On Increasing the Energy Efficiency and Performance of a Bicycle Robot Stabilization—Towards Event-Triggered Control Considerations

Abstract

This paper addresses the critical problem of stabilizing an inherently unstable bicycle robot at low or zero speeds using advanced control strategies. The key objective is to develop a feedback controller that actively operates a handlebar, as well as a reaction wheel, maintaining balance while keeping performance indices low, including energy consumption. It is the energy consumption that makes the platform attractive for the users by extending the time of operation, not only due to the actions connected to motor design and battery design, but to the control system itself. To design and verify the control law that enables stabilization, and reduces energy consumption, bicycle dynamics and controllers based on linear quadratic regulator (LQR) techniques are designed, along with their robustified variants accounting for actuator failures and model uncertainties, and an innovative event-triggered control (ETC) scheme to reduce control updates and energy use. Simulations demonstrate effective stabilization from various initial lean angles under realistic conditions, with robustness notably improved at zero speed, where balancing is most challenging. Extending control to include both reaction wheel and handlebar actuation enhances dynamic maneuverability and energy efficiency. The event-triggered approach significantly lowers computational and actuator energy demands by updating controls only when needed, reducing mechanical wear. This research contributes to electromobility by improving the control and energy efficiency of personal transport devices like electric bicycles and autonomous bicycles, which rely on stable balancing mechanisms for safety and user comfort. The findings support future experimental validation and IoT implementation, pushing forward controlled, energy-conscious stabilization for emerging personal electromobility solutions.

1. Introduction

Personal electromobility faces different challenges, spanning from battery faults, limited range, or charging infrastructure issues, especially in developing countries, which strongly affect user comfort. User comfort is further influenced by factors such as temperature impact on battery life [1] and how fast-charging stations are available. Modern and advanced control laws, also with large degrees of robustness, as well as energy management systems designed to optimize motor operation, by means of energy consumption, can strongly extend battery life, energy range, as well as energy efficiency. This might be achieved either by the construction of motors, or by the design of energy-efficient control strategies [2] to reduce the total energy consumption. Every energy-efficient control solution balances between user comfort, performance, as well as energy savings. However, every such solution contributes to user satisfaction eventually from extended battery use and contributes to pollution reduction by reducing emissions.

Modern energy storage units and energy management solutions for the means of personal electromobility present a visible decrease in energy consumption, typically achieving improvements in vehicle energy efficiency by about 10–15% in comparison to standard solutions. These numbers are even more impressive when advanced control systems are included in the loop. They are of course not only attributed to maximizing regenerative braking, reducing vehicle weight, general maintenance issues, but also to smart battery management systems, and aptly designed control laws.

Taking a look at the past years, the technology offering the greatest energy savings and increase in terms of performance for personal electromobility means is connected mainly to solid-state batteries and advanced lithium-ion batteries with silicon and graphene anodes [3]. These provide a density of energy at the level of 300–500 Wh/kg, much increased with ca. 100–270 Wh/kg for old lithium-ion batteries. Higher energy density reduces the weight of the vehicle, thus enabling the companies to support the user comfort when riding motorcycles or bicycles with self-balancing systems. These typically use gyroscopic measurements, IMUs, and are followed by advanced control algorithms to maintain stability. The balancing torques produced by such solutions are large to enable stabilization in stationary condition, of much value in the so-called inclusive mobility [4], where enhancement of user comfort, safety, and reduction in probability of accidents, is of great value.

Research on self-balancing properties in electric vehicles such as in the case of Honda or Lit Motors reveals that advanced control algorithms are needed to maintain stability, but these are often connected to extra energy consumption, where continuous operation results in its increase [5]. The current paper shows it is still possible to achieve similar aims, but with the energy of the signals greatly reduced, bridging the gap between the market demand and the availability of technology, applied to the basic electromobility unit, in the form of a bicycle.

Bicycles as an attractive means of transport offer possibilities to reduce the mobility gap for the elderly and the young. For those underprivileged, riding a bike is sometimes a great challenge and comes with a lot of effort. Also for this reason, electric bicycles have been developed, but it is the problem of stabilization that still prevails. In order to stabilize a bicycle, one needs to learn how to keep balance. However, the same can be done using effective actuation and using various techniques and control algorithms, which take advantage of a reaction wheel, handlebar control, or other approaches. It is to be kept in mind that the stabilization efficiency depends also on the linear velocity of a bicycle, and is crucial when the bicycle is at near-zero or even zero velocity. This calls for special actuation methods.

The most common technique is to use a reaction wheel to generate reaction torque to keep the bicycle in balance. The construction is relatively simple and requires a motor to drive the reaction wheel, along with proper sensors to enable stabilization. Apart from the reaction wheel, one can also use the handlebar to use the steering/heading angle to keep the balance of the bicycle, to move the center of gravity to such a position as to stabilize the structure, extending the possibility of stabilization by the reaction torque to more dynamic scenarios, such as, e.g., passing a curve [6]. Handlebar control can also be used to couple its action with the reaction wheel, to restore maneuverability in dynamic situations, as well as to recover the property in case the bicycle carries a load [7].

Such systems are usually controlled by proportional–integral–derivative controllers (PIDs) or state-vector-based controllers, on the basis of a linearized model, obtained for the upright (unstable) equilibrium point [8]. A linear quadratic control (LQR) [9,10], unfortunately requires the knowledge of the linearized dynamics. Obviously, one can also expect the linear quadratic controller with integral action to be applied as well, to reduce energy consumption. On the other side, sliding-mode controllers can be used as well, to offer agile dynamics in a closed loop along with satisfactory disturbance rejection [11].

Other approaches also use a bank of controllers to enable gain-scheduled-like control, or implement expert knowledge in fuzzy sliding-mode controllers. All the approaches try to design the steering strategy to lean the bicycle so as to enter curves, or enable combined operation coupled with the reaction wheel. Obviously, the classical PID-like control is the easiest to understand; however, it lacks robustness, and the state feedback control requires a linearized model with proper accuracy to obtain stabilization near the linearization set-point, thus is sensitive to modeling errors.

More advanced approaches, like the fuzzy controller with sliding-mode feature, require fuzzy logic expertise, replacing the knowledge about the model, whereas the other approaches consume energy to compensate for the uncertainties present in the system, by making agile moves. There are also the approaches that use model predictive control or nonlinear model predictive control to achieve stabilization and balance [10].

Every approach usually undergoes a V-cycle procedure, starting from the software-in-the-loop stage, and ending on the deployment. For the actions presented in the paper, Arduino Engineering Rev 2 Kit [12] was used, where the gyroscopic effect of the reaction wheel is used to stabilize the structure, along with the handlebar action, enabling the researchers to pursue the implementation of various control strategies eventually on the hardware. In this paper, the authors use the simulation environment of Arduino hardware under Matlab and Simulink to couple LQR control with a robustifying approach, along with the reduction of control effort by using event-triggered control to reduce the energy consumption.

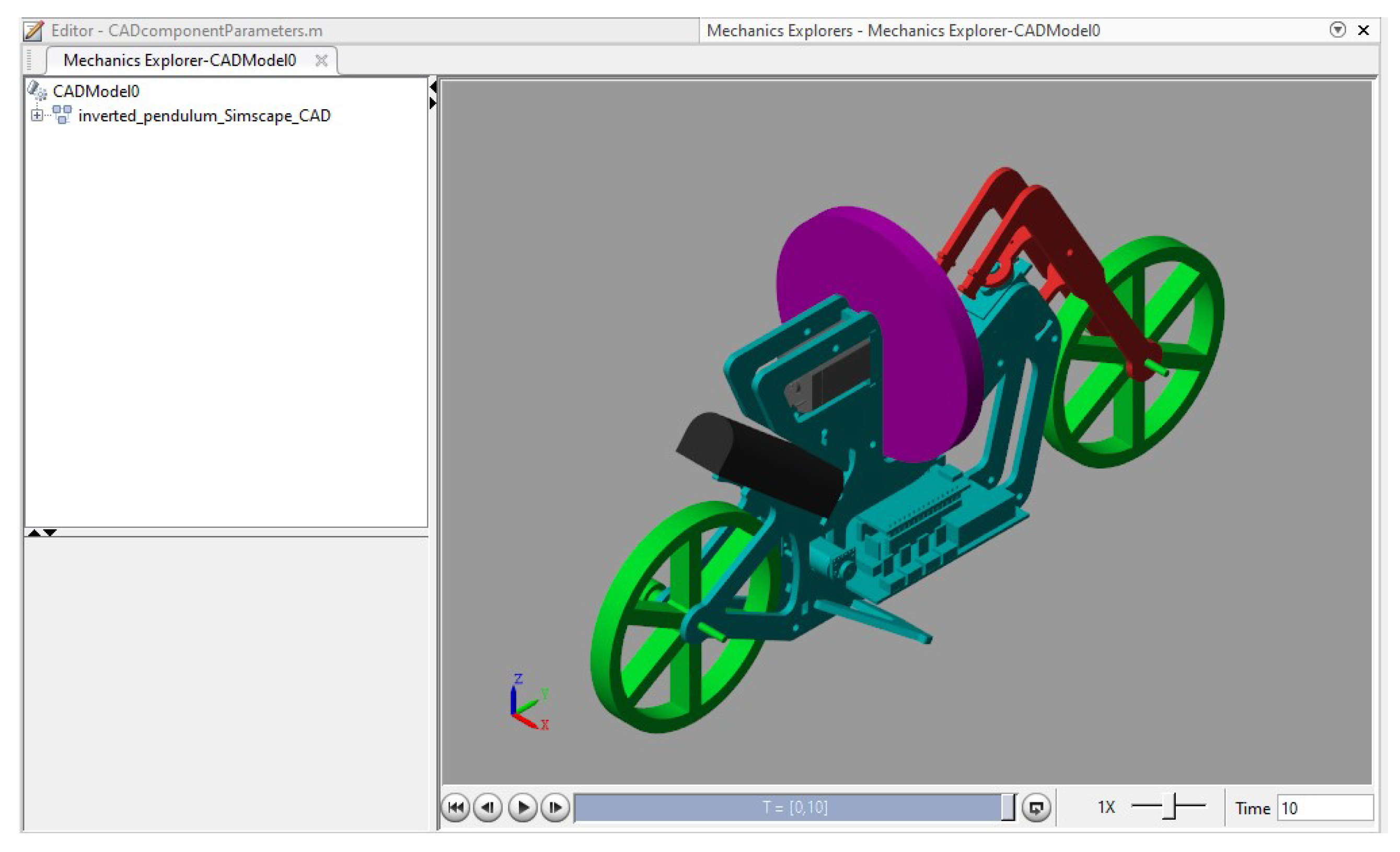
The adopted strategy forms a basic step prior to conducting experiments on the real hardware, enabling one to get a deep insight into the control strategies to be adopted, and to identify weak points of the techniques selected. It potentially allows other researchers to follow this line of inquiry and formulate their own approach, further extending the LQR capabilities. The model of the bicycle can be visualized using the Simscape library, to enable a better view of the structure during simulation, as in Figure 1. Such an approach enables one to test if all the code written fits to Arduino Nano IoT 33 board memory to enable future hardware tests.

The paper innovatively integrates classical control techniques (LQR) with a robustified version to handle actuator faults and model uncertainties, demonstrating improved performance and reliability. Another key strength is the introduction of event-triggered control (ETC), which effectively reduces the frequency of control updates, thereby lowering energy consumption and mechanical wear, an important consideration for battery-powered personal electromobility devices.

The inclusion of both reaction wheel and handlebar actuation, especially with the adoption of event-triggering mechanisms, along with introduced degrees of robustness, extend the control strategy to dynamic scenarios, enhancing maneuverability and further energy savings, which are so welcomed by the users.

A similar approach to the reduction of control updates for saturated systems can be found in [13], based on data-driven conditions. As per the connection to linear matrix inequalities, the rules obtained in the paper can be difficult to apply in real time, since the co-design of event-triggering and state feedback formulation is tightly coupled. In addition, no uncertainty can be handled here. On the contrary, the authors of [14] enable a robustification approach for additive uncertainties, unfortunately for continuous-time systems only, extending the well-established triggering conditions. The most promising alternative approach is presented in [15] for the predictive control, to adjust the sampling intervals to keep a balance between computational cost and cost of gathering the data, unfortunately, again for continuous-time systems. One of the latest approaches to the event-triggered control systems has been reported in [16], However, this technique is incomparably more demanding as far as computation burden is concerned. The natural aim is to maximize the cross-update intervals, here by the use of game theory, in a two-step fashion. In the first step, the decision whether to update or not is made; in the second step, an adaptive scheme based on dynamic programming is used. The advantage is the suitability for nonlinear multiple-input, multiple-output systems; the disadvantage is its continuous-time form, heavy computation burden, and no views toward robustification in the case of uncertain system description.

The major contribution can be listed as follows:

• Extension of a standard LQR technique to handle model uncertainty;
• Introduction of event-triggered mechanism and analysis of various performance indices to grasp the interplay between control performance and the frequency of control updates;
• Complete evaluation of the performance of the solution in the case of a single actuator (reaction wheel), and two actuators (handlebar action added);
• Critical comparison with the alternative solutions, from the viewpoint of the event-triggering strategy.

The structure of the paper is as follows: Section 2 outlines the basic model of the bicycle, Section 3 presents the considered control strategies, including LQR, linear quadratic plus integral, robustified, and event-triggered ones, along with model predictive and sliding-mode controllers. In Section 4, the results of a vast simulation campaign are presented, and finally, Section 5 outlines future research directions and presents the conclusions, paving the way to deployment on the real hardware.

2. Basic Model of the Bicycle

As per the inverted pendulum-like structure of the bicycle with a stabilizing reaction wheel, the basic motion law follows the second principle of Newton dynamics for the rotational motion, i.e.,

$$\begin{array}{ccc}\hfill T\left(t\right)& =& J\ddot{\theta }\left(t\right),\hfill \end{array}$$

(1)

where J is the moment of inertia, $\theta$ is the angle of rotation with respect to the unstable upright equilibrium point, and T is the torque exerted by the reaction wheel.

In rotational motion, torques and moments of inertia are additive, thus the torque T is a combination of the torque generated by gravity forces $T_g$, acting on the center of the mass m of the inverted pendulum rod, the torque generated by the gravity forces $T_w$, acting on the reaction wheel of mass $m_w$, and last, the torque generated by the motor of the reaction wheel $T_m$, counteracting the effects of gravity,

$$\begin{array}{ccc}\hfill T\left(t\right)& =& T_g+T_w-T_m.\hfill \end{array}$$

(2)

Let us adopt the following notation:

• $\theta$—lean angle from the upright position;
• $\dot{\theta }$—rotational velocity (lean velocity);
• $\varphi$—rotation angle of the reaction wheel;
• $\omega$—rotational velocity of the reaction wheel;
• $T_m$—torque generated by the reaction wheel.

Now, the torque can be expressed as

$$mg{l}_{r}sin\left(\theta \left(t\right)\right)+m_{w}g{l}_{w}sin\left(\theta \left(t\right)\right)-J_w(\dot{\omega }\left(t\right)+\ddot{\theta }\left(t\right))=J\ddot{\theta }\left(t\right),$$

(3)

with

• m—mass of the bicycle without the mass of the reaction wheel;
• g—gravity force;
• $l_r$—distance between the ground level and the center of mass of the bicycle;
• $m_w$—mass of the reaction wheel;
• $l_w$—distance between the ground and the axis of rotation of the reaction wheel;
• R—reaction wheel radius;
• r—inverted pendulum radius (the bicycle is treated as an inverted pendulum);
• J—auxiliary moment of inertia;
• $J_w$—moment of inertia of the reaction wheel with respect to its axis of rotation

and

$$\begin{array}{ccc}\hfill J& =& m_w(0.5R^2+l_w^2)+{\displaystyle \frac{1}{12}}m(3r^2+l_w^2)+m{l}_w^2\hfill \end{array}$$

(4)

Taking reaction wheel actions into account, the following state-space vector can be used to describe the state of the bicycle:

$$\underline{x}\left(t\right)=\left[\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\\ x_3\left(t\right)\\ x_4\left(t\right)\end{array}\right]=\left[\begin{array}{c}\theta \left(t\right)\\ \dot{\theta }\left(t\right)\\ \varphi \left(t\right)\\ \omega \left(t\right)\end{array}\right].$$

(5)

In the Engineering Rev Kit 2 documentation, one can find the nominal values of the parameters listed above, resulting in the following state-space description:

$$\underline{\dot{x}}\left(t\right)=\left[\begin{array}{c}{x}_2\left(t\right)\\ 92.1727sin\left(x_1\left(t\right)\right)-333.333u\left(t\right)\\ x_4\left(t\right)\\ -92.1727sin\left(x_1\left(t\right)\right)+11844.120u\left(t\right)\end{array}\right]=\underline{f}(t,\underline{x},u),$$

(6)

with the input signal $u\left(t\right)=T_m\left(t\right)$.

Let us linearize the nonlinear description of the model in the following unstable equilibrium point:

$$\underline{f}(t,\underline{x},u)=\underline{0}\Rightarrow {\underline{x}}_0=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],u_0=0,$$

(7)

resulting in

$$\begin{array}{ccc}\hfill \mathit{A}& =& {\left.{\displaystyle \frac{\partial \underline{f}}{\partial \underline{x}}}\right|}_{\underline{x}={\underline{x}}_0,u=u_0}=\left[\begin{array}{cccc}0& 1& 0& 0\\ 92.1727& 0& 0& 0\\ 0& 0& 0& 1\\ -92.1727& 0& 0& 0\end{array}\right],\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \underline{b}& =& {\left.{\displaystyle \frac{\partial \underline{f}}{\partial u}}\right|}_{\underline{x}={\underline{x}}_0,u=u_0}=\left[\begin{array}{c}0\\ -333.333\\ 0\\ 11844.120\end{array}\right]\hfill \end{array}$$

(9)

in the model

$$\begin{array}{c}\hfill \underline{\dot{x}}\left(t\right)=\mathit{A}\underline{x}\left(t\right)+\underline{b}u\left(t\right).\end{array}$$

(10)

Since this model reflects the real dimensions of the hardware to be used in the future research stage, the authors have decided to perform the linearization on the basis of the Simulink nonlinear model of the bicycle using the Model Linearizer Tool, assuming zero initial conditions and no constraints imposed on the control signal. This procedure resulted in the following state-space model:

$$\underline{\dot{x}}\left(t\right)=\left[\begin{array}{cccc}0& 1& 0& 0\\ 93.1217& 0& -1.0619\times {10}^{-7}& 0\\ 0& 0& 0& 1\\ -93.1250& 0& 0.0192& 0\end{array}\right]\underline{x}\left(t\right)+\left[\begin{array}{c}0\\ -246.216\\ 0\\ 11004\end{array}\right]u\left(t\right),$$

(11)

and

$$\underline{y}\left(t\right)=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\underline{x}\left(t\right)$$

(12)

as the output vector. This state-space model will eventually be taken as the source of the values of the parameters taken for further consideration.

Matrix $\mathit{A}$ of this model has the following eigenvalues:

$$\underline{\lambda }=\left[\begin{array}{c}-9.6500\\ 9.6500\\ -0.1386\\ 0.1386\end{array}\right],$$

(13)

connected to the unstable behavior of the bicycle without actuation.

3. Considered Control Strategies

3.1. Software-in-the-Loop Model Development for Reaction Wheel Actuation

In order to perform simulations of a complete setup, to reflect the behavior of the real bicycle robot, one needs to read a technical specification of the DC motor with the encoder from the setup, providing the information about the operating voltage (12 V DC) along with the stall current value of 1.85 A.

Now, the parameters of the DC motor installed in the system can be calculated from the following dependency:

$$k_t={\displaystyle \frac{M}{I}}=k_e={\displaystyle \frac{U}{\omega }},$$

(14)

where $U=12 \mathrm{V}$, $I=1.85 \mathrm{A}$, $\omega =7000 \mathrm{rpm}=733.038$${\displaystyle \frac{\mathrm{rad}}{\sec }}$. The maximum torque of the motor becomes

$$T_{\max }={\displaystyle \frac{UI}{\omega }}=0.0302 \mathrm{Nm},$$

(15)

which has been taken as the constraint level in the simulations carried out in the paper, related to the reaction wheel torque. In order to balance the system, it must hold that

$$T_{\max }\ge T_g+T_w.$$

(16)

Based on this value, one can obtain the maximum deflection of the inverted pendulum from the unstable equilibrium point, which the motor is capable of bringing back to the vertical position, by compensation of the gravity force:

$$\begin{array}{ccc}\hfill T_g& =& 0.497 \mathrm{kg}·9.807{\displaystyle \frac{\mathrm{m}}{{\sec }^2}}·0.065 \mathrm{m}·sin\left({\theta }_{max}\right),\hfill \\ \hfill T_g& =& 0.03 \mathrm{kg}·9.807{\displaystyle \frac{\mathrm{m}}{{\sec }^2}}·0.13 \mathrm{m}·sin\left({\theta }_{\max }\right),\hfill \\ \hfill T_m& =& 0.0302 \mathrm{Nm},\hfill \\ \hfill {\theta }_{\max }& =& \mathrm{asin}\left({\displaystyle \frac{0.0302}{0.355}}\right)=0.08517 \mathrm{rad}=4.{88}^{\circ }.\hfill \end{array}$$

The considered model has been discretized with $T_s=0.05 \mathrm{s}$ using step-invariant transformation into

$$\begin{array}{ccc}\hfill {\mathit{A}}_d& =& \left[\begin{array}{cccc}1.1187& 0.0520& 0& 0\\ 4.8389& 1.1187& 0& 0\\ -0.1187& -0.002& 1& 0.05\\ -4.8391& -0.1187& 0.001& 1\end{array}\right],\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\underline{b}}_d& =& \left[\begin{array}{c}-0.3138\\ -12.7941\\ 13.7609\\ 550.6824\end{array}\right],\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\mathit{C}}_d& =& \left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\hfill \end{array}$$

(19)

resulting in the following eigenvalues of ${\mathit{A}}_d$:

$${\underline{\lambda }}_A=\left[\begin{array}{c}1.6201\\ 0.6172\\ 0.9931\\ 1.007\end{array}\right].$$

(20)

3.2. LQR Controller for the Operation of the Reaction Wheel

A full-state feedback control has been used at the first stage of the research, minimizing the standard LQR performance index [17]

$$J=\sum _{t=0}^{\infty }\left({\underline{x}}_t^T\mathit{Q}{\underline{x}}_t+{\underline{u}}_t^T\mathit{R}{\underline{u}}_t\right),$$

(21)

where, $\mathit{Q}=\mathrm{diag}\left(q_i\right)$ and $\mathit{R}=\mathrm{diag}\left(r_i\right)$ have been chosen to conform to Bryson’s rule [18]:

$$q_i={\displaystyle \frac{1}{\max \mathrm{deflection}\mathrm{in}{x}_i^2}},$$

(22)

$$r_j={\displaystyle \frac{1}{\max \mathrm{deflection}\mathrm{in}{u}_j^2}}.$$

(23)

In the considered case,

$$\begin{array}{ccc}\hfill q_1& =& {\displaystyle \frac{1}{{\theta }_{\max }^2}}=137.8563,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill q_2& =& {\displaystyle \frac{1}{{\dot{\theta }}_{\max }^2}}=11.11;{\dot{\theta }}_{\max }=0.3{\displaystyle \frac{\mathrm{rad}}{\sec }},\hfill \end{array}$$

(25)

where ${\dot{\theta }}_{\max }^2$ is a halved value of the maximum rotational velocity allowing the system to stabilize subject to constraints imposed on the control signal. The other weights become

$$q_3={\displaystyle \frac{1}{{\left(60\pi \right)}^2}}=0.00168,$$

(26)

as per 30 rotations of the reaction wheel, and

$$q_4={\displaystyle \frac{1}{733.{038}^2}}=0.00000186,$$

(27)

since $733.038 {\displaystyle \frac{\mathrm{rad}}{\sec }}$ mirrors the maximal rotational velocity of the motor. The weight of the control signal is

$$\mathit{R}=R={\displaystyle \frac{1}{T_m^2}}={\displaystyle \frac{1}{{0.0302}^2}}=1096.44.$$

(28)

Following the LQR calculation of the optimal control law, one obtains

$$\begin{array}{ccc}\hfill \mathit{Q}& =& \left[\begin{array}{cccc}137.8563& 0& 0& 0\\ 0& 11.11& 0& 0\\ 0& 0& 0.00168& 0\\ 0& 0& 0& 0.00000186\end{array}\right],\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill R& =& 1096.44,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \underline{k}& =& {[0.9147,0.1026,0.0005,0.0004]}^T,\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill u_t& =& {\underline{k}}^T{\underline{x}}_t.\hfill \end{array}$$

(32)

The closed-loop system matrix

$${\mathit{A}}^c=\left[\begin{array}{cccc}0.8316& 0.0198& -0.0002& -0.0001\\ -6.8644& -0.1945& -0.0065& -0.0047\\ 12.469& 1.4105& 1.0071& 0.0551\\ 498.8918& 54.4047& 0.2826& 1.2023\end{array}\right]$$

(33)

has the following eigenvalues:

$${\underline{\lambda }}^c=\left[\begin{array}{c}0.2527\\ 0.8975+0.1018i\\ 0.8975-0.1018i\\ 0.7887\end{array}\right]$$

(34)

with all the magnitudes below 1.

The control signal in all the simulations has been constrained so as to mimic the voltage constraint of the real system at the level of 0.03 Nm.

3.3. LQI Controller for the Operation of the Reaction Wheel

The state vector has alternatively been extended with four additional entries, corresponding to integrals of the errors [19]:

$${\underline{x}}_{\mathrm{ext},t}={[{\underline{x}}_t^T,{\underline{x}}_{I,t}^T]}^T,$$

(35)

where ${\underline{x}}_{I,t}$ is the appropriate integral of the full-state vector with the vice-last component non-zero to compensate for excessive energy use connected to the rotating reaction wheel, and

$$u_t={[{\underline{k}}^T,0,0,{10}^{-9},0]}^T{\underline{x}}_{\mathrm{ext},t}.$$

(36)

The reason to affect the motion of the reaction wheel is given rise by the research reported in the paper cited above, when the wheel exhibited constant rotations when the bicycle was in an upright state, to reduce the energy consumption.

3.4. Robustified Version of the LQR Controller for the Operation of the Reaction Wheel

The robustified version of the LQR controller takes into consideration the so-called actuator failure model, which basically takes the form [19]

$$u_t^F=\rho u_t$$

where $0\le {\rho }_{-}\le \rho \le {\rho }_{+}$, ${\rho }_{-}\le 1$, ${\rho }_{+}\ge 1$ mimics the uncertainty introduced either by improper actuation, or modeling errors, in this case—introduced by the adopted linearization scheme, or mismodeling of certain phenomena. Additionally, limits imposed on the control signal also admit to such a failure model, where the calculated control signal (vector) is not all all time instants the same as the applied control signal (vector).

Having adopted this strategy, in the current paper, $0\le \delta <1$ defines the certainty level as ${\rho }_{-}=1-\delta$, ${\rho }_{+}=1+\delta$, along with the algorithm presented below, enabling one to recalculate the optimal feedback vector $\underline{k}$ to introduce robustness.

This algorithm is left here without any other description, referring the reader to the prior publication of one of the authors of this paper on the topic, providing the detailed formulae [19].

3.5. Extension of the Considered Software-in-the-Loop Model to Handlebar Actions

When the handlebar is in use, the bicycle has an additional torque exerted on the front frame, and the angle $\alpha$ refers to the angle between the planes of the two wheels. Thus, the state vector is extended to $\underline{x}\left(t\right)\in {\mathcal{R}}^6$, with $\alpha \left(t\right)$ and $\dot{\alpha }\left(t\right)$ as the last two entries (discretized when a discrete-time model is in use).

Any non-zero angle $\alpha$ results in both centrifugal force and a lean angle of the bicycle when the robot is in motion. An additional component which appears is $T_g$, which introduces an additional degree of freedom, and the so-called steer equation, whose derivation is out of the scope of this paper (strong coupling effects between lean angle, centrifugal force, net force due to gravity when the bicycle leans over, etc.) [20]. Having launched the Model Linearizer Tool in the case of the input vector

$$\underline{u}\left(t\right)=\left[\begin{array}{c}{T}_m\left(t\right)\\ T_h\left(t\right)\end{array}\right],$$

(37)

where the last component corresponds to the torque exerted on the handlebar, and discretizing the model with $T_s=0.05 \mathrm{s}$ using step-invariant method results in

$$\begin{array}{ccc}\hfill {\mathit{A}}_d^h& =& \left[\begin{array}{cccccc}1.1169& 0.0519& 0& 0& -0.0003& 0\\ 4.7663& 1.1169& 0& 0& -0.0144& -0.0003\\ -0.1169& -0.0019& 1.0000& 0.05& 0.0003& 0\\ -4.7664& -0.1169& 0.0010& 1& 0.0144& 0.0003\\ -0.0845& -0.0014& 0& 0& 1.1471& 0.0524\\ -3.5250& -0.0845& 0& 0& 6.0244& 1.1471\end{array}\right],\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\mathit{B}}_d^h& =& \left[\begin{array}{cc}-0.3260& 0.5881\\ -13.2873& 23.9097\\ 13.7687& -0.5882\\ 550.9967& -23.9149\\ -0.5882& 28.3359\\ -23.9146& 1160.1\end{array}\right],\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill C_d& =& \mathit{I}\hfill \end{array}$$

(40)

with the eigenvalues of ${\mathit{A}}_d^h$ as

$${\underline{\lambda }}^h=\left[\begin{array}{c}1.7119\\ 1.6114\\ 0.5841\\ 0.6206\\ 0.9931\\ 1.0070\end{array}\right].$$

(41)

3.6. LQR Controller for the Operation of the Reaction Wheel and the Handlebar

A full-state six-element feedback control has been used at the second stage of the research, with the entries of $\mathit{Q}$ and $\mathit{R}$ defined as in the original case, and now extended with

$$q_5={\displaystyle \frac{1}{{\left(\frac{\pi }{2}\right)}^2}}=0.4053,$$

(42)

as the maximum value of $\alpha$ is ${90}^{\circ }$, and

$$q_6={\displaystyle \frac{1}{{5.6}^2}}=0.03188,$$

(43)

since the system gets destabilized when $|\dot{\alpha }| > 5.6 {\displaystyle \frac{\mathrm{rad}}{\sec }}$, along with

$$r_2={\displaystyle \frac{1}{{0.2255}^2}}=19.6655,$$

(44)

to mimic the maximum torque generated by the handlebar motor of $0.2255$ Nm.

Following the LQR calculation of the optimal control law, one obtains

$$\begin{array}{ccc}\hfill \mathit{Q}& =& \left[\begin{array}{cccccc}137.8563& 0& 0& 0& 0& 0\\ 0& 11.111& 0& 0& 0& 0\\ 0& 0& 0.00168& 0& 0& 0\\ 0& 0& 0& 0.00000186& 0& 0\\ 0& 0& 0& 0& 0.4053& 0\\ 0& 0& 0& 0& 0& 0.03188\end{array}\right],\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill \mathit{R}& =& \left[\begin{array}{cc}1096.443138& 0\\ 0& 19.6655\end{array}\right],\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill \mathit{K}& =& \left[\begin{array}{cccccc}0.9037& 0.1014& 0.0005& 0.0004& -0.0241& -0.0022\\ 0.0543& 0.0039& 0.0001& 0& -0.0095& -0.0011\end{array}\right],\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill {\underline{u}}_t& =& \mathit{K}{\underline{x}}_t.\hfill \end{array}$$

(48)

The closed-loop system matrix

$${\mathit{A}}_h^c=\left[\begin{array}{cccccc}0.8543& 0.0211& -0.0001& -0.0001& 0.0020& 0\\ -5.9426& -0.1382& -0.0052& -0.0037& 0.0804& 0.0017\\ 12.294& 1.3923& 1.0071& 0.0549& -0.3266& -0.0298\\ 491.8737& 55.6754& 0.2824& 1.1973& -13.0639& -1.1926\\ 0.9231& 0.0486& 0.0017& 0.0011& 0.8934& 0.0213\\ 38.8828& 1.9798& 0.0681& 0.0455& -4.3679& -0.127\end{array}\right]$$

(49)

has the following eigenvalues:

$${\underline{\lambda }}_h^c=\left[\begin{array}{c}0.0004\\ 0.278\\ 0.8943+0.1041i\\ 0.8943-0.1041i\\ 0.7798\\ 0.8399\end{array}\right]$$

(50)

with all the magnitudes below 1, again.

The control signals in all the simulations have been constrained so as to mimic the voltage constraints of the real system.

3.7. Event-Triggered Control Strategy Under LQR Framework with Robustness

Let ${\underline{x}}_t^{\circ }$ denote the last received measurement of the state of a bicycle, with the corresponding control vector/signal ${\underline{u}}_t^{\circ }={\mathit{K}}^T{\underline{x}}_t^{\circ }$. The next update of the control action takes place on the basis of a triggering condition; otherwise, the control action is kept unchanged.

On the basis of [21,22], the following event-triggering condition is considered:

$$\begin{array}{c}\hfill \parallel {\underline{u}}_t^{\circ }-{\underline{u}}_{t+l}{\parallel }_2 > \gamma {\parallel {\underline{u}}_{t+l}\parallel }_2\end{array}$$

(51)

where $\gamma >0$ actually defines the threshold value, and the control action is calculated as previously discussed. As in [23], the index l increases as long as the control action is updated, saving the computational burden of the processor, and at the same time, reducing the occupation of the communication channel.

This strategy can be easily applied to the considered robustified LQR as well. Its major task is to reduce the energy consumption of the control law, as well as to reduce wear and tear effects in mechanical parts, as the input torque is altered less frequently, preserving the overall performance of the system at a similar level.

3.8. Can the ETC Mechanism Be Applied to the Other State-of-the-Art Approaches?

It is vital to show the advantage of the proposed approach in terms of computational burden, related to the necessary calculations, in comparison to the state-of-the-art solutions. The first one to compare with would be the model predictive control, where the control performance index mirrors the one from (21), though calculated for a limited number of samples in the prediction horizon N

$$J=\sum _{j=0}^{N-1}\left({\underline{x}}_{t+j}^T\mathit{Q}{\underline{x}}_{t+j}+{\underline{u}}_{t+j}^T\mathit{R}{\underline{u}}_{t+j}\right).$$

(52)

On the basis of minimization of (52), for $\underline{X}={[{\underline{x}}_{t+1}^T,\dots ,{\underline{x}}_{t+N}^T]}^T$ a set of future control inputs is calculated $\underline{U}={[{\underline{u}}_t^T,\dots ,{\underline{u}}_{t+N-1}^T]}^T$.

Using the transition matrix $\mathsf{\Phi }$, and by introduction of $\mathsf{\Gamma }$ matrix in the forms

$$\mathsf{\Phi }=\left[\begin{array}{c}\mathit{A}\\ {\mathit{A}}^2\\ ⋮\\ {\mathit{A}}^N\end{array}\right],\mathsf{\Gamma }=\left[\begin{array}{cccc}\mathit{B}& \mathbf{0}& \dots & \mathbf{0}\\ \mathit{AB}& \mathit{A}& \dots & \mathbf{0}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathit{A}}^{N-1}\mathit{B}& {\mathit{A}}^{N-2}\mathit{B}& \dots & \mathit{B}\end{array}\right],$$

the cost function can be rewritten as

$$J={\underline{X}}^T\tilde{\mathit{Q}}\underline{X}+{\underline{U}}^T\tilde{\mathit{R}}\underline{X},$$

with $\tilde{\mathit{Q}}=\mathrm{diag}\{\mathit{Q},\dots ,\mathit{Q}\}$, $\tilde{\mathit{R}}=\mathrm{diag}\{\mathit{R},\dots ,\mathit{R}\}$.

Now, substituting $\underline{X}=\mathsf{\Phi }{\underline{x}}_t+\underline{\mathsf{\Gamma }}\underline{U}$ the performance index can be rewritten as

$$\begin{array}{ccc}\hfill J& =& {(\mathsf{\Phi }{\underline{x}}_t+\underline{\mathsf{\Gamma }}\underline{U})}^T\tilde{\mathit{Q}}(\mathsf{\Phi }{\underline{x}}_t+\underline{\mathsf{\Gamma }}\underline{U})+{\underline{U}}^T\tilde{\mathit{R}}\underline{U}\to \hfill \end{array}$$

(53)

$$\begin{array}{ccc}& \to & {\displaystyle \frac{1}{2}}{\underline{U}}^T\mathit{H}\underline{U}+{\underline{U}}^T{\mathit{F}}^T{\underline{x}}_t\left(\mathrm{dropping}\mathrm{the}\mathrm{constant}\mathrm{term}\right),\hfill \end{array}$$

(54)

with

$$\begin{array}{ccc}\hfill \mathit{H}& =& 2({\mathsf{\Gamma }}^T\tilde{\mathit{Q}}\mathsf{\Gamma }+\tilde{\mathit{R}}),\hfill \\ \hfill \mathit{F}& =& 2{\mathsf{\Phi }}^T\tilde{\mathit{Q}}\mathsf{\Gamma }.\hfill \end{array}$$

Finally, the control vector in the prediction horizon of N samples becomes

$$\underline{U}=-{\mathit{H}}^{-1}\mathit{F}{\underline{x}}_t.$$

Naturally, this mechanism can allow an easy implementation of the ETC methodology, and also offers comparable performance in a finite prediction horizon, as per the same $\mathit{Q}$ and $\mathit{R}$ matrices used in comparison with the LQR approach.

In the case of a sliding-mode control, the control is aimed at keeping the states on the so-called sliding surface $\sigma \left(\underline{x}\right)$, which is selected individually for the specific system [24]. In addition, the selection criteria for this surface are also related to the desired dynamics of the closed loop, which in the considered case are of the fourth order. This control strategy is not suited for the introduction of the ETC mechanism, as it could potentially prevent the system from reaching (and staying on) the sliding surface, by infrequent changes in the controls.

In this paper, the SMC algorithm was implemented by the use of a sliding-mode controller Simulink block, developed in Matlab 2025a, where the sliding surface is automatically selected.

4. Results

4.1. Verification of the Adopted Linearization Scheme

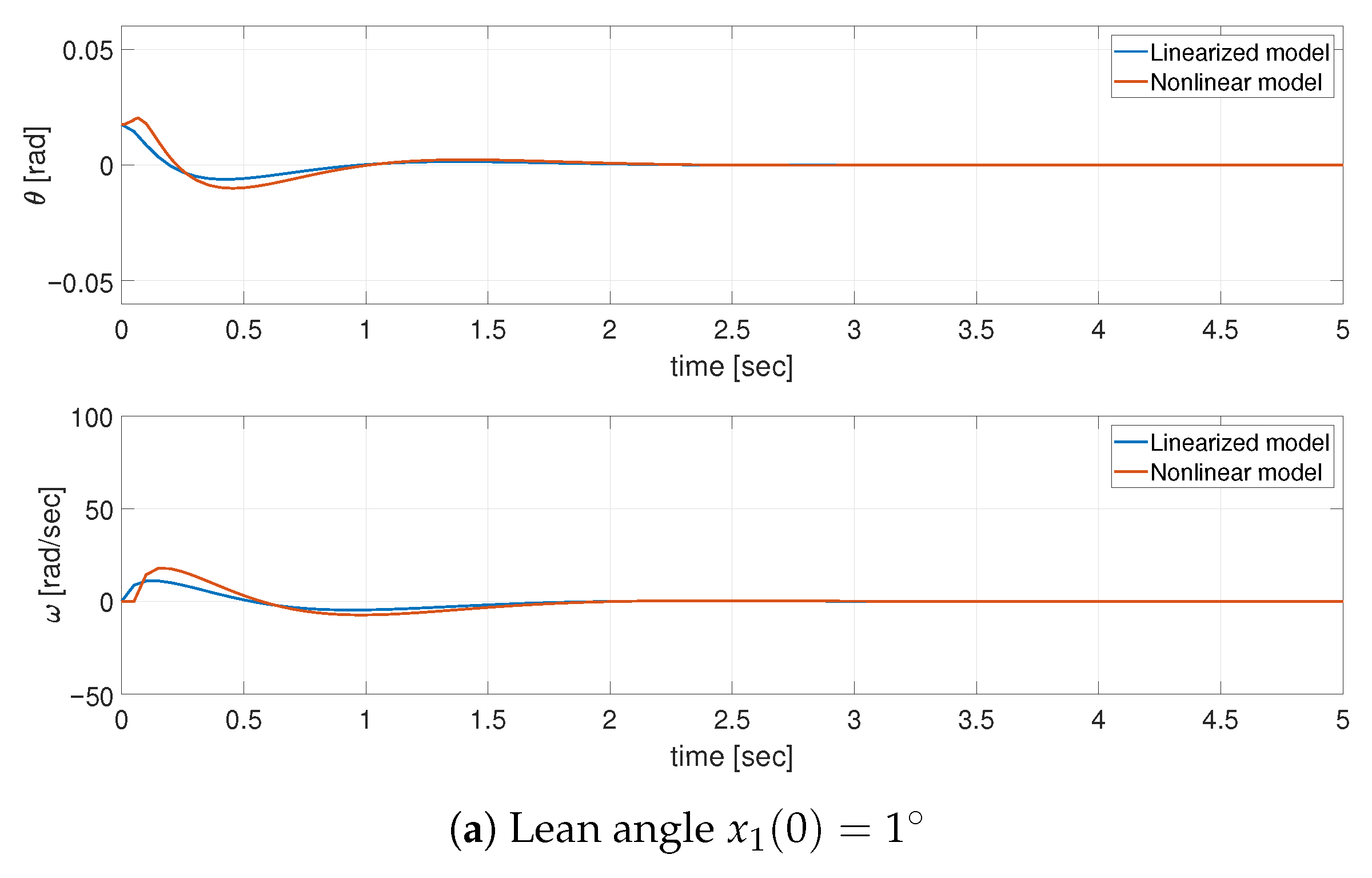
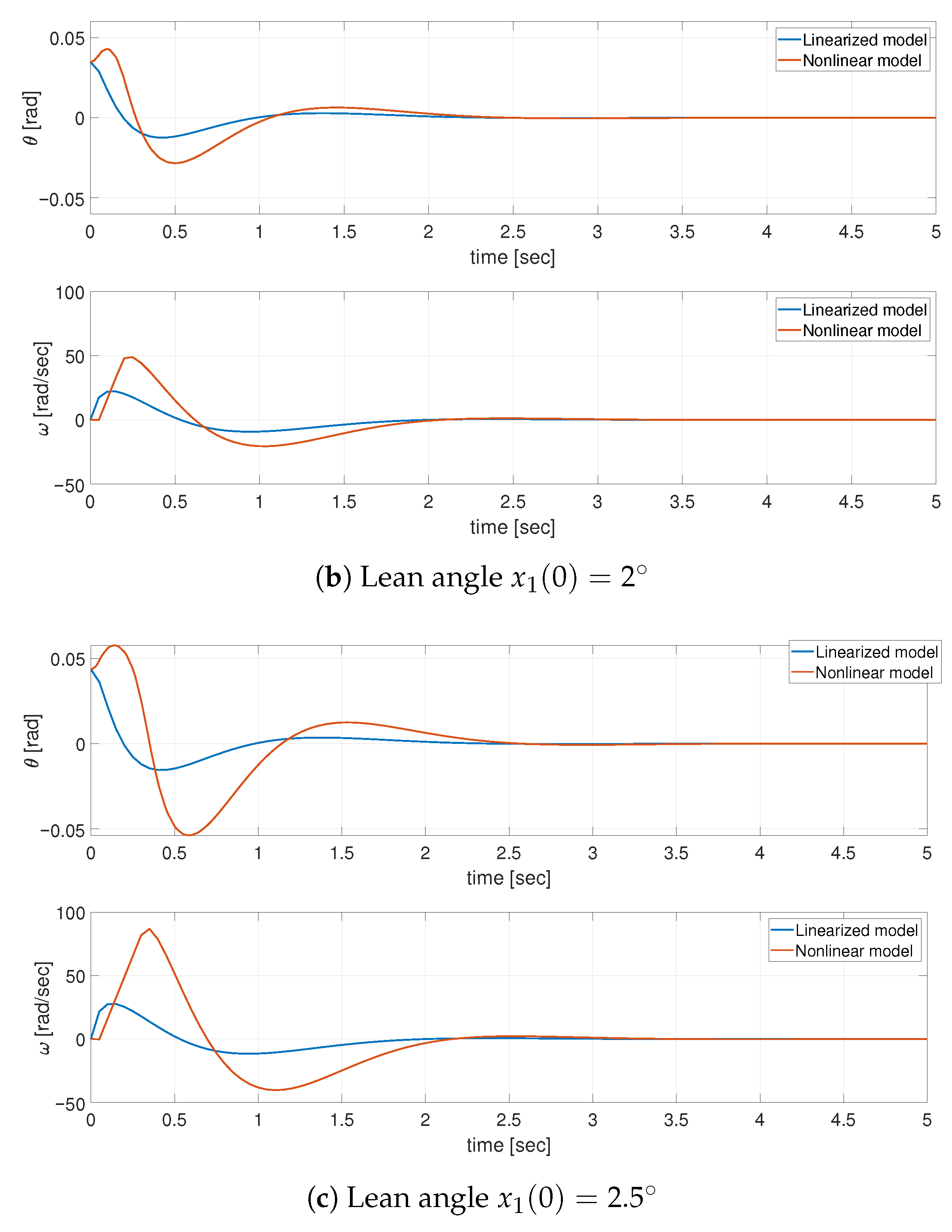
In order to clearly verify the applicability of the linearized model of the system, with the linearization point taken as

$${\underline{x}}_0=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],u_0=0,$$

and based on the LQR control law, from the range of the initial conditions allowing stabilization, three different initial conditions have been selected with the results depicted in Figure 2.

As expected, the linear model gives a worse result of approximating the nonlinear dynamics of the accurate model of the real bicycle, as per the linearization made in proximity of the unstable equilibrium point. However, on the basis of the indirect Lyapunov method [25], it is fully supported to use this linearized model as the starting point to calculate the feedback gains in the LQR control.

4.2. Simulation-Based Basin of Attraction Estimation

For the selected nonlinear control system, and the LQR gains calculated with no robustness ($\delta =0$), a set of simulations has been performed to estimate the area of initial conditions to result in attracting the $(x_1,x_2)$ phase trajectory to the origin. The results are presented in Figure 3.

The green color depicts the configuration of the initial conditions, resulting in a stable closed-loop system, whereas the red color mirrors the configurations for which it was impossible to stabilize the system, as per active constraints disabling proper stabilization.

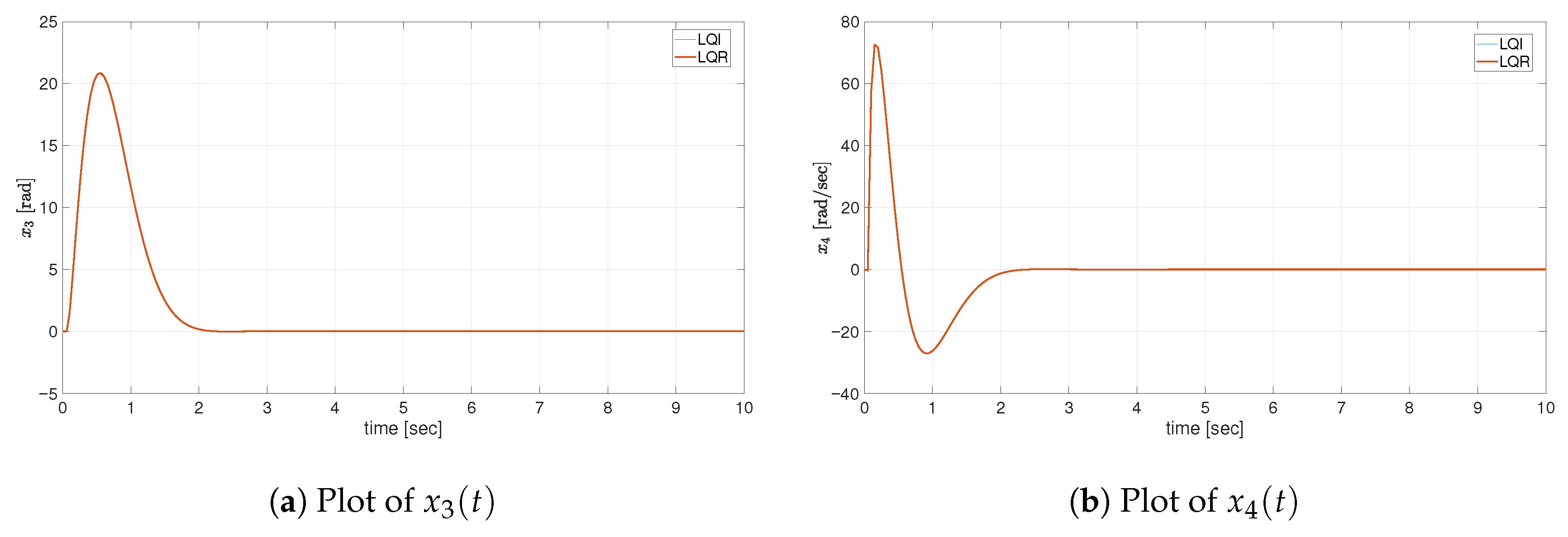
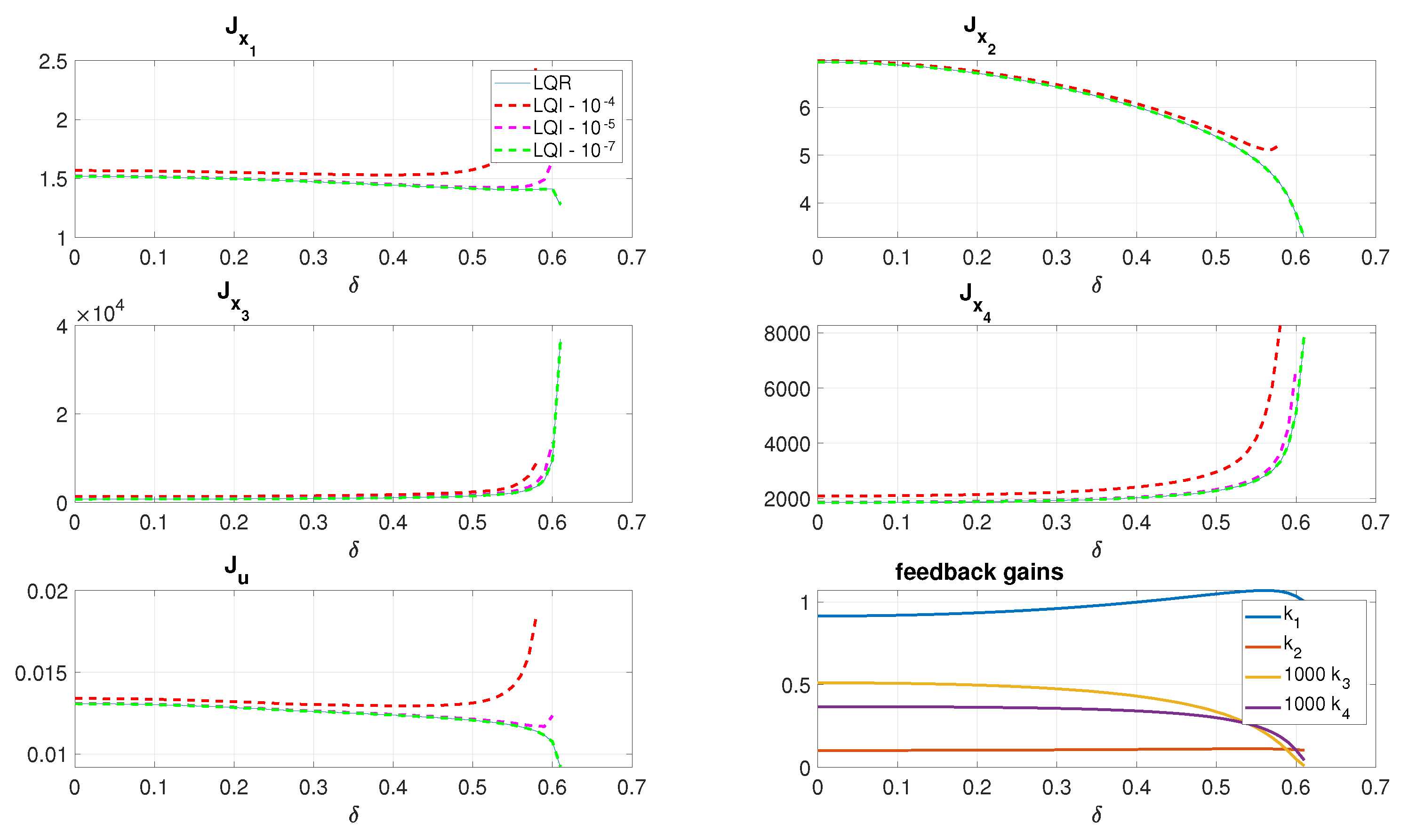
4.3. LQI Considerations

The extended control law, by adding the LQI term, surprisingly gave no improved results in terms of $x_3$ or $x_4$—it was expected that the added gain penalizing excessive rotations of the reaction wheel (extending the battery use time and keeping voltage levels with real hardware) would allow this variable to stay closer to zero. On the contrary, in the range of the feedback gain smaller than ${10}^{-7}$ in the absolute value change, only negligible changes have been observed, and for the values exceeding ${10}^{-7}$ in the absolute value change, deterioration of control performance has been observed, see Figure 4.

This could only be explained in this way that the design parameters of the LQR control law have already pushed the dynamics of the closed-loop system to its limits, with no further improvement possible. The origin of this step was the will to compare the results to [19], where a clear improvement both in energy consumption connected to constant operation of the reaction wheel, as well as improvement in overall performance, has been observed. The other reason could potentially be connected to the fact that the simulations performed used a software-in-the-loop model that does not mirror all the nonlinear phenomena connected to the real hardware.

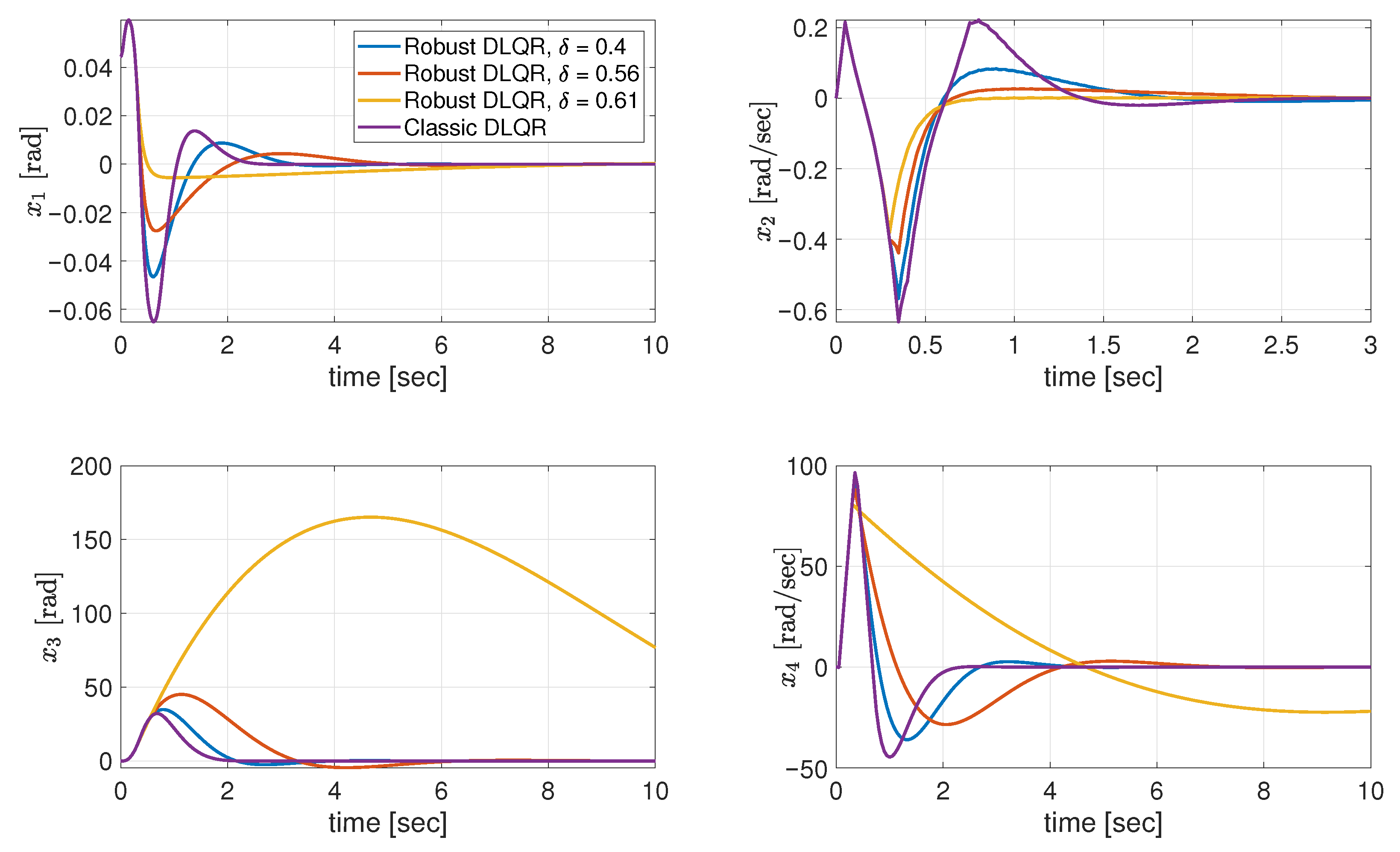
4.4. LQR-Based Stabilization of the Bicycle Using a Reaction Wheel Only with Introduced Robustness

In the control system with the LQR feedback vector calculated on the basis of the algorithm with the introduced robustness degree defined by $\delta$, a series of simulations has been performed over a grid of $\delta$ values, to depict the core differences in dynamics between the obtained control systems.

Figure 5 presents the simulation results both for the system with classical LQR ($\delta =0$), as well as for the controller taking robustness into account ($\delta >0$). It is clearly visible that the improvement in the lean angle regulation and its first derivative performance is strongly coupled with the effort of the control signal, and the energy consumed by the motor driving the reaction wheel. Relating to [19], the increase in $\delta$ allows one to take the unmodeled uncertainties inherently connected to the introduction of a linearized model into account, to improve the overall performance of the control system, as they mimic actuator fault-like behavior, where ‘inaccurate’ control signal is fed to the system (or, otherwise, ‘unexpected’ reaction to a proper control signal is observed, due to mismodeling errors).

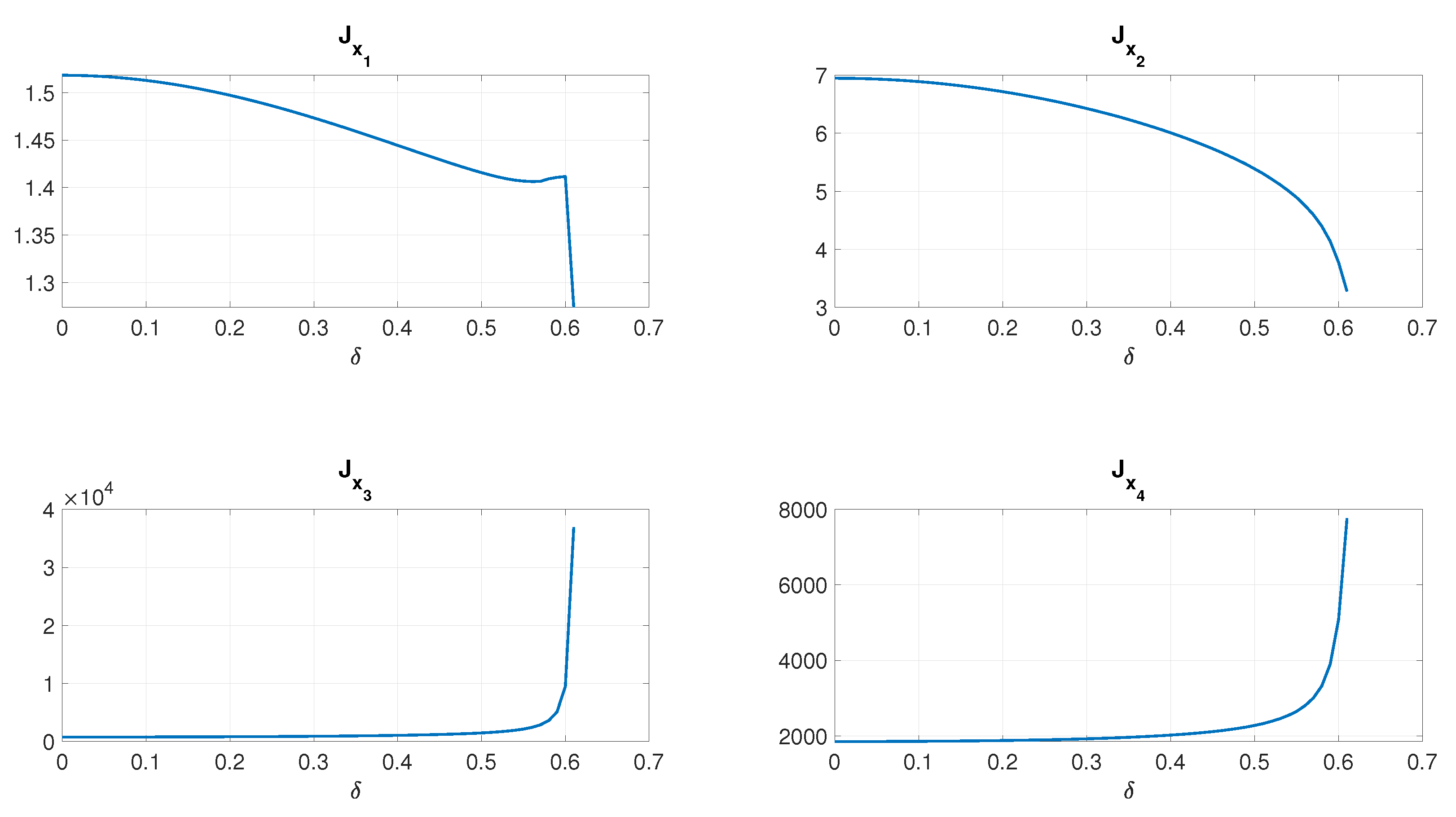
In order to evaluate the performance of the system in terms of the energy-connected performance indices, the following quantities have been calculated for every $\delta$,

$$\begin{array}{ccc}\hfill J_{x_j}& =& \sum _{i=0}^N{x}_{j,i}^2,\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill J_{u_k}& =& \sum _{i=0}^N{u}_{k,i}^2,\hfill \end{array}$$

(56)

where $j=1,\dots ,4$ refers to the state vector entry, and N is the number of samples per observation horizon, k is the control input number, and is presented in Figure 6 and Figure 7. As can be seen, introduction of robustness ($\delta >0$) enables one to obtain improved performance indices in comparison to a classical LQR control ($\delta =0$), in terms of reduction of lean angles, their derivatives, and what is of paramount importance—in terms of input energy consumption.

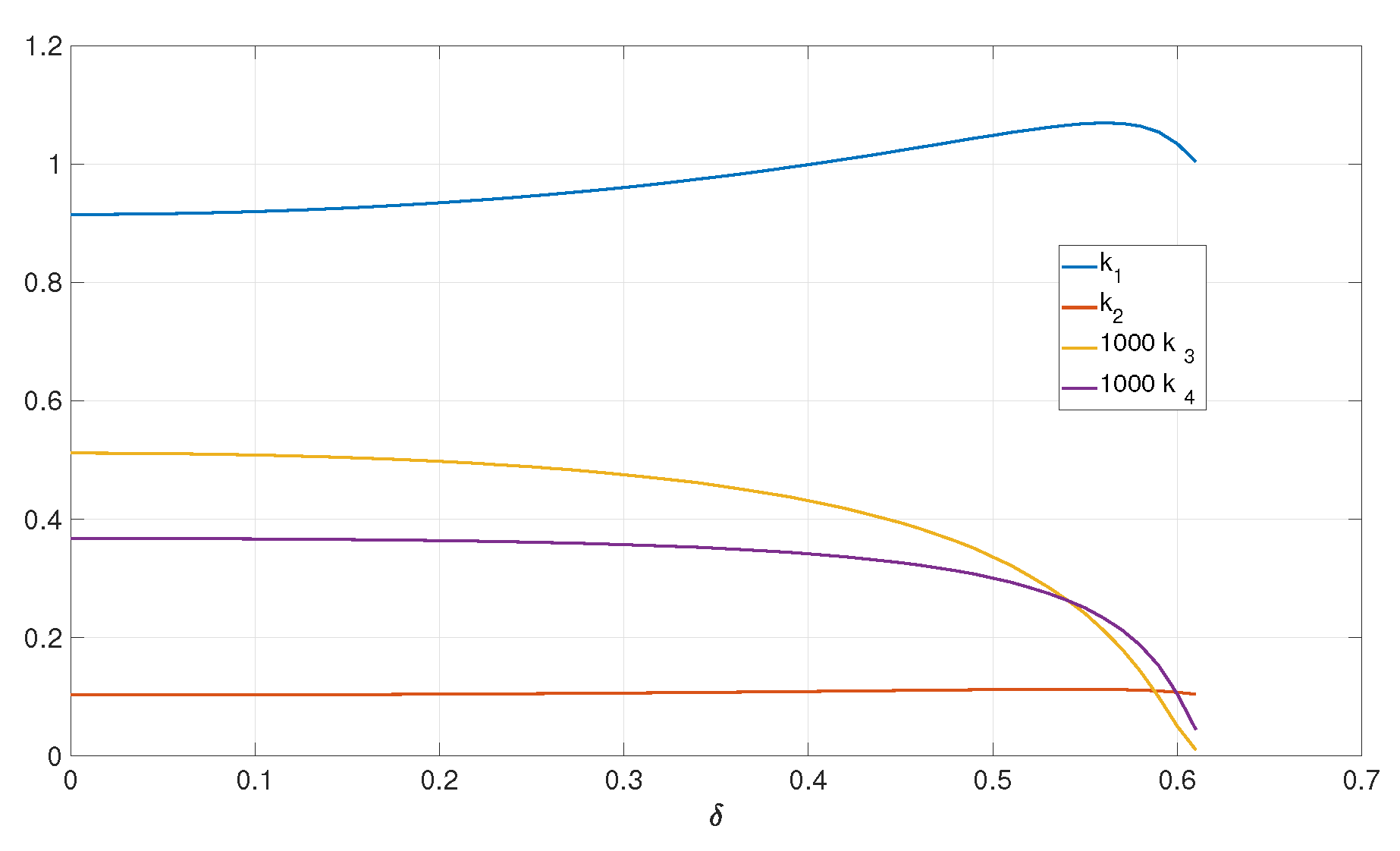
The latter is possible due to the modification of the feedback vector $\underline{k}$ by the robustifying approach to the values presented in Figure 8.

As can be seen in Figure 6 and Figure 7, it is possible to reduce the absolute value of $x_1$ and $x_2$ by a slight deterioration in the operation of the reaction wheel, while reducing the energy consumption in the control channel over a wide range of $\delta$ parameters, what is inherently connected to stability margins of a classical LQR control, supported here by the robustifying algorithm. In a real system, this would improve the performance, while increasing the battery lifetime, and prevent voltage drops.

The corresponding plots, taken for the LQI approach referred to previously, are presented in Figure 9. The results clearly indicate that there is no reason to include the LQI term in the system, as per the increase in all the performance indices’ components, when the gain attached under the LQI framework exceeds ${10}^{-7}$. On the contrary, as per the values of $x_3$ vs. the other state vector components, a decrease in this coefficient results in no impact on the overall control performance.

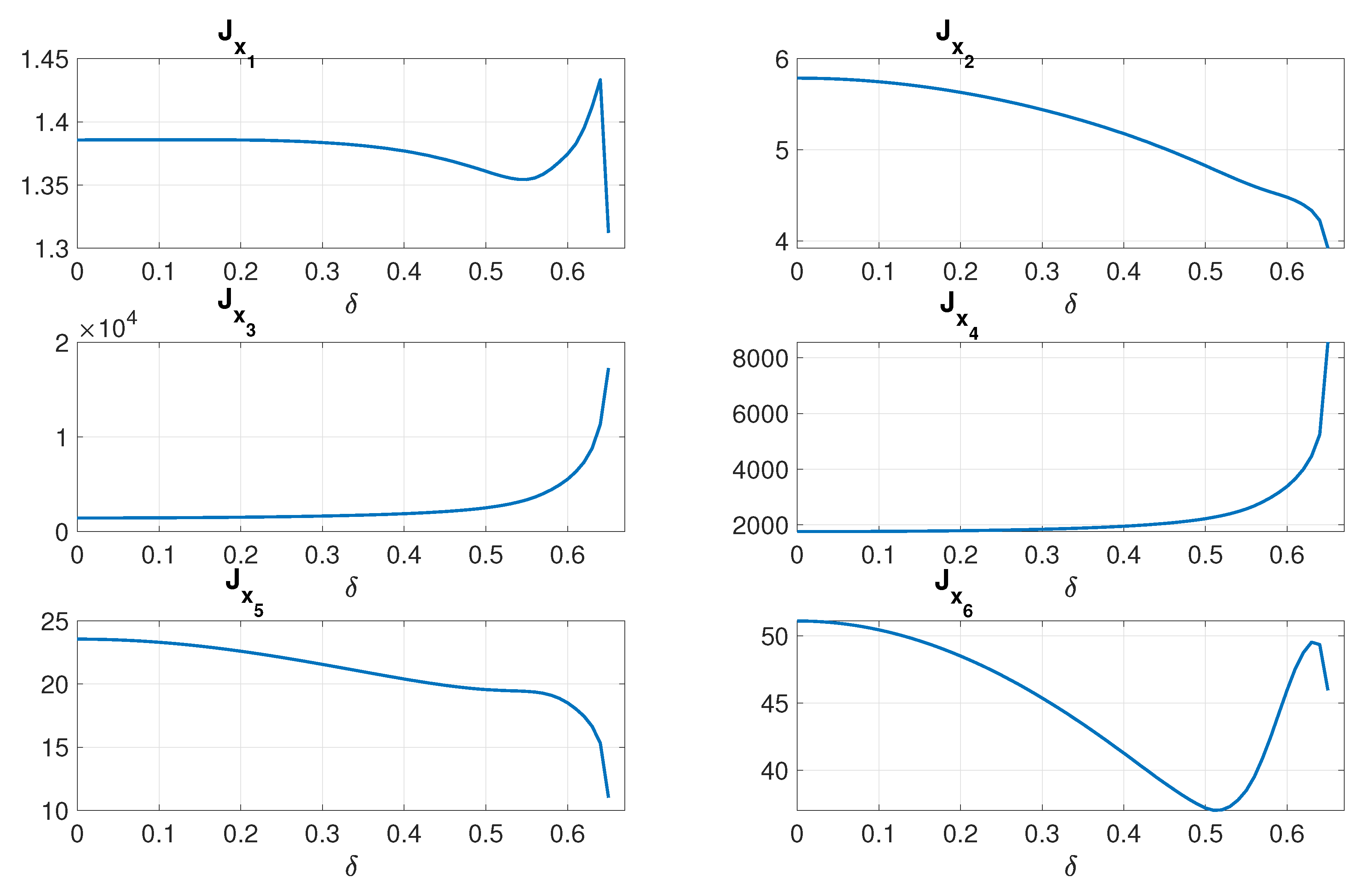
4.5. LQR-Based Stabilization of the Bicycle Using Reaction Wheel and Handlebar Actions with Introduced Robustness

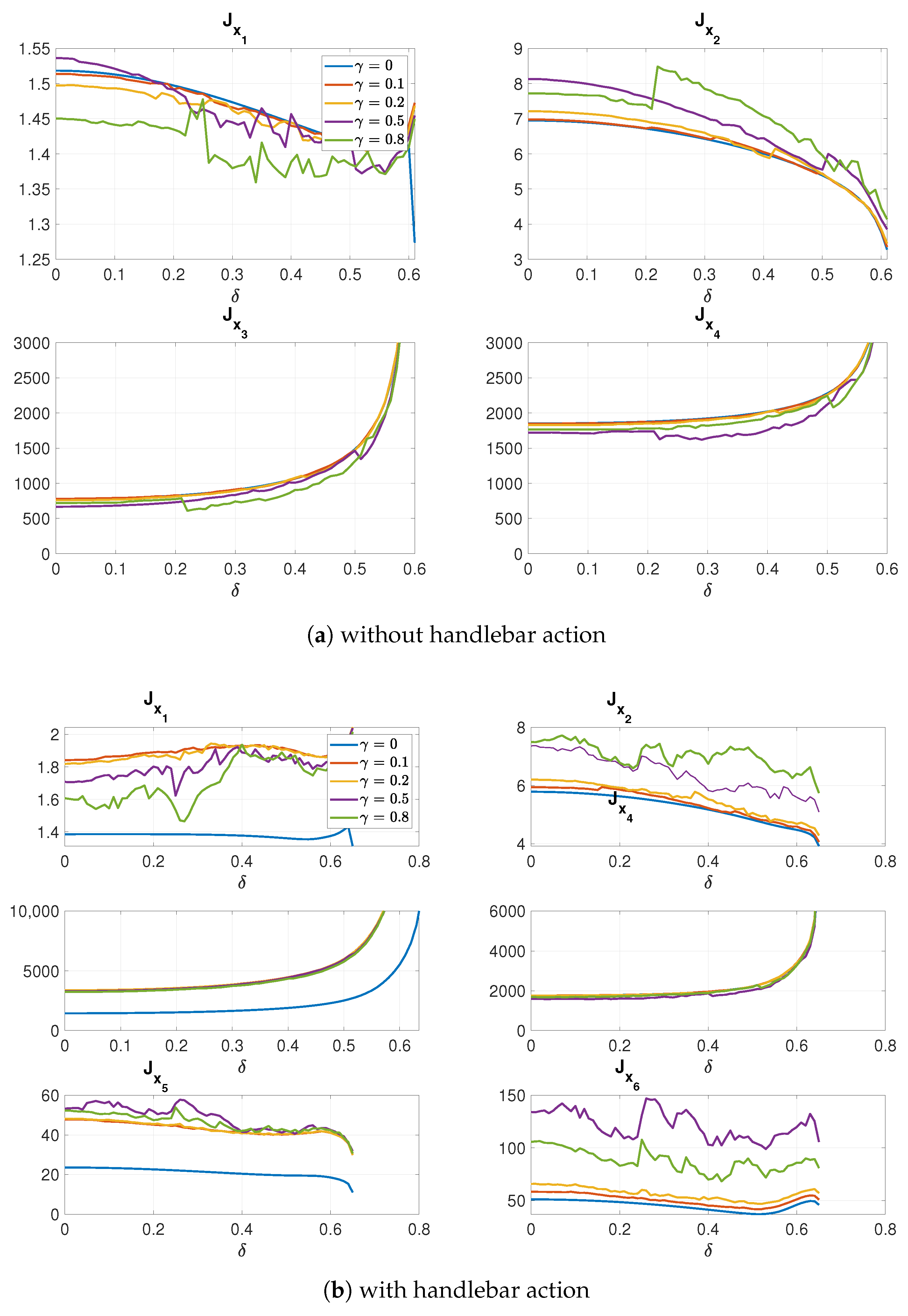
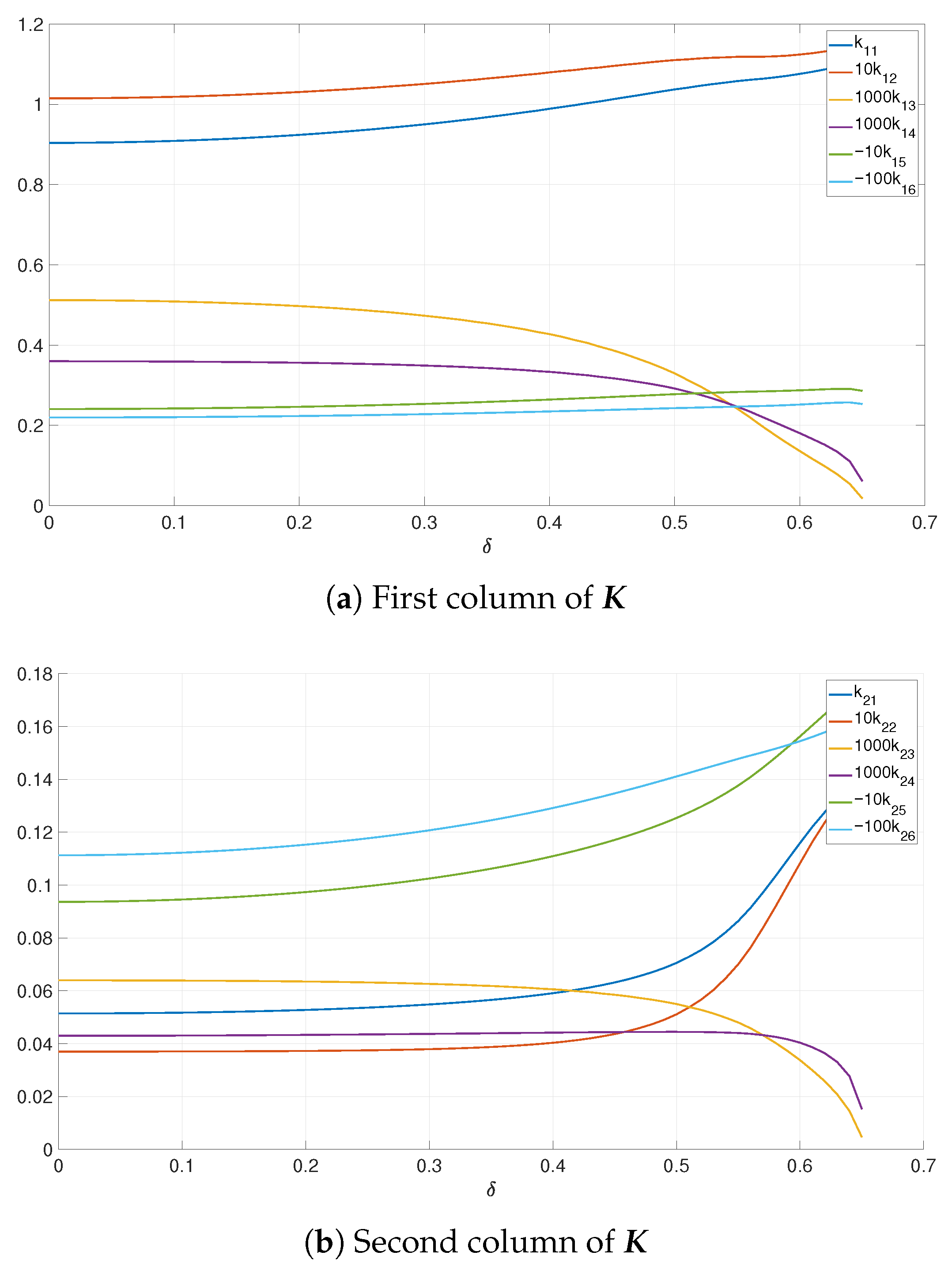
Similar tests were performed in the case of two control inputs, namely input torque to the reaction wheel ($u_1$), and to the handlebar ($u_2$). The performance indices related to components of the state vector have been presented in Figure 10, and to the control efforts in Figure 11, followed by the program of gain scheduling for various $\delta \mathrm{s}$ (Figure 12).

Again, it can be observed that the performance indices connected to the first two, and the last two components of the state vector get reduced in comparison with the classical LQR ($\delta =0$), but also comparing the first two with the case without a handlebar—the initial values of the plots with $\delta =0$ are lower in comparison with the case for a reaction wheel actuation.

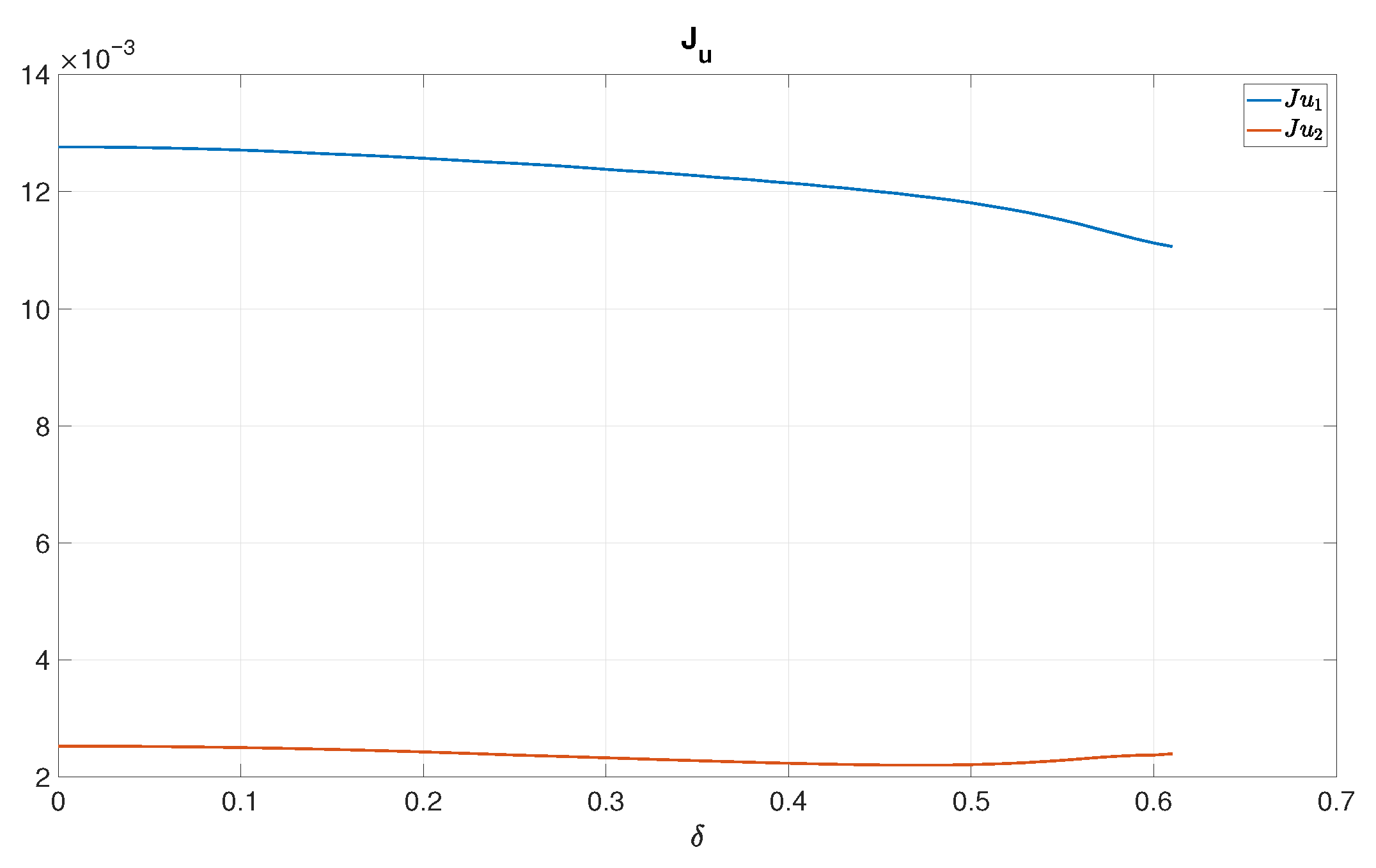
The same holds for the energy use, where the two components presented in Figure 11 have been reduced as well. Naturally, the overall consumption by summing up the two values for $\delta =0$ is greater in comparison to the situation from Figure 7; nevertheless, two control inputs are available here.

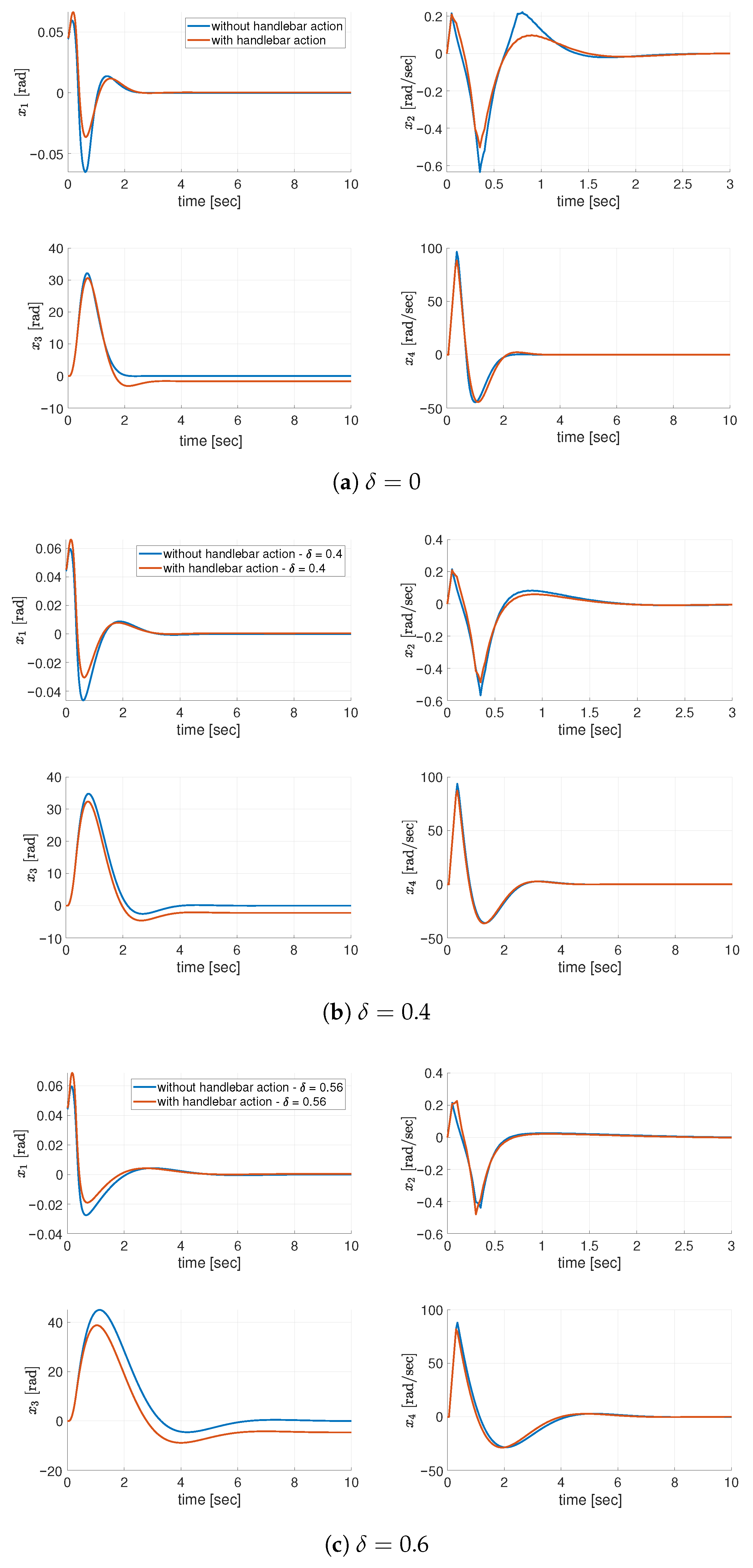
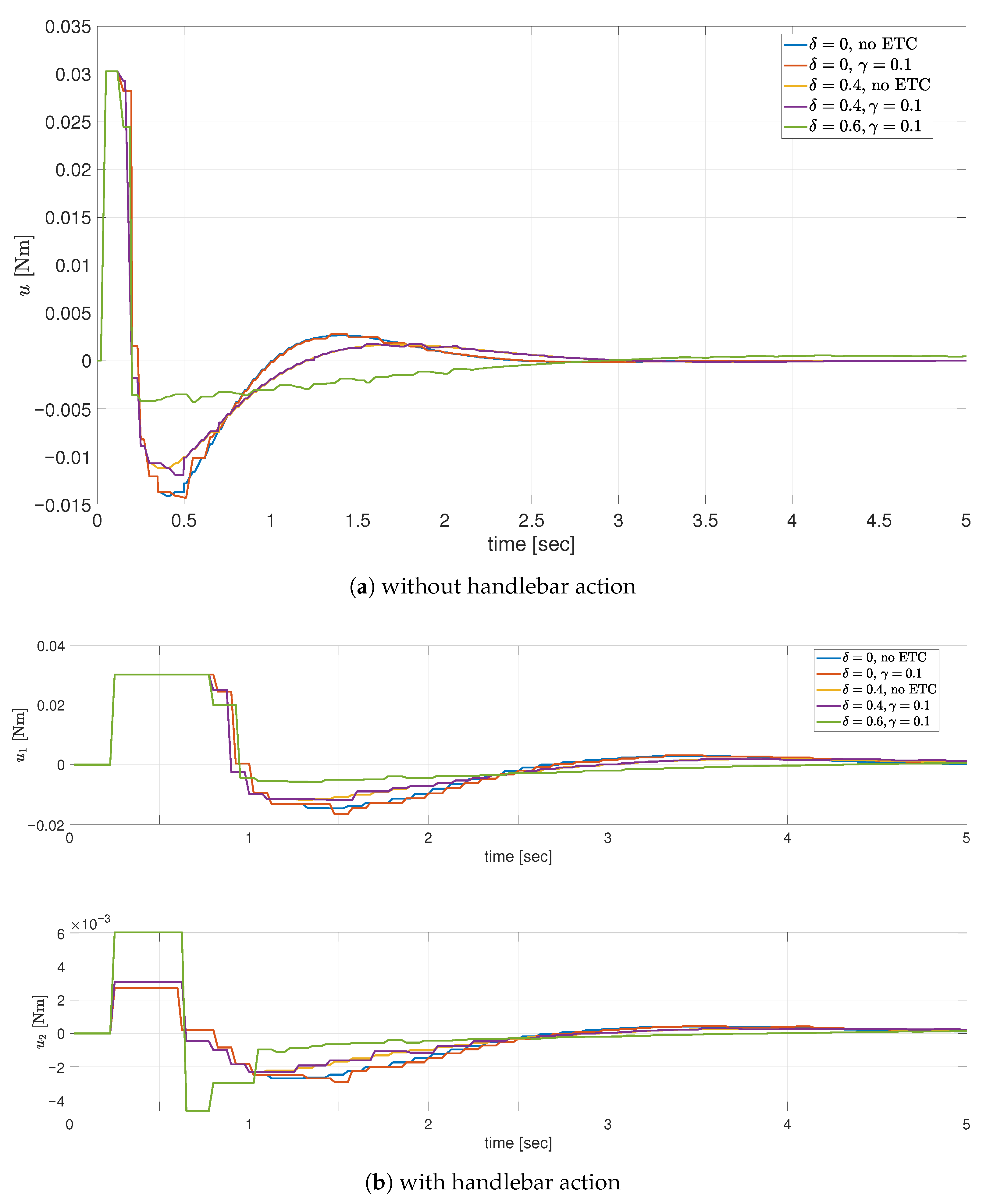
All the plots presented in Figure 13 provide a time-based comparison of the performance presenting the improvement in dynamics, of the state components (comparable between no handlebar and handlebar configurations, connected to the ability to make more agile movements, by taking advantage of the two control inputs).

It is to be mentioned again that all control inputs are saturated on the limit corresponding to the maximum torques, which can be generated by the real motors, mirrored here in the simulation environment.

4.6. Towards the Event-Triggered Control Actions in the Stabilization Task

The last stage of the research referred to the use of event-triggered control actions, to be updated whenever the considered event-triggering condition defined by $\gamma$ is met. For $\gamma =0$ one obtains the classical LQR (with $\delta =0$) or the robustified one with $\delta >0$.

At first, in the case of the situation with the reaction wheel actuation only, it can be seen in Figure 14a that the performance indices connected to the lean angle are over a wide range of $\delta$ below the case with no ETC condition. Thus, the precision of stabilization gets improved, with comparable velocities of the angular deflection, while usually providing also better results in the case of the reaction wheel operation (compare performance for $x_3$ and $x_4$).

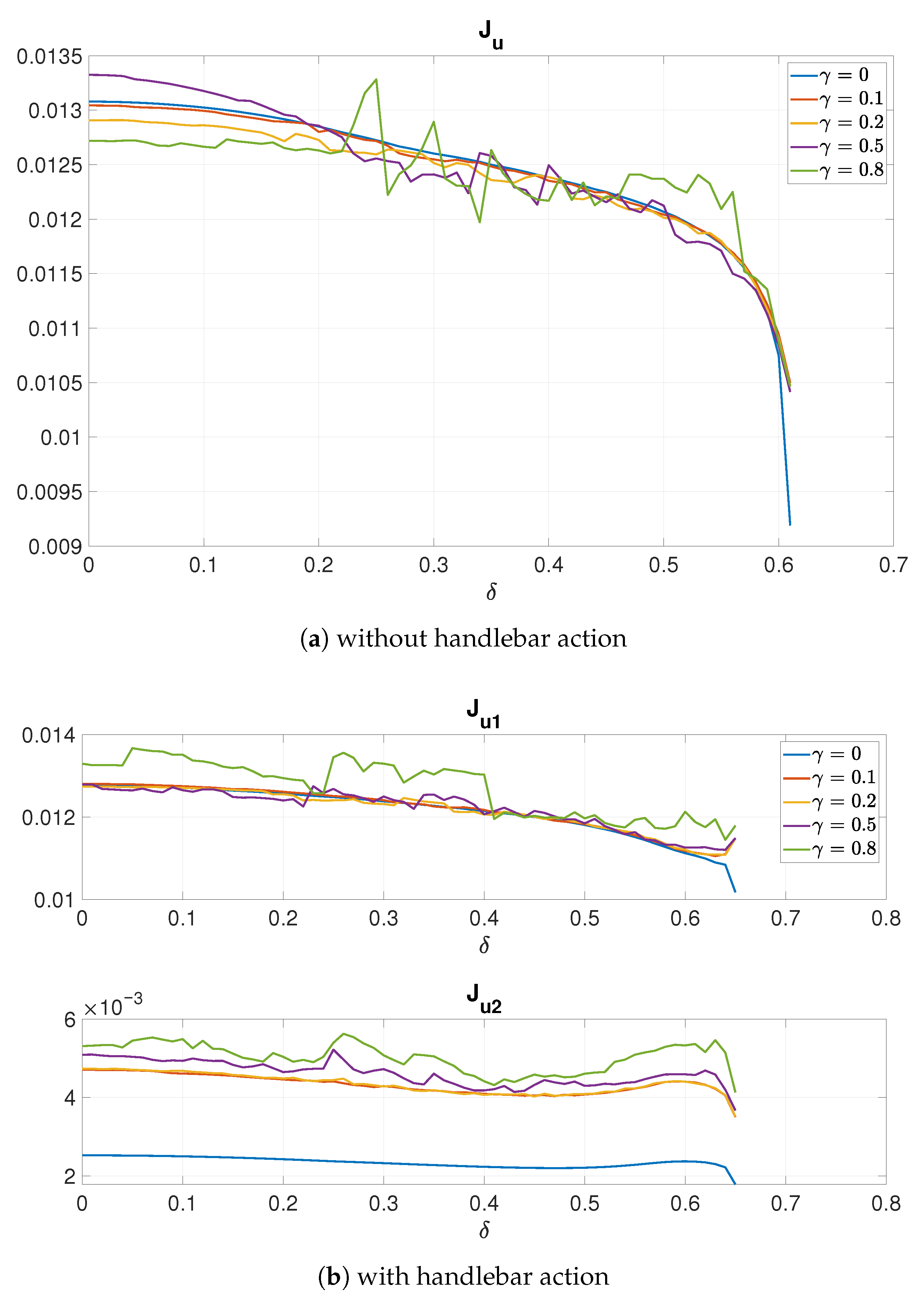
The latter is also visible in Figure 15a where one can see improvement energy consumption indices’ values, reducing with an increase in $\delta$. The less frequent the triggering is (i.e., greater values of $\gamma$), the lower energy consumption becomes. This is connected to changes in controls over time.

When two control inputs are available, it turns out that on the basis of the performance indices presented in Figure 14b that the results comparable to the single actuator only case can be seen only for greater values of $\delta$ for small values of $\gamma$, i.e., for frequent actuation. In Figure 15b, one can see no deterioration in energy consumption of the first control channel, but it is visible in the second one, as it is the handlebar which takes over the major action of improving the performance.

This can be avoided by adding linear velocity to the bicycle, to exert stabilization in motion, where far less control effort should be put into the handlebar, which will be the core of future hardware-in-the-loop experiments.

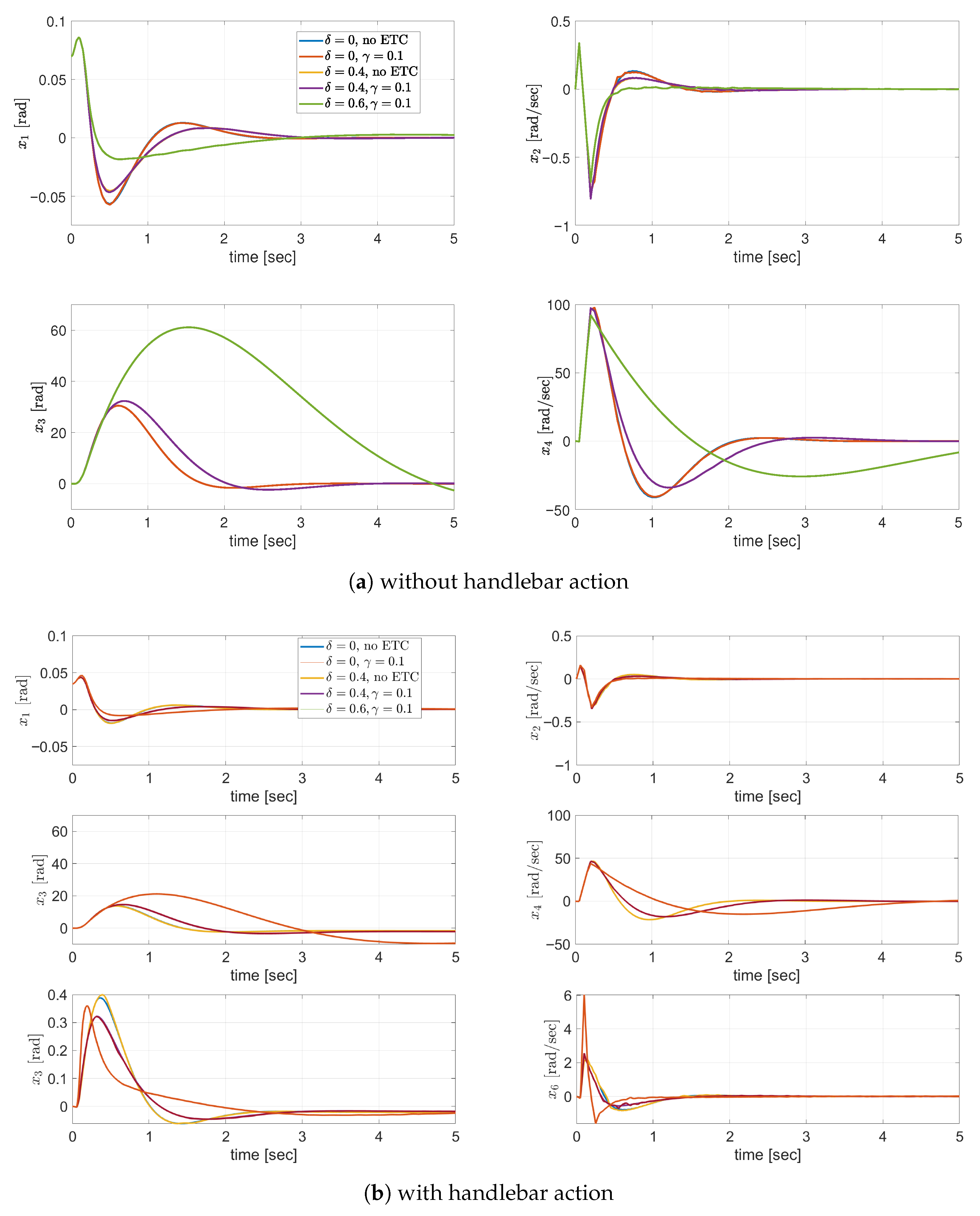
On the basis of the time plots, one can identify the reason for a potential increase in performance indices, summing up over a longer period of time. In Figure 16a when robustness is introduced, one can see a long tail in time response, and a lower speed of operation of the reaction wheel $x_4$, resulting in greater angles $x_3$. In turn, these results in terms of $x_1$ and $x_2$ and the comfort of the potential user, present no oscillatory behavior.

The same holds for the case presented in Figure 17a, where the changes in control vector have smaller absolute values and are non-zero over a wider time horizon. At the same time, they compensate model imperfections, not resulting in agile movements, aligning with the principles of robust control.

Figure 16b and Figure 17b present the plots for two control inputs, where the operation of the ETC mechanism is clearly seen. Some of the solutions in terms of time plots are similar to one another, and should be observed in terms of qualitative comparison, from the viewpoint of the performance. However, one should bear in mind that despite certain costs connected to the robustifying algorithm, in terms of a slight deterioration in channel $u_2$, the robust control law is obtained, tolerating control imperfections.

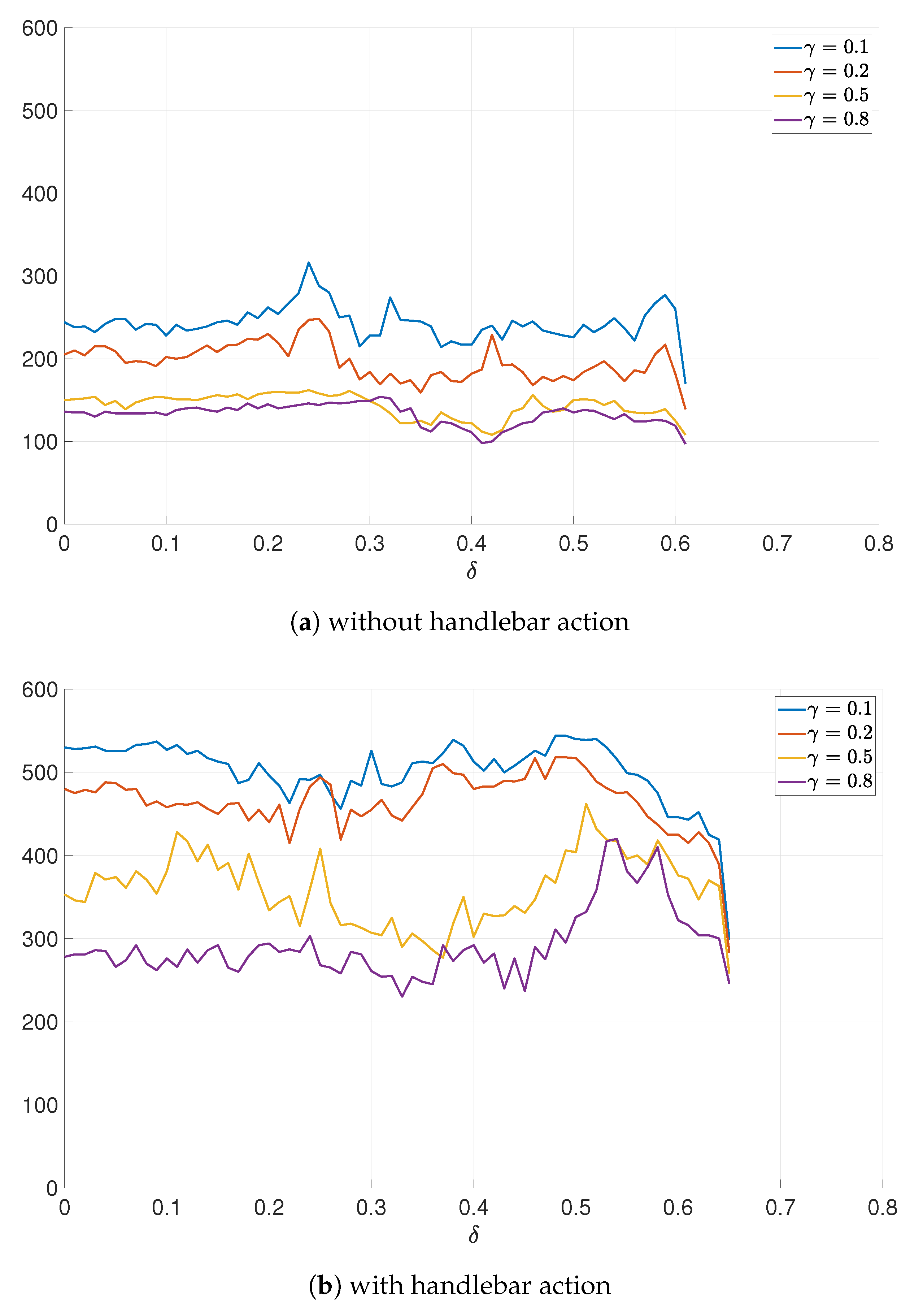
In Figure 18, the number of triggering actions has been depicted, showing the reduction from 600 in the case without ETC, down to even 100 in the case of the event-triggering mechanism considered. This admits to avoiding occupation of communication channels, in passing control actions to the system, as well as reducing frequent changes in control inputs, reducing negative effects on the mechanics of the system. One could also visualize the reduction in the computational burden of the edge devices, where less frequent control updates take place, without major deterioration of the performance, and by the use of the robustifying algorithm—improvement over a wide range of $\delta \mathrm{s}$.

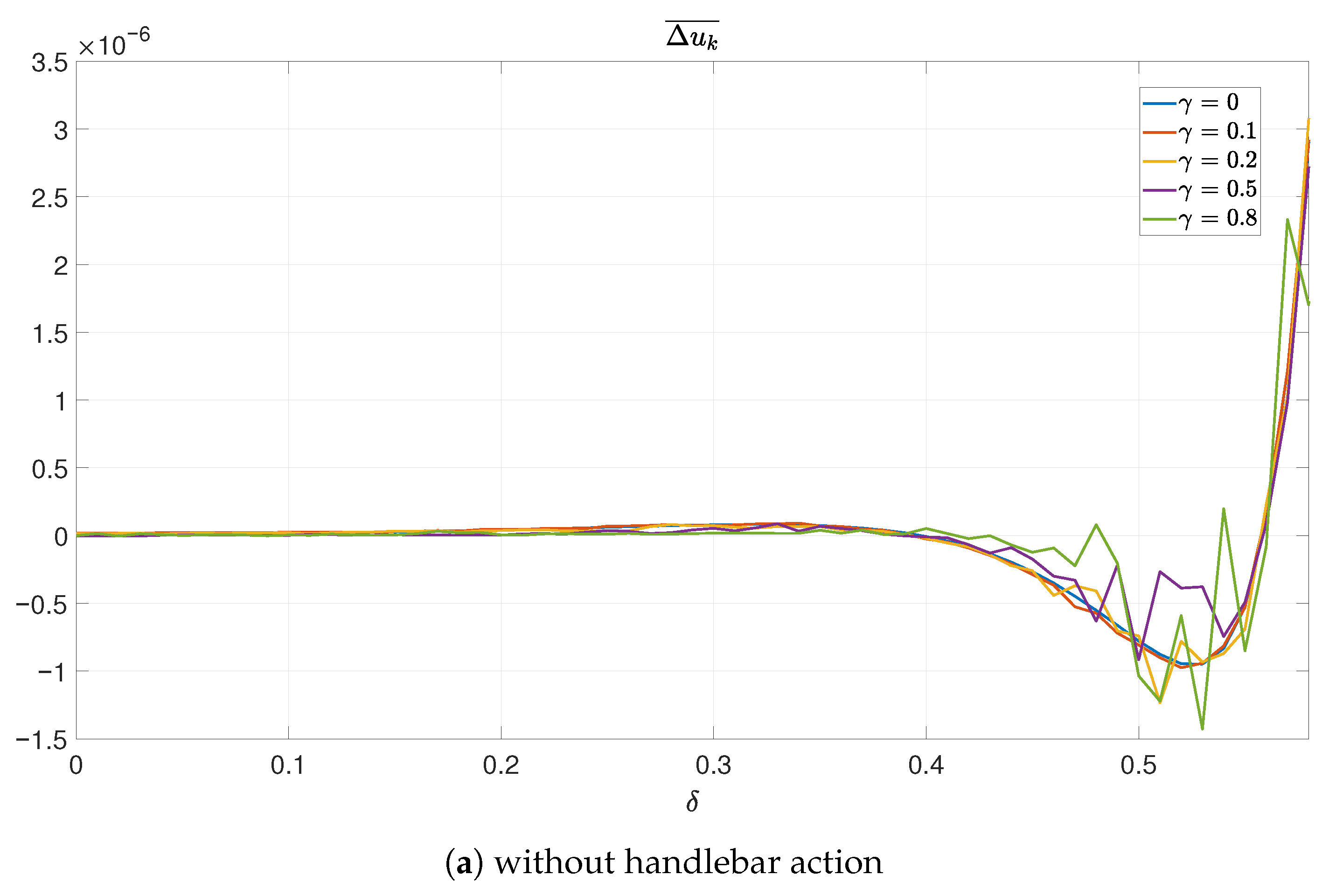
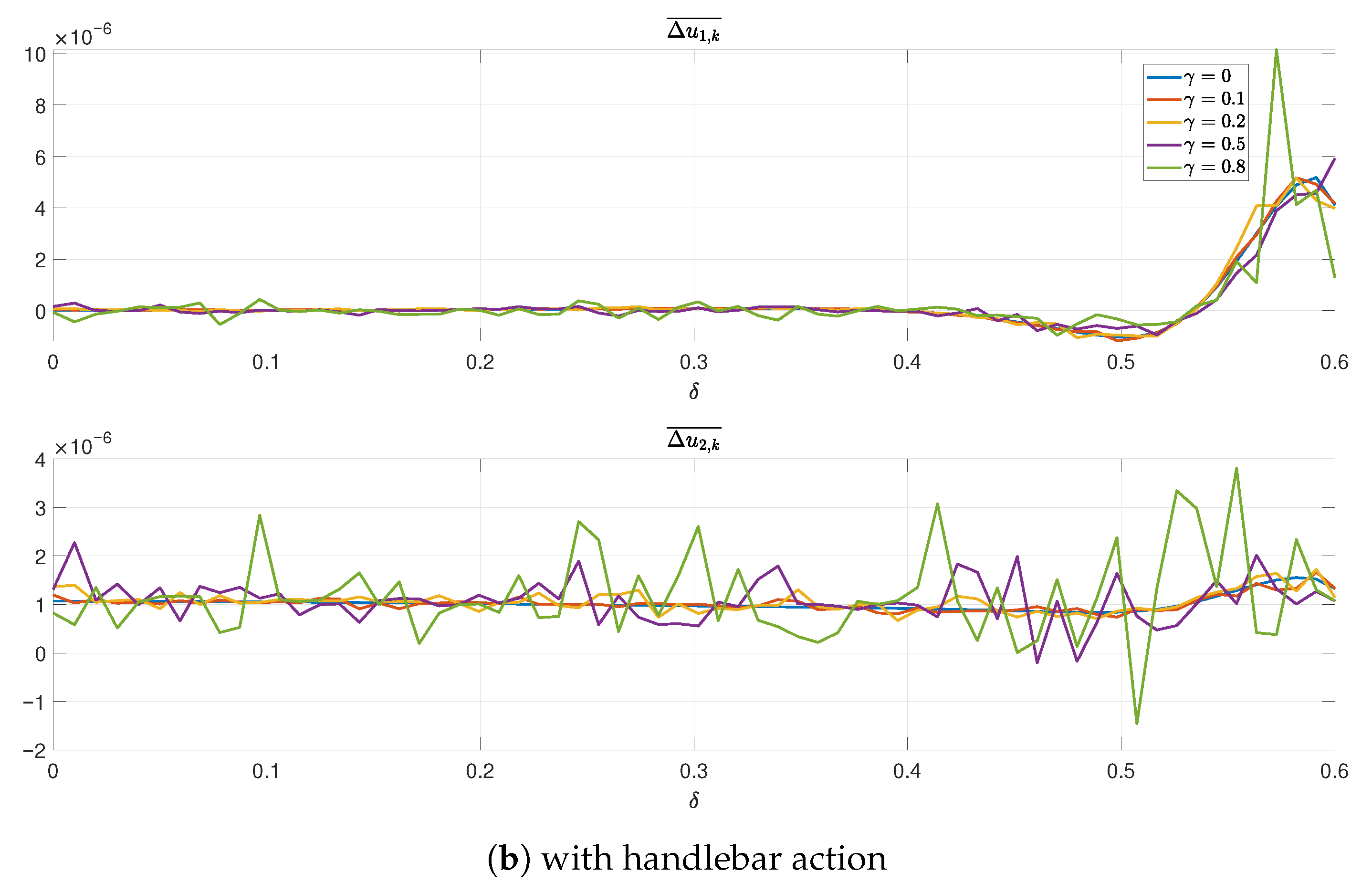
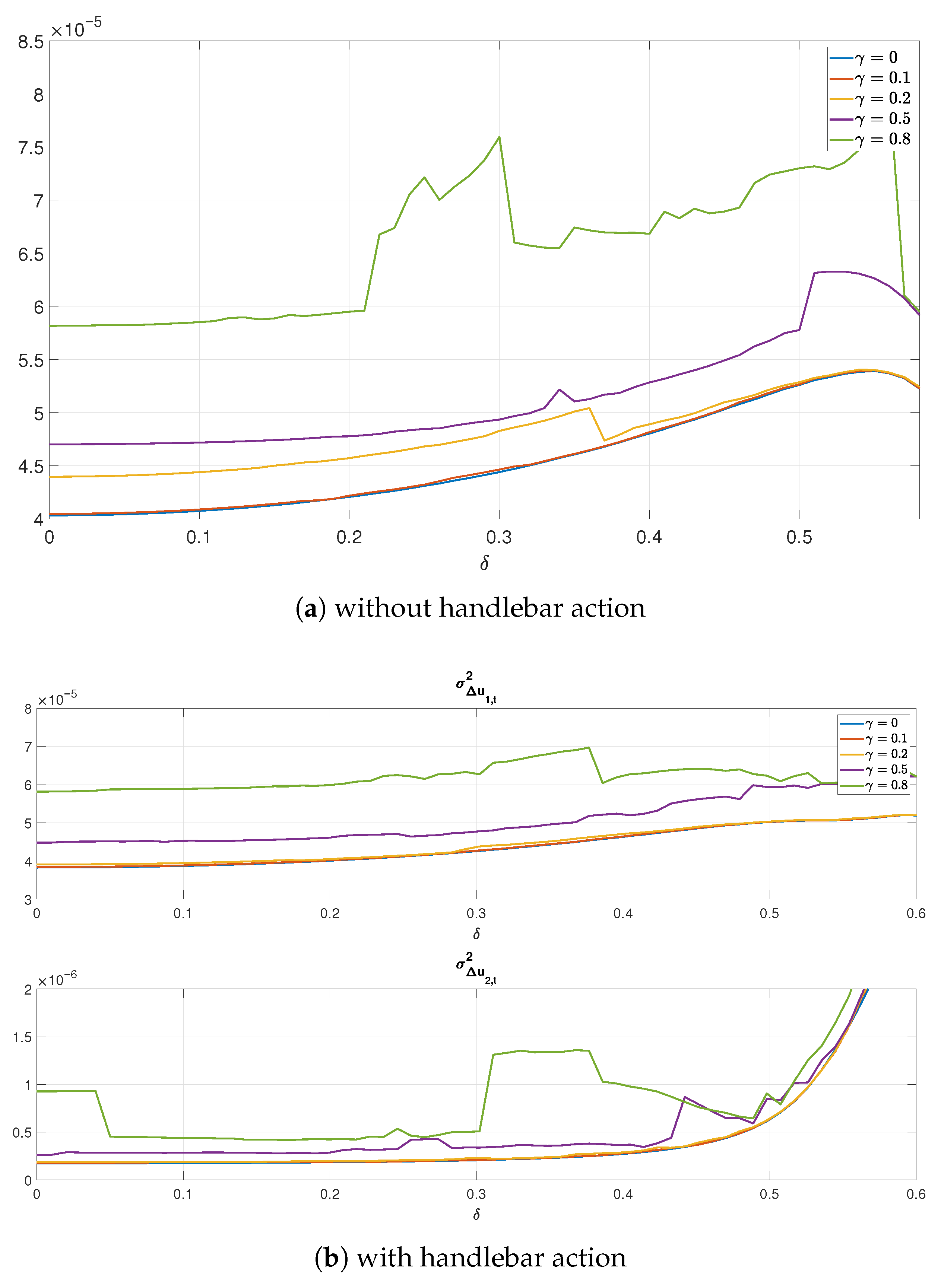
Also in terms of average value of differences across control updates is concerned (Figure 19), and their variances (Figure 20), the mean value of the control torques remains the same over the first 5 s of each simulation (there is no reason to calculate means or variance distorted by near-zero signal values in 30 s duration of the experiment), and the variance of changes is clearly greater in the case of less frequent control updates, what compensates effects of reduction of the occupation of communication channels.

Table 1. Comparison of the decrease in the best configuration of energy of the input signal and the alternative solution—reaction wheel actuation (∗ denoted skipped comparison).

vs.	LQR	LQR + $\mathit{\delta }$	ETC
LQR + $\delta$	−28%	∗	∗
ETC	−5%	−4%	∗
ETC + $\delta$	−21%	−4%	−18%

summarizes the energy reduction connected to the control input signal with reference to Figure 15a and Figure 18a, identified as the best configuration visible in the plots. These results have been obtained in the case of robustified ETC with a reduction of triggers down by −83% in the best configuration. Mean reduction of the number of triggers was $-58\%$ ($\delta =0.1$), $-67\%$ ($\delta =0.2$), $-75\%$ ($\delta =0.5$), and $-80\%$ ($\delta =0.5$).

Table 2. Comparison of the decrease in the best configuration of energy of the input signal and the alternative solution—reaction wheel and handlebar actuation (∗ denotes skipped comparison).

vs.	LQR	LQR + $\mathit{\delta }$	ETC
LQR + $\delta$	−15%	∗	∗
ETC	0%	−3%	∗
ETC + $\delta$	−7%	−3%	−9%

summarizes energy reduction (taken for channel 1, as channel 2 energy is one order of magnitude lower, thus the changes are negligible) connected to the control input signals with reference to Figure 15b and Figure 18b, identified as the best configuration visible in the plots.

These results have been obtained in the case of robustified ETC with reduction of triggers (taking two separate triggering conditions into account for two control inputs) down by −61% in the best configuration. Mean reduction of the number of triggers was $-21\%$ ($\delta =0.1$), $-24\%$ ($\delta =0.2$), $-43\%$ ($\delta =0.5$), and $-51\%$ ($\delta =0.5$).

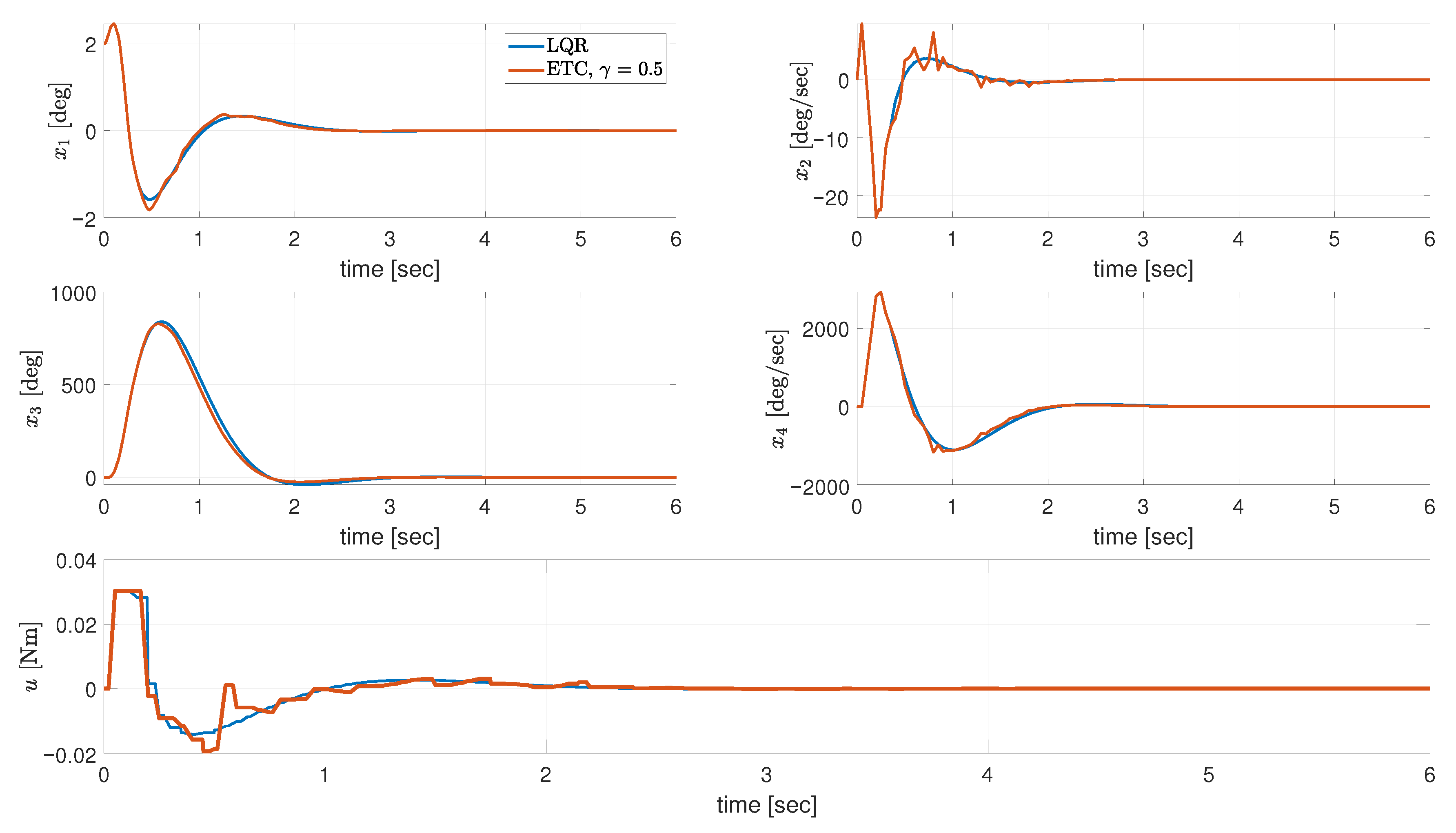
In Figure 21, a sample experimental run for $x_1\left(0\right)=2^{\circ }$, and the remaining entries of the state vector are set to zero, to compare the performance between LQR and ETC on a real platform has been added, to depict that this control scheme is deployable and allows stabilization of the bicycle robot. However, due to the issues connected to the implementation, noise mitigation, and mismodeling issues, the complete vast statistical campaign to present the properties of the considered control actions, is left as a future research direction.

The deployment on the real hardware requires necessary changes to the strategy of taking tests, initial condition changes, and at this point is premature to be presented here.

In

Table 3. Effect of $\gamma$ in ETC on the overall performance, $\delta =0$, $x_1\left(0\right)=1^{\circ }$ (bold numbers denote small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	0.538	0.538	0.536	0.537	0.530	0.531	0.540	0.533	0.520	0.544	0.543	0.519	0.519	0.519	0.519
$J_{x_2}$	2.753	2.772	2.766	2.765	2.847	2.848	2.732	2.775	3.071	3.151	3.149	3.079	3.079	3.078	3.078
$J_{x_3}$	273.0	271.1	274.9	274.1	267.3	266.9	265.2	263.4	246.0	236.7	236.9	253.9	254.9	255.1	255.0
$J_{x_4}$	656.0	654.1	655.2	655.1	647.4	648.3	651.8	639.5	619.6	624.9	624.6	617.0	617.9	618.0	618.0
$J_u$	0.0047	0.0047	0.0047	0.0047	0.0047	0.0047	0.0048	0.0047	0.0046	0.0048	0.0048	0.0046	0.0046	0.0046	0.0046
TRG [%]	0	−41.7	−40.2	−37.3	−34.7	−30.5	−27.7	−27.7	−24.7	−25.8	−25.2	−22.3	−22.2	−22.0	−21.8

and

Table 4. Effect of $\gamma$ in ETC on the overall performance, $\delta =0.3$, $x_1\left(0\right)=1^{\circ }$ (bold denotes small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	0.512	0.512	0.511	0.511	0.510	0.513	0.503	0.502	0.503	0.502	0.502	0.500	0.500	0.483	0.483
$J_{x_2}$	2.549	2.548	2.560	2.598	2.605	2.545	2.736	2.740	2.742	2.740	2.739	2.747	2.748	2.963	2.963
$J_{x_3}$	309.9	310.2	310.2	305.9	304.5	299.3	290.0	288.2	287.8	287.5	289.6	286.9	286.9	260.3	260.3
$J_{x_4}$	666.0	665.7	663.1	660.1	657.7	662.0	637.0	635.2	634.9	631.7	633.8	626.3	626.1	587.7	587.7
$J_u$	0.0045	0.0045	0.0045	0.0045	0.0045	0.0045	0.0044	0.0044	0.0044	0.0044	0.0044	0.0044	0.0044	0.0043	0.0043
TRG [%]	0	−45.2	−38.8	−32.7	−29.3	−28.5	−26.5	−27.0	−24.5	−25.2	−25.0	−26.3	−24.5	−25.0	−25.0

the comparison between different ETC versions has been presented, showing the impact of $\gamma$ on the overall performance. Starting from the bottom row, it can be easily identified that the greater the threshold value, the more frequent the updates become; thus, it is vital to keep this value low. The first two rows present the already-introduced performance indices related to the lean angle and its dynamics—the degradation does not introduce drastic changes, and is completely acceptable. The overall control energy-related performance index is also not hardly affected, which leads the way to a reduction of mechanical wear and tear effects by the introduction of ETC.

The same holds in the case when robustness is introduced to ETC ($\delta =0.3$), since not only lean angle-related performance indices are reduced by roughly 10%, but also the control effort is reduced by approximately 5–8%, whilst the control updates are reduced as well. The increase in $\gamma$ results in the same effects as in the case of no robustness introduced, since the lean angle-related performance indices get reduced, at the cost of an increase in the frequency of updates (control energy consumption decreases in such a case).

Table 5. Effect of $\gamma$ in ETC on the overall performance, $\delta =0$, $x_1\left(0\right)=2^{\circ }$ (bold denotes small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	1.518	1.519	1.514	1.518	1.497	1.496	1.494	1.528	1.479	1.537	1.536	1.533	1.450	1.450	1.450
$J_{x_2}$	6.949	6.990	6.978	6.999	7.212	7.239	7.236	7.001	7.857	8.123	8.129	8.119	7.729	7.729	7.730
$J_{x_3}$	773.3	770.5	779.6	776.0	757.75	750.0	752.7	738.8	701.4	667.6	666.8	667.6	717.0	717.0	717.2
$J_{x_4}$	1850	1849	1848	1849	1827	1815	1815	1830	1779	1769	1767	1766	1725	1725	1726
$J_u$	0.0131	0.0131	0.0130	0.0131	0.0129	0.0128	0.0128	0.0132	0.0128	0.0133	0.0133	0.0133	0.0127	0.0127	0.0127
TRG [%]	0	−42.3	−40.7	−39.3	−34.2	−31.3	−29.0	−28.2	−26.3	−25.2	−25.0	−24.3	−22.8	−23.0	−22.2

and

Table 6. Effect of $\gamma$ in ETC on the overall performance, $\delta =0.3$, $x_1\left(0\right)=2^{\circ }$ (bold denotes small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	1.476	1.476	1.468	1.472	1.471	1.484	1.481	1.447	1.446	1.445	1.447	1.437	1.431	1.418	1.426
$J_{x_2}$	6.462	6.461	6.489	6.634	6.635	6.515	6.553	7.081	7.092	7.092	7.106	7.144	7.007	6.980	7.045
$J_{x_3}$	895.3	896.2	899.7	879.5	879.5	856.1	853.4	825.1	822.0	821.4	829.4	815.7	820.0	852.0	849.1
$J_{x_4}$	1917	1916	1908	1894	1894	1908	1899	1824	1813	1812	1827	1788	1786	1774	1780
$J_u$	0.0126	0.0126	0.0126	0.0126	0.0126	0.0127	0.0127	0.0124	0.0124	0.0124	0.0124	0.0123	0.0125	0.0125	0.0126
TRG [%]	0	−49.0	−35.8	−31.7	−29.2	−28.7	−27.2	−26.3	−25.7	−25.8	−25.8	−25.7	−25.3	−25.8	−25.3

mirror the same situation, but for another initial lean angle. The control energy performance index reduction for the robustified case reaches down to 1–4%, which is less impressive, however, it is still coupled with a decrease in frequency of control updates. It is to be kept in mind though that for another $\delta$ (consult the initial tests of the impact of $\delta$), the situation might be more advantageous, as a broad range of reduction of performance indices has been identified for greater values of data, as per mismodeling errors.

Definitely, as a direction of future research, one could list the selection rule for $\gamma$ to obtain improved control performance, which would lead to the presentation of a combined, possibly weighted, performance measure capturing various features of the event-triggered control system.

4.7. Alternative Approaches—Can the ETC Mechanism Be Applied to the State-of-the-Art Methods?

It is natural to discuss whether the other state-of-the-art methods are comparable or offer similar performance in comparison to the LQR+ETC mechanism, or at least the pure LQR mechanism. For this purpose, the authors have decided to put into direct comparison the MPC method for the prediction horizon of $N=10$ samples, with $\mathit{Q}$ and $\mathit{R}$ matrices as in the case of the considered LQR algorithm. The results in terms of the performance indices are presented in

Table 7. Effect of $\gamma$ in MPC-ETC on the overall performance, $x_1\left(0\right)=1^{\circ }$ (bold denotes small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	1.219	1.218	1.219	1.221	1.232	1.238	1.235	1.225	1.211	1.215	1.224	1.232	1.239	1.273	1.354
$J_{x_2}$	2.278	2.283	2.294	2.325	2.324	2.388	2.425	2.441	2.480	2.609	2.703	2.795	2.882	2.998	3.321
$J_{x_3}$	5212	5110	5103	5108	5159	5144	5111	5134	5031	4938	4909	4876	4860	5073	5334
$J_{x_4}$	4627	4621	4620	4628	4655	4662	4647	4629	4537	4505	4524	4527	4535	4674	4957
$J_u$	0.0089	0.0089	0.0089	0.0089	0.0090	0.0090	0.0090	0.0089	0.0088	0.0089	0.0089	0.0090	0.0090	0.0093	0.0099
TRG [%]	0	−28.8	−35.5	−41.2	−40.5	−38.7	−38.0	−36.5	−38.5	−40.3	−42.3	−41.0	−40.3	−40.8	−42.0

and

Table 8. Effect of $\gamma$ in MPC−ETC on the overall performance, $x_1\left(0\right)=2^{\circ }$ (bold denotes small values).

$\mathit{\delta }$/perf.ind.	0.00	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70
$J_{x_1}$	3.463	3.463	3.468	3.517	3.533	3.527	3.503	3.438	3.481	3.411	3.438	3.428	3.598	3.566	3.625
$J_{x_2}$	5.672	5.683	5.735	5.783	5.836	5.977	6.050	6.190	6.343	6.528	6.822	7.022	7.542	7.779	8.313
$J_{x_3}$	14530	14519	14494	14739	14838	14681	14563	14206	14395	13916	13795	13614	14112	13910	13899
$J_{x_4}$	13137	13131	13137	13325	13395	13273	13192	12912	13079	12643	12687	12600	13174	12913	13072
$J_u$	0.0246	0.0246	0.0246	0.0249	0.0251	0.0250	0.0249	0.0244	0.0247	0.0242	0.0244	0.0244	0.0256	0.0255	0.0261
TRG [%]	0	−29.0	−37.7	−40.7	−39.3	−38.0	−39.8	−37.3	−38.8	−38.5	−40.0	−40.8	−41.2	−40.7	−40.5

. The calculated control vector has the first entry applied to the system, post-saturation. It can be seen that the MPC has strong averaging properties, thus the performance indices in terms of $x_1$ are almost doubled values of the LQR ones, and the improvement is observed for intermediate values of $\gamma$, since the prediction mechanism allows good control quality when the distortion of the sequence of control inputs is not present to a high extent, i.e., for low values of $\gamma$. Nevertheless, over a wide range of $\gamma \mathrm{s}$ the performance index for $x_1$ stays roughly the same, as in the case of LQR control. The averaging properties are also seen as far as $x_2$ is considered, as lower values of the performance index are visible for comparable initial lean angles, or comparable $\gamma \mathrm{s}$. That is interesting, the MPC framework has much greater control updates in comparison to the LQR case, this is why the reduction in the number of control updates is less visible for small values of $\gamma$, also in the case of the higher initial lean angle. Otherwise, the MPC controller could not get full control authority over the unstable system.

Since the performance in terms of control indices connected to the input action, along with $x_1$ as the major effect of the control effort is considered, the intermediate values of $\gamma$ are favored, to allow the ETC mechanism to mimic the trajectories feasible with $\gamma =0$.

The situation in the case of the second considered state-of-the-art solution is more complicated, as one cannot actually impose ETC mechanism without major performance deterioration, if not even instability. To keep the system on the sliding surface, the control should switch constantly, and the sequence of switch-overs cannot be modified, without divergence from the sliding motion, actually showing no features of SMC in this case.

The former is the reason why tests for various values of $\gamma$ were not performed, and the performance indices forming the first column of the to-be-conducted simulations are 7.231, 157.88, 4261.7, 2255.3, and 0.3604, respectively. This shows much greater energy of the control signal necessary to keep the system on the sliding surface, actually deterring the purpose of the paper, to introduce the ETC mechanism in order to lower the energy consumption, while maintaining the overall performance at a comparable level.

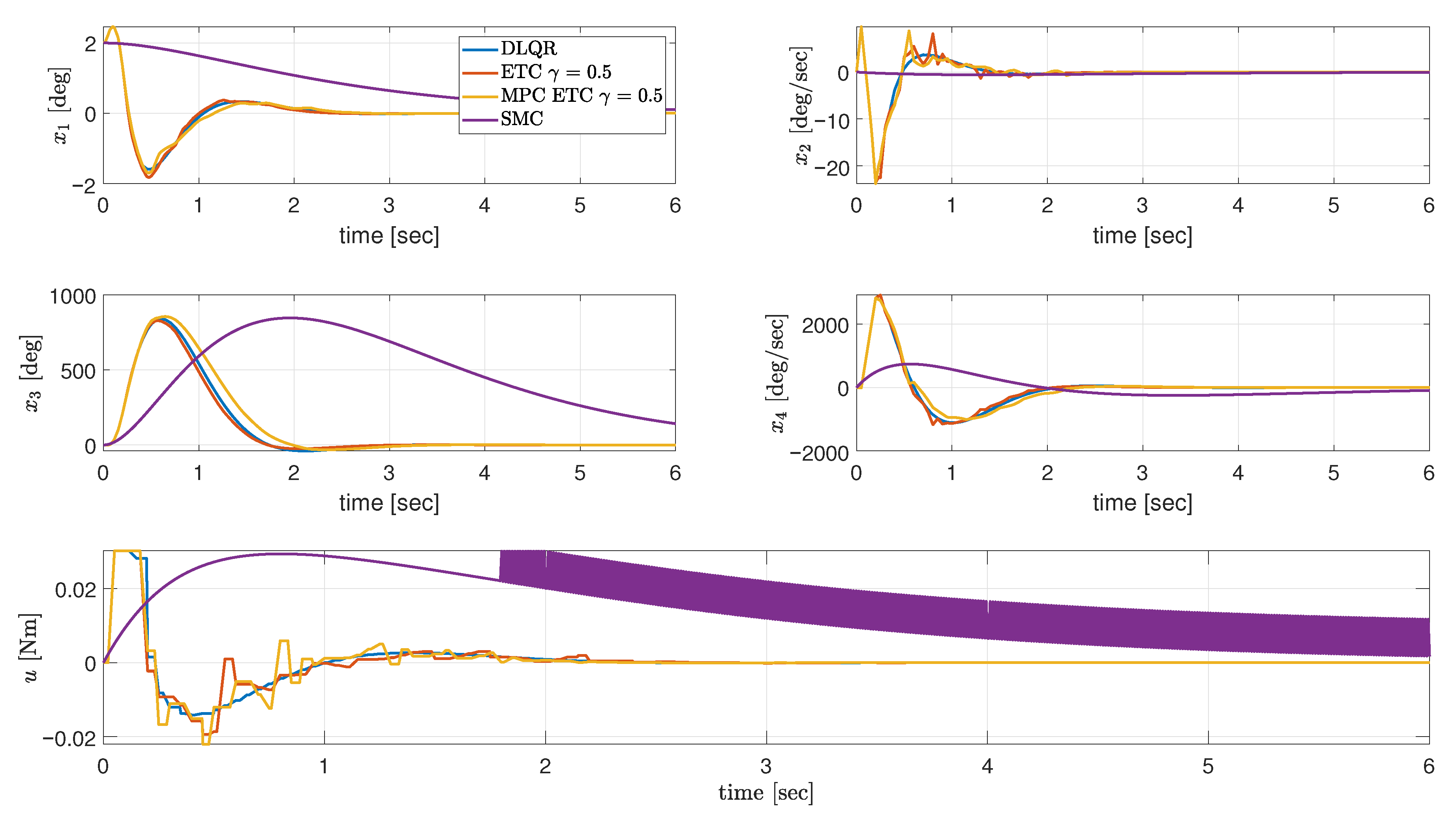
The final comparison in terms of responses to the same initial lean angle has been presented in Figure 22, where the introduction of the ETC mechanism to LQR and MPC results in comparable performance, with the LQR method more applicable in the environment where the computational burden should be lower.

A short summary of the considered approaches is presented in

Table 9. Comparison of the selected control approaches in the framework presented in the paper.

Strategy	Off-Line Calc.	Robustif.	ETC Intr’d	Post-ETC Low Perf. Degrad.
LQR	+	+	+	+
MPC	+	−	+	+
SMC	+	−	−	−

, to evaluate possible suitability for the adopted task. It is to be stressed that the strategies have been compared in their classical (most commonly met) forms, with special view of the possibility to calculate the state feedback vector off-line, to introduce robustification ($\delta$), to introduce a triggering mechanism, as well as introduction of low performance degradation in comparison to the case without ETC. As a result, the LQR method outperforms the other classical ones due to the reasons listed above in this Section.

5. Conclusions and Future Research Directions

The paper addressed the complex challenge of stabilizing an inherently unstable bicycle robot at zero speed where balancing is most difficult. The key problem here is maintaining upright balance while keeping energy consumption low—so crucial for future personal electromobility vehicles such as electric bicycles, allowing the handicapped to potentially indirectly use the proposed control solution advantages. To tackle this, the authors model bicycle dynamics and develop feedback control strategies including linear quadratic regulation, its robustified version, and an event-triggered control scheme. The approaches use reaction wheel actuation and handlebar action to stabilize the bicycle with an emphasis on (energy) efficiency. Event-triggered control significantly reduces control signal updates, thereby saving energy and reducing mechanical wear without compromising stability. Simulation results demonstrate robust stabilization across a range of initial lean angles and operational uncertainties, highlighting improved energy profiles and stability margins by means of time-domain analysis. This is particularly important for extending battery life and improving user comfort and safety in autonomous or rider-assisted vehicles. By integration of robust and event-based techniques, the study offers a promising direction for efficient balancing control in emerging personal electromobility platforms, contributing to sustainable and accessible urban mobility solutions.

Balance support is widely available beyond motorcycles and bicycles as well, also in various personal mobility units aimed at customer use, such as self-balancing scooters or wheelchairs for example. The global market demand is about to exceed USD 2.5 billion in 2025 with growth propelled not only by the adoption of energy-efficient motors, but also, as in this paper, intelligent control systems to maintain stability. All these approaches must be energy-consumption aware.

As the paper actually proposed two alternative control inputs, namely the reaction wheel torque, and the handlebar-related torque, the final discussion should also refer to different operating conditions, and the effective use of the actuators. Reaction wheels consume more electrical energy because they operate by spinning a mass to generate the input torque. This process, related to $x_3$ and $x_4$ variables, is clearly seen throughout the paper, and is connected to a sustained energy consumption, even at zero speed. In the case of the handlebar action, this input is more energy-efficient in a broader context, as per the gyroscopic effects of the front wheel and trail geometry, to get a self-stabilization property, not investigated in this paper. Nevertheless, at low or zero speeds, the reaction wheel action is preferred. At low speeds, the combination of reaction wheel and handlebar actions is most effective. The criterion that actuation to use should eventually depend on efficient control allocation, by the use of optimization, as in the case of the discussed LQR approach, where one could connect different weights to the less preferred input, and change these adaptively, subject to the change in the linear speed of the bicycle.

In the future, it is planned to use experimental validation on real hardware to confirm simulation outcomes, also in the context of more advanced control strategies as model predictive control (presented here in simulation context only) and adaptive approaches. These potentially would allow the spread control effort over a wider range of steps, in the case of predictive control, to capture the interplay between prediction horizons and control efforts better. In the case of adaptive control, it would allow alteration of control system parameters to specific conditions, as driving at zero, low, moderate, and high speeds, to build a bank of controllers to switch between. The key challenge here would be to design a switching law to change feedback gains on the basis of a specified condition. Implementing the control schemes on IoT-enabled embedded systems can potentially pave the way for intelligent, connected electromobility platforms. The authors also plan to include trajectory tracking in moving bicycles with variable velocities and external disturbances into account, including taking banked turns. This could eventually support the advantage of using a single actuation method, a combined actuation method for various conditions, as well as taking advantage of a gyroscopic effect, and self-stabilizing property support to better increase the energy efficiency. The major challenge here is to obtain results ready for generalization to other platforms with a similar mechanism of motion. The topic of balancing energy use, stability, and user comfort remains the critical goal for practical, widespread adoption.