Optimising Behavioural Control Based on Actual HVAC Use in Naturally Ventilated Buildings
Abstract
1. Introduction
2. Methodology
2.1. Construction of a Multi-Objective Database
2.1.1. Methods of Quantifying and Characterising Actual HVAC Behaviours in Building Simulation
2.1.2. Proposal of Decision Variables Based on Importance Analysis
2.1.3. Construction of a “Decision Variable-Target Variable” Mapping Database Based on Batch Simulation
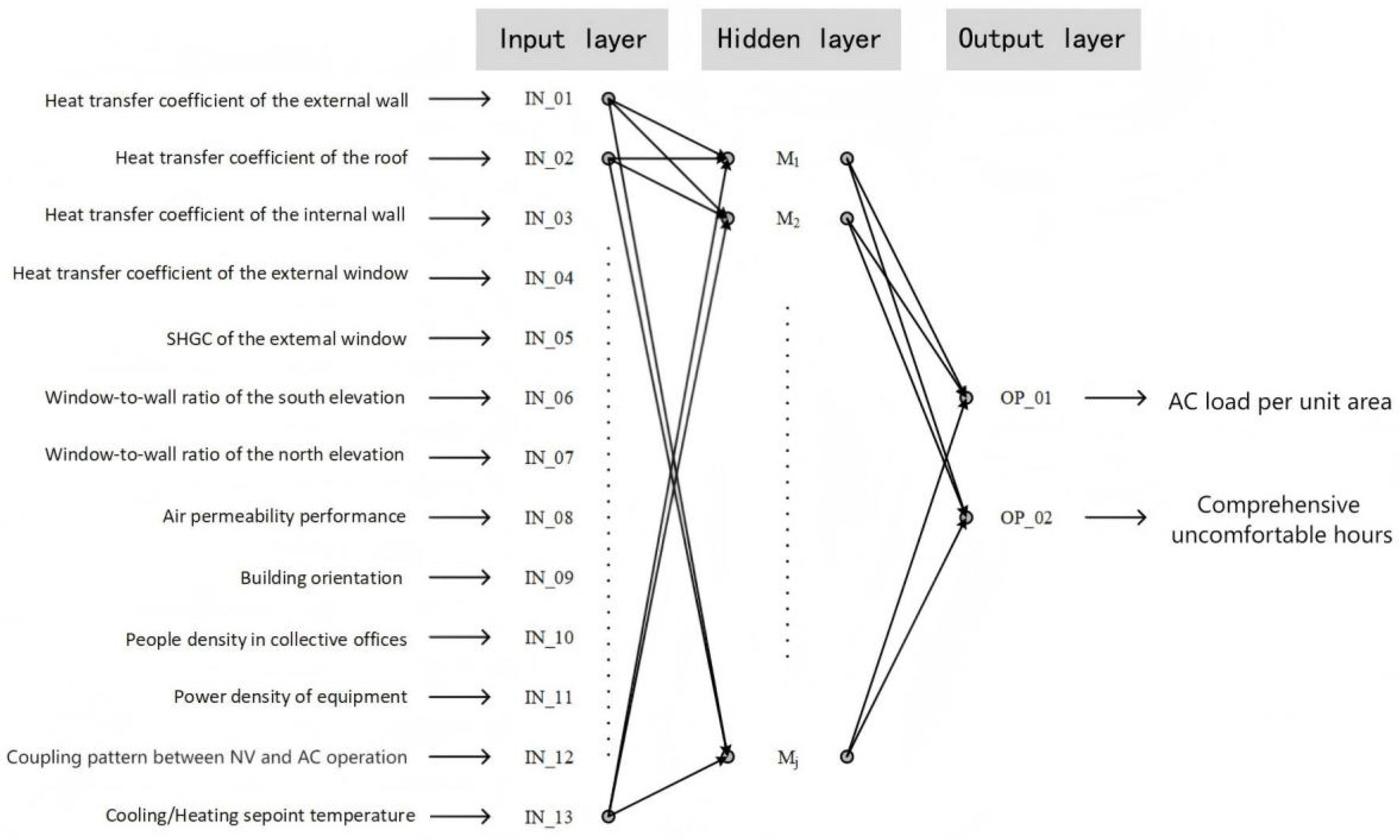
2.2. Construction of a Multi-Objective Rapid Prediction Model Based on ANN
2.3. Multi-Objective Optimisation Strategy Decision-Making Model Based on NSGA-II
2.3.1. Proposal of the Fitness Function
- (1)
- Construction of the Fitness Function
- (2)
- Range of Values for Decision Variables
- (3)
- Acquisition of Reference Values for Optimisation Objectives
- The reference standards of occupants’ behaviour are based on the typical fixed schedule of 08:00–17:00 and the stochastic behavioural schedules generated with the method described in Section 2.1.1. The method was established in the preliminary research [37];
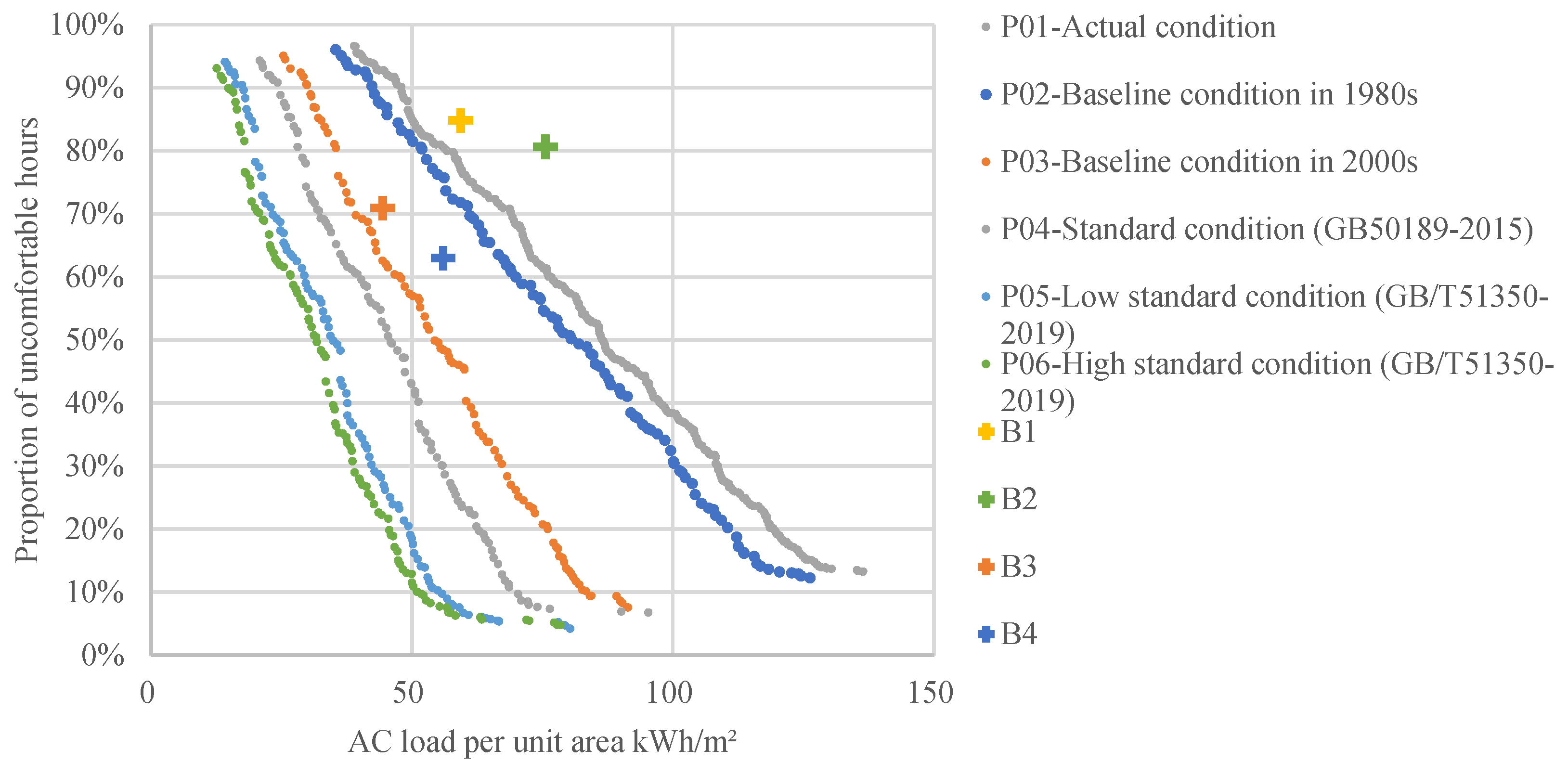
- Based on the two types of building envelope structure and HVAC behavioural patterns, the AC load per unit area and the comprehensive uncomfortable hours of the case building are worked out by EnergyPlus simulation and calculation. Equation (5) transforms the total uncomfortable hours into a proportion of those hours to enable comparative analysis. As shown in Table 6, the optimisation target for comparative analysis is set using four typical reference points: B1, B2, B3, and B4.whereis the proportion of uncomfortable hours;n is the number of air-conditioned rooms in the building;is the area of the ith room;is the simulated uncomfortable hours in the ith room;is the number of hours occupied by occupants in the ith room.
2.3.2. Algorithm Implementation of the Decision-Making Model Based on NSGA-II
- (1)
- Evaluation of target variables;
- (2)
- Control of the range of values of decision variables;
- (3)
- Control of the range of values of target variables;
- (4)
- Configuration of NSGA-II parameters.
3. Results
3.1. Construction and Calibration of the Multi-Objective Rapid Prediction Model
3.2. Construction of the Multi-Objective Optimisation Decision-Making Model
4. Discussion
4.1. Generation of Behavioural Optimisation Strategies Based on the Decision-Making Model
4.2. Generation of Integrated Optimisation Strategies Based on the Decision-Making Model
5. Conclusions
- (1)
- Take the case building as an example. A rapid prediction model for building air conditioning (AC) energy consumption and indoor thermal comfort was constructed based on a BP neural network. Using important influencing factors of the target variables as decision variables, the model efficiently and accurately predicts the AC load per unit area and the comprehensive uncomfortable hours for the case building under the various operating scenarios, providing data support for multi-objective optimisation decision-making.
- (2)
- A multi-objective optimisation decision-making model regarding AC energy consumption and indoor thermal comfort was constructed. Implementing the model generates passive optimisation strategies for the design phase, behavioural optimisation strategies for the operational phase, and integrated optimisation strategies for both phases of the case building. Furthermore, it can output corresponding strategy combinations based on predefined optimisation objectives, providing a scientific basis for building energy retrofitting and operational management.
- (3)
- Research was conducted on the application of multi-objective optimisation decision-making models, examining behavioural and integrated optimisation strategies under different operating conditions:
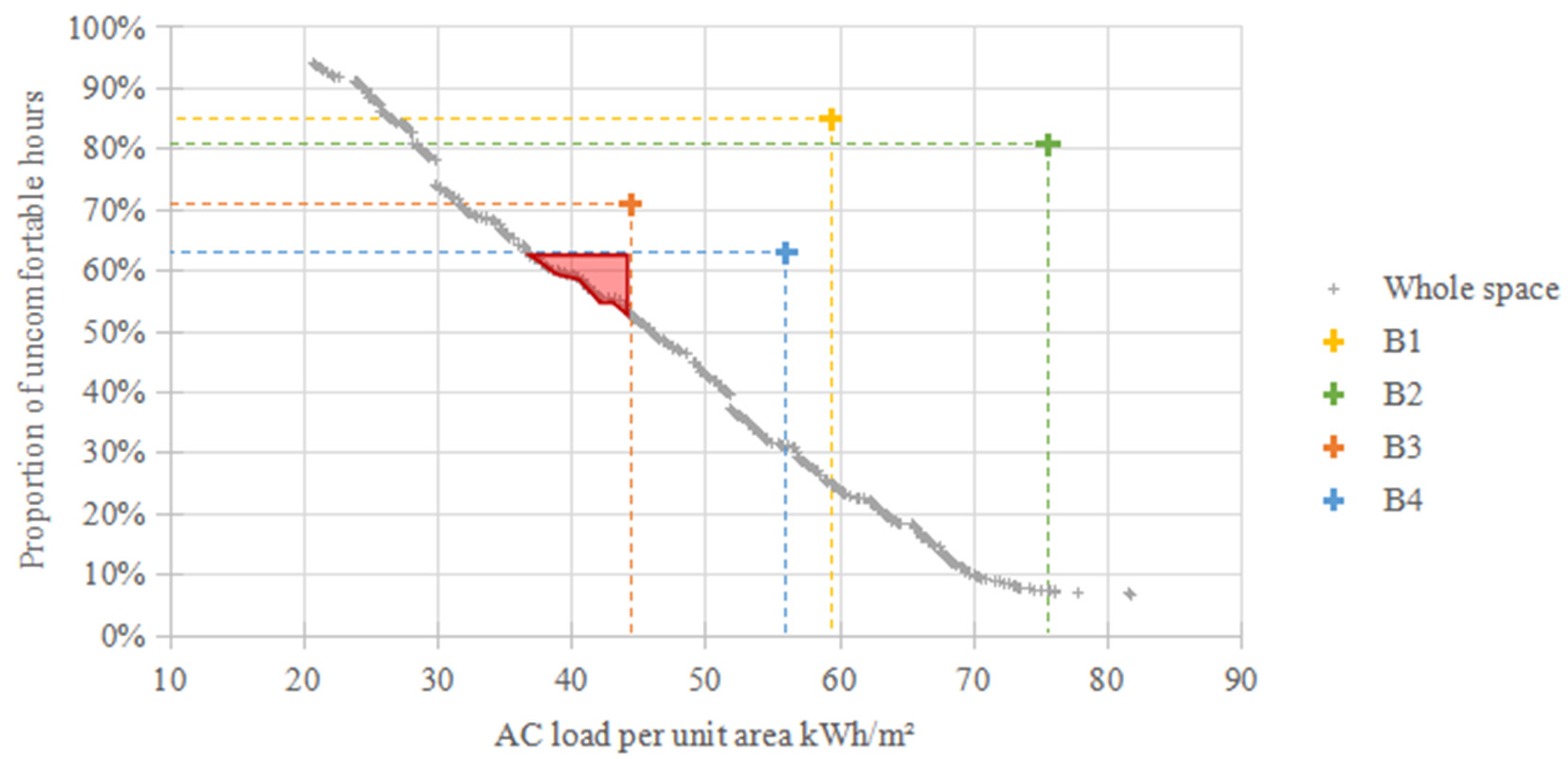
- The P04 operating condition, as outlined in the current Design standard for energy efficiency of public buildings, serves as a case study. Substantial AC energy savings and improvements in thermal comfort can be realised by adjusting the stage-based cooling/heating setpoint temperature and the coupling pattern between NV and AC operations. This has led to meeting the optimisation objectives for B1, B2, B3, and B4. Additionally, it has been demonstrated that reducing AC energy consumption to 40.7 kWh/m2 is possible while reducing the proportion of uncomfortable hours to 53%.
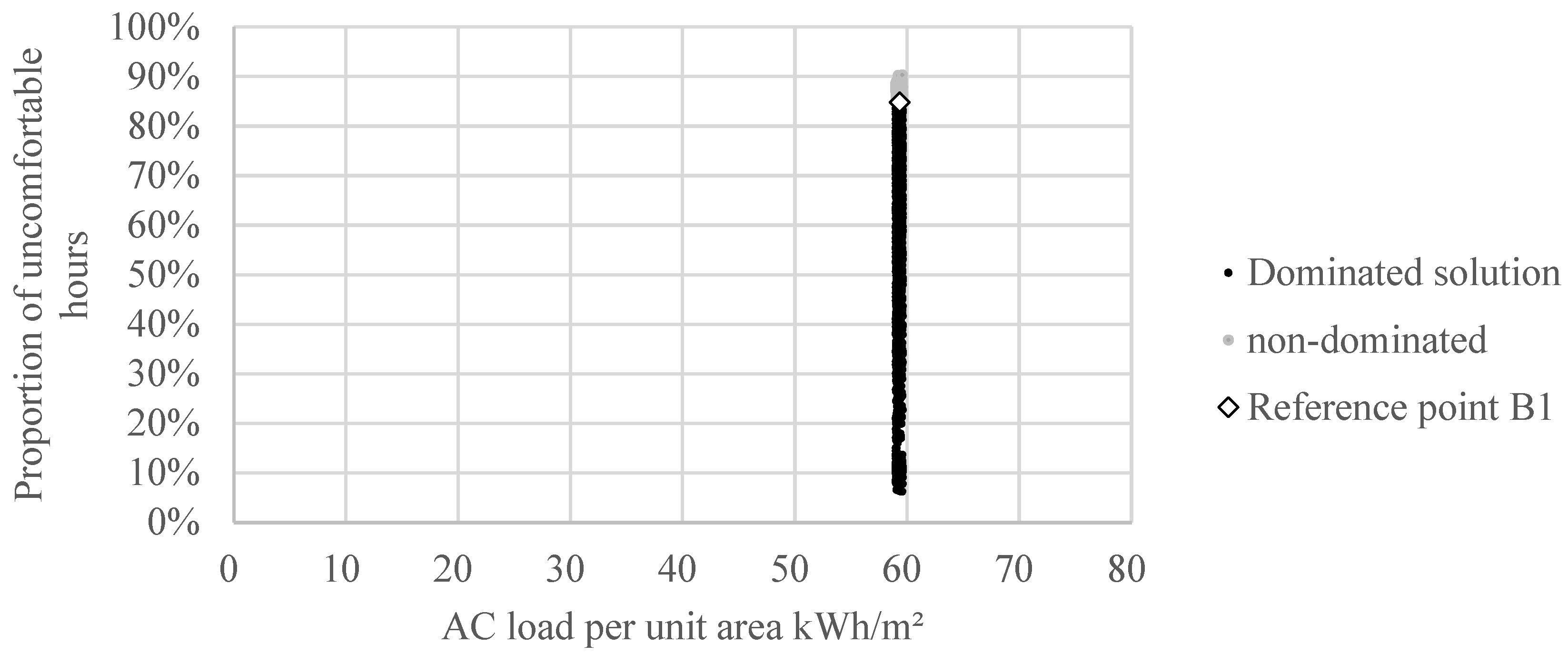
- Utilising B1 as the reference point, the multi-objective optimisation decision-making model regulates AC energy consumption limits. It combines passive and behavioural strategies to create integrated optimisation strategies for varying indoor thermal comfort levels. Consequently, the proportion of uncomfortable hours has been reduced to 6.23%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsinghua University, Building Energy Research Center. Annual Research Report on Building Energy Efficiency in China: Public Buildings; China Architecture & Building Press: Beijing, China, 2022. [Google Scholar]
- Tsinghua University, Building Energy Research Center. Annual Research Report on Building Energy Efficiency in China: Urban Residential Buildings; China Architecture & Building Press: Beijing, China, 2023. [Google Scholar]
- Dang, Y.C.; Yao, J. Multi-Objective Optimization Study of Residential Energy Consumption Based on Edh and the Stochastic Operation of Air Conditioning. J. Green Build. 2024, 19, 195–220. [Google Scholar] [CrossRef]
- Zhang, L.; Zhong, B. Partition-based building energy analysis and optimization of energy conservation. In Proceedings of the 1st International Conference on Computational Intelligence, Theory, Systems and Applications (CCITSA), Shanghai, China, 24–27 August 2015; pp. 171–176. [Google Scholar] [CrossRef]
- Ding, C.; Zhou, N. Using residential and office building archetypes for energy-efficiency solutions in an Urban Scale: A China Case Study. Energies 2020, 13, 3210. [Google Scholar] [CrossRef]
- Carlucci, S.; Pagliano, L. A review of indices for the long-term evaluation of general thermal comfort conditions in buildings. Energy Build. 2012, 53, 194–205. [Google Scholar] [CrossRef]
- Balbis-Morejón, M.; Rey-Hernández, J.M.; Amaris-Castilla, C.; Velasco-Gómez, E.; San José-Alonso, J.F.; Rey-Martínez, F.J. Experimental study and analysis of thermal comfort in a university campus building in tropical climate. Sustainability 2020, 12, 8886. [Google Scholar] [CrossRef]
- Tian, X.-Y.; Liu, W.-W.; Liu, J.-W.; Yu, B.; Zhang, J. Effects of personal heating on thermal comfort: A review. J. Cent. South Univ. 2022, 29, 2279–2300. [Google Scholar] [CrossRef]
- Shakeel, H.M.; Iram, S.; Hill, R.; Farid, H.M.A.; Sheikh-Akbari, A.; Saleem, F. A machine learning-based intelligent framework for predicting energy efficiency in next-generation residential buildings. Buildings 2025, 15, 1275. [Google Scholar] [CrossRef]
- Al-Tamimi, N. Passive design strategies for energy-efficient buildings in the Arabian desert. Front. Built Environ. 2022, 7, 805603. [Google Scholar] [CrossRef]
- Duan, Y.; Zhang, T.; Yang, Y.; Li, P.; Mo, W.; Jiao, Z.; Gao, W. A multi-objective approach to optimizing the geometry and envelope of rural dwellings for energy demand, thermal comfort, and daylight in cold regions of China: A case study of Shandong province. Energy Convers. Manag. 2024, 322, 119128. [Google Scholar] [CrossRef]
- Yaman, G.Ö. Determination of optimum passive design parameters for industrial buildings in different climate zones using an ANN–PSO energy-performance optimization model. Sustainability 2025, 17, 2357. [Google Scholar] [CrossRef]
- Xu, S.; Chen, Y.Z.; Liu, J.L.; Kang, J.; Gao, J.F.; Qin, Y.C.; Tan, W.J.; Li, G.M. Comprehensive improvement of energy efficiency and indoor environmental quality for university library atrium—A multi-objective fast optimization framework. Front. Archit. Res. 2025, 14, 449–470. [Google Scholar] [CrossRef]
- Hosamo, H.H.; Tingstveit, M.S.; Nielsen, H.K.; Svennevig, P.R.; Svidt, K. Multi-objective optimization of building energy consumption and thermal comfort based on integrated BIM framework with machine learning-NSGA II. Energy Build. 2022, 277, 112479. [Google Scholar] [CrossRef]
- Shao, T.; Zheng, W.X.; Zhang, K. Research on the establishment of rural house optimal design pattern in northwest cold region under multi-objective conditions. J. Therm. Sci. Technol. 2024, 23, 300–310. [Google Scholar] [CrossRef]
- Song, L.W. Performance optimization of high-rise residential buildings in cold regions considering energy consumption. Discov. Appl. Sci. 2025, 7, 105. [Google Scholar] [CrossRef]
- Wang, A.; Xiao, Y.; Liu, C.; Zhao, Y.; Sun, S. Multi-objective optimization of building energy consumption and thermal comfort based on SVR-NSGA-II. Case Stud. Therm. Eng. 2024, 50, 105368. [Google Scholar] [CrossRef]
- Liu, M.; Que, Y.F.; Yang, N.X.; Yan, C.Y.; Liu, Q.B. Research on Multi-Objective Optimization Design of University Student Center in China Based on Low Energy Consumption and Thermal Comfort. Energies 2024, 17, 2082. [Google Scholar] [CrossRef]
- Liu, X.B.; Wu, Y.Y.; Wu, H. Enhancing HVAC energy management through multi-zone occupant-centric approach: A multi-agent deep reinforcement learning solution. Energy Build. 2024, 303, 113770. [Google Scholar] [CrossRef]
- Li, W.; Koo, C.; Hong, T.; Oh, J.; Cha, S.H.; Wang, S.W. A novel operation approach for the energy efficiency improvement of the HVAC system in office spaces through real-time big data analytics. Renew. Sustain. Energy Rev. 2020, 127, 109885. [Google Scholar] [CrossRef]
- Ao, J.Y.; Du, C.Q.; Jing, M.Y.; Li, B.Z.; Chen, Z.Y. A method of integrating air-conditioning usage models into building simulations for predicting residential cooling energy consumption. Buildings 2024, 14, 2026. [Google Scholar] [CrossRef]
- Yao, J. Modelling and simulating occupant behaviour on air conditioning in residential buildings. Energy Build. 2018, 175, 1–10. [Google Scholar] [CrossRef]
- Virote, J.; Neves-Silva, R. Stochastic models for building energy prediction based on occupant behavior assessment. Energy Build. 2012, 53, 183–193. [Google Scholar] [CrossRef]
- Uddin, M.N.; Wei, H.-H.; Chi, H.L.; Ni, M. Influence of occupant behavior for building energy conservation: A systematic review study of diverse modeling and simulation approach. Buildings 2021, 11, 41. [Google Scholar] [CrossRef]
- Diao, L.; Sun, Y.; Chen, Z.; Chen, J. Modeling energy consumption in residential buildings: A bottom-up analysis based on occupant behavior pattern clustering and stochastic simulation. Energy Build. 2017, 147, 47–66. [Google Scholar] [CrossRef]
- Fabi, V.; Andersen, R.K.; Corgnati, S. Verification of stochastic behavioural models of occupants’ interactions with windows in residential buildings. Build. Environ. 2015, 94, 394–404. [Google Scholar] [CrossRef]
- Ren, X.; Yan, D.; Hong, T. Air-conditioning usage conditional probability model for residential buildings. Energy Build. 2020, 206, 109571. [Google Scholar] [CrossRef]
- Luo, M.H.; Jiang, K.Y.; Wang, J.L.; Feng, W.; Ma, L.; Shi, X.D.; Zhou, X. Data-driven thermal preference prediction model with embodied air-conditioning sensors and historical usage behaviors. Build. Environ. 2022, 220, 109269. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, H.; Pan, Y.; Zhang, X.; Fang, F. Research on simulation methodology of stochastic usage behavior of air conditioners in residential buildings by agent-based modeling. Build. Sci. 2017, 33, 37–44. [Google Scholar]
- Zhang, Z.C.; Yao, J.; Zheng, R.Y. Multi-objective optimization of building energy saving based on the randomness of energy-related occupant behavior. Sustainability 2024, 16, 1935. [Google Scholar] [CrossRef]
- Li, R.; Shari, Z.; Ab Kadir, M.Z.A. A Review of Multi-objective Optimization Research on Building Performance from the Perspective of Bibliometric Analysis. Energy Build. 2024, 11, e42480. [Google Scholar] [CrossRef]
- Jeong, B.; Kim, J.; Ma, Z.; Cooper, P.; de Dear, R. Identification of environmental and contextual driving factors of air-conditioning usage behaviour in Sydney residential buildings. Buildings 2021, 11, 122. [Google Scholar] [CrossRef]
- Azar, E.; O’Brien, W.; Carlucci, S.; Hong, T.; Sonta, A.; Kim, J.; Andargie, M.S.; Abuimara, T.; El Asmar, M.; Jain, R.K.; et al. Simulation-aided occupant-centric building design: A critical review of tools, methods, and applications. Energy Build. 2020, 224, 110292. [Google Scholar] [CrossRef]
- Hamed, M.M.; Alkhreasha, A.; Alshaer, A.; Olabi, A.G. Promoting sustainable development goals through energy-related behaviors of household occupants: Fostering sustainable energy solutions in developing countries. Renew. Sustain. Energy Rev. 2025, 213, 115511. [Google Scholar] [CrossRef]
- Haidar, N.; Tamani, N.; Ghamri-Doudane, Y.; Bouju, A. Towards a new graph-based occupant behavior modeling in smart buildings. In Proceedings of the 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1413–1418. [Google Scholar] [CrossRef]
- Xiang, J.; Liu, H.; Li, X.; Jones, P.; Perisoglou, E. Multi-objective optimization of ultra-low energy housing in the hot-summer cold-winter climate zone of China based on a probabilistic behavioral model. Buildings 2023, 13, 1172. [Google Scholar] [CrossRef]
- Wu, J.J.; Chen, S.Q.; Ying, X.Y.; Shu, J.B. Influencing Factors on Air Conditioning Energy Consumption of Naturally Ventilated Research Buildings Based on Actual HVAC Behaviours. Buildings 2023, 13, 2710. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 55-2017; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE): Atlanta, GA, USA, 2017.
- Feng, Y.; Li, Y. An Overview of Deep Learning Optimization Methods and Learning Rate Attenuation Methods. Hans J. Data Min. 2018, 8, 186–200. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- GB 50189-2015; Design Standard for Energy Efficiency of Public Buildings. China Architecture & Building Press: Beijing, China, 2015.
- GB/T 51350-2019; Technical Standard for Nearly Zero Energy Buildings. China Standards Press: Beijing, China, 2019.

| Characteristic Stages of AC Usage | Duration Date | |
|---|---|---|
| Cooling season | Mid-summer | 21 June~10 September |
| Early and late summer | 11 May~20 June 11 September~30 September | |
| Late spring and early autumn | 21 April~10 May 1 October~20 October | |
| Transitional period | 11 April~20 April 21 October~31 October | |
| Heating season | Early spring and late autumn | 1 November~20 November 21 March~10 April |
| Early and late winter | 11 February~20 March 21 November~10 December | |
| Mid-winter | 11 December~10 February | |
| Coupling Pattern | Feature Description |
|---|---|
| M0 | A default pattern, reflecting the actual operational characteristics of AC and NV operation. |
| M1 | Fixed ventilation in the morning: From 8:00 to 9:00, regardless of whether the air conditioner is on or off, the exterior windows are opened for a fixed period |
| M2 | Fixed ventilation overnight: From 17:00 to 8:00 the following day, regardless of whether the air conditioner is on or off, the exterior windows are open for a fixed period. |
| M3 | Opposition all day: The opening status of exterior windows and air conditioning is always in opposition between 0:00 and 24:00. |
| M4 | Opposition overnight: From 17:00 to 8:00 the following day, the opening status of exterior windows and air conditioning is always in opposition; from 8:00 to 17:00, regardless of whether the air conditioner is on or off, the exterior windows remain closed. |
| Code | Decision Variable | Unit | Relative Importance of AC Energy Consumption | Relative Importance of Thermal Comfort |
|---|---|---|---|---|
| 1 | Cooling setpoint temperature | °C | 100.0% | 100.0% |
| 2 | Air permeability performance | ach | 67.0% | 4.7% |
| 3 | Heating setpoint temperature | °C | 46.6% | 33.7% |
| 4 | People density in collective offices | m2/person | 17.3% | 0.3% |
| 5 | Coupling pattern between NV and AC operation | - | 7.8% | 0.9% |
| 6 | SHGC of the external window | - | 4.5% | 2.8% |
| 7 | Power density of equipment | W/person | 2.9% | 1.0% |
| 8 | Heat transfer coefficient of the external wall | W/(m2·K) | 2.5% | 1.4% |
| 9 | Heat transfer coefficient of the external window | W/(m2·K) | 1.8% | 0.8% |
| 10 | Heat transfer coefficient of the roof | W/(m2·K) | 1.5% | 1.3% |
| 11 | Window-to-wall ratio of the south elevation | - | 1.3% | 0.7% |
| 12 | Window-to-wall ratio of the north elevation | - | 1.2% | 0.5% |
| 13 | Heat transfer coefficient of the internal wall | W/(m2·K) | 0.9% | 0.9% |
| 14 | Building orientation | ° | 0.8% | 0.7% |
| Characteristic Stages of AC Usage | Code | Input | AC Load per Unit Area | Comprehensive Uncomfortable Hours | ||
|---|---|---|---|---|---|---|
| Output | Function Mapping Relationship | Output | Function Mapping Relationship | |||
| Late spring and early autumn | C1 | xi,C1, i ∈ [1, 13] | y1,C1 | y1,C1 = FC1(x1,C1,x2,C1,…,x13,C1) | y2,C1 | y2,C1 = PC1(x1,C1,x2,C1,…,x13,C1) |
| Early and late summer | C2 | xi,C2, i ∈ [1, 13] | y1,C2 | y1,C2 = FC2(x1,C2,x2,C2,…,x13,C2) | y2,C2 | y2,C2 = PC2(x1,C2,x2,C2,…,x13,C2) |
| Mid-summer | C3 | xi,C3, i ∈ [1, 13] | y1,C3 | y1,C3 = FC3(x1,C3,x2,C3,…,x13,C3) | y2,C3 | y2,C3 = PC3(x1,C3,x2,C3,…,x13,C3) |
| Early spring and late autumn | H1 | xi,H1, i ∈ [1, 13] | y1,H1 | y1,H1 = FH1(x1,H1,x2,H1,…,x13,H1) | y2,H1 | y2,H1 = PH1(x1,H1,x2,H1,…,x13,H1) |
| Early and late winter | H2 | xi,H2, i ∈ [1, 13] | y1,H2 | y1,H2 = FH2(x1,H2,x2,H2,…,x13,H2) | y2,H2 | y2,H2 = PH2(x1,H2,x2,H2,…,x13,H2) |
| Mid-winter | H3 | xi,H3, i ∈ [1, 13] | y1,H3 | y1,H3 = FH3(x1,H3,x2,H3,…,x13,H3) | y2,H3 | y2,H3 = PH3(x1,H3,x2,H3,…,x13,H3) |
| Type | ID | Decision Variable | Unit | Range of Values |
|---|---|---|---|---|
| Building design scheme | IN_01 | Heat transfer coefficient of the external wall | W/(m2·K) | [0.15, 2.50] |
| IN_02 | Heat transfer coefficient of the roof | W/(m2·K) | [0.15, 3.00] | |
| IN_03 | Heat transfer coefficient of the internal wall | W/(m2·K) | [1.00, 5.00] | |
| IN_04 | Heat transfer coefficient of the external window | W/(m2·K) | [2.20, 6.40] | |
| IN_05 | SHGC of the external window | - | [0.15, 1.00] | |
| IN_06 | Window-to-wall ratio of the south elevation | - | {0.4} | |
| IN_07 | Window-to-wall ratio of the north elevation | - | {0.4} | |
| IN_08 | Air permeability performance | ach | [0.1, 0.8] | |
| IN_09 | Building orientation | ° | {0} | |
| Internal disturbance elements | IN_10 | People density in collective offices | m2/person | {10} |
| IN_11 | Power density of equipment | W/person | {150} | |
| Occupants’ adaptive behaviours | IN_12 | Coupling pattern between NV and AC operation | - | {M0, M1, M2, M3, M4} |
| IN_13 | Cooling/heating setpoint temperature | °C | [18, 30] |
| Reference Point | Reference Standard for Thermal Performance of Building Envelopes | HVAC Behavioural Pattern | AC Load per Unit Area (kWh/m2) | Proportion of Uncomfortable Hours |
|---|---|---|---|---|
| B1 | Design standard for energy efficiency of public buildings (GB 50189-2015) | Stochastic behavioural schedule | 59.326 | 84.82% |
| B2 | Fixed schedule | 75.536 | 80.65% | |
| B3 | Technical standard for nearly zero energy buildings (GB/T 51350-2019) | Stochastic behavioural schedule | 44.366 | 70.93% |
| B4 | Fixed schedule | 55.942 | 63.00% |
| Code of the Prediction Model | Characteristic Stages of AC Usage | Hidden Layer Nodes | Number of Iterations | Linear Fitting of the Predicted and the Simulated Results | |
|---|---|---|---|---|---|
| AC load per unit area | Comprehensive uncomfortable hours | ||||
| C1 | Late spring and early autumn | 13 | 1900 | 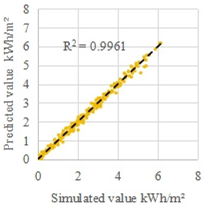 | 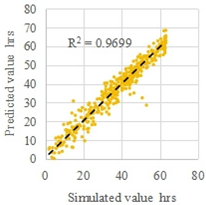 |
| MRE | 4.1% | 6.9% | |||
| C2 | Early and late summer | 9 | 1000 | 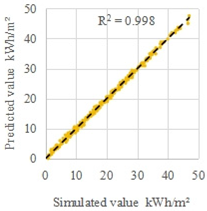 | 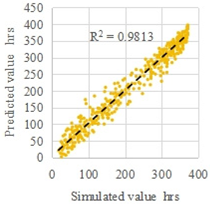 |
| MRE | 3.1% | 8.1% | |||
| C3 | Mid-summer | 11 | 2000 | 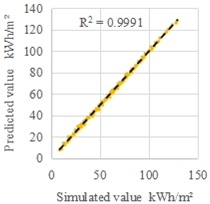 | 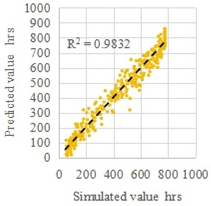 |
| MRE | 1.1% | 7.9% | |||
| H1 | Early spring and late autumn | 10 | 1610 | 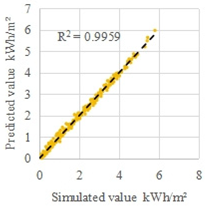 | 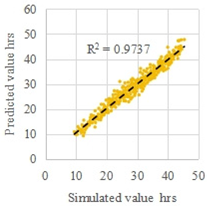 |
| MRE | 4.4% | 4.0% | |||
| H2 | Early and late winter | 11 | 1000 | 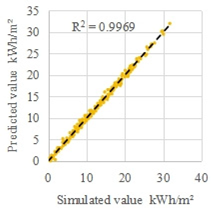 | 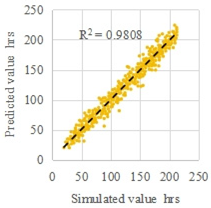 |
| MRE | 4.3% | 6.1% | |||
| H3 | Mid-winter | 10 | 1850 |  |  |
| MRE | 4.0% | 9.7% | |||
| Type | Decision Variable | Code | Unit | Range of Values | |
|---|---|---|---|---|---|
| For Behavioural Optimisation | For Integrated Optimisation | ||||
| Building design scheme | Heat transfer coefficient of the external wall | IN_01 | W/(m2·K) | Fixed values under different operating conditions | [0.15, 2.50] |
| Heat transfer coefficient of the roof | IN_02 | W/(m2·K) | [0.15, 3.00] | ||
| Heat transfer coefficient of the internal wall | IN_03 | W/(m2·K) | [1.00, 5.00] | ||
| Heat transfer coefficient of the external window | IN_04 | W/(m2·K) | [2.20, 6.40] | ||
| SHCG of the external window | IN_05 | - | [0.15, 1.00] | ||
| Window-to-wall ratio of the south elevation | IN_06 | - | {0.4} | {0.4} | |
| Window-to-wall ratio of the north elevation | IN_07 | - | {0.4} | {0.4} | |
| Air permeability performance | IN_08 | ach | Fixed values under different operating conditions | [0.1, 0.8] | |
| Building orientation (northwards deflection) | IN_09 | ° | {0} | {0} | |
| Internal disturbance elements | People density in collective offices | IN_09 | m2/person | {10} | {10} |
| Power density of equipment | IN_10 | W/person | {150} | {150} | |
| Adaptive behaviours | Coupling pattern between NV and AC operation | IN_12 | - | {M0, M1, M2, M3, M4} | {M0, M1, M2, M3, M4} |
| Cooling setpoint temperature | IN_13 | °C | [18, 30] | [18, 30] | |
| Heating setpoint temperature | °C | [18, 30] | [18, 30] | ||
| Building Design Parameters | IN_01 | IN_02 | IN_03 | IN_04 | IN_05 | IN_08 | |
|---|---|---|---|---|---|---|---|
| Heat Transfer Coefficient [W/(m2·K)] | SHGC of the External Window | Air Permeability (ach) | |||||
| Code | Operating Condition | External Wall | Roof | Internal Wall | External Window | ||
| P01 | Actual condition of the case building | 2.42 | 2.98 | 3.93 | 5.78 | 0.819 | 0.7 |
| P02 | Baseline condition of typical buildings in the 1980s | 2.0 | 1.5 | 2.0 | 6.4 | 0.8 | 0.8 |
| P03 | Baseline condition of typical buildings in the 2000s | 1.0 | 0.7 | 2.0 | 3.0 | 0.5 | 0.5 |
| P04 | Standard condition from GB 50189-2015 | 0.8 | 0.5 | 2.0 | 2.6 | 0.4 | 0.3 |
| P05 | Low standard condition from GB/T 51350-2019 | 0.4 | 0.35 | 2.0 | 2.2 | 0.15 | 0.1 |
| P06 | High standard condition from GB/T 51350-2019 | 0.15 | 0.15 | 2.0 | 2.2 | 0.15 | 0.1 |
| Parameter | Reference Point | Reference Value | Optimisation Potential Compared with the Reference Point | |||||
|---|---|---|---|---|---|---|---|---|
| P01 | P02 | P03 | P04 | P05 | P06 | |||
| AC load per unit area | B1 | 59.326 kWh/m2 | 52.86% | 40.30% | 56.75% | 34.06% | 76.22% | 78.85% |
| B2 | 75.536 kWh/m2 | 62.97% | 53.11% | 66.03% | 48.21% | 81.32% | 83.39% | |
| B3 | 44.366 kWh/m2 | 36.96% | 20.17% | 42.17% | 11.83% | 68.20% | 71.72% | |
| B4 | 55.942 kWh/m2 | 50.00% | 36.68% | 54.13% | 30.07% | 74.78% | 77.57% | |
| Proportion of uncomfortable hours | B1 | 84.82% | 92.01% | 85.58% | 90.98% | 84.27% | 95.01% | 94.29% |
| B2 | 80.65% | 91.59% | 84.84% | 90.51% | 83.46% | 94.76% | 94.00% | |
| B3 | 70.93% | 90.44% | 82.76% | 89.21% | 81.19% | 94.04% | 93.18% | |
| B4 | 63.00% | 89.24% | 80.59% | 87.86% | 78.83% | 93.29% | 92.32% | |
| Optimisation Objective | Optimal Behavioural Strategy: Cooling/Heating Setpoint Temperature (°C)|Coupling Pattern Between NV and AC Operation | Reference Point Dominance (“√” for Dominated, “×” for Non-Dominated) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proportion of Uncomfortable Hours | AC Load per Unit Area (kWh/m2) | H1 | H2 | H3 | C1 | C2 | C3 | B1 | B2 | B3 | B4 |
| 10% | 69.72 | 24|M4 | 25|M3 | 25|M4 | 26|M3 | 25|M4 | 24|M3 | × | × | × | √ |
| 20% | 63.28 | 19|M1 | 18|M4 | 25|M4 | 26|M3 | 25|M4 | 24|M4 | × | × | × | √ |
| 30% | 56.76 | 23|M1 | 23|M4 | 24|M4 | 26|M3 | 30|M2 | 24|M3 | √ | √ | × | × |
| 40% | 51.45 | 19|M4 | 18|M4 | 25|M4 | 25|M3 | 30|M2 | 25|M4 | √ | √ | √ | √ |
| 50% | 45.99 | 19|M4 | 24|M4 | 25|M4 | 27|M4 | 25|M4 | 30|M2 | √ | √ | × | √ |
| 60% | 38.62 | 24|M4 | 25|M3 | 25|M4 | 25|M0 | 30|M2 | 30|M2 | √ | √ | √ | √ |
| 70% | 31.84 | 19|M3 | 18|M0 | 25|M4 | 26|M3 | 30|M2 | 30|M2 | √ | √ | √ | × |
| 80% | 28.52 | 19|M4 | 18|M3 | 23|M4 | 26|M3 | 30|M2 | 30|M2 | √ | √ | × | × |
| 90% | 24.38 | 24|M4 | 25|M3 | 25|M4 | 26|M3 | 25|M4 | 24|M3 | × | × | × | × |
| Optimisation Objective | Behavioural Optimisation Strategy: Cooling/Heating Setpoint Temperature (°C)|Coupling Pattern Between NV and AC Operation | Reference Point Dominance (“√” for Dominated) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Proportion of Uncomfortable Hours | AC Load per Unit Area (kWh/m2) | H1 | H2 | H3 | C1 | C2 | C3 | B1 | B2 | B3 | B4 |
| 53% | 44.32 | 19|M1 | 24|M3 | 24|M4 | 27|M0 | 25|M4 | 30|M2 | √ | √ | √ | √ |
| 55% | 44.23 | 20|M1 | 22|M3 | 25|M4 | 26|M0 | 25|M3 | 30|M2 | √ | √ | √ | √ |
| 57% | 43.48 | 21|M2 | 18|M0 | 18|M0 | 27|M1 | 30|M2 | 24|M3 | √ | √ | √ | √ |
| 60% | 44.05 | 20|M0 | 18|M0 | 18|M3 | 29|M1 | 30|M4 | 24|M2 | √ | √ | √ | √ |
| 62% | 40.7 | 22|M1 | 20|M3 | 25|M4 | 29|M2 | 26|M4 | 30|M2 | √ | √ | √ | √ |
| Operating Condition | Numerical Distribution of the Cooling/Heating Setpoint Temperature | ||
|---|---|---|---|
| Heating |  | 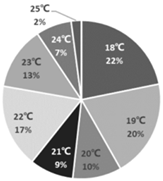 | 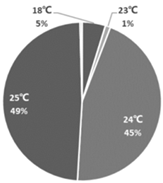 |
| H1: Early spring and late autumn | H2: Early and late winter | H3: Mid-winter | |
| Cooling | 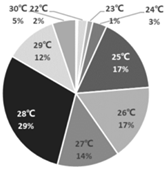 | 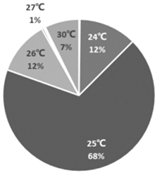 | 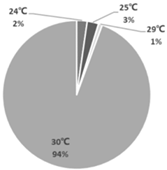 |
| C1: Late spring and early autumn | C2: Early and late summer | C3: Mid-summer | |
| Operating Condition | Numerical Distribution of the Coupling Pattern Between NV and AC Operation | ||
|---|---|---|---|
| Heating | 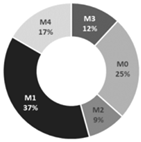 | 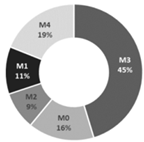 | 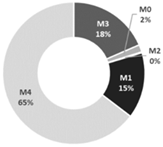 |
| H1: Early spring and late autumn | H2: Early and late winter | H3: Mid-winter | |
| Cooling | 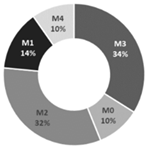 | 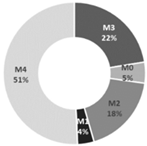 | 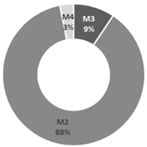 |
| C1: Late spring and early autumn | C2: Early and late summer | C3: Mid-summer | |
| Proportion of Uncomfortable Hours | Integrated Optimisation Strategy | Behavioural Optimisation Strategy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Heat Transfer Coefficient [W/(m2·K)] | SHGC of the External Window | Air Permeability (ach) | Cooling/Heating Setpoint Temperature (°C)|Coupling Pattern Between NV and AC Operation | |||||||||
| External Wall | Roof | Internal Wall | External Window | H1 | H2 | H3 | C1 | C2 | C3 | |||
| 6.23% | 0.15 | 0.15 | 1.06 | 2.2 | 0.33 | 0.1 | 24|M0 | 24|M4 | 24|M2 | 25|M0 | 24|M1 | 24|M1 |
| 10.00% | 0.15 | 0.31 | 2.81 | 2.85 | 0.29 | 0.12 | 26|M3 | 25|M1 | 24|M0 | 26|M3 | 25|M4 | 24|M1 |
| 20.00% | 0.36 | 0.31 | 3.37 | 2.77 | 0.29 | 0.11 | 27|M2 | 22|M2 | 24|M0 | 27|M0 | 25|M2 | 24|M1 |
| 30.00% | 0.41 | 0.51 | 4.24 | 2.4 | 0.22 | 0.18 | 27|M3 | 21|M1 | 24|M4 | 20|M3 | 25|M0 | 24|M1 |
| 40.00% | 0.72 | 0.48 | 3.88 | 3.94 | 0.53 | 0.1 | 29|M0 | 22|M4 | 19|M0 | 27|M4 | 24|M0 | 24|M2 |
| 50.00% | 1.6 | 0.49 | 1.06 | 3.34 | 0.59 | 0.29 | 29|M1 | 25|M4 | 18|M0 | 26|M1 | 29|M4 | 24|M4 |
| 60.00% | 1.69 | 0.67 | 3.27 | 3.11 | 0.93 | 0.26 | 20|M0 | 23|M1 | 18|M0 | 27|M0 | 29|M2 | 24|M2 |
| 70.00% | 0.42 | 1.11 | 1.2 | 3.68 | 0.25 | 0.59 | 28|M0 | 19|M2 | 22|M1 | 23|M3 | 29|M2 | 25|M2 |
| 80.00% | 0.91 | 0.69 | 1.28 | 3.78 | 0.62 | 0.53 | 24|M4 | 18|M1 | 21|M3 | 25|M4 | 26|M3 | 26|M3 |
| 84.82% | 1.38 | 1.61 | 4.45 | 3.1 | 0.47 | 0.15 | 28|M1 | 20|M2 | 29|M4 | 25|M4 | 28|M4 | 30|M1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Qiu, R.; Ying, X.; Chen, S.; Zhao, X. Optimising Behavioural Control Based on Actual HVAC Use in Naturally Ventilated Buildings. Energies 2025, 18, 6130. https://doi.org/10.3390/en18236130
Wu J, Qiu R, Ying X, Chen S, Zhao X. Optimising Behavioural Control Based on Actual HVAC Use in Naturally Ventilated Buildings. Energies. 2025; 18(23):6130. https://doi.org/10.3390/en18236130
Chicago/Turabian StyleWu, Jiajing, Rongxin Qiu, Xiaoyu Ying, Shuqin Chen, and Xueyuan Zhao. 2025. "Optimising Behavioural Control Based on Actual HVAC Use in Naturally Ventilated Buildings" Energies 18, no. 23: 6130. https://doi.org/10.3390/en18236130
APA StyleWu, J., Qiu, R., Ying, X., Chen, S., & Zhao, X. (2025). Optimising Behavioural Control Based on Actual HVAC Use in Naturally Ventilated Buildings. Energies, 18(23), 6130. https://doi.org/10.3390/en18236130






