Predictive Control Structure for a Two-Mass Drive System with a Two-Layer Observer
Abstract
1. Introduction
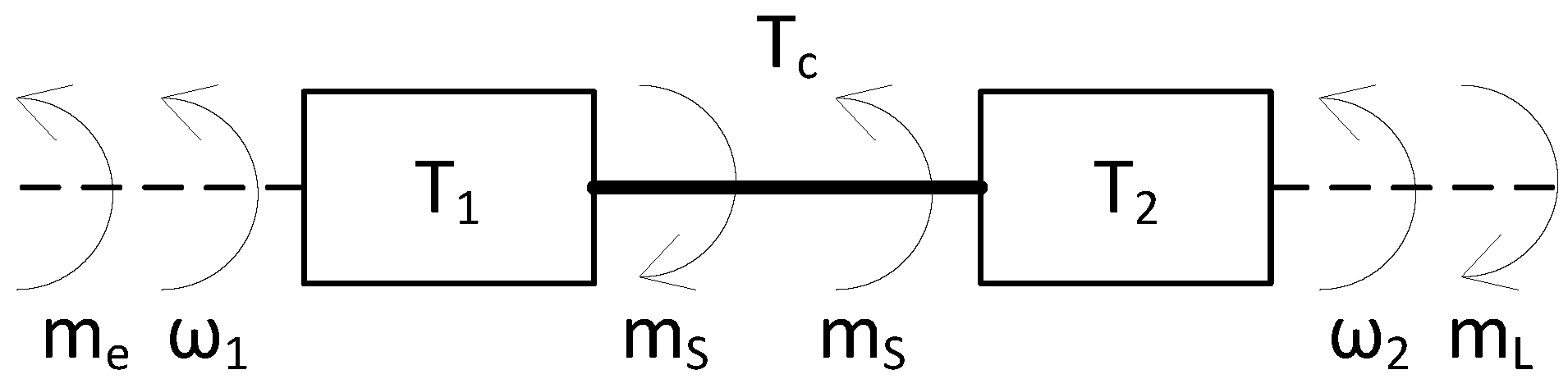
2. Mathematical Model of the Two-Mass System
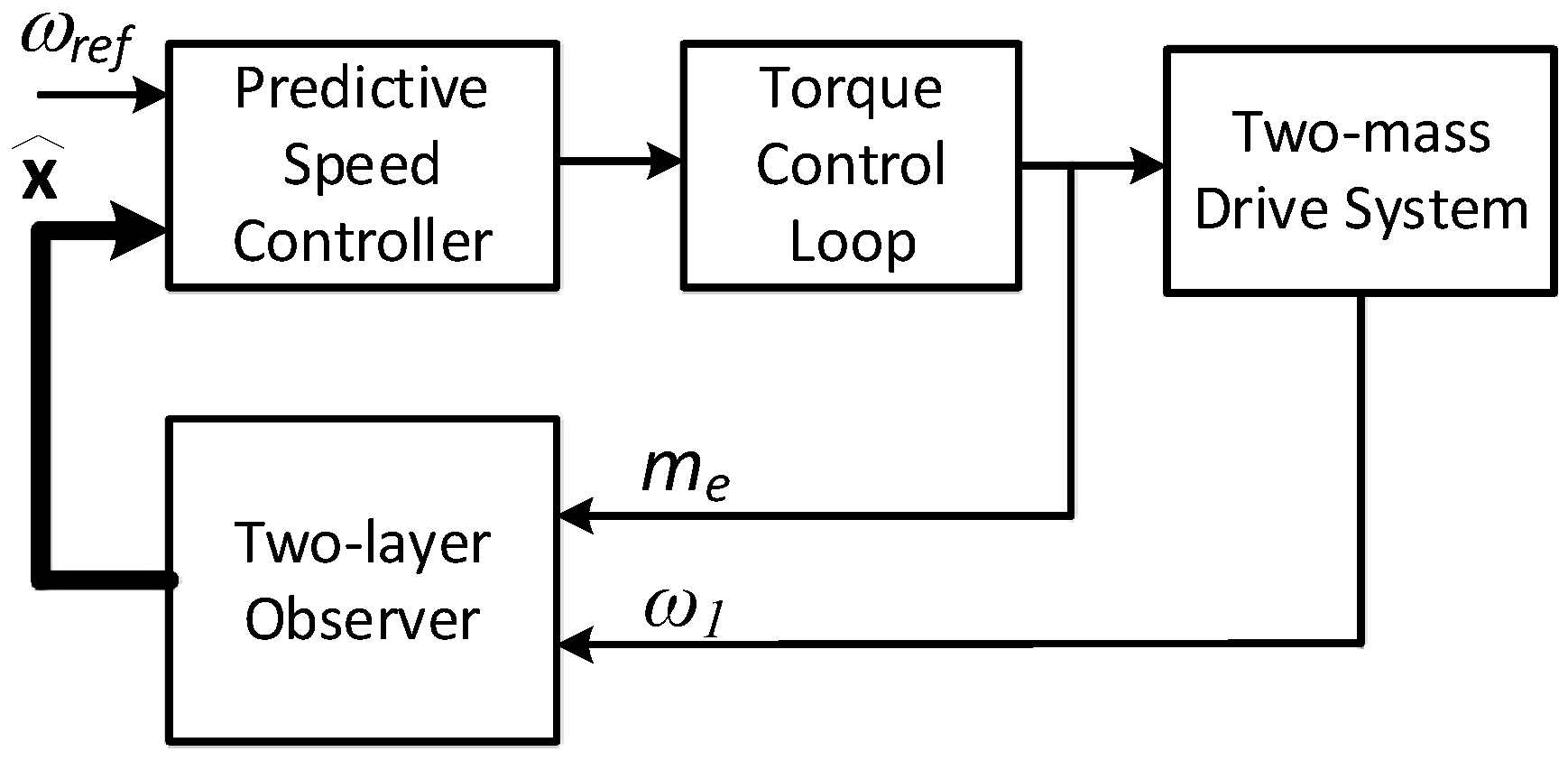
3. Control Structure with Predictive Speed Controller
4. Luenberger Observer for the Two-Mass System
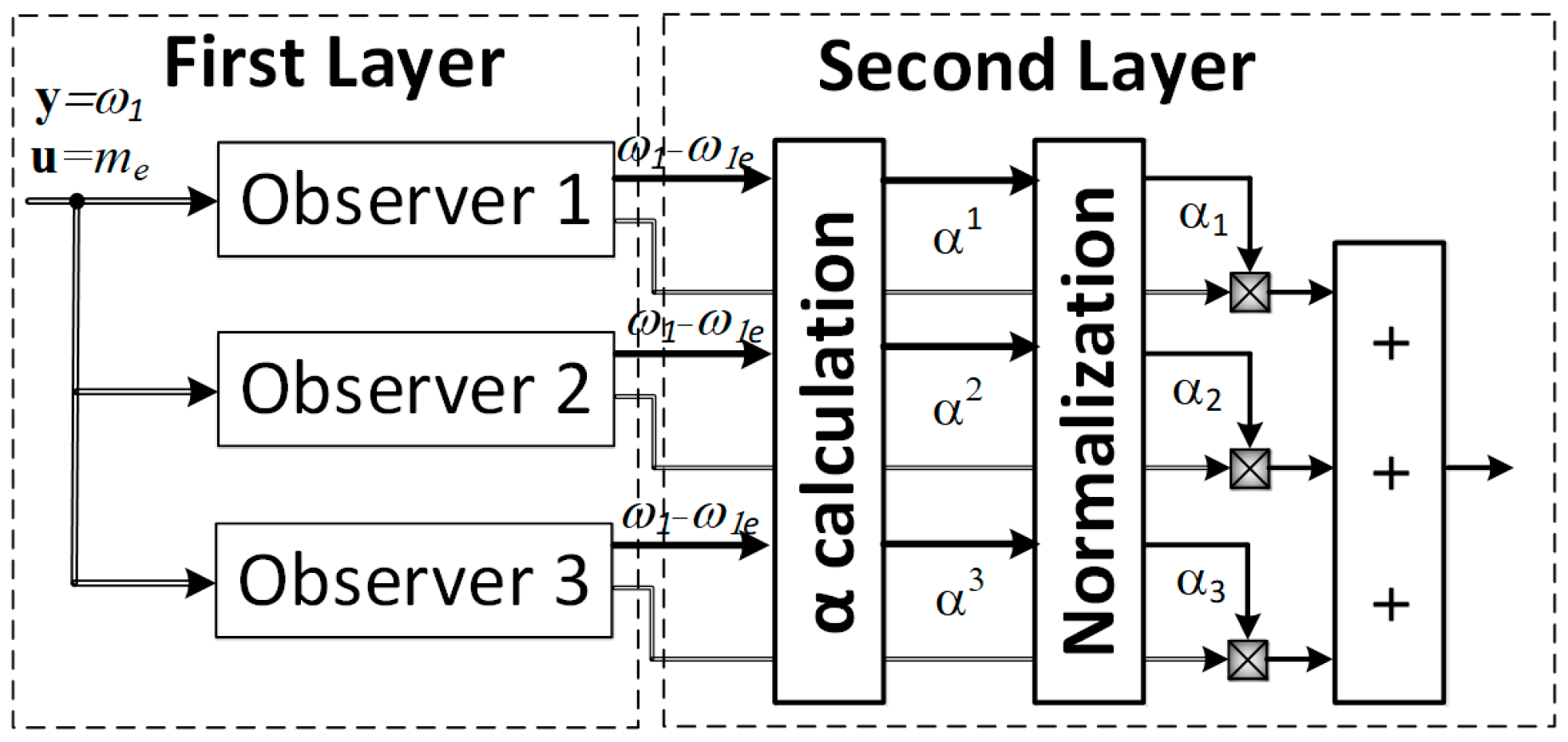
5. Two-Layer Observer
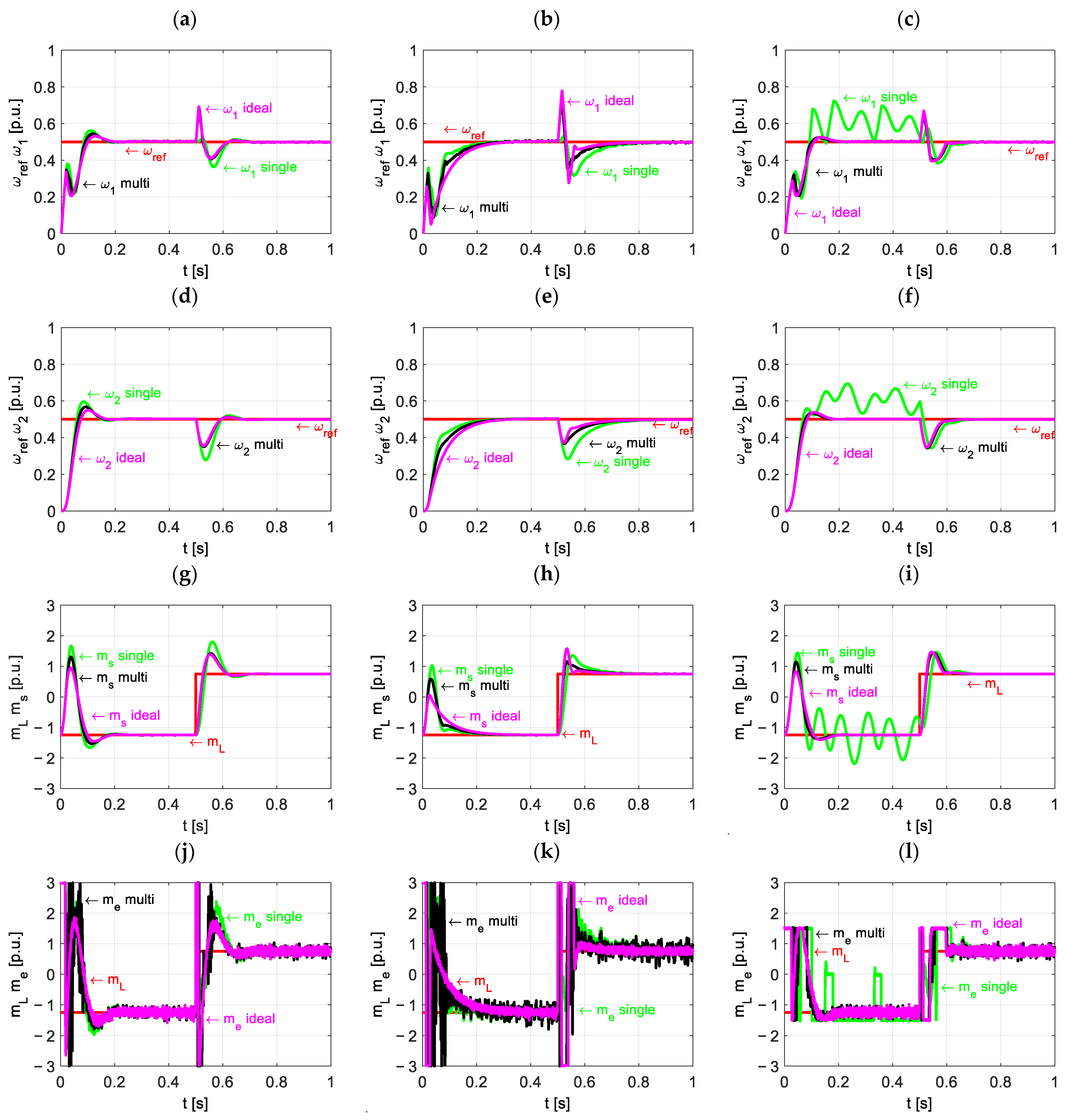
6. Results
7. Conclusions
- -
- To reach its full potential, predictive control needs a high-quality reproduction of state variables by algorithms if it is impossible to measure them.
- -
- Significant improvements in estimation dynamics, especially in cases of unknown initial state of the control object, can be achieved with the help of a two-layer observer. In the simulation studies conducted, the system with a regulator and two-layer observer obtained similar results to the model with a regulator and direct feedback from the plant.
- -
- The use of a predictive controller with a two-observer for a two-mass drive system allows the imposition of stricter torsional torque limits while maintaining a better control quality than when using a classic observer. This is possible thanks to better estimation quality.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chinoracky, R.; Stalmasekova, N.; Corejova, T. Trends in the Field of Electromobility—From the Perspective of Market Characteristics and Value-Added Services: Literature Review. Energies 2022, 15, 6144. [Google Scholar] [CrossRef]
- Adamczyk, J.; Dzikuć, M.; Dylewski, R.; Varese, E. Assessment of selected environmental and economic factors for the development of electro-mobility in Poland. Transportation 2024, 51, 2199–2223. [Google Scholar] [CrossRef]
- Kaczmarczyk, G.; Stanislawski, R.; Szrek, J.; Kaminski, M. Adaptive Sliding Mode Control Based on a Radial Neural Model Applied for an Electric Drive with an Elastic Shaft. Energies 2024, 17, 833. [Google Scholar] [CrossRef]
- Żychlewicz, M.; Kamiński, M. The LSTM Models with Gated Recurrent Unit Applied for Shaft Torque Estimation of Two-Mass System. In Proceedings of the 2025 29th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2025; pp. 295–300. [Google Scholar] [CrossRef]
- Derugo, P. Transfer Learning for Fuzzy Control of Two-Mass Drive System Using State Variables Feedback. In Proceedings of the 2023 10th International Conference on Electrical, Electronic and Computing Engineering (IcETRAN), East Sarajevo, Bosnia and Herzegovina, 5–8 June 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Kahsay, A.H.; Derugo, P.; Szabat, K.; Katsura, S. Design of Disturbance Observer-Based Robust Speed Control Structure for Two-Mass Drive System with the Help of Birch Optimization Algorithm. Energies 2025, 18, 1914. [Google Scholar] [CrossRef]
- Mohammed, A.M.; Al-Samarraie, S.A.; Jaber, A. Design of a robust controller for a gearbox connected two-mass system based on a hybrid model. FME Trans. 2022, 50, 79–89. [Google Scholar] [CrossRef]
- Kaczmarczyk, G.; Malarczyk, M.; Stanisławski, R.; Kamiński, M. Auto-Identification of Two-Mass System Parameters with Reinforcement Learning. In Proceedings of the 2025 29th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2025; pp. 289–294. [Google Scholar] [CrossRef]
- Gorla, A.; Serkies, P. Comparative Study of Analytical Model Predictive Control and State Feedback Control for Active Vibration Suppression of Two-Mass Drive. Actuators 2025, 14, 254. [Google Scholar] [CrossRef]
- Szabat, K.; Pajchrowski, T.; Tarczewski, T. Modern Electrical Drives: Trends, Problems, and Challenges. Energies 2022, 15, 160. [Google Scholar] [CrossRef]
- Kaminski, M.; Tarczewski, T. Neural Network Applications in Electrical Drives—Trends in Control, Estimation, Diagnostics, and Construction. Energies 2023, 16, 4441. [Google Scholar] [CrossRef]
- Niu, F.; Chao, X.; Zhang, Y.; Chen, J.; Li, S. MEKF-Tuned Full-State Feedback for Two-Mass Resonance Suppression. In Proceedings of the 2025 IEEE 12th International Symposium on Sensorless Control for Electrical Drives (SLED), Harbin, China, 15–17 August 2025; pp. 1–7. [Google Scholar] [CrossRef]
- Vukojičić, S.; Ristić, L.; Kvaščev, G. Industrial application of neural network-optimized model predictive control for a two mass resonant mechanical system. Electr. Eng. 2025, 107, 14121–14136. [Google Scholar] [CrossRef]
- Derugo, P.; Szabat, K. Adaptive neuro-fuzzy PID controller for nonlinear drive system. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 792–807. [Google Scholar] [CrossRef]
- Dodds, S.J.; Szabat, K. Forced Dynamic Control of Electric Drives with Vibration Modes in the Mechanical Load. In Proceedings of the IEEE 2006 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1245–1250. [Google Scholar] [CrossRef]
- Jastrzębski, M.; Kabziński, J. Adaptive Control of Two-Mass System with Nonlinear Stiffness and Backlash. In Proceedings of the 2025 29th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2025; pp. 327–332. [Google Scholar] [CrossRef]
- Wang, T.; Song, J. Research on Oscillation Suppression of Asymmetric Hydraulic Cylinder Flexible Connection Based on Luenberger Observer. In Proceedings of the 2022 3rd International Conference on Control, Robotics and Intelligent System, Virtual Event, 26–28 August 2022. [Google Scholar]
- Huang, Y.; Zhang, Z.; Huang, W.; Chen, S. DC-Link Voltage Regulation for Wind Power System by Complementary Sliding Mode Control. IEEE Access 2019, 7, 22773–22780. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Raimondo, D.M.; Limon, D.; Lazar, M.; Magni, L.; Camacho, E.F. Min-max model predictive control of nonlinear systems: A unifying overview on stability. Eur. J. Control. 2009, 15, 5–21. [Google Scholar] [CrossRef]
- Oyuela-Ocampo, J.-C.; Garcés-Ruiz, A.; Sanchez-Acevedo, S.; Ljøkelsøy, K.; D’Arco, S. Continuous Control-Set Model-Predictive Control with stability guarantee for the PWM-VSC. Control. Eng. Pract. 2025, 157, 106246. [Google Scholar] [CrossRef]
- Szabat, K.; Tran-Van, T.; Kamiński, M. A modified fuzzy luenberger observer for a two-mass drive system. IEEE Trans. Ind. Inform. 2015, 11, 531–539. [Google Scholar] [CrossRef]
- Śleszycki, K.; Wróbel, K.; Szabat, K.; Katsura, S. Parameter Identification of the Two-Mass System with the help of Multi-layer Estimator. In Proceedings of the 2021 IEEE 30th International Symposium on Industrial Electronics (ISIE), Kyoto, Japan, 20–23 June 2021. [Google Scholar] [CrossRef]
- Szabat, K.; Tokarczyk, A.; Wróbel, K.; Katsura, S. Application of the Multi-Layer Observer for a Two-Mass Drive System. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 265–270. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Śleszycki, K.; Katsura, S. States Estimation of the Two-Mass Drive System Using Multilayer Observer. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 743–748. [Google Scholar] [CrossRef]
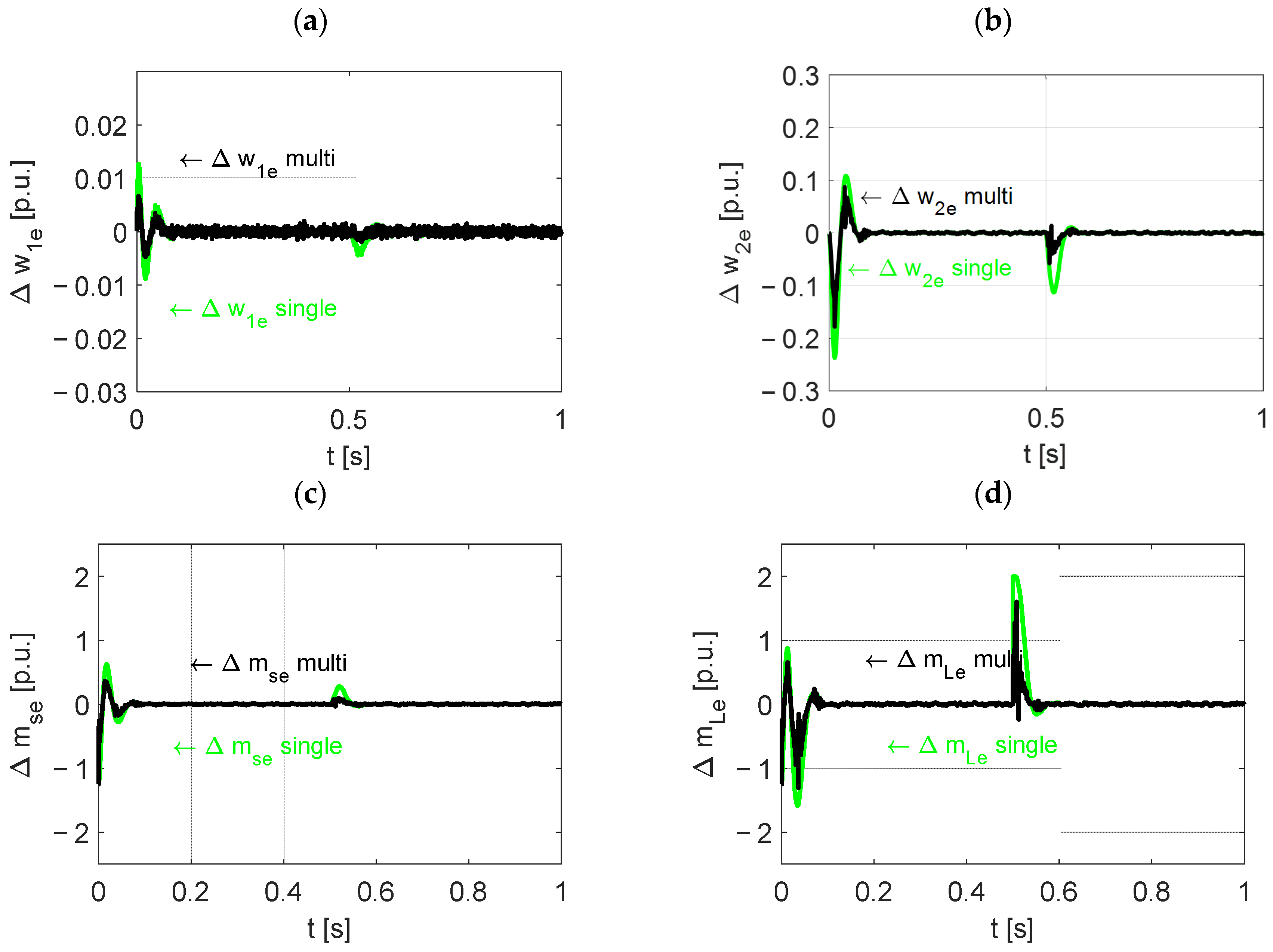

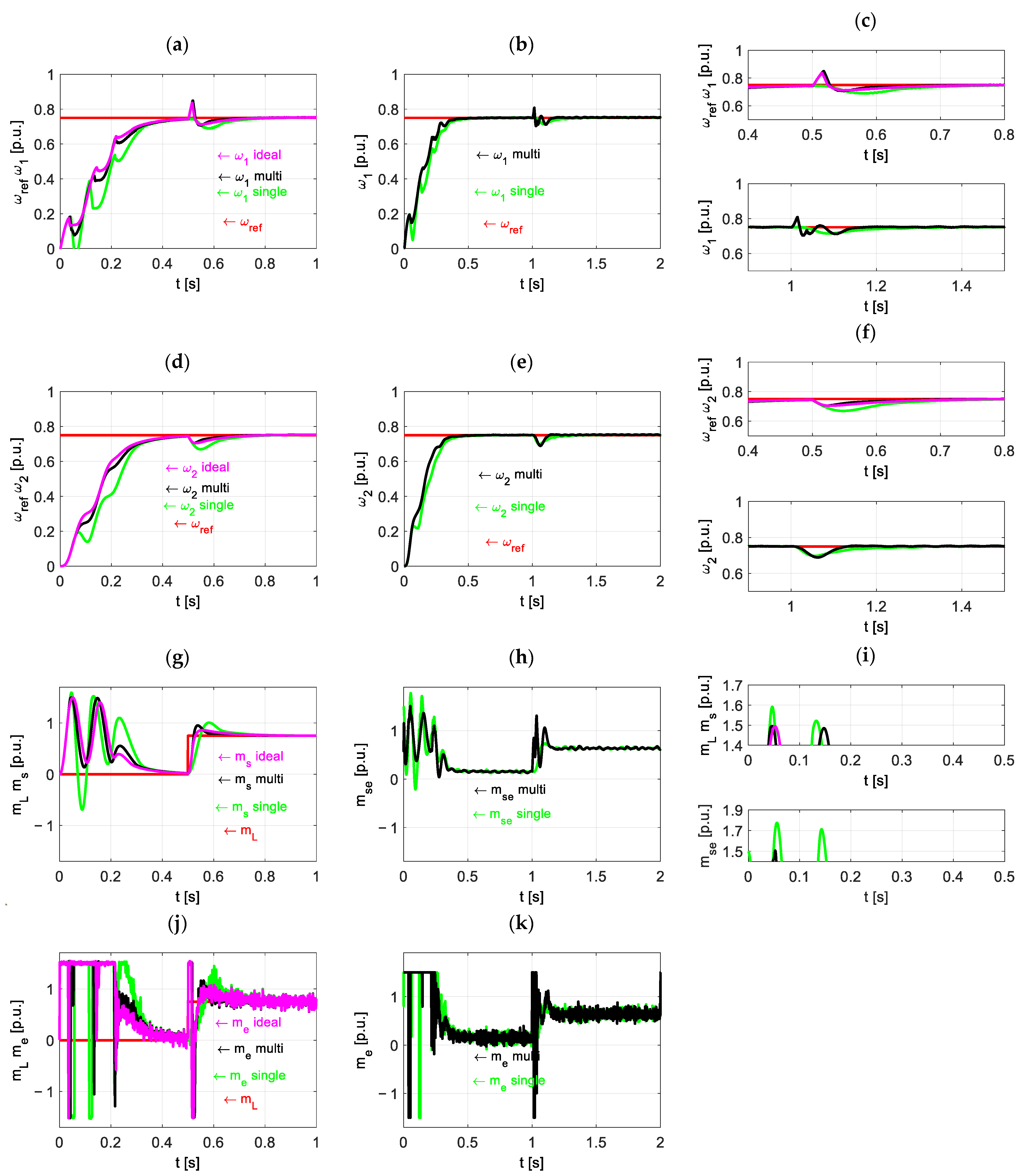
| Single Δ [-] | Two-Layer Δ [-] | Ideal Δ [-] | Single Δ [%] | Two-Layer Δ [%] | Ideal Δ [%] | ||
|---|---|---|---|---|---|---|---|
| Test 1 | ω1 | 2.89 × 10−2 | 2.92 × 10−2 | 3.01 × 10−2 | 96.1 | 97.1 | 100 |
| ω2 | 3.78 × 10−2 | 3.26 × 10−2 | 3.24 × 10−2 | 116.7 | 100.6 | 100 | |
| ms | 2.44 × 10−1 | 1.98 × 10−1 | 1.87 × 10−1 | 130.4 | 105.8 | 100 | |
| me | 4.34 × 10−1 | 4.40 × 10−1 | 4.11 × 10−1 | 105.5 | 107.0 | 100 | |
| Single Δ [-] | Two-Layer Δ [-] | Ideal Δ [-] | Single Δ [%] | Two-Layer Δ [%] | Ideal Δ [%] | ||
| Test 2 | ω1 | 4.44 × 10−2 | 4.61 × 10−2 | 5.18 × 10−2 | 85.7 | 88.9 | 100 |
| ω2 | 4.86 × 10−2 | 4.45 × 10−2 | 4.83 × 10−2 | 100.7 | 92.1 | 100 | |
| ms | 1.91 × 10−1 | 1.57 × 10−1 | 1.54 × 10−1 | 123.9 | 101.8 | 100 | |
| me | 4.47 × 10−1 | 5.28 × 10−1 | 4.65 × 10−1 | 96.1 | 113.3 | 100 | |
| Single Δ [-] | Two-Layer Δ [-] | Ideal Δ [-] | Single Δ [%] | Two-Layer Δ [%] | Ideal Δ [%] | ||
| Test 3 | ω1 | 7.45 × 10−2 | 3.19 × 10−2 | 3.31 × 10−2 | 225.1 | 96.2 | 100 |
| ω2 | 7.52 × 10−2 | 3.30 × 10−2 | 3.37 × 10−2 | 222.9 | 97.9 | 100 | |
| ms | 3.84 × 10−1 | 1.80 × 10−1 | 1.80 × 10−1 | 213.6 | 100.2 | 100 | |
| me | 5.46 × 10−1 | 3.90 × 10−1 | 3.85 × 10−1 | 141.7 | 101.2 | 100 |
| Single Δ [-] | Two-Layer Δ [-] | Single Δ [%] | Two-Layer Δ [%] | |
|---|---|---|---|---|
| ω1 | 7.24 × 10−4 | 5.13 × 10−4 | 141.1 | 100 |
| ω2 | 9.9 × 10−3 | 4.70 × 10−3 | 212.1 | 100 |
| ms | 3.21 × 10−2 | 1.67 × 10−2 | 192.2 | 100 |
| mL | 1.11 × 10−1 | 0.48 × 10−1 | 231.6 | 100 |
| DC Motor | DC Generator | |
|---|---|---|
| Manufacturer | INiME KOMEL (Sosnowiec, Poland) | INiME KOMEL (Sosnowiec, Poland) |
| Type | PZBB 22b | PZBB 22b |
| Power | 500 W | 400 W |
| Nominal voltage | 220 V | 230 V |
| Nominal armature current | 3.15 A | 3.15 A |
| Nominal excitation current | 0.254 A | 0.254 A |
| Nominal speed | 1450 rpm | 1450 rpm |
| Rotor resistance | 8.05 Ω | 8.05 Ω |
| Rotor inductance | 0.8 H | 0.8 H |
| Moment of inertia | 0.0044 kgm2 | 0.0044 kgm2 |
| Auxiliary poles resistance | 2 Ω | 2 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wróbel, K.; Śleszycki, K.K.; Majdański, P. Predictive Control Structure for a Two-Mass Drive System with a Two-Layer Observer. Energies 2025, 18, 6113. https://doi.org/10.3390/en18236113
Wróbel K, Śleszycki KK, Majdański P. Predictive Control Structure for a Two-Mass Drive System with a Two-Layer Observer. Energies. 2025; 18(23):6113. https://doi.org/10.3390/en18236113
Chicago/Turabian StyleWróbel, Karol, Kacper Krzysztof Śleszycki, and Piotr Majdański. 2025. "Predictive Control Structure for a Two-Mass Drive System with a Two-Layer Observer" Energies 18, no. 23: 6113. https://doi.org/10.3390/en18236113
APA StyleWróbel, K., Śleszycki, K. K., & Majdański, P. (2025). Predictive Control Structure for a Two-Mass Drive System with a Two-Layer Observer. Energies, 18(23), 6113. https://doi.org/10.3390/en18236113







