Generalized ANN Model for Predicting the Energy Potential of Heterogeneous Waste

Abstract

In this paper, an artificial neural network (ANN) model of the MLP 5-17-1 type was developed to predict the gross calorific value (HHV) of various waste types based on ultimate analysis. The dataset comprised heterogeneous samples, including biomass, municipal and industrial waste, sludges, and derived fuels, ensuring the model’s diversity and universality. The model achieved high accuracy (R² = 0.92; RMSE = 2.36; MAE = 1.68; MAPE = 10.99%), comparable to previous research results. The heterogeneity of the samples confirmed wide variations in composition and energy properties, which are crucial for developing a universal predictive model. The results confirm that ANN is a reliable tool for assessing the energy potential of waste and highlight the importance of expanding databases and optimizing parameters in future research.

1. Introduction

Waste management represents one of the biggest problems today [1], and it is directly related to the actions of people, whose number is rapidly increasing daily [2]. Although more technologies have been developed recently that try to reduce the mentioned problem, there is still no completely sustainable way of waste management [3]. In this context, the growing need for sustainable waste management and energy supply emphasizes the importance of the waste-to-energy process. The mentioned technologies enable the utilization of energy from different sources through thermochemical, biochemical, and chemical processes, whereby energy can be produced in different forms [4].

In this context, the principles of sustainable development of this concept consist of 5R (reduce, reuse, recycle, recovery, reclamation) and play a key role in the transition from the linear model of the economy based on the produce-use-discard pattern [5]. Emerging technologies for waste conversion and treatment have significant potential for producing clean energy and valuable products, reducing waste disposal, and supplementing recycling [6]. As waste is a valuable energy resource, it is necessary to know its characteristics, one of the most important being the higher heating value (HHV) [7].

HHV is determined in the laboratory using an adiabatic calorimeter [8]. However, it is important to note that this method requires personnel training, requires time, and is often expensive. For this reason, various equations have been used to approximate HHV as accurately as possible [9]. To create such equations, data from ultimate analysis [10] are often used as input variables, consisting of five variables: carbon (C), hydrogen (H), nitrogen (N), oxygen (O), and sulfur (S) [11]. Due to the complexity of larger datasets and their interpretation, machine learning models have been increasingly applied in recent years for modeling, approximation, and predictive analysis [12]. One of the most widely used machine learning models is the artificial neural network (ANN), which operates on the principle of the human brain, making it suitable for analyzing complex tasks [13]. ANN models are suitable for modeling nonlinear tasks, identifying patterns between input and output variables, and are based on a layered structure through which data passes [14]. On the other hand, although suitable for modeling, ANN models require parameter tuning and optimization, which is not a simple task [15]. One of the most popular types of ANN models is the multilayer perceptron (MLP), a network in which information flows unidirectionally through the input, hidden, and output layers, which are interconnected [16]. A significant number of scientific papers focus on the development of ANN models for estimating the HHV of different materials based on ultimate analysis [17,18,19,20,21]. However, most research to date has focused on specific types of raw materials, such as biomass and coal, which can significantly limit the universality of the developed model, as this approach reduces the variability of input and output data. Previous research on predicting the higher calorific value (HHV) of biomass has revealed considerable differences in both the approaches and the quality of the data used. Abdollahi et al. [22] report that earlier studies randomly used datasets from ultimate and proximate analyses, as well as their combinations, resulting in heterogeneous and difficult-to-compare models. In contrast, Köcer [23] notes that newer machine learning algorithms have improved prediction accuracy, but most developed models are still based on limited datasets and specific types of biomass, which reduces their generalizability. In this research, a new methodology is presented that integrates a highly heterogeneous dataset collected from multiple independent sources and applies standardized preprocessing and an optimized artificial neural network (ANN) architecture to achieve a universal HHV prediction model, thereby overcoming the limitations of previous studies related to narrow datasets and limited model applicability. The aim of this research is to develop and validate an artificial neural network (ANN) for the reliable prediction of the higher heating value (HHV) of biomass from various origins, using elemental composition (C, H, N, S, O) as input variables. The research involved: (1) collection and standardization of data from published sources, (2) analysis of correlations between elements and HHV, (3) development, training, and evaluation of multiple ANN model architectures, and (4) comparison of ANN performance with traditional empirical models. The ultimate goal was to define a model with an optimal balance of accuracy and generalizability, applicable to a wide range of biomasses.

2. Materials and Methods

2.1. Data Collection

The data used to develop the model included various waste types, such as agricultural biomass residues, municipal waste, sludges, digestates, and treated waste, and were collected from published scientific papers [24,25,26,27,28,29,30,31,32,33,34,35,36]. Data on the ultimate analysis of the samples (percentages of C, H, N, S, and O), as well as the higher heating value (HHV), were collected. The samples cover a wide range of materials, including biomass of plant origin (wood, agricultural residues, food) and municipal and industrial waste (plastic, paper, textiles, rubber). Such diversity confirms the high heterogeneity of the samples used in model development. The raw data used for modeling can be seen in Supplementary Table S1.

2.2. Data Preprocessing

After the data were collected, a database was created. Due to the unevenness of the data, the next step was data cleaning, standardization, and normalization. Data cleaning is the process of identifying and removing errors from the database to increase quality and consistency [37]. The data were then standardized and normalized to prepare for the creation of artificial neural network models [38,39]. To fill data gaps based on known values, the min-max scaling method was used as preparation for K-Nearest Neighbor (kNN) methods [40,41]. After these methods were implemented, the data were ready for the creation of an ANN model.

2.3. Statistical Analysis

Statistical analysis was conducted on preprocessed data (after data cleaning). For this purpose, and for visualization, a pair plot diagram was created to display distributions and correlations. The characteristics of the research variables, i.e., the descriptive statistics metrics, were also presented numerically. Statistical analysis was performed using the Python 3.14 programming language [42].

2.4. Artificial Neural Networks–Model Settings

The ANN model is constructed with an architecture comprising input, hidden, and output layers [43]. The ultimate analysis variables were used as input data, and the higher heating value (HHV) was used as the output. The model was built as a Multilayer Perceptron (MLP) [44], as such models are most suitable for generalization [45]. The architecture, specifically the number of artificial neurons in the hidden layer, is determined randomly using the trial-and-error method [46,47,48]. The data was then divided into training, testing, and validation sets in a 70:15:15 ratio [49,50,51], which is the most commonly used. The model was created using the Python programming language [42] with associated packages [52,53,54]. The ANN was trained for 100,000 cycles to obtain relevant results.

Figure 1 shows the architecture of the developed ANN model, with five artificial neurons in the input layer, seventeen in the hidden layer, and one in the output layer.

The output value of the model was calculated using the following Formula (1) [55]:

$$Y=f\cdot (b+W\cdot X)$$

(1)

where Y is the output value, f is the model function, b is the threshold, W is the weighting coefficient, and X is the model input value.

The selected methods were applied to achieve high accuracy and reliability in predicting the HHV of biomass. The artificial neural network was chosen for its ability to model complex nonlinear relationships between elemental composition (C, H, N, S, O) and HHV, which classical regression approaches cannot fully capture. Standardization, normalization, and imputation of data using the k-nearest neighbors’ method were performed to reduce the impact of outliers and information loss. Dividing the dataset into training, validation, and test sets (70:15:15) enabled assessment of the model’s generalization ability and prevented overfitting, thus ensuring the reliability and repeatability of the results.

2.5. Model Evaluation

After modeling to estimate the output value, the model needed to be evaluated. To assess the success of the model in terms of modeling error and specific regression indicators, the following metrics were used: root mean squared error (RMSE) (2), mean absolute error (MAE) (3) [56], coefficient of determination (R²) (4), and mean absolute percentage error (MAPE) (5) [57]:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{e}_i^2}}$$

(2)

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|e_i\right|}$$

(3)

$$R^2={\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left(X_i-Y_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(\overline{Y}-Y\right)}^2}}}$$

(4)

$$MAPE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|\frac{Y_i-X_i}{Y_i}\right|}$$

(5)

3. Results

Figure 2 presents a graphical representation of the scatterplot matrix and the mutual relationships among the observed variables used as input and output variables in the model.

Table 1. Descriptive statistics of the observed dataset after the cleaning, standardization, and normalization process.

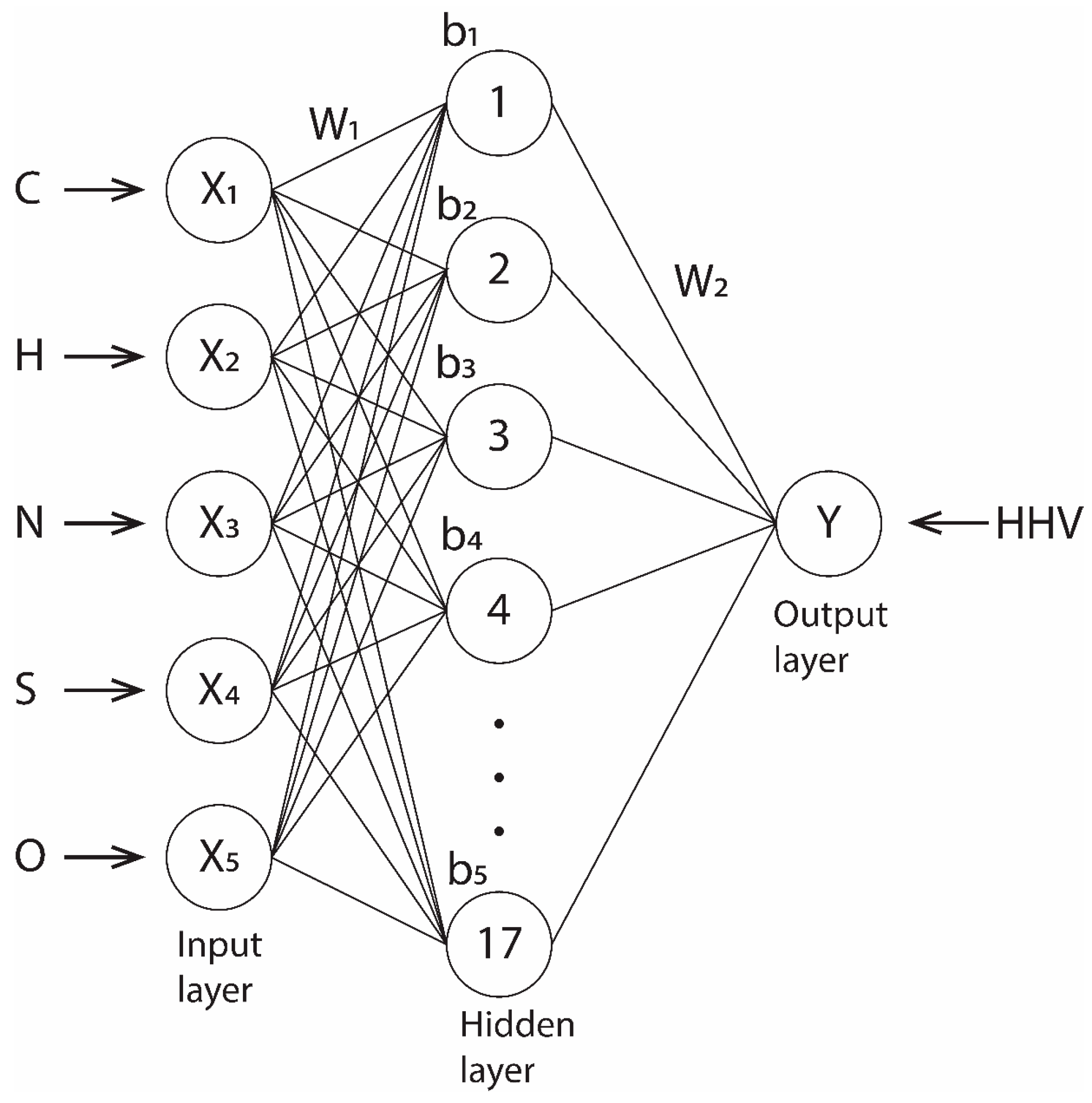
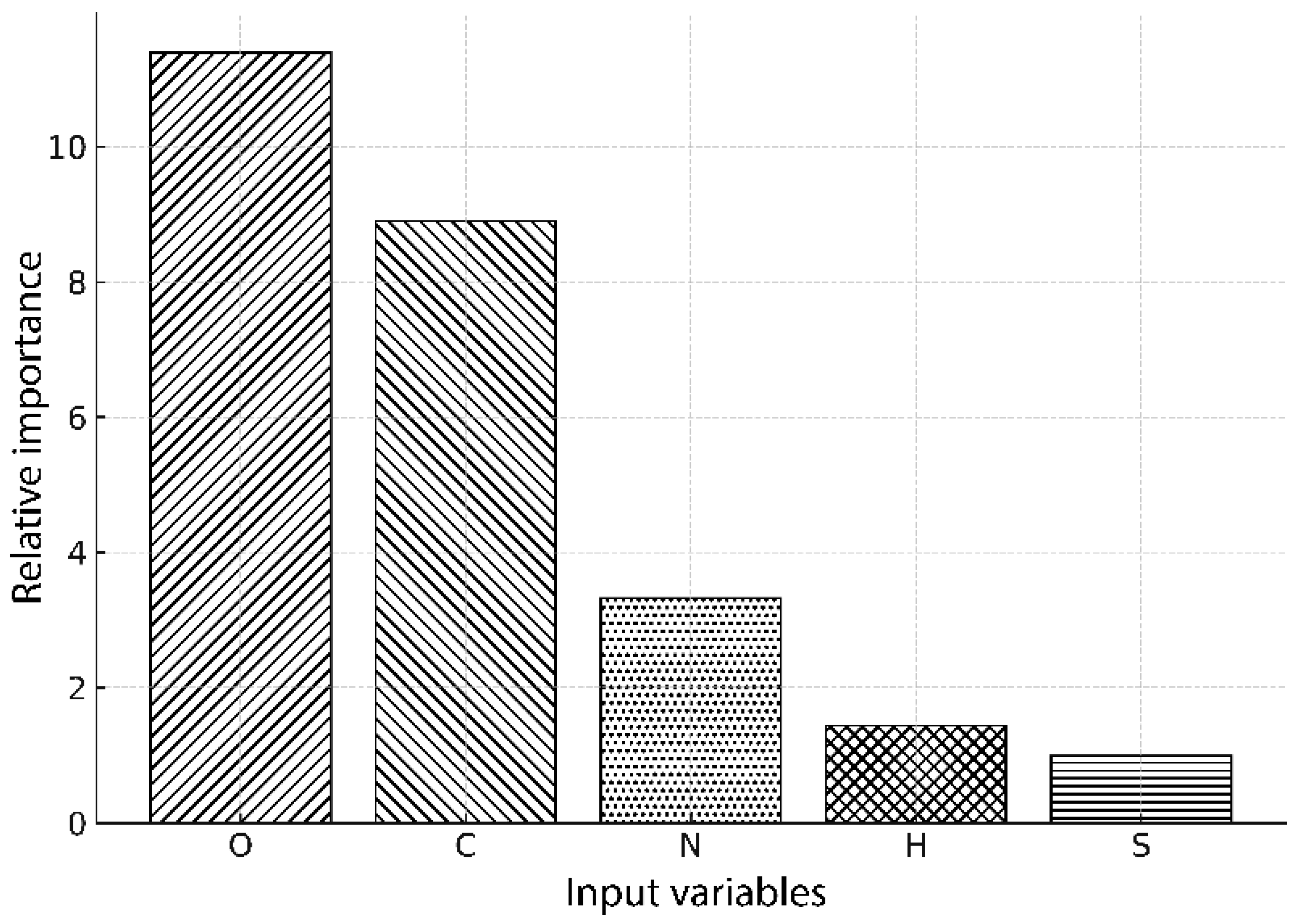
Descriptive Statistics ↓	Input Variables (%) ↓					Output Variable (MJ kg−1) ↓
	C (%)	H (%)	N (%)	S (%)	O (%)	HHV
Mean	48.62	6.37	2.35	0.37	33.35	19.59
Median	45.78	5.90	0.90	0.13	37.94	18.75
Minimum	6.27	1.09	0.01	0.00	0.00	2.80
Maximum	91.53	14.30	9.98	9.20	52.84	46.08
Std.Dev.	14.76	2.24	2.83	0.91	13.66	8.35

C—content of carbon; H—content of hydrogen; N—content of nitrogen; S—content of sulfur; O—content of oxygen; HHV—higher heating value.

presents the basic statistical characteristics of the variables used as input and output data for the model. The statistical indicators include variability, mean value, and standard deviation.

Table 1 presents the descriptive statistics of the observed variables used to develop the ANN model.

Table 2. Summary of the developed ANN MLP 5-17-1 model.

ANN Model	Performance (R2)			Error
	Training	Test	Validation	Training	Test	Validation
MLP 5-17-1	0.94	0.85	0.86	2.06	4.96	3.99

ANN—Artificial neural networks; MLP—Multilayer perceptron; R²—Coefficient of determination.

shows a summary of the developed ANN model 5-17-1.

Table 2 presents a summary of the developed ANN model, a multilayer perceptron with 5 input neurons, 17 hidden neurons, and 1 output neuron per layer, and displays the performance and model errors.

Table 3. Performance evaluation of the ANN model based on training, validation, test, and overall datasets.

Dataset	R2	RMSE	MAE	MAPE (%)
Train	0.943	2.03	1.49	8.96
Validation	0.856	2.82	1.91	15.10
Test	0.85	3.15	2.30	16.48
Overall	0.92	2.36	1.68	10.99

R²—Coefficient of determination; RMSE—Root mean squared error; MAE—Mean absolute error; MAPE—Mean absolute percentage error.

presents the model reliability metrics, including model error (RMSE, MAE, and MAPE) and the specific regression indicator (R²).

Figure 3 shows a comparison of the predicted and actual HHV values for the training, validation, and testing datasets. The histograms along the axes display the distribution of the target and predicted values.

Figure 4 shows the relative importance of the input variables of the ultimate analysis in the ANN model for HHV prediction. Relative importance refers to dimensionless values obtained from the ANN model sensitivity analysis, in which each variable is assigned a numerical importance index indicating its relative contribution to the model’s predictive accuracy.

4. Discussion

Scatterplot matrix analysis (Figure 1) shows that carbon content has a strong positive correlation with HHV (r = 0.86). García–Nieto et al. [58] conducted a correlation analysis of ultimate analysis and HHV of biomass in their research, and also found a strong positive correlation with carbon content. High carbon content indicates that samples have higher HHV [59]. Table 1 shows that the average carbon content in the samples analyzed is 48.62%, while the average HHV is 19.59 MJ kg⁻¹. The range of values indicates considerable heterogeneity in the data—for example, carbon content varies from 6.27% to 91.53%, and HHV from 2.80 to 46.08 MJ/kg. Esteves et al. [60] report that different types of biomass potentially usable as fuels exhibit substantial variation in their physicochemical characteristics and provide HHV values for wood in the range of 17–23 MJ kg⁻¹. Large variations in the proportions of individual elements and HHV result from the heterogeneity of the samples [61,62], as they are different types of waste, which was crucial for creating a more universal model with high generalization ability. For these reasons, ANN models, which are machine learning algorithms inspired by the structure and function of the human brain, are considered the most suitable for solving nonlinear problems involving large amounts of nonlinear data [63]. The ANN model developed in this research achieved coefficients of determination (R²) of 0.942 for the training dataset, 0.86 for the validation dataset, and 0.85 for the test dataset, indicating good generalization ability. The error values (2.069 for training, 3.990 for validation, and 4.964 for test) confirm the stability of the model without signs of overfitting.

The best results are achieved by the model on the training dataset (R² = 0.943; RMSE = 2.03), while slightly lower values are obtained on the validation (R² = 0.856) and test datasets (R² = 0.85), indicating good, but not perfect, generalization. Overall, the model achieves high accuracy (R² = 0.92) with acceptable error values (RMSE = 2.36; MAE = 1.68; MAPE = 10.99%), confirming its reliability in predicting the HHV of different waste types. The overall evaluation of the model shows high accuracy with R² = 0.92, indicating a strong correlation between the predictions and the actual HHV values. The error values (RMSE = 2.36; MAE = 1.68; MAPE = 10.99%) confirm that the model reliably predicts the energy potential of different waste types, with an acceptable level of deviation. Olatunji et al. [64] report RMSE of 3.587 and MAPE of 21.68. Dashti et al. [65] conducted a study comparing several machine learning models for estimating the higher heating value (HHV) of biomass using input data from proximate analysis. The ANN achieved a high regression indicator (R²) for training (0.94) and testing (0.95), and a low total error MSE (0.83), indicating the suitability of this model for this problem. In the research by Mondal and Rafizul [66], the ANN model was used to predict the calorific value of municipal waste based on proximate analysis (MC, VC, FC, Ash). After 1000 epochs, the model achieved high accuracy with R² = 0.9397, MSE = 1.599, RMSE = 1.264, MAD = 0.558, and MAPE = 0.032, confirming its ability to accurately model nonlinear relationships between the chemical composition of waste and its energy value.

Matveeva and Byckov [67] conducted research to create an ANN model for estimating the HHV of biofuels and obtained R² values of 0.82–0.87, considering the data management process. Veza et al. [68] report R² values for their model of 0.80–0.94. From all the above, it is evident that the created ANN MLP 5-17-1 model showed satisfactory performance in predicting HHV. The greatest influence on the model is exerted by the proportion of oxygen (O), followed by carbon (C), while nitrogen (N), hydrogen (H), and sulfur (S) are significantly less important. The results indicate that oxygen and carbon are the key predictors of the energy value of different types of waste, which is consistent with established patterns in the literature. Brandić et al. [18] state that the output value of HHV is mostly influenced by an increase in the variable S, while Adeleke et al. [69] report the highest influence from ash, sulfur, nitrogen, and oxygen. However, the varying influence of individual variables is determined by differences in samples, i.e., heterogeneity, as different types of waste are characterized by specific chemical compositions and energy properties [69,70,71,72]. These results are consistent with previous studies that demonstrated the effectiveness of ANN in modeling HHV based on proximate or ultimate analysis data. Compared to previous research, the developed model demonstrates equal or higher accuracy and stability, with improved generalization ability due to the broader range and greater heterogeneity of the data used.

Although the model demonstrates high performance and a high level of universality or generalization, there are key limitations that must be considered. As previously mentioned, sample heterogeneity leads to variability in the chemical composition of the analyzed samples, which can reduce model accuracy, particularly in certain subgroups. Therefore, planning and optimization are essential [73]. It is also important to emphasize that model performance depends on the quality and resolution of the input variables, as models are sensitive to poor-quality data [74]. In future research, it is advisable to build models using different data inputs while increasing the quality and quantity of the entire dataset [75]. Another key factor that can improve problem-solving is hyperparameter optimization and regularization, which can further reduce prediction errors [76].

5. Conclusions

In this study, an artificial neural network (ANN) model was developed and validated to predict the higher heating value (HHV) of various types of biomass and waste based on their elemental composition (C, H, N, S, O). The model demonstrated high accuracy (R² = 0.92; RMSE = 2.36 MJ/kg), with stable performance across training, validation, and test sets, confirming its reliability and generalizability. Analysis of variable importance showed that oxygen (O) and carbon (C) have the greatest impact on HHV, consistent with established energy laws of biomass. The scientific novelty of this work lies in the integration of a highly heterogeneous dataset collected from multiple sources and the application of standardized preprocessing and optimized ANN model architecture, enabling universal prediction of HHV for different types of biomass. The practical significance of the results is evident in the ability to rapidly assess the energy potential of waste and biomass without complex laboratory analyses, contributing to more efficient planning of energy production from renewable sources and the development of a circular economy.