Multi-Objective Optimization Strategy for Integrated Energy System Considering Mixed Participation of Aluminum Electrolysis and Hydrogen Production Industries
Abstract
1. Introduction
- (1)
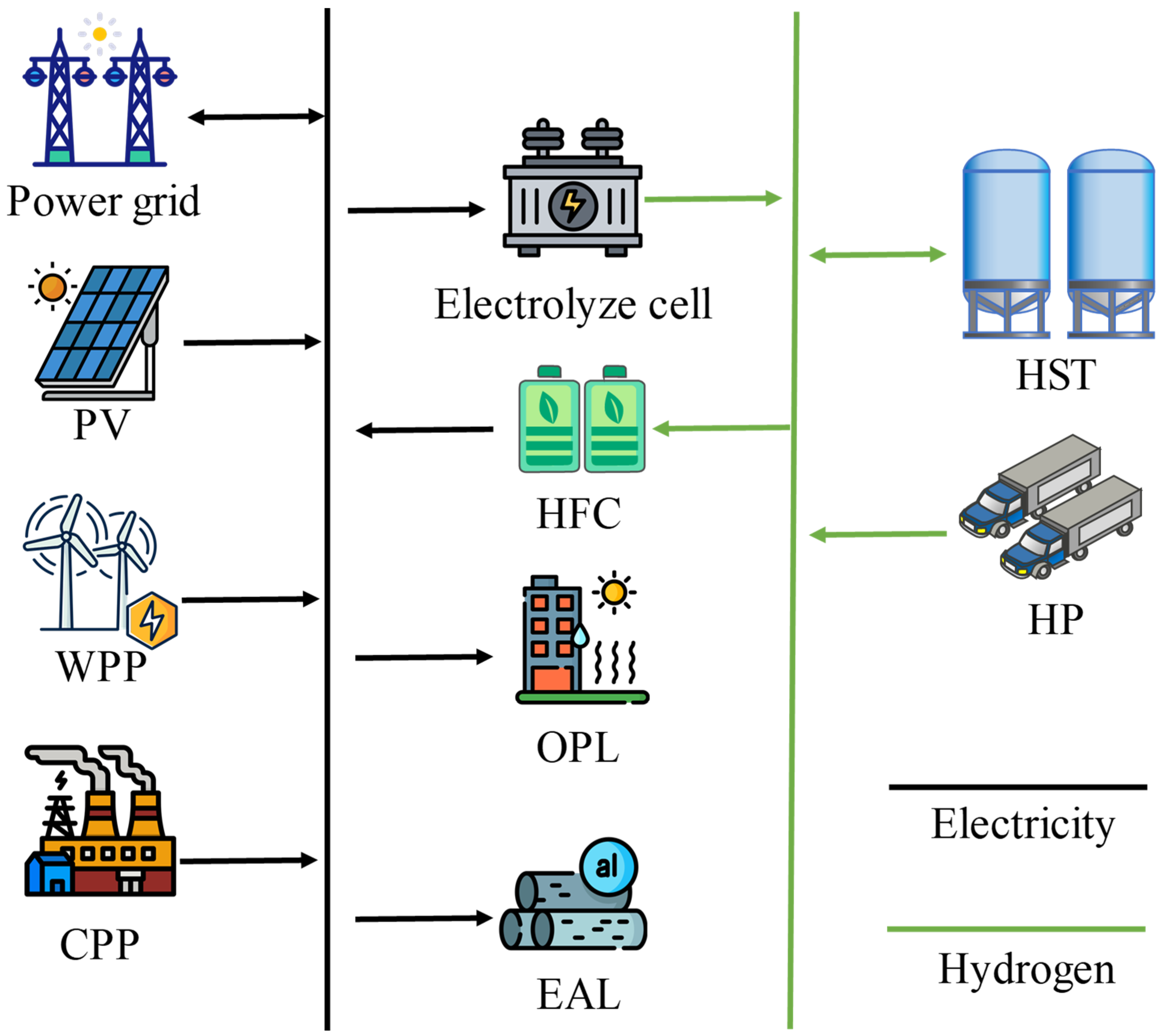
- A comprehensive energy-scheduling optimization model specifically designed for industrial parks engaged in aluminum electrolysis and hydrogen production is established. The proposed IES considers the power grid, thermal power units, new energy, electrolytic aluminum load, and ordinary load, as well as the manufacture, storage, and utilization of hydrogen.
- (2)
- An optimal scheduling method for aluminum electrolytic load is proposed. By optimizing the electrolytic aluminum load curve for the next day, the operating costs of the industrial park can be significantly reduced.
- (3)
- An objective function with a penalty term is proposed, which can adjust the total carbon emissions and operating costs according to actual conditions, greatly improving the flexibility of the system.
2. Integrated Energy Systems Framework
3. Modeling
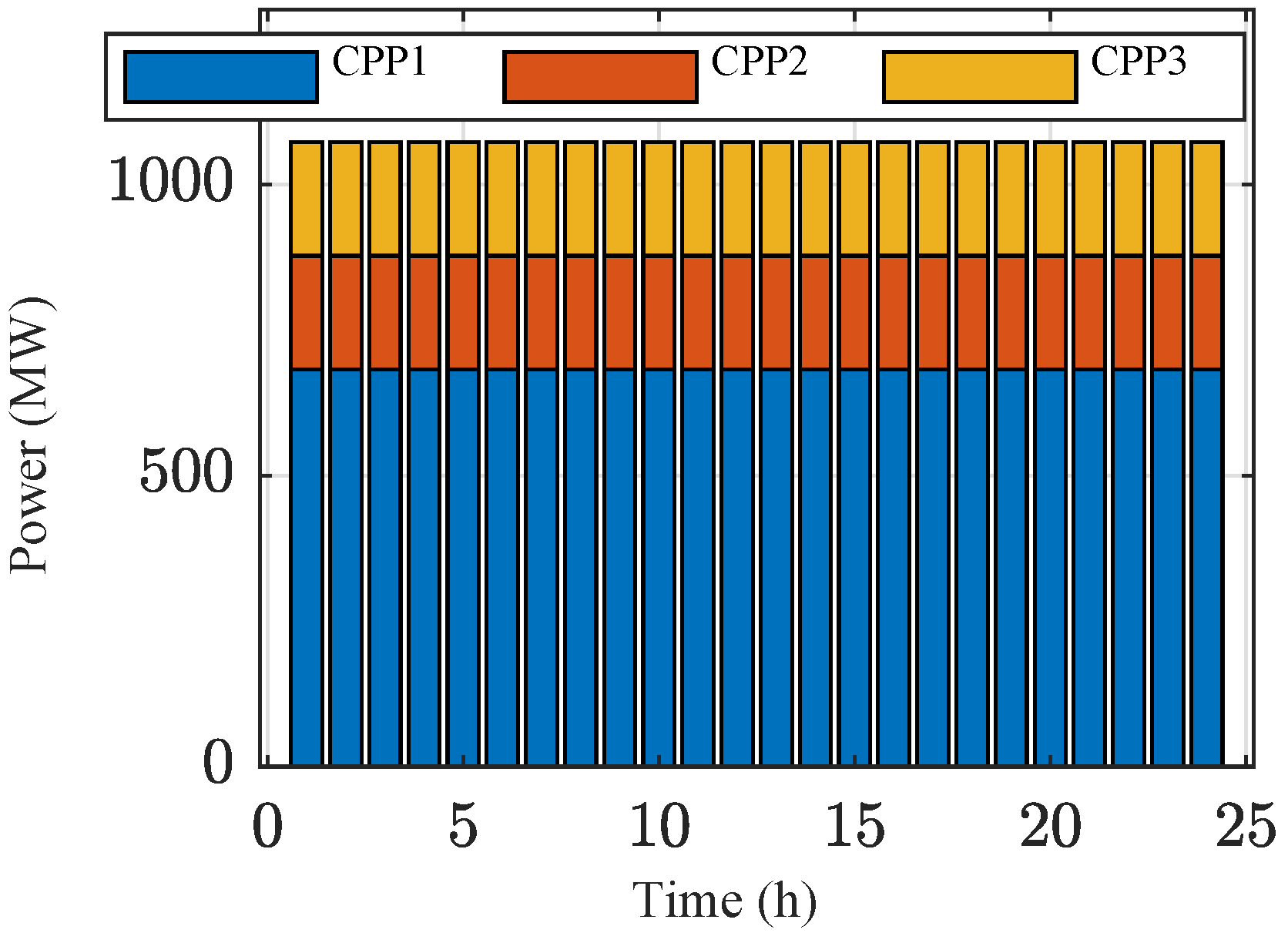
3.1. Power Supply Equipment
3.2. Controllable Load Modeling
3.2.1. Electrolytic Aluminum Load
3.2.2. Ordinary Power Load
3.3. Hydrogen Production Equipment
3.3.1. Electrolytic Cell
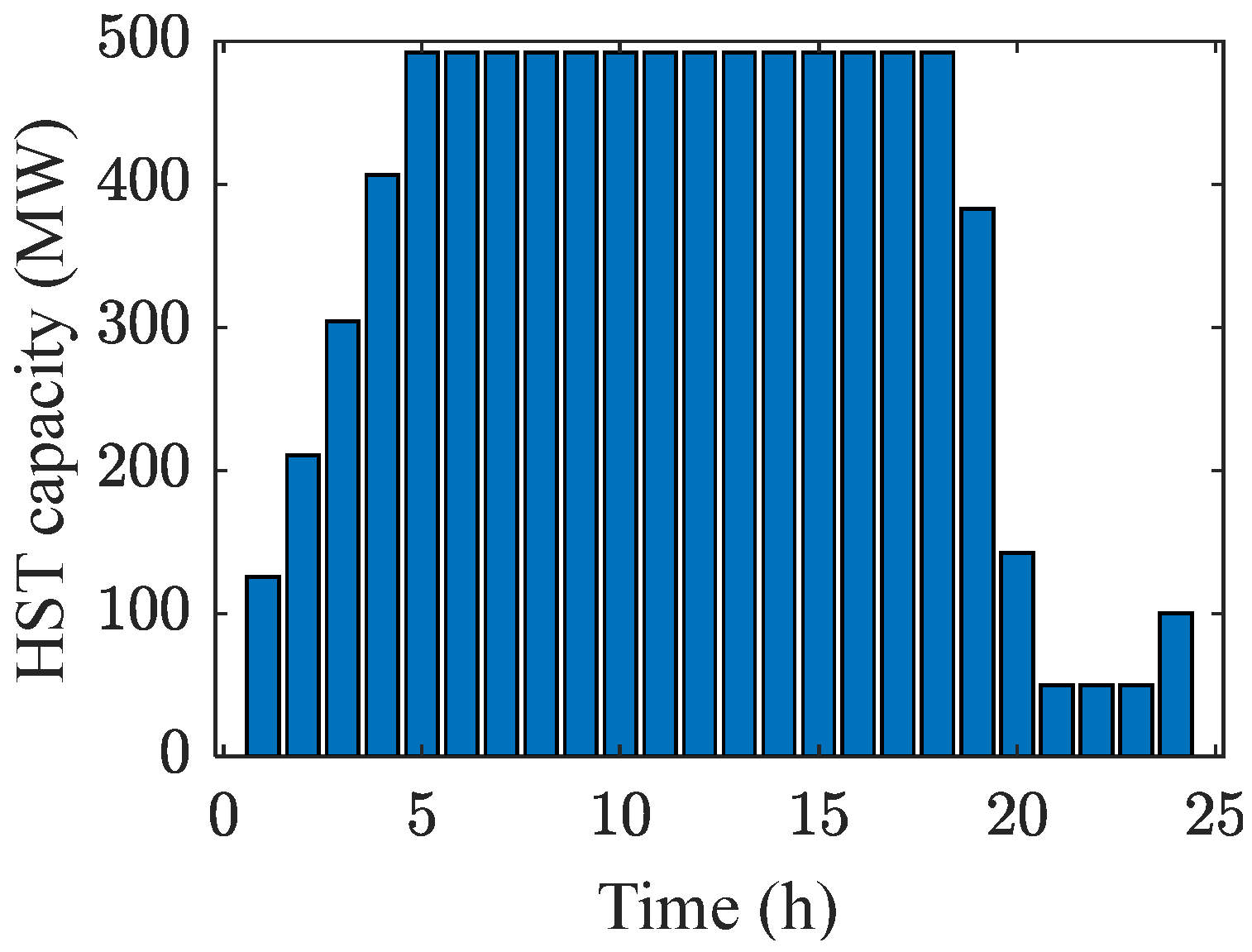
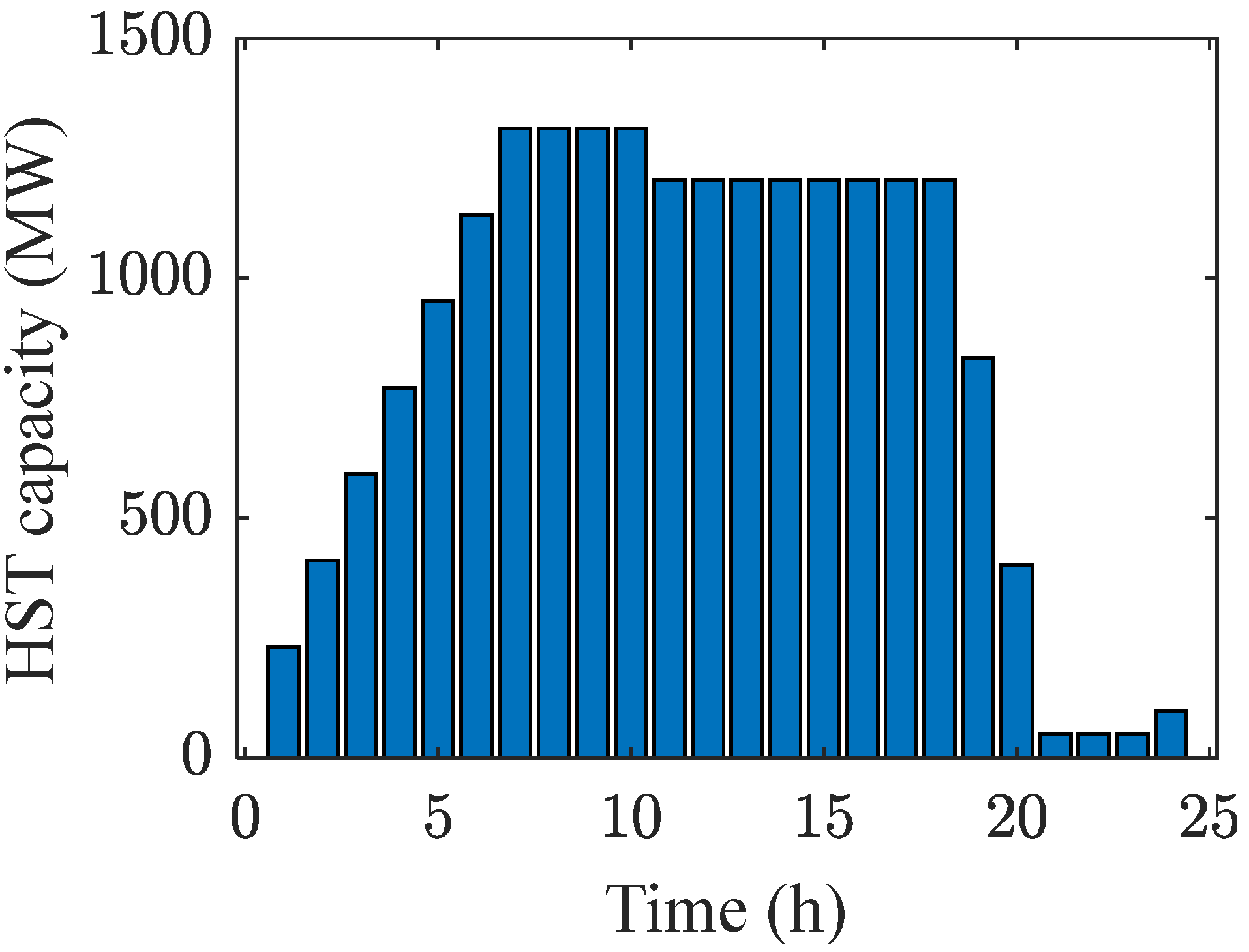
3.3.2. Hydrogen Storage Tank
3.3.3. Hydrogen Purchase
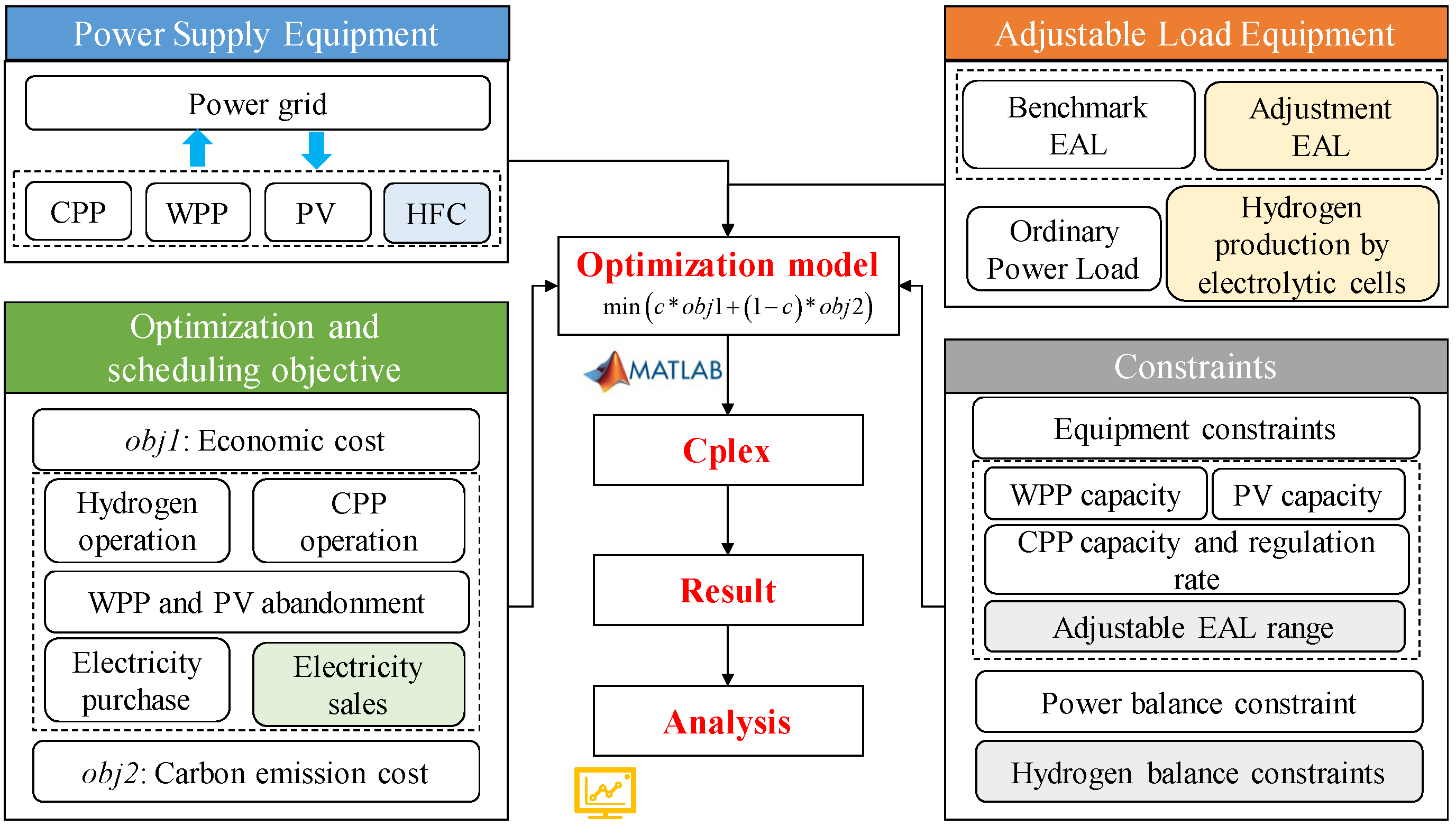
3.4. Optimization Scheduling Model
3.4.1. Objective Function
- (1)
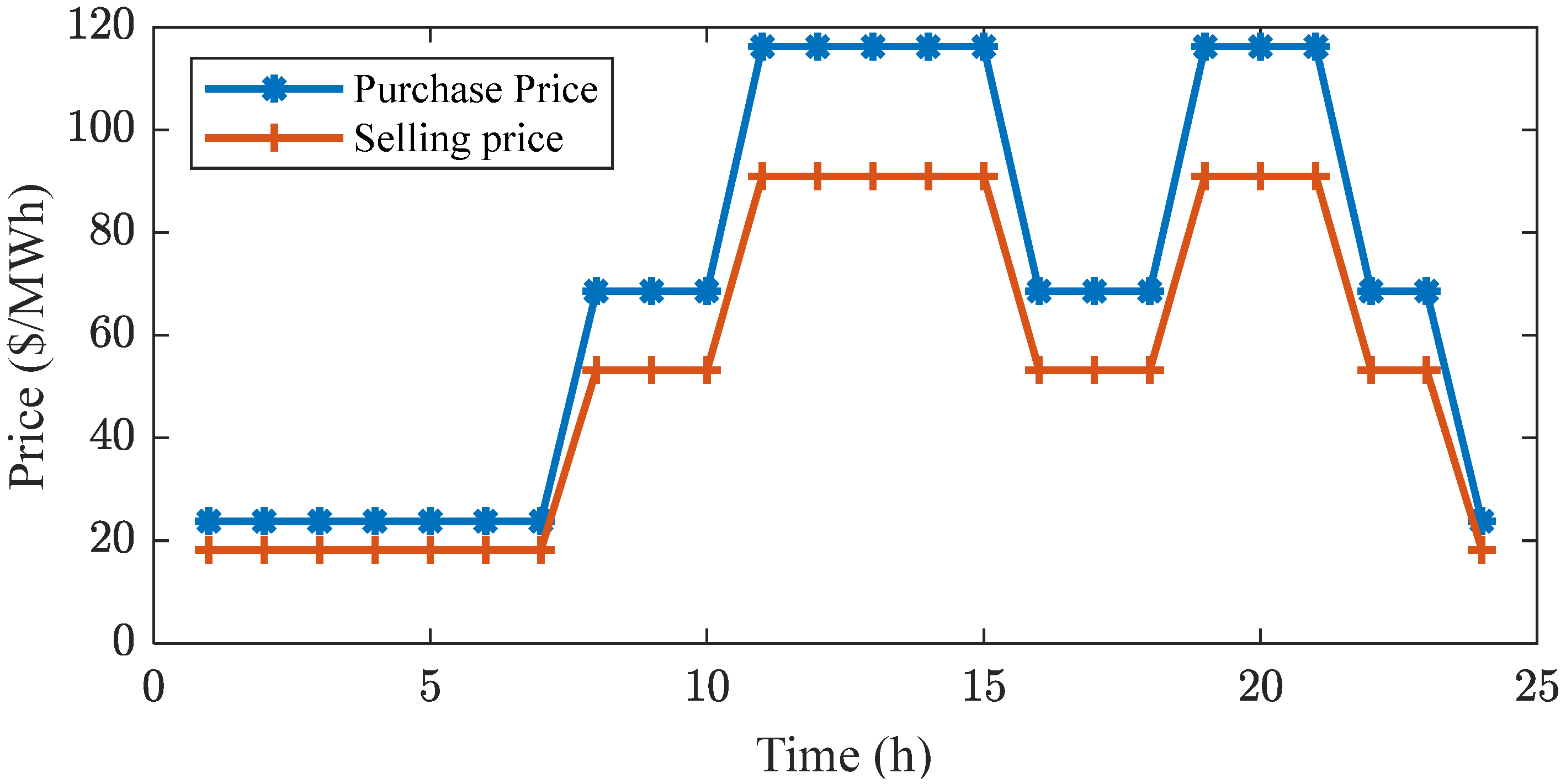
- Cost of buying electricity and selling electricity : The difference between from the grid and constitutes the grid interaction cost of this IES, which is a cost that must take into account. This cost can be expressed as follows:
- (2)
- Penalty cost of wind and solar power abandonment This cost refers to the economic losses caused by being forced to abandon wind and solar power generation due to insufficient system absorption capacity, which can be defined as shown in Equation (16):
- (3)
- Cost of the CPP : This cost refers to the power generation cost of CPP, including the nonlinear part and the advance part, defined as shown in Equation (17):
- (4)
- Hydrogen power generation cost : This part includes the daily use and maintenance costs of HFCs, HP, and HSTs, which can be defined as shown in Equation (18):
- (5)
- Hydrogen purchase cost : This part is due to the cost of purchasing hydrogen from outside, which can be defined as shown in Equation (19):
3.4.2. Constraints
4. Results and Discussion
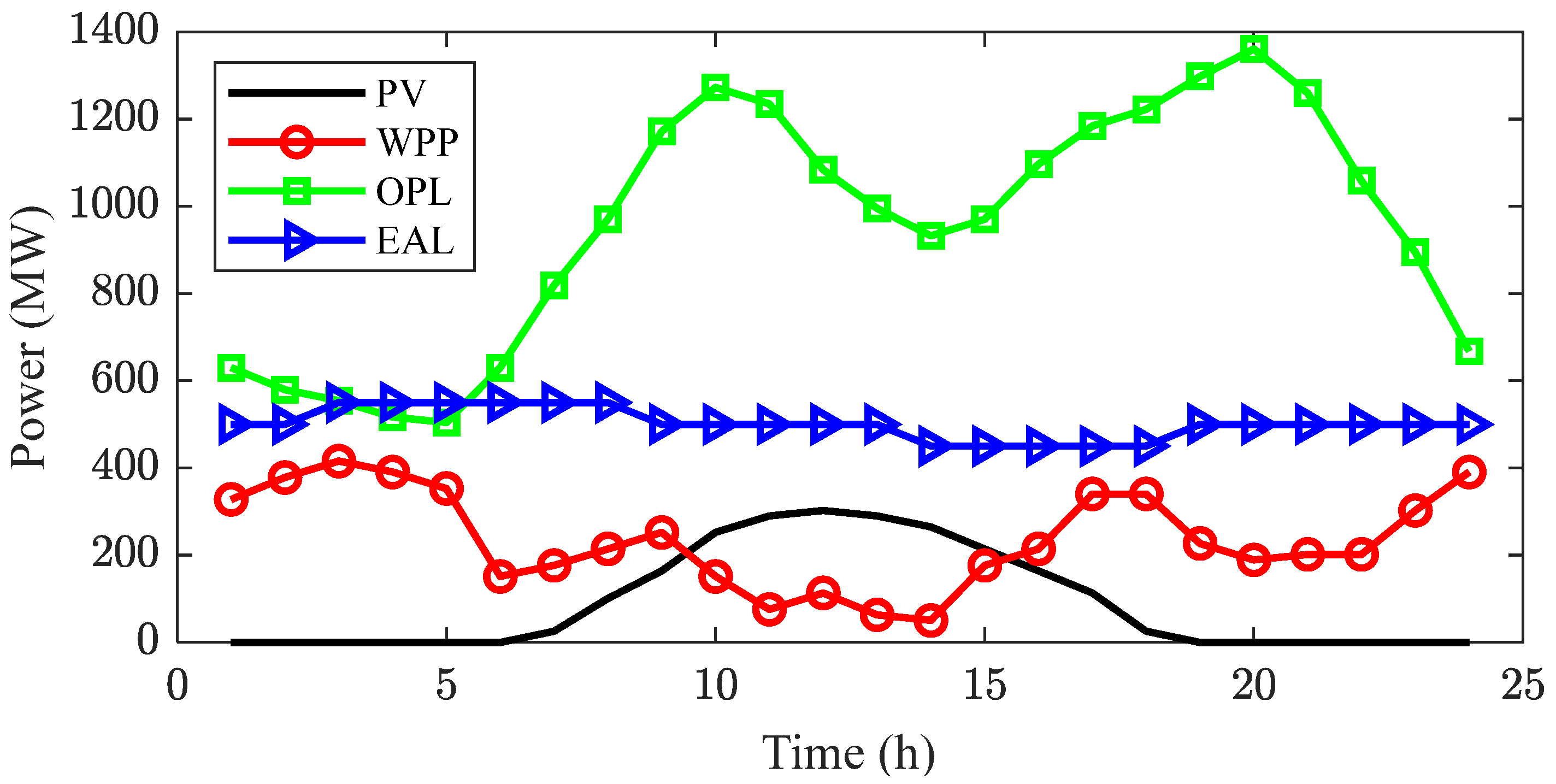
4.1. Data Description and Case Settings
4.2. Optimization Results Analysis
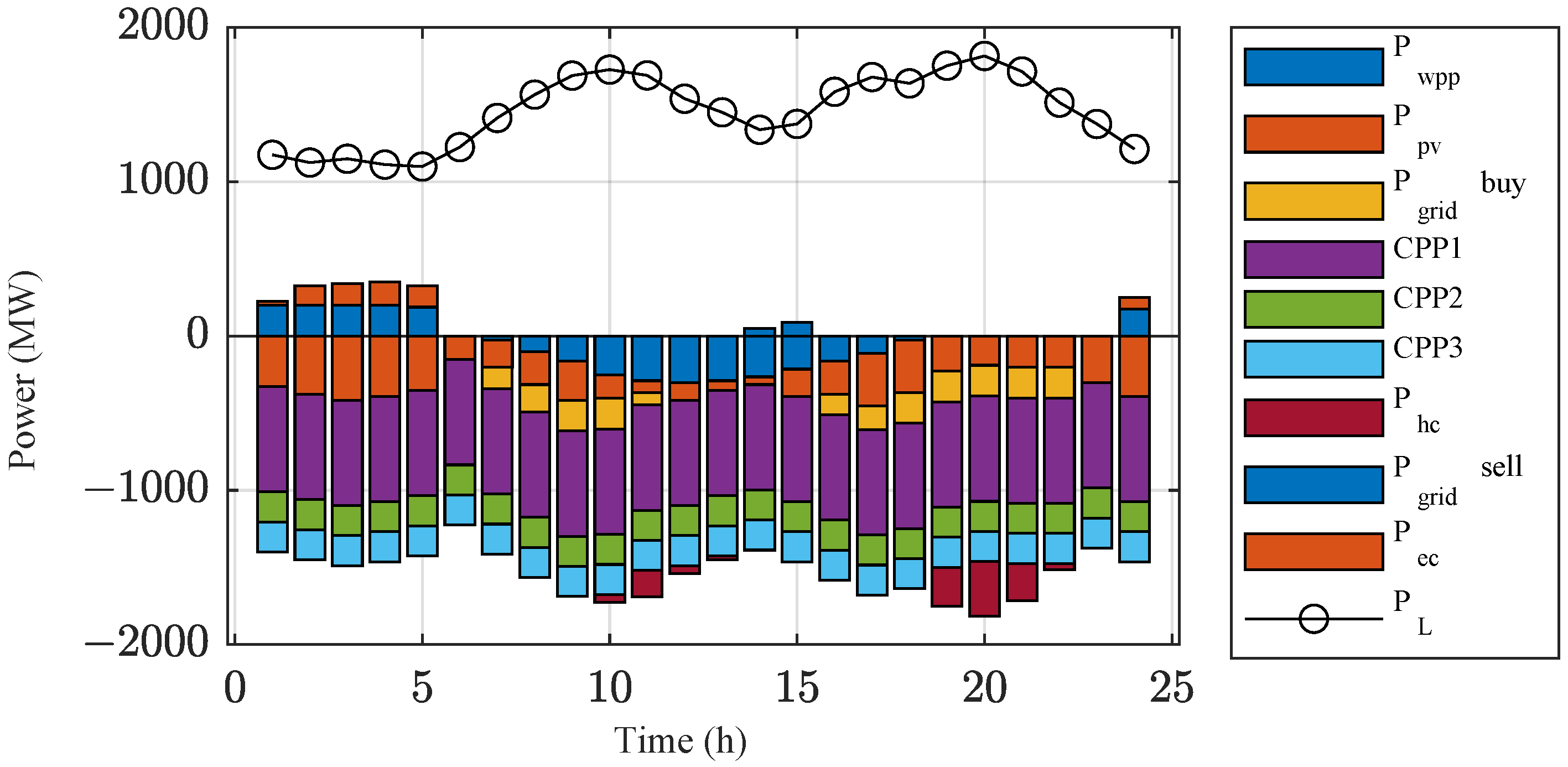
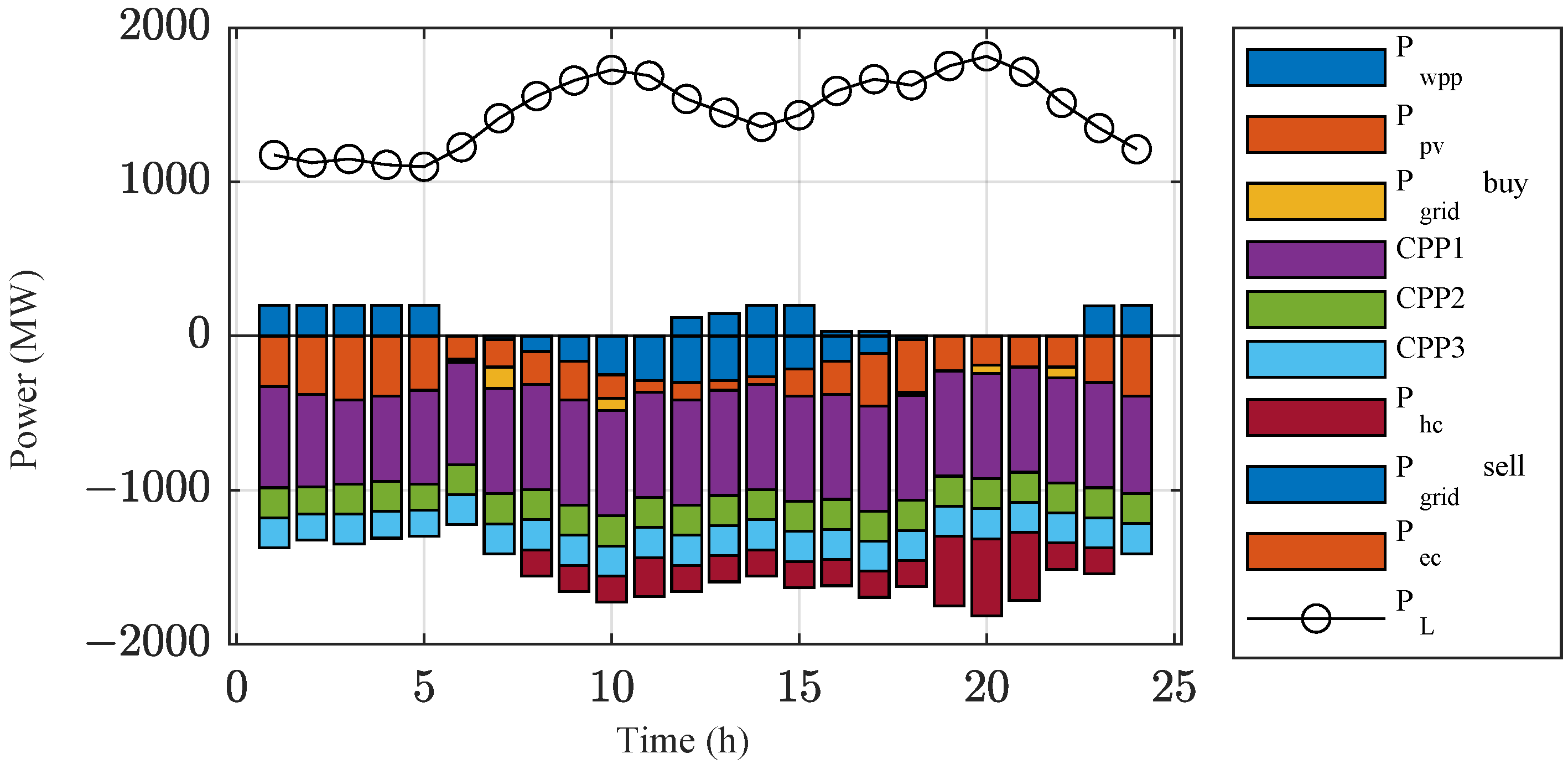
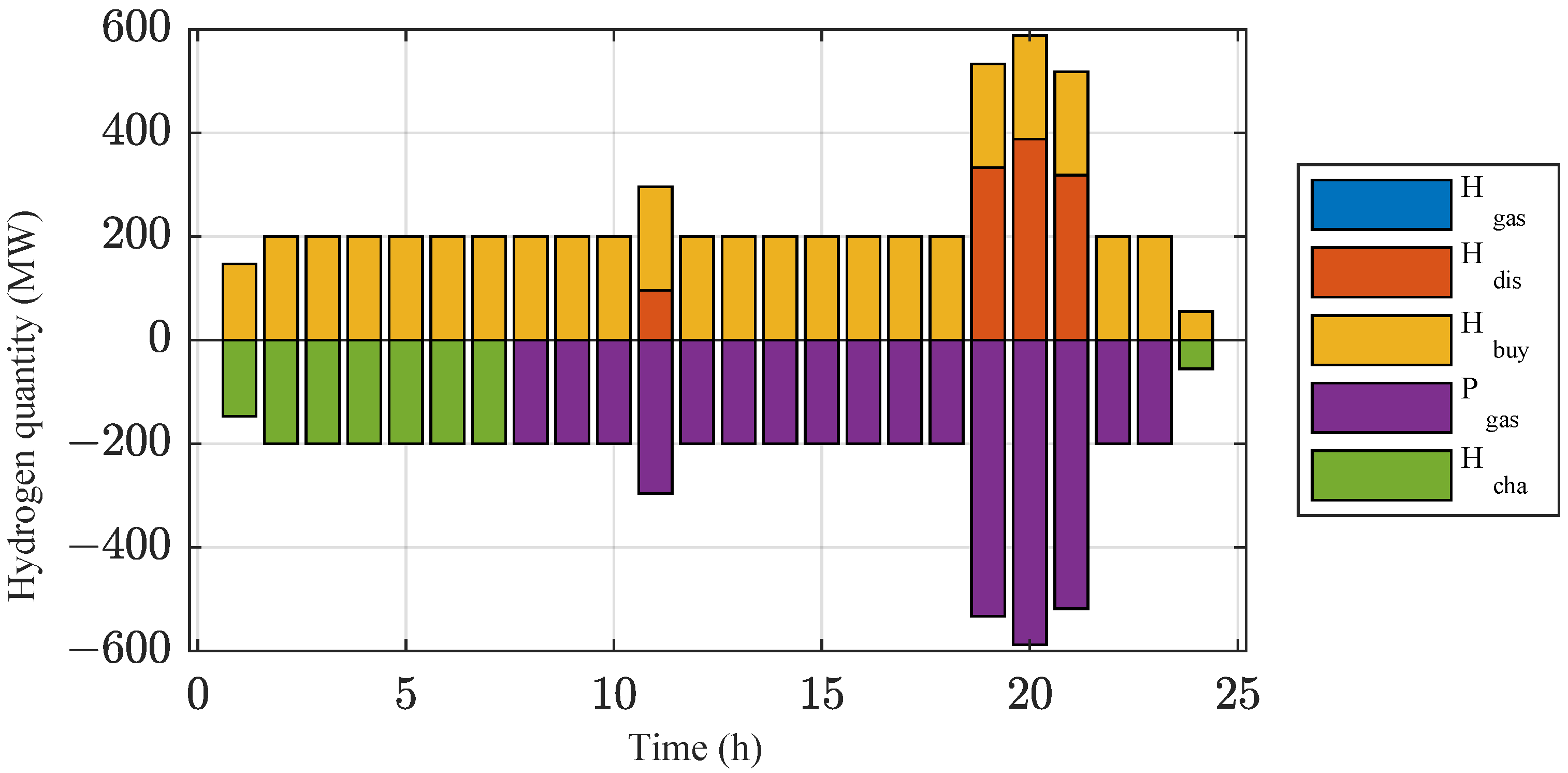
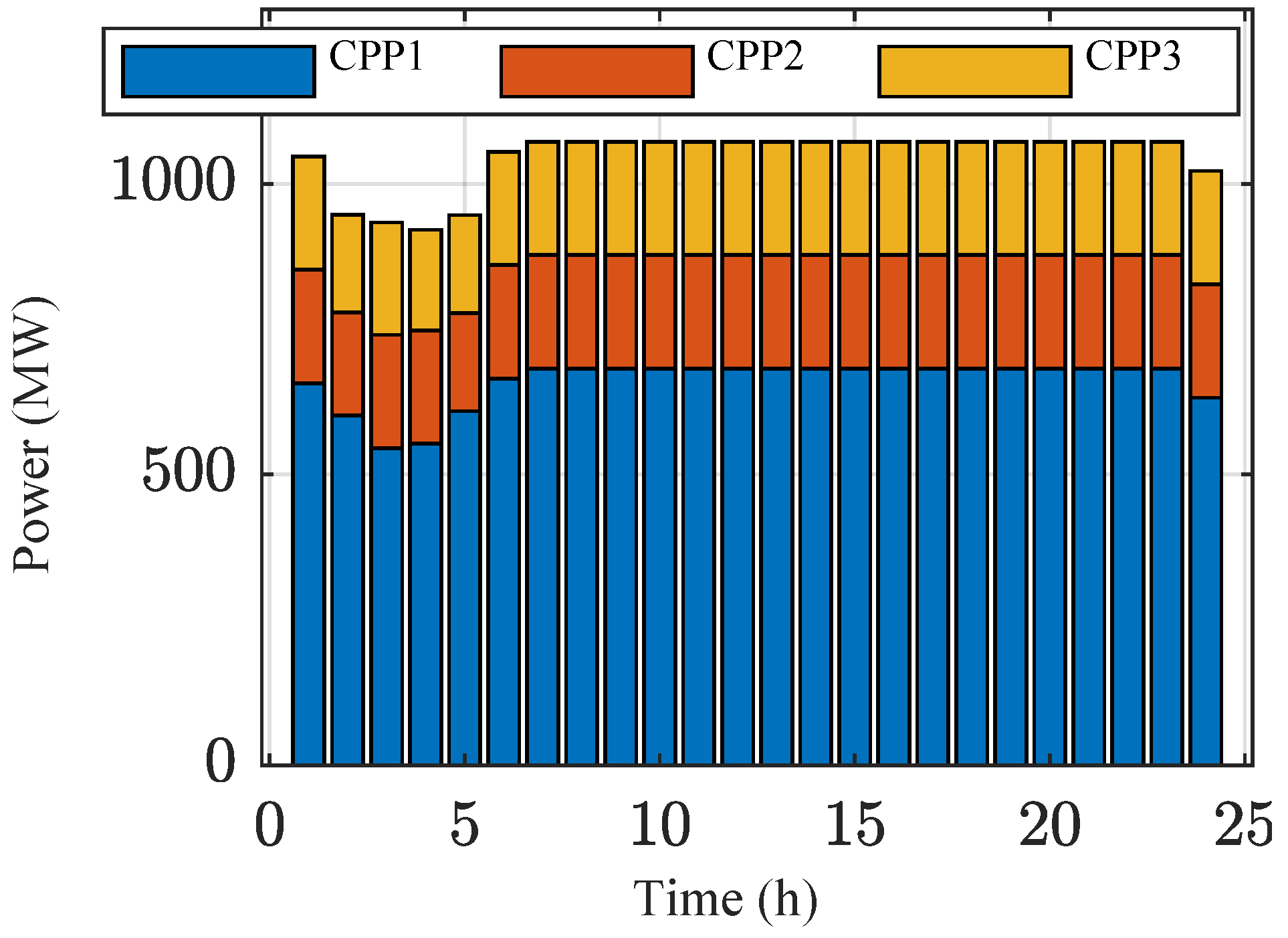
4.2.1. Analysis of Case 1 Results
4.2.2. Analysis of Case 2 Results
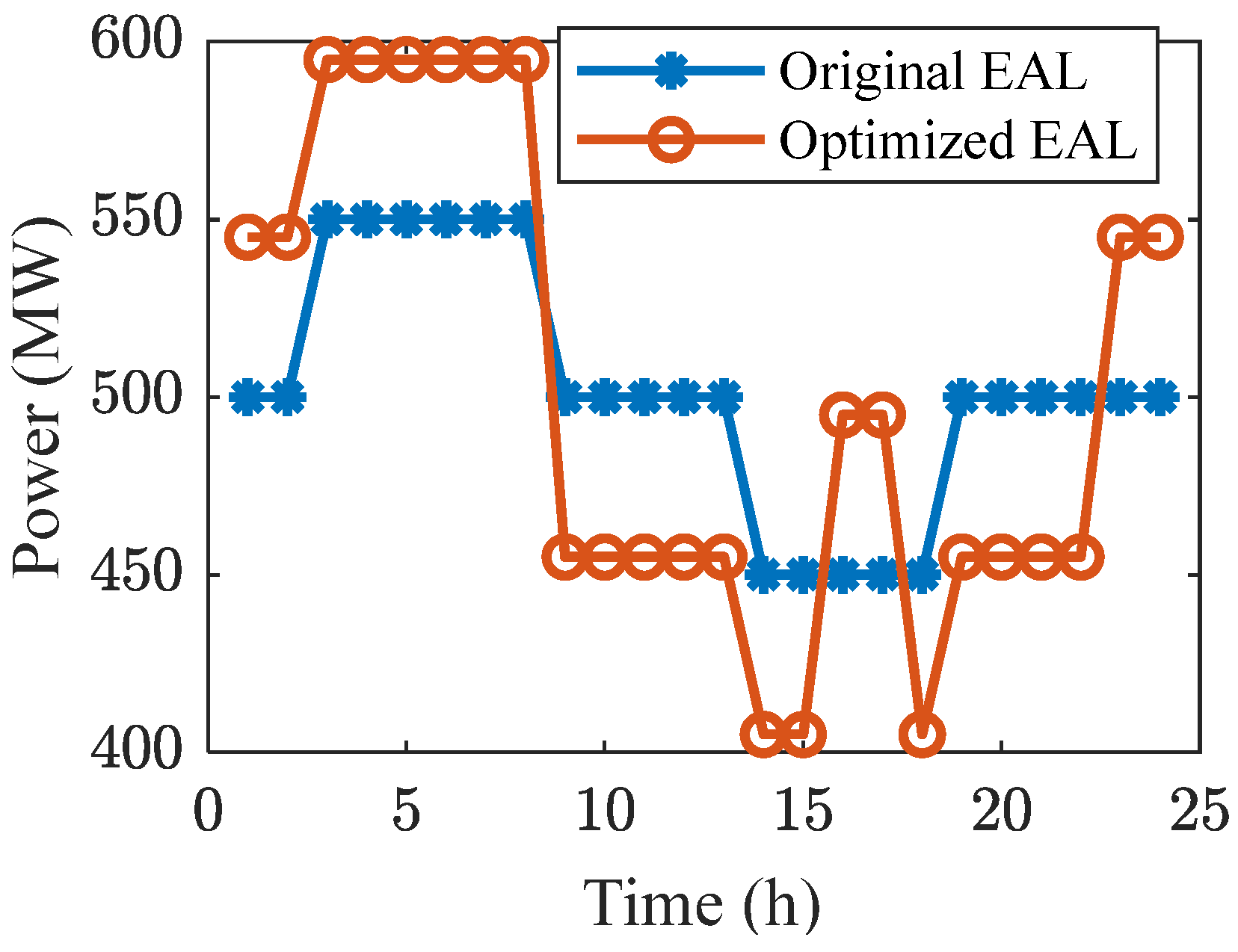
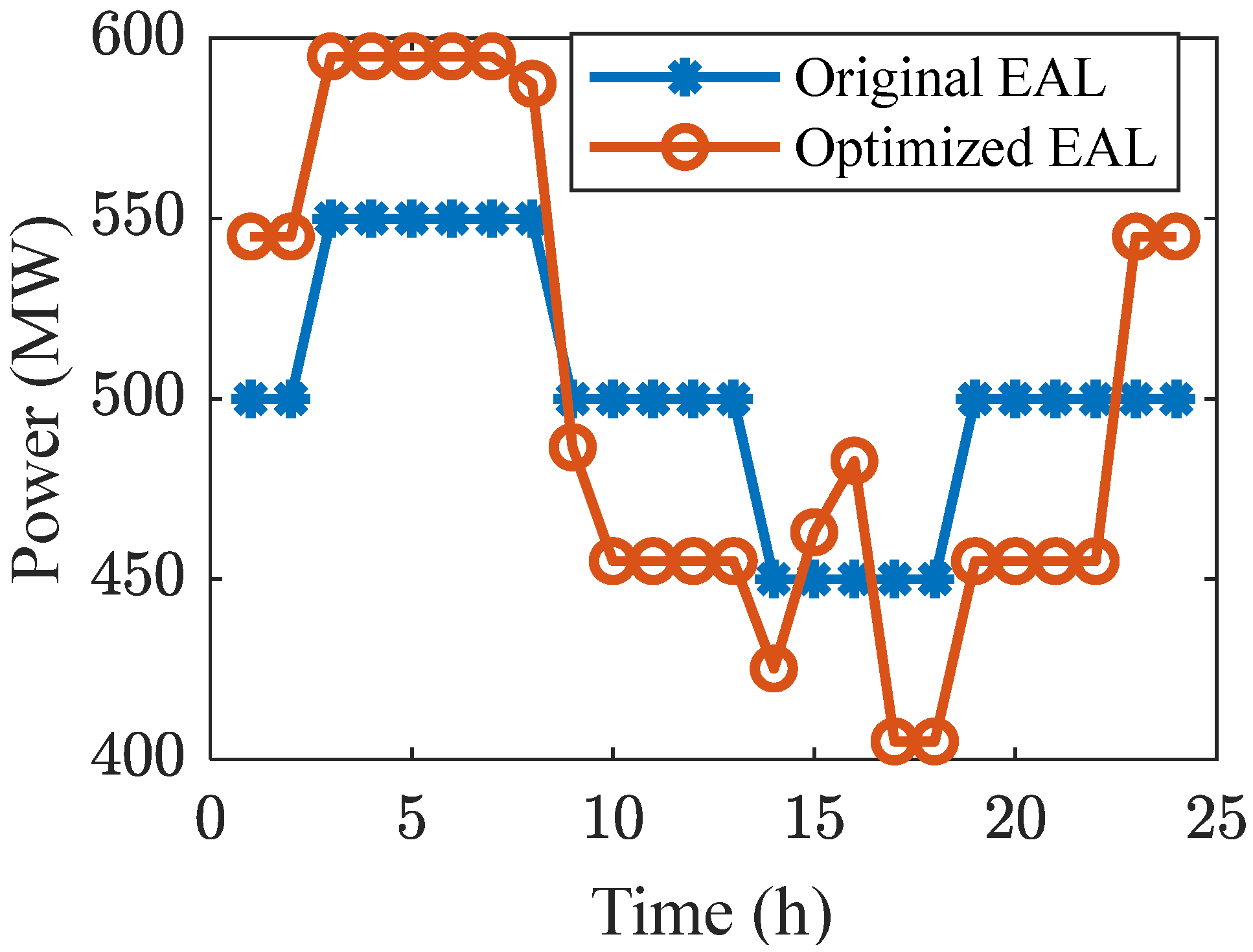
4.2.3. Optimization Effect of EAL
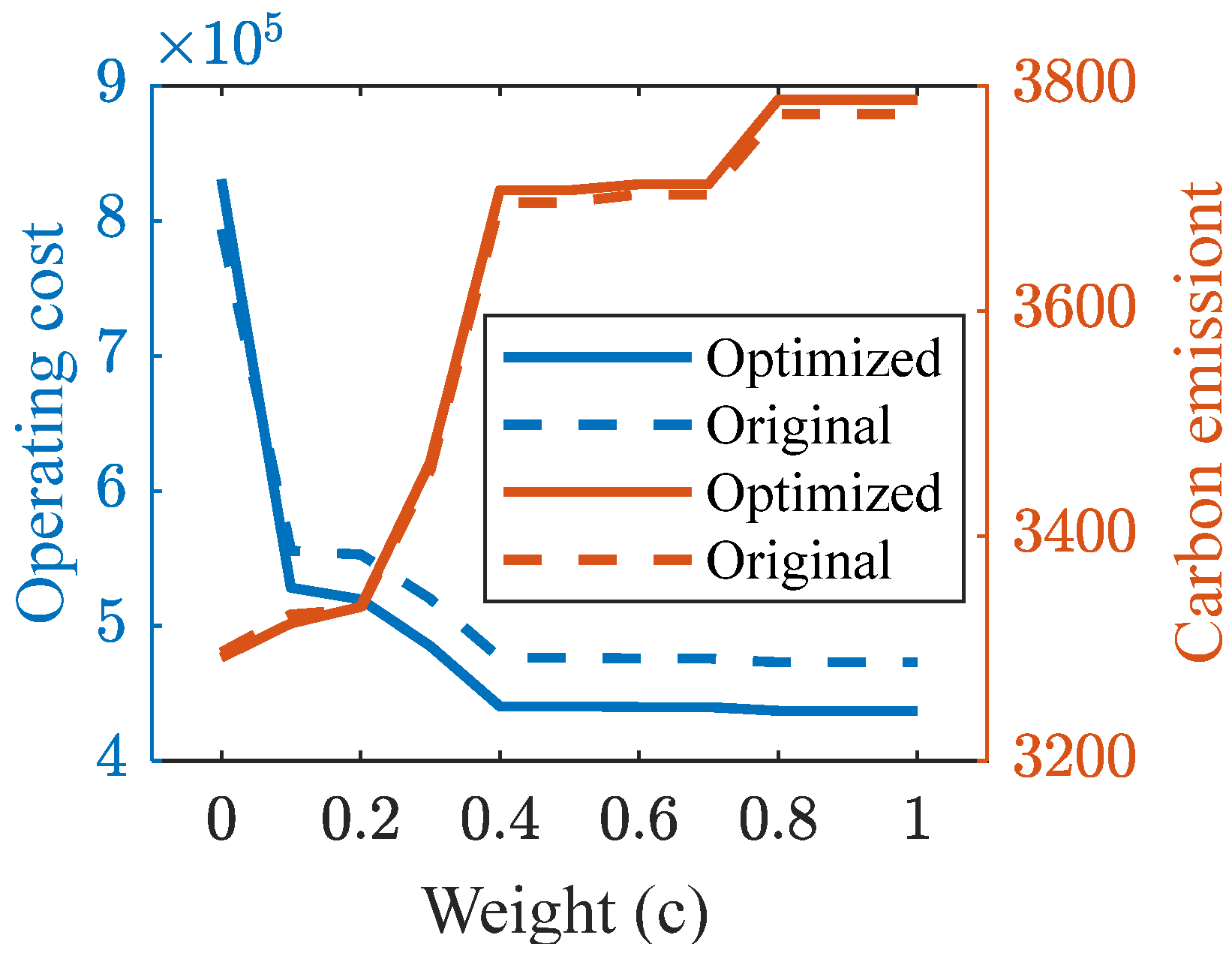
4.2.4. Sensitivity Analysis
5. Conclusions
- (1)
- This paper establishes an optimization scheduling model for an IES containing an electrolytic aluminum load, which comprehensively considers reducing the total carbon emissions of the system and the operating cost of the system. By introducing the whole industrial chain, including hydrogen electrolysis, storage, and utilization, the scheduling model can effectively reduce the carbon emissions generated by thermal power generation and electricity purchase from the large power grid.
- (2)
- The optimization method of the electrolytic aluminum load curve proposed can effectively reduce the operating costs of the system. The optimized electrolytic aluminum load can reduce the total operating cost by 7.62% at most, while the optimization result has little effect on carbon emissions.
- (3)
- The proposed objective function with penalty terms can flexibly adjust the total carbon emissions and operating costs according to actual conditions. Under an appropriate weight, carbon emissions decrease by 11.61% and operating costs drop by 34.53% versus their peak values. The changes in the weights of cost and carbon emissions show opposite trends, mainly because the cost of purchasing hydrogen is much greater than the cost of generating electricity from thermal power units.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rowaihy, F.; Hamieh, A.; Odeh, N.; Hejazi, M.; Al-Juaied, M.; Afifi, A.M.; Hoteit, H. Decarbonizing Saudi Arabia energy and industrial sectors: Assessment of carbon capture cost. Carbon Capture Sci. Technol. 2025, 14, 100375. [Google Scholar] [CrossRef]
- Lima, R.G.A.; Calili, R.F.; Almeida, M.F.L.; Silva, F.L.; Santos, S.; Velásquez, R. Estimating the potential for thermal energy efficiency in the industrial sector: A hybrid model integrating exergy analysis and long-term technology diffusion scenarios. Energy 2024, 313, 133824. [Google Scholar] [CrossRef]
- Li, Q.; Wei, F.C.; Zhou, Y.C.; Li, J.J.; Zhou, G.W.; Wang, Z.H.; Liu, J.F.; Yan, P.G.; Yu, D.R. A scheduling framework for VPP considering multiple uncertainties and flexible resources. Energy 2023, 282, 20. [Google Scholar] [CrossRef]
- Zhou, G.; Bai, M.; Li, H.; Li, J.; Li, Q.; Liu, J.; Yu, D. Multi-objective station-network synergy planning for regional integrated energy system considering energy cascade utilization and uncertainty. Energy Convers. Manag. 2024, 301, 118073. [Google Scholar] [CrossRef]
- Alizad, E.; Hasanzad, F.; Rastegar, H. A tri-level hybrid stochastic-IGDT dynamic planning model for resilience enhancement of community-integrated energy systems. Sustain. Cities Soc. 2024, 117, 105948. [Google Scholar] [CrossRef]
- Li, S.; Li, Z. Coordinating and valuing the flexibility resources in a rural integrated energy system by considering correlated source-load uncertainty. Renew. Energy 2024, 237, 121576. [Google Scholar] [CrossRef]
- Duan, J.; Tian, Q.; Liu, F.; Xia, Y.; Gao, Q. Optimal scheduling strategy with integrated demand response based on stepped incentive mechanism for integrated electricity-gas energy system. Energy 2024, 313, 133689. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, Y.; Wei, F.; Long, Z.; Li, J.; Ma, Y.; Zhou, G.; Liu, J.; Yan, P.; Yu, D. Harmonizing comfort and energy: A multi-objective framework for central air conditioning systems. Energy Convers. Manag. 2024, 314, 118651. [Google Scholar] [CrossRef]
- Lin, H.; Yan, Q.; Li, X.; Dang, J.; Yang, S.; Gejirifu, D.; Yao, L.; Wang, Y. Multi-energy coordinated and flexible operation optimization and revenue reallocation models for integrated micro energy system considering seasonal and daily load characteristics of different buildings. Energy Rep. 2022, 8, 12583–12597. [Google Scholar] [CrossRef]
- Kahraman, U.; Dincer, I. Development of a waste tires-based integrated energy system for multiple useful outputs in sustainable communities. Energy Convers. Manag. 2022, 271, 116305. [Google Scholar] [CrossRef]
- Zhu, X.; Yang, J.; Pan, X.; Li, G.; Rao, Y. Regional integrated energy system energy management in an industrial park considering energy stepped utilization. Energy 2020, 201, 117589. [Google Scholar] [CrossRef]
- Liu, S.; Ding, G.; Gu, R.; Hao, J.; Liu, P.; Qin, W.; Yu, Y.; Han, Y.; Huang, J.; He, W. Co-capture and recovery of ammonia and CO2 driven by microbial electrolysis system coupling with mineral carbon sequestration by industrial wastes. Resour. Conserv. Recycl. 2025, 212, 107931. [Google Scholar] [CrossRef]
- Yao, L.; He, T.; Luo, H. Piggybacking on past problem for faster optimization in aluminum electrolysis process design. Eng. Appl. Artif. Intell. 2023, 126, 106937. [Google Scholar] [CrossRef]
- Sun, M.; Li, B.; Liu, Z. Experimental and numerical analysis on electrolytic bubble group dynamics in the aluminum electrolysis process using the slotted anode. Powder Technol. 2023, 428, 118854. [Google Scholar] [CrossRef]
- Han, Z.; Li, Z.; Wang, W.; Liu, W.; Ma, Q.; Sun, S.; Liu, H.; Zhang, Q.; Cao, Y. Multi-Time Optimization Scheduling Strategy for Integrated Energy Systems Considering Multiple Controllable Loads and Carbon Capture Plants. Energies 2024, 17, 5995. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Ma, Z.; Wang, Y.; Li, Y. Operation optimisation of integrated energy systems based on cooperative game with hydrogen energy storage systems. Int. J. Hydrogen Energy 2023, 48, 37335–37354. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, X.; Pu, Y.; Luo, S.; Liu, H.; Chen, W. Hierarchical optimal scheduling method for regional integrated energy systems considering electricity-hydrogen shared energy. Appl. Energy 2023, 349, 121670. [Google Scholar] [CrossRef]
- Temiz, M.; Dincer, I. Solar and sodium fast reactor-based integrated energy system developed with thermal energy storage and hydrogen. Energy 2023, 284, 129275. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, Y. An economic way to reduce emissions of industrial parks with hydrogen-based integrated energy systems. Int. J. Hydrogen Energy 2025, 106, 1122–1133. [Google Scholar] [CrossRef]
- Li, W.; Liu, W.; Lin, Y.; Liu, C.; Wang, X.; Xu, J. Optimal dispatching of integrated energy system with hydrogen-to-ammonia and ammonia-mixed/oxygen-enriched thermal power. Energy 2025, 316, 134514. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, J.; Zhen, L. Optimization of integrated energy system considering multi-energy collaboration in carbon-free hydrogen port. Transp. Res. Part E Logist. Transp. Rev. 2023, 180, 103351. [Google Scholar] [CrossRef]
- Shi, M.; Vasquez, J.C.; Guerrero, J.M.; Huang, Y. Smart communities—Design of integrated energy packages considering incentive integrated demand response and optimization of coupled electricity-gas-cooling-heat and hydrogen systems. Int. J. Hydrogen Energy 2023, 48, 31063–31077. [Google Scholar] [CrossRef]
- Wang, R.; Yang, L.; Wang, X.; Zhou, Y. Low carbon optimal operation of integrated energy system based on concentrating solar power plant and power to hydrogen. Alex. Eng. J. 2023, 71, 39–50. [Google Scholar] [CrossRef]
- Yue, X.; Liao, S.; Xu, J.; Ke, D.; Wang, H.; Yang, J.; He, X. Collaborative optimization of renewable energy power systems integrating electrolytic aluminum load regulation and thermal power deep peak shaving. Appl. Energy 2024, 373, 123869. [Google Scholar] [CrossRef]
- Abdelsamie, M.M.; Hassan Ali, M.I. Technoeconomic feasibility of integrating carbon capture technology with primary aluminum production using an advanced cogeneration waste heat recovery system. Chem. Eng. J. 2025, 519, 165078. [Google Scholar] [CrossRef]
- Brough, D.; Jouhara, H. The aluminium industry: A review on state-of-the-art technologies, environmental impacts and possibilities for waste heat recovery. Int. J. Thermofluids 2020, 1–2, 100007. [Google Scholar] [CrossRef]
- Wu, K.; Jiang, M.; Huang, Y.; Dai, Z.; Wang, X.; Duan, Z.; Wang, Y.; Li, G. Optimization of multi-objective capacity allocation and performance analysis for integrated energy systems considering hydrogen storage. Energy 2025, 325, 136160. [Google Scholar] [CrossRef]
- Li, S.; Zhang, T.; Niu, L.; Yue, Q. Analysis of the development scenarios and greenhouse gas (GHG) emissions in China’s aluminum industry till 2030. J. Clean. Prod. 2021, 290, 125859. [Google Scholar] [CrossRef]
- Fan, S.L.; Ai, Q.; He, X. Risk analysis on dispatch of virtual power plant based on chance constrained programming. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2015, 35, 4025–4034. [Google Scholar]
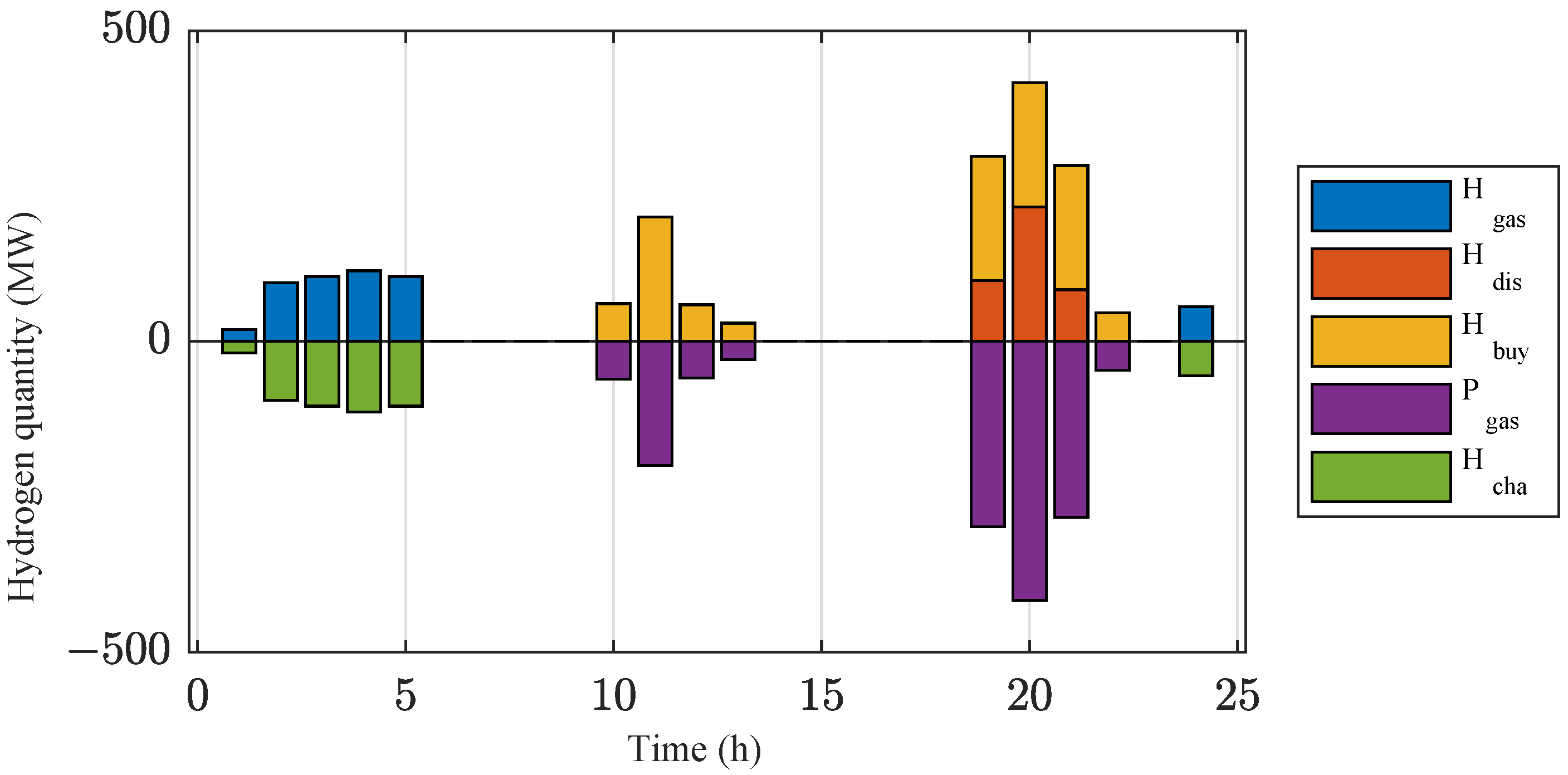
| CPP | |||||
|---|---|---|---|---|---|
| 1 | [150, 682.5] | [56, 56] | 0.00047 | 7.05 | 420 |
| 2 | [30, 195] | [26, 26] | 0.0002 | 4.23 | 970 |
| 3 | [30, 195] | [27, 27] | 0.0002 | 4.23 | 700 |
| Case 1 () | Case 2 () | Changes (Case 2 − Case 1) | Improvement (Changes/Case 2) | |
|---|---|---|---|---|
| 169,246 | 21,725.2 | −147,520.8 | −87.16% | |
| 33,756.8 | 95,854.92 | 62,098.1 | 183.96% | |
| 0 | 0 | 0 | 0.00% | |
| 189,071.8 | 184,340 | −4731.86 | −2.50% | |
| 42,772.24 | 87,147.06 | 44,374.8 | 103.75% | |
| 69,678.7 | 322,193.1 | 252,514 | 362.40% | |
| 437,010 | 519,550.6 | 82,540.6 | 18.89% | |
| 3787.56 | 3336.9 | −450.66 | −11.90% |
| Case 1 () | Case 3 () | Changes (Case 3 − Case 1) | Improvement (Changes/Case 3) | |
|---|---|---|---|---|
| 169,246 | 164,852.7 | −4393.34 | −2.67% | |
| 33,756.8 | 138,721.8 | 104,965 | 75.67% | |
| 0 | 0 | 0 | 0 | |
| 189,071.8 | 188,897.5 | −174.3 | −0.09% | |
| 42,772.24 | 58,119.88 | 15,347.6 | 26.41% | |
| 69,678.7 | 87,318.7 | 17,640 | 20.20% | |
| 437,010 | 473,057.8 | 36,047.8 | 7.62% | |
| 3787.56 | 3775.1 | −12.46 | −0.33% |
| Case 2 () | Case 4 () | Changes (Case 4 − Case 2) | Improvement (Changes/Case 4) | |
|---|---|---|---|---|
| 21,725.2 | 36,063.44 | 14,338.24 | 66.00% | |
| 95,854.92 | 83,354.6 | −12,500.3 | −13.04% | |
| 0 | 0 | 0 | 0 | |
| 184,340 | 181,993.4 | −2346.54 | −1.27% | |
| 87,147.06 | 92,300.6 | 5153.54 | 5.91% | |
| 322,193.1 | 325,888.8 | 3695.72 | 1.15% | |
| 519,550.6 | 552,891.2 | 33,340.58 | 6.42% | |
| 3336.9 | 3334.94 | −1.96 | −0.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, W.; He, B.; Cao, Z.; Liu, G.; Chuan, B.; Zhang, Q.; Cao, Y. Multi-Objective Optimization Strategy for Integrated Energy System Considering Mixed Participation of Aluminum Electrolysis and Hydrogen Production Industries. Energies 2025, 18, 6109. https://doi.org/10.3390/en18236109
Wang J, Liu W, He B, Cao Z, Liu G, Chuan B, Zhang Q, Cao Y. Multi-Objective Optimization Strategy for Integrated Energy System Considering Mixed Participation of Aluminum Electrolysis and Hydrogen Production Industries. Energies. 2025; 18(23):6109. https://doi.org/10.3390/en18236109
Chicago/Turabian StyleWang, Jinkun, Wei Liu, Baohua He, Zhendong Cao, Gang Liu, Bin Chuan, Qiang Zhang, and Yue Cao. 2025. "Multi-Objective Optimization Strategy for Integrated Energy System Considering Mixed Participation of Aluminum Electrolysis and Hydrogen Production Industries" Energies 18, no. 23: 6109. https://doi.org/10.3390/en18236109
APA StyleWang, J., Liu, W., He, B., Cao, Z., Liu, G., Chuan, B., Zhang, Q., & Cao, Y. (2025). Multi-Objective Optimization Strategy for Integrated Energy System Considering Mixed Participation of Aluminum Electrolysis and Hydrogen Production Industries. Energies, 18(23), 6109. https://doi.org/10.3390/en18236109







