Heat Dissipation and Structural Optimization of Cylindrical Lithium-Ion Batteries with Phase Change Material–Liquid Hybrid Cooling: A Numerical Study
Abstract
1. Introduction
2. Numerical Simulation
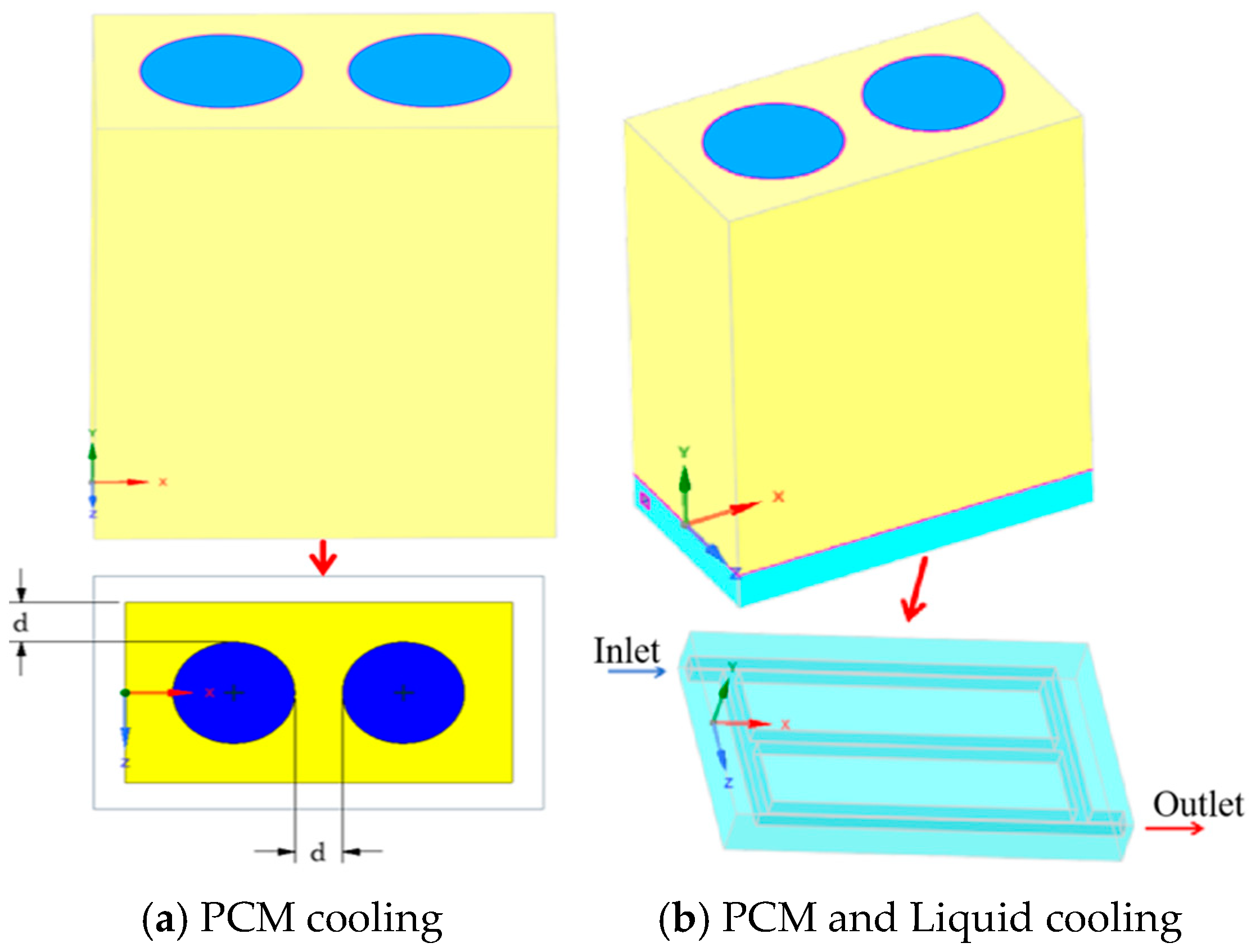
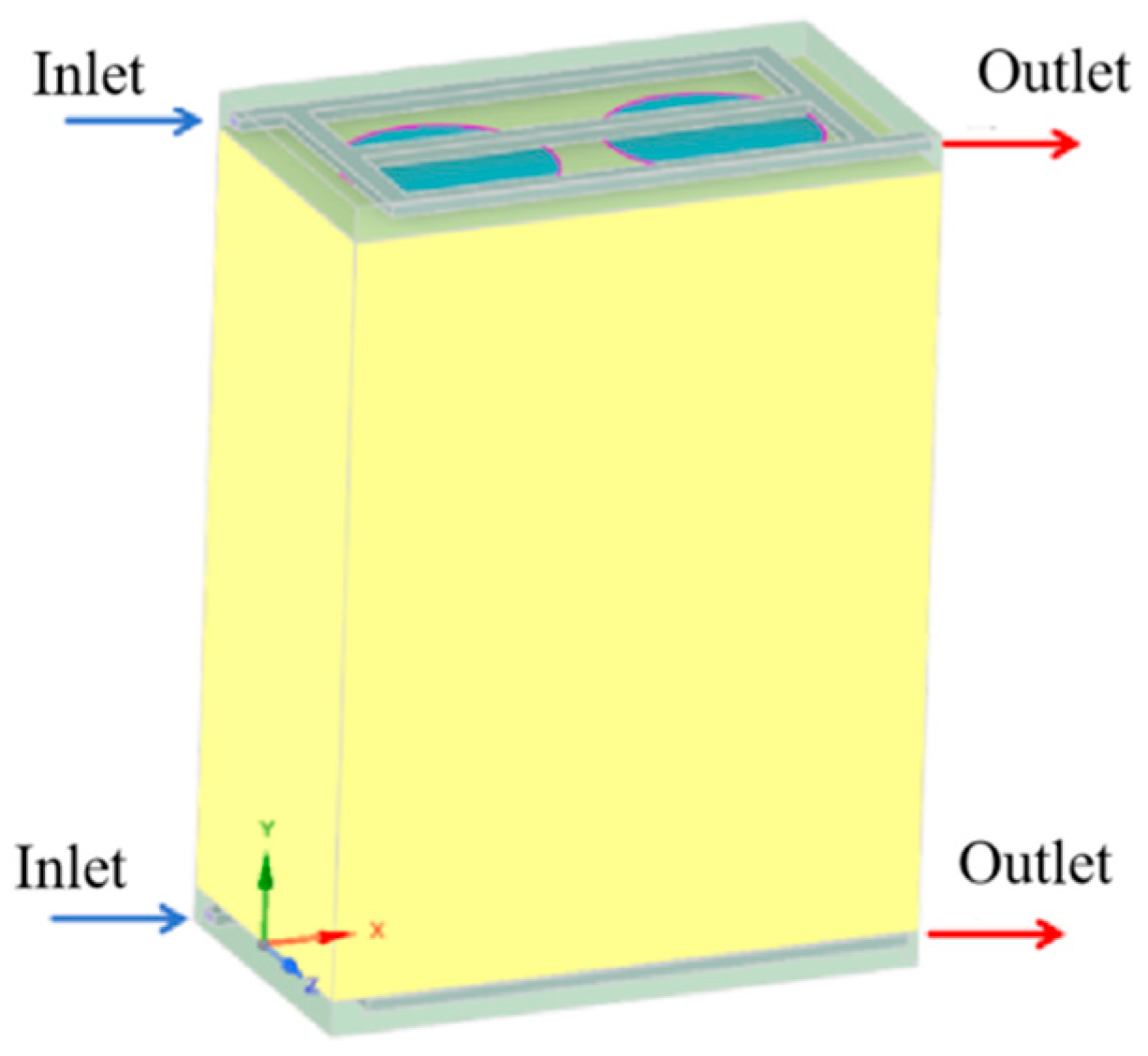
2.1. Geometrical Model
2.2. Thermal Model
2.2.1. Battery Model
- (1)
- The battery is represented as a homogeneous solid with a constant heat generation rate per unit volume, and its thermal conductivity is defined as anisotropic [26];
- (2)
- The battery’s thermophysical properties are considered constant and independent of external factors;
- (3)
- The battery’s internal heat generation is treated as uniformly distributed.
- (4)
- Thermal radiation effects are neglected.
2.2.2. Phase Change Material Cooling Model
- (1)
- The liquid PCM after melting is considered incompressible.
- (2)
- The PCM’s thermophysical properties are considered constant and independent of external conditions.
- (3)
- Thermal radiation is neglected.
- (4)
- The PCM is assumed to undergo no volume change during the phase transition process.
2.2.3. Liquid Cooling Model
- (1)
- Thermal contact resistance at the interfaces among the battery pack, PCM, and the liquid-cooling plate is neglected.
- (2)
- The coolant is treated as a single-phase, incompressible fluid under steady conditions.
- (3)
- The thermophysical properties of the liquid-cooling plate and coolant are assumed constant and temperature-independent.
2.3. Initial Conditions and Boundary Conditions
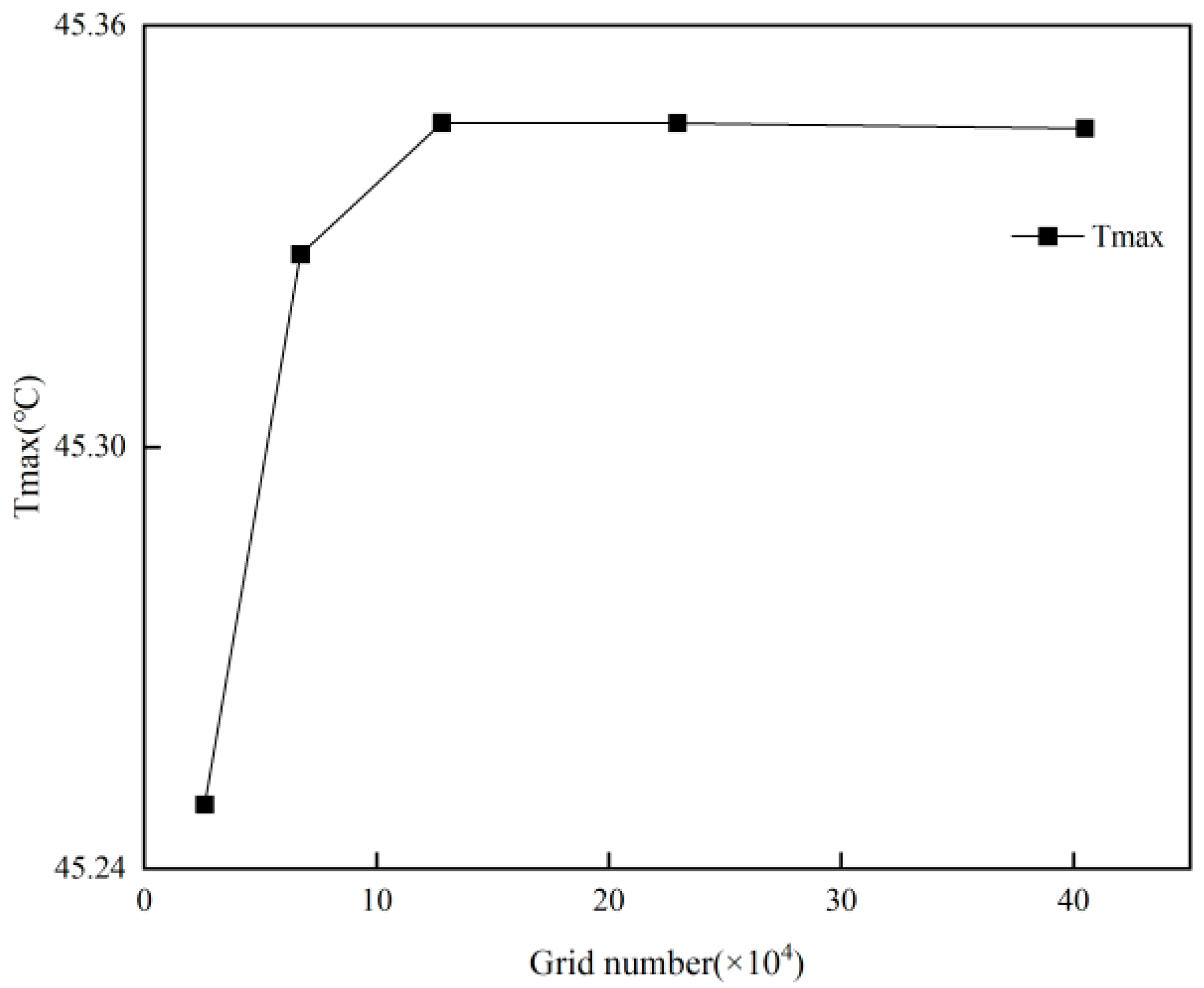
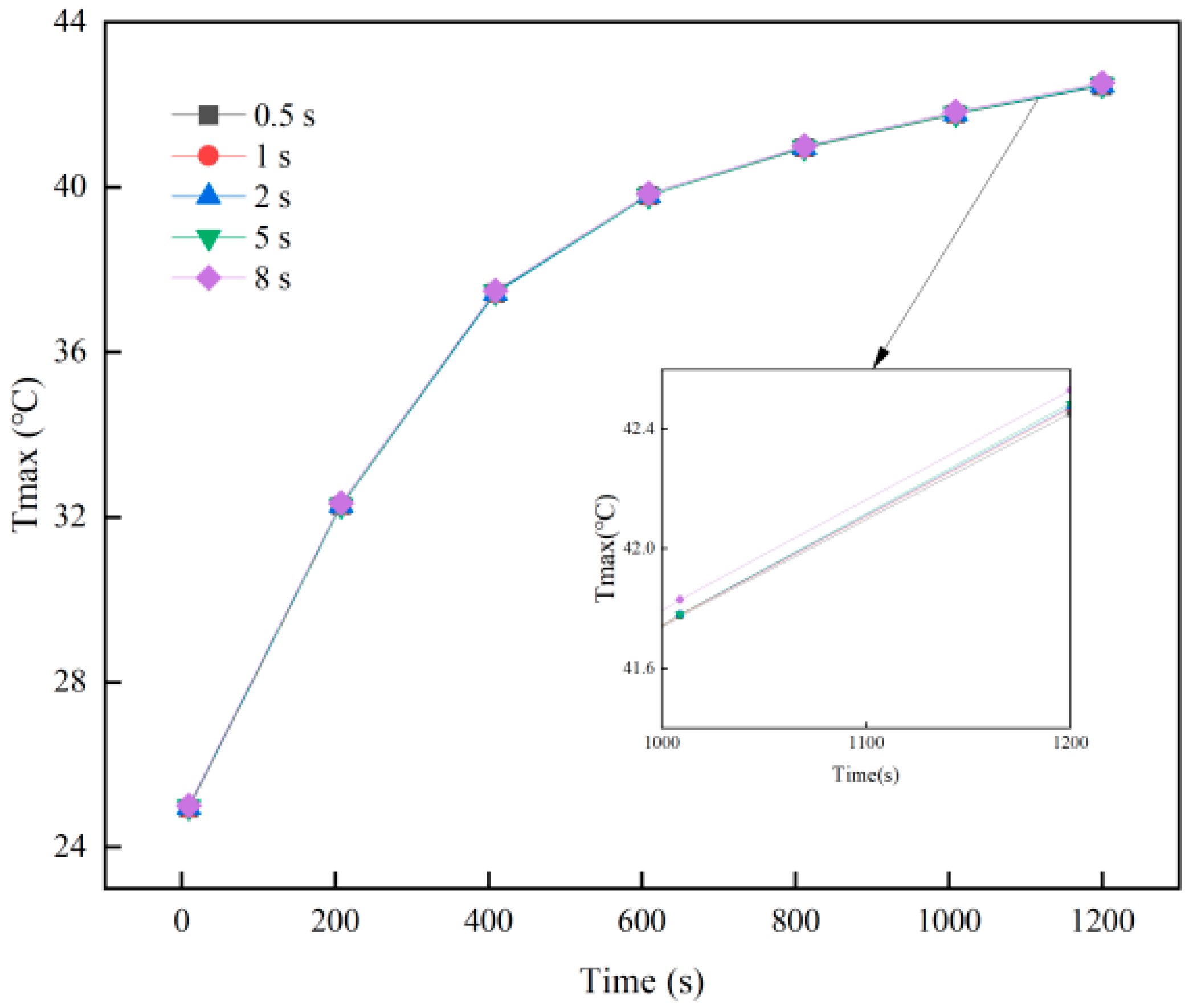
2.4. Grid Independence and Time-Step Independence Verification
3. Results and Discussion
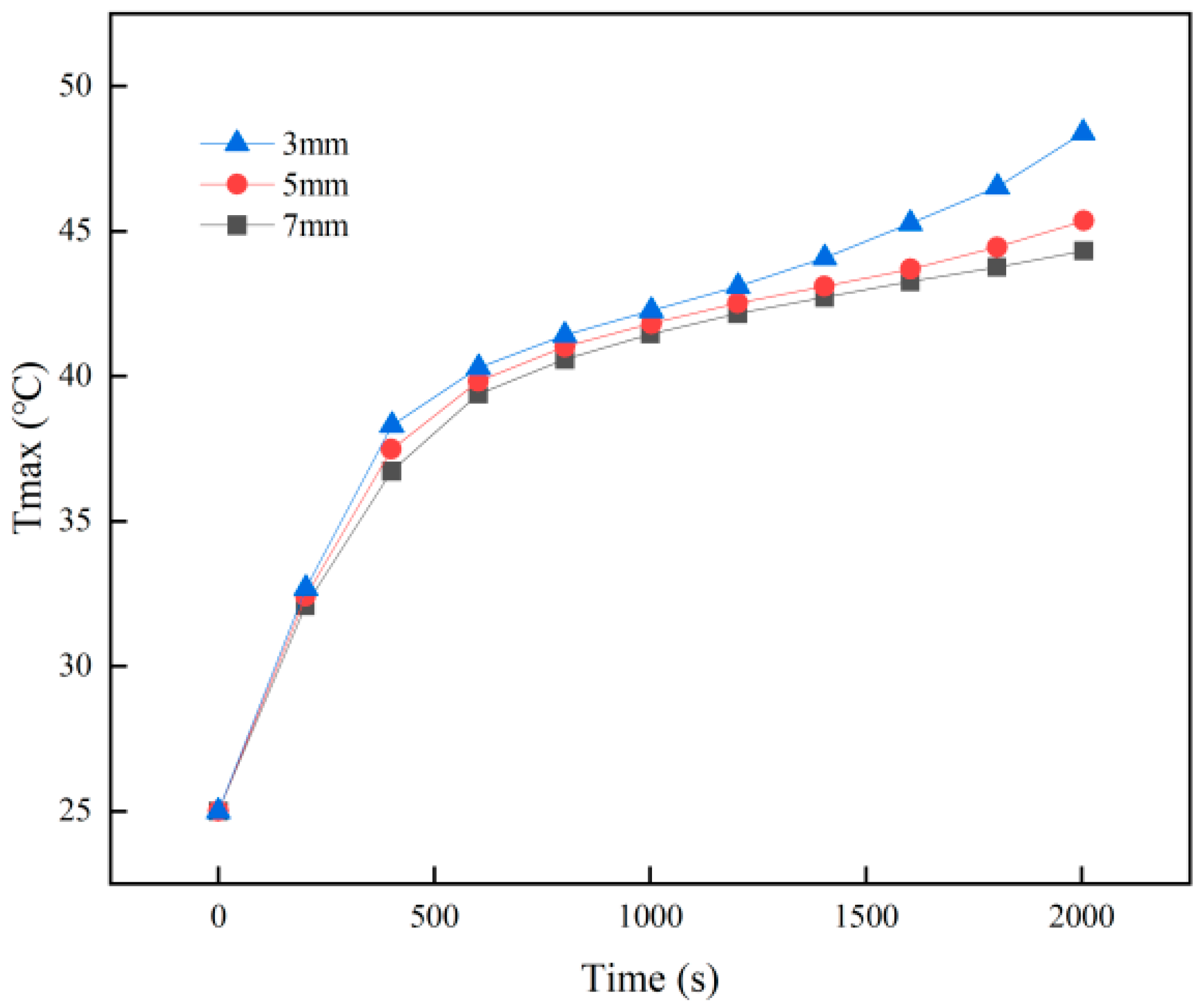
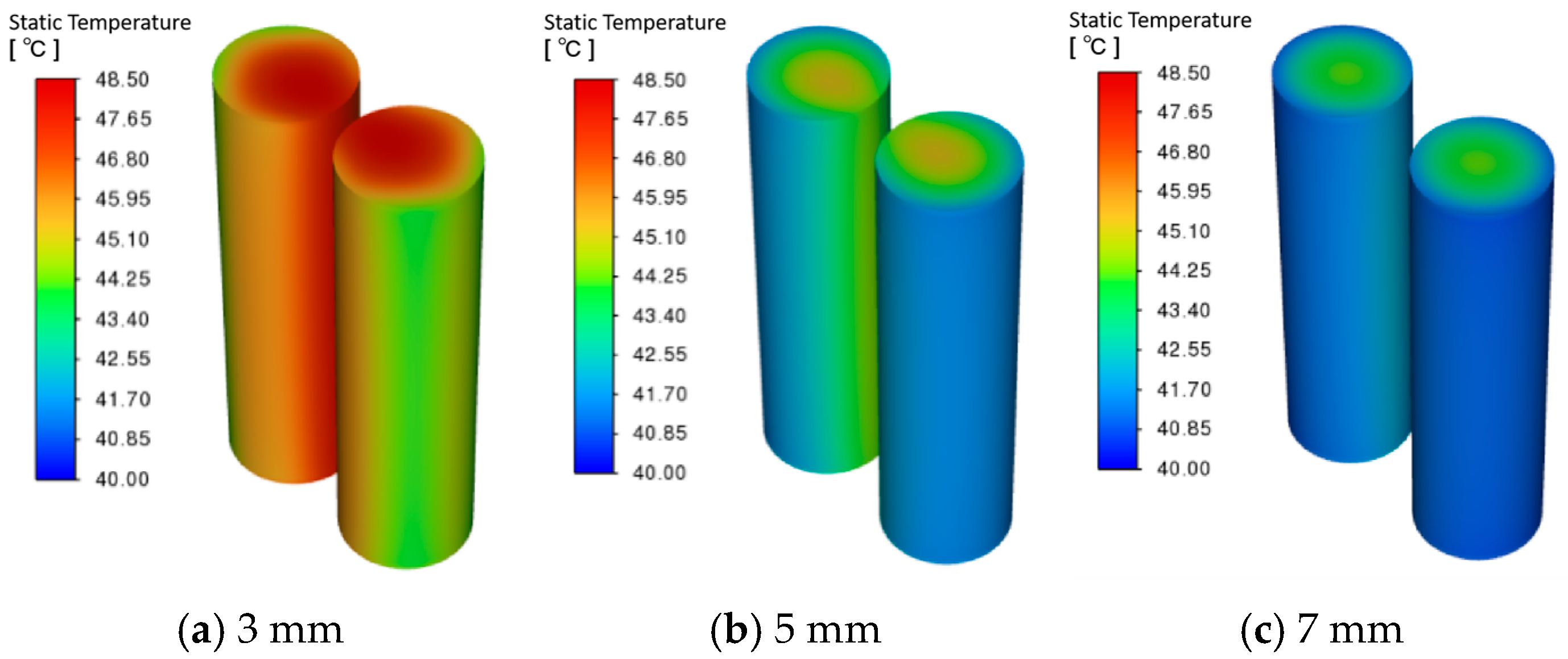
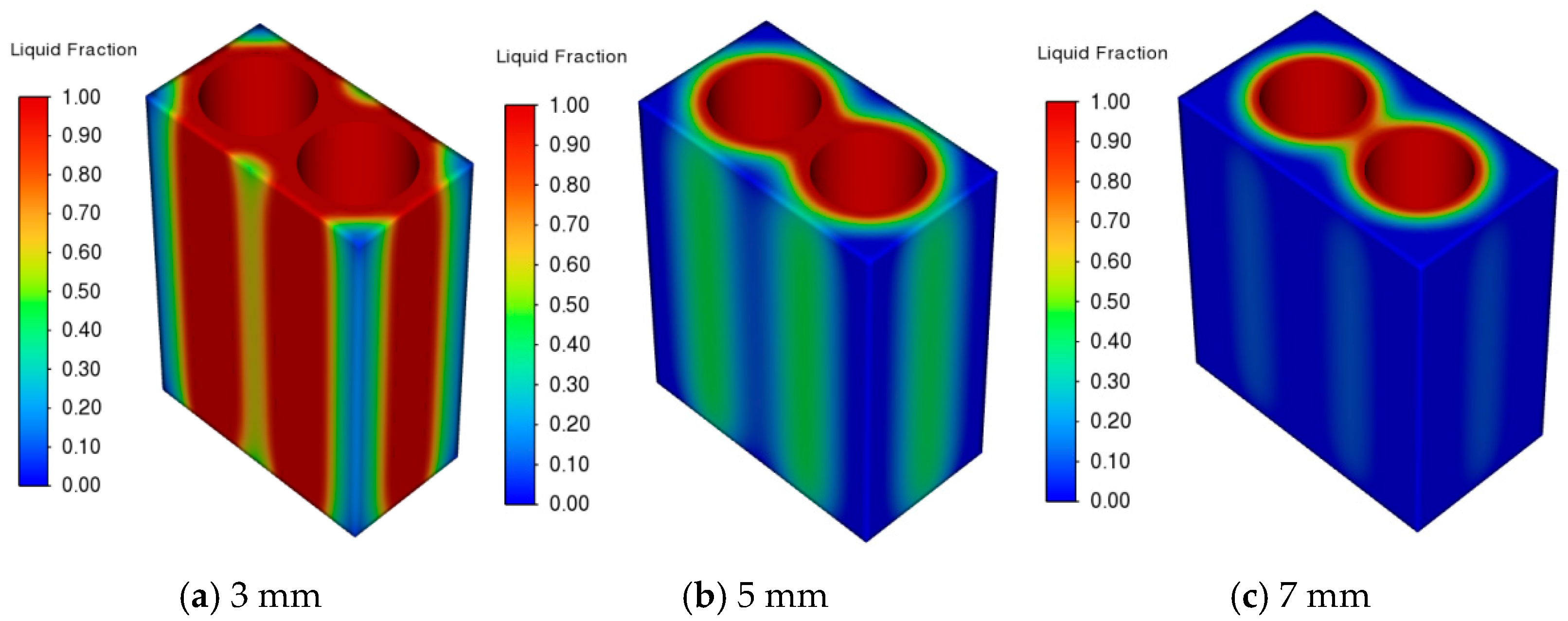
3.1. Effect of Battery Spacing on PCM–Battery Pack Cooling Performance
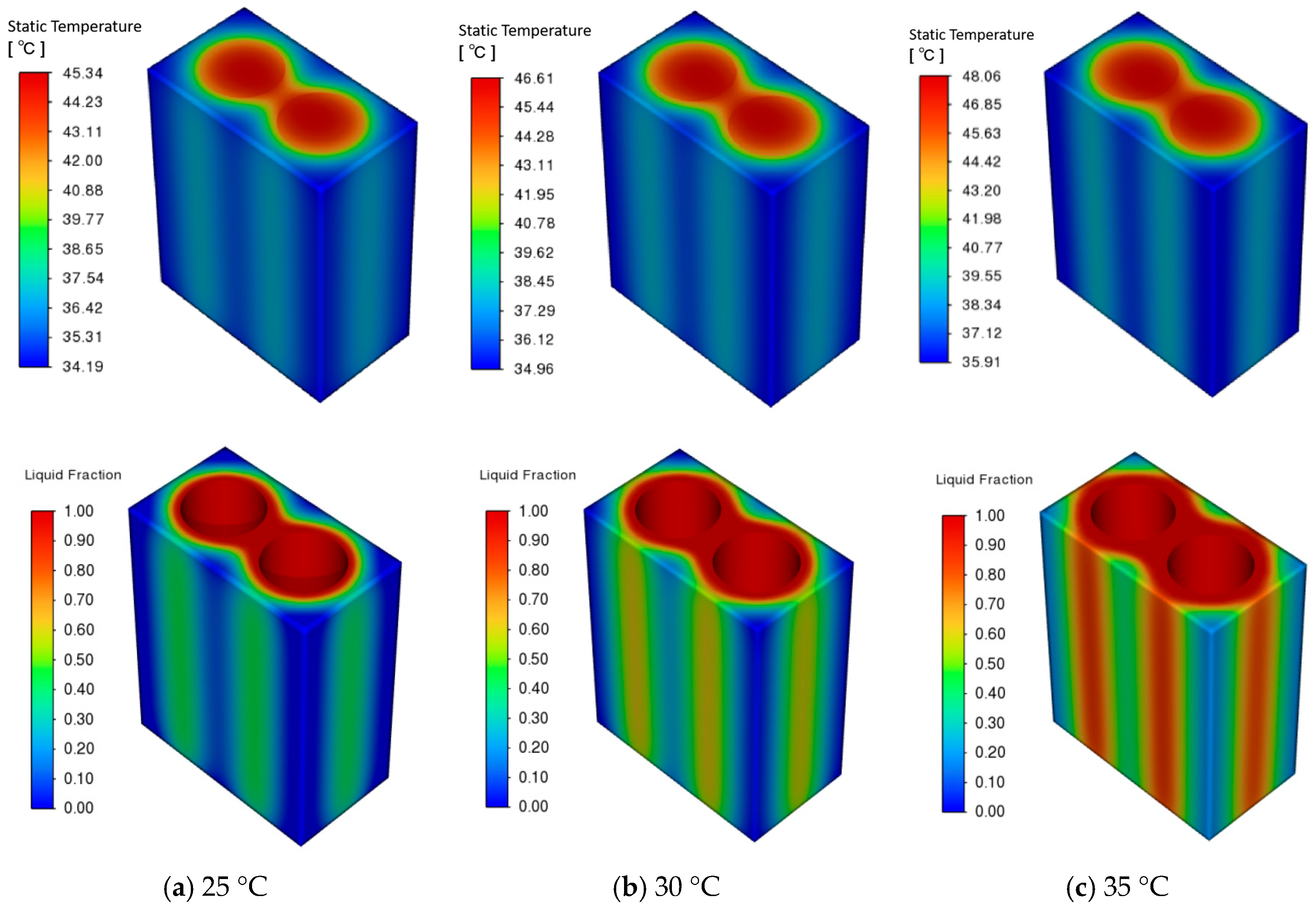
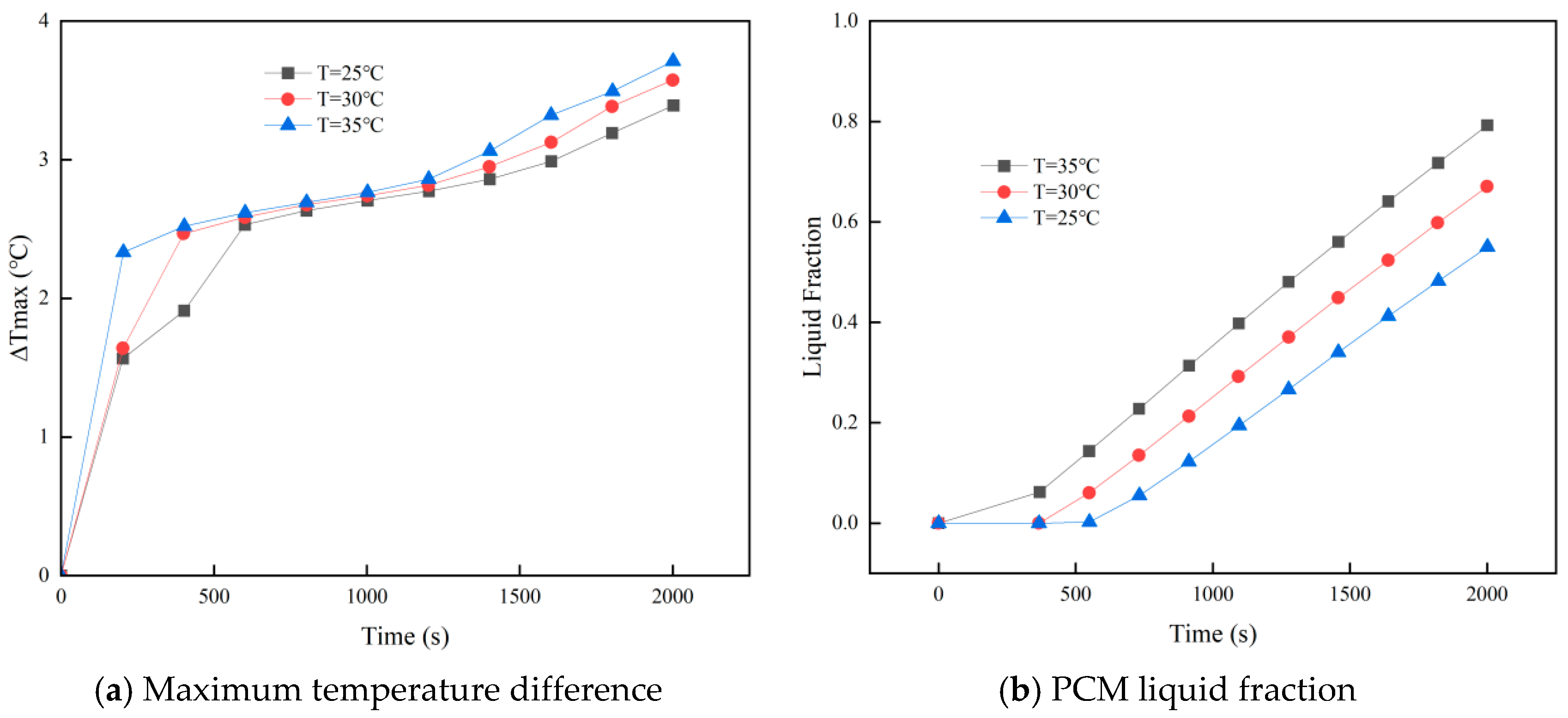
3.2. Effect of Ambient Temperature on PCM–Battery Pack Cooling Performance
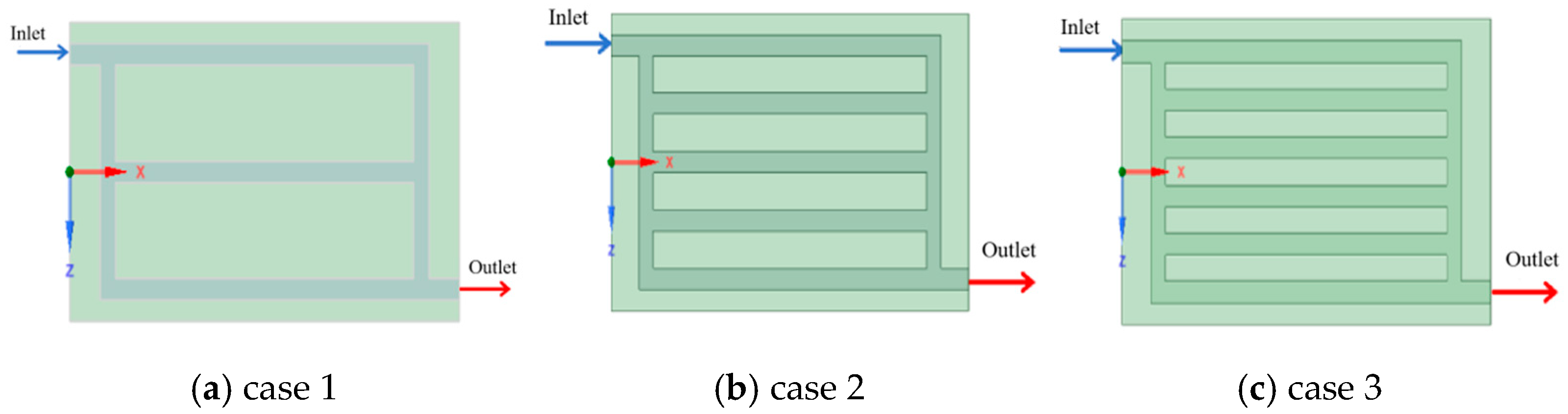
3.3. Effect of Inlet Position of the Liquid Cooling Plate on Battery Pack Heat Removal
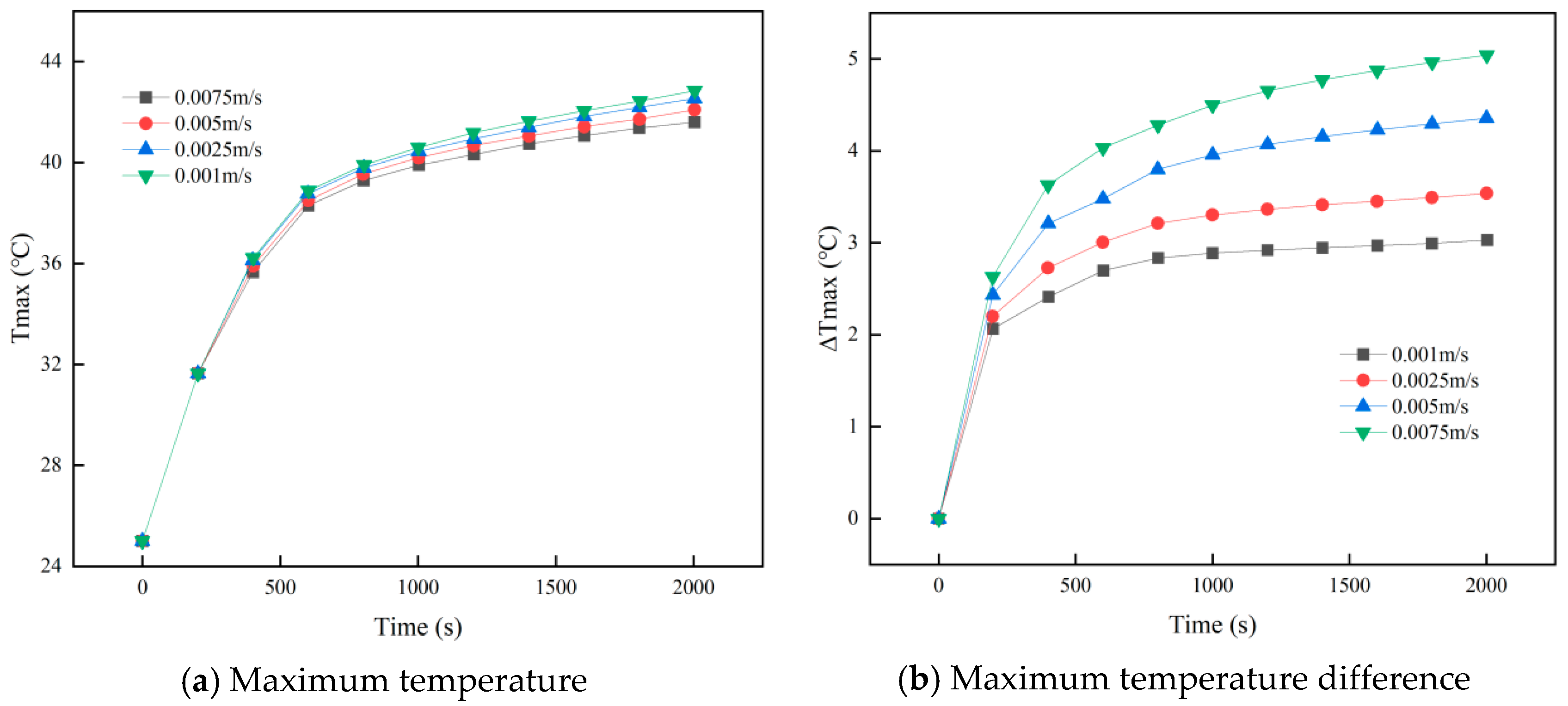
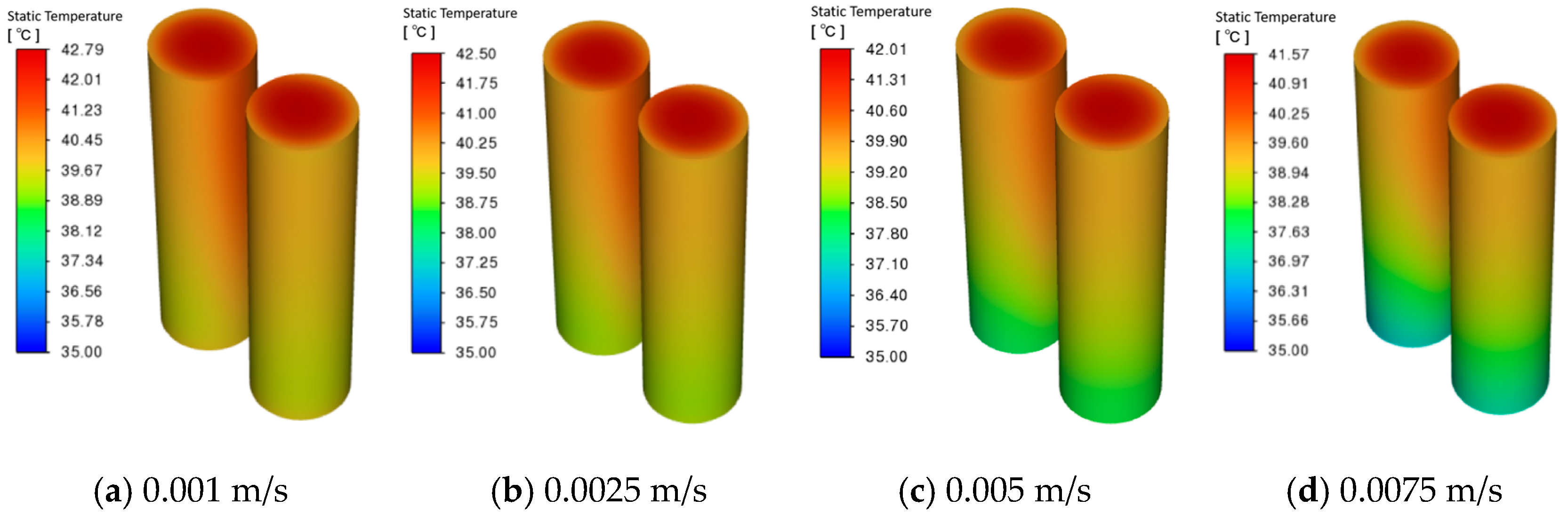
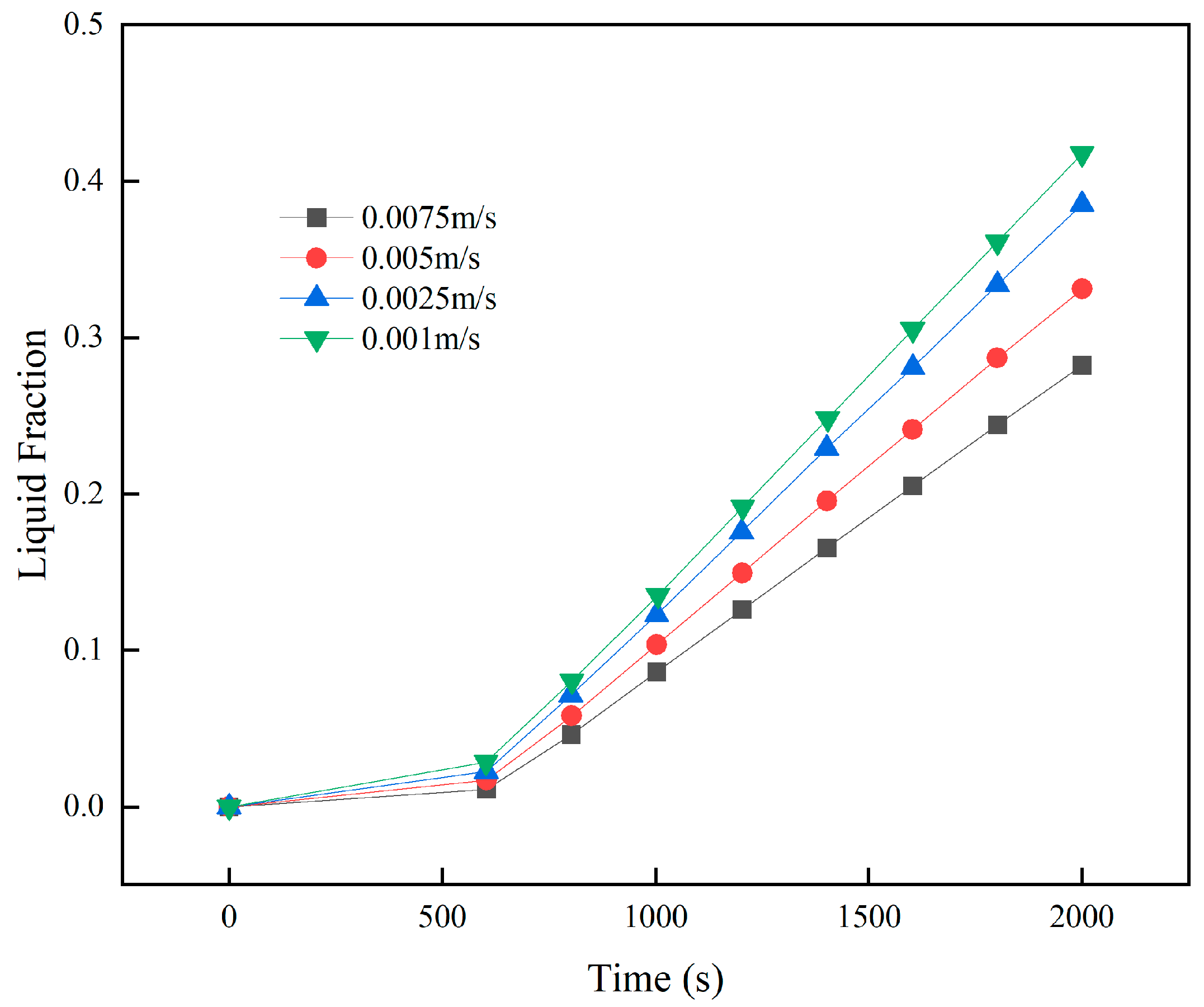
3.4. Effect of Coolant Flow Rate on Battery Pack Heat Removal
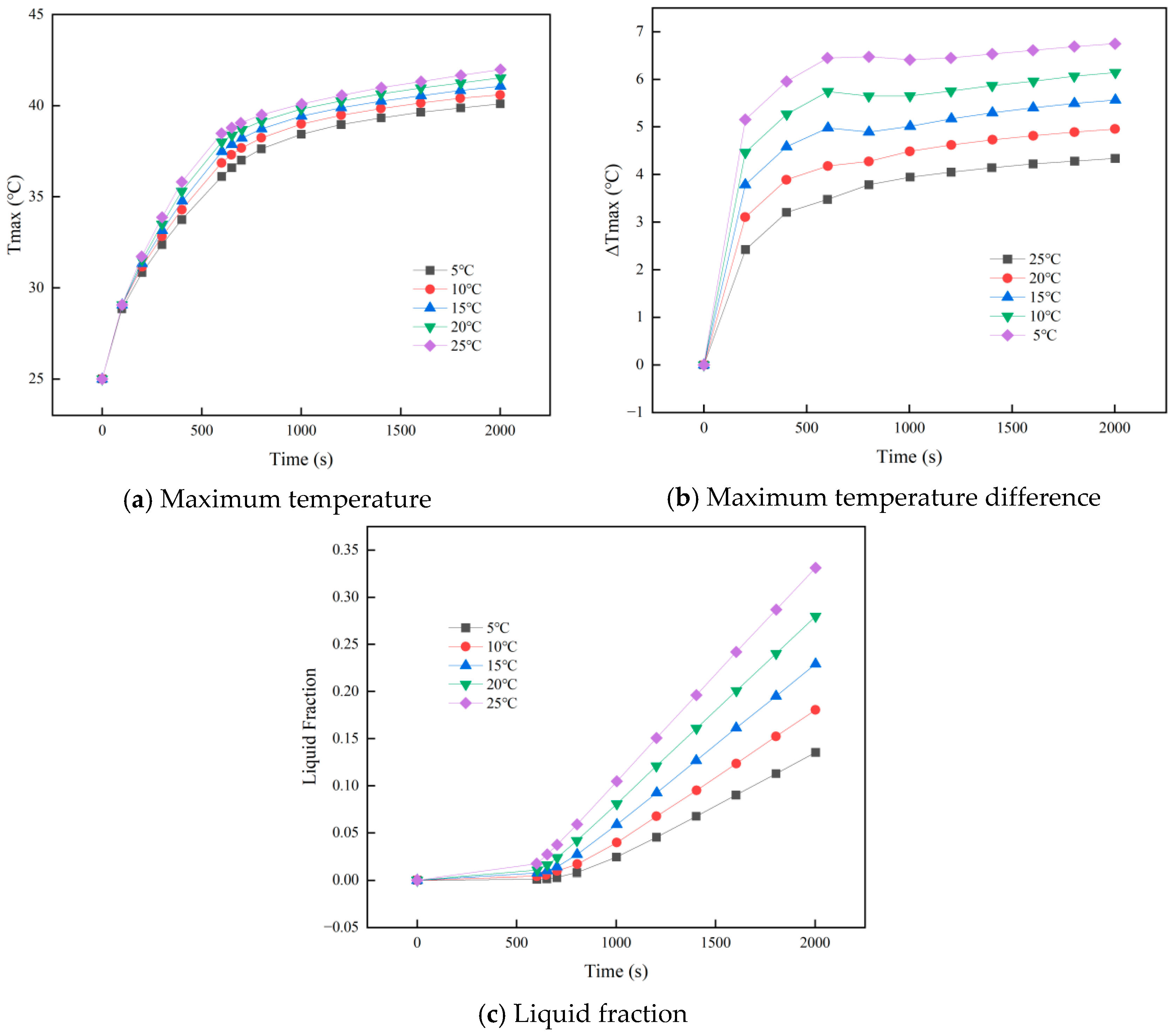
3.5. Effect of Coolant Temperature on Battery Pack Thermal Performance
3.6. Design Optimization of the PCM–Liquid Cooling Thermal Management System for Batteries
4. Conclusions
- Larger cell spacing improves PCM filling, lowering the battery pack’s peak temperature and temperature difference while increasing the PCM liquid fraction. In contrast, higher ambient temperatures raise all three metrics under identical conditions.
- When the outlet position is fixed, changing the inlet location has minimal impact on cooling performance. Higher coolant velocities reduce peak battery temperature and PCM liquid fraction, but velocities ≥ 0.0075 m/s cause the maximum temperature difference to exceed safe limits. At 0.005 m/s, lowering the coolant temperature below 15 °C further reduces the maximum temperature and PCM liquid fraction, yet increases the temperature difference beyond safe levels. Thus, coolant parameters must balance overall thermal performance.
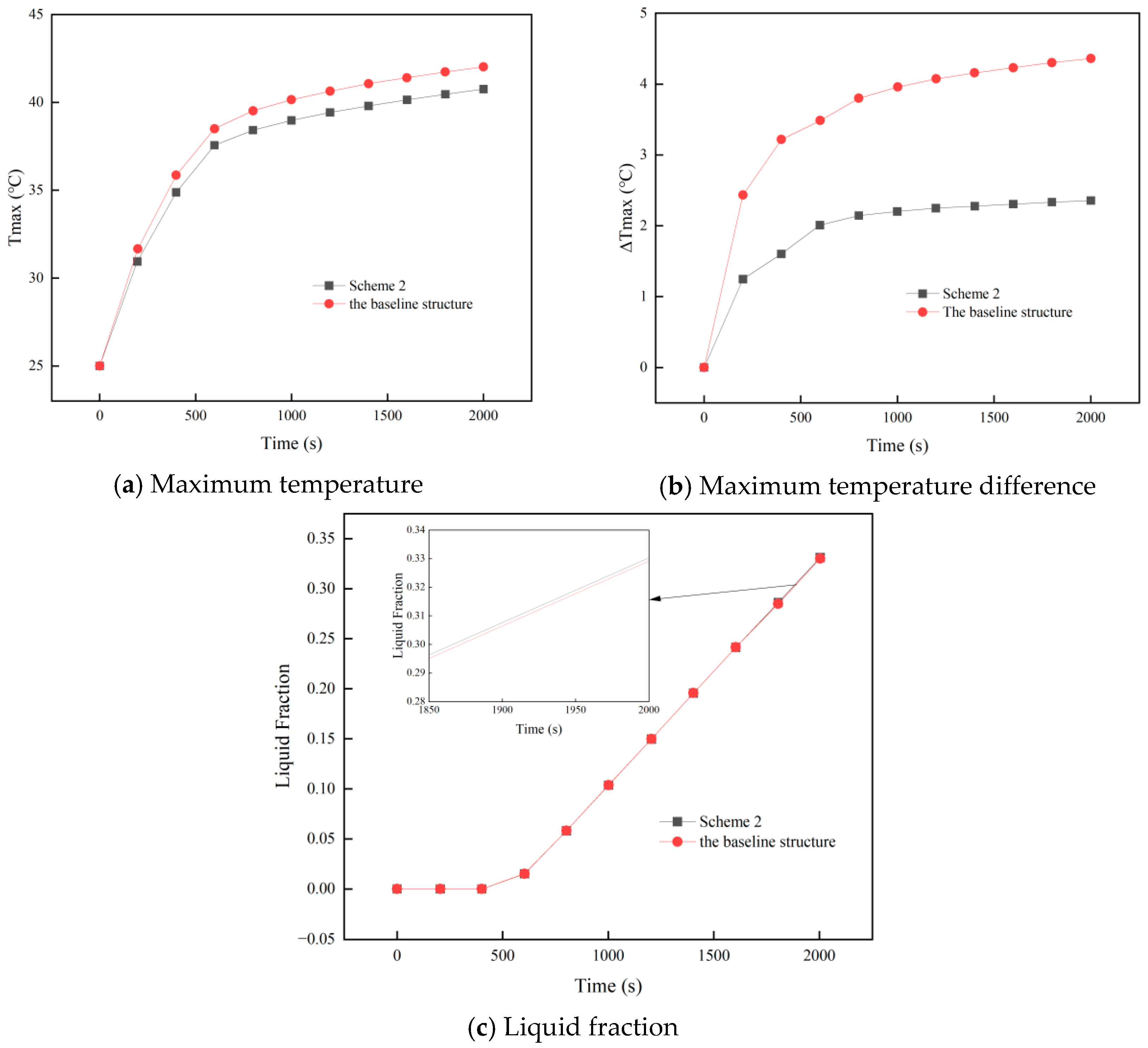
- Of the two structural optimization schemes (Scheme 1: more liquid-cooling channels; Scheme 2: evenly distributed cooling plates above and below the battery module), Scheme 2 performs better. It lowers both the peak temperature and the maximum temperature difference, enhancing thermal uniformity while maintaining PCM utilization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Ma, S.; Jin, H.; Wang, R.; Jiang, Y. Performance Analysis of Liquid Cooling Battery Thermal Management System in Different Cooling Cases. J. Energy Storage 2023, 72, 108651. [Google Scholar] [CrossRef]
- Theodore, A.M. Promising Cathode Materials for Rechargeable Lithium-Ion Batteries: A Review. J. Sustain. Energy 2023, 14, 51–58. [Google Scholar] [CrossRef]
- Qaderi, A.; Veysi, F. Investigation of a Water-NEPCM Cooling Thermal Management System for Cylindrical 18650 Li-Ion Batteries. Energy 2022, 244, 122570. [Google Scholar] [CrossRef]
- Huang, Y.; Mei, P.; Lu, Y.; Huang, R.; Yu, X.; Chen, Z.; Roskilly, A.P. A Novel Approach for Lithium-Ion Battery Thermal Management with Streamline Shape Mini Channel Cooling Plates. Appl. Therm. Eng. 2019, 157, 113623. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Yang, B.; Cai, S. A Review of Battery Thermal Management Systems Using Liquid Cooling and PCM. J. Energy Storage 2024, 76, 109836. [Google Scholar] [CrossRef]
- Ge, X.; Li, X.; Jin, Y.; Zhang, G.; Deng, J.; Ge, J. Experimental Investigation on Thermal Management System of Composite Phase Change Material Coupled with Serpentine Tubes for Battery Module. Appl. Therm. Eng. 2023, 219, 119501. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Kalogiannis, T.; Jaguemont, J.; Jin, L.; Behi, H.; Karimi, D.; Beheshti, H.; Van Mierlo, J.; Berecibar, M. A Comparative Study between Air Cooling and Liquid Cooling Thermal Management Systems for a High-Energy Lithium-Ion Battery Module. Appl. Therm. Eng. 2021, 198, 117503. [Google Scholar] [CrossRef]
- Huang, R.; Li, Z.; Hong, W.; Wu, Q.; Yu, X. Experimental and Numerical Study of PCM Thermophysical Parameters on Lithium-Ion Battery Thermal Management. Energy Rep. 2020, 6, 8–19. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Zhang, S.; Tang, B. Phase Change Materials for Lithium-Ion Battery Thermal Management Systems: A Review. J. Energy Storage 2024, 80, 110259. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Selman, J.R. A Novel Thermal Management System for Electric Vehicle Batteries Using Phase-Change Material. J. Electrochem. Soc. 2000, 147, 3231. [Google Scholar] [CrossRef]
- Xu, Q.; Huang, H.; Gu, Y.; Lin, X.-M.; Zhu, K.; Yin, M.; Li, L.; Wang, X.; Zheng, K. Performance Comparison of Phase Change Material/Liquid Cooling Hybrid Battery Thermal Management System under Different Cyclic Charging-Discharging Mode Designs. Appl. Therm. Eng. 2025, 266, 125639. [Google Scholar] [CrossRef]
- Fan, R.; Zheng, N.; Sun, Z. Evaluation of Fin Intensified Phase Change Material Systems for Thermal Management of Li-Ion Battery Modules. Int. J. Heat Mass Transf. 2021, 166, 120753. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, Z.; Xiong, X.; Zhu, J.; Gao, Q.; Wang, H.; Wu, H. Novel Concept Design of Low Energy Hybrid Battery Thermal Management System Using PCM and Multistage Tesla Valve Liquid Cooling. Appl. Therm. Eng. 2023, 220, 119680. [Google Scholar] [CrossRef]
- Patil, M.S.; Seo, J.-H.; Lee, M.-Y. A Novel Dielectric Fluid Immersion Cooling Technology for Li-Ion Battery Thermal Management. Energy Convers. Manag. 2021, 229, 113715. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, C.; Li, X.; Yang, B. A Review of Non-Uniform Load Distribution and Solutions in Data Centers: Micro-Scale Liquid Cooling and Large-Scale Air Cooling. Energies 2025, 18, 149. [Google Scholar] [CrossRef]
- Meier, M.; Strangas, E.G. Cooling Systems for High-Speed Machines—Review and Design Considerations. Energies 2025, 18, 3954. [Google Scholar] [CrossRef]
- Sun, Z.; Yao, Q.; Jin, H.; Xu, Y.; Hang, W.; Chen, H.; Li, K.; Shi, L.; Gu, J.; Zhang, Q. A Novel In-Situ Sensor Calibration Method for Building Thermal Systems Based on Virtual Samples and Autoencoder. Energy 2024, 297, 131314. [Google Scholar] [CrossRef]
- Li, L.; Xu, P.; Li, Q.; Yin, Z.; Zheng, R.; Wu, J.; Bao, J.; Bai, W.; Qi, H.; Tan, D. Multi-Field Coupling Particle Flow Dynamic Behaviors of the Microreactor and Ultrasonic Control Method. Powder Technol. 2025, 454, 120731. [Google Scholar] [CrossRef]
- Li, C.; Ding, Y.; Zhou, Z.; Jin, Y.; Ren, X.; Cao, C.; Hu, H. Parameter Optimization and Sensitivity Analysis of a Lithium-Ion Battery Thermal Management System Integrated with Composite Phase Change Material. Appl. Therm. Eng. 2023, 228, 120530. [Google Scholar] [CrossRef]
- Weng, J.; Xiao, C.; Yang, X.; Ouyang, D.; Chen, M.; Zhang, G.; Waiming, E.L.; Yuen, R.K.K.; Wang, J. An Energy-Saving Battery Thermal Management Strategy Coupling Tubular Phase-Change-Material with Dynamic Liquid Cooling under Different Ambient Temperatures. Renew. Energy 2022, 195, 918–930. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, Y.; Huang, Y. Optimisation with Adiabatic Interlayers for Liquid-Dominated Cooling System on Fast Charging Battery Packs. Appl. Therm. Eng. 2019, 147, 636–646. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Z.; Li, J.; Cao, X. Performance Analysis and Optimization of a Hybrid Battery Thermal Management System Integrating PCM with Chinese Knot-Shaped Liquid Cooling Plate. Int. Commun. Heat Mass Transf. 2024, 159, 108261. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A Critical Review of Battery Thermal Performance and Liquid Based Battery Thermal Management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Zhao, J.; Rao, Z.; Li, Y. Thermal Performance of Mini-Channel Liquid Cooled Cylinder Based Battery Thermal Management for Cylindrical Lithium-Ion Power Battery. Energy Convers. Manag. 2015, 103, 157–165. [Google Scholar] [CrossRef]
- Mousavi, S.; Siavashi, M.; Zadehkabir, A. A New Design for Hybrid Cooling of Li-Ion Battery Pack Utilizing PCM and Mini Channel Cold Plates. Appl. Therm. Eng. 2021, 197, 117398. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, L.; Wei, W.; Wen, D.; Guo, Q.; Liang, W.; Xiao, L. Study of the Thermal Properties during the Cyclic Process of Lithium Ion Power Batteries Using the Electrochemical-Thermal Coupling Model. Appl. Therm. Eng. 2018, 137, 11–22. [Google Scholar] [CrossRef]
- Pilali, E.; Soltani, M.; Hatefi, M.; Shafiei, S.; Salimi, M.; Amidpour, M. Passive Thermal Management Systems with Phase Change Material-Based Methods for Lithium-Ion Batteries: A State-of-the-Art Review. J. Power Sources 2025, 632, 236345. [Google Scholar] [CrossRef]
- Khan, S.A.; Xiangrong, L.I.; Lau, K.T.; Dong, K.; He, S.; Wabaidur, S.M.; Thakur, A.K.; Zhao, J. Metallic PCM-Based Battery Thermal Management System for Fast Charging/Discharging Applications. Int. Commun. Heat Mass Transf. 2024, 155, 107473. [Google Scholar] [CrossRef]
- He, R.; Song, K.; Wu, X.; Zhang, Q.; Zhang, K.; Su, M.; Hou, Q. Effectiveness Analysis of Novel Battery Thermal Management Systems Combining Phase Change Material and Air-Cooled Technologies. Appl. Therm. Eng. 2025, 264, 125499. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, F.; Yang, W.; Gui, Y.; Zhang, Y. A Hybrid Thermal Management System with Liquid Cooling and Composite Phase Change Materials Containing Various Expanded Graphite Contents for Cylindrical Lithium-Ion Batteries. Appl. Therm. Eng. 2022, 200, 117702. [Google Scholar] [CrossRef]



| Thermal Properties | Value |
|---|---|
| Density (kg/m3) | 2055 |
| Specific heat capacity (J/(kg·K)) | 1299 |
| Thermal conductivity (W/(m·K)) | kx: 0.9 kz: 29.6 |
| Volumetric heat source | 17,460 (1C) 70,182 (2C) 140,418 (3C) 280,706 (4C) |
| PCM | Al | Water | |
|---|---|---|---|
| Density (kg/m3) | 822 | 2719 | 998.2 |
| Specific heat capacity (J/(kg·K)) | 1770 | 871 | 4182 |
| Thermal conductivity (W/(m·K)) | 0.36 | 202.4 | 0.6 |
| Dynamic viscosity (μPa/s) | 0.00365 | - | 0.001003 |
| Melting temperature (°C) | 35/40 |
| Tmax (°C) | ∆Tmax (°C) | Liquid Fraction | |
|---|---|---|---|
| Schemes 1 | 42.50 | 3.53 | 0.3856 |
| Schemes 2 | 42.48 | 3.62 | 0.3784 |
| Schemes 3 | 42.47 | 3.63 | 0.3758 |
| Tmax (°C) | ∆Tmax (°C) | Liquid Fraction | |
|---|---|---|---|
| Case 1 | 42.01 | 4.35 | 0.329 |
| Case 2 | 42.00 | 4.40 | 0.331 |
| Case 3 | 41.98 | 4.46 | 0.327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, Z.; Wu, X.; Chen, Z.; Xiao, J.; Yang, S. Heat Dissipation and Structural Optimization of Cylindrical Lithium-Ion Batteries with Phase Change Material–Liquid Hybrid Cooling: A Numerical Study. Energies 2025, 18, 6108. https://doi.org/10.3390/en18236108
Tan Z, Wu X, Chen Z, Xiao J, Yang S. Heat Dissipation and Structural Optimization of Cylindrical Lithium-Ion Batteries with Phase Change Material–Liquid Hybrid Cooling: A Numerical Study. Energies. 2025; 18(23):6108. https://doi.org/10.3390/en18236108
Chicago/Turabian StyleTan, Zhukui, Xin Wu, Zerui Chen, Jian Xiao, and Shang Yang. 2025. "Heat Dissipation and Structural Optimization of Cylindrical Lithium-Ion Batteries with Phase Change Material–Liquid Hybrid Cooling: A Numerical Study" Energies 18, no. 23: 6108. https://doi.org/10.3390/en18236108
APA StyleTan, Z., Wu, X., Chen, Z., Xiao, J., & Yang, S. (2025). Heat Dissipation and Structural Optimization of Cylindrical Lithium-Ion Batteries with Phase Change Material–Liquid Hybrid Cooling: A Numerical Study. Energies, 18(23), 6108. https://doi.org/10.3390/en18236108






