Short-Term Load Forecasting for Electricity Spot Markets Across Different Seasons Based on a Hybrid VMD-LSTM-Random Forest Model
Abstract
1. Introduction
1.1. A Review of Artificial Intelligence and Machine Learning Methods Research
1.2. A Review of Research on Combined Forecasting Methods
1.3. Content and Contributions
2. Proposed Short-Term Load Forecasting Model
2.1. Fundamental Methods
2.1.1. Principle of VMD
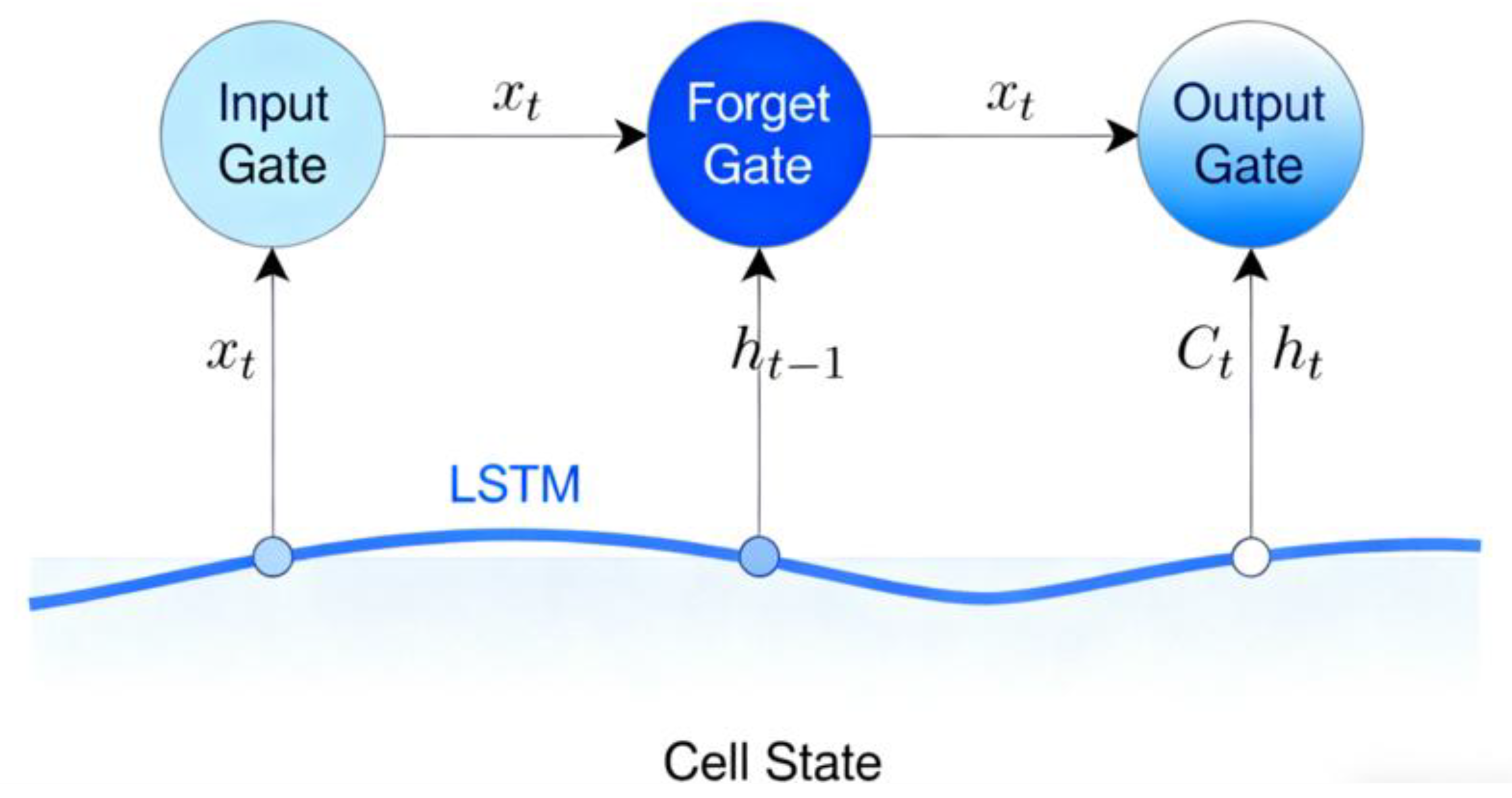
2.1.2. LSTM Neural Network
2.1.3. Random Forest Algorithm
2.1.4. Particle Swarm Optimization Algorithm
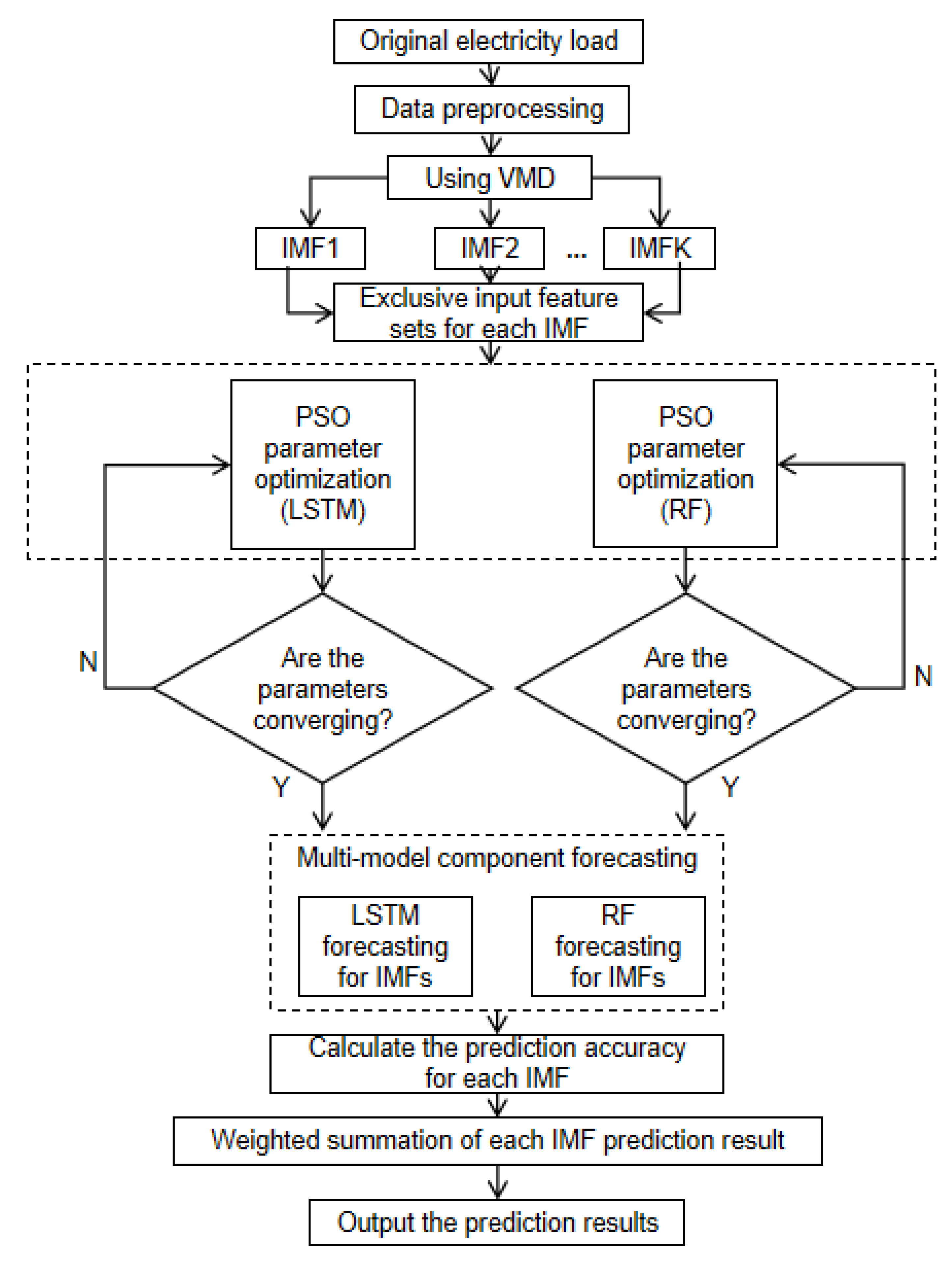
2.2. Proposed Forecasting Model
2.3. Evaluation Metrics
3. Case Study: Integrated Energy Sector
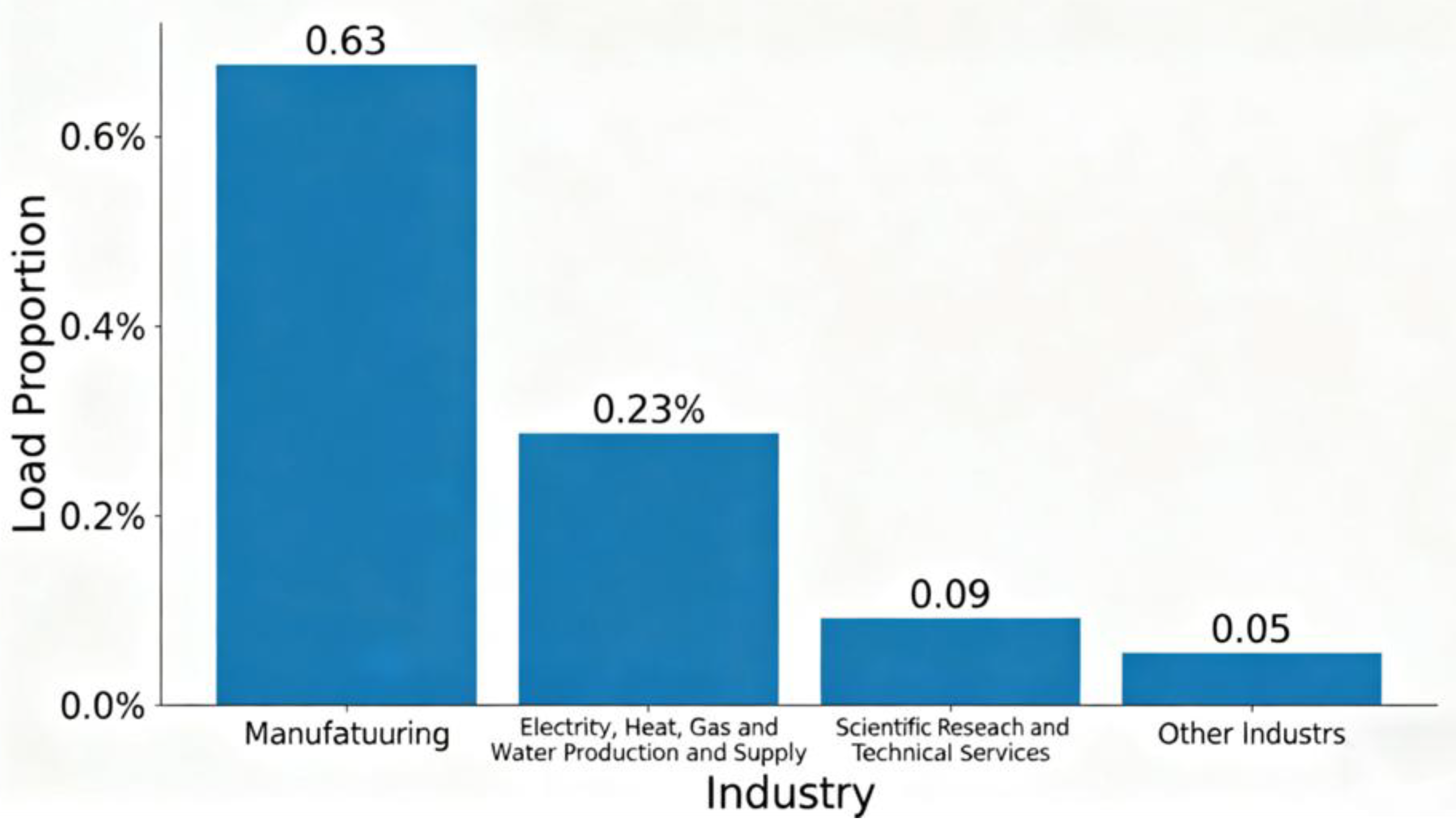
3.1. Data Source and Preprocessing
3.2. Parameter Settings
3.2.1. VMD Parameter
3.2.2. PSO Parameter
4. Results and Discussion
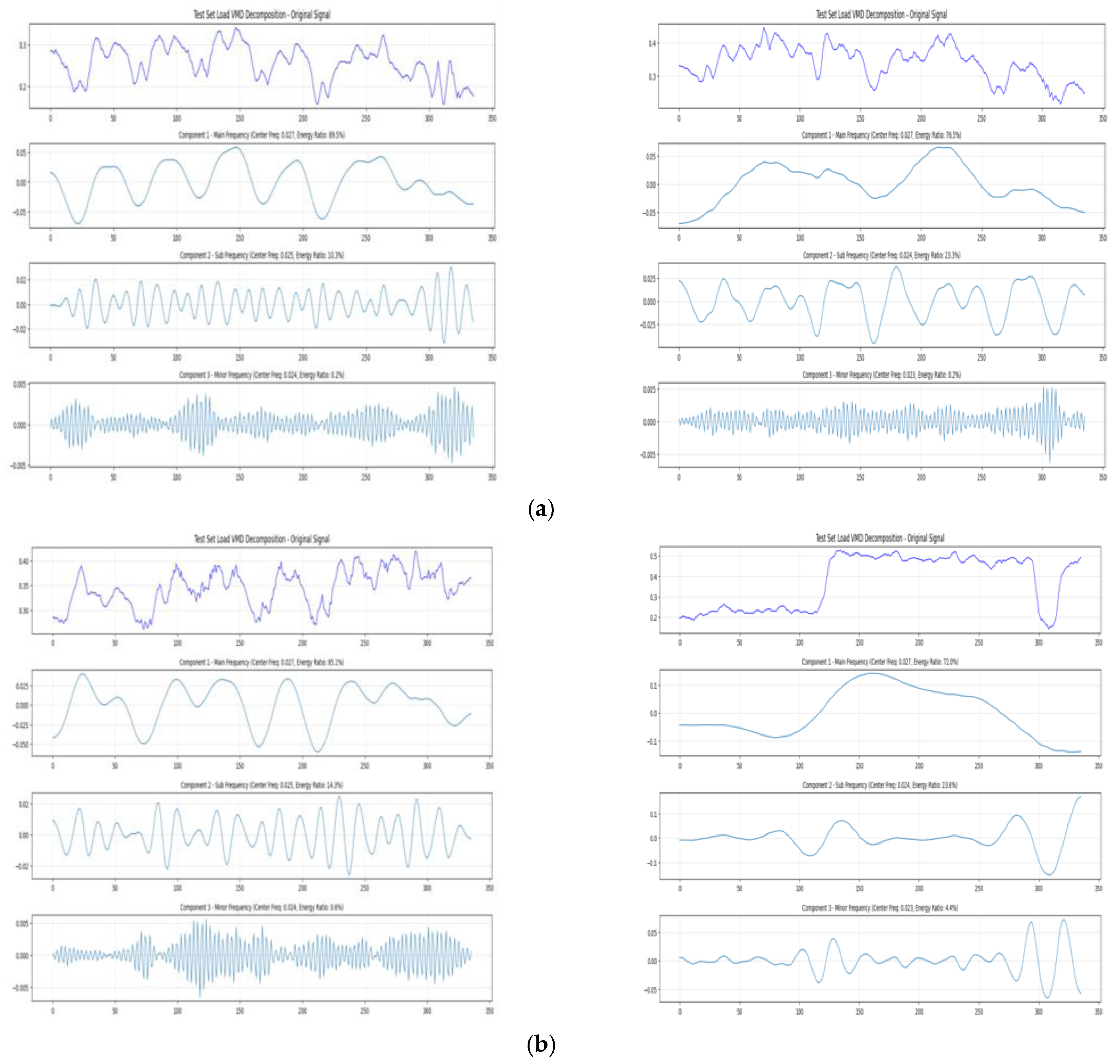
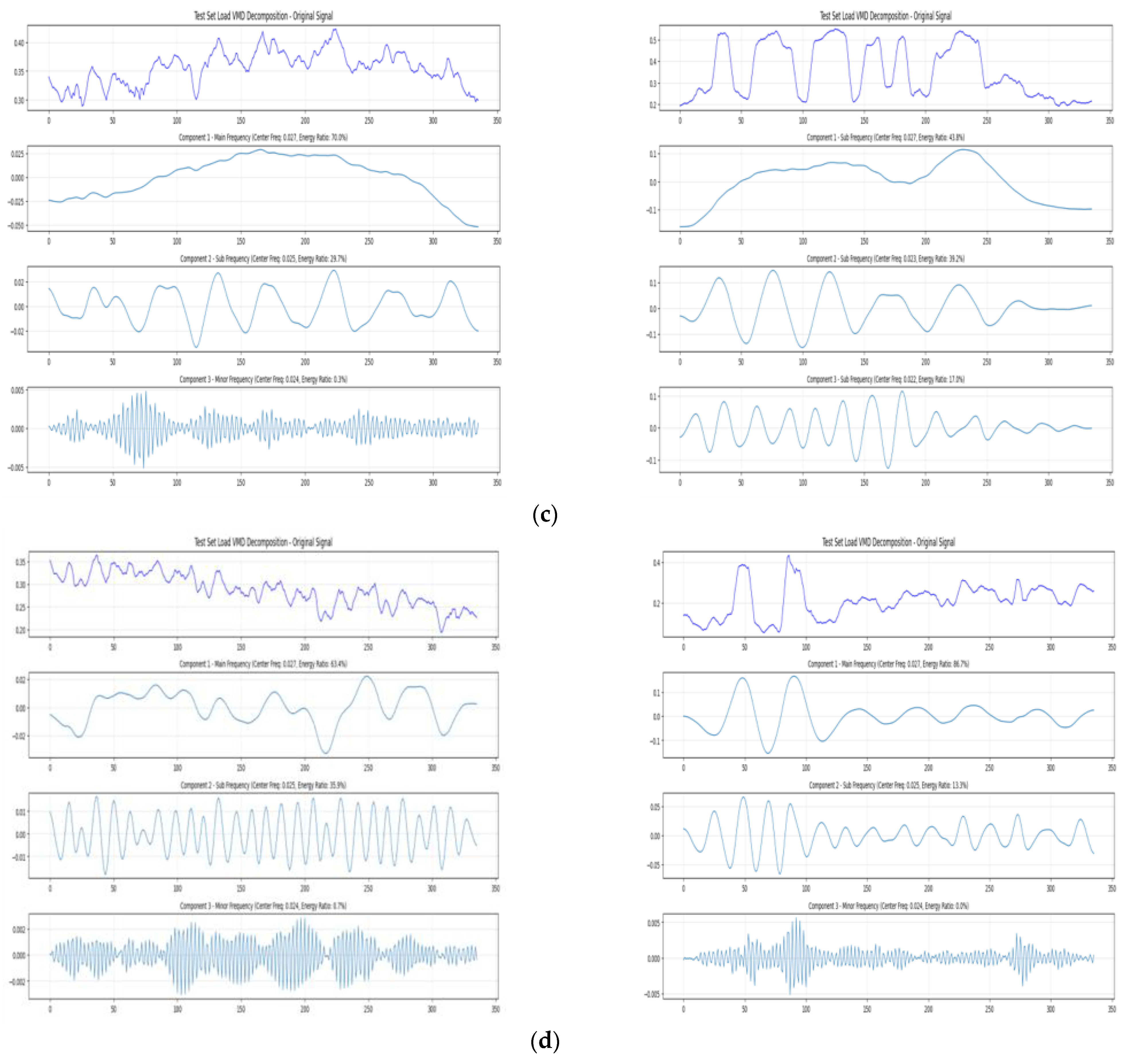
4.1. VMD Decomposition
4.2. PSO Optimization Results and Analysis
4.2.1. Analysis of Seasonal Optimization Results for LSTM Model
4.2.2. Analysis of Seasonal Optimization Results for RF Model
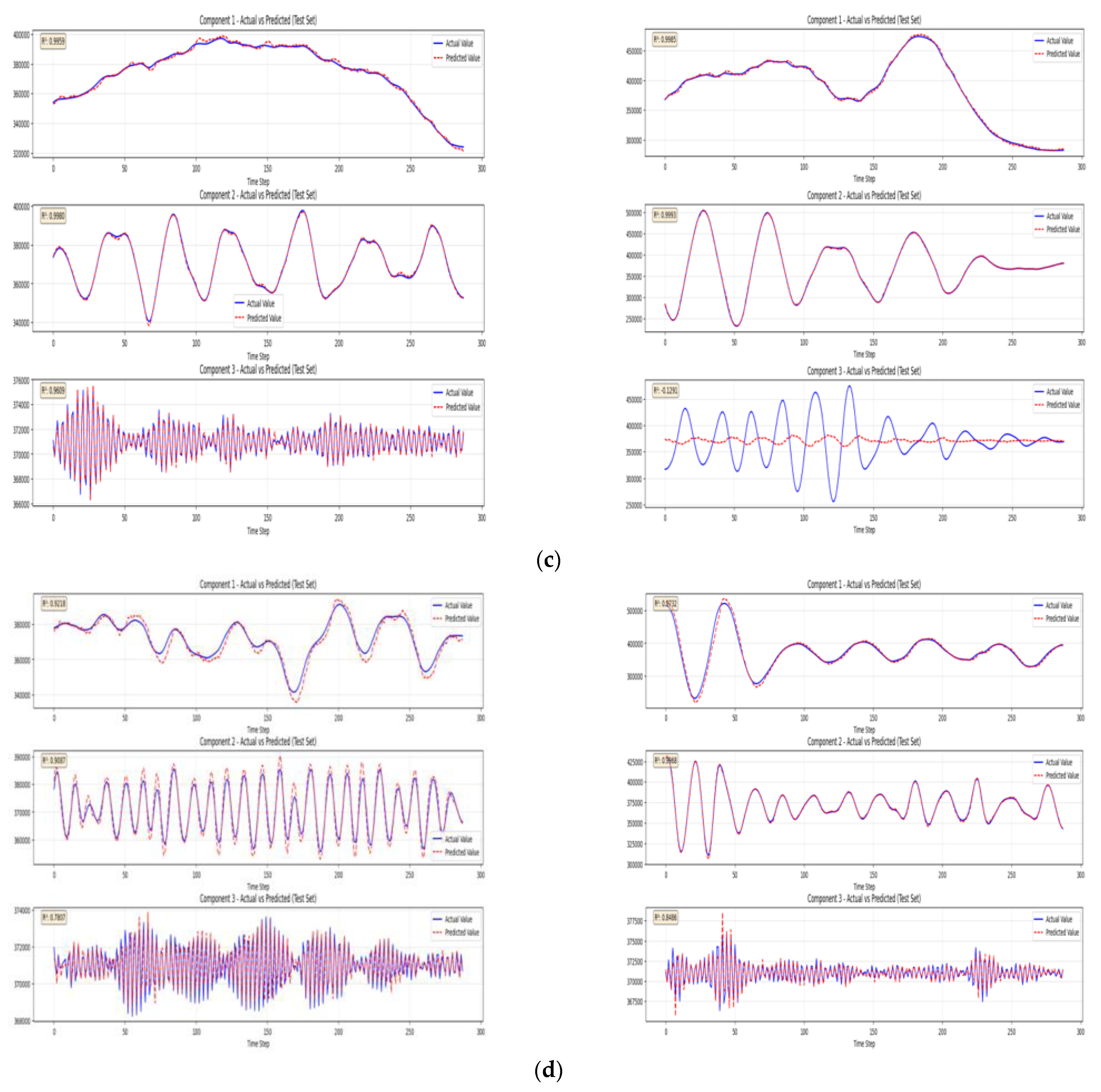
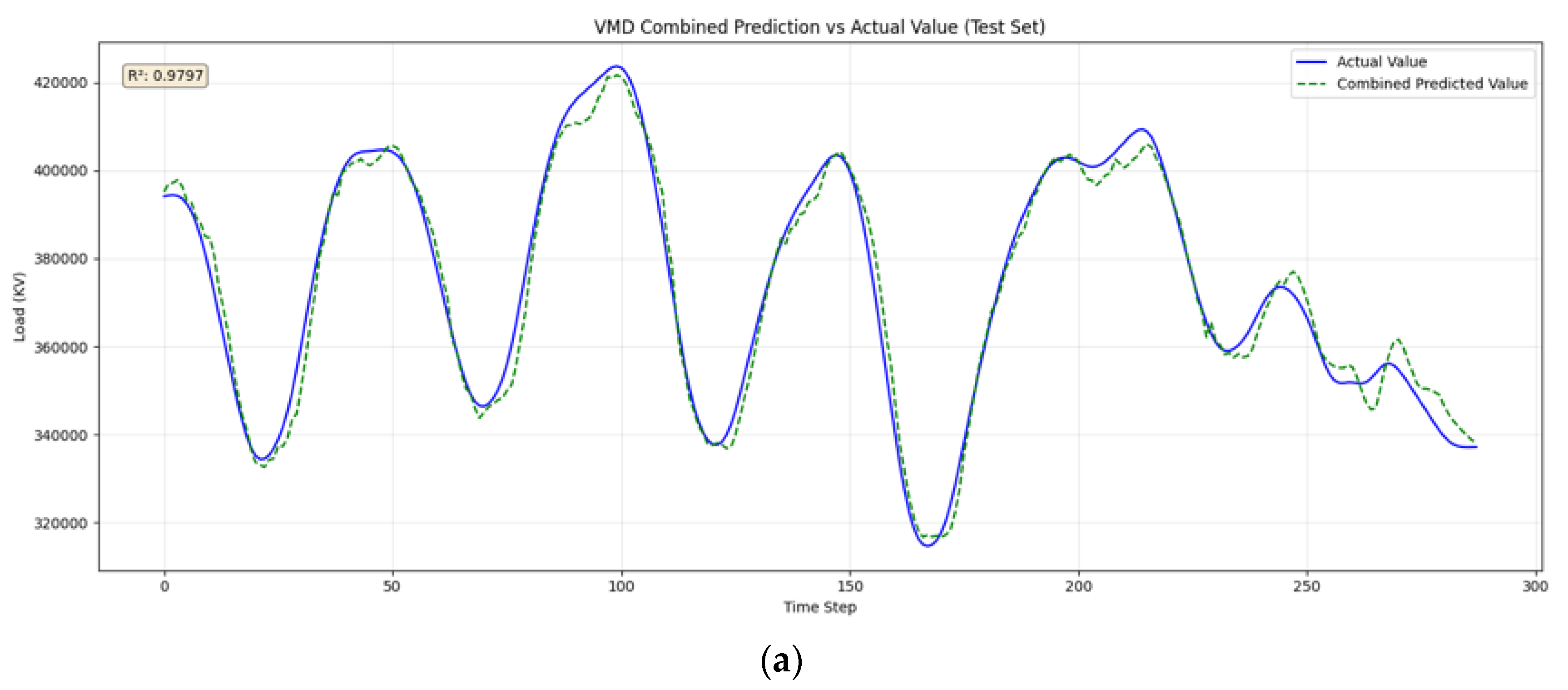
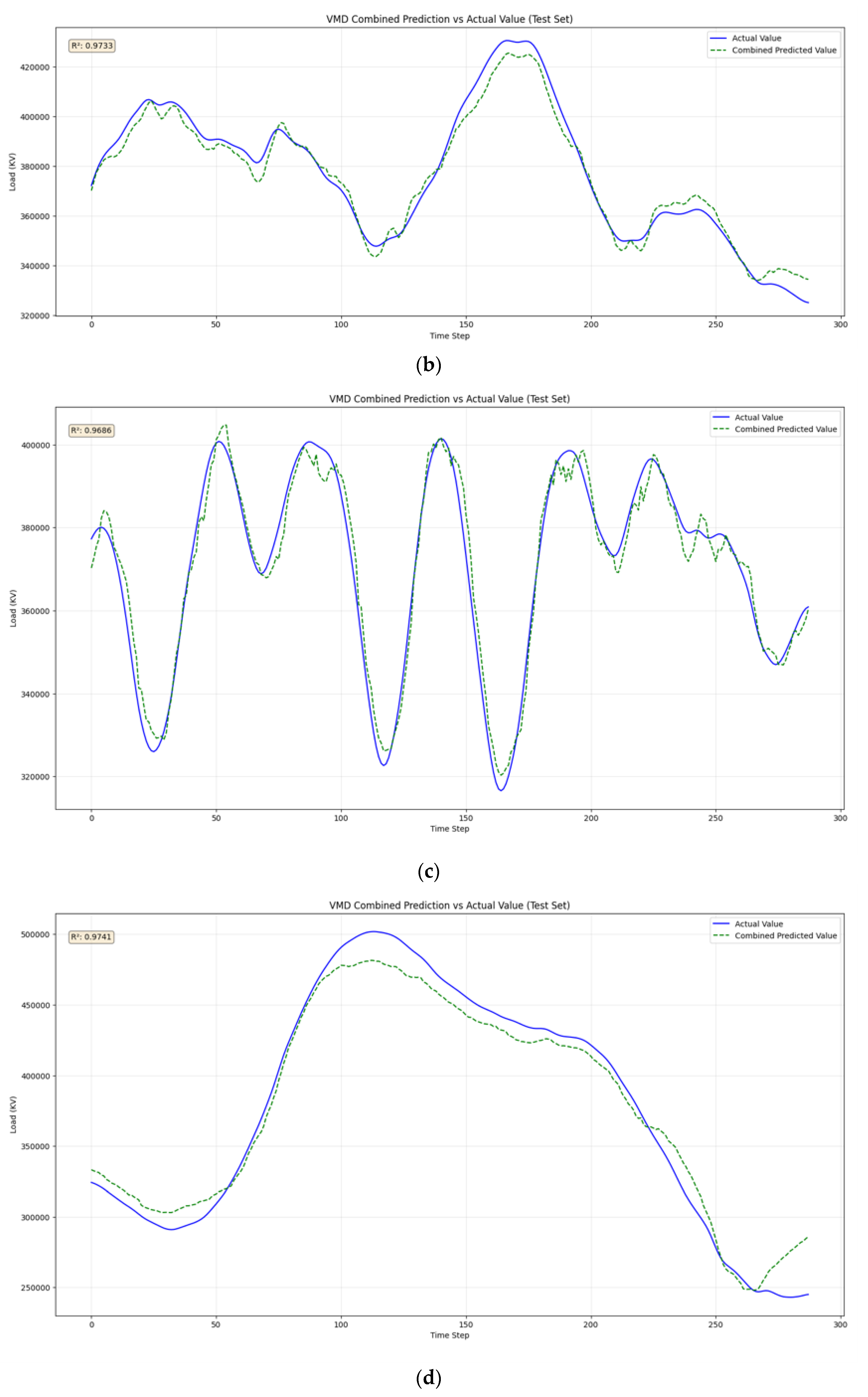
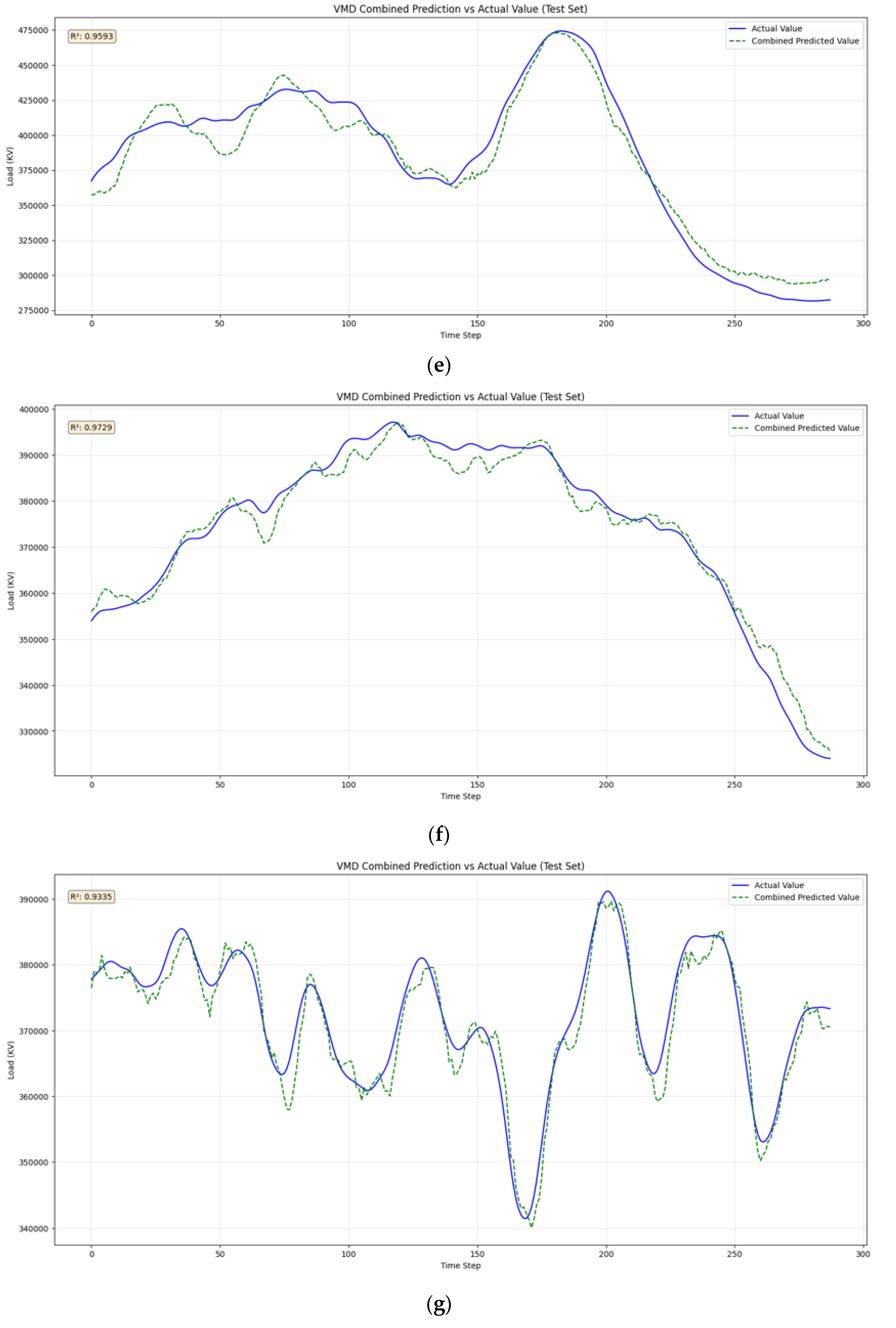
4.3. Prediction Result Comparisons
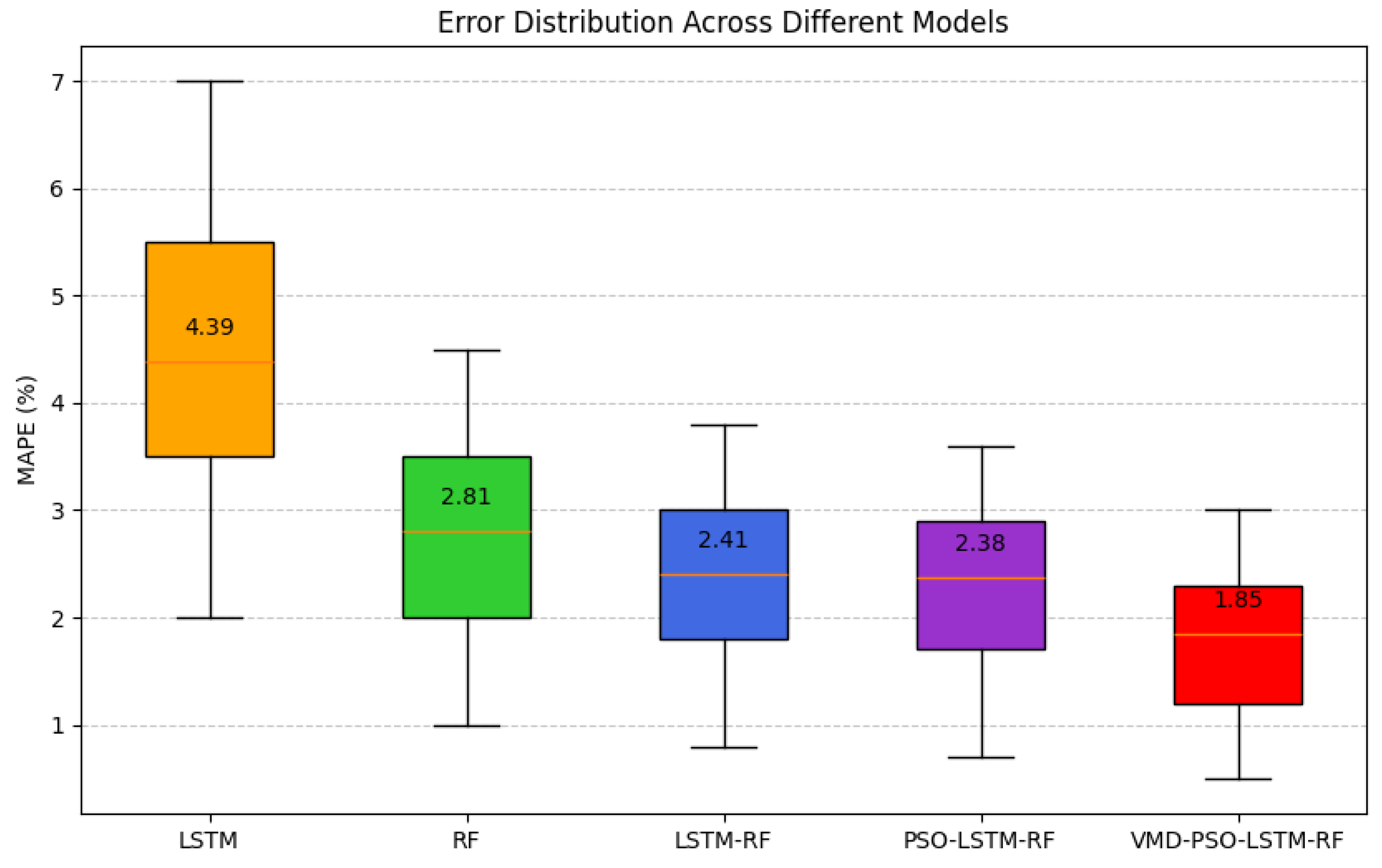
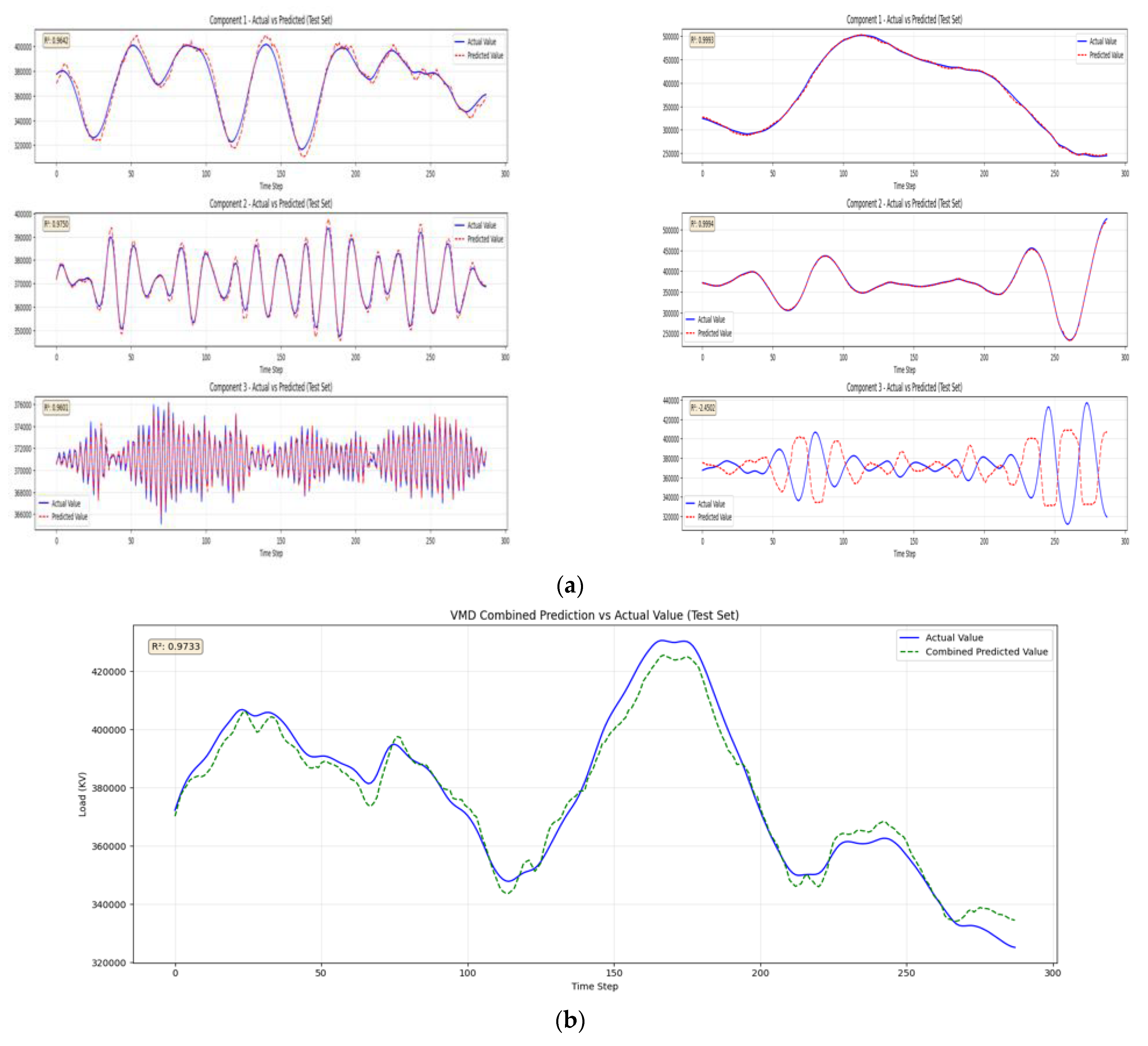
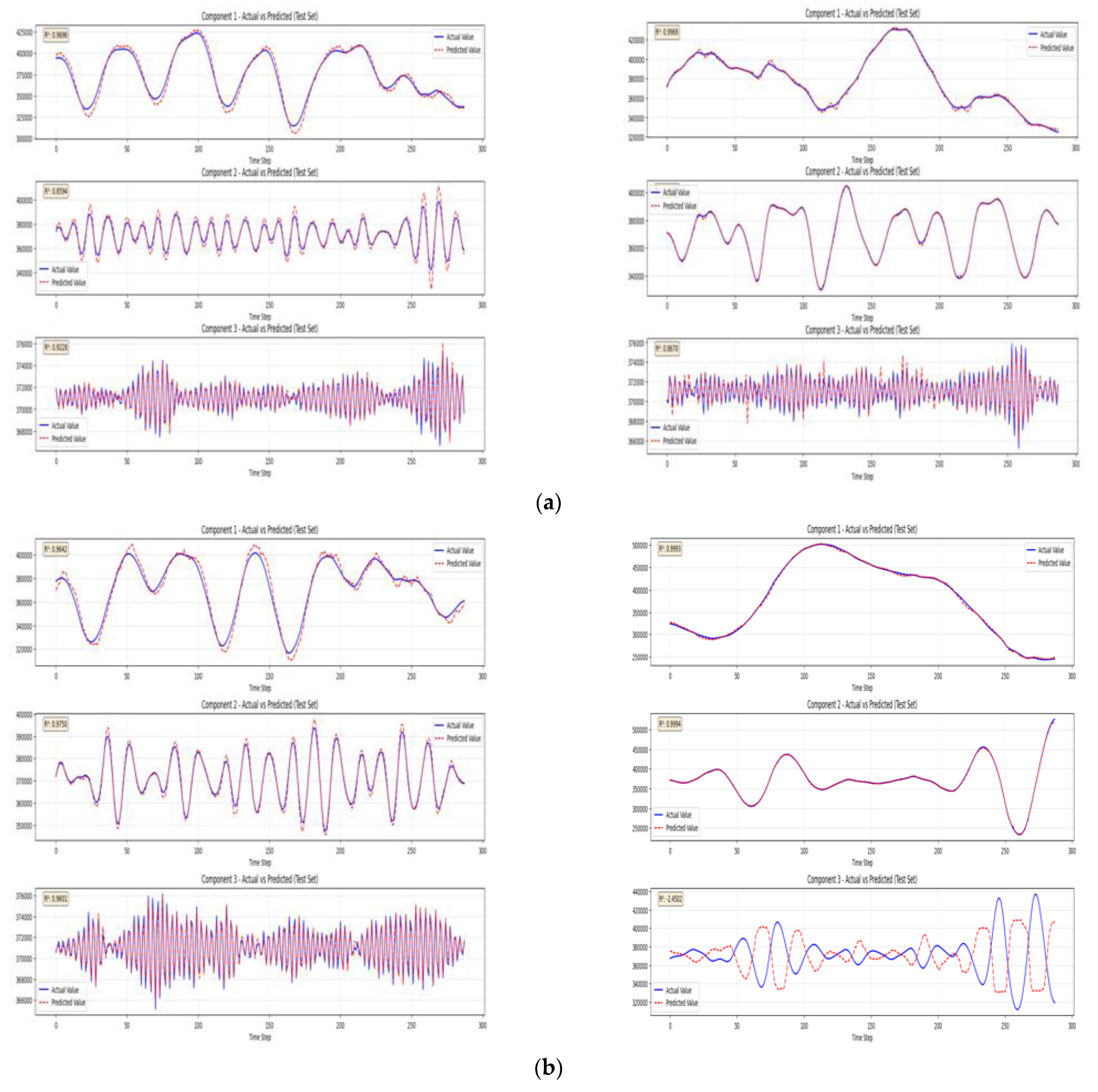
4.3.1. Model Accuracy and Fitting Performance
- The dominant frequency component reflects the main trend of the load;
- The sub-frequency component captures intraday periodic characteristics;
- The minor frequency component carries random disturbances.
4.3.2. Seasonal Adaptability
4.3.3. Electricity Market Application Value
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SVR | Support Vector Regression |
| LSTM | Long Short-Term Memory |
| RF | Random Forest |
| EMD | Empirical Mode Decomposition |
| VMD | Variational Mode Decomposition |
| MODBO | Multi-Objective Dark Bandit Optimizer |
| SVD | Singular Value Decomposition |
| RNN | Recurrent Neural Network |
| ANN | Artificial Neural Network |
| MTL | Multi-Task Learning |
| SSA | Sparrow Search Algorithm |
| EEMD | Ensemble Empirical Mode Decomposition |
| SVMD | Sparse Variational Mode Decomposition |
| IZOA | Improved Zebra Optimization Algorithm |
| IMF | Intrinsic Mode Function |
| GRU | Gated Recurrent Unit |
References
- Wang, G.; Chen, X. Power System Load Forecasting Based on Multiple Models. Adv. Appl. Math. 2024, 13, 750–759. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short term load forecasting based on ARIMA and ANN approaches. Energy Rep. 2023, 9 (Suppl. S3), 550–557. [Google Scholar] [CrossRef]
- Lu, R.; Bai, R.; Li, R.; Zhu, L.; Sun, M.; Xiao, F.; Wang, D.; Wu, H.; Ding, Y. A Novel Sequence-to-Sequence-Based Deep Learning Model for Multistep Load Forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 638–652. [Google Scholar] [CrossRef] [PubMed]
- Ortega, A.; Borunda, M.; Conde, L.; Garcia-Beltran, C. Load Demand Forecasting Using a Long-Short Term Memory Neural Network. In Advances in Computational Intelligence; Calvo, H., Martínez-Villaseñor, L., Ponce, H., Eds.; MICAI 2023; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2024; Volume 14391. [Google Scholar]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, J.; Xia, Y. Combined electricity load-forecasting system based on weighted fuzzy time series and deep neural networks. Eng. Appl. Artif. Intell. 2024, 132, 108375. [Google Scholar] [CrossRef]
- Luo, S.; Wang, B.; Gao, Q.; Wang, Y.; Pang, X. Stacking integration algorithm based on CNN-BiLSTM-Attention with XGBoost for short-term electricity load forecasting. Energy Rep. 2024, 12, 2676–2689. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, R.; Cao, J.; Tan, J. A CNN and LSTM-based multi-task learning architecture for short and medium-term electricity load forecasting. Electr. Power Syst. Res. 2023, 222, 109507. [Google Scholar] [CrossRef]
- Li, J.; Qiu, C.; Zhao, Y.; Wang, Y. A power load forecasting model based on a combined neural network. AIP Adv. 2024, 14, 045231. [Google Scholar] [CrossRef]
- Deng, S.; Dong, X.; Tao, L.; Wang, J.; He, Y.; Yue, D. Multi-type load forecasting model based on random forest and density clustering with the influence of noise and load patterns. Energy 2024, 307, 132635. [Google Scholar] [CrossRef]
- Guerra, R.R.; Vizziello, A.; Savazzi, P.; Goldoni, E.; Gamba, P. Forecasting LoRaWAN RSSI using weather parameters: A comparative study of ARIMA, artificial intelligence and hybrid approaches. Comput. Netw. 2024, 243, 110258. [Google Scholar] [CrossRef]
- Lv, L.; Wu, Z.; Zhang, J.; Zhang, L.; Tan, Z.; Tian, Z. A VMD and LSTM Based Hybrid Model of Load Forecasting for Power Grid Security. IEEE Trans. Ind. Inform. 2022, 18, 6474–6482. [Google Scholar] [CrossRef]
- Duo, Y.; Li, W.; Li, T. Short Term Power Load Forecasting Based on VMD Self Attention-LSTM. Adv. Appl. Math. 2023, 12, 1195–1206. [Google Scholar] [CrossRef]
- Dai, Y.; Yu, W. Short-term power load forecasting based on Seq2Seq model integrating Bayesian optimization, temporal convolutional network and attention. Appl. Soft Comput. 2024, 166, 112248. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Guo, K.; Liu, S.; He, D. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Appl. Sci. 2024, 14, 5966. [Google Scholar] [CrossRef]
- Li, Y. Short-Term Power Load Forecasting Modeling Based on Transfer Fuzzy System. Adv. Appl. Math. 2024, 13, 1671–1689. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Z.; Wang, D.; Wang, B.; Wang, Z.; Huang, T. Short-term photovoltaic power forecasting method considering historical information reuse and numerical weather forecasting. Renew. Energy 2025, 256, 123933. [Google Scholar] [CrossRef]
- Wang, T.; Sun, J.; Gong, D.; Wang, F.; Yue, F. A Dual-layer Decomposition and Multi-model Driven Combination Interval Forecasting Method for Short-term PV Power Generation. Expert Syst. Appl. 2025, 288, 128235. [Google Scholar] [CrossRef]
- Liu, R.; Shi, J.; Sun, G.; Lin, S.; Li, F. A Short-term net load hybrid forecasting method based on VW-KA and QR-CNN-GRU. Electr. Power Syst. Res. 2024, 232, 110384. [Google Scholar] [CrossRef]
- Li, C.; Li, G.; Wang, K.; Han, B. A multi-energy load forecasting method based on parallel architecture CNN-GRU and transfer learning for data deficient integrated energy systems. Energy 2022, 259, 124967. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Tan, M.; Liao, C.; Chen, J.; Cao, Y.; Wang, R.; Su, Y. A multi-task learning method for multi-energy load forecasting based on synthesis correlation analysis and load participation factor. Appl. Energy 2023, 343, 121177. [Google Scholar] [CrossRef]
- Huang, N.; Ren, S.; Liu, J.; Cai, G.; Zhang, L. Multi-task learning and single-task learning joint multi-energy load forecasting of integrated energy systems considering meteorological variations. Expert Syst. Appl. 2025, 288, 128269. [Google Scholar] [CrossRef]
- Li, K.; Mu, Y.; Yang, F.; Wang, H.; Yan, Y.; Zhang, C. Joint forecasting of source-load-price for integrated energy system based on multi-task learning and hybrid attention mechanism. Appl. Energy 2024, 360, 122821. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, T.; Li, J.; Li, C. A novel short-term multi-energy load forecasting method for integrated energy system based on two-layer joint modal decomposition and dynamic optimal ensemble learning. Appl. Energy 2025, 378, 124798. [Google Scholar] [CrossRef]
- Ren, X.; Tian, X.; Wang, K.; Yang, S.; Chen, W.; Wang, J. Enhanced load forecasting for distributed multi-energy system: A stacking ensemble learning method with deep reinforcement learning and model fusion. Energy 2025, 319, 135031. [Google Scholar] [CrossRef]
- Peng, D.; Liu, Y.; Wang, D.; Zhao, H.; Qu, B. Multi-energy load forecasting for integrated energy system based on sequence decomposition fusion and factors correlation analysis. Energy 2024, 308, 132796. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, P.; Ma, X.; Qian, X. Short Term Load Forecasting Method for Power System Based on Neural Network. In Proceedings of the 2024 5th International Symposium on New Energy and Electrical Technology (ISNEET), Hangzhou, China, 27–29 December 2024; pp. 481–484. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, J.; Cai, X. Intelligent analysis algorithm for power engineering data based on improved BiLSTM. Sci. Rep. 2025, 15, 15320. [Google Scholar] [CrossRef]
- Al-Selwi, S.M.; Hassan, M.F.; Abdulkadir, S.J.; Muneer, A.; Sumiea, E.H.; Alqushaibi, A.; Ragab, M.G. RNN-LSTM: From applications to modeling techniques and beyond—Systematic review. J. King Saud Univ.—Comput. Inf. Sci. 2024, 36, 102068. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Q.; Ruan, Y.; Qian, F.; Meng, H. A prediction approach with mode decomposition-recombination technique for short-term load forecasting. Sustain. Cities Soc. 2022, 85, 104034. [Google Scholar] [CrossRef]
- Ou, H.; Yao, Y.; He, Y. Missing Data Imputation Method Combining Random Forest and Generative Adversarial Imputation Network. Sensors 2024, 24, 1112. [Google Scholar] [CrossRef]
- Rani, S.; Mahmood, A.; Ahmed, U.; Razzaq, S.; Manzoor, S. A Short-Term Load Forecasting by Using Hybrid Model. In Proceedings of the 2023 20th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Bhurban, Pakistan, 22–25 August 2023; pp. 333–338. [Google Scholar] [CrossRef]
- Xu, Y.; Huang, X.; Zheng, X.; Zeng, Z.; Jin, T. VMD-ATT-LSTM electricity price prediction based on grey wolf optimization algorithm in electricity markets considering renewable energy. Renew. Energy 2024, 236, 121408. [Google Scholar] [CrossRef]
- Peng, S.; Zhu, J.; Wu, T.; Yuan, C.; Cang, J.; Zhang, K.; Pecht, M. Prediction of wind and PV power by fusing the multi-stage feature extraction and a PSO-BiLSTM model. Energy 2024, 298, 131345. [Google Scholar] [CrossRef]
- Bo, Y.; Guo, X.; Liu, Q.; Pan, Y.; Zhang, L.; Lu, Y. Prediction of tunnel deformation using PSO variant integrated with XGBoost and its TBM jamming application. Tunn. Undergr. Space Technol. 2024, 150, 105842. [Google Scholar] [CrossRef]

| Scenario | Input Variables | Model | Training Time | Refs |
|---|---|---|---|---|
| Load Forecasting | IoT data, historical load data, meteorological data, economic data, historical load data, meteorological data, time features | LSTM, LSTM-GRU, Stacking-Fusion, Reseamble-Model | Medium–Long | [17,18] |
| IoT data, historical load data, meteorological data, economic data | Shuffle-Transformer-Multi, Transformer-Attention-Net | Relatively Long | [3,19] | |
| Historical load data, meteorological data, time features, multi-energy load data | CNN-LSTM, CNN-BiGRU, ResNet-LSTM | Medium–Long | [8,20,21] | |
| Historical load data, meteorological data, multi-energy data, coupling features | Multi-task Learning, Source-Load Integrated Forecasting Model | Relatively Long | [22,23,24] | |
| Historical load data, meteorological data, multi-energy data, key features | Two-layer Joint Modal Decomposition Dynamic Ensemble Model, Stacking Ensemble, Copula Correlation Analysis Fusion | Long | [25,26,27] |
| Type | Parameter | Rage |
|---|---|---|
| Dynamic adaptable parameters | Number of Decomposition Modes | 3 |
| Penalty Factor | 2000 | |
| Basic fixed parameters | Noise Tolerance | 0 |
| Whether to Enforce DC Component Decomposition | 0 | |
| Center Frequency Initialization Method | 1 | |
| Convergence Threshold | 10−7 |
| Type | Parameter | Rage |
|---|---|---|
| Core Algorithm Parameters | Number of Particles | 20 |
| Maximum Iterations | 40 | |
| Inertia Weight | 0.9 | |
| Cognitive and Social Coefficients | 2.0 | |
| Model Parameter Rangers to Be Optimized | Number of Hidden Layer Neurons | [32,256] |
| Number of Stacked Layers | [1,5] | |
| Learning Rate | [0.0001,0.01] | |
| Number of Decision Trees | [50,150] | |
| Maximum Depth | [3,25] |
| Season | Number of Hidden Layer Neurons | Number of Stacked Layers | Learning Rate | Number of Decision Trees | Maximum Depth |
|---|---|---|---|---|---|
| Spring (case 1) | 256 | 4 | 0.01 | 100 | 17 |
| (case 2) | 239 | 1 | 0.01 | 100 | 19 |
| Summer (case 3) | 253 | 2 | 0.0001 | 100 | 20 |
| (case 4) | 224 | 1 | 0.009661 | 100 | 20 |
| Autumn (case 5) | 256 | 4 | 0.01 | 100 | 17 |
| (case 6) | 256 | 2 | 0.01 | 100 | 17 |
| Winter (case 7) | 256 | 3 | 0.01 | 100 | 17 |
| (case 8) | 256 | 4 | 0.009795 | 100 | 20 |
| Model | R2 | MAPE | RMSE | MAE |
|---|---|---|---|---|
| LSTM | 0.8651 | 4.39 | 0.0166 | 4.26 |
| RF | 0.9237 | 2.81 | 0.0125 | 2.79 |
| LSTM-RF | 0.9409 | 2.41 | 0.0106 | 2.39 |
| PSO-LSTM-RF | 0.9449 | 2.38 | 0.0110 | 2.37 |
| VMD-PSO-LSTM-RF | 0.9520 | 1.85 | 0.0098 | 1.83 |
| Jun.1 | Jun.2 (case 3) | Jul.1 | Jul.2 | Aug.1 | Aug.2 | |
|---|---|---|---|---|---|---|
| R2 | 0.9799 | 0.9686 | 0.9713 | 0.9835 | 0.9638 | 0.969 |
| RMSE | 3457.995 | 4183.216 | 3596.7316 | 6126.94 | 2847.9636 | 8746.8545 |
| MAPE | 0.73% | 0.93% | 0.80% | 1.36% | 0.61% | 1.86% |
| VMD-LSTM-RF | LSTM-RF | ||
|---|---|---|---|
| Spring (case 1) | R2 | 0.9797 | 0.9502 |
| RMSE | 3853.0036 | 8579.7107 | |
| MAPE | 0.83 | 1.07 | |
| (case 2) | R2 | 0.9733 | 0.9618 |
| RMSE | 4445.1623 | 7019.5444 | |
| MAPE | 0.98 | 0.78 | |
| Summer (case 3) | R2 | 0.9686 | 0.9206 |
| RMSE | 4183.216 | 9412.6558 | |
| MAPE | 0.93 | 1.05 | |
| (case 4) | R2 | 0.9741 | 0.9543 |
| RMSE | 13,331.1769 | 14,375.1483 | |
| MAPE | 3.18 | 1.07 | |
| Autumn (case 5) | R2 | 0.9593 | 0.9412 |
| RMSE | 12,749.6432 | 11,101.8328 | |
| MAPE | 2.58 | 1.24 | |
| (case 6) | R2 | 0.9729 | 0.9371 |
| RMSE | 3115.7979 | 6129.6015 | |
| MAPE | 0.68 | 0.69 | |
| Winter (case 7) | R2 | 0.9335 | 0.9575 |
| RMSE | 2659.8809 | 6547.8968 | |
| MAPE | 0.57 | 0.85 | |
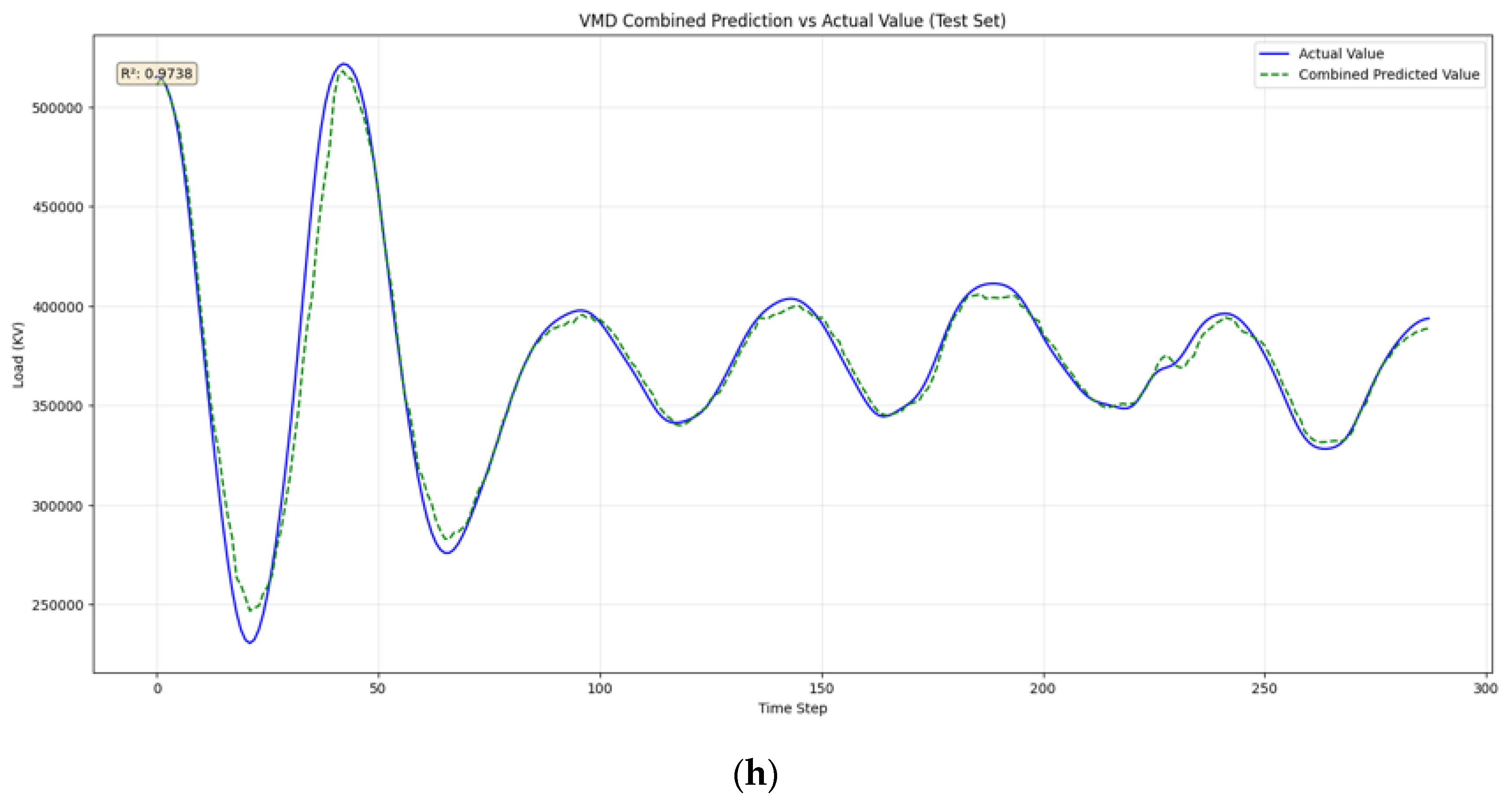
| (case 8) | R2 | 0.9738 | 0.9679 |
| RMSE | 8690.8294 | 12,031.1458 | |
| MAPE | 1.44 | 1.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Yuan, L.; Qian, F.; Song, L.; Wu, X.; Wang, L.; Dai, J.; Shen, L. Short-Term Load Forecasting for Electricity Spot Markets Across Different Seasons Based on a Hybrid VMD-LSTM-Random Forest Model. Energies 2025, 18, 6097. https://doi.org/10.3390/en18236097
Li K, Yuan L, Qian F, Song L, Wu X, Wang L, Dai J, Shen L. Short-Term Load Forecasting for Electricity Spot Markets Across Different Seasons Based on a Hybrid VMD-LSTM-Random Forest Model. Energies. 2025; 18(23):6097. https://doi.org/10.3390/en18236097
Chicago/Turabian StyleLi, Kangkang, Lize Yuan, Fanyue Qian, Lifei Song, Xinhong Wu, Li Wang, Jiefen Dai, and Lianyi Shen. 2025. "Short-Term Load Forecasting for Electricity Spot Markets Across Different Seasons Based on a Hybrid VMD-LSTM-Random Forest Model" Energies 18, no. 23: 6097. https://doi.org/10.3390/en18236097
APA StyleLi, K., Yuan, L., Qian, F., Song, L., Wu, X., Wang, L., Dai, J., & Shen, L. (2025). Short-Term Load Forecasting for Electricity Spot Markets Across Different Seasons Based on a Hybrid VMD-LSTM-Random Forest Model. Energies, 18(23), 6097. https://doi.org/10.3390/en18236097







