1. Introduction
In the past decade, climate change has led to frequent natural disasters, which seriously threaten the operation safety of power systems [
1]. To make the power grid stronger and smarter against natural disasters, reference [
2] introduced the concept of power system resilience, which has received much attention from researchers. The research on resilient power system can be divided into five categories: resilience assessment [
3], long-term resilience-oriented planning [
4], short-term preventive scheduling [
5], real-time emergency response [
6], and recovery planning post-disaster including service restoration [
7] and black-start management [
8]. Compared with long-term planning, such as line hardening in [
9], short-term preventive scheduling provides a more flexible and economical way for resilience enhancement using the existing resources and facilities against natural disasters [
10]. This paper focuses on the day-ahead preventive scheduling.
With the rapid development of hydrogen production, transportation, and storage technologies, the hydrogen-based integrated energy system (HIES) has been introduced for greenhouse gas eliminating and climate change mitigation in recent years due to its high energy density, cleanness, and sustainability. Many works have been devoted to HIES operation and planning for flexibility enhancement for economic and environmental benefits. Meanwhile, compared with modern battery-based and DC smart-grid technologies widely adopted to enhance short-term resilience [
11], HIES provides a complementary long-duration and multi-energy solution [
12], as summarized in
Table 1. Renewable energy such as solar and wind can be on-site converted into hydrogen by electrolyzers (ELZs) and stored for supply–demand balance [
13]. In addition to methanation reactor (MR) with carbon capture facilities [
14], the hydrogen-enriched compressed natural gas (HCNG) is developed by directly mixed hydrogen with natural gas [
15]. References [
16,
17,
18] studied the hydrogen supply chain coordinating the on-site hydrogen production/storage, hydrogen transportation (HT), and distribution. When the electricity or hydrogen supply is interrupted, these facilities will not work correctly, which further affects the energy supplies to customers in the HIES. Therefore, the ever-increasing inter-dependency of hydrogen systems, power systems, heat systems, and natural gas systems may result in extraordinary vulnerabilities to natural disasters in HIES operation.
Great efforts have been made to develop preventive scheduling methods for the resilient HIES against natural disasters. Among them, preventive unit commitment (UC) of key equipment such as generators and ELZs is the most widely used approach. In [
19], a bi-level UC model that performs rolling scheduling before disasters was proposed, and demonstrated its economic efficiency and high energy supply capability through simulations. To balance economic efficiency and resilience, authors in [
20] developed a multi-objective optimization model ensuring that increased operating costs do not lead to load shedding. The above-mentioned works primarily focus on electric–hydrogen coupled systems, while some recent studies have begun to consider couplings with other energy systems. For example, ref. [
14] proposed a resilient operation strategy for coordinating hydrogen conversion and production, in which HCNG were utilized as emergency energy resources transmitted through gas network system (GNS). Regarding electric–thermal coupling, several studies have explored hydrogen-assisted heat supply, including heat generation through fuel cells [
21] and heat recovery during electrolysis [
22]. However, few studies have simultaneously considered the interactions among electricity, gas, heat, and hydrogen subsystems within HIESs. Therefore, to establish practical preventive scheduling methods that reflect real HIES operations, it is essential to account for the integrated coupling of electricity, gas, heat, and hydrogen in the modeling framework.
Another effective and widely studied approach for enhancing system resilience is based on mobile energy resources (MERs). In HIESs, MERs include electric vehicles (EVs), mobile generators, and mobile energy storage systems for electricity supply, as well as fuel-cell EVs or hydrogen trucks for hydrogen delivery. To maximize their effectiveness in resilience enhancement, MERs are preventively allocated before disasters and dispatched according to preplanned strategies during disasters. In [
23], a hierarchical HIES resilience scheduling strategy was proposed, in which the upper layer coordinates energy production facilities, while the lower layer manages fuel-cell EV dispatch to maintain energy balance among microgrids. The authors in [
24] proposed a two-stage stochastic scheduling method for mobile wind turbines, which improves system resilience while reducing carbon emissions. Furthermore, to address uncertainties in disaster impacts on system operation, adaptive robust optimization (ARO)-based preventive scheduling models [
25] and corresponding high-efficiency solution algorithms [
26] have been developed. However, in most existing studies, MER routing networks are required to be predefined [
23,
24], which limits the applicability of these methods in scenarios with potential traffic disruptions. In [
27], the influence of faulted traffic roads was considered. Nevertheless, road traffic conditions, such as travel time, were assumed to be deterministic in most studies, making them unsuitable for representing the complex uncertainties introduced by disasters. Therefore, further efforts are needed to develop robust preventive scheduling methods that incorporate multiple uncertainties including faulted transportation networks.
Therefore, research gaps exist in (1) establishing a practical preventive scheduling method that accounts for the integrated coupling of electricity, gas, heat, and hydrogen in HIESs, and (2) developing robust preventive scheduling methods that incorporate multiple uncertainties, including failures in transportation networks. This paper proposes a day-ahead preventive scheduling method for HIESs that considers the uncertain impacts of natural disasters to enhance system resilience. The proposed approach realizes the integration of electricity, gas, heat, and hydrogen subsystems through energy hubs (EHs) located at the coupling points between the transmission network system (TNS) and the GNS. Furthermore, a HT model is developed to capture the uncertain impacts of road traffic disruptions, based on which an ARO-based preventive scheduling model is formulated to ensure robust and reliable operation under various disaster-induced uncertainties. The major contributions are listed as follows:
- 1.
A resilient preventive scheduling model for HIESs is proposed to mitigate the impacts of natural disasters. The model considers the coordinated operation of the TNS, GNS, and EHs to practically account for the integrated coupling of electricity, gas, heat, and hydrogen in HIESs. In particular, flexible scheduling measures such as power-to-hydrogen-and-heat (P2HH) conversion and HT scheduling are incorporated and investigated to enhance system resilience.
- 2.
An ARO-based preventive scheduling model is developed to handle uncertainties including damaged transmission lines (TLs), gas pipelines, and roads. In particular, a novel HT scheduling model is proposed to characterize the uncertainty associated with road disruptions in the second stage.
- 3.
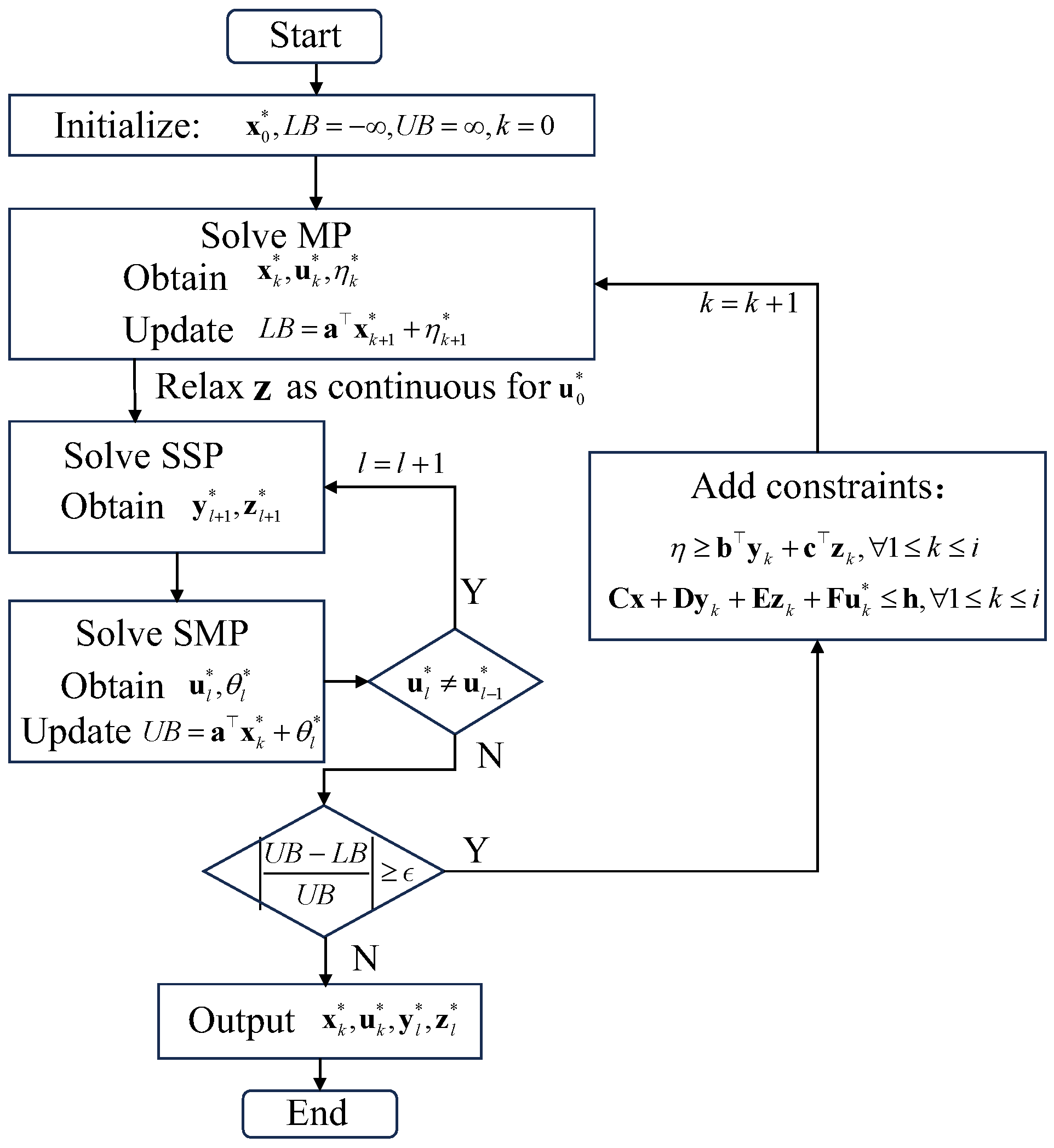
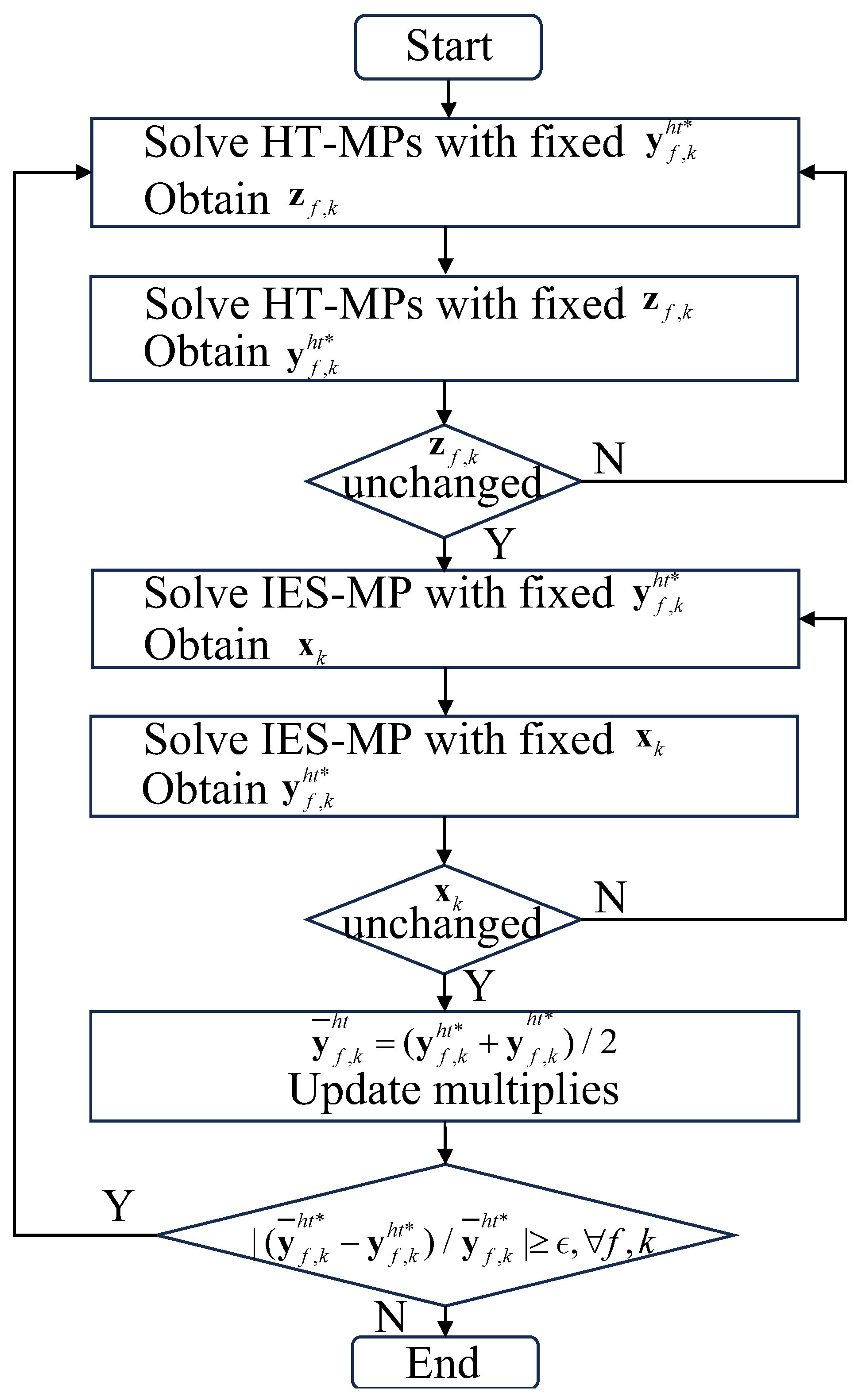
A hybrid algorithm is proposed to solve the proposed preventive scheduling model. The algorithm is developed based upon the column-and-constraint-generation (C&CG) framework and efficiently identifies near-optimal solutions for problems with a large number of integer variables by integrating analytical target cascading (ATC) and alternating optimization procedures (AOP).
The remainder of this paper is organized as follows.
Section 2 describes the formulation of the proposed preventive scheduling model.
Section 3 presents the solution methodology based on the proposed algorithm. Case studies are conducted in
Section 4, followed by conclusions in
Section 5.
4. Case Studies
The effectiveness of the proposed preventive schemes is validated on a modified 6-bus, 6-node, 6-spot system and a modified New-England 39-bus system with a Belgian 20-node gas system [
41] and a 12-spot transportation system. The models are programmed in Matlab 2020a and solved by GUROBI [
42] version 9.5 on a workstation with Intel I7 3.7 GHz CPU and 16 GB RAM. For the solver settings, the MIP gap is set at 0.1%. The relative error threshold
is set to 1% for both MP and SPs. The proposed algorithm is a deterministic mathematical optimization process that employs the Branch-and-Bound method to solve mixed-integer linear programming problems. Therefore, it does not involve any stochastic factors and does not require setting a random seed. The number of runs is determined by the number of iterations required for convergence. The time horizon
T is 24 h. For the sake of the safety of hydrogen transportation, the impacted roads are assumed to be completely interrupted. Therefore the time coefficient
is set to
T. The HT fleets are assumed to share the same travel time for a road in the RN for simplifying matters. The travel time of each road is 1h. The load shedding cost for electric power, heat, and hydrogen is 1000
$/MWh(
) and is set to 10
$/
for gas load curtailment. The transportation cost is 100
$/h according to [
17]. The capacity of each fleet is 100
. The detailed case study data and corresponding scripts can be download in the
Supplementary Materials with this paper, and will be made available online [
43].
4.1. Test 1: 6-Bus, 6-Node, 6-Spot System
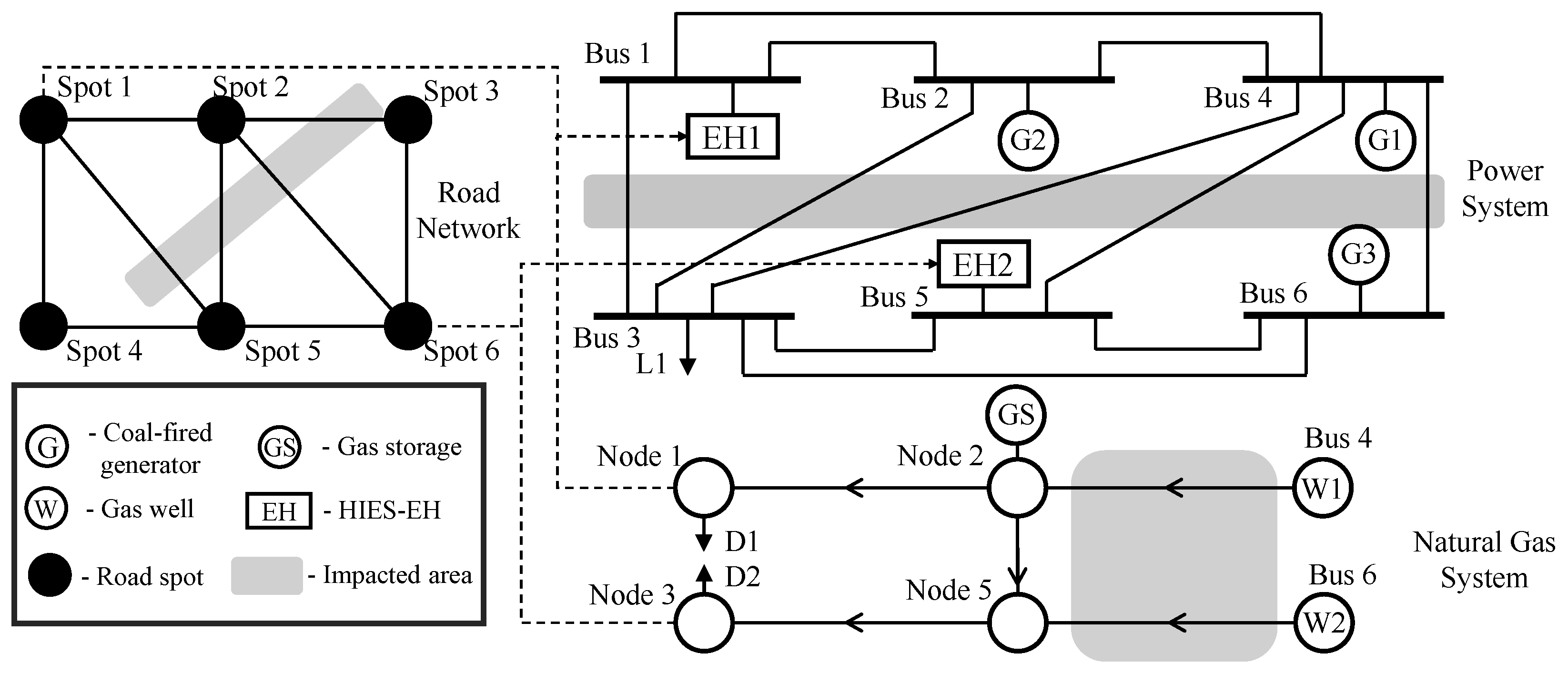
The 6-bus, 6-node, 6-spot system modified from [
44] is shown in
Figure 4, where the shaded areas represent the impacted regions. The test system includes three GTs, two EHs, two GWs, and one GS. The two EHs, which serve as the coupling points between the TNS and GNS, are located at spots 1 and 6 in the RN. Note that the detailed structure of each EH is provided in
Figure 1. Within an EH, hydrogen is produced by the ELZs or discharged from the HS, and can be transported among EHs via HT through the road network. Two HT fleets are pre-deployed at spots 1 and 6, respectively, and initially carry no stored hydrogen.
To illustrate the rationality and effectiveness of the proposed preventive schemes, we investigate a deterministic facility damage scenario under an extreme condition as following settings: TL 1-3, 2-3, 4-3, 4-5, and 4-6 are outage one by one every 1 h from 2:00; pipe 4-2 is interrupted at 2:00; roads 2-3, 2-6, 2-5, and 1-3 are interrupted one by one every 1 h from 2:00.
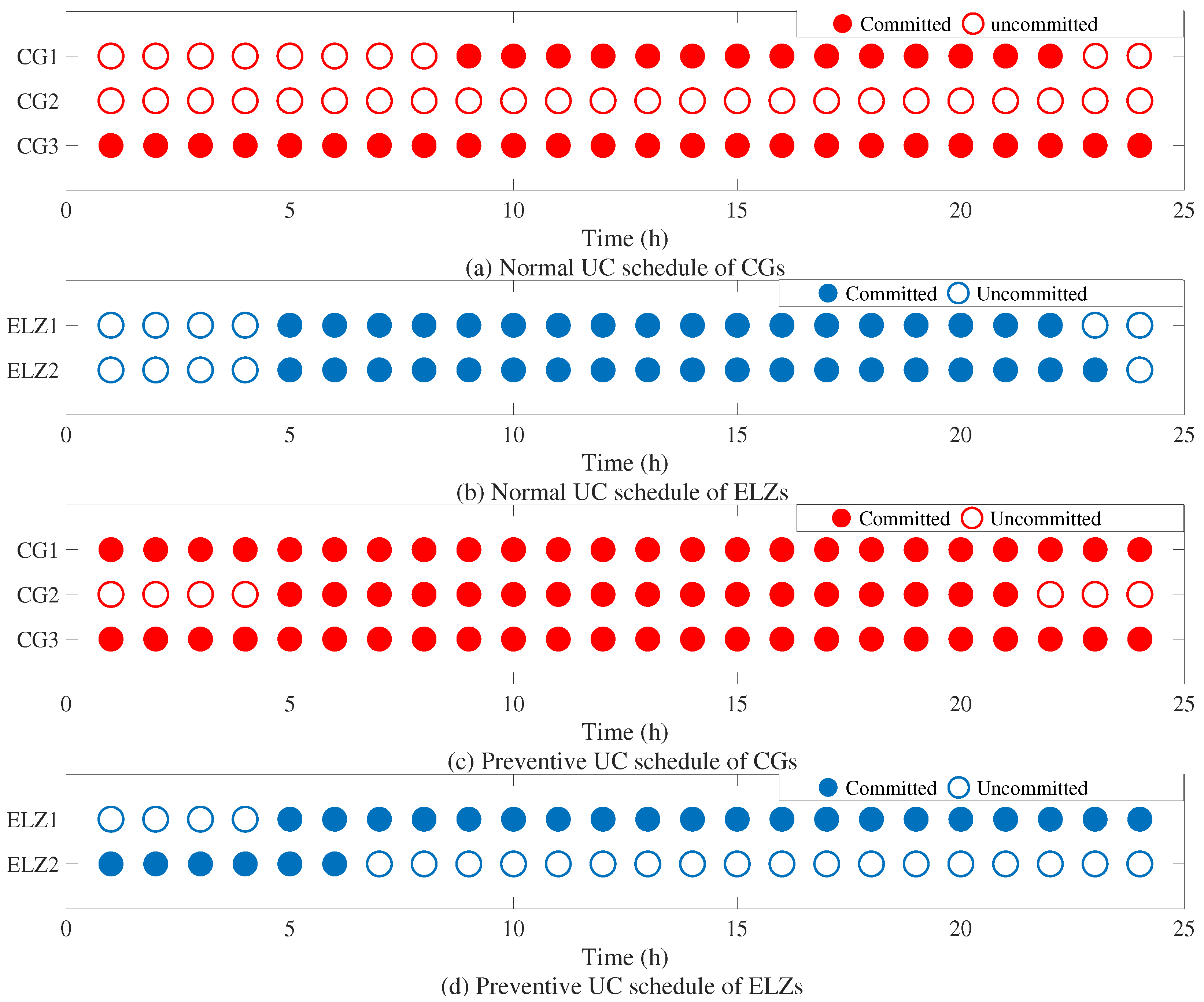
Figure 5 presents the UC schedules of the CGs and ELZs. Specifically,
Figure 5a,b show the normal UC schedules without considering facility damages, while
Figure 5c,d display the UC schedules obtained under the proposed preventive scheduling approach, which accounts for potential facility damages. In the figures, a filled circle indicates that the corresponding unit is committed, whereas a hollow circle denotes that the unit is offline. It can be observed that CG1 and CG3 are committed in all cases, whereas CG2 remains offline. This is because CG2 has a higher generation cost and is dispatched only when additional hydrogen production is required for HT in the emergency stage. In addition, ELZ2 operates from 1:00 to 6:00 because the outage of line 4-6 splits the TNS into two islanded areas, and the area containing ELZ2 experiences a power shortage as the generation capacity of CG3 is insufficient to meet the local demand. These results demonstrate that the preventive scheduling approach yields a reasonable UC pattern by proactively allocating flexible resources to mitigate islanding-induced shortages.
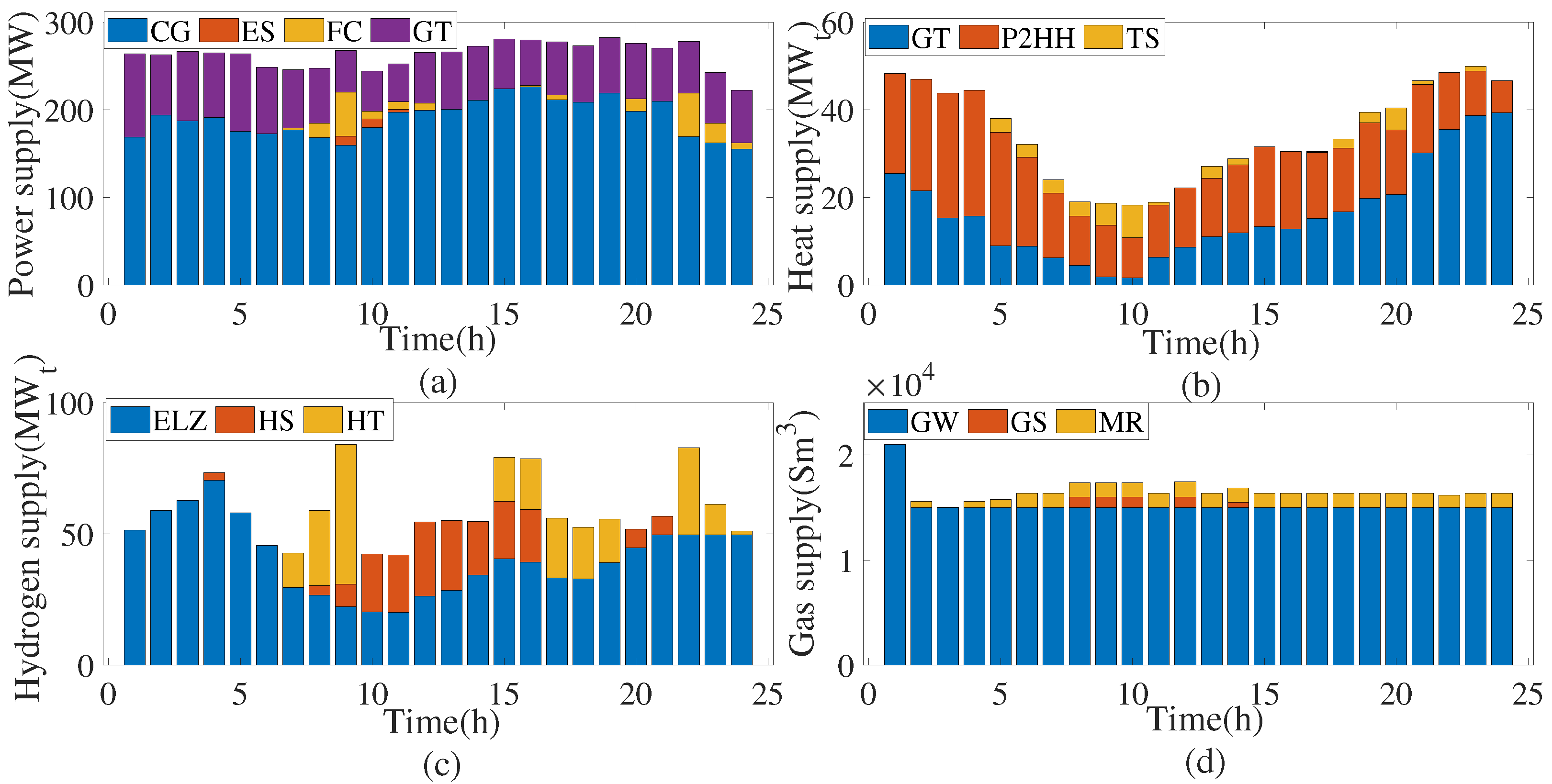
Figure 6 presents the schedules of electric power, heat, hydrogen, and natural gas supplies. As shown in
Figure 6a,c, hydrogen is transported to EH2 via HT and then converted into electricity through the FC. From
Figure 6b, approximately half of the heat demand is supplied by the ELZs through P2HH scheduling, which preserves additional natural gas for GT power generation and residential gas demand under conditions of limited gas availability. In
Figure 6d, natural gas is primarily supplied by the GW due to the capacity limits of the pipelines and the GS. Only a portion of the hydrogen is converted to natural gas for overall cost considerations. These results indicate that the system relies heavily on P2HH to alleviate natural gas shortages and on HT-to-FC conversion to support the islanded area, demonstrating the cross-energy sensitivities that highlight the need for coordinated preventive scheduling.
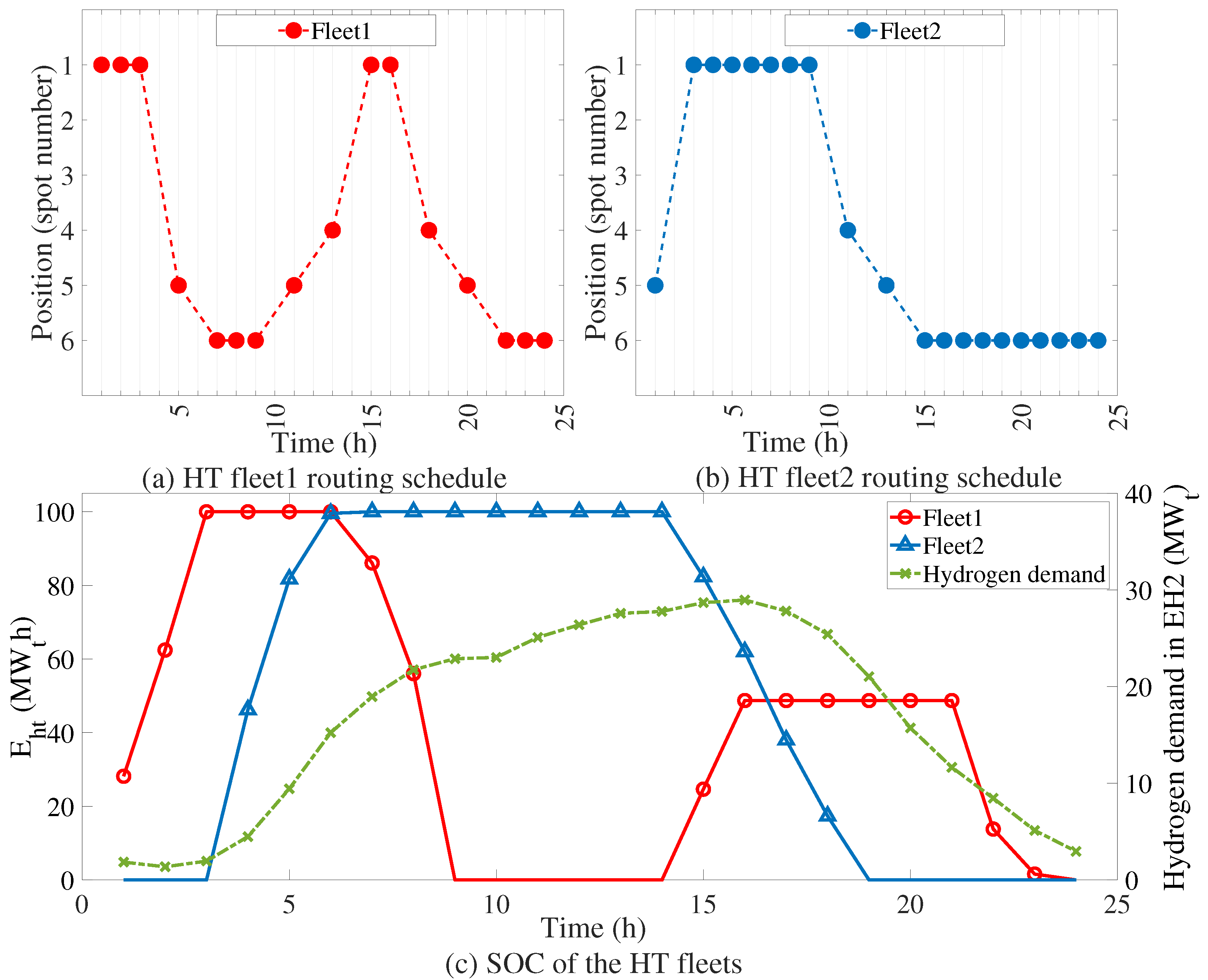
Figure 7 illustrates the routing schedules of the HT fleets as well as their charging and releasing statuses. Taking Fleet 1 as an example, it charges hydrogen at EH1 from 1:00 to 3:00, then travels along the shortest path 1-5-6 and arrives at node 6 at 6:00 to meet the upcoming hydrogen demand peak during 10:00–16:00. After fully releasing its stored hydrogen, Fleet 1 immediately returns to EH1 for the next delivery cycle. Because the shortest return path 6-5-1 becomes unavailable at 3:00 due to a road interruption, Fleet 1 must instead return via the alternative route 6-3-2-1. This routing adjustment highlights the system’s high sensitivity to road interruptions, as even a single blocked path necessitates detours and increases travel time, underscoring the importance of considering road-network uncertainty in HT scheduling.
To illustrate the effectiveness of the proposed method, five cases are considered as follows:
Case 1 (Baseline): Only UC is considered; the ELZs operate without P2HH scheduling as [
19].
Case 2: Only UC is considered; the ELZs operate with P2HH scheduling as [
13].
Case 3: One HT fleet is requisitioned, but the roads are immunity to disasters. Other settings are the same as Case 2.
Case 4: The roads can be interrupted by disasters. Other settings are the same as Case 3.
Case 5: Two HT fleets are requisitioned. Other settings are the same as Case 4.
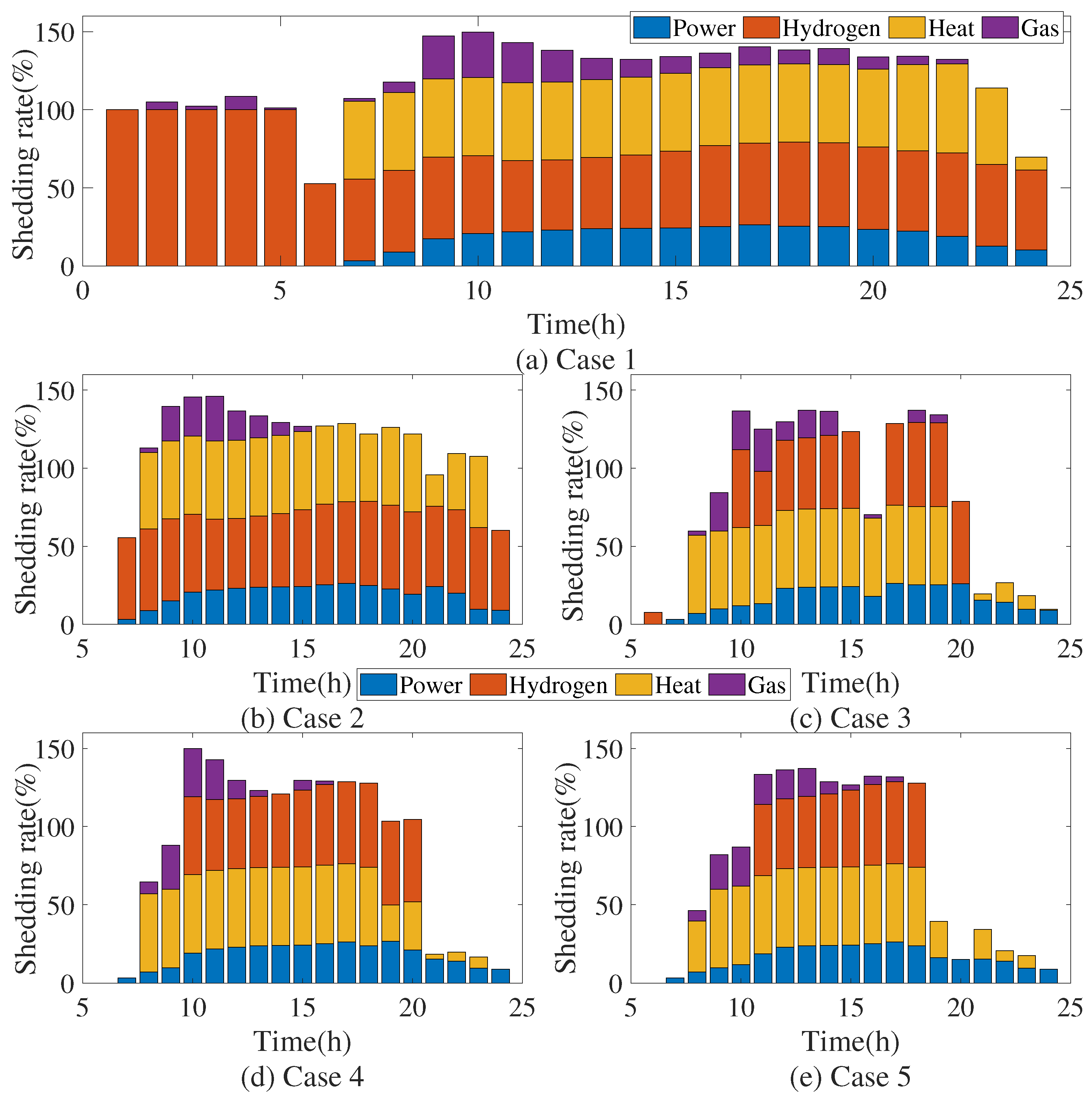
The results are given in
Table 2 and
Figure 8, where the changes compared to the baseline are indicated in bold.
Figure 8 shows that the load-shedding period becomes increasingly concentrated around the peak hours as more effective preventive schemes are adopted.
Table 2 further indicates that Case 5 achieves the lowest total cost and load shedding. By comparing Case 1 and Case 2, it can be observed that heat recovery reduces all forms of energy curtailment in the HIES. In Case 2, heat and gas curtailments directly benefit from the P2HH scheduling, decreasing by 17.33% and 31.62% to Case 1, while the reductions in power and hydrogen curtailments are comparatively smaller. When the TNS is divided into two islands, different types of energy can no longer be flexibly allocated due to interrupted power exchanges and pipeline capacity limits, which restricts the system’s ability to further reduce operational costs. The results of Case 3 to Case 5 highlight the importance of HT scheduling within the proposed preventive framework. In these cases, the total cost and load curtailments are reduced by approximately a factor of two compared with Case 2. When one HT fleet is requisitioned (Case 3–4) or two fleets are requisitioned (Case 5), the electric-power curtailment is reduced by roughly threefold and fivefold compared with Case 2, respectively. Relative to Case 4, substantially more hydrogen is transported to the energy-deficient area in Case 3 and Case 5, leading to further reductions in power and hydrogen curtailments. Overall, these results demonstrate that heat recovery, P2HH scheduling, and HT flexibility play complementary and significant roles in strengthening system resilience. By enabling cross-energy coordination and ensuring resource deliverability under disruptions, the proposed preventive schemes substantially enhance the system’s capability to withstand and recover from extreme events.
4.2. Test 2: 39-Bus, 20-Node, 12-Spot System
To verify the effectiveness and computational performances of the proposed ARO-based preventive scheduling with the uncertainties of facility damage, a larger 39-bus, 20-node, 12-spot system is used in this test. The system contains five CGs, five EHs, two GSs, and three GWs. Four HT fleets are requisitioned and pre-deployed at spots 3, 11, 6, and 2, respectively. The updating step in Algorithm 2 is set to 2.
To evaluate the sensitivity of the scheduling results to the robustness budgets
, the outcomes of the proposed preventive schemes under different budget levels are summarized in
Table 3. The initial values of
,
, and
are set to 5, 4, and 2, respectively. When
increases to 6, the failure of transmission lines 39-1, 4-3, 17-16, 16-15, 28-26, and 29-6 divides the TNS into four islanded subsystems under the worst-case scenario. In this case, generation resources become highly unevenly distributed, with no CG in the island containing EH1 and four CGs concentrated in the area of EH4. This imbalance leads to power load curtailment and results in a 44% increase in the total system cost, which subsequently drives higher levels of heat, hydrogen, and gas load shedding. Similarly, when
rises to 5, pipelines 3-4, 4-8, 7-10, 8-11, and 11-12 fail in the worst-case scenario. Although the gas load curtailment increases by 61%, the load shedding of power, heat, and hydrogen rises by less than 10%, indicating that the integrated energy system maintains a relatively high level of resilience against limited natural gas supply disruptions. For the transportation network, increasing
by one unit (while keeping other budgets constant) leads to a 4% increase in total cost and a 10% increase in average load shedding. These results highlight that road accessibility plays a critical role in maintaining the efficiency of HT scheduling and, consequently, the overall resilience of the HIES. This finding is consistent with the trends observed in
Table 2 from Test 1.
Table 4 illustrates the computational performances of the proposed preventive schemes solved by different methodologies. The budgets
are respectively set at 6, 4, 3. When the nested C&CG is adopted directly, the solver is stuck when solving SMP, making the day-ahead scheduling fail. When the AOP is used in the inner C&CG loop, a near-optimal solution, with a deviation of 2% from the solution by the C&CG-AOP algorithm, is obtained in 25214s. The iterations of MP and SP, respectively, are 8 and 26 for the two algorithms. The solution time is further reduced by 21% using the proposed ATC-C&CG-AOP algorithm compared to the C&CG-AOP algorithm. Overall, simulation results on the 39-bus, 20-node, 12-spot test system demonstrate that the proposed strategy effectively reduces shedding costs. In addition, the ATC–C&CG–AOP algorithm exhibits clear advantages in convergence and computational efficiency, particularly in solving the MP.
5. Conclusions
This paper proposes an ARO-based resilient preventive scheduling approach that incorporates the interactions among multiple energy systems, P2HH, and HT scheduling in HIESs to mitigate the impacts of natural disasters. The model accounts for road interruptions as well as failures of TLs and pipelines caused by disasters. To improve computational efficiency, an ATC–C&CG–AOP hybrid algorithm is developed to solve the proposed ARO model. Case studies conducted on two test systems demonstrate that the proposed preventive scheduling model effectively reduces operational costs and load curtailments. Simulation results show that coordinating P2HH and HT reduces power, heat, hydrogen, and gas load curtailments by 14.35%, 43.39%, 49.97%, and 40.32%, respectively, and lowers operational costs by 14.60%. Moreover, the proposed hybrid algorithm enhances computational efficiency, reducing solution time by 21% with only a 2% deviation from the solution obtained using the conventional C&CG–AOP algorithm.
The proposed preventive scheduling approach has several limitations. First, the uncertainties of loads and renewable generation are not considered, which limits applicability in future energy systems with high renewable penetration. Future work will incorporate both disaster-induced uncertainties and source–load uncertainties and develop enhanced optimization models capable of handling all these factors simultaneously. Moreover, hydrogen transportation may pose potential safety risks, unlike natural gas, because hydrogen has several hazardous characteristics, including high leakage propensity, low minimum ignition energy, and a wide flammable range [
45]. Therefore, safety-oriented scheduling strategies for hydrogen transportation can be further investigated in future research.