Effects of Wellbore Parameters on the Performance of an Open-Loop Geothermal System with Horizontal Well
Abstract
1. Introduction
2. Materials and Methods
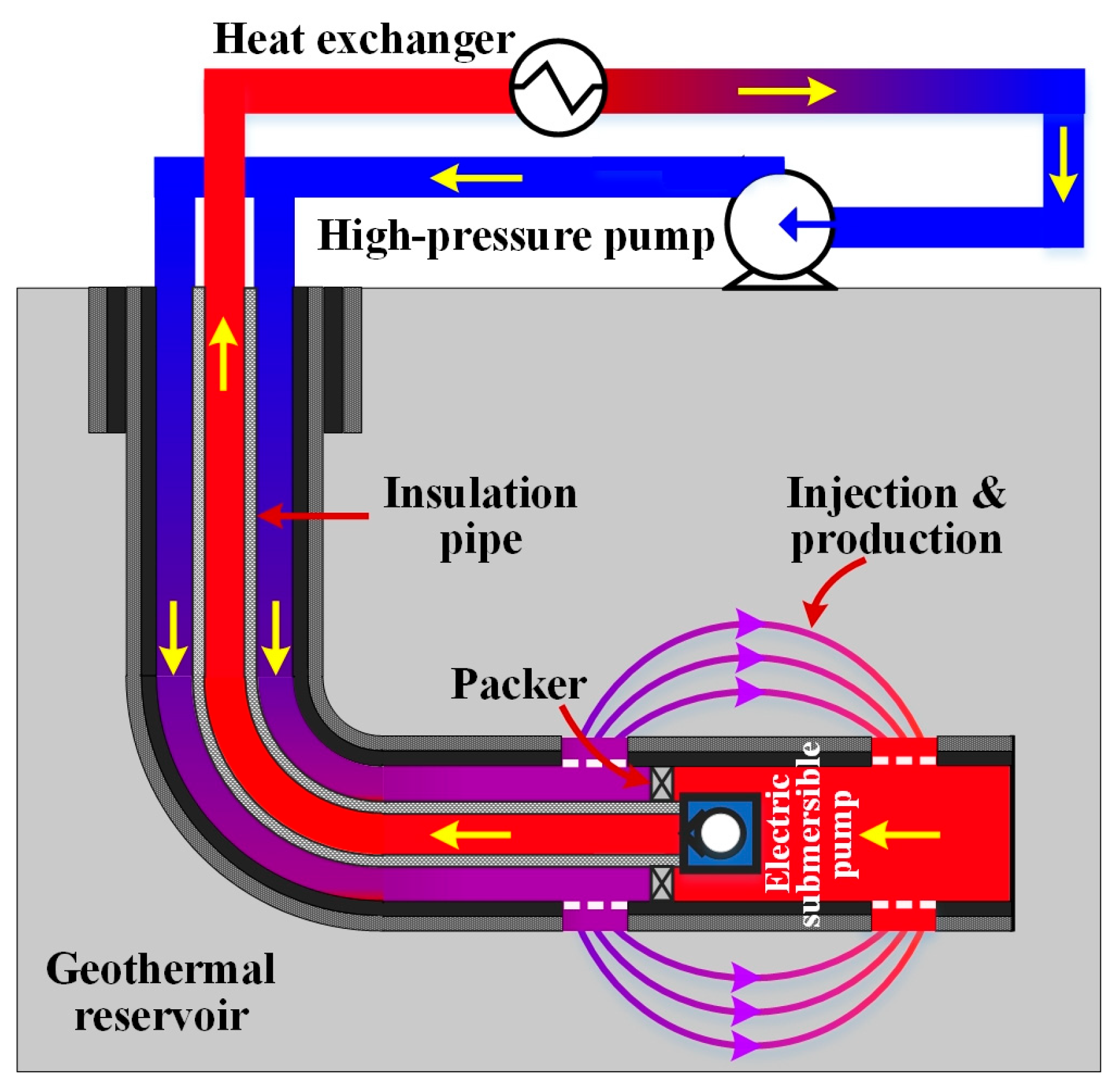
2.1. Model Assumptions
- (1)
- (2)
- In non-aquifer zones adjacent to the wellbore, heat transfer occurs exclusively by conduction in the rock matrix.
- (3)
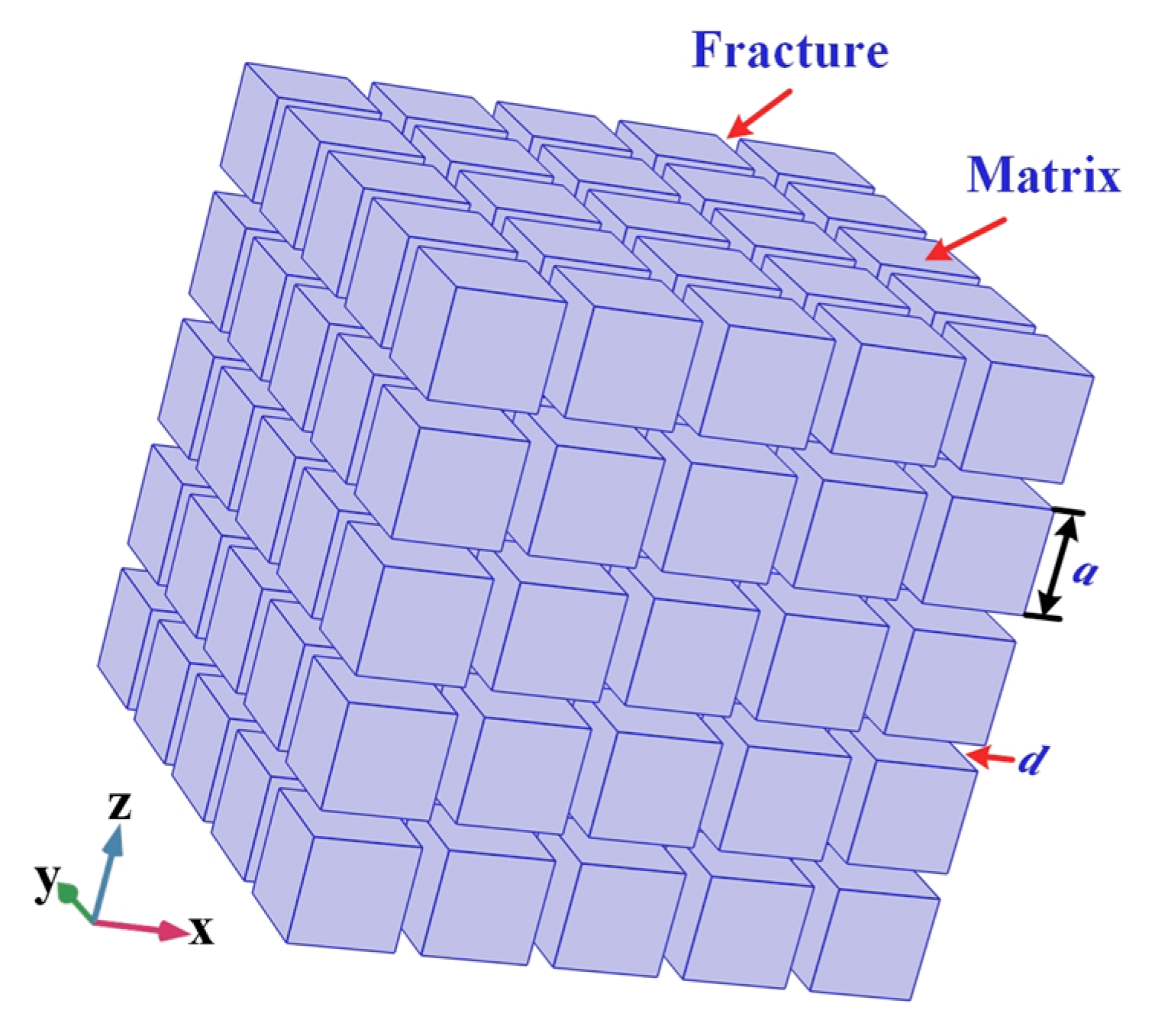
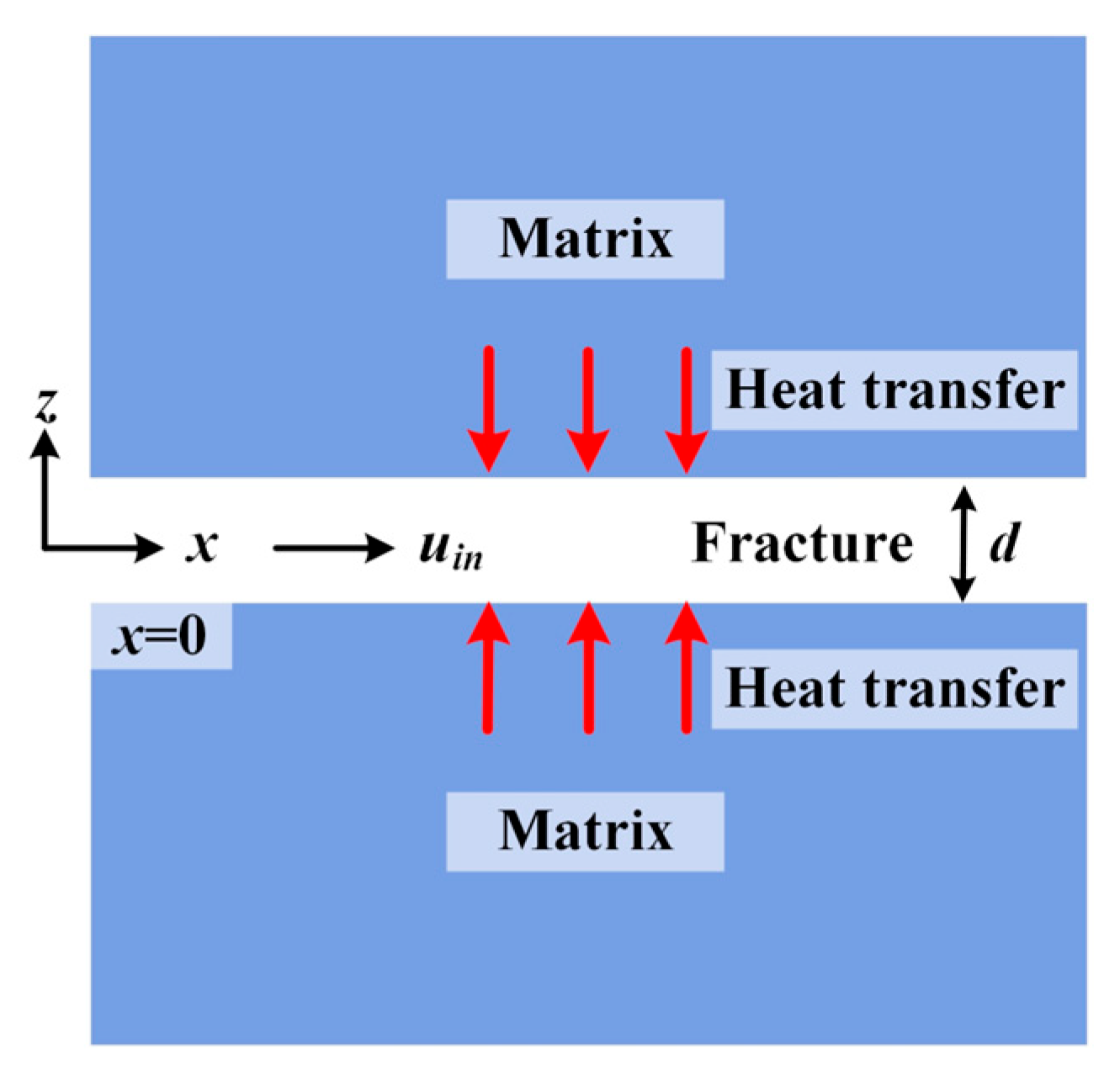
- The fractured geothermal reservoir (aquifer zone) is described based on the dual-porosity theory to ensure calculational efficiency. It conceptualizes the system as two superimposed continua (see Figure 2) [12]: a matrix region providing storage capacity, and a fracture region offering dominant flow channels.
- (4)
- The influence of formation deformation on porosity and permeability in the reservoir is neglected.
2.2. Governing Equations
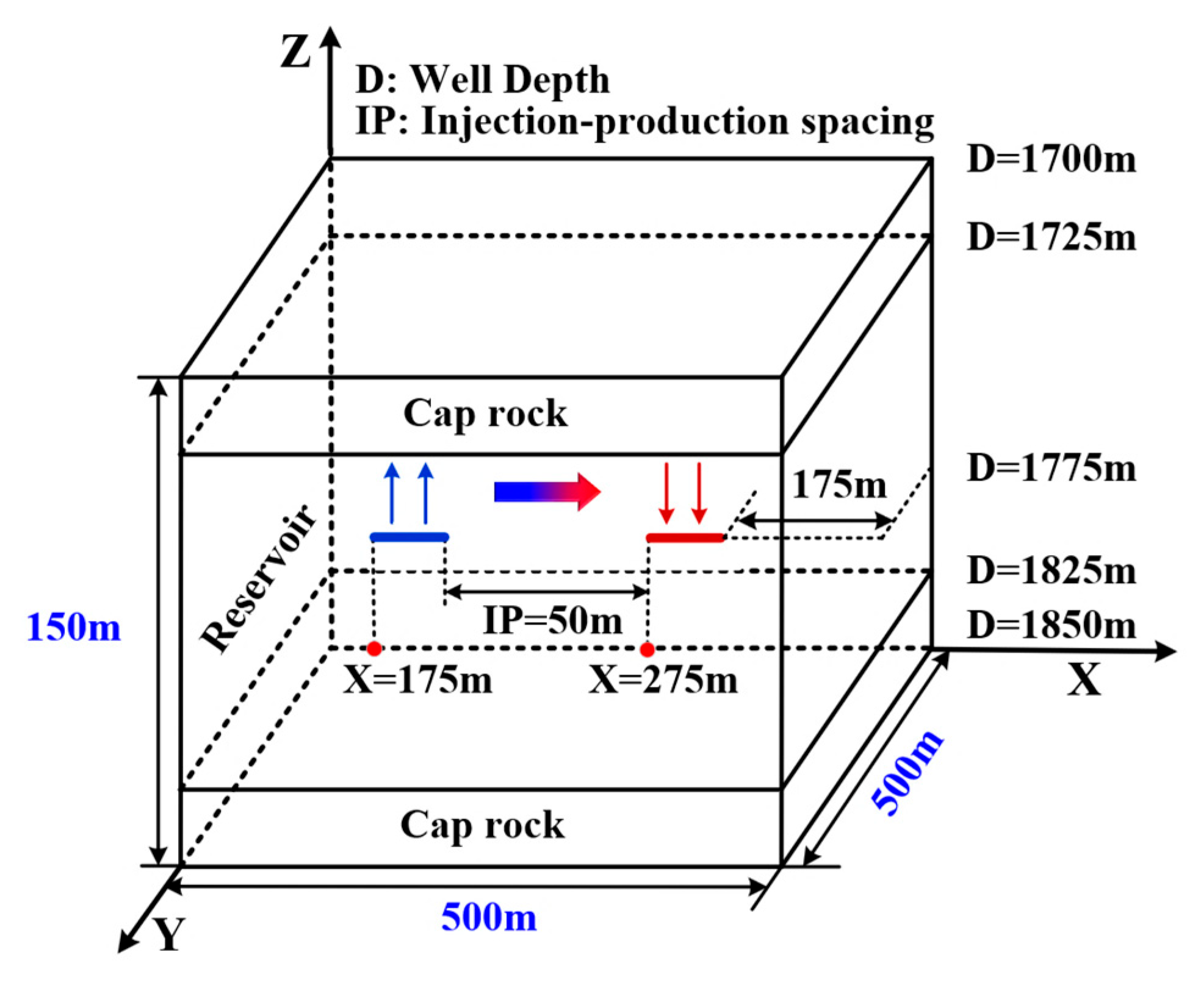
2.3. Geometric Model
2.4. Initial and Boundary Conditions for the Numerical Model
2.5. Numerical Calculation
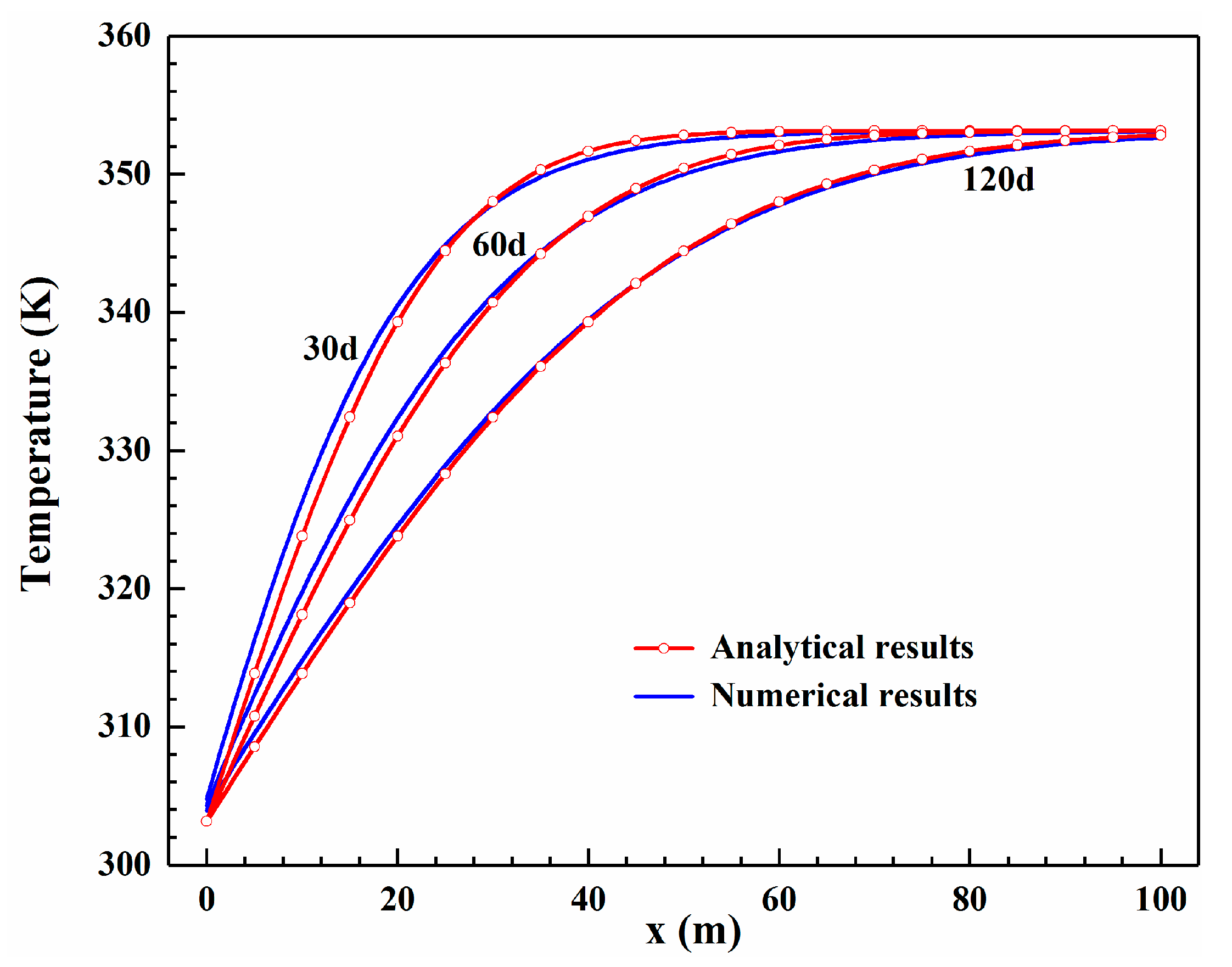
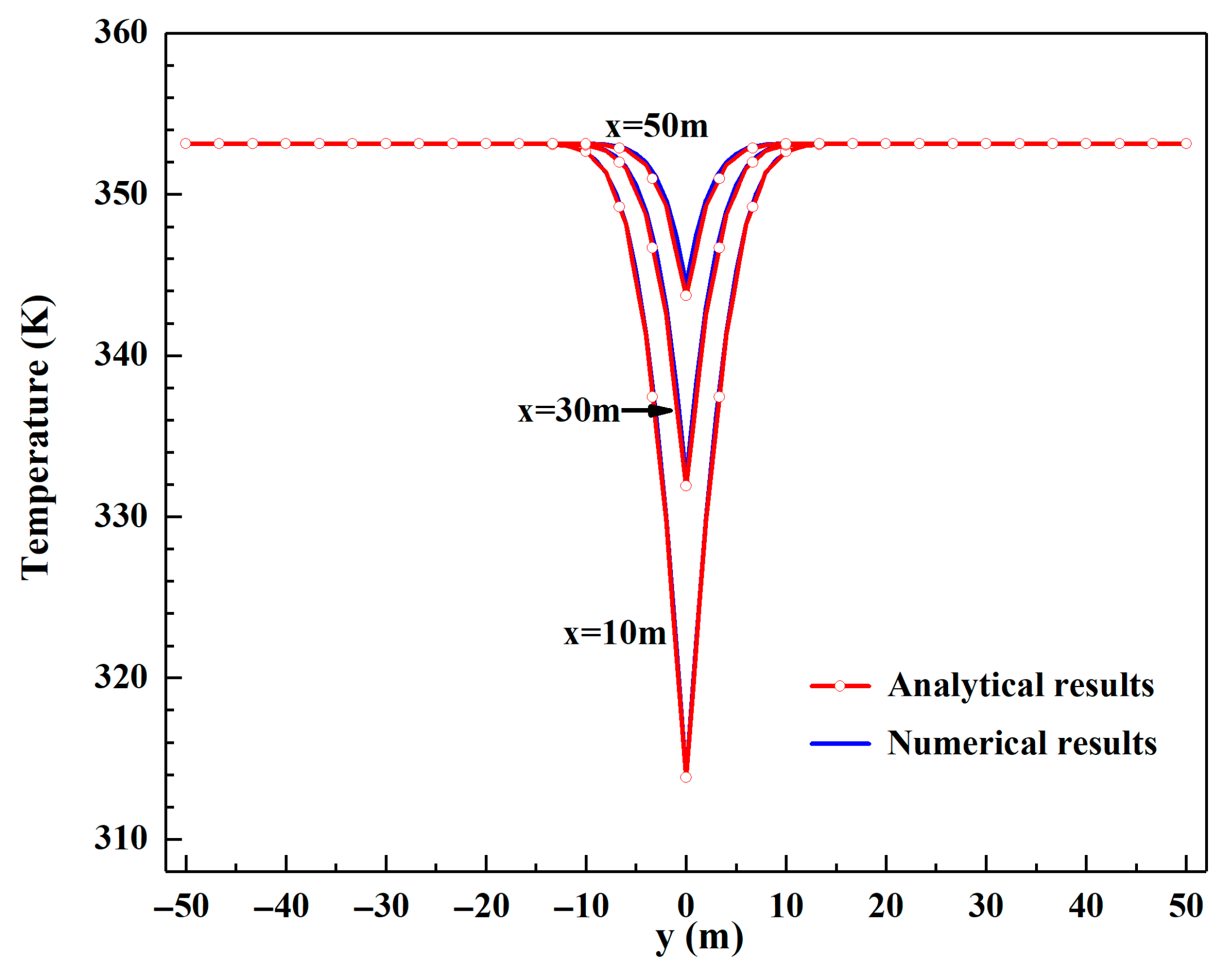
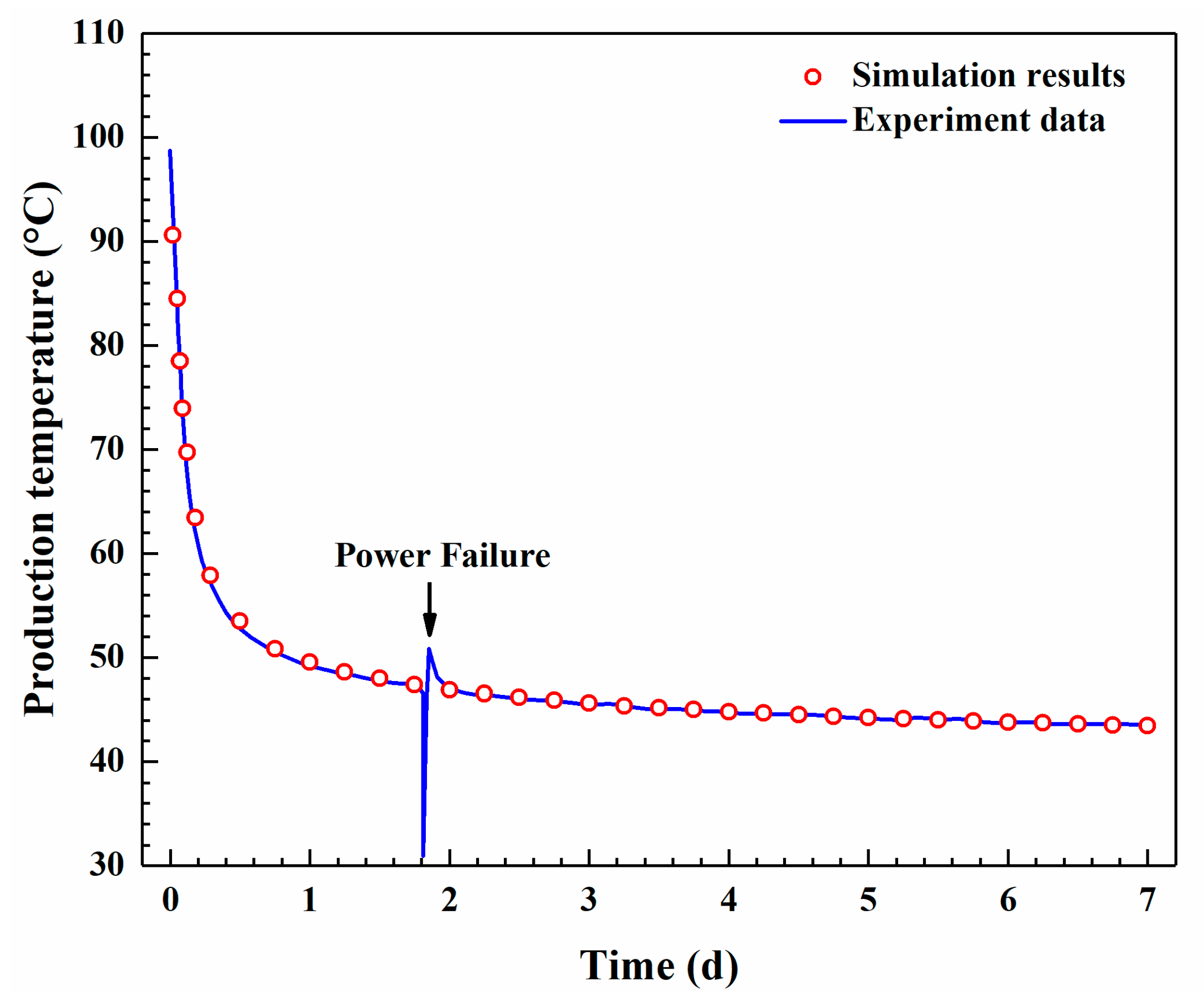
2.6. The Validation for the Numerical Model
3. Results
3.1. Influences of Various Wellbore Parameters
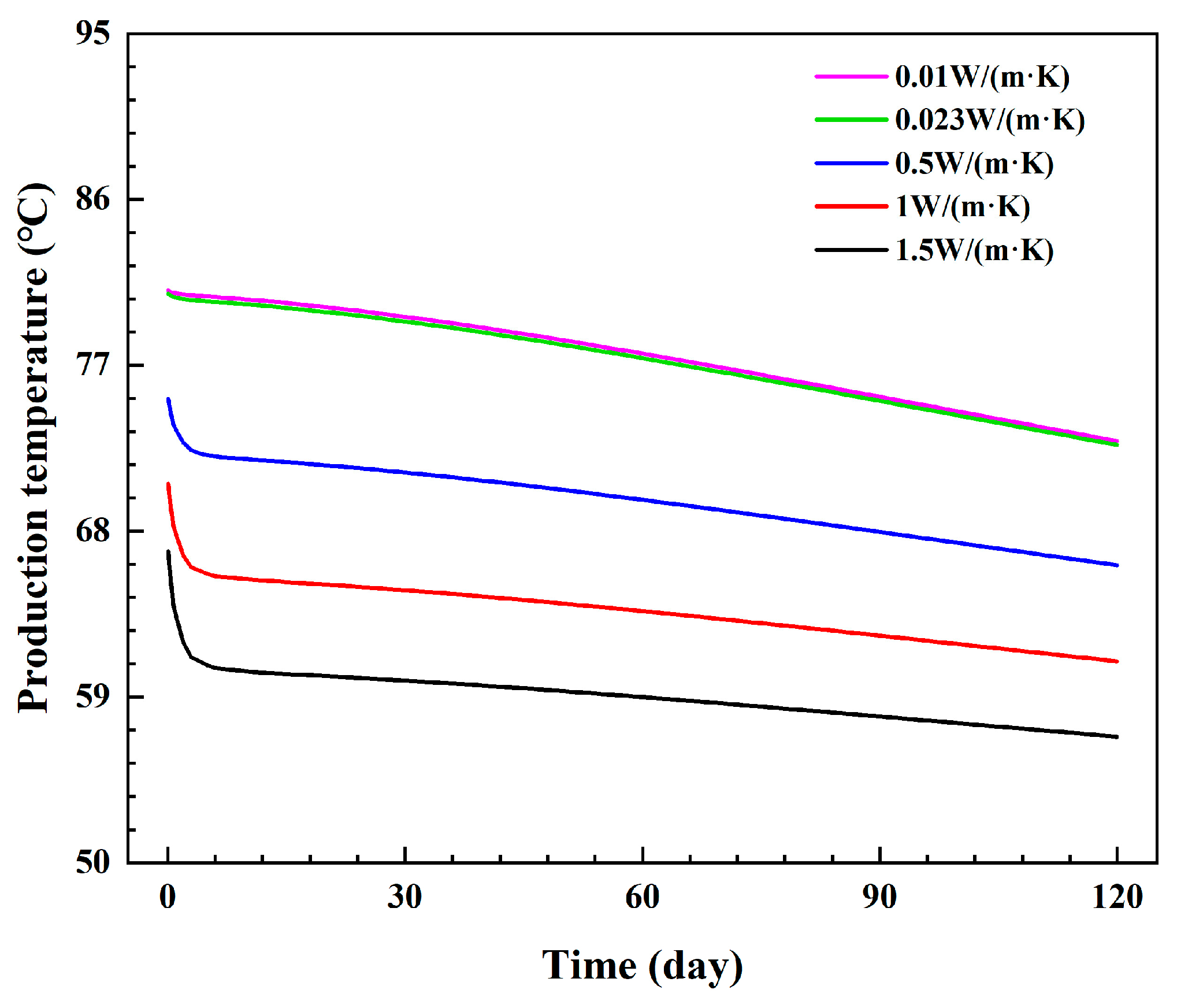
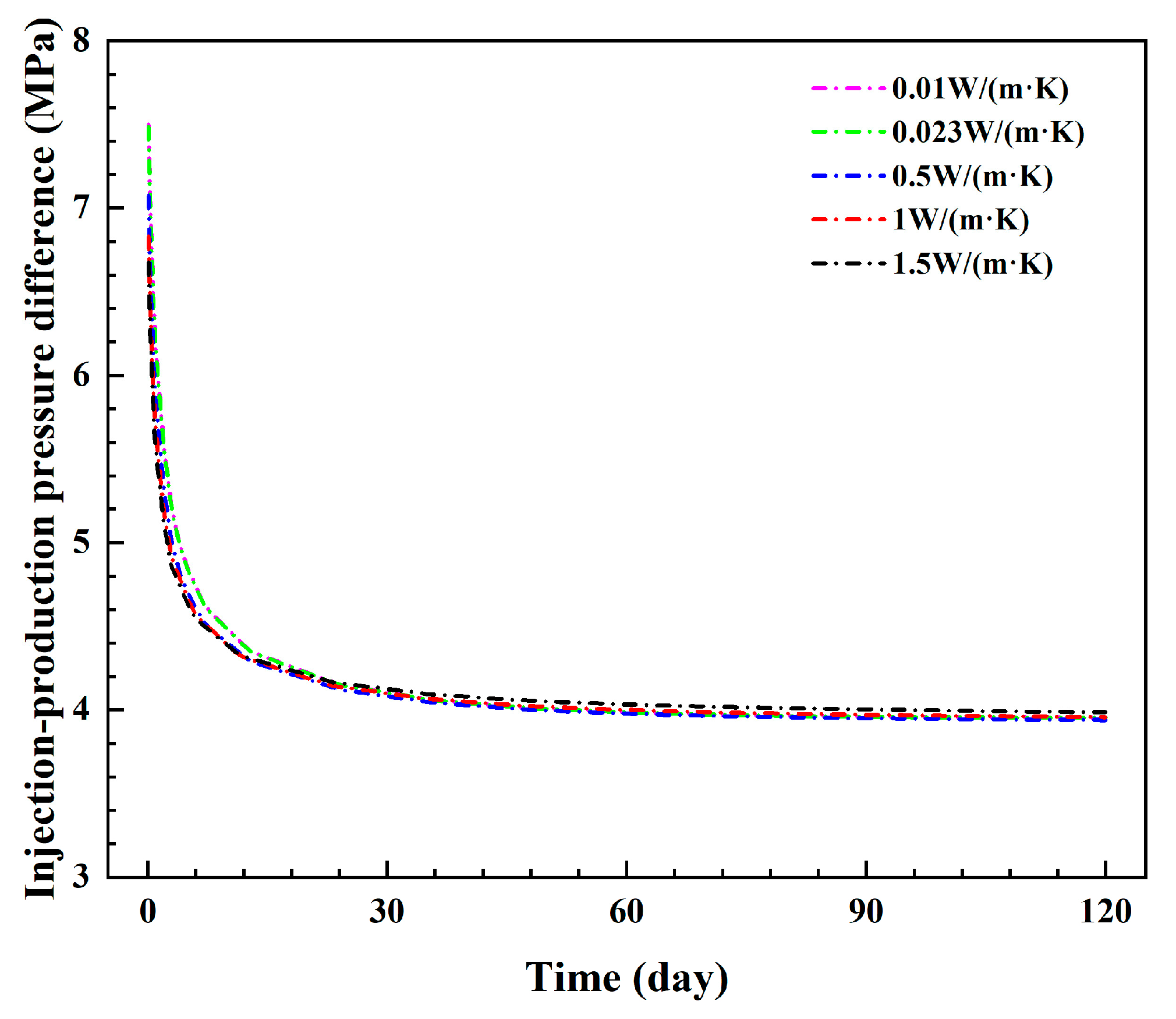
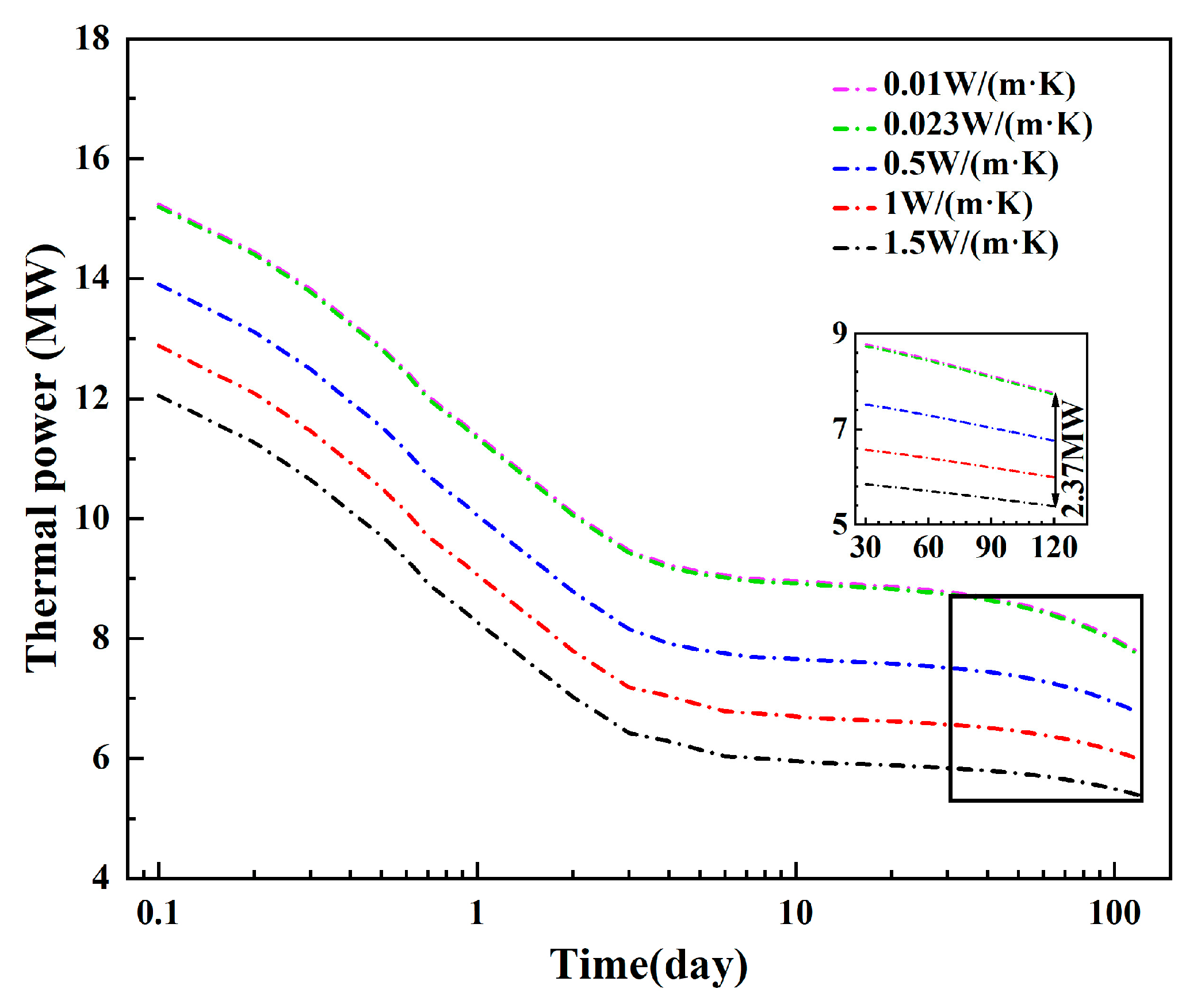
3.1.1. Influence of the Thermal Conductivity of the Insulated Pipe
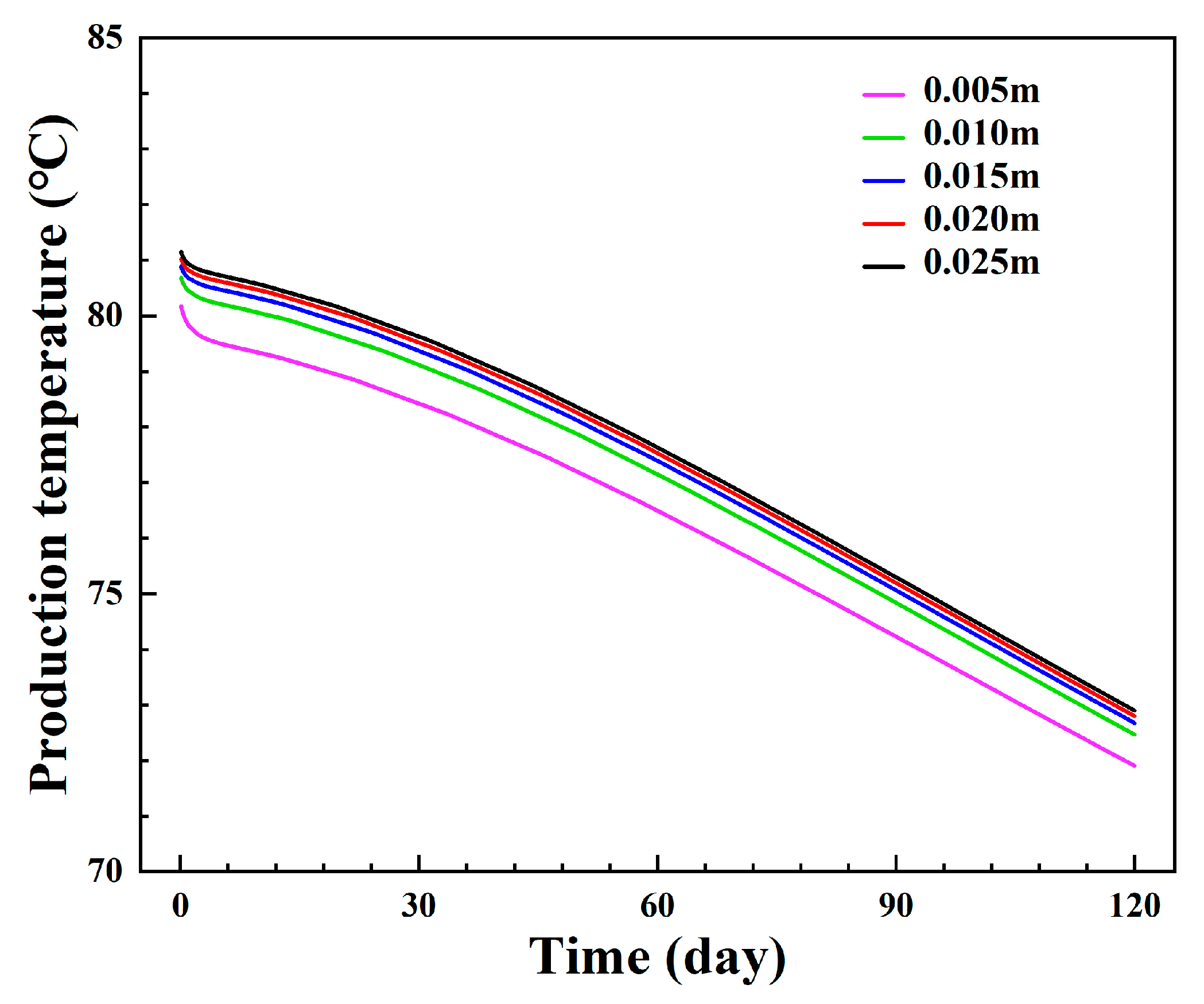
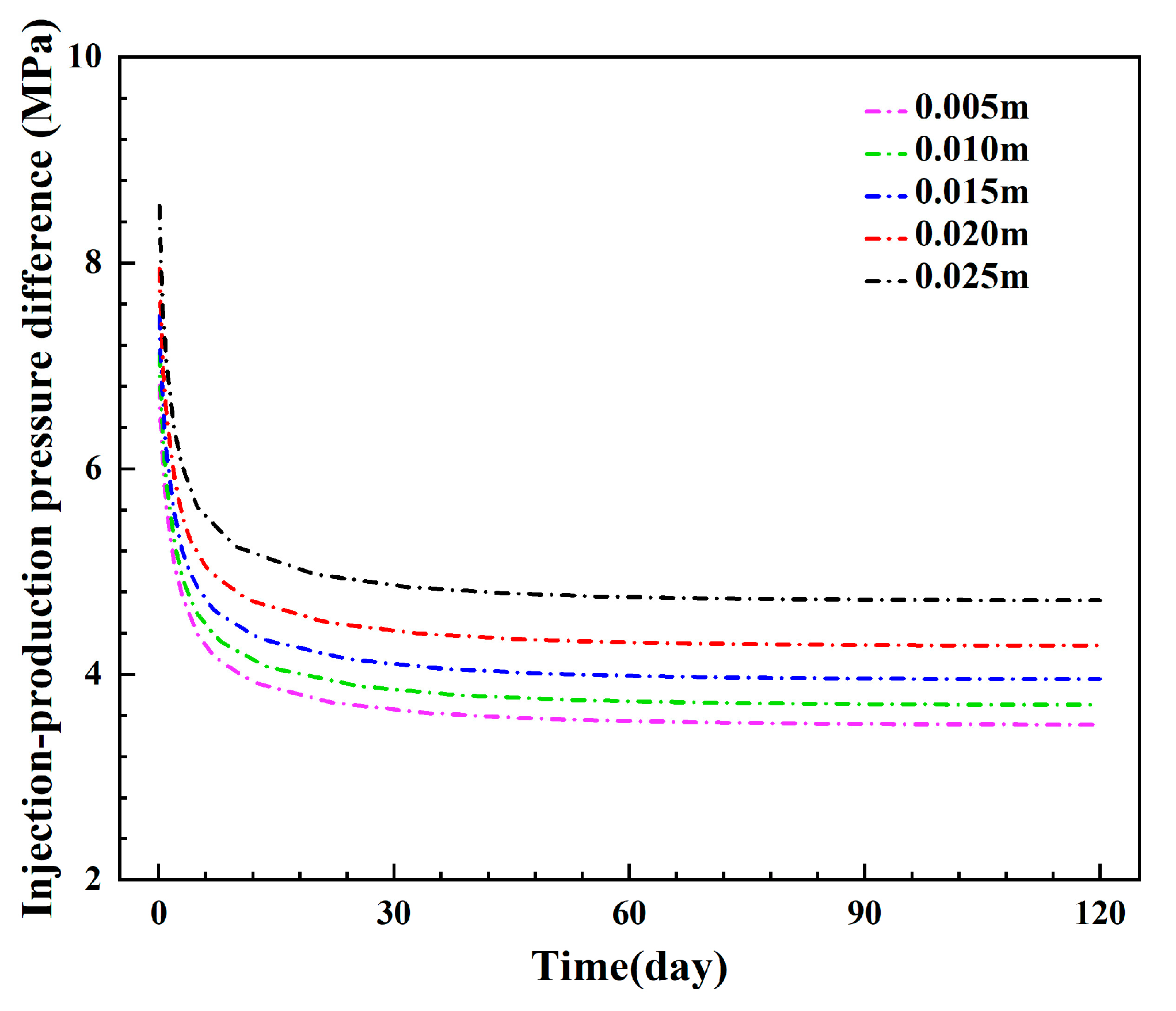
3.1.2. Influence of the Thickness of the Insulated Pipe
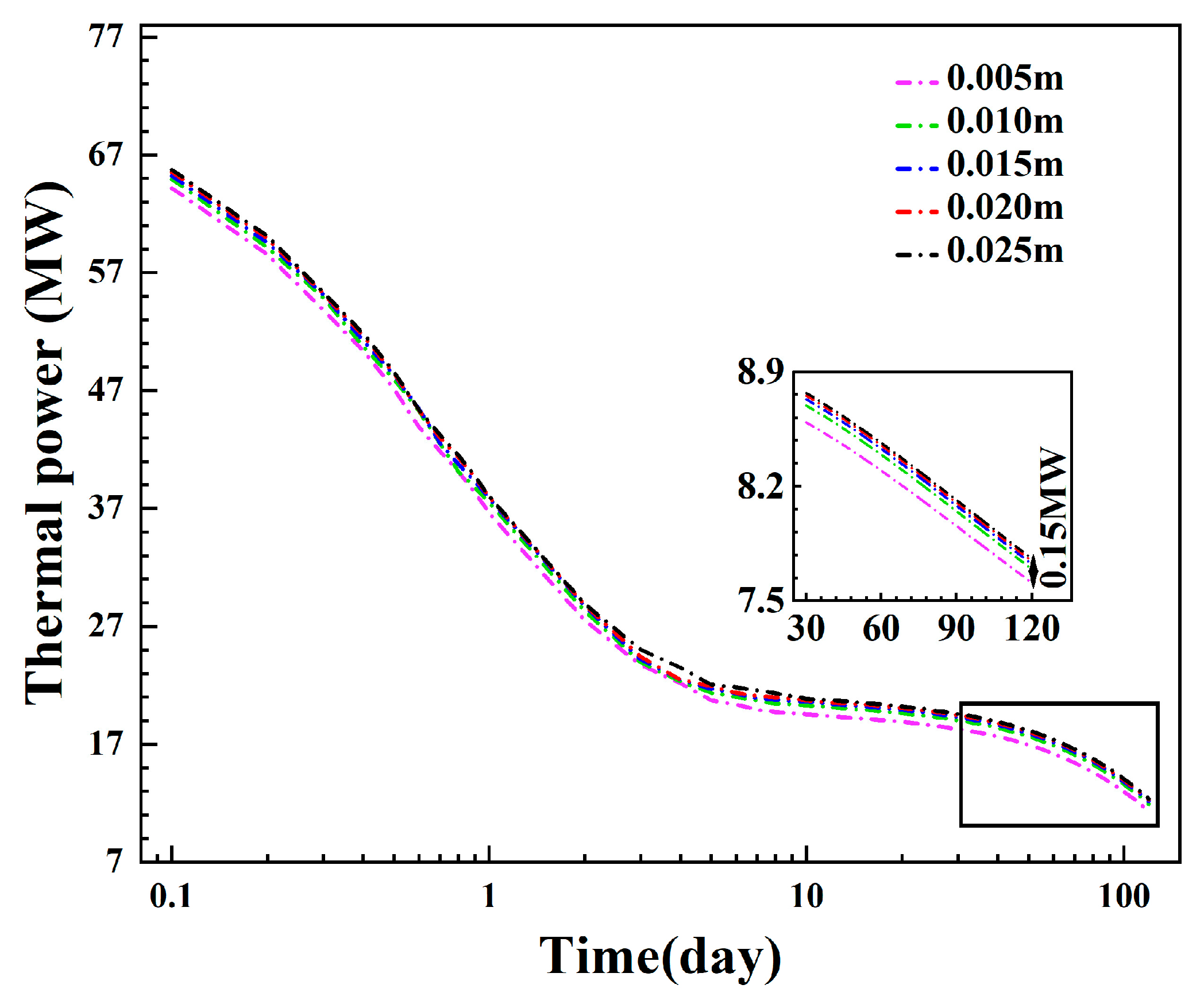
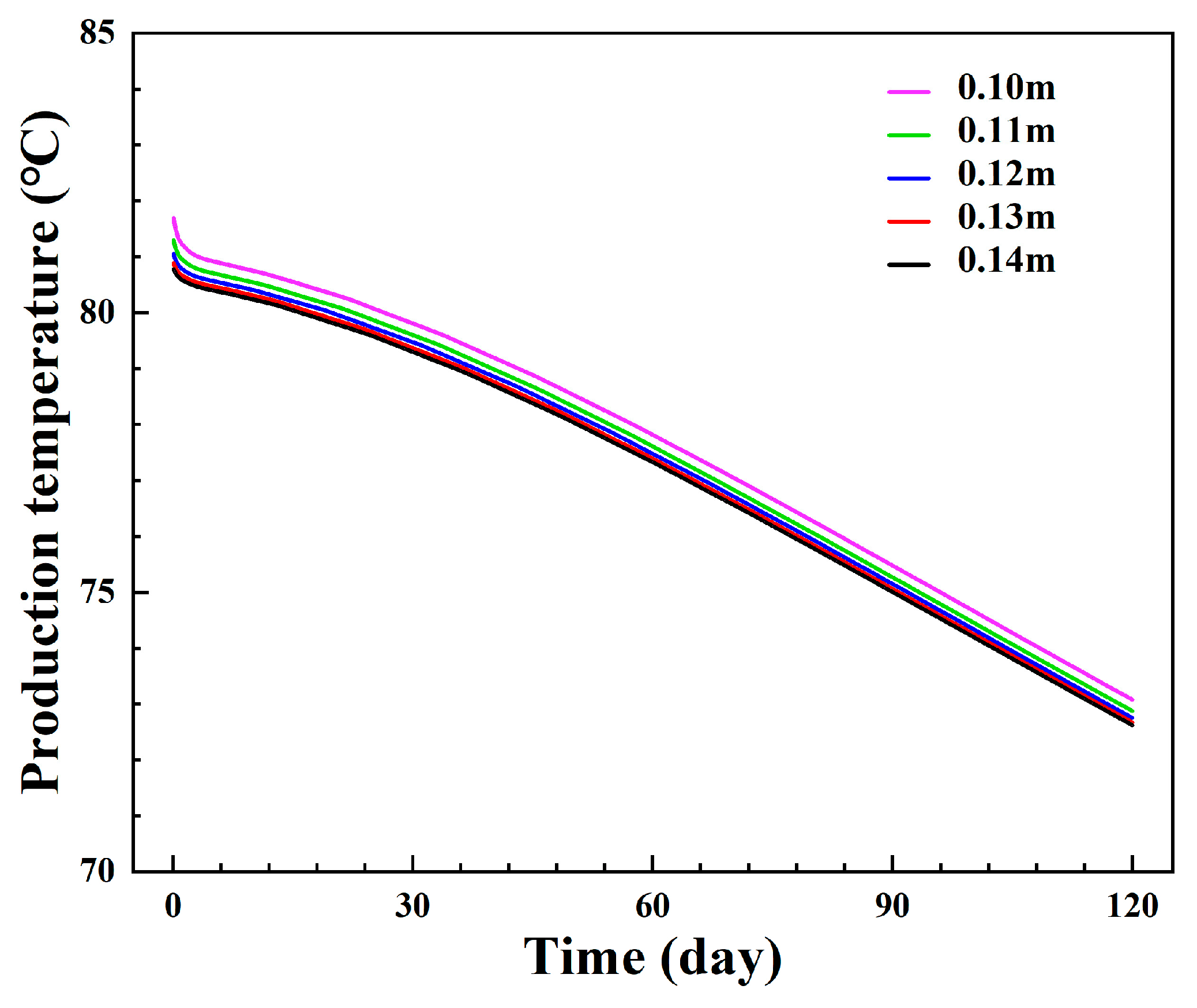
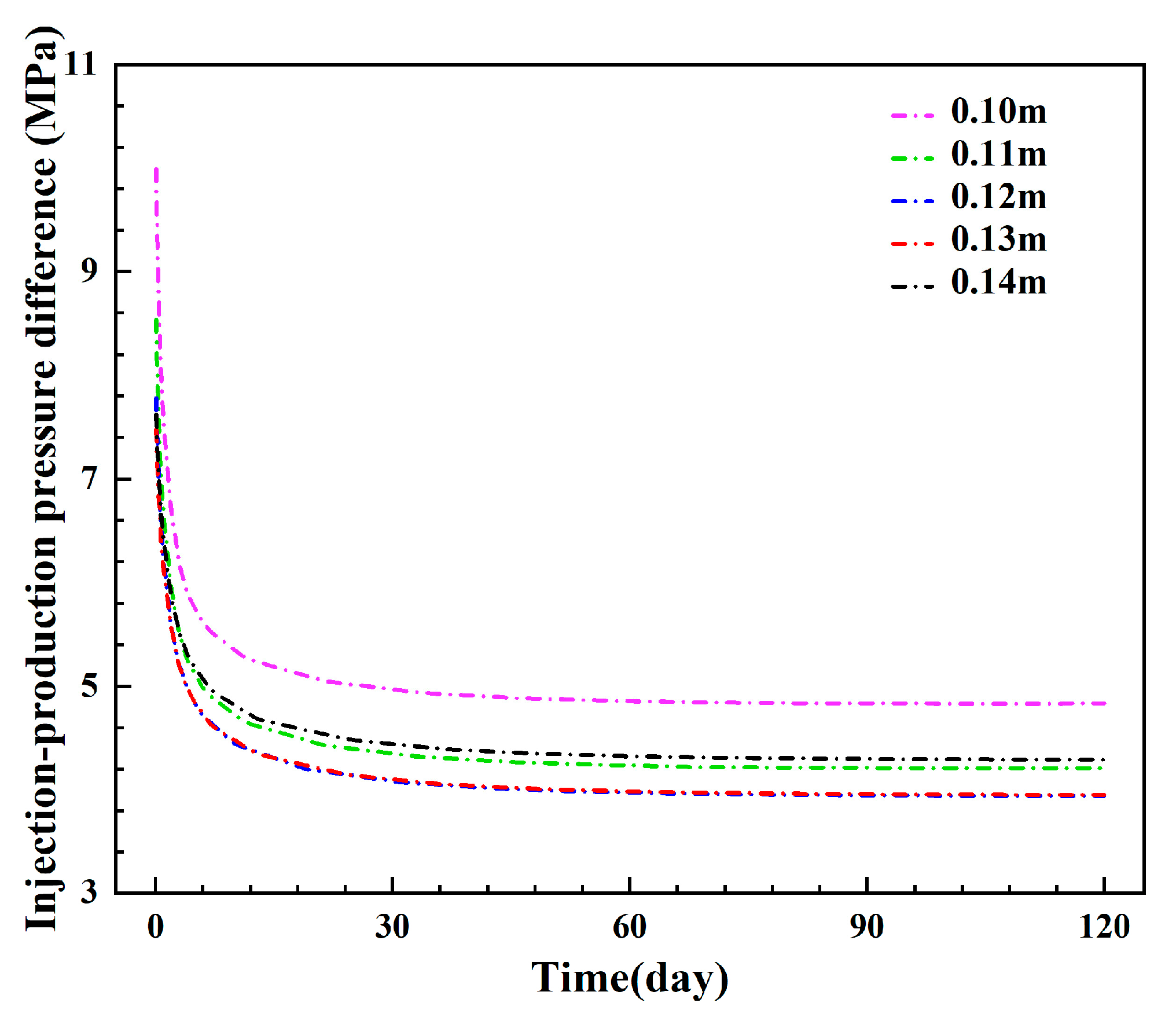
3.1.3. Influence of the Diameter of the Insulated Pipe
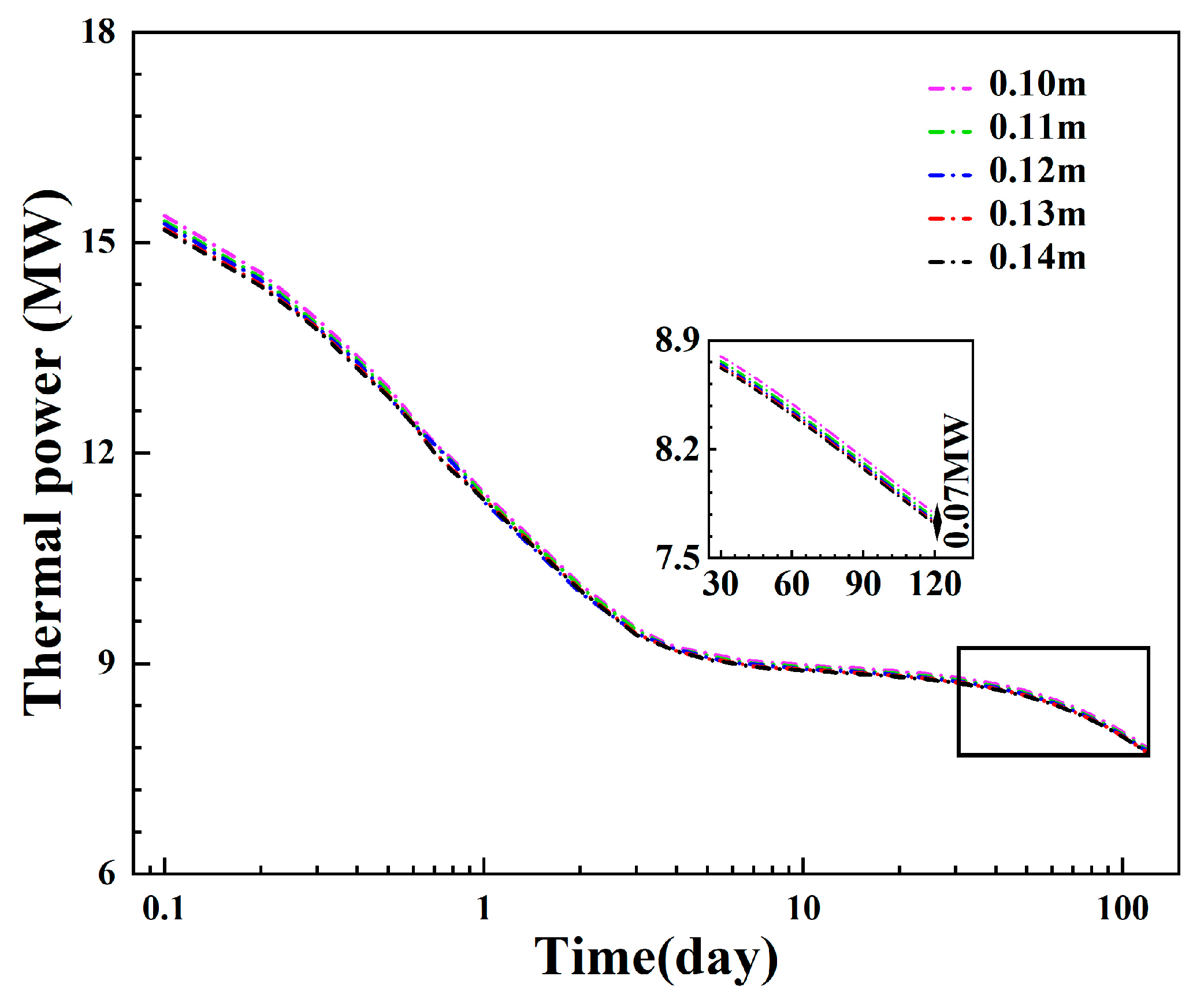
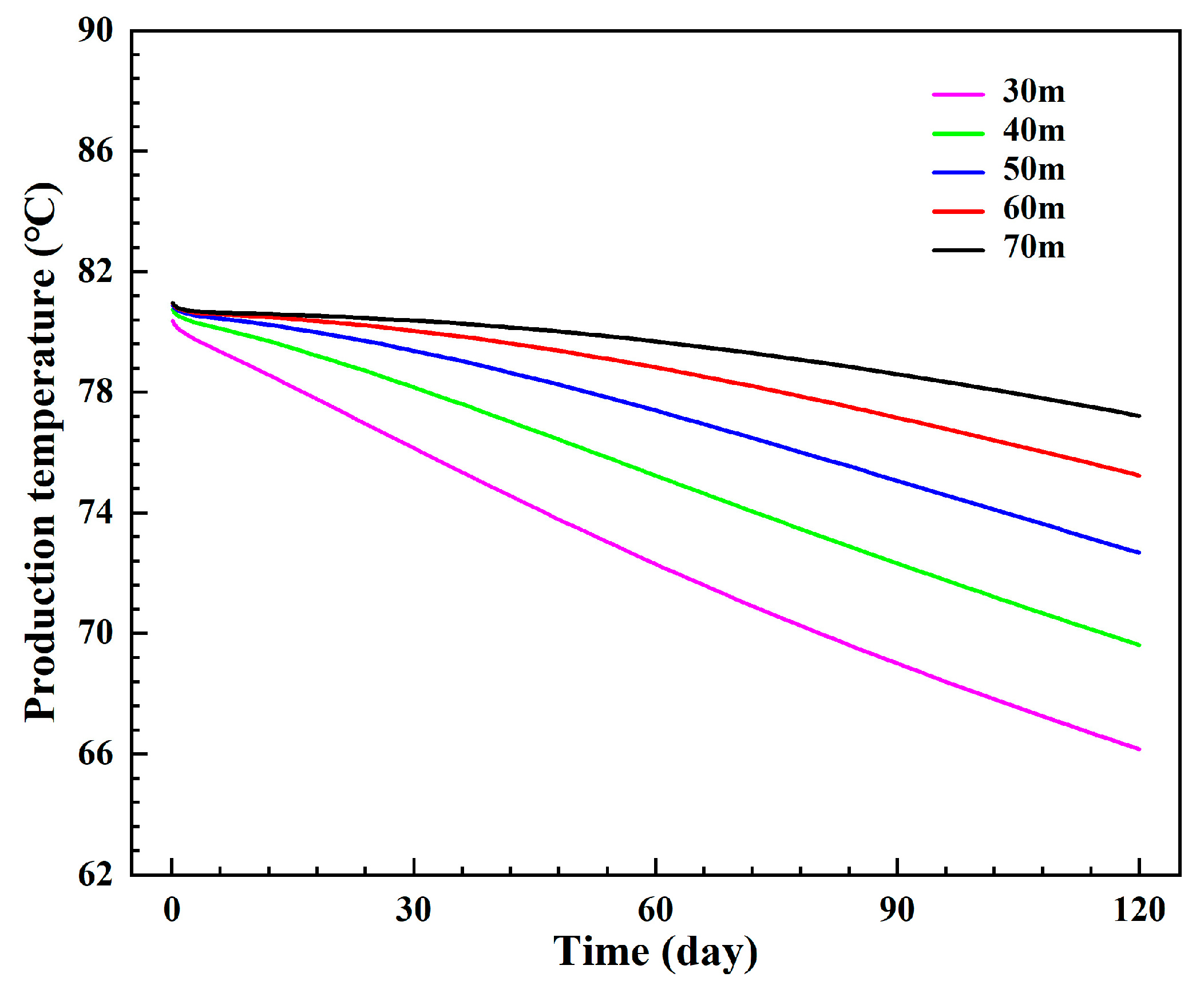
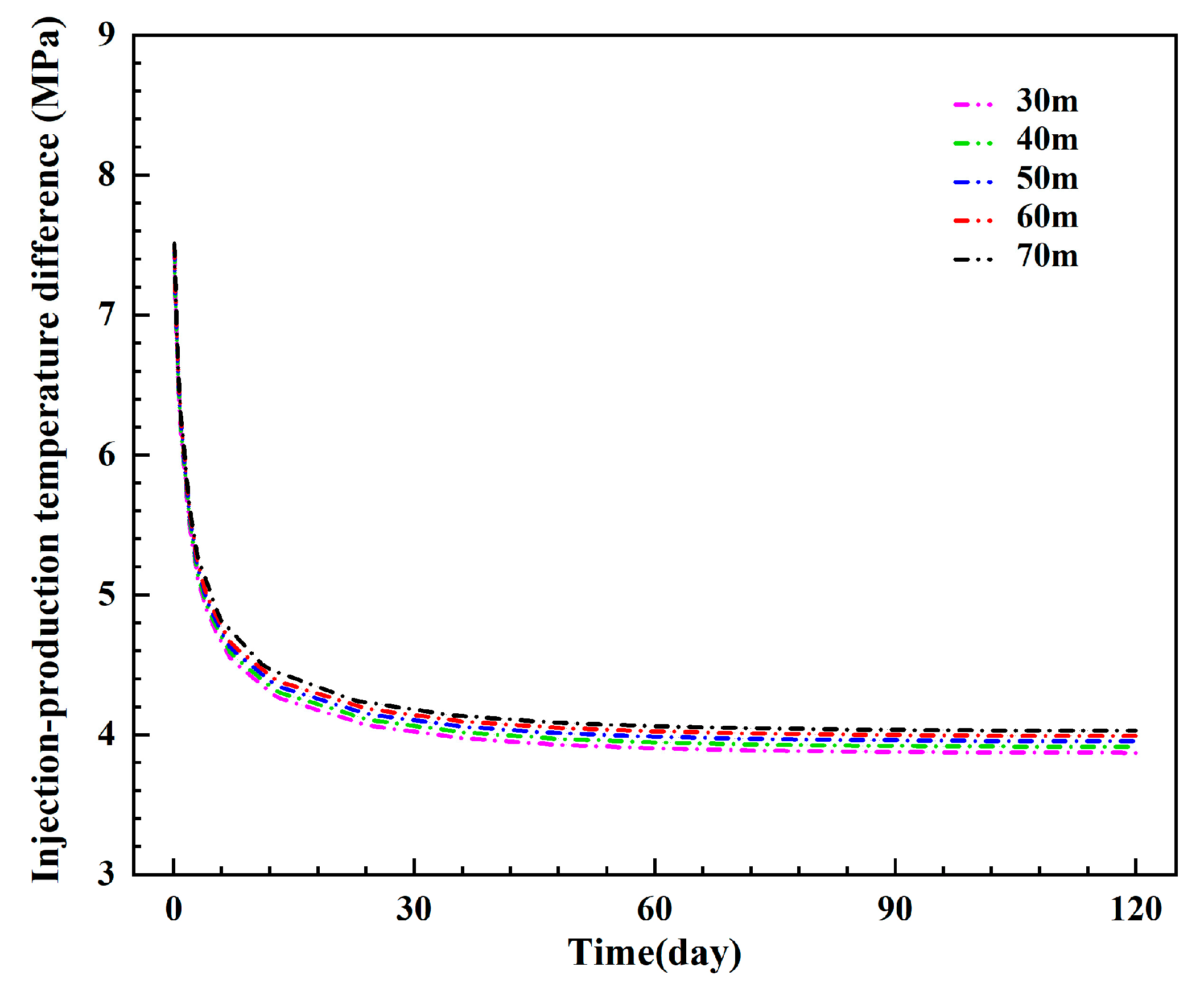
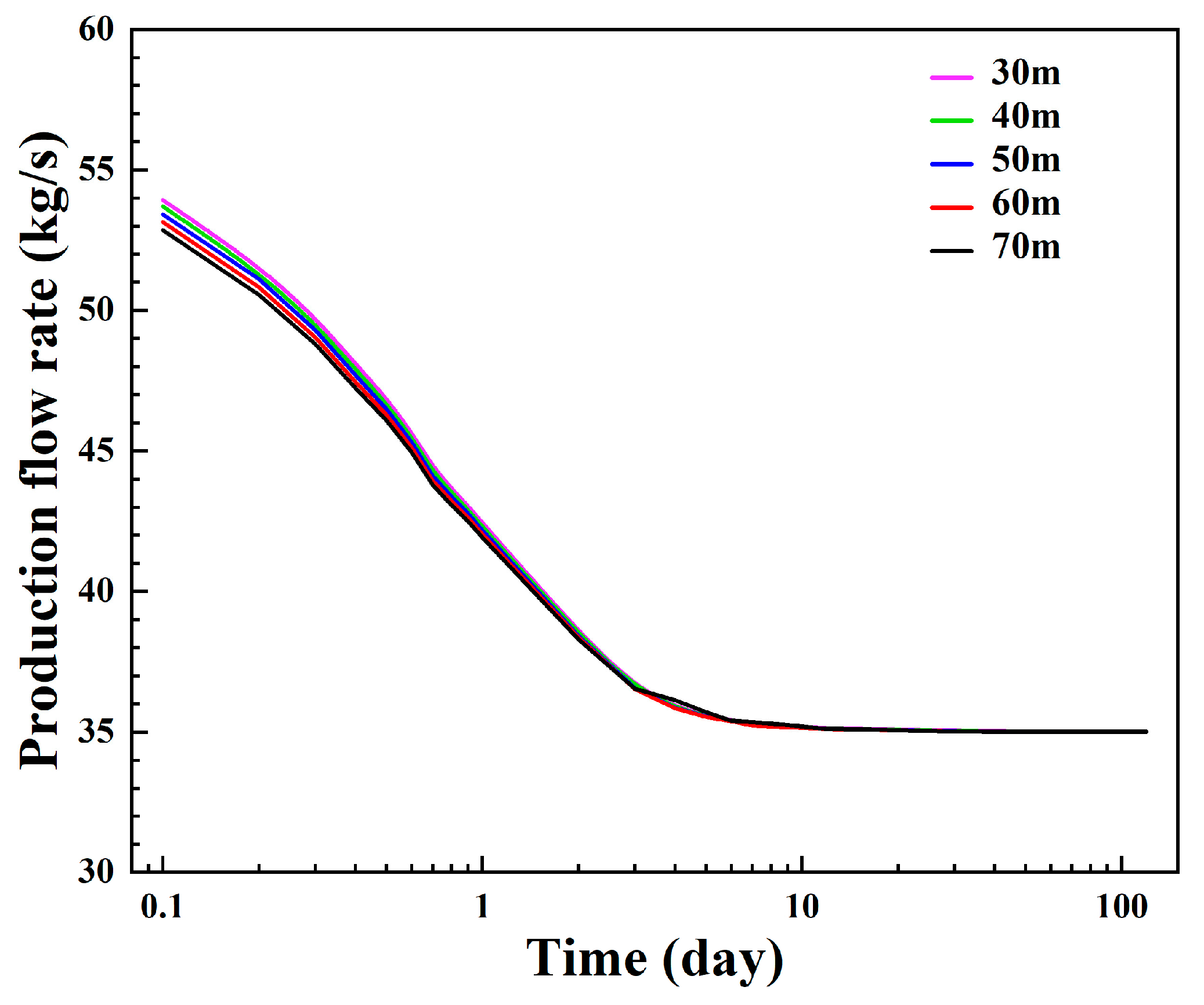
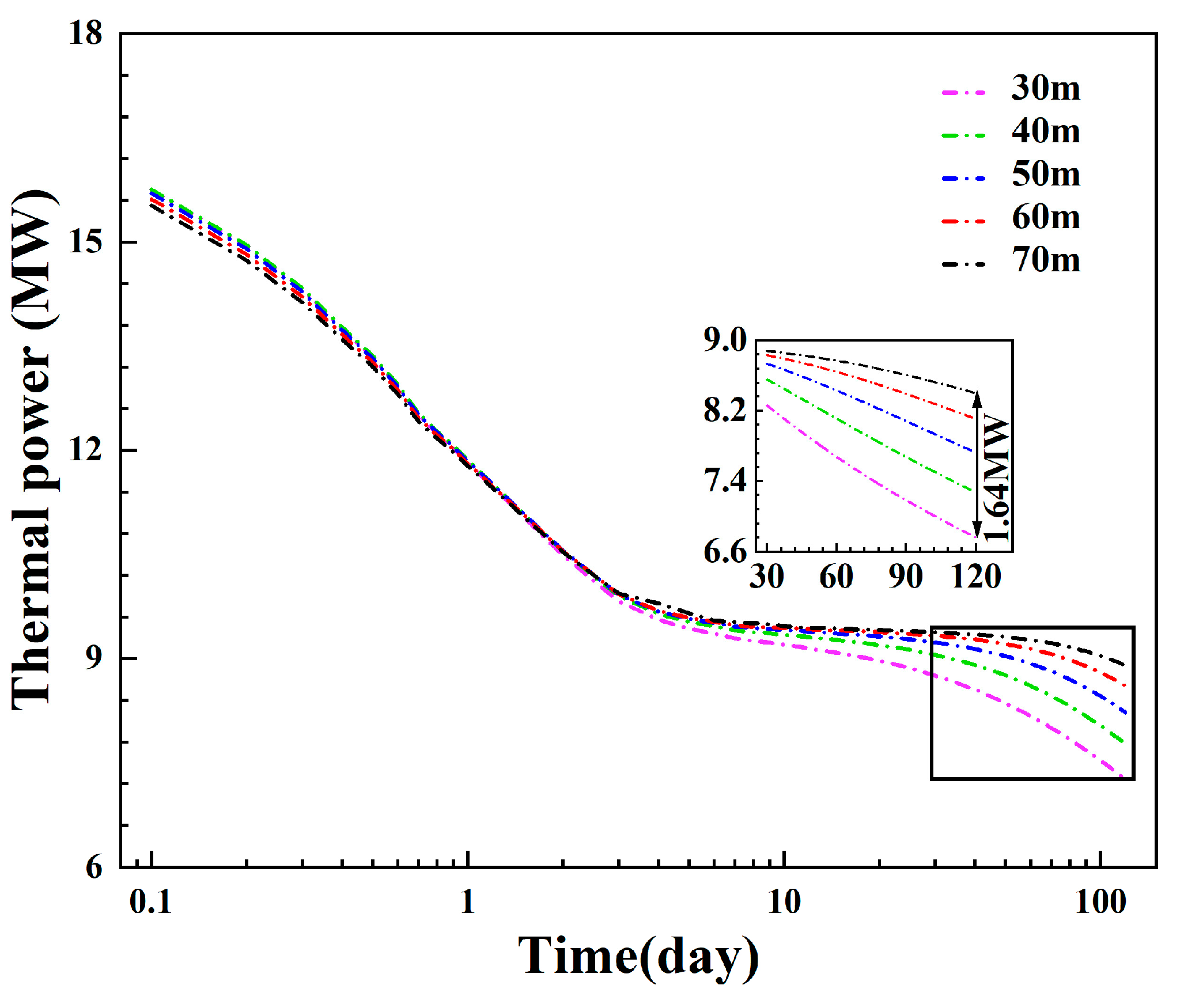
3.1.4. Influence of the Injection–Production Spacing
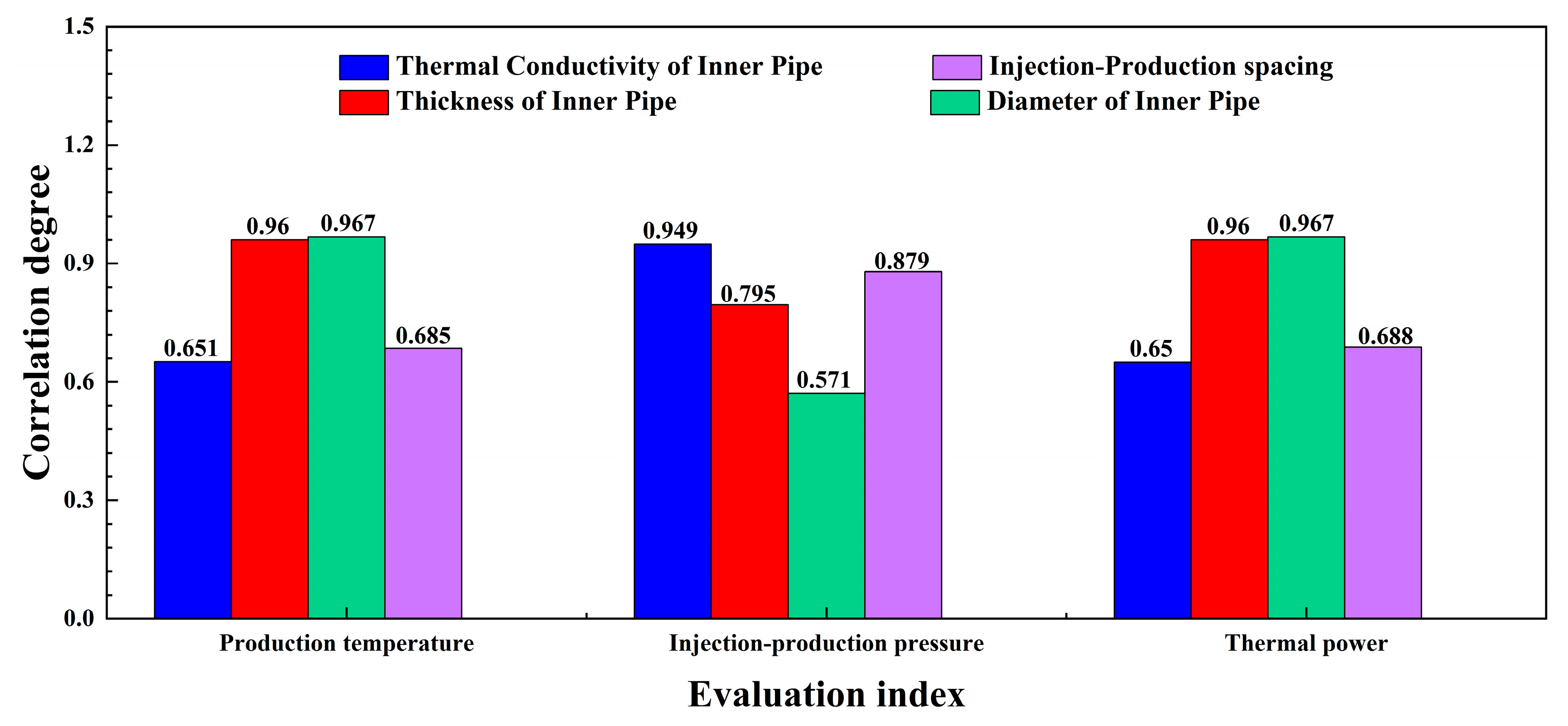
3.2. Sensitivity Analysis of Various Parameters
4. Conclusions
- (1)
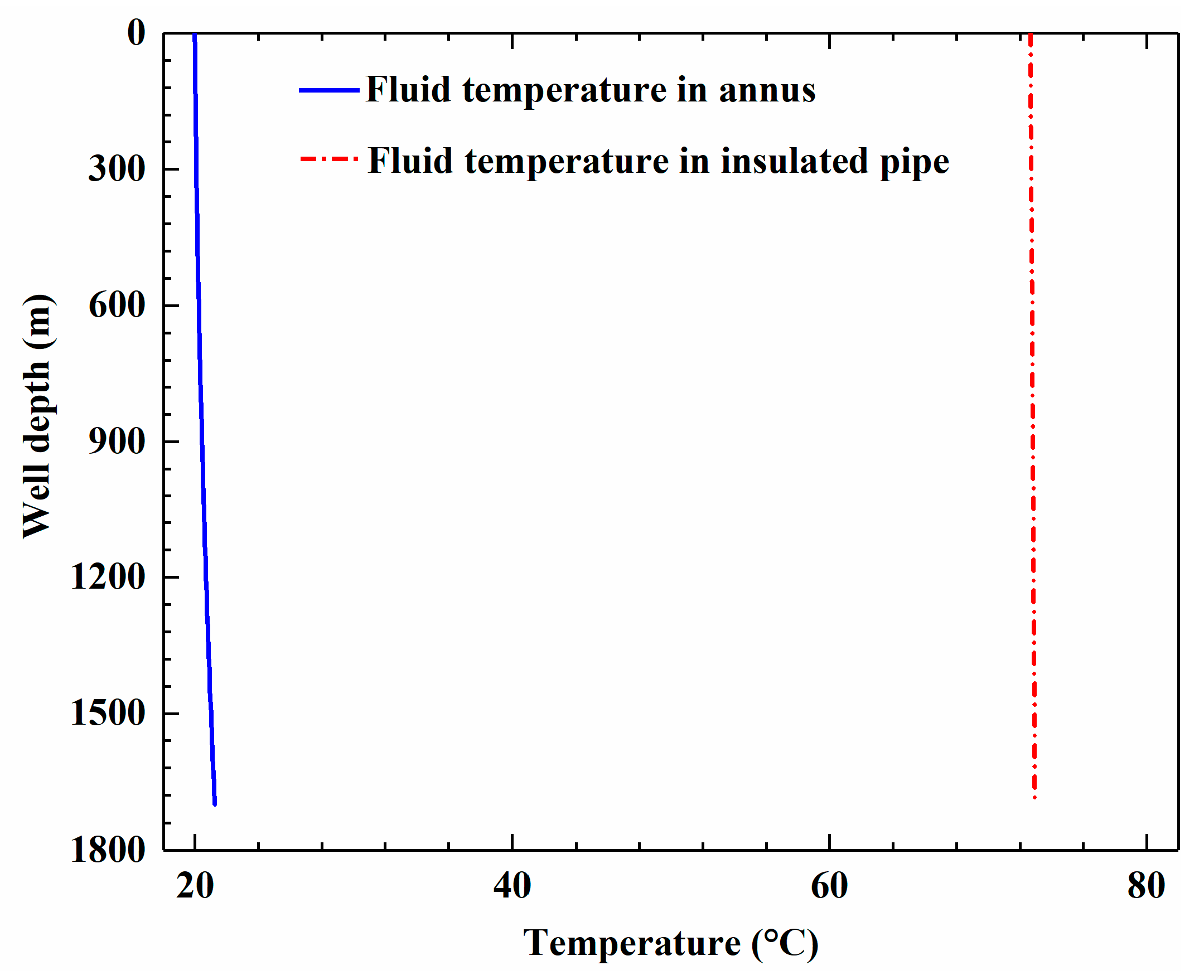
- The insulated pipe plays a key role in the heat loss of the production fluid, and the temperature decrease is only 0.29 °C after 120 days if the inner pipe has an excellent insulation performance. The fluid temperature increase in the annulus is only 1.24 °C after 120 days, while it exceeds 50 °C in the geothermal reservoir. Thus, the fractured reservoir dominates the heat extraction capacity of the injection fluid.
- (2)
- The inner pipe’s thermal conductivity can significantly impact the production temperature and thermal power. To ensure heat output, it is necessary to use an insulated inner pipe with a low thermal conductivity. The production temperature decrease is negligible when the inner pipe’s thermal conductivity is less than 0.023 W/(m·K). Appropriate reductions in the inner pipe’s thickness can help to reduce the injection–production pressure difference, and a thickness of 0.015 m is appropriate to decrease the heat loss and obtain a relatively low injection–production pressure difference.
- (3)
- The diameter of the inner pipe can affect the injection–production pressure difference by changing the flow spaces of the inner pipe and the annulus, and the injection–production pressure difference is the lowest when the inner pipe’s diameter is 0.12 m or 0.13 m. A longer injection section can effectively delay thermal breakthrough and reduce the injection–production pressure difference. The thermal breakthrough is limited if the injection–production spacing exceeds 70 m.
- (4)
- For the production temperature and thermal power, the sensitivity of the wellbore parameters is ranked as follows: thermal conductivity of insulated pipe > injection–production spacing. For the injection–production pressure difference, the sensitivity of the wellbore parameters is ranked as follows: diameter of the insulated pipe > thickness of the insulated pipe > injection–production spacing. Hence, sufficient attention should be paid to the diameter and thickness of the insulated pipe to ensure effective regulation of the injection–production pressure difference in the production of a geothermal system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Af | Transfer area of the fractures, m2 |
| Am | Transfer area of the matrix, m2 |
| Ac | Cross-section area of flow channel, m2 |
| C | Thermal capacity of the solid component, (J/(kg·K)) |
| cf, in | Thermal capacity of inlet fluid, J/(kg·K) |
| cf, out | Thermal capacity of outlet fluid, J/(kg·K) |
| cs | Thermal capacity of rock, J/(kg·K) |
| di | Inner pipe diameter, m |
| hin | Convective heat transfer coefficient between produced fluid and wellbore, W/(m2·K) |
| hm | Heat transfer coefficient between injected and produced fluid, W/(m2·K) |
| hlm | Heat transfer coefficient between fracture fluid and solid component, W/(m2·K) |
| Mmf | Mass exchange rate from matrix to fractures, kg/(m3·s) |
| e | Surface roughness of pipe, μm |
| fD | Darcy friction factor |
| kf | Fracture permeability, m2 |
| km | Matrix permeability, m |
| Nu | Nusselt number |
| P | Thermal power, MW |
| p | Pressure, Pa |
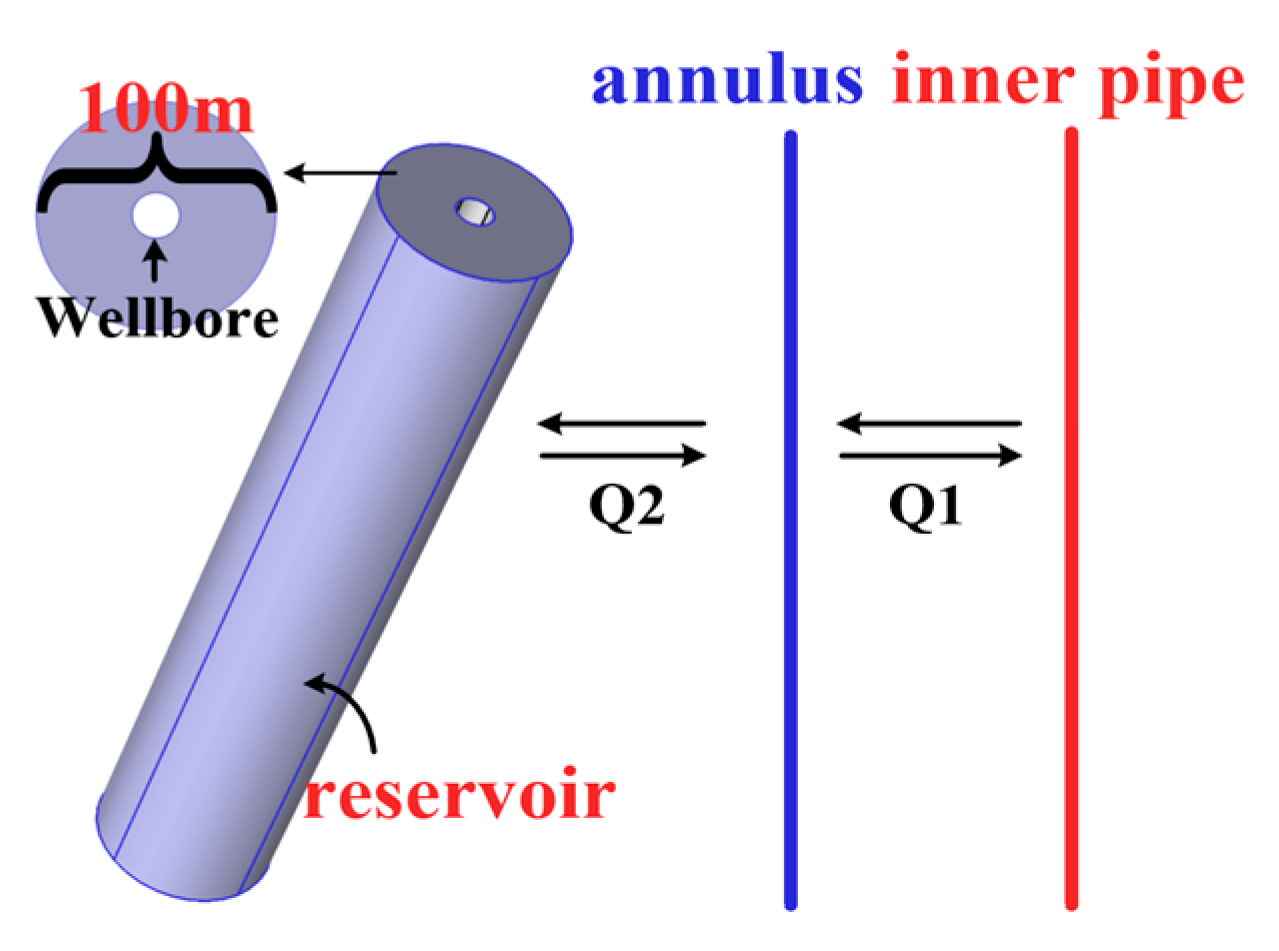
| Q1 | Heat transfer from the produced fluid to injected fluid, W |
| Q2 | Heat transfer from the surrounding formation to injected fluid, W |
| qin | Volumetric flow rate of injected fluid, m3/s |
| qout | Volumetric flow rate of produced fluid, m3/s |
| Re | Reynolds number |
| ri,ro | Inner and outer radius of the pipe, m |
| Tin | Temperature of inlet fluid, K |
| Tout | Temperature of outlet fluid, K |
| uf | Darcy velocity in the fractures, m/s |
| um | Darcy velocity in the matrix, m/s |
Greek Symbols
| α | Thermal diffusivity, m2/s |
| βs | Compressibility coefficient of the solid phase in the rock, Pa−1 |
| γ | Gravitational acceleration, m/s2 |
| λ | Thermal conductivity, W/(m·K) |
| λf | Thermal conductivity of fluid, W/(m·K) |
| λs | Thermal conductivity of rock, W/(m·K) |
| λeff | Effective thermal conductivity of the formation, W/(m·K) |
| ρf | Density of working fluid, kg/m3 |
| ρf, in | Density of inlet fluid, kg/m3 |
| ρf, out | Density of outlet fluid, kg/m3 |
| ρs | Density of rock, kg/m3 |
| ƞp | Pump efficiency |
| μf | Viscosity of working fluid, Pa·s |
| φm | Formation porosity |
| φf | Fracture porosity |
References
- Iacobuţă, G.I.; Brandi, C.; Dzebo, A.; Duron, S.D.E. Aligning climate and sustainable development finance through an SDG lens. The role of development assistance in implementing the Paris Agreement. Glob. Environ. Chang. 2022, 74, 102509. [Google Scholar] [CrossRef]
- Babaei, M.; Nick, H.M. Performance of low-enthalpy geothermal systems: Interplay of spatially correlated heterogeneity and well-doublet spacings. Appl. Energy 2019, 253, 113569. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, Y. Investigation on the effect of symmetrical multi-well layout on geothermal energy extraction from a fractured granitic reservoir: A case study in the Gonghe Basin, Northwestern China. Energy Rep. 2021, 7, 7741–7758. [Google Scholar] [CrossRef]
- Song, X.; Wang, G.; Shi, Y.; Li, R.; Xu, Z.; Zheng, R.; Wang, Y.; Li, J. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system. Energy 2018, 164, 1298–1310. [Google Scholar] [CrossRef]
- Ke, T.; Huang, S.; Xu, W.; Li, X. Study on heat extraction performance of multiple-doublet system in Hot Sedimentary Aquifers: Case study from the Xianyang geothermal field, Northwest China. Geothermics 2021, 94, 102131. [Google Scholar] [CrossRef]
- Sørensen, S.N.; Reffstrup, J. Prediction of Long-Term Operational Conditions for Single-Well Groundwater Heat Pump Plants. In Proceedings of the 27th Intersociety Energy Conversion Engineering Conference, San Diego, CA, USA, 3–7 August 1992. [Google Scholar]
- Capozza, A.; De Carli, M.; Zarrella, A. Investigations on the influence of aquifers on the ground temperature in ground-source heat pump operation. Appl. Energy 2013, 107, 350–363. [Google Scholar] [CrossRef]
- Wang, G.; Song, X.; Shi, Y.; Zheng, R.; Li, J.; Li, Z. Production performance of a novel open loop geothermal system in a horizontal well. Energy Convers. Manag. 2020, 206, 112478. [Google Scholar] [CrossRef]
- Horne, R. Design Considerations of a Down-Hole Coaxial Geothermal Heat Exchanger. Geothermal Resources Council Transactions. Available online: https://www.osti.gov/biblio/6166794 (accessed on 1 September 1980).
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Transient heat transfer in a coaxial borehole heat exchanger. Geothermics 2014, 51, 470–482. [Google Scholar] [CrossRef]
- Holmberg, H.; Acuña, J.; Næss, E.; Sønju, O.K. Thermal evaluation of coaxial deep borehole heat exchangers. Renew. Energy 2016, 97, 65–76. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Song, X.; Shi, Y.; Li, G.; Yang, R.; Wang, G.; Zheng, R.; Li, J.; Lyu, Z. Numerical simulation of heat extraction performance in enhanced geothermal system with mul-tilateral wells. Appl. Energy 2018, 218, 325–337. [Google Scholar] [CrossRef]
- Wang, G.; Ma, X.; Song, X.; Li, G. Production enhancement analysis of a supercritical CO2 multi-stage EGS with horizontal wells. Renew. Energy 2025, 256, 124111. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Xie, Y.; Zhang, Y.; Gao, X.; Ma, J. Long-term thermal performance analysis of deep coaxial borehole heat exchanger based on field test. J. Clean. Prod. 2021, 278, 123396. [Google Scholar] [CrossRef]
- Cai, X.; Liu, Z.; Xu, K.; Li, B.; Zhong, X.; Yang, M. Numerical simulation study of an Enhanced Geothermal System with a five-spot pattern horizontal well based on thermal-fluid-solid coupling. Appl. Therm. Eng. 2025, 258, 123396. [Google Scholar] [CrossRef]
- Shi, Y.; Song, X.; Wang, G.; McLennan, J.; Forbes, B.; Li, X.; Li, J. Study on wellbore fluid flow and heat transfer of a multilateral-well CO2 enhanced geothermal system. Appl. Energy 2019, 249, 14–27. [Google Scholar] [CrossRef]
- Benson, A.-L.; Clarkson, C.; Zeinabady, D. Analysis of enhanced geothermal system flowback and circulation test data for fracture and reservoir characterization. Geoenergy Sci. Eng. 2025, 245, 213532. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, X.; Wang, G.; Ma, F. Characteristics, Formation Periods, and Controlling Factors of Tectonic Fractures in Carbonate Geothermal Reservoirs: A Case Study of the Jixianian System in the Xiong’an New Area, China. Acta Geol. Sin.-Engl. Ed. 2023, 97, 1625–1639. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, G.; Zhang, C.; Hu, J.; Shi, Y.; Wang, Y.; Hu, S. Thermal regime of the lithosphere and geothermal potential in Xiong’an New Area. Energy Explor. Exploit. 2018, 37, 787–810. [Google Scholar] [CrossRef]
- Allahvirdizadeh, P. A review on geothermal wells: Well integrity issues. J. Clean. Prod. 2020, 275, 124009. [Google Scholar] [CrossRef]
- Wei, G.; Liu, Y.; Zhang, X.; Yu, F.; Du, X. Thermal conductivities study on silica aerogel and its composite insulation materials. Int. J. Heat Mass Transf. 2011, 54, 2355–2366. [Google Scholar] [CrossRef]
- Cheng, A.H.; Ghassemi, A.; Detournay, E. Integral equation solution of heat extraction from a fracture in hot dry rock. Int. J. Numer. Anal. Methods Géoméch. 2001, 25, 1327–1338. [Google Scholar] [CrossRef]
- Morita, K.; Bollmeier, W.; Mizogami, H. Experiment to Prove the Concept of the Downhole Coaxial Heat Exchanger (DCHE) in Hawaii. Geothermal Resources Council Transactions. 1992. Available online: https://scholarspace.manoa.hawaii.edu/items/29af4c5a-281a-4ab3-95c5-d719663234cd (accessed on 4 October 1992).
- Chakraborty, S.; Datta, H.N.; Chakraborty, S. Grey relational analysis-based optimization of machining processes: A compre-hensive review. Process Integr. Optim. Sustain. 2023, 7, 609–639. [Google Scholar] [CrossRef]

| Items | Value | Items | Value |
|---|---|---|---|
| Inner diameter of insulated pipe (m) | 0.13 | Outer diameter of cement (m) | 0.3111 |
| Outer diameter of insulated pipe (m) | 0.16 | Thermal conductivity of insulated pipe (W/(m·K)) | 0.023 |
| Inner diameter of annulus (m) | 0.2224 | Thermal conductivity of casing (W/(m·K)) | 43.75 |
| Outer diameter of casing (m) | 0.2445 | Thermal conductivity of cement (W/(m·K)) | 0.7 |
| Items | Cap Rock | Reservoir Matrix | Reservoir Fracture |
|---|---|---|---|
| Density(kg/m3) | 2600 | 2500 | Water |
| Thermal Conductivity (W/(m·K)) | 2.1 | 3.0 | Water |
| Heat Capacity (J/(kg·K)) | 850 | 870 | Water |
| Porosity (%) | 3 | 7 | 100 |
| Permeability (m2) | 10−18 | 10−15 | 10−12 |
| Items | Cap Rock |
|---|---|
| Density of Water ρf | 1000 kg/m3 |
| Thermal Capacity of Water cf | 4200 J/(kg·K) |
| Viscosity of Water μf | 0.001 Pa·s |
| Density of Matrix ρs | 2700 kg/m3 |
| Thermal Capacity of Matrix cs | 1000 J/(kg·K) |
| Thermal Conductivity of Matrix λs | 2.5 W/(m·K) |
| Flow Velocity uin | 0.01 m/s |
| Inlet Temperature Tin | 303.15 K |
| Initial Temperature of Matrix Ti | 353.15 K |
| Fracture Aperture d | 0.001 m |
| Items | Value | Items | Value |
|---|---|---|---|
| Thermal Conductivity of Formation (W/(m·K)) | 1.6 | Inner Radius of Inner Pipe (m) | 0.0506 |
| Thermal Conductivity of Cement (W/(m·K)) | 0.99 | Outer Radius of Inner Pipe (m) | 0.0890 |
| Thermal Conductivity of Casing (W/(m·K)) | 46.1 | Inner Radius of Casing (m) | 0.1617 |
| Thermal Conductivity of Inner Pipe (W/(m·K)) | 0.06 | Inner Radius of Cement (m) | 0.1778 |
| Thermal Capacity of Formation (J/(kg·K)) | 870 | Inner Radius of Wellbore (m) | 0.2159 |
| Density of Formation (kg/m3) | 3050 | Well Depth (m) | 876.5 |
| Wellbore Parameters | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| Production Temperature (°C) | 72.882 °C | 71.905 °C | 73.080 °C | 66.157 °C |
| 72.675 °C | 72.467 °C | 72.878 °C | 69.619 °C | |
| 66.146 °C | 72.675 °C | 72.754 °C | 72.675 °C | |
| 60.934 °C | 72.801 °C | 72.675 °C | 75.240 °C | |
| 56.838 °C | 72.899 °C | 72.625 °C | 77.215 °C |
| Wellbore Parameters | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| Injection–Production Pressure (MPa) | 3.954 MPa | 3.512 MPa | 4.833 MPa | 3.871 MPa |
| 3.953 MPa | 3.705 MPa | 4.209 MPa | 3.913 MPa | |
| 3.940 MPa | 3.953 MPa | 3.943 MPa | 3.953 MPa | |
| 3.957 MPa | 4.280 MPa | 3.953 MPa | 3.991 MPa | |
| 3.986 MPa | 4.721 MPa | 4.292 MPa | 4.027 MPa |
| Wellbore Parameters | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| Thermal Power (MW) | 7.757 MW | 7.612 MW | 7.786 MW | 6.759 MW |
| 7.726 MW | 7.695 MW | 7.756 MW | 7.272 MW | |
| 6.758 MW | 7.726 MW | 7.738 MW | 7.726 MW | |
| 5.988 MW | 7.745 MW | 7.726 MW | 8.107 MW | |
| 5.385 MW | 7.759 MW | 7.719 MW | 8.401 MW |
| Reference Sequence | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| 1.000 | 1.000 | 0.986 | 1.000 | 0.857 |
| 1.000 | 0.997 | 0.994 | 0.997 | 0.902 |
| 1.000 | 0.908 | 0.997 | 0.996 | 0.941 |
| 1.000 | 0.836 | 0.999 | 0.994 | 0.974 |
| 1.000 | 0.780 | 1.000 | 0.993 | 1.000 |
| Reference Sequence | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| 1.000 | 0.992 | 0.744 | 1.000 | 0.961 |
| 1.000 | 0.992 | 0.785 | 0.871 | 0.972 |
| 1.000 | 0.988 | 0.837 | 0.816 | 0.982 |
| 1.000 | 0.993 | 0.907 | 0.818 | 0.991 |
| 1.000 | 1.000 | 1.000 | 0.888 | 1.000 |
| Reference Sequence | Inner Pipe Thermal Conductivity | Inner Pipe Thickness | Inner Pipe Diameter | Injection–Production Spacing |
|---|---|---|---|---|
| 1.000 | 1.000 | 0.981 | 1.000 | 0.805 |
| 1.000 | 0.996 | 0.992 | 0.996 | 0.866 |
| 1.000 | 0.871 | 0.996 | 0.994 | 0.920 |
| 1.000 | 0.772 | 0.998 | 0.992 | 0.965 |
| 1.000 | 0.694 | 1.000 | 0.991 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Li, Y.; Wang, G.; Xia, H.; Gu, F.; Zhang, Y.; Gao, Y.; Sun, J. Effects of Wellbore Parameters on the Performance of an Open-Loop Geothermal System with Horizontal Well. Energies 2025, 18, 6090. https://doi.org/10.3390/en18236090
Xiao L, Li Y, Wang G, Xia H, Gu F, Zhang Y, Gao Y, Sun J. Effects of Wellbore Parameters on the Performance of an Open-Loop Geothermal System with Horizontal Well. Energies. 2025; 18(23):6090. https://doi.org/10.3390/en18236090
Chicago/Turabian StyleXiao, Li, Youwu Li, Gaosheng Wang, Haobin Xia, Feng Gu, Yue Zhang, Ying Gao, and Jingyao Sun. 2025. "Effects of Wellbore Parameters on the Performance of an Open-Loop Geothermal System with Horizontal Well" Energies 18, no. 23: 6090. https://doi.org/10.3390/en18236090
APA StyleXiao, L., Li, Y., Wang, G., Xia, H., Gu, F., Zhang, Y., Gao, Y., & Sun, J. (2025). Effects of Wellbore Parameters on the Performance of an Open-Loop Geothermal System with Horizontal Well. Energies, 18(23), 6090. https://doi.org/10.3390/en18236090






