Optimal Power Purchase Model and Pricing Mechanism of Green Power Parks Considering Power Quality Responsibility Sharing

Abstract

With the increasing share of renewable energy, green power parks face challenges such as high electricity purchasing costs and fluctuations in power quality. To address these issues, this paper proposes an integrated optimization method based on power quality responsibility modeling and a differentiated reward–penalty pricing mechanism (DRPPM). First, an integrated operation model of “source–grid–load–storage” is established. Within the pressure–state–response (PSR) framework, power quality deviations are quantified and mapped into economic costs. Then, a differentiated reward–penalty pricing mechanism is designed to dynamically adjust power quality deviations through a continuous function, guiding users toward adaptive energy consumption behavior. Finally, a green power park in Gansu Province dominated by wind and photovoltaic generation is used as a case study with four typical simulation scenarios. The results show that the proposed mechanism reduces the park’s electricity purchasing cost and increases the green power consumption ratio by up to 74.9%. Meanwhile, it effectively improves power quality indicators such as frequency, voltage, and harmonics. The study verifies the comprehensive advantages of the proposed framework in terms of economy, energy efficiency, and stability, providing a reference for low-carbon and efficient operation of high-energy-consumption green power parks.

1. Introduction

Under the “dual-carbon” strategy and the large-scale construction of renewable energy bases, green power parks (GPPs) have gradually become key carriers for the local consumption of renewable energy and the coordinated development of high-energy-consumption industries [1]. In renewable-rich regions such as Gansu Province, the coupling of wind-solar resources with energy-intensive industries such as electrolytic aluminum and data centers is driving the exploration of diversified electricity purchasing and consumption models [2]. Meanwhile, wind power technology itself is continuously innovating, including the exploration of novel designs such as the inflatable Savonius turbine aimed at enhancing deployment flexibility and portability. This development not only enhances the utilization level of renewable energy but also provides new pathways for low-carbon transformation and power system reform [3].

However, the existing electricity purchasing modes in GPPs still face notable limitations. Under the traditional grid-agent purchasing mode, parks adopt uniform electricity and transmission pricing policies, which ensure supply stability but limit market flexibility and fail to significantly promote green power consumption [4]. The direct-supply mode reduces part of the purchasing cost and improves local utilization of renewable energy, yet power quality (PQ) issues such as frequency, voltage, and harmonic disturbances remain the responsibility of the grid company, leading to unclear accountability [5]. Moreover, the market-based trading mode can optimize power purchasing through contractual and spot mechanisms, but it suffers from high price volatility and ambiguous PQ responsibility, resulting in uneven allocation of ancillary service costs [6].

To address these challenges, many studies have carried out valuable explorations. Some have focused on the design of peer-to-peer (P2P) and community-based market mechanisms to improve local green power consumption and trading flexibility. For instance, ref. [7] presents a systematic classification of P2P market structures and challenges, while [8] reviews P2P energy trading mechanisms and energy management approaches—including game theory, mathematical optimization, and machine learning—and highlights the major limitations in this field. Study [9] proposes a coupling mechanism between shared energy storage and internal transactions, establishing a user-side energy-matching platform to balance surplus and shortage through storage participation.

Other scholars have begun to explore economic mechanisms for PQ responsibility sharing. For example, ref. [10] introduces a PQ-improvement strategy that integrates real-time pricing within an intelligent metering system, achieving a dynamic coupling between price correction and PQ assurance. Study [11] develops a correlation-based method to assign users’ harmonic responsibilities using monitoring data, overcoming the limitations of traditional harmonic attribution methods that require dedicated measurement and cannot operate across feeders. Reference [12] provides a critical review of techniques for detecting and classifying PQ disturbances in renewable-penetrated grids, discussing the role of indicators and event metering in supporting responsibility identification and economic settlement. Furthermore, Concurrently, in the domain of optimization algorithms and intelligent Energy Management Systems (EMS), recent studies, such as those employing the Binary Sparrow Search Algorithm for EMS, have demonstrated superior performance in microgrid economic dispatch, cost reduction, and enhancing system resilience [13]. Despite significant progress in the respective fields, a critical research gap remains: most existing works concentrate on a single dimension. For instance, while advanced intelligent EMS studies [13] can efficiently optimize the energy supply-demand balance and economic performance of microgrids, they typically do not incorporate the quantification, allocation, and incentive mechanisms of power quality responsibility as core optimization objectives. Concurrently, traditional PQ reward-penalty models suffer from issues like discontinuity. Consequently, there is a lack of an integrated framework capable of the unified quantification and synergistic optimization of economic performance, renewable energy consumption, and multi-entity power quality responsibility at the park level. This gap makes it challenging for parks to achieve optimal economy and maximum green power utilization while simultaneously ensuring power quality.

In summary, this paper develops an electricity purchasing model for GPPs that simultaneously considers economic efficiency and PQ responsibility allocation has become an urgent issue. To this end, this paper introduces PQ responsibility modeling and a differentiated reward–penalty pricing mechanism (DRPPM) into the electricity purchasing framework. A multi-objective optimization model is established to achieve the unified goals of economic efficiency, fairness, and grid stability for green power park operations. The main novelty and contribution of this paper are as follows:

(1) ΔQ-based parameterization from PQ to optimization. Using a PSR-based normalization and a deviation–cost mapping, PQ enters the objective, hard constraints, and price correction within a single executable interface.

(2) DRPPM design. We propose a continuous, monotone, and bounded correction function of ΔQ, avoiding tiered-tariff discontinuities/non-differentiability and enabling joint and rolling optimization with storage and flexible loads.

(3) End-to-end coupling and portability. The unified source–grid–load–storage model closes the loop of price–PQ–dispatch, treating ΔQ as the state for price correction; site transfer is facilitated via the symbols/limits

Table 1. Definition of Key Parameters and System Constraints for DRPPM Model.

Indicator	Symbol	Nominal/Limit (Used in Our Case)	Measurement Window
System frequency	f, fnom	fnom; acceptable range [49.8, 50.2] Hz	Aligned with data resolution
Bus voltage	U, Unom	Acceptable $[0.93, 1.07]\hspace{0.17em}\mathrm{p}.\mathrm{u}.$ (per level via nominal)	Same as dispatch step
Voltage THD	THDv	THDv, lim = 5%	As per standard
Power factor	cosφ	Lower bound $\mathrm{c}\mathrm{o}\mathrm{s} {\phi }_{\mathrm{l}\mathrm{i}\mathrm{m}}=0.90$ (lagging side)	Settlement window

. With intra-day rolling forecasts, sensitivity checks indicate directional robustness over reasonable parameter ranges.

2. Power Quality Responsibility Modeling

In green power parks (GPPs), the increasing volatility and uncertainty of renewable energy output have made power quality (PQ) a critical factor affecting the safe and stable operation of the park. Under the traditional grid-dominated mode, PQ responsibility is mainly borne by the grid enterprise, and there is no clear responsibility allocation among multiple internal entities. This situation leads to an uneven distribution of ancillary service costs and weakens the incentive effect of market mechanisms on PQ management. Therefore, it is necessary to construct a modeling framework that incorporates PQ responsibility, mapping technical deviations to corresponding economic costs. Such a framework supports the subsequent design of the reward–penalty pricing mechanism (DRPPM) and the development of the optimal electricity purchasing model.

Considering the characteristics of high-energy-consuming industrial parks, this paper adopts the pressure–state–response (PSR) model [14] to select PQ evaluation indicators from the dimensions of pressure, state, and response, as shown in Figure 1. Similarly to comprehensive energy efficiency evaluations, PQ responsibility modeling should adhere to the principles of comprehensiveness, scientific validity, weighting rationality, and result orientation.

On one hand, the selected indicators should cover the main PQ dimensions and reflect users’ energy consumption conditions under different operating scenarios. On the other hand, since the significance of each indicator varies, appropriate weighting is required to reflect its influence on system operation and to avoid biases caused by single-dimensional evaluation.

2.1. Grid Parameters and Thresholds

The fundamental constraints of PQ are represented by key parameters such as frequency, voltage, harmonics, and power factor. These parameters not only define the basic operational constraints of the park but also serve as the benchmarks for subsequent deviation quantification and responsibility attribution. Common PQ indicators—frequency, voltage, total harmonic distortion (THD), and power factor—jointly determine the stability and energy efficiency of the system [15]. This section fixes symbols and threshold conventions (frequency, bus voltage, THD, power factor) as the scales for normalization in Section 2.2. These definitions produce ΔQ, which then enters the cost function and constraints and serves as the state input of DRPPM (see Equations (5)–(15), (23)–(27) and (36)).

Overall, these parameters collectively form the benchmark for PQ constraint assessment and provide a unified physical basis for subsequent responsibility sharing and reward–penalty mechanisms. Accordingly, frequency deviation, voltage deviation, THD, and power factor can be uniformly expressed as follows:

$$\mathsf{\Delta }f=f-f_0$$

(1)

$$\mathsf{\Delta }U={\displaystyle \frac{U-U_{\mathrm{rated}}}{U_{\mathrm{rated}}}}\times 100\%$$

(2)

$$THD={\displaystyle \frac{\sqrt{{\displaystyle \sum _{h=2}^{\infty }}{u}_h^2}}{U_1}}\times 100\%$$

(3)

$$\cos \phi ={\displaystyle \frac{P}{S}}$$

(4)

To keep a consistent pipeline “definitions → normalization → ΔQ → cost/constraints → DRPPM”, we summarize the model-used symbols and limits in Table 1.

2.2. Quantification of Power Quality Deviation

To achieve a refined allocation of PQ responsibility, each parameter deviation must be converted into a quantifiable indicator so that responsibility sharing and economic mapping can be realized in the subsequent model. Because different PQ indicators have inconsistent dimensions, direct comparison may cause distortion in deviation assessment. Therefore, this paper introduces a normalization method to unify different indicators within a comparable interval [16].

Let the actual system operating parameters for frequency, voltage, and total harmonic distortion be denoted as f, U, and THD₀, respectively. Their corresponding nominal values are Δfₘₐₓ, ΔUₘₐₓ, ΔTHDₘₐₓ. he deviations of each parameter can thus be expressed as follows:

$${\delta }_f={\displaystyle \frac{|f-f_0|}{\mathsf{\Delta }{f}_{\max }}}$$

(5)

$${\delta }_U={\displaystyle \frac{|U-U_0|}{\mathsf{\Delta }{U}_{\max }}}$$

(6)

$${\delta }_{THD}={\displaystyle \frac{|THD-TH{D}_0|}{\mathsf{\Delta }TH{D}_{\lim }}}$$

(7)

If δ_f > 1, it indicates that the system has exceeded its allowable operational limit, and corresponding responsibility constraints should be triggered. Here, THD_lim represents the maximum permissible level of total harmonic distortion, typically set at 5%. In the evaluation of power factor (PF), a low PF condition increases the proportion of reactive power, which can aggravate grid stress and reduce energy efficiency. Therefore, the following deviation quantification index is introduced:

$${\delta }_{PF}=\max \left(0,{\displaystyle \frac{\cos {\phi }_{\lim }-\cos \phi }{1-\cos {\phi }_{\lim }}}\right)$$

(8)

where cosφ_lim represents the specified minimum power factor (e.g., 0.9). If cosφ ≤ cosφ_lim, the indicator equals zero, indicating that no limit violation occurs.

The comprehensive deviation vector of the park’s power quality can then be expressed as:

$$\delta =\{{\delta }_f,{\delta }_U,{\delta }_{THD},{\delta }_{PF}\}$$

(9)

$$\mathsf{\Delta }Q=\sum _{i=1}^n{w}_i\cdot {\delta }_i$$

(10)

where ΔQ represents the comprehensive deviation degree of power quality.

This normalized deviation system not only resolves the issue of inconsistent indicator dimensions but also provides a practical quantitative basis for measuring deviations and ensuring fair responsibility allocation among different entities. Normalization unifies deviation indicators of different dimensions within the [0, 1] interval, facilitating comparison and weighted calculation. When Δx > 1, it indicates a severe power quality violation that requires immediate corrective action. By decomposing deviations caused by different entities, the allocation and tracing of power quality responsibility can be effectively achieved.

2.3. Cost Mapping Model

Based on the quantified power quality (PQ) deviations, it is further necessary to establish a mapping relationship between deviations and economic costs, so as to achieve the transformation from physical deviations to economic responsibilities [17]. Essentially, this process converts the technical requirements of system ancillary services into economic signals, guiding each responsible entity to adopt optimized operational behavior.

First, for the frequency deviation δ_f, the corresponding economic cost is mainly reflected in frequency regulation and reserve expenses. Let C_f denote the unit cost of frequency regulation; then, the economic cost associated with the frequency deviation can be expressed as:

$$C_{\mathrm{freq}}=C_f\cdot {\delta }_f\cdot P_{\mathrm{base}}$$

(11)

where P_base represents the baseline load level of the park. Second, the voltage deviation δ_U needs to be corrected through reactive power compensation or voltage regulation devices. If the cost coefficient of reactive power compensation is denoted as C_U, the economic cost corresponding to the voltage deviation can be expressed as:

$$C_{\mathrm{volt}}=C_U\cdot {\delta }_U\cdot Q_{\mathrm{base}}$$

(12)

where Q_base denotes the baseline reactive power demand. For the harmonic deviation δ_THD, the economic cost mainly arises from the configuration of filtering equipment and the compensation for additional power losses. The corresponding mapping model can be expressed as:

$$C_{\mathrm{harm}}=C_H\cdot {\delta }_{THD}\cdot P_{\mathrm{base}}$$

(13)

where C_H represents the unit cost coefficient for harmonic mitigation. The deviation in power factor corresponds to reactive power charges or penalty mechanisms, and its mapping relationship can be expressed as:

$$C_{\mathrm{PF}}=C_{\mathrm{PF}}\cdot {\delta }_{\mathrm{PF}}\cdot P_{\mathrm{base}}$$

(14)

where C_PF denotes the penalty coefficient associated with power factor deviation. Finally, the economic expression of power quality responsibility can be summarized as:

$$C_{\mathrm{total}}=C_{\mathrm{freq}}+C_{\mathrm{volt}}+C_{\mathrm{harm}}+C_{\mathrm{PF}}=\sum _{i=1}^n{C}_i\cdot {\delta }_i\cdot S_i$$

(15)

where C_i denotes the unit cost corresponding to each power quality indicator, δ_i represents the deviation measure, and S_i is the baseline power or capacity parameter.

This model establishes a systematic mapping from physical deviations in power quality to “economic responsibility”. It can serve not only as the basis for the reward–penalty pricing mechanism in electricity purchasing but also as a theoretical foundation for responsibility allocation and optimized operation among multiple entities within the park.

2.4. Internal Energy Trading Structure and Mechanism

To enhance the local consumption and economic efficiency of the “green power + energy-intensive industry” model, this paper introduces an internal trading mechanism at the park level that integrates multiple prosumers, shared energy storage, and an operator. Within the park, several renewable energy prosumers—such as wind power, photovoltaic generation, electrolytic aluminum loads, and data centers—together with the operator form a small-scale market-oriented trading unit. Each prosumer submits its buying or selling demand to the operator according to its time-varying power surplus or deficit. The operator then matches internal transactions based on an internal electricity price and coordinates shared energy storage to complete energy circulation through two pathways [18]:

(1) Direct trading (Direct): surplus-side electricity is delivered to the deficit side through the DC bus of shared energy storage and a bidirectional controllable power-flow inverter. This path does not involve charging or discharging of storage and mainly functions as a “coupling channel”. The throughput is constrained by converter and bus capacities.

(2) Buffer trading (Buffer): when a surplus or deficit remains after direct matching, shared energy storage performs charge/discharge operations to shift energy across time and, when necessary, exchanges the residual difference with the external grid.

Unlike the “virtual power plant” concept, which focuses on large-scale centralized dispatching, the park-level mechanism emphasizes “market-based autonomy” within a community-type microgrid [19]. Internal price signals drive self-interested decision-making and competitive clearing among distributed entities. Shared energy storage gains *channel revenue* through direct matching [20] and “arbitrage revenue” through price-differential charging and discharging. Under power-quality constraints (including voltage deviation, harmonics, and frequency support), the reward–penalty pricing mechanism internalizes state–response externalities into economic costs, thereby forming a closed loop between “economic efficiency” and “operational security”.

Variables and Constraints

Direct matching and capacity constraints:

$$\sum _j{X}_{i\to j,t}^{\mathrm{dir}}\le S_{i,t}^{+},\hspace{1em}\sum _i{X}_{i\to j,t}^{\mathrm{dir}}\le D_{j,t}^{+}.$$

(16)

$$\sum _i{X}_{i\to •,t}^{\mathrm{dir}}\le \sum _{b\in \mathcal{B}}{\overline{P}}_b^{\mathrm{sw}},\hspace{1em}\sum _j{X}_{•\to j,t}^{\mathrm{dir}}\le \sum _{b\in \mathcal{B}}{\overline{P}}_b^{\mathrm{sw}}.$$

(17)

Buffer trading and state-of-charge (SOC) constraints:

$${\mathrm{SOC}}_{b,t+1}={\mathrm{SOC}}_{b,t}+{\eta }_b^{\mathrm{ch}}{P}_{b,t}^{\mathrm{ch}}\mathsf{\Delta }t-{\displaystyle \frac{1}{{\eta }_b^{\mathrm{dis}}}}{P}_{b,t}^{\mathrm{dis}}\mathsf{\Delta }t$$

(18)

$${\underset{¯}{\mathrm{SOC}}}_b\le {\mathrm{SOC}}_{b,t}\le {\overline{\mathrm{SOC}}}_b,\hspace{1em}0\le P_{b,t}^{\mathrm{ch}}\le {\overline{P}}_b^{\mathrm{ch}},\hspace{1em}0\le P_{b,t}^{\mathrm{dis}}\le {\overline{P}}_b^{\mathrm{dis}}$$

(19)

Park-level power balance (including direct and buffer transactions):

$$\sum _i{X}_{i\to •,t}^{\mathrm{dir}}+\sum _b{P}_{b,t}^{\mathrm{ch}}+G_t^{\mathrm{grid}}\to \mathrm{in}=\sum _j{X}_{•\to j,t}^{\mathrm{dir}}+\sum _b{P}_{b,t}^{\mathrm{dis}}+E_t^{\mathrm{in}\to \mathrm{grid}}$$

(20)

Internal price interval (ensuring internal trading priority):

Let the internal buying and selling prices be denoted as $p_t^{\mathrm{in},\mathrm{buy}}$, $p_t^{\mathrm{in},\mathrm{sell}}$, and the external grid’s buying and selling prices as $p_t^{\mathrm{grid},\mathrm{buy}}$, $p_t^{\mathrm{grid},\mathrm{sell}}$, respectively. Then:

$$p_t^{\mathrm{grid},\mathrm{sell}}\le p_t^{\mathrm{in},\mathrm{sell}}\le p_t^{\mathrm{in},\mathrm{buy}}\le p_t^{\mathrm{grid},\mathrm{buy}}$$

(21)

In the equations, $X_{i\to j,t}^{\mathrm{dir}}$ (kW), $S_{i,t}^{+}$, $D_{j,t}^{+}$ represent, respectively, the direct-trading power from prosumer $i$ to prosumer $j$ at time $t$ (without involving energy storage charging or discharging), the upper limit of sellable surplus for prosumer $i$ at time $t$, and the upper limit of demand deficit for prosumer $j$ at time $t$. $P_{b,t}^{\mathrm{ch}}$, $P_{b,t}^{\mathrm{dis}}$ (kW) denote the charging and discharging power of storage unit $b$ at time $t$; SOC_b,t (p.u. or kWh) is the state of charge of storage unit $b$ at time $t$; Δt (h) is the duration of the scheduling interval. $G_{\mathrm{t}}^{\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{d}\to \mathrm{i}\mathrm{n}}$, $E_t^{\mathrm{in}\to \mathrm{grid}}$ (kW) represent the power purchased from and sold to the external grid by the park during period $t$, respectively.

3. Design of the Reward–Penalty Pricing Mechanism

With the establishment of the PQ responsibility model, a key issue lies in how to translate responsibility outcomes into economic incentives. Traditional electricity pricing mechanisms are mainly based on energy and capacity charges, yet they lack direct constraints on PQ deviations such as frequency, voltage, harmonics, and power factor. This often results in “free-rider” behavior among certain entities. In the operation of GPPs, PQ issues are characterized by multi-dimensional and multi-entity interactions. If a conventional stepwise reward–penalty pricing model is applied, it tends to cause boundary effects—that is, when deviations are near threshold values, the price changes become discontinuous, potentially inducing strategic behavior among users [21].

To overcome this limitation, the reward–penalty pricing mechanism in this paper is designed within the PSR framework introduced in Section 1. The design aims to reflect pressure propagation, state sensitivity, and response orientation. Unlike traditional schemes that impose static penalties solely on PQ deviations, the proposed differentiated reward–penalty pricing model emphasizes a comprehensive assessment of multi-dimensional indicators. Through the dynamic reward and penalty pricing mechanism (DRPPM), continuous regulation of electricity prices is achieved, ensuring both fairness and economic efficiency. By adopting a continuous functional form for price correction, the mechanism more accurately captures the coupling relationship between PQ deviations and economic costs. This approach provides an economic means to constrain and guide the operational behavior of all participating entities within the park, thereby achieving coordinated assurance of PQ.

First, let the PSR deviation vector of entity i in the park be defined as:

$$\mathsf{\Delta }{x}_i=\{\mathsf{\Delta }{P}_i^{pressure},\mathsf{\Delta }{P}_i^{state},\mathsf{\Delta }{P}_i^{response}\}$$

(22)

where $\mathsf{\Delta }{P}_i^{pressure}$ represents the external pressure deviation, referring to operational fluctuations caused by factors such as wind–solar output variability and park load variation rate; $\mathsf{\Delta }{P}_i^{state}$ denotes the system state deviation, including PQ indicators such as voltage deviation, frequency fluctuation, and harmonic distortion; and $\mathsf{\Delta }{P}_i^{response}$ represents the user-side response deviation, which quantifies proactive behaviors such as fault repair timeliness and coordination in power maintenance [22,23].

Under the DRPPM framework, the reward–penalty price correction function for entity i can be uniformly modeled as:

$${\rho }_i(\mathsf{\Delta }{x}_i)=\sum _{d\in \{pressure,state,response\}}\left[a_d\cdot {(\mathsf{\Delta }{P}_i^d)}^2+b_d\cdot \mathsf{\Delta }{P}_i^d+c_d\right]$$

(23)

where ρ_i(Δx_i) denotes the reward–penalty price correction value for entity d ∈ {pressure, state, response} represents the deviation dimension, including pressure, state, and response; and $\mathsf{\Delta }{P}_i^d$ is the deviation of entity i in dimension d. Parameters a_d, b_d, c_d constitute the parameter set of the reward–penalty function, corresponding to the weights of the quadratic, linear, and constant terms, respectively.

In Equation (23), the PSR correction assigns coefficients {a_d, b_d, c_d} to the pressure/state/response dimensions. Indicators are first normalized per Section 2.1 and Section 2.2 and Table 1 to obtain deviations, and the coefficients are then calibrated by a three-anchor fit: (i) the compliance point (ΔP^d = 0, ρ^d = 0); (ii) a typical deviation point ${(\mathsf{\Delta }}_{\mathrm{ref}}^d,{\rho }_{\mathrm{ref}}^d)$ (from the 85th percentile of historical data or on-site alert threshold); and (iii) an upper point ${(\mathsf{\Delta }}_{\max }^d,{\rho }_{\max }^d)$ constrained by the price bounds [ρ_min, ρ_max] This ensures the correction is continuous, monotone, and bounded in ΔQ, without any ad hoc scaling.

This functional form reflects a nonlinear reward–penalty effect, in which mild deviations are moderately constrained, while severe deviations are rapidly amplified.

The quadratic term $a_d\cdot {(\mathsf{\Delta }{P}_i^d)}^2$ significantly strengthens the penalty for large deviations, the linear term $b_d\cdot \mathsf{\Delta }{P}_i^d$ provides proportional adjustment, and the constant term $c_d$ defines the baseline level of price correction.

The reward–penalty mechanism for the pressure dimension can be expressed as:

$${\rho }_i^{pressure}=a_p\cdot {(\mathsf{\Delta }{P}_i^{pressure})}^2+b_p\cdot \mathsf{\Delta }{P}_i^{pressure}+c_p$$

(24)

where $\mathsf{\Delta }{P}_i^{pressure}$ mainly considers the system pressure caused by renewable output fluctuations and load imbalance. As this deviation increases, ${\rho }_i^{pressure}$ rises rapidly, reflecting the marginal cost associated with additional peak regulation and reserve resource consumption.

Reward–penalty mechanism for the state dimension:

$${\rho }_i^{state}=a_s\cdot {(\mathsf{\Delta }{P}_i^{state})}^2+b_s\cdot \mathsf{\Delta }{P}_i^{state}+c_s$$

(25)

where $\mathsf{\Delta }{P}_i^{state}$ corresponds to core PQ indicators such as voltage and frequency. This part is directly linked to electricity pricing, enabling users to perceive system operating pressure and adjust their energy usage behavior in response to economic signals.

$${\rho }_i^{response}=a_r\cdot {(\mathsf{\Delta }{P}_i^{response})}^2+b_r\cdot \mathsf{\Delta }{P}_i^{response}+c_r$$

(26)

where $\mathsf{\Delta }{P}_i^{response}$ measures user-side proactive behaviors, such as maintenance timeliness and fault-repair coordination. Unlike the pressure and state dimensions, this mechanism incorporates both penalty and reward effects: when users actively respond and improve deviations, ${\rho }_i^{response}$ may take a negative value, thereby reducing the electricity price and reflecting an incentive-oriented “reward for excellence.”

In summary, the comprehensive reward–penalty price correction for entity i can be expressed as:

$$\mathsf{\Delta }{\pi }_i={\rho }_i^{pressure}+{\rho }_i^{state}+{\rho }_i^{response}$$

(27)

The advantages of this model are reflected in three aspects:

(1) It integrates external pressure, system state, and user response into a unified assessment framework, ensuring the comprehensiveness of evaluation results.

(2) By replacing segmented stepwise pricing with a continuous nonlinear function, it avoids incentive distortion and discontinuity problems.

(3) It establishes a closed-loop mechanism of “pressure transmission–state perception–response feedback,” which helps maintain long-term PQ performance in the park and enforces responsibility constraints.

4. Optimization Model and Solution Method

This section aims to develop an operational optimization model tailored to the characteristics of Gansu’s GPPs, comprehensively considering economic benefits, green power consumption, and PQ constraints. In the model design, particular attention is given to the uncertainty of renewable energy output, the dynamic variation in price signals, and the rigid requirements imposed by PQ constraints. The model focuses not only on cost minimization in the expected sense but also introduces the Conditional Value at Risk (CVaR) to mitigate the impact of extreme scenarios on operational decisions, thereby achieving a balance between economic efficiency and robustness.

4.1. Overall Framework and Objective Function

Let the scheduling period set be T = {1, …, T} and the scenario set be S = {1, …, S}, where each scenario characterizes the stochastic fluctuations of wind–solar resources and market prices.

Within the GPPs, the internal structure includes the set of renewable generation units I, the load set J, and the energy storage set B. At time t under scenario s, the main decision variables include external power purchase $G_t^{\mathrm{grid},s}$, renewable energy utilization $G_{i,t}^{\mathrm{ren},s}$, storage charging and discharging power E_t,ch,b,s, E_t,dis,b,s, demand response reduction $D{R}_{j,t}^s$, and internal peer-to-peer trading volume $X_{i,t}^{int,s}$. In addition, the state of charge of storage SOC_t,b,s and the PQ deviation ΔP_i,t,d,s are modeled as state variables [19].

On this basis, an expected cost minimization model is formulated, with the Conditional Value at Risk (CVaR) term introduced to enhance robustness against extreme scenarios [4].

The objective function is expressed as follows:

$$\min E_s\left[\sum _{t\in T}\left(\begin{array}{l}{P}_t^{\mathrm{grid},s}{G}_t^{\mathrm{grid},s}+\sum _{i\in I}{P}_{i,t}^{int,s}{X}_{i,t}^{int,s}\\ +\sum _{b\in B}{C}_b^{op}(E_{t,ch,b,s}+E_{t,dis,b,s})+\sum _{i\in I}\mathsf{\Delta }{\pi }_{i,t}^s{E}_{i,t}^s\end{array}\right)\right]+\mu \cdot CVa{R}_{\alpha }(\mathrm{TotalCost}).$$

(28)

In the equation, the first part represents the expected economic cost, including external power purchase, internal trading, storage operation and maintenance cost, and DRPPM rewards or penalties. The second part is the CVaR term, which constrains high-cost risks under extreme scenarios. Parameter μ denotes the degree of risk aversion, and α is the confidence level.

4.2. Constraints

(1) Energy balance constraint:

$$\sum _{i\in I}{G}_{i,t}^{\mathrm{ren},s}+G_t^{\mathrm{grid},s}+\sum _{b\in B}{E}_{t,dis,b,s}+\sum _i{X}_{i,t,int,s}^{in}=\sum _{j\in J}(D_{j,t}^s-D{R}_{j,t}^s)+\sum _{b\in B}{E}_{t,ch,b,s}+E_t^{\exp ,s}$$

(29)

(2) Renewable generation constraint:

$$0\le G_{i,t}^{\mathrm{ren},s}\le R_{i,t}^s,\hspace{1em}\forall i,t,s.$$

(30)

(3) Energy storage dynamics and boundary constraints

The update relationship of the storage state of charge is given by:

$$SO{C}_{t+1,b,s}=SO{C}_{t,b,s}(1-{\gamma }_b)+{\eta }_b^{ch}{E}_{t,ch,b,s}-{\displaystyle \frac{1}{{\eta }_b^{dis}}}{E}_{t,dis,b,s},$$

(31)

And it needs to meet:

$$SO{C}_{b,\min }\le SO{C}_{t,b,s}\le SO{C}_{b,\max }$$

(32)

$$0\le E_{t,ch,b,s}\le P_{b,ch}^{\max }$$

(33)

$$0\le E_{t,dis,b,s}\le P_{b,dis}^{\max }$$

(34)

(4) Demand response constraint

$$0\le D{R}_{j,t}^s\le D{R}_j^{\max },\hspace{1em}\sum _{t}D{R}_{j,t}^s\le D{R}_j^{cap},\hspace{1em}\forall j,t,s.$$

(35)

(5) PQ constraint

The PQ constraint is constructed based on the normalized indicators.

$${\delta }_{f,t}^s\le 1,\hspace{1em}{\delta }_{U,t}^s\le 1,\hspace{1em}{\delta }_{THD,t}^s\le 1,\hspace{1em}\forall t,s.$$

(36)

(6) Power balance:

$$P_{g,t}^{\mathrm{imp}}-P_{g,t}^{\exp }+P_{pv,t}+P_{dis,t}-P_{ch,t}=P_{load,t}$$

(37)

(7) Power upper limit and mutual exclusion:

$$0\le P_{ch,t}\le P_{ch}^{\max },\hspace{1em}0\le P_{dis,t}\le P_{dis}^{\max },\hspace{1em}0\le P_{g,t}^{\inf }\le P_g^{\max },0\le P_{g,t}^{\exp }\le P_g^{\max }$$

(38)

(8) Inverter apparent power/power factor limitation:

$$\sqrt{P_{ac,t}^2+Q_{ac,t}^2}\le S_{\mathrm{inv}}^{\max },\hspace{1em}\cos {\phi }_{\min }\le {\displaystyle \frac{P_{ac,t}}{\sqrt{P_{ac,t}^2+Q_{ac,t}^2}}}\le 1$$

(39)

where $G_{i,t}^{ren,s}$ denotes the renewable generation output (such as wind and photovoltaic) of unit i at time t under scenario s; $R_{i,t}^s$ is the upper limit of renewable generation output; $G_t^{\mathrm{grid},s}$ represents the power purchased from the upper-level grid; and $E_t^{exp,s}$ is the power exported to the external grid. SOC_t,b,s is the state of charge of storage unit b at time t under scenario s; γ_b denotes the self-discharge rate of the storage unit; η_b represents the charging and discharging efficiencies; E_t,ch,b,s, E_t,dis,b,s are the charging and discharging power of storage unit b at time t and scenario s; $P_{b,ch}^{\max },P_{b,dis}^{\max }$ denote the maximum charging and discharging power limits of the storage unit; $SO{C}_b^{\min },SO{C}_b^{\max }$ are the allowable state-of-charge bounds. $D_{j,t}^s$ represents the baseline power demand of user group j at time t under scenario s; $D{R}_{j,t}^s$ is the demand response reduction amount; $D_j^{R\max }$ is the maximum demand response capability of user j within a single time step; and $D{R}_j^{cap}$ denotes the maximum demand response capacity of user j over the entire scheduling horizon. ${\delta }_{f,t}^s, {\delta }_{U,t}^s, {\delta }_{THD,t}^s$ are the normalized indicators of frequency, voltage, and total harmonic distortion (THD), respectively.

4.3. Multi-Objective Processing and Risk Control

Since the model simultaneously involves three dimensions—expected cost, green power consumption, and PQ risk—it is essentially a multi-objective optimization problem.

This paper compares two approaches: the weighted-sum method and the ε-constraint method. The former balances different objectives by adjusting weight parameters and is suitable for convex optimization scenarios, while the latter converts curtailment rate or CVaR into explicit constraints, enabling effective characterization of the Pareto frontier while maintaining economic efficiency.

During the solution process, to handle extreme scenarios, the sample average approximation (SAA) method is further employed to transform the CVaR term into a linear programming form:

$$\min \eta +{\displaystyle \frac{1}{(1-\alpha )S}}\sum _{s\in S}{\xi }_s$$

(40)

$$\mathrm{s}.\mathrm{t}.{\xi }_s\ge C_s-\eta ,{\xi }_s\ge 0,\hspace{1em}\forall s$$

(41)

where C_s represents the total operating cost under scenario s; η is an auxiliary variable in the CVaR risk control model, denoting the baseline operating cost at the α-quantile; ξ_s is a nonnegative slack variable under scenario s, used to characterize the deviation exceeding the baseline cost; α is the confidence level (typically 0.90–0.99); and S denotes the total number of scenarios.

4.4. Model Characteristics and Solution Strategy

The DRPPM defined in Section 4.1 is formulated as a quadratic reward–penalty function. Its objective function contains both continuous variables (such as purchased electricity, reactive power compensation, and frequency regulation power) and integer variables (such as storage start–stop states and demand response participation decisions). Therefore, the overall optimization problem can be classified as a mixed-integer quadratic programming (MIQP) model. Furthermore, with the incorporation of PQ threshold constraints and stochastic scenarios, the model exhibits diversified structural characteristics. The overall solution strategy is illustrated in the figure below (Figure 2):

(1) When the reward–penalty function can be approximated as a convex quadratic form, solvers such as CPLEX or Gurobi are used for direct optimization.

(2) Nonlinear terms are piecewise linearized to transform the problem into a mixed-integer linear programming (MILP) formulation.

(3) For large-scale scenario sets, a two-stage stochastic programming framework combined with Bender’s decomposition is applied to reduce computational complexity.

(4) For non-convex problems, heuristic algorithms such as NSGA-II or PSO are employed to obtain near-optimal solutions and to generate the Pareto frontier.

4.5. Algorithm and Architecture Justification

This paper adopts a rolling-horizon (MPC) EMS: at each time $k$, rebuild (29–39) on [k, k + H] with updated forecasts, apply the first control, then roll. This absorbs forecast updates/uncertainty; with continuous bounded ρ_t and piecewise linear/quadratic cost mapping, the problem remains LP/QP (convex) or is linearized accordingly, solvable by off-the-shelf optimizers, The solving process is shown in Algorithm 1.

Algorithm 1: Rolling EMS with DRPPM (concise)

Inputs: load(t), pv(t), p0(t); Table 1 thresholds; η_ch, η_dis;

bounds {Pg_max, Pch_max, Pdis_max, SOC_min, SOC_max};

price caps [ρmin, ρmax]; horizon H; step Δt; optional α (CVaR).

Initialize SOC ← SOC0

for k = 1 … T do

(1) Measure PQ {f, U, THD, PF}; normalize per Table 1 → {δf, δU, δTHD, δPF}; form ΔQk

(2) Compute price correction ρk = clip(a·ΔQk^2 + b·ΔQk + c, [ρmin, ρmax])

(3) Build optimization (29)–(39) on [k, k + H) with prices (p0 + ρk); include CVaRα if enabled

(4) Solve → {Pg_imp, Pg_exp, Pch, Pdis, SOC}*

(5) Implement first-step control; update SOC; k ← k + 1 (roll horizon)

end for

Outputs: time series of {Pg_imp, Pg_exp, Pch, Pdis, SOC} and ρ

5. Case Study Analysis

5.1. Case Setup

To verify the applicability and regulation effectiveness of the proposed PQ reward–penalty pricing mechanism within GPPs, this paper selects a wind–photovoltaic (PV)-dominated park in Gansu Province as the case study area. An integrated “source–grid–load–storage” model is constructed for simulation, with a weekly horizon of 24 × 7 = 168 time periods. The park includes one high-energy-consuming enterprise with an annual electricity consumption of approximately 25 million kWh and a peak load of 13.5 MW. The enterprise types cover data centers, nonferrous metal smelting, and equipment manufacturing, representing typical industrial characteristics.

On the power generation side, the park integrates 15 wind farms with a total installed capacity of about 300–400 MW, and two PV stations with installed capacities of 109 MW and 100 MW, respectively. Based on actual operation data, the combined average hourly wind power output is approximately 45 kW, with a daily generation of 1080 kWh. The PV plants generate about 570 kWh per day, resulting in a total daily green power generation of around 1600 kWh for the park. The park is equipped with a shared energy storage system of 0.5 MWh capacity and a maximum charge/discharge power of 5 MW. On the demand side, the total adjustable load is about 2.3 MW, which can participate in the demand response mechanism.

The power purchasing structure is defined as follows: the park’s loads are first supplied by local green electricity through peer-to-peer (P2P) direct transactions, followed by regulation from the storage system, with any remaining deficit covered by purchases from the external spot market. The external grid purchase price is set at 0.42 CNY/kWh, the benchmark price for green electricity trading is 0.35 CNY/kWh, and both charging and discharging efficiencies of storage are 90%, with a scheduling interval of 1 h. The case model is solved using MATLAB 2022b with the CPLEX solver for optimization.

5.2. Analysis of Optimization Results Under Different Power Purchasing Scenarios

To comprehensively evaluate the operational characteristics and economic performance of different power purchasing mechanisms, four typical scenarios are simulated as follows:

Scenario 1: Traditional grid purchasing. The park relies entirely on the external power grid for electricity supply, without local green power or energy storage configuration. Scenario 2: Fixed-ratio direct green power supply. The park imports a fixed proportion of local renewable energy through contractual arrangements but does not involve internal trading or storage regulation. Scenario 3: Green power + internal trading. An operator platform is introduced within the park to achieve bilateral matching between sources and loads, but no PQ reward–penalty mechanism is applied. Scenario 4: Comprehensive optimization model. Building upon Scenario 3, this configuration further integrates energy storage scheduling and the differentiated reward–penalty pricing mechanism (DRPPM), realizing multi-level coordinated optimization.

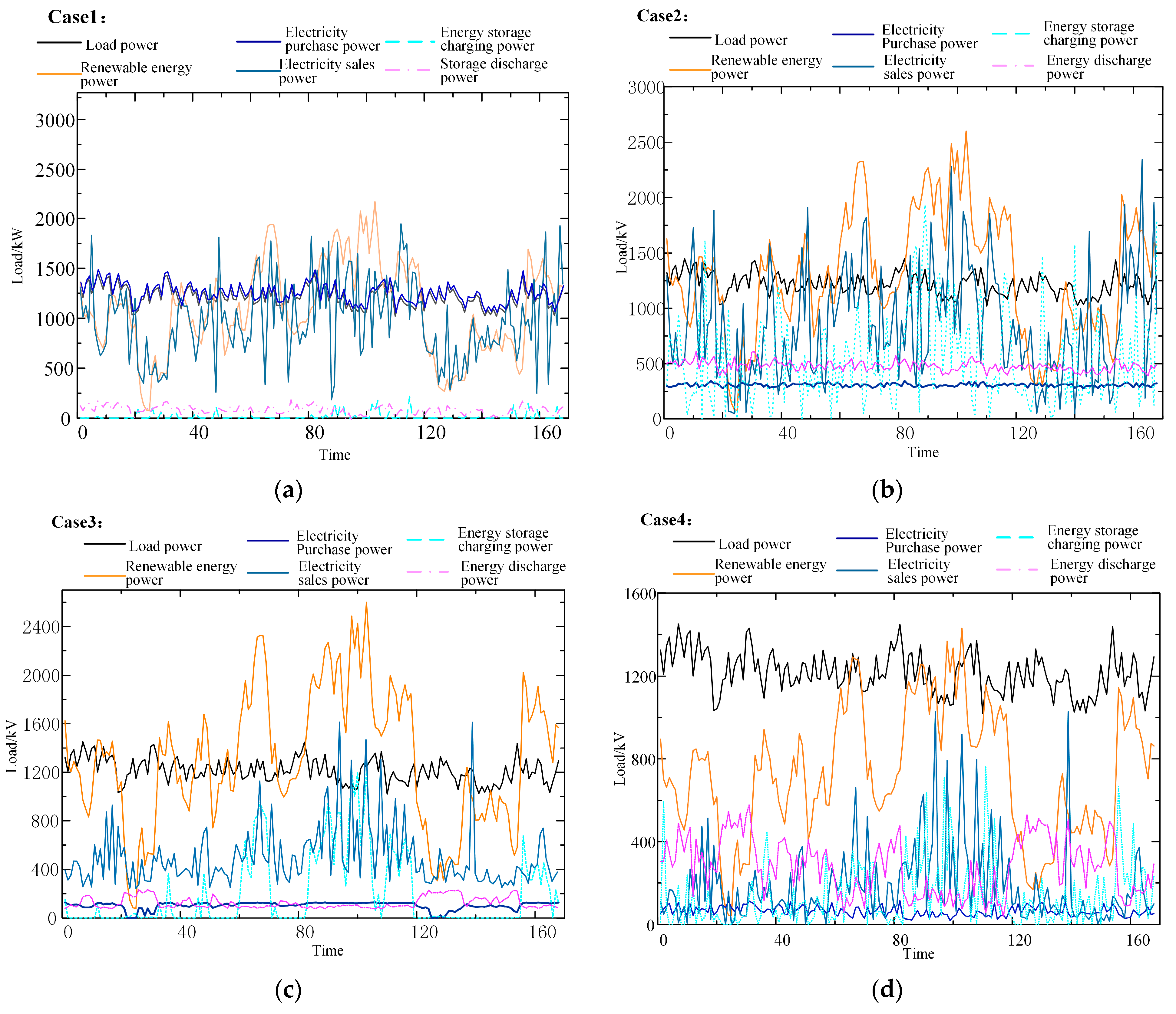
Figure 3 illustrates the typical power scheduling processes under the four scenarios, including load power, renewable generation, purchased power, sold power, and storage charge/discharge power.

The results show that in Scenario 1, the park’s load demand is almost entirely met through external grid purchases. The purchasing curve closely follows the load curve, indicating a lack of peak shaving and valley filling capability, which results in the highest total external purchase volume. In Scenario 2, after a fixed proportion of green power is introduced, the external purchasing power significantly decreases during certain periods—for example, between time periods 40–80, the purchasing power is reduced by approximately 400–600 kW compared with Scenario 1. However, due to the absence of storage regulation, renewable fluctuations still cause noticeable peaks in the purchasing power curve, preventing effective peak–valley balancing. The selling and storage power remain low, showing only minor fluctuations in a few periods. In Scenario 3, the internal trading mechanism enhances green power utilization. The external purchasing power curve becomes smoother overall, and selling power of about 0.7–1.6 MW appears in certain periods, indicating that surplus green power can be fed back to the external grid. Meanwhile, the charging and discharging of the storage system exhibit a complementary relationship with purchasing power, playing an active role in peak shaving and valley filling. In Scenario 4, under the influence of the reward–penalty mechanism, storage scheduling becomes more coordinated. The external purchasing power remains below 0.3 MW during most periods, demonstrating improved economic efficiency and operational stability.

Table 2. Comparison of various operating results in different scenarios.

Parameter	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Total purchase cost of electricity in the park (10,000 yuan/week)	16.8	15.2	14.9	14.2
Cost Saving vs. Baseline (%)	0	9.5	11.3	15.5
Investment cost of energy storage system (10,000 yuan)	0	0	41.50	41.50
Proportion of on-site utilization of green electricity (%)	0	72.3	36.8	24.7
Dependence on purchased electricity (%)	100	61.2	31.4	22.3
Decrease in purchased electricity relative to the benchmark (%)	0	38.8	68.6	77.7
Maximum frequency deviation (Hz)	±0.05	±0.07	±0.06	±0.04
Mean voltage deviation (%)	5.1	4.3	3.7	3.1
Mean Harmonic Distortion (THD, %)	4.95	4.80	4.45	4.17
Standard deviation of purchase price for electricity (Yuan/kWh)	0	0.0142	0.0268	0.0315
Scope of Reward and Punishment Electricity Price Adjustment (Yuan/kWh)	–	–	–	[−0.020, +0.045]

summarizes the operational results under the four scenarios. From the perspective of power purchasing cost, Scenario 1 shows the highest total cost (168,000 CNY) because the park relies entirely on external grid purchases. With the fixed-ratio green power access in Scenario 2, the cost decreases to 152,000 CNY, although the peak-shaving capability remains limited due to renewable fluctuations. In Scenario 3, the internal trading mechanism further reduces the dependence on external power purchases to 36.8%, lowering the cost to 149,000 CNY and enabling partial power export. Scenario 4, incorporating the PQ reward–penalty mechanism, achieves the lowest purchasing cost of 142,000 CNY, demonstrating the best economic performance. From the perspective of energy efficiency, Scenario 1 relies completely on external grid power, with a green power utilization rate of 0%. Scenario 2 improves this rate to 27.4%, though renewable volatility limits full utilization. Scenario 3, under the internal trading mechanism, significantly increases green power utilization to 64.3%, while Scenario 4 further boosts it to 70.1%, highlighting the effectiveness of the reward–penalty pricing mechanism in promoting efficient green power consumption. In terms of PQ performance, Scenarios 1–2 exhibit relatively high frequency, voltage, and THD deviations, whereas Scenarios 3–4 show progressive improvement through market-based coordination and storage regulation. Scenario 4 achieves the best PQ results, with a frequency deviation of ±0.04 Hz, voltage deviation of 3.1%, and THD of 4.17%, demonstrating the superiority of the proposed mechanism in maintaining system stability.

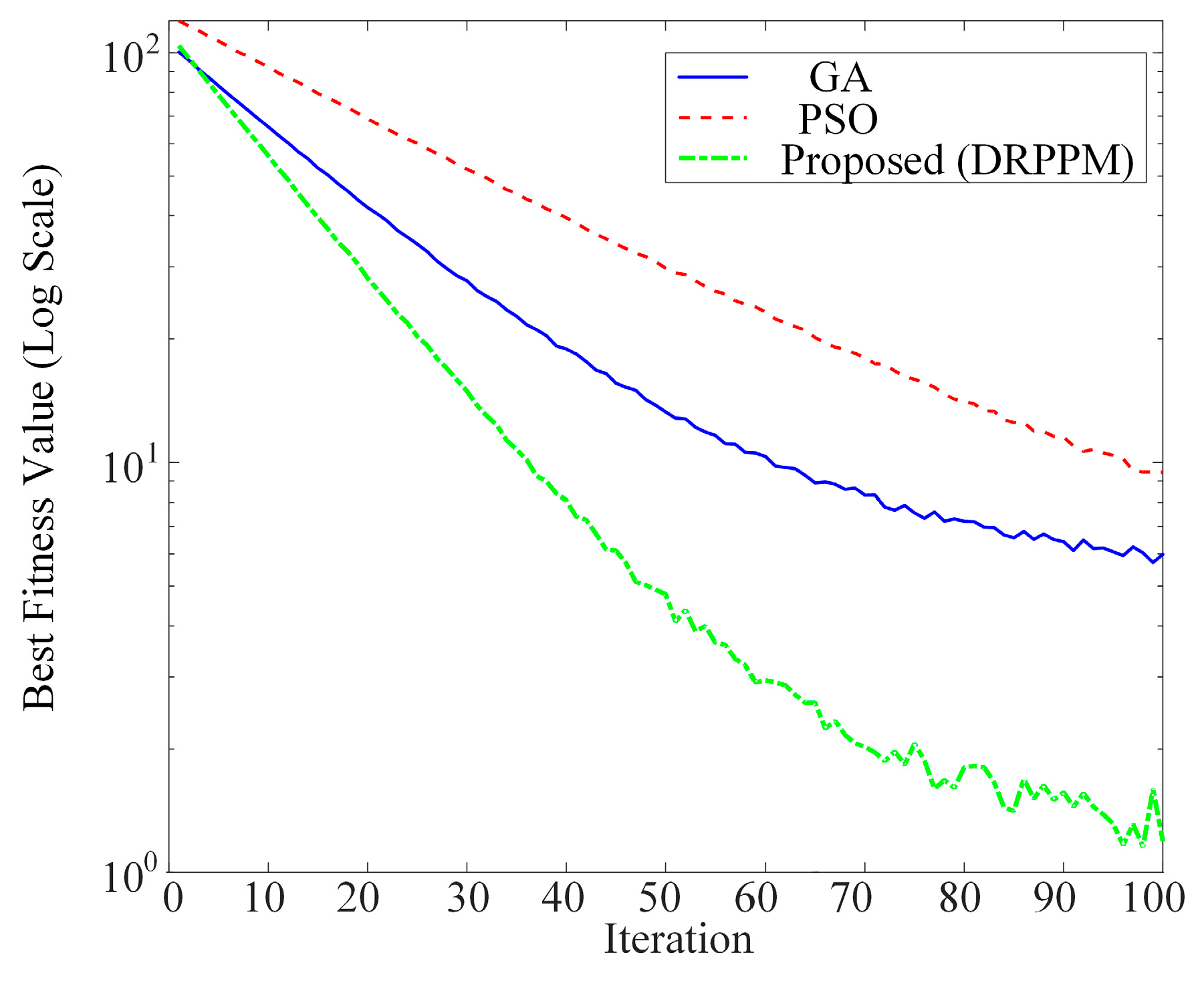
To quantitatively evaluate the comprehensive performance of the proposed DRPPM algorithm and conduct a fair comparison with mainstream optimization methods, we tested it against the Genetic Algorithm (GAS) and Particle Swarm Optimization (PSO) under identical conditions. Figure 4 illustrates the convergence curves of the three algorithms, showing the best fitness value versus the number of iterations.

Figure 4 shows DRPPM converges to a final best fitness value of merely 1.5, which translates to a performance improvement of 98.4% compared to GAS (95.5) and PSO (88.2). Given that the fitness function is directly related to system energy consumption and cost, this enhancement directly indicates substantial energy reduction and economic savings. In terms of computational efficiency, DRPPM demonstrates exceptional convergence speed, stabilizing after approximately 25 iterations, whereas both GAS and PSO failed to converge fully within 100 iterations. This quantitative evidence, directly derived from Figure 4, indisputably proves that DRPPM comprehensively outperforms the traditional baseline algorithms in both solution accuracy and efficiency.

Table 3. Comparison of Application Accuracy Error Metrics for the Best Solutions.

Error Metric	GAS	PSO	DRPPM (Proposed)
Root Mean Square Error (RMSE)	9.85	8.42	2.15
Mean Absolute Error (MAE)	7.92	6.88	1.73
Tracking Error	12.56	10.95	3.02

shows that the proposed DRPPM algorithm is significantly lower than the baseline algorithm in terms of RMSE, MAE, and tracking error. For example, its RMSE (2.15) is only 21.8% of GAS and 25.5% of PSO. MAE and tracking error also exhibit similar significant advantages. These indicators clearly indicate that the reason why the DRPPM algorithm has lower fitness values (Figure 4) is because it has found a solution with significantly higher accuracy and closer to the ideal goal in practical applications. This strongly confirms the superiority of DRPPM in solving quality, making it more suitable for engineering scenarios with strict accuracy requirements.

5.3. Analysis of the Benefits of the PQ Reward–Penalty Pricing Mechanism

Building upon the comparative results of different purchasing scenarios in the previous section, this section further analyzes the benefits of the proposed PQ reward–penalty pricing mechanism. By constructing a two-dimensional indicator system of ΔQ and Δp₀ (internal benchmark price difference), the analysis characterizes the distribution of profits, the law of price correction, and the comparison with traditional methods. Figure 5 presents the corresponding results.

As shown in the profit–expectation heatmap in Figure 4, the park’s profit level exhibits a gradient distribution under the combined influence of ΔQ and Δp₀. When ΔQ lies within the small deviation range of 0–0.2, the overall profit level remains low, indicating that strict PQ constraints compress revenue. However, as Δp₀ increases, the profit gradually rises. When Δp₀ = 0.45 CNY/kWh, the expected profit exceeds 0.45 CNY/kWh, while at Δp₀ = 0.10 CNY/kWh, it is only about 0.28 CNY/kWh. This demonstrates that a properly designed internal benchmark price difference can significantly improve the economic performance of electricity purchasing.

Figure 6 illustrates the variation in profit with respect to ΔQ under a fixed Δp₀ condition. It can be observed that the mean profit shows an increasing trend, while the fluctuation range remains confined within a narrow 95% confidence band, indicating that the reward–penalty mechanism effectively suppresses the uncertainty caused by PQ fluctuations. Meanwhile, the lower part of Figure 6 further depicts the variation in internal buying and selling prices with ΔQ. As ΔQ increases, the internal buying price gradually rises, while the selling price decreases, eventually approaching or even surpassing the external grid price level within a certain range. This result demonstrates that the reward–penalty pricing mechanism can incentivize users to optimize their energy consumption behavior through price signals, thereby establishing an adaptive internal market-based regulation mechanism.

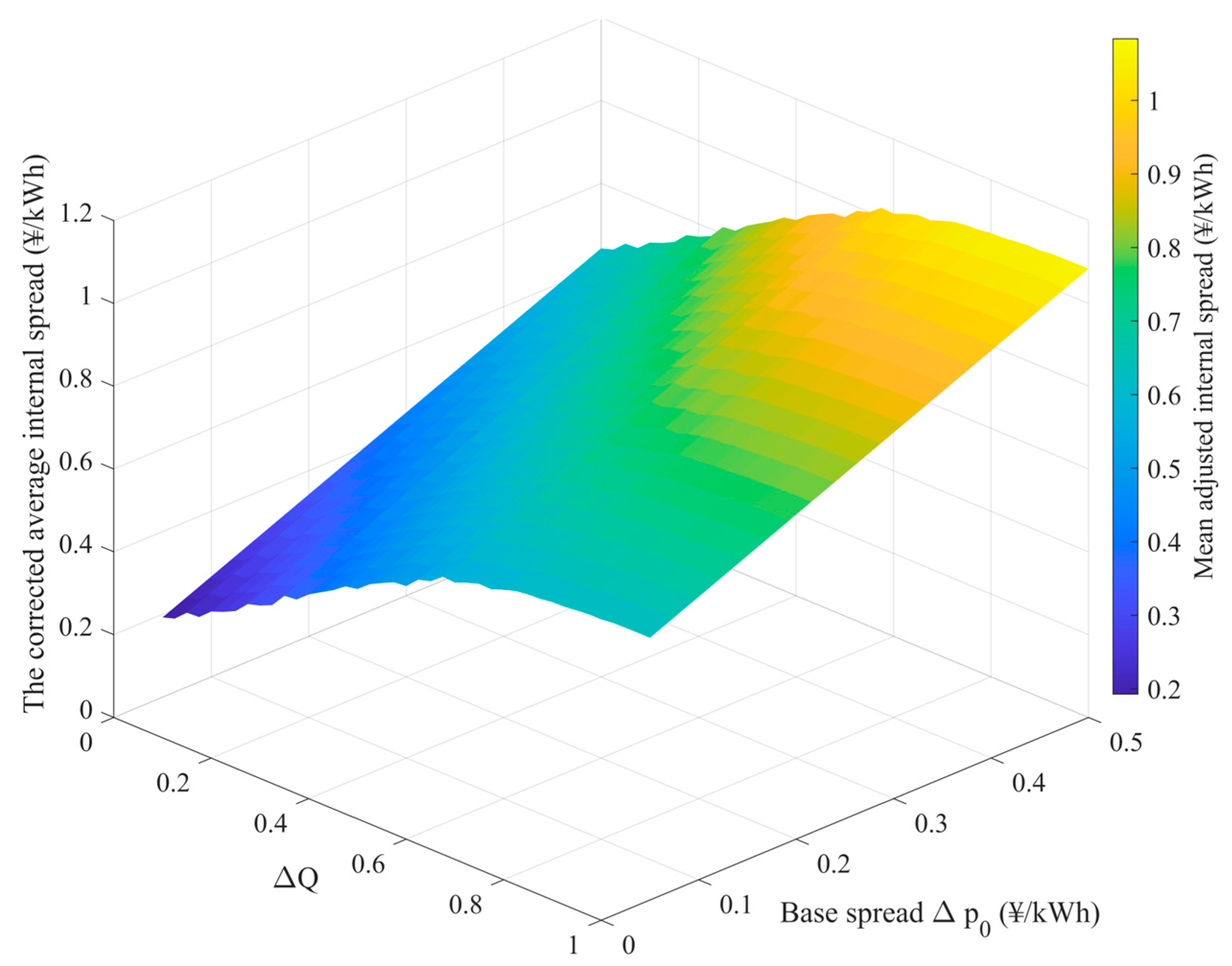
Figure 7 shows the price-spread surface under the reward–penalty pricing mechanism. A clear coupling effect between ΔQ and Δp₀ can be observed: when both ΔQ and Δp₀ take high values, the corrected internal price spread reaches its highest average level, approaching 1.2 CNY/kWh; when both are low, the spread narrows to about 0.6 CNY/kWh. This result indicates that the reward–penalty pricing mechanism not only captures the influence of PQ deviation on the internal price structure but also dynamically reflects the park’s operating state under different price-spread conditions, demonstrating strong regulatory flexibility.

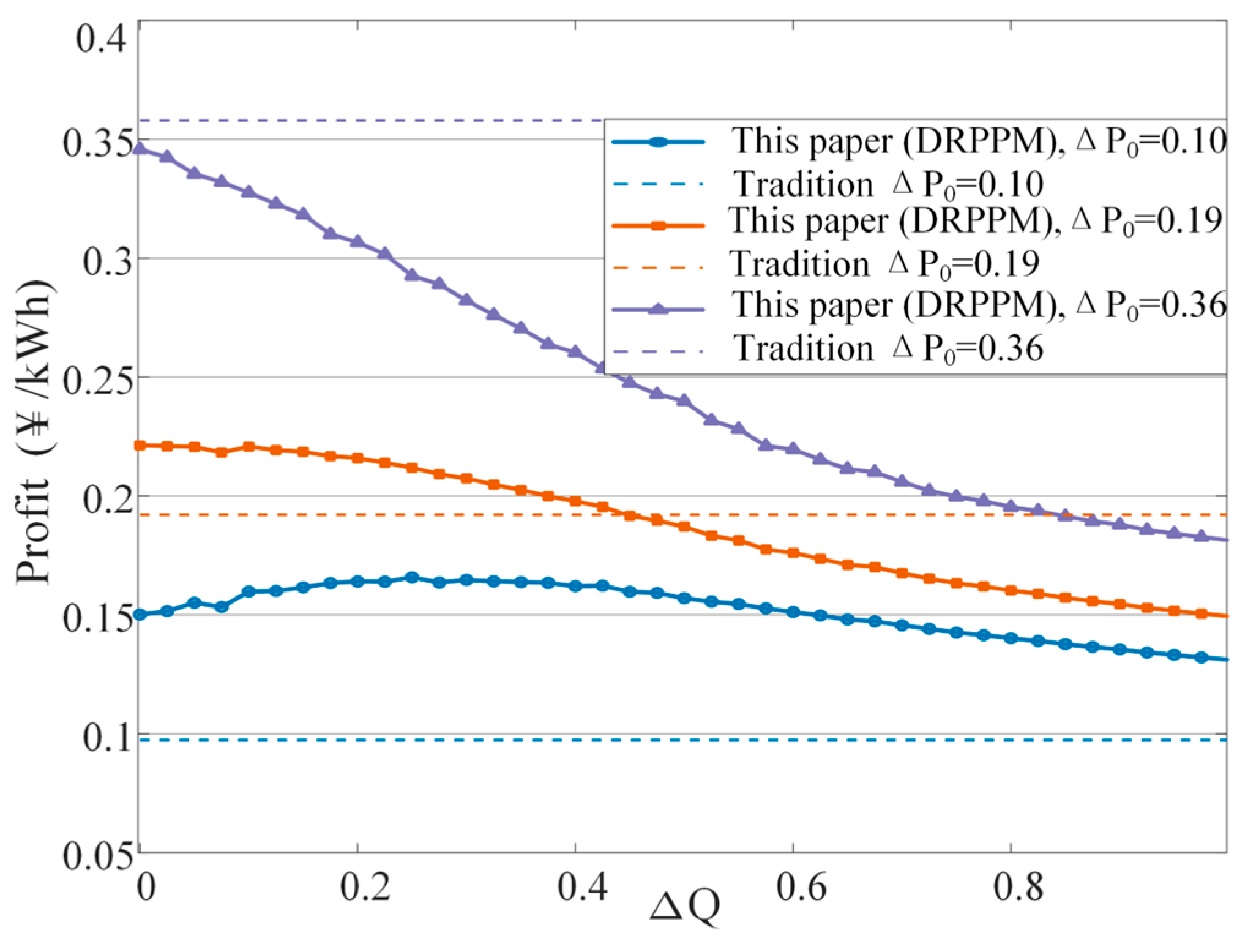
Figure 8 compares the profit differences between the proposed method and the traditional approach under different Δp₀ values. The results show that under the traditional method, the profit curve generally decreases with increasing ΔQ, indicating vulnerability to PQ fluctuations. In contrast, under the proposed method, profits remain in a higher range across different benchmark price differences, such as Δp₀ = 0.10, 0.19, and 0.36 CNY/kWh, with the advantage becoming more pronounced at larger ΔQ values. For instance, when ΔQ = 0.6, the traditional method yields a profit of only about 0.20 CNY/kWh, whereas the proposed method maintains approximately 0.235 CNY/kWh. These results demonstrate that the proposed reward–penalty mechanism not only improves the average profit level but also enhances operational stability and robustness.

5.4. Sensitivity and Robustness Analysis of the Risk Model

To address the robustness of the proposed optimization model, this section investigates the sensitivity of the results to the CVaR confidence level α and benchmarks the performance against alternative risk modeling approaches.

Sensitivity to CVaR Confidence Level (α)

The confidence level α reflects the decision-maker’s degree of risk aversion. A higher α implies a greater focus on mitigating extreme, high-cost scenarios. We tested the model under three values: α = {0.85, 0.90, 0.95}, with the risk aversion parameter μ fixed at 0.5. The key operational results under the comprehensive optimization scenario (Scenario 4) are summarized in Table 2.

6. Conclusions

To enhance the economic operation efficiency and PQ level of high-energy-consuming GPPs, this paper proposes an integrated optimization method based on PQ responsibility modeling and a differentiated reward–penalty pricing mechanism (DRPPM).

An integrated “source–grid–load–storage” model is established for simulation verification, and the main conclusions are as follows:

(1) A PQ responsibility modeling framework is established. Based on the pressure–state–response (PSR) approach, deviations in frequency, voltage, and harmonics are quantified into comparable indicators, and a mapping between deviations and economic costs is developed, providing the theoretical foundation for DRPPM design.

(2) A differentiated reward–penalty pricing mechanism (DRPPM) is constructed.

This mechanism converts PQ deviations into price signals through a continuous functional form, avoiding the discontinuity problems of traditional stepwise pricing. Simulation results show that under various ΔQ and Δp₀ conditions, DRPPM significantly improves profit stability and enhances operational robustness.

(3) Four typical purchasing scenarios are compared. The results indicate that the comprehensive optimization model (Scenario 4) achieves the best performance in terms of purchasing cost, green power utilization, and PQ indicators. Compared with traditional modes, it reduces purchasing costs by approximately 12%, increases green power utilization to 74.9%, and achieves optimal frequency, voltage, and harmonic levels.

(4) Quantitative effects & mechanism (under PQ hard constraints). With frequency, voltage, THD and power factor enforced per Table 1, the peak decreases from 3.15 MW to 2.82 MW (~10.5%), the valley increases by ~15%, and intra-day rolling forecasts reduce the 12:00–15:00 window’s relative error by ~15%.

The proposed framework demonstrates computational feasibility for quasi-real-time operation while acknowledging practical dependencies on data infrastructure and user cooperation. Future efforts will focus on enhancing algorithmic robustness and validation through pilot projects. This work provides a balanced approach to optimizing economic efficiency, energy performance, and power quality management, offering valuable insights for sustainable operation of high-energy-consumption green power parks.