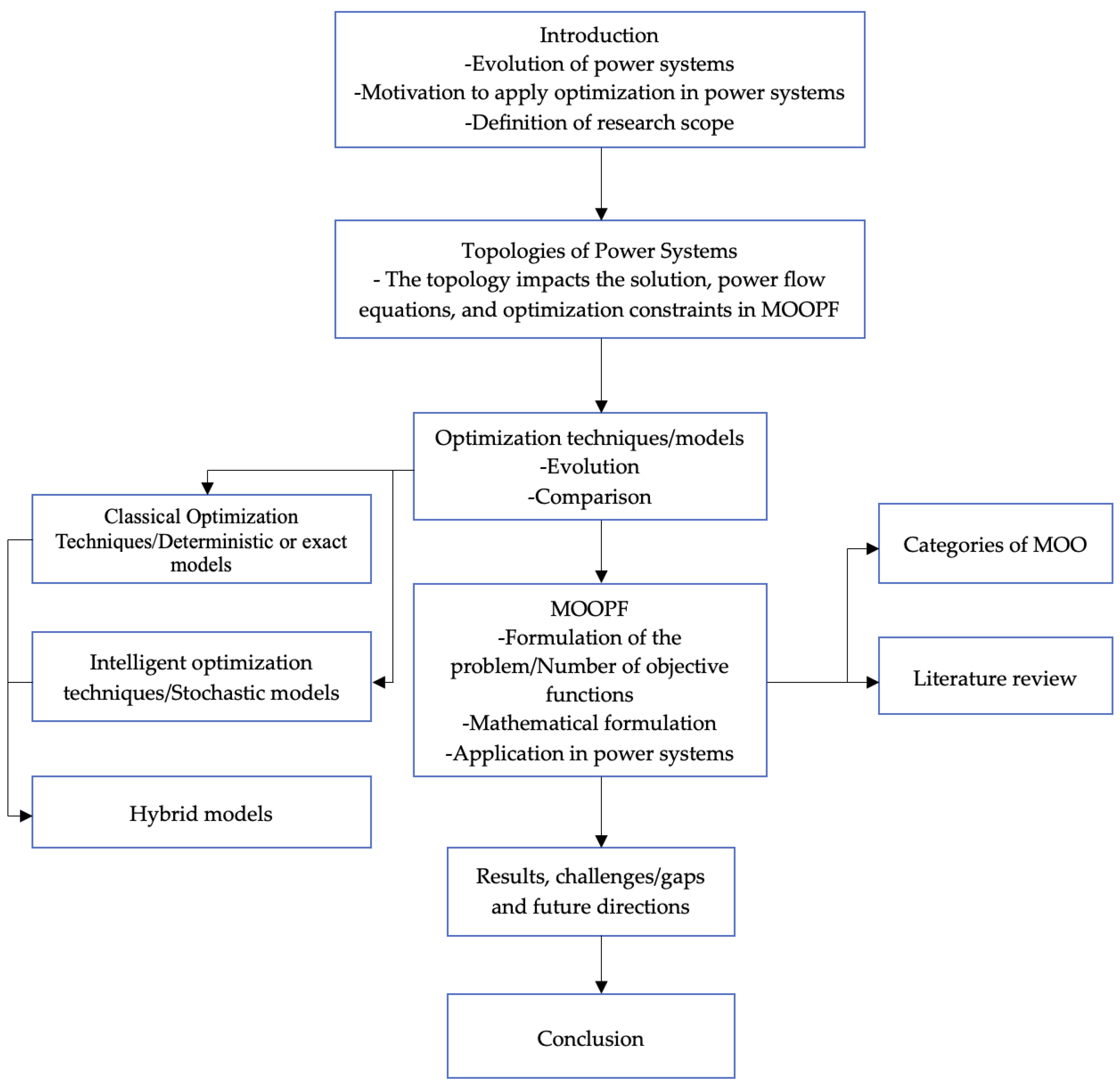
Multi-Objective Optimization of Load Flow in Power Systems: An Overview
Abstract
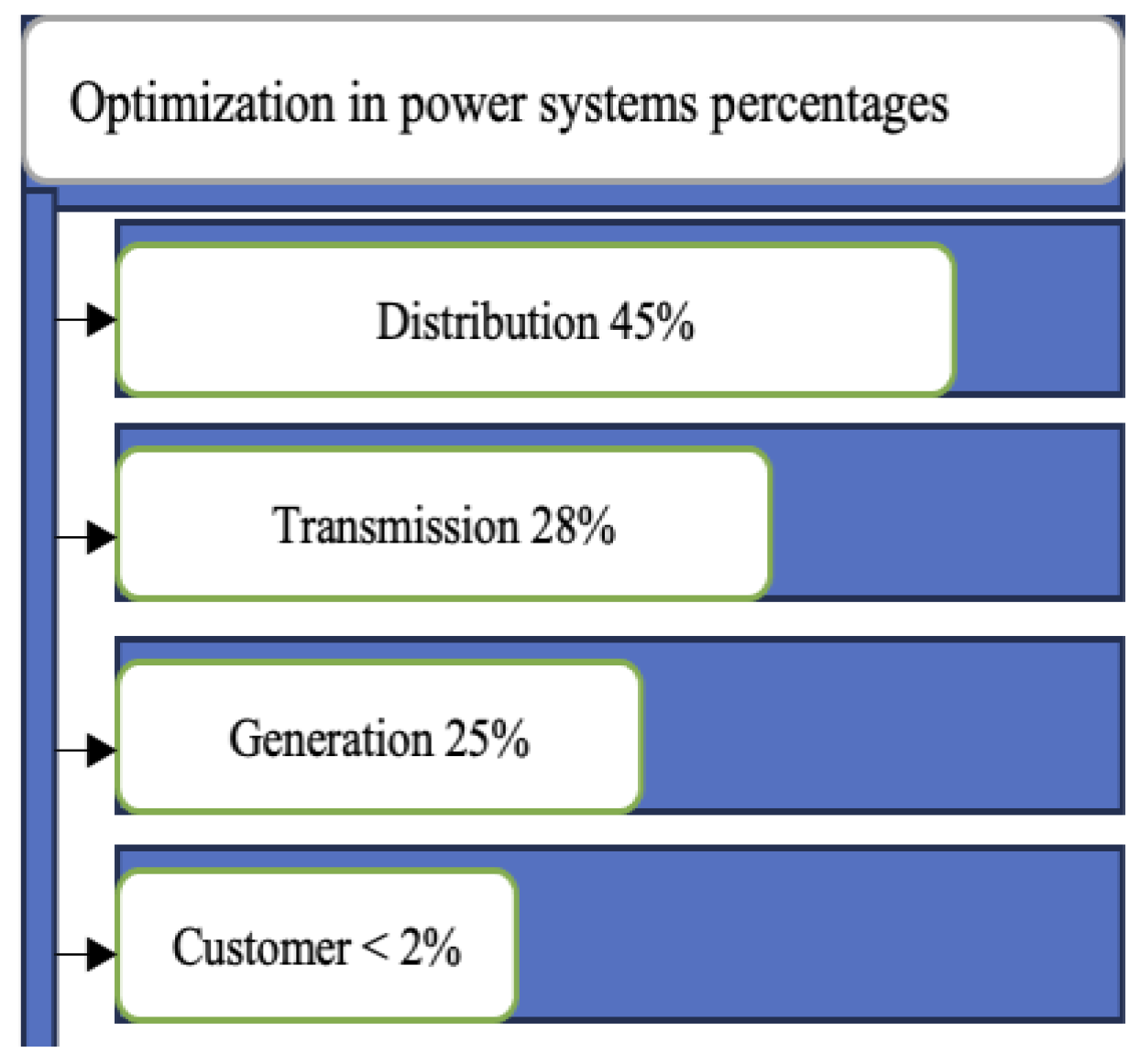
1. Introduction
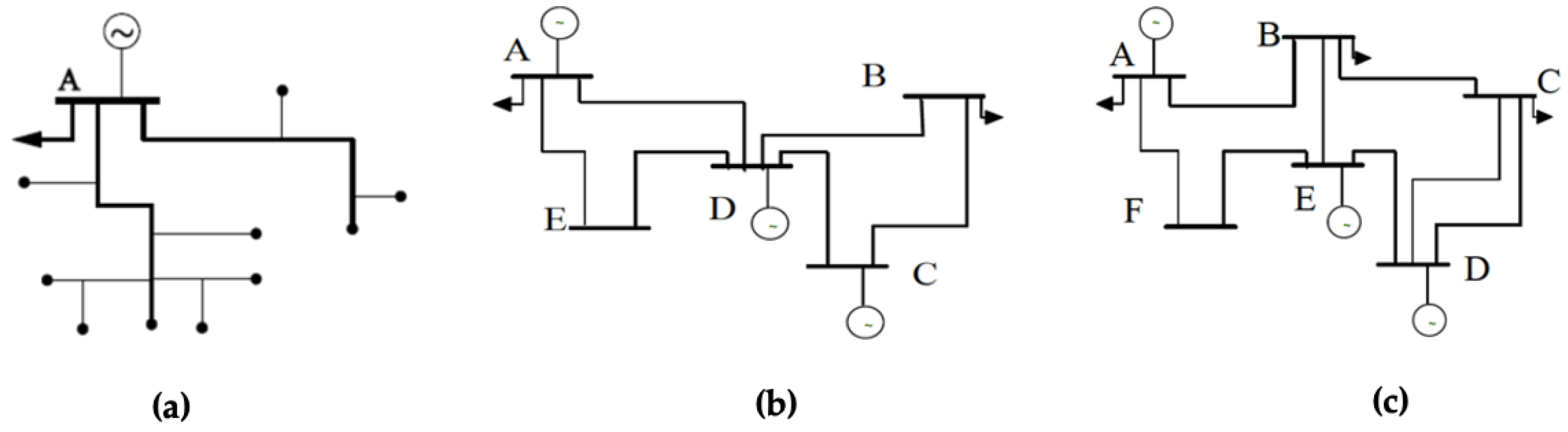
2. Topologies of Power Systems
2.1. Radial or Star Networks
2.2. Loop Networks
2.3. Mesh or Connected Networks
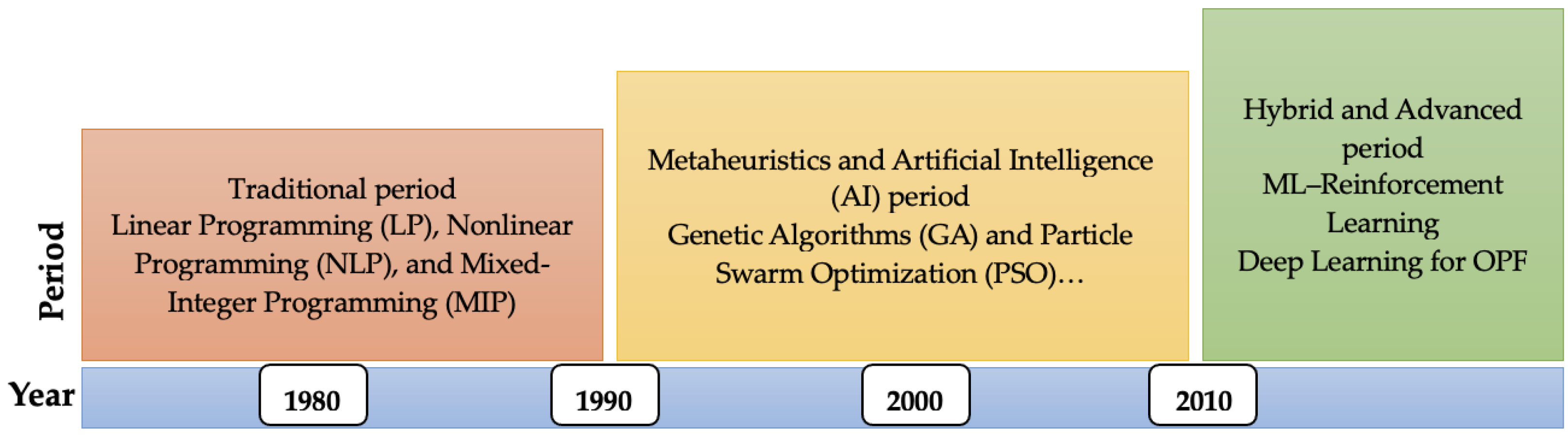
3. Optimization Techniques
3.1. Classical Optimization Techniques
3.2. Intelligent Optimization Techniques
4. Multi-Objective Optimization in Power Systems
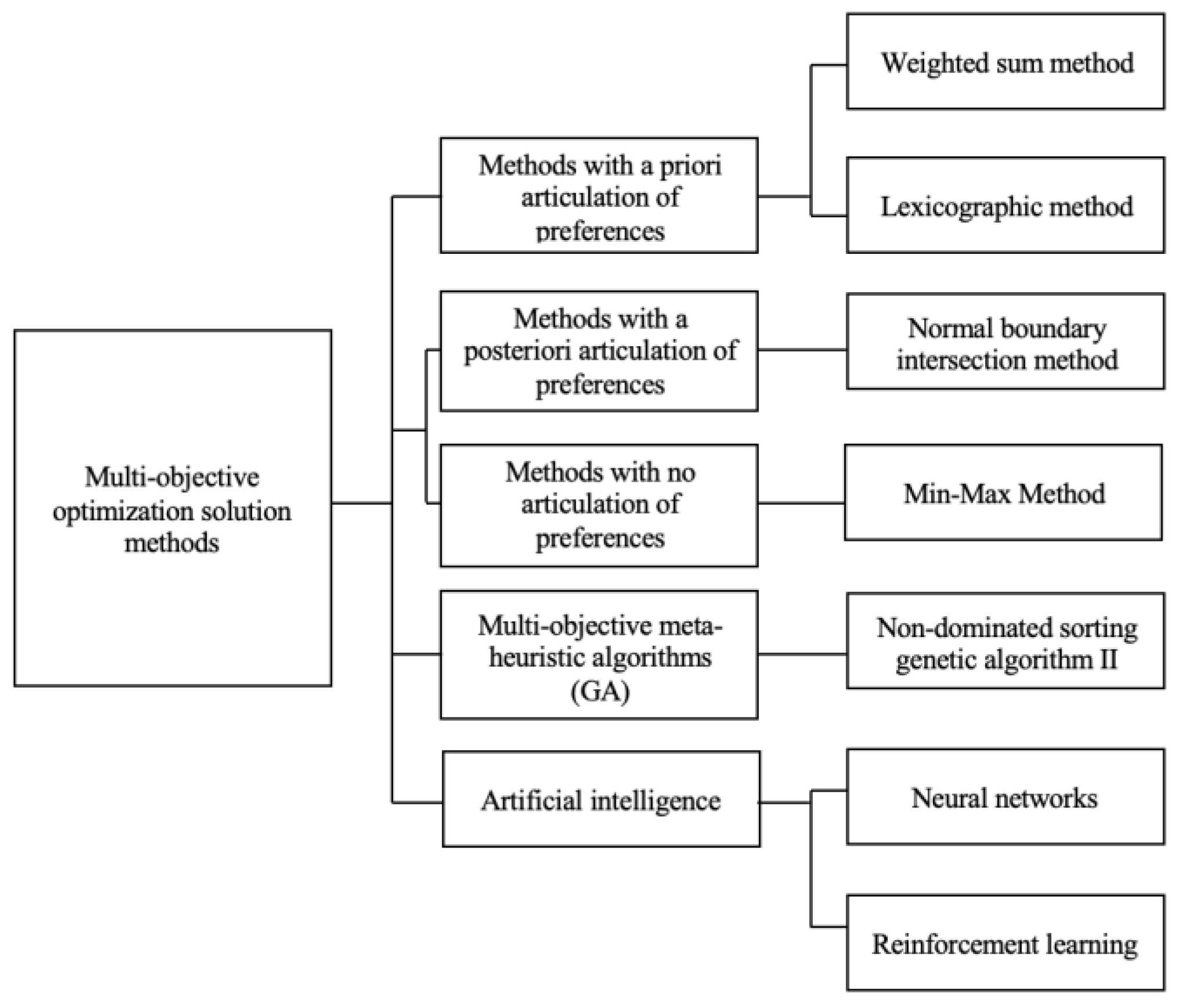
4.1. Categories of Multi-Objective Optimization Algorithm
4.2. Literature Review
5. Results, Challenges and Future Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony |
| ABX | Adapted Binary Crossover |
| ACNSDE | Adaptive Crossover Non-Dominated Sorting Differential Evolution |
| ACO | Ant Colony Optimization |
| ADNs | Active Distribution Networks |
| AHP | Analytic Hierarchy Process |
| AI | Artificial Intelligence |
| ALO | Ant Lion Optimization |
| ANNs | Artificial Neural Networks |
| APSOA | Adaptive Parallel Seeker Optimization Algorithm |
| ATC | Analytical Target Cascading |
| BAG | Bat Algorithm with Generalized Flight |
| BBO | Biogeography-Based Optimization |
| BPSO-SFLA | Binary Particle Swarm Optimization–Shuffled Frog Leaping Algorithm |
| CD | Crowding Distance |
| CDMTMO | Constrained Dynamic Multitasking Multi-Objective Optimization |
| CFD/CFI | Constraint Feasibility Degree/Index |
| COSR | Constraint-Objective Sorting Rule |
| CPS | Classification-Based Pre-Selection |
| DCM | Data Clustering Method |
| DDPG | Deep Deterministic Policy Gradient |
| DEA-EMA | Data Envelopment Analysis and Electromagnetism-like Algorithm |
| DGs | Distributed Generators |
| DMOGWO | Distributed Multi-Objective Grey Wolf Optimiser |
| DOPF | Dynamic Optimal Power Flow |
| DR | Demand Response |
| DRL | Deep Reinforcement Learning |
| EAs | Evolutionary Algorithms |
| EO | Equilibrium Optimiser |
| ESSs | energy storage systems |
| EWOA | Enhanced Wombat optimization Algorithm |
| FAHSPSO-DE | Fuzzy Adaptive Hybrid Particle Swarm Optimization-Differential Evolution |
| FCM | Fuzzy C-Means |
| FMOPF | Fuzzy Multi-Objective Optimal Power Flow |
| GA | Genetic Algorithms |
| GEWA | Generalized Evolutionary Walk Algorithm |
| GOA | Gazelle Optimization Algorithm |
| GOA | Grasshopper optimization Algorithm |
| GRP | Grey Relational Projection |
| GSA | Gravitational Search Algorithm |
| GTO | Giant Trevally Optimizer |
| GW | Gigawatt |
| GWO | Glow Warm Optimization |
| GWO | Gray Wolf Optimization |
| HBA | Honey Badger Algorithm |
| HDEED | Hybrid Dynamic Economic Emission Dispatch |
| HDI | Human Development Index |
| HFABC | Hybrid Fruit fly-based Artificial Bee Colony |
| HFSSA | Hybrid Flying Squirrel Search Algorithm |
| HHO | Harris Hawks Optimization |
| HRES | Hybrid Renewable Energy Systems |
| HWMSFLA-PSO | Hybrid Wavelet Mutation-based Shuffled Frog Leaping method and Particle Swarm Optimization |
| IAOA | Improved Archimedes optimization Algorithm |
| IEEE | Institute of Electrical and Electronics Engineers |
| IGDT | Information Gap Decision Theory |
| IMOPSO | Improved Multi-Objective Particle Swarm Optimization |
| IP | Integer Programming |
| IPFCs | Interline Power Flow Controllers |
| IRENA | International Renewable Energy Agency |
| ISPEA2 | Improved Strength Pareto Evolutionary method 2 |
| KnEA | Knee Point-Driven Evolutionary Algorithm |
| LCOE | Levelized Cost of Energy |
| LMIPSs | large-scale multi-area interconnected power systems |
| LP | Linear Programming |
| LPSP | Loss of Power Supply Probability |
| MCS-OPF | Monte Carlo simulation–Optimal Power Flow |
| MES | Multi-Energy System |
| MF | Moth Flame |
| MFO_PDU | Moth-Flame Optimization Method with a Position Disturbance Updating |
| MG-ASTGCN | Multi-Grained Attention-Based Spatial-Temporal Graph Convolution Network |
| MGs | microgrids |
| MIP | Mixed-Integer Programming |
| MJAYA | Modified JAYA |
| MOADE | Multi-Objective Adaptive Differential Evolution |
| MOCOA-ML | Multi-Objective Coyote optimization Algorithm with Meta-Lamarckian Learning |
| MOCSA | Multi-Objective Cuckoo Search Algorithm |
| MODA | Multi-Objective Dragonfly Algorithm |
| MODE | Multi-Objective Differential Evolution |
| MOEA | Multi-Objective Evolutionary Algorithm |
| MOEA/D | Multi-Objective Evolutionary Algorithm based on Decomposition |
| MOHHO | Multi-Objective Horse Herd Optimization Algorithm |
| MOMICA | Multi-Objective Modified Imperialist Competitive Algorithm |
| MOO | Multi-Objective Optimization |
| MOOPF | Muti-Objective Optimal Power Flow |
| MOPFA | Multi-Objective Pathfinder Algorithm |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| MORPD | Multi-Objective Optimal Reactive Power Dispatch |
| MOSAO | Multi-objective Snow Ablation Optimiser |
| MOSGA | Multi-Objective Search Group Algorithm |
| MOTEO | Multi-Objective Thermal Exchange optimization |
| MOWDO | Multi-Objective Wind Driven optimization |
| MPIO | Modified Pigeon-Inspired Optimization |
| MRFO | Manta Ray Foraging Optimization |
| NIDE | New Improved Differential Evolution |
| NLP | Nonlinear Programming |
| NNC | Normalized Normal Constraint |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm |
| NSHFABC | Non-Dominated Sorting Hybrid Fruit Fly-Based Artificial Bee Colony |
| OPF | Optimal Power Flow |
| PESA | Pareto Envelope-based Selection Algorithm |
| PFI | Power Flow Index |
| PFM | Penalty Function Method |
| POA | Pelican Optimization Algorithm |
| POPF | Probabilistic Optimum Power Flow |
| POSs | Pareto optimum solutions |
| PSO | Particle Swarm Optimization |
| PV | Photovoltaic |
| QO-BBO | Quasi-Oppositional Biogeography-Based Optimization |
| QP | Quadratic programming |
| RESs | Renewable Energy Sources |
| SAA | Sample Average Approximation |
| SELM | Stacked Extreme Learning Machine |
| SHO | Sea Horse Optimizer |
| SMA | Slime Mould Algorithm |
| SOCR | Second-Order Conic Relaxation |
| SOPs | Soft Open Points |
| SSA | Salp Swarm Algorithm |
| SSOA | Synergistic Swarm Optimization Algorithm |
| ST | Spatial-Temporal |
| TCSCs | Thyristor-Controlled Series Compensators |
| TSA | Time Series Aggregation |
| TW | Terawatt |
| UMGF | Universal Moment Generating Function |
| VCPSO | variable constants particle swarm optimization |
| VD | Voltage Deviation |
| VSI | Voltage Stability Index |
| WOA | Whale Optimization Algorithm |
| WT | Wind Turbine |
| WTLBO | Weighted Teaching-Learning-Based Optimization |
References
- Bollen, M.; Hassan, F. Introduction. Integration of Distributed Generation in the Power System; Hanzo, L., Abhari, R., Eds.; IEEE press on power engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 1–5. [Google Scholar]
- Grainger, J.J.; Stevenson, W.D. Power Systems Analysis; Stephen, W., Ed.; Electrical and computer engineering; McGraw-Hill: New York, NY, USA, 1994; pp. 329–376. [Google Scholar]
- Valle, Y.D.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Comp. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Liang, J.; Venayagamoorthy, G.K.; Harley, R.G. Wide-Area Measurement Based Dynamic Stochastic Optimal Power Flow Control for Smart Grids with High Variability and Uncertainty. IEEE Trans. Smart Grid 2012, 3, 59–69. [Google Scholar] [CrossRef]
- Alamo, D.H.; Medina, R.N.; Ruano, S.D.; García, S.S.; Moustris, K.P.; Kavadias, K.K.; Zafirakis, D.; Tzanes, G.; Zafeiraki, E.; Spyropoulos, G.; et al. An Advanced Forecasting System for the Optimum Energy Management of Island Microgrids. Energy Procedia 2019, 159, 111–116. [Google Scholar] [CrossRef]
- Wei, M. Multi-Objective Optimisation of Highly Distributed Power System Management. Doctorate Thesis, University of Edinburgh, Scotland, UK, 2020. [Google Scholar]
- Yan, C.; Wang, F.; Pan, Y.; Shan, K.; Kosonen, R. A multi-timescale cold storage system within energy flexible buildings for power balance management of smart grids. Renew. Energy 2020, 161, 626–634. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Elavarasan, R.M. Many-Objective Gradient-Based Optimizer to Solve Optimal Power Flow Problems: Analysis and Validations. Eng. Appl. Artif. Intell. 2021, 106, 104479. [Google Scholar] [CrossRef]
- Scheibe, C.; Kuri, A.; Feng, Y.; Zhao, L.; Xiong, X.; La Seta, P.; Liang, X.P.; Knödtel, J.; Holzinger, P.; Reichenbach, M.; et al. Interfacing Real-Time and Offline Power System Simulation Tools Using UDP or FPGA Systems. Electr. Power Syst. Res. 2022, 212, 108490. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-Objective Optimization Methods and Application in Energy Saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]
- Vallés, M.; Reneses, J.; Frías, P.; Mateo, C. Economic Benefits of Integrating Active Demand in Distribution Network Planning: A Spanish Case Study. Electr. Power Syst. Res. 2016, 136, 331–340. [Google Scholar] [CrossRef]
- Karmellos, M.; Mavrotas, G. Multi-Objective Optimization and Comparison Framework for the Design of Distributed Energy Systems. Energy Convers. Manag. 2019, 180, 473–495. [Google Scholar] [CrossRef]
- Li, B.; Zhang, J. A Review on the Integration of Probabilistic Solar Forecasting in Power Systems. Sol. Energy 2020, 210, 68–86. [Google Scholar] [CrossRef]
- Fadaee, M.; Radzi, M.A.M. Multi-Objective Optimization of a Stand-Alone Hybrid Renewable Energy System by Using Evolutionary Algorithms: A Review. Renew. Sustain. Energy Rev. 2012, 16, 3364–3369. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; Duan, Z.; Chen, C. A Review on Multi-Objective Optimization Framework in Wind Energy Forecasting Techniques and Applications. Energy Convers. Manag. 2020, 224, 113324. [Google Scholar] [CrossRef]
- Barakat, S.; Osman, A.I.; Tag-Eldin, E.; Telba, A.A.; Abdel Mageed, H.M.; Samy, M.M. Achieving Green Mobility: Multi-Objective Optimization for Sustainable Electric Vehicle Charging. Energy Strategy Rev. 2024, 53, 101351. [Google Scholar] [CrossRef]
- Khan, T.; Ullah, Z.; Agyekum, E.B.; Hasanien, H.M.; Yu, M. Multi-objective optimization of combined heat and power system integrated with multi-energy storage systems for rural communities. J. Energy Storage 2024, 99, 113433. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.; Maleki, A.; Ochbelagh, D.R. Multi-objective optimization of hybrid energy systems using gravitational search algorithm. Nat. Sci. Rep. 2025, 15, 2550. [Google Scholar] [CrossRef] [PubMed]
- Shaier, A.A.; Elymany, M.M.; Enany, M.A.; Elsonbaty, N.A. Multi-objective optimization and algorithmic evaluation for EMS in a HRES integrating PV, wind, and backup storage. Nat. Sci. Rep. 2025, 15, 1147. [Google Scholar] [CrossRef]
- Mena, R.; Hennebel, M.; Li, Y.F.; Zio, E. A multi-objective optimization framework for risk-controlled integration of renewable generation into electric power systems. Energy 2016, 106, 712–727. [Google Scholar] [CrossRef]
- Cheraghi, R.; Jahangir, M.H. Multi-objective optimization of a hybrid renewable energy system supplying a residential building using NSGA-II and MOPSO algorithms. Energy Convers. Manag. 2023, 294, 117515. [Google Scholar] [CrossRef]
- Mundra, P.; Arya, A.; Gawre, S.K. A Multi-Objective Optimization Based Optimal Reactive Power Reward for Voltage Stability Improvement in Uncertain Power System. J. Electr. Eng. Technol. 2021. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, B.; Deng, J. Multi-Objective Optimization Strategy for Distribution Network Considering V2G-Enabled Electric Vehicles in Building Integrated Energy System. Prot. Control. Mod. Power Syst. 2020, 5, 7. [Google Scholar] [CrossRef]
- Zhang, T.; Li, W.; Wang, R. Surrogated-Assisted Multimodal Multi-Objective Optimization for Hybrid Renewable Energy System. Complex Intell. Syst. 2023, 9, 4075–4087. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H. Multi-Objective Optimization and Performance Assessments of an Integrated Energy System Based on Fuel, Wind and Solar Energies. Entropy 2021, 23, 431. [Google Scholar] [CrossRef]
- Deng, H.; Xu, Y. Distributed Alternating Direction Method of Multipliers for Multi-Objective Optimization. Adv. Pure Math. 2022, 12, 249–259. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, J.; Lv, F.; Jing, W. Multi-Objective Optimization Evaluation Index System of Power System Resilience Considering Economy. In Proceedings of the CMAAE 2021: 2021 International Conference on Mechanical, Aerospace and Automotive Engineering, Changsha, China, 3–5 December 2021; pp. 20–27. [Google Scholar]
- Anoune, K.; Bouya, M.; Astito, A.; Abdellah, A. Ben Sizing Methods and Optimization Techniques for PV-Wind Based Hybrid Renewable Energy System: A Review. Renew. Sustain. Energy Rev. 2018, 93, 652–673. [Google Scholar] [CrossRef]
- Ge, X.; Ahmed, F.W.; Rezvani, A.; Aljojo, N.; Samad, S.; Foong, L.K. Implementation of a Novel Hybrid BAT-Fuzzy Controller Based MPPT for Grid-Connected PV-Battery System. Control Eng. Pract. 2020, 98. [Google Scholar] [CrossRef]
- He, P.; Fang, Q.; Jin, H.; Ji, Y.; Gong, Z.; Dong, J. Coordinated Design of PSS and STATCOM-POD Based on the GA-PSO Algorithm to Improve the Stability of Wind-PV-Thermal-Bundled Power System. Int. J. Electr. Power Energy Syst. 2022, 141, 108208. [Google Scholar] [CrossRef]
- Vadivelu, K.R.; Marutheeswar, G.V. Multi Objective Optimization Based optimal Reactive Power Planning Using Improved Differential Evolution Incorporating FACTS. Int. J. Electr. Eng. Inform. 2015, 7, 630. [Google Scholar] [CrossRef]
- Chen, W.; Ren, H.; Zhou, W. Review of multi-objective optimization in long-term energy system models. Glob. Energy Interconnect. 2023, 6, 645–666. [Google Scholar] [CrossRef]
- García-Martínez, E.; Espinosa-Juárez, S.; Pérez-Rojas, C. A Multi-Objective Optimal Reconfiguration of Electrical Networks to Improve Power Quality Aspects. In Proceedings of the IEEE International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 1–5. [Google Scholar]
- Grond, M.O.W.; Luong, N.H.; Morren, J.; Slootweg, J.G. Multi-objective optimization techniques and applications in electric power systems. In Proceedings of the IEEE 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A. Adaptive Multi Objective Parallel Seeker Optimization Algorithm for Incorporating TCSC Devices into Optimal Power Flow Framework. IEEE Access 2019, 7, 36934–36947. [Google Scholar] [CrossRef]
- Bourennani, F. Leadership-Based Multi-Objective Optimization with Applications in Energy Systems. Doctorate Thesis, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2013. [Google Scholar]
- Nallolla, C.A.; Vijayapriya, P.; Chittathuru, D.; Padmanaban, S. Multi-Objective Optimization Algorithms for a Hybrid AC/DC Microgrid Using RES: A Comprehensive Review. Electronics 2023, 12, 1062. [Google Scholar] [CrossRef]
- Ge, L.; Li, Y.; Li, Y.; Yan, J.; Sun, Y. Smart Distribution Network Situation Awareness for High-Quality Operation and Maintenance: A Brief Review. Energies 2022, 15, 828. [Google Scholar] [CrossRef]
- He, H.; Wu, K. Research on Multi-Objective Optimization of Energy Power System Under Low Carbon Constraints. J. Phys. Conf. Ser. 2023, 2442, 012022. [Google Scholar] [CrossRef]
- Alzahrani, A.; Hafeez, G.; Ali, S.; Murawwat, S.; Khan, M.I.; Rehman, K.; Abed, A.M. Multi-Objective Energy Optimization with Load and Distributed Energy Source Scheduling in the Smart Power Grid. Sustainability 2023, 15, 9970. [Google Scholar] [CrossRef]
- Rahnamafard, Y. Multi-Objective Optimization Application in Power Systems. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2019. [Google Scholar]
- Mishra, S. Multi-Objective Optimization Methods for Various Power System Problems. J. Microcontroll. Eng. Appl. 2022, 9, 35–39. [Google Scholar] [CrossRef]
- McGranaghan, M.F.; Dugan, R.C.; Beaty, H.W. Electrical Power Systems Quality; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Zaro, F.R.; Abido, M.A. Multi-Objective Particle Swarm Optimization for Optimal Power Flow in a Deregulated Environment of Power Systems. In Proceedings of the IEEE 11th International Conference on Intelligent Systems Design and Applications, Cordoba, Spain, 22–24 November 2011; pp. 1–6. [Google Scholar]
- Yahui, L.; Yang, L. Two-Step Many-Objective Optimal Power Flow Based on Knee Point-Driven Evolutionary Algorithm. Energy Econ. Environ. Ind. Prod. Process. 2018, 6, 250. [Google Scholar]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Gharibzadeh, M.; Vahed, A.A. Multi-objective optimal power flow considering the cost, emission, voltage deviation and power losses using multi-objective modified imperialist competitive algorithm. Energy 2014, 78, 276–289. [Google Scholar] [CrossRef]
- Alajmi, B.N.; AlHajri, M.F.; Ahmed, N.A.; Abdelsalam, I.; Marei, M.I. Multi-objective Optimization of Optimal Placement and Sizing of Distributed Generators in Distribution Networks. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 817–833. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wan, L.; Gu, Q. Multi-objective optimal power flow with stochastic wind and solar power. Appl. Soft Comput. 2022, 114, 108045. [Google Scholar] [CrossRef]
- Ayalew, F.; Hussen, S.; Pasam, G.K. Optimization techniques in Power System: Review. Int. J. Eng. Appl. Sci. Technol. 2019, 3, 8–16. [Google Scholar]
- Bush, B.; Chen, Y.; Ofori-Boateng, D.; Gel, Y.R. Topological Machine Learning Methods for Power System Responses to Contingencies: Preprint. Available online: https://docs.nrel.gov/docs/fy21osti/77899.pdf (accessed on 9 November 2025).
- Yaldız, A.; Gökçek, T.; Ateş, Y.; Erdinç, O. Overview and Advancement of Power System Topology Addressing Pre- and Post-Event Strategies under Abnormal Operating Conditions. Sustain. Energy Grids Netw. 2024, 40, 101562. [Google Scholar] [CrossRef]
- El Berkaoui, A.; Bahsine, S.; Oukennou, A.; Nouh, F.A.; Rzine, B. Distribution Network Topology Planning and Optimization: A Brief Review. In Proceedings of the E3S Web of Conferences; EDP Sciences, Surakarta City, Indonesia, 27–28 September 2023; Volume 469. [Google Scholar] [CrossRef]
- Hines, P.; Blumsack, S.; Sanchez, E.C.; Barrows, C. The Topological and Electrical Structure of Power Grids. In Proceedings of the Proceedings of the Annual Hawaii International Conference on System Sciences, Kauai, HI, USA, 5–8 January 2010. [Google Scholar]
- Mokryani, G. Distribution Network Types and Configurations. In Future Distribution Networks; AIP Publishing: Melville, NY, USA, 2022; pp. 1–18. [Google Scholar] [CrossRef]
- Wang, C.; An, J.; Mu, G. Power System Network Topology Identification Based on Knowledge Graph and Graph Neural Network. Front. Energy Res. 2021, 8, 613331. [Google Scholar] [CrossRef]
- GE, H.; XU, B.; CHEN, W.; ZHANG, X.; BI, Y. Topology Identification of Low Voltage Distribution Network Based on Current Injection Method. Arch. Electr. Eng. 2021, 70, 297–306. [Google Scholar] [CrossRef]
- Luan, W.; Xu, D.; Liu, B.; Jiang, W.; Feng, L.; Liu, W. Improved Topology Identification for Distribution Network with Relatively Balanced Power Supplies. IET Energy Syst. Integr. 2024, 6, 162–173. [Google Scholar] [CrossRef]
- Cavraro, G.; Kekatos, V.; Zhang, L.; Giannakis, G.B. Learning Power Grid Topologies. In Advanced Data Analytics for Power Systems; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Zhu, J.; Member, S.; Hwang, A. Sadjadpour, Real Time Congestion Monitoring and Management of Power Systems. In Proceedings of the 2005 IEEE/PES Transmission & Distribution Conference & Exposition: Asia and Pacific, Dalian, China, 15–18 August 2005. [Google Scholar]
- Nyingu, B.T.; Masike, L.; Mbukani, M.W.K. Optimal Sizing of Residential Photovoltaic (PV)—Battery Power System in an Off-grid Configuration. In Proceedings of the IEEE PES/IAS PowerAfrica, Johannesburg, South Africa, 7–10 October 2024. [Google Scholar]
- Bre, F.; Fachinotti, V.D. A Computational Multi-Objective Optimization Method to Improve Energy Efficiency and Thermal Comfort in Dwellings. Energy Build. 2017, 154, 283–294. [Google Scholar] [CrossRef]
- Kuroda, K.; Magori, H.; Ichimura, T.; Yokoyama, R. A Hybrid Multi-Objective Optimization Method Considering Optimization Problems in Power Distribution Systems. J. Mod. Power Syst. Clean Energy 2015, 3, 41–50. [Google Scholar] [CrossRef]
- Finke, J.; Bertsch, V. Implementing a Highly Adaptable Method for the Multi-Objective Optimization of Energy Systems. 2022. Available online: https://mpra.ub.uni-muenchen.de/115504/ (accessed on 9 November 2025).
- Subramanyan, K.; Diwekar, U.M.; Goyal, A. Multi-Objective Optimization for Hybrid Fuel Cells Power System under Uncertainty. J. Power Sources 2004, 132, 99–112. [Google Scholar] [CrossRef]
- Crespo-Sánchez, G.; Pérez-Abril, I. Multi-Objective Reconfiguration of the Distribution Systems by Using NSGA-II and Local Improvement. Dyna 2023, 90, 89–96. [Google Scholar] [CrossRef]
- Pathe, S.; Bertsch, V. Multi-Objective Energy System Modeling of the Rhenish Mining Area Minimizing Costs and Environmental Impacts. In Proceedings of the International Conference on Applied Energy, Bangkok, Thailand, 29 November–5 December 2021. [Google Scholar]
- Pindoriya, N.M.; Singh, S.N.; Lee, K.Y. A Comprehensive Survey on Multi-objective Evolutionary Optimization in Power System Applications. In Proceedings of the IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Muralitharan, K.; Sakthivel, R.; Shi, Y. Multi-objective Optimization Technique for Demand Side Management with Load Balancing Approach in Smart Grid. Neurocomputing 2016, 177, 110–119. [Google Scholar] [CrossRef]
- Kheiri, F. A Review on Optimization Methods Applied in Energy-Efficient Building Geometry and Envelope Design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Elkholy, A.M.; Panfilov, D.I.; ELGebaly, A.E. Comparative Analysis of FACT Devices for Optimal Improvement of Power Quality in Unbalanced Distribution Systems. Sci. Rep. 2025, 15, 2672. [Google Scholar] [CrossRef] [PubMed]
- Farhat, M.; Kamel, S.; Abdelaziz, A.Y. Modified Tasmanian Devil Optimization for Solving Single and Multi-Objective Optimal Power Flow in Conventional and Advanced Power Systems. Cluster Comput. 2025, 28, 105. [Google Scholar] [CrossRef]
- Güven, A.F.; Yörükeren, N.; Mengi, O.Ö. Multi-Objective Optimization and Sustainable Design: A Performance Comparison of Metaheuristic Algorithms Used for on-Grid and off-Grid Hybrid Energy Systems. Neural Comput. Appl. 2024, 36, 7559–7594. [Google Scholar] [CrossRef]
- Risi, B.G.; Riganti-Fulginei, F.; Laudani, A. Modern Techniques for the Optimal Power Flow Problem: State of the Art. Energies 2022, 15, 6387. [Google Scholar] [CrossRef]
- Siddaiah, R.; Saini, R.P. A Review on Planning, Configurations, Modeling and Optimization Techniques of Hybrid Renewable Energy Systems for off Grid Applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
- Rajput, S.K.; Dheer, D.K. Forecasting Power-Factor Reductions in Rooftop PV-Integrated Industrial Power Systems: Mathematical Modelling and Experimental Validation. Sustain. Energy Grids Netw. 2023, 33, 100974. [Google Scholar] [CrossRef]
- Sharafi, M.; ElMekkawy, T.Y. Stochastic Optimization of Hybrid Renewable Energy Systems Using Sampling Average Method. Renew. Sustain. Energy Rev. 2015, 52, 1668–1679. [Google Scholar] [CrossRef]
- Yang, J.; Su, C. Robust Optimization of Microgrid Based on Renewable Distributed Power Generation and Load Demand Uncertainty. Energy 2021, 223, 120043. [Google Scholar] [CrossRef]
- Rivas-Dávalos, F.; Moreno-Goytia, E.; Gutiérrez-Alacaraz, G.; Tovar-Hernández, J. Evolutionary Multi-Objective Optimization in Power Systems: State-of-the-Art. In Proceedings of the IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; Volume 451. [Google Scholar]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Bansal, R.C. Optimization Methods for Electric Power Systems: An Overview. Int. J. Emerg. Electr. Power Syst. 2005, 2, 1–23. [Google Scholar] [CrossRef]
- Frank, S.; Rebennack, S. An introduction to optimal power flow: Theory, formulation, and examples. IIE Trans. Oper. Eng. Anal. 2016, 48, 1172–1197. [Google Scholar] [CrossRef]
- Zhu, J. Optimization of Power System Operation; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Mangasarian, O.L. A Newton Method for Linear Programming. J. Optim. Theory Appl. 2004, 121, 1–18. [Google Scholar] [CrossRef]
- Özlü, I.A.; Baimakhanov, O.; Saukhimov, A.; Ceylan, O. A Heuristic Methods-Based Power Distribution System Optimization Toolbox. Algorithms Plan. Oper. Power Syst. 2021, 15, 14. [Google Scholar] [CrossRef]
- Gavrilas, M. Heuristic and metaheuristic optimization techniques with application to power systems. In Proceedings of the 12th WSEAS International Conference on Mathem Methods And Comput Techniques in Electrical Engineer, Timișoara, Romania, 21–23 October 2010; pp. 1–10. [Google Scholar]
- Shaheen, A.M.; Spea, S.R.; Farrag, S.M.; Abido, M.A. A review of meta-heuristic algorithms for reactive power planning problem. Ain Shams Eng. J. 2018, 9, 215–231. [Google Scholar] [CrossRef]
- Eriksson, E.L.V.; Gray, E.M.A. Optimization of Renewable Hybrid Energy Systems—A Multi-Objective Approach. Renew. Energy 2019, 133, 971–999. [Google Scholar] [CrossRef]
- Dang, J.; Zhang, S.; Wang, Y.; Yan, Y.; Jia, R.; Liu, G. Multi-Objective Power Supply Restoration in Distribution Networks Based on Graph Calculation and Information Collected by Multi-Source Sensors. Sensors 2025, 25, 768. [Google Scholar] [CrossRef]
- Liang, R.H.; Wu, C.Y.; Chen, Y.T.; Tseng, W.T. Multi-Objective Dynamic Optimal Power Flow Using Improved Artificial Bee Colony Algorithm Based on Pareto Optimization. Int. Trans. Electr. Energy Syst. 2016, 26, 692–712. [Google Scholar] [CrossRef]
- Jamal, R.; Zhang, J.; Men, B.; Khan, N.H.; Ebeed, M.; Kamel, S. Solution to the Deterministic and Stochastic Optimal Reactive Power Dispatch by Integration of Solar, Wind-Hydro Powers Using Modified Artificial Hummingbird Algorithm. Energy Rep. 2023, 9, 4157–4173. [Google Scholar] [CrossRef]
- Bauer, R.; Mühlpfordt, T.; Ludwig, N.; Hagenmeyer, V. Analytical Uncertainty Propagation for Multi-Period Stochastic Optimal Power Flow. Sustain. Energy Grids Netw. 2023, 33, 100969. [Google Scholar] [CrossRef]
- Fathy, A.; Yousri, D.; Abdelaziz, A.Y.; Ramadan, H.S. Robust Approach Based Chimp Optimization Algorithm for Minimizing Power Loss of Electrical Distribution Networks via Allocating Distributed Generators. Sustain. Energy Technol. Assess. 2021, 47, 101359. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. Solving Optimal Power Flow Problem with Stochastic Wind–Solar–Small Hydro Power Using Barnacles Mating Optimizer. Control Eng. Pract. 2021, 106, 104672. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal Power Flow Solutions Using Differential Evolution Algorithm Integrated with Effective Constraint Handling Techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Grangereau, M.; van Ackooij, W.; Gaubert, S. Multi-Stage Stochastic Alternating Current Optimal Power Flow with Storage: Bounding the Relaxation Gap. Electr. Power Syst. Res. 2022, 206, 107774. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Wang, L.; Yan, X.; Hu, C. Optimal Power Flow by Means of Improved Adaptive Differential Evolution. Energy 2020, 198, 117314. [Google Scholar] [CrossRef]
- Grover-Silva, E.; Heleno, M.; Mashayekh, S.; Cardoso, G.; Girard, R.; Kariniotakis, G. A Stochastic Optimal Power Flow for Scheduling Flexible Resources in Microgrids Operation. Appl. Energy 2018, 229, 201–208. [Google Scholar] [CrossRef]
- Grover-Silva, E.; Girard, R.; Kariniotakis, G. Optimal Sizing and Placement of Distribution Grid Connected Battery Systems through an SOCP Optimal Power Flow Algorithm. Appl. Energy 2018, 219, 385–393. [Google Scholar] [CrossRef]
- Lai, L.L.; Ma, J.T.; Yokoyama, R.; Zhao, M. Improved Genetic Algorithms for Optimal Power Flow under Both Normal and Contingent Operation States. Int. J. Electr. Power Energy Syst. 1997, 19, 287–292. [Google Scholar] [CrossRef]
- Abaci, K.; Yamacli, V. Differential Search Algorithm for Solving Multi-Objective Optimal Power Flow Problem. Int. J. Electr. Power Energy Syst. 2016, 79, 1–10. [Google Scholar] [CrossRef]
- Costa, A.L.; Costa, A.S. Energy and Ancillary Service Dispatch through Dynamic Optimal Power Flow. Electr. Power Syst. Res. 2007, 77, 1047–1055. [Google Scholar] [CrossRef]
- Adhikari, A.; Jurado, F.; Naetiladdanon, S.; Sangswang, A.; Kamel, S.; Ebeed, M. Stochastic Optimal Power Flow Analysis of Power System with Renewable Energy Sources Using Adaptive Lightning Attachment Procedure Optimizer. Int. J. Electr. Power Energy Syst. 2023, 153, 109314. [Google Scholar] [CrossRef]
- Surender Reddy, S.; Srinivasa Rathnam, C. Optimal Power Flow Using Glowworm Swarm Optimization. Int. J. Electr. Power Energy Syst. 2016, 80, 128–139. [Google Scholar] [CrossRef]
- Kumar, S.; Chaturvedi, D.K. Optimal Power Flow Solution Using Fuzzy Evolutionary and Swarm Optimization. Int. J. Electr. Power Energy Syst. 2013, 47, 416–423. [Google Scholar] [CrossRef]
- Ali, S.S.; Choi, B.J. State-of-the-Art Artificial Intelligence Techniques for Distributed Smart Grids: A Review. Electronics 2020, 9, 1030. [Google Scholar] [CrossRef]
- Li, Y. Advanced Intelligent Optimization Algorithms for Multi-Objective Optimal Power Flow in Future Power Systems: A Review. arXiv 2024, arXiv:2404.09203. [Google Scholar] [CrossRef]
- Lissa, P.; Deane, C.; Schukat, M.; Seri, F.; Keane, M.; Barrett, E. Deep Reinforcement Learning for Home Energy Management System Control. Energy AI 2021, 3, 100043. [Google Scholar] [CrossRef]
- Sun, B.; Song, M.; Li, A.; Zou, N.; Pan, P.; Lu, X.; Yang, Q.; Zhang, H.; Kong, X. Multi-Objective Solution of Optimal Power Flow Based on TD3 Deep Reinforcement Learning Algorithm. Sustain. Energy Grids Netw. 2023, 34, 101054. [Google Scholar] [CrossRef]
- Al Khafaf, N.; Wang, J.; Jalili, M.; Sokolowski, P. A Deep Learning Approach for Detecting Distributed Generation in Residential Customers. Sustain. Energy Grids Netw. 2023, 33, 100966. [Google Scholar] [CrossRef]
- Rocha, H.R.O.; Honorato, I.H.; Fiorotti, R.; Celeste, W.C.; Silvestre, L.J.; Silva, J.A.L. An Artificial Intelligence Based Scheduling Algorithm for Demand-Side Energy Management in Smart Homes. Appl. Energy 2021, 282, 116145. [Google Scholar] [CrossRef]
- Huang, N.; Wang, S.; Wang, R.; Cai, G.; Liu, Y.; Dai, Q. Gated Spatial-Temporal Graph Neural Network Based Short-Term Load Forecasting for Wide-Area Multiple Buses. Int. J. Electr. Power Energy Syst. 2023, 145, 108651. [Google Scholar] [CrossRef]
- Jackson, D.; Belakaria, S.; Cao, Y.; Doppa, J.R.; Lu, X. Machine Learning Enabled Design Automation and Multi-Objective Optimization for Electric Transportation Power Systems. IEEE Trans. Transp. Electrif. 2022, 8, 1467–1481. [Google Scholar] [CrossRef]
- Judge, M.A.; Franzitta, V.; Curto, D.; Guercio, A.; Cirrincione, G.; Khattak, H.A. A Comprehensive Review of Artificial Intelligence Approaches for Smart Grid Integration and Optimization. Energy Convers. Manag. X 2024, 24, 100724. [Google Scholar] [CrossRef]
- Abraham, A.; Jain, L.; Goldberg, R. Evolutionary Multi-objective Optimization: Theoretical Advances and Applications; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Zhang, M.; Li, Y. Multi-Objective Optimal Reactive Power Dispatch of Power Systems by Combining Classification- Based Multi-Objective Evolutionary Algorithm and Integrated Decision Making. IEEE Access Artif. Intell. Technol. Electr. Power Syst. 2020, 8, 38198–38209. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, H.M. Evaluation of Multi-Objective Optimization Techniques for Resilience Enhancement of Electric Vehicles. Electronics 2021, 10, 3030. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms. Soft Comput. Fusion. Found. Methodol. Appl. 2020, 24, 2999–3023. [Google Scholar] [CrossRef]
- Avvari, R.K.; Kumar, D.M.V. Multi-Objective Optimal Power Flow including Wind and Solar Generation Uncertainty Using New Hybrid Evolutionary Algorithm with Efficient Constraint Handling Method. Int. Trans. Electr. Energy Syst. 2022, 2022, 7091937. [Google Scholar] [CrossRef]
- Zhang, B.; Che, A. An Enhanced Decomposition-Based Multi-Objective Evolutionary Algorithm with Neighborhood Search for Multi-Resource Constrained Job Shop Scheduling Problem. Swarm Evol. Comput. 2025, 93, 101834. [Google Scholar] [CrossRef]
- Zainal, M.I.; Yasin, Z.M.; Zakaria, Z. Optimizing Voltage Profile and Loss Minimization using Cuckoo Search Algorithm. In Proceedings of the 11th IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 3–4 April 2021; pp. 1–7. [Google Scholar]
- Ang, S.; Leeton, U.; Kulworawanichpong, T.; Chayakulkeeree, K. Multi-Objective Real Power Loss and Voltage Deviation Minimization for Grid Connected Micro Power System Using Whale Optimization Algorithm. Int. Energy J. 2018, 18, 297–310. [Google Scholar]
- Rajalashmi, K.; Prabha, S.U. Hybrid Swarm Algorithm for Multiobjective Optimal Power Flow Problem. Circuits Syst. 2016, 7, 3589–3603. [Google Scholar] [CrossRef]
- Muangkhiew, P.; Chayakulkheeree, K. Multi-Objective Optimal Power Flow Using Fuzzy Satisfactory Stochastic Optimization. Int. Energy J. 2022, 22, 281–290. [Google Scholar]
- Prioste, F.B. Optimal Power Flow Using Genetic Algorithm. Soc. Bras. Inteligência Comput. 2021, SC2021, 1–6. [Google Scholar]
- Arouna, O.; Imano, A.M.; Maurel, A.G.; Antoine, V.; Mitterand, D.; François-Xavier, F.; Ramanou, B.; Herman, T. Multi-objective Optimization of the Voltage Static Stability Margin of a Distribution Network by Genetic Algorithms. Am. J. Eng. Res. (AJER) 2020, 9, 155–165. Available online: https://www.ajer.org/papers/certificates/vol9(4)/AJER-17.pdf (accessed on 9 November 2025).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multi-Objective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-Objective Optimization Using Genetic Algorithms: A Tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Naderi, E.; Narimani, H.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Marzband, M.; Lehtonen, M. State-of-the-Art of Optimal Active and Reactive Power Flow: A Comprehensive Review from Various Standpoints. Processes 2021, 9, 1319. [Google Scholar] [CrossRef]
- Mallala, B.; Papana, V.P.; Sangu, R.; Palle, K.; Chinthalacheruvu, V.K.R. Multi-Objective Optimal Power Flow Solution Using a Non-Dominated Sorting Hybrid Fruit Fly-Based Artificial Bee Colony. J. Energ. 2022, 15, 4063. [Google Scholar] [CrossRef]
- Huy, T.H.B.; Kim, D.; Vo, D.N. Multi-objective Optimal Power Flow Using Multi-Objective Search Group Algorithm. IEEE Access 2022, 10, 77837–77856. [Google Scholar] [CrossRef]
- Li, N.; Zhou, G.; Zhou, Y.; Deng, W.; Luo, Q. Multi-objective pathfinder algorithm for multi-objective optimal power flow problem with random renewable energy sources: Wind, photovoltaic and tidal. Sci. Rep. 2023, 13, 10647. [Google Scholar] [CrossRef]
- Islam, M.Z.; Wahab, N.I.A.; Veerasamy, V.; Hizam, H.; Mailah, N.F.; Guerrero, J.M.; Nasir, M.N.M. A Harris Hawks Optimization Based Single- and Multi-Objective Optimal Power Flow Considering Environmental Emission. Sustainability 2020, 12, 5248. [Google Scholar] [CrossRef]
- Lei, X.; Yang, Z.; Yu, J.; Zhao, J.; Gao, Q.; Yu, H. Data-driven Optimal Power Flow: A Physics-Informed Machine Learning Approach. IEEE Trans. Power Syst. 2021, 36, 346–354. [Google Scholar] [CrossRef]
- Li, J.; Zhang, R.; Wang, H.; Liu, Z.; Lai, H.; Zhang, Y. Deep Reinforcement Learning for Optimal Power Flow with Renewables Using Spatial-Temporal Graph Information. J. Latex Cl. Files 2021, 14, 1–11. [Google Scholar]
- Balasubbareddy, M.; Dwivedi, D.; Prasad, P.V. Optimal power flow solution using HFSS Algorithm. J. Electr. Electron. Eng. Res. 2023, 12, 1–11. [Google Scholar] [CrossRef]
- Al-Kaabi, M.; Dumbrava, V.; Eremia, M. A Slime Mould Algorithm Programming for Solving Single and Multi-Objective Optimal Power Flow Problems with Pareto Front Approach: A Case Study of the Iraqi Super Grid High Voltage. Energies 2022, 15, 1–33. [Google Scholar] [CrossRef]
- Hilawie, A.; Shewarega, F. Improved Multi Objective Particle Swarm Optimization Based Reactive Power Optimization for Ensuring Voltage Security of Power Systems. Eng. Res. Express 2023, 4, 045062. [Google Scholar] [CrossRef]
- Yalcinoz, T.; Rudion, K. Multi-Objective Environmental-Economic Load Dispatch Considering Generator Constraints and Wind Power Using Improved Multi-Objective Particle Swarm Optimization. Adv. Electr. Comput. Eng. 2020, 20, 3–10. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal Reactive Power Dispatch for Real Power Loss Minimization and Voltage Stability Enhancement Using Artificial Bee Colony Algorithm. Microprocess. Microsyst. 2020, 76, 103085. [Google Scholar] [CrossRef]
- Prajapati, B.S.; Srivastava, L. Multi-objective reactive power optimization using Artificial Bee Colony Algorithm. Int. J. Eng. Innov. Technol. (IJEIT) 2012, 2, 126–131. [Google Scholar]
- Rezaei Adaryani, M.; Karami, A. Artificial Bee Colony Algorithm for Solving Multi-Objective Optimal Power Flow Problem. Int. J. Electr. Power Energy Syst. 2013, 53, 219–230. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, X.; Wang, F.; Mao, Y. Multi-Objective Optimal Power Flow Problem Using Constrained Dynamic Multitasking Multi-Objective Optimization Algorithm. Swarm Evol. Comput. 2025, 93, 101850. [Google Scholar] [CrossRef]
- Yin, L.; Sun, Z. Distributed Multi-Objective Grey Wolf Optimizer for Distributed Multi-Objective Economic Dispatch of Multi-Area Interconnected Power Systems. Appl. Soft Comput. 2022, 117, 108345. [Google Scholar] [CrossRef]
- Chen, G.; Qian, J.; Zhang, Z.; Li, S. Application of Modified Pigeon-Inspired Optimization Algorithm and Constraint-Objective Sorting Rule on Multi-Objective Optimal Power Flow Problem. Appl. Soft Comput. J. 2020, 92, 106321. [Google Scholar] [CrossRef]
- Rezaeian-Marjani, S.; Ebrahimi, H.; Tousi, B. Probabilistic Multi-Objective Optimization Method for Interline Power Flow Controller (IPFC) Allocation in Power Systems. IET Gener. Transm. Distrib. 2022, 16, 4951–4962. [Google Scholar] [CrossRef]
- Praveen, J.; Rao, B.S. Multi-Objective Optimization for Optimal Power Flow with IPFC using PSO. In Proceedings of the 3rd International Conference on Electrical Energy Systems (ICEES), Chennai, India, 17–19 March 2016. [Google Scholar]
- Guerraiche, K.; Dekhici, L.; Chatelet, E.; Zeblah, A. Multi-Objective Electrical Power System Design Optimization Using a Modified Bat Algorithm. Energies 2021, 14, 3956. [Google Scholar] [CrossRef]
- Zhao, Y.; Xue, Y.; Zhang, R.; Yin, J.; Yang, Y.; Chen, Y. Multi-Objective Optimization Operation of Multi-Agent Active Distribution Network Based on Analytical Target Cascading Method. Energies 2024, 17, 5022. [Google Scholar] [CrossRef]
- Alsokhiry, F. Leveraging Harris Hawks Optimization for Enhanced Multi-Objective Optimal Power Flow in Complex Power Systems. Energies 2025, 18, 18. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Arasteh, H.; Shafiekhani, M.; Kia, M.; Guerrero, J.M. Multi-Objective Operation of Microgrids Based on Electrical and Thermal Flexibility Metrics Using the NNC and IGDT Methods. Int. J. Electr. Power Energy Syst. 2023, 144, 108617. [Google Scholar] [CrossRef]
- HASHEMI, S.I.N.A.; LESANI, H.; AGHAMOHAMMADI, M.R. An Integrated Approach for Incorporation of Voltage and Transient Stabilities into Optimal Power Flow Study. Electr. Power Syst. Res. 2022, 206, 107784. [Google Scholar] [CrossRef]
- Kharrich, M.; Mohammed, O.H.; Alshammari, N.; Akherraz, M. Multi-Objective Optimization and the Effect of the Economic Factors on the Design of the Microgrid Hybrid System. Sustain. Cities Soc. 2021, 65, 102646. [Google Scholar] [CrossRef]
- Choobineh, M.; Mohagheghi, S. A Multi-Objective Optimization Framework for Energy and Asset Management in an Industrial Microgrid. J. Clean. Prod. 2016, 139, 1326–1338. [Google Scholar] [CrossRef]
- Aghajani, G.; Ghadimi, N. Multi-Objective Energy Management in a Micro-Grid. Energy Rep. 2018, 4, 218–225. [Google Scholar] [CrossRef]
- Reina, J.; Ortiz, R.; Lopez-Santiago, D.M. Multi-Objective Optimization of Multi-Energy Systems Planning in Remote Zones: The Bahía Málaga Colombian Case. DYNA 2023, 90, 56–65. [Google Scholar] [CrossRef]
- Hassan, A.S.; Sun, Y.; Wang, Z. Multi-Objective for Optimal Placement and Sizing DG Units in Reducing Loss of Power and Enhancing Voltage Profile Using BPSO-SFLA. Energy Rep. 2020, 6, 1581–1589. [Google Scholar] [CrossRef]
- Oloulade, A.; Imano, A.M.; Fifatin, X.; Vianou, A.; Tamadaho, H.; Badarou, R. Multi-Objective Optimization of the Safe Operation of the Electrical Distribution System by Placing D-FACTS and Network Reconfiguration. J. Power Energy Eng. 2019, 7, 94–113. [Google Scholar] [CrossRef]
- Vaithiyanathan, V.; Mani, V.; Govindasamy, S.; Selvaraj, J. A Multi-Objective Time–Series Optimization for Optimum Planning Design of Integrative Power System with the Effects of Multi-Dimensional Sources of Uncertainty. Electr. Power Compon. Syst. 2024, 52, 891–904. [Google Scholar] [CrossRef]
- Naderi, E.; Mirzaei, L.; Trimble, J.P.; Cantrell, D.A. Multi-Objective Optimal Power Flow Incorporating Flexible Alternating Current Transmission Systems: Application of a Wavelet-Oriented Evolutionary Algorithm. Electr. Power Compon. Syst. 2024, 52, 766–795. [Google Scholar] [CrossRef]
- Ermiş, S. Multi-Objective Optimal Power Flow Using a Modified Weighted Teaching-Learning Based Optimization Algorithm. Electr. Power Compon. Syst. 2023, 51, 2536–2556. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S.S. Multi-Objective Optimal Power Flow Using Biogeography-Based Optimization. Electr. Power Compon. Syst. 2010, 38, 1406–1426. [Google Scholar] [CrossRef]
- Roy, P.K.; Mandal, D. Quasi-Oppositional Biogeography-Based Optimization for Multi-Objective Optimal Power Flow. Electr. Power Compon. Syst. 2011, 40, 236–256. [Google Scholar] [CrossRef]
- Zhu, J.H.; Wang, J.S.; Zhang, X.Y.; Wang, Y.C.; Song, H.M.; Zheng, Y.; Liu, X. Multi-Objective Coyote Optimization Algorithm Based on Hybrid Elite Framework and Meta-Lamarckian Learning Strategy for Optimal Power Flow Problem. Artif. Intell. Rev. 2024, 57, 117. [Google Scholar] [CrossRef]
- Roselyn, J.P.; Devaraj, D. Adaptive Multi Objective Differential Evolution with Fuzzy Decision Making in Preventive and Corrective Control Approaches for Voltage Security Enhancement. J. Franklin Inst. 2018, 355, 4553–4582. [Google Scholar] [CrossRef]
- Naderi, E.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Lehtonen, M. A Novel Hybrid Self-Adaptive Heuristic Algorithm to Handle Single- and Multi-Objective Optimal Power Flow Problems. Int. J. Electr. Power Energy Syst. 2021, 125, 106492. [Google Scholar] [CrossRef]
- Jiekang, W.; Zhuangzhi, G.; Fan, W. Short-Term Multi-Objective Optimization Scheduling for Cascaded Hydroelectric Plants with Dynamic Generation Flow Limit Based on EMA and DEA. Int. J. Electr. Power Energy Syst. 2014, 57, 189–197. [Google Scholar] [CrossRef]
- Li, J.; Wen, M.; Zhou, Z.; Wen, B.; Yu, Z.; Liang, H.; Zhang, X.; Qin, Y.; Xu, C.; Huang, H. Multi-Objective Optimization Method for Power Supply and Demand Balance in New Power Systems. Int. J. Electr. Power Energy Syst. 2024, 161, 110204. [Google Scholar] [CrossRef]
- Ali, S.; Ullah, K.; Hafeez, G.; Khan, I.; Albogamy, F.R.; Haider, S.I. Solving Day-Ahead Scheduling Problem with Multi-Objective Energy Optimization for Demand Side Management in Smart Grid. Eng. Sci. Technol. Int. J. 2022, 36, 101135. [Google Scholar] [CrossRef]
- Falke, T.; Krengel, S.; Meinerzhagen, A.K.; Schnettler, A. Multi-Objective Optimization and Simulation Model for the Design of Distributed Energy Systems. Appl. Energy 2016, 184, 1508–1516. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Li, Y. Research and Application of a Hybrid Forecasting Framework Based on Multi-Objective Optimization for Electrical Power System. Energy 2018, 148, 59–78. [Google Scholar] [CrossRef]
- Akdag, O. A Improved Archimedes Optimization Algorithm for Multi/Single-Objective Optimal Power Flow. Electr. Power Syst. Res. 2022, 206, 107796. [Google Scholar] [CrossRef]
- Premkumar, M.; Hashim, T.J.T.; Ravichandran, S.; Sin, T.C.; Chandran, R.; Alsoud, A.R.; Jangir, P. Optimal Operation and Control of Hybrid Power Systems with Stochastic Renewables and FACTS Devices: An Intelligent Multi-Objective Optimization Approach. Alex. Eng. J. 2024, 93, 90–113. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, C.; Ma, J.; Qiu, W.; Liu, S.; Lin, Z.; Qian, M.; Zhu, L.; Zhao, D. Multi-Objective Optimization Strategy of Multi-Sources Power System Operation Based on Fuzzy Chance Constraint Programming and Improved Analytic Hierarchy Process. Energy Rep. 2021, 7, 268–274. [Google Scholar] [CrossRef]
- Abubakar, A.; Mohammad, M.B. Multi-Objective Genetic Algorithm Optimization of Thermal Limit Parameters for Low-Frequency Oscillation Control in Power Systems. Int. J. Res. Innov. Appl. Sci. 2024, 9, 536–540. [Google Scholar] [CrossRef]
- Nwachukwu, T.; Ranade, S.; Rawn, B. Exploring Multi-Objective Transmission Planning for Investment-Constrained Power Systems. In Proceedings of the IEEE PowerAfrica Conference, Venue, Virtual, 25–28 August 2020. [Google Scholar]
- Wang, Z.; Zhang, Z.; Luo, F.; Qiu, X.; Zhang, X.; Duan, J. Optimal Configuration of Soft Open Point and Energy Storage Based on Snowflake-Shaped Grid Characteristics and Sensitivity Analysis. Appl. Sci. 2024, 14, 503. [Google Scholar] [CrossRef]
- Pandya, S.B.; Ravichandran, S.; Manoharan, P.; Jangir, P.; Alhelou, H.H. Multi-Objective Optimization Framework for Optimal Power Flow Problem of Hybrid Power Systems Considering Security Constraints. IEEE Access 2022, 10, 103509–103528. [Google Scholar] [CrossRef]
- Akbel, M.; Kahraman, H.T.; Duman, S.; Temel, S. A Clustering-Based Archive Handling Method and Multi-Objective Optimization of the Optimal Power Flow Problem. Appl. Intell. 2024, 54, 11603–11648. [Google Scholar] [CrossRef]
- Chew, B.S.H.; Xu, Y.; Wu, Q. Voltage Balancing for Bipolar DC Distribution Grids: A Power Flow Based Binary Integer Multi-Objective Optimization Approach. IEEE Trans. Power Syst. 2019, 34, 28–39. [Google Scholar] [CrossRef]
- Chen, H.; Gao, L.; Zhang, Z. Multi-Objective Optimal Scheduling of a Microgrid with Uncertainties of Renewable Power Generation Considering User Satisfaction. Int. J. Electr. Power Energy Syst. 2021, 131, 107142. [Google Scholar] [CrossRef]
- Liu, Y.; Ćetenović, D.; Li, H.; Gryazina, E.; Terzija, V. An Optimized Multi-Objective Reactive Power Dispatch Strategy Based on Improved Genetic Algorithm for Wind Power Integrated Systems. Int. J. Electr. Power Energy Syst. 2022, 136, 107764. [Google Scholar] [CrossRef]
- Aghajani, G.R.; Shayanfar, H.A.; Shayeghi, H. Presenting a Multi-Objective Generation Scheduling Model for Pricing Demand Response Rate in Micro-Grid Energy Management. Energy Convers. Manag. 2015, 106, 308–321. [Google Scholar] [CrossRef]
- Ghiasi, M. Detailed Study, Multi-Objective Optimization, and Design of an AC-DC Smart Microgrid with Hybrid Renewable Energy Resources. Energy 2019, 169, 496–507. [Google Scholar] [CrossRef]
- Agrawal, S.; Pandya, S.; Jangir, P.; Kalita, K.; Chakraborty, S. A Multi-Objective Thermal Exchange Optimization Model for Solving Optimal Power Flow Problems in Hybrid Power Systems. Decis. Anal. J. 2023, 8, 100299. [Google Scholar] [CrossRef]
- Morshed, M.J.; Ben Hmida, J.; Fekih, A. A Probabilistic Multi-Objective Approach for Power Flow Optimization in Hybrid Wind-PV-PEV Systems. Appl. Energy 2018, 211, 1136–1149. [Google Scholar] [CrossRef]
- Roberts, J.J.; Marotta Cassula, A.; Silveira, J.L.; da Costa Bortoni, E.; Mendiburu, A.Z. Robust Multi-Objective Optimization of a Renewable Based Hybrid Power System. Appl. Energy 2018, 223, 52–68. [Google Scholar] [CrossRef]
- Wang, R.; Xiong, J.; He, M.; Gao, L.; Wang, L. Multi-Objective Optimal Design of Hybrid Renewable Energy System under Multiple Scenarios. Renew. Energy 2020, 151, 226–237. [Google Scholar] [CrossRef]
- Wang, R.; Li, G.; Ming, M.; Wu, G.; Wang, L. An Efficient Multi-Objective Model and Algorithm for Sizing a Stand-Alone Hybrid Renewable Energy System. Energy 2017, 141, 2288–2299. [Google Scholar] [CrossRef]
- Sarshar, J.; Moosapour, S.S.; Joorabian, M. Multi-Objective Energy Management of a Micro-Grid Considering Uncertainty in Wind Power Forecasting. Energy 2017, 139, 680–693. [Google Scholar] [CrossRef]
- Mayer, M.J.; Szilágyi, A.; Gróf, G. Environmental and Economic Multi-Objective Optimization of a Household Level Hybrid Renewable Energy System by Genetic Algorithm. Appl. Energy 2020, 269, 115058. [Google Scholar] [CrossRef]
- Liu, Z.F.; Li, L.L.; Liu, Y.W.; Liu, J.Q.; Li, H.Y.; Shen, Q. Dynamic Economic Emission Dispatch Considering Renewable Energy Generation: A Novel Multi-Objective Optimization Approach. Energy 2021, 235, 121407. [Google Scholar] [CrossRef]
- Elattar, E.E.; ElSayed, S.K. Modified JAYA Algorithm for Optimal Power Flow Incorporating Renewable Energy Sources Considering the Cost, Emission, Power Loss and Voltage Profile Improvement. Energy 2019, 178, 598–609. [Google Scholar] [CrossRef]
- Alzahrani, A.; Rahman, M.U.; Hafeez, G.; Rukh, G.; Ali, S.; Murawwat, S.; Iftikhar, F.; Haider, S.I.; Khan, M.I.; Abed, A.M. A Strategy for Multi-Objective Energy Optimization in Smart Grid Considering Renewable Energy and Batteries Energy Storage System. IEEE Access 2023, 11, 33872–33886. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; De Stasio, C.; Mauro, G.M.; Vanoli, G.P. Multi-Objective Optimization of the Renewable Energy Mix for a Building. Appl. Therm. Eng. 2016, 101, 612–621. [Google Scholar] [CrossRef]
- Bandaru, S.; Ng, A.H.C.; Deb, K. Data Mining Methods for Knowledge Discovery in Multi-Objective Optimization: Part A—Survey. Expert. Syst. Appl. 2017, 70, 139–159. [Google Scholar] [CrossRef]
- Ida Evangeline, S.; Rathika, P. Wind Farm Incorporated Optimal Power Flow Solutions through Multi-Objective Horse Herd Optimization with a Novel Constraint Handling Technique. Expert. Syst. Appl. 2022, 194, 116544. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, L.; Xing, Z.; Jiang, Z.; Xu, J. Multi-Objective Coordinated Optimization of Power System with Wind Power Accommodation. Energy Rep. 2022, 8, 188–195. [Google Scholar] [CrossRef]
- Nagarajan, K.; Rajagopalan, A.; Bajaj, M.; Raju, V.; Blazek, V. Enhanced Wombat Optimization Algorithm for Multi-Objective Optimal Power Flow in Renewable Energy and Electric Vehicle Integrated Systems. Results Eng. 2025, 25, 103671. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. A Probabilistic Multi-Objective Approach for Power Flow Optimization in Hybrid Wind-Based Power Systems Using Grasshopper Optimization Algorithm. Int. J. Swarm Intell. Res. 2020, 11, 61–86. [Google Scholar] [CrossRef]
- Bisht, Y.S.; Poornima, E.; Aysola, S.C.; Sood, S.; Balassem, Z.A.; Kumar, S.; Cajla, P.; Khandelwal, U. Hybrid Renewable Energy System Design Using Multi-Objective Optimization. E3S Web Conf. 2024, 581, 01036. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies 2017, 10, 674. [Google Scholar] [CrossRef]
- Zhao, L.; Meng, X.; Yang, L.; Wei, J. Unified Multi-Objective Optimization for Regional Power Systems with Unequal Distribution of Renewable Energy Generation and Load. Eng. Rep. 2023, 5, 12768. [Google Scholar] [CrossRef]
- Xing, Q.; Cheng, M.; Liu, S.; Xiang, Q.; Xie, H.; Chen, T. Multi-Objective Optimization and Dispatch of Distributed Energy Resources for Renewable Power Utilization Considering Time-of-Use Tariff. Front. Energy Res. 2021, 9, 647199. [Google Scholar] [CrossRef]
- Liu, B.; Peng, Z.; Liao, S.; Liu, T.; Lu, J. A multi-objective optimization model for the coordinated operation of hydropower and renewable energy. Front. Energy Res. 2023, 11, 1193415. [Google Scholar] [CrossRef]
- Ma, X.; Liang, C.; Dong, X.; Li, Y. Multi-objective reactive power optimization strategy of power system considering large-scale renewable integration. Front. Energy Res. 2023, 11, 1213154. [Google Scholar] [CrossRef]
- Sadeghi, S.; Ameri, M. Multi-objective Optimization of PV-SOFC-GT-Electrolyser Hybrid System. J. Ren. Energy Env. 2015, 2, 47–58. [Google Scholar]
- Nagaleshmi, P. Solution for optimal power flow problem in wind energy system using hybrid multi objective artificial physical optimization algorithm. Intern. J. Power Electron. Drive Syst. 2019, 10, 486–503. [Google Scholar] [CrossRef]
- Barbosa, A.M.; Rotella Junior, P.; Peruchi, R.S.; Rocha, L.C.S.; Pires, A.L.G.; Janda, K. Stochastic multi-objective optimization of hybrid distributed power generation with battery storage systems. Energy Sources Part B Econ. Plan. Policy 2025, 20, 2504487. [Google Scholar] [CrossRef]
- Ndjependa, P.R.; Boum, A.T.; Essiane, S.N. A novel approach of a dynamic multi objective optimization of a power distribution system. J. Electr. Syst. Infor. Techn. 2021, 8, 17. [Google Scholar] [CrossRef]
- Pandya, S.B.; Kalita, K.; Čep, R.; Jangir, P.; Chohan, J.S.; Abualigah, L. Multi-objective Snow Ablation Optimization Algorithm: An Elementary Vision for Security-Constrained Optimal Power Flow Problem Incorporating Wind Energy Source with FACTS Devices. Int. J. Comput. Intell. Syst. 2024, 17, 33. [Google Scholar] [CrossRef]
- Seyam, S.; Al-Hamed, K.H.M.; Qureshy, A.M.M.I.; Dincer, I.; Agelin-Chaab, M.; Rahnamayan, S. Multi-objective Optimization of Hydrogen Production in Hybrid Renewable Energy Systems. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; Volume 8790299. [Google Scholar] [CrossRef]
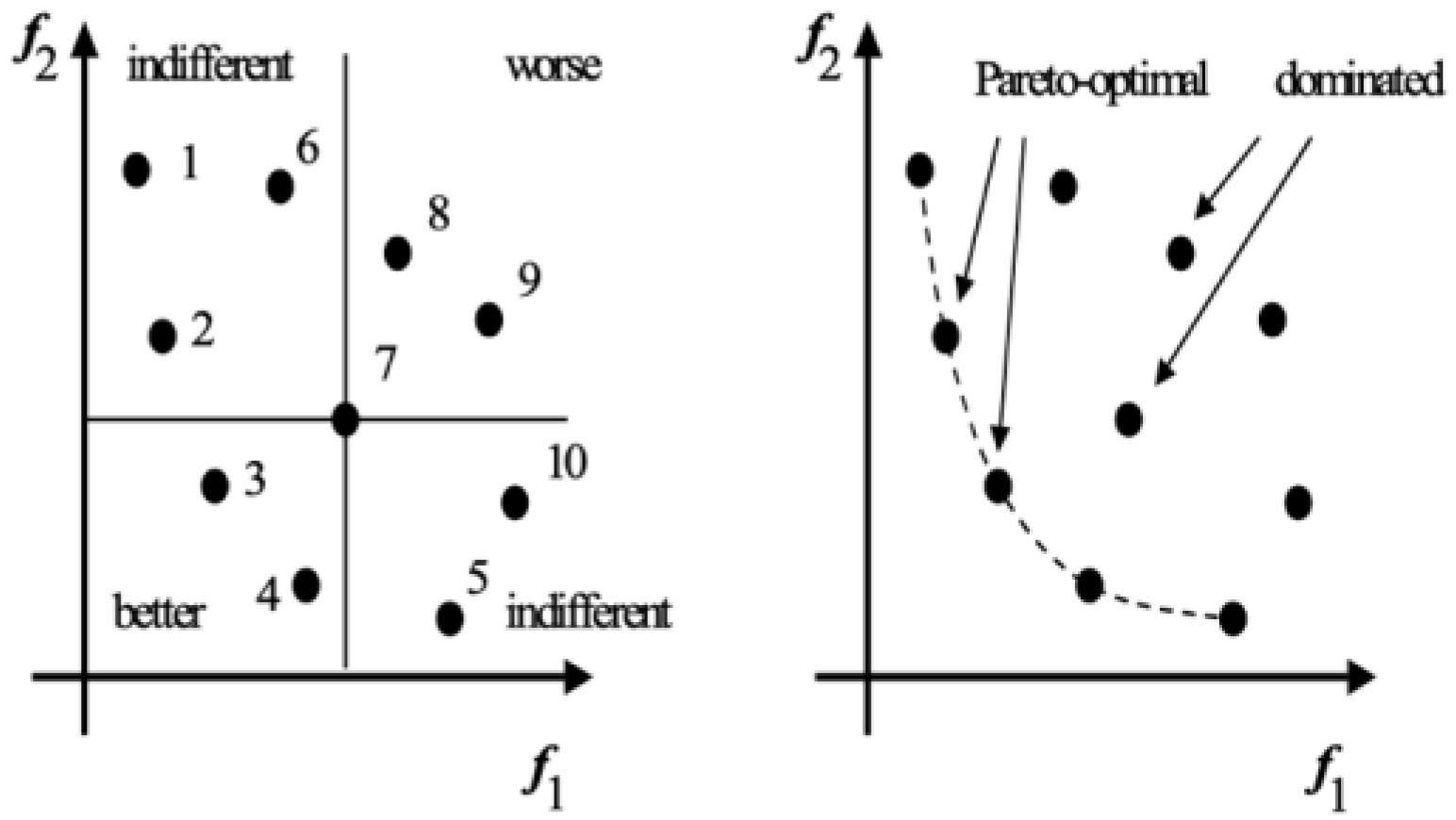
| Feature | Classical Optimization | Intelligent Optimization |
|---|---|---|
| Method | Exact/Deterministic | Non-exact/Stochastic |
| Math model | Explicit mathematical model | Black-box models |
| Intricacy handling | Limited | High |
| Result | One optimal solution | Multiple (global optimum) |
| Speed | Fast (for basic models) | Slower (for iterative search) |
| Global search | Local minima propensity | Improved capability |
| Computation Time | Shorter (small, convex systems) | Higher (large, complex systems) |
| Convergence behavior | Quickly (convex) | Global/near-global solutions |
| Solution Quality | Exact/near-exact (convex, smooth) | High-quality |
| CFD/CFI (Constraint Feasibility Degree/Index) | CFD = 0 (satisfaction of constraints) | CFD > 0 |
| Handling of CFD/CFI | Enforced rigidly (mathematically) | Flexible |
| Numerical Stability | High (Jacobian/Hessian well-conditioned) | Stable (Algorithmic adjustment) |
| Implementation Difficulty | Simpler | Difficult |
| Scalability | Effective (small, medium systems) | Adaptable (Large systems) |
| Solution | CO2 (kg/h) | Cost ($/h) | VD |
|---|---|---|---|
| 1 | 400 | 900 | 0.016 |
| 2 | 300 | 950 | 0.014 |
| 3 | 200 | 1000 | 0.011 |
| Year | Electrical Network Reconfiguration | Economic Dispatch/Optimal Power Flow | Power Distribution Planning | Operational Planning with RESs Integration |
|---|---|---|---|---|
| 2010 | [161] | |||
| 2011 | [44] | |||
| 2012 | [162] | |||
| 2013 | ||||
| 2014 | [46] | |||
| 2015 | [48] | |||
| 2016 | [123] | [20] | ||
| 2017 | ||||
| 2018 | [45,122] | |||
| 2019 | [33] | [35] | ||
| 2020 | [115,117,127,144,145] | [125] | ||
| 2021 | [120] | [124] | [147] | [22,84,134] |
| 2022 | [48] | [123,129,130,131,132,136,143] | [129] | |
| 2023 | [47] | [135,137,160] | [21] | |
| 2024 | [163] | |||
| 2025 | [18,19] |
| Approach (Method) | References |
|---|---|
| GOA, GTO, HBA, MRFO, POA, SHO, SSOA | [19] |
| MCS-OPF | [20] |
| BHA, DE, NIDE | [22,31] |
| Tabu Search | [33] |
| APSOA | [35] |
| MOPSO, IMOPSO, PSO, VCPSO, GA, GWO, ALO, WOA, FMOPF, DMOGWO, BPSO-SFLA, MOCOA-ML | [44,47,84,122,123,137,143,156,163] |
| MO-CSA, ABC, ACO, MPIO-PFM | [120,121,144] |
| KnEA, FCM, GRP | [45] |
| MOMICA | [46] |
| NSGA, NSGA-II, ACNSDE, CPF, NSGSA | [18,21,48,125] |
| CPSMOEA, MOEA/D, BA-GEWA(BAG)-UMGF | [115,117,118,147] |
| GAOPF, NLP-OPF | [124] |
| HFABC, NSHFABC, BBO, QO-BBO | [129,161,162] |
| MOSGA | [130] |
| MOPFA | [131] |
| HHO | [132] |
| SELM, DRL, DDPG, MG-ASTGCN, WTLBO | [133,134,160] |
| HFSSA | [135] |
| SMA | [136] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyingu, B.T.; Masike, L.; Mbukani, M.W.K. Multi-Objective Optimization of Load Flow in Power Systems: An Overview. Energies 2025, 18, 6056. https://doi.org/10.3390/en18226056
Nyingu BT, Masike L, Mbukani MWK. Multi-Objective Optimization of Load Flow in Power Systems: An Overview. Energies. 2025; 18(22):6056. https://doi.org/10.3390/en18226056
Chicago/Turabian StyleNyingu, Bansendeka Theo, Lebogang Masike, and Mwana Wa Kalaga Mbukani. 2025. "Multi-Objective Optimization of Load Flow in Power Systems: An Overview" Energies 18, no. 22: 6056. https://doi.org/10.3390/en18226056
APA StyleNyingu, B. T., Masike, L., & Mbukani, M. W. K. (2025). Multi-Objective Optimization of Load Flow in Power Systems: An Overview. Energies, 18(22), 6056. https://doi.org/10.3390/en18226056








