Abstract
Unbalanced active distribution networks must be carefully analyzed to minimize undesirable implications from internal unbalances and the incorporation of intermittent sources, such as DG (Distributed Generation). A coordinated voltage regulation mechanism is being created employing a MAS (Multi-Agent System) control structure to solve the difficulties mentioned earlier. The proposed technique increases coordination between DGs and Shunt capacitors (SCs) to optimize the voltage profile and reduce overall power losses, along with voltage and current unbalanced factors in the proposed unbalanced 3-phase radial distribution network. To ensure improved real-time monitoring, PMUs (Phasor Measurement Units) measure the state parameters of the above-regulated distribution network in realtime. Because it does not necessitate the placement of PMUs at all nodes for total network observability, it is a cost-effective technique for estimating network state. The IEEE standard, a 25-bus unbalanced 3-phase distribution network feeder, is used to assess the viability of the recommended technique. MATLAB R2024a programming is used to simulate the case studies.
1. Introduction
Due to unpredictable power supply, distribution networks become more complex when integrating intermittent sources, like distributed generation (DG). Enhancing the utilization of energy depends on managing DG in unbalanced networks effectively. Internal unbalances in active distribution networks can impair stability and effectiveness and affect the quality of consumers’ power. These unbalances must be corrected for distribution systems to be dependable and effective. This research intends to improve unbalance in the system and DG integration for reliable power delivery. The continuous enlargement of the distribution network due to increasing load demand and substantial evolution of distributed generation (DG) is one of the critical research areas in the electrical engineering domain. DG penetration into distribution networks transforms them from passive to active systems, which could impact the entire power system’s dynamics, particularly the distribution networks [1]. Power electronic voltage source inverters are frequently used to interface DG systems. Power quality will be a significant challenge in networks with increased power electronics interfacing with DGs and loads as well as increased nonlinear loads. Among the many power quality challenges, unbalanced voltage is one of the most serious [2]. Voltage regulation becomes difficult when network voltages are unbalanced because the unbalanced voltage’s negative-sequence component causes oscillations with a double fundamental frequency in both reactive and active power injections [3]. Moreover, an unbalanced network can support less photovoltaic (PV) generation before the critical voltage limit is reached [4].
Many scholarly contributions have been made to address the issues mentioned earlier. Based on strong and weak mutual Var compensation effects, a novel inter-phase coordinated consensus technique is proposed in the paper [5] to overcome the voltage regulation challenges arising from unbalanced photovoltaic systems. In coordination with the distribution system operator, an ideal hierarchical control technique is proposed for handling reactive power injection of electrical vehicle chargers located geologically nearby. This system uses a linear quadratic regulator (LQR) that prevents voltage sag/swell [6]. Voltage source converters (VSCs) are used as reactive power sources in the proposed controller. It coordinates with conventional controllers without substantially modifying the current distribution grid’s control and operation architecture [7]. The distributed voltage control scheme based on the time-graded control strategy is presented. In case of regulative need, the coordination scheme enables prioritization of control devices adjustments in for photovoltaic plants, ensuring they are configured prior to the other connected devices according to the time synchronization schedule [8]. In [9], a novel controller parameter tuning method is proposed based on a virtual-time delay scheme to moderate the adverse effects of simultaneous and non-simultaneous operations of traditional voltage regulating devices and distributed generation units. In reference [10], an innovative multi-phase zonal-based coordination method is proposed to control network voltages within limits and mitigate the overuse of regulating devices. The authors of [11] presented an integrated multi-agent system architecture in which each voltage regulator is treated as an independent control agent that operates based on changes in the network topology to minimize voltage deviations. The research paper in ref. [12] provides a hybrid online approach for optimum coordination of plug-in electric vehicles (PEVs) that performs voltage regulation and improves voltage unbalance with local auxiliary voltage assistance through dynamic PEV switching. An on-load tap changer’s post-contingency slow-timescale curative activities are coordinated with solar inverters and battery energy storage system’s fast-timescale curative activities using a multi-time scale optimization method in [13]. The differential evolution optimization technique is used to elucidate the coordination between electric vehicles and distributed generations to improve the distribution system’s performance [14]. A two-stage stochastic approach using the co-optimization method is presented to handle short and long-term period voltage issues [15]. The research paper in reference [16] provides a two-level coordination model for distributed generation and soft open point scheduling in unbalanced distribution networks considering their regulating capacities. In the studies, a multi-objective optimization model is used to coordinate the operation of fast and slow voltage regulators [17,18,19].
The papers in references [20,21,22] tackles real-time voltage control in power systems using a unique algorithm called EC-MADRL. Its operation is analogous to a strategy game involving various components like energy storage, compensators, and flexible loads, intending to minimize power loss from solar panels. The algorithm is designed to be efficient and flexible, and simulations show that it works better than other methods, ensuring stable voltage while wasting as little solar power as possible, on IEEE 33-bus test systems. The papers in references [23,24,25] presents an innovative voltage regulator control strategy for unbalanced distribution systems (UDS) with photovoltaic (PV) integration. Using a multi-agent system (MAS) architecture, it optimizes voltage regulation while adapting to changing UDS conditions [26]. This method ensures robust performance under normal operation and during system failures, as demonstrated throughsimulations on IEEE 34-node and 123-node distribution test feeders with high PV penetration and varying sun profiles [27,28,29,30]. The reference papers [31,32] present a cooperative voltage control strategy using a multi-agent system to manage high PV penetration challenges. It optimizes voltage regulation by coordinating voltage regulators with PV inverter reactive power control [33]. Simulations on IEEE 34-bus and 123-bus test feeders demonstrate their effectiveness under diverse 24 h operating conditions [11]. The paper in [34] introduces a distributed multi-objective optimization model to coordinate PV inverter fast dispatch with the slower dispatch of on-load tap changers and capacitor banks in unbalanced three-phase distribution systems. While existing studies often rely on centralized control, this approach decentralizes the coordination, mitigating single points of failure and reducing the computational load for more effective voltage regulation.
When viewed in the context of earlier studies, the need for a distinct approach becomes clear. While several methods have been proposed for voltage regulation in distribution networks, most are developed for balanced systems, rely on centralized control, or consider the operation of a single type of device, such as DG units, shunt capacitors, or OLTCs in isolation. In contrast, the present work adopts a coordinated MAS framework that integrates optimal PMU placement for cost-effective real-time monitoring and complete system observability. The method simultaneously coordinates DGs and SCs through voltage-sensitivity and loss-sensitivity analysis, with specific emphasis on unbalanced three-phase radial distribution networks. The proposed approach is flexible and scalable, making it applicable to any radial feeder irrespective of feeder length, lateral complexity, or variations in the X/R ratio. This combination of MAS-based coordination, PMU-assisted monitoring, and joint DG–SC operation in unbalanced networks has not been reported in earlier literature and constitutes the key distinguishing feature of this study.
This paper presents a coordinated operation of DGs and SCs in an unbalanced distribution network for voltage regulation to minimize voltage deviation, power loss, and voltage and current balance factors and improve the overall network’s voltage profile. The MAS technique is employed in this work for optimal voltage regulator selection, and it is simulated on an IEEE 3-phase, 25-bus unbalanced radial distribution network.
The following are the major contributions of this paper:
- (1)
- Introduced a Multi-Agent System (MAS) approach for optimal operation of Distributed Generators (DGs) and Switchable Capacitors (SCs) in unbalanced distribution networks, specifically targeting efficient voltage regulation.
- (2)
- Integrates an optimal PMU placement strategy within the proposed MAS framework to enable cost-effective real-time monitoring and ensure full observability of unbalanced radial networks, thereby supporting the coordinated operation of DGs and SCs.
- (3)
- The usage of PMUs helps to monitor the electrical parameters (voltage/current) via a conjoint time basis for synchronization, which helps the MAS controller get its agent’s data at specified timestamp events.
- (4)
- The proposed technique can be applied to any UDN radial structure, regardless of the feeder length, innumerable laterals/sub-laterals, or X/R ratio fluctuations.
2. Problem Formulation
Inherently, distribution systems are unbalanced. An unbalanced system, as used in the context of electrical distribution systems, is one in which the three phases of the system (often denoted by the letters A, B, and C) do not have equal voltage magnitudes or phase angles. In an unbalanced system, one or more of the following conditions may exist:
- ➢
- Voltage Magnitude Unbalance: The three phases’ voltages have different magnitudes. This indicates that a phase’s voltage may be higher or lower than the other phases.
- ➢
- Phase Angle Unbalance: The phase angles of the voltages in the three phases are not evenly spaced at 120 degrees. This can lead to phase shifts between the phases, causing various issues in the system.
- ➢
- Asymmetrical Load: The load connected to each phase is different. Some phases may carry significantly more load than others, leading to an uneven power distribution.
Systems can become out of balance for several reasons, such as an uneven load distribution, system flaws, or an unbalance in the generation sources. Managing unbalanced systems can be tricky since they can lead to problems like unstable voltage and fluctuations, which can lead to a rise in distribution system losses and decreased power quality and cause problems for connected equipment. Resources are not used effectively because some phases can be overloaded while others need to be utilized more. Research in this area, as mentioned in the previous context, is crucial for optimizing the performance of distribution networks, especially in the presence of distributed generation and other complex loads. Advanced control and regulation techniques are needed to address these challenges. To avoid catastrophic errors due to internal unbalances in the system, careful analysis of the distribution system with a detailed component model is required.
2.1. Feeder Modeling of 3-Phase Unbalanced Distribution Network
Since the distribution network is made up of single, two, and three phase non-converting phase lines serving unbalanced loads, mutual and self-impedance conditions of the line conductors need to be maintained, and the path of return conductor to earth for unbalanced current needs to be considered. Using modified Carson equations [18], a 4 × 4 primitive impedance matrix can be written for a three-phase feeder with a neutral conductor, shown in Figure 1.
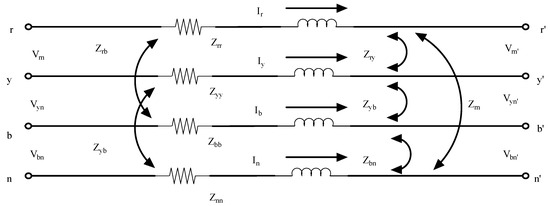
Figure 1.
3-Phase line section model. Where are the phase voltages of the phases () and the neutral conductor(n). , , , and represent self-impedances and are mutual impedances, respectively, in ohms per meter [Ω/m]. are the branch currents. are the phase voltages, the phases (), and the neutral conductor ().
Thus, the receiving end voltages (Vr, Vy, Vb, and Vn) are related to the sending end side (Vr′, Vy′, Vb′, and Vn′) of the network depicted in Figure 1, as
After applying Kron’s reduction method, the neutral or ground wire’s effects are still present in the model, as shown in Equation (3). The phase impedance matrix is given as
The receiving end voltages can be correlated with the sending end voltages of the depicted feeder in Figure 1 in the following manner:
The relevant load current injections Iir, Iiy, and Iib for bus i, corresponding to phases ‘r’, ‘y’, and ‘b’, are calculated as a function of bus voltage Vir, Vir, and Vir.
Power fed into the phaser of the line (Figure 1) at the sending end bus is Vr·(Ir)*, and at the receiving end bus is Vr′·(Ir)*. Therefore, real and reactive power losses for phaser in the line () may be written as:
Similarly, for phase-y and phase-b
2.2. Need for Voltage Regulation in an Unbalanced Active Distribution System
2.2.1. Effect of DG Integration
DG integration makes the distribution system active rather than passive since it changes the power flow and voltage profiles. DG penetration into the distribution system (DS) will cause the voltage at the point of connection of the DG to rise above the receiving end voltage, and power will be flowing both directions [19].
2.2.2. Effect of Unbalance in the Network
A voltage unbalance condition occurs when the line or phase voltages in a three-phase system deviate from their nominal balance state. A significant unbalance could drastically reduce equipment life cycles, speed up the additional component cycle, and significantly increase network operating and maintenance costs. A lower level of unbalance is desirable for improved system operation. According to IEEE standards, the percentage of unbalance is given in (11) and (12) is defined as follows [20]. A single line diagram of an electrical distribution network’s equivalent branch is shown in Figure 2.
where is the negative-sequence voltage component and is the positive-sequence voltage component.
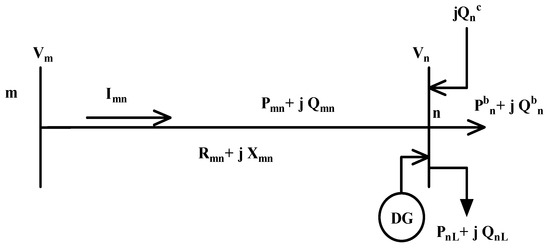
Figure 2.
Single line diagram of an electrical distribution network’s equivalent branch [21].
Current unbalance is caused by load deficiencies, which travel to the transformer and generate three-phase voltage unbalance. Even slight voltage unbalances considerably disrupt the current waveform on all the loads connected at the transformer level.
where are the negative- and positive-sequence current components, respectively. According to IEEE standards, voltage unbalance should be less than 3%, and current unbalance should be less than 20% under normal operating conditions. The +ve (positive) and −ve (negative) sequence components of voltage and current are V1,V2 and I1,I2 respectively, while the voltage and current unbalance factors are V2/V1 and I2/I1. As per standards, the nodes are presumed to be in the normal operating range [21,35].
Historically, distribution networks were passive and radial, ensuring stability under most conditions; therefore, stability concerns were not considered when designing distribution networks. Nonetheless, as the load unbalance and DG penetration of networks grows, their contribution to network security increases over time. As a result, voltage regulation is essential in these circumstances.
A sensitivity-based voltage regulation solution based on the MAS coordinated algorithm is implemented to overcome the aforementioned problems. For this study, two sensitivity techniques are being investigated as follows. The sensitivity-based methods for DG selection and capacitor placement are detailed in Section 2.3 and Section 2.4.
2.3. Sensitivity Matrix Formulation for Voltage Regulation Using DG
In an unbalanced distribution network, voltage profile optimization is a significant challenge that can be performed by selecting the optimal DG units. Therefore, satisfactory results can only be obtained if assigned to the most appropriate nodes. Nonetheless, determining the optimal voltage-sensitive bus installed for DG selection is difficult. Voltage sensitivity analysis has been addressed in various ways in the literature. This section describes the evaluation of buses that are the most sensitive to DG selection. Equations (13) and (14) represent the real and reactive power of a node in a ‘k’ bus network [22,23,24].
From Equations (13) and (14), is the number of nodes to a specific node, and are the voltage magnitudes of the nth and mth nodes, and are the voltage phase angles at node m, n, and are the node admittance magnitude and angle.
For the k-bus network, Equations (13) and (14) represent ‘2n’ active power flow equations. Taking the partial derivative of (14) to voltage yields Equations (15) and (16).
As a result, the change in voltage equation at a node ‘m’ in response to the change in P and Q on every system node ‘n’ is reduced to (17)
The decoupled load flow nodal equation is expressed in matrix form as follows:
Equation (17) shows that the DG corresponding to node m is the one with the highest sensitivity value.
2.4. Loss Sensitivity Factor (LSF) Matrix Formulation for Capacitor Selection
Loss sensitivity analysis identifies the network’s sensitive buses to install shunt capacitors (SCs) [25]. The buses with the highest LSF values are regarded as the most sensitive buses in the network. Equations (20) and (21) can indicate the active and reactive power losses that have occurred throughout branch “mn”, respectively.
By taking partially derivative Equations (20) and (21) concerning reactive power injection, the LSF value of every node in a distribution system is derived as follows.
Buses with high LSF values are designated as sensitive buses for the installation of shunt capacitors.
3. Methodology
Multi-agent systems (MAS), the focus of this research, comprise autonomous entities called agents. Agents collaborate to complete tasks, but their intrinsic ability to learn and make independent judgments allows them to be more flexible. Through encounters with the other agents and the environment, agents learn new situations and activities. Agents then use their knowledge to identify and execute activities in the environment to achieve their tasks. MAS is highly suited to tackling problems in various technological applications due to its adaptability [26].
For the analysis of this proposed study, MAS architecture is divided into two sections: Agent control process and Management control process (Task manager).
- (1)
- Agent control: The DG and SC agents will have access to the details of the network’s installed DG and SCs and will regulate voltage locally. When a coordinated operation of voltage regulators is required, they interact with the MAS controller, which passes the duties to the agents to complete.
- (2)
- Management control: The management controller receives data from the PMU agent and communicates with each DG/SC agent as needed.
PMU agent is a real-time monitoring device that continuously measures and stores data from the agents in the distribution network [27]. The functional interaction between DG agents, SC agents, the PMU agent, and the MAS task manager for coordinated voltage regulation in an active UDN is illustrated in Figure 3.
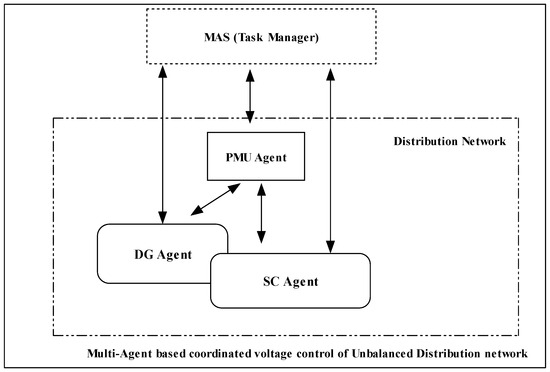
Figure 3.
Block diagram of coordinated operation of voltage regulators in Active UDN using MAS Architecture.
3.1. Algorithm for DG Agent
The following steps represented in Algorithm 1 are used in the DG agent-based strategy for optimal selection of DGs for voltage regulation and loss minimization.
| Algorithm 1: Voltage regulation of UDN using DG agent, based on sensitivity approach |
|
The procedural steps outlined above for the DG agent are represented in the coordination flow diagram in Figure 4, which visualizes the decision-making process and tie-resolution logic used in the MAS.
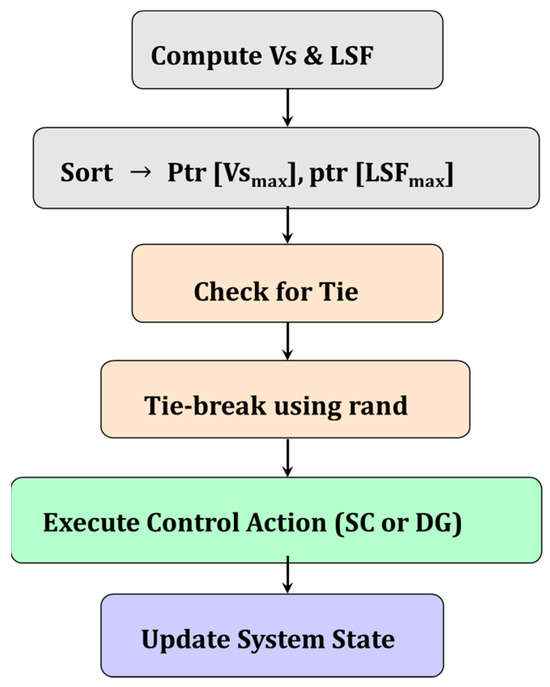
Figure 4.
Flow diagram of MAS coordination and tie-resolution logic.
3.2. Algorithm for SC Agent
The SC agent-based approach for optimal selection of SCs problem to minimize the loss takes the following steps as per Algorithm 2.
| Algorithm 2: Voltage regulation of UDN using SC agent, employing Loss sensitivity factor (LSF) approach |
|
Similarly, the SC agent’s selection and coordination process, as explained above, is incorporated within the overall MAS control logic illustrated in Figure 5.
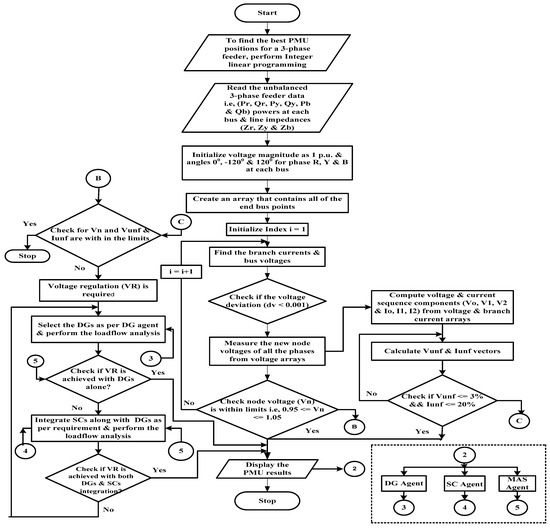
Figure 5.
Flowchart of coordinated operation of voltage regulators in Active UDN using MAS Architecture.
3.3. Coordinated Operation of Voltage Regulators in Active UDN Using MAS Topology
In the proposed MAS, the supervisory controller computes the voltage sensitivity vector Vs and the line sensitivity factor vector LSF at each coordination cycle. These are sorted in descending order to form the index arrays ptr[Vsmax] and ptr[LSFmax], which identify the most effective control candidates among the shunt capacitors (SCs) and distributed generators (DGs). The controller first attempts to select the top-ranked agent from ptr[Vsmax] or ptr[LSFmax], depending on the control objective. If two or more agents have equal sensitivity values within a predefined threshold (e.g., ±0.5%), a pseudo-random function (rand) is applied to select one agent, while the others are deferred to the next cycle. This prevents simultaneous conflicting actions on the same bus or feeder section. The random function is seeded once per cycle to ensure reproducibility in simulation while still introducing variability for fairness. The coordination cycle follows four steps: (i) compute ptr[Vsmax] and ptr[LSFmax]; (ii) apply sensitivity-based ranking; (iii) resolve ties using rand; and (iv) execute the selected control action and update the system state before the next cycle. This lightweight approach avoids explicit inter-agent communication yet ensures that only one control action is applied per location per cycle, thereby preventing oscillations and instability. The stepwise coordination process is illustrated in Figure 4.
The coordinated operation of voltage regulators in an active unbalanced distribution network (UDN) implemented though the proposed multi-agent system (MAS) architecture, as shown in Figure 5.
3.4. PMU (Phasor Measurement Unit)
Integrating a PMU into a bus will measure the voltage at the node and the currents from all the other buses connected to that bus as the output. It would be severely expensive to just place them everywhere. So, the optimal placement of PMUs is important in the elimination of redundant cost and information; when placed everywhere, there would be redundancy in the current data while also achieving total observability of the given system [28,29].
ILP (Integer Linear Programming)
ILP is the method used generally to minimize a linear function(x) based on some constraints. Here, we are trying to minimize the X (optimal placement solution) based on the constraint of X .
Following is the optimal placement problem for N-bus systems formulated as an ILP.
where
- Objective: Minimize the sum of PMU placements
- Variables:
- N: Number of buses in the system
- X: Binary vector representing PMU placement decisions
- TPMU (a, b) = 1, if a = b=1, if a and b are connected=0, if otherwise
- Tpmu: Connection matrix indicating bus connections
- bpmu: Inequality constraints vector
Where ‘k represents all’ to ‘buses connected to’ from ‘bus a’. X is PMU placement vector of binary values (0, 1), with 1 (ones) indicating placement buses, is the inequality constraints vector, and a and b are from and to buses in the network.
This pseudocode outlines the ILP formulation for the PMU placement problem. It aims to minimize the total number of PMUs placed while ensuring that each bus connected to others has at least one PMU. The constraints are based on the connection matrix ‘Tpmu’ and the inequality constraints vector ‘bpmu’. The objective is to optimize the placement of PMUs in the power system for effective monitoring while considering connectivity and constraint requirements.
This study uses PMU technology to measure the network’s voltage and current parameters. Various strategies have been used to solve the Optimal Placement problem (OPP). This method presents the implementation of PMU optimal allocation utilizing the Integer Linear Programming approach for full observability of the system, which brings the electric utility network closer to intelligent grid communication technologies to enhance system monitoring settings. For the state estimation of an unbalanced, 3-phase, IEEE 25-bus radial distribution network, the methodology proposed in [30] is being used.
Although the proposed MAS framework was evaluated on the IEEE 25-bus unbalanced radial feeder, which is widely used as a benchmark in voltage regulation studies, the approach is not limited to small-scale systems. The MAS architecture’s distributed decision-making and limited communication requirements make it inherently scalable to larger, more complex distribution networks. This scalability, combined with the optimal PMU placement strategy, enables efficient monitoring and control without a proportional increase in computational burden.
4. Results and Discussions
The proposed methodology is being used on a 25-bus, unbalanced 3-phase radial distribution system. The rated line voltage is 4.16 kV, the base MVA is 100, and the system data is given in [31].
An ILP analysis is utilized to identify the best PMU location for the test system. By implementing MATLAB programming, the simulation is completed for comprehensive system observability. The single-line diagram of the unbalanced 25-bus radial distribution system, as depicted in Figure 6, illustrates the network topology used in this study.
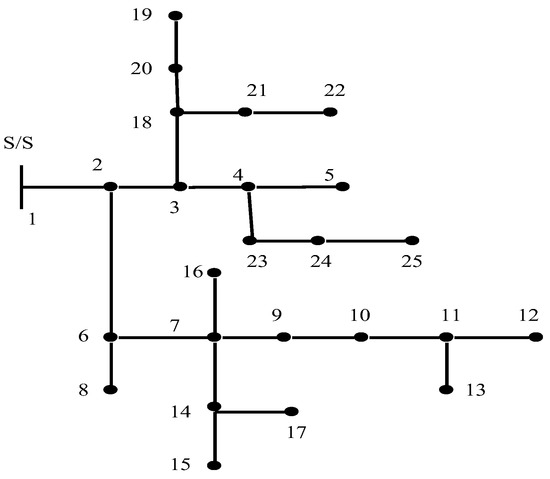
Figure 6.
A single line representation of an unbalanced 25 bus, radial distribution system.
Table 1 shows the necessary number of PMUs and their positions in the test feeder for total system observability.

Table 1.
Recommended PMU locations of a 25-bus unbalanced radial distribution system.
The percentage unbalance in the 3-phase feeder is considered as follows. It is assumed that the load in the R-phase remains the same as in a balanced system, and the Y-phase load is reduced by x% while the B-phase load is increased by y% from the base case.
The case study analysis considers three scenarios: a system without voltage regulators, DG integration, and SC and DG integration. A detailed discussion of each scenario follows.
4.1. Scenario1—Without DG/SC Integration
In this case, the percentage of load unbalance is taken in steps of 10%, 20%, 30%, and 40% to observe the effect of unbalance in the system without DG/SC integration. With 10% in the load unbalance, the total load of phase R is 1333.8 kVA, phase Y is 1226.2 kVA, and phase B is 1465.9 kVA; with 20% in the load unbalance, the total load of phase R is 1333.8 kVA, phase Y is 1089.96 kVA, and phase B is 1599.23 kVA; with 30% in the load unbalance, the total load of phase R is 1333.8 kVA, phase Y is 953.71 kVA, and phase B is 1732.50 kVA; and with 40% in the load unbalance, the total load of phase R is 1333.8 kVA, phase Y is 817.47 kVA, and phase B is 1865.77 kVA, with power factor (PF) = 0.8.
Table 2 presents voltage magnitudes (VRph, VYph, and VBph in p.u.) without DG/SC. Figure 7 shows the voltage profile of 25-bus unbalanced 3-phase radial feeder networks without DG/SC using a PMU setup.

Table 2.
Voltage magnitude (p.u.) results of unbalanced loading without DG/SC based on PMU data.
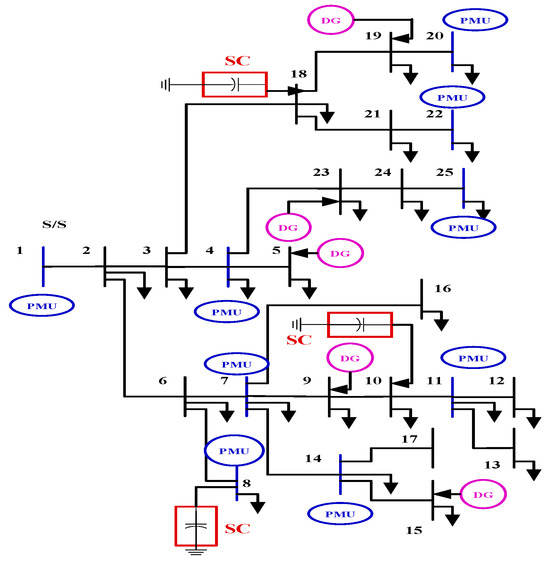
Figure 7.
Modified diagram of 25-bus unbalanced, radial distribution test system with DGs, SCs, and PMU installation.
From the test results of scenario 1, as there is no change in load, the voltage profile of phase-R remains the same compared with the other two phases of the 3-phase feeder. The voltage profile of phase Y improved as the unbalance percentage increased, whereas the phase-B voltage magnitude profile was reduced with the increase in the percentage unbalance. Despite improvements in some phase voltage profiles, these unbalances caused some node voltage to fall below specifications, increasing the total power loss of the system.
Also, the analysis is being extended further by calculating the voltage and current unbalance factors of the above cases, which are tabulated in Table 3. It is noticed that the voltage unbalance factors are within the standard limits (i.e., <3%), but the current unbalance factor is increased to above the limit (i.e., <20%) in one of the cases as the load unbalance increases. The corresponding voltage profile of the 25-bus, 3-phase unbalanced feeder under various unbalance levels without DG/SC integration is shown in Figure 8.

Table 3.
Voltage and current unbalance factor of a 25-bus unbalanced system with various loading conditions.
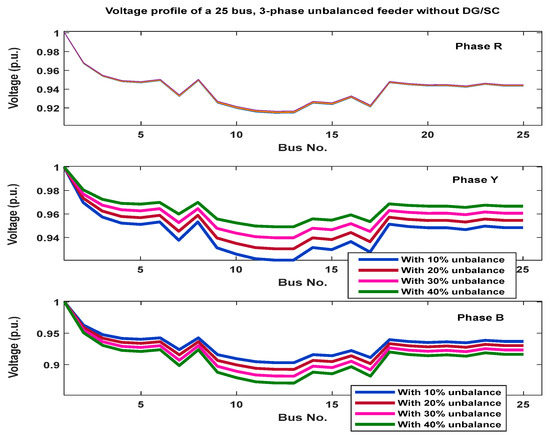
Figure 8.
Voltage profile of a 25 bus, 3-phase unbalanced feeder without DG/SC.
4.2. Scenario2—With DG Integration
In this scenario, the percentages of load unbalance are taken as 30% and 40%, respectively, and DGs are incorporated as needed at each step of change in unbalance. Table 4 displays the real power (Pr), apparent power (Py), and reactive power (Qr, Qy, and Qb) generated by each Distributed Generator (DG) for each of the specified unbalanced percentages (30% and 40%).

Table 4.
DG penetration and power generation at various buses for load unbalance scenarios.
Figure 9 and Figure 10 show the voltage profile, Table 5 and Table 6 compare voltage magnitude measurements (VRph, VYph, and VBph in p.u.), and Table 7 and Table 8 compare the voltage and current unbalanced factors of the test system with and without DG considering 30% and 40% unbalanced loading, whereas Table 8 presents the total power loss of the network. Table 5 represents the voltage magnitude (p.u.) results of the test system with 30% unbalanced loading, DG using PMU measurement. The table illustrates voltage magnitude results for a test system under unbalanced loading conditions, incorporating Distributed Generation (DG) at varying levels (10%, 15%, and 20%). It compares voltage magnitudes (VRph, VYph, and VBph) with and without DG. Through these comparisons, the impact of DG integration on system stability and voltage regulation can be observed, offering insights into the effectiveness of DG in mitigating voltage fluctuations and enhancing system performance under different loading conditions. Table 6 provides data examining voltage and current unbalance factors under a 30% unbalanced loading scenario, while varying the levels of Distributed Generation (DG) penetration. It compares these factors across different DG penetration levels: without DG/SC, with 10% DG, 15% DG, and 20% DG. This comparison allows for an assessment of how the integration of DG impacts both voltage and current unbalance factors, providing insights into the effectiveness of DG in mitigating unbalance issues within the system. Table 7 presents voltage magnitude results per unit (p.u.) obtained from PMU data under 40% unbalanced loading, both with and without Distributed Generation (DG). It compares voltage magnitudes for Red (VRph), Yellow (VYph), and Blue (VBph) phases across different DG penetration levels (0%, 10%, 15%, and 20%). This comparison enables an assessment of how DG integration influences voltage stability and regulation amidst unbalanced loading conditions.
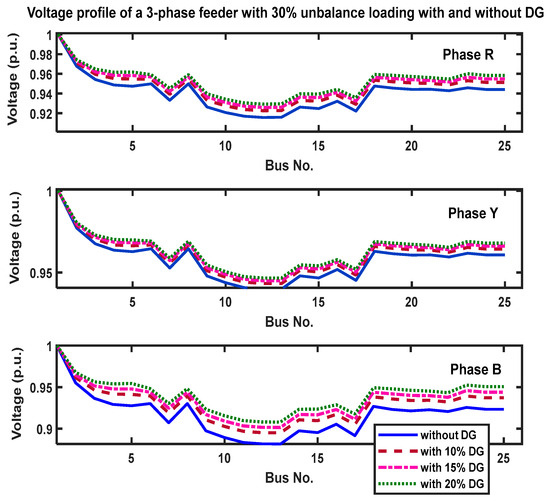
Figure 9.
Voltage profile of a 3-phase feeder with 30% unbalanced loading, with and without DG.
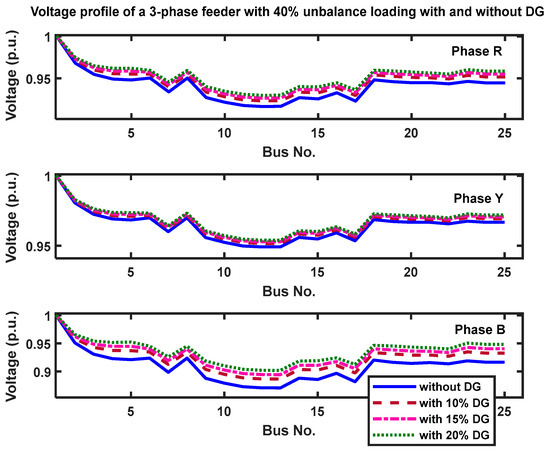
Figure 10.
Voltage profile of a 3-phase feeder with 40% unbalanced loading, with and without DG.

Table 5.
Voltage magnitude (p.u.) results of the test system with 30% unbalanced loading, DG using PMU measurement.

Table 6.
Voltage and current unbalance factors with 30% unbalance loading and various DG penetration levels.

Table 7.
Voltage magnitude (p.u.) results of PMU data with 40% unbalanced loading and DG.

Table 8.
Voltage and current unbalance factor with 40% unbalance loading with various DG penetration levels.
Table 8 provides data that outline the voltage profile of a 3-phase feeder under a 40% unbalanced loading condition, comparing scenarios with and without Distributed Generation (DG). It further examines voltage and current unbalance factors across various DG penetration levels (0%, 10%, 15%, and 20%). This comparison allows for an assessment of how the integration of DG impacts the voltage profile and unbalance factors, providing insights into the effectiveness of DG in mitigating unbalance issues within the feeder system. Table 9 presents total power loss data for a 25-bus, unbalanced 3-phase radial distribution system with varying levels of Distributed Generation (DG) integration. The first column denotes the percentage of unbalanced loading, with variations of 30% and 40%. The subsequent columns represent different levels of DG penetration. The second column shows the net real power loss in kilowatts (kW), while the last column displays the net reactive power loss in kilovolt-amperes reactive (kVAR). This data allows for an analysis of how DG integration impacts power losses under different degrees of unbalanced loading, providing insights into the system’s efficiency and performance.

Table 9.
Total power loss of 25-bus, unbalanced 3-phase radial distribution system with DG integration.
The following are the main conclusions drawn from the test results of scenario 2:
- (a)
- Voltage Profile Improvement: The voltage profiles of all three phases in the distribution system significantly improve by introducing DGs at different penetration levels. As a result, the system’s voltage levels are more consistent and closer to the intended nominal values.
- (b)
- Reduction in Total Power Losses: The total power losses within the distribution network are significantly reduced as the DG penetration levels rise. DGs assist in reducing losses by producing power closer to the load centers.
- (c)
- Compliance with Unbalance Limits: The voltage and current unbalance factors remain within the prescribed limits, demonstrating that the distribution system runs within the acceptable limits.
Nevertheless, some node voltages in each phase are still below the lower limit. Hence, a further improvement in voltage regulation is desirable.
4.3. Scenario3—With DG and SC Integration
In scenario 3, the percentage of load unbalance is considered the same as in previous cases. SCs with ratings of 300 kVAR, 150 kVAR, and 300 kVAR have been installed at buses 8, 10, and 18 together with the existing DGs to improve the system conditions further from the above two scenarios.
Figure 11 and Figure 12 depict the voltage profile, while Table 10 and Table 11 compare voltage magnitude (VRph, VYph and VBph in p.u.) measurements, and Table 12 and Table 13 compare the voltage and current unbalanced factors of the test system with and without DG under 30% and 40% unbalanced loading, respectively. Table 14 represents the network’s total power loss.
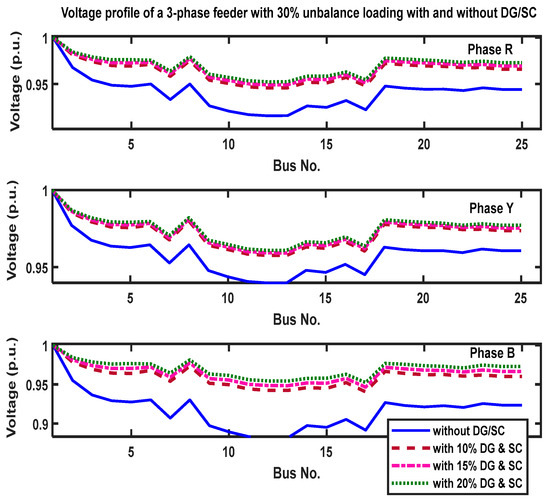
Figure 11.
Voltage profile of a 3-phase feeder with 30% unbalanced loading, with and without DG/SC.
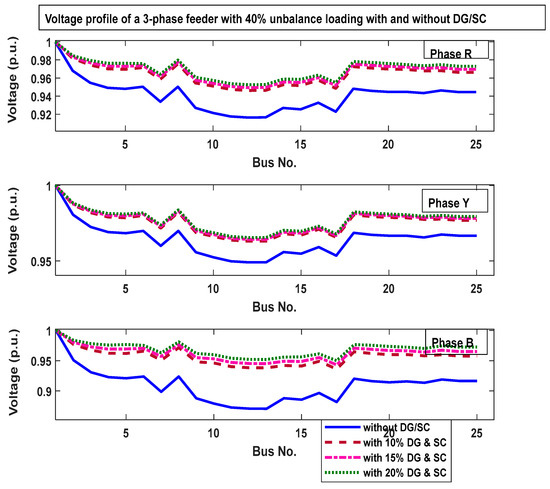
Figure 12.
Voltage profile of a 3-phase feeder with 40% unbalanced loading, with and without DG/SC.

Table 10.
Voltage magnitude (p.u.) results of PMU data with 30% unbalanced loading, DG and SC.

Table 11.
Voltage and current unbalance factors with 30% unbalance loading, DG and SC.

Table 12.
Voltage magnitude (p.u.) results of PMU data with 40% unbalanced loading, DG and SC.

Table 13.
Voltage and current unbalance factor with 40% unbalance loading, DG and SC.

Table 14.
Total power loss of 25-bus, unbalanced 3-phase radial distribution system with DG and SC integration.
Table 10 presents voltage magnitude results (in p.u.) from PMU data in a system experiencing 30% unbalanced loading. It integrates Distributed Generation (DG) and shunt capacitor (SC). The first column shows voltage magnitudes for Red (VRph), Yellow (VYph), and Blue (VBph) phases without DG or SC. Subsequent columns display voltage magnitudes with increasing DG and SC integration (at 10%, 15%, and 20%). This data enables analysis of how DG and SC affect voltage stability and regulation under unbalanced loading, offering insights into their efficacy in enhancing system performance. Table 11 presents voltage and current unbalance factors under a 30% unbalanced loading scenario, incorporating Distributed Generation (DG) and shunt capacitors (SC) at various penetration levels. The first column represents unbalance factors without DG or SC, while subsequent columns denote increasing levels of DG and SC integration (10%, 15%, and 20%). This data allows for an assessment of how the combination of DG and SC influences both voltage and current unbalance factors, providing insights into the effectiveness of DG and SC in mitigating unbalance issues within the system. Table 12 presents voltage magnitude data in per unit (p.u.) obtained from Phasor Measurement Unit (PMU) readings. It analyzes the impact of integrating Distributed Generation (DG) and shunt capacitors (SC) under 40% unbalanced loading. The baseline column shows voltage without DG or SC. Subsequent columns indicate voltage with increasing DG and SC levels (10%, 15%, and 20%). This data aids in understanding the influence of DG and SC on voltage stability and regulation.
From the results of the three scenarios, it is observed that, without voltage regulating devices, as the load unbalancing increases in the distribution network, most of the node voltage magnitudes are below the lower limit. Though the voltage unbalance factors are within acceptable limits, the current unbalance factors are beyond the limit. When DGs and SCs are integrated into the network, considerable losses are minimized. The voltage profile is improved by bringing all node voltage magnitudes within limits. Also, the percentages of voltage and current unbalance factors are dropped compared to the unregulated scenario. Table 13 presents voltage and current unbalance factors under a 40% unbalanced loading scenario, considering the integration of both Distributed Generation (DG) and shunt capacitors (SC) at various penetration levels (10%, 15%, and 20%). The first column represents unbalance factors without DG or SC, while subsequent columns display results with increasing levels of DG and SC integration. This data allows for an evaluation of how the combination of DG and SC impacts voltage and current unbalance factors, providing insights into their effectiveness in mitigating unbalance issues within the system. The Table 14 illustrates the total power loss data for a 25-bus unbalanced 3-phase radial distribution system with integrated Distributed Generation (DG) and shunt capacitors (SC). It displays the percentage of unbalanced loading at 30% and 40%, while also presenting the net real power loss in kilowatts (kW) and net reactive power loss in kilovolt-amperes reactive (kVAR) across different levels of DG penetration. This data enables an assessment of how the integration of DG and SC impacts power losses under varying degrees of unbalanced loading, providing valuable insights into the efficiency and performance of the distribution system
The identified PMU locations for IEEE-34 or IEEE-123 bus test system and presented in Table 15. Additionally, a validation process is conducted to ensure the accuracy and reliability of the proposed scheme. The procedure is explained in Algorithm 3 and corresponding results are given in Table 16.

Table 15.
Optimal placement of PMUs in unbalanced radial IEEE bus systems.

Table 16.
Validation table for Phasor Measurement Units.
Validation involves closely examining the results produced by an algorithm. This algorithm serves the primary goal of confirming the connectivity of all buses to Phasor Measurement Units (PMUs). To do this, the buses were divided into two different vectors: one for the buses connected to the PMU and another for the ones not. A thorough inspection used a branch vector to compare every bus (Comp_vector) connected to the PMUs. The findings were then saved in a “Ver” vector (initialized as an empty vector) and then populated with the bus numbers related to PMU-connected buses. The “Ver” vector must contain all the outstanding bus (Out_bus) numbers for a system to be considered fully observable. On the other hand, an imperfect match signifies a deficiency in total observability, implying possible errors in the determined ideal PMU positions.
| Algorithm 3: Validation of Optimal PMU Placement Solution of Unbalanced radial networks |
|
4.4. Robustness and External Corroboration Across Test Systems
The proposed MAS controller relies on local measurements (positive/negative-sequence voltage V1, V2) and agent-level arbitration rules, with actuation through DG reactive power set-points and shunt capacitors. The sensitivity matrix used for selection depends on feeder impedance s and injections but does not require feeder-specific controller gains. Consequently, for radial distribution networks with per-section R/X in typical ranges and unbalance ≤5%, the following qualitative behavior holds: (i) minimum phase voltage improves monotonically with DG penetration up to the point of local over-voltage constraints; (ii) moderate SC sizing (≈10–15% of local kvar) reduces phase-spread without inducing excessive circulating reactive power; and (iii) under load growth up to ≈1.2 p.u., MAS coordination maintains Vmin within statutory limits provided DG support ≥20% of peak load.
Published studies on IEEE 33- and 69-bus feeders employing MAS-based coordination and sensitivity/OPF-guided voltage control report the same trends with respect to DG penetration, unbalance level, and reactive compensation. These reports indicate improvements in minimum bus voltage and reduced inter-phase dispersion comparable to those observed in our 25-bus case. Together with the mechanism above, this supports portability of the proposed scheme to standard feeders of different sizes and impedances. We will provide full IEEE 33-/69-bus scenario sweeps (voltage envelopes, losses, tap actions) as an extended dataset in a follow-up technical note.
5. Conclusions
This work analyses a 3-phase, 25-bus unbalanced distribution network for steady-state performance. This research provides an effective and efficient coordinated voltage control mechanism based on the MAS approach. The scheme optimizes the voltage profile to minimize the unbalance, voltage deviation, and losses in an active UDN. The DG/SC agents have the sensitivity indices of all DGs and SCs linked in the network and allow voltage regulation to be made locally on the most sensitive nodes. When a coordinated action of voltage regulators is desired, they communicate with the MAS controller, which then delegates the tasks to the agents based on the available information from the PMU agent database. Thus, coordinated voltage regulation is accomplished by optimally choosing the exact number of devices, eliminating the need for other voltage regulators in the network. As the PMUs are already installed in the network, a separate memory unit for the MAS structure can be avoided, making the scheme cost-effective. The voltage and current parameters of the network are measured using an online estimation technique based on PMU. A PMU allows one to measure the voltage phasor of the bus in real time and the current phasor of all lines connected to the bus. Due to this capability of PMU, all buses adjacent to it are observable. The optimum PMU allocation on the test system is elucidated using an integer linear programming approach. An improved voltage profile of the system and a substantial reduction in voltage and current unbalance and power loss are exhibited as a result of optimal operations of DGs and SCs in the network.
Author Contributions
Conceptualization, S.T., D.N.G. and R.S.S.N.; methodology, S.T., D.N.G. and R.S.S.N.; software, S.T.; formal analysis, A.A. and S.R.A.; validation, A.A. and S.R.A.; investigation, A.A.; writing—original draft preparation, S.T., D.N.G. and R.S.S.N.; writing—review and editing, A.A. and S.R.A.; visualization, A.A.; supervision, A.A. and S.R.A.; project administration, A.A. and S.R.A.; funding acquisition, A.A. and S.R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors gratefully acknowledge the valuable support of Yogesh Ramaswamy and A. Mutharasan during the early stages of this work. Their assistance in preliminary analysis, validation activities, and constructive discussions contributed to shaping the direction of the study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Azadani, E.N.; Canizares, C.A.; Olivares, D.E.; Bhattacharya, K. Stability analysis of unbalanced distribution systems with synchronous machine and DFIG based distributed generators. IEEE Trans. Smart Grid. 2014, 5, 2326–2338. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W.; Wu, B. Control strategies of three-phase distributed generation inverters for grid unbalanced voltage compensation. IEEE Trans. Pow. Electron. 2016, 31, 5228–5241. [Google Scholar] [CrossRef]
- Kabiri, R.; Holmes, D.G. McGrath, B.P. Control of active and reactive power ripple to mitigate unbalanced grid voltages. IEEE Trans. Ind. Appl. 2016, 52, 1660–1668. [Google Scholar] [CrossRef]
- Weckx, S.; Driesen, J. Load balancing with EV chargers and PV inverters in unbalanced distribution grids. IEEE Trans. Sustain. Energy 2015, 6, 635–643. [Google Scholar] [CrossRef]
- Wang, L.; Yan, R.; Bai, F.; Saha, T.; Wang, K. A distributed inter-phase coordination algorithm for voltage control with unbalanced PV integration in LV systems. IEEE Trans. Sustain. Energy 2020, 11, 2687–2697. [Google Scholar] [CrossRef]
- Mejia-Ruiz, G.E.; Cárdenas-Javier, R.; Paternina, M.R.A.; Rodríguez-Rodríguez, J.R.; Ramirez, J.M.; Zamora-Mendez, A. Coordinated optimal volt/var control for distribution networks via D-PMUs and EV chargers by exploiting the Eigensystem realization. IEEE Trans. Smart Grid 2021, 12, 2425–2438. [Google Scholar] [CrossRef]
- Ahmed, M.; Bhattarai, R.; Hossain, S.J.; Abdelrazek, S.; Kamalasadan, S. Coordinated voltage control strategy for voltage regulators and voltage source converters integrated distribution system. IEEE Trans. Ind. Appl. 2019, 55, 4235–4246. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B.H.; Jahanbakhsh, F. Distributed control of voltage regulating devices in the presence of high PV penetration to mitigate ramp-rate issues. IEEE Trans. Smart Grid 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Ranamuka, D.; Agalgaonkar, A.P.; Muttaqi, K.M. Innovative Volt/VAr control philosophy for future distribution systems embedded with voltage-regulating devices and distributed renewable energy resources. IEEE Syst. J. 2019, 13, 3153–3164. [Google Scholar] [CrossRef]
- Chamana, M.; Chowdhury, B.H. Optimal voltage regulation of distribution networks with cascaded voltage regulators in the presence of high PV penetration. IEEE Trans. Sustain. Energy 2018, 9, 1427–1436. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N.; Mahmoud, K.; Lehtonen, M. An effective coordination strategy for voltage regulation in distribution system containing high intermittent photovoltaic penetrations. IEEE Access 2021, 9, 117404–117414. [Google Scholar] [CrossRef]
- Jabalameli, N.; Ghosh, A. Online centralized coordination of charging and phase switching of PEVs in unbalanced LV networks with high PV penetrations. IEEE Syst. J. 2021, 15, 1015–1025. [Google Scholar] [CrossRef]
- Zafar, R.; Ravishankar, J.; Fletcher, J.E.; Pota, H.R. Multi-timescale voltage stability-constrained Volt/VAR optimization with battery storage system in distribution grids. IEEE Trans. Sustain. Energy 2020, 11, 868–878. [Google Scholar] [CrossRef]
- Islam, M.R.; Lu, H.; Hossain, J.; Li, L. Multiobjective optimization technique for mitigating unbalance and improving voltage considering higher penetration of electric vehicles and distributed generation. IEEE Syst. J. 2020, 14, 3676–3686. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Q.; Wang, Z. Cooperative peak shaving and voltage regulation in unbalanced distribution feeders. IEEE Trans. Power Syst. 2021, 36, 5235–5244. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, N.; Chung, C.Y.; Wang, Q. Coordinated planning of converter-based DG units and soft open points incorporating active management in unbalanced distribution networks. IEEE Trans. Sustain. Energy 2020, 11, 2015–2027. [Google Scholar] [CrossRef]
- Tatikayala, V.K.; Dixit, S. Multi-stage voltage control in high photovoltaic based distributed generation penetrated distribution system considering smart inverter reactive power capability. Ain Shams Eng. J. 2024, 15, 102265. [Google Scholar] [CrossRef]
- Kryonidis, G.C.; Malamaki, K.-N.D.; Gkavanoudis, S.I.; Oureilidis, K.O.; Kontis, E.O.; Mauricio, J.M.; Maza-Ortega, J.M.; Demoulias, C.S. Distributed reactive power control scheme for the voltage regulation of unbalanced LV grids. IEEE Trans. Sustain. Energy 2020, 12, 1301–1310. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Hossain, M.J.; Pota, H.R. Voltage variation on distribution networks with distributed generation: Worst case scenario. IEEE Syst. J. 2014, 8, 1096–1103. [Google Scholar] [CrossRef]
- Wang, H.; Yan, Z.; Shahidehpour, M.; Zhou, Q.; Xu, X. Optimal energy storage allocation for mitigating the unbalance in active distribution network via uncertainty quantification. IEEE Trans. Sustain. Energy 2021, 12, 303–313. [Google Scholar] [CrossRef]
- Yao, M.; Hiskens, I.A.; Mathieu, J.L. Mitigating voltage unbalance using distributed solar photovoltaic inverters. IEEE Trans. Power Syst. 2021, 36, 2642–2651. [Google Scholar] [CrossRef]
- Mendonca, T.R.F.; Green, T.C. Distributed active network management based on locally estimated voltage sensitivity. IEEE Access 2019, 7, 105173–105185. [Google Scholar] [CrossRef]
- Jhala, K.; Natarajan, B.; Pahwa, A. Probabilistic Voltage Sensitivity Analysis (PVSA)—A Novel Approach to Quantify Impact of Active Consumers. IEEE Trans. Power Syst. 2018, 33, 2518–2527. [Google Scholar] [CrossRef]
- Zad, B.B.; Lobry, J.; Vallée, F. A New Voltage Sensitivity Analysis Method for Medium-Voltage Distribution Systems Incorporating Power Losses Impact. Electr. Power Compon. Syst. 2018, 46, 1540–1553. [Google Scholar] [CrossRef]
- Dixit, M.; Kundu, P.; Jariwala, H.R. Optimal integration of shunt capacitor banks in distribution networks for assessment of techno-economic asset. Comput. Electr. Engg. 2018, 71, 331–345. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-agent systems: A survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Yasinzadeh, M.; Akhbari, M. Detection of PMU spoofing in power grid based on phasor measurement analysis. IET Gener. Transm. Distrib. 2018, 12, 1980–1987. [Google Scholar] [CrossRef]
- Chauhan, K.; Sodhi, R. Placement of Distribution-Level Phasor Measurements for Topological Observability and Monitoring of Active Distribution Networks. IEEE Trans. Instrum. Meas. 2020, 69, 3451–3460. [Google Scholar] [CrossRef]
- Koochi, M.H.R.; Hemmatpour, M.H. A general PMU placement approach considering both topology and system aspects of contingencies. Int. J. Electr. Power Energy Syst. 2020, 118, 105774. [Google Scholar] [CrossRef]
- Tangi, S.; Gaonkar, D.N. Voltage Estimation of Active Distribution Network Using PMU Technology. IEEE Access 2021, 9, 100436–100446. [Google Scholar] [CrossRef]
- Taher, S.A.; Karimi, M.H. Optimal reconfiguration and DG allocation in balanced and unbalanced distribution systems. Ain Shams Eng. J. 2014, 5, 735–749. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, L.; Yue, D.; Dou, C.; Xie, X.; Chen, L. Coordinated voltage regulation of high renewable-penetrated distribution networks: An evolutionary curriculum-based deep reinforcement learning approach. Int. J. Electr. Power Energy Syst. 2023, 149, 108995. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N.; Mahmoud, K.; Zoka, Y.; Sasaki, Y. Optimal Voltage Control Strategy for Voltage Regulators in Active Unbalanced Distribution Systems Using Multi-Agents. IEEE Trans. Power Syst. 2020, 35, 1023–1035. [Google Scholar] [CrossRef]
- Zhang, Q.; Dehghanpour, K.; Wang, Z. Distributed CVR in Unbalanced Distribution Systems with PV Penetration. IEEE Trans. Smart Grid 2019, 10, 5308–5319. [Google Scholar] [CrossRef]
- Kersting, W.H. The whys of distribution system analysis. IEEE Ind. Appl. Mag. 2011, 17, 59–65. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).