A Fuzzy Division Control Strategy for Flywheel Energy Storage to Assist Primary Frequency Regulation of Hydropower Units
Abstract
1. Introduction
- (1)
- To develop an adaptive frequency division control strategy based on fuzzy logic that dynamically allocates power commands between FESS and HPU;
- (2)
- To design a state of charge (SOC)-based output limitation mechanism for FESS that prevents over-charge/discharge while maintaining regulation capability;
- (3)
- To verify through simulations that the proposed strategy can significantly improve the primary frequency regulation performance while reducing the operational pressure on hydropower units.
2. A Model of FESS-Assisted HPU for PFR
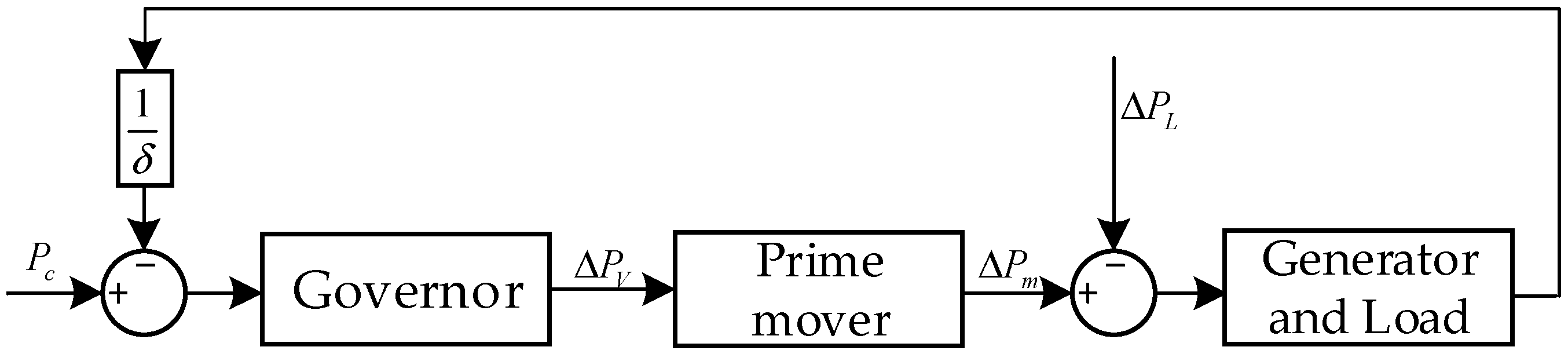
2.1. HPU Model
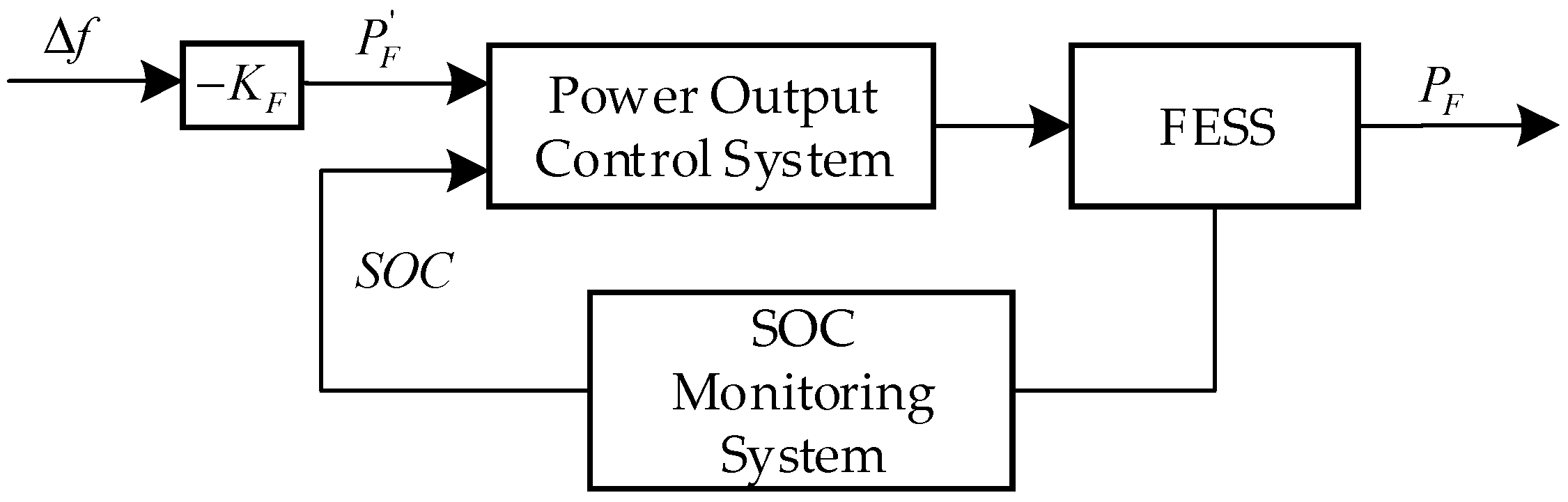
2.2. FESS Model
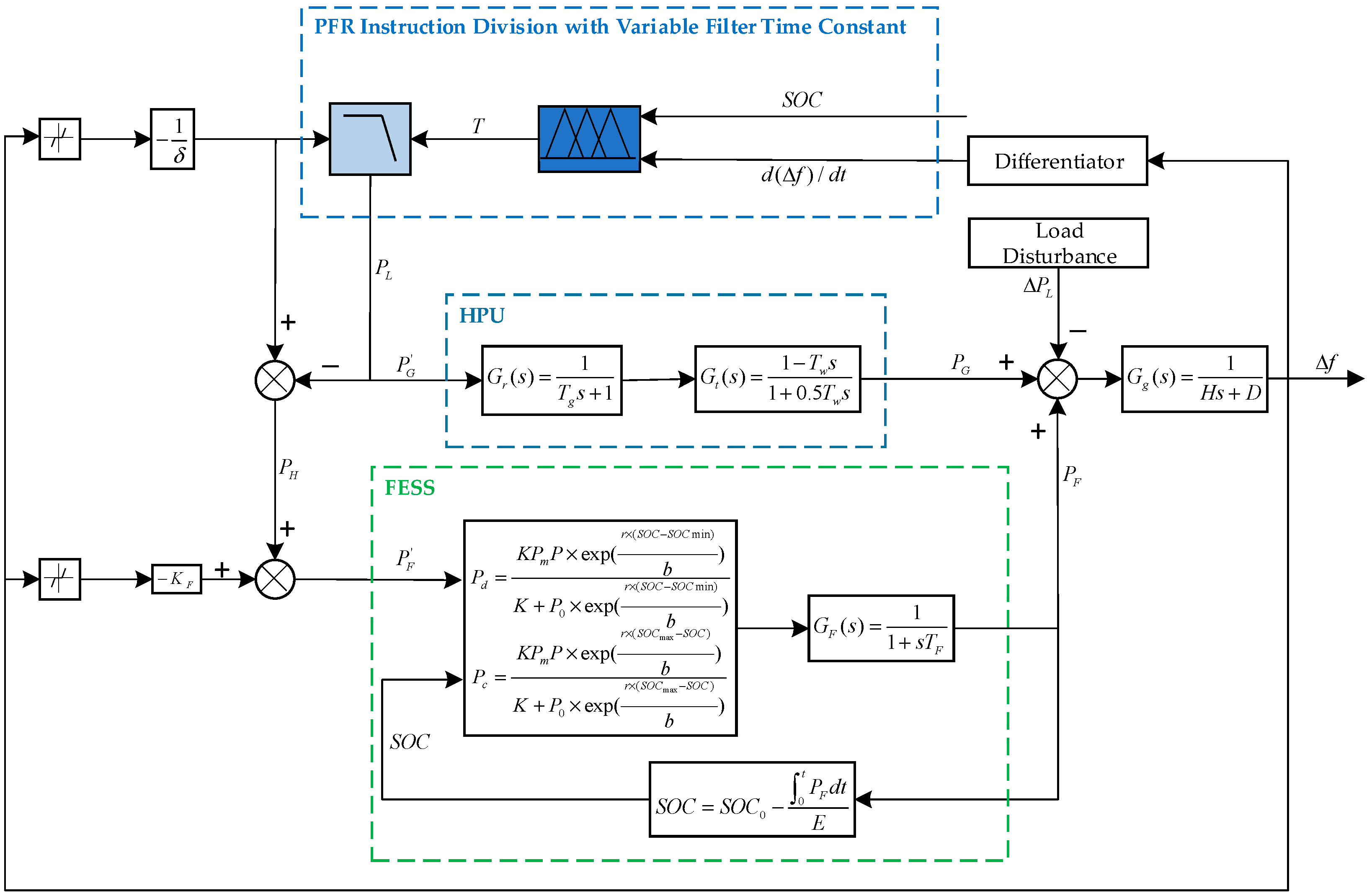
3. Control Strategy for PFR of FESS-Assisted HPU
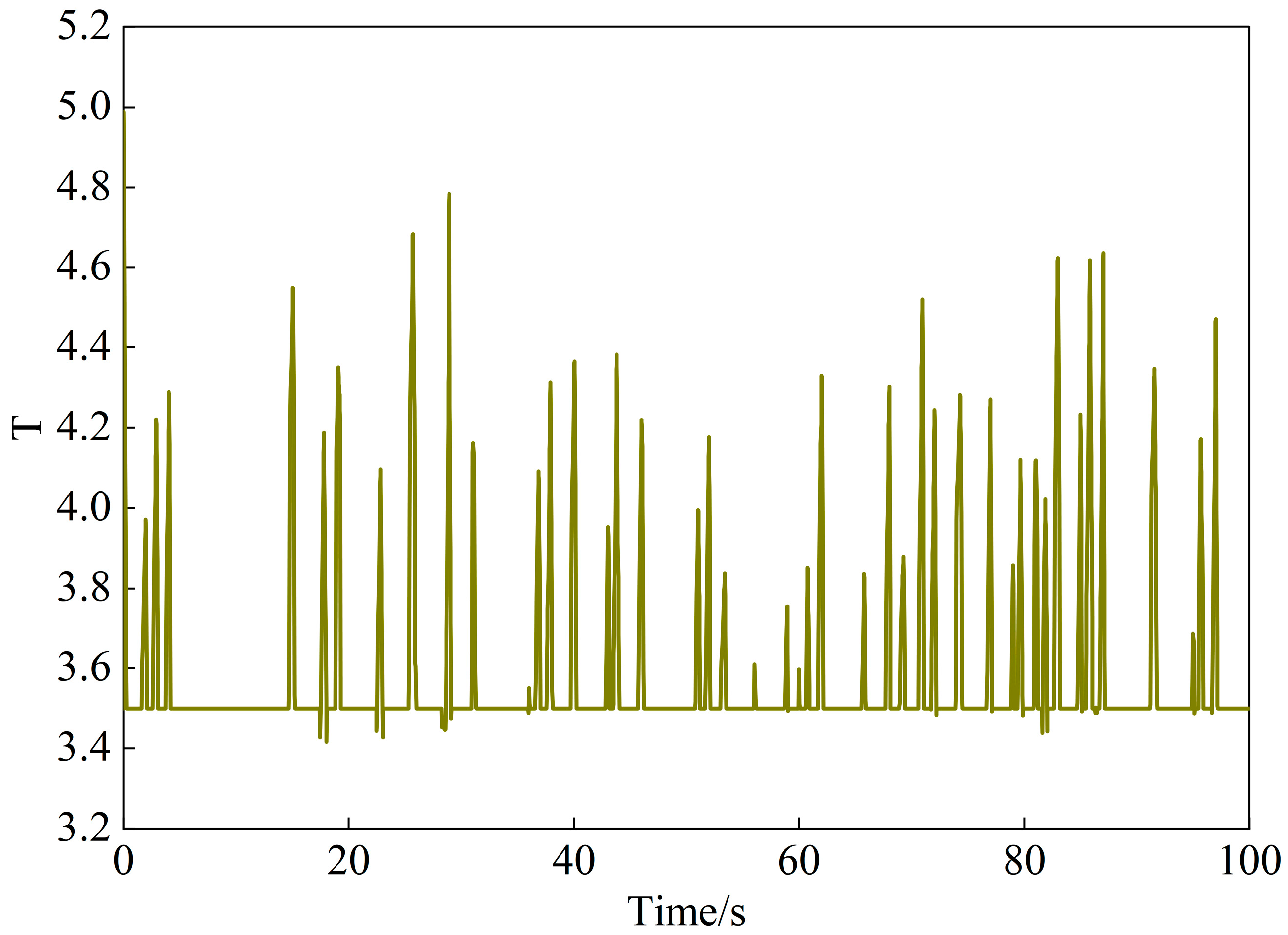
3.1. PFR Instruction Division with Variable Filter Time Constant
3.2. Fuzzy Controller Design
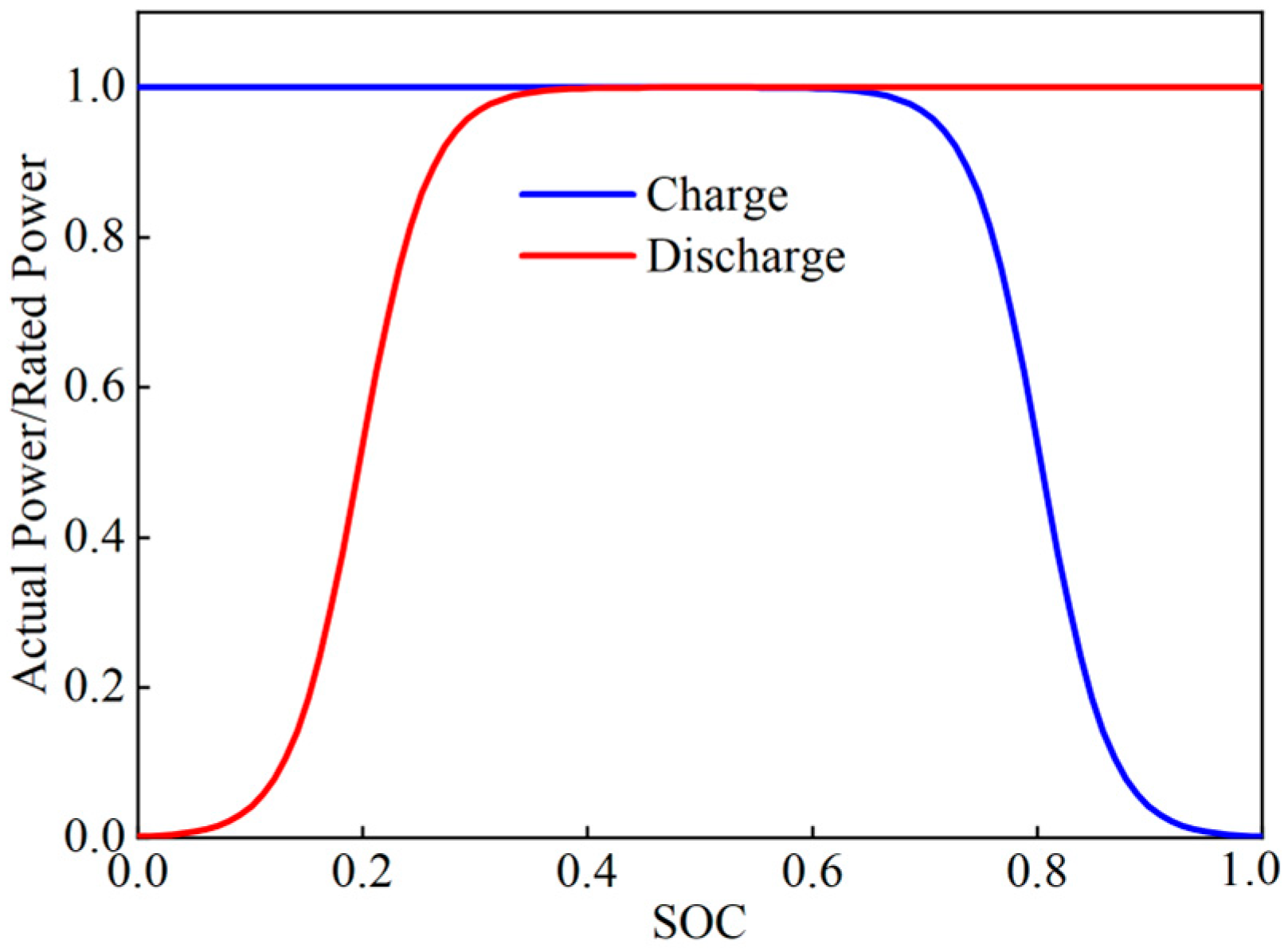
3.3. FESS Output Control
- (1)
- Hz
- (2)
- Hz
- (3)
- Hz
4. Simulation Analysis
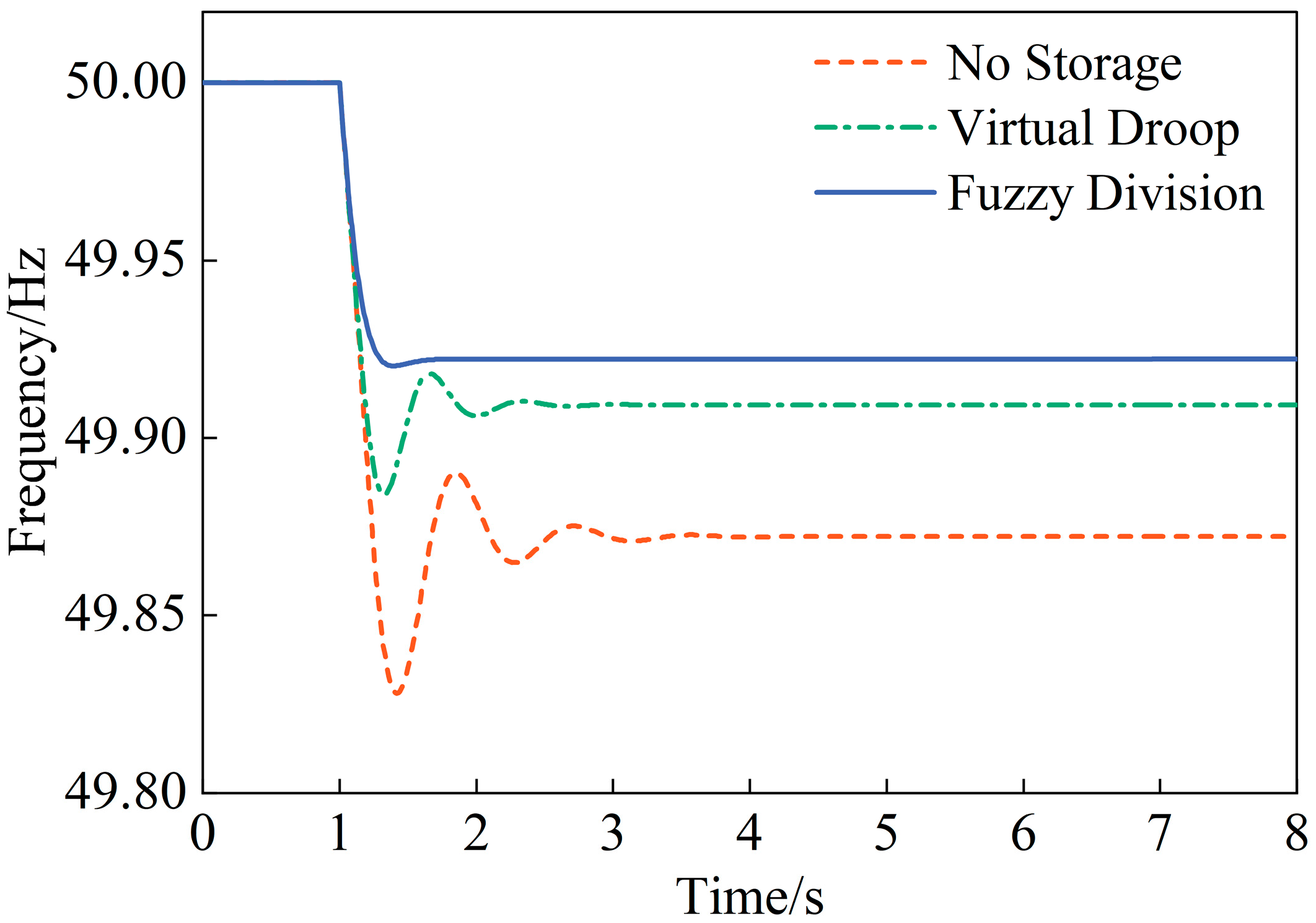
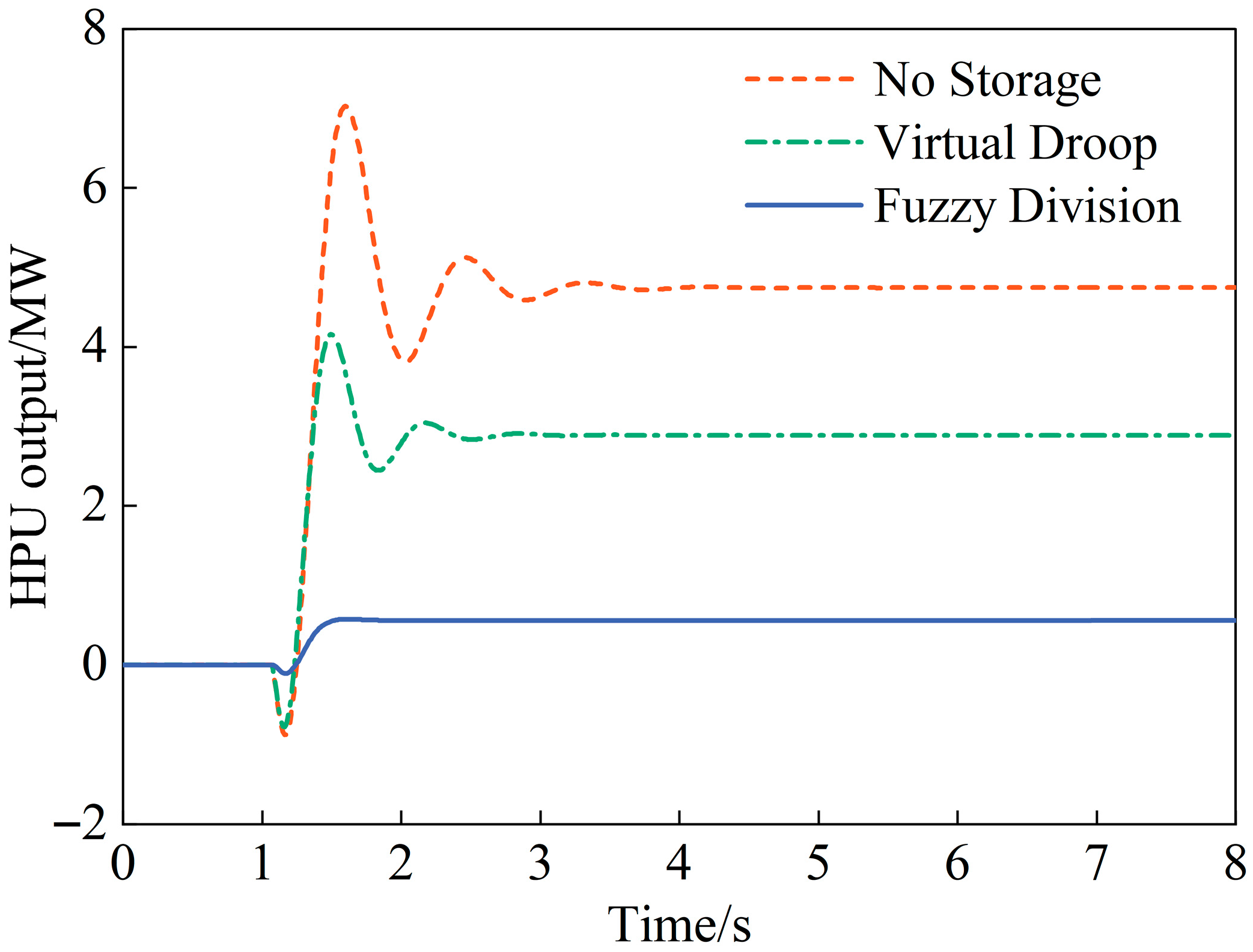
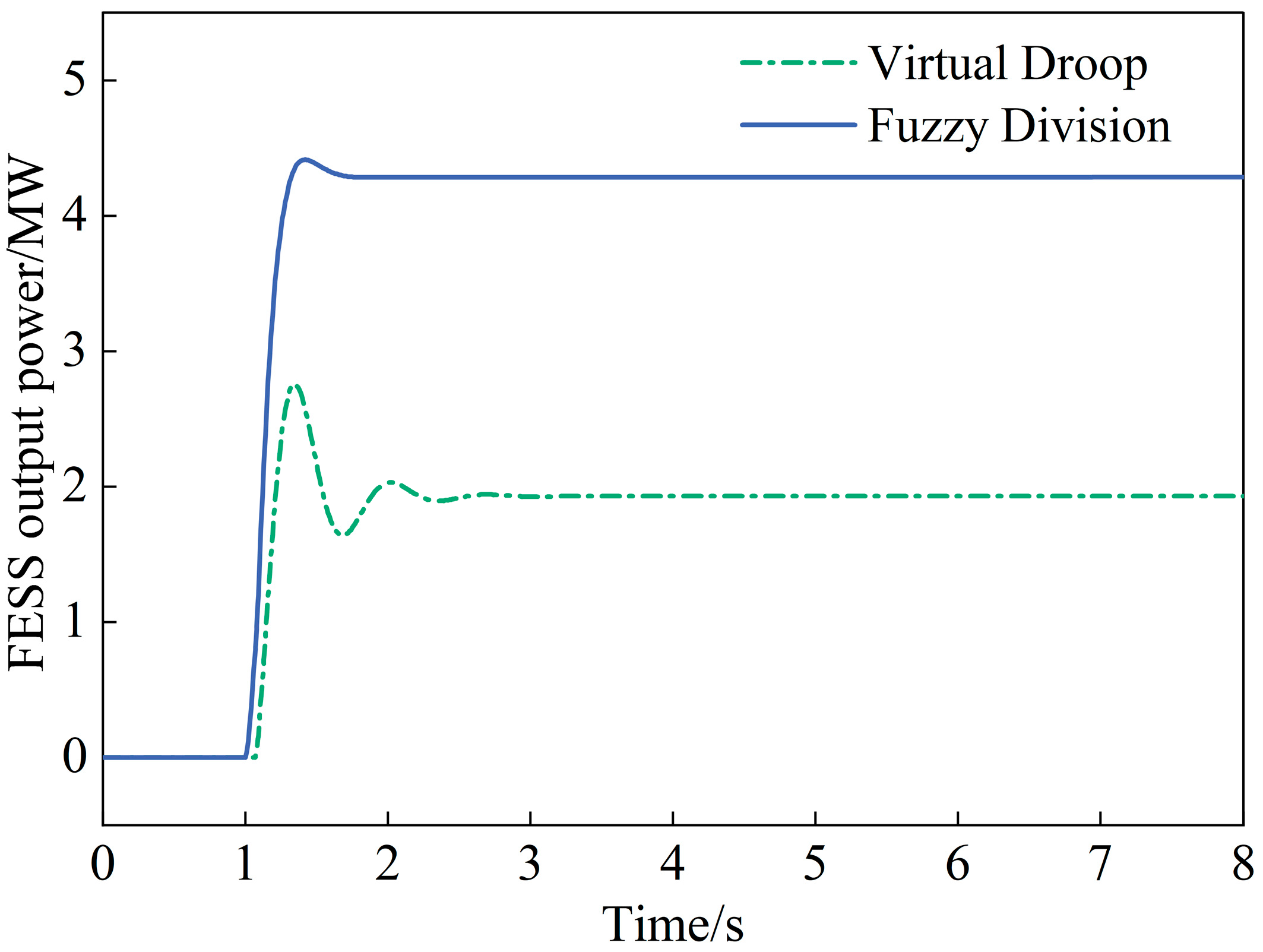
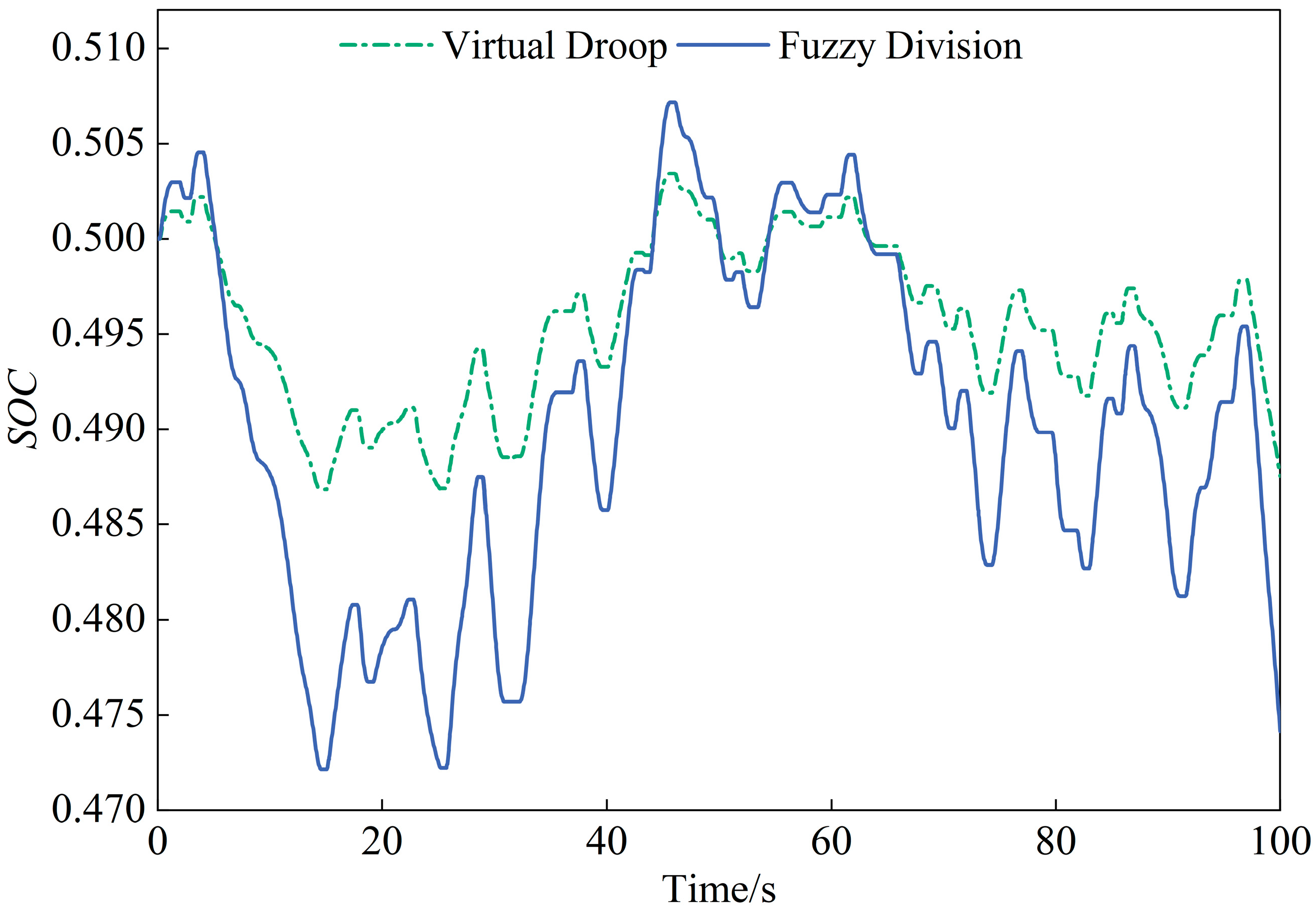
4.1. Step Disturbance
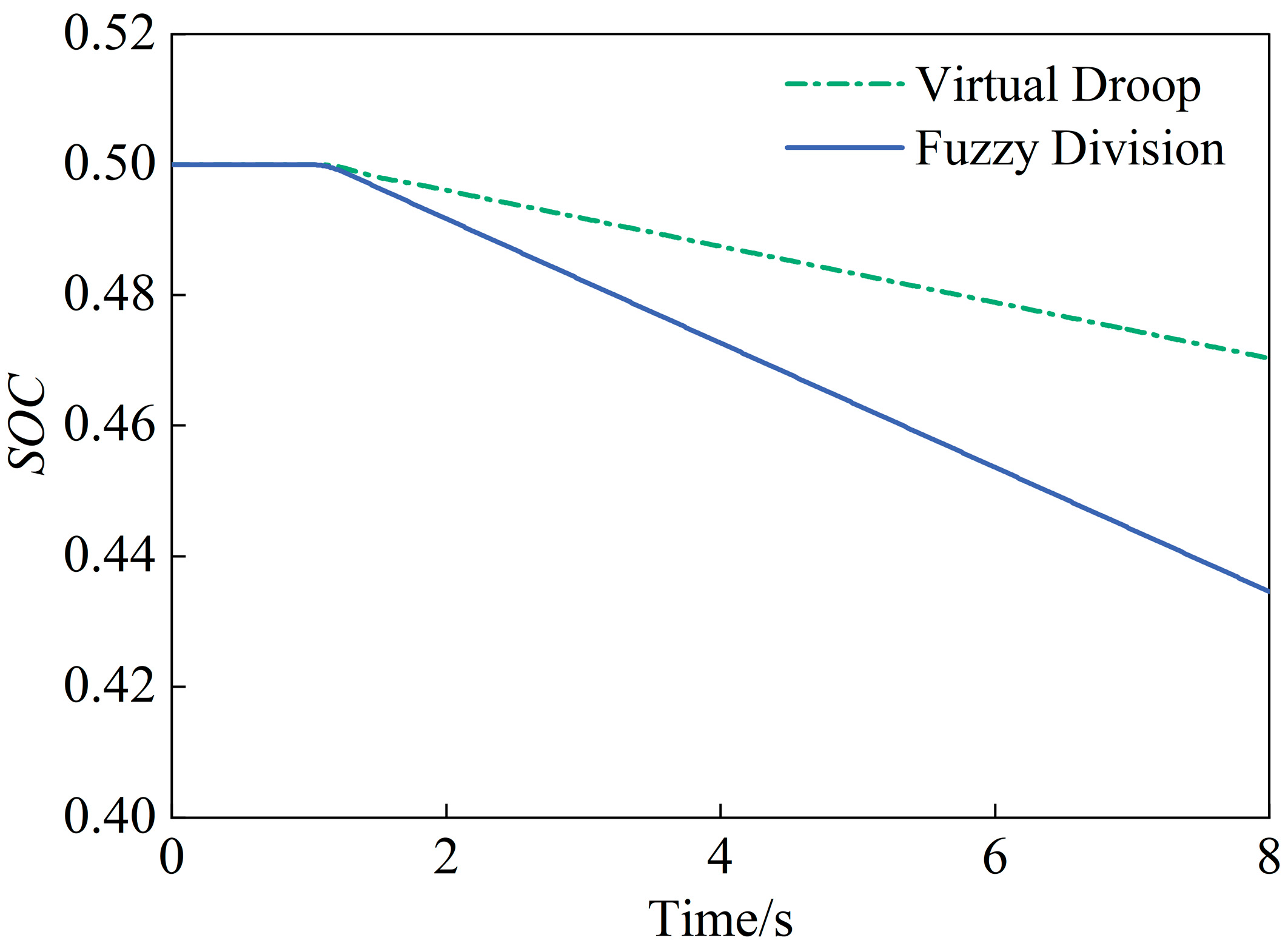
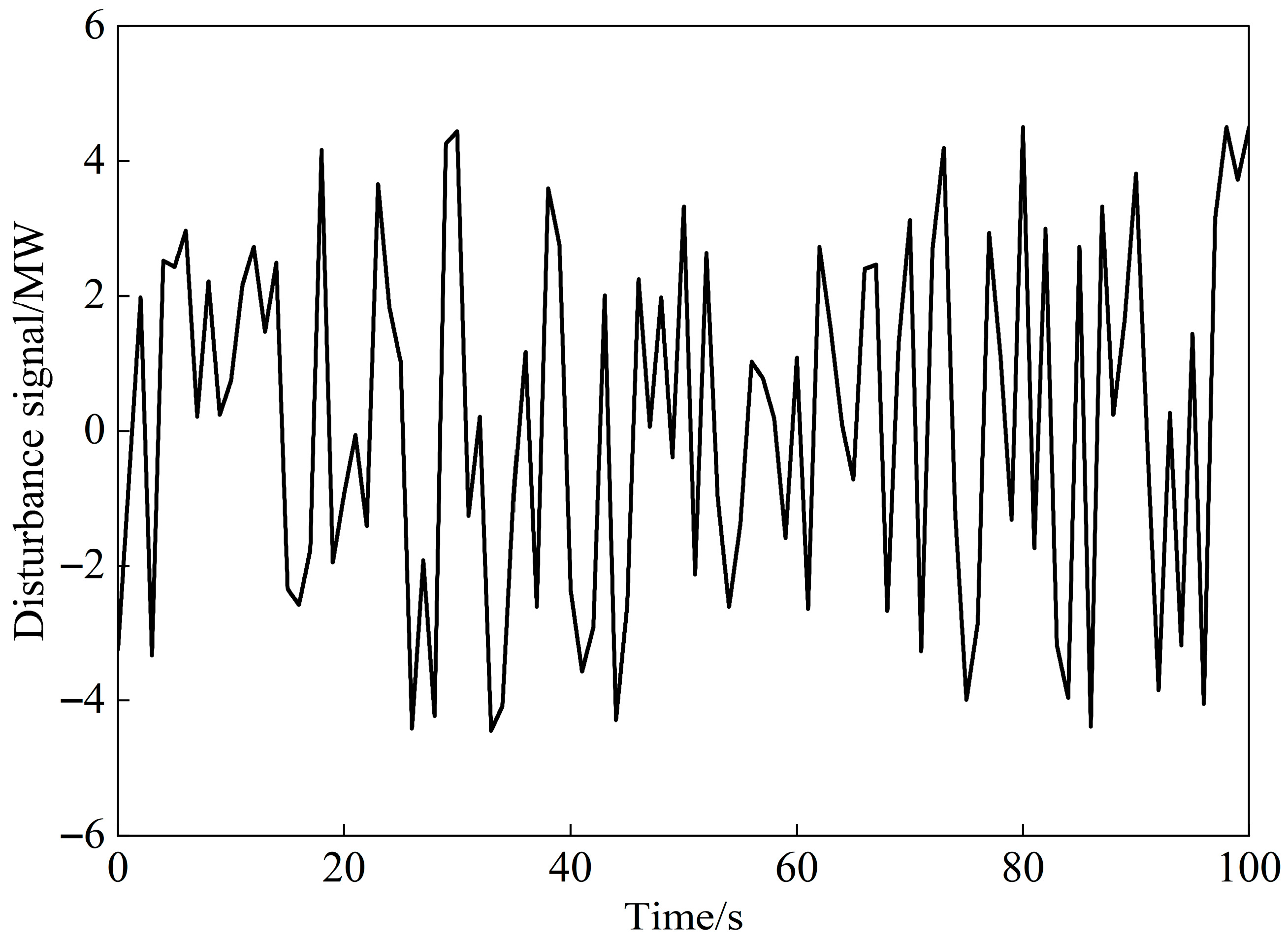
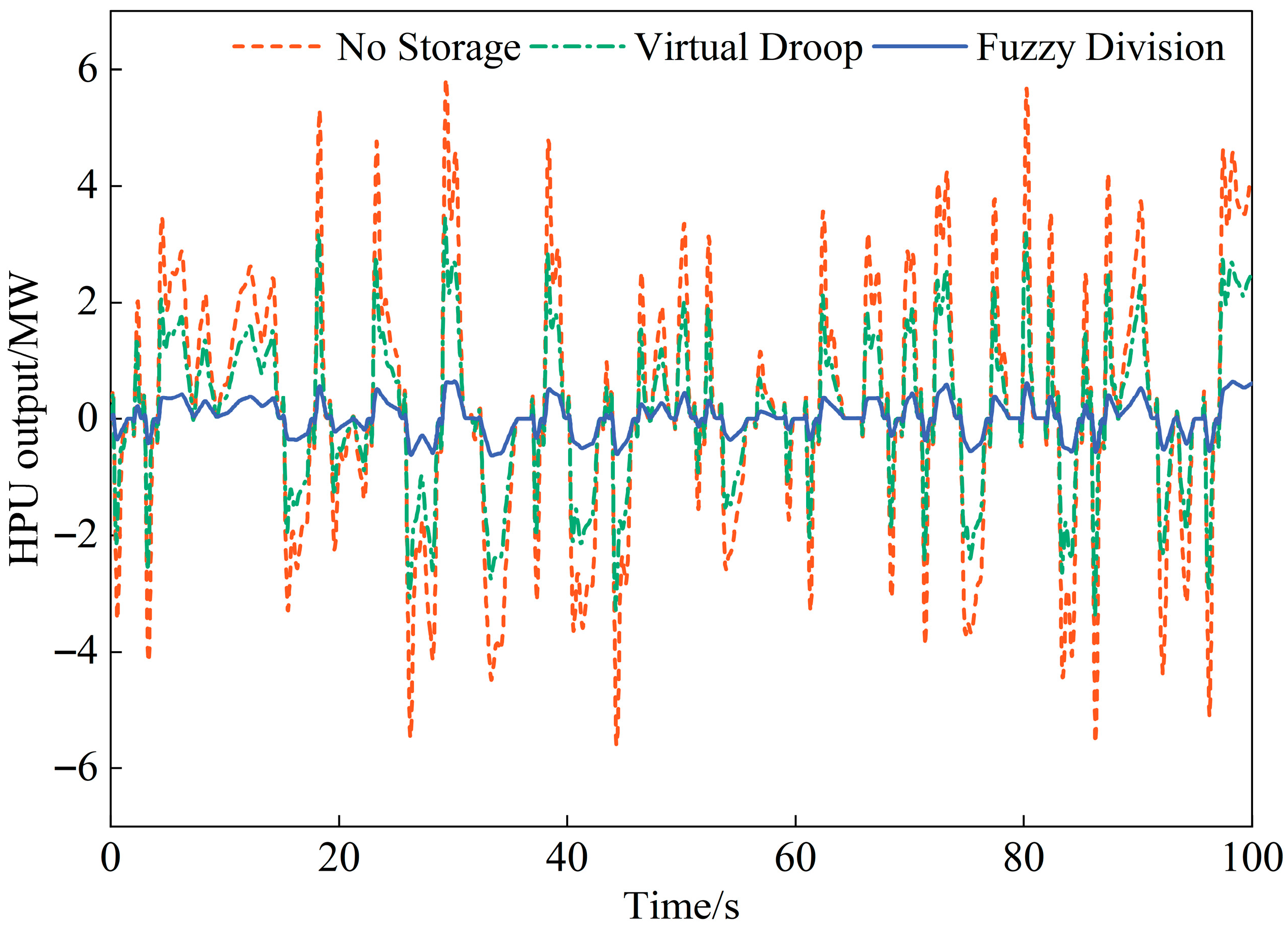
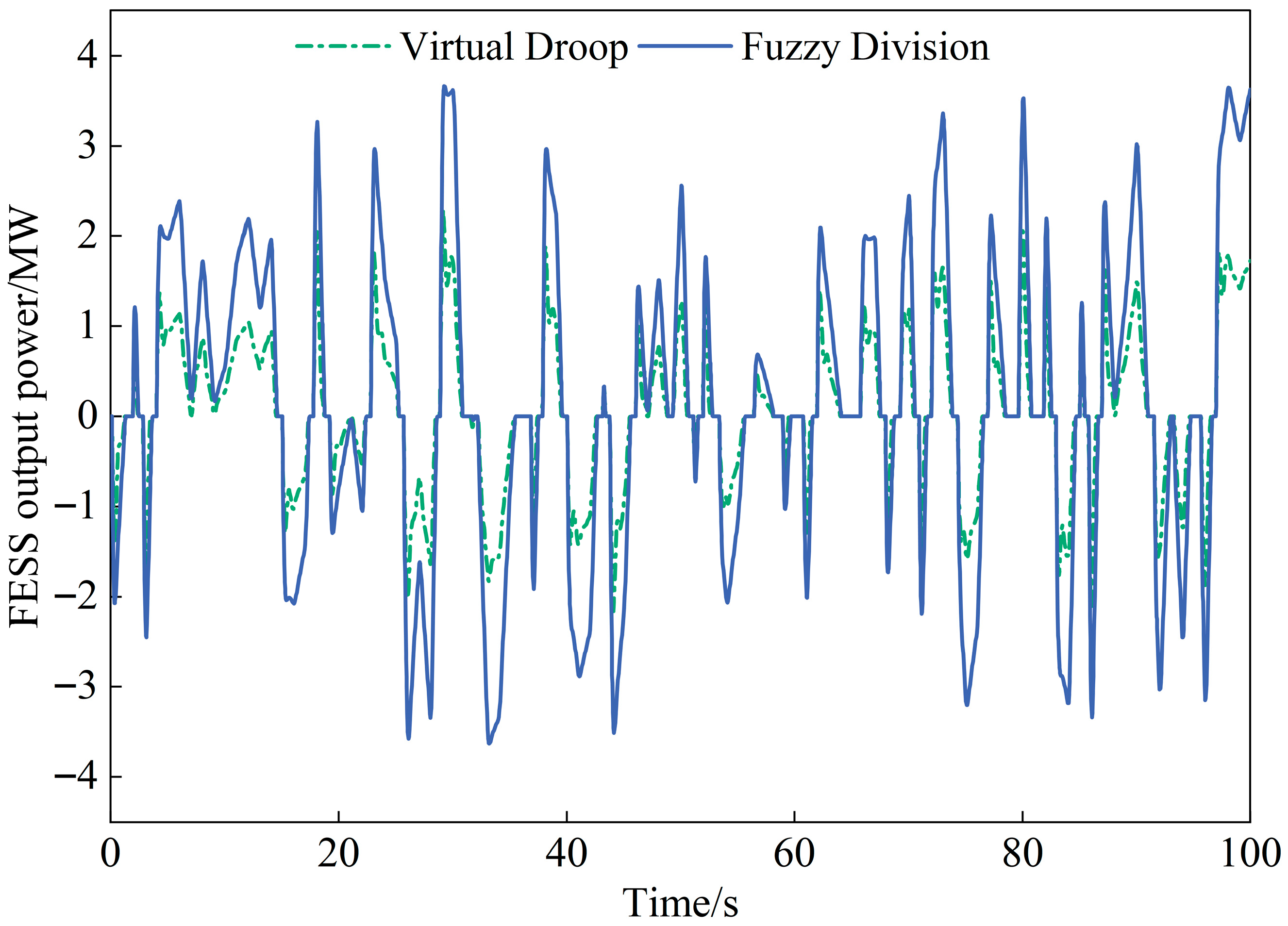
4.2. Continuous Disturbance
5. Conclusions
- (1)
- Enhanced frequency regulation performance: The integration of the FESS significantly improves the system’s frequency response. Under a step disturbance, the proposed strategy reduces the maximum frequency deviation by 53.49% and improves the steady-state frequency by 39.06% compared to HPU-only operation, outperforming conventional virtual droop control. During continuous fluctuations, the strategy effectively suppresses frequency deviations and improves the HPU’s own regulatory performance.
- (2)
- Improved operational conditions for the HPU: The FESS mitigates mechanical stress on the HPU. The fuzzy frequency division control strategy leverages the flywheel’s rapid response to prevent sudden, large power changes in the HPU during step disturbances. Under continuous disturbances, the HPU’s output power fluctuations are significantly reduced, minimizing equipment wear. This enables the power plant to reliably provide more ancillary services, enhancing its economic value.
- (3)
- Optimized role of FESS: The proposed strategy fully utilizes the power-type characteristics of the FESS. It enables the flywheel to provide higher short-term power during initial stage of a step disturbance and undertake a larger share of the regulating burden during continuous fluctuations. This proactively meets PFR demands and effectively reduces the strain on the HPU.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Etanya, T.F.; Tsafack, P.; Ngwashi, D.K. Grid-Connected Distributed Renewable Energy Generation Systems: Power Quality Issues, and Mitigation Techniques—A Review. Energy Rep. 2025, 13, 3181–3203. [Google Scholar] [CrossRef]
- Zhou, D.; Pan, X.; Sun, X.; Hu, F. Resilience Assessment Framework for High-Penetration Renewable Energy Power System. Sustainability 2025, 17, 2058. [Google Scholar] [CrossRef]
- Sadeghian, O.; Shotorbani, A.M.; Ghassemzadeh, S.; Mohammadi-Ivatloo, B. Energy Management of Hybrid Fuel Cell and Renewable Energy Based Systems-A Review. Int. J. Hydrogen Energy 2025, 107, 135–163. [Google Scholar] [CrossRef]
- Gonzalez-Salazar, M.; Poganietz, W.R. Evaluating the Complementarity of Solar, Wind and Hydropower to Mitigate the Impact of El Nino Southern Oscillation in Latin America. Renew. Energy 2021, 174, 453–467. [Google Scholar] [CrossRef]
- Zhang, C.; Cao, W.; Xie, T.; Wang, C.; Shen, C.; Wen, X.; Mao, C. Operational Characteristics and Optimization of Hydro-PV Power Hybrid Electricity System. Renew. Energy 2022, 200, 601–613. [Google Scholar] [CrossRef]
- Zhao, X.; Ren, Y.; Sha, Y.; Zhang, L.; Hou, S.; Xiao, F.; Chen, F.; Chen, S.; He, K.; Luo, L.; et al. Research on the Impact of Hydro-PV Complementary System Operation on Power Grid Based on New Energy Consumption. Math. Probl. Eng. 2022, 2022, 8459948. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, S.; Zhang, J. Adaptive PID Control of Hydropower Units Based on Particle Swarm Optimization and Fuzzy Inference. Water 2025, 17, 1512. [Google Scholar] [CrossRef]
- Dong, W.; Cao, Z.; Zhao, P.; Yang, Z.; Yuan, Y.; Zhao, Z.; Chen, D.; Wu, Y.; Xu, B.; Venkateshkumar, M. A Segmented Optimal PID Method to Consider Both Regulation Performance and Damping Characteristic of Hydroelectric Power System. Renew. Energy 2023, 207, 1–12. [Google Scholar] [CrossRef]
- Jia, Y.; Tan, B.; Zhang, W.; Jiang, D.; Yang, C.; Wen, Y. A Novel Control Strategy for Hydraulic Turbines to Consider Both Primary Frequency Regulation and Ultra-Low Frequency Oscillation Suppression. Energies 2024, 17, 1067. [Google Scholar] [CrossRef]
- Liu, Z.; Yan, Z.; Zhang, H.; Xie, H.; Zou, Y.; Zheng, Y.; Xiao, Z.; Chen, F. Suppression and Analysis of Low-Frequency Oscillation in Hydropower Unit Regulation Systems with Complex Water Diversion Systems. Energies 2024, 17, 4831. [Google Scholar] [CrossRef]
- Chen, G.; Tang, F.; Shi, H.; Yu, R.; Wang, G.; Ding, L.; Liu, B.; Lu, X. Optimization Strategy of Hydrogovernors for Eliminating Ultralow-Frequency Oscillations in Hydrodominant Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1086–1094. [Google Scholar] [CrossRef]
- Lu, X.; Li, C.; Liu, D.; Wang, H.; Zhu, Z.; Ta, X.; Xu, R. Correlating Analysis and Optimization between Hydropower System Parameters and Multi-Frequency Oscillation Characteristics. Energy 2024, 304, 131789. [Google Scholar] [CrossRef]
- Liao, Y.; Yang, W.; Wang, Z.; Huang, Y.; Chung, C.Y. Mechanism of Primary Frequency Regulation for Battery Hybridization in Hydropower Plant. CSEE J. Power Energy Syst. 2024, 10, 2127–2137. [Google Scholar] [CrossRef]
- Feng, C.; Mai, Z.; Wu, C.; Zheng, Y.; Zhang, N. Advantage of Battery Energy Storage Systems for Assisting Hydropower Units to Suppress the Frequency Fluctuations Caused by Wind Power Variations. J. Energy Storage 2024, 78, 109989. [Google Scholar] [CrossRef]
- Ojo, Y.; Alam, S.M.S.; Balliet, W.H.; Mosier, T.M. Frequency Response Improvement in a Standalone Small Hydropower Plant Using Battery Storage. IEEE Trans. Energy Convers. 2024, 39, 2701–2717. [Google Scholar] [CrossRef]
- Gerini, F.; Vagnoni, E.; Seydoux, M.; Cherkaoui, R.; Paolone, M. Enhanced Frequency Containment Reserve Provision from Battery Hybridized Hydropower Plants: Theory and Experimental Validation. Electr. Power Syst. Res. 2024, 235, 110765. [Google Scholar] [CrossRef]
- Shu, H.; He, Y.; Wang, G.; Zhang, H.; Shi, B.; Luo, S. Research on Water Hammer Effect and Cooperative Frequency Regulation Technology of PV-HBESS Compensated Hydroturbine. IEEE Trans. Sustain. Energy 2025, 16, 919–932. [Google Scholar] [CrossRef]
- Esparcia, E.A.; Castro, M.T.; Odulio, C.M.F.; Ocon, J.D. A Stochastic Techno-Economic Comparison of Generation-Integrated Long Duration Flywheel, Lithium-Ion Battery, and Lead-Acid Battery Energy Storage Technologies for Isolated Microgrid Applications. J. Energy Storage 2022, 52, 104681. [Google Scholar] [CrossRef]
- Dragoni, E. Mechanical Design of Flywheels for Energy Storage: A Review with State-of-the-Art Developments. Proc. Inst. Mech. Eng. Pt. L J. Mater. Des. Appl. 2019, 233, 995–1004. [Google Scholar] [CrossRef]
- Tziovani, L.; Hadjidemetriou, L.; Charalampous, C.; Tziakouri, M.; Timotheou, S.; Kyriakides, E. Energy Management and Control of a Flywheel Storage System for Peak Shaving Applications. IEEE Trans. Smart Grid 2021, 12, 4195–4207. [Google Scholar] [CrossRef]
- Cai, X.; Li, X.; He, X.; Yang, Z.; Peng, D.; Ao, C. Research and Simulation of Hydraulic Turbine Speed Control System Based on Fuzzy Control. Procedia Comput. Sci. 2024, 241, 397–402. [Google Scholar] [CrossRef]
- He, L.; Li, W. Research and simulation of hydraulic turbine speed control system based on fuzzy control. Energy Storage Sci. Technol. 2021, 10, 1679–1686. [Google Scholar] [CrossRef]
- Wen, S.; Gong, Y.; Zhao, Z.; Mu, X.; Zhao, S. Power Grid Primary Frequency Control Strategy Based on Fuzzy Adaptive and State-of-Charge Self-Recovery of Flywheel-Battery Hybrid Energy Storage System. Energies 2025, 18, 1536. [Google Scholar] [CrossRef]
- Qin, H.; Qin, L.; Bai, X.; Li, C. A control strategy of flywheel energy storage system participating frequency regulation with pumped storage. Energy Storage Sci. Technol. 2022, 11, 3915–3925. [Google Scholar] [CrossRef]
- Lu, E.; Chen, L.; Li, J.; Yao, L.; Zheng, B.; Mo, B. Research on power system frequency regulation based on improved fuzzy control. Power Syst. Prot. Control. 2017, 45, 46–52. [Google Scholar] [CrossRef]
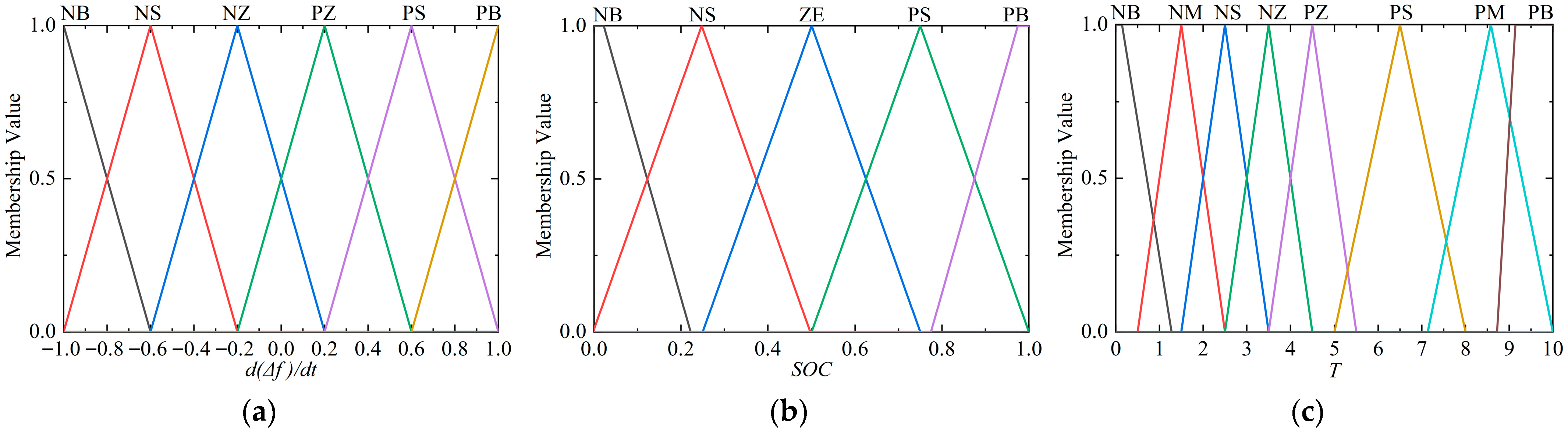

| NB | NS | ZE | PS | PB | |
|---|---|---|---|---|---|
| NB | NB | NM | PS | PM | PB |
| NS | NB | NS | PZ | PS | PM |
| NZ | NM | NS | NZ | PZ | PS |
| PZ | PS | PZ | NZ | NS | NM |
| PS | PM | PS | PZ | NS | NB |
| PB | PB | PM | PS | NM | NB |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.04 | 1 | ||
| 0.05 | 16.7 | ||
| 0.1 | 0.02 | ||
| 5 | 0.5 |
| Control Strategies | Nadir Frequency/Hz | Steady-State Frequency/Hz | HPU | FESS | ||
|---|---|---|---|---|---|---|
| Peak Power Output/MW | Steady-State Value/MW | Peak Power Output/MW | Steady-State Value/MW | |||
| No Storage | 49.828 | 49.872 | 7.023 | 4.744 | / | / |
| Virtual Droop | 49.884 | 49.909 | 4.151 | 2.889 | 2.756 | 1.929 |
| Fuzzy Division | 49.920 | 49.922 | / | 0.558 | 4.412 | 4.287 |
| Control Strategies | Frequency Nadir/Hz | Frequency Peak/Hz | RMSE/Hz |
|---|---|---|---|
| No Storage | 49.852 | 50.144 | 0.0621 |
| Virtual Droop | 49.898 | 50.098 | 0.0484 |
| Fuzzy Division | 49.915 | 50.084 | 0.0474 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, P.; Xu, N.; Lu, J.; Miao, D.; Ma, Q.; Zhang, T.; Zhang, H. A Fuzzy Division Control Strategy for Flywheel Energy Storage to Assist Primary Frequency Regulation of Hydropower Units. Energies 2025, 18, 6032. https://doi.org/10.3390/en18226032
Li Z, Gao P, Xu N, Lu J, Miao D, Ma Q, Zhang T, Zhang H. A Fuzzy Division Control Strategy for Flywheel Energy Storage to Assist Primary Frequency Regulation of Hydropower Units. Energies. 2025; 18(22):6032. https://doi.org/10.3390/en18226032
Chicago/Turabian StyleLi, Zhengfa, Peina Gao, Ning Xu, Jian Lu, Dong Miao, Qiong Ma, Tian Zhang, and Hao Zhang. 2025. "A Fuzzy Division Control Strategy for Flywheel Energy Storage to Assist Primary Frequency Regulation of Hydropower Units" Energies 18, no. 22: 6032. https://doi.org/10.3390/en18226032
APA StyleLi, Z., Gao, P., Xu, N., Lu, J., Miao, D., Ma, Q., Zhang, T., & Zhang, H. (2025). A Fuzzy Division Control Strategy for Flywheel Energy Storage to Assist Primary Frequency Regulation of Hydropower Units. Energies, 18(22), 6032. https://doi.org/10.3390/en18226032





