Addressing Frequency Stability in Islanded Microgrids with Multi-VSGs: A Review of Control Strategies

Abstract

With increasing penetration of renewable energy sources, virtual synchronous generator (VSG) control is playing an increasingly vital role in islanded microgrids’ frequency stabilization. However, frequency stability becomes a critical challenge when multiple VSGs operate in parallel within an islanded microgrid. This paper conducts in-depth research on frequency stability control in islanded microgrids with multi-VSGs. The prevailing frequency modeling approaches and underlying mechanisms of frequency instability are analyzed. Furthermore, both conventional and emerging machine learning-based frequency stability control strategies are comprehensively surveyed. Finally, potential research directions are outlined to facilitate future advancements.

1. Introduction

With the rapid development of distributed energy technologies, islanded microgrids have emerged as a key solution for local utilization of renewable energy [1]. The microgrids are gradually evolving toward larger scale and greater diversity. Owing to the widespread deployment of power electronic converters, microgrids exhibit high control flexibility and improved dispatchability [2]. However, the lack of rotational inertia in power electronic interface devices [3] significantly reduces equivalent system inertia [4]. Consequently, frequency response deteriorates, increasing the challenge of maintaining system stability. Under such conditions, novel grid-forming control technologies are urgently required to enhance frequency regulation and improve overall system stability.

To address this challenge, VSG control was proposed [5]. The virtual synchronous generator (VSG) provides virtual inertia and damping, thereby enhancing the frequency support capability of islanded microgrids [6,7]. Due to its superior frequency regulation capabilities, VSG has become a key technology for the stabilization of islanded microgrids [8].

In high-power microgrids, a single VSG is not enough to support the grid. Therefore, multiple VSGs are typically required to operate in parallel to increase power capacity [9]. Although such multi-VSG configurations improve power supply reliability, they introduce complexities in frequency dynamics. These complexities primarily originate from disparities in control parameters [10] and nonlinear coupling among system components [11], jointly posing new challenges to frequency stability control [12]. Current research on frequency stability in multi-VSG systems predominantly focuses on conventional control approaches, including droop control [13], secondary frequency regulation [14], and virtual-inertia-based methods [15]. However, these strategies are typically constrained by fixed-parameter designs, limited adaptability, and heavy reliance on communication infrastructure. With the development of machine learning techniques, data-driven frequency control has attracted more and more attention. These methods have shown strong potential in frequency deviation mitigation, oscillation suppression, and multi-agent coordination [16].

This paper aims to systematically review the frequency modeling and control methods for islanded multi-VSG parallel systems. The frequency stability issues are thoroughly analyzed. Conventional and machine learning-based frequency control approaches are investigated. Emerging trends in frequency stability control are also discussed. This paper is arranged as follows: frequency modeling methods for multi-VSG systems are introduced in Section 2; the frequency stability issues in multi-machine systems are analyzed in Section 3; conventional and machine learning-based frequency stability control techniques are reviewed in Section 4; and future research trends are discussed in Section 5.

2. Frequency Modeling Methods for Islanded Microgrids with Multi-VSGs

2.1. Principle of VSG Control

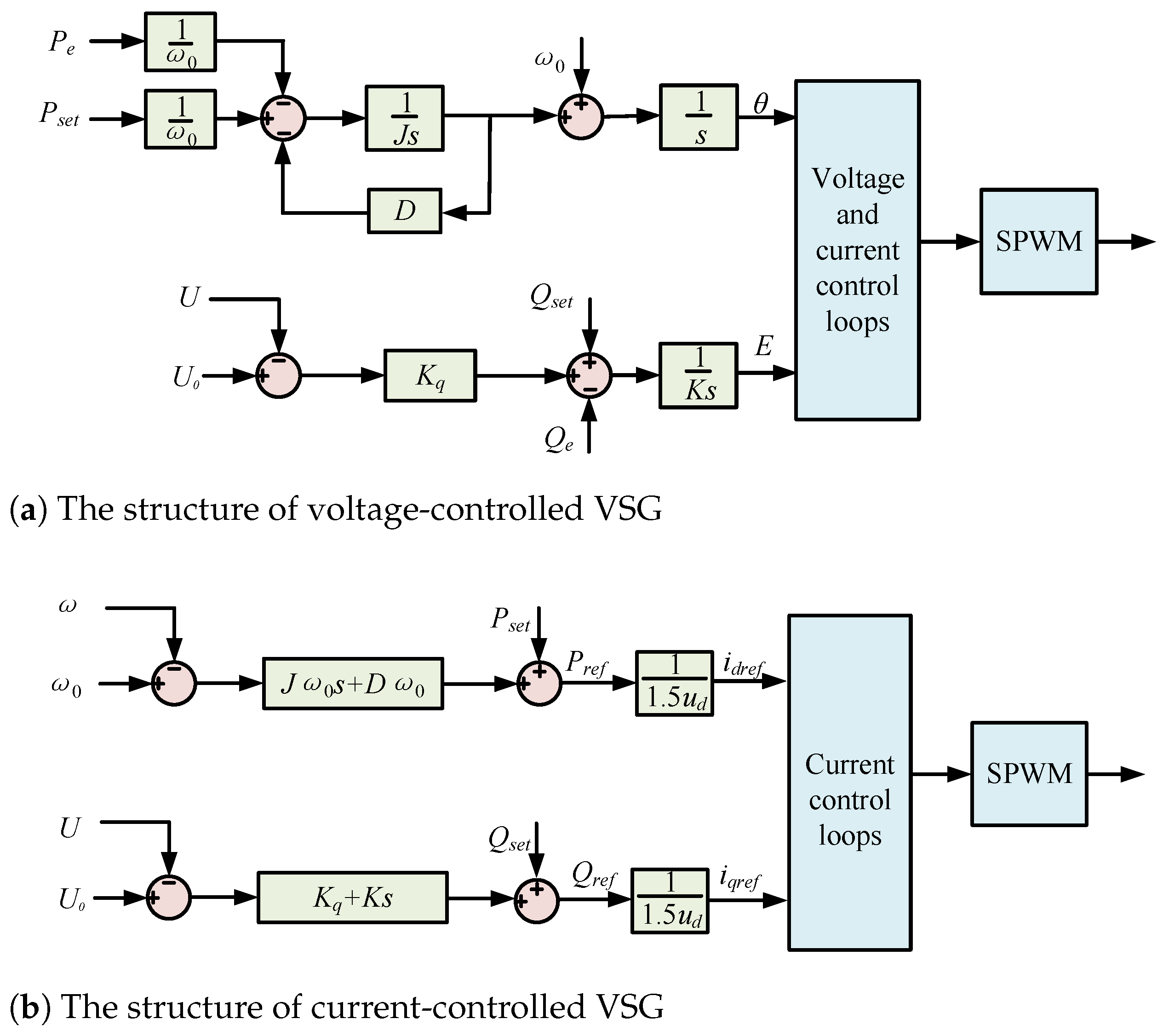
VSG control is equivalent to the operation of a synchronous generator [17]. Based on the control structure, VSGs are mainly classified into voltage-controlled VSG and current-controlled VSG [18], which are shown in Figure 1a and Figure 1b, respectively.

Here, ${\omega }_0$ and $\omega$ represent the grid angular frequency and the VSG angular frequency, respectively. J and D denote the virtual inertia and damping coefficient. $\theta$ is the phase angle of the VSG. E is the output voltage of the VSG. $P_{set}$ and $P_e$ are the active power reference setpoint and the actual active power, respectively. $U_0$ and U refer to the grid voltage and the VSG output voltage. $K_q$ is the reactive power droop coefficient, and K is the integral gain of the reactive power control loop. $Q_{set}$ and $Q_e$ denote the reactive power reference setpoint and the actual reactive power, respectively. $P_{ref}$ and $Q_{ref}$ are the final active and reactive power reference inputs to the VSG control. $u_d$ is the d-axis component of the grid voltage vector. $i_{dref}$ and $i_{qref}$ are the d- and q-axis reference currents for the current control loop, respectively.

The output characteristics of voltage-controlled VSG emulate those of a voltage source with low output impedance. This configuration exhibits the inherent capability to autonomously establish and maintain system frequency and voltage [19]. Consequently, this topology is predominantly employed in weak grid applications [20]. The governing active and reactive power control equations can be expressed as follows:

$$\left\{\begin{array}{c}J{\omega }_0{\displaystyle \frac{d\omega }{dt}}=P_{set}-P_e+D{\omega }_0({\omega }_0-\omega )\hfill \\ \omega =s\theta \hfill \\ E={\displaystyle \frac{1}{Ks}}[Q_{set}-Q_e+K_q(U-U_0)]\hfill \end{array}\right.$$

(1)

The structure of the current-controlled VSG is depicted in Figure 1b. Its output exhibits characteristics of a current source with high output impedance. Frequency establishment in this current-controlled VSG is facilitated by an external phase-locked loop (PLL) [21]. Consequently, its operational structure aligns more closely with conventional PQ-controlled inverters. This configuration is particularly suitable for strong grid applications [22]. The governing power control equations are expressed as follows:

$$\left\{\begin{array}{c}{P}_{ref}=(J{\omega }_{0}s+D{\omega }_0)({\omega }_0-\omega )+P_{set}\hfill \\ Q_{ref}=(Ks+K_q)(U-U_0)+Q_{set}\hfill \end{array}\right.$$

(2)

The comparison between the two types of VSGs is shown in

Table 1. Comparison between voltage-controlled VSG and current-controlled VSG.

Category	Frequency Formation	Grid Adaptability	Source Model	References
Voltage-Controlled VSG	Capable of autonomous frequency formation	Suitable for weak grids and islanded microgrids	Constant voltage source model	[19,20]
Current-Controlled VSG	Depend on grid frequency	Suitable for strong grids and grid-connected scenarios	Constant current source model	[21,22]

.

In summary, compared to current-controlled VSG, the voltage-controlled VSG demonstrates superior suitability for islanded operation owing to its inherent capability to autonomously establish frequency. Therefore, the subsequent modeling and control analysis will be conducted based on the voltage-controlled VSG.

2.2. Frequency Modeling Methods for Islanded Microgrids with Multi-VSGs

In islanded microgrids employing multiple voltage-controlled VSGs, the frequency dynamics exhibit strongly nonlinear characteristics with multi-timescale behavior [23]. To accurately analyze frequency stability issues, it is crucial to select proper modeling methods [24,25]. Current research on VSG frequency modeling has developed diverse approaches, which primarily include small-signal modeling, impedance modeling, nonlinear time-domain simulation, graph-theory and the network-dynamics method, and the data-driven method.

2.2.1. Small-Signal Modeling

The small-signal modeling method, a classical approach widely used for frequency stability analysis, constructs the state-space model of islanded microgrids with multi-VSGs. The system frequency stability is then assessed through eigenvalue analysis of the system matrix after formulating the state equations.

$$\left\{\begin{array}{c}\Delta \dot{x}=A\Delta x+B\Delta u\hfill \\ \Delta y=C\Delta x+D\Delta u\hfill \end{array}\right.$$

(3)

where $\Delta x$ represents the state variables of the VSG system, $\Delta u$ denotes the input disturbance, and $\Delta y$ is the output variables of the VSG system.

In [26], the small-signal model was employed to investigate frequency response and stability boundaries of multi-VSGs. The significant influence of control parameters on oscillation modes was revealed. Based on this, the model was extended to coupled frequency and voltage scenarios in [27], improving its applicability. Meanwhile, the impact of communication delays on small-signal stability was analyzed from a network perspective in [28]. To enhance modeling accuracy, a more detailed small-signal modeling framework was constructed in [29], effectively improving the stability evaluation capability of multi-machine systems. Furthermore, an optimization method for control parameters was proposed based on eigenvalue sensitivity analysis in [30].

While this method proves effective for analyzing system dynamics under small disturbances, its ability to capture large-disturbance behavior remains limited.

2.2.2. The Impedance Modeling Method

The impedance modeling method is widely used for small-signal stability studies. It characterizes the system frequency response by developing frequency-domain impedance models for multi-VSGs. Subsequently, system frequency stability is assessed by applying the Nyquist criterion to the impedance ratio derived from these models.

$$\left[\begin{array}{c}{V}_d\\ V_q\end{array}\right]=\left[\begin{array}{cc}{Z}_{dd}\left(s\right)& Z_{dq}\left(s\right)\\ Z_{qd}\left(s\right)& Z_{qq}\left(s\right)\end{array}\right]\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]$$

(4)

where $V_{dq}$ and $I_{dq}$ denote the dq-axis voltage and current of the VSG, respectively. $Z_{dd}$ and $Z_{qq}$ represent the self-impedances on the dq-axes, and $Z_{dq}$ and $Z_{qd}$ describe the cross-coupling terms between the dq-axes.

In [31,32], impedance-based analysis was used to investigate the coordinated effects of virtual inertia and damping on frequency response, providing guidance for controller parameter design. In [33], an impedance network model tailored for frequency stability analysis was developed. The model was further refined in [34] by incorporating detailed VSG control loops. Additionally, a system-level impedance-based stability assessment method for VSGs was proposed in [35,36], enabling effective prediction of system oscillation boundaries.

While this method provides intuitive insights into how control parameters affect stability margins, significant limitations persist in online modeling implementation and accuracy verification for complex systems.

2.2.3. Nonlinear Time-Domain Simulation

The nonlinear time-domain simulation method enables real-time frequency stability analysis by numerically solving the system’s nonlinear differential equations, facilitating detailed observation of transient behaviors and dynamic responses under various disturbance scenarios. In [37], the combined effects of virtual inertia and damping were investigated under nonlinear conditions. In [38], the nonlinear recovery mechanism of the VSG system was examined in depth. Transient stability boundaries were analyzed from a simulation perspective in [39], and further modeling extensions for transient stability assessment were introduced in [40].

Although this approach achieves high numerical accuracy and flexibility, it requires substantial computational resources, particularly when detailed modeling and long dynamic time scales are considered. The computational burden can be reduced by using simplified models, such as averaged converter models or reduced-order dynamic representations, depending on the dynamics of interest.

2.2.4. The Graph-Theory and Network-Dynamics Method

The graph-theory and network-dynamics method analyzes frequency stability by modeling the interconnections and interactions among VSG units as a graph topology. System-wide dynamic behavior and synchronization properties are then studied through eigenvalue analysis of the resulting Laplacian matrix.

$$J\dot{\omega }+D\omega =P_e-L\theta$$

(5)

where L denotes the Laplacian matrix of the graph.

In [41], graph-theoretical methods were applied to frequency analysis of multi-VSG systems. The constraints imposed by network topology on frequency dynamics were revealed. In [42], graph neural networks were introduced to enable online frequency prediction and coordinated optimization control. A graph-based model for microgrid frequency synchronization assessment was proposed in [43]. In [44], the propagation of disturbances under topological changes was investigated with respect to frequency stability. In [45], a topology-aware adaptive synchronization controller was developed to achieve dynamic consistency among VSG units.

While this method effectively characterizes network-topological dynamics, it also leads to a significant increase in model complexity.

2.2.5. The Data-Driven Method

The data-driven method leverages deep learning and reinforcement learning techniques to extract frequency dynamics from large-scale datasets, enabling predictive frequency modeling and control through learned representations.

In [46], deep reinforcement learning was applied to realize zero steady-state frequency error under multiple disturbance scenarios. In [47], a data-driven framework for frequency stability assessment was proposed. Dynamic evaluation and early warning of system states were achieved. In [48], frequency disturbance trend prediction was achieved using a long short-term memory (LSTM) network model. In [49], graph neural networks were introduced into frequency control tasks. Distributed coordination capability was significantly enhanced. In [50], a reinforcement learning-based control strategy was proposed. Strong nonlinear modeling and self-learning capabilities were demonstrated.

While offering strong adaptability to complex operating conditions, this method exhibits high dependence on data quality.

Comparative analyses of the five frequency modeling approaches are summarized in

Table 2. Comparison of VSG frequency modeling methods.

Method Category	Applicable Disturbance Range	Typical Applications	Main Limitations	References
Small-signal modeling	Small disturbances	Stability boundary analysis	Poor at capturing large disturbance	[26,27,28,29,30]
Impedance modeling	Small to medium disturbances	Frequency response analysis, control design	Poor at capturing large disturbance; depend on accurate parameter identification	[31,32,33,34,35,36]
Nonlinear time-domain simulation	Small to large disturbances	Control strategy validation; transient analysis	High computational burden	[37,38,39,40]
Graph-theory and network-dynamics	Small to medium disturbances	Topology analysis	High model complexity	[41,42,43,44,45]
Data-driven methods	Small to large disturbances	Frequency prediction online; adaptive control	Reliance on large high-quality datasets	[46,47,48,49,50]

.

As evident in Table 2, the impedance modeling method achieves an optimal balance between theoretical rigor and computational efficiency. This approach retains frequency-domain analytical advantages while maintaining dynamic modeling capabilities, making it uniquely suitable for investigating frequency response characteristics. Consequently, impedance modeling was used in this study to investigate the mechanisms underlying frequency stability.

3. Frequency Stability Analysis of Islanded Microgrids with Multi-VSGs

To further investigate the underlying mechanisms of frequency stability, this study established a frequency-domain impedance model of islanded microgrids with multi-VSGs.

3.1. Frequency Impedance Modeling of Islanded Microgrids with Multi-VSGs

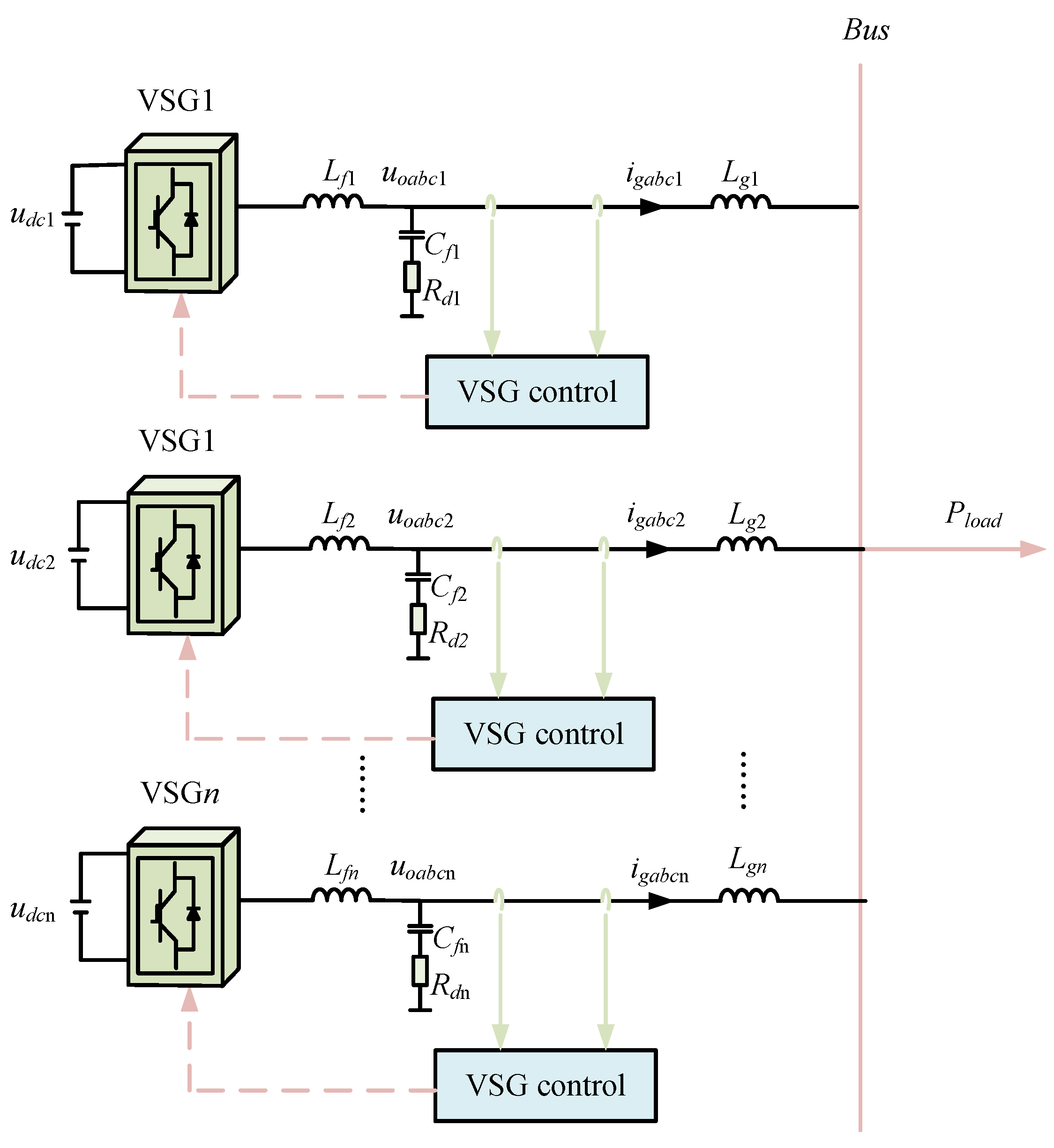
The main topology of a typical islanded microgrid with multi-VSGs is illustrated in Figure 2. In this configuration, each VSG is connected to the common AC bus through its corresponding line impedance. Given that the system investigated in this paper is a small-capacity islanded microgrid with short lines, the line reactance is dominant while the resistance can be reasonably neglected, and the line impedance is thus considered predominantly inductive. However, in low-voltage or long-line networks where the line resistance becomes non-negligible, this assumption may lead to deviations in subsequent stability analyses [51]. Moreover, since the phase angle difference ${\delta }_i$ between the output voltage of the VSG and the common bus is typically small in practice, it is reasonable to apply the approximations: $sin{\delta }_i\approx {\delta }_i,cos{\delta }_i\approx 1$. Under this condition, the active power output $P_{ei}$ of the ith VSG, as depicted in Figure 2, can be expressed as

$$P_{ei}={\displaystyle \frac{E_i{U}_{bus}}{X_{ti}}}{\delta }_i=k_{pi}{\delta }_i=k_{pi}{\displaystyle \frac{{\omega }_i-{\omega }_{bus}}{s}}$$

(6)

where $X_{ti}$ denotes the total reactance composed of the ith VSG and its associated line reactance; $U_{bus}$ is the voltage magnitude of AC bus; $E_i$ represents the output voltage of the ith VSG; $k_{pi}$ denotes the active power-frequency gain; ${\omega }_{bus}$ refers to the angular frequency of the bus voltage.

Here, $u_{dci}$ represents the DC-side voltage of the ith inverter, where i = 1, 2,…, n; $u_{oabci}$ denotes the output voltage of the ith VSG; $i_{gabci}$ is the load-side current of the ith VSG. The parameters $L_{fi}$, $C_{fi}$ and $R_{di}$ denote the filter inductance, capacitance and damping resistance of the ith VSG, respectively. $L_{gi}$ denotes the equivalent inductance on the load side. $P_{load}$ represents the total active load power.

Neglecting the transmission lines loss, the total load power satisfies:

$$\sum _{i=1}^n{P}_{ei}=P_{Load}$$

(7)

By linearizing Equation (1), the transfer function $G_i$ between the output angular frequency deviation $\Delta {\omega }_i$ and the active power deviation $\Delta P_{ei}$ for each VSG can be obtained:

$${\displaystyle \frac{\Delta {\omega }_i}{\Delta P_{ei}}}=-{\displaystyle \frac{1}{J_i{\omega }_{0}s+D_i{\omega }_0}}=G_i$$

(8)

By linearizing and combining Equations (6)–(8), the transfer function from the bus angular frequency deviation $\Delta {\omega }_{bus}$ to the active power deviation $\Delta P_{ei}$ of $VS{G}_i$ can be derived as

$$\left\{\begin{array}{c}{\displaystyle \frac{\Delta P_{ei}}{\Delta {\omega }_{bus}}}=-{\displaystyle \frac{k_{pi}{\omega }_0(J_{i}s+D_i)}{J_i{\omega }_0{s}^2+D_i{\omega }_{0}s+k_{pi}}}={\displaystyle \frac{1}{Z_i}}\hfill \\ {\displaystyle \frac{\Delta {\omega }_{bus}}{\Delta P_{load}}}={\displaystyle \frac{1}{{\sum }_{i=1}^n{Z}_i}}\hfill \end{array}\right.$$

(9)

where $\Delta$ denotes small-signal deviations, $J_i$ denotes the virtual inertia of the ith VSG, $D_i$ is the damping coefficient of the ith VSG, $Z_i$ represents the frequency impedance of the ith VSG.

From Equation (9), the active power response of $VS{G}_i$ under load disturbances can be expressed as follows:

$${\displaystyle \frac{\Delta P_{ei}}{\Delta P_{load}}}={\displaystyle \frac{\frac{1}{Z_i}}{{\sum }_{i=1}^n\frac{1}{Z_i}}}$$

(10)

Substituting Equations (8) and (10), the angular frequency response of $VS{G}_i$ under load disturbances in an islanded microgrid with multi-VSGs can be obtained:

$${\displaystyle \frac{\Delta {\omega }_{ei}}{\Delta P_{load}}}={\displaystyle \frac{\frac{G_i}{Z_i}}{{\sum }_{i=1}^n\frac{1}{Z_i}}}$$

(11)

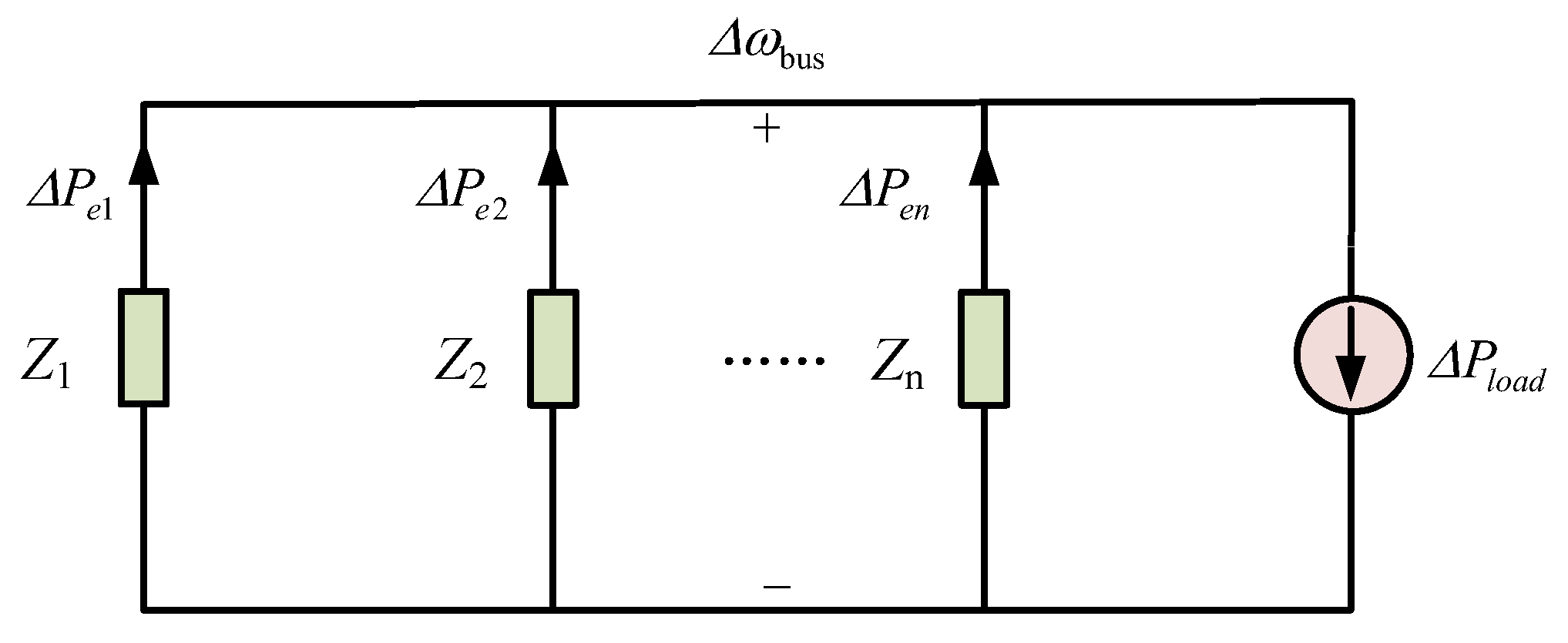
The equivalent circuit model of the multi-VSG system is subsequently derived from Equations (8)–(11) and is shown in Figure 3.

3.2. Frequency Stability Analysis in Islanded Microgrids with Multi-VSG

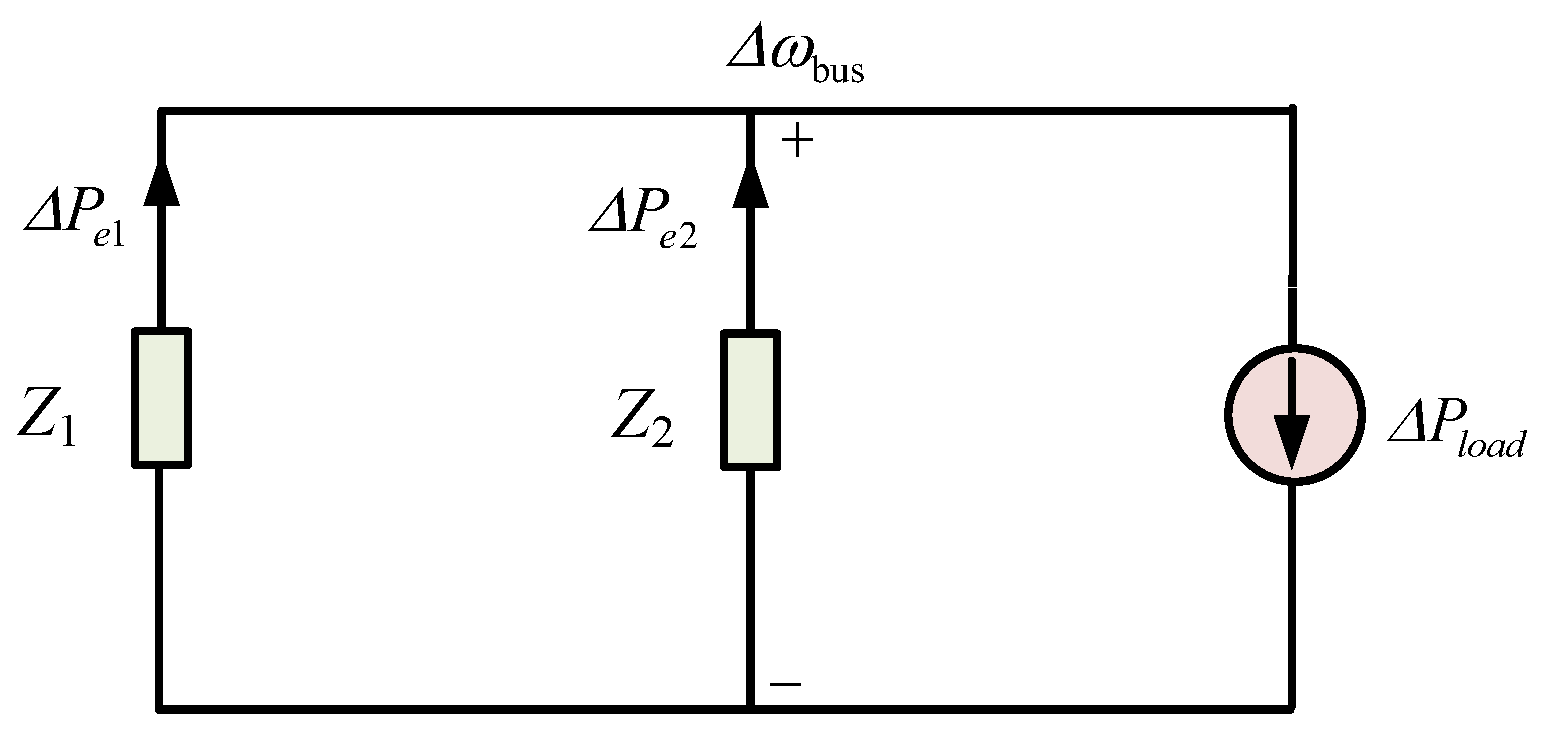
To further investigate the mechanism of frequency stability, this study analyzes a dual-VSG islanded system as a representative case. The corresponding equivalent circuit is presented in Figure 4.

Based on Equation (8), the frequency responses of the two VSGs under active power variation can be expressed as:

$$\left\{\begin{array}{c}{\displaystyle \frac{\Delta {\omega }_1}{\Delta P_{e1}}}=-{\displaystyle \frac{1}{J_1{\omega }_{0}s+D_1{\omega }_0}}\hfill \\ {\displaystyle \frac{\Delta {\omega }_2}{\Delta P_{e2}}}=-{\displaystyle \frac{1}{J_2{\omega }_{0}s+D_2{\omega }_0}}\hfill \end{array}\right.$$

(12)

From Equation (11), the frequency responses to load disturbances can be derived as

$$\left\{\begin{array}{c}{\displaystyle \frac{\Delta {\omega }_1}{\Delta P_{load}}}=-{\displaystyle \frac{k_{p1}}{(J_1{\omega }_0{s}^2+D_1{\omega }_{0}s+k_{p1}){\sum }_{i=1}^2\frac{k_{pi}{\omega }_0(J_{i}s+D_i)}{J_i{\omega }_0{s}^2+D_i{\omega }_{0}s+k_{pi}}}}\hfill \\ {\displaystyle \frac{\Delta {\omega }_1}{\Delta P_{load}}}=-{\displaystyle \frac{k_{p2}}{(J_2{\omega }_0{s}^2+D_2{\omega }_{0}s+k_{p2}){\sum }_{i=1}^2\frac{k_{pi}{\omega }_0(J_{i}s+D_i)}{J_i{\omega }_0{s}^2+D_i{\omega }_{0}s+k_{pi}}}}\hfill \end{array}\right.$$

(13)

The above expressions establish the fundamental dynamic model of the dual-VSG system. Based on these frequency response functions, two critical aspects influencing frequency stability can be identified. First, frequency deviation is an inherent characteristic of VSG control under load disturbances. Second, during transients, mismatches in the dynamic responses of multiple VSGs can induce low-frequency oscillations. To further investigate these mechanisms, the following subsections provide a detailed analysis.

3.2.1. Frequency Deviation and Mitigation Methods

Applying the final value theorem to Equation (12) yields the following steady-state values:

$$\left\{\begin{array}{c}\Delta {\omega }_{1s}=-\underset{s\to 0}{lim}s{\displaystyle \frac{1}{J_1{\omega }_{0}s+D_1{\omega }_0}}{\displaystyle \frac{\Delta P_{e1}}{s}}=-{\displaystyle \frac{1}{D_1{\omega }_0}}\Delta P_{e1}\hfill \\ \Delta {\omega }_{2s}=-\underset{s\to 0}{lim}s{\displaystyle \frac{1}{J_2{\omega }_{0}s+D_2{\omega }_0}}{\displaystyle \frac{\Delta P_{e2}}{s}}=-{\displaystyle \frac{1}{D_2{\omega }_0}}\Delta P_{e2}\hfill \end{array}\right.$$

(14)

where $\Delta {\omega }_{1s}$ and $\Delta {\omega }_{2s}$ are the steady-state values of $\Delta {\omega }_1$ and $\Delta {\omega }_2$, respectively.

Equation (14) reveals that frequency deviation is an inherent characteristic of VSG control under load disturbances. This deviation is directly proportional to the magnitude of the load variations and inversely proportional to the damping coefficient.

To mitigate frequency deviation, two primary approaches exist. First, increasing the damping coefficient of each VSG directly reduces the deviation. Second, Second, coordinated parameter tuning across VSGs can achieve power sharing proportional to their rated capacities, minimizing the overall steady-state frequency deviation in the parallel system. The corresponding coordination condition is given by Equation (15).

$${\displaystyle \frac{\Delta P_{e1}}{D_1}}={\displaystyle \frac{\Delta P_{e2}}{D_2}}$$

(15)

By combining the principle of proportional load sharing according to capacity with Equation (15), the parameter condition for minimizing frequency deviation is derived:

$${\displaystyle \frac{D_1}{D_2}}={\displaystyle \frac{\Delta P_{e1}}{\Delta P_{e2}}}={\displaystyle \frac{S_1}{S_2}}$$

(16)

where $S_1$ and $S_2$ are the rate capacity the of VSG1 and VSG2, respectively.

Since parameter tuning alone cannot fully restore frequency, secondary frequency regulation must be implemented. This is typically achieved by employing an integral controller to eliminate the steady-state deviation, which can be expressed as

$$P_{sec}=K_i\int \Delta fdt$$

(17)

where $P_{sec}$ is the compensation power of secondary frequency regulation, $K_i$ is the integral gain, and $\Delta f$ is frequency deviation value.

Additionally, feedforward compensation based on load disturbance detection and forecasting can be applied to eliminate frequency deviations.

$$P_f=K_f\Delta P_{loade}$$

(18)

where $P_f$ is the feedforward compensation power, which denotes the residual power required to compensate the remaining frequency deviation after the VSG’s primary regulation, $K_f$ is the feedforward gain, and $\Delta P_{loade}$ represents the estimated load disturbance. In practical applications, $\Delta P_{loade}$ usually obtained through machine learning models. By injecting $P_f$ into the active power–frequency control loop, the residual power deficit during load disturbances can be compensated, thereby eliminating frequency deviations.

3.2.2. Low-Frequency Oscillation and Suppression Methods

According to Equation (13), ensuring consistent frequency responses among all VSGs during transients is essential for preventing low-frequency oscillations [52]. This consistency requires satisfying the following condition:

$${\displaystyle \frac{k_{p1}}{J_1{\omega }_0(s^2+\frac{D_1}{J_1}s+\frac{k_{p1}}{J_1{\omega }_0})}}={\displaystyle \frac{k_{p2}}{J_2{\omega }_0(s^2+\frac{D_2}{J_2}s+\frac{k_{p2}}{J_2{\omega }_0})}}$$

(19)

To ensure this, the system must satisfy the following condition:

$$\left\{\begin{array}{c}{\displaystyle \frac{J_1}{k_{p1}}}={\displaystyle \frac{J_2}{k_{p2}}}\hfill \\ {\displaystyle \frac{D_1}{k_{p1}}}={\displaystyle \frac{D_2}{k_{p2}}}\hfill \end{array}\right.$$

(20)

However, the parameter requirements specified in Equation (20) are often difficult to satisfy in practice, potentially resulting in low-frequency oscillations.

Effective oscillation suppression strategies can be inferred from the system dynamics. Equation (19) indicates that increasing the damping coefficient D and reducing the virtual inertia J enhances system damping, thereby accelerating oscillation decay. Simultaneously, Equation (20) suggests that system-level parameter coordination can achieve consistent responses among multiple VSG nodes, reducing the risk of system-level low-frequency oscillations.

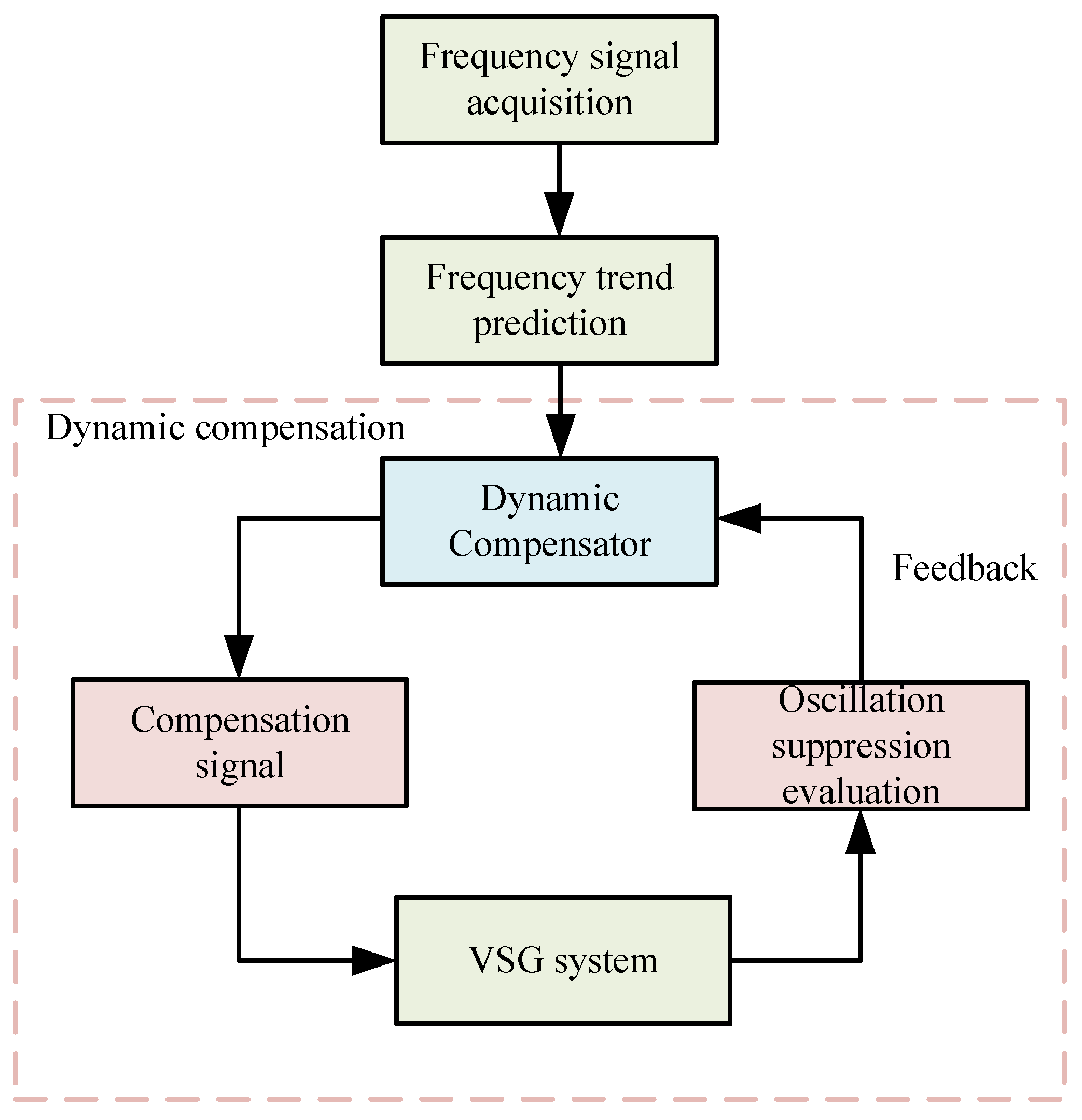
Furthermore, when oscillations cannot be entirely eliminated through parameter adjustment, proactive prediction and dynamic compensation techniques can be employed to suppress persistent low-frequency oscillations.

$$U_{osc}=K_{dyn}{x}_e$$

(21)

Here, $U_{osc}$ is the compensation signal of dynamic compensation, $K_{dyn}$ is the dynamic compensation gain, $x_e$ represents the estimated oscillation signal derived from machine learning prediction or modal identification. By injecting $U_{osc}$ into the active power–frequency control loop, the oscillatory power associated with low-frequency modes can be effectively compensated, thereby eliminating low-frequency oscillations.

4. Frequency Stabilization Control Strategies for Islanded Microgrids with Multi-VSGs

As analyzed in the preceding section, frequency deviation and low-frequency oscillation constitute the two primary frequency stability challenges in islanded microgrids with multi-VSGs. Frequency deviation drives the system away from its nominal operating frequency, adversely impacting stable active power sharing between sources and loads [53]. Low-frequency oscillation can induce persistent power swings [54], potentially leading to VSG disconnection from the grid. Consequently, developing effective control strategies targeting these two issues is essential for ensuring stable system operation.

The following sections systematically review mainstream conventional and machine learning-based strategies for addressing frequency deviation and low-frequency oscillation, comparing their respective characteristics.

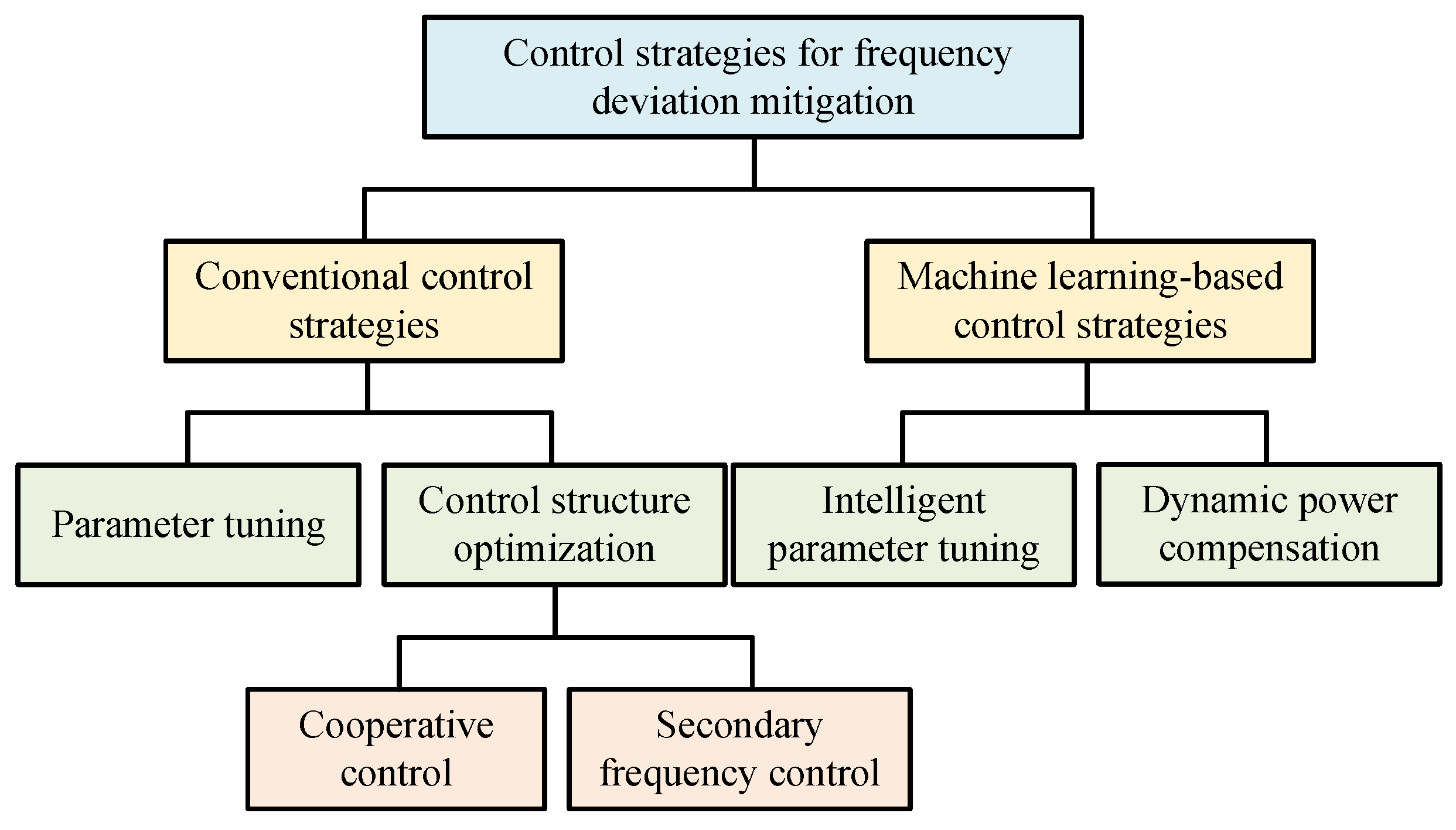
4.1. Control Strategies for Frequency Deviation Mitigation

Based on the analysis in Section 3.2, the current control strategies for mitigating frequency deviations can be categorized into four primary types: (1) Parameter tuning; (2) Control structure optimization; (3) Intelligent parameter tuning based on machine learning; (4) Dynamic power compensation based on machine learning.

These strategies can be further divided into two major categories, as illustrated in Figure 5: (1) Conventional control strategies, including parameter tuning and control structure optimization; (2) Machine learning-based control strategies, involving intelligent parameter tuning and dynamic power compensation.

4.1.1. Conventional Control Strategies

Conventional control strategies are grounded in classical control theory. These strategies primarily aim to mitigate frequency deviations by tuning controller parameters or modifying control structures. Existing research within this domain predominantly focuses on two key aspects:

(1) Parameter Tuning

Equation (14) indicates that optimizing key parameters, particularly the damping coefficient, directly mitigates steady-state frequency deviation. This principle has been supported by prior studies.

In [55,56], frequency deviation was suppressed by introducing rate-of-change-of-frequency (ROCOF) feedback and additional damping. In [57], a self-adaptive virtual droop control method was proposed, where the damping coefficient D was dynamically adjusted based on load variation, effectively reducing long-term frequency offset. In [58], a model reference adaptive system was developed for real-time tuning of inertia and damping, achieving minimal frequency deviation. In [59], a multi-objective optimization algorithm was used to jointly tune J and D, balancing steady-state frequency accuracy and dynamic response, and significantly reducing frequency deviation.

(2) Control Structure Optimization

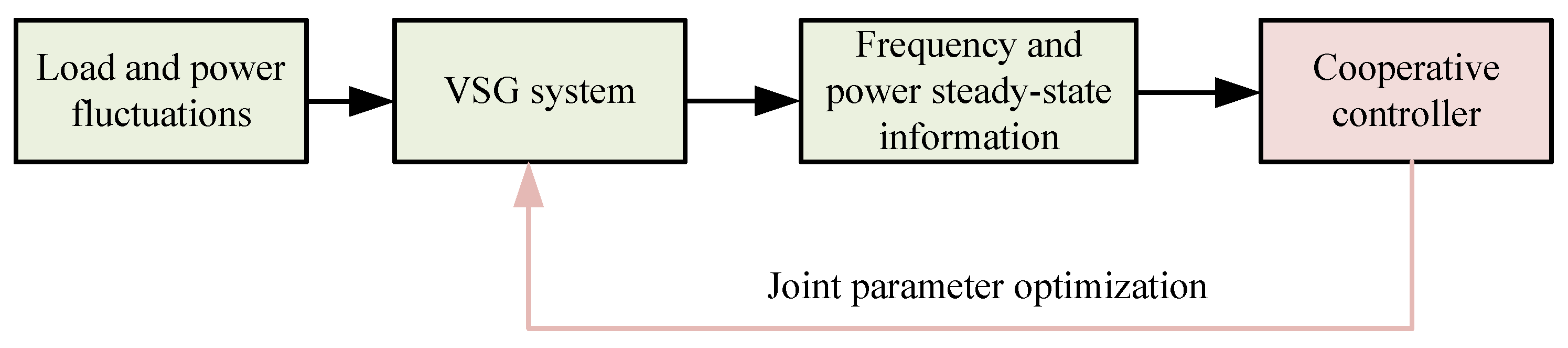
This work primarily concentrates on two research directions: cooperative control and secondary frequency control.

Cooperative control, as indicated by Equations (15) and (16) and depicted in Figure 6, coordinates the parameters of multiple VSGs to achieve power sharing proportional to their rated capacities, thereby minimizing the overall steady-state frequency deviation. In [60], a centralized optimization platform was developed to jointly tune the control parameters of multiple VSGs, aiming to achieve capacity-proportional power sharing while suppressing steady-state frequency deviation. In [61,62], a centralized MPC framework was proposed to jointly optimize multiple VSG parameters, achieving capacity-proportional power sharing and improved steady-state frequency performance. In [63], a distributed optimization algorithm was introduced to coordinate parameter tuning via limited communication, ensuring capacity-proportional power sharing and reducing the steady-state frequency error of the system.

The secondary frequency control, as derived in Equation (17) and illustrated in Figure 7, mitigates steady-state frequency deviation by introducing a power compensation term into the VSG control loop, thereby restoring the system frequency to its nominal value.

In [64], long-term frequency correction was performed using integral droop control. An MPC-based secondary frequency regulation strategy was proposed in [65], where an input observer was employed to estimate disturbances, significantly improving frequency deviation suppression. In [66], the secondary frequency control mechanism was modified to ensure frequency recovery to the nominal value. In [67], a distributed secondary frequency control strategy was designed based on a linear active disturbance rejection control (LADRC) algorithm. Frequency restoration was achieved under communication constraints and disturbance uncertainties. An enhanced robust PI controller was developed in [68], providing strong resistance to communication delays and improving frequency recovery performance. In [69], a graph-theory-based consensus algorithm was applied to realize decentralized secondary frequency control. Both frequency restoration consistency and active power sharing were ensured. In [70], a distributed event-triggered secondary frequency control strategy was proposed. Progressive frequency convergence was achieved while significantly reducing the communication burden.

4.1.2. Machine Learning-Based Control Strategies

The rapid development of artificial intelligence has enabled machine learning to provide novel optimization solutions for frequency deviation control in VSG systems. Current research primarily focuses on two methods.

(1) Intelligent Parameter Tuning

The damping coefficient D adjustment to reduce steady-state frequency deviation can be realized via machine learning techniques. In [71], a deep neural network was employed to model the nonlinear relationship between frequency states and damping coefficients. Adaptive parameter tuning was achieved under various disturbance conditions. In [72,73], deep reinforcement learning models were applied to jointly regulate virtual inertia and damping coefficients in complex frequency evolution scenarios. In [74], convolutional neural networks (CNN) were introduced to classify disturbance patterns, and optimal parameter sets were dynamically selected based on classification results. Accurate damping adjustment under varying conditions was ensured. In [75], LSTM networks were used to capture the evolving trend of frequency deviations. Time-sequenced adjustment of damping coefficients was achieved, resulting in improved dynamic performance and steady-state accuracy.

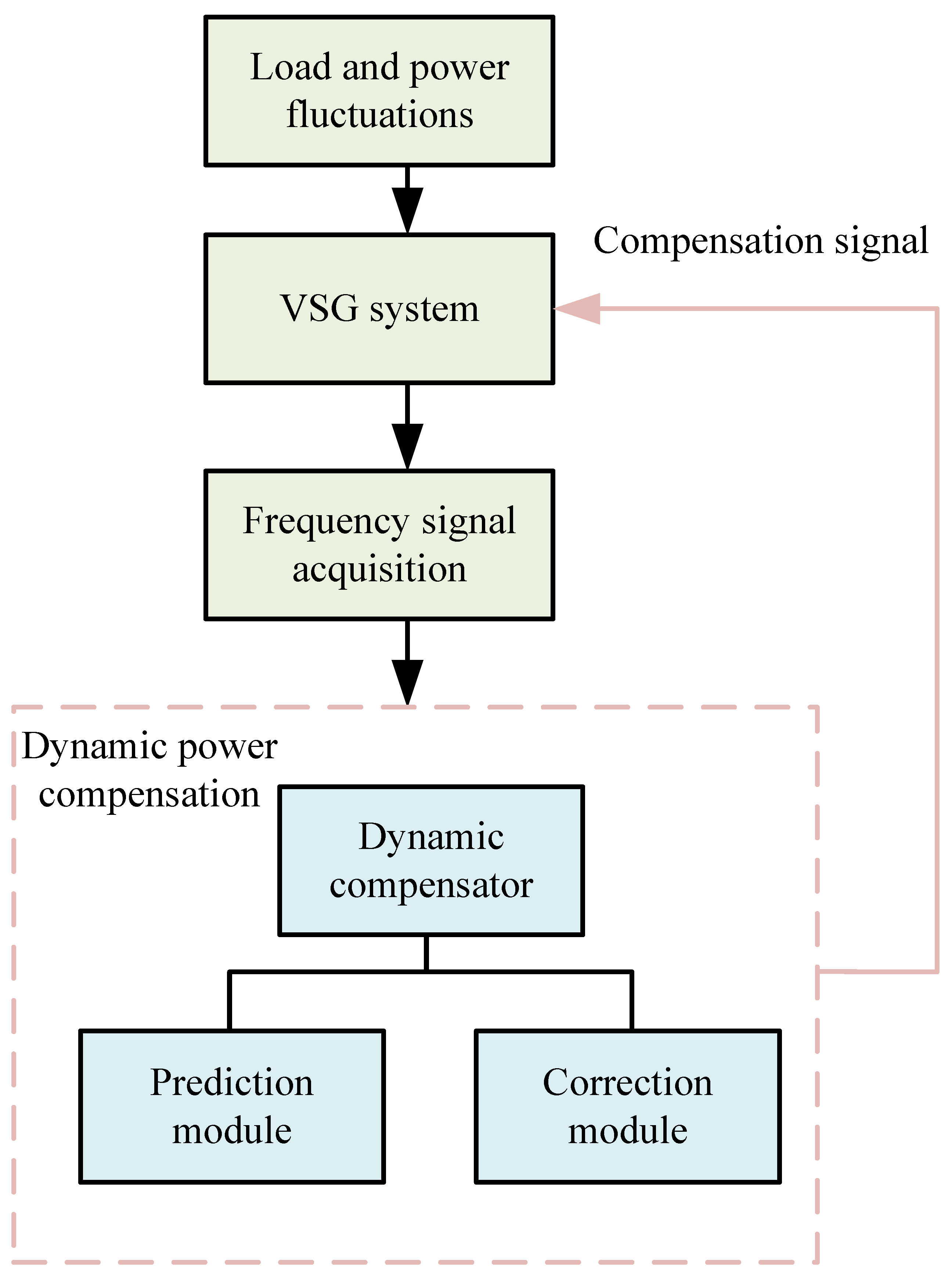
(2) Dynamic Power Compensation

As indicated by Equation (18), feedforward compensation power is proportional to the predicted load disturbance, which can be obtained in real time via machine learning to enhance frequency correction. This is primarily achieved through dynamic compensation, as illustrated in Figure 8.

In [76], Graph Convolutional Network-LSTM (GCN-LSTM) model was combined to jointly forecast system frequency and disturbance signals, providing accurate temporal features for feedforward compensation. In [77], reinforcement learning and disturbance observers were used to detect and compensate disturbances in real time. In [78], LSTM-based forecasting of future load variations was implemented, enabling dynamic feedforward control adjustment.

Table 3. Comparison of control strategies for frequency deviation mitigation.

Category	Method Subtype	Advantages	Disadvantages	Example Methods	References
Conventional control strategies	Parameter tuning	Clear control principles; fast response	Poor adaptability	Damping coefficient tuning	[55,56,57,58,59]
Conventional control strategies	Control structure optimization	Strong coordination	Strong communication dependency	Cooperative control; secondary control	[60,61,62,63,64,65,66,67,68,69,70]
Machine learning-based control strategies	Intelligent parameter tuning	High adaptability	High data dependency	LSTM; CNN	[71,72,73,74,75]
Machine learning-based control strategies	Dynamic power compensation	Real-time prediction and adjustment capability	Complex training process	Reinforcement learning; LSTM	[76,77,78]

summarizes the comparative analysis of the discussed control strategies for frequency deviation mitigation.

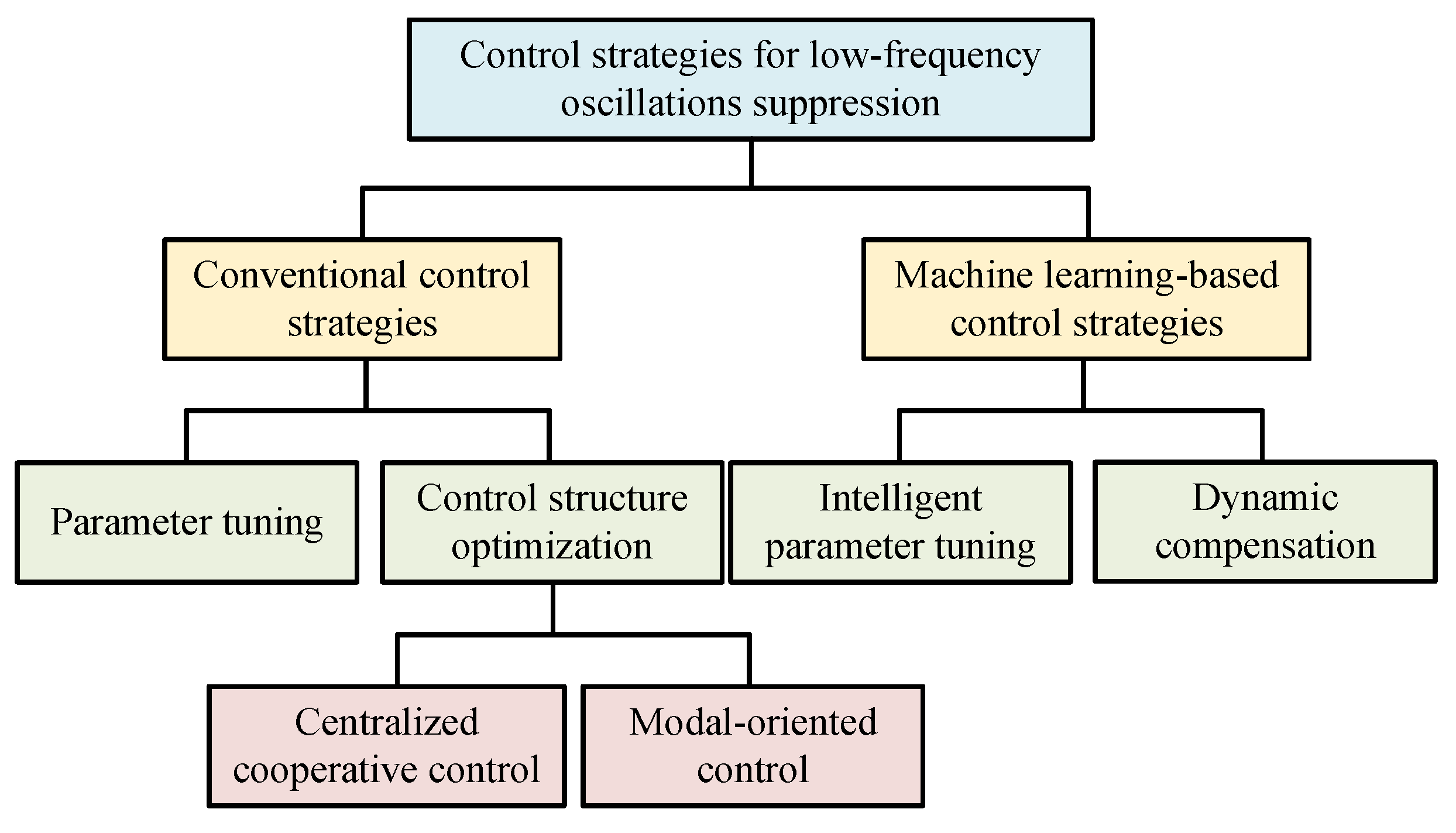
4.2. Control Strategies for Low-Frequency Oscillation Suppression

Based on the previous analysis in Section 3.2, current control strategies for low-frequency oscillation suppression can be categorized into four primary approaches: (1) Parameter tuning; (2) Control structure optimization; (3) Intelligent parameter tuning based on machine learning; (4) Dynamic compensation based on machine learning.

These strategies can be categorized into two broad categories, as illustrated in Figure 9: (1) Conventional control strategies, including parameter tuning and control structure optimization; (2) Machine learning-based control strategies, including intelligent parameter tuning and dynamic compensation.

4.2.1. Conventional Control Strategies

Conventional control strategies for low-frequency oscillation suppression are fundamentally grounded in modal analysis and frequency-domain response theory. These approaches enhance system stability through parameter optimization and control structure optimization.

(1) Parameter Tuning

As shown in Equation (19), increasing D and reducing J enhance system damping and accelerate oscillation decay. Consistent with this, studies show that optimized J and D significantly improve modal damping and frequency response. In [79], it was shown that decreasing J helps smooth the frequency dynamics. In [80], increasing D was found to significantly improve the low-frequency modal behavior. An adaptive inertia-damping coordination scheme was proposed in [81], enabling dynamic parameter tuning under varying operating conditions. In [82], an online parameter tuning strategy was developed using modal sensitivity analysis. A parameter tuning method based on eigenvalue sensitivity analysis was employed in [83] to optimize the system response characteristics. In [84], an adaptive parameter tuning method based on joint optimization of response amplitude and rate was proposed, further suppressing oscillation.

(2) Control Structure Optimization

Control structure optimization strategies can be classified into two principal categories: centralized coordination control and modal-oriented control.

Centralized coordination control, as shown in Equation (20) and illustrated in Figure 10, employs system-level parameter coordination to synchronize VSG dynamic responses and damp low-frequency oscillations. This synchronization relies on system-wide information exchange for frequency synchronization. In [85], a centralized coordinator framework was introduced, where unified parameter optimization was performed for all VSG nodes. This achieved consistent frequency response. In [86], a modal-bandwidth coupling design was proposed, effectively mitigating instability caused by modal interactions and enhancing global coordination.

As demonstrated in Equation (21) and depicted in Figure 11, modal-oriented control injects feedforward compensation signal within the VSG controller, boosting modal damping to stabilize frequency dynamics. In [87], a lead-lag compensator was introduced to rapidly damp the target mode, improving the frequency response dynamic behavior. In [88], an adaptive modal-oriented control strategy was developed by integrating online modal identification and gain adjustment, enhancing the system adaptability to disturbances. In [89,90], feedback control was designed based on modal observers, enabling real-time perception and accurate oscillatory behavior suppression.

4.2.2. Machine Learning-Based Control Strategies

Advancements in intelligent algorithms have enabled machine learning techniques to demonstrate superior capability in suppressing low-frequency oscillation. Current research primarily focuses on two methods:

(1) Intelligent Parameter Tuning

Machine learning techniques enable the intelligent adjustment of system parameters to proactively suppress oscillatory modes. In [91], supervised learning was used to predict inertia and damping parameters matched to oscillation characteristics. In [92], a CNN-LSTM model was developed for intelligent inertia selection. In [93], a soft actor critic (SAC) model was introduced to construct parameter adjustment, enabling effective suppression of oscillations. In [94], a hierarchical regulation network was designed to identify disturbance types and determine optimal parameters accordingly.

(2) Dynamic Compensation

As demonstrated in Equation (21) and illustrated in Figure 12, dynamic compensation proactively identifies oscillatory components via machine learning and injects a feedforward compensation signal into the VSG controller to effectively suppress persistent low-frequency oscillations.

In [95], a neural network-based gain generation mechanism was proposed to support frequency-dependent compensation. In [96], LSTM and autoencoders were combined to recognize and compensate oscillation trends in advance. In [97], a Transformer model was applied for time-series forecasting, enabling proactive control during the early oscillation stage. In [98], a deep reinforcement learning model was applied to construct an optimal frequency compensation strategy, enabling proactive suppression of low-frequency oscillations. In [99,100], a twin-delayed deep deterministic policy gradient (TD3) was proposed to improve VSG frequency response and reduce low-frequency oscillations.

A comparative analysis of control strategies for low-frequency oscillation suppression is presented in

Table 4. The comparison of control strategies for low-frequency oscillation suppression.

Category	Method Subtype	Advantages	Disadvantages	Example Methods	References
Conventional control strategies	Parameter tuning	Clear principle	Poor adaptability	Inertia/damping tuning	[79,80,81,82,83,84]
Conventional control strategies	Control structure optimization	Strong coordination	Complex structure	Modal feedback control; Lead-lag compensators	[85,86,87,88,89,90]
Machine learning-based control strategies	Intelligent parameter tuning	High adaptability	High data dependency	SAC; LSTM	[91,92,93,94]
Machine learning-based control strategies	Dynamic compensation	Fast response; predictive and compensatory ability	Complex training process	Reinforcement learning; Transformer	[95,96,97,98,99]

.

5. Conclusions and Outlook

This paper presents a comprehensive review of frequency stability control in islanded microgrids with multi-VSGs. The main findings and insights are summarized as follows:

First, mainstream modeling approaches for VSGs have been comprehensively summarized, including small-signal, impedance-based, nonlinear time-domain, graph-theoretic, network-dynamics, and data-driven methods. Their respective characteristics are comparatively analyzed in terms of computational complexity, theoretical rigor, and applicability under different operating conditions. Comparative analysis indicates that frequency-domain impedance modeling achieves an optimal balance between theoretical rigor and computational efficiency, making it particularly suitable for mechanism exploration and stability assessment in multi-VSG systems.

Second, two representative frequency stability problems—frequency deviations and low-frequency oscillations—are analyzed in depth. Existing studies reveal that, in islanded multi-VSG systems, frequency deviations primarily originate from the inherent characteristics of VSGs, while inaccurate active power sharing can aggravate the deviation. Low-frequency oscillations are mainly caused by the dynamic coupling among VSG units. These findings provide theoretical guidance for the design of frequency stabilization control strategies.

Third, frequency control strategies are classified into conventional and intelligent approaches. Conventional methods, such as secondary frequency control and cooperative control, remain predominant due to their transparent structure and technological maturity. Conversely, machine learning techniques, such as intelligent parameter tuning and dynamic power compensation, demonstrate superior capabilities in nonlinear system modeling and real-time disturbance recognition under complex operating conditions, representing a promising research avenue.

Future research on frequency stability control for islanded VSG systems can prioritize the following directions:

1. Develop hybrid modeling frameworks, integrating physical principles with data-driven techniques to enhance model interpretability and adaptability.

2. Establish distributed multi-agent reinforcement learning architectures to facilitate autonomous and coordinated control among VSG units.

3. Investigate online learning and adaptive control mechanisms to improve dynamic response performance under varying operating conditions.

Advancing these research fronts can lay a solid foundation from conventional control paradigms towards intelligent coordinated control within islanded microgrids with multi-VSGs. This progression will establish a robust foundation for developing next-generation microgrids featuring high penetration of renewable energy resources.