Optimizing Fault-Ride-Through Strategies of Renewable Generation for the Enhancement of Power System Transient Stability and Security

Abstract

As renewable energy sources increasingly penetrate power systems, ensuring operational stability during grid faults poses a significant challenge. Conventional fault-ride-through (FRT) control strategies often lack systematic parameter optimization, resulting in limited support for transient rotor angle stability and inadequate suppression of transient overvoltages. This paper introduces a comprehensive optimization framework to address these shortcomings. We first develop a novel quasi-steady-state model that accurately captures critical states governing transient stability and voltage security. Variational analysis at these states yields gradient information to guide stability enhancement. Leveraging this insight, we propose a gradient-informed optimization approach to tune FRT parameters, simultaneously improving transient rotor angle stability and mitigating overvoltages. The effectiveness of the proposed model and method is demonstrated through simulations on a benchmark renewable-integrated power system.

1. Introduction

In recent years, China has been developing the new power system characterized by high proportion of renewables and high proportion of power electronics. Renewable energy sources (RES), particularly wind power and photovoltaics (PV), have shown a steadily increasing contribution to the overall electricity generation. By 2030, the total installed capacity of wind and PV power in China is projected to reach 1200 GW, accounting for the largest share in the national power generation [1,2]. The grid integration of renewable energy systems involves dynamic processes across multiple timescales. Additionally, considering different system operation modes, there are switching processes between various control modes. To some extent, the replacement of traditional power sources will reduce the grid’s voltage support capability and short-circuit capacity. As a result, this will significantly increase the risk of voltage instability. Therefore, the power system stability issues have become increasingly prominent [3,4].

In addressing power system transient stability, time-domain simulation remains the mainstream methodology. This approach has virtually no restrictions on the complexity of component models. Furthermore, the analysis results obtained are relatively accurate and reliable [5]. In contrast to simulation methods, the direct method for transient stability analysis employs a direct characterization of the stability region in state space. This technique eliminates the requirement for post-fault integration computations and provides direct access to stability margin information. What’s more, both rotor angle and voltage stability problems could be effectively analyzed and addressed in power system stability assessment [6].

Regarding the transient rotor angle issue, through simulations, reference [7] suggests that replacing traditional synchronous machines with high-proportion renewable energy negatively impacts rotor angle stability. The study in reference [8] considers the impact of the renewable-to-thermal power ratio at the sending end on rotor angle stability focusing on the coupling effects of wind power, thermal power and direct current (DC) systems. References [9,10] apply the extended equal-area criterion, equating the power of wind farms to the mechanical power of synchronous generators, while also considering the impact of wind turbine control on the equivalent mechanical power. They analyze the changes in the acceleration and deceleration areas after system faults. Reference [11] uses a Taylor expansion to transform the rotor motion equations into polynomials, then it proposes a polynomial-based method for estimating the power system’s attraction domain, employing a two-stage iterative process of s-optimization and V-optimization through sum-of-squares programming.

Regarding transient voltage stability problem, numerous studies have proposed analytical approaches and solutions, which can be summarized as follows: Reference [12] analyzes the transient voltage behavior of power systems with high penetration of power-electronic-interfaced renewables using a differential-algebraic equation framework, demonstrating the evolution of system instability modes. Reference [13] proposes using the impedance modulus ratio to measure voltage instability and obtains an approximate relationship between load shedding and voltage instability indices through time-domain simulation. Reference [14] correlates the energy function of the DC-link voltage with the equivalent rotor angle dynamics to characterize instability, proposing an innovative technique for transient voltage stability evaluation. Reference [15] employs capacitor energy storage and alternating current (AC) side potential energy as its energy function, developing a passivity-based control strategy designed to enhance transient stability.

References [16,17,18] collectively demonstrate that the reactive current injection coefficient critically impacts the transient synchronization stability of renewable energy systems during faults. While [16,17] focus on its influence and propose adaptive adjustment, [18] further investigates its matching with grid parameters, highlighting that a mismatch can cause instability. Research on enhancing FRT capability in doubly fed induction generators (DFIGs) currently pursues three major pathways. One primary area involves the implementation of advanced control strategies, including the coordination of sliding mode and model predictive control [19] and the application of adaptive backstepping techniques [20], which are designed to achieve superior dynamic performance and increased robustness. Second, reconstructing control mechanisms from new physical perspectives, for instance, by analyzing rotor-port impedance characteristics [21] or deepening the understanding of the transient process in demagnetization control [22] to fundamentally enhance stability. Third, refined solutions for specific fault scenarios, including addressing over-modulation issues under asymmetrical faults [23], optimizing cooperative strategies for symmetrical faults [24,25], and extending research to converter systems based on modular multilevel converter (MMC) [26]. These advancements collectively drive FRT technology for DFIG toward smarter, more precise, and more reliable development. However, current research primarily relies on simulations and qualitative analysis to propose control strategies, leaving room for further optimization of control parameters.

In this paper, a quasi-steady-state (QSS) model for RES is first established, where RES are regarded as injected currents controlled by nodal voltages. By employing an alternating iterative method, various electrical quantities of the generators are solved and then linearized to obtain gradient information for these electrical quantities concerning the control parameters of RES. Subsequently, the causes of rotor angle stability issues and transient overvoltage problems are separately investigated and parameter scan is conducted to qualitatively analyze the impact of RES control parameters on stability problems. Based on the gradient descent method, quantitative calculations are performed in the direction of the negative gradient to obtain an optimal set of control parameters that most benefit the respective stability problems. Finally, the proposed method is tested on the Chinese Society for Electrical Engineering- frequency stability (CSEE-FS) system to validate its effectiveness.

2. Quasi-Steady-State Model of Renewable Energy and Its Sensitivity Analysis

2.1. Overview of QSS Model

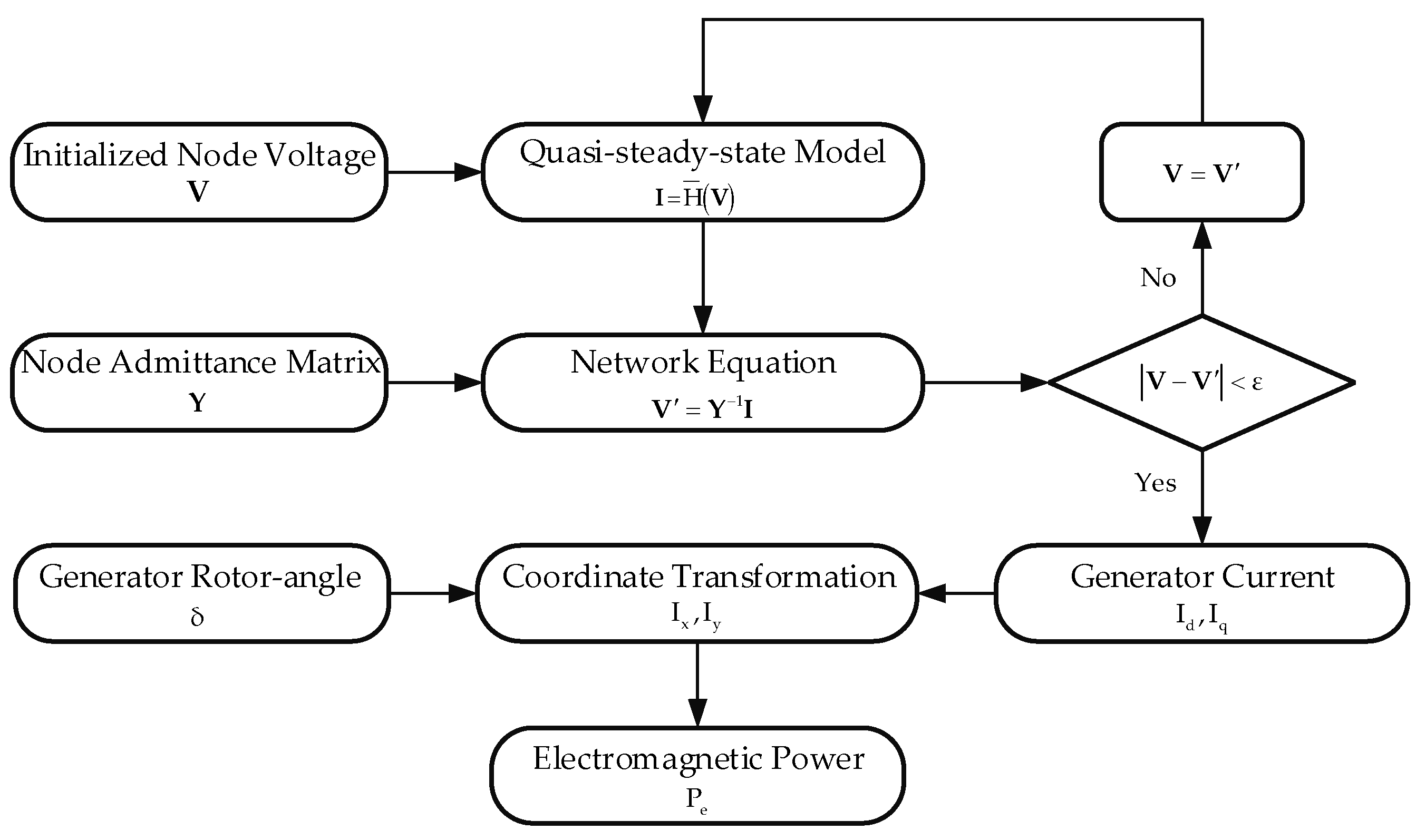
The QSS model for modern power systems is founded upon the inherent property of timescale separation between electromechanical dynamics and electromagnetic transients. That is, each moment of the electromechanical transients corresponds to a quasi-steady-state equilibrium of the electromagnetic process. Given that the dynamic response of measurement and control in power electronic equipment is at timescale of electromagnetic transients, it is reasonable to represent the power electronics by quasi-steady-state models. Consequently, the differential model governing the underlying behavior of power electronic equipment gives way to a set of switched algebraic equations:

$$0=\mathrm{R}\left(\mathrm{y},\dot{\mathrm{V}}\right),$$

(1)

$$\dot{\mathrm{I}}=\overline{\mathrm{H}}\left(\mathrm{y},\dot{\mathrm{V}}\right),$$

(2)

where the algebraic variable $\mathrm{y}$ is the internal operating state of the device, and the voltage phasor and the current injection phasor at the connection point of the device are denoted $\dot{\mathrm{V}}$ and $\dot{\mathrm{I}}$, respectively. The possibly non-smooth and non-linear functions $\mathrm{R}\left(·\right)$ and $\overline{\mathrm{H}}\left(·\right)$ capture the underlying physical law and the switching behavior of the device.

Meanwhile, the network equations are given by

$$Y\dot{\mathrm{V}}=\dot{\mathrm{I}},$$

(3)

where Y is the network admittance matrix. Specifically, the injected current phasors $\dot{\mathrm{I}}$ at each node can be calculated from the quasi-steady-state models of each component and be described as

$$\dot{\mathrm{I}}={\dot{\mathrm{I}}}_{\mathrm{G}}+{\dot{\mathrm{I}}}_{\mathrm{R}}+{\dot{\mathrm{I}}}_{\mathrm{L}}$$

(4)

where ${\dot{\mathrm{I}}}_{\mathrm{G}}$, ${\dot{\mathrm{I}}}_{\mathrm{R}}$ and ${\dot{\mathrm{I}}}_{\mathrm{L}}$ are the injected current of synchronous generators, renewable generation units and loads in the xy coordinate frame. Their specific forms are detailed in Section 2.3, Section 2.4 and Section 2.5, respectively.

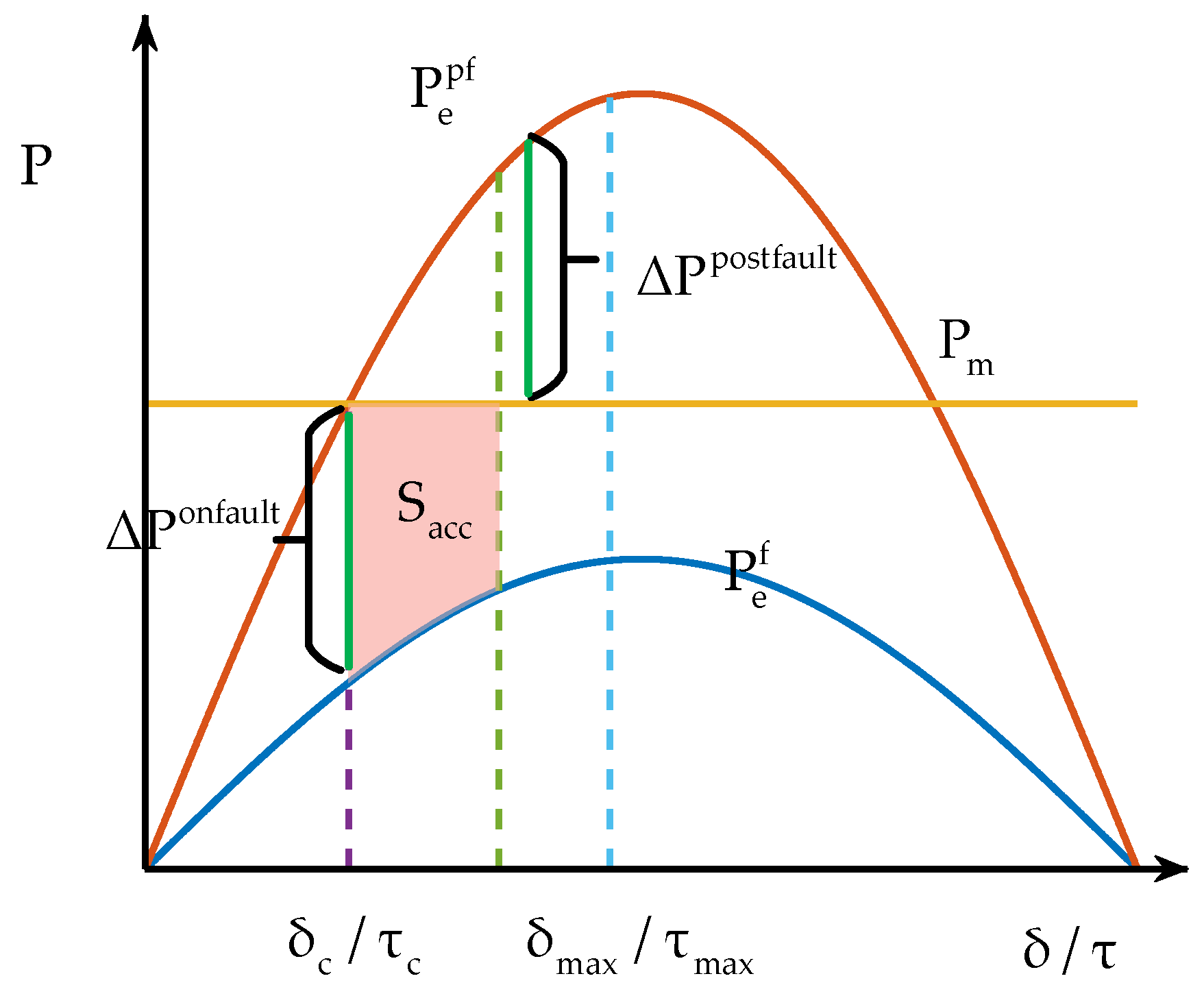
By assigning different values to the internal states of synchronous generators, the proposed model can characterize various critical quasi-steady states, such as the instant immediately following a fault, the moment after fault clearing, and the post-fault steady state. Unlike conventional transient models, which rely on differential-algebraic equations, these reduced models consist of switched nonlinear algebraic equations. Solving these equations directly yields the desired critical quasi-steady states without requiring full time-domain simulations. Furthermore, variational analysis at these states provides valuable sensitivity information for control design and optimization.

2.2. Quasi-Steady-State Model of Renewable Generation Unit

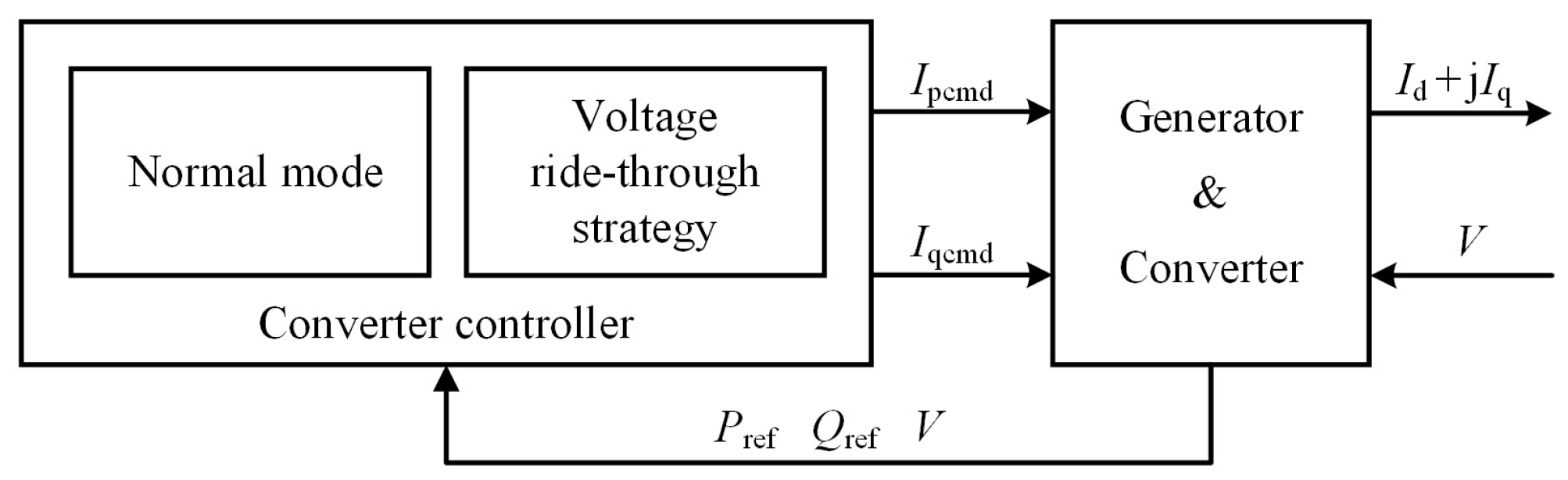
As illustrated in Figure 1, the converter control system is capable of transitioning between the standard operation mode and the FRT mode, depending on the voltage level measured at the point of common coupling (PCC). Under either normal operation or fault ride-through control, the renewable generation system connects to the grid via a voltage source converter (VSC) and operates in a current regulation mode governed by voltage control. For instance, under normal operation, a wind generation system employs coordinated control of optimal rotor speed, active power, and reactive power. In the QSS condition, the coordination between optimal speed regulation and active power management is expressed through an algebraic relation.

$$\left\{\begin{array}{l}{\mathrm{\omega }}_{\mathrm{g}\mathrm{e}\mathrm{n}}=\mathrm{f}\left({\mathrm{P}}_{\mathrm{W}\mathrm{T}\mathrm{T}}\right)={\mathrm{\omega }}_{\mathrm{r}\mathrm{e}\mathrm{f}},\\ {\mathrm{P}}_{\mathrm{W}\mathrm{T}\mathrm{T}}={\mathrm{P}}_{\mathrm{r}\mathrm{e}\mathrm{f}},\end{array}\right.$$

(5)

where ${\mathrm{\omega }}_{\mathrm{gen}}$ and ${\mathrm{\omega }}_{\mathrm{ref}}$ are, respectively, the measurement and reference of its rotational speed. In addition, ${\mathrm{P}}_{\mathrm{W}\mathrm{T}\mathrm{T}}$ and ${\mathrm{P}}_{\mathrm{ref}}$ are the measurement and reference of the active power. Similarly to the active power control, the QSS model of the reactive power control takes the form

$${\mathrm{Q}}_{\mathrm{WTT}}={\mathrm{Q}}_{\mathrm{ref}},$$

(6)

where ${\mathrm{Q}}_{\mathrm{WTT}}$ corresponds to the reactive power measurement, while ${\mathrm{Q}}_{\mathrm{ref}}$ indicates its reference value within the control scheme. The current injection under normal control mode is given by

$$\left\{\begin{array}{l}{\mathrm{i}}_{\mathrm{d}1}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{WTT}}}{\mathrm{V}}},\\ {\mathrm{i}}_{\mathrm{q}1}={\displaystyle \frac{{\mathrm{Q}}_{\mathrm{WTT}}}{\mathrm{V}}},\end{array}\right.$$

(7)

where ${\mathrm{i}}_{\mathrm{d}1}$ and ${\mathrm{i}}_{\mathrm{q}1}$ are the currents in local $\mathrm{dq}$ coordinate. On the other hand, the current injection for the LVRT mode is usually a linear function of the voltage magnitude. The transient model features four active power control strategies and three reactive power control strategies; the control strategies are as follows:

The active current control method:

• Specified current control:

$${\mathrm{i}}_{\mathrm{d}2}={\displaystyle \frac{{\mathrm{I}}_{\mathrm{P}}\mathrm{N}}{{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(8)

where ${\mathrm{i}}_{\mathrm{d}2}$ represents the axis current during the ride-through mode, ${\mathrm{I}}_{\mathrm{P}}$ is the active current control setpoint, $\mathrm{N}$ denotes the total count of renewable energy plants and ${\mathrm{I}}_{\mathrm{base}}$ represents individual current reference value for each renewable energy unit.

2.

Specified current as a percentage of the initial current control:

$${\mathrm{i}}_{\mathrm{d}2}={\mathrm{K}}_{\mathrm{I}}\%{\mathrm{I}}_{\mathrm{P}0},$$

(9)

where ${\mathrm{K}}_{\mathrm{I}}\%$ is the active current percentage setpoint and ${\mathrm{I}}_{\mathrm{P}0}$ is the initial active current.

3.

Specified power setpoint:

$${\mathrm{i}}_{\mathrm{d}2}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{L}\mathrm{V}}\mathrm{N}}{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(10)

where ${\mathrm{P}}_{\mathrm{L}\mathrm{V}}$ is the active power setpoint, ${\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}$ is the voltage of the point of interconnection and ${\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}$ is the capacity benchmark value of the power system.

4.

Specified power station initial power percentage control.

$${\mathrm{i}}_{\mathrm{d}2}={\displaystyle \frac{{\mathrm{K}}_{\mathrm{P}}\%{\mathrm{P}}_0}{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}},$$

(11)

where ${\mathrm{K}}_{\mathrm{P}}\%$ is the active power percentage setpoint and ${\mathrm{P}}_0$ is the initial active power.

Reactive current control method:

1.

Voltage-controlled reactive current control method.

$${\mathrm{i}}_{\mathrm{q}2}=-{\displaystyle \frac{{\mathrm{K}}_{\mathrm{Q}}\left({\mathrm{V}}_{\mathrm{L}\mathrm{i}\mathrm{n}}-{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}\right){\mathrm{S}}_{\mathrm{m}\mathrm{ac}}}{{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(12)

where ${\mathrm{i}}_{\mathrm{q}2}$ represents the q axis current during the ride-through mode, ${\mathrm{K}}_{\mathrm{Q}}$ is the reactive current calculation coefficient, ${\mathrm{V}}_{\mathrm{L}\mathrm{i}\mathrm{n}}$ is the LVRT threshold and ${\mathrm{S}}_{\mathrm{m}\mathrm{ac}}$ is the capacity benchmark value for each renewable energy unit.

2.

Specified power setpoint.

$${\mathrm{i}}_{\mathrm{q}2}=-{\displaystyle \frac{{\mathrm{Q}}_{\mathrm{L}\mathrm{V}}\mathrm{N}}{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(13)

where ${\mathrm{Q}}_{\mathrm{L}\mathrm{V}}$ is the reactive power setpoint.

3.

Specified current control.

$${\mathrm{i}}_{\mathrm{q}2}=-{\displaystyle \frac{{\mathrm{I}}_{\mathrm{Q}}\mathrm{N}}{{\mathrm{I}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}},$$

(14)

where ${\mathrm{I}}_{\mathrm{Q}}$ is the reactive current control setpoint.

Considering the transition between standard operation and LVRT modes, the current injection of the generation unit can be expressed as

$$\left\{\begin{array}{l}{\mathrm{i}}_{\mathrm{d}}=(1-\mathrm{LF})\cdot {\mathrm{i}}_{\mathrm{d}1}+\mathrm{LF}\cdot {\mathrm{i}}_{\mathrm{d}2},\\ {\mathrm{i}}_{\mathrm{q}}=(1-\mathrm{LF})\cdot {\mathrm{i}}_{\mathrm{q}1}+\mathrm{LF}\cdot {\mathrm{i}}_{\mathrm{q}2},\end{array}\right.$$

(15)

where $\mathrm{L}\mathrm{F}=0$ represents the normal mode and $\mathrm{L}\mathrm{F}=1$ indicates the ride-through mode.

Considering that the d and q axes of renewable energy units are synchronized using a phase-locked loop (PLL), the injected current ${\dot{\mathrm{I}}}_{\mathrm{R}}$ of the renewable energy unit in the xy coordinate frame is determined by the following equation:

$${\dot{\mathrm{I}}}_{\mathrm{R}}={\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}({\mathrm{i}}_{\mathrm{d}}+\mathrm{j}{\mathrm{i}}_{\mathrm{q}})$$

(16)

where θ is the phase angle corresponding to the voltage at the PCC.

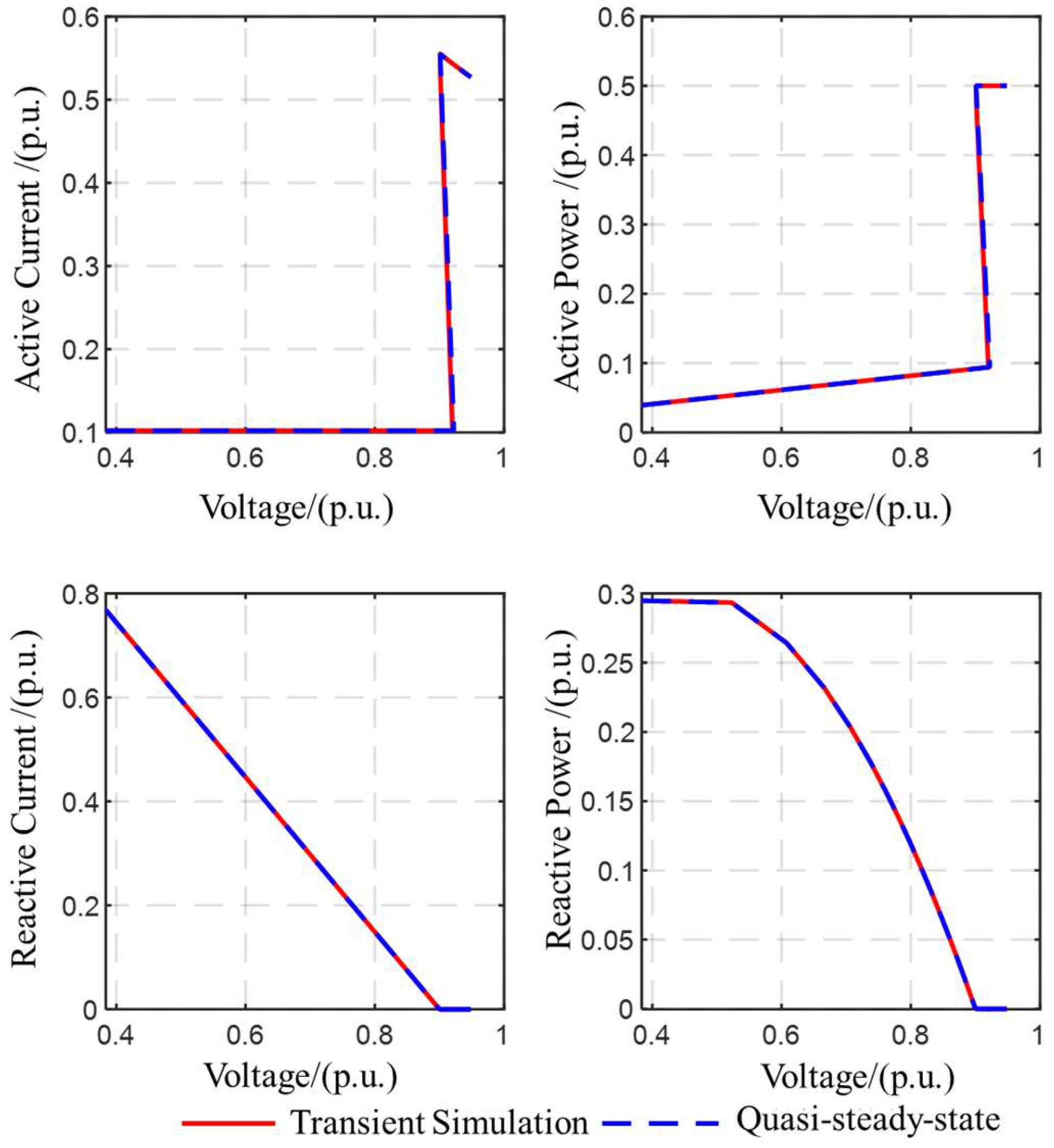
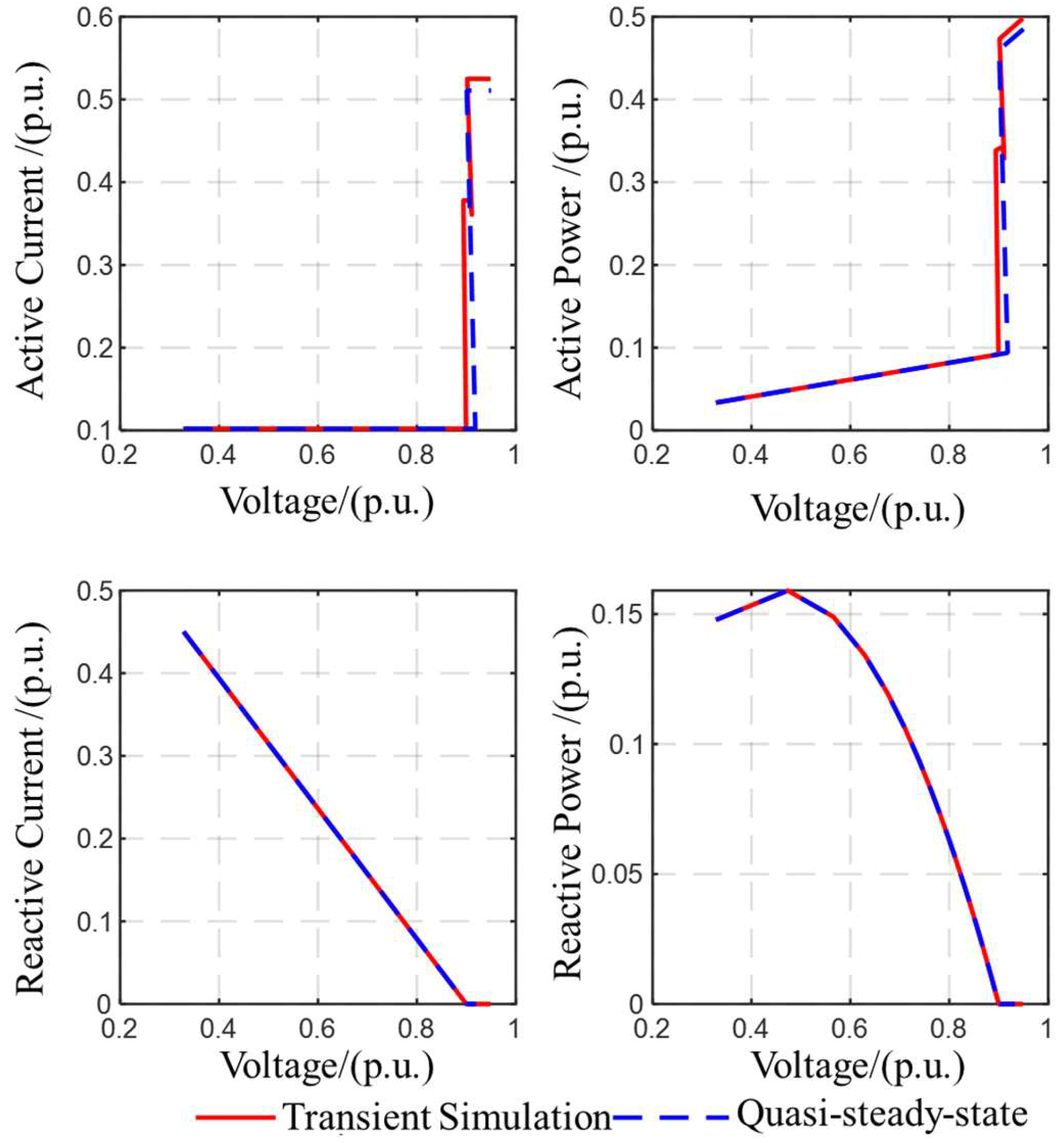
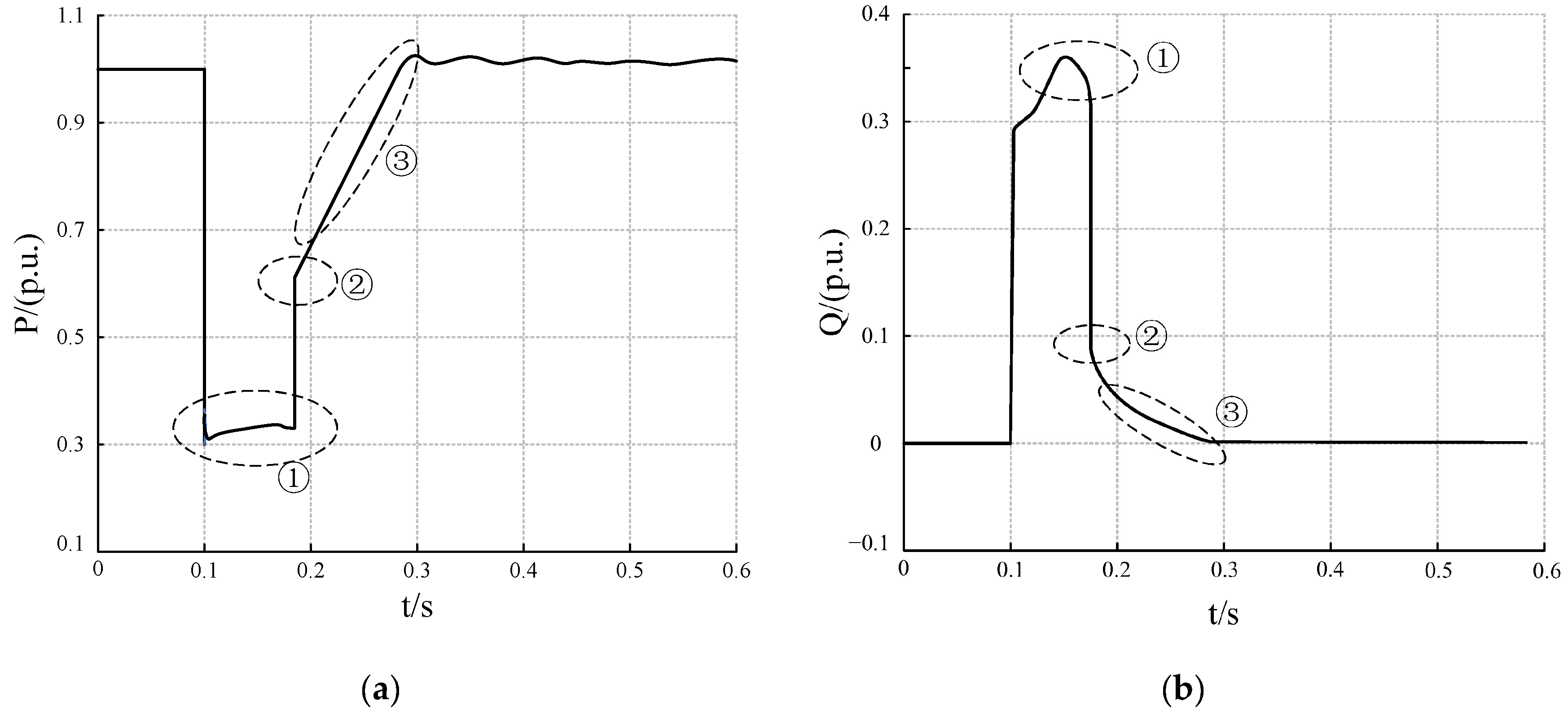
To verify the QSS model of the described FRT control strategy, the case study adopts a single-machine infinite bus (SMIB) system integrated with renewable energy units (wind turbines or PV units). To validate the QSS representation of the proposed FRT control approach, the case study employs a single-machine infinite bus (SMIB) configuration coupled with RES, such as wind turbines or photovoltaic systems. A three-phase short-circuit fault is selected as the disturbance type, with fault initiating at 0 s and lasting for 10 cycles. The steady-state values of current and power in both the active and reactive components are selected for comparison. The corresponding results are illustrated in Figure 2 and Figure 3. The results indicate that the values are essentially consistent, thus verifying the correctness of the QSS model.

Specifically, regarding the active current, it remains constant at a relatively low level during the low-voltage ride through (LVRT) period. Under normal voltage conditions, wind turbines exhibit a decreasing characteristic, while PV units maintain a constant output. Furthermore, a recovery segment can be observed in the curve. This is primarily because after the fault occurs, the voltage begins to drop from the normal level. When it decreases to 0.9 p.u., the RES enter the LVRT state. At this point, the control strategy increases reactive power output to support voltage recovery, resulting in the voltage during the LVRT period occasionally exceeding 0.9 p.u. Additionally, in the transient simulation of the PV unit, the active current exhibits an intermediate value for a certain period. This occurs because the voltage fluctuates near the critical point of FRT, repeatedly entering and exiting the FRT state. As a result, the electrical quantities are actually in a periodic variation state rather than reaching a steady state, making it difficult to obtain their true steady-state values. The active power shows characteristics similar to the active current, but it exhibits an increasing trend during the FRT period. Under normal conditions, wind turbines implement constant power control, whereas PV units adopt constant current control. The reactive current curve demonstrates an initial decrease followed by stabilization, and the reactive power curve behaves similarly. However, at lower voltage levels (e.g., 0.5 p.u.), the rate of reactive power increase slows down, and in the case of photovoltaic units, the reactive power may even decrease.

2.3. QSS Model of Synchronous Generator

Under steady operating conditions, the electromotive forces (EMFs) ${\mathrm{E}}_{\mathrm{d}}^{\prime }$ and ${\mathrm{E}}_{\mathrm{d}}^{\prime }$ correspond to the d- and q-axis windings, respectively. The steady-state equation for the transient EMF of a synchronous generator is

$$\left\{\begin{array}{l}{\mathrm{V}}_{\mathrm{d}}+{\mathrm{R}}_{\mathrm{a}}{\mathrm{I}}_{\mathrm{d}}-{\mathrm{x}}_{\mathrm{q}}^{\prime }{\mathrm{I}}_{\mathrm{q}}={\mathrm{E}}_{\mathrm{d}}^{\prime },\\ {\mathrm{V}}_{\mathrm{q}}+{\mathrm{R}}_{\mathrm{a}}{\mathrm{I}}_{\mathrm{q}}+{\mathrm{x}}_{\mathrm{d}}^{\prime }{\mathrm{I}}_{\mathrm{d}}={\mathrm{E}}_{\mathrm{q}}^{\prime },\end{array}\right.$$

(17)

where ${\mathrm{V}}_{\mathrm{d}}$ and ${\mathrm{V}}_{\mathrm{q}}$ represent the terminal voltage in the dq coordinate system of the generator, ${\mathrm{x}}_{\mathrm{d}}^{\prime }$ and ${\mathrm{x}}_{\mathrm{q}}^{\prime }$ represent the direct-axis and quadrature-axis transient reactance of the generator and ${\mathrm{R}}_{\mathrm{a}}$ denotes the stator winding resistance.

To solve for ${\mathrm{I}}_{\mathrm{d}}$ and ${\mathrm{I}}_{\mathrm{d}}$ from Equation (17), we conclude

$$\left\{\begin{array}{l}{\mathrm{I}}_{\mathrm{d}}={\displaystyle \frac{{\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{R}}_{\mathrm{a}}-{\mathrm{R}}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{d}}+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }-{\mathrm{V}}_{\mathrm{q}}{\mathrm{X}}_{\mathrm{q}}^{\prime }}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{q}}^{\prime }{\mathrm{X}}_{\mathrm{d}}^{\prime }}},\\ {\mathrm{I}}_{\mathrm{q}}={\displaystyle \frac{{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{R}}_{\mathrm{a}}-{\mathrm{R}}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{q}}-{\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{d}}^{\prime }+{\mathrm{V}}_{\mathrm{d}}{\mathrm{X}}_{\mathrm{d}}^{\prime }}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{q}}^{\prime }{\mathrm{X}}_{\mathrm{d}}^{\prime }}},\end{array}\right.$$

(18)

Considering that the synchronous machine’s dq reference frame is aligned with the rotor angular position, the injected current ${\dot{\mathrm{I}}}_{\mathrm{G}}$ of the synchronous machine in the xy coordinate frame is thus determined by the following equation:

$${\dot{\mathrm{I}}}_{\mathrm{G}}={\mathrm{e}}^{\mathrm{j}(\mathrm{\delta }-{\displaystyle \frac{\mathsf{\pi }}{2}})}({\mathrm{I}}_{\mathrm{d}}+\mathrm{j}{\mathrm{I}}_{\mathrm{q}})$$

(19)

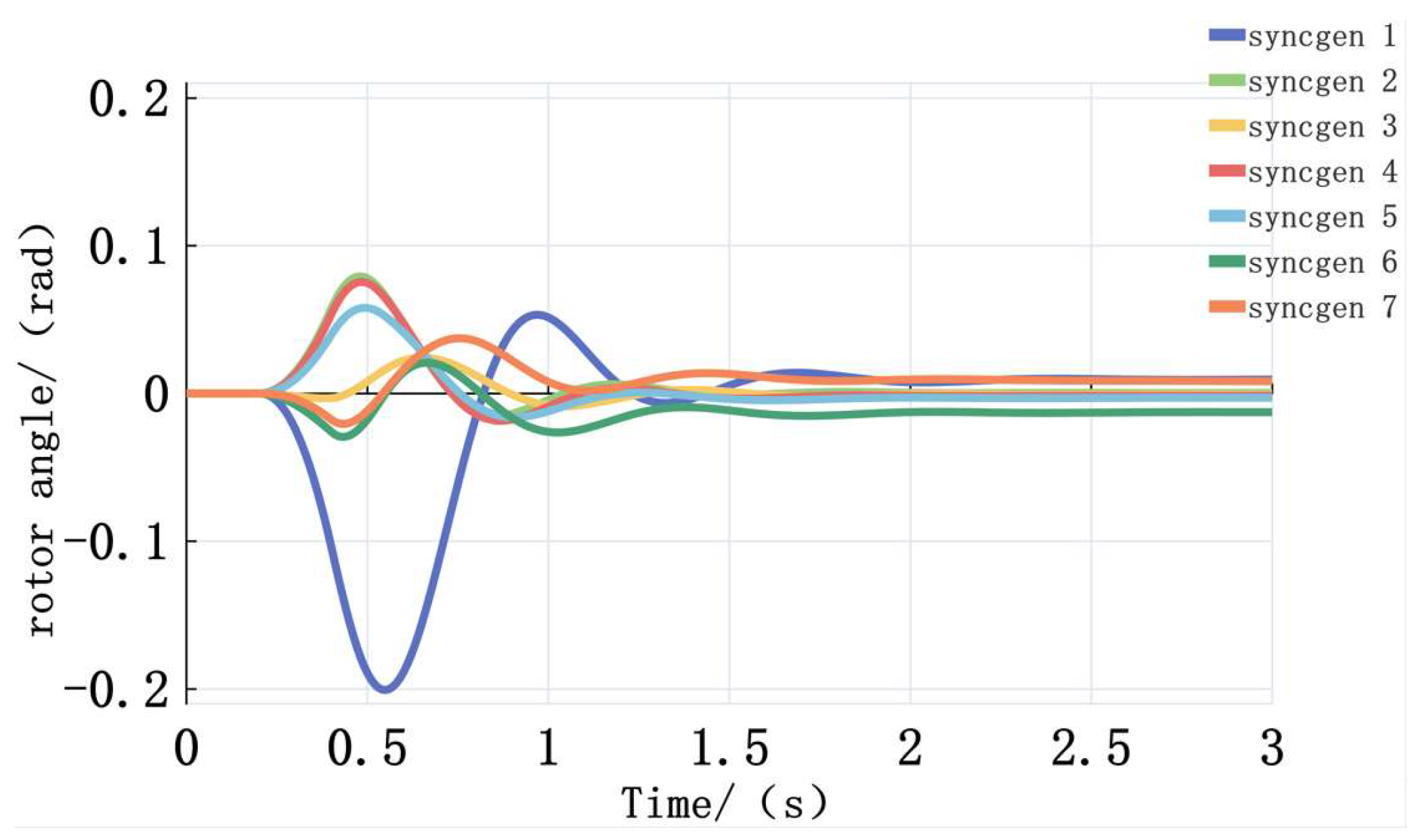
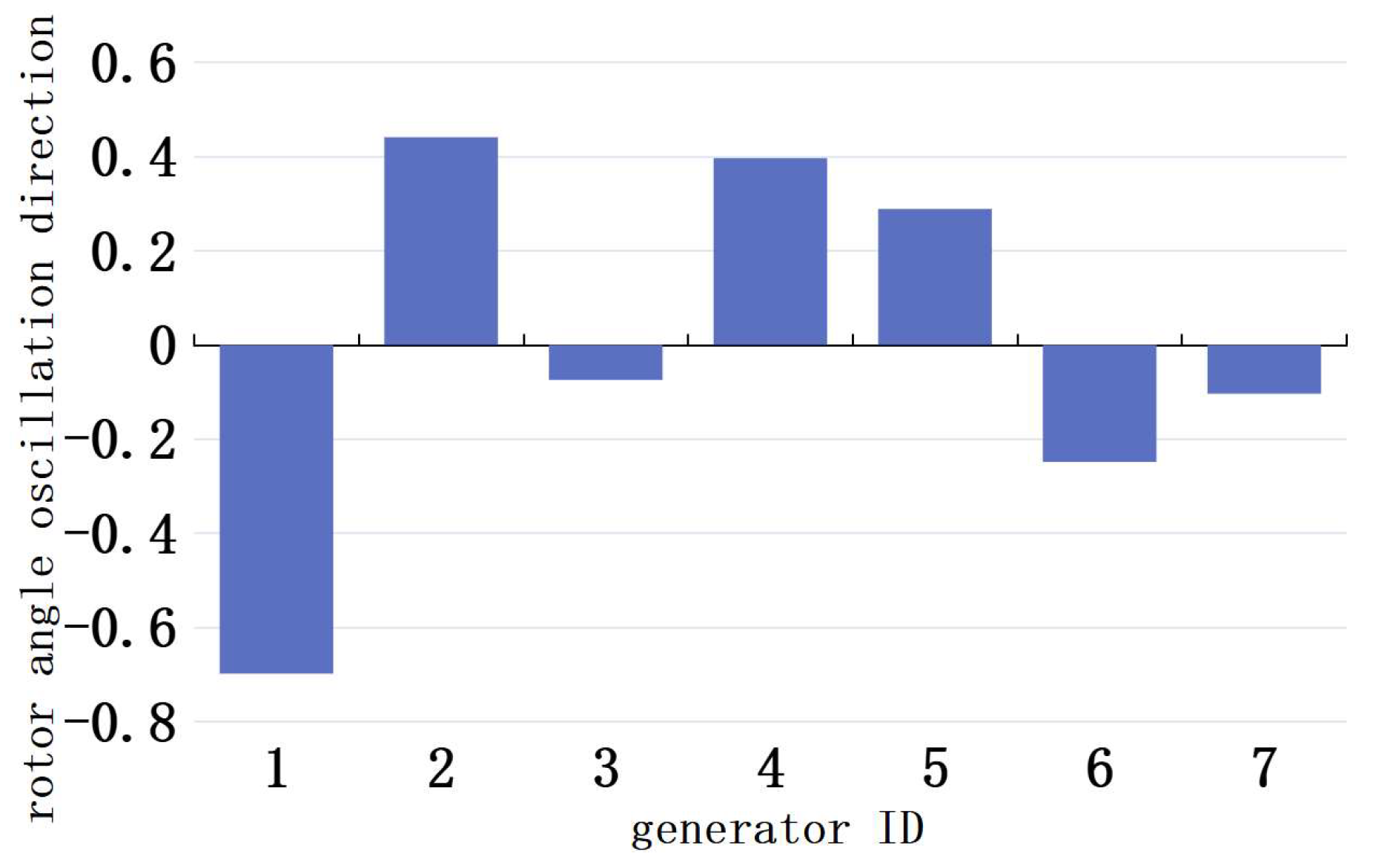
For the instant immediately following a fault, the rotor angle δ remains unchanged at this moment since the synchronous machine controllers do not have time to respond. While for the moment after fault clearing, given the short duration of faults, the rotor angle can be assumed to change linearly.

2.4. QSS Model of Load

The load is modeled as a voltage-dependent ZIP model:

$$\left\{\begin{array}{l}{\mathrm{P}}_{\mathrm{L}}={\mathrm{P}}_0[{\mathrm{a}}_{\mathrm{P}}{({\displaystyle \frac{\mathrm{V}}{{\mathrm{V}}_0}})}^2+{\mathrm{b}}_{\mathrm{P}}({\displaystyle \frac{\mathrm{V}}{{\mathrm{V}}_0}})+{\mathrm{c}}_{\mathrm{P}}]\\ {\mathrm{Q}}_{\mathrm{L}}={\mathrm{Q}}_0[{\mathrm{a}}_{\mathrm{Q}}{({\displaystyle \frac{\mathrm{V}}{{\mathrm{V}}_0}})}^2+{\mathrm{b}}_{\mathrm{Q}}({\displaystyle \frac{\mathrm{V}}{{\mathrm{V}}_0}})+{\mathrm{c}}_{\mathrm{Q}}]\end{array}\right.$$

(20)

where ${\mathrm{P}}_{\mathrm{L}}$ and ${\mathrm{Q}}_{\mathrm{L}}$ represent active power and reactive power, ${\mathrm{P}}_0$, ${\mathrm{Q}}_0$ and ${\mathrm{V}}_0$ denote initial active power, reactive power and voltage magnitude. The coefficients ${\mathrm{a}}_{\mathrm{P}}$ (${\mathrm{a}}_{\mathrm{Q}}$), ${\mathrm{b}}_{\mathrm{P}}$ (${\mathrm{b}}_{\mathrm{Q}}$), and ${\mathrm{c}}_{\mathrm{P}}$ (${\mathrm{c}}_{\mathrm{Q}}$) specify the portions of Z, I and P characteristics in the active (reactive) load, satisfying the following constraint:

$$\left\{\begin{array}{c}{\mathrm{a}}_{\mathrm{P}}+{\mathrm{b}}_{\mathrm{P}}+{\mathrm{c}}_{\mathrm{P}}=1\\ {\mathrm{a}}_{\mathrm{Q}}+{\mathrm{b}}_{\mathrm{Q}}+{\mathrm{c}}_{\mathrm{Q}}=1\end{array}\right.$$

(21)

Considering the connection equations between the loads and the network, we have

$$\left\{\begin{array}{l}0={\mathrm{P}}_{\mathrm{L}}+{\mathrm{V}}_{\mathrm{L}\mathrm{x}}{\mathrm{I}}_{\mathrm{L}\mathrm{x}}+{\mathrm{V}}_{\mathrm{L}\mathrm{y}}{\mathrm{I}}_{\mathrm{L}\mathrm{y}}\\ 0={\mathrm{Q}}_{\mathrm{L}}+{\mathrm{V}}_{\mathrm{L}\mathrm{y}}{\mathrm{I}}_{\mathrm{L}\mathrm{x}}-{\mathrm{V}}_{\mathrm{L}\mathrm{x}}{\mathrm{I}}_{\mathrm{L}\mathrm{y}}\end{array}\right.$$

(22)

Thus, we can get the injected current ${\dot{\mathrm{I}}}_{\mathrm{L}}={\mathrm{I}}_{\mathrm{L}\mathrm{x}}+\mathrm{j}{\mathrm{I}}_{\mathrm{L}\mathrm{y}}$ of the synchronous machine in the xy coordinate frame.

2.5. Solution of the QSS Model

After adopting the QSS model for renewable energy sources, it can be treated as an injected current that depends on the nodal voltage. Based on this, the network equations of the system can be solved using the alternating iteration method. The corresponding flowchart is shown in Figure 4 and the detailed procedure is described as follows:

1.

Establish the system’s admittance matrix.

2.

Initialize the system’s nodal voltages, currents, and generator rotor angles.

3.

Calculate the injected current from each component to the system based on the QSSS model of the renewable energy sources.

4.

With the injected currents, calculate the nodal voltages of the system.

5.

After iteration and convergence, calculate the electromagnetic power of each generator.

2.6. Sensitivity Analysis of the Quasi-Steady State

2.6.1. Linearization of the Network Equations

Assume that the power network includes $\mathrm{n}$ nodes, with devices using coordinate system $\mathrm{d}\mathrm{q}$, and the network adopting synchronous coordinate system $\mathrm{x}\mathrm{y}$. The current injected by the devices into the network is $I_d+\mathrm{j}{I}_q$, and the nodal current balance of the system is formulated as

$$Y\left[V\right]{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}=\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\left(I_d+\mathrm{j}{I}_q\right),$$

(23)

where $Y$ is the network’s admittance matrix, $\left[V\right]\subset {ℝ}^{\mathrm{n}\times \mathrm{n}}$ is the diagonal matrix, $\theta \subset {ℝ}^{\mathrm{n}}$ represents the phase angles of each node in the system’s $\mathrm{xy}$ reference coordinate system. When performing linearization on Equation (23) at the equilibrium point, the result would be

$$Y\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\Delta V+\mathrm{j}\mathrm{Y}\left[V\right]\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\Delta \theta =\mathrm{j}\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\left[I_d+\mathrm{j}{I}_q\right]\Delta \theta +\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\left(\Delta I_d+\mathrm{j}\Delta I_q\right),$$

(24)

Given the following substitutions, ${\mathbf{V}}^{\prime }=\left[V\right]\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]$, ${\mathbf{I}}^{\prime }=\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\left[I_d+\mathrm{j}{I}_q\right]$, Equation (24) is reformulated in a compact form as follows:

$$\left(\begin{array}{cc}\mathrm{Re}\left\{Y\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\right\}& \mathrm{Re}\left\{\mathrm{j}\left(Y\left[V^{\prime }\right]-\left[I^{\prime }\right]\right)\right\}\\ \mathrm{Im}\left\{Y\left[{\mathrm{e}}^{\mathrm{j}\mathrm{\theta }}\right]\right\}& \mathrm{Im}\left\{\mathrm{j}\left(Y\left[V^{\prime }\right]-\left[I^{\prime }\right]\right)\right\}\end{array}\right)\left(\begin{array}{c}\Delta V\\ \Delta \theta \end{array}\right)=\left(\begin{array}{cc}\left[\cos \theta \right]& -\left[\sin \theta \right]\\ \left[\sin \theta \right]& \left[\cos \theta \right]\end{array}\right)\left(\begin{array}{c}\Delta I_d\\ \Delta I_q\end{array}\right).$$

(25)

Here, Equation (18) is the linearization expression of the network equation. Thus, we obtain the partial derivatives of the voltage magnitude and phase angle with respect to I_d and I_q, for subsequent use in the chain rule during gradient calculation.

2.6.2. Linearization of Generator Active Power

Linearize Equation (18), we have

$$\left(\begin{array}{c}\Delta {\mathrm{I}}_{\mathrm{d}}\\ \Delta {\mathrm{I}}_{\mathrm{q}}\end{array}\right)=\left(\begin{array}{cc}-{\displaystyle \frac{{\mathrm{R}}_{\mathrm{a}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}& -{\displaystyle \frac{{\mathrm{X}}_{\mathrm{q}}^{\prime }}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}\\ {\displaystyle \frac{{\mathrm{X}}_{\mathrm{d}}^{\prime }}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}& -{\displaystyle \frac{{\mathrm{R}}_{\mathrm{a}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}\end{array}\right)\left(\begin{array}{c}\Delta {\mathrm{V}}_{\mathrm{d}}\\ \Delta {\mathrm{V}}_{\mathrm{q}}\end{array}\right),$$

(26)

The coordinate transformation equation for the generator terminal voltage is

$${\mathrm{V}}_{\mathrm{dq}}={\mathrm{e}}^{\mathrm{j}\left({\displaystyle \frac{\mathrm{\pi }}{2}}-\mathrm{\delta }\right)}{\mathrm{V}}_{\mathrm{x}\mathrm{y}}={\mathrm{e}}^{\mathrm{j}\left({\displaystyle \frac{\mathrm{\pi }}{2}}-\mathrm{\delta }+\mathrm{\theta }\right)}\mathrm{V},$$

(27)

Linearize Equation (27), we have

$$\left(\begin{array}{c}\Delta {\mathrm{V}}_{\mathrm{d}}\\ \Delta {\mathrm{V}}_{\mathrm{q}}\end{array}\right)=\left(\begin{array}{cc}\sin \left(\mathrm{\delta }-\mathrm{\theta }\right)& -\cos \left(\mathrm{\delta }-\mathrm{\theta }\right)\mathrm{V}\\ \cos \left(\mathrm{\delta }-\mathrm{\theta }\right)& \sin \left(\mathrm{\delta }-\mathrm{\theta }\right)\mathrm{V}\end{array}\right)\left(\begin{array}{c}\Delta \mathrm{V}\\ \Delta \mathrm{\theta }\end{array}\right),$$

(28)

The electromagnetic power of the generator is

$${\mathrm{P}}_{\mathrm{e}}=\mathrm{Re}\left(\left({\mathrm{V}}_{\mathrm{d}}+\mathrm{j}{\mathrm{V}}_{\mathrm{q}}\right){\left({\mathrm{I}}_{\mathrm{d}}+\mathrm{j}{\mathrm{I}}_{\mathrm{q}}\right)}^{*}\right)={\mathrm{V}}_{\mathrm{d}}{\mathrm{I}}_{\mathrm{d}}+{\mathrm{V}}_{\mathrm{q}}{\mathrm{I}}_{\mathrm{q}},$$

(29)

Linearize Equation (29), we have

$$\Delta {\mathrm{P}}_{\mathrm{e}}=\Delta {\mathrm{V}}_{\mathrm{d}}{\mathrm{I}}_{\mathrm{d}}+\Delta {\mathrm{V}}_{\mathrm{q}}{\mathrm{I}}_{\mathrm{q}}+{\mathrm{V}}_{\mathrm{d}}\Delta {\mathrm{I}}_{\mathrm{d}}+{\mathrm{V}}_{\mathrm{q}}\Delta {\mathrm{I}}_{\mathrm{q}},$$

(30)

Substitute Equations (26) and (28) into (30), and simplify to obtain

$$\Delta {\mathrm{P}}_{\mathrm{e}}={\left(\begin{array}{c}{\mathrm{I}}_{\mathrm{d}}-{\displaystyle \frac{{\mathrm{R}}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{d}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}+{\displaystyle \frac{{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{V}}_{\mathrm{q}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}\\ {\mathrm{I}}_{\mathrm{q}}-{\displaystyle \frac{{\mathrm{X}}_{\mathrm{q}}^{\prime }{\mathrm{V}}_{\mathrm{d}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}-{\displaystyle \frac{{\mathrm{R}}_{\mathrm{a}}{\mathrm{V}}_{\mathrm{q}}}{{{\mathrm{R}}_{\mathrm{a}}}^2+{\mathrm{X}}_{\mathrm{d}}^{\prime }{\mathrm{X}}_{\mathrm{q}}^{\prime }}}\end{array}\right)}^{\mathrm{T}}\left(\begin{array}{cc}\sin \left(\mathrm{\delta }-\mathrm{\theta }\right)& -\cos \left(\mathrm{\delta }-\mathrm{\theta }\right)\mathrm{V}\\ \cos \left(\mathrm{\delta }-\mathrm{\theta }\right)& \sin \left(\mathrm{\delta }-\mathrm{\theta }\right)\mathrm{V}\end{array}\right)\left(\begin{array}{c}\Delta \mathrm{V}\\ \Delta \mathrm{\theta }\end{array}\right).$$

(31)

Here, Equation (31) is the linearization expression of generator’s active power output.

2.6.3. Disturbance Analysis of the Generator’s Electromagnetic Power

The electromagnetic power of the generator is expressed as

$${\mathrm{P}}_{\mathrm{e}}={\mathrm{V}}_{\mathrm{d}}{\mathrm{I}}_{\mathrm{d}}+{\mathrm{V}}_{\mathrm{q}}{\mathrm{I}}_{\mathrm{q}}$$

(32)

Combine the steady-state equation of the transient electromotive force and the equation of the generator and network interface

$${\mathrm{E}}_{\mathrm{d}}^{\prime }={\mathrm{V}}_{\mathrm{d}}+{\mathrm{R}}_{\mathrm{a}}{\mathrm{I}}_{\mathrm{d}}-{\mathrm{x}}_{\mathrm{q}}^{\prime }{\mathrm{I}}_{\mathrm{q}},$$

(33)

$${\mathrm{E}}_{\mathrm{q}}^{\prime }={\mathrm{V}}_{\mathrm{q}}+{\mathrm{R}}_{\mathrm{a}}{\mathrm{I}}_{\mathrm{q}}+{\mathrm{x}}_{\mathrm{d}}^{\prime }{\mathrm{I}}_{\mathrm{d}},$$

(34)

$$\mathrm{V}\angle \mathrm{\theta }={\mathrm{e}}^{\mathrm{j}\left({\displaystyle \frac{\mathrm{\pi }}{2}}-\mathrm{\delta }\right)}\left({\mathrm{V}}_{\mathrm{d}}+\mathrm{j}{\mathrm{V}}_{\mathrm{q}}\right),$$

(35)

By eliminating ${\mathrm{I}}_{\mathrm{d}}$, ${\mathrm{I}}_{\mathrm{q}}$, ${\mathrm{V}}_{\mathrm{d}}$ and ${\mathrm{V}}_{\mathrm{q}}$, and express ${\mathrm{P}}_{\mathrm{e}}$ as a function of the nodal voltage magnitude $\mathrm{V}$ and phase angle $\mathrm{\theta }$, we can obtain

$${\mathrm{P}}_{\mathrm{e}}={\displaystyle \frac{\mathrm{V}\left(2\cos \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{r}}_{\mathrm{a}}\right)+2\sin \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{r}}_{\mathrm{a}}+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)-\mathrm{V}\left({\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)\sin \left(2\left(\mathrm{\delta }-\mathrm{\theta }\right)\right)-2{\mathrm{r}}_{\mathrm{a}}\mathrm{V}\right)}{2\left({{\mathrm{r}}_{\mathrm{a}}}^2-{\mathrm{x}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)}},$$

(36)

Then, differentiate with respect to $\mathrm{V}$ and $\mathrm{\theta }$ to obtain

$${\displaystyle \frac{\partial {\mathrm{P}}_{\mathrm{e}}}{\partial \mathrm{V}}}={\displaystyle \frac{\cos \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{r}}_{\mathrm{a}}\right)+\sin \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{r}}_{\mathrm{a}}+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)-\mathrm{V}\left({\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)\sin \left(2\left(\mathrm{\delta }-\mathrm{\theta }\right)\right)-2{\mathrm{r}}_{\mathrm{a}}\mathrm{V}}{{{\mathrm{r}}_{\mathrm{a}}}^2-{\mathrm{x}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }}}$$

(37)

$${\displaystyle \frac{\partial {\mathrm{P}}_{\mathrm{e}}}{\partial \mathrm{\theta }}}={\displaystyle \frac{\mathrm{V}\left(\sin \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{r}}_{\mathrm{a}}\right)-\cos \left(\mathrm{\delta }-\mathrm{\theta }\right)\left({\mathrm{E}}_{\mathrm{d}}^{\prime }{\mathrm{r}}_{\mathrm{a}}+{\mathrm{E}}_{\mathrm{q}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)+\mathrm{V}\left({\mathrm{x}}_{\mathrm{d}}^{\prime }+{\mathrm{x}}_{\mathrm{q}}^{\prime }\right)\cos \left(2\left(\mathrm{\delta }-\mathrm{\theta }\right)\right)\right)}{{{\mathrm{r}}_{\mathrm{a}}}^2-{\mathrm{x}}_{\mathrm{d}}^{\prime }{\mathrm{x}}_{\mathrm{q}}^{\prime }}}$$

(38)

2.6.4. Sensitivity Analysis of the Voltage at PCC with Respect to the New Energy Control Strategy

As described in Section 2.2, regarding the new energy model with control strategy switching, the new energy units exhibit different fault ride-through methods influenced by the control mode. Since each control mode is represented by a first-order polynomial equation, the partial derivatives of voltage and adjustable parameters are directly computed for each mode. The corresponding sensitivity information is then the linear increment under disturbance.

Normal control mode:

The active current control method:

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=-{\displaystyle \frac{{\mathrm{P}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}^2}}.$$

(39)

Reactive current control method:

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}={\displaystyle \frac{{\mathrm{Q}}_{\mathrm{r}\mathrm{e}\mathrm{f}}}{{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}^2}}.$$

(40)

Fault ride-through control mode:

The active current control method:

1.

Specified current control:

$${\displaystyle \frac{\partial {\mathrm{i}}_{\mathrm{d}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=0.$$

(41)

2.

Specified current as a percentage of the initial current control:

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=0.$$

(42)

3.

Specified power setpoint:

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=-{\displaystyle \frac{{\mathrm{P}}_{\mathrm{s}\mathrm{e}\mathrm{t}\_\mathrm{H}\mathrm{V}}\mathrm{N}}{{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}^2}}.$$

(43)

4.

Specified power station initial power percentage control.

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=-{\displaystyle \frac{{\mathrm{K}}_{\mathrm{s}\mathrm{e}\mathrm{t}\_\mathrm{H}\mathrm{V}}\%{\mathrm{P}}_0}{{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}^2}}.$$

(44)

Reactive current control method:

1.

Voltage-controlled reactive current control method.

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}={\displaystyle \frac{{\mathrm{K}}_{\mathrm{Q}\_\mathrm{H}\mathrm{V}}{\mathrm{S}}_{\mathrm{m}\_\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}{{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}}}.$$

(45)

2.

Specified power setpoint.

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=-{\displaystyle \frac{{\mathrm{Q}}_{\mathrm{set}\_\mathrm{H}\mathrm{V}}\mathrm{N}}{{\mathrm{S}}_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}}{{\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}^2}}.$$

(46)

3.

Specified current control.

$${\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}3}}{\partial {\mathrm{V}}_{\mathrm{P}\mathrm{C}\mathrm{C}}}}=0.$$

(47)

3. Analyzing the Impact of LVRT Parameters

3.1. The Influence of LVRT Parameters on Transient Stability

3.1.1. The Indicator of Transient Rotor Angle Stability

During the electromechanical transient analysis of a power system, electromagnetic transients evolve much more rapidly than electromechanical transients. This discrepancy arises from the much faster dynamic response of power electronic devices compared to the rotational speed of synchronous machine rotors. Consequently, the electromechanical transient dynamics of the whole system are described through the following differential–algebraic formulation:

$$\dot{x}=\mathrm{f}(x,\omega ,V),$$

(48)

$$\dot{\mathsf{\delta }}=\mathsf{\omega },$$

(49)

$$\dot{\mathsf{\omega }}={\mathbf{M}}^{-1}{\mathbf{P}}_{\mathbf{m}}-{\mathbf{M}}^{-1}{\mathbf{P}}_{\mathbf{e}}(\mathsf{\delta },\mathbf{V}),$$

(50)

$$\mathbf{YV}=\mathbf{I}(\mathbf{x},\mathsf{\delta },\mathbf{V}).$$

(51)

They characterize all dynamic response processes excluding the rotor motion of the generator and represent the equations governing the rotor motion, where $\mathbf{M}$ is a diagonal matrix formed by the inertia time constants of the generator rotor. ${\mathbf{P}}_{\mathbf{m}}$ and ${\mathbf{P}}_{\mathbf{e}}$ represent the mechanical power and electromagnetic power of the generator, respectively. $\mathbf{Y}$ demonstrates the network equations of the power system, $\mathbf{V}$ represents the nodal voltage, and $\mathbf{I}$ is the currents injected into the nodes by all devices, such as $\mathbf{I}={\mathbf{i}}_{\mathbf{d}}+\mathbf{j}{\mathbf{i}}_{\mathbf{q}}$. If there are N generators in the system, $\mathsf{\delta }$, $\mathsf{\omega }$, ${\mathbf{P}}_{\mathbf{m}}$ and ${\mathbf{P}}_{\mathbf{e}}$ are N-dimensional vectors.

Model reduction involves simplifying a complex mathematical or computational model while retaining its essential characteristics. This process often entails eliminating or approximating certain components or dynamics of the system, resulting in a reduced-order model. This streamlined model is computationally more efficient while still providing accurate representations of the system’s behavior within specific operating conditions or constraints. The essence of model reduction is to confine the trajectories of a complex system to an invariant manifold. In the context of power system rotor angle stability analysis, this means constraining the angle information of N generators to a one-dimensional invariant manifold.

$$\delta =\mathrm{h}(\mathrm{\tau })={\delta }_e+\mathrm{\tau }\eta ,$$

(52)

${\delta }_e$ denotes the pre-fault steady-state position of the generators. From the same system and the same fault, it obtains the information of the rotor angle variation in all generators over time, denoted as historical data $\left\{\widehat{\mathsf{\delta }}\right({\mathrm{t}}_1),\widehat{\mathsf{\delta }}\left({\mathrm{t}}_2\right),\dots ,\widehat{\mathsf{\delta }}({\mathrm{t}}_{\mathrm{N}}\left)\right\}$. Then, under the premise of the one-dimensional linear invariant manifold, each column vector of matrix $\widehat{\mathbf{\Delta }}=[\widehat{\mathsf{\delta }}\left({\mathrm{t}}_1\right)-{\mathsf{\delta }}_{\mathrm{e}},\widehat{\mathsf{\delta }}\left({\mathrm{t}}_2\right)-{\mathsf{\delta }}_{\mathrm{e}},\dots ,\widehat{\mathsf{\delta }}\left({\mathrm{t}}_{\mathrm{N}}\right)-{\mathsf{\delta }}_{\mathrm{e}}]$ is situated in the subspace spanned by vector $\eta$. To ensure the aforementioned premises hold, it is necessary to select vector $\mathsf{\eta }$ to align with the directions of the column vectors of matrix $\mathbf{\Delta }$ as much as possible. This involves considering the following optimization problem:

$$\underset{{‖\mathsf{\eta }‖}_2=1}{\mathbf{max}}{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{N}}{\left[{\left(\mathsf{\delta }({\mathrm{t}}_{\mathrm{k}}\right)-{\mathsf{\delta }}_{\mathrm{e}})}^{\mathrm{T}}{\mathsf{\eta }}_{\mathrm{m}}\right]}^2},$$

(53)

It is equivalent to

$$\underset{{‖\mathsf{\eta }‖}_2=1}{\mathbf{max}}{\mathsf{\eta }}^{\mathrm{T}}\widehat{\mathbf{\Delta }}{\widehat{\mathbf{\Delta }}}^{\mathrm{T}}\mathsf{\eta },$$

(54)

The optimal solution to the above optimization problem corresponds to the eigenvector $\widehat{\mathbf{\Delta }}{\widehat{\mathbf{\Delta }}}^{\mathrm{T}}$ associated with the largest eigenvalue ${\lambda }_{\mathrm{m}}$ of the symmetric matrix ${\mathbf{\eta }}_{\mathrm{m}}$. The expression of the one-dimensional linear invariant manifold is as follows:

$$\delta =\mathrm{h}(\mathrm{\tau })={\delta }_e+\mathrm{\tau }{\eta }_m,$$

(55)

We can then approximately use the value of $\mathrm{\tau }$ to represent the rotor angle information of all generators, thereby achieving model reduction in the system. The reduced-order rotor motion equations are as follows:

$$\dot{\mathrm{\tau }}={\displaystyle \frac{\mathrm{d}\mathrm{\tau }}{\mathrm{dt}}},$$

(56)

$$\ddot{\mathrm{\tau }}={\eta }^{\mathrm{T}}[M^{-1}{P}_{\mathrm{m}}-M^{-1}{P}_{\mathrm{e}}(\mathrm{h}(\mathrm{\tau }),V)].$$

(57)

From Equations (56) and (57), it can be inferred that the system can be equivalently modeled as an SMIB system. $\mathrm{\tau }$ is analogous to the rotor angle of the generator in the system, and ${\mathrm{\tau }}_{\max }$ denotes the overall system’s rotor angle deviation magnitude. Improving this indicator is expected to strengthen the system’s rotor angle stability under transient conditions.

Furthermore, we define ${\mathrm{P}}_{\mathrm{m}}={\eta }^{\mathrm{T}}{M}^{-1}{P}_{\mathrm{m}}$ and ${\mathrm{P}}_{\mathrm{e}}\left(\mathrm{\tau }\right)={\eta }^{\mathrm{T}}{M}^{-1}{P}_{\mathrm{e}}$. Here, we use the superscript “f” to indicate the variables during the fault-on period and use superscript “pf” to indicate variables during the post-fault period. We assume that the system experiences a fault at t = 0, at which point $\mathrm{\tau }=0$. At $\mathrm{t}={\mathrm{t}}_{\mathrm{c}}$, the fault is cleared, corresponding to a fault clearance $\mathrm{\tau }$ value of ${\mathrm{\tau }}_{\mathrm{c}}$. By rearranging (57), we obtain

$${\displaystyle \frac{\mathrm{d}\mathrm{\tau }}{\mathrm{dt}}}\mathrm{d}({\displaystyle \frac{\mathrm{d}\mathrm{\tau }}{\mathrm{dt}}})=({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(\mathrm{\tau }))\mathrm{d}\mathrm{\tau }$$

(58)

Integrating (58), we get

$${\displaystyle {\int }_0^{\frac{\mathrm{d}{\mathrm{\tau }}_{\mathrm{c}}}{\mathrm{dt}}}\frac{\mathrm{d}\mathrm{\tau }}{\mathrm{dt}}}\mathrm{d}({\displaystyle \frac{\mathrm{d}\mathrm{\tau }}{\mathrm{dt}}})={\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }$$

(59)

Next,

$$\mathrm{d}\mathrm{t}={\displaystyle \frac{1}{2\sqrt{{\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }}}}\mathrm{d}\mathrm{\tau }$$

(60)

Integrating (60), we get

$${\mathrm{t}}_{\mathrm{c}}={\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}\frac{1}{2\sqrt{{\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }}}}\mathrm{d}\mathrm{\tau }$$

(61)

when specifying ${\mathrm{\tau }}_{\mathrm{c}}$, which is the $\mathrm{\tau }$ value of fault clearance, we can find the relationship between ${\mathrm{\tau }}_{\mathrm{c}}$ and ${\mathrm{t}}_{\mathrm{c}}$. Not only that,

$${\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau })\mathrm{d})\mathrm{\tau }+{\displaystyle {\int }_{{\mathrm{\tau }}_{\mathrm{c}}}^{{\mathrm{\tau }}_{\max }}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{p}\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }=0$$

(62)

From (62), we can also determine ${\mathrm{\tau }}_{\max }$ of the rotor angle swing after the fault. When we consider the equilibrium points after clearing the fault as ${\mathrm{\tau }}_{\mathrm{e}1}^{\mathrm{p}\mathrm{f}}$ and ${\mathrm{\tau }}_{\mathrm{e}2}^{\mathrm{p}\mathrm{f}}$,

$${\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau })\mathrm{d})\mathrm{\tau }+{\displaystyle {\int }_{{\mathrm{\tau }}_{\mathrm{c}\mathrm{c}}}^{{\mathrm{\tau }}_{\mathrm{e}2}^{\mathrm{p}\mathrm{f}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{p}\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }=0$$

(63)

We can obtain the critical $\mathrm{\tau }$ value ${\mathrm{\tau }}_{\mathrm{c}\mathrm{c}}$ for fault clearing in the system from (63). Furthermore, from (61), we can derive the critical fault-clearing time ${\mathrm{t}}_{\mathrm{c}\mathrm{c}}$ for the system.

$${\mathrm{t}}_{\mathrm{c}\mathrm{c}}={\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}\mathrm{c}}}\frac{1}{2\sqrt{{\displaystyle {\int }_0^{{\mathrm{\tau }}_{\mathrm{c}}}({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}^{\mathrm{f}}(}\mathrm{\tau }))\mathrm{d}\mathrm{\tau }}}}\mathrm{d}\mathrm{\tau }$$

(64)

3.1.2. The Relationship Between the Transient Rotor Angle Indicator and the Critical Quasi-Steady-State

In an SMIB system or a system analogous to the SMIB, the transient behavior of the rotor angle can be evaluated through the application of the equal-area principle. By applying this method, one can solve for parameters like ${\mathrm{\delta }}_{\max }$ or ${\mathrm{\tau }}_{\max }$, as shown in Figure 5. Under particular fault conditions and durations, decreasing the accelerating portion and expanding the decelerating portion contribute to lowering the generator’s ${\mathrm{\delta }}_{\max }$ or ${\mathrm{\tau }}_{\max }$, thereby enhancing the system’s ability to maintain rotor angle stability during transients.

Furthermore, lowering the power imbalance that occurs during fault initiation (i.e., decreasing the acceleration area) $\Delta {\mathrm{P}}^{ \mathrm{o}\mathrm{n}\mathrm{f}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{t}}$, or increasing the relative unbalanced power after the fault clearing (increasing the deceleration area) $\Delta {\mathrm{P}}^{ \mathrm{p}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{f}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{t}}$, can both reduce the system’s ${\mathrm{\delta }}_{\max }$ or ${\mathrm{\tau }}_{\max }$ and thus improve the system’s ability to maintain rotor angle stability during transient disturbances. Therefore, both the power imbalance occurring at fault initiation and that remaining after fault clearance are crucial factors influencing the rotor angle and transient stability of the system. This paper mainly investigates how the power imbalance occurring during fault initiation affects the rotor angle stability of the system.

3.1.3. Analysis of LVRT Parameter Scanning Results for Rotor Angle Stability

This paper adopts the control modes for renewable energy during fault conditions as specified current (percentage of initial current) control and voltage-controlled reactive current control. Therefore, the main focus is on the active power control parameter ${\mathrm{K}}_{\mathrm{P}}$ and reactive power control parameter ${\mathrm{K}}_{\mathrm{Q}}$. This paper analyzes the CSEE-FS standard test case, with its model framework diagram shown below, it includes hydropower, thermal power, wind power, and photovoltaic sources, with a 500 kV AC and ±500 kV DC as the main grid structure and its specific framework is shown in Figure 6 [27]. The specific data for the test case can be found in

Table A1. Overview of the Power Transmission Network.

Voltage Level	Bus Number	Bus Type
500	16	AC transmission grid
220	19	medium/high transformer
210	6	DC rectifier side
199	6	DC inverter side
sum	47	/

,

Table A2. Overview of Transmission Lines and Transformers.

Type	Number		Note
AC line	31	500 kV	AC transmission network framework: 11 lines
		220 kV	New energy transmission lines: 20 lines
Two-Winding Transformer	47	20/525 kV	Conventional unit step-up transformers: 7 units
		0.4/38.5 kV	New energy box-type transformers: 20 units
		0.69/38.5 kV
		38.5/230 kV	New energy station step-up transformers: 20 units
Three-Winding Transformer	15	Voltage/kV	525/230/37
DC line	3	Rated voltage/kV	$\pm$500
		Rated power/MW	5000

,

Table A3. Overview of Installed Power Capacity.

Bus	Conventional Power Generator		Renewable Energy Generator
	Fossil Fuel	Hydropower	Wind Power	Solar Power
B01	600	/	1050	1050
B02	600	/	/	/
B03	1000	/	1050	1650
B04	600	/	/	/
B05	/	1000	1050	1050
B06	/	1000	/	/
B07	600	600	/	/
sum	3400	2000	3150	3750

and

Table A4. System Load Condition.

Bus	Active Load/MW	Reactive Load/Mvar
B01	1100	360
B02	700	220
B03	900	300
B04	429.1	78
B05	500	170
B07	1223	400
sum	4852.1	1528

in the Appendix A. By keeping one parameter constant and gradually changing the other, the quasi-steady state and system indicators are obtained, as shown in

Table 1. Impact of LVRT active parameters on rotor angle stability.

${\mathit{K}}_{\mathit{P}}$	10	20	30	40	50	60	70	80
${\mathrm{\tau }}_{\max }$	1.063	1.016	1.044	1.058	1.077	1.088	1.207	1.544
$\Delta {\mathrm{P}}^{ \mathrm{o}\mathrm{n}\mathrm{f}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{t}}(\mathrm{k}\mathrm{W})$	2.401	1.985	2.045	2.217	2.364	2.963	3.145	3.946

and

Table 2. Impact of LVRT reactive parameters on rotor angle stability.

${\mathit{K}}_{\mathit{Q}}$	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1
${\mathrm{\tau }}_{\max }$	1.108	1.098	1.089	1.081	1.077	1.071	1.071	1.060
$\Delta {\mathrm{P}}^{ \mathrm{o}\mathrm{n}\mathrm{f}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{t}}(\mathrm{k}\mathrm{W})$	3.021	2.457	2.451	2.434	2.364	2.347	2.347	2.301

.

It can be observed that when ${\mathrm{K}}_{\mathrm{Q}}$ is maintained at 1.5, as ${\mathrm{K}}_{\mathrm{P}}$ increases from 10 to 70, the system’s rotor angle stability index gradually improves. This is because, after a fault, excessive renewable energy is disconnected due to control strategies, while the renewable energy that remains in operation generates more active power, helping to mitigate the rotor angle issue. However, when the coefficient increases from 70 to 90, the rotor angle stability index gradually deteriorates. This occurs as, under fault conditions, the surplus real power output from renewable-based generators leads to a continuous decline in the system’s bus voltage. When the voltage drops too low, it negatively affects the rotor angle, leading to a worsening of the rotor angle stability index. When ${\mathrm{K}}_{\mathrm{P}}$ is maintained at 50, and ${\mathrm{K}}_{\mathrm{Q}}$ increases from 0.7 to 2.1, the system’s rotor angle stability index generally improves. This is because the system’s increased reactive power generation helps raise the transient voltage after a fault, thereby enhancing the stability of the system’s rotor angle. However, identifying the optimal ranges of these two parameters to ensure system stability necessitates solid mathematical foundations for theoretical support.

3.2. The Influence of LVRT Parameters on Overvoltage

3.2.1. Mechanism in Formation of Transient Overvoltage

The occurrence of transient overvoltage is closely related to renewable energy generation. The control strategy under fault conditions is shown in Figure 7, where

• ① represents the control strategy during LVRT, such as specifying current or specifying power;
• ② represents the initial value of the power recovery;
• ③ represents the power recovery process.

As illustrated in the figure, during LVRT operation, renewable generation raises reactive power output to keep the bus voltage within an acceptable range. Once the fault has been removed, the system voltage rapidly recovers to its nominal value. However, due to the lag in the control strategy, reactive power remains at a higher level. Subsequently, the system voltage exhibits a further rise at the early stage of fault recovery. Subsequently, the control strategy is adjusted to reduce reactive power output, causing the voltage to decrease. Consequently, a transient overvoltage tends to appear at the initial phase of the recovery process in renewable energy systems.

For the High-voltage direct current (HVDC) transmission system, transient overvoltage observed at the source terminal mainly originates from the commutation failure and the subsequent recovery of the inverter circuit. During commutation failure events, the interruption of DC power transmission leads to a corresponding decrease in reactive power consumption at both terminal converter stations. The short-term inability to disconnect AC filters promptly results in substantial reactive power surplus, consequently inducing the transient overvoltage.

Based on the gradient descent method, the optimization of LVRT parameters aims to proactively limit the post-fault reactive power output of inverters, thereby directly mitigating the root cause of transient overvoltage. In contrast, conventional damping or reactive power compensation methods primarily rely on dissipating energy through damping devices or compensation equipment, thus suppressing overvoltage after it occurs. Therefore, in principle, optimizing LVRT parameters offers a more direct and effective approach to suppressing transient overvoltage.

3.2.2. Relationship Between Transient Over-Voltage and Key Quasi-Steady-State

Typically, the fault duration is short and the corresponding change in the generator’s rotor angle is not significant. This allows us to approximate the rotor angle linearly throughout the fault duration. In the absence of system damping, the rotor motion of the generator is governed by the following dynamic equation:

$$\dot{\mathrm{\delta }}={\mathrm{\omega }}_{\mathrm{s}}\left(\mathrm{\omega }-1\right),$$

(65)

$${\mathrm{T}}_{\mathrm{J}}\dot{\mathrm{\omega }}={\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}},$$

(66)

where ${\mathrm{\omega }}_{\mathrm{s}}$ denotes the synchronous angular frequency, which is related to the system’s frequency ${\mathrm{f}}_{\mathrm{n}}$ as: ${\mathrm{\omega }}_{\mathrm{s}}=2\mathrm{\pi }{\mathrm{f}}_{\mathrm{n}}$, ${\mathrm{T}}_{\mathrm{J}}$ represents the inertia time constant. Integrating both sides of Equation (66) gives

$${\displaystyle {\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_1}\dot{\mathrm{\omega }}\mathrm{d}\mathrm{t}}={\displaystyle {\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_1}\frac{{\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}}{{\mathrm{T}}_{\mathrm{J}}}\mathrm{d}\mathrm{t}},$$

(67)

where ${\mathrm{t}}_0$ denotes the fault initiation time, when the system operates under steady-state conditions and ${\mathrm{t}}_1$ represents the fault clearing time. Then we have

$${\mathrm{\omega }}_1={\mathrm{\omega }}_0+{\displaystyle \frac{{\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}}{{\mathrm{T}}_{\mathrm{J}}}}{\mathrm{t}}_{\mathrm{d}\mathrm{u}\mathrm{r}},$$

(68)

where ${\mathrm{\omega }}_0$ represents the generator’s angular frequency under steady state, ${\mathrm{\omega }}_1$ represents the generator’s angular frequency at ${\mathrm{t}}_1$, and ${\mathrm{t}}_{\mathrm{d}\mathrm{u}\mathrm{r}}$ represents the fault duration, defined as ${\mathrm{t}}_{\mathrm{d}\mathrm{u}\mathrm{r}}={\mathrm{t}}_1-{\mathrm{t}}_0$. Integrating both sides of Equation (65) gives

$${\displaystyle {\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_1}\dot{\mathrm{\delta }}\mathrm{d}\mathrm{t}}={\displaystyle {\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_1}{\mathrm{\omega }}_{\mathrm{s}}\left(\mathrm{\omega }-1\right)\mathrm{d}\mathrm{t}},$$

(69)

Combining with Equation (68), then we have

$${\mathrm{\delta }}_1={\mathrm{\delta }}_0+{\displaystyle \frac{{\mathrm{\omega }}_{\mathrm{s}}\left({\mathrm{P}}_{\mathrm{m}}-{\mathrm{P}}_{\mathrm{e}}\right)}{2{\mathrm{T}}_{\mathrm{J}}}}{{\mathrm{t}}_{\mathrm{d}\mathrm{u}\mathrm{r}}}^2,$$

(70)

where δ₀ denotes the rotor angle of the generator in steady-state operation, and δ₁ denotes the rotor angle at time t₁.

For permanent fault conditions, such as post-fault line disconnection, the admittance matrix experiences two changes throughout the process: the admittance matrix for the pre-fault condition is $\mathrm{Y}$, for the fault condition is ${\mathrm{Y}}^{\prime }$, and for the post-fault condition is ${\mathrm{Y}}^{″}$. As mentioned before, transient overvoltage occurs at the initial stage of fault recovery, hence the corresponding admittance matrix should be ${\mathrm{Y}}^{″}$. By integrating the quasi-steady-state models of each component and the commutation failure DC information during the fault, the post-fault voltage levels at each node are calculated to obtain the transient overvoltage assessment results.

3.2.3. Analysis of LVRT Parameter Scanning Results for Transient Overvoltage Stability

This section performs a parameter scan focusing on transient overvoltage, utilizing the same renewable energy control strategy as described in Section 3.1.3 and CSEE-FS system in Figure 6. The parameter scan still focuses on the active power support coefficient ${\mathrm{K}}_{\mathrm{P}}$ and reactive power support coefficient ${\mathrm{K}}_{\mathrm{Q}}$. As illustrated in Figure 8, ${\mathrm{K}}_{\mathrm{P}}$ shows distinct behavior in response to overvoltage events induced by inverter commutation failure and DC block faults. When ${\mathrm{K}}_{\mathrm{P}}$ is relatively high, such as ${\mathrm{K}}_{\mathrm{P}}=60$, voltage oscillation will happen resulting from the saturation of the renewable energy converters. When ${\mathrm{K}}_{\mathrm{P}}=100$, the transient overvoltage caused by DC commutation failure can be effectively relieved, while it will simultaneously aggravate the situation during subsequent DC blocking. Therefore, the control parameters for each renewable energy plant should be tuned according to specific gradient descent directions and regional factors.

As shown in Figure 9, ${\mathrm{K}}_{\mathrm{Q}}$ is insensitive to transient overvoltage caused by commutation failure. However, a reasonable support coefficient can improve transient overvoltage stability caused by blocking faults. When the system’s global reactive power support coefficient is adjusted from an initial value of ${\mathrm{K}}_{\mathrm{Q}}=1.5$ to ${\mathrm{K}}_{\mathrm{Q}}=1.0$, the transient overvoltage caused by DC blocking is better than in other scenarios.

4. Optimization Algorithm

4.1. Gradient Descent Algorithm for Transient Enhancement

The gradient direction represents the most effective direction for improving a given objective. As will be demonstrated in the following case studies, parameter optimization via the gradient descent method leads to improvements across different safety and stability issues.

Gradient Descent is an optimization algorithm designed to determine the function’s minimum point. The corresponding flowchart is shown in Figure 10 and the operational principle can be summarized as follows:

• Initialize power system parameters: Select a starting point as the initial parameters: ${\mathrm{K}}_{\mathrm{P}}^0=20,{\mathrm{K}}_{\mathrm{Q}}^0=1.5$.
• Determine the loss functions for different problems: ${\mathrm{P}}_{\mathrm{\eta }}={\eta }^{\mathrm{T}}{M}^{-1}{P}_{\mathrm{m}}-{\eta }^{\mathrm{T}}{M}^{-1}{P}_{\mathrm{e}}$ is for transient rotor angle stability issues, $\mathrm{V}$ is for transient overvoltage issues.
• Compute the gradient of the FRT control parameters relative to the loss function: this gradient indicates how the loss function varies along each parameter dimension. ${\displaystyle \frac{\partial {\mathrm{P}}_{\mathrm{\eta }}}{\partial \mathrm{p}}}$ is the gradient of control parameter p with respect to the rotor angle loss function, and ${\displaystyle \frac{\partial \mathrm{V}}{\partial \mathrm{p}}}$ is the gradient of control parameter p with respect to the voltage loss function.
• Update parameters: Use the gradient information to update the fault ride-through parameters to reduce the value of the loss function. The parameter update method involves adjusting the parameters in the direction opposite to the gradient.
• Iterative update: Continue executing steps 2 and 3 until the termination condition is satisfied, such as reaching the predefined upper limit of iterations or achieving a sufficiently small loss function value.
• Output results: The final fault ride-through control parameter values are the parameter values that minimize the loss function, representing the final optimization result.

4.2. Gradient Direction for Transient Stability Enhancement

The disturbance analysis of the relative unbalanced power in the quasi-steady state during or after a fault can be performed using the chain rule. This helps identify the parameter adjustment direction that enhances the system’s transient angle stability. Specifically, during the fault, the relative unbalanced power should be reduced. To achieve this, the derivative information of the parameters with respect to the unbalanced power needs to be calculated, as shown in Equation (71), which indicates the direction for parameter adjustment. By adjusting the parameters in the direction where the derivative information is negative and iterating using gradient descent, the derivative information gradually approaches zero. The parameters obtained at this point will be the most beneficial for the system’s angle stability.

$$\begin{array}{c}{\displaystyle \frac{\partial {\mathrm{P}}_{\mathrm{\eta }}}{\partial \mathrm{p}}}={\displaystyle \frac{\partial {\eta }^{\mathrm{T}}[M^{-1}{P}_{\mathrm{m}}-M^{-1}{P}_{\mathrm{e}}(g(\mathrm{\tau }),h(\mathrm{\tau }),V)]}{\partial \mathrm{V}}}\cdot \left({\displaystyle \frac{\partial \mathrm{V}}{\partial {\mathrm{I}}_{\mathrm{d}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}}}{\partial \mathrm{p}}}+{\displaystyle \frac{\partial \mathrm{V}}{\partial {\mathrm{I}}_{\mathrm{q}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}}}{\partial \mathrm{p}}}\right)\\ +{\displaystyle \frac{\partial {\eta }^{\mathrm{T}}[M^{-1}{P}_{\mathrm{m}}-M^{-1}{P}_{\mathrm{e}}(g(\mathrm{\tau }),h(\mathrm{\tau }),V)]}{\partial \mathrm{\theta }}}\cdot \left({\displaystyle \frac{\partial \mathrm{\theta }}{\partial {\mathrm{I}}_{\mathrm{d}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}}}{\partial \mathrm{p}}}+{\displaystyle \frac{\partial \mathrm{\theta }}{\partial {\mathrm{I}}_{\mathrm{q}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}}}{\partial \mathrm{p}}}\right),\end{array}$$

(71)

4.3. Gradient Direction for Over-Voltage Suppression

For analyzing post-fault voltage variations, we examine how injected currents relate to the nodal voltages through the network equation. By employing the chain rule, we obtain gradient information of the voltage magnitude with respect to the control parameters of renewable energy generation, as shown in Equation (72), where V represents voltage, p represents the control parameter of RES, ${\mathrm{I}}_{\mathrm{d}}$ denotes d-axis current of the generator and ${\mathrm{I}}_{\mathrm{q}}$ is the q-axis current. The negative gradient information indicates the direction to suppress transient overvoltage. The series of parameters represent the optimal results for transient over-voltage stability.

$${\displaystyle \frac{\partial \mathrm{V}}{\partial \mathrm{p}}}={\displaystyle \frac{\partial \mathrm{V}}{\partial {\mathrm{I}}_{\mathrm{d}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{d}}}{\partial \mathrm{p}}}+{\displaystyle \frac{\partial \mathrm{V}}{\partial {\mathrm{I}}_{\mathrm{q}}}}\cdot {\displaystyle \frac{\partial {\mathrm{I}}_{\mathrm{q}}}{\partial \mathrm{p}}}.$$

(72)

5. Results and Discussion

5.1. Results for Transient Rotor Angle Stability Enhancement

To analyze the transient stability following a grounding fault at the B06-B07 terminal cleared after 0.1 s, Figure 11 illustrates the time evolution of each generator’s rotor angle in the CSEE-FS system. The invariant manifold information obtained using the invariant manifold reduction method is shown in Figure 12, which clearly displays the oscillation direction of each generator’s rotor angle. After model reduction, the time-domain simulation curve of the reduced-order model is shown in Figure 13.

This case study mainly focuses on parameter optimization for ${\mathrm{K}}_{\mathrm{P}}$ and ${\mathrm{K}}_{\mathrm{Q}}$ during FRT. Initially, the relative imbalance across the entire system is determined through the QSS modeling approach described previously. Then, the relative imbalance power gradient is evaluated for each control parameter, the updated parameters are re-applied to the system, and this iteration continues until the gradient becomes zero. Ultimately, the minimum relative imbalance power and the optimal parameters are determined. Some of the renewable energy parameter optimizations before and after are shown in

Table 3. Optimization results of LVRT parameters for rotor angle stability.

Renewable Energy Unit Name	(Before Optimization)		(After Optimization)
	${\mathbf{K}}_{\mathbf{P}}$	${\mathbf{K}}_{\mathbf{Q}}$	${\mathbf{K}}_{\mathbf{P}}$	${\mathbf{K}}_{\mathbf{Q}}$
WT03-1	30	1.8	0	1.82
WT03-2	30	1.8	0	1.82
WT03-3	30	1.8	0	1.82
WT04-1	30	1.8	0	1.78
WT04-2	30	1.8	0	1.78
WT04-3	30	1.8	0	1.74
WT04-4	30	1.8	0	1.74
WT05-1	30	1.8	0	1.74
WT05-2	30	1.8	100	1.83
WT05-3	30	1.8	100	1.83

. In this case study, the relative imbalance power calculated using the quasi-steady-state method before optimization was 0.361, and the relative imbalance power after optimization was 0.148. Correspondingly, ${\mathrm{\tau }}_{\max }$ changed from 0.205 to 0.145. This demonstrates that a smaller acceleration area leads to better stability of the generators’ rotor angles. Figure 14 presents the simulation results over time before and after parameter optimization, while Figure 15 depicts the temporal evolution of each generator’s rotor angle corresponding to the same conditions.

5.2. Results for Transient Over-Voltage Suppression

The test is conducted based on the CSEE-FS standard example, as shown in Figure 6. A three-phase grounding fault is applied at node B10 on the line “B10-B05”, lasting for 0.1 s.

Based on the provided fault information, the admittance matrix should reflect the network configuration during fault conditions, denoted as ${\mathrm{Y}}^{\prime }$. Combining the quasi-steady-state models of the various components, calculations are performed to obtain the LVRT information for the renewable energy system throughout the fault duration. Subsequently, following fault clearance without line disconnection, the admittance matrix should be modified to the post-recovery network configuration, denoted as ${\mathrm{Y}}^{″}$. It is assumed that the initial current values during the fault restoration are equal to those during the fault. Finally, calculations are carried out to determine the voltage levels at each node after fault restoration and the transient overvoltage assessment result is obtained.

Table 4. Optimization results of LVRT parameters for overvoltage.

Renewable Energy Unit Name	Before Optimization		After Optimization
	${\mathbf{K}}_{\mathbf{P}}$	${\mathbf{K}}_{\mathbf{Q}}$	${\mathbf{K}}_{\mathbf{P}}$	${\mathbf{K}}_{\mathbf{Q}}$
PV01-1	80	1.2	0	6.9
PV01-2	80	1.2	0	5.6
PV01-3	80	1.2	0	1.0
PV03-1	80	1.2	0	2.8
WT01-1	80	1.5	0	1.8
WT01-2	80	1.5	0	1.6
WT01-3	80	1.5	0	1.7
WT03-1	80	1.5	0	1.4
WT03-3	80	1.5	0	1.7

presents the renewable energy settings for the system prior to and following parameter tuning. (${\mathrm{K}}_{\mathrm{P}}$ denotes the proportion of the active current or output of the renewable generator relative to its baseline during the LVRT interval). The temporal voltage at node B10 and the renewable unit’s active power, both pre- and post-optimization, are depicted in Figure 16 and Figure 17. From the result graph, it can be observed that the transient overvoltage occurs at $\mathrm{t}=1.6 \mathrm{s}$ before parameter optimization. After parameter optimization, the strategy results in a reduction in the renewable generator’s active power between 1.5 s and 1.6 s, and the transient overvoltage moment is shifted to $\mathrm{t}=1.5 \mathrm{s}$. Meanwhile, the transient overvoltage magnitude dropped from an initial value of 1.0763 p.u. down to 1.01 p.u., indicating an improvement in voltage stability. In practical power systems, 1.05 p.u. can be considered the operational security boundary. Therefore, reducing the overvoltage down to 1.01 p.u. achieves a transition from an unsafe operating state to a safe operating state, significantly improving the overall reliability and dynamic performance of the system.

6. Conclusions

This paper proposes a comprehensive approach for optimizing FRT control parameters of RES to enhance both transient rotor angle stability and transient overvoltage security in power systems. The main contributions and findings are summarized as follows:

Quasi-steady-state modeling effectively simplifies the representation of RES as voltage-controlled current sources, enabling efficient and accurate sensitivity analysis and gradient computation. This approach facilitates a clear understanding of the influence of FRT parameters on stability within an acceptable error margin.

For transient rotor angle stability, the reduction in the relative unbalanced power during faults is identified as a key factor. Through gradient-based optimization, the relative unbalanced power was reduced from 0.361 to 0.148, while the maximum rotor angle swing ${\mathrm{\tau }}_{\max }$ decreased from 0.205 to 0.145, an improvement of about 29.3%. This significantly enhances the system’s transient synchronization stability.

For transient overvoltage suppression, the optimized control parameters effectively limit reactive power output during fault recovery, reducing the peak overvoltage at node B10 from 1.0763 p.u. to 1.01 p.u., a reduction of 6.16%. More importantly, this brings the system from an unsafe operating state (above 1.05 p.u.) to a secure operating region, demonstrating the practical effectiveness of the proposed method.

In summary, the study introduces an effective and computationally efficient approach for renewable energy FRT optimization, advancing both conceptual understanding and practical techniques for improving system stability. In future studies, the methodology will be applied to multi-objective optimization and adaptive control strategies that respond dynamically to changing grid conditions.