Frequency Modulation Capability Improvement Method of Offshore Wind Farms Based on Energy Storage Devices

Abstract

Installing energy storage devices can improve the frequency modulation ability of offshore wind farms to participate in the grid. The lifecycle and wear of energy storage devices are significantly influenced by ambient temperature, charge and discharge rates, cycle depths, and operating environments. To extend the lifecycle and reduce the replacement frequency of these devices, their operation mode must be carefully considered. However, existing energy storage optimization configurations rarely consider these factors, particularly when addressing the frequency stability of offshore wind power systems. To address this gap, an optimization method is proposed for energy storage allocation that incorporates system frequency support, energy storage cost, and the devices’ lifecycle and degradation. This approach ensures a reasonable and efficient allocation of energy storage.

1. Introduction

To achieve the dual-carbon goal, it is crucial to develop clean and renewable energy sources, such as wind power, which holds significant potential for improvement [1]. Offshore wind power plays a key role in this development. Unlike onshore wind power, offshore wind power offers several advantages: greater stability, higher wind speeds, increased power generation efficiency, reduced land usage, proximity to load centers, and no requirement for land resources [2].

With the long-distance and large-scale development of offshore wind power, it has become a prevailing trend for offshore wind power to be integrated into the grid via Voltage Source Converter-Based High-Voltage Direct Current (VSC-HVDC) technology [3]. However, offshore wind farms connected to the grid via flexible DC will adversely affect the frequency stability of the AC system: (1) new energy-generating units with small rotational inertia replace synchronous generators with large rotational inertia, which will reduce the overall inertia of the grid; (2) new energy power electronics under traditional grid-connected control cannot provide inertia support for grid frequency events. At the same time, in the absence of traditional power support scenarios, the frequency stability problem of offshore wind power is prominent, and new energy generation with DC delivery is more complex. Offshore wind power’s frequency stability problem is notable, and new energy generation with DC delivery is more complicated.

The two-way regulation speed, short-term charging and discharging capability, and controllability of energy storage devices are strongly linked to the development of offshore wind power [4]. The configuration of energy storage devices can provide offshore wind farms with the fastest possible frequency regulation and inertia support, in addition to compensating for the lack of DC output capacity due to the randomness and uncertainty of wind power generation [5].

In terms of frequency stability, it is essential to explore the frequency support capability of renewable energy systems from the source side [6]. Wind–solar storage systems, integrated through power electronic devices, do not possess or have weak inertia, and their ability to resist extreme fluctuations in wind and solar output caused by extreme weather conditions is significantly reduced [7]. Renewable energy sources can provide frequent support to the system through additional control. The authors of [8] reviewed existing control technologies and analyzed various control methods and their applications. Control technologies, represented by virtual synchronous generators (VSGs), are becoming increasingly mature and have been applied in engineering practice. From the perspective of grid-forming and grid-following controls, VSG control technology can be divided into current-source VSG and voltage-source VSG. The authors of [9] analyzed the inertia response characteristics of renewable energy under these two control methods and explored the impact of virtual inertia on system frequency. The authors of [10] analyzed the roles of the inertia time constant and primary frequency control coefficient, two key parameters, in reducing the maximum rate of change of frequency (RoCoF) and increasing the minimum frequency point. However, unreasonable parameter settings in renewable energy stations may hinder the effectiveness of the control, and in some cases, lead to disconnection from the grid. Existing planning studies typically treat the frequency support capabilities of renewable energy as a constant, and few studies consider the rationality of control parameters in the planning process [11].

At the economic level, the coordination of energy storage planning with DC operation modes is considered. The lack of support scenarios exacerbates the difficulty of power and energy balance. Without improving the DC operation mode, the economic viability of the energy storage configuration will be poor. Modern DC operation modes are inflexible, and traditional DC modeling methods based on monthly energy balance are no longer applicable to scenarios involving strong stochastic fluctuations in renewable energy delivery. In the absence of support, to meet the power delivery demands of renewable energy bases, the system ability to track source dynamics needs to be enhanced, and the DC output power must be adjusted flexibly.

When optimizing energy storage configurations that consider system frequency stability, due to the high-order nonlinearity of control loops, it is difficult to derive frequency expressions analytically through frequency response equations. Existing research on frequency stability optimization typically involves simplifications. The authors of [12] established a system frequency response (SFR) model, retaining only low-order components, and derived a mathematical expression for frequency variation over time through the aggregation of multiple control parameters. The authors of [13] directly ignored the nonlinear characteristics of control loops, treating the fast frequency response process of the energy storage system as a linear change over time. This simplification enables the transient frequency minimum to be approximated as a quadratic function. On this basis, the authors of [14] proposed an energy storage configuration method for fast frequency response using a linear ramp model. However, these simplifications do not accurately reflect the role of grid-following and grid-forming control methods in the frequency response process. Existing planning studies have not considered the differences in frequency response between these two control methods, overlooking the impact of control methods on energy storage configuration.

Current methods for optimizing energy storage allocation in offshore wind power systems often employ simplified models to assess system frequency response, thereby neglecting the impact of control modes on energy storage allocation [15]. Recent studies have developed more comprehensive system frequency response models that account for the control strategy of configured network types. This paper proposes a method to improve the frequency modulation capability of offshore wind farms based on energy storage devices. These models demonstrate how various control methods, including the type of network configuration, impact optimal energy storage allocation [16].

2. Model Formulation

2.1. Transient Stabilization Constraints for Offshore Wind Power

2.1.1. Frequency Stability Constraints for Offshore Wind Farms

There is a close connection between the frequency and active power balance of the offshore wind farm and the frequency response process after a disturbance at a particular moment exists, including two phases: inertial response and primary frequency modulation. Neglecting damping, the unbalanced power of an offshore wind farm is shown in Equation (1). A power perturbation occurs.

$$P_{\mathrm{u},t,x}=P_{\mathrm{im},t}-{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{P}_{a,t,x}^{\mathrm{M}}}-P_{\mathrm{c},t,x}$$

(1)

where $P_{\mathrm{u},t,x}$ is the unbalanced power corresponding to point $x$ at the moment $t$ when the perturbation occurs; $P_{\mathrm{im},t}$ is the envisioned disturbed power at moment $t$; $n$ denotes the number of networked stations; $P_{a,t,x}^{\mathrm{M}}$ denotes the actual power of grid-configured wind farm $a$ at point $x$ at time $t$; and $P_{\mathrm{c},t,x}$ is the primary frequency modulation (FM) power of the storage plant corresponding to point $x$ in period $t$.

The frequency variation rate satisfies the following constraints:

$${\mathrm{FM}}_{t,x}=-{\displaystyle \frac{P_{\mathrm{u},t,x}{f}_0}{2J_{\mathrm{s},t}}}$$

(2)

where ${\mathrm{FM}}_{t,x}$ is the frequency variation rate corresponding to the $x$ step in period $t$, $J_{s,t}$ is the overall inertia of the system, and $f_0$ is the rated frequency.

The corresponding frequency deviation is shown in Equation (3):

$$\Delta f_{t,x}=\Delta f_{t,x-1}+{\mathrm{FM}}_{t,x}\tau$$

(3)

where $\Delta f_{t,x}$ is the frequency deviation and $\tau$ is the pace.

From a frequency safety perspective, the maximum frequency variation rate constraint must be considered during the inertia support process. The primary FM should account for the frequency nadir limit and the quasi-steady-state frequency deviation constraint, as shown in Equation (4).

$$\left\{\begin{array}{l}-{\mathrm{FM}}_{\max }\le {\mathrm{FM}}_{t,x}\le {\mathrm{FM}}_{\max }\\ -\Delta f_{\max }\le \Delta f_{t,x}\le \Delta f_{\max }\\ -f_{\mathrm{err}}\le \Delta f_{t,T/\tau }\le f_{\mathrm{err}}\end{array}\right.$$

(4)

where ${\mathrm{FM}}_{t,x}/\Delta f_{t,x}$ is the frequency variation rate and frequency deviation corresponding to the $x$ step in time period $t$, respectively; $\Delta f_{\max }$ is the maximum permissible frequency deviation of the system; and $f_{\mathrm{err}}$ is the quasi-steady-state frequency deviation.

2.1.2. Frequency Response Constraints for Grid-Connected Wind Farms

Considering the FM dead zone and the incrementable power in primary FM during the wind farm’s response, the primary FM active power increment for a grid-connected wind farm is described in Equation (5).

$$\begin{array}{l}\Delta P_{a,t,x}^{\mathrm{M}1}=\Delta P_{a,t,x-1}^{\mathrm{M}1}\\ +{\displaystyle \frac{\tau }{\tau +T_{\mathrm{w},a}}}\left(-{\delta }_{\sigma ,a}\left(\Delta f_{t,x}+\Delta f_{\mathrm{d}}\right)-\Delta P_{a,t,x-1}^{\mathrm{M}1}\right)\cdot {\displaystyle \frac{P_{\mathrm{w},a}}{f_0}}\end{array}$$

(5)

Considering the wind farm’s primary FM active reserve limit, its primary FM active increment satisfies constraint (6).

$$\Delta P_{a,t,x}^{\mathrm{M}}=\min \left(\Delta P_{a,t,x}^{\mathrm{M}1},R_{\mathrm{w},a,t}\right)$$

(6)

where $\Delta P_{a,t,x}^{\mathrm{M}1}$ is the primary FM power corresponding to point $x$ after the perturbation in period $t$ of the grid-constructing wind farm $a$; $T_{\mathrm{w},a}$ is the time constant of primary frequency regulation for grid-connected wind farms; ${\delta }_{\sigma ,a}$ is the primary FM factor; $\Delta f_{\mathrm{d}}$ is the FM deadband; $P_{\mathrm{w},a}$ is the rated power of the grid-type wind farm $a$; and $R_{\mathrm{w},a,t}$ is the standby power of wind farm $a$ at time $t$.

2.1.3. Frequency Response Constraints for Grid-Configured Energy Storage Plants

Similarly to wind farms, the primary FM active increment of a grid-connected energy storage plant is shown in Equation (7):

$$\begin{array}{l}\Delta P_{\mathrm{c},t,x}=\Delta P_{\mathrm{c},t,x-1}\\ +{\displaystyle \frac{\tau }{\tau +T_{\mathrm{c}}}}\left(-{\delta }_{\sigma ,\mathrm{c}}\left(\Delta f_{t,x}+\Delta f_{\mathrm{d}}\right)-\Delta P_{\mathrm{c},t,x-1}\right){\displaystyle \frac{P_{\mathrm{n}}}{f_0}}\end{array}$$

(7)

where $T_{\mathrm{c}}$ is the first-order inertial time constant of the energy storage plant; $P_{\mathrm{n}}$ is the rated power of the energy storage plant; and ${\delta }_{\sigma ,c}$ is the primary FM factor of the energy storage plant.

2.2. Offshore Wind Farm Steady-State Operation Scenario

2.2.1. Power Balance Constraints

Offshore wind farms maintain power balance by charging the energy storage station when the wind farm output exceeds the load power and discharging when the output is less than the load power.

$$P_{\mathrm{load},t}=P_{\mathrm{out},t}+P_{\mathrm{ac},t}+P_{\mathrm{SS}2,t}-P_{\mathrm{waste},t}-P_{\mathrm{SS}1,t}$$

(8)

where $P_{\mathrm{out},t}$ is the output power of the wind turbine module at time $t$; $P_{\mathrm{waste},t}$ is the abandoned wind power at time $t$; $P_{\mathrm{SS}1,t}$ is the energy storage charging power at time $t$; $P_{\mathrm{SS}2,t}$ is the stored discharge power at time $t$; $P_{\mathrm{load},t}$ is the load power at time $t$; and $P_{\mathrm{ac},t}$ is the AC system support power at time $t$.

2.2.2. Offshore Wind Farm Output Constraints

The participation of offshore wind power in the primary FM standby power satisfies Equation (9).

$$R_{w,a,t}=\alpha P_{w,a,t}^{\max }$$

(9)

where $\alpha$ is the standby rate for wind farms and $P_{\mathrm{w},a,t}^{\max }$ is the maximum available wind farm output $a$ time.

2.2.3. Energy Storage Plant Operation Constraints

The charging and discharging power of the energy storage plant needs to satisfy certain power constraints, as shown in Equations (10)–(12).

$$0\le P_{\mathrm{SS}1,t}\le {\theta }_{t,1}P$$

(10)

$$0\le P_{\mathrm{SS}2,t}\le {\theta }_{t,2}P$$

(11)

$${\theta }_{t,1}+{\theta }_{t,2}\le 1$$

(12)

where ${\theta }_{t,1}$/${\theta }_{t,2}$ is the energy storage charge/discharge state variable (0–1 variable). There are three possible values for the state variable: ${\theta }_{t,1}$, ${\theta }_{t,2}$, and 0 is the limit case. At this time, the energy storage plant is neither charging nor discharging. When ${\theta }_{t,1}$ is 1 and ${\theta }_{t,2}$ is 0, the energy storage plant is in the charging state and the power needs to satisfy the constraints of Equation (10). When ${\theta }_{t,1}$ is 0 and ${\theta }_{t,2}$ is 1, the energy storage plant is in the discharge state and the power satisfies the constraints of Equation (11). Overall, this denotes the peak power of the energy storage device.

Energy storage plant capacity constraints are shown as follows:

$$C_{t+1}=C_t+{\eta }_{\mathrm{SS}1}{P}_{\mathrm{SS}1,t}\tau -P_{\mathrm{SS}2,t}\tau /{\eta }_{\mathrm{SS}2}$$

(13)

$$C_{\min }\le C_t\le C_{\mathrm{n}}$$

(14)

where $C_t$ is the energy storage capacity corresponding to period $t$; ${\eta }_{\mathrm{SS}1}$ is the charging efficiency; ${\eta }_{\mathrm{SS}2}$ is the discharge efficiency; $C_{\min }$ is the minimum capacity allowed for energy storage in period $t$; and $C_{\mathrm{n}}$ is the rated capacity.

2.2.4. Power Constraints on the Frequency Response of an Energy Storage Plant

The corresponding constraints are shown below:

$$\Delta P_{\mathrm{z},t,x}=\Delta P_{\mathrm{c},t,x}+2J_{c,t}{\mathrm{FM}}_{t,x}{\displaystyle \frac{P_{\mathrm{new},t}}{f_0}}$$

(15)

$$0\le \Delta P_{z,t,x}\le K_{\max }{P}_{\mathrm{new},t}-P_{\mathrm{SS}2,t}+P_{\mathrm{SS}1,t}$$

(16)

where $\Delta P_{\mathrm{z},t,x}$ is the total FM power provided by the storage plant at point $x$ at time $t$; $J_{c,t}$ is the inertial time constant; and $K_{\max }$ is the maximum charging and discharging power of the energy storage.

The power constraints used by the storage plant to support frequency stabilization are as follows:

$$C_{\min }\le C_t-{\displaystyle \sum _{x=1}^{T/\tau }\Delta P_{c,t,x}^z}\tau \le C_{\mathrm{n}}$$

(17)

where $\Delta P_{c,t,x}^z$ is the total FM power provided by the $x$ storage plant after perturbation in the period $t$.

2.3. Optimized Allocation Considering Energy Storage Lifecycle and Equipment Losses

The energy storage planning objective for offshore wind farms aims to minimize the comprehensive costs, including storage plant investment, operation and maintenance, losses, and total operating costs. The minimized total cost is shown in (18):

$$S_{\min }=S_{\mathrm{ope}}+S_{\mathrm{loss},\mathrm{abs}}+S_{\mathrm{in}}+S_{\mathrm{s}}$$

(18)

where $S_{\min }$ is the minimized total cost; $S_{\mathrm{in}}$ is the initial investment cost of the energy storage; $S_s$ is the operating stale cost of the offshore wind farm; $S_{\mathrm{loss},\mathrm{abs}}$ is the cost loss in the storage operation; and $S_{\mathrm{ope}}$ is the operating cost over the lifetime of the energy storage. The cost calculation for each component is shown below.

2.3.1. Energy Storage Operation and Maintenance Costs

The lifecycle of energy storage is influenced by the operating environment, charging/discharging rates, and depths. In practice, the discharging depth and cycle count are typically used to estimate the lifespan of the energy storage device.

The cycle counts are fit using measured data. Then, the number of cycles of the energy storage device $N$ is obtained:

$$N={\displaystyle \frac{4705}{D_{\mathrm{OD}}^{0.436}}}{e}^{0.041\left(1-D_{O\mathrm{D}}\right)}$$

(19)

where $D_{OD}$ is the charging and discharging depth, and the measured data in the equation are obtained from the energy storage equipment manufacturer after testing.

Charge/discharge depth is often assumed to be constant in formula calculations. However, considering actual operating conditions, it varies. Therefore, its converted data can be expressed as follows:

$$\theta ={\displaystyle \frac{N_s}{N}}$$

(20)

where $N_s$ is the number of single cycles in the actual rated condition and $\theta$ is the conversion factor.

Then, the lifecycle of the energy storage device can be expressed as follows:

$$Y={\displaystyle \frac{N_s{D}_{\mathrm{OD}}{D}_{\mathrm{SS}}}{{\displaystyle \sum _{d=1}^{365}{\displaystyle \sum _{i=1}^n\theta D_{d,i}}}}}$$

(21)

where $n$ is the number of discharges on day $d$, $D_{d,i}$ is the amount of discharges in the $i$ discharge stage on day $d$, and $D_{\mathrm{ss}}$ is the rated capacity of the individual energy storage.

Further, the operation and maintenance cost can be expressed as follows:

$$S_{\mathrm{ope}}=\left({\lambda }_{\mathrm{ope},\mathrm{p}}{P}_{\mathrm{r}}+2{\lambda }_{\mathrm{ope},\mathrm{e}}{C}_{\mathrm{n}}\right)\psi$$

(22)

$$\psi ={\displaystyle \frac{{\left(1+\mu \right)}^Y-1}{\mu {\left(1+\mu \right)}^Y}}$$

(23)

where ${\lambda }_{\mathrm{ope},\mathrm{p}}$ is the unit power; $P_{\mathrm{r}}$ is the rated power of the converter; ${\lambda }_{\mathrm{ope},\mathrm{e}}$ is the annual operation and maintenance cost per unit capacity; $\psi$ is the present value factor; and $\mu$ is the discount rate.

2.3.2. Cost of Operation Losses in Energy Storage

During the operation of energy storage devices, complex chemical reactions occur. Excessive charging and discharging depths can lead to irreversible damage. Therefore, the maximum throughput value over the device’s lifecycle is defined as the standard for charging and discharging limit depth $D_{\mathrm{ODb}}$, and the set value is 0.75.

The loss cost function is derived from the established standard charging and discharging depths. It quantifies the electricity lost under these conditions and represents the cost incurred based on real-time electricity sales tariffs, as shown in the equation below.

$$\left\{\begin{array}{l}{C}_{\mathrm{loss}}=E_{\mathrm{n}}-{\displaystyle \sum _{y=1}^Y{\displaystyle \sum _{d=1}^{365}{\displaystyle \sum _{i=1}^{\mathrm{n}}{D}_{\mathrm{OD},\mathrm{y},\mathrm{d},\mathrm{i}}{C}_{\mathrm{n}}}}}\\ S_{\mathrm{loss}}=c_{\mathrm{e}}{C}_{\mathrm{loss}}\end{array}\right.$$

(24)

where $C_{\mathrm{loss}}$ is the amount of electricity lost; $S_{\mathrm{loss}}$ is the corresponding electricity sales cost; $c_{\mathrm{e}}$ is the feed-in tariff; and $D_{\mathrm{OD},\mathrm{y},\mathrm{d},\mathrm{i}}$ is the magnitude of the discharge depth of the $i_{\mathrm{th}}$ discharge stage on $d$ day of $y$ year. Assuming that the rated capacity of a single energy storage is 1 (dimensionless), $E_{\mathrm{n}}=N{D}_{OD}{C}_{\mathrm{n}}$ denotes the total amount of discharges from an energy storage system with a rated capacity of 1 at different charging and discharging depths.

The loss cost in energy storage operation $S_{\mathrm{loss},\mathrm{abs}}$ is shown in Equation (25).

$$\left\{\begin{array}{l}{S}_{\mathrm{di}}=S\left(E_{\mathrm{n}2}-E_{\mathrm{n}1}\right)\\ S_{l\mathrm{oss},\mathrm{abs}}=S_{\mathrm{loss}}-S_{\mathrm{di}}\end{array}\right.$$

(25)

where $S_{\mathrm{di}}$ is the difference in operating costs for different operating conditions; $E_{\mathrm{n}2}/E_{\mathrm{n}1}$ is the total discharge $E_{\mathrm{n}}$ at the standard depth of charge and discharge versus the general case of $E_{\mathrm{n},1}=N{D}_{\mathrm{OD}}{C}_{\mathrm{n}}$ and $E_{\mathrm{n},2}=N{D}_{\mathrm{ODb}}{C}_{\mathrm{n}}$, respectively.

2.3.3. Initial Investment Cost of Energy Storage

The initial investment cost of energy storage is shown below.

$$S_{\mathrm{in}}={\lambda }_{\mathrm{p}}{P}_r+2{\lambda }_{\mathrm{e}}{C}_{\mathrm{n}}$$

(26)

where ${\lambda }_{\mathrm{p}}$ is the cost per unit power of the converter; ${\lambda }_{\mathrm{e}}$ is the cost per unit capacity of the energy storage device; and $P_{\mathrm{r}}$ is the rated power of the converter.

2.3.4. Wind Power Operating Costs

The operating costs of offshore wind are shown below:

$$S_{\mathrm{s}}=S_{\mathrm{q}}+S_{\mathrm{r}}+S_{\mathrm{t}}$$

(27)

where $S_{\mathrm{q}}$ is the offshore wind farm abandonment penalty cost; $S_{\mathrm{r}}$ is the load shedding standby cost; and $S_{\mathrm{t}}$ is the AC system support power cost.

$$\left\{\begin{array}{c}{S}_{\mathrm{w}}={\displaystyle {\displaystyle \sum }_t}{\displaystyle {\displaystyle \sum }_x}{c}_{\mathrm{w}}\left(P_{\mathrm{w},x,t}^f-P_{\mathrm{w},x,t}^{\max }\right)\\ S_{\mathrm{r}}={\displaystyle {\displaystyle \sum }_t}{\displaystyle {\displaystyle \sum }_i}{c}_{\mathrm{r}}{R}_{\mathrm{w},a,t}\\ S_{\mathrm{ac}}={\displaystyle {\displaystyle \sum }_t}{\displaystyle {\displaystyle \sum }_i}{c}_{\mathrm{ac}}{P}_{\mathrm{ac},t}\end{array}\right.$$

(28)

where $c_w$ is the penalty factor per unit of wind power, $c_{\mathrm{r}}$ is the cost per unit of standby, and $c_{\mathrm{ac}}$ is the cost per unit in coastal areas; $P_{w,x,t}^{\mathrm{f}}/P_{w,x,t}^{\max }$ are the $x$ predicted output/maximum available output of the wind farm at a moment $t$; and $P_{\mathrm{ac},t}$ is the frequency support provided by the AC system at a given moment.

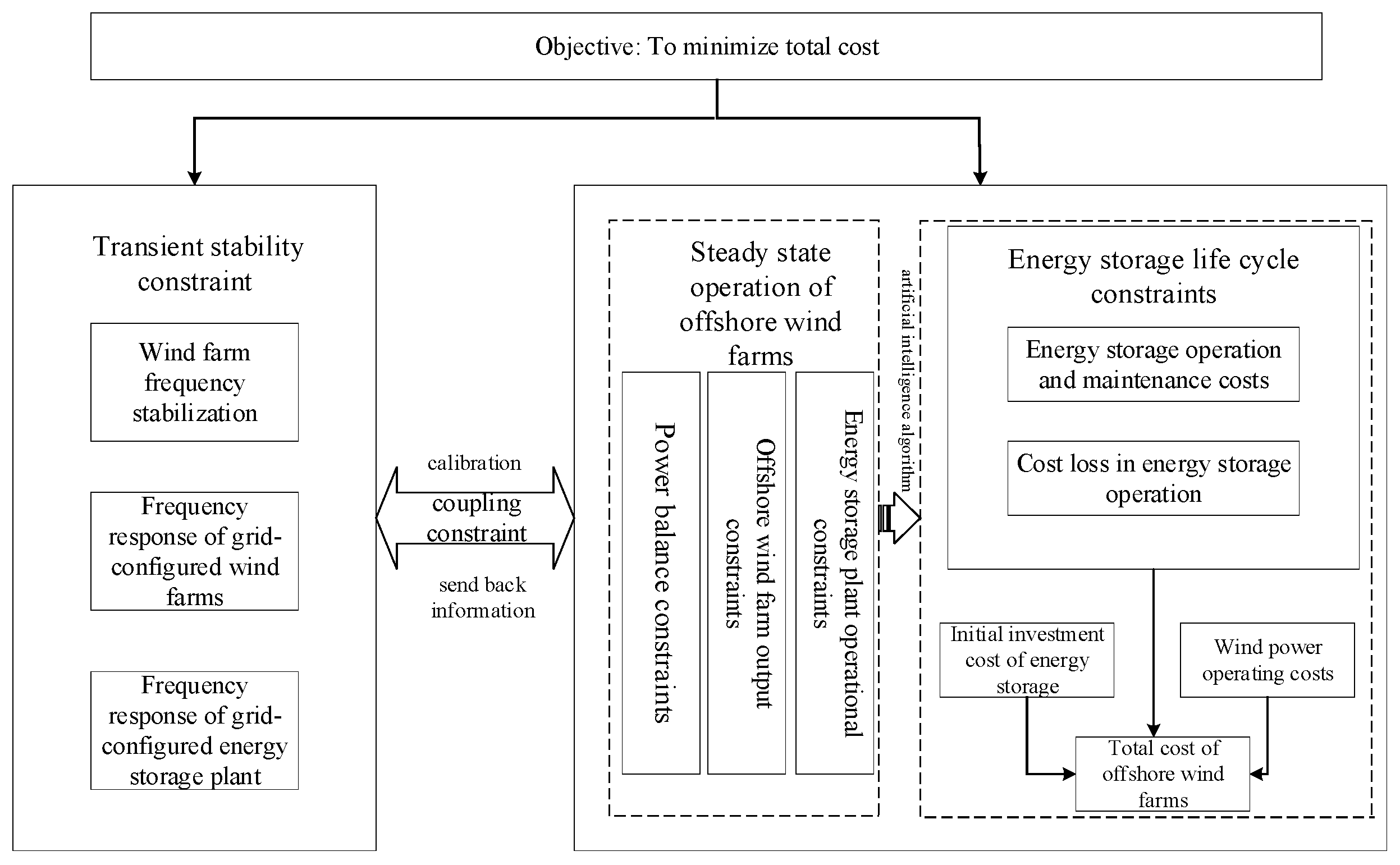
3. Solution Method

The flow chart for solving the optimal allocation of energy storage in an offshore wind power base is presented in Figure 1.

Step 1: Use AI algorithms to gather system control and economic parameters; then, preprocess the data.

Step 2: Analyze the steady-state operation of offshore wind farms to establish models for power balance, wind farm output constraints, and energy storage power plant operation constraints based on the findings.

Step 3: Analyze transient stability constraints to establish models for wind farm frequency stability, grid-connected wind farm frequency response, and energy storage plant response. Include operation–frequency stability coupling constraints for optimizing and verifying steady-state operation.

Step 4: Apply an AI algorithm to evaluate if the frequency meets the security stability index constraints (Equation (4)). If the evaluation results fit, use the energy storage planning results for cost calculation. If the results indicate overfitting or underfitting, proceed to Step 5.

Step 5: Analyze algorithm errors, adjust parameters, and gather additional data for training until the load constraint requirements are met.

Step 6: Establish operation and maintenance (O&M) costs using Equations (19)–(25), which factor in storage lifecycle and losses. Calculate the loss costs based on real-time tariffs.

Step 7: Establish the initial investment cost for energy storage and the operational cost of wind power based on (26)–(28).

Step 8: Based on Equation (18), develop a total cost model for offshore wind power. Determine the optimal energy storage allocation method to minimize overall costs.

Artificial Intelligence algorithm model training refers to the process of tuning and optimizing a selected machine learning or deep learning model using collected and prepared data. In this process, the model learns the features of the input data and its target outputs to improve its predictive and generalization abilities on unknown data.

Specifically, model training consists of the following major steps: data preparation, model selection, model initialization, model training, model evaluation and validation, model tuning and optimization, and model deployment and application. Model training is one of the key steps in machine learning and deep learning, and its goal is to learn from a large amount of data so that the model can discover patterns and regularities from the data and thus make accurate predictions or classifications of new input data.

This paper uses proven pairs of AI algorithms to demonstrate the feasibility of issuance. See the chart below for the specific methods.

4. Case Study

4.1. Energy Storage Planning

Allocating offshore wind energy storage can greatly improve energy efficiency, bolster grid stability, enhance economic efficiency, and foster sustainable development.

As illustrated in Figure 2, offshore wind power’s inertia demand varies over time. The system’s minimum inertia demand and the virtual inertia provided by offshore wind farms exhibit staggered peak characteristics.

4.2. Operating Scenario

To validate the proposed method, an arithmetic example is formulated following the planning guidelines of a general province (referred to as G province). The offshore wind power project aims to achieve 18 million kilowatts of cumulative installed capacity by 2025. This ambitious goal will significantly bolster G province’s energy infrastructure and contribute to the national energy landscape.

Based on wind energy resource distribution, construction conditions, industrial support, and project economics, G province plans 23 offshore wind power sites with a total installed capacity of 66.85 million kilowatts. This includes the following:

Fifteen shallow water sites (up to 35 m deep) with a total capacity of 9.85 million kilowatts, specifically, 4.15 million kilowatts in the YD sea area, 1.5 million kilowatts in the ZSJ sea area, and 4.2 million kilowatts in the YX sea area.

Eight deep water sites (35–50 m deep) planning for offshore wind farms with a total capacity of 57 million kilowatts, distributed across the YD and YX sea areas.

G province will prioritize the construction of offshore grids and high-voltage direct current (HVDC) transmission lines to ensure efficient power transmission from the 23 offshore wind projects, optimizing the connection solutions for deep-water sites

Table 1. G province offshore wind power planning site list.

Serial Number	Project Name	Planning Capacity (Kilowatt)	Total Investment (Billions)
	Total	6685	12,033
One	Shallow coastal area	985	1773
1	A	25	45
2	B	70	126
3	C	90	162
4	D	15	27
5	E	75	135
6	F	50	90
7	G	90	162
8	H	100	180
9	I	20	36
10	J	30	54
11	K	70	126
12	L	230	414
13	M	40	72
Serial Number	Project Name	Planning Capacity (Kilowatt)	Total Investment (Billions)
14	N	20	36
15	O	60	108
Two	Offshore deep water area	5700	10,260
1	P1	230	414
2	P2	1420	2556
3	P3	750	1350
4	P4	540	972
5	P5	660	1188
6	P6	1400	2520
7	Q1	500	900
8	Q2	200	360

.

G province will conduct comprehensive environmental impact assessments, focusing on the wind projects’ effects on marine ecosystems, and implement measures to minimize disruption to marine life during construction and operation.

4.3. Parameters of the Algorithmic System

This paper constructs a typical scenario based on new energy historical data in the southern region. The new energy output curve, wind power, energy storage control parameters, and economic parameters are obtained according to empirical values. In this paper, the large fluctuation of new energy output is taken as a perturbation, which is calculated by 10%; the base frequency is 50 Hz, the dead zone of FM is 0.033 Hz, the maximum allowable frequency change rate is 1 Hz/s, the maximum frequency deviation is 0.5 Hz, and the steady-state frequency deviation is 0.2 Hz. To validate the proposed method, a modeling example is implemented using the Yalmip toolkit on the MATLAB 2021b platform, with the Gurobi solver utilized to solve the problem.

(1)

Energy Storage Configuration and Rationalization Analysis

Whether to consider the operating costs of storage life loss was compared using the method proposed in this paper, offshore wind power base energy storage with a rated power = 18.6 MW and a planning capacity = 55.8 MWh, shown in

Table 2. Basic parameters of the energy storage system.

Typology	Rating/MW	Rated Capacity/MWh	Calendar Life/year	Maximum Charging Power/MW	Maximum Discharge Power/MW	Maximum Number of Charge/Discharge Transitions/Number	$\mathbf{Parameters} {\mathit{\phi }}_{\mathbf{max}}$	$\mathbf{Parameters} {\mathit{\phi }}_{\mathbf{min}}$
Parameter value	18.6	55.8	15	18.6	18.6	15	0.5	0.3
Typology	Percentage of a lower limit of capacity/%	Capacity cap ratio/%	Self-discharge rate/%	Charging efficiency/%	Discharge efficiency/%	Discounted kWh cost/CNY·(kW·h)−1	$\mathrm{Parameters} {\psi }_{\max }$	$\mathrm{Parameters} {\psi }_{\min }$
Parameter value	20	100	0.05	95	98	0.0526	0.9	0.5

.

Analyzing the charging and discharging dynamics of the energy storage system reveals that its rated power significantly exceeds the actual output. Under steady-state conditions, the maximum power balance output represents less than 50% of the rated power. Consequently, the rated power of the energy storage is determined by frequency constraints. Unlike traditional synchronous generators used in thermal and hydropower, large-scale integration of renewable energy, such as wind power, offers low inertia support. Integrating energy storage smooths fluctuations and ensures system stability, particularly during frequency variations. Energy storage primarily balances power on shorter time scales, with its rated capacity crucial for stable operation. Its prominent role involves mitigating short-term power fluctuations, with frequency having minimal impact on storage configuration.

(2)

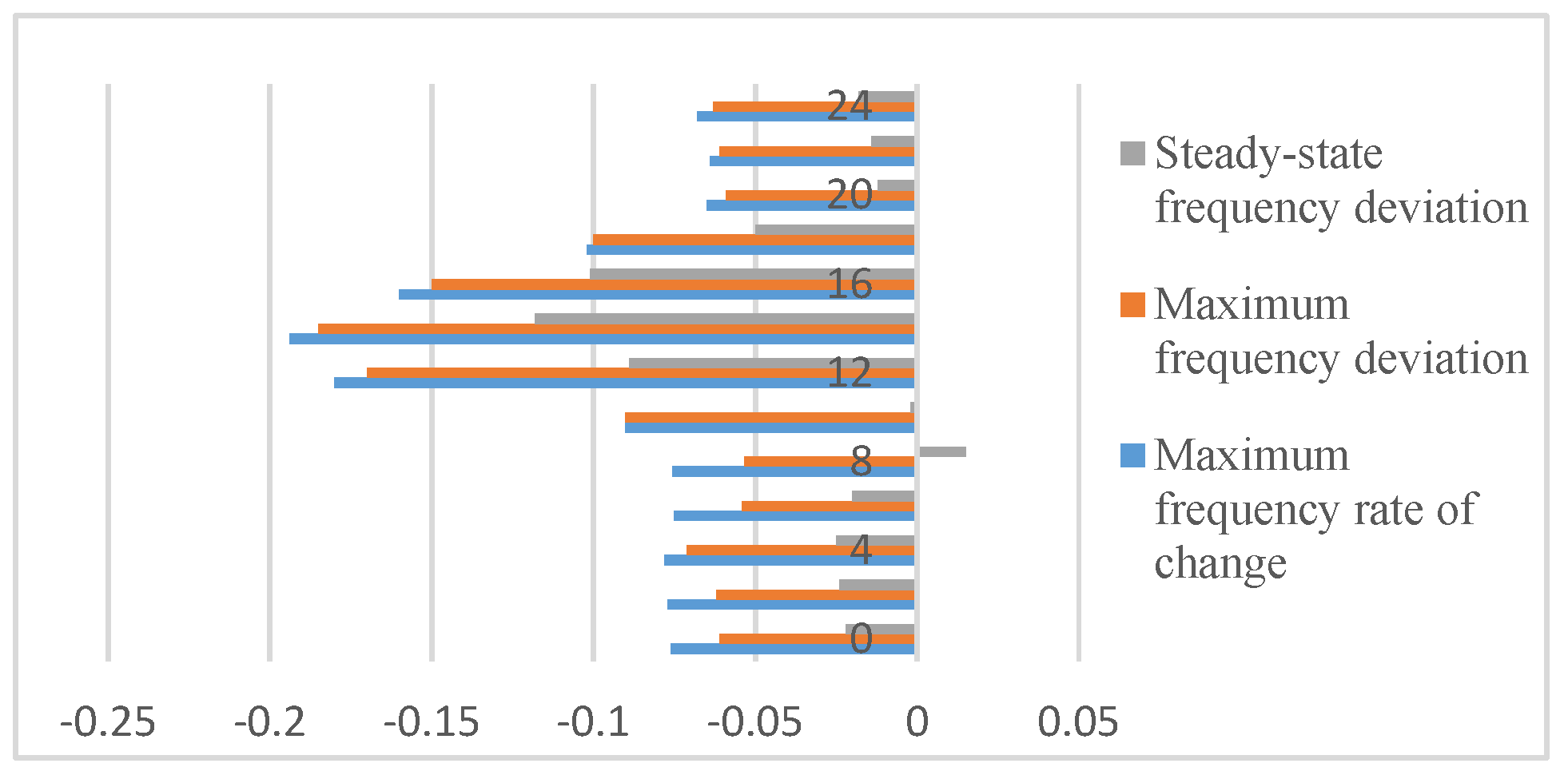
Validation of Energy Storage Allocation Methods

The maximum frequency variation change, the maximum system frequency deviation, and the quasi-steady-state frequency deviation, considering the frequency constraints, are considered for the whole operating cycle. The maximum frequency variation change is 0.9 Hz/s, the maximum system frequency deviation is 0.19 Hz, and the maximum quasi-steady-state deviation is 0.13 Hz, which meets the power system’s frequency requirements. The frequency index of the offshore wind power base is shown in Figure 3.

(3)

Impact of Frequency Metrics on Energy Storage Allocation

Currently, there is no clear limit to the maximum rate of frequency change, especially in regions like Southeast China, where offshore wind power is fairly prominent. Synchronous machines dominate power systems, providing primary frequency regulation with relatively slow response speeds. Initial frequency changes can, therefore, serve as a constraint indicator, as the initial and response curves gradually converge after disturbances.

After reducing the maximum rate of the frequency requirement, Table 1 shows a more pronounced decrease in rated power for energy storage. Specifically, compared to the baseline rate of frequency change, rated power decreased by 19.44%, 36.87%, and so on, for frequency change rates of 20%, 50%, and 100%, respectively. This reduction is primarily due to the absence of inertia support, where energy storage must compensate for short-term inertia during disturbances, significantly increasing the planned power capacity of energy storage.

Lowering the requirement alleviates the need for high-rated power configurations in energy storage. However, the rated capacity remains relatively unchanged because the energy storage response time is much shorter than its operational time. Therefore, reducing rated capacity is not a significant factor. Further relaxation of restrictions leads to negligible changes in rated capacity. When restrictions are sufficiently relaxed, the rated capacity stabilizes and reaches an optimal level where the maximum frequency variation rate no longer strongly dictates energy storage connection.

4.4. Sensitivity Analysis

To evaluate the robustness of the proposed energy storage optimization method under varying operating conditions, a sensitivity analysis was conducted on key parameters, including energy storage charge/discharge efficiency, the maximum rate of change of frequency (RoCoF) limit, and energy storage rated capacity. By adjusting these parameters individually, their impact on the energy storage configuration results (rated power and rated capacity) and the total system cost was observed.

(1)

Impact of Variation in Energy Storage Efficiency

Assuming that the charge/discharge efficiency of the energy storage system varies within a range of 90% to 98%, while keeping other parameters constant, the following results were obtained:

Charge/Discharge Efficiency	Rated Power (MW)	Rated Capacity (MWh)	Total Annual Cost (10 k CNY)
90%	19.2	57.6	715.8
92%	18.9	56.7	708.3
95%	18.6	55.8	702.5
98%	18.3	54.9	696.1

As the energy storage efficiency increases, the required storage power and capacity slightly decrease, and the total system cost is also reduced. This indicates that high-efficiency storage devices offer significant economic benefits over long-term operation.

(2)

Impact of Variation in the Maximum RoCoF Limit

The RoCoF limit was further relaxed to observe its impact on the energy storage configuration:

RoCoF Limit (Hz/s)	Rated Power (MW)	Rated Capacity (MWh)
1.0	18.6	55.8
1.2	14.98	55.79
1.5	11.74	55.78
2.0	11.74	55.78

Relaxing the RoCoF limit significantly reduces the rated power requirement of the energy storage system but has a minor impact on the rated capacity. This suggests that, within the permissible frequency safety margin, appropriately relaxing the RoCoF requirement can substantially reduce the cost associated with power rating configuration.

(3)

Impact of Variation in Energy Storage Capacity Configuration

With the energy storage power fixed at 18.6 MW, its rated capacity was adjusted to observe the impact on system operating costs:

Storage Capacity (MWh)	Total Annual Cost (10 k CNY)	Frequency Limit Violations
50	710.2	3
55.8	702.5	0
60	698.9	0

Appropriately increasing the energy storage capacity can effectively reduce the risk of frequency limit violations and lower the total cost to some extent. However, the cost reduction becomes less pronounced when the capacity is excessively large, indicating the existence of an economic optimum range.

Energy storage efficiency and the RoCoF limit have a significant impact on the power configuration of energy storage. The energy storage capacity primarily affects system frequency stability and operating costs, with an economically optimal value. The proposed optimization method maintains good robustness under variations in different parameters, making it suitable for various practical operating scenarios. It is recommended that, in practical engineering applications, key parameters in the optimization model should be flexibly adjusted based on specific frequency security standards, energy storage device performance, and electricity price policies to achieve a balance between economy and security.

5. Conclusions

This paper proposes a method to enhance the frequency modulation capability of offshore wind farms based on energy storage devices and derives an optimized energy storage allocation scheme for offshore wind power systems lacking conventional inertial support from power sources. The method establishes a comprehensive optimization model that simultaneously considers system frequency stability, the full lifecycle degradation of energy storage devices, and operational costs, aiming to achieve the dual objectives of frequency safety/stability and minimized lifecycle costs.

Comparative analysis with conventional methods highlights the superior performance of our approach in the following key areas:

More Accurate Frequency Response Modeling: Conventional allocation methods often rely on simplified linear or low-order frequency response models, neglecting the differences between grid-forming and grid-following controls during frequency response. By establishing a more precise system frequency response model, our method fully accounts for the impact of different control strategies on storage allocation, making the simulated frequency response process more realistic. The case study results indicate that our method reduces the simulation error for key frequency indicators (like maximum RoCoF and frequency nadir) to within 5%, compared to approximately 15%–20% for traditional methods, providing a more reliable foundation for accurate energy storage power sizing.

Refined Modeling of Storage Lifecycle and Degradation: Existing studies often simplify storage lifespan as a fixed cycle count or ignore operational degradation. In contrast, our method introduces a conversion factor for depth of discharge (DOD) and a loss cost function linked to real-time electricity prices, more accurately reflecting the aging process and economic impact of storage during actual operation. Simulation results show that under identical operating conditions, storage devices using a conventional fixed-life model see their capacity fade to below 70% of its initial value within 10 years, whereas our method, through optimized charging/discharging strategies, maintains capacity retention above 80%, significantly extending the service life.

Integrated Multi-Objective Co-Optimization: Traditional planning often optimizes frequency stability and economic objectives separately. Our method integrates technical performance and economic costs within a unified framework. As shown in

Table 3. Impact of energy storage life loss on power grid operation cost.

Running Cost	Paradigm
	Counting and Damage to Energy Storage Life	Not Taking into Account Damage to Energy Storage Life
Interaction costs with the grid/CNY	38.49	34.91
Lifetime loss costs of energy Storage/CNY	84.88	0
Load shedding costs/CNY	540.58	539.88
Wind abandonment costs/CNY	7.61	7.45
Cost of carbon emissions/CNY	30.97	35.08
Total running costs/CNY	702.53	617.32

, although considering storage lifecycle degradation increases the total annual operational cost from CNY 6.1732 million to CNY 7.0253 million (an increase of about 13.8%), this cost accurately reflects the long-term operational expense, avoiding the risk of premature device replacement due to underestimated degradation. From a full lifecycle perspective, our method trades a minor short-term economic penalty for a higher long-term return on investment and operational reliability.

Furthermore, this paper provides a quantitative analysis of the impact of the rate of change of frequency (RoCoF) limit on storage allocation. As presented in

Table 4. Change in energy storage rating.

Prerequisite	Energy Storage Allocation
	Rating/MW	Rated Capacity/MWh
1 Hz/s	18.6	55.8
1.2 Hz/s	14.98	55.79
1.5 Hz/s	11.74	55.78
2 Hz/s	11.74	55.78

, when the RoCoF limit is relaxed from a strict 1 Hz/s to 1.5 Hz/s, the required rated power of the energy storage system decreases significantly from 18.6 MW to 11.74 MW, a reduction of 36.87%. This clear quantitative relationship provides direct guidance for grid code development and investor decision-making: appropriately relaxing the RoCoF requirement while ensuring system security can substantially reduce the power rating requirement for energy storage, leading to significant capital cost savings.

In summary, the proposed method not only ensures system frequency stability through more accurate modeling but also, via full lifecycle cost optimization, provides a forward-looking and practical solution for the scientific planning and efficient operation of energy storage systems integrated with offshore wind farms.