A Cluster-Based Filtering Approach to SCADA Data Preprocessing for Wind Turbine Condition Monitoring and Fault Detection
Abstract
1. Introduction
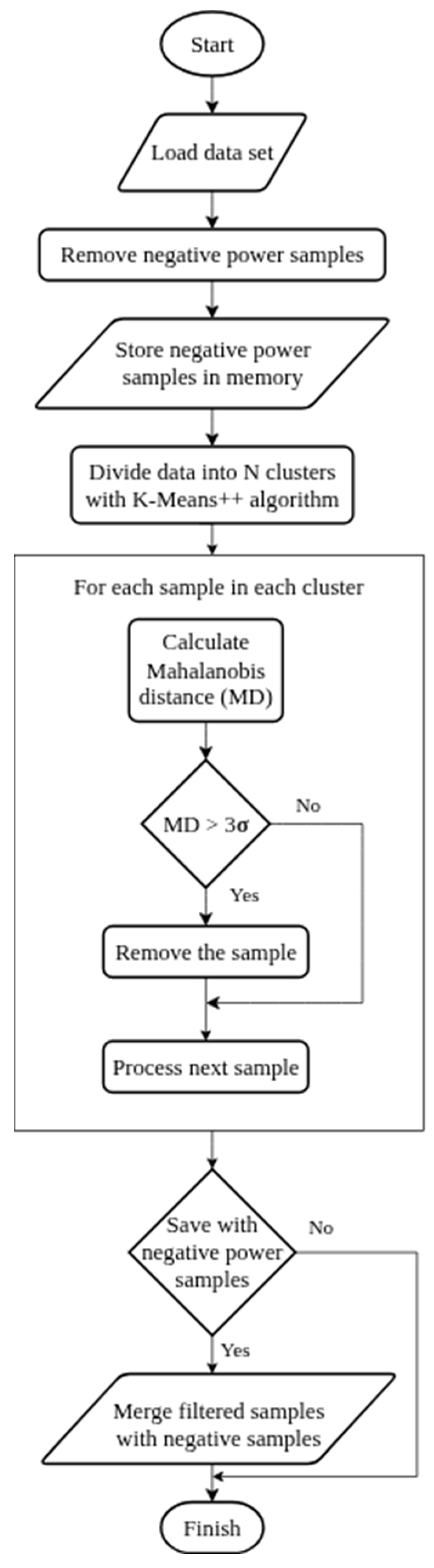
2. A Cluster-Based Filtering Approach to SCADA Data Preprocessing
- The workflow starts by identifying negative power samples in the generated power parameter of the dataset. These identified rows are stored separately for later use and removed from the main table to allow focused processing of variables relevant to outlier detection. The preserved negative samples retain their original indices, ensuring they can be seamlessly reintegrated with the processed dataset later without requiring reindexing.
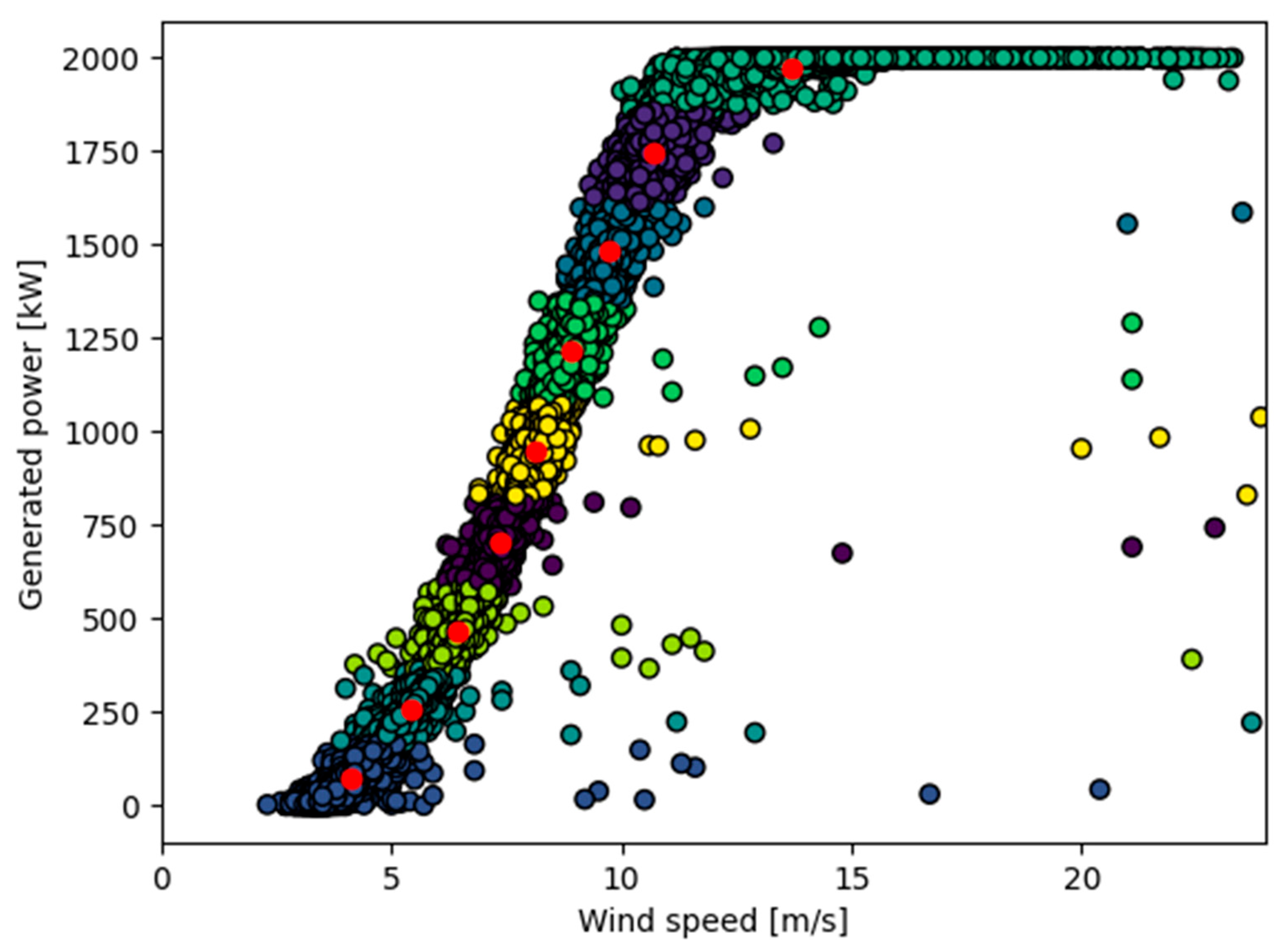
- The data containing only nonnegative generated power samples is then grouped into clusters using the K-Means++ algorithm. The optimal number of clusters is determined using the “Elbow method,” where the within-cluster sum of squares is plotted against the number of clusters. This plot enables a heuristic decision, balancing cluster compactness with computational efficiency. The cutoff point at which the metric is achieving steady state is typically selected as the desired number of clusters. Each cluster is represented by its centroid, which corresponds to the mean value of all data points within that cluster.
- To detect outliers, a criterion is established to determine whether a data sample deviates abnormally from others in the same cluster. The measure used is the distance between the cluster’s centroid and the sample under examination. In this approach, the Mahalanobis distance is employed, as it accounts for potential skewness in the data distribution. A sample is classified as an outlier if its distance exceeds a predefined threshold.
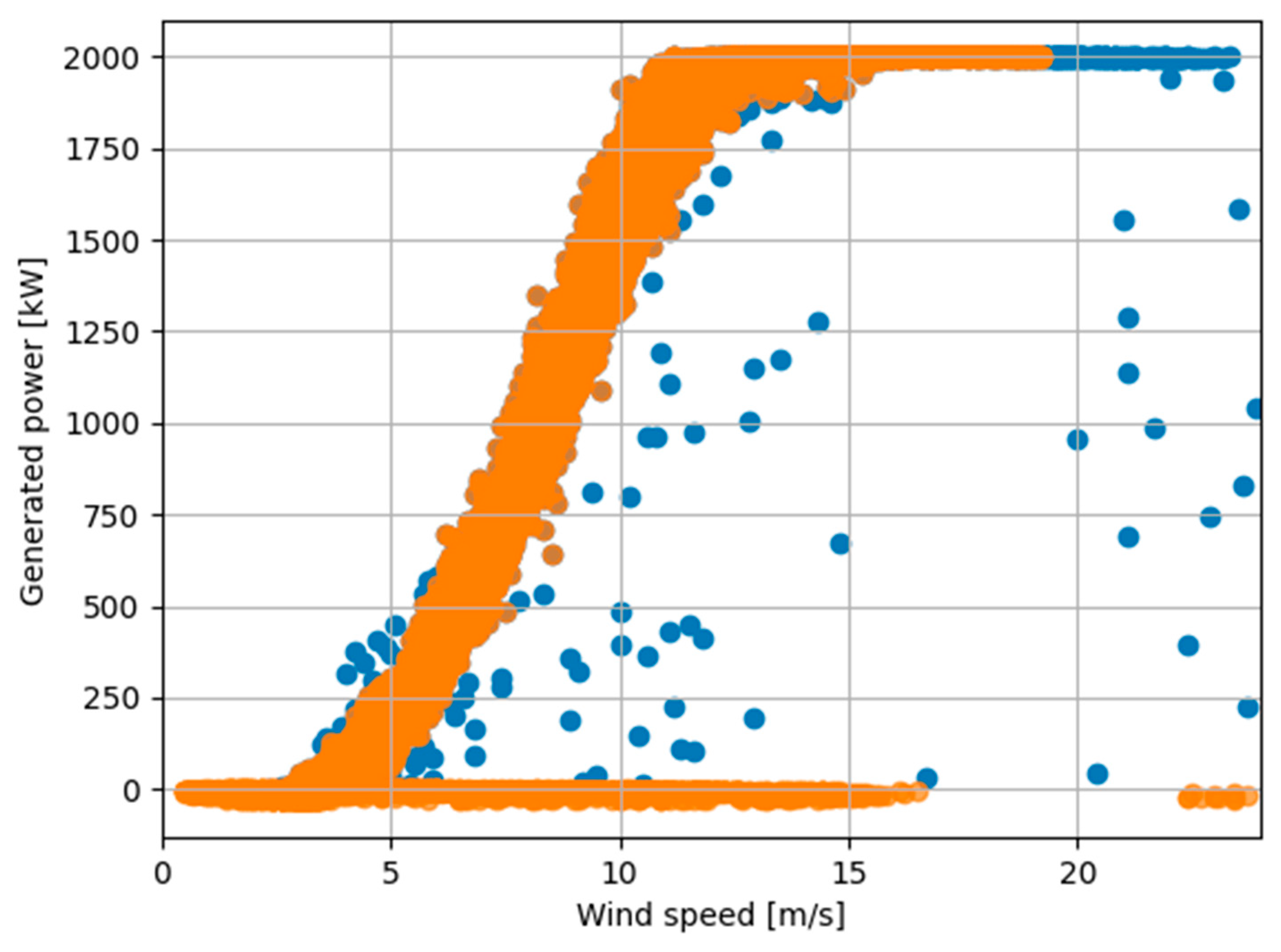
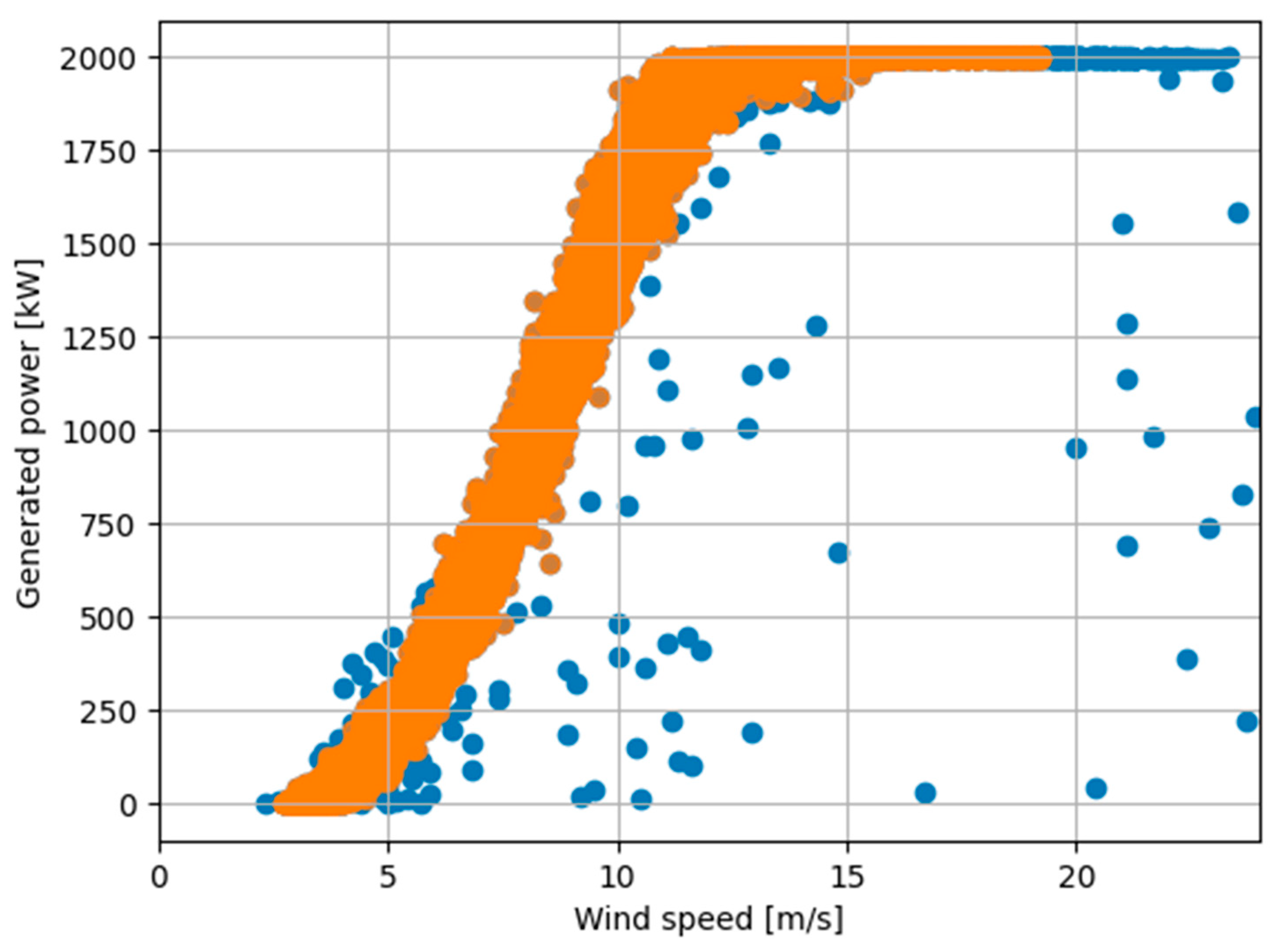
- In this study, the outlier detection threshold is set to three standard deviations (three sigma). Any sample with a distance exceeding this threshold is classified as an outlier and subsequently removed from the dataset. To evaluate the impact of outliers on the fault detection process, this study applies two threshold settings: a 95% confidence interval, which excludes 5% of samples per cluster, and a 99% confidence interval, which excludes 1% of samples per cluster.
- Finally, for this study, the negative power samples are either merged back into the filtered dataset or excluded entirely. This process produces two distinct cleaned datasets—one including negative power values and one without—both free from outliers.
3. Case Study: Energias de Portugal Wind Farm
3.1. A Short Description of the Wind Farm
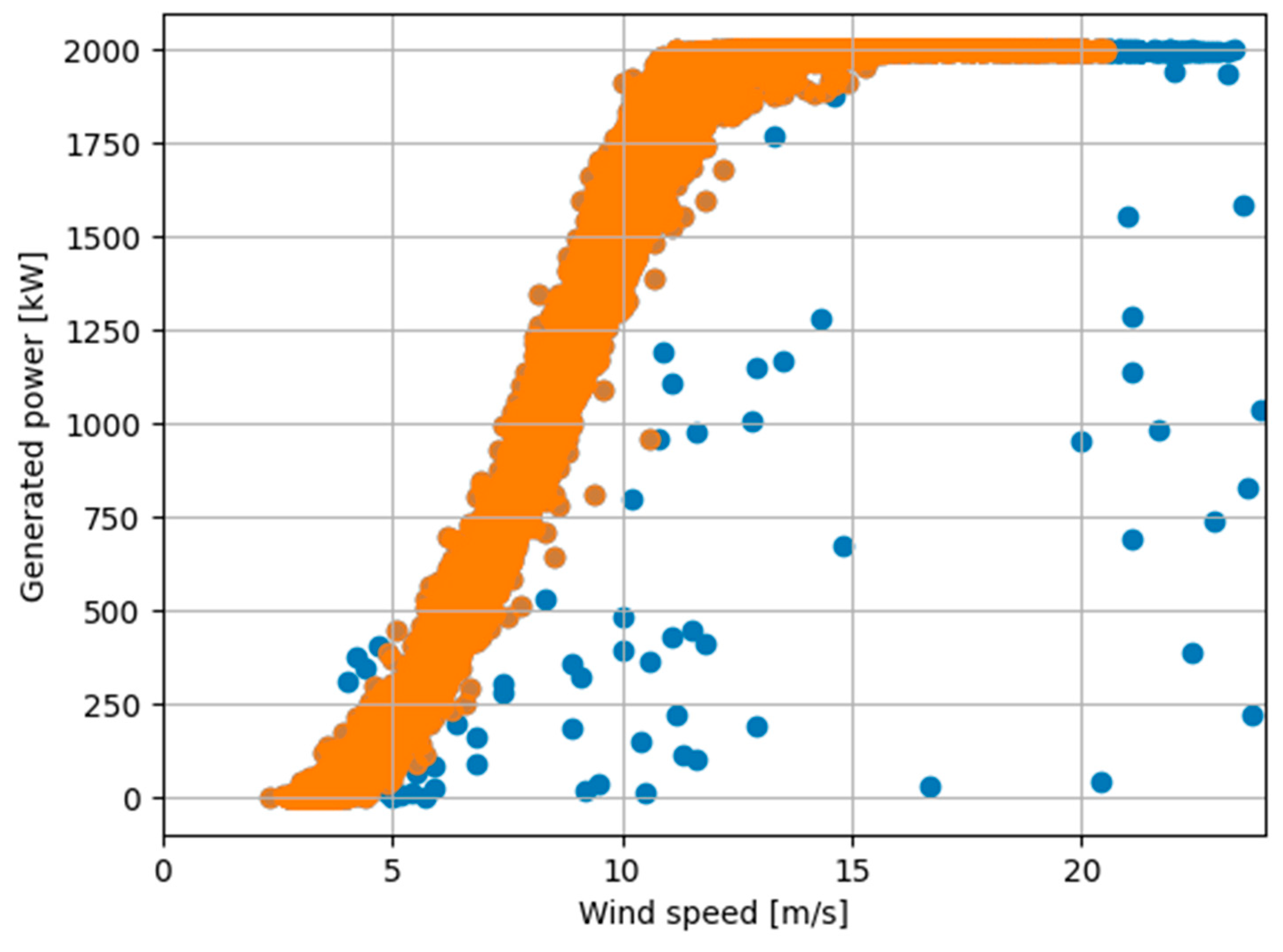
3.2. Data Preprocessing Results for Wind Turbines
4. Validation Using a Real Generator Fault
4.1. Description of a Real Generator Fault in Wind Turbine T07
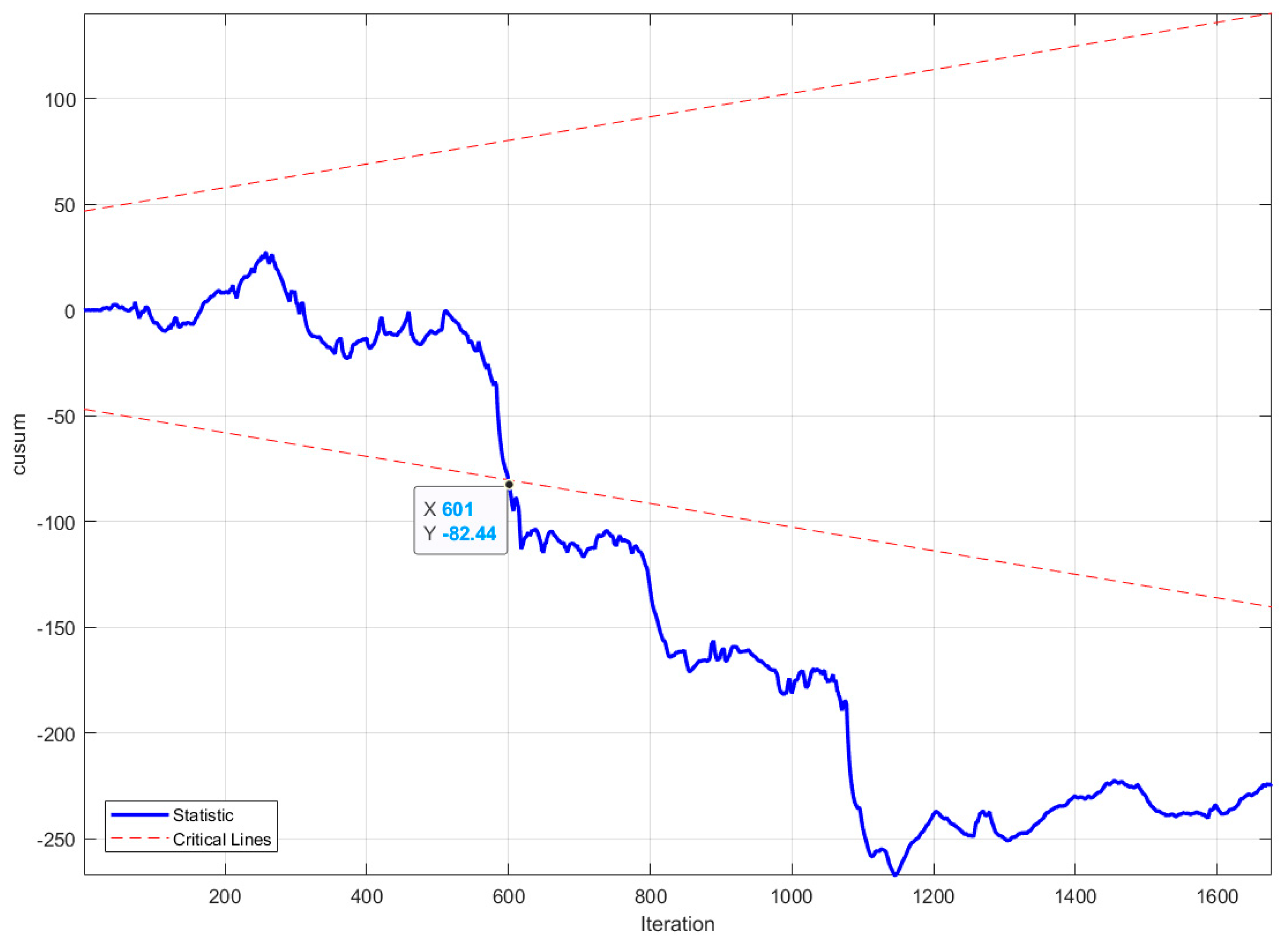
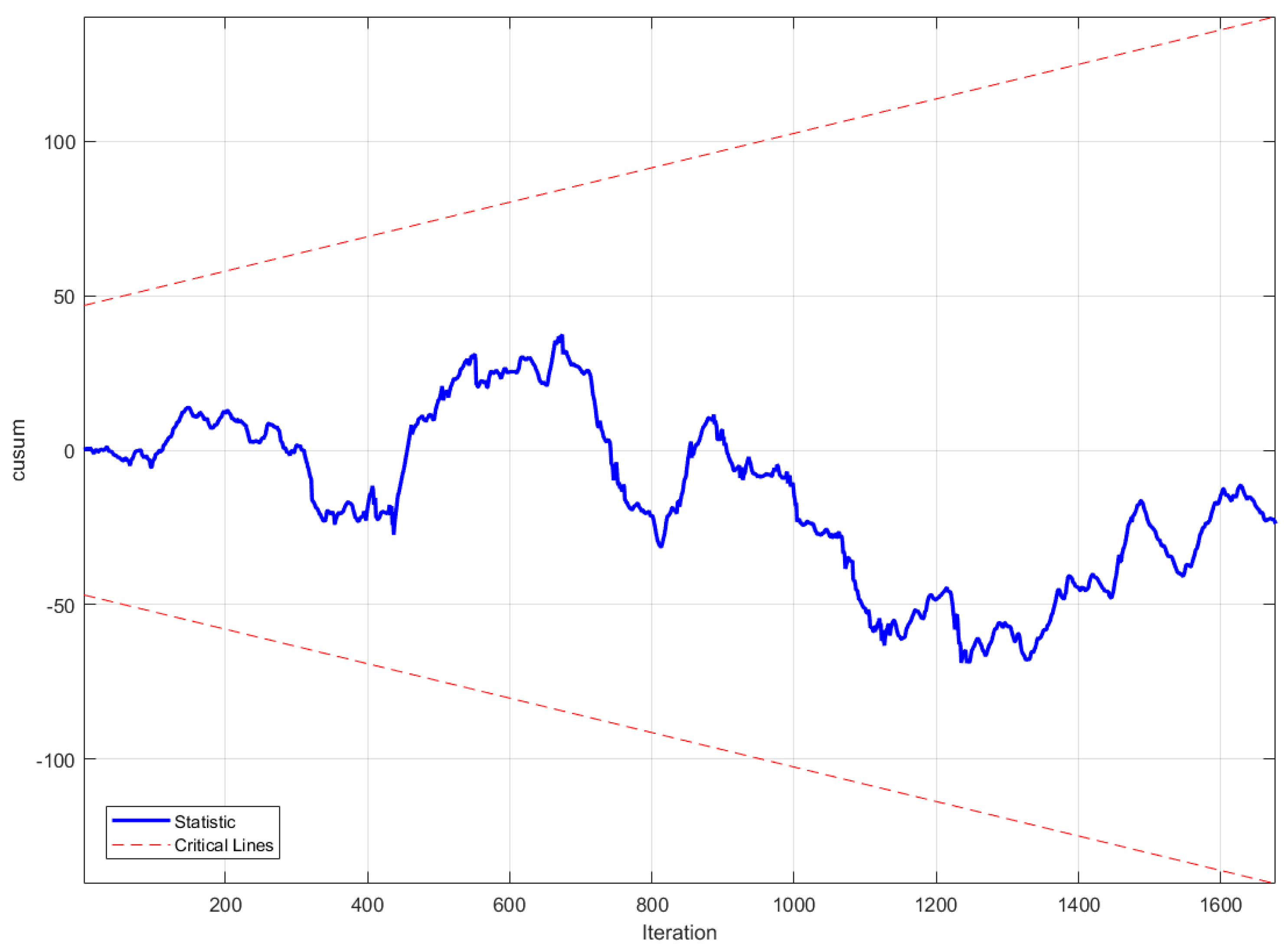
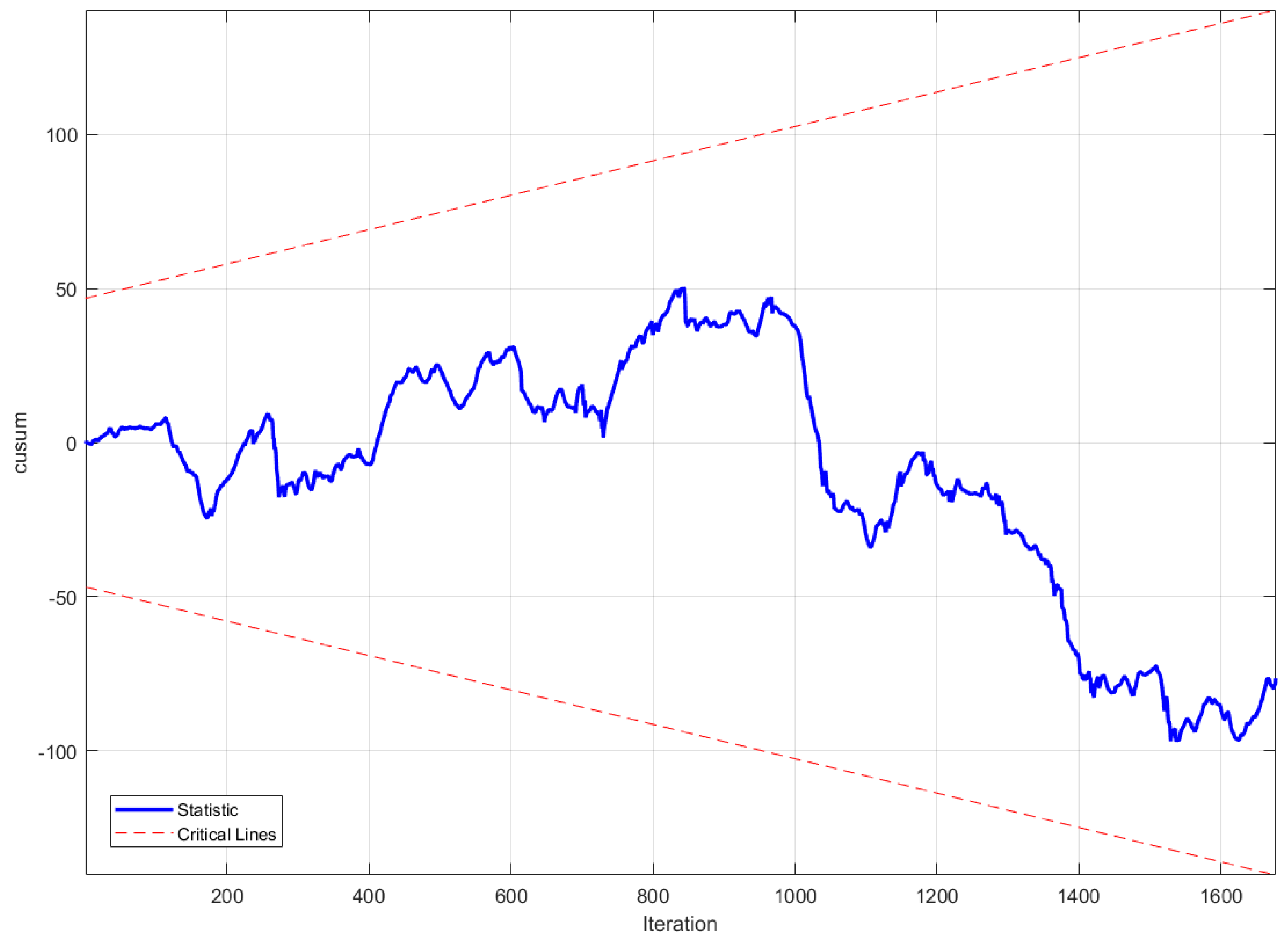
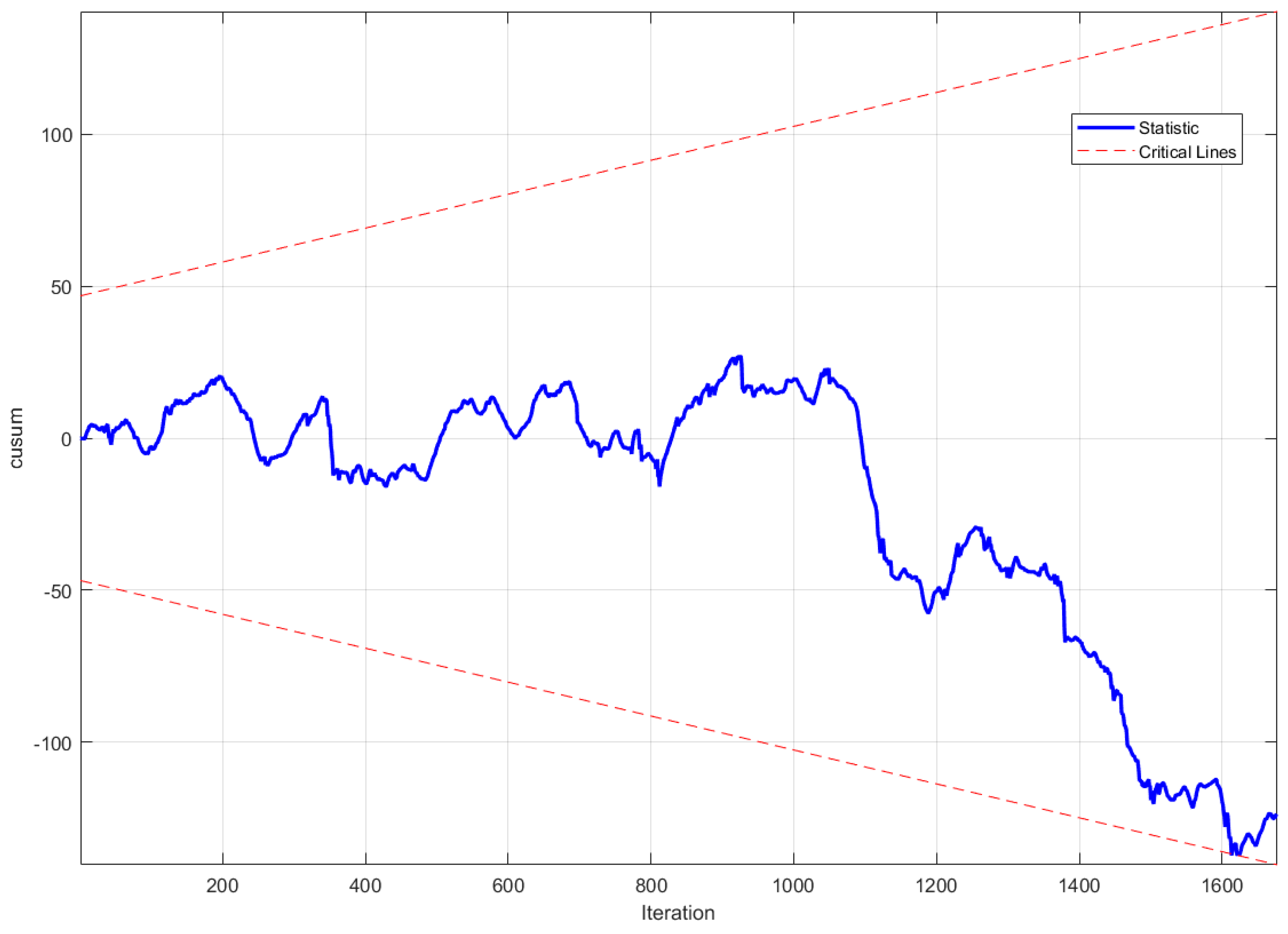
4.2. CUSUM Test-Based Method for Detecting Structural Changes in SCADA Data
- Null hypothesis (): The regression coefficients remain constant throughout the sample.
- Alternative hypothesis (): The coefficients vary over time, implying structural instability.
- If the CUSUM statistic crosses the critical boundaries, reject (indicating instability of regression coefficients).
- Otherwise, do not reject (i.e., regression coefficients are stable).
4.3. Fault Detection Results
4.4. Comparison and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SCADA | Supervisory Control and Data Acquisition |
| CUSUM | Cumulative Sum |
| ADF | Augmented Dickey-Fuller |
| LSTM | Long-Short Term Memory |
| XGBoost | Extreme Gradient Boosting |
| IQR | Interquartile Range |
| MLR | Multiple Linear Regression |
| OLS | Ordinary Least Squares |
References
- Global Wind Report 2025; Global Wind Energy Council: Brussels, Belgium, 2025; published on 23 April 2025; Available online: https://www.gwec.net/reports/globalwindreport (accessed on 15 August 2025).
- WWEA Annual Report 2024: A Challenging Year for Windpower; World Wind Energy Association: Bonn, Germany, 2025; Available online: https://wwindea.org/AnnualReport2024 (accessed on 15 August 2025).
- Chatterjee, J.; Dethlefs, N. Scientometric Review of Artificial Intelligence for Operations & Maintenance of Wind Turbines: The Past, Present and Future. Renew. Sustain. Energy Rev. 2021, 144, 111051. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Hu, W.; Yan, X. Anomaly Detection and Fault Analysis of Wind Turbine Components Based on Deep Learning Network. Renew. Energy 2018, 127, 825–834. [Google Scholar] [CrossRef]
- Meyer, A. Multi-Target Normal Behaviour Models for Wind Farm Condition Monitoring. Appl. Energy 2021, 300, 117342. [Google Scholar] [CrossRef]
- Castellani, F.; Natili, F.; Astolfi, D.; Vidal, Y. Wind Turbine Gearbox Condition Monitoring through the Sequential Analysis of Industrial SCADA and Vibration Data. Energy Rep. 2024, 12, 750–761. [Google Scholar] [CrossRef]
- Olabi, A.G.; Wilberforce, T.; Elsaid, K.; Sayed, E.T.; Salameh, T.; Abdelkareem, M.A.; Baroutaji, A. A Review on Failure Modes of Wind Turbine Components. Energies 2021, 14, 5241. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox Condition Monitoring in Wind Turbines: A Review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, Y.; Wang, Q. Fault Detection in Wind Turbine Generators Using a Meta-Learning-Based Convolutional Neural Network. Mech. Syst. Signal Process. 2023, 200, 110528. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.-C. A Review of Machine Learning Techniques for Wind Turbine’s Fault Detection, Diagnosis, and Prognosis. Int. J. Green Energy 2024, 21, 771–786. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, J.; Zhang, Q.; Xu, R. Advances and Trends in Intelligent Maintenance for Wind Turbine Systems. Sustain. Energy Technol. Assess. 2025, 80, 104398. [Google Scholar] [CrossRef]
- Yan, M.; Hui, S.C.; Jiang, N.; Li, N. A Review on Data-Driven Prognostics and Health Management for Wind Turbine Systems. Eng. Appl. Artif. Intell. 2025, 159, 111484. [Google Scholar] [CrossRef]
- Hussain, M.; Hussain Mirjat, N.; Shaikh, F.; Luxmi Dhirani, L.; Kumar, L.; Sleiti, A.K. Condition Monitoring and Fault Diagnosis of Wind Turbine: A Systematic Literature Review. IEEE Access 2024, 12, 190220–190239. [Google Scholar] [CrossRef]
- Murgia, A.; Verbeke, R.; Tsiporkova, E.; Terzi, L.; Astolfi, D. Discussion on the Suitability of SCADA-Based Condition Monitoring for Wind Turbine Fault Diagnosis through Temperature Data Analysis. Energies 2023, 16, 620. [Google Scholar] [CrossRef]
- Cambron, P.; Masson, C.; Tahan, A.; Pelletier, F. Control Chart Monitoring of Wind Turbine Generators Using the Statistical Inertia of a Wind Farm Average. Renew. Energy 2018, 116, 88–98. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, S.; Zhang, H.; Yang, G. Wind Power Prediction Based on Multi-Class Autoregressive Moving Average Model with Logistic Function. J. Mod. Power Syst. Clean Energy 2022, 10, 1184–1193. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Zhang, G. Probabilistic Power Curve Estimation Based on Meteorological Factors and Density LSTM. Energy 2023, 269, 126768. [Google Scholar] [CrossRef]
- Pozo, F.; Vidal, Y.; Salgado, Ó. Wind Turbine Condition Monitoring Strategy through Multiway PCA and Multivariate Inference. Energies 2018, 11, 749. [Google Scholar] [CrossRef]
- Letzgus, S. Change-Point Detection in Wind Turbine SCADA Data for Robust Condition Monitoring with Normal Behaviour Models. Wind Energy Sci. 2020, 5, 1375–1397. [Google Scholar] [CrossRef]
- Dao, P.B. Condition Monitoring and Fault Diagnosis of Wind Turbines Based on Structural Break Detection in SCADA Data. Renew. Energy 2022, 185, 641–654. [Google Scholar] [CrossRef]
- Bilendo, F.; Lu, N.; Badihi, H.; Meyer, A.; Cali, Ü.; Cambron, P. Multitarget Normal Behavior Model Based on Heterogeneous Stacked Regressions and Change-Point Detection for Wind Turbine Condition Monitoring. IEEE Trans. Ind. Inform. 2024, 20, 5171–5181. [Google Scholar] [CrossRef]
- Dao, P.B. A CUSUM-Based Approach for Condition Monitoring and Fault Diagnosis of Wind Turbines. Energies 2021, 14, 3236. [Google Scholar] [CrossRef]
- Latiffianti, E.; Sheng, S.; Ding, Y. Wind Turbine Gearbox Failure Detection Through Cumulative Sum of Multivariate Time Series Data. Front. Energy Res. 2022, 10, 904622. [Google Scholar] [CrossRef]
- Dao, P.B. On Wilcoxon Rank Sum Test for Condition Monitoring and Fault Detection of Wind Turbines. Appl. Energy 2022, 318, 119209. [Google Scholar] [CrossRef]
- Dao, P. Condition Monitoring of Wind Turbines Based on Cointegration Analysis of Gearbox and Generator Temperature Data. Diagnostyka 2018, 19, 63–71. [Google Scholar] [CrossRef]
- Sun, X.; Xue, D.; Li, R.; Li, X.; Cui, L.; Zhang, X.; Wu, W. Research on Condition Monitoring of Key Components in Wind Turbine Based on Cointegration Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2019, 575, 012015. [Google Scholar] [CrossRef]
- Qadri, B.A.; Ulriksen, M.D.; Damkilde, L.; Tcherniak, D. Cointegration for Detecting Structural Blade Damage in an Operating Wind Turbine: An Experimental Study. In Dynamics of Civil Structures, Volume 2; Pakzad, S., Ed.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer International Publishing: Cham, Switzerland, 2020; pp. 173–180. ISBN 978-3-030-12114-3. [Google Scholar]
- Xu, M.; Li, J.; Wang, S.; Yang, N.; Hao, H. Damage Detection of Wind Turbine Blades by Bayesian Multivariate Cointegration. Ocean Eng. 2022, 258, 111603. [Google Scholar] [CrossRef]
- Dao, P.B. On Cointegration Analysis for Condition Monitoring and Fault Detection of Wind Turbines Using SCADA Data. Energies 2023, 16, 2352. [Google Scholar] [CrossRef]
- Dao, P.B.; Barszcz, T.; Staszewski, W.J. Anomaly Detection of Wind Turbines Based on Stationarity Analysis of SCADA Data. Renew. Energy 2024, 232, 121076. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-Term Offshore Wind Power Forecasting—A Hybrid Model Based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and Deep-Learning-Based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Hsu, J.-Y.; Wang, Y.-F.; Lin, K.-C.; Chen, M.-Y.; Hsu, J.H.-Y. Wind Turbine Fault Diagnosis and Predictive Maintenance Through Statistical Process Control and Machine Learning. IEEE Access 2020, 8, 23427–23439. [Google Scholar] [CrossRef]
- Udo, W.; Muhammad, Y. Data-Driven Predictive Maintenance of Wind Turbine Based on SCADA Data. IEEE Access 2021, 9, 162370–162388. [Google Scholar] [CrossRef]
- Knes, P.; Dao, P.B. Machine Learning and Cointegration for Wind Turbine Monitoring and Fault Detection: From a Comparative Study to a Combined Approach. Energies 2024, 17, 5055. [Google Scholar] [CrossRef]
- Kiczek, B.; Batsch, M. Exploration of Unsupervised Deep Learning-Based Gear Fault Detection for Wind Turbine Gearboxes. Energies 2025, 18, 3630. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Li, L.-W.; Wei, H.-L.; Li, M.; Lv, M.-Y.; Zhang, Y. Periodic-Enhanced Informer Model for Short-Term Wind Power Forecasting Using SCADA Data. IEEE Trans. Sustain. Energy 2025, 16, 2573–2585. [Google Scholar] [CrossRef]
- Ansari, S.; Nassif, A.B.; Mahmoud, S.; Majzoub, S.; Almajali, E.; Jarndal, A.; Bonny, T.; Alnajjar, K.A.; Hussain, A. Impact of Outliers on Regression and Classification Models: An Empirical Analysis. In Proceedings of the 2024 17th International Conference on Development in eSystem Engineering (DeSE), Khorfakkan, United Arab Emirates, 6 November 2024; IEEE: New York, NY, USA, 2024; pp. 211–218. [Google Scholar]
- Vamsikrishna, B.; Manikanta, K.R.N.; Sai Kiran, D.V.N.K.; Reddy Pothireddy, K.M.; Vuddanti, S. Outliers Detection and Imputation in Wind Speed Data and Forecasting Using LSTM. In Proceedings of the 2024 IEEE 4th International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 31 July 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Khan, Z.; Naeem, M.; Khalil, U.; Khan, D.M.; Aldahmani, S.; Hamraz, M. Feature Selection for Binary Classification Within Functional Genomics Experiments via Interquartile Range and Clustering. IEEE Access 2019, 7, 78159–78169. [Google Scholar] [CrossRef]
- Komadina, A.; Martinić, M.; Groš, S.; Mihajlović, Ž. Comparing Threshold Selection Methods for Network Anomaly Detection. IEEE Access 2024, 12, 124943–124973. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Zhang, Y.; Deng, C. Analysis of SCADA Data Preprocessing Methods for Wind Power Farms. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15 December 2023; IEEE: New York, NY, USA, 2023; pp. 3578–3583. [Google Scholar]
- Long, H.; Sang, L.; Wu, Z.; Gu, W. Image-Based Abnormal Data Detection and Cleaning Algorithm via Wind Power Curve. IEEE Trans. Sustain. Energy 2020, 11, 938–946. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Huang, C. A Fast Abnormal Data Cleaning Algorithm for Performance Evaluation of Wind Turbine. IEEE Trans. Instrum. Meas. 2020, 70, 1–12. [Google Scholar] [CrossRef]
- Su, Y.; Chen, F.; Liang, G.; Wu, X.; Gan, Y. Wind Power Curve Data Cleaning Algorithm via Image Thresholding. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; IEEE: New York, NY, USA, 2019; pp. 1198–1203. [Google Scholar]
- Zheng, L.; Zhu, L.; Wen, W.; Li, J.; Zhang, C. Three-Stage Composite Outlier Identification of Wind Power Data: Integrating Physical Rules with Regression Learning and Mathematical Morphology. IEEE Trans. Instrum. Meas. 2025, 74, 1–13. [Google Scholar] [CrossRef]
- Thorndike, R.L. Who Belongs in the Family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Ketchen, D.J., Jr.; Shook, C.L. The Application of Cluster Analysis in Strategic Management Research: An Analysis and Critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Energias De Portugal (EDP) Wind Farm SCADA Datasets. Available online: https://www.edp.com/en/innovation/open-data/data (accessed on 17 July 2025).
- Turner, P. Power Properties of the CUSUM and CUSUMSQ Tests for Parameter Instability. Appl. Econ. Lett. 2010, 17, 1049–1053. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for Testing the Constancy of Regression Relationships Over Time. J. R. Stat. Soc. Ser. B 1975, 37, 149–192. [Google Scholar] [CrossRef]
- Chow, G.C. Tests of Equality between Sets of Coefficients in Two Linear Regressions. Econometrica 1960, 28, 591–605. [Google Scholar] [CrossRef]
- Al Hassan, A.; Dao, P.B. Bridging Data and Diagnostics: A Systematic Review and Case Study on Integrating Trend Monitoring and Change Point Detection for Wind Turbines. Energies 2025, 18, 5166. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; Simoudis, E., Han, J., Fayyad, U.M., Eds.; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN Revisited, Revisited: Why and How You Should (Still) Use DBSCAN. ACM Trans. Database Syst. 2017, 42, 19. [Google Scholar] [CrossRef]



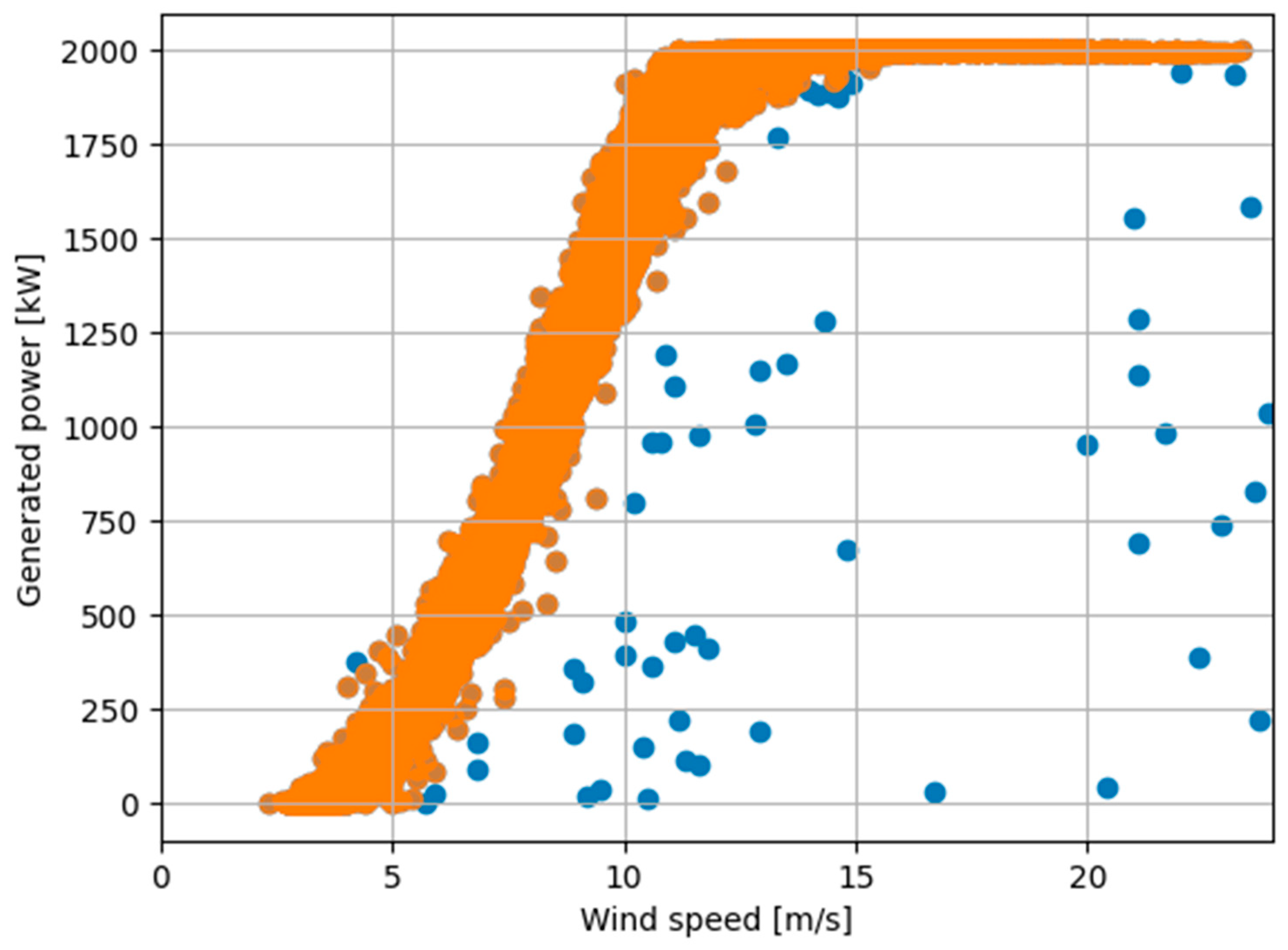
| Fault ID | Fault Type | Occurrence Time | Sample Index |
|---|---|---|---|
| F1 | Generator bearing damage | 20 August 2017, at 06:08 | 32,730 |
| F2 | Generator damage | 21 August 2017, at 14:47 | 32,920 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kijanowski, K.; Barszcz, T.; Dao, P.B. A Cluster-Based Filtering Approach to SCADA Data Preprocessing for Wind Turbine Condition Monitoring and Fault Detection. Energies 2025, 18, 5954. https://doi.org/10.3390/en18225954
Kijanowski K, Barszcz T, Dao PB. A Cluster-Based Filtering Approach to SCADA Data Preprocessing for Wind Turbine Condition Monitoring and Fault Detection. Energies. 2025; 18(22):5954. https://doi.org/10.3390/en18225954
Chicago/Turabian StyleKijanowski, Krzysztof, Tomasz Barszcz, and Phong Ba Dao. 2025. "A Cluster-Based Filtering Approach to SCADA Data Preprocessing for Wind Turbine Condition Monitoring and Fault Detection" Energies 18, no. 22: 5954. https://doi.org/10.3390/en18225954
APA StyleKijanowski, K., Barszcz, T., & Dao, P. B. (2025). A Cluster-Based Filtering Approach to SCADA Data Preprocessing for Wind Turbine Condition Monitoring and Fault Detection. Energies, 18(22), 5954. https://doi.org/10.3390/en18225954







