1. Introduction
Many newcomer countries face common challenges during the early stages of nuclear power deployment, such as maturing regulatory capacity, evolving emergency infrastructure, and comparatively less reliable grid systems, which can heighten exposure to Loss of Offsite Power (LOOP) and subsequent Station Blackout (SBO). This study employs a country-specific case study approach, concentrating on Uganda, to evaluate SBO risk by formulating a time-dependent probabilistic model tailored to its infrastructure conditions. Uganda’s pursuit of nuclear energy under its Vision 2040 framework reflects a national commitment to meeting rising electricity demand, projected to reach 52 GW by 2040, through sustainable and resilient power generation [
1]. With the successful completion of the International Atomic Energy Agency (IAEA) INIR Phase 1, as well as bilateral cooperation with experienced nuclear states, the country is advancing toward adopting the APR1400 reactor design, favored for its well-validated safety profile and global deployment record [
2].
However, integrating nuclear power into the national grid presents significant reliability challenges. Uganda’s transmission and distribution system experiences high losses, averaging approximately 15% annually [
3], and is prone to major disturbances; for instance, a nationwide blackout occurred during a load rejection test at the newly completed Karuma Hydropower Plant in June 2024 [
4]. Recent performance data indicate a customer-weighted national System Average Interruption Duration Index (SAIDI) of approximately 780–950 min/year and a System Average Interruption Frequency Index (SAIFI) of 11–14 outages/year for the 2021–2023 period. These values reflect utility-level data weighted by customer share, covering approximately 92.5% of the connected customer base [
5]. In contrast, South Africa’s Eskom grid, serving the continent’s only operational nuclear power plant, reports significantly better reliability, with SAIDI of 200–300 min/year and SAIFI of 5–7 outages/year [
6]. Such reliability differences place Uganda in a lower grid performance category, implying a substantially higher risk of LOOP events. Given Uganda’s limited redundancy and the long transmission distances from the proposed nuclear plant site to major load centers, such conditions significantly increase the probability of SBO events, where all AC power required for core cooling and safe shutdown is lost [
7].
Following the Fukushima Daiichi accident, the U.S. nuclear industry proposed and developed Flexible and Diverse Coping Strategies (FLEX) to mitigate such events by deploying portable, redundant equipment capable of restoring essential safety functions during extended power outages [
8]. Existing FLEX frameworks, designed for advanced programs, have not been systematically tested in newcomer settings marked by grid instability, logistical constraints, and human-factor delays. This study quantifies how component failure rates, offsite power recovery delays, and FLEX deployment timing/reliability shape time-dependent SBO risk in a newcomer context and evaluates the contribution of non-AC coping systems. The goal is to guide infrastructure design, emergency preparedness, and regulatory oversight for Uganda’s safe, reliable nuclear deployment.
While time-dependent SBO risk models are well-established, as shown by foundational work such as NUREG/CR-6890, they have been developed and calibrated for established nuclear fleets operating within high-reliability electrical grids rather than in the operational context of a newcomer program like Uganda’s. This context is defined by high grid losses, long transmission distances, and frequent offsite power interruptions, where such factors affect the SBO risk profile and challenge the direct application of existing PRA parameters. This study focuses on the application and parameterization of this established framework to a relatively unexplored, high-risk context. It provides a quantitative analysis that (i) parameterizes an SBO model with country-specific, data-informed inputs reflecting a low-reliability grid; (ii) quantifies the comparative risk-reduction benefit of AC-only versus non-AC (TDP) coping strategies under these specific conditions; and (iii) derives a set of actionable, evidence-based recommendations for mitigation priorities for a newcomer nation, balancing on-site FLEX reliability against strategic grid-strengthening investments.
2. Materials and Methods
The methodological framework for this study adopts a 72 h mission time consistent with post-Fukushima practice, reflecting the window in which coping systems must sustain essential safety functions to avert core damage during SBO. Two operational cases are defined to span available coping strategies over this period, reflecting Uganda’s grid-reliability constraints and slower emergency response.
All component failures and recoveries are modeled as statistically independent to maintain tractability while providing transparent analytical foundations suitable for newcomer program assessment. Common-cause failures (CCFs) and explicit human-reliability analysis (HRA) are excluded owing to the absence of Uganda-specific empirical data. CCFs can correlate outages across nominally independent AC sources like the EDG and AAC source through shared environment, maintenance or procedural practices, or support systems, thereby increasing joint-failure probabilities. HRA affects FLEX success through action errors or delays during activation, staging, transport, connection, and sustained operation, which can increase the effective deployment time.
These factors are methodologically excluded. For a newcomer context, no defensible, data-informed parameterization for CCF dependence or HRA (HEPs, PSFs) is available. This lack of data means that any attempt to include these factors would rely on non-transferable, speculative inputs. Such an approach would reduce the model’s transparency and, more importantly, introduce its own distorting bias to the absolute risk. A transparent exclusion is therefore the more defensible choice. Given these conditions, the probabilities from this model are interpreted as conditional on these assumptions, while the comparative findings between FLEX equipment reliability and deployment timing remain reliable.
For conservatism, one EDG is credited as reliably available despite design redundancy to reflect plausible CCFs, maintenance unavailability, and start-up delays, all risks experienced in newcomer contexts with logistical and infrastructure constraints. Similarly, one TDP is credited as available to simplify the model by removing complex common-cause treatment, and reflect the likely limitations of Uganda’s first-of-a-kind nuclear program in terms of operational maturity, logistics, and maintenance capacity. Although steam-driven, the TDP depends on Class 1E DC for control and valve actuation and is therefore only credited within the existing DC endurance window of 16 h unless FLEX DC support is assumed [
9]. This scope clarification does not affect the results of this study. This intentionally conservative treatment of safety-critical systems is appropriate for early-stage assessments [
10], and provides lower-bound estimates of system performance.
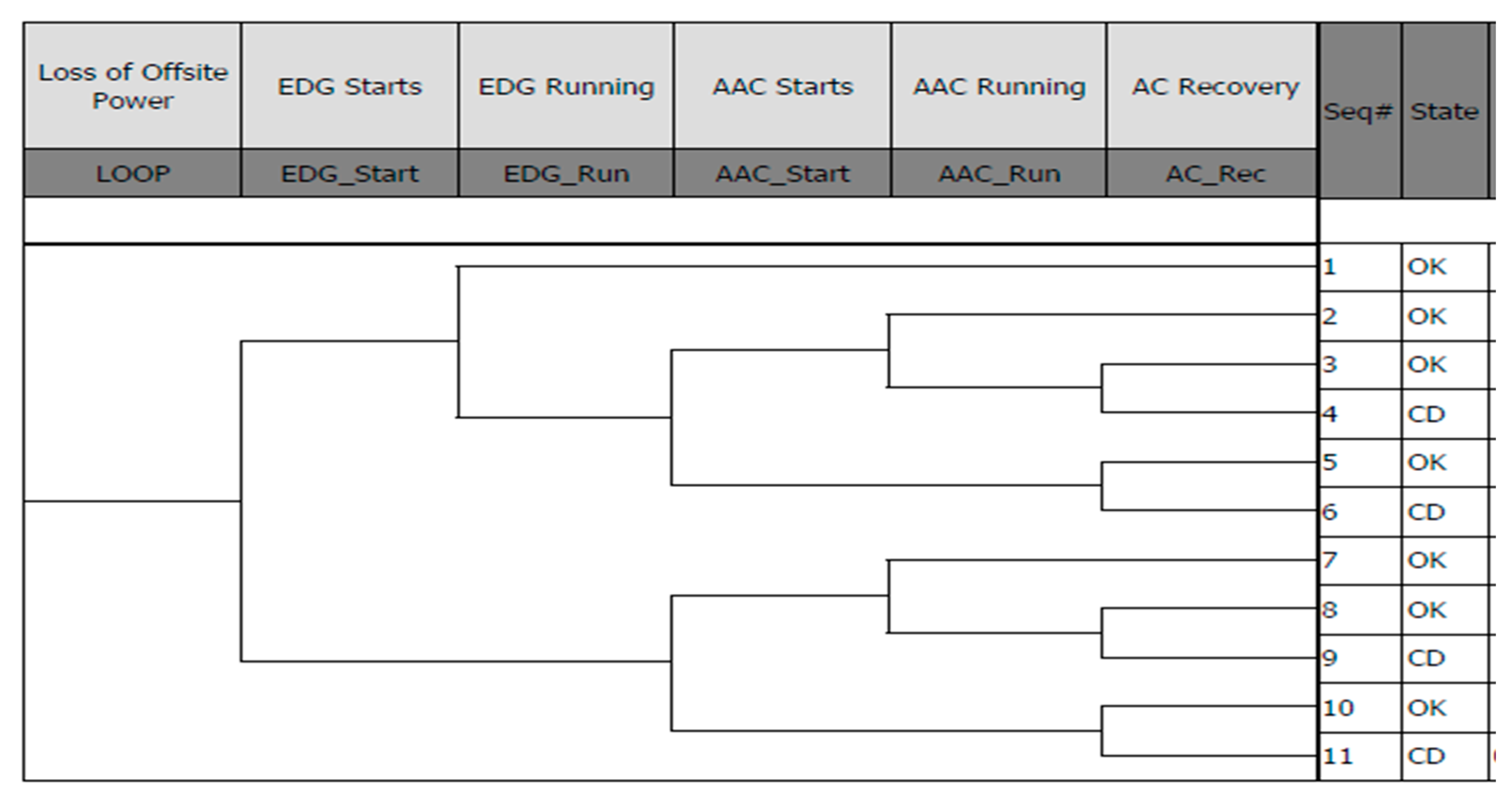
2.1. Case 1: AC Supply Only (EDG, AAC, and Offsite Power)
This case represents the baseline SBO coping configuration for Uganda’s proposed nuclear program and relies solely on AC power recovery pathways. The configuration comprises an EDG, an AAC source modeled as a backup to the EDG, and offsite power recovery characterized by a two-parameter Weibull distribution that captures the time-varying probability of grid restoration. The event tree,
Figure 1, illustrates the sequential logic of LOOP initiation, EDG startup and operation, AAC activation, and eventual offsite recovery [
11]. Core damage (CD) occurs in sequences where all AC sources fail or recovery is delayed beyond coping capacity.
2.2. Case 2: AC Supply with TDP
This case extends the baseline configuration by introducing the TDP, modeled as a non-AC coping system. The TDP is assumed to actuate automatically at LOOP initiation (τ = 0), providing auxiliary feed water independent of AC sources. By providing immediate non-AC cooling capacity, it diversifies coping strategies and reduces reliance on AC restoration. The event tree for this case, as shown in
Figure 2 below, expands upon Case 1 by including the TDP branch. Sequences leading to core damage are reduced, demonstrating structurally how the TDP improves resilience against SBO progression.
2.3. FLEX Deployment
FLEX is modeled as a staged coping measure, activated at defined time windows to add an AC-recovery pathway during prolonged SBO, and its effect depends on timely deployment and equipment reliability. This study compares a baseline AC-only configuration with a FLEX-enhanced case, assuming FLEX is realistically deployable only after initial commercial operation. The framework reflects Uganda’s conditions, such as grid instability, long transmission distances, limited redundancy, and constraints such as slower mobilization, fewer mobile assets, and geographic barriers that can delay response. It further integrates AC and non-AC coping measures with delayed deployment to quantify risk-mitigation potential in a developing nuclear program. Consistent with international studies, FLEX effectiveness is shown to depend strongly on local infrastructure and environmental conditions. This approach provides a context-specific basis for assessing SBO risk in Uganda, accounting for both technological measures and systemic limitations of early-phase nuclear programs.
In this study, FLEX deployment is defined as the on-site activation and connection of pre-staged portable equipment by plant operators to restore or maintain AC power and cooling following a station blackout. The deployment window begins once operators determine that installed systems are unavailable or insufficient to maintain core cooling, and the scope includes equipment retrieval from protected on-site storage, transfer to designated tie-in points, electrical and hydraulic connections, and startup and operation until safety functions are re-established.
Consistent with industry guidance such as NEI 12-06, installed capabilities are treated as the baseline configuration. Two FLEX options extend this baseline; Option 1 models on-site activation of pre-staged portable resources as the primary early-recovery pathway once installed systems are inadequate; Option 2 adds integration of offsite resources, when access permits, to support sustained recovery. This structure aligns with established practice while reflecting a single-site newcomer context with potentially constrained regional logistics. Given Uganda’s infrastructure conditions, priority is placed on site-held portable resources that can be deployed under degraded external support. The Gas Turbine Generator (GTG) was considered the primary pre-staged resource due to its rapid start-up, minimal infrastructure needs, and adaptability to local conditions [
12].
These definitions and assumptions establish when FLEX is credited, how it is initiated, and which resources are modeled. The subsequent analysis specifies parameter values and distributions, evaluates SBO risk for the baseline and FLEX-enhanced configurations. Results are reported as incremental risk reduction over the mission time with sensitivity to deployment timing and equipment reliability, providing a transparent, reproducible basis for assessing FLEX contributions to mitigating SBO risk in Uganda.
2.4. Mathematical Formulation
All failure probabilities are expressed as functions of time, denoted by τ, representing the number of hours elapsed since the initiating LOOP event [
12]. This approach allows for dynamic assessment of system unavailability, particularly relevant in contexts such as Uganda’s, where grid-related outages are often prolonged and uncertain.
2.4.1. Component Modeling
The EDG is modeled with a constant fail-to-run rate, where λ
E is the run failure rate (in h
−1), and the probability density function (PDF) for its failure at time τ is given by:
In the event of EDG failure, the AAC source begins operation, where λ
A is the fail-to-run rate (in h
−1), and t
E the time at which the EDG fails and the AAC starts. Its conditional failure probability density function at time τ, given activation at t
E, is defined as:
This shows the delay in AAC activation that occurs after EDG failure, allowing the model to accurately represent the sequence of dependent system responses.
Offsite power recovery follows a Weibull survival function to represent the non-recovery behavior over time. This distribution accommodates the increasing likelihood of restoration as time progresses, a characteristic feature of developing grid systems [
13]. It is given by:
where
β is the shape parameter and
η is the scale parameter. This function is particularly suited for modeling offsite power behavior where uncertainties in restoration timelines are significant [
14].
As a non-AC measure, always available from τ = 0, the running failure probability of the TDP is given below, where λ
TDP is the failure rate and τ is the elapsed time since LOOP initiation.
The
Table 1 shows the base failure rates for the components considered in this model, with the EDG failure rate from the APR1400 Design Control Document: Chapter 19, and the AAC and TDP failure rates from NUREG/CR-6928 (2020 Update) [
15,
16].
In the absence of Uganda-specific operating experience, the run-failure rates above are used as a baseline from the U.S. and Korea’s mature-industry datasets, an approach consistent with IAEA Safety Standards guidance [
17] for pre-construction assessment. This is because they are known, mechanism-based, and widely employed in PRA. In order to prevent introducing unverified bias, numerical rescaling of these component rates is not considered. As Uganda’s program matures and operational experience accumulates, these parameters should be refined with plant-specific data.
2.4.2. FLEX Deployment Model
FLEX success is modeled with a survival function that defines the likelihood that it has not restored AC power by any time τ, where τ represents the elapsed time since the initiating LOOP event. The function is defined as:
where τ
F denotes the time at which FLEX is deployed, and λ
F represents the constant failure rate of FLEX in restoring AC power once operational. This failure rate relates to equipment reliability, which can also be given in terms of Mean Time To Failure (MTTF) that is given as 1/λ
F (h). This function assumes that FLEX has no mitigating effect before deployment and that its failure to restore power follows an exponential decay function post-deployment.
2.4.3. Joint SBO Probability
For Case 1, the Joint Probability of Total AC Loss at Time τ is the probability that both EDG and AAC have failed and offsite power has not been restored by τ, and it is given by
Substituting Equations (1), (3) and (5),
Therefore, the probability of SBO occurring anytime up to τ is given by
FLEX is later integrated by substituting Equations (7) and (12):
For Case 2, the joint probability is derived by substituting Equation (6) into (12) and is given by
With the integration of FLEX in this case, the joint probability is given by considering Equations (7) and (15):
2.4.4. FLEX Risk Reduction Model
In this study, the SBO probability following FLEX deployment can be expressed as:
where
k ∈ (0, 1) represents the FLEX effectiveness factor achieved immediately upon successful deployment at time τ
F. The relative risk reduction, R(τ), as a result of FLEX is quantified through the standard risk reduction metric:
Substituting Equations (17) and (18),
This formulation reflects that FLEX yields no risk reduction before deployment (τ < τ
F), attains its maximum effect immediately after deployment, and can decline thereafter due to equipment wear, environmental challenges, and resource depletion. In this study, k = 0.8 is adopted as a conservative engineering bound consistent with best-estimate-plus-uncertainty practice for safety analyses in situations where uncertainties cannot be fully quantified from operational data or in the absence of plant-specific data [
18,
19].
The 20% effectiveness reduction (1 − k) provides a structured allowance for un-modeled implementation uncertainties such as equipment deployment challenges under extreme environmental conditions like seismic damage or flooding; human reliability uncertainties in extended accident scenarios; equipment degradation effects under sustained emergency operation beyond design specifications; and interface compatibility issues between portable equipment and plant systems under degraded conditions.
These considerations align with the beyond-design-basis mitigation framework [
20], and FLEX guidance, emphasizing performance-based coping capability, reasonable protection of equipment, and site-wide implementation following loss of all AC power. This approach provides appropriate conservatism for epistemic uncertainties while maintaining physically realistic risk reduction estimates necessary for regulatory decision-making and operational planning.
3. Results and Discussion
This section presents and discusses results from the developed model, focusing on (i) offsite power recovery characterized with a Weibull distribution; (ii) baseline time-dependent SBO risk for Case 1 (AC-only) and Case 2 (with TDP); (iii) the effect of FLEX deployment across the 72 h mission; and (iv) a sensitivity evaluation quantifying how FLEX effectiveness impacts risk reduction.
3.1. Offsite Power Recovery
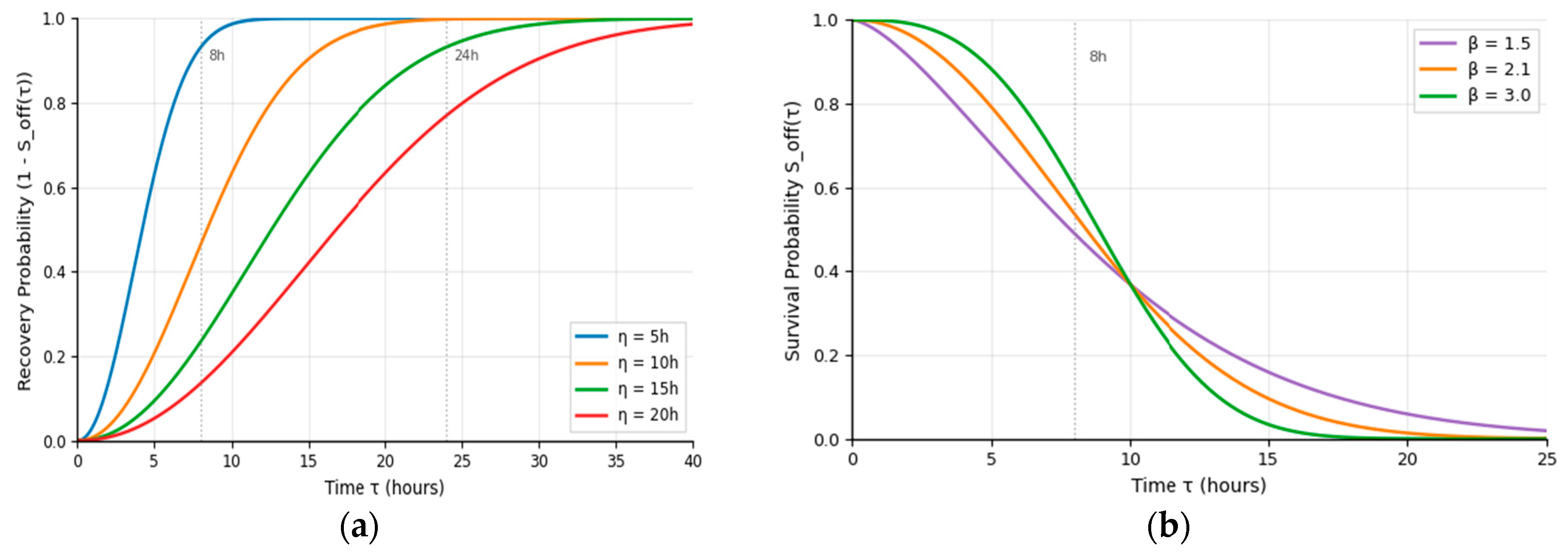
The restoration of offsite AC power following LOOP events is characterized using a two-parameter Weibull distribution as defined in Equation (5), where the survival function Soff(τ) governs the probability of non-recovery over time. This framework enables systematic evaluation of grid reliability effects on SBO risk for newcomer nuclear programs.
Figure 3a demonstrates the influence of the Weibull scale parameter η on recovery characteristics, with shape parameter β fixed at 2.1. The scale parameter directly controls restoration timing, where larger η values indicate slower grid recovery capability. Increasing η from 5 h to 20 h produces a proportional increase in median recovery time from 4.2 h to 16.8 h. This parameter variation results in correspondingly delayed restoration across all time horizons, emphasizing the critical role of grid infrastructure quality in determining SBO vulnerability windows.
Figure 3b illustrates the effect of the shape parameter β on recovery probability distribution, with scale parameter η held constant at 10 h. Lower β values (1.5) produce exponential-like behavior with rapid initial recovery, while higher β values (3.0) concentrate recovery events around the median time with reduced uncertainty. Despite these distributional differences, the median recovery time remains approximately constant at 8 h across all β variations, confirming that the scale parameter primarily determines restoration timing while the shape parameter governs temporal uncertainty.
For Uganda’s grid conditions, the baseline parameters β = 2.1 and η = 10 h reflect reliability constraints and susceptibility to major disturbances such as infrastructural and logistical challenges. The selected Weibull parameters are benchmarked against outage duration data from mature U.S. nuclear programs, where median restoration times typically fall between 2–8 h depending on outage type.
The parameter η = 10 h represents a conservative extension beyond typical mature-program recovery values (5–7 h, per NUREG/CR-6890) to account for Uganda’s documented grid reliability constraints. This selection is informed by Uganda’s SAIDI/SAIFI performance relative to nuclear-operating countries and provides an appropriate baseline for strategic planning purposes. Although country-specific comparisons with other newcomer programs are beyond this study’s scope, model behavior is examined over a reasonable range of parameter values to establish generalizability.
This parameter combination yields 50% recovery probability at 8 h, substantially exceeding typical values for mature nuclear programs and the non-recovery probability exceeds 60% during the first 8 h, emphasizing the critical dependence on on-site coping systems during initial SBO phases. This produces an extended vulnerability window where FLEX deployment becomes essential for sustained plant safety. The intermediate recovery window (8–24 h) aligns with typical FLEX activation timelines, and the residual 5% non-recovery at 72 h supports the post-Fukushima 72 h mission time adopted for newcomer programs. These calibrated assumptions are propagated through the SBO calculations by integrating Equation (5) within the analytical framework, anchoring the results to Uganda’s grid conditions.
3.2. Baseline SBO Risk Assessment
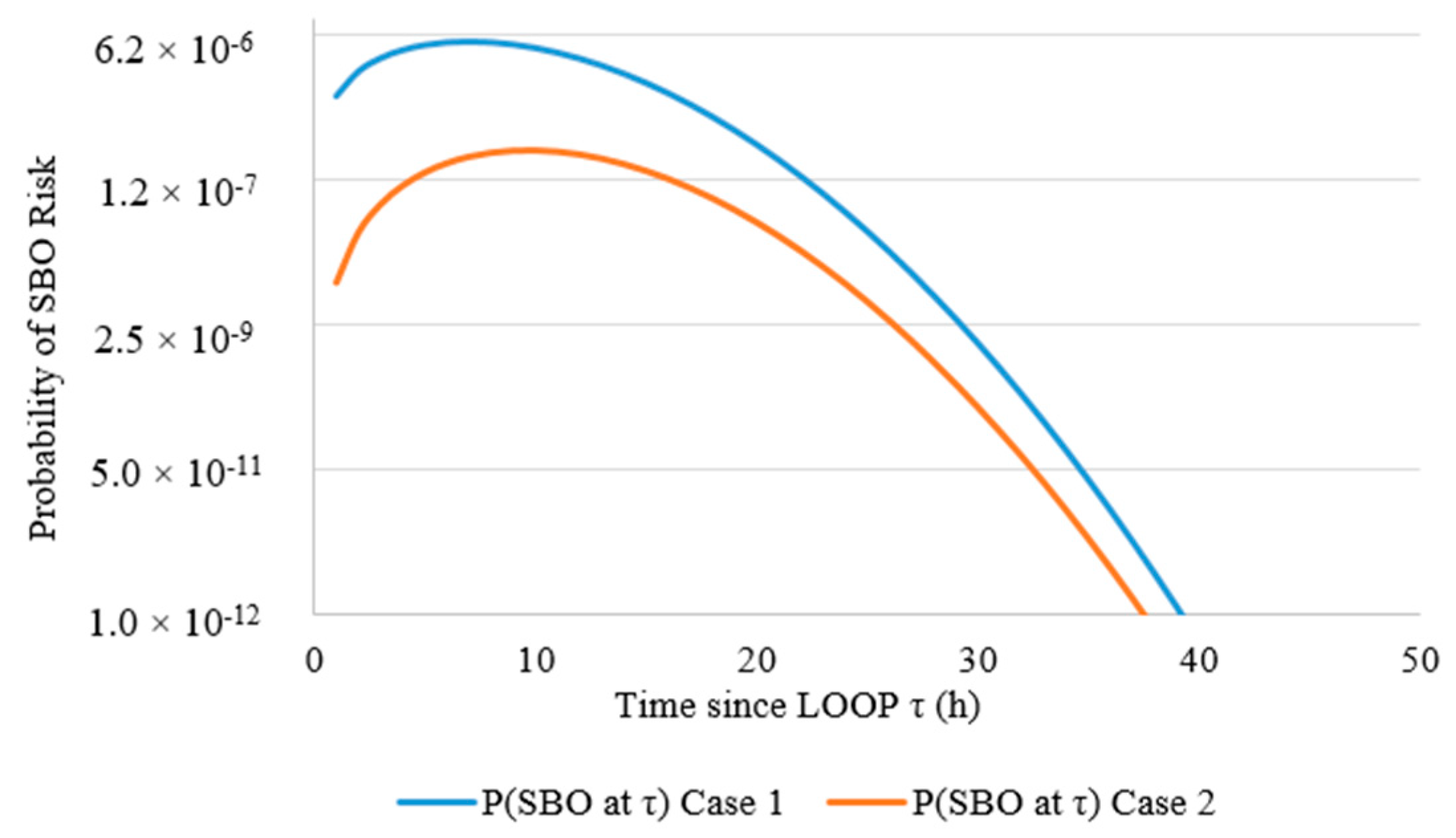
An analysis of the instantaneous SBO probabilities shows the dynamic nature of the plant’s vulnerability over the mission time. As shown in
Figure 4, the instantaneous risk at a given time τ, for both cases, rises to a peak within the first 12 h before declining as the likelihood of offsite power recovery increases. This peak identifies the period of maximum vulnerability for the plant. This comparison also shows that the SBO risk for Case 2 is substantially lower than for Case 1 as shown in
Table 2 This is as a result of the TDP, which provides a continuous safety margin, effectively reducing the rate of risk accumulation over the mission time.
When results are summarized across the 72 h mission window, the mean ratio (C2/C1) is 0.20, confirming that the TDP provides an additional benefit. This emphasizes the relative scaling of SBO risk between the two cases, which offers a more transparent basis for comparison. Values below 1.0 × 10−12 are not considered, consistent with PRA truncation practices.
3.3. FLEX-Enhanced Scenario Performance
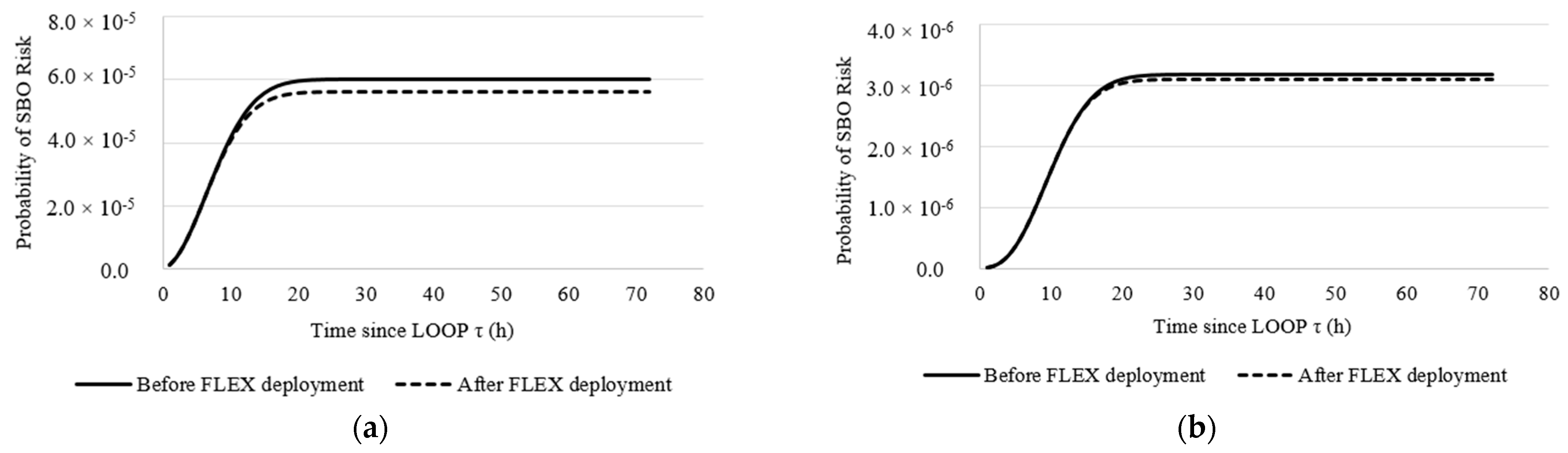
Figure 5a,b show the cumulative SBO risk for Case 1 and Case 2, respectively, comparing baseline conditions with FLEX-enhanced scenarios. Deployment times were selected from the peaks of the instantaneous-risk profiles, with τ
F = 6 h for Case 1 and τ
F = 12 h for Case 2, reflecting the later vulnerability peak once the TDP is available. The failure rate of FLEX equipment was considered as λ
F = 0.02, representing a conservative risk informed assumption for a newcomer nuclear program facing grid reliability, infrastructural and logistical challenges.
In Case 1, the baseline and FLEX curves are indistinguishable up to 6 h, when installed AC systems dominate risk accumulation. Following FLEX activation, its trajectory remains uniformly below baseline, reflecting a gradual mitigation effect. However, the initial accumulation rate in Case 2 is lower because the TDP suppresses early vulnerability. FLEX is deployed at 12 h, near the later peak in instantaneous risk and the divergence between the baseline and FLEX curves is correspondingly smaller than in Case 1. This is because the TDP is considered to have removed most of the early risk before FLEX is engaged.
The more defined downward shift in Case 1 highlights the role of FLEX as the primary mitigation measure when only installed AC is available, whereas in Case 2, FLEX provides an additional advantage to an already effective coping mechanism. Case 2 maintains a consistently lower cumulative risk across the mission time, demonstrating the advantage of combining diversified non-AC capability with FLEX.
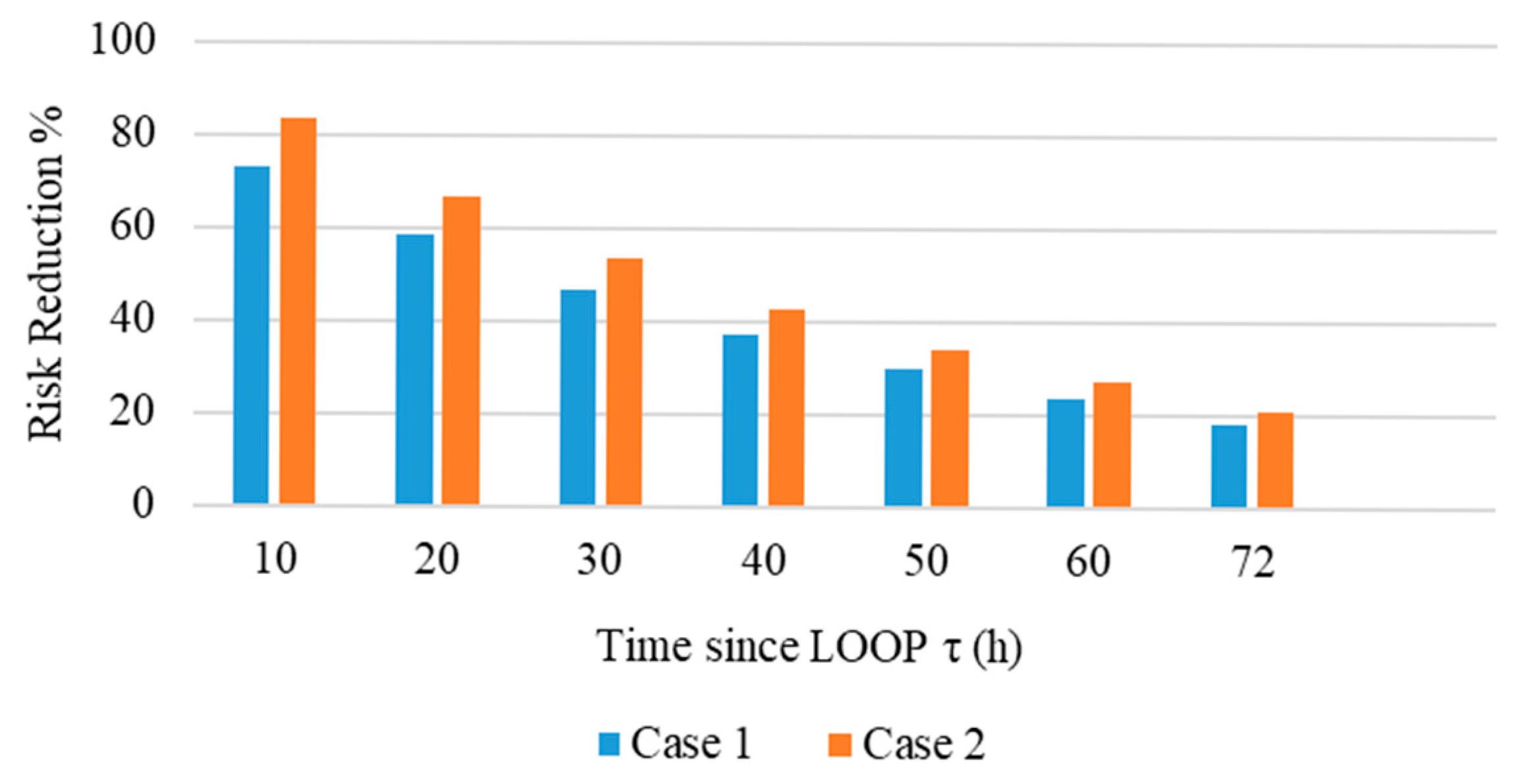
Figure 6 shows these effects in terms of percentage reduction across the mission time from Equation (19). FLEX offers substantial early benefits in both cases, followed by a gradual decline in percentage reduction with progression in time, due to increasing exposure time and the rising probability of portable-equipment failure. Following deployment, Case 2 achieves a higher percentage risk reduction than Case 1 across the 72 h mission time. This is due to the later deployment timing, which shortens the operating window at any given time τ and results in a lower cumulative failure probability for the FLEX equipment, therefore sustaining a stronger SBO mitigating effect.
The baseline and range-based restoration profiles are consistent with empirically observed LOOP restoration patterns documented in Idaho National Laboratory (INL) multi-decade updates [
21]. The model structure also aligns with the benchmark framework in NUREG/CR-6890 for SBO treatment [
22]. Crediting non-AC coping (TDP/FLEX) is consistent with NEI 12-06 and NRC/EPRI guidance on modeling and crediting FLEX in PRA. Peer-reviewed quantification reports a reduction of 90% in the CDF for a Pressurized Water Reactor (PWR) when FLEX is modeled [
23], supporting the Case 2 vs. Case 1 outcomes, with plant and grid differences acknowledged.
3.4. FLEX Integration Analysis
The effectiveness of FLEX deployment is evaluated using the risk reduction metric defined in Equation (17), examining how equipment reliability (λF) and deployment timing (τF) influence SBO mitigation across the 72 h mission window. Equation (19) reveals that risk reduction depends exponentially on equipment MTTF and linearly on elapsed deployment time, providing the analytical foundation for parameter assessment.
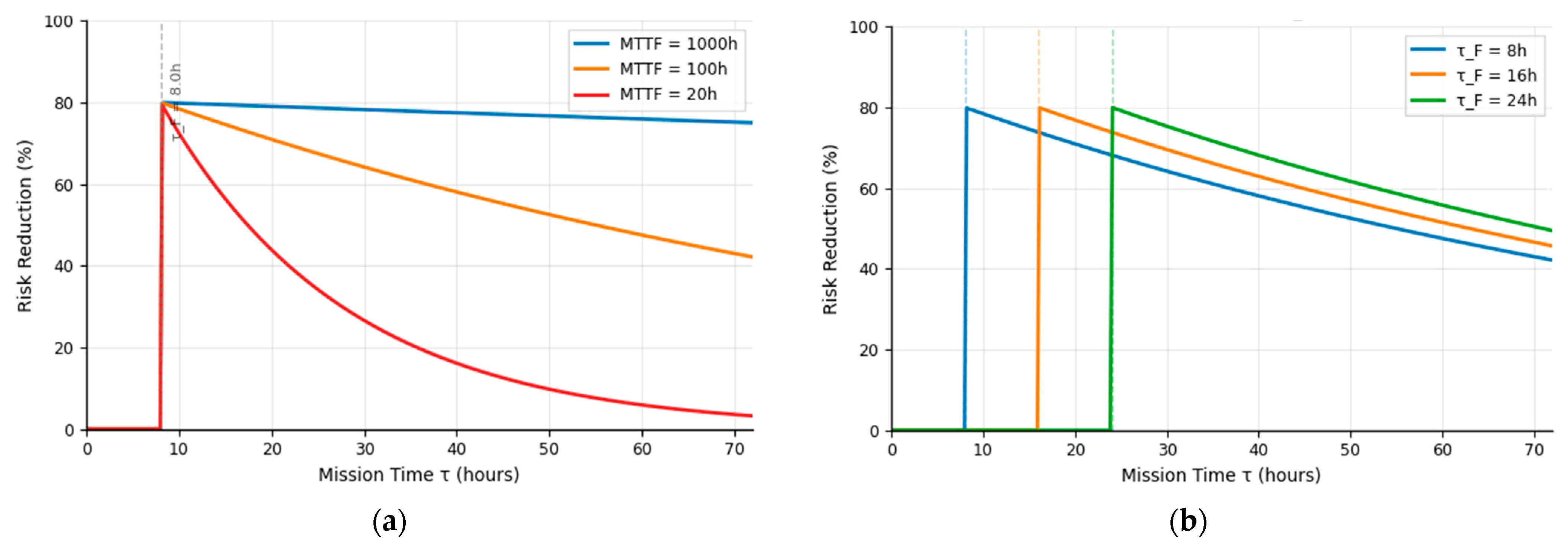
The reliability analysis shows the dominant effect of equipment MTTF on FLEX effectiveness as shown in
Figure 7a. High-reliability systems (MTTF = 1000 h, λF = 0.001 h
−1) maintain approximately 75% risk reduction throughout the mission window, while moderate reliability equipment (MTTF = 100 h, λF = 0.010 h
−1) achieves 60% reduction, and low-reliability systems (MTTF = 20 h, λF = 0.050 h
−1) provide only 25% benefit by 72 h. The exponential relationship predicted by Equation (18) is evident in the separation between reliability curves. The reliability sensitivity analysis spans two orders of magnitude in equipment MTTF (10 h to 1000 h), with low-reliability scenarios (MTTF ≤ 50 h) accounting for likely degradation from newcomer-specific operational challenges including limited maintenance infrastructure, environmental stressors, and reduced operational maturity. This range provides country-relevant sensitivity bounds for Uganda’s context.
The deployment timing analysis confirms the secondary influence of τ
F on system effectiveness as shown in
Figure 7b. Varying deployment time from 8 h to 24 h produces modest changes in risk reduction profiles, with all curves converging to approximately 45–50% effectiveness at 72 h regardless of deployment timing. This convergence behavior reflects the linear dependence on (τ − τ
F) in Equation (18), demonstrating that timing effects are substantially smaller than reliability effects.
The convergence is expected because FLEX functions act in partially overlapping operational windows, early DC bridging and TDP start-up transition into fuel or endurance-limited operation. It is observed that the time of deployment has diminishing influence, while equipment reliability (sustained running capability) becomes the dominant driver of risk reduction at later times.
The quantitative results in
Table 3 below validate Equation (19) predictions. Zero values at 8 h reflect the physical reality that FLEX provides no benefit at deployment initiation (τ − τ
F = 0). The analysis identifies distinct performance thresholds: MTTF ≥ 200 h delivers substantial risk reduction benefit 58.1% at 72 h, while MTTF ≥ 1000 h provides the highest benefit exceeding 75% at 72 h. Meanwhile, MTTF ≤ 50 h provides limited improvement below 25%. The low-reliability scenarios analyzed account for possible degradation from newcomer-specific operational challenges including limited maintenance infrastructure, environmental stressors, and reduced operational maturity, providing country-relevant sensitivity bounds for Uganda’s context.
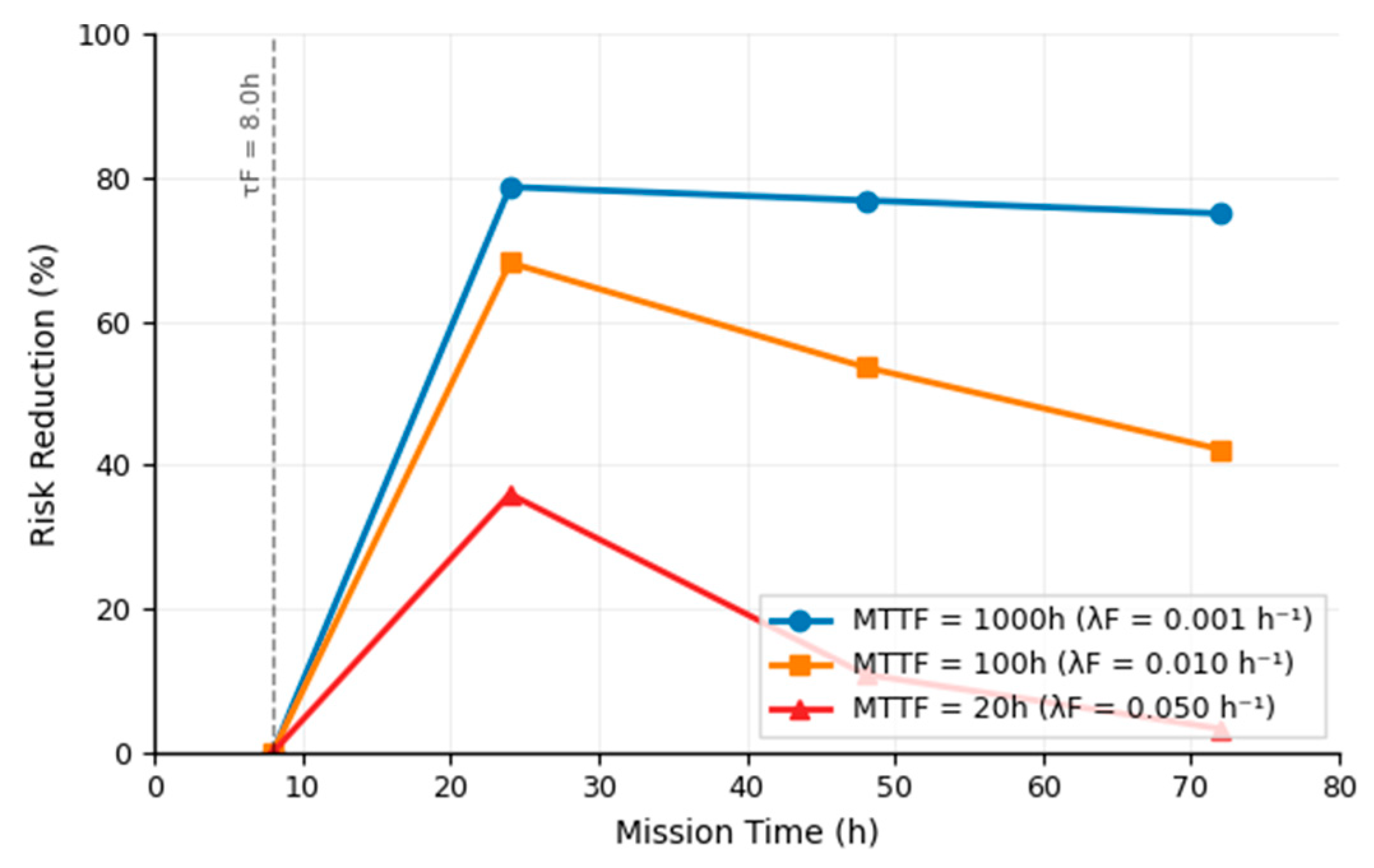
The temporal evolution analysis confirms that sustained FLEX operation becomes increasingly effective with extended mission duration as shown in
Figure 8. High-reliability systems (MTTF = 1000 h) achieve peak effectiveness of 75% at 24 h and maintain this level through 72 h, while moderate systems (MTTF = 100 h) show gradual improvement reaching 42% at 72 h. Low-reliability systems (MTTF = 20 h) demonstrate poor performance across all mission times, reaching only 3% maximum effectiveness at 72 h.
This analytical framework establishes clear guidance for newcomer nuclear programs. Equipment reliability has a greater impact than deployment timing, indicating that investment should prioritize high-reliability FLEX systems rather than rapid response capabilities. Pre-staged gas turbine generators with MTTF ≥ 200 h offer optimal risk reduction, while portable equipment with MTTF < 50 h should serve only supplementary roles.
3.5. FLEX Implementation Limitations and Model Implications
The practical implementation of FLEX in a newcomer program, according to this study, is directly affected by the equipment reliability (λF) and deployment timing (τF). For λF, practical support factors, such as dependence on imported spares and vendor services, can potentially extend repair cycles and delay corrective maintenance, and degrade in-service equipment reliability. Other factors like insufficient periodic run-tests, inadequate fuel conditioning, and lack of sheltered, climate-controlled storage, will measurably increase λF over the plant lifetime.
For τF, human and logistical factors are of critical importance. Limited hands-on training, underdeveloped procedures and limited supervisory capacity can increase the time required for activation, staging, connection, and refueling of FLEX equipment. Logistical limitations such as poor site access, blocked pathways, or non-redundant communications can make rapid deployment windows (<8 h) unachievable under adverse conditions, reinforcing industry guidance to pre-stage equipment near safety-related loads where possible.
A mature regulatory and quality-assurance (QA) framework is required to keep both λF and τF aligned with design assumptions through surveillance, configuration control, and feedback from drills and inspections. These factors affect the key parameters tested in the sensitivity analysis, showing that lower MTTF and delayed deployment directly reduce FLEX effectiveness. Therefore, the risk reduction results from this study should be considered as an optimistic upper bound. In order to achieve this in practice, there is need to invest in life-cycle spares and vendor support, maintenance and testing to ensure reliability, periodic integrated drills to ensure effective deployment, and secured logistics pathways and refueling access. This shows that high FLEX equipment reliability and rapid deployment are the key factors to consider when mitigating SBO risk.
4. Conclusions and Recommendations
4.1. Summary of Key Findings
The purpose of this study was to identify critical vulnerabilities and determine how flexible mitigation options could strengthen plant reliability in the case of a newcomer nuclear program, such as Uganda’s, facing challenges like grid unreliability, developing regulatory capacity, and constrained emergency response infrastructure. The results showed that SBO risk is most severe in the early hours after LOOP occurs, highlighting the importance of early coping capacity.
Incorporation of the TDP provided a vital non-AC pathway for decay heat removal, substantially reducing SBO risk compared to conventional AC-dependent coping as in the baseline case. It was observed that FLEX equipment reliability dominates deployment timing effects, with high-reliability systems achieving up to 75% risk reduction at 72 h, while low-reliability equipment provides limited improvement below 25%. The mathematical framework reveals that risk reduction increases exponentially with equipment MTTF and linearly with elapsed deployment time. This establishes clear performance thresholds for newcomer nuclear programs.
4.2. Practical Recommendations for Uganda’s Newcomer Program
To directly address the practical implementation challenges discussed in
Section 3.5, such as logistical constraints and limited local expertise, the following recommendations provide a clear path forward. A full implementation feasibility study to analyze Uganda’s current capacity is a separate, vital step that is outside the scope of this technical risk assessment. Rather, the quantitative targets presented in this study define the necessary performance that Uganda’s program must procure and train for to ensure a high level of safety, providing the technical foundation for that future feasibility study.
High-reliability FLEX equipment meeting the MTTF ≥ 200 h threshold identified in this analysis is commercially available from established nuclear industry suppliers. Field-proven gas turbine generators, such as those used in U.S. FLEX programs, demonstrate this level of reliability and can be procured through bilateral cooperation agreements or direct commercial channels. FLEX deployment procedures can be developed using standard simulator-based training, consistent with international guidance (e.g., NEI 12-06) and with technical support from the reactor vendor. Infrastructure requirements, such as protected on-site storage and pre-engineered connection points, are standard in post-Fukushima plant designs. These pathways demonstrate that the technical targets established here are achievable through conventional nuclear industry practices.
The results obtained offer direct, quantifiable policy recommendations for operators, and regulators in Uganda’s nuclear program. They provide a quantitative basis for Performance Targets; for example, primary FLEX systems should have a minimum target MTTF ≥ 200 h, and deployment procedures must be periodically validated to achieve a rapid deployment time of <8 h in the event of offsite power non-recovery.
This study also supports the adoption of a Dual-Track Infrastructure Strategy given Uganda’s specific grid constraints such as long transmission distances, high outage frequencies, and relatively slow restoration times. The immediate response to this should be the prioritization of on-site, pre-staged resources, considering high-reliability Gas Turbine Generators as the primary, non-grid-dependent coping mechanism. This must be complemented by a strategic, long-term national policy for grid infrastructure development, aimed at improving reliability (i.e., reducing the offsite power recovery scale parameter η) and strengthening resilience to large disturbances such as the June 2024 blackout.
As Uganda’s regulatory capacity advances, it should consider integrating FLEX performance into its licensing requirements. This can be done through:
Setting clear minimum targets such as MTTF ≥ 200 h for primary FLEX equipment
Carrying out verification and surveillance through periodic run-tests, load-banking and equipment storage checks
Conducting quarterly drills that exercise activation, staging or transportation, connection and refueling of FLEX equipment
Reporting Key Performance Indicators (KPIs) such as achieved MTTF, start-success rate, fail-to-run events, observed deployment time and variance, with trend analysis and corrective actions when thresholds are missed
Carrying out configuration control through change management for equipment, procedures, and interfaces, as well as supplier quality assurance (life-cycle spares, vendor support contracts) to sustain performance
Conducting annual independent audits and regulator-observed drills
Prioritizing logistics readiness through enhancement of infrastructure to prevent delays in equipment transportation; secured, all-weather access and fuel resupply; and redundant communications
These measures align plant operations with Phase-2 expectations by linking quantified FLEX targets to measurable oversight, ensuring performance is demonstrated, documented, and resilient throughout the plant lifetime.
4.3. Areas for Future Study
This work motivates a phased program of research to strengthen both the risk model and the decision framework as Uganda-specific evidence accumulates. In the near term, the model should be extended to include explicit dependence and human performance: common-cause failures (CCFs) for EDG/AAC/FLEX groupings, a consistent human-reliability analysis (HRA) for activation, staging or transportation, connection, and maintenance tasks, and a separation of fail-to-start and fail-to-run modes for EDG/AAC/TDP/FLEX with full time-dependent integration [
24]. These enhancements will move the present bounding treatment to a data-driven representation and refine absolute risk [
25], while preserving traceability.
With a calibrated model in place, decision-support analyses should quantify the economics of alternative portfolios. A formal cost–benefit analysis (CBA) can compare on-site versus offsite FLEX and gas-turbine generators (GTG) versus diesel power packages under Uganda’s infrastructure constraints, reporting risk reduction per unit cost and accounting for schedule and supply chain risk [
26]. Full life-cycle costs should be evaluated alongside quantified risk reduction, explicitly incorporating reliability-centered maintenance (periodic run-tests, load-banking, fuel conditioning and sheltered storage), life-cycle spares, and vendor support. Using equipment MTTF and deployment time as the key drivers, such analyses would identify the least-cost mixes that sustain high reliability and rapid deployment.
The scope should also expand to integrate national infrastructure trends and external factors that shape initiating-event frequency (LOOP) and offsite power recovery. As new hydropower assets are commissioned and policies to reduce transmission losses (up to 15%) take effect, the LOOP frequency and offsite power recovery profile should be re-estimated and fed back into the model. In doing so, including probabilistic uncertainty propagation of (β, η) parameters using country-specific restoration datasets as they mature will quantify credibility intervals around the risk metrics. In addition, further research into alternative energy sources and advanced grid technologies should be considered. One such innovation is the integration of Fault Current Limiters (FCLs) with Line Commutated Converter (LCC) grids, which represent a more economical grid-forming technology [
27]. This combined architecture is designed to provide fault ride-through and support the controlled energization of priority loads. This approach is particularly advantageous for developing grids where cost-effectiveness is a primary concern.