Comparative Study of Steady-State Efficiency Maps and Time-Stepping Methods for Induction Motor Drive Cycle Performance Analysis
Abstract
1. Introduction
Contribution of This Paper
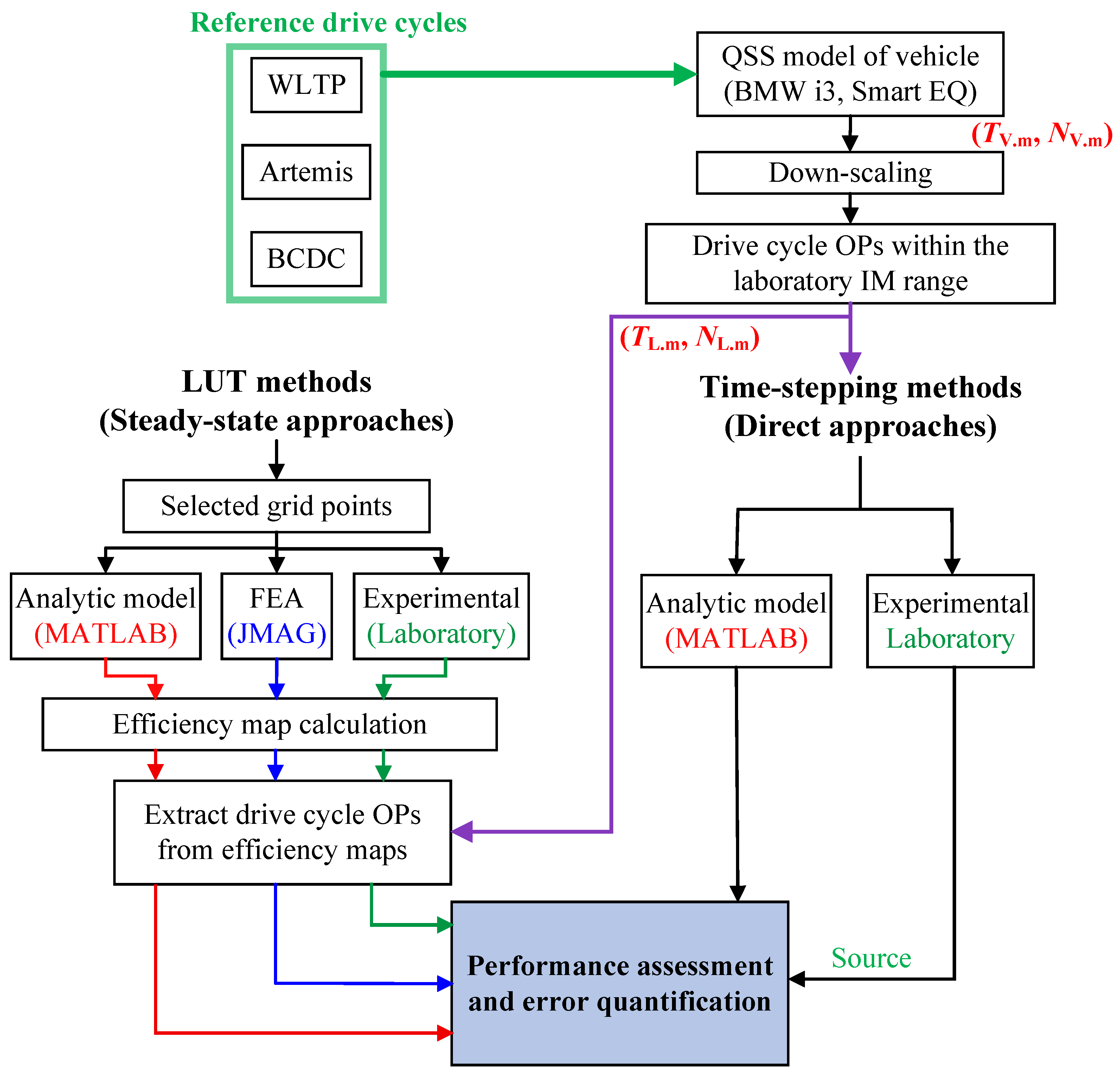
2. Test Cases, Modeling, and Experimental Setup
2.1. Methodology and Test Case Overview

| Specifications of Vehicle Motors | ||
|---|---|---|
| Parameters | Vehicles | |
| BMW i3 | Smart EQ | |
| Max. Power | 125 | 60 |
| Max. Torque | 250 | 160 |
| Rated Speed | 4800 | 3600 |
| Maximum Speed | 11,400 | 11,475 |
| Laboratory Motor Specification | ||
| Parameters | Values | |
| Max. Power | 4.4 | |
| Max. Torque | 24.7 | |
| Rated Speed | 1430 | |
| Maximum Speed | 2850 | |
2.2. Setting Up the Models
2.2.1. Analytic Model
2.2.2. FEA Model
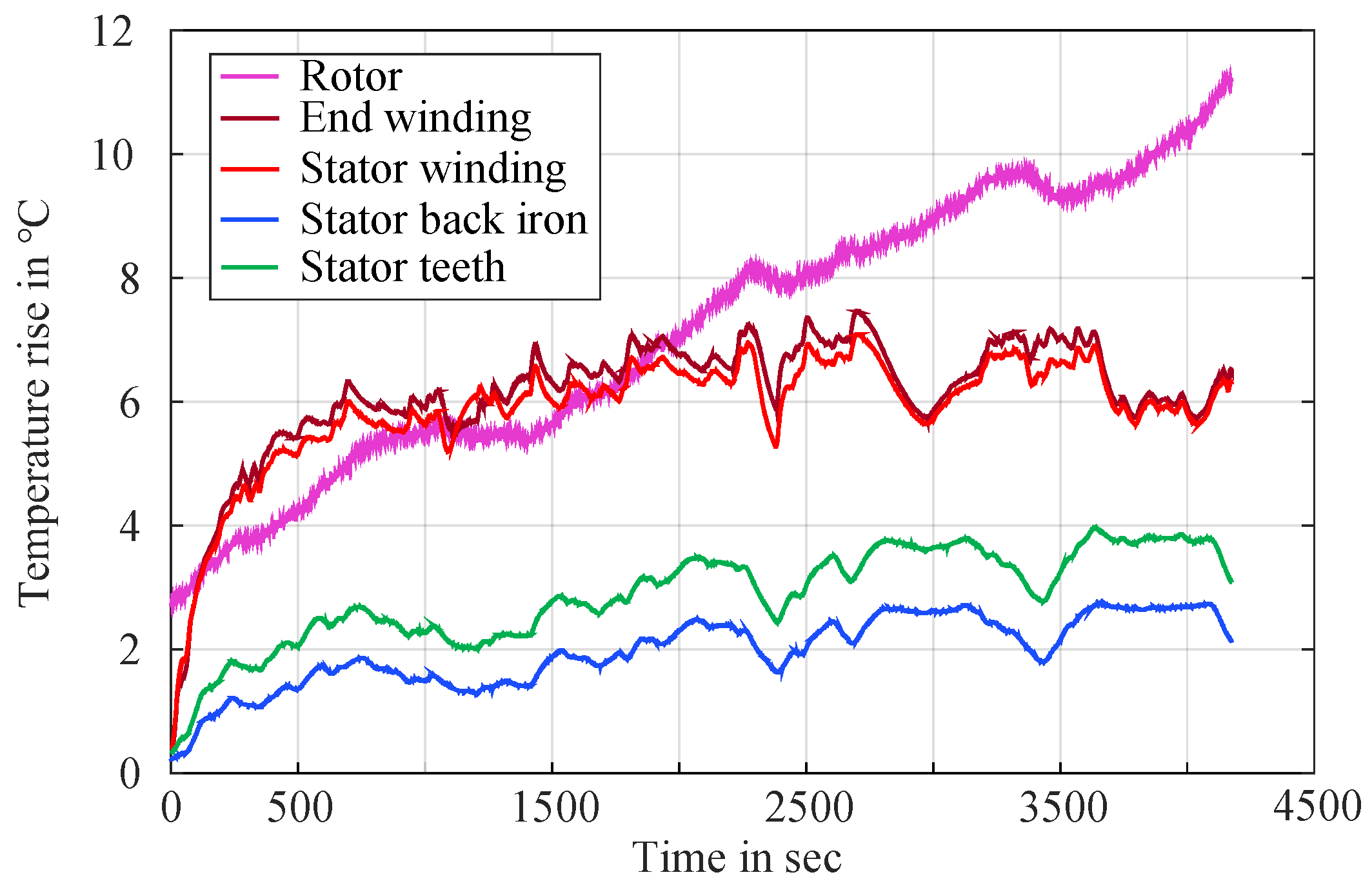
2.3. Test Bench Setup and Configuration
3. Results of Analysis
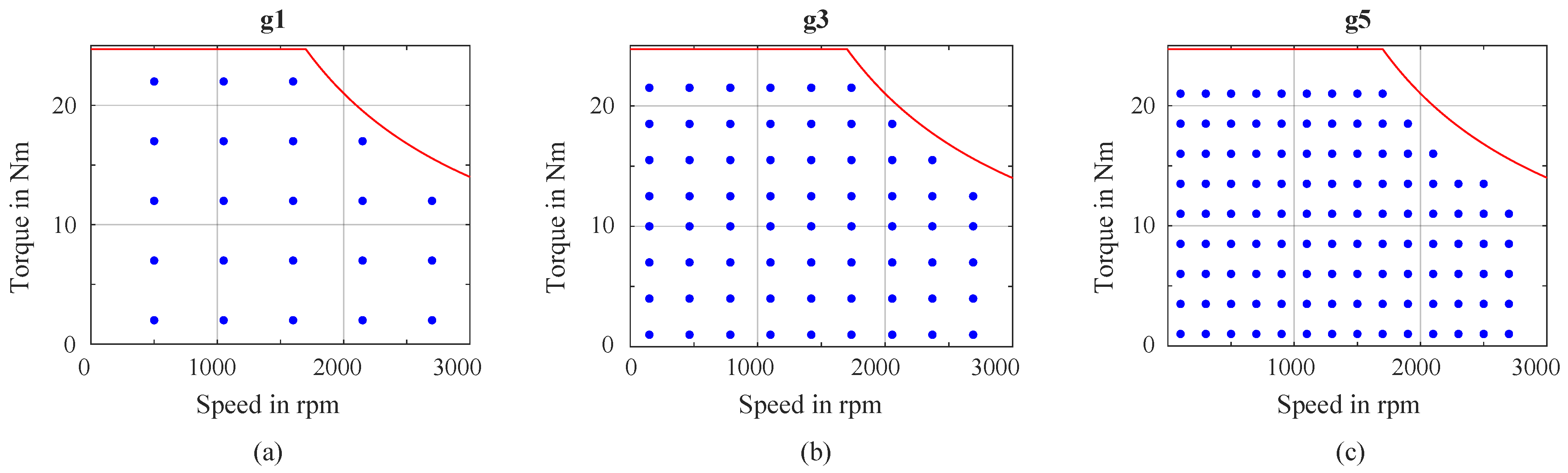
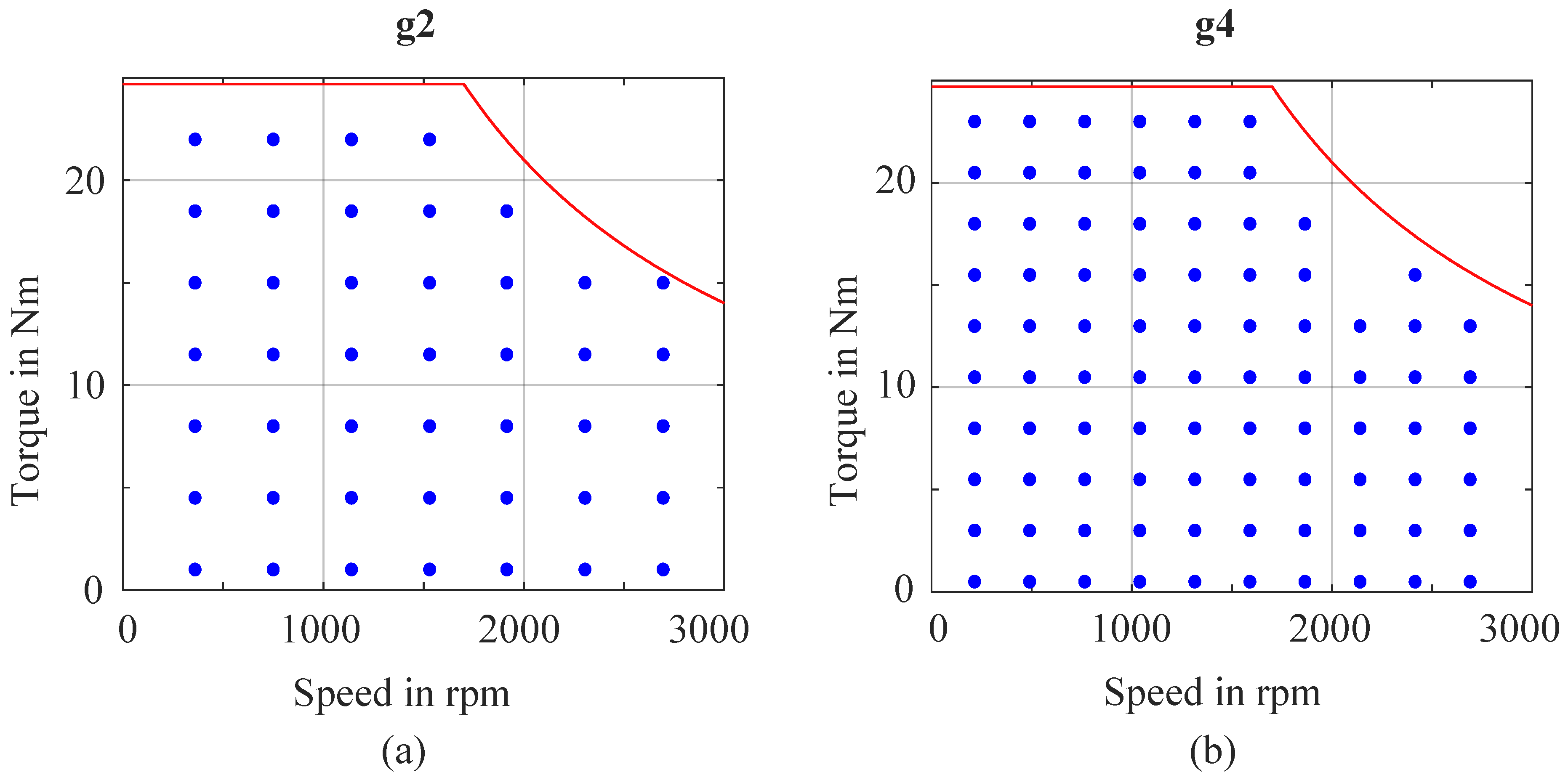
3.1. Steady-State Efficiency Map Analysis
3.2. Direct Time-Stepping Analysis
3.2.1. Analytic Model
3.2.2. Experimental Direct Method (Baseline Measurement)
4. Discussions of Results
4.1. Energy Conversion and Loss Analysis
4.1.1. Computation Method
4.1.2. Results and Discussion
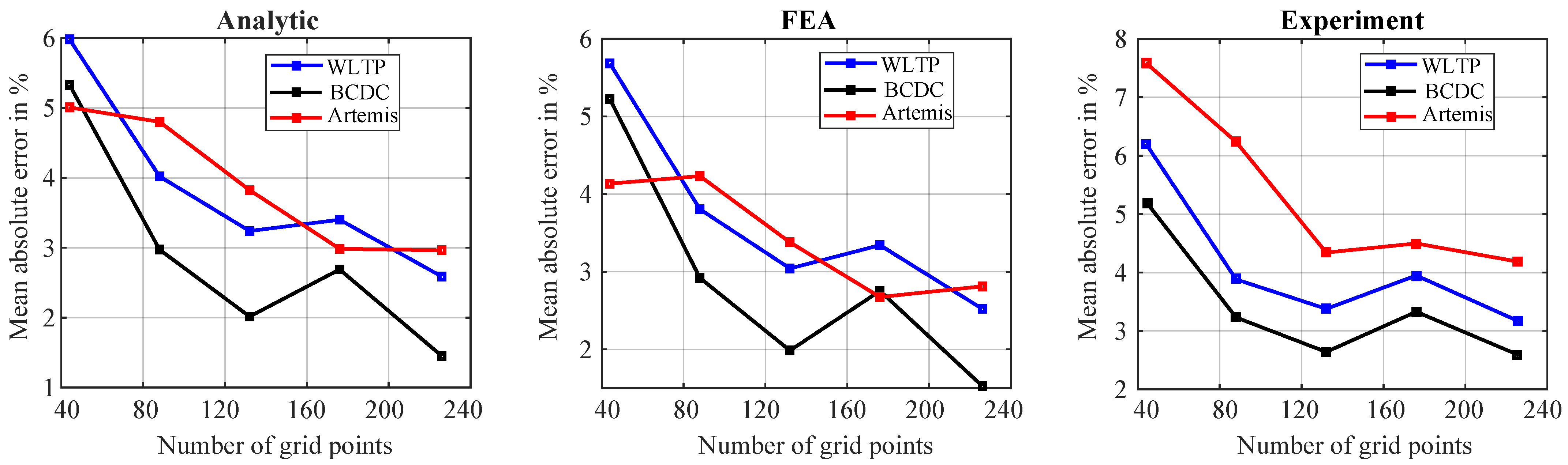
4.2. Error Analysis of Drive Cycle OP Efficiency
4.2.1. Evaluation Method
4.2.2. LUT-Based Method Analysis
4.2.3. Time-Stepping Analytic Method Analysis
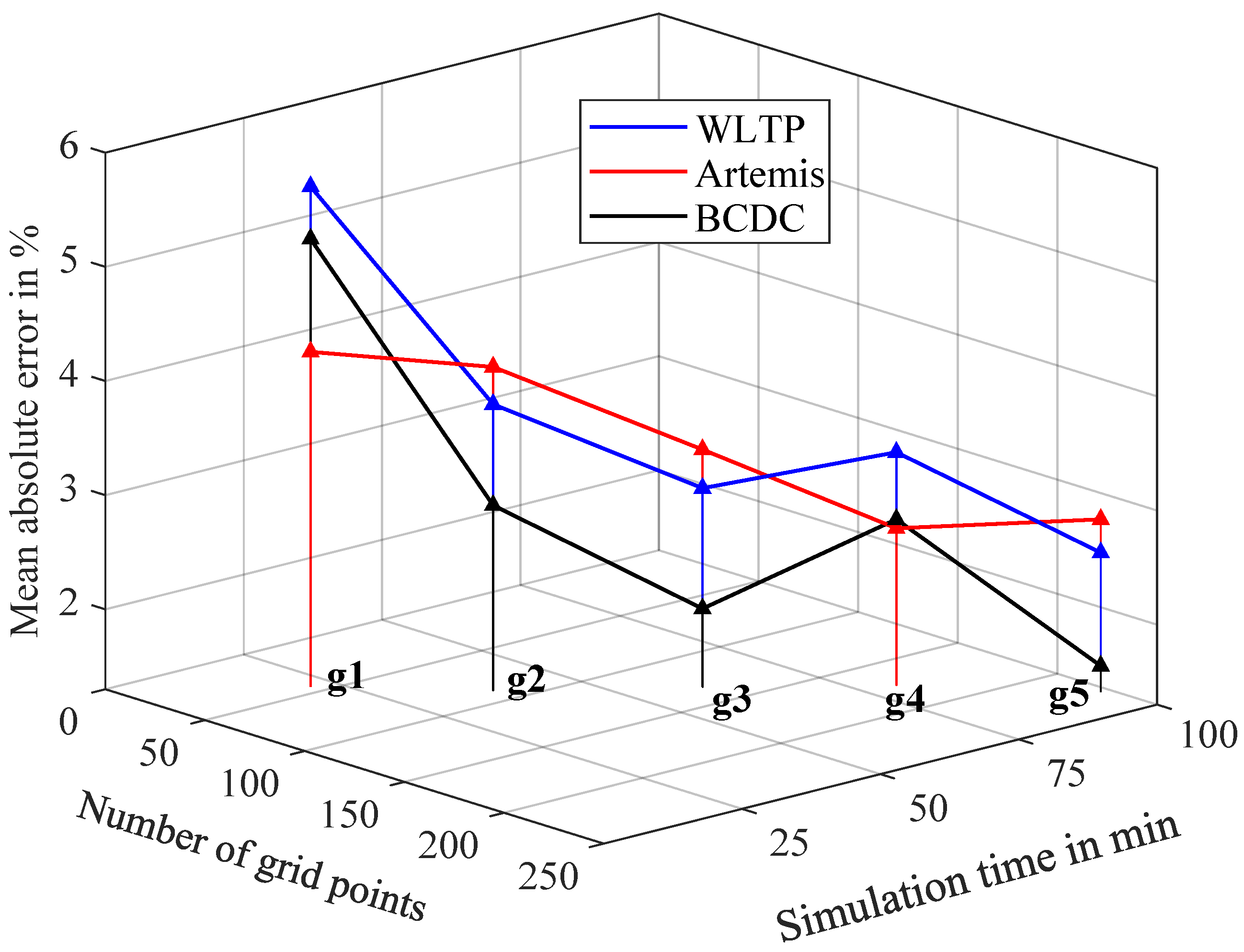
4.3. Effect of Grid Placement and Temperature on Efficiency Maps
4.3.1. Effect of Grid Placement on Efficiency Maps
4.3.2. Effect of Temperature on Efficiency Maps
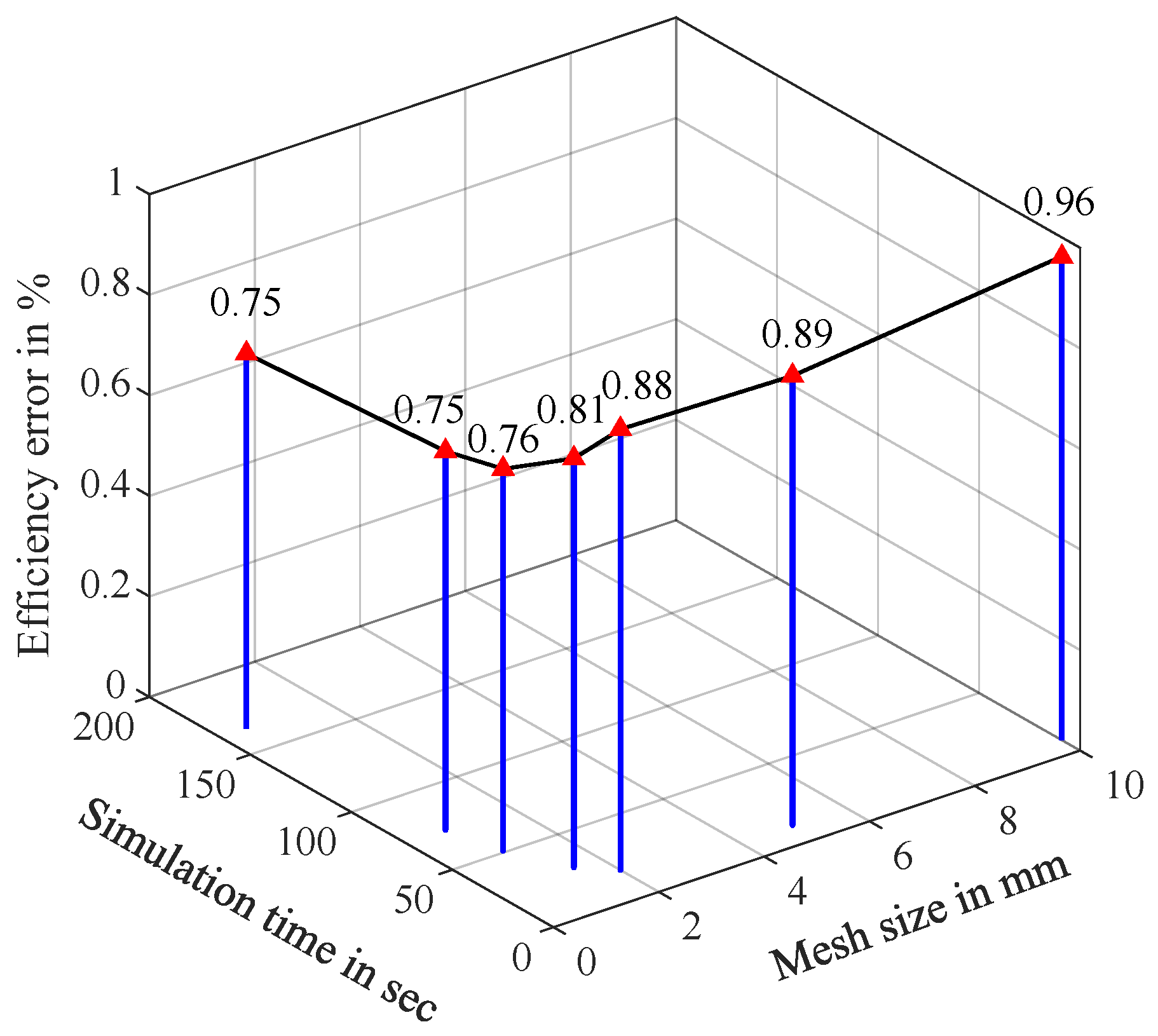
5. Analysis of Accuracy Factors and Computational Efficiency
5.1. Factors Influencing Performance Prediction Accuracy of the Methods
5.2. Computational Efficiency of Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Type of Measurement | Device | Accuracy |
|---|---|---|
| Data recorder | HBM Gen 3i [42] | 2 MS/s |
| Torque | HBM T10F 100 Nm [47] | |
| Temperature (stator sensors) | PT1000 thermocouples [48] | °C |
| Temperature (rotor sensors) | RS T Type thermocouples [49] | °C |
| IM rotor position | RI 76TD 2048ppr [50] | |
| Current | LEM IT 60-S [43] | 0.02725% |
| Voltage | HBM Gen 3i equipped with GEN Series GN610 [51] | 0.02% |
References
- Heidarikani, K.; Dhakal, P.K.; Seebacher, R.; Muetze, A. Quantification of Steady-State Efficiency Maps and Time-Stepping Solutions for Drive Cycle Performance Analysis of Induction Motors. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Guo, D.; Yang, F.; Zhang, Z.; Zhao, M. Drive-Cycle-Based Configuration Design and Energy Efficiency Analysis of Dual-Motor 4WD System with Two-Speed Transmission for Electric Vehicles. IEEE Trans. Transp. Electrif. 2024, 10, 1887–1899. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Y.; Ma, J.; Liu, G.; Li, D.; Qu, R. Fast Evaluation of Driving Cycle Efficiency of Interior Permanent Magnet Synchronous Machines for Electric Vehicles Considering Step-Skewing. IEEE Trans. Ind. Appl. 2024, 60, 4396–4407. [Google Scholar] [CrossRef]
- Mariasiu, F. Performance Analysis and Simulation of Electric Vehicles. Energies 2025, 18, 2365. [Google Scholar] [CrossRef]
- Huynh, T.A.; Chen, P.H.; Hsieh, M.F. Analysis and Comparison of Operational Characteristics of Electric Vehicle Traction Units Combining Two Different Types of Motors. IEEE Trans. Veh. Technol. 2022, 71, 5727–5742. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Baker, N.J. Design Optimization of Induction Motors with Different Stator Slot Rotor Bar Combinations Considering Drive Cycle. Energies 2024, 17, 154. [Google Scholar] [CrossRef]
- Praslicka, B.; Ma, C.; Taran, N. A Computationally Efficient High-Fidelity Multi-Physics Design Optimization of Traction Motors for Drive Cycle Loss Minimization. IEEE Trans. Ind. Appl. 2023, 59, 1351–1360. [Google Scholar] [CrossRef]
- Krishnamoorthy, S.; Panikkar, P.P.K. A comprehensive review of different electric motors for electric vehicles application. Int. J. Power Electron. Drive Syst. 2024, 15, 74. [Google Scholar] [CrossRef]
- Mavlonov, J.; Ruzimov, S.; Tonoli, A.; Amati, N.; Mukhitdinov, A. Sensitivity Analysis of Electric Energy Consumption in Battery Electric Vehicles with Different Electric Motors. World Electr. Veh. J. 2023, 14, 36. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, F.; Chen, F.; Wu, C.; Wang, Q.; He, Z.; Lu, S. Energy-efficient Train Control: A Comparative Study based on Permanent Magnet Synchronous Motor and Induction Motor. IEEE Trans. Veh. Technol. 2024, 73, 16148–16159. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.H.; Sul, S.K. FEA-Assisted Experimental Parameter Map Identification of Induction Motor for Wide-Range Field-Oriented Control. IEEE Trans. Power Electron. 2024, 39, 1353–1363. [Google Scholar] [CrossRef]
- Roshandel, E.; Mahmoudi, A.; Soong, W.L.; Kahourzade, S. Optimal Design of Induction Motors Over Driving Cycles for Electric Vehicles. IEEE Trans. Veh. Technol. 2023, 72, 15548–15562. [Google Scholar] [CrossRef]
- Roshandel, E.; Mahmoudi, A.; Kahourzade, S.; Soong, W.L. Efficiency Maps of Electrical Machines: A Tutorial Review. IEEE Trans. Ind. Appl. 2023, 59, 1263–1272. [Google Scholar] [CrossRef]
- Stiscia, O.; Rubino, S.; Vaschetto, S.; Cavagnino, A.; Tenconi, A. Accurate Induction Machines Efficiency Mapping Computed by Standard Test Parameters. IEEE Trans. Ind. Appl. 2022, 58, 3522–3532. [Google Scholar] [CrossRef]
- Lanzara, G. Electric Motor Test Bench for Efficiency Maps Generation. Master’s Thesis, Politecnico di Torino, Torino, Italy, 2021. [Google Scholar]
- Karkkainen, H.; Aarniovuori, L.; Niemela, M.; Pyrhonen, J. Converter-Fed Induction Motor Efficiency: Practical Applicability of IEC Methods. IEEE Ind. Electron. Mag. 2017, 11, 45–57. [Google Scholar] [CrossRef]
- Sano, H.; Semba, K.; Suzuki, Y.; Yamada, T. Investigation in the accuracy of FEA Based Efficiency Maps for PMSM traction machines. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 2061–2066. [Google Scholar] [CrossRef]
- Ragazzo, P.; Dilevrano, G.; Bojoi, A.; Ferrari, S.; Pellegrino, G. Fast Efficiency Mapping Procedure for PMSM Accounting for the PWM Supply Impact. In Proceedings of the 2024 IEEE International Conference on Industrial Technology (ICIT), Bristol, UK, 25–27 March 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Heidarikani, K.; Dhakal, P.K.; Seebacher, R.; Muetze, A. Baseline Determination for Drive Cycle Performance Analysis of Induction Motors. In Proceedings of the 2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chiang Mai, Thailand, 28 November–1 December 2023. [Google Scholar] [CrossRef]
- Dhakal, P.K.; Heidarikani, K.; Seebacher, R.; Muetze, A. Baseline Determination for Drive Cycle Performance Analysis of Permanent Magnet Synchronous Motors. In Proceedings of the 2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chiang Mai, Thailand, 28 November–1 December 2023. [Google Scholar] [CrossRef]
- Pastellides, S.; Gerber, S.; Wang, R.J.; Kamper, M. Evaluation of Drive Cycle-Based Traction Motor Design Strategies Using Gradient Optimisation. Energies 2022, 15, 1095. [Google Scholar] [CrossRef]
- Hwang, S.W.; Ryu, J.Y.; Chin, J.W.; Park, S.H.; Kim, D.K.; Lim, M.S. Coupled Electromagnetic-Thermal Analysis for Predicting Traction Motor Characteristics According to Electric Vehicle Driving Cycle. IEEE Trans. Veh. Technol. 2021, 70, 4262–4272. [Google Scholar] [CrossRef]
- Mısır, O.; Akar, M. Efficiency and Core Loss Map Estimation with Machine Learning Based Multivariate Polynomial Regression Model. Mathematics 2022, 10, 3691. [Google Scholar] [CrossRef]
- Oyamada, M.; Kunimatsu, S.; Mizumoto, I. Performance Prediction of Electric Motors via Deep Learning. IEEJ J. Ind. Appl. 2023, 12, 238–243. [Google Scholar] [CrossRef]
- Gong, Y.; Gneiting, A.; Weigel, S.; Parspour, N.; An, Z. Surrogate Model Based Drive Cycle Modelling and Optimization of Synchronous Reluctance Machines for Electric Vehicles. IEEE Trans. Magn. 2025, 61, 8101906. [Google Scholar] [CrossRef]
- Carbonieri, M.; Leonardo, L.D.; Bianchi, N.; Tursini, M.; Villani, M.A.; Popescu, M. Cage Losses in Induction Motors Considering Harmonics: A New Finite Element Procedure and Comparison with the Time-Domain Approach. IEEE Trans. Ind. Appl. 2022, 58, 1931–1940. [Google Scholar] [CrossRef]
- Dhakal, P.K.; Heidarikani, K.; Seebacher, R.; Muetze, A. Efficiency Map Versus Time-Stepping Solutions for Drive Cycle Performance Analysis of Permanent Magnet Synchronous Motors. In Proceedings of the 2024 27th International Conference on Electrical Machines and Systems (ICEMS), Fukuoka, Japan, 26–29 November 2024. [Google Scholar] [CrossRef]
- Fan, D.; Zhu, X.; Quan, L.; Han, P.; Xiang, Z.; Wu, J. Driving Cycle Design Optimization of Less-Rare-Earth PM Motor Using Dimension Reduction Method. IEEE Trans. Energy Convers. 2023, 38, 1614–1625. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Nerg, J.; Pyrhönen, J.; Ruotsalainen, S.; Kennel, R. Drive Cycle Analysis of a Permanent-Magnet Traction Motor Based on Magnetostatic Finite-Element Analysis. IEEE Trans. Veh. Technol. 2015, 64, 1249–1254. [Google Scholar] [CrossRef]
- Malarselvam, V.; Carunaiselvane, C. Energy Efficient Analysis of Electric Vehicle Motor Under Drive Cycle Influence. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 17–20 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lacock, S.; du Plessis, A.A.; Booysen, M.J. Electric Vehicle Drivetrain Efficiency and the Multi-Speed Transmission Question. World Electr. Veh. J. 2023, 14, 342. [Google Scholar] [CrossRef]
- Bhaktha, B.S.; Jose, N.; Vamshik, M.; Pitchaimani, J.; Gangadharan, K.V. Driving Cycle-Based Design Optimization and Experimental Verification of a Switched Reluctance Motor for an E-Rickshaw. IEEE Trans. Transp. Electrif. 2024, 10, 9959–9974. [Google Scholar] [CrossRef]
- Islam, M.S.; Safayet, A.; Islam, M. A Fast Computation Method to Calculate Performances of an Electric Propulsion System for Drive Cycles. In Proceedings of the 2024 IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 20–24 October 2024; pp. 2308–2314. [Google Scholar] [CrossRef]
- Dhakal, P.K.; Heidarikani, K.; Muetze, A. Down-scaling of drive cycles for experimental drive cycle analyses. In Proceedings of the 12th International Conference on Power Electronics, Machines and Drives (PEMD 2023), Brussels, Belgium, 23–24 October 2023; Volume 2023, pp. 271–276. [Google Scholar] [CrossRef]
- DieselNet. Emission Test Cycles. Available online: https://dieselnet.com/standards/cycles/index.php (accessed on 18 August 2025).
- BMW Group. Technical Data BMW i3 (120Ah). Available online: https://www.press.bmwgroup.com/global/article/detail/T0148284EN/the-bmw-i3?language=en (accessed on 1 September 2025).
- Smart. Smart EQ Fortwo Coupe. Available online: https://ev-database.org/car/1230/Smart-EQ-fortwo-coupe (accessed on 1 September 2025).
- Heidarikani, K.; Dhakal, P.K.; Muetze, A.; Seebacher, R. CREATOR Case: Induction Motor Data; Graz University of Technology: Graz, Austria, 2024; Version Number: 1. [Google Scholar] [CrossRef]
- MathWorks. MATLAB. Available online: https://www.Mathworks.com/products/matlab.html (accessed on 10 September 2025).
- JSOL. Simulation Technology for Electromechanical Design: JMAG. Available online: https://www.jmag-international.com/ (accessed on 16 September 2025).
- dSPACE. User Documentation, MicroLabBox. Available online: https://www.dspace.com/en/pub/home/support/documentation.cfm?helpsetid=MicroLabBox&externalid=Container_3161d161-cef9-4fa6-8fa4-4f3fbcfd0c77_–_&Language=en-us&Release=RLS2025-A (accessed on 19 September 2025).
- HBK. “eDrive Power Analyzer, 6CH, 2MS/s, GEN3iA”. Available online: https://www.hbkworld.com/en/products/instruments/power-analyser/edrive/1-edrv-6p-3i (accessed on 17 September 2025).
- LEM. IT 60-S ULTRASTAB High Accurate Current Transducer. 2025. Available online: https://www.lem.com/en/product-list/it-60s-ultrastab (accessed on 17 September 2025).
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- OpenAI. ChatGPT-4o. Available online: https://openai.com/chatgpt (accessed on 17 September 2025).
- HBK. T10F: Tried and Tested Torque Flange for Many Application. 2020. Available online: https://www.hbm.com/en/2379/t10f-torque-meter-with-an-extremely-short-design/ (accessed on 17 September 2025).
- Heinz Meßwiderstände GmbH. PT1000 Temperature Sensors| H. Heinz Meßwiderstaende GmbH. Available online: https://heinz-messwiderstaende.de/en/products/ (accessed on 18 September 2025).
- RS Components. RS PRO Type T Exposed Junction Thermocouple. 2025. Available online: https://at.rs-online.com/web/p/thermoelemente/8479681 (accessed on 17 September 2025).
- Hengstler. ICURO RI76TD/1024AD.4O32RF Incremental Encoders. 2025. Available online: https://de.hengstler.com/produkte/drehgeber/inkrementaldrehgeber/ri76/ri76td1024ad4o32rf (accessed on 18 September 2025).
- HBK. GEN Series GN610 Isolated 1 kV 2 MS/s Input Card. 2025. Available online: https://www.hbm.com/5892/genesis-highspeed-high-voltage-card-gn610b-gn611b/?product_type_no=Card%20for%20High%20Voltage%20ISO:%201000V (accessed on 17 September 2025).

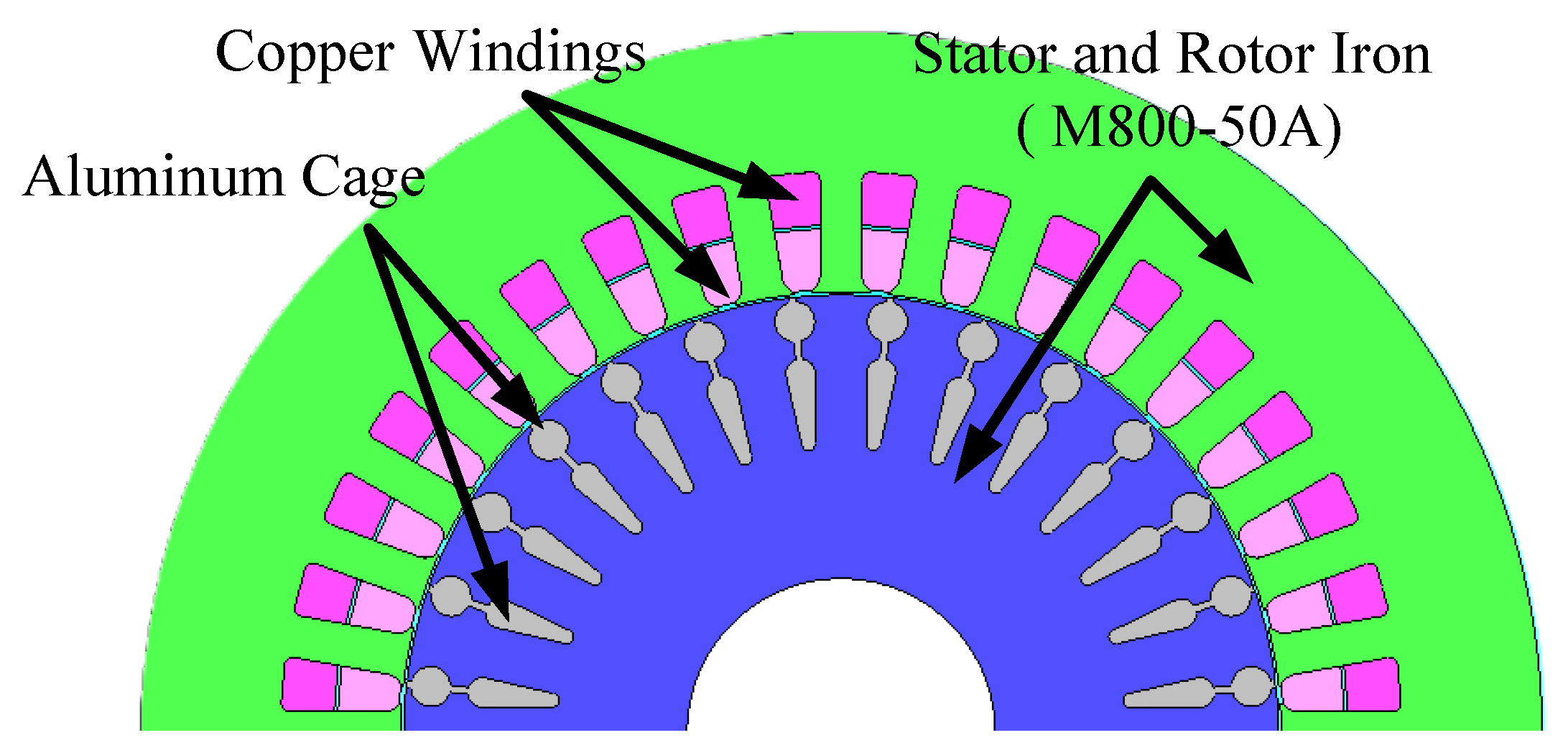
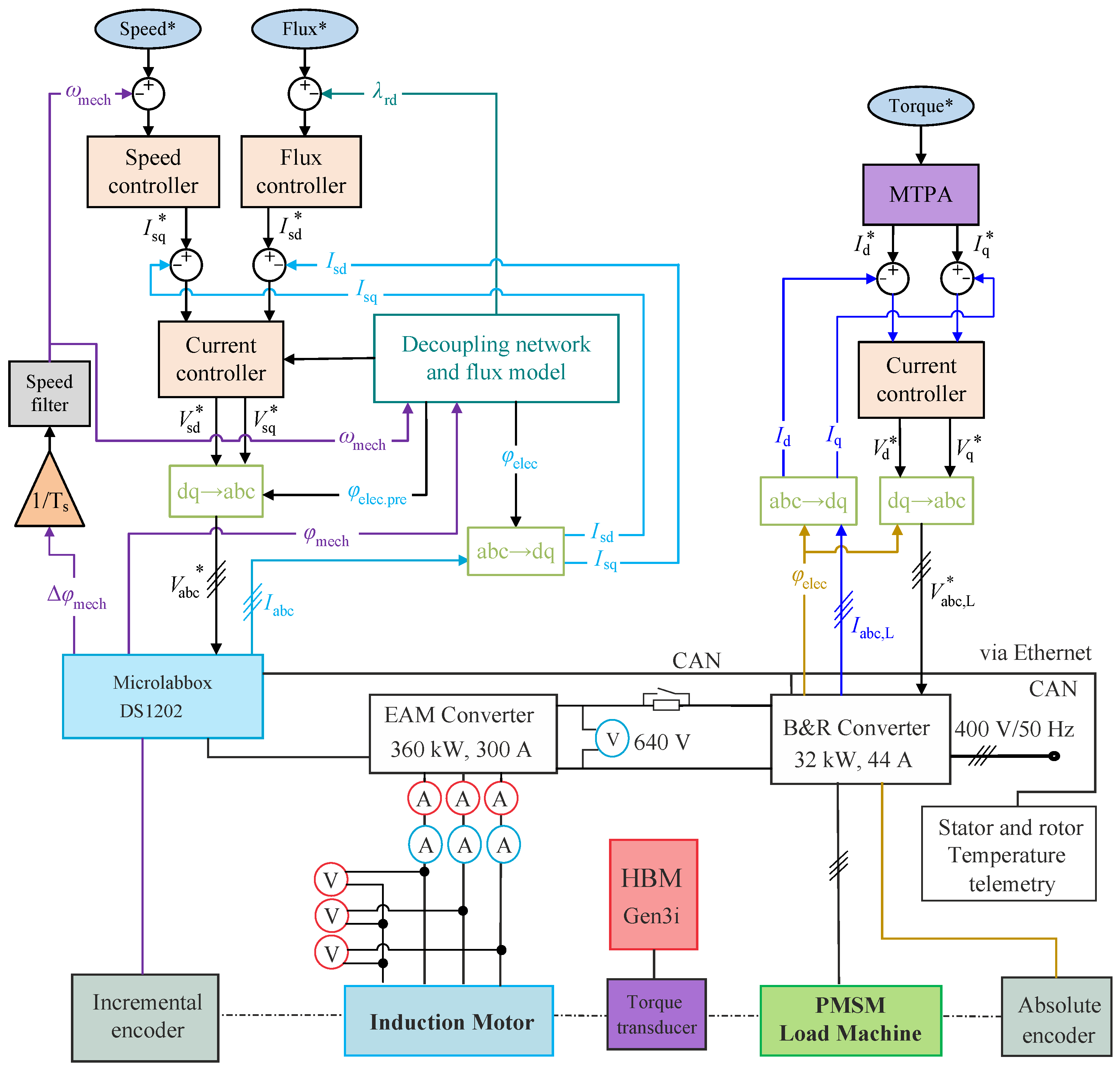

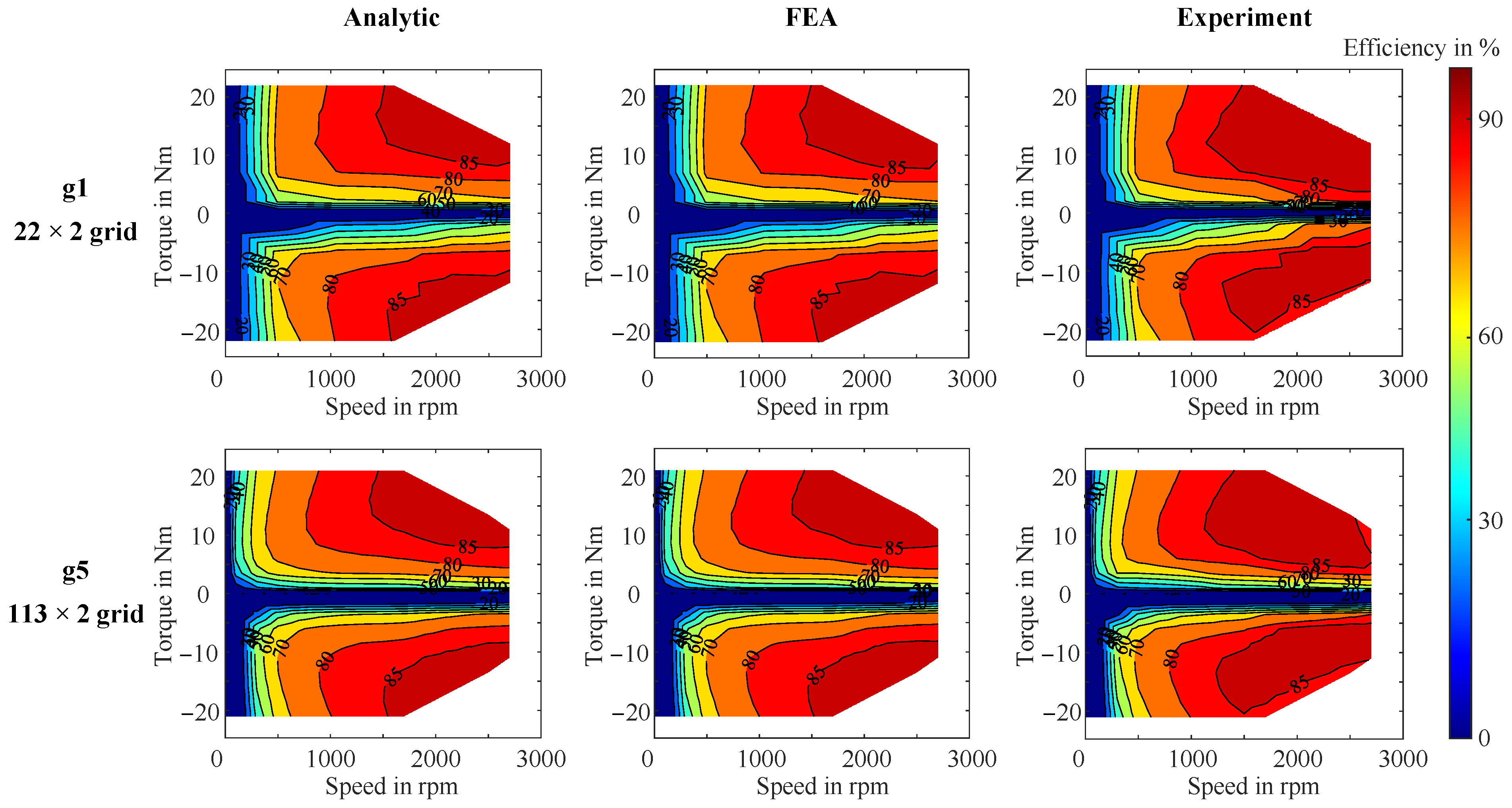
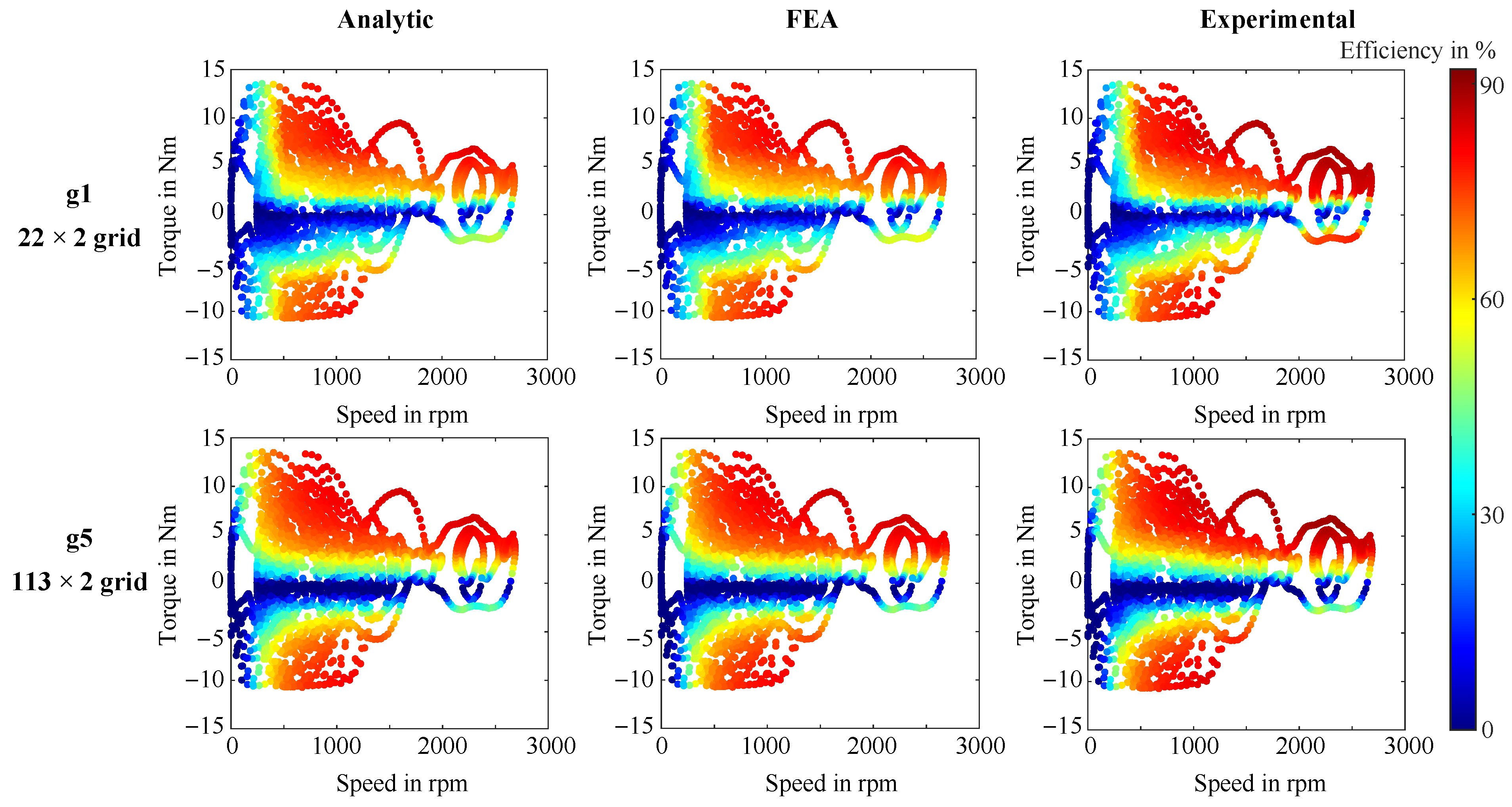
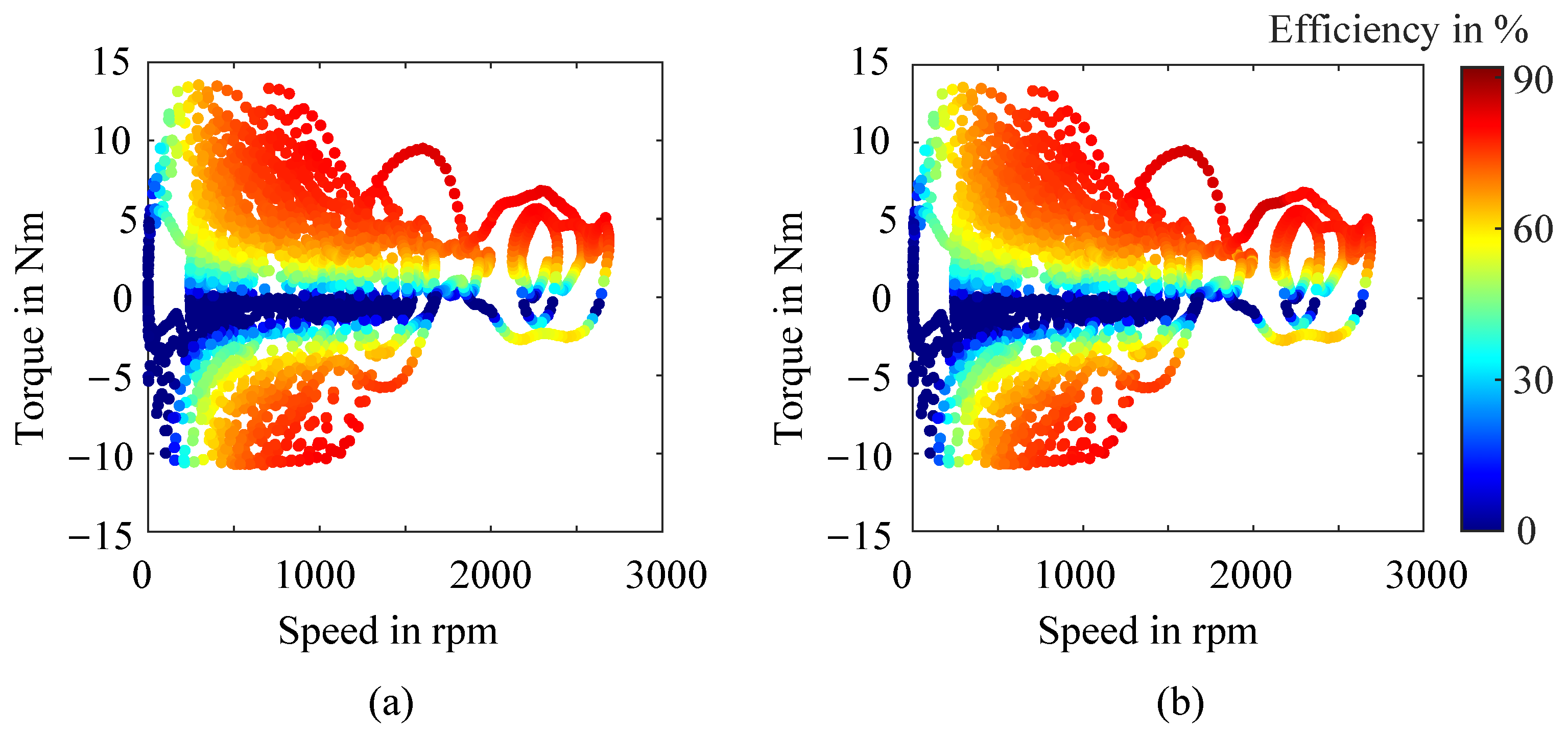
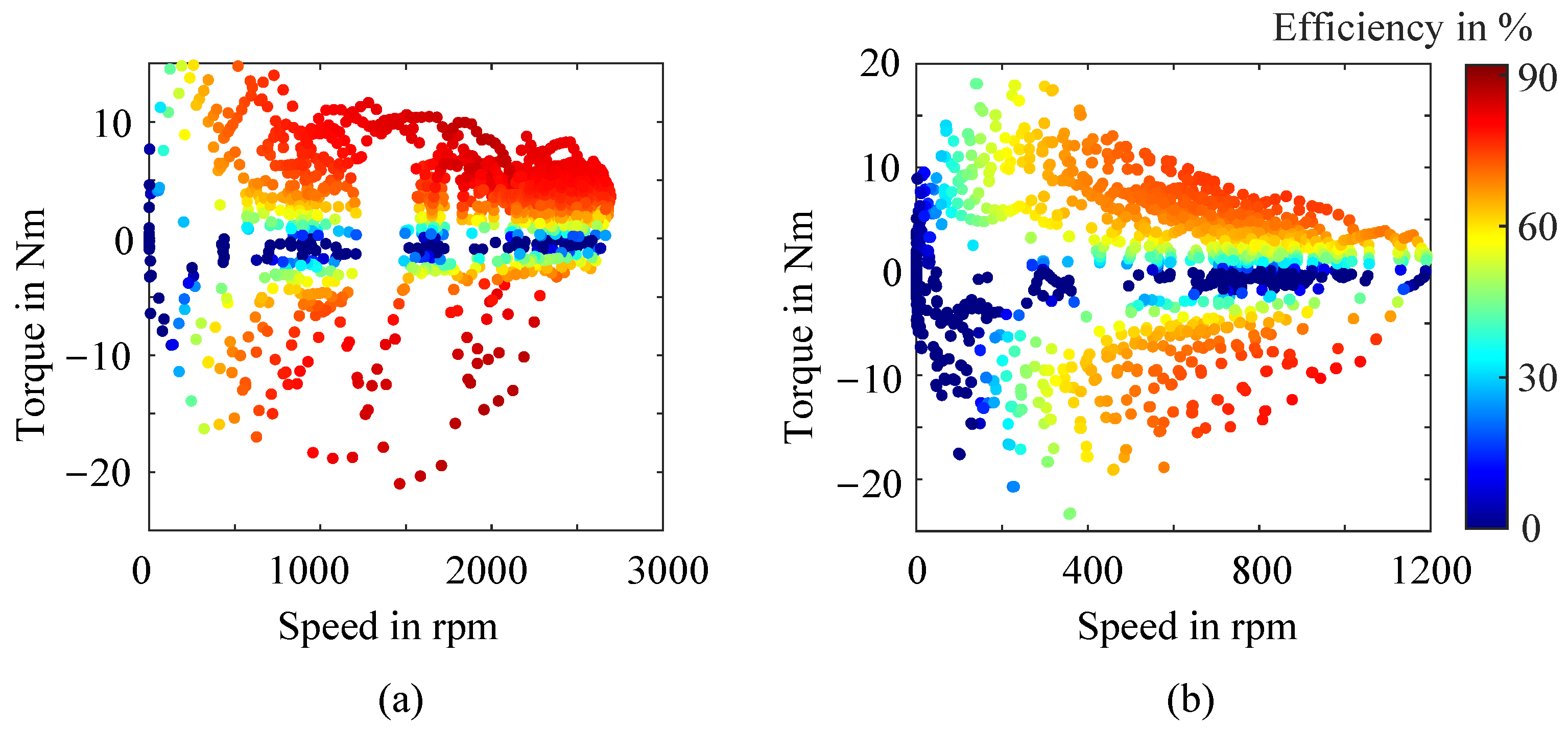
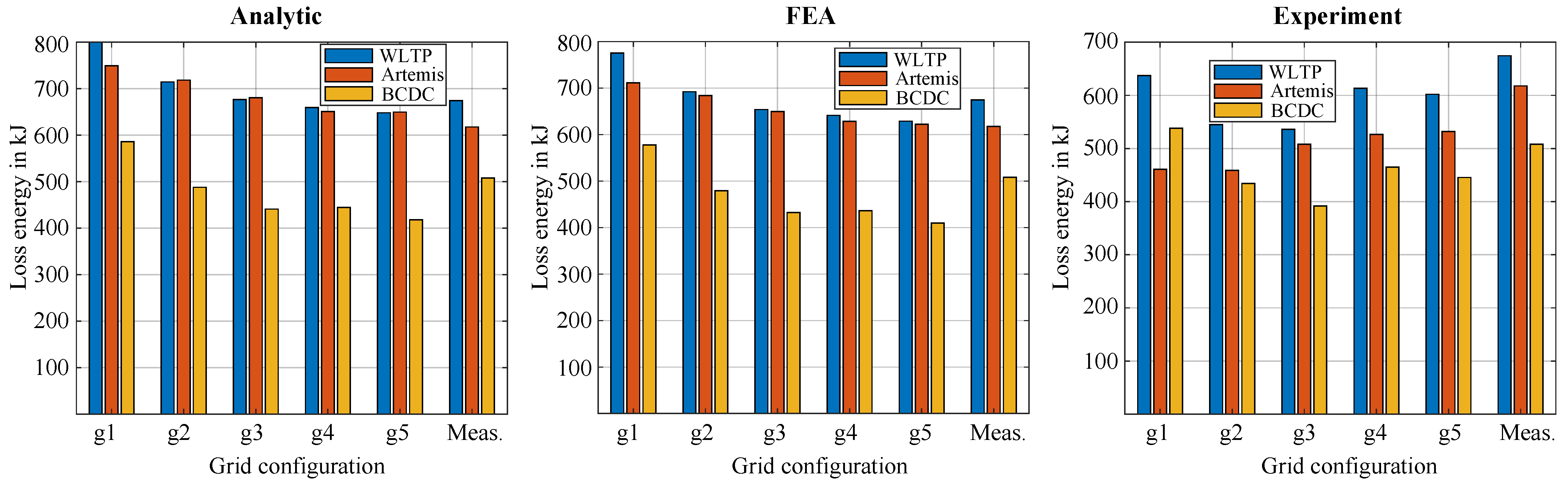
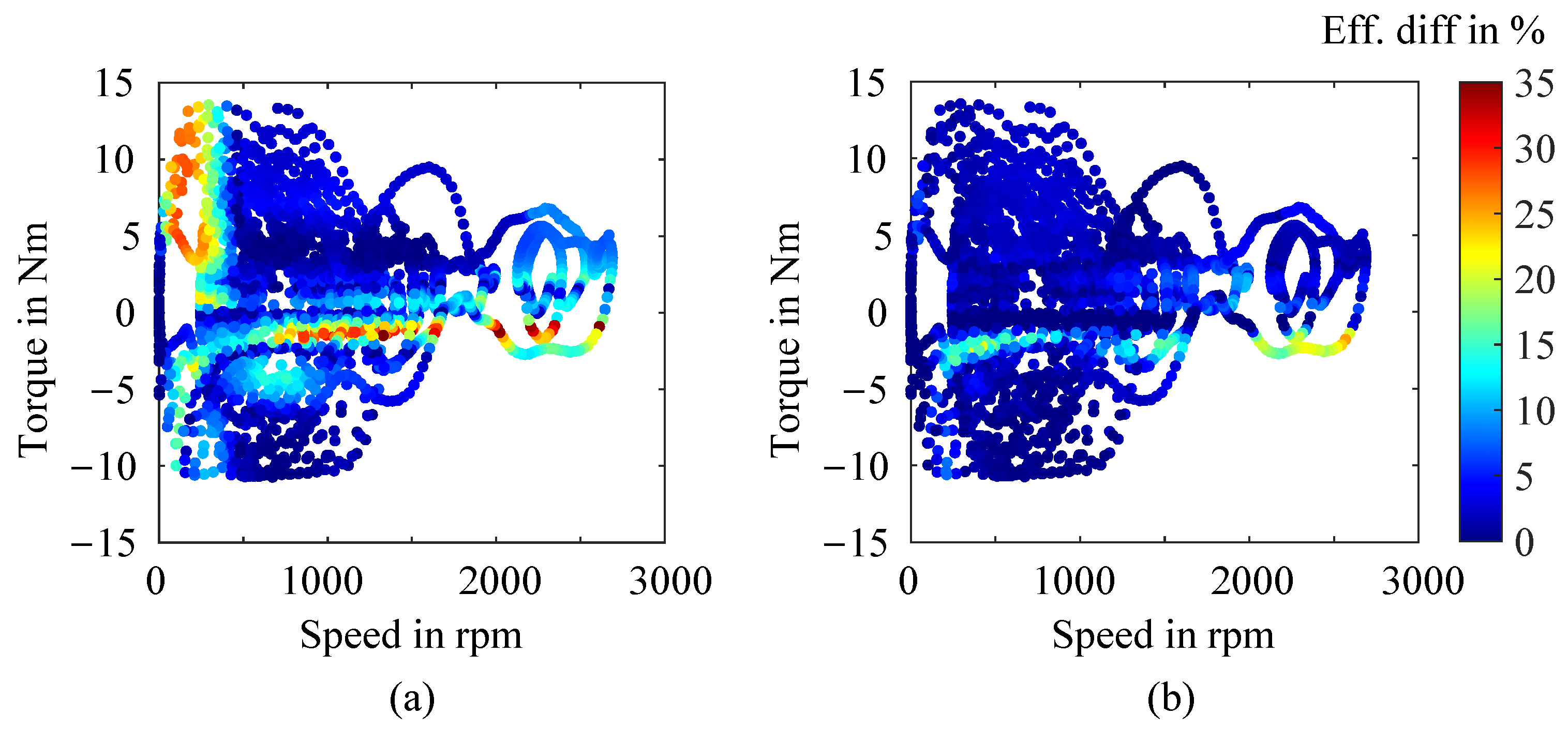
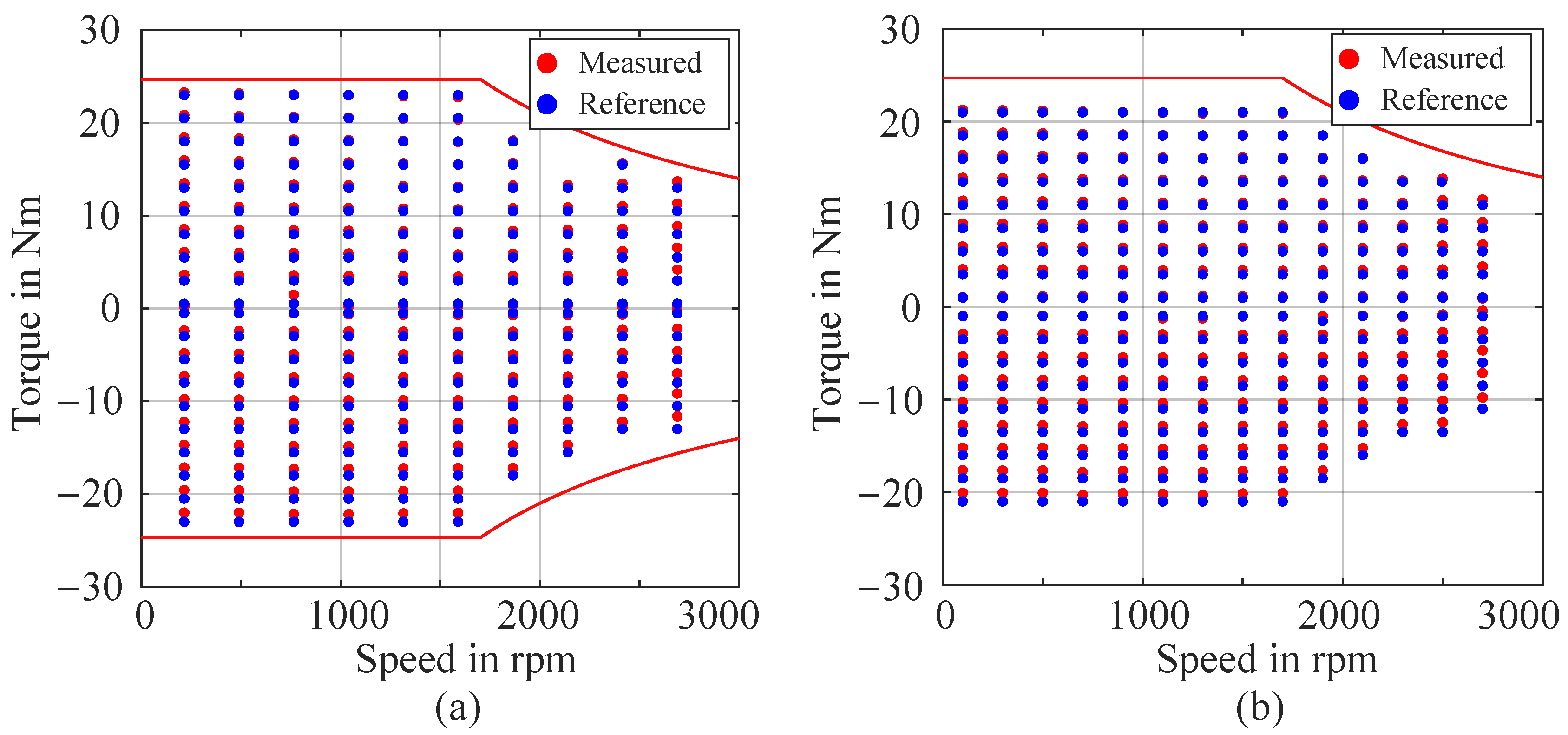
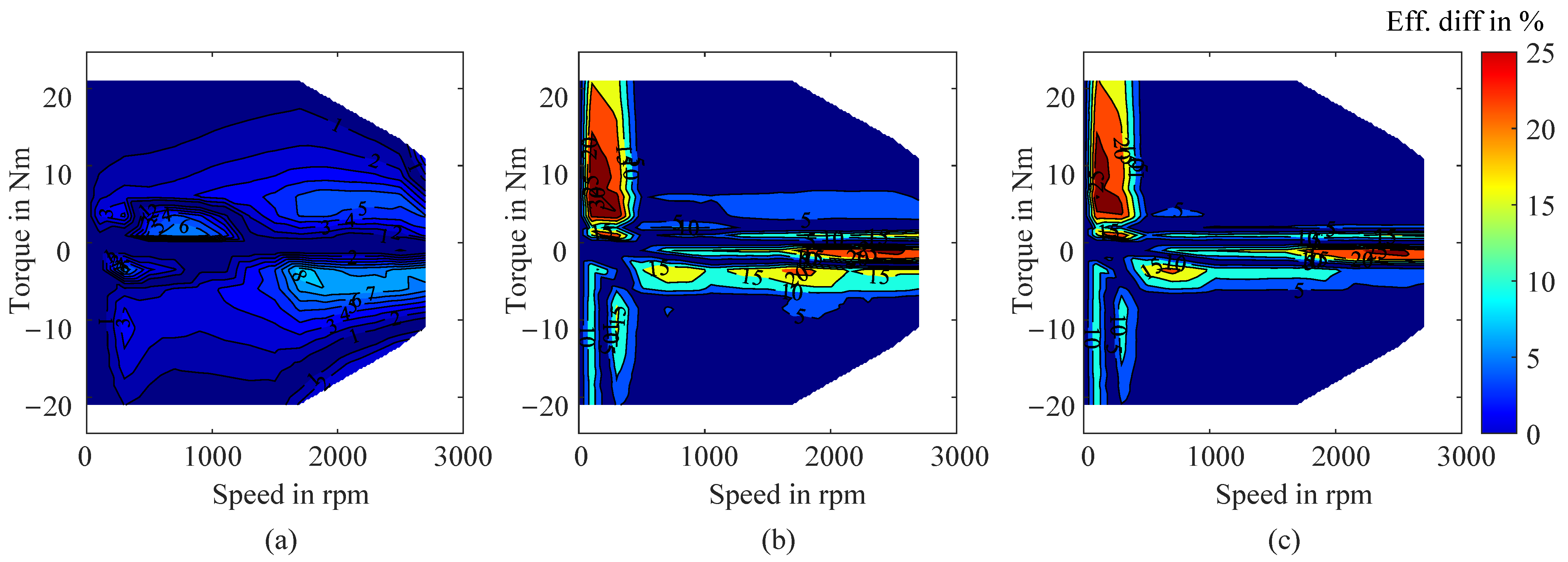

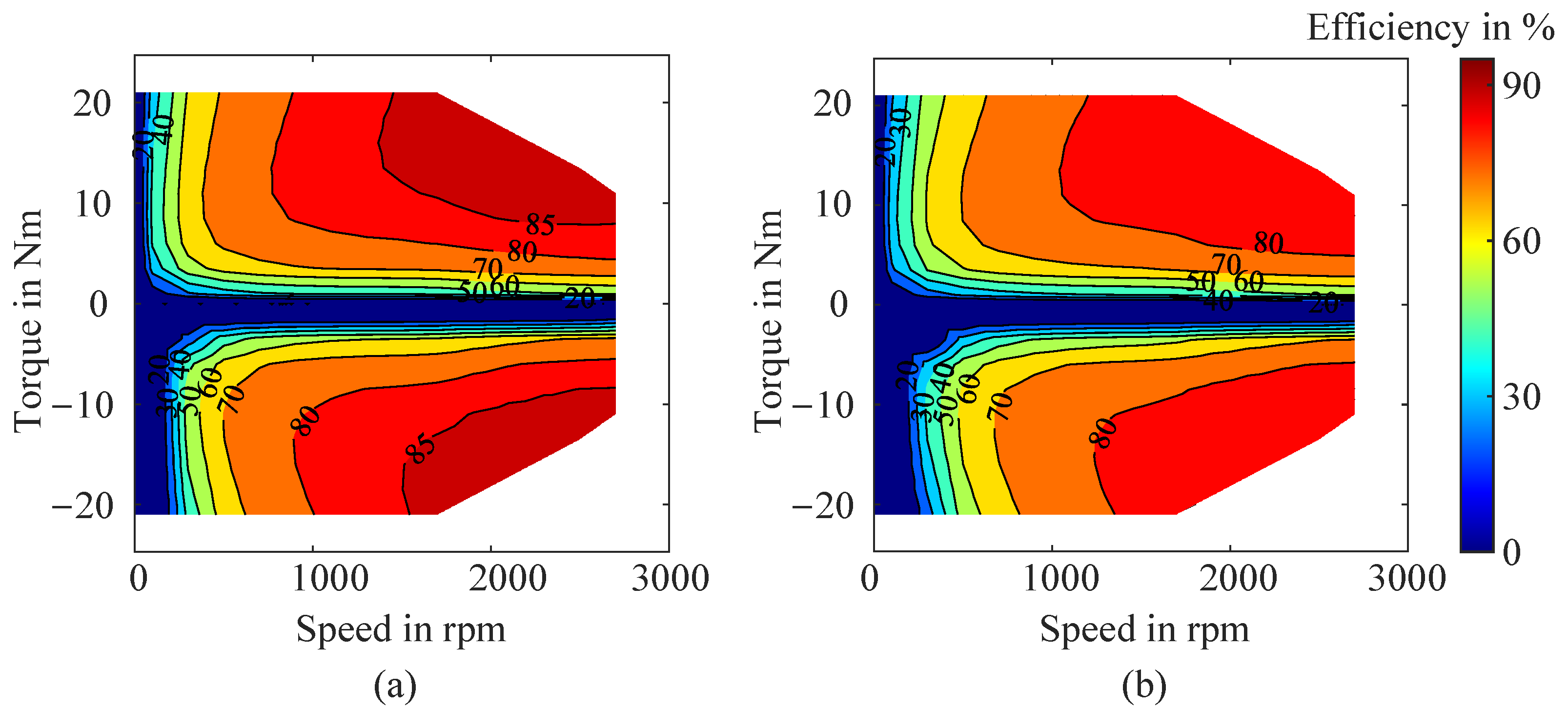
| Parameter | BMW i3 Drive Cycles | Smart EQ Drive Cycles | ||||
|---|---|---|---|---|---|---|
| WLTP | Artemis | BCDC | WLTP | Artemis | BCDC | |
| Energy efficiency | 52.54% | 70.61% | 28.40% | 58.25% | 73.64% | 37.80% |
| Total input energy | 1421 kJ | 2101.4 kJ | 709.3 kJ | 1339.3 kJ | 2093.3 kJ | 806.3 kJ |
| Total output energy | 746.3 kJ | 1482 kJ | 201.6 kJ | 780.3 kJ | 1541.6 kJ | 304.8 kJ |
| Method | Grid | BMW i3 Drive Cycles | Smart EQ Drive Cycles | ||||
|---|---|---|---|---|---|---|---|
| WLTP | Artemis | BCDC | WLTP | Artemis | BCDC | ||
| Analytic | g1 | 48.28% | 66.44% | 25.57% | 53.94% | 70.51% | 34.65% |
| g2 | 51.09% | 67.37% | 29.22% | 56.70% | 72.28% | 37.34% | |
| g3 | 52.45% | 68.55% | 31.35% | 57.93% | 73.16% | 38.83% | |
| g4 | 53.08% | 68.51% | 31.18% | 58.13% | 73.84% | 38.58% | |
| g5 | 53.53% | 69.55% | 32.52% | 58.93% | 73.82% | 39.84% | |
| FEA | g1 | 49.06% | 67.60% | 25.87% | 54.71% | 71.54% | 35.18% |
| g2 | 51.89% | 68.46% | 29.59% | 57.49% | 73.19% | 37.93% | |
| g3 | 53.31% | 69.55% | 31.79% | 58.76% | 73.99% | 39.51% | |
| g4 | 53.79% | 70.26% | 31.60% | 58.81% | 74.47% | 39.18% | |
| g5 | 54.28% | 70.46% | 32.95% | 59.65% | 74.59% | 40.44% | |
| Experiment | g1 | 53.95% | 76.31% | 27.24% | 59.69% | 79.51% | 38.19% |
| g2 | 57.81% | 76.38% | 31.70% | 63.41% | 80.09% | 42.35% | |
| g3 | 58.20% | 74.50% | 33.97% | 63.61% | 78.05% | 43.75% | |
| g4 | 54.90% | 73.82% | 30.23% | 60.15% | 78.38% | 39.86% | |
| g5 | 55.36% | 73.61% | 31.14% | 60.96% | 78.07% | 41.18% | |
| Parameter | BMW i3 | Smart EQ | ||||
|---|---|---|---|---|---|---|
| WLTP | Artemis | BCDC | WLTP | Artemis | BCDC | |
| Energy efficiency | 52.69% | 69.31% | 29.30% | 57.53% | 73.01% | 37.37% |
| MAE | 1.04% | 1.69% | 0.97% | 1.09% | 1.39% | 0.90% |
| Method | Grid | BMW i3 Drive Cycles | Smart EQ Drive Cycles | ||||
|---|---|---|---|---|---|---|---|
| WLTP | Artemis | BCDCs | WLTP | Artemis | BCDC | ||
| Analytic | g1 | 5.98% | 5.01% | 5.33% | 6.22% | 4.63% | 5.52% |
| g2 | 4.02% | 4.80% | 2.97% | 4.23% | 3.88% | 3.95% | |
| g3 | 3.24% | 3.82% | 2.02% | 3.45% | 3.13% | 3.01% | |
| g4 | 3.40% | 2.99% | 2.69% | 3.69% | 2.59% | 3.42% | |
| g5 | 2.59% | 2.96% | 1.45% | 2.74% | 2.54% | 2.43% | |
| FEA | g1 | 5.68% | 4.13% | 5.22% | 5.89% | 3.90% | 5.27% |
| g2 | 3.81% | 4.23% | 2.92% | 3.99% | 3.63% | 3.78% | |
| g3 | 3.04% | 3.38% | 1.99% | 3.21% | 2.98% | 2.84% | |
| g4 | 3.34% | 2.67% | 2.75% | 3.57% | 2.59% | 3.34% | |
| g5 | 2.52% | 2.81% | 1.53% | 2.61% | 2.60% | 2.33% | |
| Experiment | g1 | 6.20% | 7.59% | 5.21% | 5.96% | 7.25% | 4.94% |
| g2 | 3.88% | 6.24% | 3.23% | 3.63% | 6.31% | 3.27% | |
| g3 | 3.38% | 4.34% | 2.64% | 3.13% | 4.47% | 2.70% | |
| g4 | 3.95% | 4.50% | 3.33% | 4.19% | 5.03% | 3.71% | |
| g5 | 3.17% | 4.18% | 2.59% | 3.33% | 4.69% | 2.47% | |
| Factors | LUT-Based | Time-Stepping |
|---|---|---|
| Interpolation errors | ●●●●● | ○○○○○ |
| Reference vs. measured OPs in experimental LUT method | ●●●○○ | ○○○○○ |
| Friction and mechanical loss modeling | ●●●●○ | ●●●○○ |
| Thermal effects and mismatch | ●○○○○ | ●○○○○ |
| Inaccurate iron loss modeling | ●●●○○ | ●●●○○ |
| Control strategy differences | ●○○○○ | ●○○○○ |
| Mesh quality in FEA | ●○○○○ | ○○○○○ |
| Method | Grid | No. of Points | Simulation Time |
|---|---|---|---|
| Direct Analytic | – | 3600 (WLTP) | 8 min |
| – | 2136 (Artemis) | 4 min | |
| – | 3480 (BCDC) | 7 min | |
| LUT-based Analytic | g1 | 22 × 2 | 7 s |
| g2 | 44 × 2 | 15 s | |
| g3 | 66 × 2 | 22 s | |
| g4 | 88 × 2 | 30 s | |
| g5 | 113 × 2 | 38 s | |
| LUT-based FEA | g1 | 22 × 2 | 21 min |
| g2 | 44 × 2 | 38 min | |
| g3 | 66 × 2 | 60 min | |
| g4 | 88 × 2 | 76 min | |
| g5 | 113 × 2 | 98 min | |
| LUT-based Experiment | g1 | 22 × 2 | 22.5 min |
| g2 | 44 × 2 | 44.5 min | |
| g3 | 66 × 2 | 66.5 min | |
| g4 | 88 × 2 | 88.5 min | |
| g5 | 113 × 2 | 113.5 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heidarikani, K.; Dhakal, P.K.; Seebacher, R.; Muetze, A. Comparative Study of Steady-State Efficiency Maps and Time-Stepping Methods for Induction Motor Drive Cycle Performance Analysis. Energies 2025, 18, 5928. https://doi.org/10.3390/en18225928
Heidarikani K, Dhakal PK, Seebacher R, Muetze A. Comparative Study of Steady-State Efficiency Maps and Time-Stepping Methods for Induction Motor Drive Cycle Performance Analysis. Energies. 2025; 18(22):5928. https://doi.org/10.3390/en18225928
Chicago/Turabian StyleHeidarikani, Kourosh, Pawan Kumar Dhakal, Roland Seebacher, and Annette Muetze. 2025. "Comparative Study of Steady-State Efficiency Maps and Time-Stepping Methods for Induction Motor Drive Cycle Performance Analysis" Energies 18, no. 22: 5928. https://doi.org/10.3390/en18225928
APA StyleHeidarikani, K., Dhakal, P. K., Seebacher, R., & Muetze, A. (2025). Comparative Study of Steady-State Efficiency Maps and Time-Stepping Methods for Induction Motor Drive Cycle Performance Analysis. Energies, 18(22), 5928. https://doi.org/10.3390/en18225928








