Parameter Optimization for Dual-Mode Operation of Unitized Regenerative Fuel Cells via Steady-State Simulation
Abstract
1. Introduction
2. Numerical Method
2.1. Geometric Configuration
2.2. Assumptions
- (1)
- The flow within the URFC is laminar, and the effect of gravity is neglected;
- (2)
- Evaporation of water and transfer of concentrated substances at the anode side are neglected;
- (3)
- All gases are considered as ideal gases and are incompressible;
- (4)
- PEM is fully hydrated;
- (5)
- The only manner in which water is transported across the membrane is considered to be electro-osmotic resistance. The effects of diffusion and pressure are ignored;
- (6)
- PEM is non-permeable to substances;
- (7)
- Thermal contact resistance between layers is ignored;
- (8)
- All operations are considered as steady state.
2.3. Governing Equations
2.4. Boundary Conditions
3. Experimental Validation
3.1. Test Rig Design
3.2. Parametric Study
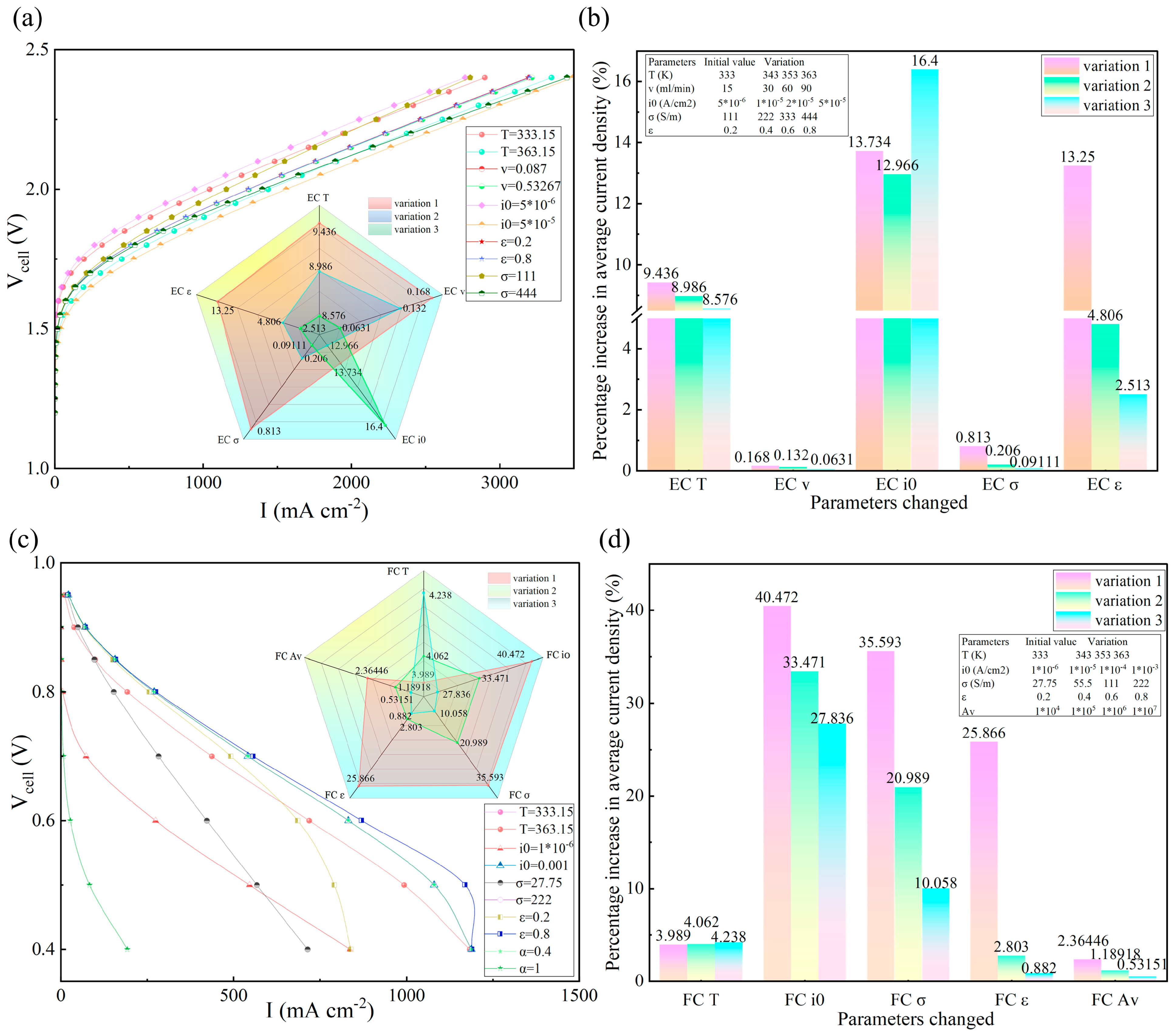
3.2.1. Sensitivity of Flow Rates
3.2.2. Differentiation of Dual Modes of Temperature Regulation
FC Mode
EC Mode
3.2.3. The Central Role of Exchange Current Density
FC Mode
EC Mode
3.2.4. Positive Gain Characteristics of Membrane Conductivity Tending to Decay
3.2.5. Differential Response of Porosity Regulation for GDL on Both Sides
FC Mode
EC Mode
3.2.6. Marginal Effect of Active Specific Surface Area
3.2.7. Summary
FC Mode
EC Mode
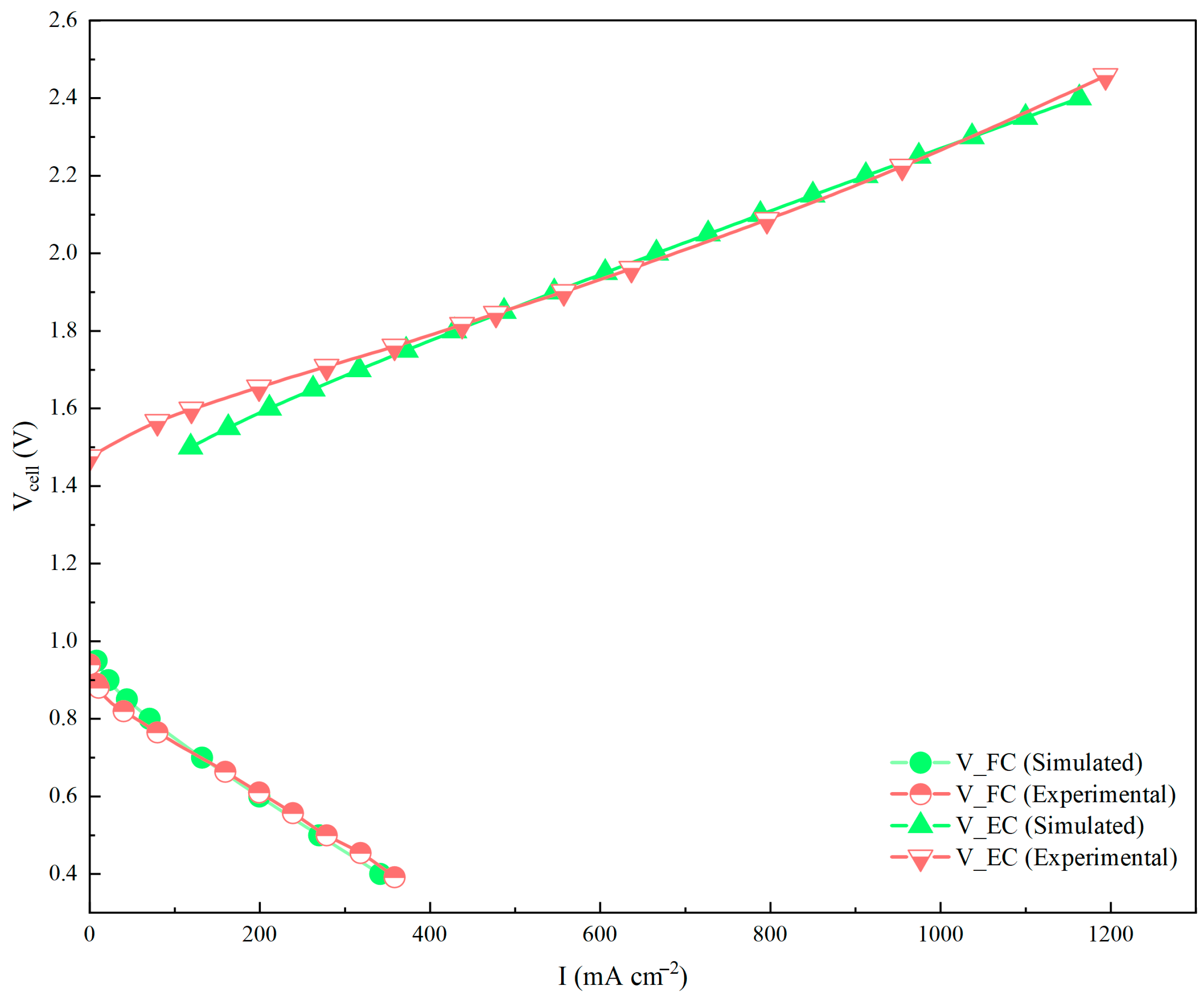
3.3. Experimental Verification
4. Results and Discussions
4.1. Numerical Results
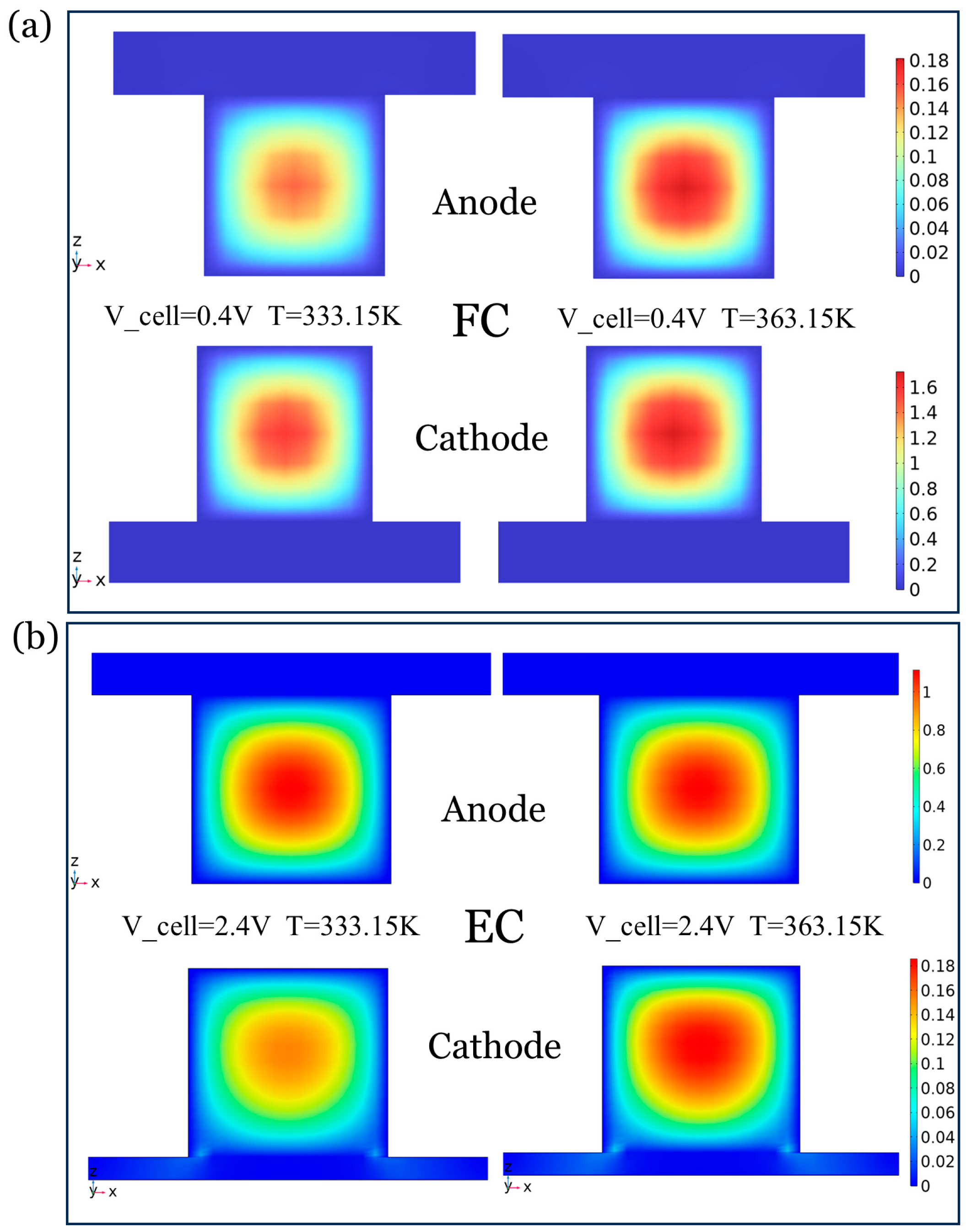
4.1.1. Heat–Mass Transfer Analysis at Different Temperatures
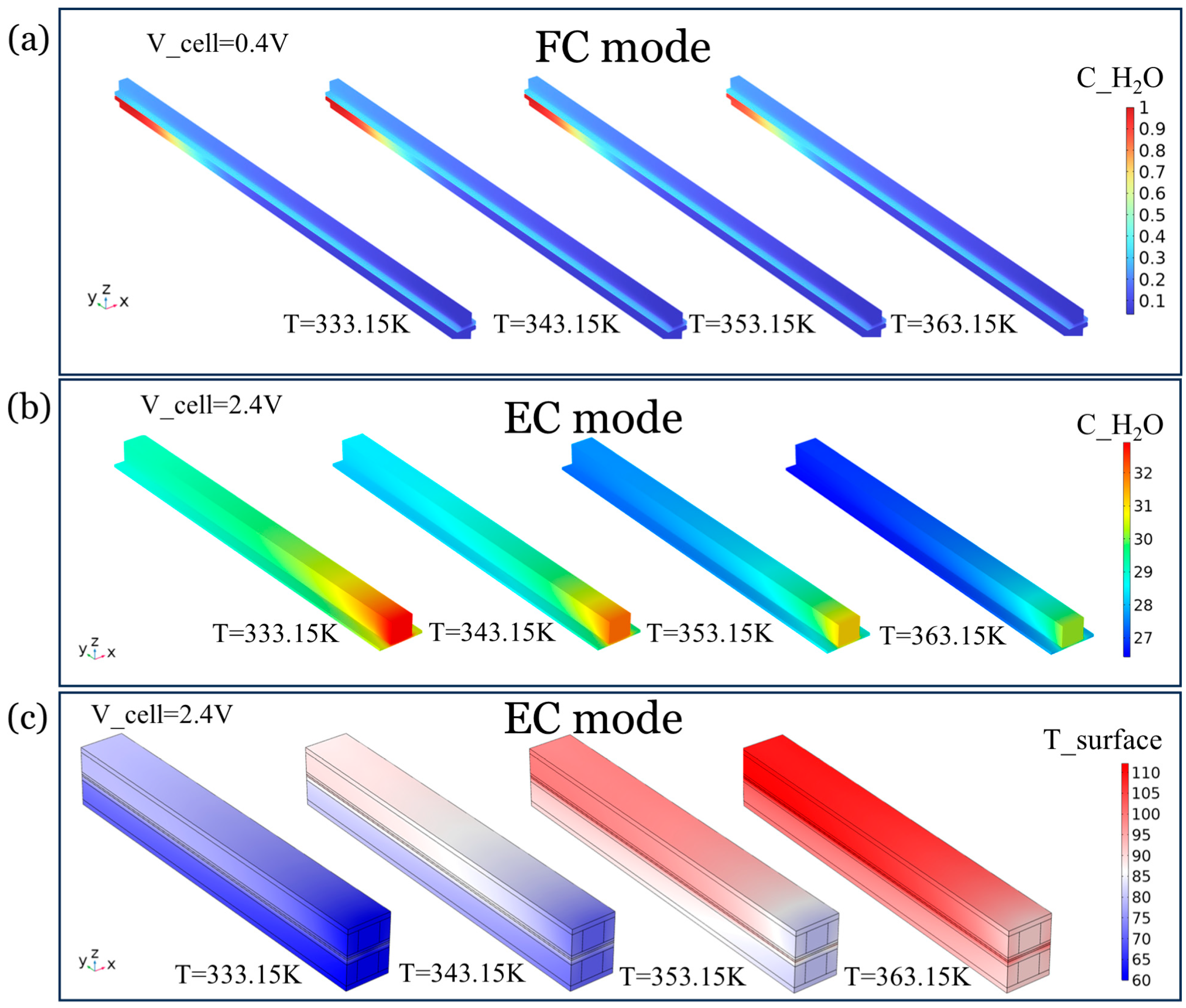
4.1.2. Coupling of Temperature and Concentration Fields in FC Modes
4.1.3. Heat–Mass Coupling in the EC Modes
4.1.4. Sensitivity Mechanisms of Flow Velocity in EC Modes
5. Conclusions
- (a)
- The parametric contradictions between FC and EC modes were successfully reconciled by a coupled multi-physical field model (COMSOL®), which reveals the mechanisms by different operating conditions and structural parameters on the performance of the dual modes. In particular, both FC and EC modes are sensitive to temperature, exchange current density, and conductivity. Thus, the modeling process is well guided by the parameter determinations.
- (b)
- A dual mechanism of action was observed for temperature (333–353 K), where high temperature induced membrane dehydration with accelerated gas depletion in FC modes, which resulted in performance degradation (−4.2% to −4.0%). For the EC modes, the high temperature accelerates the electrochemical kinetics and enhances the liquid water mobility, which facilitates the mass transfer and promotes the detachment of gas bubbles, which greatly reduces the polarization loss (gain of 8.6–9.4%).
- (c)
- Sensitivity analysis determines the optimal interval of key structural parameters: the porosity of GDL needs to be >0.4 in FC mode to avoid water flooding, and the conductivity >222 S/m in EC mode inhibits ohmic loss effectively. Breaking the threshold will trigger nonlinear performance degradation (e.g., FC current density gain plummets 25.87–0.88% at porosity > 0.4).
- (d)
- The increase in flow rates for the EC modes (15–90 mL/min) resulted in a current density gain of only 0.36%, with diminishing marginal benefits. Higher flow rates (>60 mL/min) could not significantly improve the species concentration gradient due to turbulent shear effects, which suggests that the channel’s design needs to be synergistically optimized with other parameters.
- (e)
- The spatial distribution analysis reveals that the temperature increase in the FC modes leads to the enrichment of liquid water (>0.8 mol/m3) at the anode exit, while the EC mode inlet forms a low-temperature and high-concentration boundary layer, which emphasizes the strong coupling characteristics of the water-phase equilibrium and the heat–mass transfer in the dual modes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| density | |
| fluid flow velocity vector | |
| mass source term | |
| dynamic viscosity | |
| p | pressure |
| K | permeability |
| porosity | |
| temperature | |
| diffusion flux | |
| diffusion coefficient | |
| mass fraction | |
| molar mass | |
| molar fraction | |
| effective transfer factor | |
| fluid tortuosity factor | |
| effective conductivity | |
| effective ionic conductivity | |
| potential | |
| ionic potential | |
| thermal conductivity of the porous medium | |
| fluid thermal conductivity | |
| thermal dispersion coefficient | |
| α | transfer coefficient |
| R | molar gas constant |
| F | Faraday constant |
| overpotential | |
| Av | active specific surface area |
References
- Lee, J.J.; Jeong, K.; Kwon, S.; Yook, H.; Kim, S.M.; Han, J.W.; Choi, J.; Park, J.H. ‘Magic methyl effect’ in 2-benzylpyridine-based H2 storage materials: Enhanced H2 storage/release performances. Energy Storage Mater. 2024, 67, 103259. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Ahmad, M.; Sun, X.; Liu, C.; Chen, S.; Zhang, J.; Luo, J.; Fu, X. Dual Hydrogen-Producing Formaldehyde-Water fuel cell for pollutant treatment and valuable chemical Co-generation. Chem. Eng. J. 2025, 505, 159653. [Google Scholar] [CrossRef]
- Ga, S.; An, N.; Lee, G.Y.; Joo, C.; Kim, J. Economic analysis with multiscale high-throughput screening for covalent organic framework adsorbents in ammonia-based green hydrogen separation. Renew. Sustain. Energy Rev. 2024, 189, 113989. [Google Scholar] [CrossRef]
- Wang, Y.; Leung, D.Y.C.; Xuan, J.; Wang, H. A review on unitized regenerative fuel cell technologies, part-A: Unitized regenerative proton exchange membrane fuel cells. Renew. Sustain. Energy Rev. 2016, 65, 961–977. [Google Scholar] [CrossRef]
- Hu, Y.; Li, Y.; Ren, P.; Wang, D.; Song, X.; Zhu, Z.; Zhang, L.; Pei, P. Impedance Investigation and Switching Strategy Study of Constant-Electrode Unitized Regenerative Fuel Cell from Electrolytic Cell Through Purging to Fuel Cell. Energy 2024, 32, 137327. [Google Scholar] [CrossRef]
- Da Silva, G.C.; Fernandes, M.R.; Ticianelli, E.A. Activity and Stability of Pt/IrO2 Bifunctional Materials as Catalysts for the Oxygen Evolution/Reduction Reactions. ACS Catal. 2018, 8, 2081–2092. [Google Scholar] [CrossRef]
- Lim, A.; Kim, J.; Lee, H.J.; Kim, H.; Yoo, S.J.; Jang, J.H.; Young Park, H.; Sung, Y.; Park, H.S. Low-loading IrO2 supported on Pt for catalysis of PEM water electrolysis and regenerative fuel cells. Appl. Catal. B Environ. 2020, 272, 118955. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Ma, Y.; Cheng, J.; Zhong, H.; Song, S.; Ma, H. A novel bifunctional electrocatalyst for unitized regenerative fuel cell. J. Power Sources 2010, 195, 142–145. [Google Scholar] [CrossRef]
- Peng, X.; Taie, Z.; Liu, J.; Zhang, Y.; Peng, X.; Regmi, Y.N.; Fornaciari, J.C.; Capuano, C.; Binny, D.; Kariuki, N.N.; et al. Hierarchical electrode design of highly efficient and stable unitized regenerative fuel cells (URFCs) for long-term energy storage. Energy Environ. Sci. 2020, 13, 4872–4881. [Google Scholar] [CrossRef]
- Regmi, Y.N.; Peng, X.; Fornaciari, J.C.; Wei, M.; Myers, D.J.; Weber, A.Z.; Danilovic, N. A low temperature unitized regenerative fuel cell realizing 60% round trip efficiency and 10,000 cycles of durability for energy storage applications. Energy Environ. Sci. 2020, 13, 215–296. [Google Scholar] [CrossRef]
- Lim, A.; Lee, J.S.; Lee, S.; Lee, S.Y.; Kim, H.; Yoo, S.J.; Jang, J.H.; Sung, Y.; Park, H.S. Polymer electrolyte membrane unitized regenerative fuel cells: Operational considerations for achieving high round trip efficiency at low catalyst loading. Appl. Catal. B Environ. 2021, 297, 120458. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-physical modeling and parameter identification method for dynamic model with unmeasurable state in 10-kW scale proton exchange membrane fuel cell system. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, M.; Yu, Z.; Yao, S.; Wang, J.; Qiu, D.; Peng, L. A novel cooperative design with optimized flow field on bipolar plates and hybrid wettability gas diffusion layer for proton exchange membrane unitized regenerative fuel cell. Energy 2022, 239, 122375. [Google Scholar] [CrossRef]
- Choe, S.; Lee, B.; Cho, M.K.; Kim, H.; Henkensmeier, D.; Yoo, S.J.; Kim, J.Y.; Lee, S.Y.; Park, H.S.; Jang, J.H. Electrodeposited IrO2/Ti electrodes as durable and cost-effective anodes in high-temperature polymer-membrane-electrolyte water electrolyzers. Appl. Catal. B Environ. 2018, 226, 289–294. [Google Scholar] [CrossRef]
- Lim, A.; Jeong, H.; Lim, Y.; Kim, J.Y.; Park, H.Y.; Jang, J.H.; Sung, Y.; Kim, J.M.; Park, H.S. Amphiphilic Ti porous transport layer for highly effective PEM unitized regenerative fuel cells. Sci. Adv. 2021, 7, eabf7866. [Google Scholar] [CrossRef]
- Yilmaz, A.; Komini Babu, S.; Kissane, J.; Pasaogullari, U.; Spendelow, J.S. Stratified Porous Transport Layers for Unitized Reversible Fuel Cells. ACS Appl. Energ. Mater. 2025, 8, 1986–1993. [Google Scholar] [CrossRef]
- Komini Babu, S.; Yilmaz, A.; Uddin, M.A.; Lamanna, J.; Baltic, E.; Jacobson, D.L.; Pasaogullari, U.; Spendelow, J.S. A goldilocks approach to water management: Hydrochannel porous transport layers for unitized reversible fuel cells. Adv. Energy Mater. 2023, 13, 3952. [Google Scholar] [CrossRef]
- Kusoglu, A.; Weber, A.Z. New Insights into Perfluorinated Sulfonic-Acid Ionomers. Chem. Rev. 2017, 117, 987–1104. [Google Scholar] [CrossRef]
- Tian, Y.; Hong, J.; Cao, D.; You, S.; Song, Y.; Cheng, B.; Wang, Z.; Guan, D.; Liu, X.; Zhao, Z.; et al. Visualizing Eigen/Zundel cations and their interconversion in monolayer water on metal surfaces. Science 2022, 377, 315–319. [Google Scholar] [CrossRef]
- Du, Y.; Li, Y.; Ren, P.; Zhang, L.; Wang, D.; Xu, X. Oxygen Transfer at Mesoscale Catalyst Layer in Proton Exchange Membrane Fuel Cell: Mechanism, Model and Resistance Characterization. Chem. Eng. J. 2024, 494, 153021. [Google Scholar] [CrossRef]
- Ma, M.; Shen, L.; Zhao, Z.; Guo, P.; Liu, J.; Xu, B.; Zhang, Z.; Zhang, Y.; Zhao, L.; Wang, Z. Activation methods and underlying performance boosting mechanisms within fuel cell catalyst layer. Escience 2024, 4, 100254. [Google Scholar] [CrossRef]
- Guo, H.; Guo, Q.; Ye, F.; Ma, C.F.; Liao, Q.; Zhu, X. Improving the electric performance of a unitized regenerative fuel cell during mode switching through mass transfer enhancement. Energy Convers. Manag. 2019, 188, 27–39. [Google Scholar] [CrossRef]
- Guo, H.; Guo, Q.; Ye, F.; Ma, C.F.; Zhu, X.; Liao, Q. Three-dimensional two-phase simulation of a unitized regenerative fuel cell during mode switching from electrolytic cell to fuel cell. Energy Convers. Manag. 2019, 195, 989–1003. [Google Scholar] [CrossRef]
- Yelegen, N.; Kümük, B.; Kaplan, R.N.; İlbaş, M.; Kaplan, Y. Numerical and experimental studies on unitized regenerative proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2023, 48, 12969–12981. [Google Scholar] [CrossRef]
- Guo, H.; Song, J.; Ye, F.; Chong Fang, M.A. Dynamic response during mode switching of unitized regenerative fuel cells with orientational flow channels. Renew. Energy 2022, 188, 698–710. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Wu, L.; Bao, Z.; Zu, B.; Jiao, K. A 3-D multiphase model of proton exchange membrane electrolyzer based on open-source CFD. Digit. Chem. Eng. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Falcão, D.S.; Pinto, A.M.F.R. A review on PEM electrolyzer modelling: Guidelines for beginners. J. Clean. Prod. 2020, 261, 121184. [Google Scholar] [CrossRef]
- Shen, W.; Su, H.; Gao, J.; Fan, L.; Zhang, G.; Zhou, S. A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control. Energies 2025, 18, 2443. [Google Scholar] [CrossRef]
- Lv, L.; Pei, P.; Ren, P.; Wang, H.; Wang, G. Exploring Performance Degradation of Proton Exchange Membrane Fuel Cells Based on Diffusion Transformer Model. Energies 2025, 18, 1191. [Google Scholar] [CrossRef]
- Fu, X.; Pei, P.; Ren, P.; Zhu, Z.; Wang, H.; Song, X.; Wang, Z. On-board and in-situ identification of cell-individual hydrogen crossover in fuel cell stacks based on electrochemical dynamics during shutdown. Chem. Eng. 2025, 506, 159952. [Google Scholar] [CrossRef]
- Deng, L.; Jin, L.; Yang, L.; Feng, C.; Tao, A.; Jia, X.; Geng, Z.; Zhang, C.; Cui, X.; Shi, J. Bubble Evolution Dynamics in Alkaline Water Electrolysis. Escience 2024, 5, 100353. [Google Scholar] [CrossRef]
- Ren, P.; Fu, X.; Pei, P.; Li, Y.; Zhu, Z.; Wang, H.; Song, X.; Wang, Z. Bridging the gap between prediction and real-time diagnosis of water failures in proton exchange membrane fuel cell stacks via gas distribution characterization. Appl. Energy 2025, 389, 125755. [Google Scholar] [CrossRef]
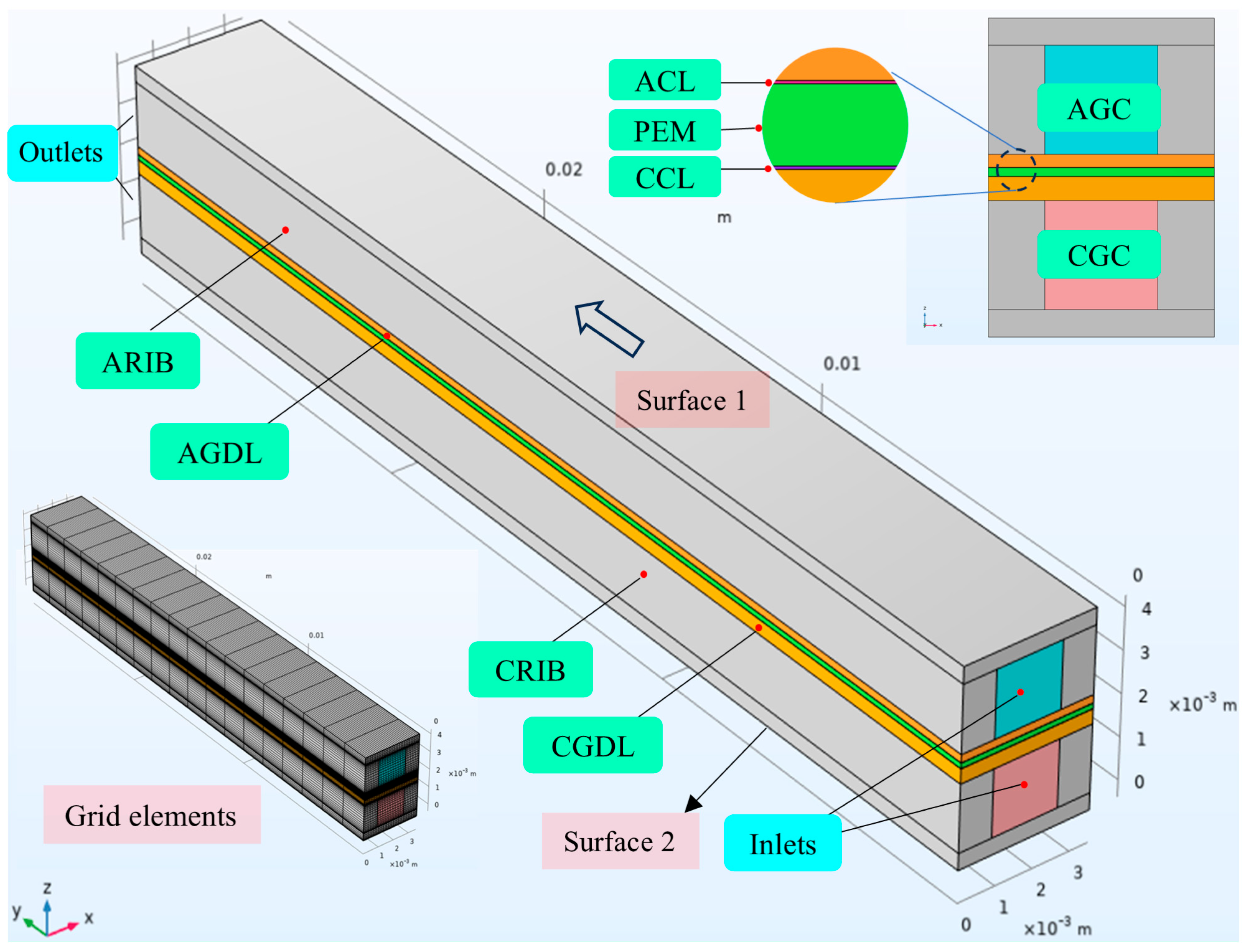
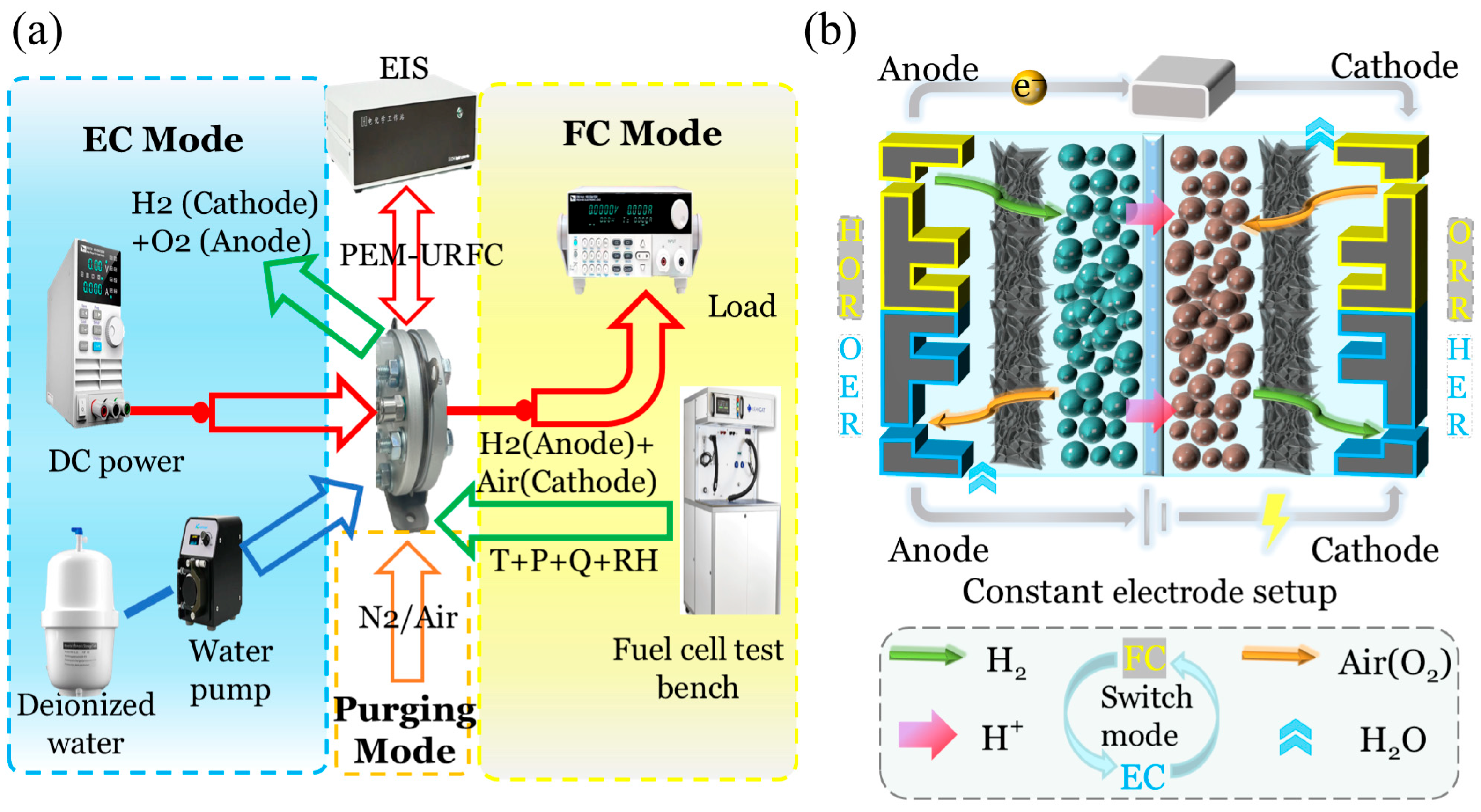

| Subdomains | Symbols | Values (mm) |
|---|---|---|
| Gas channels | LCH, HCH, WCH | 30, 1.6, 1.76 |
| Bipolar plates | LBP, HBP, WBP | 30, 2, 3.5 |
| Ribs | δRib, WRib, LRib | 1.6, 1.76, 30 |
| Gas diffusion layers | δGDL, WGDL, LGDL | 0.35, 3.5, 30 |
| Catalyst layers | δCL, WCL, LCL | 0.005, 3.5, 30 |
| Proton exchange membrane | δm, Wm, Lm | 0.127, 3.5, 30 |
| Description | Symbol | Unit | Value (EC) | Value (FC) |
|---|---|---|---|---|
| Flow rates | v | m3/s | 2.5 × 10−7 | -- |
| Cell temperature | T | K | 303.15 | 333.15 |
| Anode reference exchange current density | i0,a | A/m2 | 2 × 10−5 | 1 × 10−3 |
| Conductivity of GDL | σGDL | S/m | 222 | 222 |
| Porosity of GDL | εGDL | \ | 0.6 | 0.6 |
| Description | Symbol | Unit | Value (EC) | Value (FC) |
|---|---|---|---|---|
| Anode porosity | εaL∕GDL, εaCL | \ | 0.4, 0.3 | 0.4, 0.3 |
| Cathode porosity | εcL∕GDL, εcCL | \ | 0.4, 0.3 | 0.4, 0.3 |
| Anode permeability | ΚaL∕GDL, ΚaCL | μm2 | 118, 23.6 | 118, 23.6 |
| Cathode permeability | ΚcL∕GDL, ΚcCL | μm2 | 118, 23.6 | 118, 23.6 |
| Anode conductivity | κaL∕GDL, κaCL | S/m | 20,000, 10, 5000 | 20,000, 10, 5000 |
| Cathode conductivity | κcL∕GDL, κcCL | S/m | 20,000, 10, 5000 | 20,000, 10, 5000 |
| MEM Conductivity | κMEM | S/m | 9.825 | 9.825 |
| Cell temperature | T | K | 303.15 | 363.15 |
| Reference pressure | Pref | atm | 1 | 1 |
| Reference exchange current density | j0a, j0c | A/m3 | 0.05, 3000 | 0.001, 100 |
| Charge transfer coefficients | αa, αc | \ | 0.5, 0.5 | 0.5, 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Li, Y.; Li, Y.; Yang, F.; Zhang, B.; Wang, D. Parameter Optimization for Dual-Mode Operation of Unitized Regenerative Fuel Cells via Steady-State Simulation. Energies 2025, 18, 5899. https://doi.org/10.3390/en18225899
Hu Y, Li Y, Li Y, Yang F, Zhang B, Wang D. Parameter Optimization for Dual-Mode Operation of Unitized Regenerative Fuel Cells via Steady-State Simulation. Energies. 2025; 18(22):5899. https://doi.org/10.3390/en18225899
Chicago/Turabian StyleHu, Yuhang, Yijia Li, Yuehua Li, Fang Yang, Bin Zhang, and Dan Wang. 2025. "Parameter Optimization for Dual-Mode Operation of Unitized Regenerative Fuel Cells via Steady-State Simulation" Energies 18, no. 22: 5899. https://doi.org/10.3390/en18225899
APA StyleHu, Y., Li, Y., Li, Y., Yang, F., Zhang, B., & Wang, D. (2025). Parameter Optimization for Dual-Mode Operation of Unitized Regenerative Fuel Cells via Steady-State Simulation. Energies, 18(22), 5899. https://doi.org/10.3390/en18225899







