Flame Speciation and Laminar Burning Velocity of Tetralin Flames Under Atmospheric Pressure
Abstract
1. Introduction
2. Experiment and Modeling
2.1. Mache–Hebra Nozzle Burner
2.2. MBMS Setup
- −
- direct calibration against gas mixtures with known mole fractions of the target species;
- −
- −
- determination from an elemental material balance (C, O, H, and Ar) for the most abundant species.
2.3. TICS Calculations
2.4. Kinetic Simulations
3. Results and Discussion
3.1. Preliminary Analysis
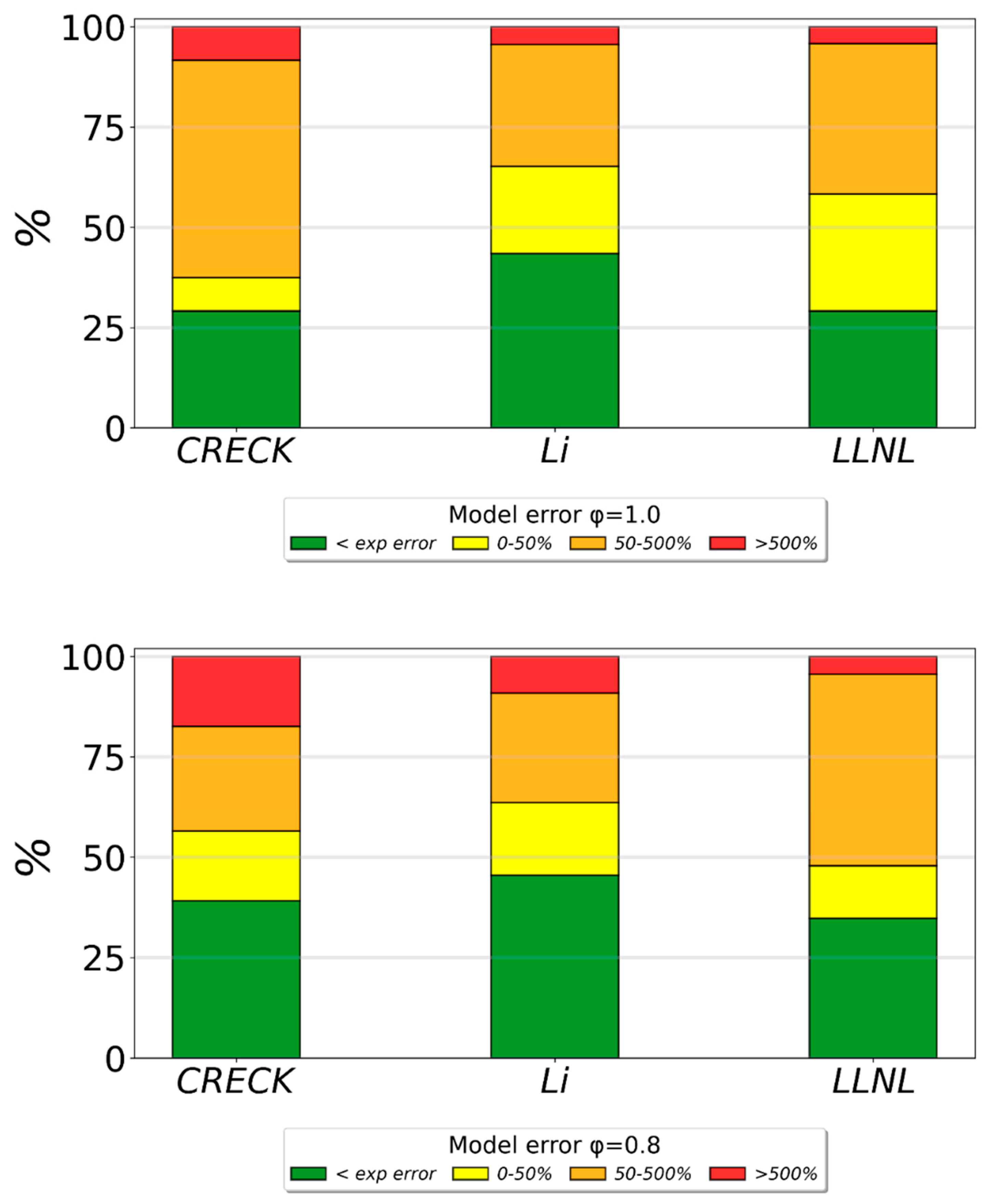
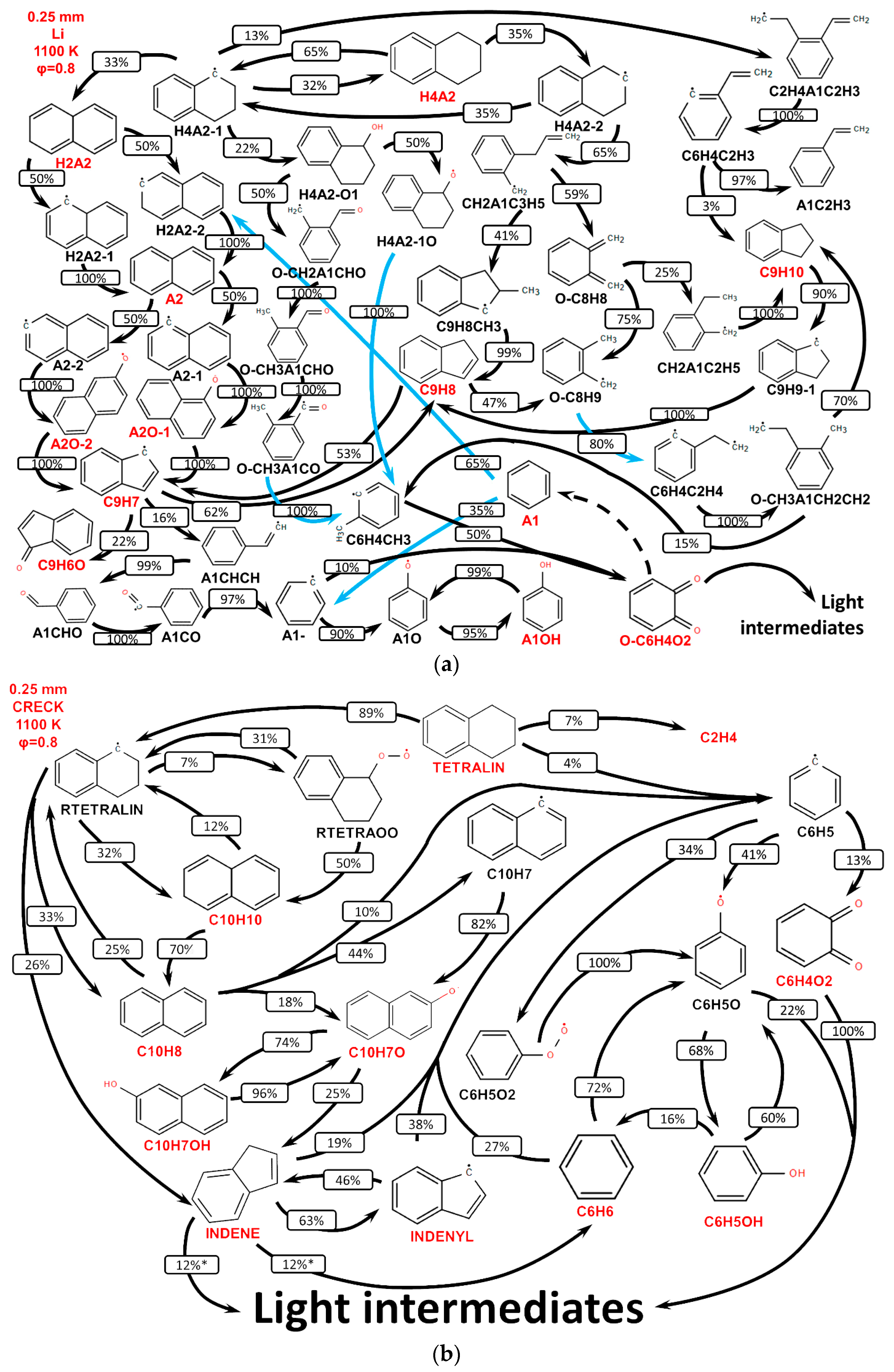
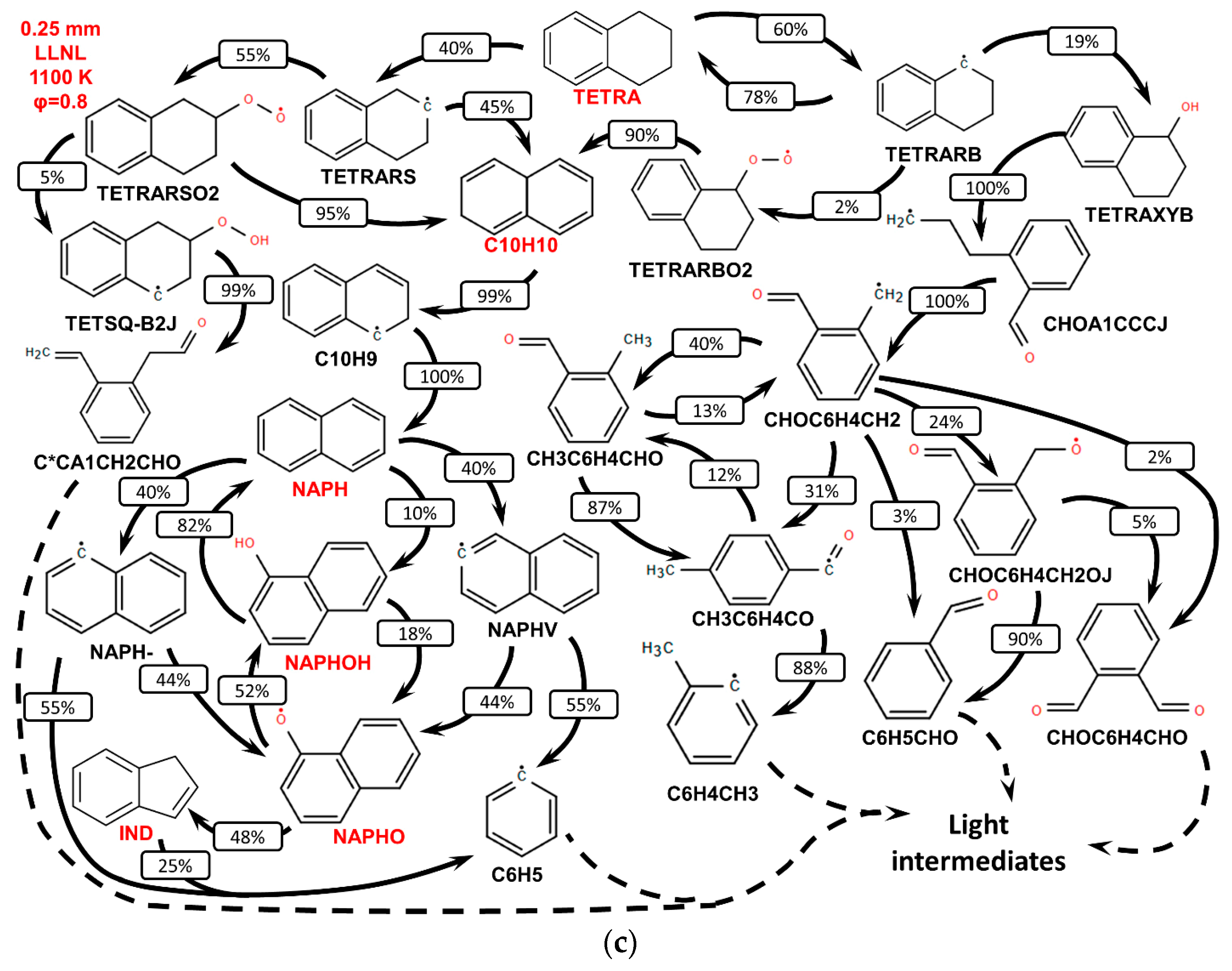
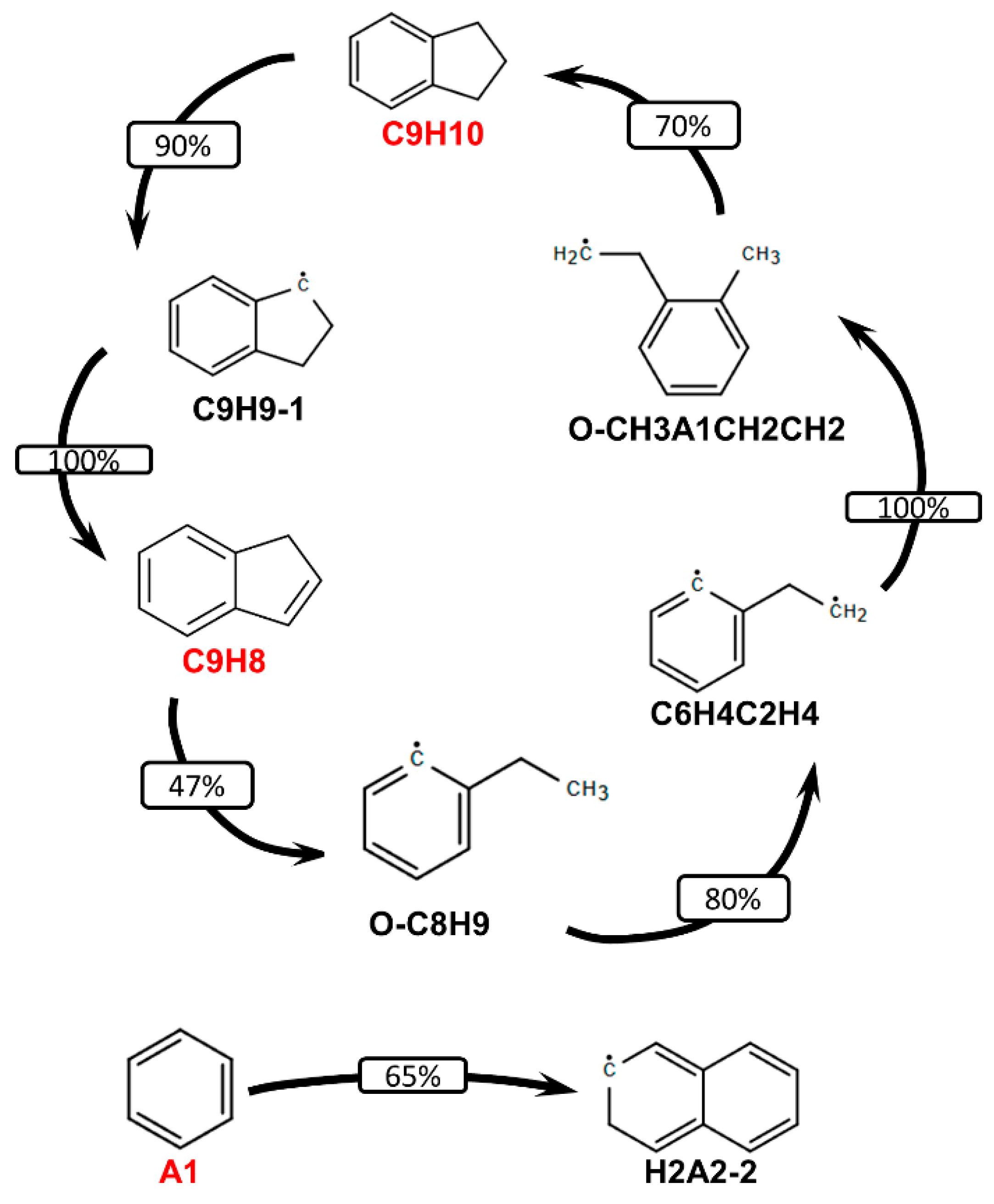
3.2. Validation of Models Against Experimental Data: Chemical Flame Structure
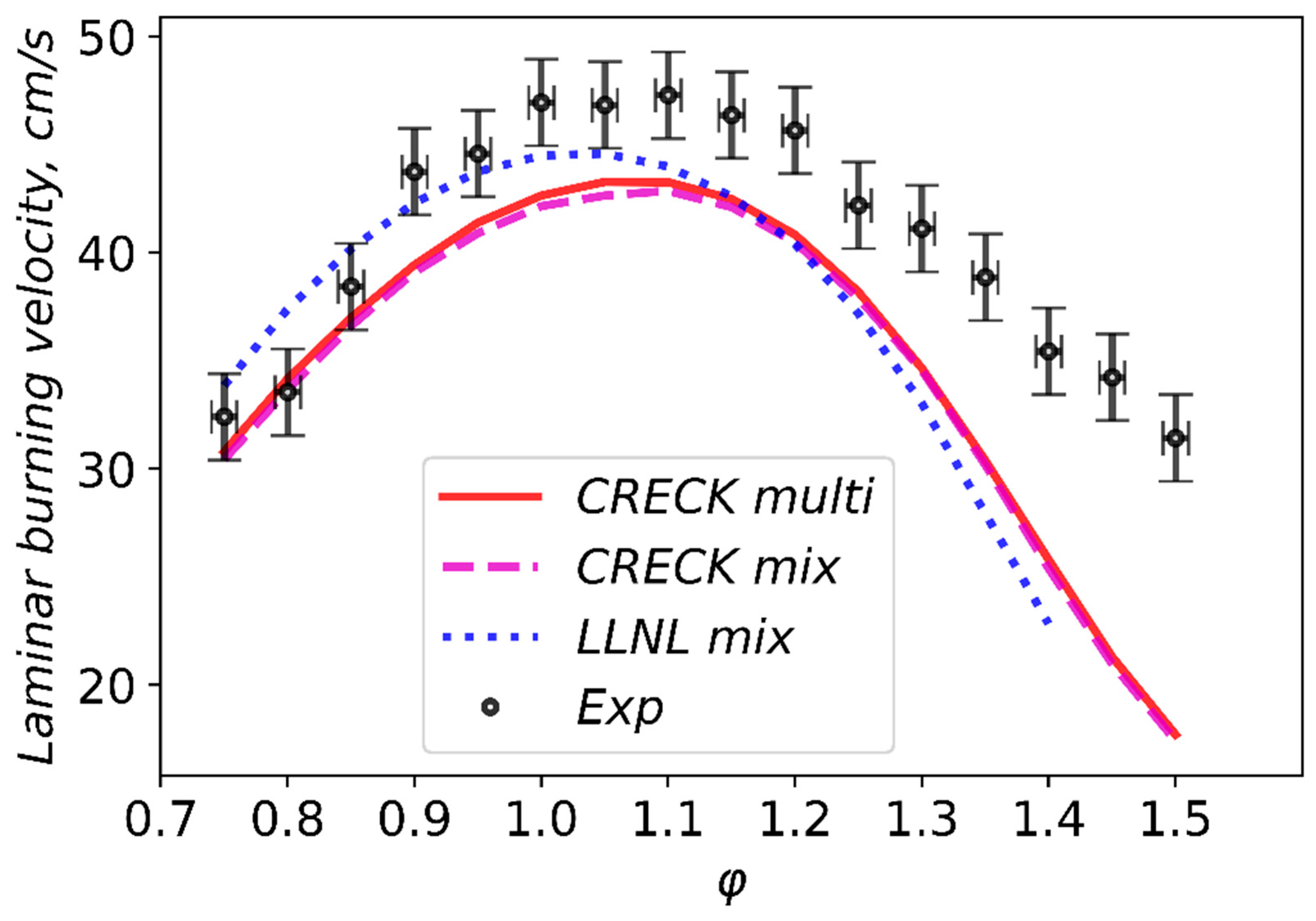
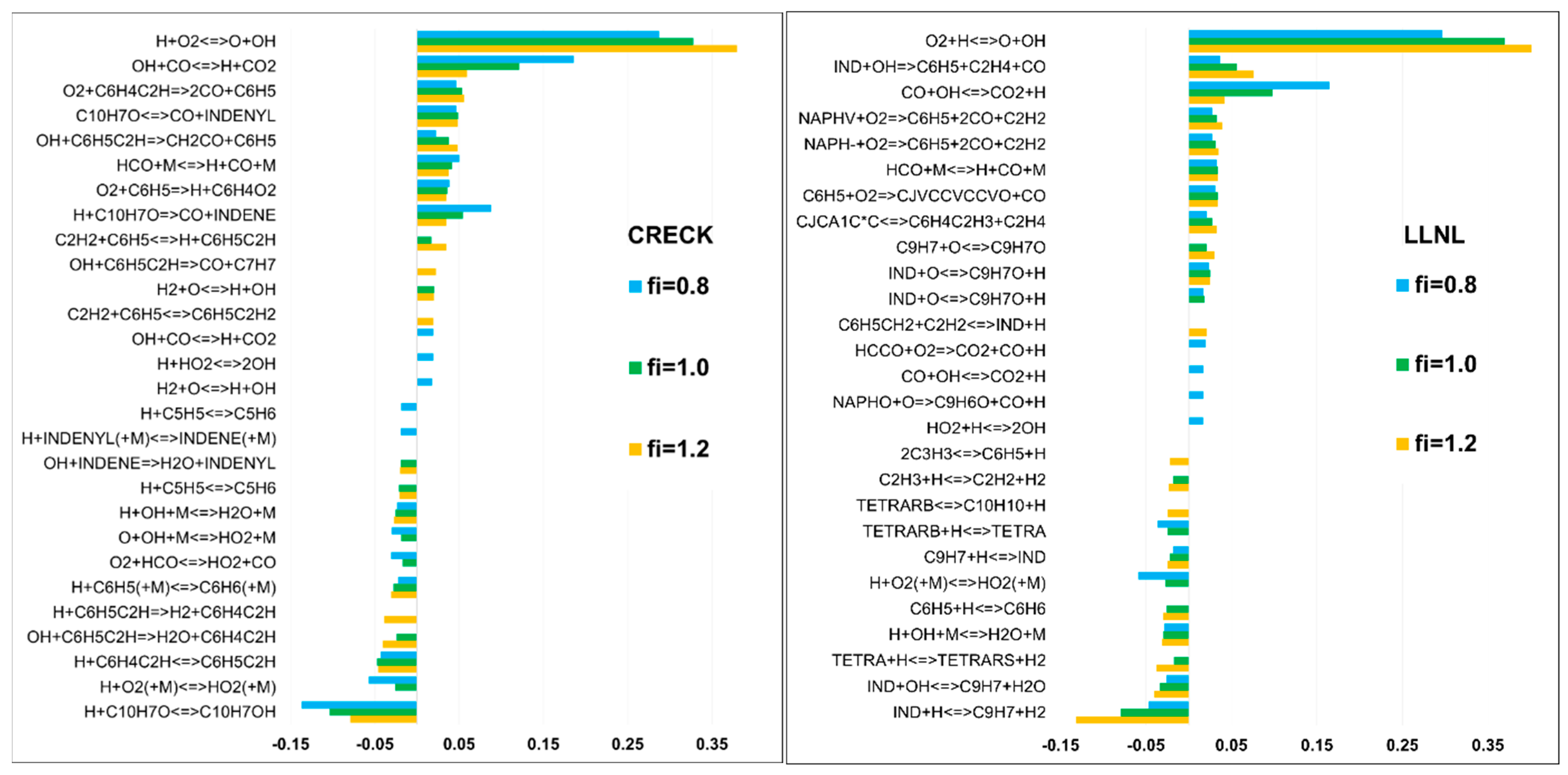
3.3. Validation of Models Against Experimental Data: Laminar Burning Velocity
4. Conclusions
- (1)
- The primary decomposition kinetics of tetralin under flame conditions (i.e., those leading to C10 intermediates versus ring-opening reactions) remain poorly understood. These inconsistencies result in different ratios of heavy cyclic hydrocarbons to light hydrocarbon components within the reaction networks. The kinetic parameters of the corresponding pathways should be refined to ensure their accuracy across the full range of temperature conditions, including flames.
- (2)
- The transition pathways between the C10 and monoaromatic pools are strongly governed by the indene/indenyl subchemistry, which mole fraction profiles were not reproduced properly by the models.
- (3)
- The C10H7O, C6H5C2H, and C6H5 radicals were identified as the principal fuel-derived intermediates controlling the laminar burning velocity. Taking into account low predictive capability of the models against these intermediates, revising the rate constants and uncertain branching ratios for corresponding H-abstraction and β-scission channels is expected to substantially improve model predictions.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Morales, M.H.; Tsapenkov, K.D.; Zubrilin, I.A.; Yakushkin, D.V.; Semenikhin, A.S.; Sazhin, S.S.; Matveev, S.G. Formulation of Surrogates of Hydrocarbon Fuels Using Selected Physico-Chemical Properties Related to Atomization, Heating, Evaporation and Combustion Behaviours. Combust. Sci. Technol. 2024, 196, 4269–4291. [Google Scholar] [CrossRef]
- Poutsma, M.L. Free-Radical Thermolysis and Hydrogenolysis of Model Hydrocarbons Relevant to Processing of Coal. Energy Fuels 1990, 4, 113–131. [Google Scholar] [CrossRef]
- Violi, A.; Yan, S.; Eddings, E.G.; Sarofim, A.F.; Granata, S.; Faravelli, T.; Ranzi, E. Experimental Formulation and Kinetic Model for JP-8 Surrogate Mixtures. Combust. Sci. Technol. 2002, 174, 399–417. [Google Scholar] [CrossRef]
- Anand, K.; Ra, Y.; Reitz, R.D.; Bunting, B. Surrogate Model Development for Fuels for Advanced Combustion Engines. Energy Fuels 2011, 25, 1474–1484. [Google Scholar] [CrossRef]
- Pitz, W.J.; Mueller, C.J. Recent Progress in the Development of Diesel Surrogate Fuels. Prog. Energy Combust. Sci. 2011, 37, 330–350. [Google Scholar] [CrossRef]
- Mueller, C.J.; Cannella, W.J.; Bays, J.T.; Bruno, T.J.; DeFabio, K.; Dettman, H.D.; Gieleciak, R.M.; Huber, M.L.; Kweon, C.-B.; McConnell, S.S.; et al. Diesel Surrogate Fuels for Engine Testing and Chemical-Kinetic Modeling: Compositions and Properties. Energy Fuels 2016, 30, 1445–1461. [Google Scholar] [CrossRef]
- Abdul Jameel, A.G.; Naser, N.; Issayev, G.; Touitou, J.; Ghosh, M.K.; Emwas, A.-H.; Farooq, A.; Dooley, S.; Sarathy, S.M. A Minimalist Functional Group (MFG) Approach for Surrogate Fuel Formulation. Combust. Flame 2018, 192, 250–271. [Google Scholar] [CrossRef]
- Wu, Z.; Mao, Y.; Raza, M.; Zhu, J.; Feng, Y.; Wang, S.; Qian, Y.; Yu, L.; Lu, X. Surrogate Fuels for RP-3 Kerosene Formulated by Emulating Molecular Structures, Functional Groups, Physical and Chemical Properties. Combust. Flame 2019, 208, 388–401. [Google Scholar] [CrossRef]
- Wang, M.; Kukkadapu, G.; Fang, R.; Pitz, W.J.; Sung, C.-J. Autoignition Study of Iso-Cetane/Tetralin Blends at Low Temperature. Combust. Flame 2021, 228, 415–429. [Google Scholar] [CrossRef]
- Issayev, G.; Djebbi, K.; Kukkadapu, G.; Mehl, M.; Wagnon, S.W.; Pitz, W.J.; Farooq, A. Experimental and Kinetic Modeling Study of Tetralin: A Naphtheno-Aromatic Fuel for Gasoline, Jet and Diesel Surrogates. Proc. Combust. Inst. 2021, 38, 641–649. [Google Scholar] [CrossRef]
- Bounaceur, R.; Scacchi, G.; Marquaire, P.-M.; Dominé, F. Mechanistic Modeling of the Thermal Cracking of Tetralin. Ind. Eng. Chem. Res. 2000, 39, 4152–4165. [Google Scholar] [CrossRef]
- Poutsma, M.L. Progress toward the Mechanistic Description and Simulation of the Pyrolysis of Tetralin. Energy Fuels 2002, 16, 964–996. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Wang, Z.; Ye, L.; Cai, J.; Cheng, Z.; Qi, F. Experimental and Kinetic Modeling Study of Tetralin Pyrolysis at Low Pressure. Proc. Combust. Inst. 2013, 34, 1739–1748. [Google Scholar] [CrossRef]
- Yang, Y.; Boehman, A.L. Oxidation Chemistry of Cyclic Hydrocarbons in a Motored Engine: Methylcyclopentane, Tetralin, and Decalin. Combust. Flame 2010, 157, 495–505. [Google Scholar] [CrossRef]
- Dagaut, P.; Ristori, A.; Frassoldati, A.; Faravelli, T.; Dayma, G.; Ranzi, E. Experimental Study of Tetralin Oxidation and Kinetic Modeling of Its Pyrolysis and Oxidation. Energy Fuels 2013, 27, 1576–1585. [Google Scholar] [CrossRef]
- Kukkadapu, G.; Weber, B.W.; Sung, C.-J. Autoignition Study of Tetralin in a Rapid Compression Machine at Elevated Pressures and Low-to-Intermediate Temperatures. Fuel 2015, 159, 436–445. [Google Scholar] [CrossRef]
- Wang, H.; Gerken, W.J.; Wang, W.; Oehlschlaeger, M.A. Experimental Study of the High-Temperature Autoignition of Tetralin. Energy Fuels 2013, 27, 5483–5487. [Google Scholar] [CrossRef]
- Raza, M.; Qian, Y.; Wang, S.; Mao, Y.; Zhu, J.; Lu, X. The Experimental Study of Autoignition of Tetralin at Intermediate-to-High Temperatures. Fuel 2020, 266, 117081. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Mai, T.V.-T.; Huynh, L.K. Ab Initio Kinetics of OH-Initiated Oxidation of Tetralin: New Insight into a Mixed Saturated-Unsaturated Ring Compound. Fuel 2024, 374, 132427. [Google Scholar] [CrossRef]
- Li, Y.; Zou, J.; Yuan, W.; Cao, C.; Zhang, Y.; Qi, F.; Yang, J. Unraveling Chemical Structure of Laminar Premixed Tetralin Flames at Low Pressure with Photoionization Mass Spectrometry and Kinetic Modeling. Int. J. Chem. Kinet. 2020, 53, 154–163. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.; Kelley, A.P.; Law, C.K. Hierarchical and Comparative Kinetic Modeling of Laminar Flame Speeds of Hydrocarbon and Oxygenated Fuels. Prog. Energy Combust. Sci. 2012, 38, 468–501. [Google Scholar] [CrossRef]
- Mache, H.; Hebra, A. Zur Messung Der Verbrennungsgeschwindigkeit Explosiver Gasgemische. Sitzungsberichte Akad. Wiss. Math.-Naturwissenschaftliche Kl. 1941, 150_2a, 157–174. [Google Scholar]
- Andrews, G.E.; Bradley, D. Determination of Burning Velocities: A Critical Review. Combust. Flame 1972, 18, 133–153. [Google Scholar] [CrossRef]
- Gerasimov, I.E.; Knyazkov, D.A.; Shmakov, A.G.; Paletsky, A.A.; Shvartsberg, V.M.; Bolshova, T.A.; Korobeinichev, O.P. Inhibition of Hydrogen–Oxygen Flames by Iron Pentacarbonyl at Atmospheric Pressure. Proc. Combust. Inst. 2011, 33, 2523–2529. [Google Scholar] [CrossRef]
- Mazas, A.N.; Fiorina, B.; Lacoste, D.A.; Schuller, T. Effects of Water Vapor Addition on the Laminar Burning Velocity of Oxygen-Enriched Methane Flames. Combust. Flame 2011, 158, 2428–2440. [Google Scholar] [CrossRef]
- Osipova, K.N.; Bolshova, T.A.; Korobeinichev, O.P.; Kuibida, L.V.; Shmakov, A.G. Effect of Addition of Methyl Hexanoate and Ethyl Pentanoate on the Structure of Premixed N-Heptane/Toluene/O2/Ar Flame. Energy Fuels 2019, 32, 4585–4597. [Google Scholar] [CrossRef]
- Knyazkov, D.A.; Bolshova, T.A.; Dmitriev, A.M.; Shmakov, A.G.; Korobeinichev, O.P. The Effect of Methyl Pentanoate Addition on the Structure of a Non-Premixed Counterflow n-Heptane/O2 Flame. Energy Fuels 2018, 32, 2397–2406. [Google Scholar] [CrossRef]
- Matyushkov, V.V.; Chernov, A.A.; Dmitriev, A.M.; Shmakov, A.G. Chemical Structure of Lean and Stoichiometric Laminar Flames of Methylcyclohexane at Atmospheric Pressure. Energies 2024, 17, 6154. [Google Scholar] [CrossRef]
- Bolshova, T.; Shvartsberg, V.; Dmitriev, A.; Knyazkov, D. Flame Structure and a Compact Reaction Mechanism for Combustion of Dimethyl Ether at Atmospheric Pressure. Fuel 2019, 255, 115752. [Google Scholar] [CrossRef]
- Knyazkov, D.A.; Dmitriev, A.M.; Korobeinichev, O.P.; Osipova, K.N.; Pio, G.; Shmakov, A.G.; Salzano, E. Structure of Premixed Flames of Propylene Oxide: Molecular Beam Mass Spectrometric Study and Numerical Simulation. Proc. Combust. Inst. 2021, 38, 2467–2475. [Google Scholar] [CrossRef]
- Botha, J.P.; Spalding, D.B. The Laminar Flame Speed of Propane/Air Mixtures with Heat Extraction from the Flame. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 225, 71–96. [Google Scholar] [CrossRef]
- Dmitriev, A.M.; Agafontsev, M.V.; Loboda, E.L.; Knyazkov, D.A.; Korobeinichev, O.P. Measuring the Surface Temperature of a Molecular Beam Probe in the Flame Front at Pressures of 1–5 Atm. Combust. Explos. Shock. Waves 2019, 55, 555–561. [Google Scholar] [CrossRef]
- Kaskan, W.E. The Dependence of Flame Temperature on Mass Burning Velocity. Proc. Combust. Inst. 1957, 6, 134–143. [Google Scholar] [CrossRef]
- Shaddix, C.R. Correcting Thermocouple Measurements for Radiation Loss: A Critical Review; Sandia National Labs: Livermore, CA, USA, 1999. [Google Scholar]
- Cool, T.A.; Nakajima, K.; Taatjes, C.A.; McIlroy, A.; Westmoreland, P.R.; Law, M.E.; Morel, A. Studies of a Fuel-Rich Propane Flame with Photoionization Mass Spectrometry. Proc. Combust. Inst. 2005, 30, 1681–1688. [Google Scholar] [CrossRef]
- Dmitriev, A.M.; Knyazkov, D.A.; Bolshova, T.A.; Shmakov, A.G.; Korobeinichev, O.P. The Effect of Methyl Pentanoate Addition on the Structure of Premixed Fuel-Rich n-Heptane/Toluene Flame at Atmospheric Pressure. Combust. Flame 2015, 162, 1964–1975. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Irikura, K.K.; Rudd, M.E.; Ali, M.A.; Stone, P.M. Electron-Impact Cross Sections for Ionization and Excitation Database. Available online: https://www.nist.gov/pml/electron-impact-cross-sections-ionization-and-excitation-database (accessed on 26 October 2016).
- Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Ingman, V.M.; Schaefer, A.J.; Andreola, L.R.; Wheeler, S.E. QChASM: Quantum Chemistry Automation and Structure Manipulation. WIREs Comput. Mol. Sci. 2021, 11, e1510. [Google Scholar] [CrossRef]
- Schaefer, A.J.; Ingman, V.M.; Wheeler, S.E. SEQCROW: A ChimeraX Bundle to Facilitate Quantum Chemical Applications to Complex Molecular Systems. J. Comput. Chem. 2021, 42, 1750–1754. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom-Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Singh, S.; Modak, P.; Antony, B.; Kwon, D.-C.; Song, M.-Y.; Yoon, J.-S. Total Ionization Cross Section of Cyclic Organic Molecules. J. Chem. Phys. 2019, 150, 064313. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Irikura, K.K. Semi-Empirical Estimation of Ion-Specific Cross Sections in Electron Ionization of Molecules. J. Chem. Phys. 2016, 145, 224102. [Google Scholar] [CrossRef]
- Plasma Basic Data. Available online: http://plasma.mathboylinlin.com/ (accessed on 12 September 2025).
- Kukkadapu, G.; Whitesides, R.; Wang, M.; Wagnon, S.W.; Mehl, M.; Westbrook, C.K.; McCormick, R.; Sung, C.-J.; Pitz, W.J. Development of a Diesel Surrogate for Improved Autoignition Prediction: Methodology and Detailed Chemical Kinetic Modeling. Appl. Energy Combust. Sci. 2023, 16, 100216. [Google Scholar] [CrossRef]
- Tsang, W.; Cui, J.P. Homogeneous Gas-Phase Decyclization of Tetralin and Benzocyclobutene. J. Am. Chem. Soc. 1990, 112, 1665–1671. [Google Scholar] [CrossRef]
- Karir, G.; Mendez-Vega, E.; Portela-Gonzalez, A.; Saraswat, M.; Sander, W.; Hemberger, P. The Elusive Phenylethynyl Radical and Its Cation: Synthesis, Electronic Structure, and Reactivity. Phys. Chem. Chem. Phys. 2024, 26, 18256–18265. [Google Scholar] [CrossRef] [PubMed]
- Mao, Q.; Pratali Maffei, L.; Pitsch, H.; Faravelli, T. Theoretical Study of Important Phenylacetylene Reactions in Polycyclic Aromatic Hydrocarbon Growth. Combust. Flame 2024, 261, 113300. [Google Scholar] [CrossRef]

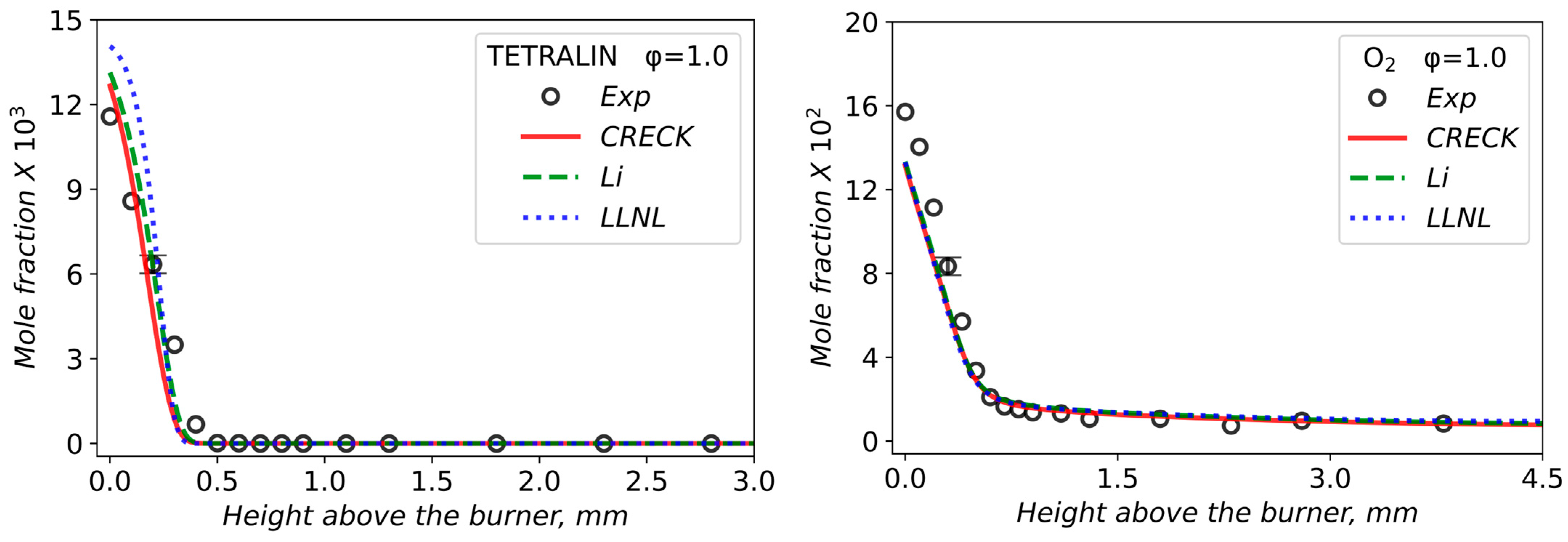
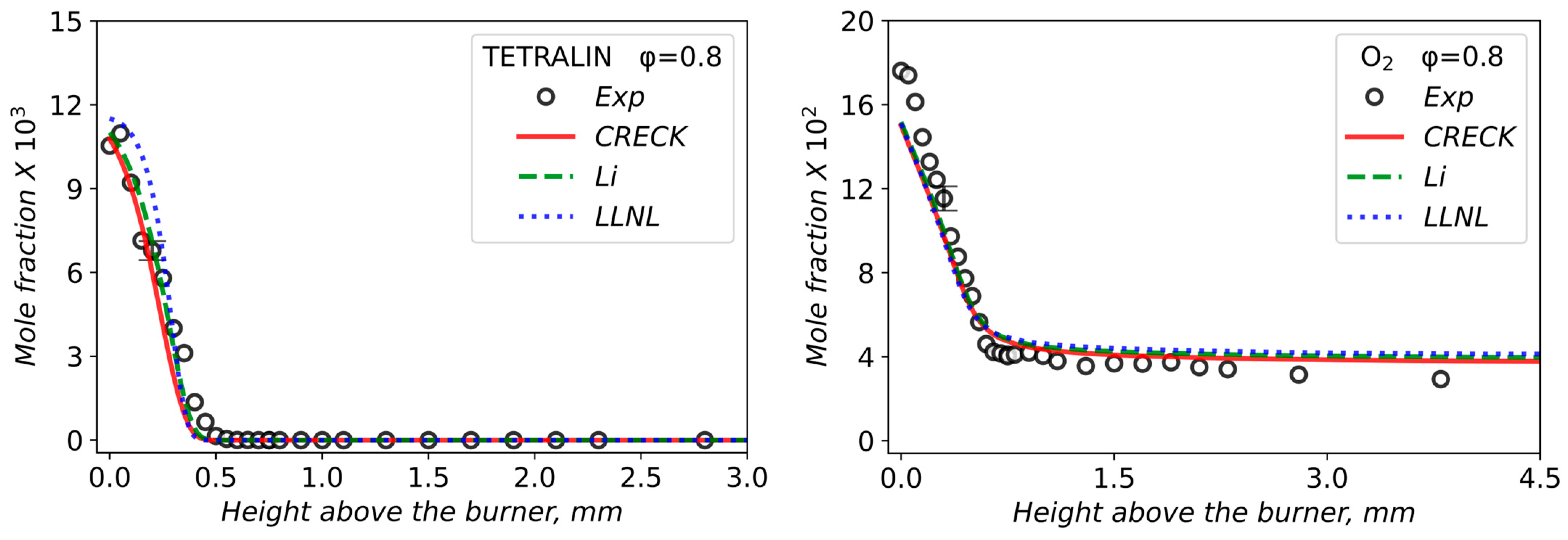
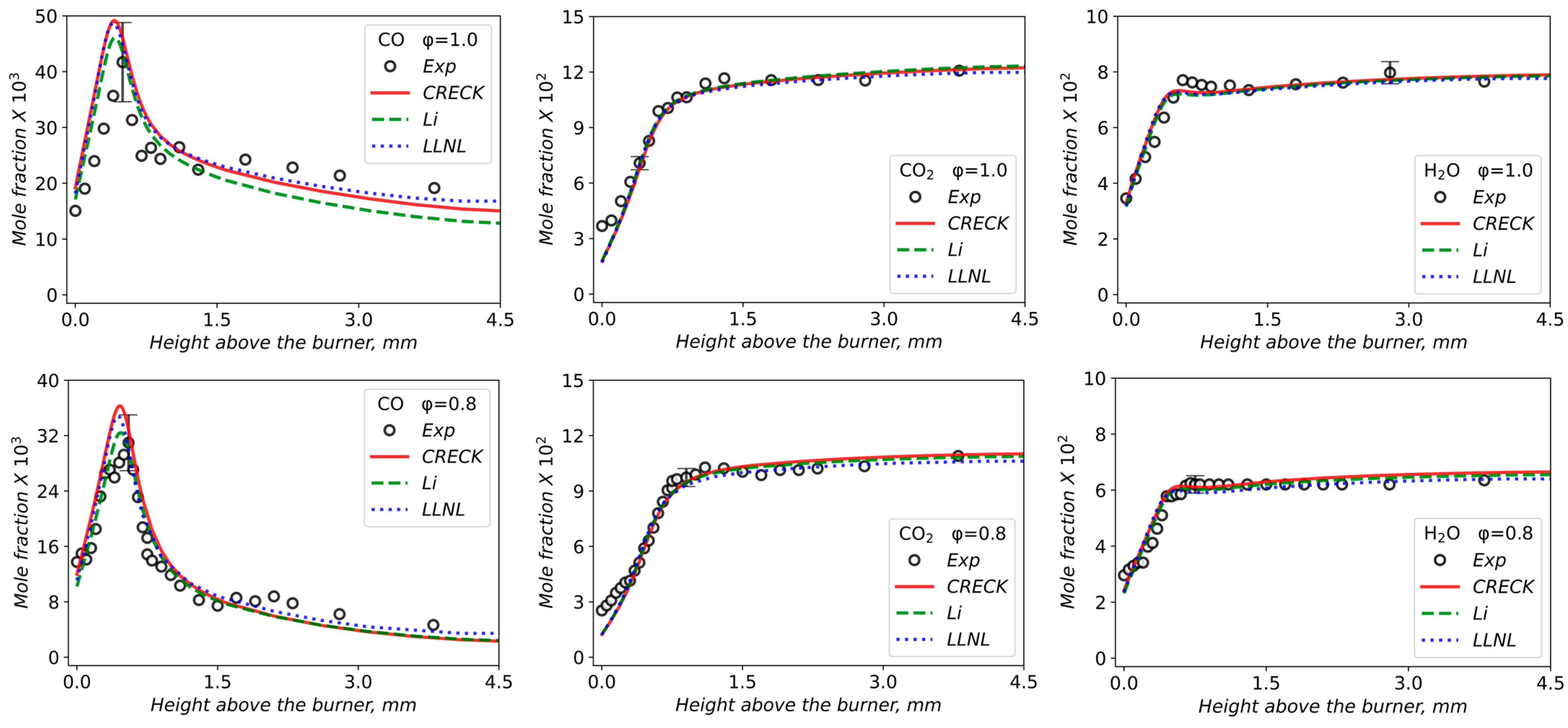
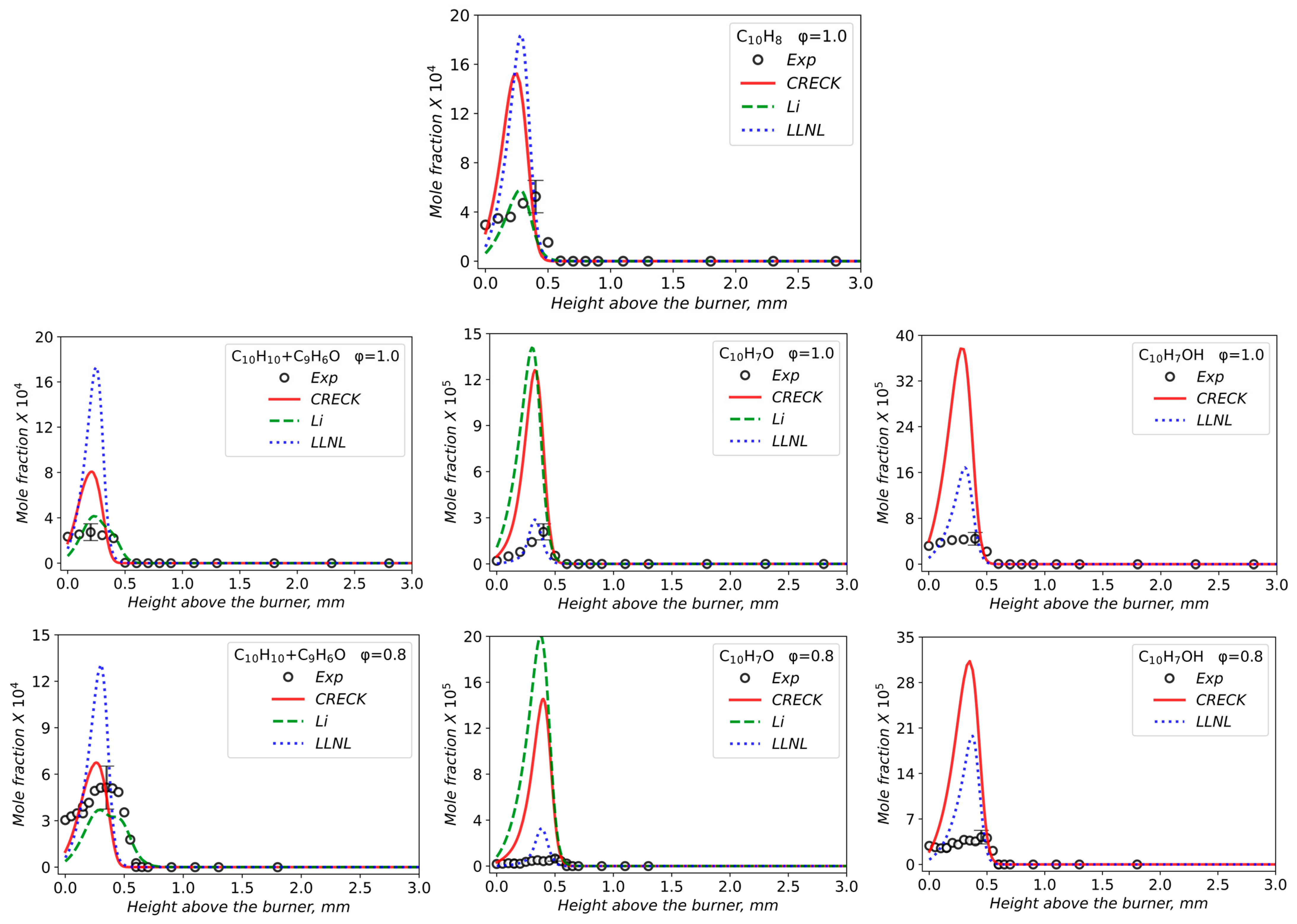

| φ | X (Tetralin) | X (O2) | X (Ar) | Qv, cm3/s | Qm, g/(s·cm2) |
|---|---|---|---|---|---|
| 1.00 ± 0.01 | 0.0142 ± 0.0001 | 0.186 ± 0.001 | 0.800 ± 0.008 | 25 ± 1 | 0.020 ± 0.001 |
| 0.80 ± 0.01 | 0.0116 ± 0.0001 | 0.188 ± 0.001 | 0.800 ± 0.008 | 25 ± 1 | 0.020 ± 0.001 |
| m/z | Species | Considered as | IE, eV | E, eV | Calibration Method |
|---|---|---|---|---|---|
| 15 | CH3 | Methyl radical | 9.8 | 16.2 | RICS |
| 17 | OH | Hydroxyl radical | 13.0 | 16.2 | RICS |
| 18 | H2O | Water | 12.6 | 16.65 | Element balance |
| 26 | C2H2 | Acetylene | 11.4 | 12.3 | Direct |
| 28 | C2H4 | Ethylene | 10.5 | 12.3 | Direct |
| 28 | CO | Carbon monoxide | 14 | 14.35 | Element balance |
| 30 | CH2O | Formaldehyde | 10.9 | 11.5 | RICS |
| 30 | C2H6 | Ethane | 11.5 | 12.3 | Direct |
| 32 | O2 | Molecular oxygen | 12.0 | 14.35 | Element balance |
| 42 | C3H6 +CH2CO | Propene, ketene | 9.7 | 14.35 | Direct |
| 44 | CO2 | Carbon dioxide | 13.8 | 15.4 | Element balance |
| 76 | C6H4 | Benzyne | 9.0 | 15 | RICS |
| 78 | C6H6 | Benzene + fulvene | 9.2 | 15 | Direct |
| 92 | C7H8 + C6H4O | Toluene + cyclohexadienenone | 8.8 | 15 | RICS |
| 94 | C6H5OH | Phenol | 8.5 | 15 | RICS |
| 102 | C6H5C2H | Phenylacetylene | 8.8 | 15 | RICS |
| 108 | C6H4O2 + CH3C6H4OH + C6H5CH2OH + C6H5OCH3 | Benzoquinone + cresols + Benzyl alcohol + anisole | 10 | 15 | RICS |
| 115 | C9H7 | Indenyl radical | 8.4 | 15 | RICS |
| 116 | C9H8 | Indene | 8.1 | 15 | RICS |
| 118 | C8H6O + C9H10 | Benzofuran + indan | 8.4 | 15 | RICS |
| 128 | C10H8 | Naphthalene | 8.1 | 15 | RICS |
| 130 | C10H10 + C9H6O | Dihydronaphthalene + indenone | 8.1 | 15 | RICS |
| 132 | C10H12 | Tetralin | 8.5 | 18 | element balance |
| 143 | C10H7O | Naphthol radical | 8.1 | 15 | RICS |
| 144 | C10H7OH | Naphthol | 7.9 | 15 | RICS |
| Compound | σ (wB97XD), Å2 | σ (wB97X), Å2 |
|---|---|---|
| Benzene | 2.517 | 2.263 |
| 1,2-Dihydronaphthalene | 4.348 | 3.897 |
| α-Cresol | 3.266 | 2.930 |
| o-Cresol | 3.032 | 2.707 |
| m-Cresol | 3.109 | 2.767 |
| p-Cresol | 3.101 | 2.760 |
| Indane | 3.596 | 3.250 |
| Indene | 3.886 | 3.505 |
| Indenyl radical | 4.000 | 3.610 |
| α-Naphthol | 4.156 | 3.743 |
| α-Naphthoxy radical | 3.596 | 3.214 |
| β-Naphthol | 4.293 | 3.869 |
| β-Naphthoxy radical | 3.479 | 3.105 |
| o-1-Phenylyldioxyl radical | 2.258 | 2.026 |
| Phenol | 2.661 | 2.382 |
| Benzyne | 2.433 | 2.201 |
| Cyclohexdienenone | 2.163 | 1.918 |
| p-Benzoquinone | 1.655 | 1.463 |
| o-Benzoquinone | 1.794 | 1.596 |
| Anisole | 3.053 | 2.739 |
| Benzofuran | 3.286 | 2.964 |
| Indenone | 3.134 | 2.805 |
| Naphthalene | 4.156 | 3.749 |
| Phenylacetylene | 3.297 | 2.958 |
| Toluene | 2.961 | 2.647 |
| Reactions | A 1 | n | E, cal/mol |
|---|---|---|---|
| H4A2 = H4A2-1 + H | 3.24E + 116 | −28.775 | 151,649.4 |
| H4A2 = H4A2-2 + H | 3.24E + 116 | −28.775 | 164,149.4 |
| C9H7 => C7H5 + C2H2 | 1.526E + 108 | −25.979 | 180,259 |
| o-C6H4 + C3H3 => C9H7 | 7.46E + 100 | −25.035 | 61,535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matyushkov, V.V.; Chernov, A.A.; Novikov, M.V.; Osipova, K.N.; Bolshova, T.A.; Dmitriev, A.M.; Knyazkov, D.A.; Shmakov, A.G. Flame Speciation and Laminar Burning Velocity of Tetralin Flames Under Atmospheric Pressure. Energies 2025, 18, 5878. https://doi.org/10.3390/en18225878
Matyushkov VV, Chernov AA, Novikov MV, Osipova KN, Bolshova TA, Dmitriev AM, Knyazkov DA, Shmakov AG. Flame Speciation and Laminar Burning Velocity of Tetralin Flames Under Atmospheric Pressure. Energies. 2025; 18(22):5878. https://doi.org/10.3390/en18225878
Chicago/Turabian StyleMatyushkov, Vladislav V., Anatoly A. Chernov, Mikhail V. Novikov, Ksenia N. Osipova, Tatyana A. Bolshova, Artëm M. Dmitriev, Denis A. Knyazkov, and Andrey G. Shmakov. 2025. "Flame Speciation and Laminar Burning Velocity of Tetralin Flames Under Atmospheric Pressure" Energies 18, no. 22: 5878. https://doi.org/10.3390/en18225878
APA StyleMatyushkov, V. V., Chernov, A. A., Novikov, M. V., Osipova, K. N., Bolshova, T. A., Dmitriev, A. M., Knyazkov, D. A., & Shmakov, A. G. (2025). Flame Speciation and Laminar Burning Velocity of Tetralin Flames Under Atmospheric Pressure. Energies, 18(22), 5878. https://doi.org/10.3390/en18225878






