Multi-Criteria Model Predictive Controller for Hybrid Heating Systems in Buildings
Abstract
1. Introduction
1.1. Related Work
1.2. Research Aims and Contributions
- A multi-objective predictive controller designed to consider cost, emissions, and comfort level of the building’s indoor environment. The hybrid heating system is supplied by a heat pump and district heating.
- Proposing an MPC and a system architecture to assist the process of applying it to real-world hybrid-heated buildings
- Competitiveness analysis of district heating versus heat pumps in the Swedish energy market using real-world data.
- In a sensitivity analysis, investigating the control behavior under different cost, emission and outdoor weather condition scenarios.
2. Materials and Methods
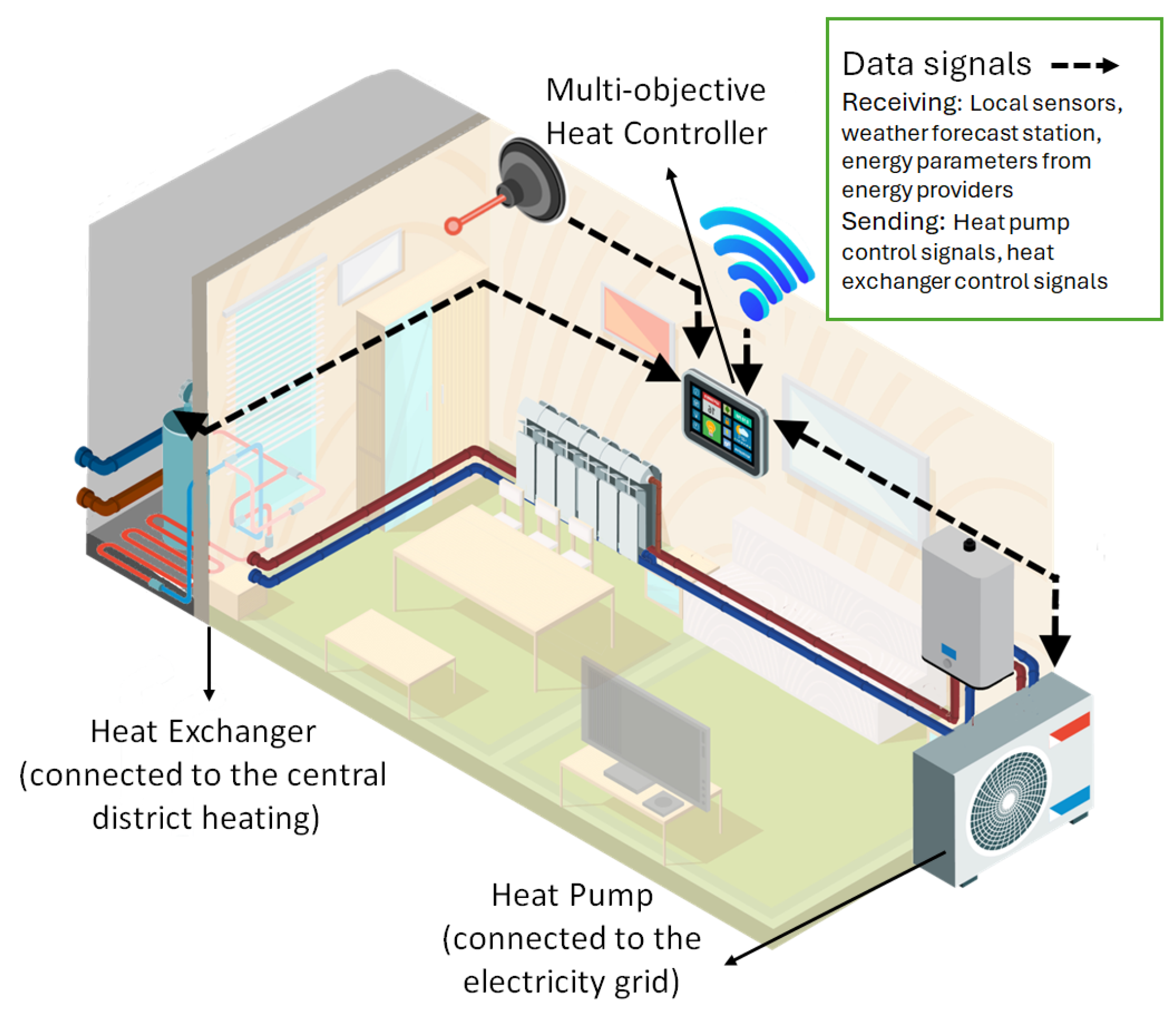
2.1. System Overview—Hybrid Heating System
2.2. System Architecture: Cloud and Local Data
2.3. State-Space Building Model
2.4. Multi-Objective Model Predictive Controller (MO-MPC)
- The cost objective has a value between 251 and 368.
- The emission objective has a value between 2.0 and 17.2.
- The discomfort index objective has a value between 1 and 192.
| Algorithm 1 Multi-Objective Model Predictive Controller |
|
3. Results
- The changes in building insulation wear and tear and efficiency of the heating systems are negligible during the simulation period.
- The size of the heating systems is selected in the sense that each heating resource can independently supply the building’s heating demand.
- The heating demand consists only of the space heating, and the domestic hot water demand is not considered.
3.1. Case Study
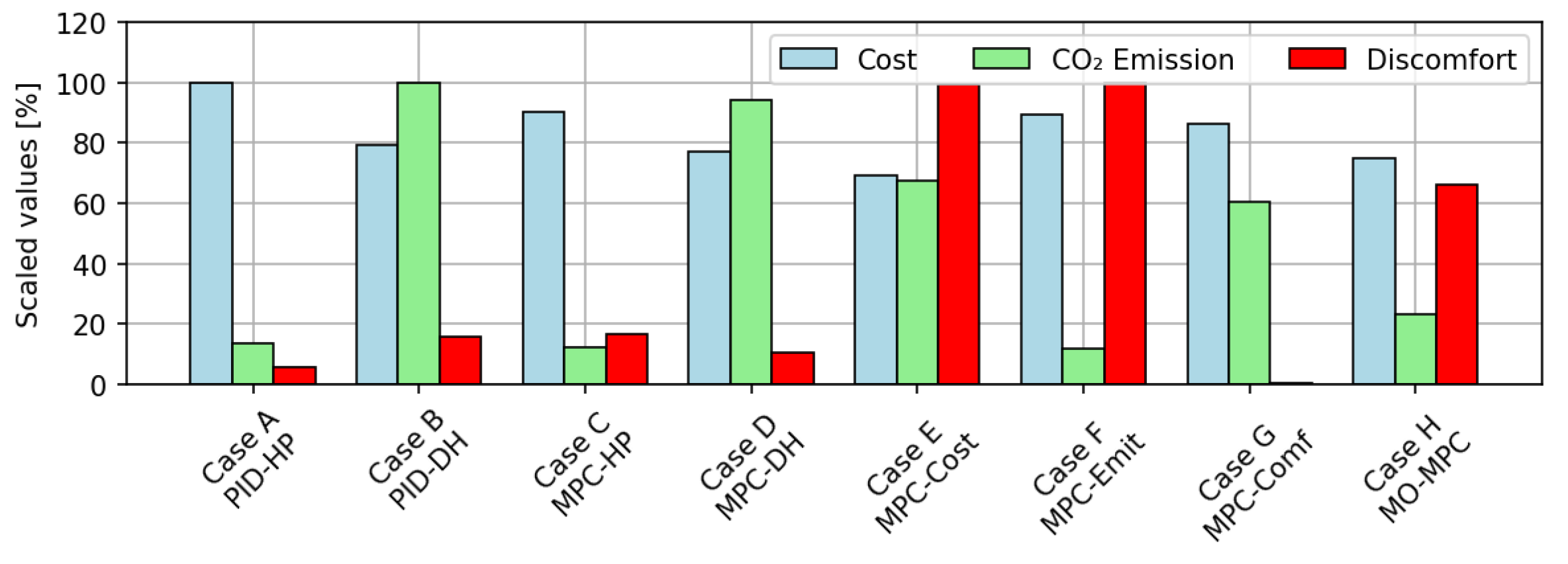
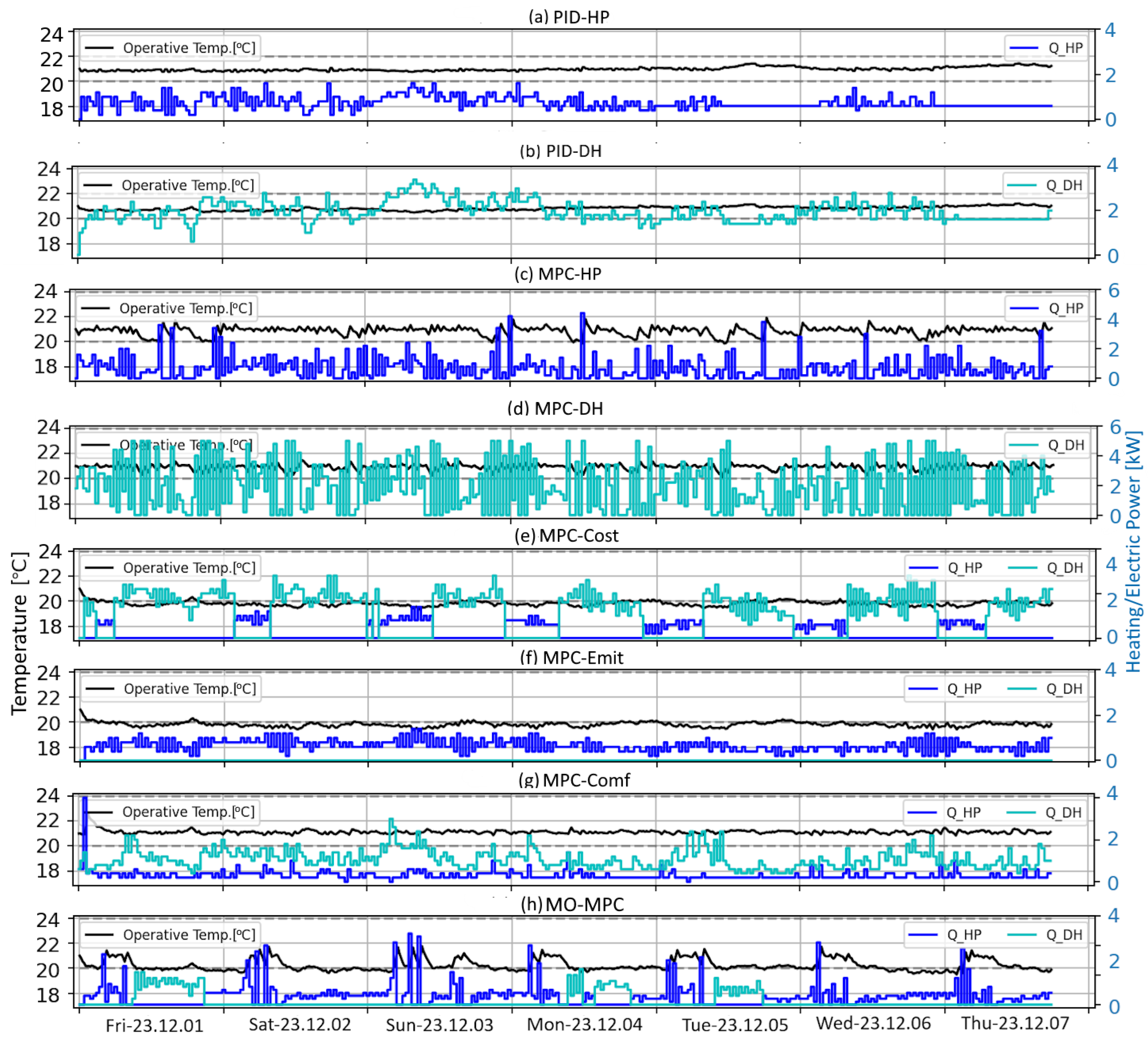
3.2. Simulation Results
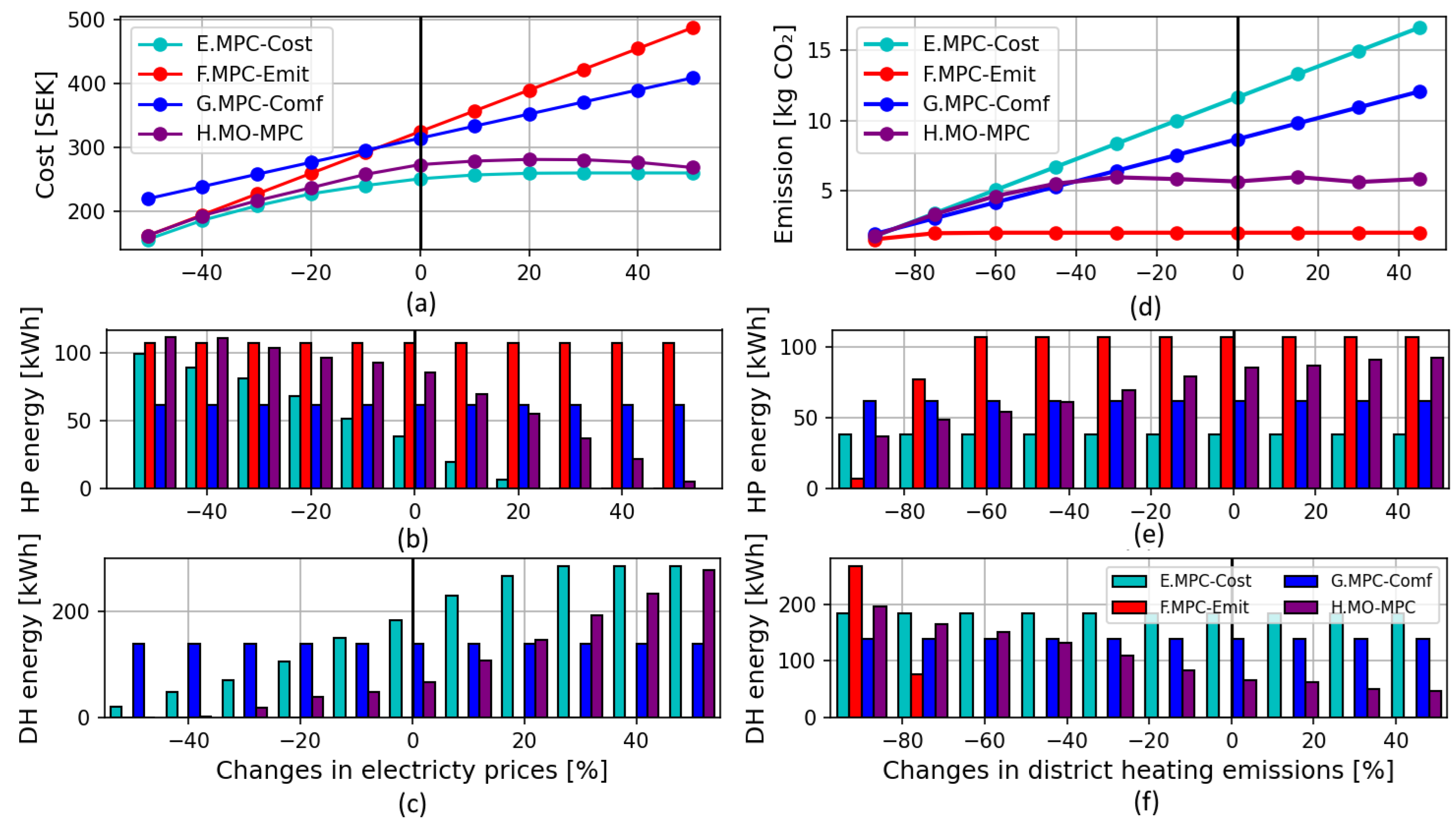
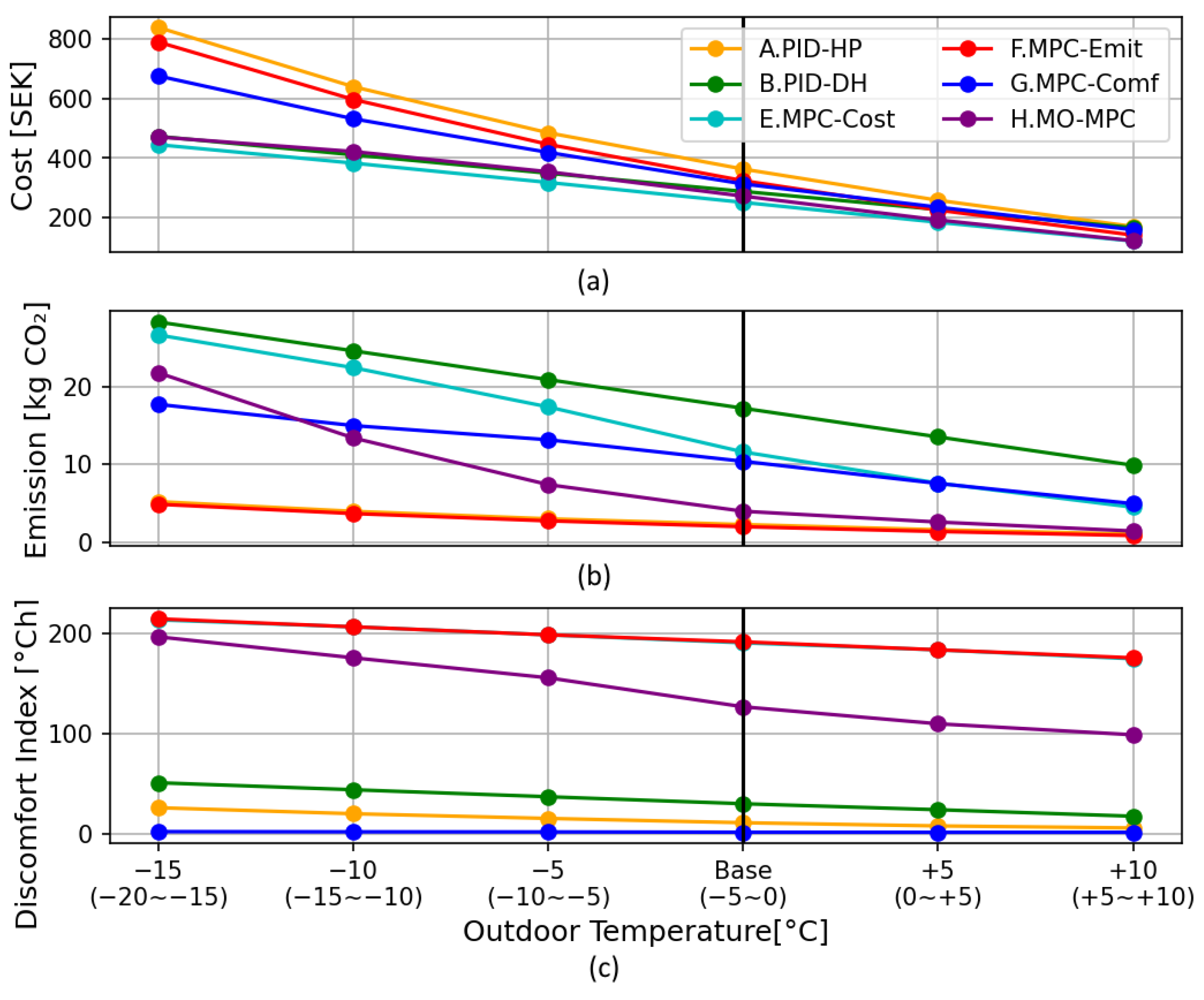
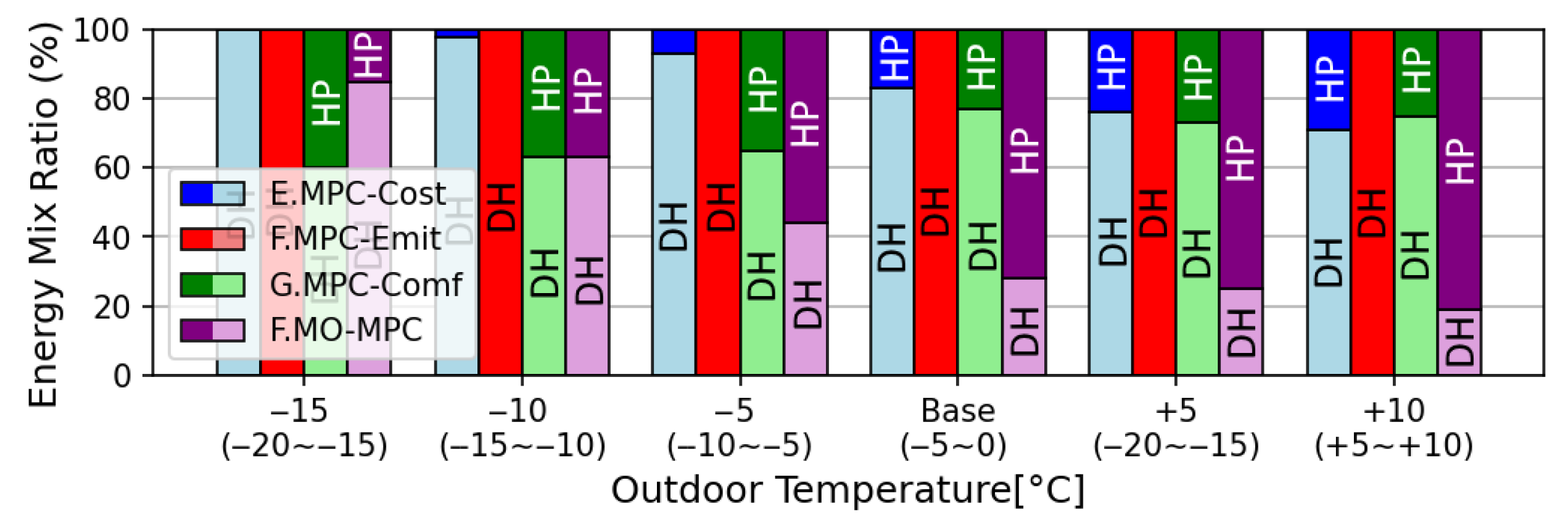
3.3. Sensitivity Analysis
3.3.1. Price Changes
3.3.2. Emission Changes
3.3.3. Weather Changes
4. Discussion
5. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DH | District Heating |
| HP | Heat Pump |
| MPC | Model Predictive Controller |
| MO-MPC | Multi-Objective Model Predictive Controller |
| PID | Proportional–Integral–Derivative |
| RBC | Rule-Based Controller |
| RC | Resistor–Capacitor |
| AHU | Air Handling Unit |
| COP | Coefficient of Performance |
| I.I.D. | Independent and Identically Distributed |
Appendix A. Gray-Box Model of the Building
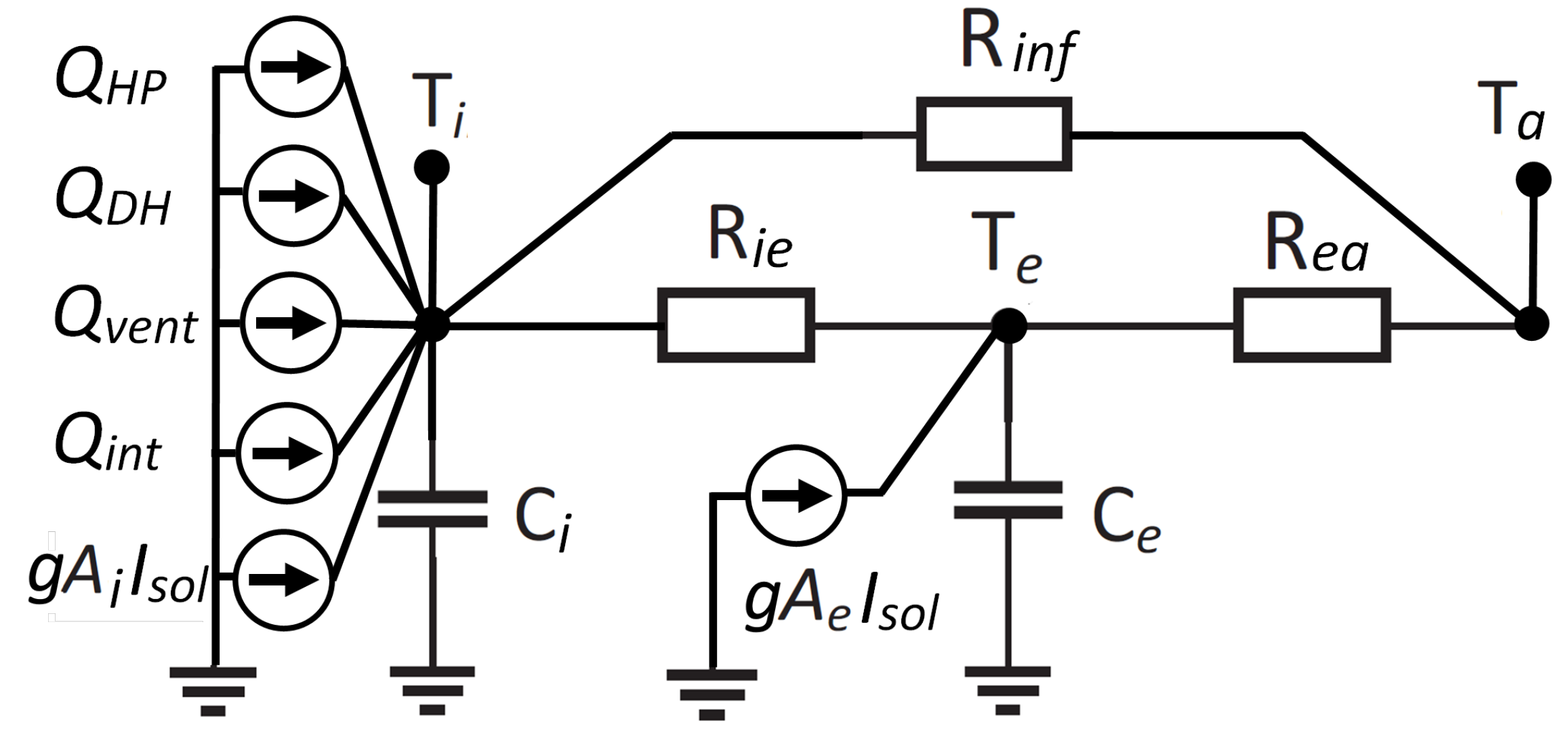
| Model Name | [°C/kWh] | [°C/kWh] | [°C/kWh] | [kWh/°C] | [kWh/°C] | [m2] | [m2] |
|---|---|---|---|---|---|---|---|
| 3R2Csto | 58.49 | 1.15 | 15.75 | 1.15 | 4.22 | 1.56 | 0.122 |
Appendix B. Discomfort Index—Operative Temperature
References
- European Heat Pump Association. Decarb Heat. 2023. Available online: https://www.ehpa.org/news-and-resources/campaigns/decarb-heat (accessed on 20 April 2025).
- Eurostats. Electricity and Heat Statistics. 2024. Available online: https://www.ec.europa.eu/eurostat/statistics-explained/index.php?title=Electricity_and_heat_statistics (accessed on 20 April 2025).
- Werner, S. European District Heating Price Series, DiVA Portal. 2016. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1067605 (accessed on 30 October 2025).
- Sayegh, M.A.; Jadwiszczak, P.; Axcell, B.; Niemierka, E.; Bryś, K.; Jouhara, H. Heat pump placement, connection and operational modes in European district heating. Energy Build. 2018, 166, 122–144. [Google Scholar] [CrossRef]
- European Heat Pump Association. European Heat Pump Market Statistics Report. 2023. Available online: https://www.ehpa.org/wp-content/uploads/2023/06/EHPA_market_report_2023_Executive-Summary.pdf (accessed on 20 April 2025).
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Maddalena, E.T.; Lian, Y.; Jones, C.N. Data-driven methods for building control—A review and promising future directions. Control Eng. Pract. 2020, 95, 104211. [Google Scholar] [CrossRef]
- Reda, F.; Paiho, S.; Pasonen, R.; Helm, M.; Menhart, F.; Schex, R.; Laitinen, A. Comparison of solar assisted heat pump solutions for office building applications in Northern climate. Renew. Energy 2020, 147, 1392–1417. [Google Scholar] [CrossRef]
- Hermansen, R.; Smith, K.; Thorsen, J.E.; Wang, J.; Zong, Y. Model predictive control for a heat booster substation in ultra low temperature district heating systems. Energy 2022, 238, 121631. [Google Scholar] [CrossRef]
- Abokersh, M.H.; Valles, M.; Saikia, K.; Cabeza, L.F.; Boer, D. Techno-economic analysis of control strategies for heat pumps integrated into solar district heating systems. J. Energy Storage 2021, 42, 103011. [Google Scholar] [CrossRef]
- Liu, D.x.; Lei, H.Y.; Li, J.S.; Dai, C.s.; Xue, R.; Liu, X. Optimization of a district heating system coupled with a deep open-loop geothermal well and heat pumps. Renew. Energy 2024, 223, 119991. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Huang, K.; Feng, G.; Li, X.; Cui, Y. Research on solar-air source heat pump coupled heating system based on heat network in severe cold regions of China. Energy Built Environ. 2024. [Google Scholar] [CrossRef]
- Fiorentini, M.; Heer, P.; Baldini, L. Design optimization of a district heating and cooling system with a borehole seasonal thermal energy storage. Energy 2023, 262, 125464. [Google Scholar] [CrossRef]
- Xue, T.; Jokisalo, J.; Kosonen, R. Cost-Effective Control of Hybrid Ground Source Heat Pump (GSHP) System Coupled with District Heating. Buildings 2024, 14, 1724. [Google Scholar] [CrossRef]
- Knudsen, M.D.; Petersen, S. Demand response potential of model predictive control of space heating based on price and carbon dioxide intensity signals. Energy Build. 2016, 125, 196–204. [Google Scholar] [CrossRef]
- Tarragona, J.; Fernández, C.; Cabeza, L.F.; de Gracia, A. Economic evaluation of a hybrid heating system in different climate zones based on model predictive control. Energy Convers. Manag. 2020, 221, 113205. [Google Scholar] [CrossRef]
- Baeten, B.; Rogiers, F.; Helsen, L. Reduction of heat pump induced peak electricity use and required generation capacity through thermal energy storage and demand response. Appl. Energy 2017, 195, 184–195. [Google Scholar] [CrossRef]
- Finck, C.; Li, R.; Zeiler, W. Optimal control of demand flexibility under real-time pricing for heating systems in buildings: A real-life demonstration. Appl. Energy 2020, 263, 114671. [Google Scholar] [CrossRef]
- Aruta, G.; Ascione, F.; Bianco, N.; Mauro, G.M.; Vanoli, G.P. Optimizing heating operation via GA-and ANN-based model predictive control: Concept for a real nearly-zero energy building. Energy Build. 2023, 292, 113139. [Google Scholar] [CrossRef]
- Qi, D.; Liu, Y.; Zhao, C.; Dong, Y.; Song, B.; Li, A. Thermal response and performance evaluation of floor radiant heating system based on fuzzy logic control. Energy Build. 2024, 313, 114232. [Google Scholar] [CrossRef]
- Underwood, C. Fuzzy multivariable control of domestic heat pumps. Appl. Therm. Eng. 2015, 90, 957–969. [Google Scholar] [CrossRef]
- Yang, J.; Wang, H.; Cheng, L.; Gao, Z.; Xu, F. A review of resistance–capacitance thermal network model in urban building energy simulations. Energy Build. 2024, 323, 114765. [Google Scholar] [CrossRef]
- ISO 13790:2008; Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling. 2nd ed. ISO: Geneva, Switzerland, 2008.
- VDI 6007-1; Calculation of Transient Thermal Response of Rooms and Buildings—Modelling of Rooms. German Association of Engineers (VDI): Düsseldorf, Germany, 2012.
- Vivian, J.; Zarrella, A.; Emmi, G.; De Carli, M. An evaluation of the suitability of lumped-capacitance models in calculating energy needs and thermal behaviour of buildings. Energy Build. 2017, 150, 447–465. [Google Scholar] [CrossRef]
- Yu, X.; Skeie, K.S.; Knudsen, M.D.; Ren, Z.; Imsland, L.; Georges, L. Influence of data pre-processing and sensor dynamics on grey-box models for space-heating: Analysis using field measurements. Build. Environ. 2022, 212, 108832. [Google Scholar] [CrossRef]
- Knudsen, M.D.; Georges, L.; Skeie, K.S.; Petersen, S. Experimental test of a black-box economic model predictive control for residential space heating. Appl. Energy 2021, 298, 117227. [Google Scholar] [CrossRef]
- Klanatsky, P.; Veynandt, F.; Heschl, C. Grey-box model for model predictive control of buildings. Energy Build. 2023, 300, 113624. [Google Scholar] [CrossRef]
- Wang, X.; Tian, S.; Ren, J.; Jin, X.; Zhou, X.; Shi, X. A novel resistance-capacitance model for evaluating urban building energy loads considering construction boundary heterogeneity. Appl. Energy 2024, 361, 122896. [Google Scholar] [CrossRef]
- Kastner, P.; Dogan, T. Towards Auto-Calibrated UBEM Using Readily Available, Underutilized Urban Data: A Case Study for Ithaca, NY. Energy Build. 2024, 317, 114286. [Google Scholar] [CrossRef]
- Bacher, P.; Madsen, H. Identifying suitable models for the heat dynamics of buildings. Energy Build. 2011, 43, 1511–1522. [Google Scholar] [CrossRef]
- NIBE. F2050 Air Source Heat Pump. Available online: https://www.nibe.eu/en-gb/products/heat-pumps/air-source-heat-pumps/f2050 (accessed on 20 April 2025).
- Google. Google Colaboratory. Available online: https://colab.research.google.com/ (accessed on 30 October 2025).
- Python Language Reference, Version 3.11; Python Software Foundation: Wake Forest, NC, USA, 2025. Available online: http://www.python.org (accessed on 30 October 2025).
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- The Joint Research Centre: EU Science Hub. Photovoltaic Geographical Information System (PVGIS). 2023. Available online: https://joint-research-centre.ec.europa.eu/photovoltaic-geographical-information-system-pvgis_en (accessed on 20 April 2025).
- E.on. Electricity Prices Hour by Hour. 2023. Available online: https://www.eon.se/el/elpriser/aktuella (accessed on 20 April 2025).
- E.on. District Heating Small Home 2023. 2023. Available online: https://www.eon.se/fjarrvarme/priser (accessed on 20 April 2025).
- Nowtricity. Real Time Live Emissions from Energy Production by Country. 2023. Available online: https://www.nowtricity.com/country/sweden (accessed on 20 April 2025).
- Piltz Vitanc, L.; Hinsegård, M. Emission Factors and Methods Used in Climate Impact Assessments of Energy Use in Swedish Heated Buildings-Assessing District Heating and Electricity as Energy Source. 2023. Available online: https://lup.lub.lu.se/student-papers/search/publication/9122136 (accessed on 30 October 2025).
- Gadd, H.; Werner, S. Daily heat load variations in Swedish district heating systems. Appl. Energy 2013, 106, 47–55. [Google Scholar] [CrossRef]
- Paris, B.; Eynard, J.; Grieu, S.; Talbert, T.; Polit, M. Heating control schemes for energy management in buildings. Energy Build. 2010, 42, 1908–1917. [Google Scholar] [CrossRef]
- Sameti, M.; Haghighat, F. Optimization approaches in district heating and cooling thermal network. Energy Build. 2017, 140, 121–130. [Google Scholar] [CrossRef]
- O’Dwyer, E.; De Tommasi, L.; Kouramas, K.; Cychowski, M.; Lightbody, G. Prioritised objectives for model predictive control of building heating systems. Control Eng. Pract. 2017, 63, 57–68. [Google Scholar] [CrossRef]
- Mattson, C.A.; Messac, A. Pareto frontier based concept selection under uncertainty, with visualization. Optim. Eng. 2005, 6, 85–115. [Google Scholar] [CrossRef]
- Ritchie, M.; Engelbrecht, J.; Booysen, M. A probabilistic hot water usage model and simulator for use in residential energy management. Energy Build. 2021, 235, 110727. [Google Scholar] [CrossRef]
- Gelažanskas, L.; Gamage, K.A. Forecasting hot water consumption in residential houses. Energies 2015, 8, 12702–12717. [Google Scholar] [CrossRef]
- Sartori, I.; Walnum, H.T.; Skeie, K.S.; Georges, L.; Knudsen, M.D.; Bacher, P.; Candanedo, J.; Sigounis, A.M.; Prakash, A.K.; Pritoni, M.; et al. Sub-hourly measurement datasets from 6 real buildings: Energy use and indoor climate. Data Brief 2023, 48, 109149. [Google Scholar] [CrossRef]
- ISO 7726:1998; Ergonomics of the Thermal Environment—Instruments for Measuring Physical Quantities. ISO: Geneva, Switzerland, 1998.
- Olesen, B.W.; Wang, H.; Kazanci, O.B. The Effect of Room Temperature Control by Air-Or Operative Temperature on Thermal Comfort and Energy Use. In Proceedings of the Building Simulation 2019; IBPSA: Brussels, Belgium, 2019; Volume 16, pp. 2086–2093. [Google Scholar]



| Ref. | Method | Building Model | Energy Type(s) | Objective(s) | Results |
|---|---|---|---|---|---|
| [8] | Rule-based | White | District heating, heat pump, solar energy | Energy efficiency, renewable use | Up to 25% on-site renewable use in solar-assisted heat pump scenario and lowering heat pump input temperature from 5 to 10 degrees. |
| [9] | MPC, rule-based | White | Low-temperature district heating, heat pump, thermal storage | Economic | 23% cost saving with dynamic electricity prices. As a result of load shifting with the multiple input energies and thermal storage. |
| [10] | Rule-based | White | District heating, heat pump, thermal storage, gas boiler, solar fields | Economic | Solar fields, electricity grid, and natural gas resources are optimally allocated. In the best case, 7% economic savings and 75% use of solar fields are achieved. |
| [11] | Rule-based | White | District heating, heat pump | Energy efficiency, resource sizing, investment | The setting and optimal size of a heat pump that has the most efficiency coupled with the district heating. |
| [12] | Rule-based | White | District heating, heat pump, thermal storage, solar energy | Economic, renewable use | Solar-assisted heat pump compared to a normal one can save up to 50.9% energy and 28% cost. |
| [13] | Rule-based | White | District heating, heat pump, thermal storage, solar energy | Economic, Environment | More than 27% reduction in CO2 emission of electricity use when using the thermal storage and load shifting, and an extra 3.9–9.7% reduction potential when using solar-assisted heat pumps. |
| [14] | Rule-based | White | District heating, heat pump, | Economic, environment | A 2.2% reduction in annual energy cost while increasing the CO2 emission slightly, in the optimal solution. |
| [15] | MPC, PID | White | Heat pump | Economic, environment | An MPC with different penalty weights was assessed. Depending on the weights, savings on cost and emissions can be achieved. |
| [16] | MPC, rule-based | White | Heat pump, solar energy, thermal storage | Economic, renewable use | MPC strategy has 16–22% cost savings compared to rule-based algorithm while significantly decreasing the power purchased from grid and promoting on-site renewable use. |
| [17] | MPC | Gray | Heat pump | Economic, Environment, Sizing | Adding the thermal storage increases the load-shifting abilities, while decreasing the peak demand by 11%. |
| [18] | MPC, rule-based | Black | Heat pump, thermal storage, solar energy | Economic, demand prediction | The MPC, compared to the rule-based strategy, enables demand flexibility and optimize energy consumption, leading to lower overall energy cost. |
| [19] | MPC | Black | Economic, comfort | A cost savings of up to 26% with an improved comfort level is achieved through the proposed GA- and ANN-based MPC strategy compared to the reference control strategy. | |
| [20] | Fuzzy-logic, PID | White | Ground source heat pump, thermal storage | Energy efficiency | With the optimal control strategy, more than 200 kWh has been saved while the predicted mean vote (PMV) index has improved greatly. |
| [21] | Fuzzy-logic | - | Heat pump, thermal storage | Energy efficiency | The fuzzy multi-variable controller can achieve 20% energy saving while improving the temperature setpoint tracking. |
| This paper | MPC, PID | Gray | District heating, heat pump | Economic, environment, comfort | (refer to Section 3). |
| Case | Description | Energy Source(s) | Objective(s) | |||
|---|---|---|---|---|---|---|
|
Heat
Pump |
District
Heating | Cost | Emission | Comfort | ||
| A | PID-HP | ✓ | - | - | - | - |
| B | PID-DH | - | ✓ | - | - | - |
| C | MPC-HP | ✓ | - | ✓ | ✓ | ✓ |
| D | MPC-DH | - | ✓ | ✓ | ✓ | ✓ |
| E | MPC-Cost | ✓ | ✓ | ✓ | - | - |
| F | MPC-Emission | ✓ | ✓ | - | ✓ | - |
| G | MPC-Comfort | ✓ | ✓ | - | - | ✓ |
| H | MO-MPC | ✓ | ✓ | ✓ | ✓ | ✓ |
| Definition | Symbol | Value | |
|---|---|---|---|
| HP | Model | - | F2050-6 [32] |
| Type | - | air-to-water [32] | |
| Max. electrical power [kW] | 6 [32] | ||
| Min. power [kW] | - | 0 | |
| Coefficient of Performance | Acc. to Equation (6) [32] | ||
| DH | Max. heating power [kW] | 6 | |
| Min. power [kW] | - | 0 | |
| Heat exchanger efficiency | 0.98 |
| Definition | Symbol | Value | |
|---|---|---|---|
| MPC | Type | - | Discrete MPC |
| Optimization type | - | Non-Linear | |
| Operative temp. low/up setpoint [°C] | 20/24 | ||
| Comfort zone operative temp. [°C] | / | 21/23 | |
| Simulation Horizon [hr] | 168 | ||
| Simulation Sample time [min] | 15 | ||
| Control horizon [hr] | 6 | ||
| Control signal interval [min] | - | 30 | |
| PID | Operative temp. setpoint [°C] | - | 21–23 |
| Proportional factor | - | 5.0 | |
| Integral factor | - | 0.1 | |
| Derivative factor | - | 0.05 | |
| Control signal interval [min] | - | 30 |
| Case | Objective | Energy Consumption | Operative Temp. | |||||
|---|---|---|---|---|---|---|---|---|
|
Cost
[SEK] |
Emission
[kg CO2] |
Discomfort
Index [°Ch] |
District
Heating [kWh] |
Heat
Pump [kWh] |
Total
[kWh] |
Min.
[°C] |
Max.
[°C] | |
| A.PID-HP | 363 | 2.3 | 11 | 0 | 120 | 120 | 20.6 | 21.7 |
| B.PID-DH | 288 | 17.2 | 30 | 317 | 0 | 317 | 20.5 | 21.4 |
| C.MPC-HP | 327 | 2.1 | 32 | 0 | 115 | 115 | 19.8 | 21.4 |
| D.MPC-DH | 280 | 16.2 | 20 | 308 | 0 | 308 | 20.1 | 21.4 |
| E.MPC-Cost | 251 | 11.6 | 191 | 184 | 38 | 222 | 19.7 | 21.0 |
| F.MPC-Emit | 325 | 2.0 | 192 | 0 | 107 | 107 | 19.7 | 21.0 |
| G.MPC-Comf | 313 | 10.4 | 1 | 175 | 51 | 226 | 20.8 | 24.3 |
| H.MO-MPC | 272 | 4.0 | 127 | 96 | 38 | 134 | 19.8 | 23.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soleimani, A.; Davidsson, P.; Malekian, R.; Spalazzese, R. Multi-Criteria Model Predictive Controller for Hybrid Heating Systems in Buildings. Energies 2025, 18, 5839. https://doi.org/10.3390/en18215839
Soleimani A, Davidsson P, Malekian R, Spalazzese R. Multi-Criteria Model Predictive Controller for Hybrid Heating Systems in Buildings. Energies. 2025; 18(21):5839. https://doi.org/10.3390/en18215839
Chicago/Turabian StyleSoleimani, Ali, Paul Davidsson, Reza Malekian, and Romina Spalazzese. 2025. "Multi-Criteria Model Predictive Controller for Hybrid Heating Systems in Buildings" Energies 18, no. 21: 5839. https://doi.org/10.3390/en18215839
APA StyleSoleimani, A., Davidsson, P., Malekian, R., & Spalazzese, R. (2025). Multi-Criteria Model Predictive Controller for Hybrid Heating Systems in Buildings. Energies, 18(21), 5839. https://doi.org/10.3390/en18215839








