Energy Management of Hybrid Energy System Considering a Demand-Side Management Strategy and Hydrogen Storage System

Abstract

A hybrid energy system (HES) integrates various energy resources to attain synchronized energy output. However, HES faces significant challenges due to rising energy consumption, the expenses of using multiple sources, increased emissions due to non-renewable energy resources, etc. This study aims to develop an energy management strategy for distribution grids (DGs) by incorporating a hydrogen storage system (HSS) and demand-side management strategy (DSM), through the design of a multi-objective optimization technique. The primary focus is on optimizing operational costs and reducing pollution. These are approached as minimization problems, while also addressing the challenge of achieving a high penetration of renewable energy resources, framed as a maximization problem. The third objective function is introduced through the implementation of the demand-side management strategy, aiming to minimize the energy gap between initial demand and consumption. This DSM strategy is designed around consumers with three types of loads: sheddable loads, non-sheddable loads, and shiftable loads. To establish a bidirectional communication link between the grid and consumers by utilizing a distribution grid operator (DGO). Additionally, the uncertain behavior of wind, solar, and demand is modeled using probability distribution functions: Weibull for wind, PDF beta for solar, and Gaussian PDF for demand. To tackle this tri-objective optimization problem, this work proposes a hybrid approach that combines well-known techniques, namely, the non-dominated sorting genetic algorithm II and multi-objective particle swarm optimization (Hybrid-NSGA-II-MOPSO). Simulation results demonstrate the effectiveness of the proposed model in optimizing the tri-objective problem while considering various constraints.

1. Introduction

The rapid growth of hybrid energy systems (HESs), which combine renewable and conventional energy sources within a unified operational structure, is being driven by a range of environmental concerns, economic considerations, and operational needs. These systems integrate variable renewables such as photovoltaic solar and wind energy with controllable conventional units, helping to lower greenhouse gas emissions while maintaining a reliable electricity supply [1]. Additionally, HES significantly strengthens grid infrastructure by incorporating advanced energy storage solutions like electrochemical batteries and hydrogen storage systems (HSS). These technologies support functions such as frequency regulation, peak demand reduction, and quick system recovery following disturbances [2]. Their economic and technical viability is further supported by resource scheduling optimization, demand forecasting, and favorable policy incentives. As a result, HESs are becoming increasingly attractive in both developed and developing markets [3]. Continuous improvements in renewable generation technologies, smart grid management, and digital control systems are expected to further accelerate their deployment, ultimately contributing to a more resilient and low-carbon energy network [4,5]. At the same time, implementing demand-side management (DSM) strategies requires bidirectional communication systems that allow real-time data exchange between consumers and utilities. This ensures dynamic load control and higher system efficiency.

Despite their advantages, the deployment of HES involves significant operational and control-related difficulties. One of the primary challenges is the coordination of distributed energy resources, as the unpredictable nature of renewables leads to variations and uncertainty in supply–demand balance [6,7]. These variations can result in voltage instability, frequency deviations, and reduced power quality, which are less prominent in traditional centralized grids [8]. To manage these challenges, advanced control strategies, predictive energy flow algorithms, and adaptive optimization techniques are necessary to ensure consistent and reliable power delivery [9,10,11]. Renewable energy technologies remain crucial to the global energy transition due to their carbon-neutral nature, safety, and resistance to fuel price fluctuations [12,13,14]. However, the intermittent nature of these resources, along with limitations in large-scale energy storage, presents ongoing research challenges. Key issues include improving storage duration, lifecycle efficiency, and cost-effectiveness [15,16].

One increasingly promising option for renewable energy storage is the use of hydrogen. Hydrogen offers benefits such as ease of storage, transportability, and broad availability [17,18]. Hydrogen storage systems are recognized as cost-efficient solutions for capturing excess renewable electricity, with applications extending from stationary storage to transportation and international energy trade [19,20]. A few studies [21,22,23,24] highlight the essential role of hydrogen in building a hydrogen-based energy economy where renewables meet most or all energy needs. This transition is advancing in sectors like electricity generation, industrial production, and transportation, offering a clear path toward deep decarbonization [25,26,27,28].

Hydrogen is particularly useful in smart microgrid applications. Its high energy density and multi-functional characteristics make it ideal for storing electricity. Surplus energy generated during off-peak times can be converted into hydrogen through electrolysis, stored in compressed or liquid form, and later converted back into electricity during peak periods. Advancements in electrolyzer technologies, including proton exchange membrane (PEM) and solid oxide electrolyzers, have significantly increased efficiency, making hydrogen a more viable option for grid-scale storage [29,30,31]. However, barriers remain. These include high capital investment requirements, conversion losses across the hydrogen lifecycle, and the environmental impact of large-scale hydrogen production. Ongoing research is focusing on reducing costs, improving system efficiency, and enabling green hydrogen production using only renewable energy sources [32].

Hydrogen also plays an important role in smart grids by helping mitigate the variability of renewable energy sources and increasing grid reliability. Although batteries, particularly lithium-ion types, are widely used in smart grid systems due to their high efficiency, scalability, and rapid response times [33,34], they face challenges such as limited cycle life, performance degradation, and material supply constraints. These limitations have encouraged interest in hybrid storage systems.

Combining hydrogen and battery technologies is gaining traction as a hybrid energy storage strategy that leverages the complementary strengths of both. In smart grid settings, this combination allows for a continuous and flexible energy supply, especially in areas that rely heavily on intermittent sources such as solar and wind power [35]. Batteries provide fast-responding, short-term energy balancing, while hydrogen supports long-duration and large-scale storage. When used together, these technologies create a robust energy storage framework capable of maintaining supply reliability regardless of weather conditions or fluctuating electricity demand. Empirical evidence suggests that integrated hydrogen–battery systems can improve grid performance, lower emissions, and support the broader integration of renewable energy [36,37,38].

Although several important performance goals for HES have been identified in existing literature, many unresolved issues remain [39,40]. One major challenge involves determining the optimal size of system components to achieve multiple objectives. These objectives include minimizing operational costs, reducing emissions, maximizing renewable energy usage, and improving supply–demand alignment, all while ensuring power reliability and availability [41,42,43,44]. Balancing these competing goals makes system optimization particularly complex.

Moreover, operating a fully integrated HES requires detailed monitoring and control across multiple subsystems. Each element must work in coordination, often through real-time, bidirectional communication between energy providers and users to support DSM practices [45,46,47,48]. The control system becomes a critical part of the infrastructure, managing how generation, storage, and consumption interact. Well-designed control strategies can enhance system-wide performance, although maintaining effective operator engagement in decentralized and distributed systems remains a challenge [49,50,51,52].

Additional complexity arises when incorporating multiple energy storage types, especially in hybrid configurations involving both battery systems and hydrogen storage. Batteries excel at short-duration balancing and rapid discharge, while hydrogen is better suited for long-term energy storage. However, combining these systems presents unique design and control challenges. Accurate modeling of uncertainties in load demand and renewable generation is necessary. Effective operation depends on advanced optimization techniques that can balance technical performance, cost constraints, and environmental impact. While integrating hydrogen and battery technologies in HES shows promise for creating stable and sustainable energy systems, the widespread implementation of such systems remains a major focus of ongoing research [53,54,55,56,57].

Table 1. Comparison of existing and proposed studies [58].

References	Objectives	Techniques	Optimization	Limitations
[41]	Minimization of total cost	Constraint and Column Generation Algorithm	Single-objective	Emission and energy gap not considered
[42]	Enhancement of control performance	Genetic Algorithm (GA)	Single-objective	Economic cost and emission factors omitted
[43]	Reduction in operational cost and improvement of stability	Asynchronous Advantage Actor–Critic (A3C) Reinforcement Learning	Bi-objective	Environmental emissions not evaluated
[44]	Minimization of capital and replacement expenditures	Mixed-Integer Quadratic Constrained Programming (MIQCP)	Bi-objective	Energy balance and emissions disregarded
[45]	Minimization of energy deficit and demand mismatch	Improved Harmony Search integrated with GIS	Single-objective	Emission impacts not assessed
[46]	Optimization of levelized cost of energy	Particle Swarm Optimization (PSO) combined with Ant Colony Optimization (ACO)	Single-objective	Emissions not considered
[47]	Cost reduction	Artificial Bee Colony–Particle Swarm Optimization (ABC–PSO)	Single-objective	Environmental impact excluded
[48]	Minimization of operational cost and economic performance assessment	Adaptive Inertia Weight PSO (PSO-AIW) and Constriction Factor PSO (PSO-CF)	Bi-objective	Energy gap and emission parameters omitted
[49]	Minimization of energy consumption cost	Mixed-Integer Linear Programming (MILP)	Single-objective	Energy gap and emissions not included
This study	Minimization of operational cost and pollutant emissions, reduction in energy gap, and enhancement of renewable energy penetration	Hybrid NSGA-II–MOPSO	Tri-objective	–

shows the oomparison of existing and proposed studies.

Accordingly, this research emphasizes the energy management of distribution networks that incorporate demand-side management (DSM), battery systems, and hydrogen storage systems (HSS). The primary aim is to formulate a multi-objective framework that includes minimizing both operational costs and environmental emissions, along with maximizing the integration of renewable energy sources. Additionally, the third objective is introduced through the DSM framework, which focuses on reducing the discrepancy between the initial energy demand and actual consumption. The core contributions of this study are outlined as follows:

• Implementation of a hybrid energy storage architecture that combines hydrogen and battery systems to ensure coordinated and efficient energy delivery.
• Identification and mitigation of key challenges in hybrid energy systems, including increasing energy demand, cost escalation, and emissions, accompanied by a strategic planning model to address these concerns.
• Formulation of a multi-objective optimization strategy for distribution systems aimed at minimizing operational expenses, lowering pollutant levels, and enhancing the share of renewable energy in the energy mix.
• Integration of a DSM framework supported by two-way communication between consumers and utilities, combined with a hybrid optimization algorithm (Hybrid-MOPSO-NSGA-II), to solve the complex tri-objective optimization problem efficiently.

The structure of the paper is arranged as follows: Section 2 outlines the formulation of the research problem. Section 3 describes the configuration and components of the proposed system. In Section 4, a comprehensive explanation of the adopted methodology is provided. Section 5 presents the simulation outcomes along with an analysis of system performance. Lastly, Section 6 summarizes the main conclusions and offers insights into future research directions.

2. Problem Statement

The HES faces substantial challenges, including a growing rate of energy consumption, cost inefficiencies due to multiple energy sources, and an increase in emissions from non-renewable resources. The key issue is the lack of an efficient energy management strategy for distribution grids that can effectively integrate hydrogen storage and demand-side management while optimizing operational costs, reducing pollution, and maximizing renewable energy utilization. To address this complex tri-objective optimization problem comprehensively, the research proposes a hybrid approach that combines established optimization techniques, specifically, NSGA-II and MOPSO, into a unified framework known as Hybrid-NSGA-II-MOPSO. This study aims to validate how the proposed model can be applied in addressing the tri-objective optimization problem while accounting for a range of real-world operational constraints.

3. Proposed System Model Overview and Analysis

This research addresses a tri-objective optimization problem for a distribution grid that integrates renewable energy sources along with a demand-side management (DSM) approach. The objectives of the optimization focus on lowering operational expenses and environmental pollution, enhancing the share of renewable energy integration, and narrowing the gap between the original demand and the optimized level of consumption. To solve this complex model, a hybrid optimization algorithm combining MOPSO and NSGA-II is employed, considering multiple operational constraints. The energy flow of the proposed system is illustrated in Figure 1.

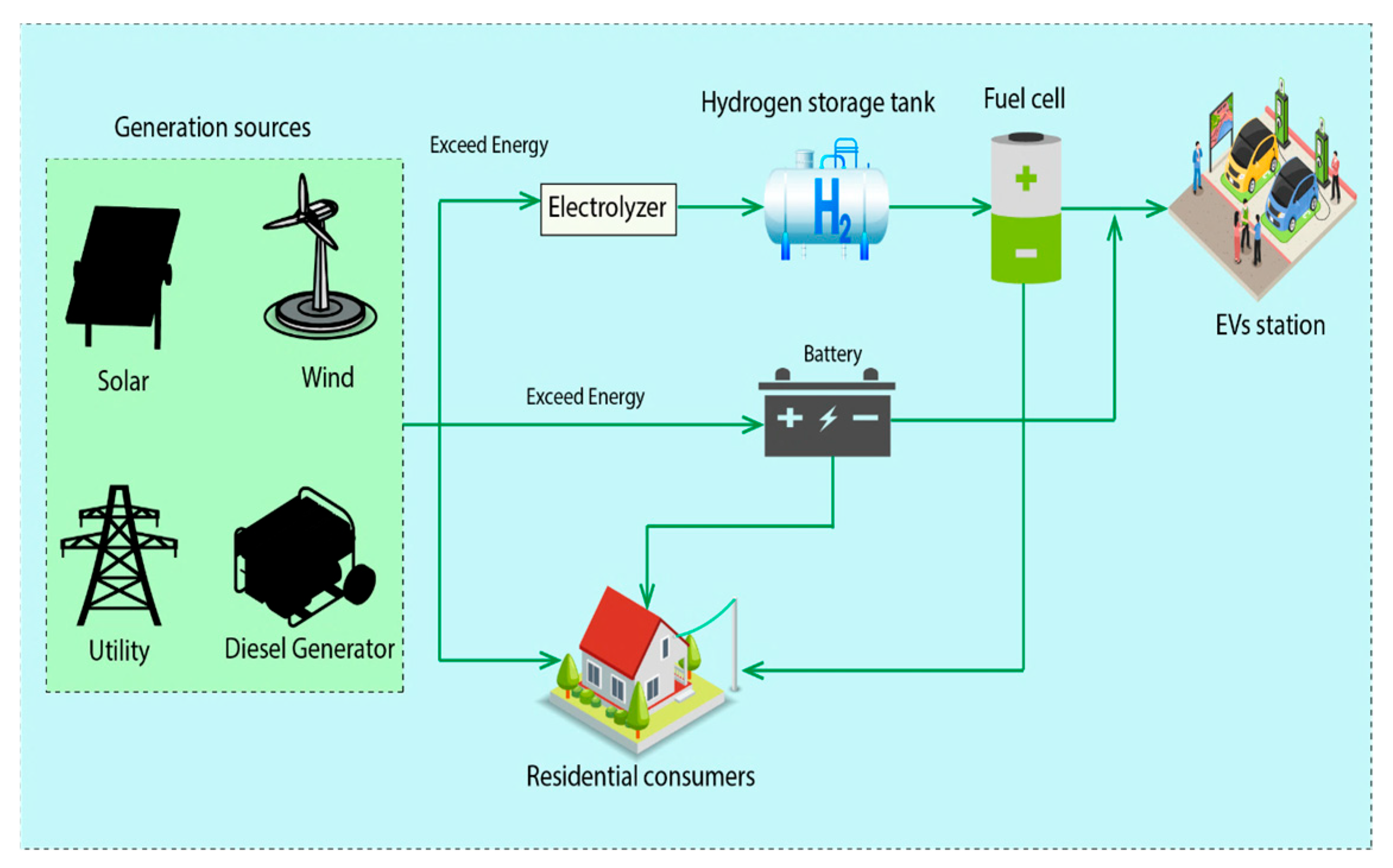
3.1. Smart Grid Overview and Working Mechanism

The schematic representation of the proposed residential smart grid is illustrated in Figure 1. The system integrates multiple key components, including distributed energy resources (DERs), residential consumers, an electric vehicle (EV) charging station, and energy storage systems. The DERs consist of solar photovoltaic (PV) panels, wind turbines (WTs), a diesel generator (DG), and a utility grid supply. Excess energy generated from these sources is directed either to a battery storage system or an electrolyzer, which converts the surplus into hydrogen for storage. The stored hydrogen is later utilized by a fuel cell to support EV charging and meet residential demand. Consumers are served from both the grid and storage systems, and their loads are categorized into sheddable, non-sheddable, and shiftable types to support demand-side management (DSM). Technical constraints on each resource and system component are also considered. The model is solved using a Hybrid-NSGA-II-MOPSO optimization approach to generate a set of non-dominated solutions, and a decision-making mechanism is then applied to select the most suitable solution from the Pareto front.

When solar output declines, household electricity needs are sustained through the coordinated use of battery storage, hydrogen reserves, and the utility grid, thereby maintaining an uninterrupted supply of power. Similarly, in the absence of wind generation, the combined support of solar energy, battery systems, hydrogen storage, and grid infrastructure provides a stable and reliable source of electricity. In addition, surplus energy from renewable generation can be effectively allocated to charging electric vehicles at designated stations, fostering the development of sustainable and environmentally conscious transportation. This comprehensive energy management framework not only improves overall efficiency in resource utilization but also substantially reduces reliance on conventional non-renewable sources [51,52,53].

3.2. Uncertain Systems Modeling

Because renewable energy sources are inherently uncertain, forecasting their output is essential prior to their integration with power grids. Probability density functions (PDFs) are employed to represent the variability of wind and solar resources. Specifically, wind uncertainty is characterized using the Weibull PDF, photovoltaic generation is described through the beta PDF, and load demand is represented by the Gaussian PDF [54,55,56].

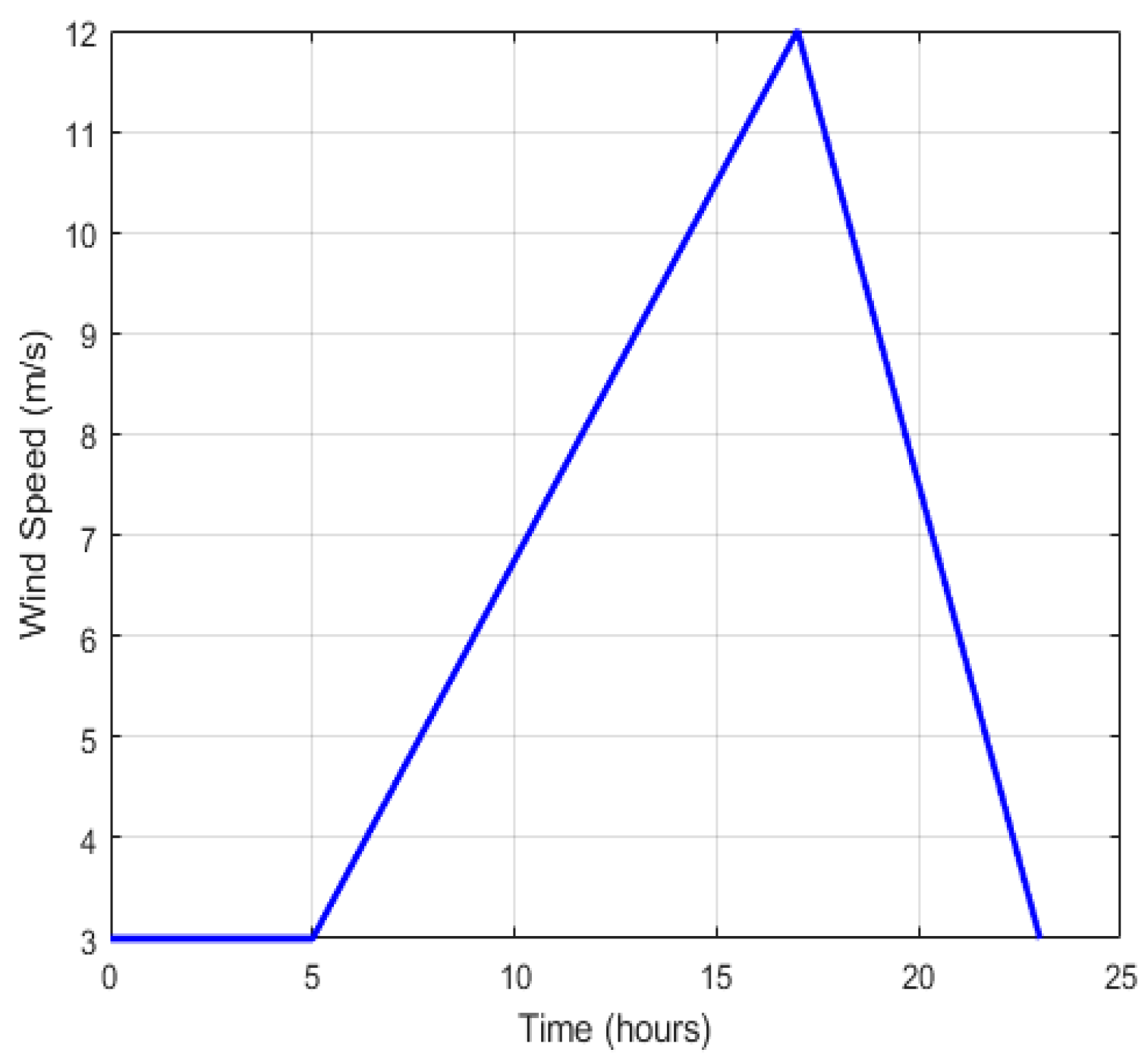
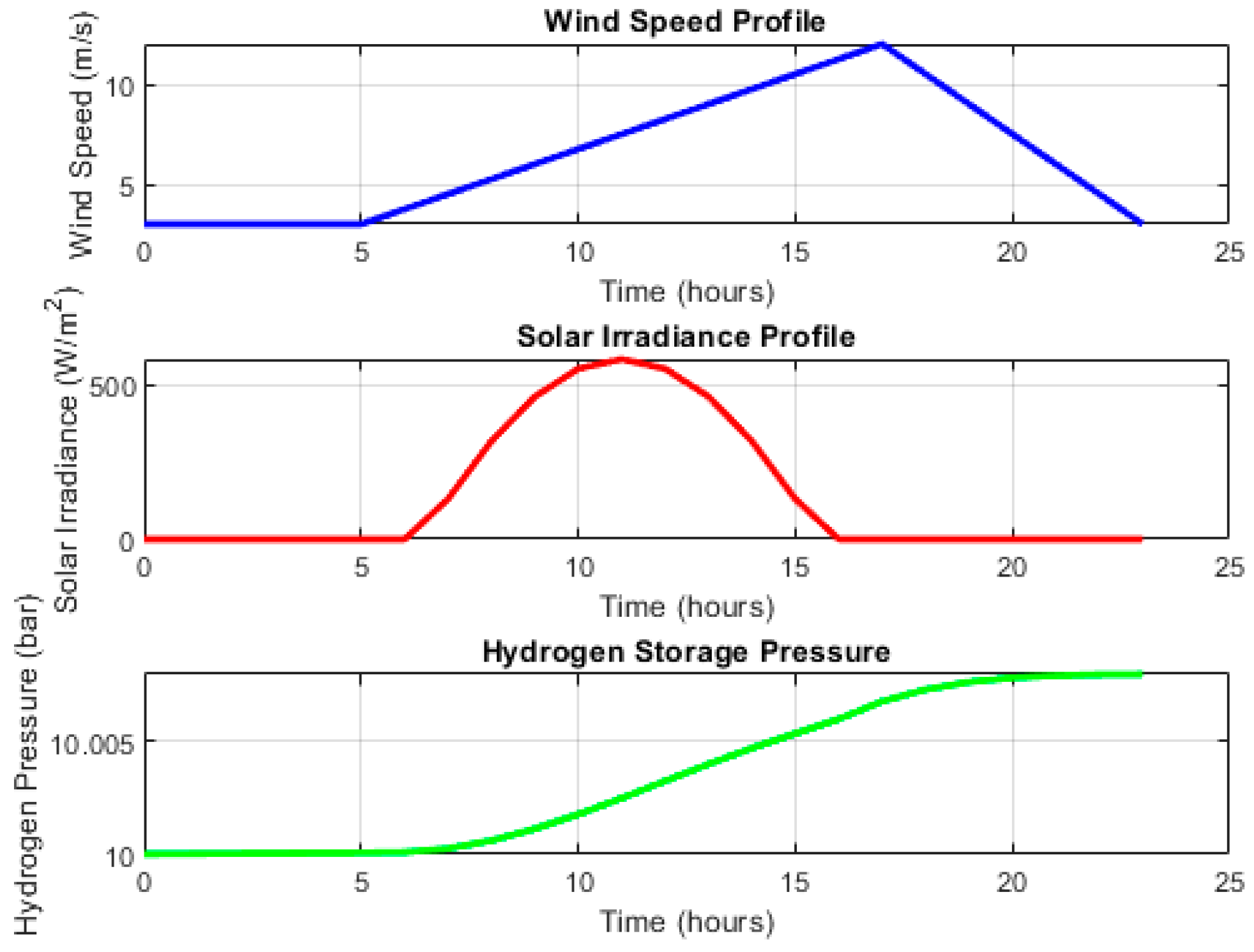
3.2.1. Wind System Modeling

Due to the inherent unpredictability of wind energy, the Weibull probability density function (PDF) is commonly applied to represent the variable characteristics of wind speed [51]. The power generated by wind turbines is expressed in Equation (1).

$$W_{wt}\left(s\right)=\left\{\begin{array}{c}0 if S\le S_{ci}\\ W_{wt}\times \left({\displaystyle \frac{s-S_{ci}}{S_r-S_{ci}}}\right) if S_{ci}\le s\le S_{co}\\ 0 if S_{co}\le s\end{array}\right.$$

(1)

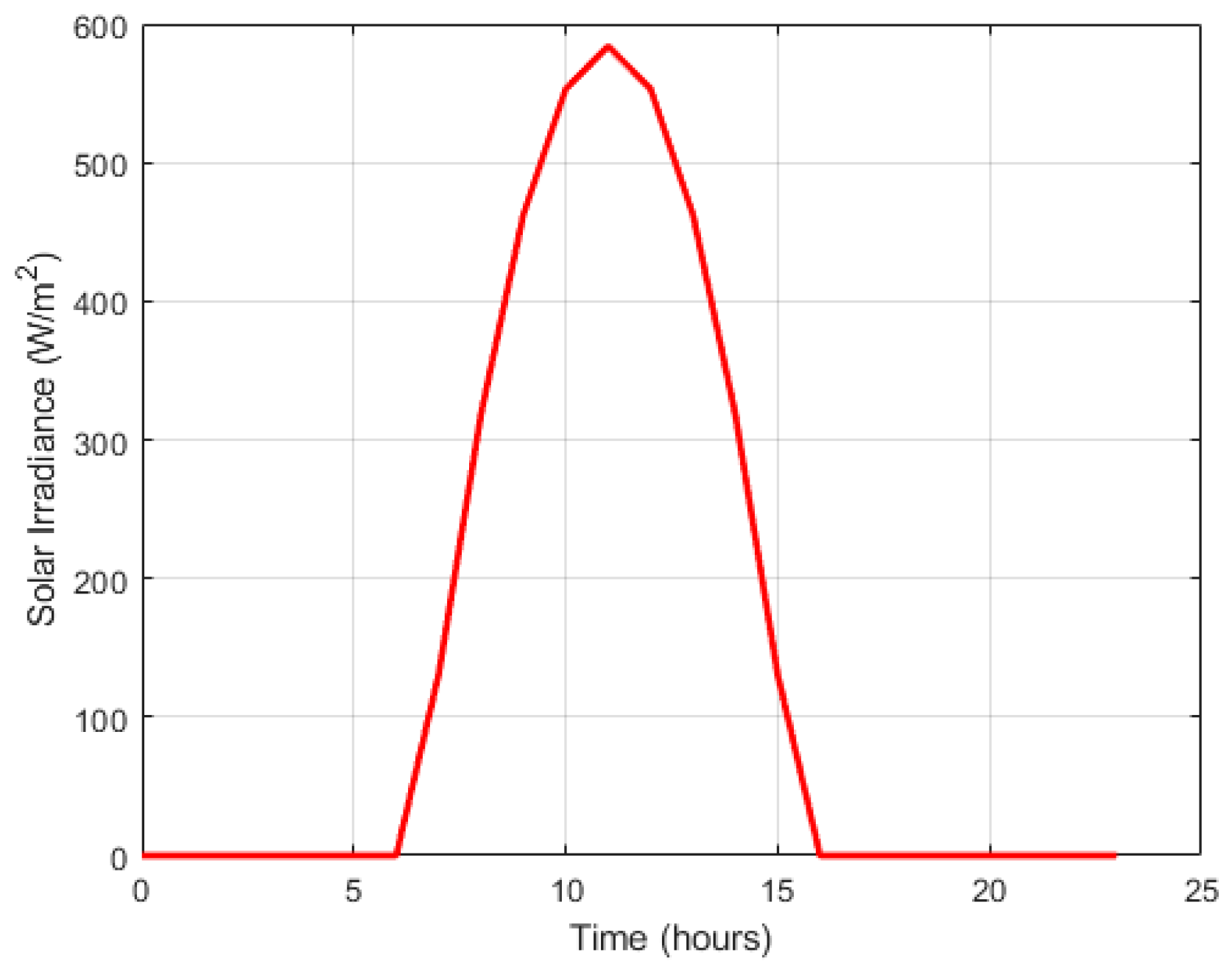
3.2.2. Solar System Modeling

In this study, PDF beta is used for modeling the intermittent behavior of solar irradiance [51]. The output power of solar energy is modeled in Equation (2) as follows:

$$W_{PV}\left(si\right)={\eta }_{PV}\times A\times si$$

(2)

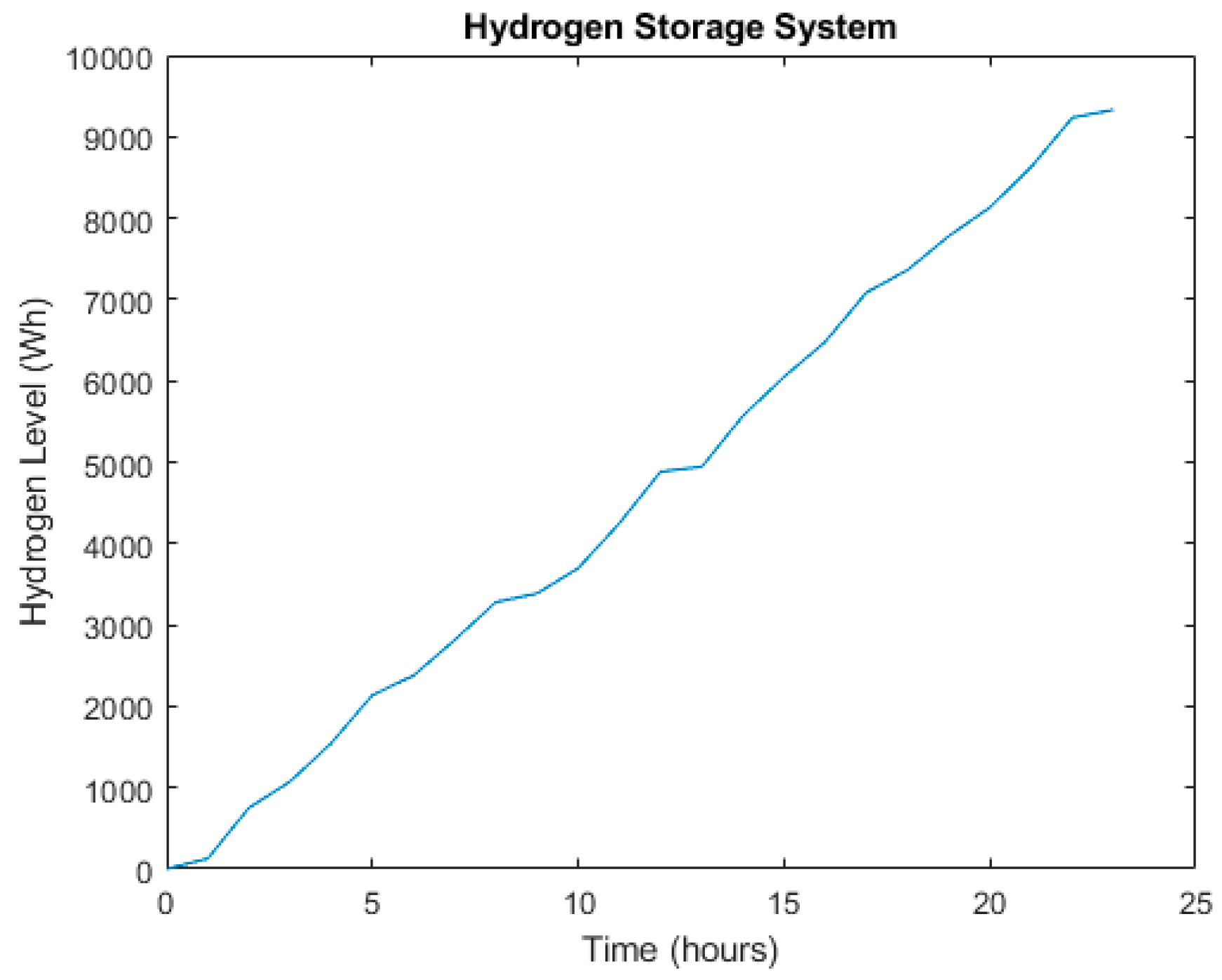
3.2.3. Hydrogen Storage System Modeling

The hydrogen storage system (HSS) consists of three main components: the electrolyzer (EL), hydrogen storage tanks (HTS), and the fuel cell (FC). This system functions such that, during the charging process, the electrolyzer (EL) generates hydrogen, which is then stored in the HTS units. During the discharge phase, the hydrogen stored in the tanks is utilized by the fuel cell (FC) to produce electrical energy. A detailed mathematical representation of this system is provided in Equation (3). Equation (8) models hydrogen production by the electrolyzer, while Equation (4) defines the conversion of stored hydrogen into electricity through the fuel cell [52].

$${G_H}^{FC}\left(sc, t, hyd\right)={\displaystyle \frac{W_{FC}(sc, t, hyd)}{{\eta }_{FC} . {H_{L}V}_H}} \forall sc, t, hyd$$

(3)

$${G_H}^{EL}\left(sc, t, hyd\right)={\displaystyle \frac{{{\eta }_{EL} . W}_{EL}(sc, t, hyd)}{{H_{L}V}_H}} \forall sc, t, hyd$$

(4)

where ${G_H}^{FC}$, ${G_H}^{EL}$ indicate the hydrogen generation and consumption in time slot t; $W_{FC}$, $W_{EL}$ represent the power of FC and EL; ${\eta }_{FC}$, ${\eta }_{EL}$ show the efficiency of FC and EL; and ${H_{L}V}_H$ represents lowering the hydrogen heating value, respectively.

The model also accounts for the limitations inherent in both the generation and consumption of hydrogen molecules by the EL and the fuel cell FC. These limitations are addressed through Equations (5) and (6), respectively, ensuring a more accurate representation of the system’s behavior.

$${G_H}^{FC,min}\le {G_H}^{FC}\left(sc,t,hyd\right)\le {G_H}^{FC,max}\forall sc,t,hyd$$

(5)

$${G_H}^{EL,min}\le {G_H}^{EL}\left(sc,t,hyd\right)\le {G_H}^{EL,max}\forall sc,t,hyd$$

(6)

3.2.4. Demand Modeling

In this study, the uncertain nature of demand is modeled using a Gaussian PDF. To predict the intermittent parameters such as wind speed, solar irradiance, and demand, several scenarios are generated using the Monte Carlo simulation. The occurrence probability of each scenario is modeled in Equation (7) as follows:

$${\rho }_s={{\rho }_s}^{WT}\times {{\rho }_s}^{PV}\times {{\rho }_s}^L$$

(7)

where ${\rho }_s$, ${{\rho }_s}^{WT}$, ${{\rho }_s}^{PV}$, ${{\rho }_s}^L$ show the probability of scenario s, probability of the WT in scenario s, and probability of the demand in scenario s, respectively.

3.2.5. Battery Storage System Modeling

To strengthen the operational flexibility and reliability of the hybrid energy system (HES), a battery energy storage system (BESS) model is integrated within the optimization framework. The BESS serves as a critical component for mitigating the inherent variability of renewable energy sources and for maintaining grid load balance under dynamic operating conditions. In developing the battery model, both technical constraints and operational characteristics are explicitly formulated to ensure a realistic representation of its behavior within the system. These include constraints related to charging and discharging limits, state of charge (SOC) boundaries, efficiency factors, and degradation considerations. Such modeling not only guarantees operational feasibility but also allows the optimization algorithm to schedule energy storage more effectively, aligning charging during periods of surplus renewable generation with discharging during peak demand intervals.

State of Charge (SOC)

The battery system supports the smart grid by storing excess renewable energy and discharging it during demand peaks or supply shortages. The battery’s state of charge (SOC) at time t is modeled as follows:

$$SOC\left(t\right)=SOC\left(t-1\right)+{\displaystyle \frac{{\eta }_{ch}.p_{ch}\left(t\right)-\frac{p_{ch}\left(t\right)}{{\eta }_{dis}}}{C_{but}}} \forall t$$

(8)

where ${\eta }_{ch}$ and ${\eta }_{dis}$ are the charging and discharging efficiencies, respectively, and $C_{but}$ is the battery capacity.

SOC Constraints

$${SOC}_{min}\le SOC\left(t\right)\le {SOC}_{max} \forall t$$

(9)

These ensure the battery operates within safe and practical limits.

Charging/Discharging Power Limits

$$0{ \le p}_{ch}\left(t\right) \le p_{ch}^{max} , 0{ \le p}_{dis}\left(t\right) \le p_{dis}^{max} \forall t$$

(10)

The integration of the battery energy storage system (BESS) into the proposed model facilitates optimized scheduling of charging and discharging operations. This enables surplus renewable generation to be absorbed during low-demand intervals and subsequently discharged during peak load periods, thereby improving overall system flexibility and reliability. Within the Hybrid-NSGA-II-MOPSO optimization framework, the operational dynamics of the BESS are co-optimized alongside other system components. This joint optimization process aims to simultaneously reduce operational costs, lower pollutant emissions, and mitigate energy imbalances, while at the same time enhancing the penetration level of renewable energy resources [57,58].

3.3. Objective Functions

3.3.1. First Objective Function (f1)

The first objective function focuses on evaluating the operational cost and environmental emissions associated with the proposed smart grid (SG). This includes the fuel and running costs of the diesel generator (DG), the degradation-related expenses of the battery system, as well as the operating costs of both the electrolyzer and the fuel cell within the hydrogen storage system. In addition, emissions from the utility grid (UG) and diesel generators are also taken into account. The complete formulation is presented in Equation (11).

$$\begin{array}{cc}\hspace{1em}\hspace{1em}\hspace{1em}\mathit{min}{f}_1=\hfill & {\displaystyle \sum _{sc=1}^{SC}}{\rho }_{sc}{\displaystyle \sum _{t=1}^T}[{\displaystyle \sum _{dg=1}^{DG}}{O}_{cost}(sc, t, dg)\hfill \\ & \hspace{1em}\hspace{1em} +{\displaystyle \sum _{batt=1}^{BATT}}{O_{cost}}^{charge}\left(sc, t, batt\right)\hfill \\ & \hspace{1em}\hspace{1em} +{\displaystyle \sum _{batt=1}^{BATT}}{O_{cost}}^{discharge}(sc, t, batt)\hfill \\ & \hspace{1em}\hspace{1em} +{\displaystyle \sum _{Hyd=1}^{HYD}}{O}_{cost Hyd}\left(sc, t, hyd\right)\hfill \\ & \hspace{1em}\hspace{1em} +{\sum }_{d=1}^D{Em}_{DG}\left(t,d\right)+{Em}_{UG}\left(t\right)]\hfill \end{array}$$

(11)

In Equation (11), the first component represents the operational cost of the diesel generators (DGs). The second and third components correspond to the charging and discharging costs of the battery system used to supply both the electric vehicle (EV) station and local demand. The fourth component accounts for the operational expenses of the hydrogen storage system, including the costs of the electrolyzer and fuel cell. Finally, the fifth component captures the pollution emissions attributed to the operation of both the diesel generators and the utility grid (UG). In Equation (1), ${\rho }_{sc}$, $O_{cost}$, ${O_{cost}}^{charge}$, ${O_{cost}}^{discharge}$, ${Em}_{DG}$, ${Em}_{UG}$ represent the probability of each scenario in the system model, operational cost, and cost of charging and discharging, emission of DGs and UG, respectively.

3.3.2. Second Objective Function (f2)

Managing load consumption is a critical aspect of modern power systems, especially when integrating renewable energy sources. In this study, a mathematical formulation for load consumption management is developed and represented through Equations (12)–(14). Specifically, Equation (12) aims to minimize the energy gap between the system’s initial demand and its optimized consumption level. The initial energy demand is defined in Equation (10), while the optimal power consumption value is described in Equation (11):

$$\mathit{min}f2=\sum _{sc=1}^{SC}{\rho }_{sc}\sum _{t=1}^T\left|W_{original}\left(sc, t\right)-W_{optiml}\right|$$

(12)

where $W_{original}\left(sc,t\right)$, $W_{optiml}$, and ${\rho }_{sc}$ in Equation (12) indicate the original power, the optimal value of power, and the probability of scenarios, respectively.

$$\begin{gathered} W_{original}\left(sc,t\right)=D_T\left(sc,t\right)+W_{EL}\left(sc,t,hyd\right)+W_{wind}\left(sc,t\right)+W_{pv}\left(sc,t\right) \\ \hspace{1em}\hspace{1em}+W_{batt}\left(sc,t,batt\right)-D_{unmet}\left(sc,t\right)\forall sc,t,hyd,batt \end{gathered}$$

(13)

where $D_T\left(sc,t\right)$, $W_{EL}\left(sc,t,hyd\right)$, $W_{wind}\left(sc,t\right)$, $W_{pv}\left(sc,t\right)$, $W_{batt}\left(sc,t,batt\right)$, and $D_{unmet}\left(sc,t\right)$ in Equation (13) represent the total demand, power of electrolyzer, power of wind, power generated by PV, power of battery, and unmet demand in time slot t, respectively.

$$W_{optiml}={\displaystyle \frac{ \sum _{t\in T}{W}_{original}\left(sc, t\right)}{T}} \forall sc,t$$

(14)

3.3.3. Third Objective Function (f3)

A high level of renewable energy integration for meeting system demand has a significant influence on reducing operational costs. Therefore, this aspect is considered the third objective function in the proposed system framework. When demand is met primarily through renewable sources, the system naturally operates at a lower cost. The cost-effectiveness achieved through renewable energy utilization is evident. This objective function is defined as the ratio of the total energy generated by wind turbine (WT) and photovoltaic (PV) systems to the total energy demand of the system over the entire operational period. The corresponding mathematical representation is provided in Equation (15):

$$\mathit{Max}f3=\sum _{sc=1}^{SC}{\rho }_{sc}\sum _{t=1}^T\left[{\displaystyle \frac{\sum _{wt=1}^{WT}{W}_{wt}\left(sc, t, wt\right)+\sum _{pv=1}^{PV}{W}_{pv}\left(sc, t, pv\right)}{D_T\left(sc,t\right)}}\right]$$

(15)

where $W_{wt}\left(sc,t,wt\right)$, $W_{pv}\left(sc,t,pv\right)$, $D_T\left(sc,t\right)$, and ${\rho }_{sc}$ indicate the power generated by wind, PV, total demand required, and probability of scenarios in time slot t, respectively.

To ensure a fair and balanced evaluation of the three objective functions, min–max normalization was applied. This method scales each objective value to a standardized range between 0 and 1, which prevents disparities in magnitude from influencing the optimization process or skewing the results.

Moreover, since the proposed optimization framework is based on a Pareto-front methodology using the Hybrid-NSGA-II-MOPSO algorithm, no explicit weighting was assigned to any of the objectives. Instead, the algorithm maintains solution diversity and fairness across the objective space by employing non-dominated sorting and crowding distance techniques. This approach allows the algorithm to generate a well-distributed set of non-dominated solutions, from which the most suitable option can be selected based on specific application goals.

3.4. Demand-Side Management Strategy and Classification of Loads

To strengthen the operational flexibility and reliability of the hybrid energy system (HES), a battery energy storage system (BESS) model is integrated within the optimization framework. The BESS serves as a critical component for mitigating the integral flexibility of renewable energy sources and for maintaining grid load balance under dynamic operating conditions. In developing the battery model, both technical constraints and operational characteristics are explicitly formulated to ensure a realistic representation of its behavior within the system. These include constraints related to charging and discharging limits, state of charge (SOC) boundaries, efficiency factors, and degradation considerations. Such modeling not only guarantees operational feasibility but also allows the optimization algorithm to schedule energy storage more effectively, aligning charging during periods of surplus renewable generation with discharging during peak demand intervals.

3.4.1. Demand Shifting Modeling

The demand shifting (DS) strategy is designed to redistribute a portion of the residential energy consumption from high-demand periods (peak hours) to low-demand intervals (off-peak hours). The primary objective of this approach is to smooth the overall demand profile, thereby minimizing stress on the distribution grid, enhancing operational stability, and ensuring more efficient utilization of distributed energy resources (DERs). By strategically rescheduling flexible loads, the DS strategy contributes not only to peak load reduction but also to cost minimization and improved system reliability.

The mathematical representation of the DS model is provided in Equations (16) and (17), which formally describe the operational mechanism of shifting demand across different time steps. Furthermore, Equation (18) defines the computation of the residential demand shifting (RDS) load at each time interval, incorporating the amount of demand shifted from an original peak time step ttt to a new off-peak time step t1t_1t1 within a given scenario scscsc [20].

This formulation captures the dynamics of load redistribution under the DS framework, allowing the optimization algorithm to determine how much demand can be reallocated without violating user comfort constraints or system operational limits. In essence, the RDS model quantifies the extent of energy reallocation from peak to off-peak periods, enabling effective demand-side management (DSM) and ensuring a more balanced interaction between supply and demand.

$$D_{LS}\left(sc, t\right)=\sum _{t1}\sum _{ls=1}^{LS}{D}_{LS}\left(sc, t1, t\right)-\sum _{ls=1}^{LS}{D}_{LS}\left(sc, t1, t\right) \forall sc,ls,t$$

(16)

Equation (14) is introduced to control the participation level of the RDS system within the demand-shifting framework. It defines specific boundaries that limit how actively the RDS system can be involved in the load management process. These constraints are necessary to ensure that the strategy operates within acceptable limits and remains consistent with the overall objectives and operational requirements of the system.

$$0\le \sum _{t1}\sum _{ls=1}^{LS}{D}_{LS}\left(sc, t1, t\right)\le r\times \sum _{ls=1}^{LS}{D}_{LS}\left(sc, t\right) \forall sc,ls,t$$

(17)

Here, r is a predefined participation ratio (e.g., 0.2 or 20%) indicating the maximum allowable portion of the load that can be shifted. This constraint ensures that DSM operations remain within technical and behavioral limits of the residential load structure.

This DSM formulation directly contributes to the second objective function (f₂) of the optimization model, where the energy gap between original and optimized demand is minimized. The mismatch is expressed in Equation (11) and helps reduce reliance on costly or emission-intensive sources during peak hours.

3.4.2. Classification of Loads

In this study, the loads are divided into three categories: sheddable, non-sheddable, and shiftable loads [54].

3.5. Constraints’ Modeling

The objective functions considered in this research focus on three key aspects: minimizing operational costs and emissions from the generation side, reducing the energy gap between the initial load demand and its optimized consumption on the demand side, and increasing the share of renewable energy sources in the system. These objectives are optimized subject to several constraints, including the technical limitations of the diesel generators and the overall power balance of the system. The mathematical representation of these objectives and constraints is provided as follows:

Power Balance Constraints

The power balance constraint applies to each time step and under every system condition. It is formulated in Equation (18) [54]. This constraint ensures that the total energy produced by all available sources, including diesel generators (DGs), photovoltaic (PV) arrays, wind turbines (WTs), and fuel cells (FCs), is equal to the total energy demand of the system. The demand encompasses the energy needed for charging electric vehicles (EVs), the electricity consumed by the electrolyzer (EL), and is adjusted by subtracting any portion of demand that remains unmet.

$$\begin{array}{c}{\displaystyle \sum _{d=1}^D}{W}_d\left(sc, t\right)+{\displaystyle \sum _{pv=1}^{PV}}{W}_{pv}\left(sc,t\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{wt=1}^{WT}}{W}_{wt}\left(sc,t\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{hyd=1}^{HYD}}{W}_{fc}\left(sc,t\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=D_{eq}\left(sc,t\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{lg}^{LG}}{W_{EVs}}^{charge}\left(sc,t\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _{hyd=1}^{HYD}}{W}_{EL}\left(sc, t\right)-D_{unmet}\left(sc, t\right) \forall sc, t\hfill \end{array}$$

(18)

Equation (18) plays a vital role as a system constraint, ensuring that power generation and consumption always remain balanced. It confirms that the energy produced from various sources adequately meets the system’s total demand, while accounting for temporal variations and different operational scenarios. Maintaining this balance is essential for ensuring the system’s reliability and operational efficiency. By incorporating renewable sources such as photovoltaic (PV) systems and wind turbines (WTs), and by minimizing any unmet demand, the equation contributes to improved system stability and supports the broader goal of sustainability.

3.6. Technical DG Constraints

The operational constraints associated with diesel generators (DGs) are formulated through Equations (16)–(22). Equation (16) defines the lower and upper output limits of DGs, capturing their allowable range of operation. The minimum required uptime and downtime durations are specified using Equations (19) and (20), respectively, as detailed in reference [20]. In addition, the constraints related to the permissible rates of increase and decrease in DG output are represented by Equations (21) and (22), which address ramp-up and ramp-down limitations.

$${W_d}^{min}\le W_d\left(sc, t\right)\le {W_d}^{max} \forall sc, t, d$$

(19)

$${\vartheta }^{0n}\left(sc, t, d\right)+\sum _{\tau =t+1}^{\mathit{min}\left(T, t-1+MU\right)}{\vartheta }^{0ff}\left(sc, \tau , d\right)\le 1 \forall sc, t, d$$

(20)

$${\vartheta }^{0ff}\left(sc, t, d\right)+\sum _{\tau =t+1}^{\mathit{min}\left(T, t-1+MD\right)}{\vartheta }^{0n}\left(sc, \tau , d\right)\le 1 \forall sc, t, d$$

(21)

$$W_d\left(sc, t,d\right)-W_d\left(sc, t-1,d\right)\le RU \forall sc,t,d$$

(22)

$$W_d\left(sc, t-1,d\right)-W_d\left(sc, t,d\right)\le RD \forall sc,t,d$$

(23)

where RU, RD, MU, MD, ${\vartheta }^{0ff}$, and ${\vartheta }^{0n}$ in the above Equations represent the ramp-up and ramp-down time of DGs, the minimum-up and minimum-down time of DGs, and binary variables of DGs. Its operation takes place using on = 1 and off = 0.

The parameter values used in this study, such as residential load profiles, generation mix percentages, and storage system capacities, were selected based on standard practices in recent literature and reflect realistic values for typical smart grid applications [58]. The generation mix of wind, solar, diesel, and utility supply aligns with general renewable integration goals, while the sizing of storage components ensures reliable operation under variable conditions. These assumptions provide a representative basis for evaluating the performance of the proposed model without introducing case-specific bias.

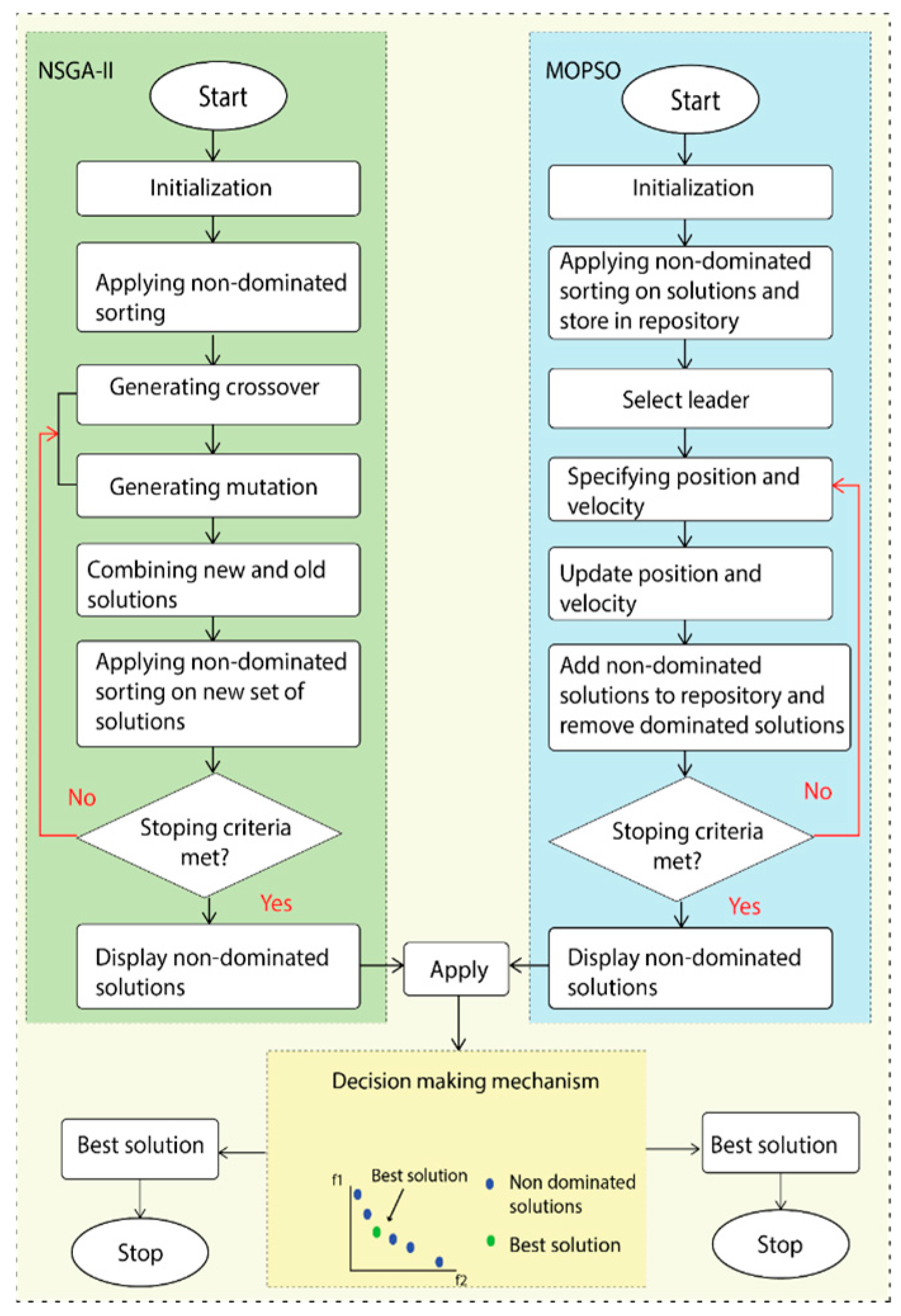
4. Hybrid MOPSO-NSGA-II Algorithm for Solving the Proposed Smart Grid Problem

This research introduces a hybrid MOPSO-NSGA-II algorithm to address non-linear and complex optimization problems that involve searching within a high-dimensional and challenging solution space. The objective of employing this hybrid method is to strengthen the algorithm’s search capabilities by integrating the distinct strengths of MOPSO and NSGA-II. While each algorithm uses a different mechanism for navigating the search space, their combination allows for a more effective balance between exploration and exploitation. This integration helps mitigate the risk of convergence to local optima.

To further improve the distribution and diversity of the Pareto optimal solutions and avoid early convergence, the population is divided into two groups. This division is based on ranks assigned through non-domination sorting. A comprehensive explanation of the individual algorithms and their features can be found in references [55,56,57,58].

In practical optimization tasks, it is common to encounter multiple objectives that must be optimized simultaneously. These objectives are often conflicting and not directly comparable, which makes it impossible to determine a single solution that optimizes all targets at once. As a result, the outcome of such problems is a set of trade-off solutions rather than one globally optimal point. To handle this complexity, the proposed tri-objective problem is addressed using the hybrid MOPSO-NSGA-II approach, and its mathematical representation is provided in Equation (22).

$$\left\{\begin{array}{c}Min f1, f2 and Max f3\\ subject \\ to\\ constrains\end{array}\right\}$$

(24)

The following sequence outlines the implementation steps of the proposed Hybrid MOPSO-NSGA-II algorithm for solving the smart grid (SG) optimization problem:

• Step 1: Define smart grid system parameters

• ▪ Determine the total energy demand of the proposed power network.
• ▪ Set the upper limits for all decision variables.
• ▪ Set the lower limits for all decision variables.
• ▪ Identify the total number of decision variables involved.

• Step 2: Initialize MOPSO algorithm parameters

• ▪ Define the size of the solution repository.
• ▪ Assign values for the cognitive and social acceleration coefficients (c1 and c2).
• ▪ Set the inertia weight (W).
• ▪ Establish a method for leader selection within the swarm.

• Step 3: Configure NSGA-II parameters

• ▪ Specify the maximum number of iterations.
• ▪ Set the size of the population.
• ▪ Define crossover probability or method.
• ▪ Choose the mutation approach and rate.

• Step 4: Evaluate the objective functions of the smart grid (f1, f2, and f3)

• ▪ Compute all three objective functions.
• ▪ Provide these calculated values as inputs to the optimization algorithm.

• Step 5: Perform non-dominated sorting

• ▪ Rank the solutions based on Pareto dominance.

• Step 6: Execute the MOPSO algorithm

• ▪ Begin the exploration phase to identify diverse regions of the solution space.

• Step 7: Execute the NSGA-II algorithm

• ▪ Begin the exploitation phase to refine the solutions and improve convergence.

• Step 8: Implement the decision-making strategy

• ▪ Apply a mechanism to select the best compromise solution from the Pareto front.

• Step 9: Terminate the algorithm

• ▪ Stop the process once the predefined stopping criteria are satisfied.

The complete flow of the proposed Hybrid MOPSO-NSGA-II approach is illustrated in Figure 2.

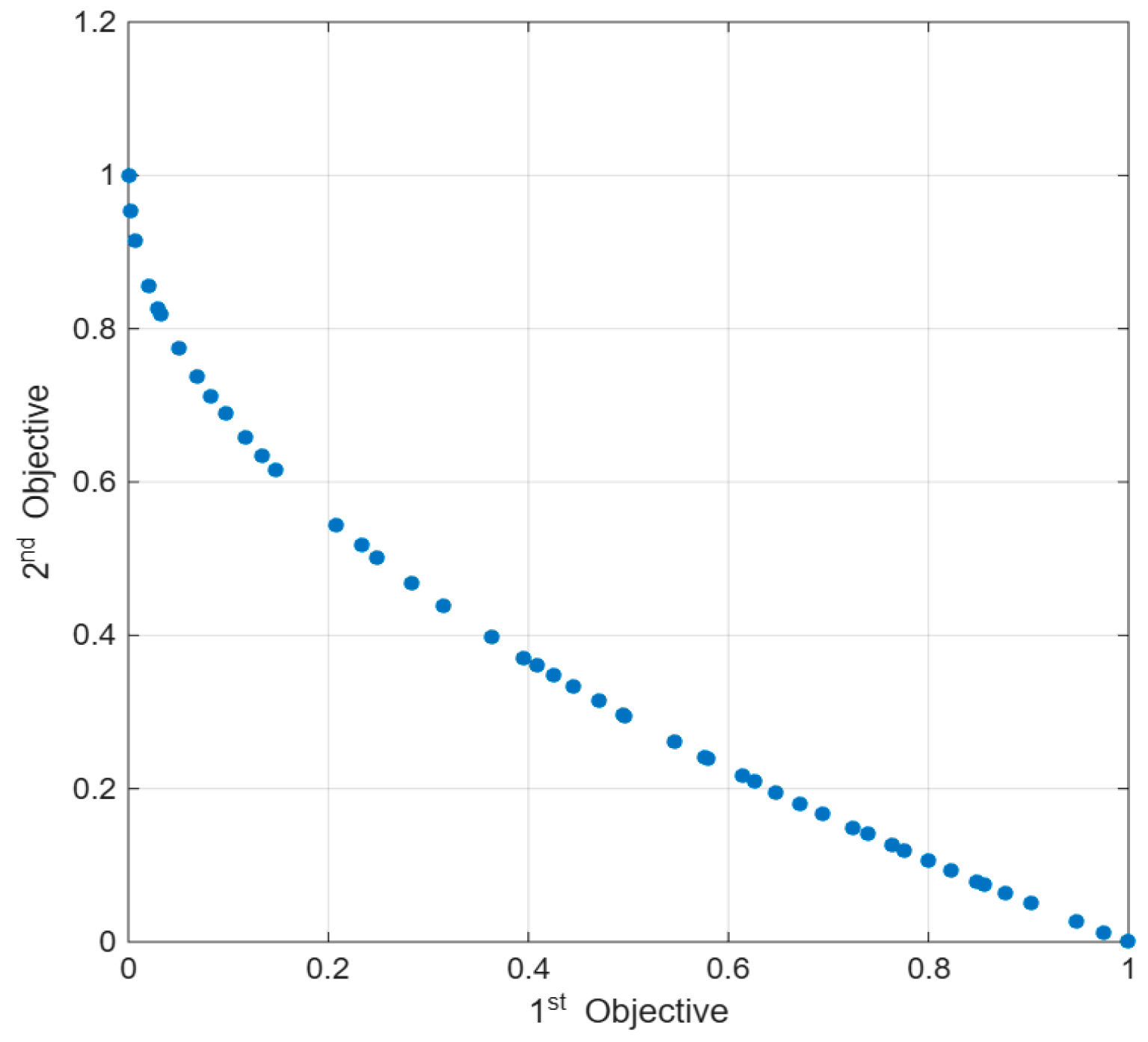
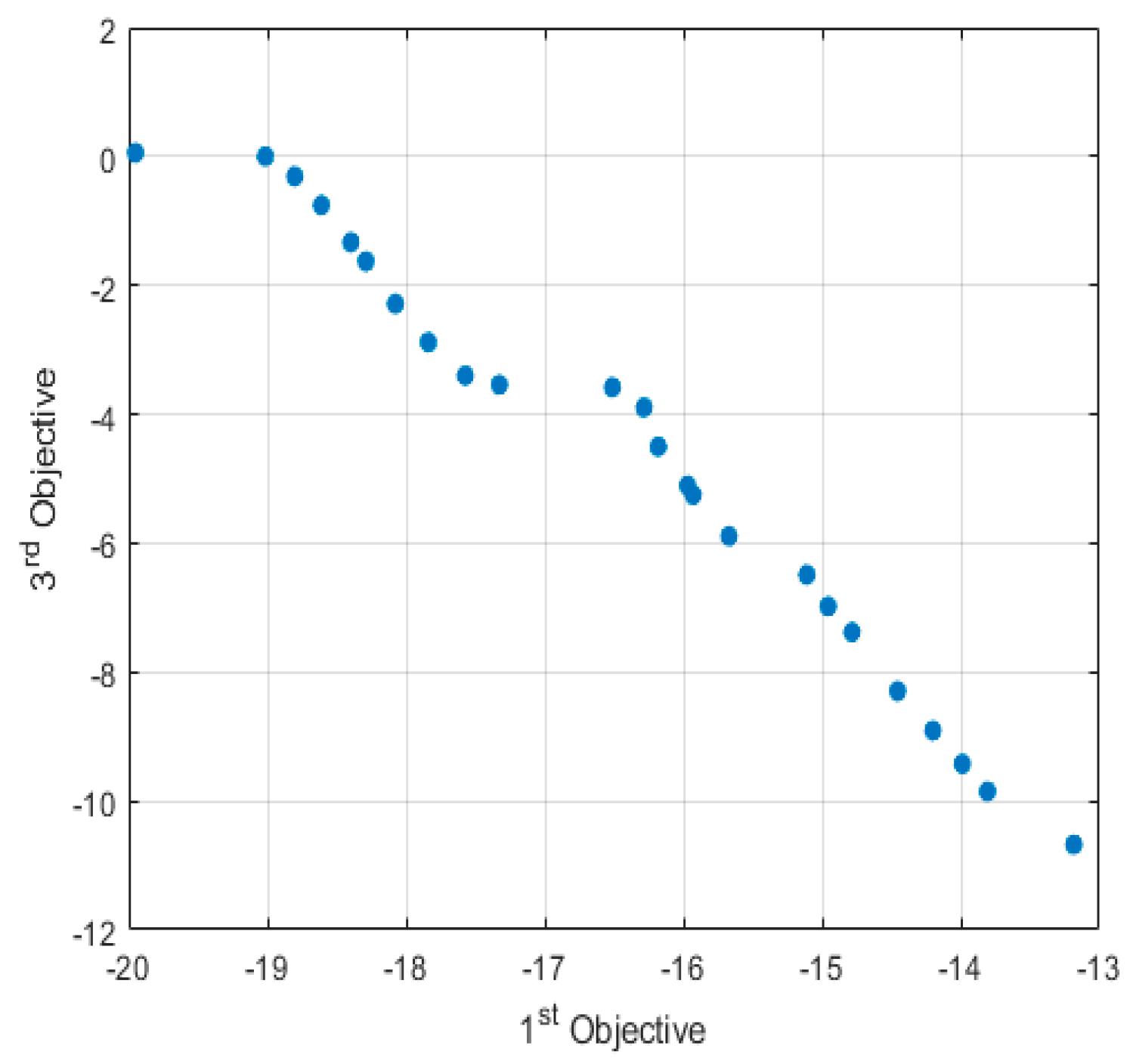
5. Simulations and Results

The Hybrid-NSGA-II-MOPSO optimization framework is applied to the residential smart distribution grid in order to address tri-objective functions under a demand-side management (DSM) scheme. Within this framework, residential loads are classified into sheddable, non-sheddable, and shiftable categories, enabling a more precise representation of consumer behavior and flexibility in demand response.

The temporal variability of renewable resources is characterized through detailed simulations: Figure 3 presents the hourly wind speed profile, while Figure 4 illustrates the solar irradiance pattern over the same horizon. The dynamics of hydrogen energy storage are shown in Figure 5, complemented by the hydrogen pressure evolution depicted in Figure 6. The performance of the battery energy storage system (BESS) is analyzed through its state of charge (SOC), as presented in Figure 7, with a full charge–discharge cycle profile provided in Figure 8. In addition, Figure 9 illustrates the price signal trajectory, which is integrated into the optimization framework to capture cost variability and influence consumer-side decision-making.

The operational characteristics and technical parameters of the proton exchange membrane (PEM) fuel cell and electrolyzer systems, which are integral to the hydrogen storage cycle, are summarized in

Table 2. Fuel cell design and operating parameters [58].

Parameter	Value
Current density	$1100 \mathrm{A}/{\mathrm{m}}^2$
Area of cell	$0.1 {\mathrm{m}}^2$
Heat rate of fuel cell	$1518 \mathrm{W}$
Fuel cell operating pressure	$100 \mathrm{k}\mathrm{P}\mathrm{a}$
Fuel cell operating temperature	$80 °\mathrm{C}$

and

Table 3. PEM electrolyzer design and operating parameters [58].

Parameter	Value
Cathode activation energy	$\mathrm{18,000} \mathrm{j}/\mathrm{m}\mathrm{o}\mathrm{l}$
Anode activation energy	$\mathrm{76,000} \mathrm{j}/\mathrm{m}\mathrm{o}\mathrm{l}$
Temperature	$80 °\mathrm{C}$
Thickness of membrane	$0.1 \mathrm{m}\mathrm{m}$

, respectively. These parameters form the basis for system-level modeling and optimization, ensuring that the interaction between electrochemical components, storage devices, and demand-side flexibility is accurately represented within the hybrid optimization algorithm.

In order to demonstrate the proposed model’s efficiency, the simulation of this model is planned and implemented in four different modes.

(1)

First objective optimization;

(2)

First and second objective optimization;

(3)

First and third objective optimization;

(4)

Tri-objective simultaneous optimization.

By implementing these four distinct modes, the proposed model’s efficiency is thoroughly evaluated, and its performance is quantified across a spectrum of optimization objectives. The four modes are explained in detail as follows:

• First objective (operational cost and pollution emission optimization)

In the first simulation scenario, the optimization problem is formulated to simultaneously minimize the operational cost of the smart distribution grid and the associated pollution emissions. The underlying aim is to achieve an optimal trade-off between economic efficiency and environmental sustainability. To this end, the Hybrid-NSGA-II-MOPSO algorithm is employed, which effectively generates a Pareto front of non-dominated solutions, offering a diverse set of trade-offs between the two conflicting objectives.

A structured decision-making framework is subsequently applied to identify the most suitable operating point from the Pareto set. Among the solutions generated, the 15th point—highlighted in black in Figure 8—is selected as the optimal compromise solution. Simulation results demonstrate that, under this configuration, the proposed approach yields a 12% reduction in operational cost alongside a 7% decrease in pollution emissions compared to baseline operation. These findings validate the effectiveness of the Hybrid-NSGA-II-MOPSO technique in achieving cost–emission co-optimization within a residential smart grid environment.

2.

First and second objective optimization

In the second simulation scenario, the optimization framework is extended to address a broader set of objectives, thereby testing the robustness of the proposed model under multi-criteria conditions. Specifically, the Hybrid-NSGA-II-MOPSO algorithm is applied to simultaneously minimize operational costs, reduce pollutant emissions, and mitigate the energy gap between supply and demand. This formulation captures the inherent trade-offs among economic, environmental, and reliability-driven performance indicators.

The metaheuristic search process yields a Pareto front consisting of non-dominated solutions, from which the most appropriate operating point is selected through the integrated decision-making mechanism. Among the solutions generated, the 20th point—highlighted in Figure 9—is identified as the optimal compromise solution. Quantitative results indicate that the adoption of this solution leads to an 11% reduction in operational costs, a 7% reduction in emissions, and a 13% decrease in the energy gap compared to baseline operation. These outcomes underscore the capacity of the Hybrid-NSGA-II-MOPSO approach to effectively balance multiple conflicting objectives, thereby enhancing both system sustainability and operational reliability within residential smart grid applications.

3.

First and third objective optimization

This simulation scenario introduces a distinct set of optimization goals compared to the previous mode. It focuses specifically on the first and third objectives of the system model, highlighting their importance within the overall optimization framework. The purpose of this mode is to evaluate the model’s flexibility in addressing varying optimization criteria and to verify its effectiveness under different operational conditions. In this case, two objectives are targeted: the minimization of operational cost and environmental emissions, and the maximization of renewable energy integration. The optimization process is carried out using the proposed Hybrid MOPSO-NSGA-II algorithm. A decision-making mechanism is then applied to select the most suitable solution from the set of Pareto-optimal or non-dominated outcomes, as illustrated in Figure 10.

In terms of performance, the results show a 10% reduction in both operational costs and emissions when treating them as minimization objectives. Simultaneously, the penetration level of renewable energy sources is improved by 15%, reflecting the algorithm’s ability to enhance sustainability while maintaining cost efficiency.

4.

First, second, and third objective (tri-objective) simultaneous optimization

The final simulation scenario explores a more advanced level of complexity by implementing a tri-objective optimization framework. In this setting, the model seeks to optimize all three defined objectives at the same time. This reflects practical energy system conditions, where multiple objectives must be balanced concurrently, despite potential conflicts among them. The purpose of this mode is to assess how effectively the proposed model can manage these competing goals and adapt to multifaceted operational challenges.

To thoroughly examine this capability, the tri-objective model is applied to three distinct case studies:

(a)

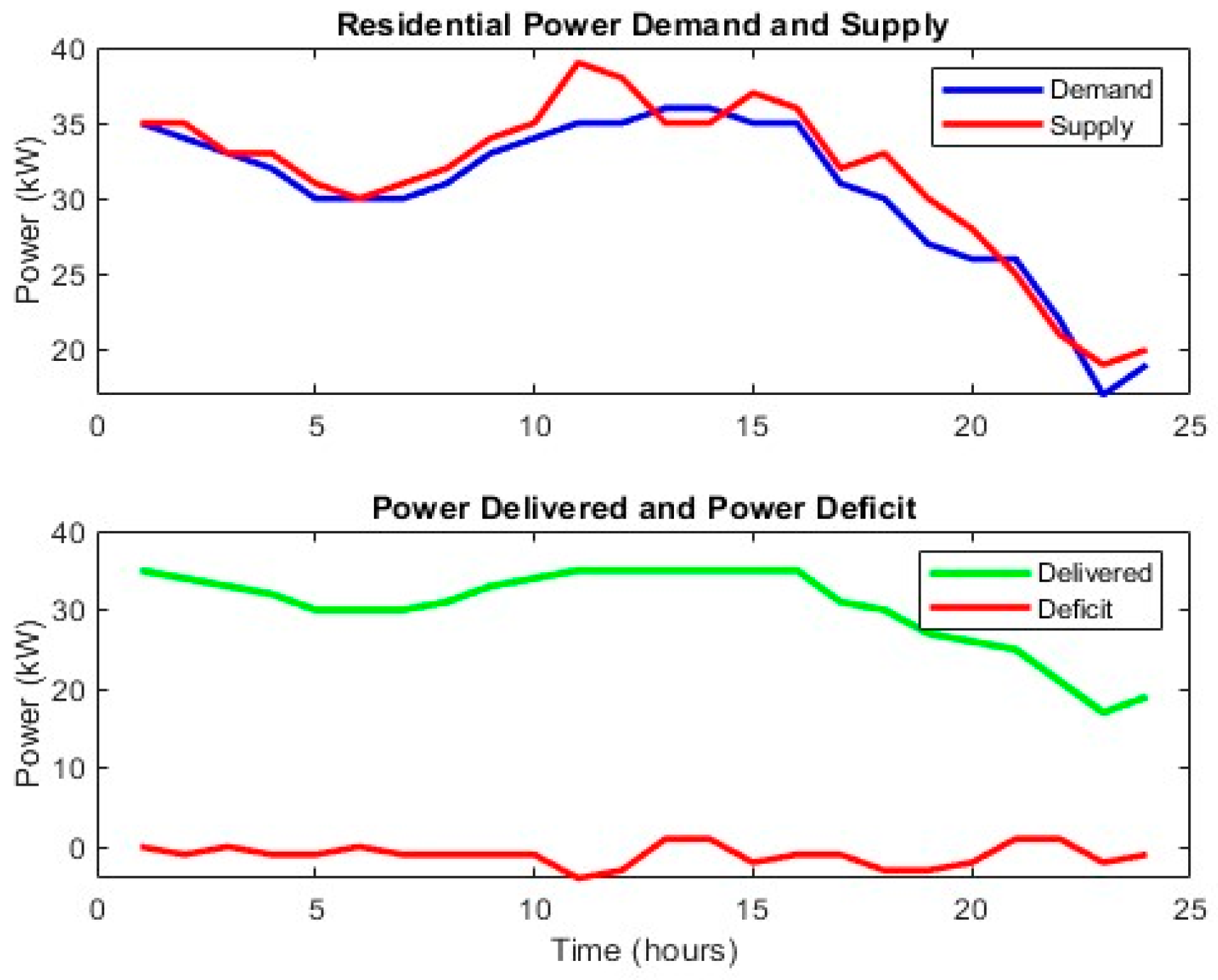
Case Study 1: standard system operation without additional strategies;

(b)

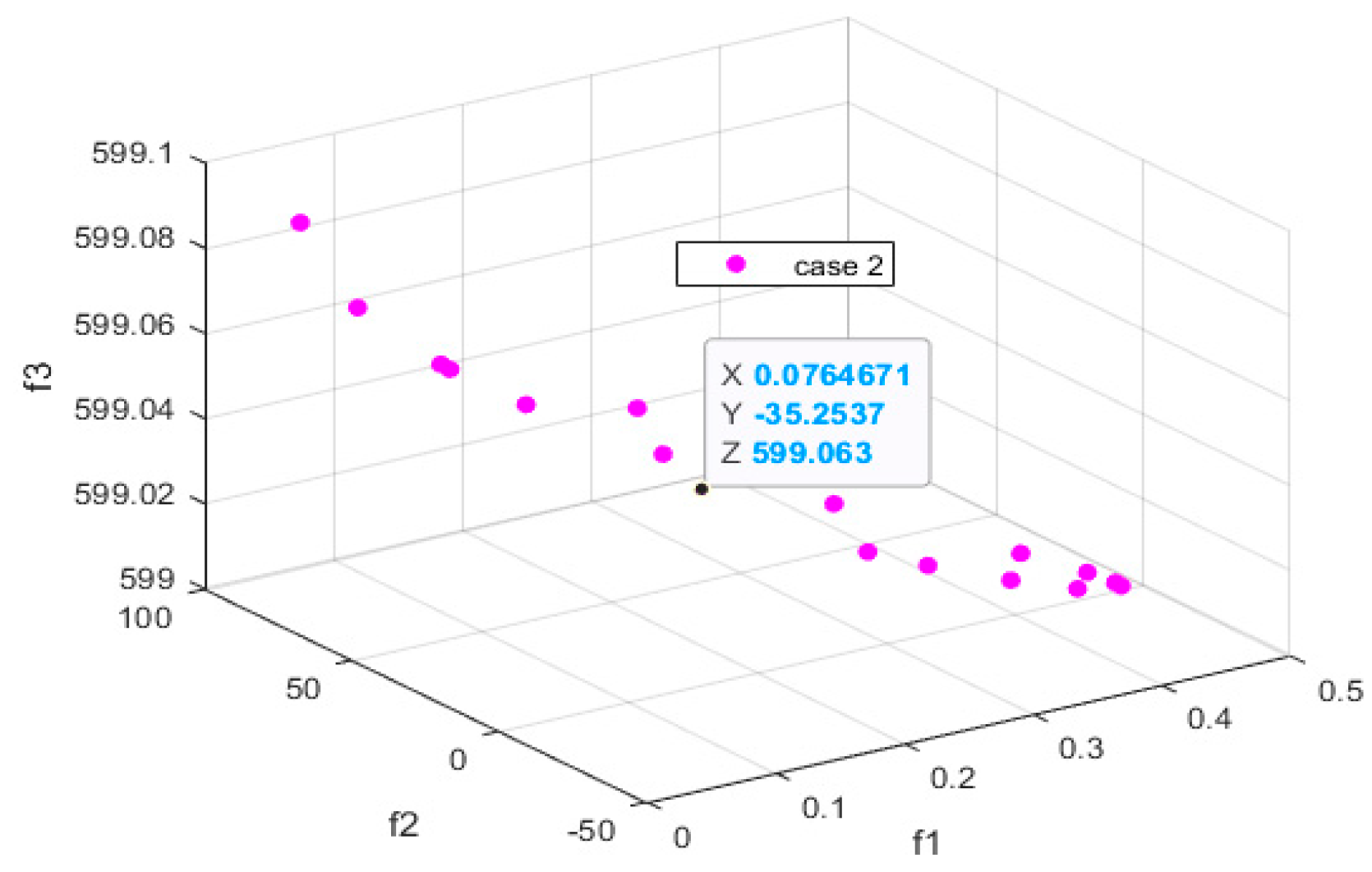
Case Study 2: operation incorporating both demand-side management (DSM) and battery storage;

(c)

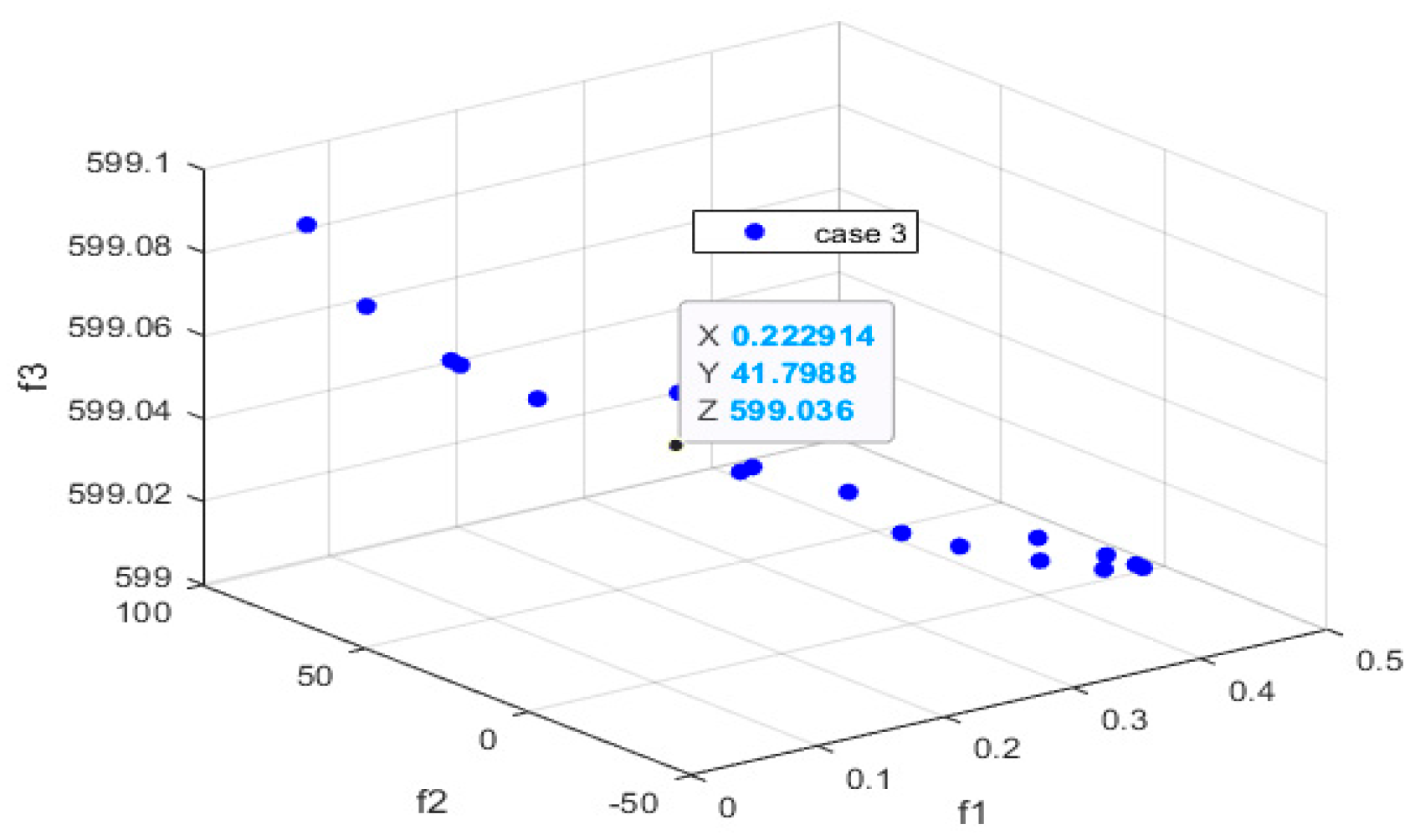
Case Study 3: operation involving DSM along with both battery and hydrogen storage technologies.

The implementation of DSM strategies and energy storage configurations across these scenarios is summarized in

Table 4. Different case studies for tri-objective optimization using Hybrid-NSGA-II-MOPSO.

Case Studies	Sources	Involvement	DSM Strategy
Basic operation	Wind	✓
	Solar	✓
	Battery	✓	NA
	Hydrogen	--
	Utility	✓
	Diesel generator	✓
Operation with DSM and battery	Wind	✓
	Solar	✓
	Battery	✓	✓
	Hydrogen
	Utility	✓
	Diesel generator
Operation with DSM considering both battery and hydrogen	Wind	✓
	Solar	✓
	Battery	✓	✓
	Hydrogen	✓
	Utility	✓
	Diesel generator	--

.

Table 5. Involvement of sources in different simulation studies [58].

Simulation Modes	Wind	Solar	Utility	Battery	Hydrogen	DGs
Case study 1	20%	35%	40%	5%	--	--
Case study 2	25%	30%	40%	3%	2%	--
Case study 3	34%	36%	11%	8%	11%	--

provides further detail on the energy sources utilized in each simulation setup.

The tri-objective problem is addressed using the Hybrid MOPSO-NSGA-II optimization approach across all three case studies. The first case, referred to as “basic operation,” serves as the control scenario, offering baseline results without any advanced optimization strategies. The second case introduces DSM in combination with battery storage, creating a more flexible and responsive energy management system. The third case represents the most sophisticated configuration, integrating both battery and hydrogen storage alongside DSM, and illustrates a highly coordinated and resilient approach to energy optimization.

Details regarding the role of DSM and the integration of various energy sources in each case study are provided in Table 5. A comprehensive analysis of these case studies and the results obtained is presented in the subsequent section.

(a)

Case study 1: Basic operation

This case study illustrates the system’s default mode of operation, where no advanced energy storage technologies or strategic enhancements are applied. It serves as the foundational scenario, offering a reference point for evaluating improvements in subsequent cases. The outcomes from Case Study 1 indicate elevated levels of operational cost and environmental emissions, highlighting the need for more efficient and sustainable energy management solutions. The Pareto-optimal set generated using the Hybrid MOPSO-NSGA-II algorithm, along with the best solution identified through the decision-making process, is presented in Figure 10.

Figure 10. Basic operation using Hybrid-NSGA-II-MOPSO.

Figure 10. Basic operation using Hybrid-NSGA-II-MOPSO.

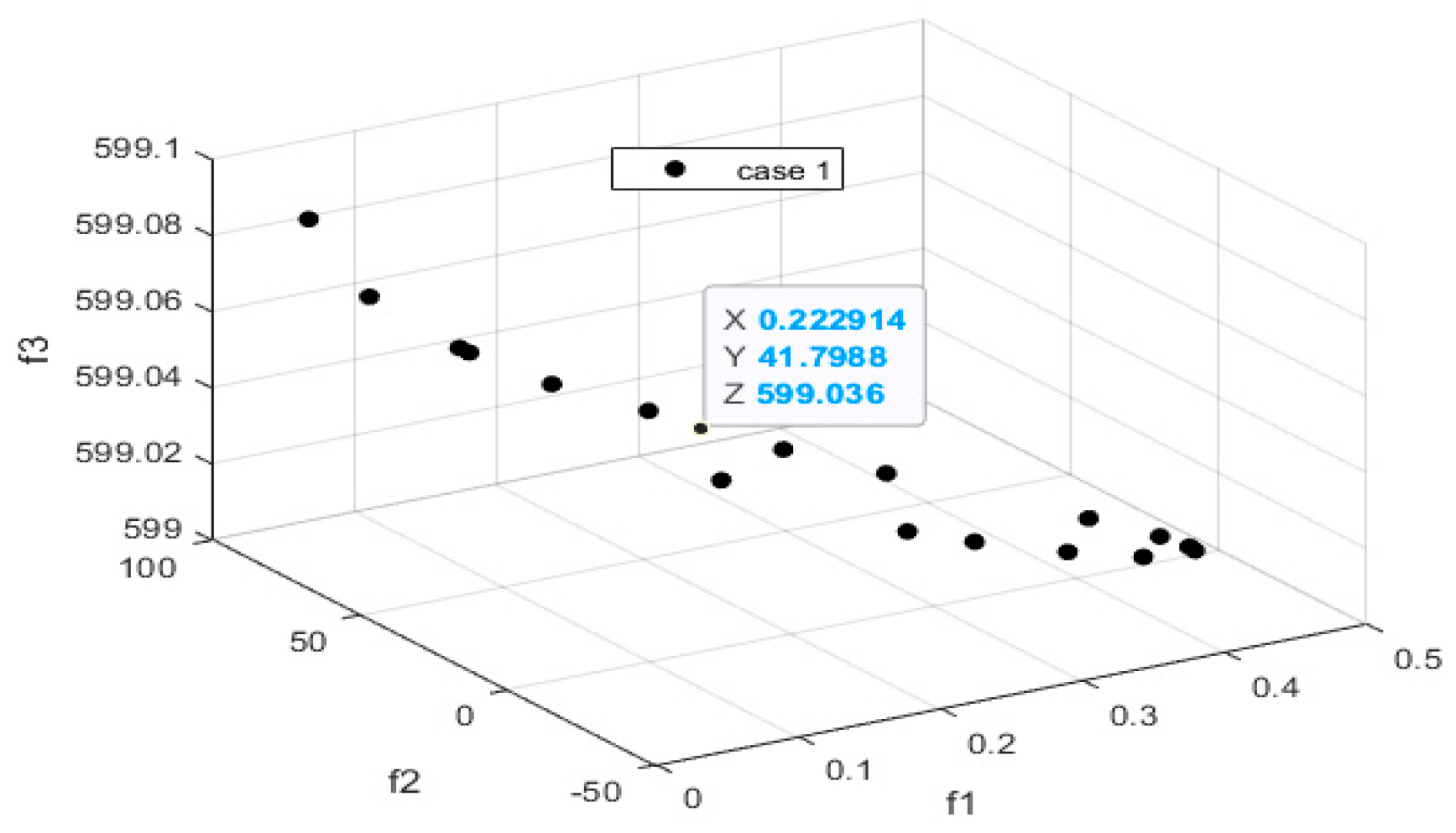
(b)

Case study 2: Operation with DSM and Battery

The second case study, titled “operation with DSM and battery,” incorporates two important components aimed at improving energy system performance. A demand-side management (DSM) strategy is implemented to optimize consumption behavior and reduce peak demand, while battery storage is introduced to capture surplus energy and supply it during high-demand periods. The integration of these elements increases the system’s operational flexibility and enhances its ability to function efficiently during peak load conditions, thereby lowering dependency on the utility grid.

The results from this scenario demonstrate significant performance gains. Specifically, operational costs were reduced by 4.1 percent, pollution emissions declined by 9 percent, and the energy gap between initial demand and optimized consumption was lowered by 12.5 percent. These improvements were achieved using the Hybrid MOPSO-NSGA-II optimization method. The findings underscore the advantages of combining DSM with battery storage to achieve economic and environmental benefits. Additionally, the share of renewable energy in the supply mix increased by 7 percent, indicating progress toward a cleaner and more sustainable energy system.

Figure 11 presents the Pareto-optimal solutions derived through the Hybrid MOPSO-NSGA-II approach, along with the optimal solution selected through the decision-making mechanism.

(c)

Case study 3: Operation with DSM considering both battery and hydrogen

The third and most comprehensive case study, referred to as “operation with DSM including both battery and hydrogen storage,” represents the highest level of advancement in the proposed energy management framework. This scenario integrates demand-side management (DSM) with a dual-storage system composed of battery and hydrogen technologies. By combining these two storage solutions, the model enhances system responsiveness and promotes a sustainable energy strategy that is both adaptive and environmentally responsible.

The outcomes of this scenario demonstrate significant improvements across all key performance indicators. Utilizing the Hybrid MOPSO-NSGA-II optimization technique, the system achieved a 5.4 percent reduction in operational costs, a 13 percent decrease in emissions, and a 14.5 percent reduction in the energy gap. The inclusion of hydrogen storage notably contributed to these improvements, further enhancing the system’s ability to manage energy demand effectively. Additionally, the share of renewable energy sources in the total supply increased by 15 percent, indicating a strong progression toward sustainability.

These results highlight the substantial benefits of integrating both advanced storage systems and DSM strategies. This combined approach supports lower operational costs, reduces environmental impact, narrows the energy demand–supply gap, and significantly boosts the integration of renewable energy.

The comparison between the system’s energy supply before and after optimization is presented in Figure 12, demonstrating a significant shift in overall performance. In the initial, pre-optimization state, the energy supply was inadequate to meet system demand. This shortfall created an energy deficit that negatively affected the operation and efficiency of the entire infrastructure. Figure 13 illustrates the Pareto-optimal set derived through the Hybrid MOPSO-NSGA-II algorithm, along with the optimal solution selected using the decision-making process.

Following the implementation of the proposed optimization strategy, which included demand-side management, battery storage, and hydrogen storage systems, the situation improved substantially. The optimized configuration enabled the energy supply to not only meet but also exceed the system’s total demand.

The surplus energy produced in this scenario was directed toward powering the electric vehicle (EV) charging station, ensuring it received the additional electricity required for operation. This improvement eliminated the prior supply deficiency and contributed to the system’s environmental objectives by facilitating the adoption of clean transportation technologies.

The optimization process not only resolved the mismatch between energy supply and demand but also created opportunities for sustainable energy use. It allowed for excess power to be utilized in promoting green technologies, thereby advancing both operational efficiency and ecological sustainability. The final demand and supply status of the system, under the third case study, is illustrated in Figure 14.

To better illustrate the progressive improvements achieved through each case study, a comparative summary of key performance indicators: operational cost, pollution emissions, energy gap, and renewable energy penetration before and after optimization is provided in

Table 6. Comparative results before and after optimization across case studies using Hybrid-NSGA-II-MOPSO [58].

Simulation Modes	Optimization Elements	Operational Cost	Pollution Emissions	Energy Gap	Renewable Energy Penetration
Case study 1	Basic operation (No DSM, No hydrogen)	High	High	High	Low (Baseline)
Case study 2	DSM + Battery	−4.1%	−9%	−12.5%	+7%
Case study 3	DSM + Battery + Hydrogen Storage	−9.5% (total)	−22% (total)	−26% (total)	+22% (total)

. This comparison clearly demonstrates the effectiveness of integrating DSM strategies, battery systems, and hydrogen storage in enhancing the performance of the smart distribution grid.

6. Conclusions

In this study, a tri-objective optimization problem concerning energy management in distribution grids was addressed through the analysis of three distinct case studies using the proposed Hybrid-NSGA-II-MOPSO algorithm. The three objectives were minimizing operational cost and emissions, minimizing the energy gap between forecasted and optimized demand, and maximizing the penetration of renewable energy sources.

In the first case study, the basic operation of the distribution grid was analyzed without incorporating demand-side management (DSM) or energy storage systems. As expected, this scenario resulted in the highest operational costs and pollution emissions due to the absence of flexibility and storage mechanisms.

In the second case, the implementation of DSM and a battery storage system led to notable improvements. Operational costs and emissions were reduced by 4.1% and 9%, respectively, while the energy gap narrowed by 12.5%. Additionally, renewable energy penetration increased by 7%, indicating a shift toward cleaner energy usage.

In the final case study, further improvements were achieved by integrating both battery and hydrogen storage systems alongside DSM. Compared to case 2, operational costs were reduced by an additional 5.4%, emissions decreased by 14.5%, and the energy gap was reduced by 13.5%. Renewable energy penetration increased significantly by 15%, confirming the enhanced performance and sustainability of the proposed model.

While the main focus of this study was on validating the effectiveness of the hybrid optimization approach, this work acknowledges that a benchmark comparison with standalone algorithms such as NSGA-II or MOPSO was not included. This is recognized as a limitation, and a detailed comparative analysis using performance metrics such as convergence speed, hypervolume, and spacing index will be explored in future work.

Additionally, the successful implementation of DSM strategies and hybrid storage integration is not solely dependent on technical optimization. Practical deployment requires enabling communication architectures such as IEC 61850 or 5G to support real-time control and data exchange between distributed grid operators (DGOs) and consumers. Moreover, user acceptance and trust are crucial for DSM adoption. As a potential solution, emerging technologies like smart metering and blockchain may enhance transparency and participation in DSM programs. These aspects will be considered in future extensions of this research.

7. Future Work

In future research, this work will be extended in several directions:

• A comparative benchmarking study will be conducted to evaluate the performance of the proposed Hybrid-NSGA-II-MOPSO algorithm against standalone NSGA-II and MOPSO methods, using standard convergence and diversity metrics.
• Artificial intelligence-based techniques will be explored to enable more accurate techno-economic analysis of the distribution grid.
• AI and machine learning methods will also be applied to enhance control, forecasting, and real-time optimization of power flow.
• Further investigation into capital and operating cost modeling will be performed to support investment and planning decisions in smart grid deployment.