Application of the WRF Model for Operational Wind Power Forecasting in Northeast Brazil
Abstract
1. Introduction
2. Materials and Methods
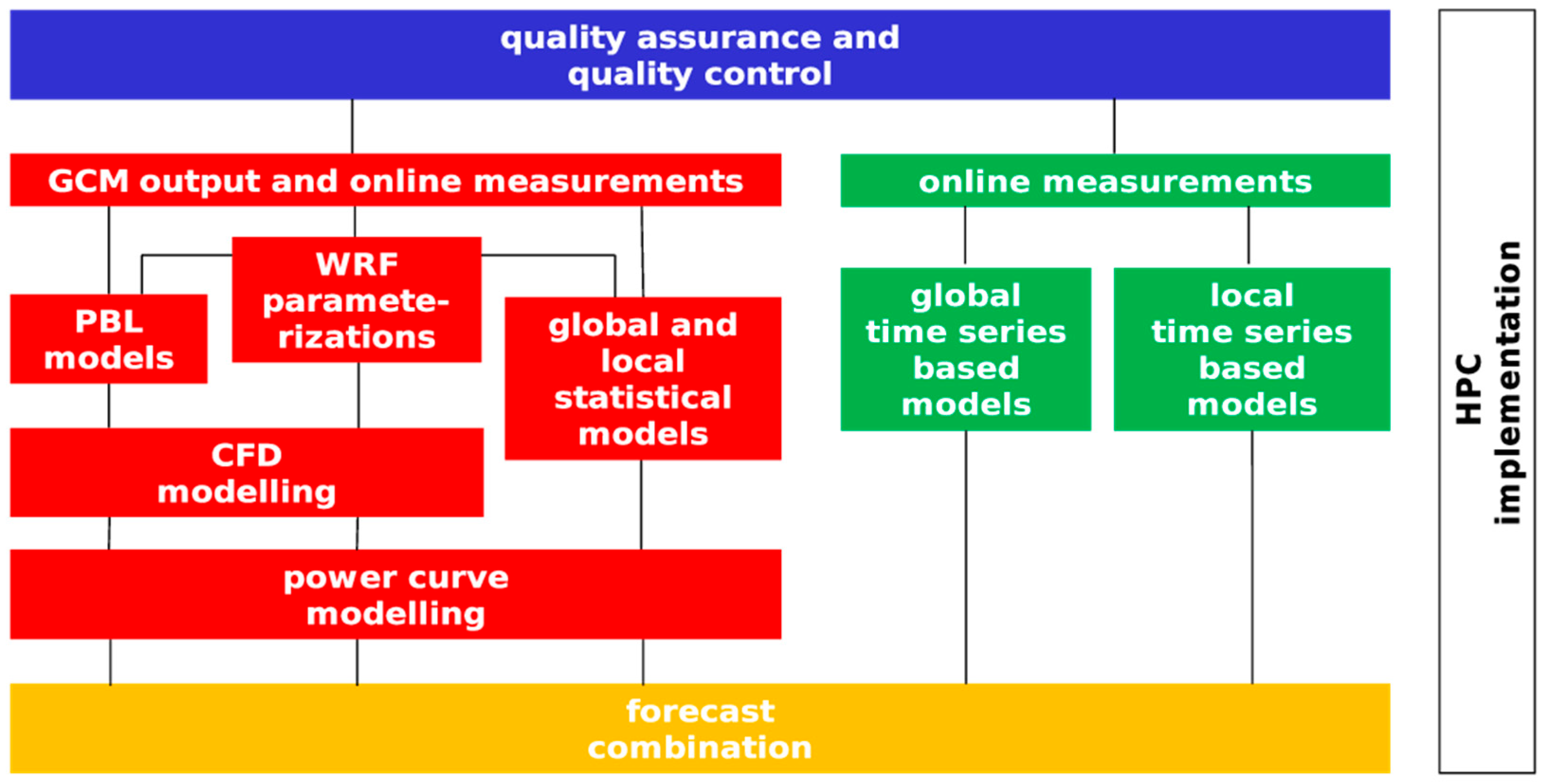
2.1. CER-UFPE Wind Power Forecasting Tool
2.2. Infrastructure
2.3. Observational Dataset
2.4. Geographic Dataset
2.5. Physical Parameterization
2.6. Data Assimilation and Forecast Runs
2.7. Post-Processing
2.8. Statistical Analysis
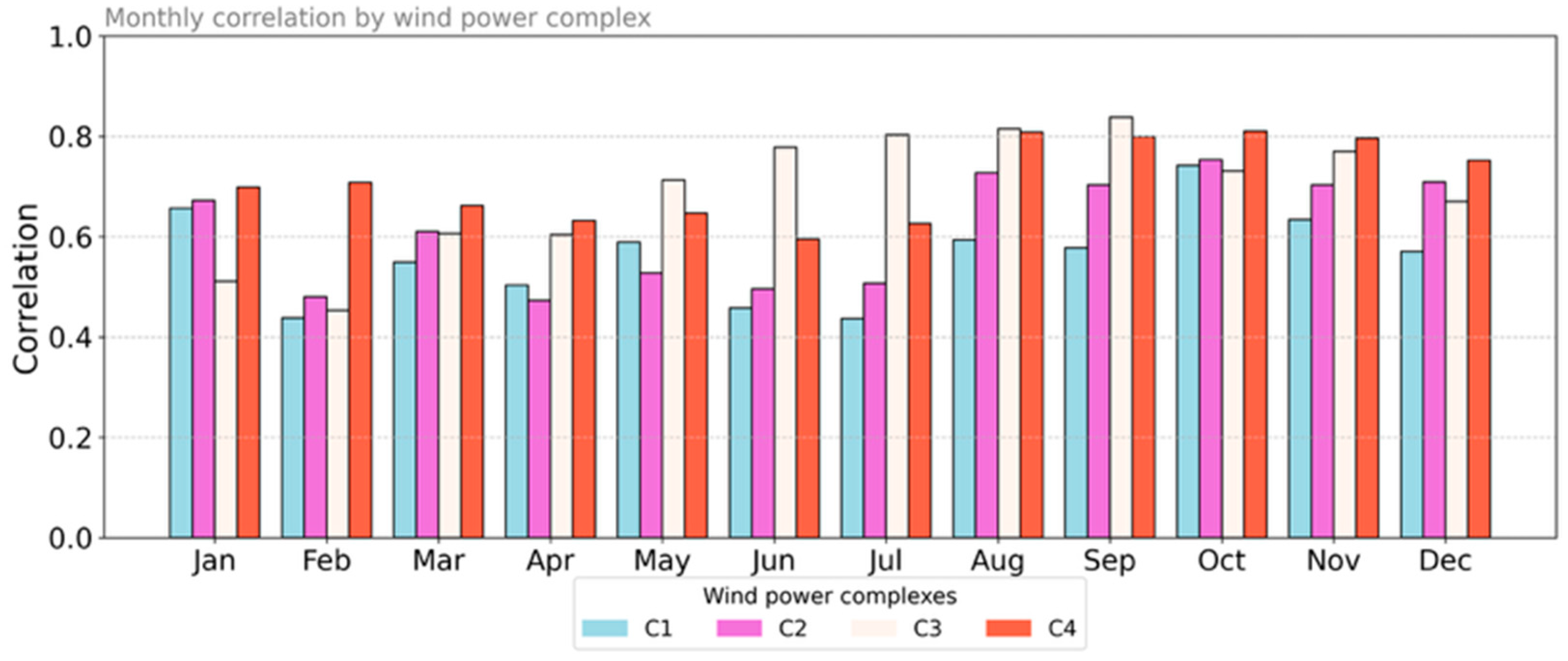
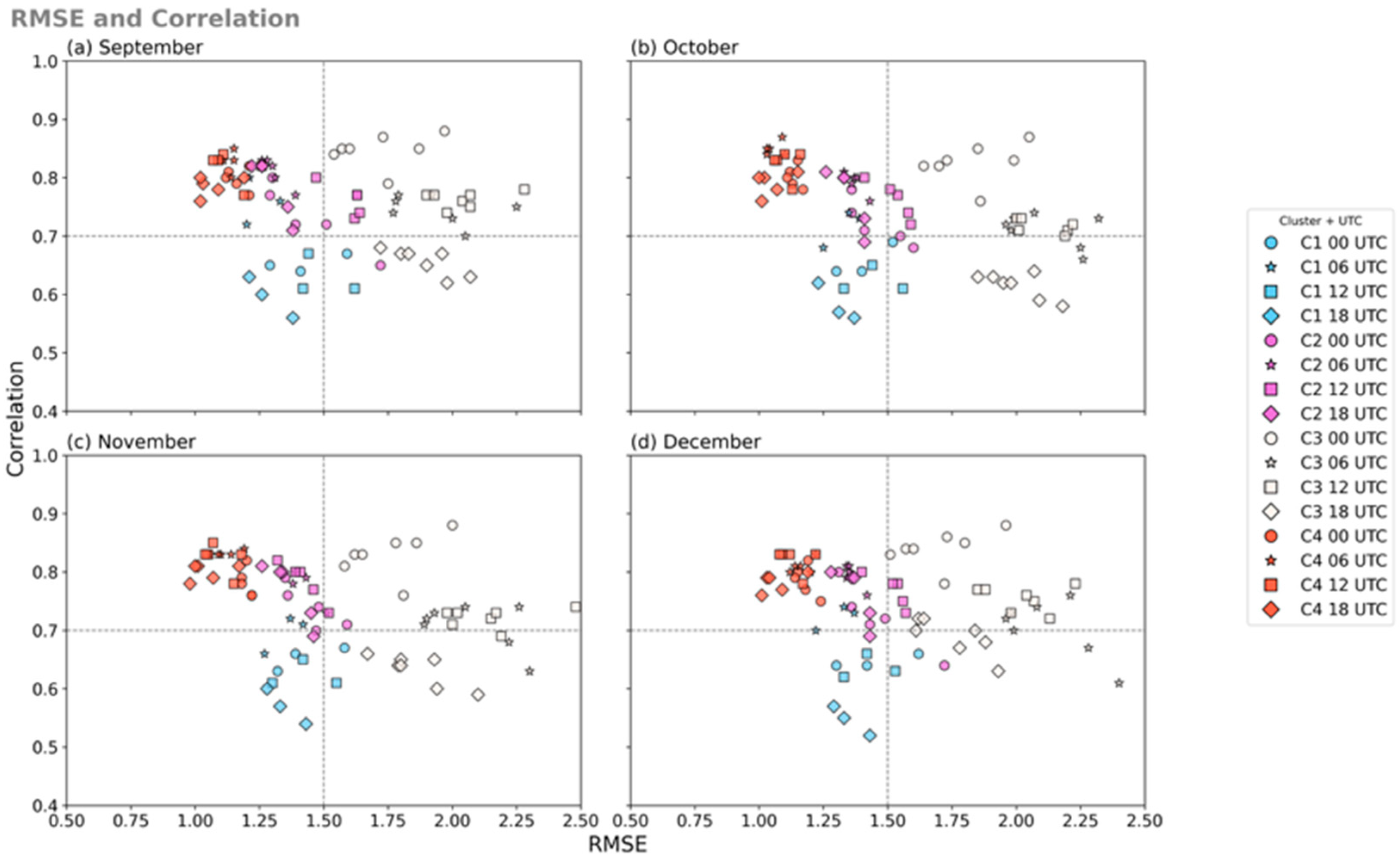
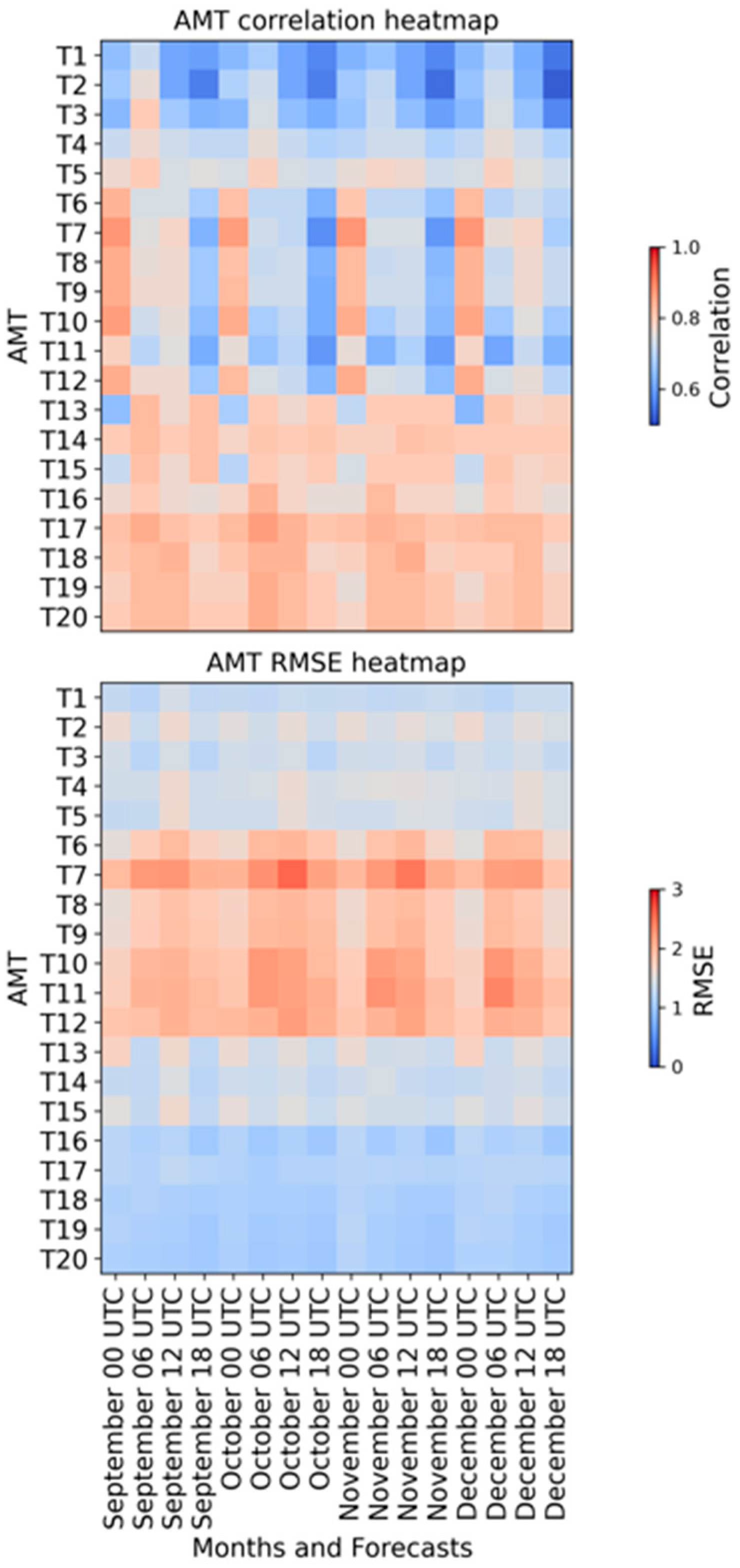
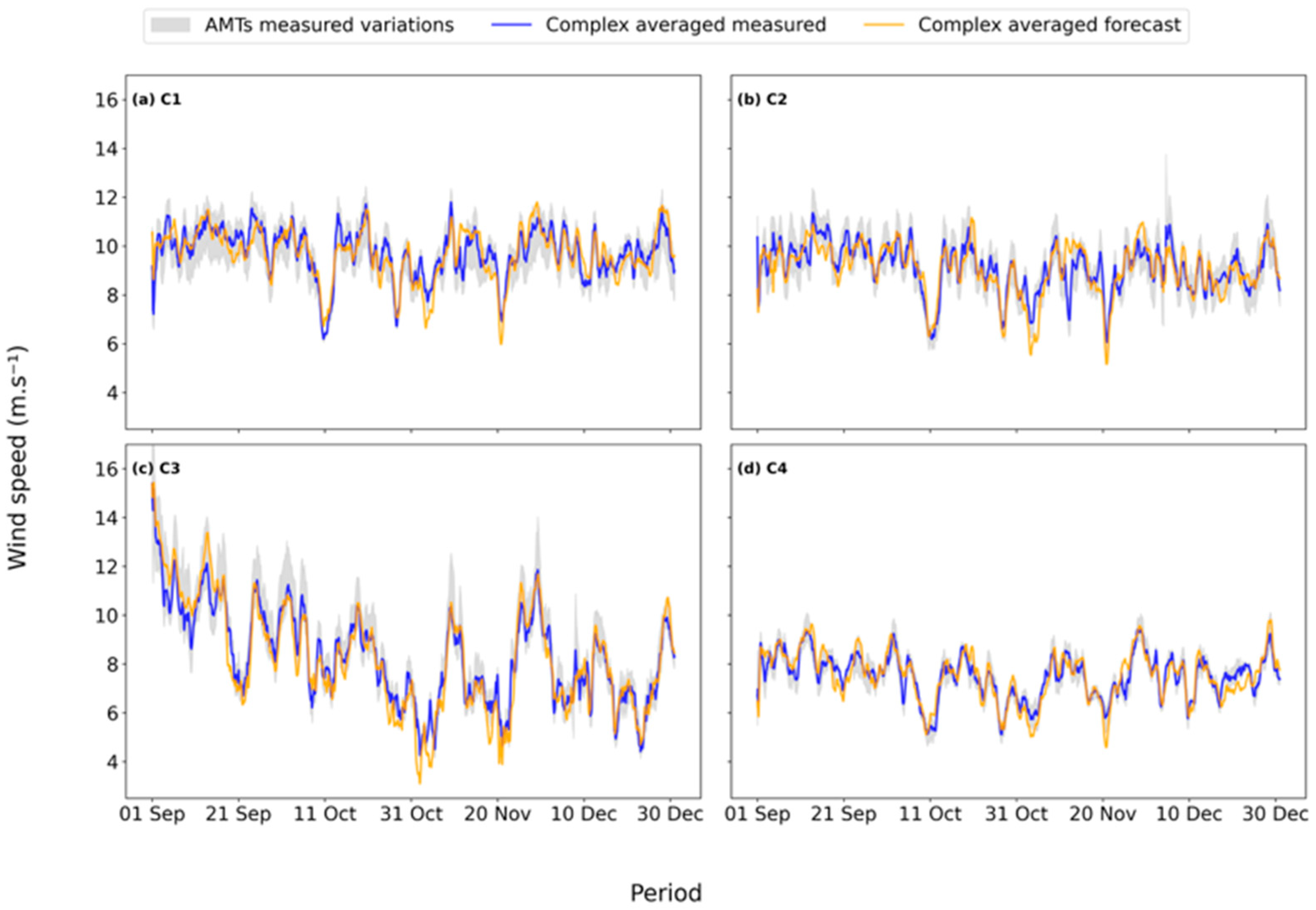
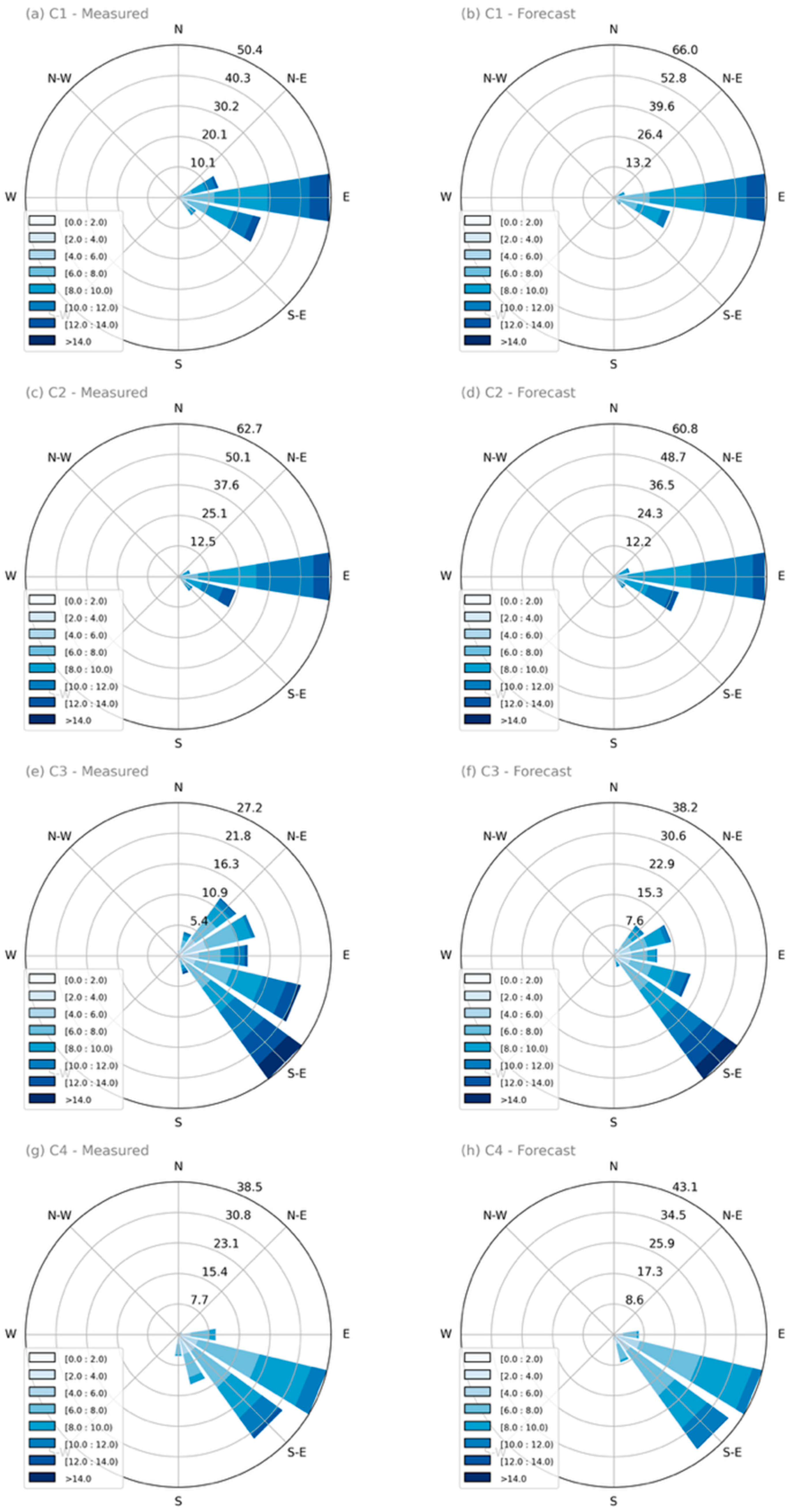
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Operador Nacional do Sistema Elétrico (ONS). O Sistema em Números. Programa Mensal de Operação. Available online: https://www.ons.org.br/paginas/sobre-o-sin/o-sistema-em-numeros (accessed on 17 February 2025).
- Agência Nacional de Energia Elétrica (ANEEL). SIGA Sistema de Informação de Geração Aneel. Available online: https://app.powerbi.com/view?r=eyJrIjoiNGE3NjVmYjAtNDFkZC00MDY4LTliNTItMTVkZTU4NWYzYzFmIiwidCI6IjQwZDZmOWI4LWVjYTctNDZhMi05MmQ0LWVhNGU5YzAxNzBlMSIsImMiOjR9 (accessed on 17 February 2025).
- de Jong, P.; Barreto, T.B.; Tanajura, C.A.S.; Kouloukoui, D.; Oliveira-Esquerre, K.P.; Kiperstok, A.; Torres, E.A. Estimating the Impact of Climate Change on Wind and Solar Energy in Brazil Using a South American Regional Climate Model. Renew. Energy 2019, 141, 390–401. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Costoya, X.; deCastro, M.; Gómez-Gesteira, M. Wind Energy Resource over Europe under CMIP6 Future Climate Projections: What Changes from CMIP5 to CMIP6. Renew. Sustain. Energy Rev. 2021, 151, 111594. [Google Scholar] [CrossRef]
- Araújo, J.C.H.; Souza, W.F.d.; Meireles, A.J.d.A.; Brannstrom, C. Sustainability Challenges of Wind Power Deployment in Coastal Ceará State, Brazil. Sustainability 2020, 12, 5562. [Google Scholar] [CrossRef]
- Cacciuttolo, C.; Navarrete, M.; Cano, D. Advances, Progress, and Future Directions of Renewable Wind Energy in Brazil (2000–2025–2050). Appl. Sci. 2025, 15, 5646. [Google Scholar] [CrossRef]
- Gehrke, P.; Goretti, A.A.T.; Ávila, L.V. Impactos Da Matriz Energética No Desenvolvimento Sustentável Do Brasil. Rev. Adm. UFSM 2021, 14, 1032–1049. [Google Scholar] [CrossRef]
- Martinez, A.; Iglesias, G. Climate Change and Wind Energy Potential in South America. Sci. Total Environ. 2024, 957, 177675. [Google Scholar] [CrossRef]
- Souza, N.B.P.; Nascimento, E.G.S.; Moreira, D.M.; Souza, N.B.P.; Nascimento, E.G.S.; Moreira, D.M. Performance Evaluation of the WRF Model in a Tropical Region: Wind Speed Analysis at Different Sites. Atmósfera 2023, 36, 253–277. [Google Scholar] [CrossRef]
- Chkeir, S.; Anesiadou, A.; Mascitelli, A.; Biondi, R. Nowcasting Extreme Rain and Extreme Wind Speed with Machine Learning Techniques Applied to Different Input Datasets. Atmos. Res. 2023, 282, 106548. [Google Scholar] [CrossRef]
- Garcia, D.W.; Reboita, M.S.; Carvalho, V.S.B. Sensitivity Analysis and Performance Evaluation of the WRF Model in Forecasting an Extreme Rainfall Event in Itajubá, Southeast Brazil. Atmosphere 2025, 16, 548. [Google Scholar] [CrossRef]
- Garcia, D.W.; Reboita, M.S.; Carvalho, V.S.B. Evaluation of WRF Performance in Simulating an Extreme Precipitation Event over the South of Minas Gerais, Brazil. Atmosphere 2023, 14, 1276. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, L.; Yu, M.; Chen, X. Response of Extreme Rainfall to Atmospheric Warming and Wetting: Implications for Hydrologic Designs Under a Changing Climate. J. Geophys. Res. Atmos. 2023, 128, e2022JD038430. [Google Scholar] [CrossRef]
- Correia Filho, W.L.F.; De Oliveira-Júnior, J.F.; De Barros Santiago, D.; De Bodas Terassi, P.M.; Teodoro, P.E.; De Gois, G.; Blanco, C.J.C.; De Almeida Souza, P.H.; da Silva Costa, M.; Gomes, H.B.; et al. Rainfall Variability in the Brazilian Northeast Biomes and Their Interactions with Meteorological Systems and ENSO via CHELSA Product. Big Earth Data 2019, 3, 315–337. [Google Scholar] [CrossRef]
- Ramos, D.N.d.S.; Fernandez, J.P.R.; Fisch, G. Evolution of the Planetary Boundary Layer on the Northern Coast of Brazil during the CHUVA Campaign. Atmos. Res. 2018, 203, 298–310. [Google Scholar] [CrossRef]
- Fesquet, C.; Drobinski, P.; Barthlott, C.; Dubos, T. Impact of Terrain Heterogeneity on Near-Surface Turbulence Structure. Atmos. Res. 2009, 94, 254–269. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Mechem, D.B.; Anderson, M.C. Surface Heterogeneity Impacts on Boundary Layer Dynamics via Energy Balance Partitioning. Atmos. Chem. Phys. 2011, 11, 3403–3416. [Google Scholar] [CrossRef]
- Lohou, F.; Lothon, M.; Bastin, S.; Brut, A.; Canut, G.; Cohard, J.-M.; Cheruy, F.; Couvreux, F.; Dupont, S.; Lafont, S.; et al. Model and Observation for Surface–Atmosphere Interactions over Heterogeneous Landscape: MOSAI Project. J. Eur. Meteorol. Soc. 2025, 3, 100019. [Google Scholar] [CrossRef]
- Huang, H.; Margulis, S.A. On the Impact of Surface Heterogeneity on a Realistic Convective Boundary Layer. Water Resour. Res. 2009, 45, W04425. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Fundamentals of Atmospheric Modeling; Cambridge University Press: Cambridge, UK, 2005; ISBN 9780521548656. [Google Scholar]
- Hong, S.-P. Different Numerical Techniques, Modeling and Simulation in Solving Complex Problems. J. Mach. Comput. 2023, 3, 58. [Google Scholar] [CrossRef]
- Dameris, M.; Jöckel, P. Numerical Modeling of Climate-Chemistry Connections: Recent Developments and Future Challenges. Atmosphere 2013, 4, 132–156. [Google Scholar] [CrossRef]
- Lynch, P. The Origins of Computer Weather Prediction and Climate Modeling. J. Comput. Phys. 2008, 227, 3431–3444. [Google Scholar] [CrossRef]
- Gross, M.; Wan, H.; Rasch, P.J.; Caldwell, P.M.; Williamson, D.L.; Klocke, D.; Jablonowski, C.; Thatcher, D.R.; Wood, N.; Cullen, M.; et al. Physics–Dynamics Coupling in Weather, Climate, and Earth System Models: Challenges and Recent Progress. Mon. Weather Rev. 2018, 146, 3505–3544. [Google Scholar] [CrossRef]
- Benavente, N.R.; Vara-Vela, A.L.; Nascimento, J.P.; Acuna, J.R.; Damascena, A.S.; de Fatima Andrade, M.; Yamasoe, M.A. Air Quality Simulation with WRF-Chem over Southeastern Brazil, Part I: Model Description and Evaluation Using Ground-Based and Satellite Data. Urban. Clim. 2023, 52, 101703. [Google Scholar] [CrossRef]
- Figueroa, S.N.; Bonatti, J.P.; Kubota, P.Y.; Grell, G.A.; Morrison, H.; Barros, S.R.M.; Fernandez, J.P.R.; Ramirez, E.; Siqueira, L.; Luzia, G.; et al. The Brazilian Global Atmospheric Model (BAM): Performance for Tropical Rainfall Forecasting and Sensitivity to Convective Scheme and Horizontal Resolution. Weather Forecast. 2016, 31, 1547–1572. [Google Scholar] [CrossRef]
- Freitas, S.R.; Panetta, J.; Longo, K.M.; Rodrigues, L.F.; Moreira, D.S.; Rosário, N.E.; Silva Dias, P.L.; Silva Dias, M.A.F.; Souza, E.P.; Freitas, E.D.; et al. The Brazilian Developments on the Regional Atmospheric Modeling System (BRAMS 5.2): An Integrated Environmental Model Tuned for Tropical Areas. Geosci. Model. Dev. 2017, 10, 189–222. [Google Scholar] [CrossRef]
- Mantovani Júnior, J.A.; Aravéquia, J.A.; Carneiro, R.G.; Fisch, G. Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin. Atmosphere 2023, 14, 850. [Google Scholar] [CrossRef]
- Holtslag, A.A.M. Introduction to the Third GEWEX Atmospheric Boundary Layer Study (GABLS3). Bound. Layer. Meteorol. 2014, 152, 127–132. [Google Scholar] [CrossRef]
- Huang, L.; Bai, L. Evaluation of Planetary Boundary Layer Schemes on the Urban Heat Islands in the Urban Agglomeration over the Greater Bay Area in South China. Front. Earth Sci. 2023, 10, 1065074. [Google Scholar] [CrossRef]
- Kepert, J.D. Choosing a Boundary Layer Parameterization for Tropical Cyclone Modeling. Mon. Weather Rev. 2012, 140, 1427–1445. [Google Scholar] [CrossRef]
- KoHler, M.; Ahlgrimm, M.; Beljaars, A. Unified Treatment of Dry Convective and Stratocumulus-Topped Boundary Layers in the ECMWF Model. Q. J. R. Meteorol. Soc. 2011, 137, 43–57. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Stefanova, L.; Misra, V. Tropical Meteorology: An Introduction; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-1461474081. [Google Scholar]
- Mahrt, L. Stably Stratified Atmospheric Boundary Layers. Annu. Rev. Fluid. Mech. 2014, 46, 23–45. [Google Scholar] [CrossRef]
- Sandu, I.; Beljaars, A.; Bechtold, P.; Mauritsen, T.; Balsamo, G. Why Is It so Difficult to Represent Stably Stratified Conditions in Numerical Weather Prediction (NWP) Models? J. Adv. Model. Earth Syst. 2013, 5, 117–133. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating Winds and Vertical Wind Shear from Weather Research and Forecasting Model Forecasts Using Seven Planetary Boundary Layer Schemes. Wind. Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Olson, J.B.; Kenyon, J.S.; Djalalova, I.; Bianco, L.; Turner, D.D.; Pichugina, Y.; Choukulkar, A.; Toy, M.D.; Brown, J.M.; Angevine, W.M.; et al. Improving Wind Energy Forecasting through Numerical Weather Prediction Model Development. Bull. Am. Meteorol. Soc. 2019, 100, 2201–2220. [Google Scholar] [CrossRef]
- Pryor, S.C.; Shepherd, T.J.; Volker, P.J.H.; Hahmann, A.N.; Barthelmie, R.J. “Wind Theft” from Onshore Wind Turbine Arrays: Sensitivity to Wind Farm Parameterization and Resolution. J. Appl. Meteorol. Climatol. 2020, 59, 153–174. [Google Scholar] [CrossRef]
- Cruz, M.T.; Simpas, J.B.; Sorooshian, A.; Betito, G.; Cambaliza, M.O.L.; Collado, J.T.; Eloranta, E.W.; Holz, R.; Topacio, X.G.V.; Del Socorro, J.; et al. Impacts of Regional Wind Circulations on Aerosol Pollution and Planetary Boundary Layer Structure in Metro Manila, Philippines. Atmos. Environ. 2023, 293, 119455. [Google Scholar] [CrossRef]
- Han, S.; Hao, T.; Yang, X.; Yang, Y.; Luo, Z.; Zhang, Y.; Tang, Y.; Lu, M. Land-Sea Difference of the Planetary Boundary Layer Structure and Its Influence on PM2.5—Observation and Numerical Simulation. Sci. Total Environ. 2023, 858, 159881. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, J.; Svensson, G. Wind Turning in the Planetary Boundary Layer in CMIP6 Models. J. Clim. 2023, 36, 5729–5742. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4.3; 2021. Available online: https://opensky.ucar.edu/islandora/object/technotes%3A576 (accessed on 20 July 2021).
- Wang, W.; Bruyère, C.; Duda, M.; Dudhia, J.; Gill, D.; Kavulich, M.; Werner, K.; Chen, M.; Lin, H.-C.; Michalakes, J.; et al. Weather Research & Forecasting Model ARW Version 4 Modeling System User’s Guide; EUA: Boulder, CO, USA, 2019. [Google Scholar]
- Otero-Casal, C.; Patlakas, P.; Prósper, M.A.; Galanis, G.; Miguez-Macho, G. Development of a High-Resolution Wind Forecast System Based on the WRF Model and a Hybrid Kalman-Bayesian Filter. Energies 2019, 12, 3050. [Google Scholar] [CrossRef]
- Delfino, R.J.; Bagtasa, G.; Hodges, K.; Vidale, P.L. Sensitivity of Simulating Typhoon Haiyan (2013) Using WRF: The Role of Cumulus Convection, Surface Flux Parameterizations, Spectral Nudging, and Initial and Boundary Conditions. Nat. Hazards Earth Syst. Sci. 2022, 22, 3285–3307. [Google Scholar] [CrossRef]
- Pedruzzi, R.; Andreão, W.L.; Baek, B.H.; Hudke, A.P.; Glotfelty, T.W.; Dias de Freitas, E.; Martins, J.A.; Bowden, J.H.; Pinto, J.A.; Alonso, M.F.; et al. Update of Land Use/Land Cover and Soil Texture for Brazil: Impact on WRF Modeling Results over São Paulo. Atmos. Environ. 2022, 268, 118760. [Google Scholar] [CrossRef]
- Slingo, J.; Palmer, T. Uncertainty in Weather and Climate Prediction. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 4751–4767. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Yang, J.; Zeng, Y.; Zhang, Q.; Liu, Y.; Gu, J.; Dietrich, S.; Sun, H.; Wang, H.; Yang, J.; et al. Improving Forecast of Severe Oceanic Mesoscale Convective Systems Using FY-4A Lightning Data Assimilation with WRF-FDDA. Remote Sens. 2022, 14, 1965. [Google Scholar] [CrossRef]
- Bughici, T.; Lazarovitch, N.; Fredj, E.; Tas, E. Evaluation and Bias Correction in WRF Model Forecasting of Precipitation and Potential Evapotranspiration. J. Hydrometeorol. 2019, 20, 965–983. [Google Scholar] [CrossRef]
- Jiménez, P.A.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. Quality Assurance of Surface Wind Observations from Automated Weather Stations. J. Atmos. Ocean. Technol. 2010, 27, 1101–1122. [Google Scholar] [CrossRef]
- Fang, J.; Peringer, A.; Stupariu, M.S.; Pǎtru-Stupariu, I.; Buttler, A.; Golay, F.; Porté-Agel, F. Shifts in Wind Energy Potential Following Land-Use Driven Vegetation Dynamics in Complex Terrain. Sci. Total Environ. 2018, 639, 374–384. [Google Scholar] [CrossRef]
- López-Espinoza, E.D.; Zavala-Hidalgo, J.; Mahmood, R.; Gómez-Ramos, O. Assessing the Impact of Land Use and Land Cover Data Representation on Weather Forecast Quality: A Case Study in Central Mexico. Atmosphere 2020, 11, 1242. [Google Scholar] [CrossRef]
- Luu, L.N.; van Meijgaard, E.; Philip, S.Y.; Kew, S.F.; de Baar, J.H.S.; Stepek, A. Impact of Surface Roughness Changes on Surface Wind Speed Over Western Europe: A Study With the Regional Climate Model RACMO. J. Geophys. Res. Atmos. 2023, 128, e2022JD038426. [Google Scholar] [CrossRef]
- Kendzierski, S. Impact of WRF Model Parameterization Settings on the Quality of Short-Term Weather Forecasts over Poland. Atmosphere 2024, 15, 1425. [Google Scholar] [CrossRef]
- Fernández-González, S.; Martín, M.L.; García-Ortega, E.; Merino, A.; Lorenzana, J.; Sánchez, J.L.; Valero, F.; Rodrigo, J.S. Sensitivity Analysis of the WRF Model: Wind-Resource Assessment for Complex Terrain. J. Appl. Meteorol. Climatol. 2018, 57, 733–753. [Google Scholar] [CrossRef]
- Adomako, A.B.; Yusup, Y.; Elsebakhi, E.; Jaafar, M.H.; Ishak, M.I.S.; Hwee San, L.; Ahmad, M.I. Sensitivity Analysis and Validation of WRF-ARW Parameterizations for Potential Solar and Wind Energy Sources over Malaysia. Weather Forecast. 2024, 39, 1833–1847. [Google Scholar] [CrossRef]
- Keshtgar, M.; Siadatmousavi, S.M. Sensitivity Analysis of WRF Model to Physical Parameterization for the Characterization of Coastal and Offshore Wind Patterns in Caspian Sea Region. Theor. Appl. Climatol. 2025, 156, 10. [Google Scholar] [CrossRef]
- Zhang, T.; Cao, L.; Li, S.; Zhan, C.; Wang, J.; Zhao, T. Comprehensive Sensitivity Analysis of the WRF Model for Meteorological Simulations in the Arctic. Atmos. Res. 2024, 299, 107200. [Google Scholar] [CrossRef]
- Hong, S.; Lim, J. The WRF Single-Moment 6-Class Microphysics Scheme (WSM6). J. Korean Meteorol.-Ical Soc. 2006, 42, 129–151. [Google Scholar]
- Ma, L.M.; Tan, Z.M. Improving the Behavior of the Cumulus Parameterization for Tropical Cyclone Prediction: Convection Trigger. Atmos. Res. 2009, 92, 190–211. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative Forcing by Long-Lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J. Improving the Representation of Resolved and Unresolved Topographic Effects on Sur-face Wind in the Wrf Model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.Y. Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray-Zone Resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; Cuenca, R.H. Implementation and Verification of the Unified NOAH Land Surface Model in the WRF Model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 12–16 January 2004; pp. 11–15. [Google Scholar]
- Von Storch, H.; Langenberg, H.; Feser, F. A Spectral Nudging Technique for Dynamical Downscaling Purposes. Mon. Weather Rev. 2000, 128, 3664–3673. [Google Scholar] [CrossRef]
- von Storch, J.-S. What Determines the Spectrum of a Climate Variable at Zero Frequency? J. Clim. 1999, 12, 2124–2127. [Google Scholar] [CrossRef]
- Miguez-Macho, G.; Stenchikov, G.L.; Robock, A. Spectral Nudging to Eliminate the Effects of Domain Position and Geometry in Regional Climate Model Simulations. J. Geophys. Res. Atmos. 2004, 109, D13104. [Google Scholar] [CrossRef]
- Gómez, B.; Miguez-Macho, G. Spectral Nudging in the Tropics. Earth Syst. Dyn. Discuss. 2020, 1–26. [Google Scholar] [CrossRef]
- Otte, T.L.; Nolte, C.G.; Otte, M.J.; Bowden, J.H. Does Nudging Squelch the Extremes in Regional Climate Modeling? J. Clim. 2012, 25, 7046–7066. [Google Scholar] [CrossRef]
- Bowden, J.H.; Otte, T.L.; Nolte, C.G.; Otte, M.J. Examining Interior Grid Nudging Techniques Using Two-Way Nesting in the WRF Model for Regional Climate Modeling. J. Clim. 2012, 25, 2805–2823. [Google Scholar] [CrossRef]
- Warner, T.T. Quality Assurance in Atmospheric Modeling. Bull. Am. Meteorol. Soc. 2011, 92, 1601–1610. [Google Scholar] [CrossRef]
- Saikrishna, T.S.; Ramu, D.A.; Prasad, K.B.R.R.H.; Osuri, K.K.; Rao, A.S. High Resolution Dynamical Downscaling of Global Products Using Spectral Nudging for Improved Simulation of Indian Monsoon Rainfall. Atmos. Res. 2022, 280, 106452. [Google Scholar] [CrossRef]
- Sun, W.; Liu, Z.; Song, G.; Zhao, Y.; Guo, S.; Shen, F.; Sun, X. Improving Wind Speed Forecasts at Wind Turbine Locations over Northern China through Assimilating Nacelle Winds with WRFDA. Weather Forecast. 2022, 37, 545–562. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna. In Proceedings of the Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; ACM: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]
- Sayeed, A.; Choi, Y.; Jung, J.; Lops, Y.; Eslami, E.; Salman, A.K. A Deep Convolutional Neural Network Model for Improving WRF Simulations. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 750–760. [Google Scholar] [CrossRef]
- Hugeback, K.K.; Gallus, W.A.; Villegas Pico, H.N. Machine Learning–Adjusted WRF Forecasts to Support Wind Energy Needs in Black Start Operations. Weather Forecast. 2023, 38, 1553–1561. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Yang, Y.; Wang, Y.; Luo, W.; Zhou, X. Enhancing Weather Forecast Accuracy Through the Integration of WRF and BP Neural Networks: A Novel Approach. Earth Space Sci. 2024, 11, e2024EA003613. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, Z.; Li, Y. Deep-Learning Correction Methods for Weather Research and Forecasting (WRF) Model Precipitation Forecasting: A Case Study over Zhengzhou, China. Atmosphere 2024, 15, 631. [Google Scholar] [CrossRef]
- Liu, H.; Tan, Z.; Wang, Y.; Tang, J.; Satoh, M.; Lei, L.; Gu, J.; Zhang, Y.; Nie, G.; Chen, Q. A Hybrid Machine Learning/Physics-Based Modeling Framework for 2-Week Extended Prediction of Tropical Cyclones. J. Geophys. Res. Mach. Learn. Comput. 2024, 1, e2024JH000207. [Google Scholar] [CrossRef]
- Hu, W.; Ghazvinian, M.; Chapman, W.E.; Sengupta, A.; Ralph, F.M.; Delle Monache, L. Deep Learning Forecast Uncertainty for Precipitation over the Western United States. Mon. Weather Rev. 2023, 151, 1367–1385. [Google Scholar] [CrossRef]
- Gurgel, A.d.R.C.; Sales, D.C.; Lima, K.C. Wind Power Density in Areas of Northeastern Brazil from Regional Climate Models for a Recent Past. PLoS ONE 2024, 19, e0307641. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Schumacher, V.; Fernández, A.; Justino, F.; Comin, A. WRF High Resolution Dynamical Downscaling of Precipitation for the Central Andes of Chile and Argentina. Front. Earth Sci. 2020, 8, 328. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Introduction to Special Section: Regional Climate Modeling Revisited. J. Geophys. Res. Atmos. 1999, 104, 6335–6352. [Google Scholar] [CrossRef]
- Golzio, A.; Ferrarese, S.; Cassardo, C.; Diolaiuti, G.A.; Pelfini, M. Land-Use Improvements in the Weather Research and Forecasting Model over Complex Mountainous Terrain and Comparison of Different Grid Sizes. Bound. Layer. Meteorol. 2021, 180, 319–351. [Google Scholar] [CrossRef]
- Gnedin, N.Y.; Semenov, V.A.; Kravtsov, A.V. Enforcing the Courant–Friedrichs–Lewy Condition in Explicitly Conservative Local Time Stepping Schemes. J. Comput. Phys. 2018, 359, 93–105. [Google Scholar] [CrossRef]
- Das, M.K.; Das, M.K.; Chowdhury, A.M.; Das, S. Sensitivity Study with Physical Parameterization Schemes for Simulation of Mesoscale Convective Systems Associated with Squall Events. Int. J. Earth Atmos. Sci. 2015, 2, 20–36. [Google Scholar]

| Wind Power Complex | Distance from Coastline | Topography |
|---|---|---|
| C1 | 0.5 km | Transition sea–land |
| C2 | 6.2 km; 2.5 km | Flat terrain |
| C3 | >400 km | High altitude plateau |
| C4 | 15.5 km | Low altitude plateau |
| Module | Parameterizations | References |
|---|---|---|
| Microphysics | WSM6 | [60] |
| Cumulus | Kain–Fritsch | [61,62] |
| Longwave/shortwave radiation | RRTMG | [63] |
| Surface physics | Revised MM5 Scheme | [64] |
| Planetary boundary layer | Shin-Hong | [65] |
| Soil physics | NOAH | [66] |
| September | October | November | December | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | |
| MBE (m.s−1) | 0.13 | 0.17 | −0.20 | −0.08 | 0.05 | 0.00 | 0.30 | −0.10 | 0.07 | 0.08 | 0.25 | 0.06 | −0.03 | 0.03 | −0.04 | 0.05 |
| MAE (m.s−1) | 0.98 | 0.87 | 1.12 | 0.74 | 0.86 | 0.86 | 1.25 | 0.74 | 1.01 | 1.05 | 1.37 | 0.76 | 0.88 | 0.83 | 1.26 | 0.74 |
| 0.86 | 0.93 | 1.06 | 0.96 | 0.87 | 0.92 | 1.02 | 0.96 | 1.02 | 1.11 | 1.09 | 1.00 | 0.85 | 0.92 | 0.99 | 0.97 | |
| RMSE (m.s−1) | 1.24 | 1.12 | 1.45 | 1.00 | 1.08 | 1.09 | 1.70 | 0.98 | 1.36 | 1.41 | 1.82 | 1.00 | 1.13 | 1.07 | 1.65 | 0.94 |
| nRMSE (%) | 12.93 | 9.77 | 10.35 | 11.05 | 11.60 | 9.82 | 13.03 | 9.17 | 12.54 | 11.56 | 12.99 | 9.91 | 11.27 | 9.81 | 13.05 | 9.84 |
| 0.68 | 0.81 | 0.89 | 0.84 | 0.79 | 0.85 | 0.79 | 0.86 | 0.66 | 0.80 | 0.80 | 0.85 | 0.62 | 0.83 | 0.71 | 0.82 | |
| September | October | November | December | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | C1 | C2 | C3 | C4 | |
| MBE (m.s−1) | 0.05 | −0.05 | −0.30 | 0.02 | 0.02 | −0.08 | 0.10 | −0.02 | 0.25 | 0.02 | −0.10 | −0.01 | 0.06 | −0.04 | 0.04 | 0.01 |
| MAE (m.s−1) | 0.94 | 0.81 | 1.00 | 0.61 | 0.96 | 0.88 | 1.07 | 0.68 | 0.91 | 0.89 | 1.11 | 0.64 | 0.83 | 0.74 | 1.10 | 0.67 |
| 0.71 | 0.97 | 0.89 | 0.86 | 0.79 | 0.81 | 0.85 | 0.87 | 0.82 | 0.84 | 0.84 | 0.93 | 0.79 | 0.84 | 0.77 | 0.93 | |
| RMSE (m.s−1) | 1.19 | 1.05 | 1.28 | 0.80 | 1.21 | 1.10 | 1.43 | 0.86 | 1.16 | 1.16 | 1.44 | 0.82 | 1.07 | 0.94 | 1.45 | 0.84 |
| nRMSE (%) | 12.66 | 9.45 | 9.28 | 9.07 | 12.76 | 10.38 | 11.42 | 7.62 | 11.43 | 9.77 | 10.52 | 8.08 | 11.33 | 9.03 | 11.70 | 9.44 |
| 0.67 | 0.83 | 0.90 | 0.90 | 0.72 | 0.85 | 0.83 | 0.89 | 0.71 | 0.83 | 0.85 | 0.90 | 0.63 | 0.86 | 0.71 | 0.86 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, T.; Costa, A.; Vilela, O.C.; Willmersdorf, R.; dos Santos Júnior, J.V.; Alves, L.H.B.; Tyaquiçã, P.; de Lima, M.F.S.; de Souza, H.R.B.; Veleda, D. Application of the WRF Model for Operational Wind Power Forecasting in Northeast Brazil. Energies 2025, 18, 5731. https://doi.org/10.3390/en18215731
Silva T, Costa A, Vilela OC, Willmersdorf R, dos Santos Júnior JV, Alves LHB, Tyaquiçã P, de Lima MFS, de Souza HRB, Veleda D. Application of the WRF Model for Operational Wind Power Forecasting in Northeast Brazil. Energies. 2025; 18(21):5731. https://doi.org/10.3390/en18215731
Chicago/Turabian StyleSilva, Thiago, Alexandre Costa, Olga C. Vilela, Ramiro Willmersdorf, José Vailson dos Santos Júnior, Luís Henrique Bezerra Alves, Pedro Tyaquiçã, Mateus Francisco Silva de Lima, Herbert Rafael Barbosa de Souza, and Doris Veleda. 2025. "Application of the WRF Model for Operational Wind Power Forecasting in Northeast Brazil" Energies 18, no. 21: 5731. https://doi.org/10.3390/en18215731
APA StyleSilva, T., Costa, A., Vilela, O. C., Willmersdorf, R., dos Santos Júnior, J. V., Alves, L. H. B., Tyaquiçã, P., de Lima, M. F. S., de Souza, H. R. B., & Veleda, D. (2025). Application of the WRF Model for Operational Wind Power Forecasting in Northeast Brazil. Energies, 18(21), 5731. https://doi.org/10.3390/en18215731







