Mitigating Energy Losses Under Incremental Load Variations in Distributed Power-Flow Systems While Ensuring User Comfort

Abstract

Renewable energy sources (RESs) such as photovoltaic (PV) and fuel cells (FCs) introduce variability that complicates reliable, loss-aware operation of distributed power-flow systems (DPFSs) in smart homes. Frequent charge/discharge cycling of energy storage systems (ESSs) can inflate losses and jeopardize user comfort when generation and demand are mismatched. This paper addresses the gap in multi-load, multi-source coordination under fluctuating RESs by proposing a Multiple-Load Power-Flow Assignment (MPFA) framework that explicitly minimizes storage-related losses while maintaining demand satisfaction. We evaluate four logical interconnection scenarios among generators (PGs), loads (PLs), and storage (PSs), and compare three control algorithms—total-demand-based (TDPF), adaptive-demand-based (ADPF), and grid-based (GBPF). Using measured PV/FC data across seasons, MPFA consistently reduces storage-related losses as interconnections increase, with GBPF guaranteeing full daily demand satisfaction by flexibly supplementing local generation with grid power. ADPF performs strongly when grid support is limited by prioritizing critical loads and optimizing storage utilization. The results provide actionable guidance for designing smart-home energy management that emphasizes sustainability, reliability, and user comfort.

1. Introduction

The rapid advancement of smart home technologies and the increasing adoption of Renewable Energy Sources (RESs) have revolutionized the way energy is generated, stored, and consumed. Smart homes, equipped with intelligent energy management systems, enable efficient utilization of energy resources while enhancing user comfort and reducing operational costs. The urgent need to reduce ${\mathrm{CO}}_2$ emissions and mitigate the impact of conventional energy sources on the environment has led to a global shift towards RES power generation. This transition addresses environmental concerns and the dwindling reserves of traditional energy sources such as oil and gas. RESs such as photovoltaic (PV), biomass, and wind offer clean and efficient alternatives to conventional power generation methods [1,2].

Smart home systems have evolved significantly with advancements in the Internet, transforming traditional homes into interconnected spaces where appliances and devices communicate seamlessly [3]. Modern smart homes often incorporate RESs like PVs and Fuel Cells (FCs) alongside conventional appliances, creating more sustainable and efficient energy ecosystems [4]. Through integration with RESs, smart home systems can optimize energy usage, reduce dependence on fossil fuels, and minimize environmental impact. As these systems continue to evolve, they promise to revolutionize modern living by providing personalized, interconnected, and energy-efficient environments. These systems gather energy profiles and oversee automation controls, managing the ON/OFF operations of Home Appliances and Devices (HADs) efficiently [5].

However, the integration of RESs, such as solar PV systems and wind turbines, into the smart home environment introduces significant challenges due to their inherent variability and intermittency. Fluctuations in energy generation can lead to imbalances between supply and demand, resulting in energy losses, reduced system efficiency, and potential disruptions in power supply. These fluctuations in energy generation can lead to instability in the DPFS, making it difficult to maintain a reliable and consistent power supply [6].

Deploying Energy Storage Systems (ESSs) has emerged as a practical solution to mitigate power fluctuations and enhance power system reliability. To tackle the changes in power from renewable energy and the varying needs of electricity in a system, using ESSs is an effective solution [7,8]. This flexibility helps manage situations where we have too much power when demand is low or not enough power during peak times. Using ESSs to store surplus power and supply it when needed effectively mitigates these fluctuations.

This paper investigates the impact of fluctuating energy generation on multiple load operations in smart homes and evaluates energy loss within the DPFS. In this work, we introduce the Multiple-Load Power-Flow Assignment (MPFA) approach, which aims to minimize power storage losses and ensure the maximum demand of power loads is satisfied. The DPFS framework is designed to dynamically allocate power flows between energy generators, loads, and storage units, taking into account the variability of RESs and the diverse demand patterns of smart homes. Through extensive simulations, we explore four distinct scenarios of power flow interactions between generators, loads, and storage systems. Our results demonstrate significant reductions in primary and secondary storage losses, highlighting the effectiveness of the proposed MPFA approach. Furthermore, the framework ensures that the maximum demand of power loads is consistently met, even under fluctuating generation conditions.

Fluctuating renewable energy production leads to temporal mismatches between generation and demand in smart homes, causing intermittent under- or over-supply conditions. Such fluctuations can result in frequent charging/discharging of storage units, increasing energy losses and reducing system efficiency. The proposed MPFA framework addresses these challenges by dynamically re-allocating power flows among generators, storage systems, and multiple loads in real time. Through the integration of the ADPF and GBPF algorithms, the MPFA approach adaptively balances supply–demand mismatches, prioritizes critical loads, and leverages both local storage and grid power to maintain continuous operation with minimized losses.

2. Related Work

The integration of Renewable Energy Sources (RESs) into power systems has been extensively studied in recent years, driven by the global push toward sustainable and resilient energy infrastructures. Researchers have explored various facets of RES integration, encompassing energy generation, storage, and consumption, with a sustained focus on optimizing power flow and minimizing energy losses. This section provides a comprehensive review of key studies in the field, highlighting seminal contributions and identifying persisting gaps that the current research aims to address.

For instance, one study examined the impact of solar irradiance fluctuations on power grid stability and proposed a dynamic energy management system to mitigate these effects [1]. In a related effort, another work introduced a linear programming-based approach to optimize energy storage sizing under operational safety conditions to ensure stable grid performance [7]. Similarly, a battery energy storage system (BESS) optimization model was developed with the primary objective of minimizing overall energy costs [9], while another contribution addressed dual power load scenarios by introducing novel load-shifting algorithms that significantly reduce energy losses [10]. Further discussions appear in studies that extend grid optimization [5,11].

More recently, researchers proposed an energy management approach that prioritizes the utilization of stored power in energy storage systems (ESSs) during periods when the System Marginal Price (SMP) is high, while also considering household appliance efficiency ratings and noise limitations [12,13]. In cases where ESS reserves are depleted, their strategy shifts toward operating high-power and high-efficiency appliances to achieve cost-effective energy consumption under conditions of low grid demand [3,11,12,13,14,15]. Another line of research advanced the field by applying ESS to mitigate photovoltaic (PV) fluctuations, introducing a control strategy that regulates the state of charge (SoC) and determines output power based on super short-term PV forecasts [16,17]. Similarly, ref. [18] presents an optimization-based sizing routine for battery energy storage systems (BESSs) aimed at ensuring adequacy and small-signal stability in hybrid power systems. These contributions highlight the growing importance of coordinated control and appropriate storage sizing—topics directly aligned with the objectives of this study. This method incorporates rolling prediction theory, ensuring real-time regulation at every sampling point, and further develops an ESS sizing framework to evaluate the combined technical and economic performance of the system [19,20]. Moreover, rolling, short-horizon forecasting has also been used to regulate PV-driven variability in real time [16], while recent work develops adequacy- and stability-oriented BESS sizing for hybrid microgrids [18].

The historical evolution of power system flexibility has also been explored, with one study emphasizing that cloud transients cause rapid PV output variations which significantly influence voltage levels in low-voltage (LV) grids with high PV penetration [21]. Such variations may cause power-quality violations; their effects were analyzed via load-flow assessments under multiple scenarios [21]. In addition, a comprehensive review highlighted the main characteristics of flexible power systems, identifying flexibility sources, evaluation parameters, and the broader impacts of variable renewable energy penetration on transient stability, small-signal stability, and frequency response [6]. A decentralized droop control method based on battery state of charge was proposed to enable reliable power exchange among clustered nanogrids without inter-unit communication, reducing line losses and ensuring scalability [22]. Building on droop concepts, adaptive droop control further enhances voltage regulation and coordinated power exchange in DC nanogrids [23]. Renewable-integrated DC nanogrids with distributed control have been shown suitable for rural/remote electrification scenarios [24]. To further improve resource sharing and transient control, a multi-agent distributed control strategy employing augmented Lagrangian optimization has been introduced, achieving optimal power distribution with minimized losses [24]. Additionally, cooperative game-theoretic approaches, such as Nash Bargaining Solution (NBS) based energy management, have been applied to nanogrids to ensure fair and efficient allocation of resources, enhancing battery lifespan and renewable utilization while maintaining robust bus voltage regulation [25].

Despite substantial progress in the domains of RES integration, ESS optimization, and power flow management, several critical gaps persist in the literature. First, most existing studies focus on single-load scenarios, often neglecting the complexities inherent in multiple-load operations within smart homes. Second, the impact of fluctuating energy generation on energy losses in DPFS remains underexplored. Third, there is a lack of comprehensive frameworks that simultaneously integrate RESs, ESSs, and multiple loads to optimize power flow allocation and minimize energy losses. Finally and most importantly, the literature rarely considers user comfort or satisfaction, particularly when power demand cannot be fully met, an essential aspect for practical deployment in real-world smart home environments [11,14,15,26]. Recent works underscore these gaps. For example, presents a multi-objective optimization model for smart home energy management that incorporates user comfort as a critical constraint, revealing significant trade-offs between energy efficiency and occupant satisfaction [11,14,15,26]. One study investigates the coordinated operation of multiple loads, ESSs, and PV systems, and demonstrates that incorporating user preferences leads to both improved energy utilization and enhanced comfort [27,28]. Similarly, Kiani et al. introduce a demand-side management approach using reinforcement learning [29], where user comfort is explicitly modeled and optimized, further emphasizing the necessity of considering end-user experience in future smart grid research. While single-source or single-load optimization is well-studied, the coupling of multi-source–multi-storage–multi-load systems introduces complex energy loss and control challenges. Additionally, the risk of thermal runaway in ESSs poses reliability and safety concerns in residential applications [30,31]. Authors in [32] propose a shrinking-horizon control architecture for bidirectional home charging (V2H/H2V), improving load balancing and reducing operational costs within HEMS.

Due to the intermittent and fluctuating nature of renewable sources such as solar and wind, achieving a stable, large-scale energy supply remains challenging. Hydrogen energy offers significant potential as a complementary pathway in the clean energy transition. Through water electrolysis, surplus renewable power can be converted into hydrogen for long-term storage and later reconverted into electricity via proton-exchange-membrane fuel cells [33], with advances in PEMFC membrane materials (e.g., SPEEK) enabling this conversion step [34]. For a system-level overview of power-to-hydrogen and long-term storage, see [35]. This integrated hydrogen–electricity pathway supports deep decarbonization and enhances the flexibility of distributed energy systems.

The contributions of this research are threefold: (i) the development of a dynamic power flow allocation framework for smart home energy systems, (ii) the evaluation of energy losses under multiple operational scenarios, and (iii) the demonstration of the DPFS algorithm’s capability to satisfy load demands while minimizing storage losses. By addressing key challenges of RES integration, this work provides an effective approach for optimizing energy management in future smart homes.

Table 1 summarizes the key contributions, strengths, and limitations of existing studies on multi-load or multi-source power flow control and energy management in smart homes. As shown, most prior works focus on single-load or cost-oriented optimization, whereas the proposed MPFA framework uniquely emphasizes multi-load coordination under fluctuating renewable conditions while ensuring user comfort.

Table 1. Summary of related work and strengths of the proposed MPFA framework.

Study	Main Focus	Strengths	Limitations
[1]	Dynamic EMS for PV fluctuation mitigation.	Improves grid stability; adaptive response to irradiance changes.	Focuses on single-load; ignores ESS losses.
[7]	ESS sizing via linear programming.	Ensures safe operation and SoC management.	Ignores multi-load and RES variability.
[9]	Cost minimization model for BESS.	Reduces operational cost; enhances ESS use.	Static model; lacks real-time adaptability.
[10]	Dual-load shifting algorithm.	Lowers losses under dual-load operation.	Limited scalability to multi-load systems.
[12,13]	Smart home scheduling with SMP pricing.	Considers appliance efficiency and user comfort.	Excludes RES uncertainty and loss modeling.
[21]	PV-induced voltage fluctuation in LV grids.	Highlights grid flexibility challenges.	No mitigation strategy provided.
[6]	Review of flexibility in RES systems.	Comprehensive theoretical overview.	Lacks quantitative smart home validation.
[22,23,24,25]	Nanogrid droop (SoC/adaptive) and cooperative microgrid control.	Improves DC-bus voltage regulation and fair power sharing; enables rural/remote electrification and islanded operation; MPC-based optimal power flows for cooperative microgrids;	Droop does not explicitly optimize economics; cooperative/MPC methods can require more tuning/communication; scope often beyond single-home scale.
[11,14,15,27,28,29]	User comfort in multi-load energy management.	Balances comfort and energy efficiency.	Does not address DPFS losses or fluctuation effects.
Proposed MPFA	Multi-load power flow optimization under RES fluctuation.	Integrates RES, ESS, and loads; minimizes storage loss; maintains comfort and stability.	Current model omits degradation and converter losses (future work).

3. System Model

This section provides an in-depth description of the Distributed Power Flow System (DPFS) implemented in a smart home environment. The DPFS enables optimal energy management by coordinating multiple power generation sources, flexible energy storage systems, and diverse household loads. Through real-time power flow control and adherence to operational constraints, the DPFS ensures reliable, efficient, and sustainable operation of the residential microgrid.

3.1. Overview of System Architecture

As illustrated in Figure 1, the DPFS is architected around three fundamental subsystems:

Figure 1. System model of the DPFS in a smart home environment, illustrating three power generation units (PV, FC, UG), two storage systems, and eight power loads.

• Power Generation Systems (PGs): Responsible for producing electrical energy from renewable and conventional sources.
• Power Storage Systems (PSs): Facilitate temporal balancing of supply and demand by storing surplus energy and discharging it as needed.
• Power Loads (PLs): Represent the consumption profile of the household through various appliances and devices.

All subsystems are interconnected via a central electrical bus, supporting bidirectional energy transfer and intelligent coordination.

3.2. Performance Metrics

User comfort and demand satisfaction are used as system-level metrics. We define

$$U_c=1-{\displaystyle \frac{T_{int}}{T_{tot}}},D_s={\displaystyle \frac{E_{\mathrm{supplied}}}{E_{\mathrm{demanded}}}}\times 100\%,$$

where $T_{int}$ is the total interruption time over the horizon $T_{tot}$, and $E_{\mathrm{supplied}}$, $E_{\mathrm{demanded}}$ are cumulative energy supply and demand, respectively.

3.3. Power Generation Systems (PGs)

The power generation subsystem comprises the following:

• PV Panels: Generate variable renewable energy based on solar irradiance.
• Fuel Cells (FC): Provide semi-controllable renewable generation through hydrogen-based electrochemical reactions.
• Utility Grid (UG): Functions as a fully controllable generator, supplementing local generation to guarantee demand satisfaction.

Let J be the total number of PGs. For the j-th PG at time t:

• $P{G}_j^f\left(t\right)$: Fluctuating RESs generation (e.g., PV, FC)
• $P{G}_j^c\left(t\right)$: Controllable generation (e.g., UG)

Subject to generation bounds:

$$\begin{array}{cc}\hfill {\mathcal{P}}_{P{G}_j^c}^{min}& \le {\mathcal{P}}_{P{G}_j^c}\left(t\right)\le {\mathcal{P}}_{P{G}_j^c}^{max},\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{P{G}_j^f}^{min}& \le {\mathcal{P}}_{P{G}_j^f}\left(t\right)\le {\mathcal{P}}_{P{G}_j^f}^{max}.\hfill \end{array}$$

(2)

3.4. Power Storage Systems (PSs)

The power storage subsystem introduces flexibility and robustness, enabling the DPFS to buffer renewable fluctuations and optimize energy usage. Each PS can be categorized as primary ($P{S}_p$) or secondary ($P{S}_s$), designed for different cycling profiles.

Let H denote the total number of PS units. Each storage system h at time t is defined by

• $So{C}_h^{ini}$: Initial state of charge.
• $So{C}_h^{min},So{C}_h^{max}$: Minimum and maximum SoC bounds.
• ${\eta }_c$: Charging efficiency.
• ${\eta }_d$: Discharging efficiency.
• $ES{S}_h$: Storage capacity (Wh or kWh).

3.4.1. Stored Energy and SoC Dynamics

Let n index time steps with step size $\Delta t$. The total stored energy in the h-th PS at time t is given by

$$\begin{array}{cc}\hfill E_{{\mathrm{PS}}_h}[n+1]& =E_{{\mathrm{PS}}_h}\left[n\right]+{\eta }_c{\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left[n\right]\Delta t-{\displaystyle \frac{1}{{\eta }_d}}{\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left[n\right]\Delta t,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill E_{{\mathrm{PS}}_h}\left[0\right]& =So{C}_h^{ini}ES{S}_h,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill So{C}_h[n+1]& =So{C}_h\left[n\right]+{\displaystyle \frac{{\eta }_c\Delta t}{ES{S}_h}}{\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left[n\right]-{\displaystyle \frac{\Delta t}{{\eta }_{d}ES{S}_h}}{\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left[n\right],\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill So{C}_h^{min}& \le So{C}_h\left[n\right]\le So{C}_h^{max}.\hfill \end{array}$$

(6)

where $E_{{\mathrm{PS}}_h}^{ini}$ is the initial stored energy, ${\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)$ is the charging power, and ${\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)$ is the discharging power.

The initial stored energy is computed as

$$E_{{\mathrm{PS}}_h}^{ini}=So{C}_h^{ini}·ES{S}_h$$

(7)

The state of charge evolves according to

$$So{C}_h\left(t\right)=So{C}_h^{ini}+{\displaystyle \frac{{\eta }_c}{ES{S}_h}}{\int }_0^t{\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(\tau \right)d\tau -{\displaystyle \frac{1}{{\eta }_{d}ES{S}_h}}{\int }_0^t{\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(\tau \right)d\tau$$

(8)

The SoC is subject to operational limits:

$$So{C}_h^{min}\le So{C}_h\left(t\right)\le So{C}_h^{max}$$

(9)

3.4.2. Charging and Discharging Constraints

Charging and discharging power are bounded:

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\mathrm{PS}}_h^{in}}^{min}& \le {\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)\le {\mathcal{P}}_{{\mathrm{PS}}_h^{in}}^{max},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\mathrm{PS}}_h^{out}}^{min}& \le {\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)\le {\mathcal{P}}_{{\mathrm{PS}}_h^{out}}^{max},\hfill \end{array}$$

(11)

and cannot occur simultaneously. A simple complementarity condition is

$${\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right){\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)=0,$$

(12)

or, equivalently, with binary auxiliaries $u_h^c\left(t\right),u_h^d\left(t\right)\in \{0,1\}$,

$$\begin{array}{cc}\hfill u_h^c\left(t\right)+u_h^d\left(t\right)& \le 1,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)& \le u_h^c\left(t\right){\mathcal{P}}_{{\mathrm{PS}}_h^{in}}^{max},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)& \le u_h^d\left(t\right){\mathcal{P}}_{{\mathrm{PS}}_h^{out}}^{max}.\hfill \end{array}$$

(15)

3.4.3. Energy Loss Calculations

Energy losses occur inside storage during charge/discharge due to imperfect efficiencies:

$$\begin{array}{cc}\hfill P_{loss}^{h_c}\left(t\right)& =\left(1-{\eta }_c\right){\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill P_{loss}^{h_d}\left(t\right)& =\left(\frac{1}{{\eta }_d}-1\right){\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right).\hfill \end{array}$$

(17)

where $P_{loss}^{h_c}\left(t\right)$ and $P_{loss}^{h_d}\left(t\right)$ denote charging and discharging losses, respectively.

Total storage-related loss at the bus.

$$P_{\mathrm{loss},\mathrm{tot}}\left(t\right)=\sum _h\left[P_{loss}^{h_c}\left(t\right)+P_{loss}^{h_d}\left(t\right)\right]=\sum _h\left[(1-{\eta }_c){\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)+\left(\frac{1}{{\eta }_d}-1\right){\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)\right].$$

(18)

To incorporate degradation, the aging cost $C_{deg}$ is defined as

$$C_{deg}\left(t\right)=k_{cyc}{\displaystyle \frac{E_{cyc}\left(t\right)}{E_{rated}}}+k_T{(T\left(t\right)-25)}^2,$$

where $k_{cyc}$ and $k_T$ are empirically derived coefficients. This formulation captures cycle-life and temperature-induced capacity fade consistent with Li-ion models in [36]. Including $C_{deg}$ allows evaluating long-term operational costs alongside instantaneous losses. The present storage model neglects degradation and temperature effects for simplicity.

3.5. Power Loads (PLs)

The PL subsystem models residential energy consumption through both controllable and fluctuating loads:

• Controllable Loads (${\mathit{PL}}^{\mathit{c}}$): Schedulable devices (e.g., air conditioner, washing machine).
• Fluctuating Loads (${\mathit{PL}}^{\mathit{f}}$): Non-shiftable, variable demand devices (e.g., refrigerator, lights).

Let K be the number of loads. The k-th load at time t is represented as

• $P{L}_k^c\left(t\right)$: Controllable demand.
• $P{L}_k^f\left(t\right)$: Fluctuating demand.

With respective power constraints:

$$\begin{array}{cc}\hfill {\mathcal{P}}_{P{L}_k^c}^{min}& \le {\mathcal{P}}_{P{L}_k^c}\left(t\right)\le {\mathcal{P}}_{P{L}_k^c}^{max}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\mathcal{P}}_{P{L}_k^f}^{min}& \le {\mathcal{P}}_{P{L}_k^f}\left(t\right)\le {\mathcal{P}}_{P{L}_k^f}^{max}\hfill \end{array}$$

(20)

3.6. Power Flow and System Balance

All components interact via a central power bus. The instantaneous system-wide power balance at time t is

$${\mathcal{P}}_{\mathrm{PG}}\left(t\right)+\sum _h{\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)={\mathcal{P}}_{\mathrm{PL}}\left(t\right)+\sum _h{\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)+P_{\mathrm{loss},\mathrm{tot}}\left(t\right).$$

(21)

where ${\mathcal{P}}_{\mathrm{PG}}\left(t\right)$ and ${\mathcal{P}}_{\mathrm{PL}}\left(t\right)$ denote aggregate generated and consumed power, respectively, and $P_{\mathrm{loss},\mathrm{tot}}\left(t\right)$ is the aggregate storage-related loss defined in the Section 3.4.3.

Cumulative energy for generation and consumption over time horizon $[0,t]$ is

$$\begin{array}{cc}\hfill E_{P{G}_j^c}& ={\int }_0^t{\mathcal{P}}_{P{G}_j^c}\left(\tau \right)d\tau \hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill E_{P{G}_j^f}& ={\int }_0^t{\mathcal{P}}_{P{G}_j^f}\left(\tau \right)d\tau \hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill E_{P{L}_k^c}& ={\int }_0^t{\mathcal{P}}_{P{L}_k^c}\left(\tau \right)d\tau \hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill E_{P{L}_k^f}& ={\int }_0^t{\mathcal{P}}_{P{L}_k^f}\left(\tau \right)d\tau \hfill \end{array}$$

(25)

3.7. Logical Connections in DPFS

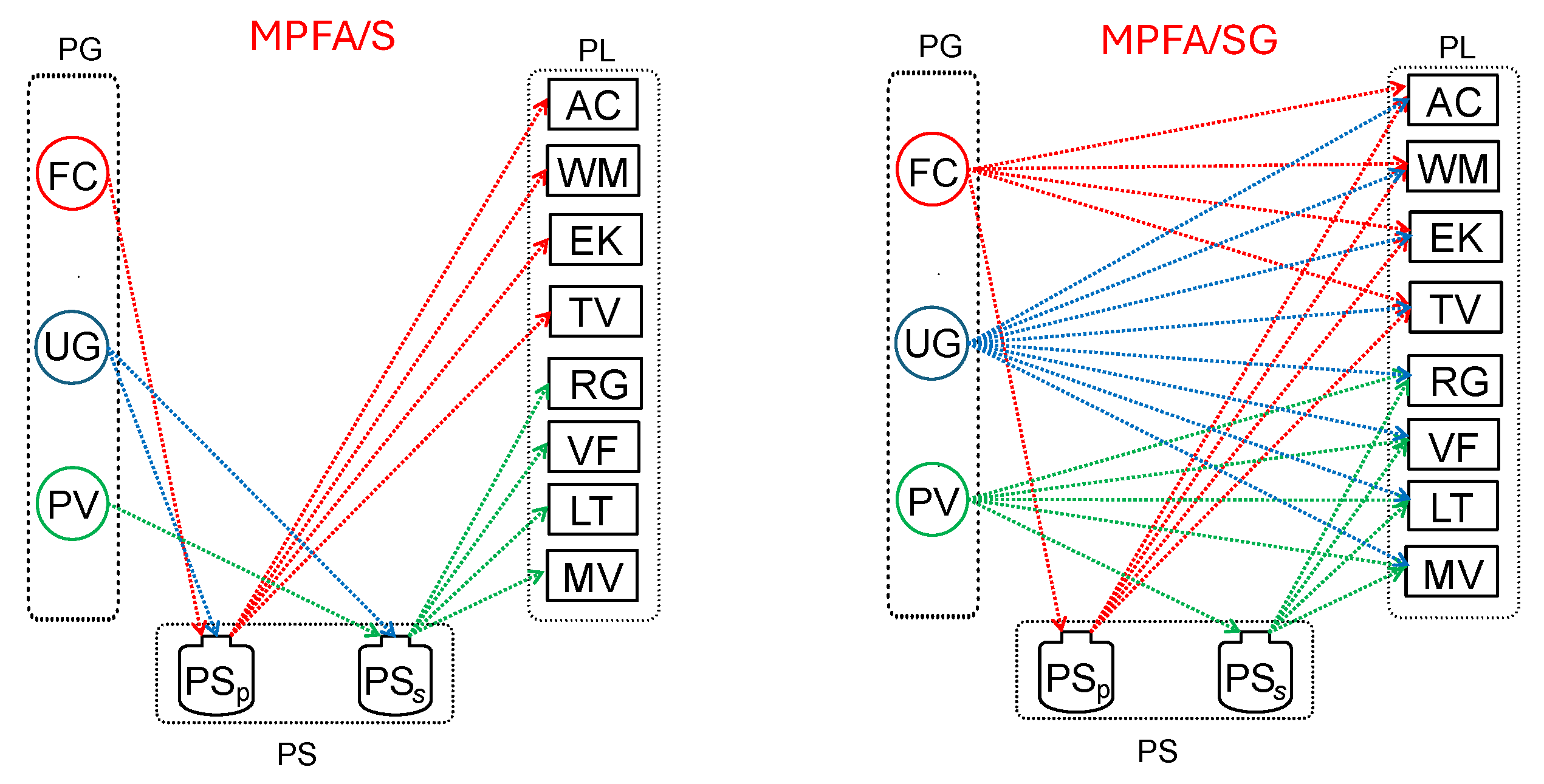
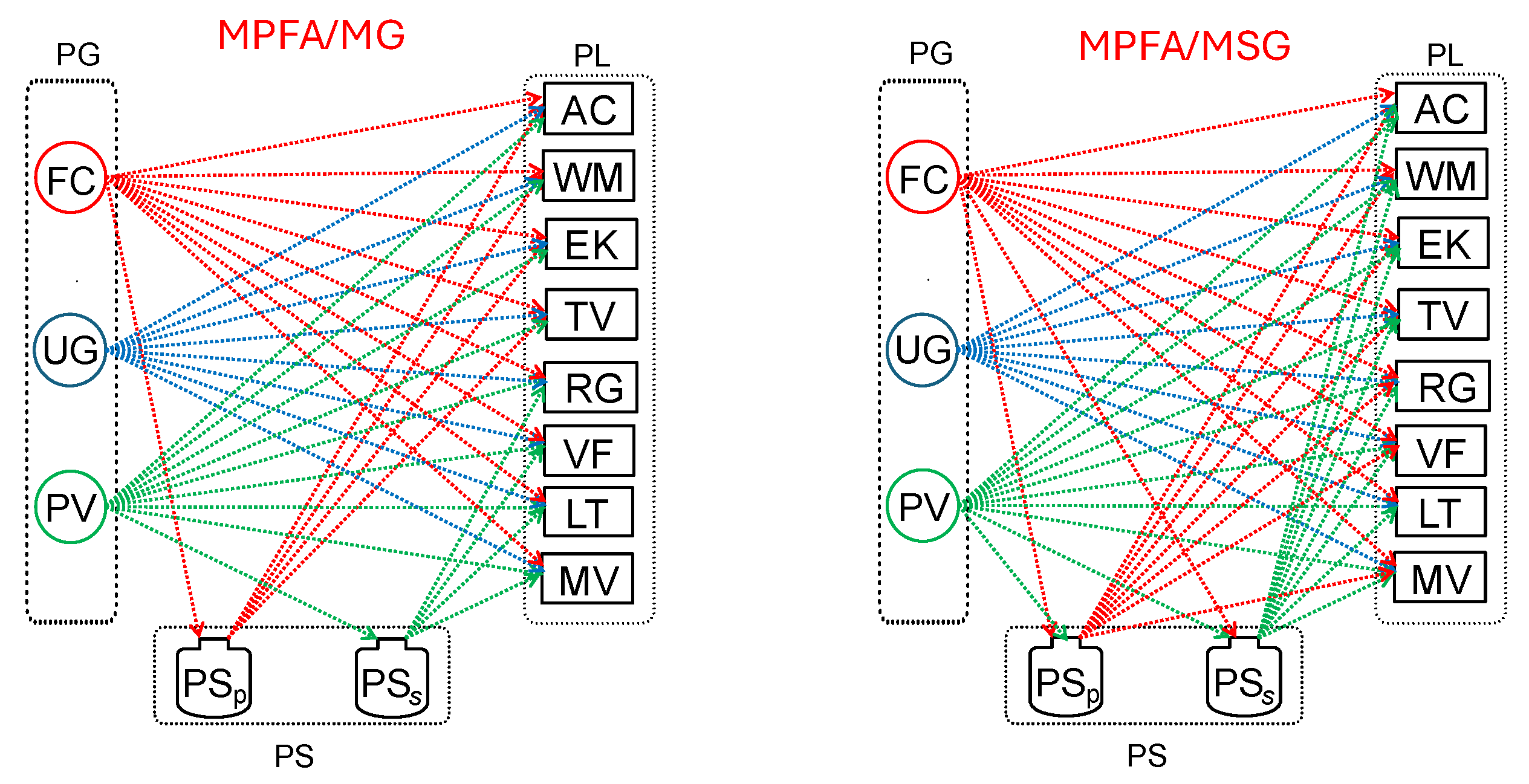
We examine four power-flow assignment scenarios in Table 2 that differ in how power generators (PGs), power storage systems (PSs), and power loads (PLs) are interconnected. (1) MPFA/S (multi-load, single storage): multiple PLs are supplied via a single PS; a single RES-based PG (optionally backed by the UG) charges that PS (Figure 2). (2) MPFA/SG (multi-load, single generator): multiple PLs are connected to a single RES PG and a single PS (Figure 2). (3) MPFA/MG (multi-load, multiple generators): multiple PLs are supplied by multiple RES PGs and a single PS (Figure 3). (4) MPFA/MSG (multi-load, multiple generators and storages): multiple PL sets can draw from all RES PGs, the UG, and multiple PSs (Figure 3).

Table 2. Summary of MPFA scenarios in the DPFS.

Scenario	Power Generators (PGs)	Power Storages (PSs)	Description
MPFA/S	1	1	Single PG–single PS configuration
MPFA/SG	1	1	Single RES PG and single PS supplying multiple loads
MPFA/MG	3	1	Multiple PGs with single PS
MPFA/MSG	3	2	Multiple PGs and PSs, fully integrated DPFS

Figure 2. Logical connection for MPFA/S and MPFA/SG.

Figure 3. Logical connection for MPFA/MG and MPFA/MSG.

4. DPFS Algorithms

This section introduces three power flow algorithms designed for the DPFS: the Total-Demand-Based Power Flow (TDPF) algorithm, the Adaptive-Demand-Based Power Flow (ADPF) algorithm, and the Grid-Based Power Flow (GBPF) algorithm. These algorithms are foundational for managing the smart home DPFS by dynamically balancing supply, demand, and storage resources in real time, optimizing energy usage, and prioritizing user comfort and system reliability.

4.1. Overview of Power Flow Algorithms

In Algorithm 1 represent the TDPF, ADPF, and GBPF algorithms differ in their operational logic, their handling of load priorities, and the manner in which they utilize available energy resources including renewable generation, energy storage, and the external utility grid. Their integration enables the DPFS to flexibly adapt to changes in renewable output, user demand, and energy storage status.

Algorithm 1 MPFA Power-Flow Management (bus-level allocation under TDPF/ADPF/GBPF).

Require: ${\mathcal{P}}_{P{L}_k}\left(t\right)$ for all k, ${\mathcal{P}}_{P{G}_j}\left(t\right)$ for all j, ${\mathcal{P}}_{{\mathrm{PS}}_h^{in}}\left(t\right)$ and ${\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)$ for all h, and ${\mathcal{P}}_{\mathrm{grid}}\left(t\right)$ 1: for each time step t do 2:      Compute total demand: $P_{\mathrm{demand},\mathrm{tot}}\left(t\right)={\sum }_{k\in K}{\mathcal{P}}_{P{L}_k}\left(t\right)$ 3:      Compute total supply: $P_{\mathrm{supply},\mathrm{tot}}\left(t\right)={\sum }_{j\in J}{\mathcal{P}}_{P{G}_j}\left(t\right)$ 4:      Compute available discharge from storage: $P_{\mathrm{storage},\mathrm{tot}}\left(t\right)={\sum }_{h\in H}{\mathcal{P}}_{{\mathrm{PS}}_h^{out}}\left(t\right)$ 5:      if TDPF or GBPF mode then 6:           if $P_{\mathrm{demand},\mathrm{tot}}\left(t\right)\le P_{\mathrm{supply},\mathrm{tot}}\left(t\right)$ then 7:                 Serve all ${\mathcal{P}}_{P{L}_k}\left(t\right)$, charge PSs subject to ${\eta }_c$ and bounds 8:                 Record charging losses 9:           else if $P_{\mathrm{demand},\mathrm{tot}}\left(t\right)\le P_{\mathrm{supply},\mathrm{tot}}\left(t\right)+P_{\mathrm{storage},\mathrm{tot}}\left(t\right)$ then 10:               Discharge PSs with ${\eta }_d$ to meet deficit, record losses 11:         else if GBPF mode and $P_{\mathrm{demand},\mathrm{tot}}\left(t\right)\le P_{\mathrm{supply},\mathrm{tot}}\left(t\right)+P_{\mathrm{storage},\mathrm{tot}}\left(t\right)+{\mathcal{P}}_{\mathrm{grid}}\left(t\right)$ then 12:                Draw remaining deficit from grid 13:                Serve all ${\mathcal{P}}_{P{L}_k}\left(t\right)$, update energy accounting 14:         else 15:                Curtail loads (TDPF only; GBPF curtails only if a grid cap binds) 16:    else if ADPF mode then 17:          Sort loads by priority (essential → non-essential) 18:          Allocate ${\mathcal{P}}_{P{G}_j}\left(t\right)$ to high-priority ${\mathcal{P}}_{P{L}_k}\left(t\right)$ first 19:          If ${\mathcal{P}}_{P{G}_j}\left(t\right)$ is exhausted, use PSs 20:          If PSs are exhausted, curtail lowest priority ${\mathcal{P}}_{P{L}_k}\left(t\right)$ as needed 21:          Compute and record energy losses

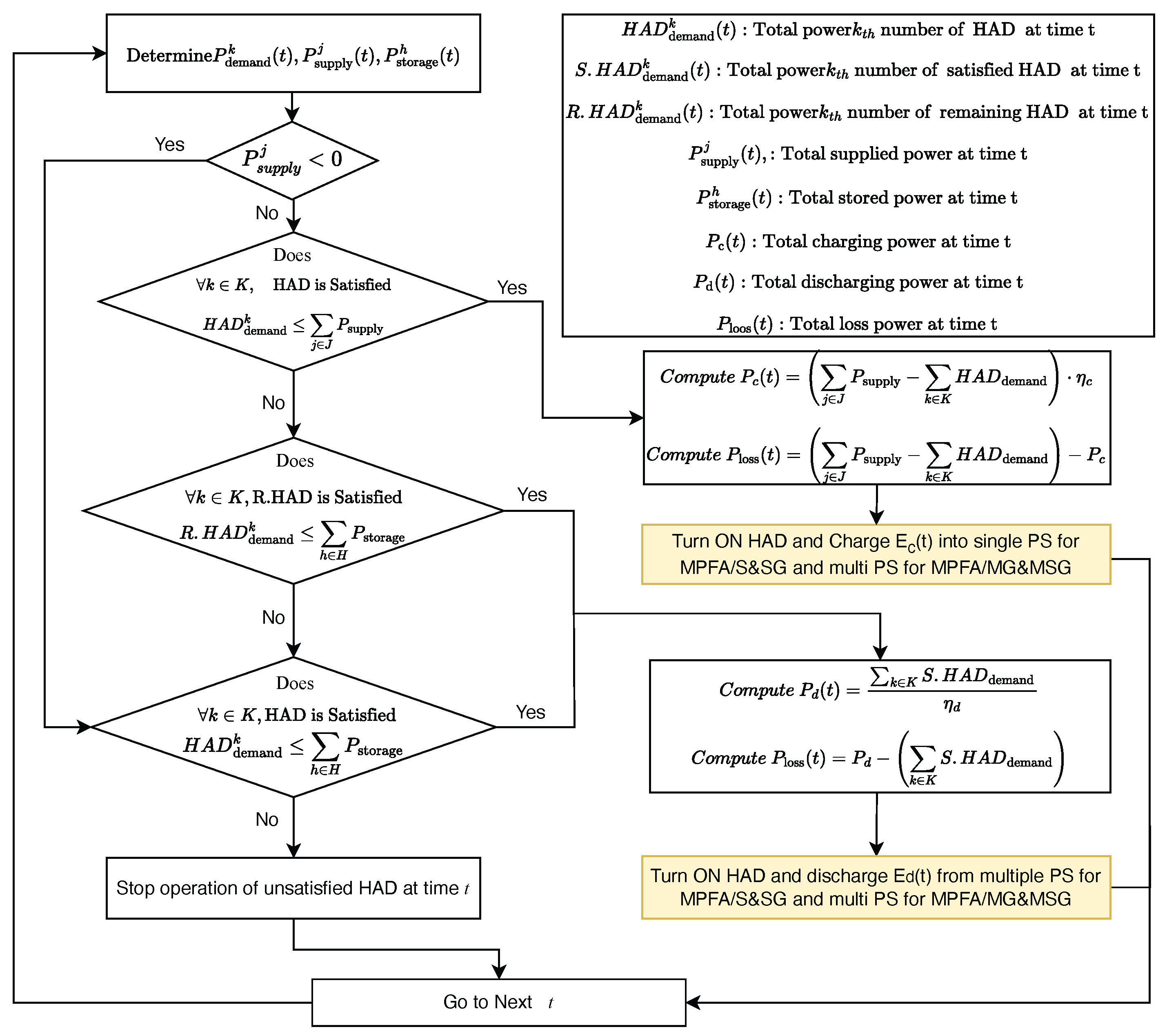
4.1.1. Total-Demand-Based Power Flow (TDPF) Algorithm

The Total-Demand-Based Power Flow (TDPF) algorithm is depicted in Figure 4 and constitutes a baseline approach to power management in the DPFS. This algorithm operates by first evaluating the total power demand of the system at each discrete time interval and comparing it to the sum of the available power supply from Power Generation (PGs) and Power Storage Systems (PSs).

Figure 4. Flowchart of Total-Demand-Based Power Flow (TDPF) algorithm.

If the available supply is sufficient to meet the total demand, all household Power Loads (PLs) are powered accordingly, maximizing user comfort and uninterrupted operation of appliances. In this scenario, any surplus power after meeting demand is allocated to charging the PSs with a charging efficiency factor ${\eta }_{\mathrm{c}}$, and any residual energy loss resulting from charging inefficiencies is computed and recorded for system analysis and optimization.

Conversely, if the supply is insufficient to meet the total demand, the algorithm suspends the operation of HADs, which may include flexible loads or critical appliances, to prevent over-discharge and ensure safe operation of the DPFS. Although this may lead to user discomfort due to interrupted appliance use, it preserves the integrity of storage systems and prevents excessive battery cycling or blackout conditions. This stepwise logic ensures that energy is allocated efficiently, losses are minimized, and system stability is maintained under varying operational and environmental conditions.

4.1.2. Adaptive-Demand-Based Power Flow (ADPF) Algorithm

The Adaptive-Demand-Based Power Flow (ADPF) algorithm, as illustrated in Figure 5, enhances flexibility by introducing adaptive load prioritization. Unlike the TDPF, which treats all loads equally, the ADPF algorithm recognizes the varying importance of different household appliances and assigns higher priority to essential or critical loads (such as medical equipment, refrigeration, or heating/cooling systems).

Figure 5. Flowchart of Adaptive-Demand-Based Power Flow (ADPF) algorithm.

During each time step, the ADPF algorithm first attempts to satisfy the demand of prioritized loads using the available supply from RES PGs and PSs units. If the available supply is sufficient, the surplus is charged to PSs with efficiency ${\eta }_{\mathrm{c}}$ and losses are computed as before. If the available supply is not sufficient, the algorithm allocates stored energy (if available) to power the remaining prioritized loads, discharging PSs with efficiency ${\eta }_{\mathrm{d}}$ and again computing corresponding losses. When neither PGs nor PSs can fully meet demand, the algorithm systematically turns off the lowest priority or non-critical loads, thereby minimizing user discomfort by ensuring that essential services remain operational. This adaptive approach optimizes energy usage and minimizes the impact of supply shortages on user comfort.

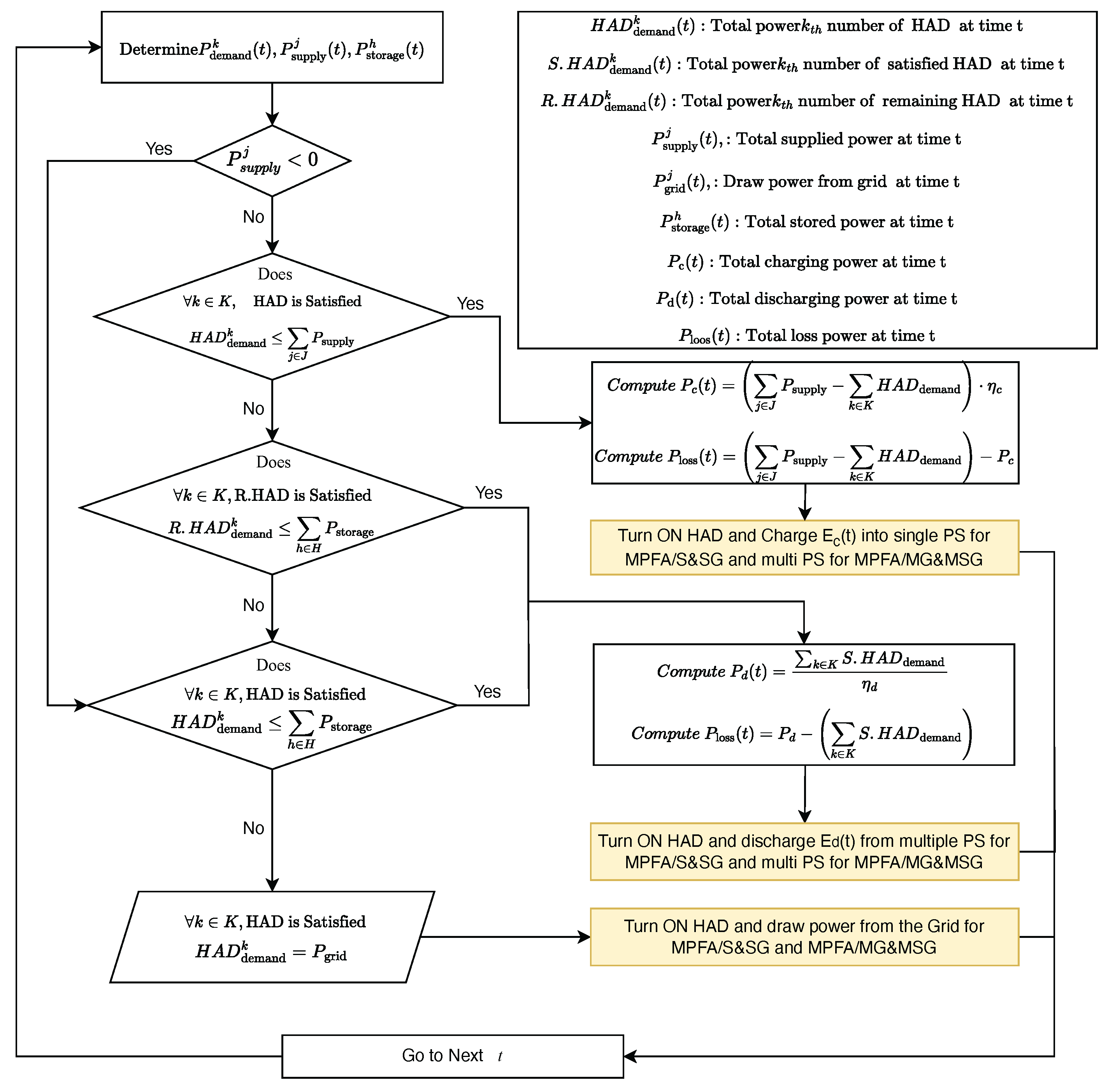
4.1.3. Grid-Based Power Flow (GBPF) Algorithm

The Grid-Based Power Flow (GBPF) algorithm, shown in Figure 6, introduces the external utility grid as an additional energy source to further enhance the reliability and resilience of the DPFS. This approach first allocates power from RES PGs and storage units, maximizing local RES PGs and PSs energy utilization. If the combined supply from local sources is insufficient to meet the full household demand, the GBPF algorithm automatically engages the external grid, which supplies the remaining demand and thus ensures that no load curtailment occurs. This operational paradigm guarantees user comfort and the seamless operation of all loads at all times.

Figure 6. Flowchart of Grid-Based Power Flow (GBPF) algorithm.

By using the grid only when local sources are insufficient, the GBPF algorithm maximizes the economic and ecological benefits of RES energy while maintaining the capability to fully satisfy demand. This approach provides system-level reliability and stability, minimizes the risk of service interruptions, and can reduce storage cycling (lower storage-related losses) at the expense of potentially higher imported energy when RES are scarce.

4.2. Algorithmic Logic and Stepwise Description

The detailed operational logic of each algorithm is as follows:

Total-Demand-Based Power Flow (TDPF) Algorithm:

• At each time step t, the algorithm first checks whether there is any available power supply.
• If the total demand is less than or equal to the total supply, the surplus power is used to charge the storage units with efficiency ${\eta }_{\mathrm{c}}$, and any residual energy loss is computed.
• If the demand exceeds the supply but remains less than or equal to the combined available power from supply and storage, the deficit is met by discharging storage with efficiency ${\eta }_{\mathrm{d}}$, and corresponding losses are calculated.
• If only storage is available and sufficient to meet the demand, the storage discharges accordingly.
• If none of these conditions are satisfied, all HAD operations are suspended for that time step.
• This logic ensures that energy is allocated efficiently, minimizes losses, and maintains system stability under varying operational and environmental conditions.

Adaptive-Demand-Based Power Flow (ADPF) Algorithm:

• This algorithm governs the allocation of stored and supplied energy to meet demand in real time at each time step t.
• If supply is available and exceeds the total HAD demand, the surplus energy is stored after accounting for charging efficiency ${\eta }_{\mathrm{c}}$, and any losses are computed.
• In the absence of sufficient supply, the algorithm checks whether the stored energy can satisfy the HAD demand. If so, the storage discharges energy based on the discharging efficiency ${\eta }_d$, with the corresponding energy loss calculated.
• In cases where stored energy is insufficient, the algorithm defaults to discharging what is available from the multiple power sources (e.g., MPFA/S&G or MPFA/MG&MSG configurations).
• This process ensures optimal utilization of energy resources and maintains the operation of HAD systems while minimizing energy losses.

Grid-Based Power Flow (GBPF) Algorithm:

• The GBPF algorithm manages energy distribution by coordinating supplied, stored, and demanded energy at each time step t.
• When there is a positive supply, the algorithm first checks if the total HAD demand is less than or equal to the available supply.
• If true, and the HAD demand is fully met by the supply, the excess supply is partially stored in the energy storage system after accounting for the charging efficiency ${\eta }_c$. The energy loss in this case is the difference between the remaining supply and the amount successfully stored.
• If the HAD demand exceeds the current supply but can still be met by combining supply with stored energy, the required deficit is discharged from storage based on the discharging efficiency ${\eta }_d$, and losses are computed accordingly.
• In both scenarios, HAD systems are activated and energy is either charged into or discharged from single or multiple power sources (e.g., MPFA/S&G or MPFA/MG&MSG).
• If the combined available supply and storage are insufficient to meet demand, all HAD operations are halted for that time step to prevent instability.
• This strategy ensures optimal grid-supported energy flow, maintains HAD operation when feasible, and prevents overuse of limited resources.

For completeness and reproducibility, a generic pseudocode structure encompassing the operational flow of these algorithms is presented below.

Figure 4, Figure 5 and Figure 6 provide flowchart representations for the TDPF, ADPF, and GBPF algorithms, respectively, depicting their decision-making process and operational flow.

In summary, the TDPF, ADPF, and GBPF algorithms together provide a robust, flexible, and adaptive power management framework for the DPFS. By considering total demand, load priority, and grid integration, these algorithms enable real-time optimization of energy flows, minimize system losses, maintain user comfort, and ensure reliable smart home operation under a wide range of supply, storage, and demand scenarios. Their modular design allows for seamless integration and future extension within advanced residential energy management systems.

4.3. Computational Remarks and Guarantees

Each algorithm operates in a single pass per time step with arithmetic over J generators, H storages, and K loads. The per-step time is $O(J+H+K)$ for TDPF and GBPF; ADPF adds a priority sort of loads $O(KlogK)$ (or $O\left(K\right)$ with bucketed priorities). Feasibility is always achieved under GBPF (assuming ${\mathcal{P}}_{\mathrm{grid}}\left(t\right)$ is adequate). Under fixed ${\eta }_c,{\eta }_d$, storage bounds, and complementarity, the energy state $E_{{\mathrm{PS}}_h}\left[n\right]$ remains within $[So{C}_h^{min}ES{S}_h,So{C}_h^{max}ES{S}_h]$ provided the charging/discharging limit constraints hold. Optimality (loss-minimality) is not claimed for TDPF/ADPF but is empirically evaluated; extending MPFA with optimization-based dispatch is left to future work.

5. Numerical Simulations

This section presents the simulation setup and scenarios considered to evaluate the proposed Multiple-Load Power Flow Assignment (MPFA) approach in a smart home environment. The Distributed Power Flow System (DPFS) consists of three key components: power generators (PGs), power loads (PLs), and power storage systems (PSs). The PGs include a photovoltaic (PV) array, a fuel cell (FC), and the utility grid (UG), each playing a crucial role in supplying energy to household appliances. The PLs comprise various essential household HADs, including an air conditioner (AC), washing machine (WM), ventilation fan (VF), light (LT), electric kettle (EK), microwave (MV), television (TV), and refrigerator (RG), all of which are modeled based on their real-time usage patterns in a smart home. The PSs include two dedicated storage units, PS1 and PS2, which manage fluctuations in energy demand and supply.

5.1. Simulation Scenarios and Setup

The simulation framework is developed using Python, incorporating real experimental data from both the FC and PV systems obtained from the iHouse setup. To comprehensively assess the impact of power flow strategies, the study explores four distinct MPFA scenarios: MPFA/S, MPFA/SG, MPFA/MG, and MPFA/MSG. These scenarios are designed to analyze how different energy sources and storage mechanisms contribute to energy distribution, loss minimization, and demand satisfaction. The evaluation is conducted using three power-flow algorithms—TDPF, ADPF, and GBPF—each offering unique insights into system performance under varying energy conditions.

The operation of the FC is modeled based on the ENE-FARM framework, in Table 3 with its active operational hours set from 00:00 to 05:00 and 16:00 to 23:59 across all seasons to optimize energy availability [10,37]. Although the current FC model assumes stable operation, in practice FC performance degrades due to component aging and reversible voltage losses. For PV generation, actual recorded data is used to reflect seasonal variations, with representative dates selected for each season: winter (11 January), spring (23 April), summer (14 June), and autumn (17 October). The utility grid is considered a controllable energy source and is available 24/7, providing an additional layer of stability to the energy supply.

Table 3. Main experimental parameters used in the simulation.

Component	Specification/Setting
PV system	Model: 1.0 kW mono-crystalline PV array; tilt angle: 30°; efficiency: 18%;
Fuel cell (FC)	Model: Toshiba ENE-FARM household FC system; type: PEMFC; rated electrical output: 700 W; thermal output: 1.0 kW; hydrogen supply pressure: 1.3 bar; reaction temperature: 70 °C; overall system efficiency: 90% (electric 40%, heat 50%).

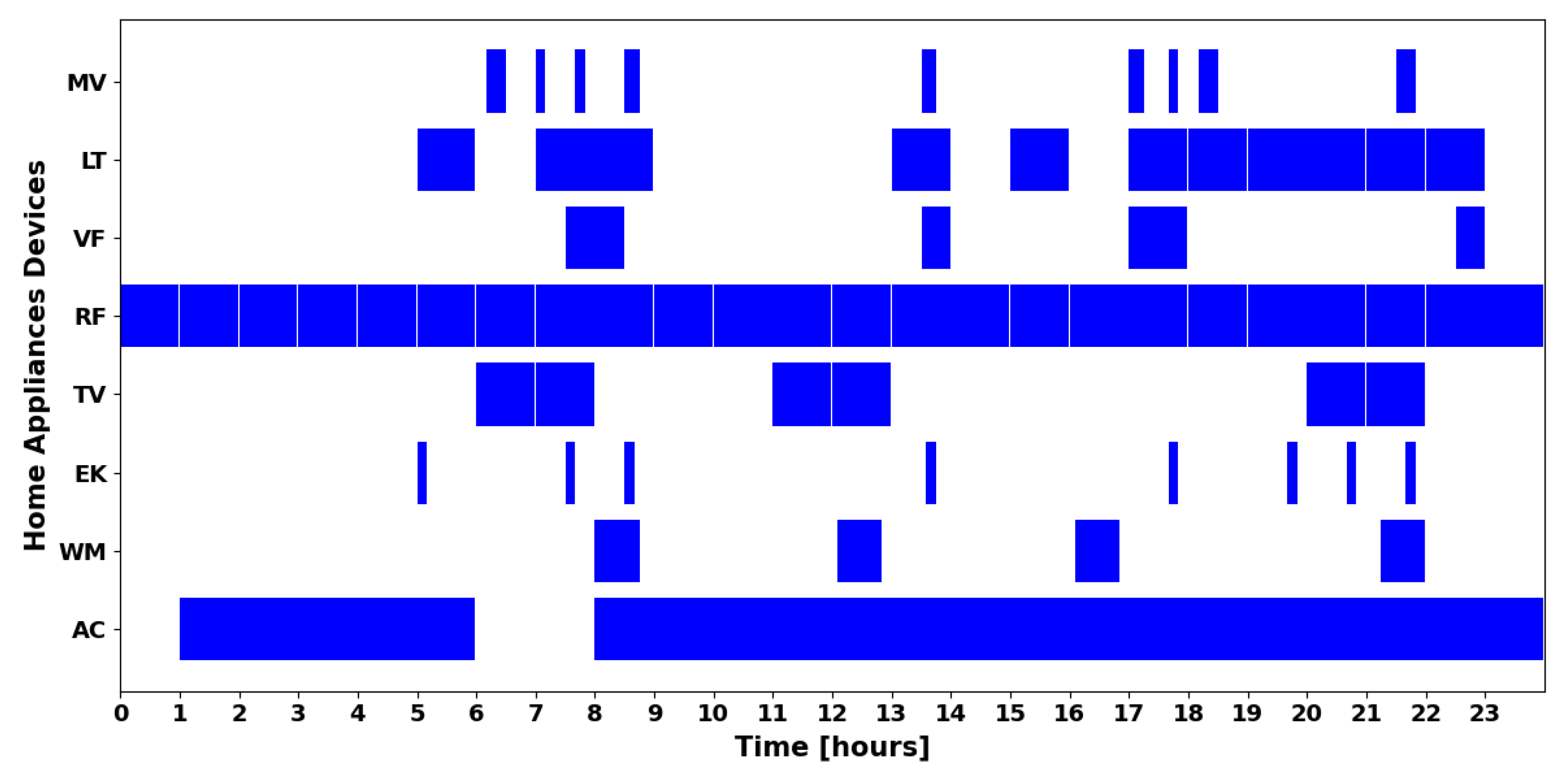
Regarding household appliance PLs, the simulation considers the most relevant and frequently used HADs in a smart home environment. A detailed 24 h operational profile of these appliances is depicted in Figure 7 and Table 4, illustrating the variations in energy demand throughout the day. Notably, the air conditioner (AC) operates for 21 h, reflecting its significant role in maintaining indoor comfort, while the refrigerator (RG) remains active continuously for 24 h to ensure food preservation. The operational schedules of other household appliances are also taken into account, aligning with the daily energy consumption patterns of typical users.

Figure 7. Household activity schedule for the operation of HADs.

Table 4. Power ratings of home appliances across seasons.

Season	Home Appliance Power Ratings (W)
	AC	WM	EK	TV	RG	VF	LT	MV
Winter	890	500	600	120	150	66	36.8	1000
Summer	790	350	600	120	250	111	36.8	1000
Autumn	380	450	600	120	200	36	36.8	1000
Spring	380	350	600	120	200	36	36.8	1000

For both PSs, the initial, minimum, and maximum state of charge (SoC) are 21%, 20%, and 94%, respectively. Both PSs have charging efficiency ${\eta }_c$ and discharging efficiency ${\eta }_d$ of 92%. This setup allows for a realistic assessment of power flow strategies and their effectiveness in balancing supply and demand while minimizing losses within the DPFS.

5.2. Power Profile Results and Discussion

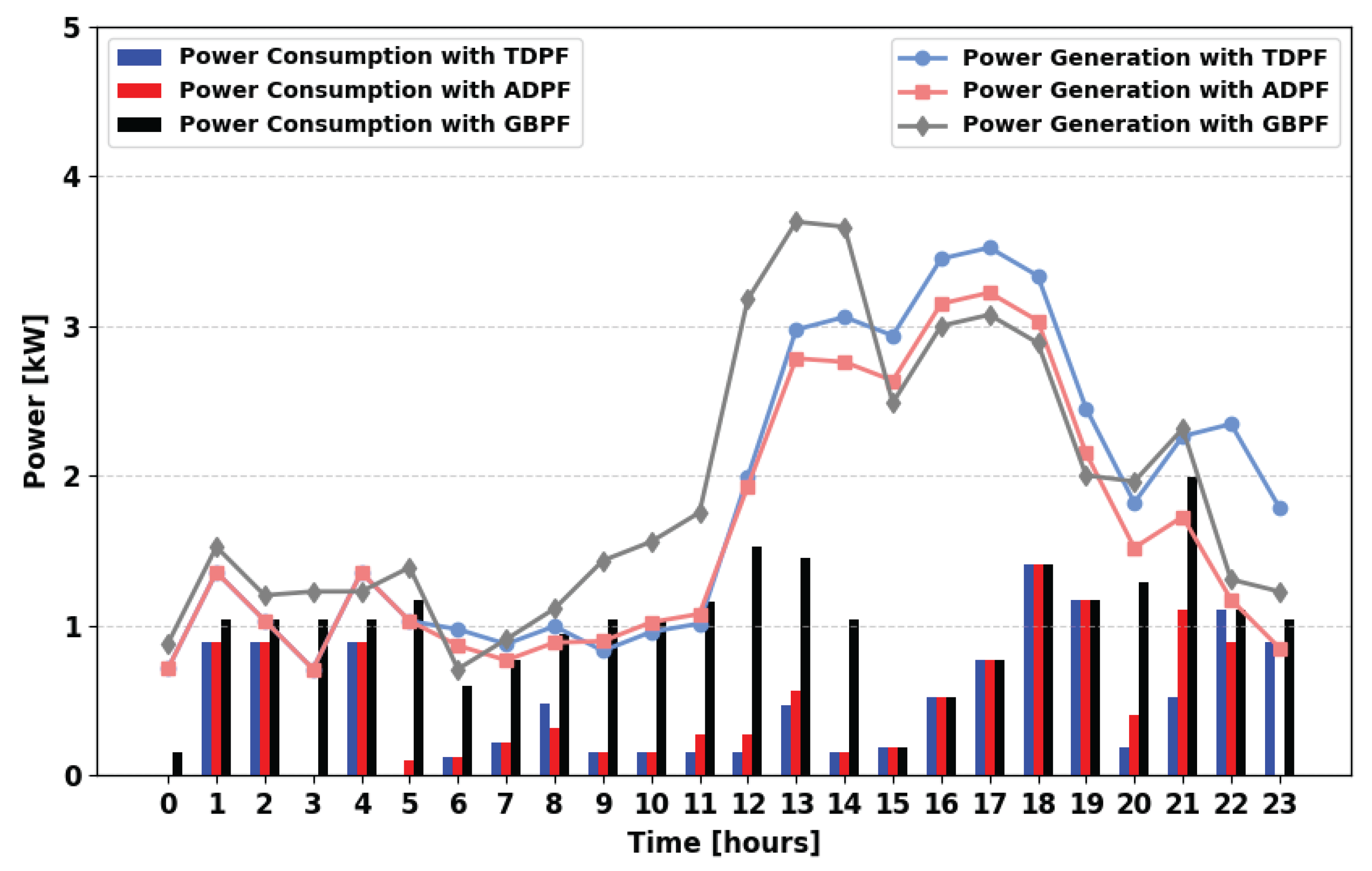
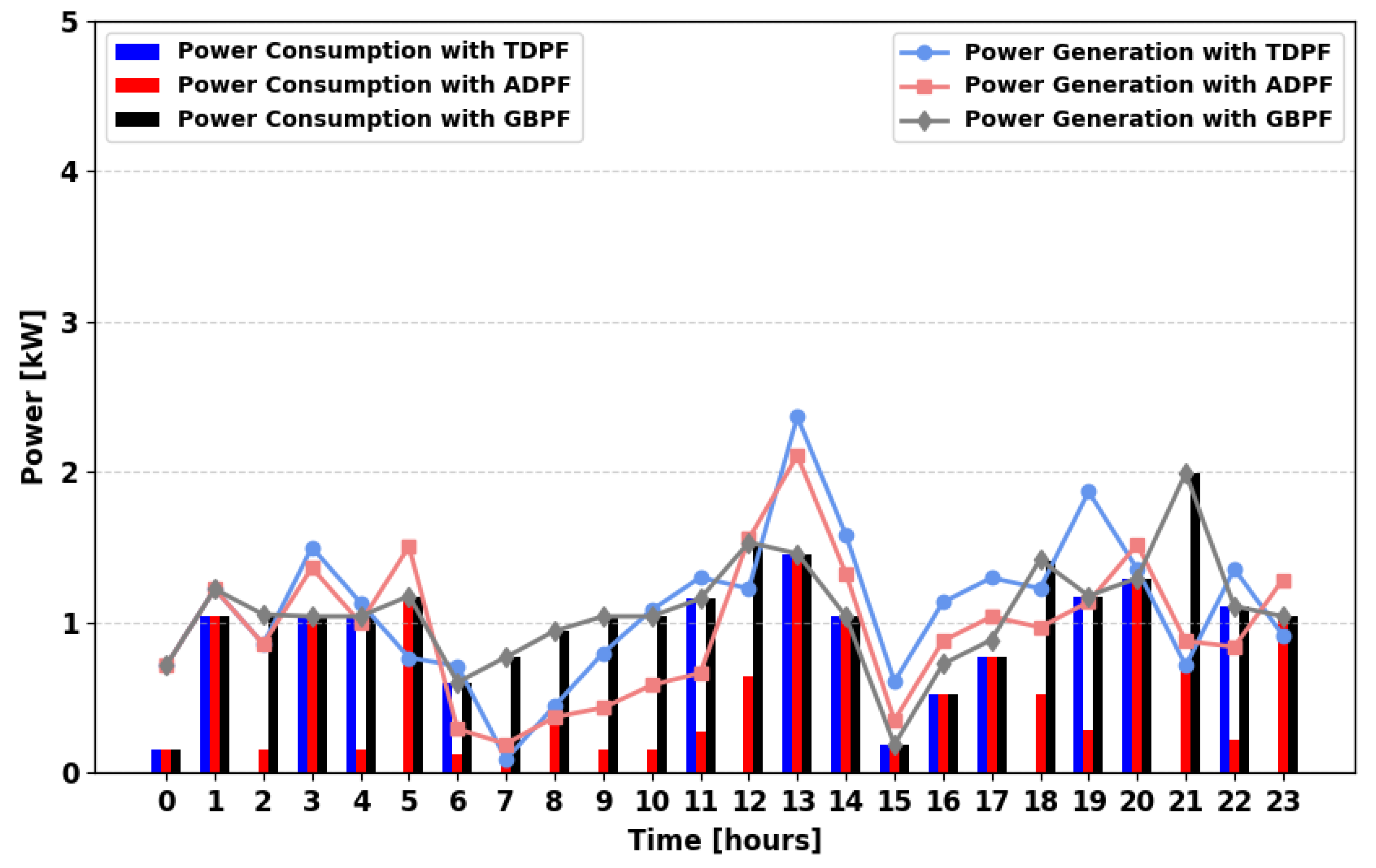
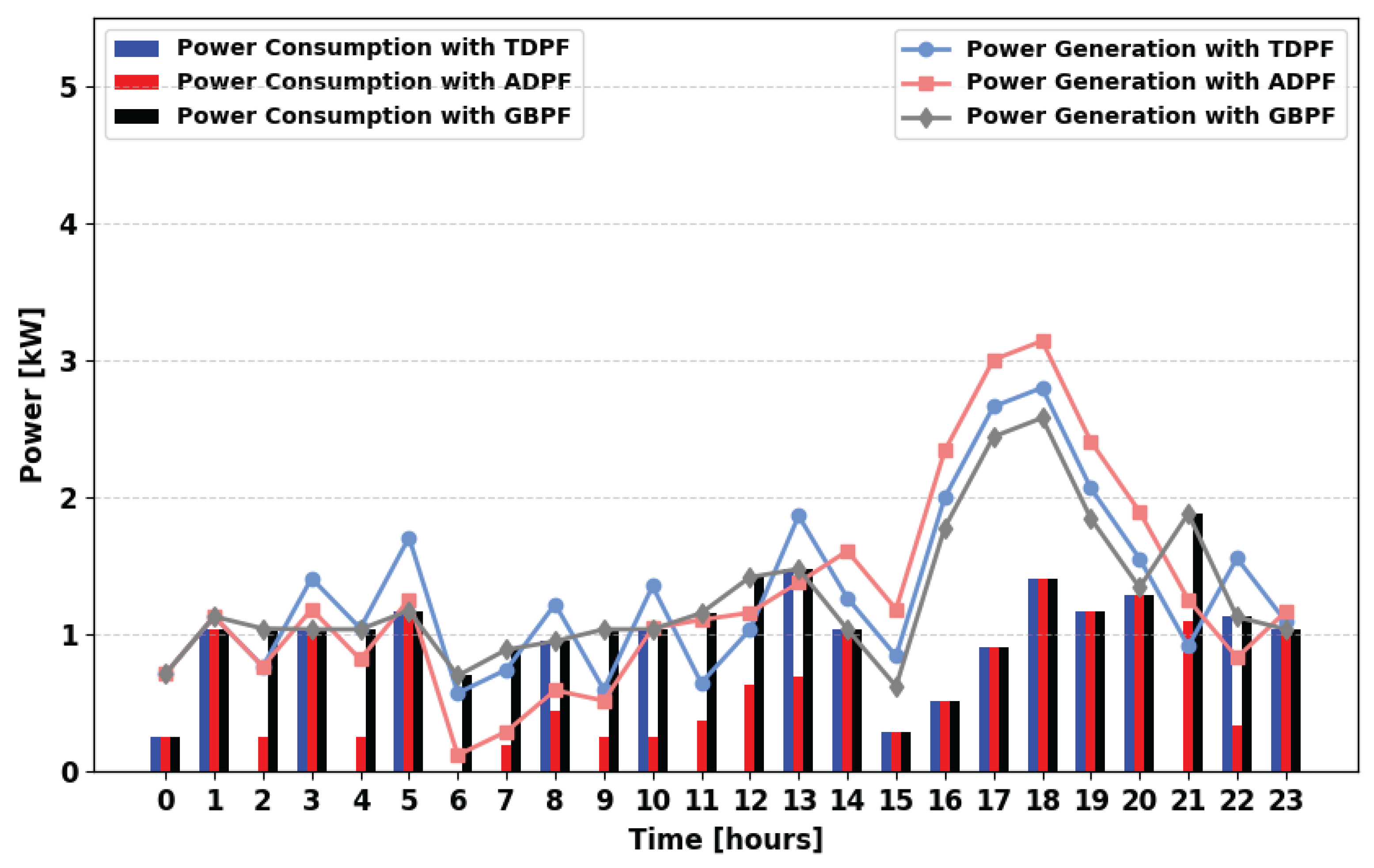
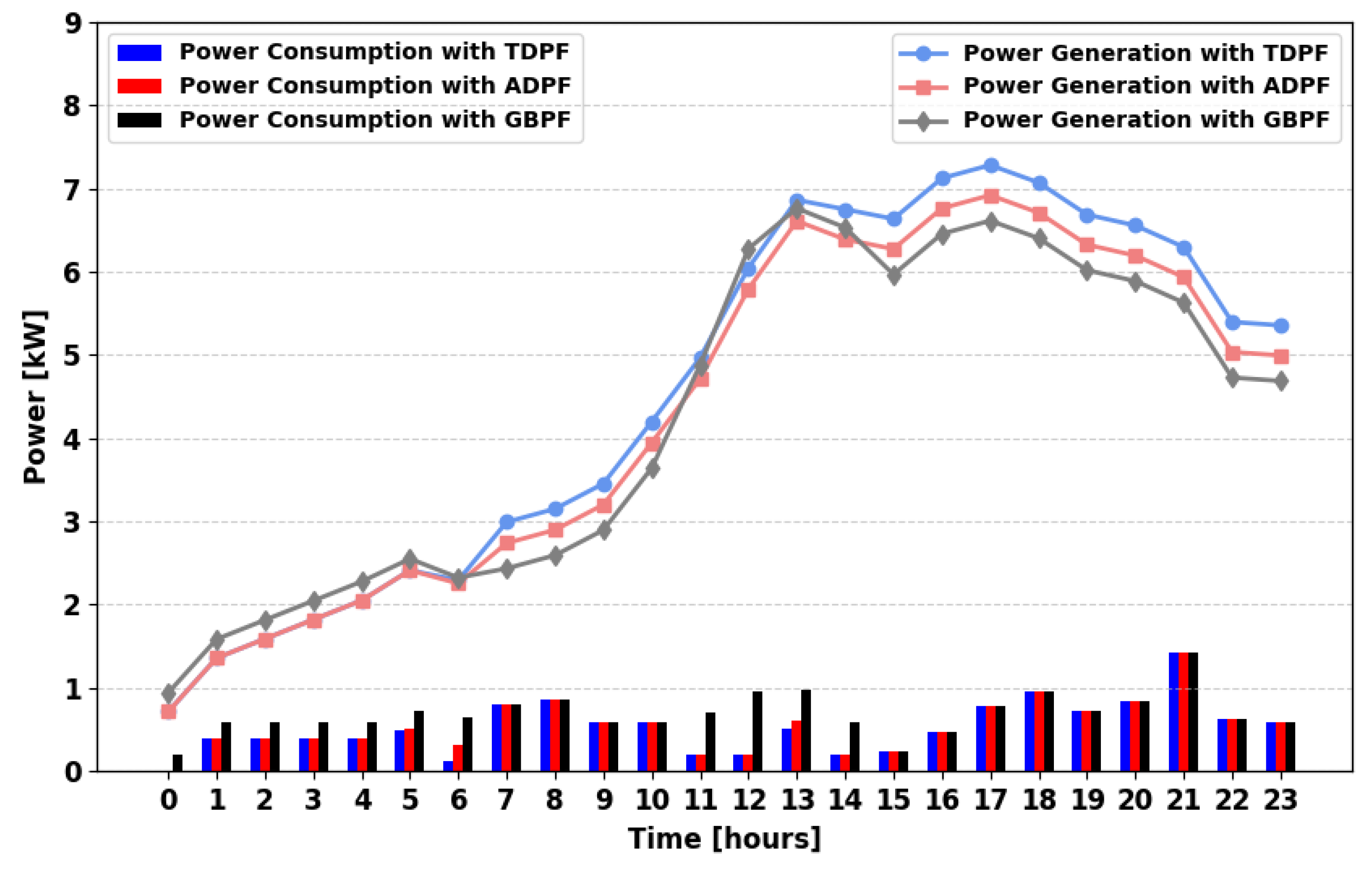
The simulation results presented in Figure 8 illustrate the power consumption and supply profiles for the first scenario for the winter season (MPFA/S). Both TDPF and ADPF algorithms achieve similar levels of demand fulfillment throughout the day. However, at 13:00, 14:00, 21:00, and 22:00 the ADPF algorithm exhibits higher demand satisfaction than TDPF. This indicates the effectiveness of ADPF in dynamically adjusting power allocation, ensuring better utilization of available storage energy.

Figure 8. Power supply and consumption in winter with MPFA/S.

In this section, power flow scenarios and algorithms are tested and verified for the winter season. The power supply and consumption profiles reflect the operational strategies of the implemented power flow algorithms. The total power supply in the ADPF and TDPF approaches is primarily sourced from FC, PV, and PSs, while the GBPF algorithm integrates power from PV, FC, PSs, and the UG to meet the power demand. The total daily power demand during winter is 24.51 kWh.

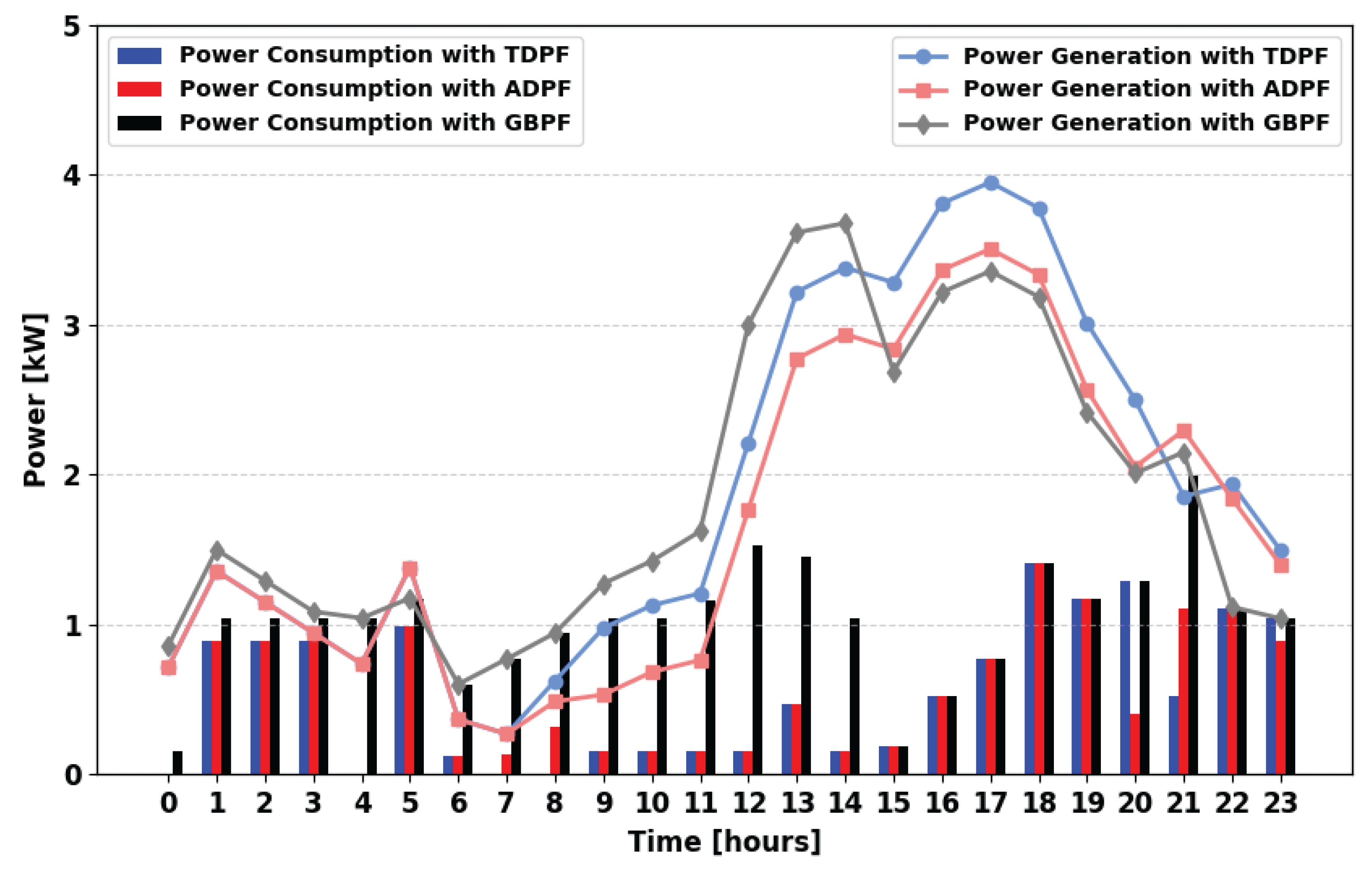
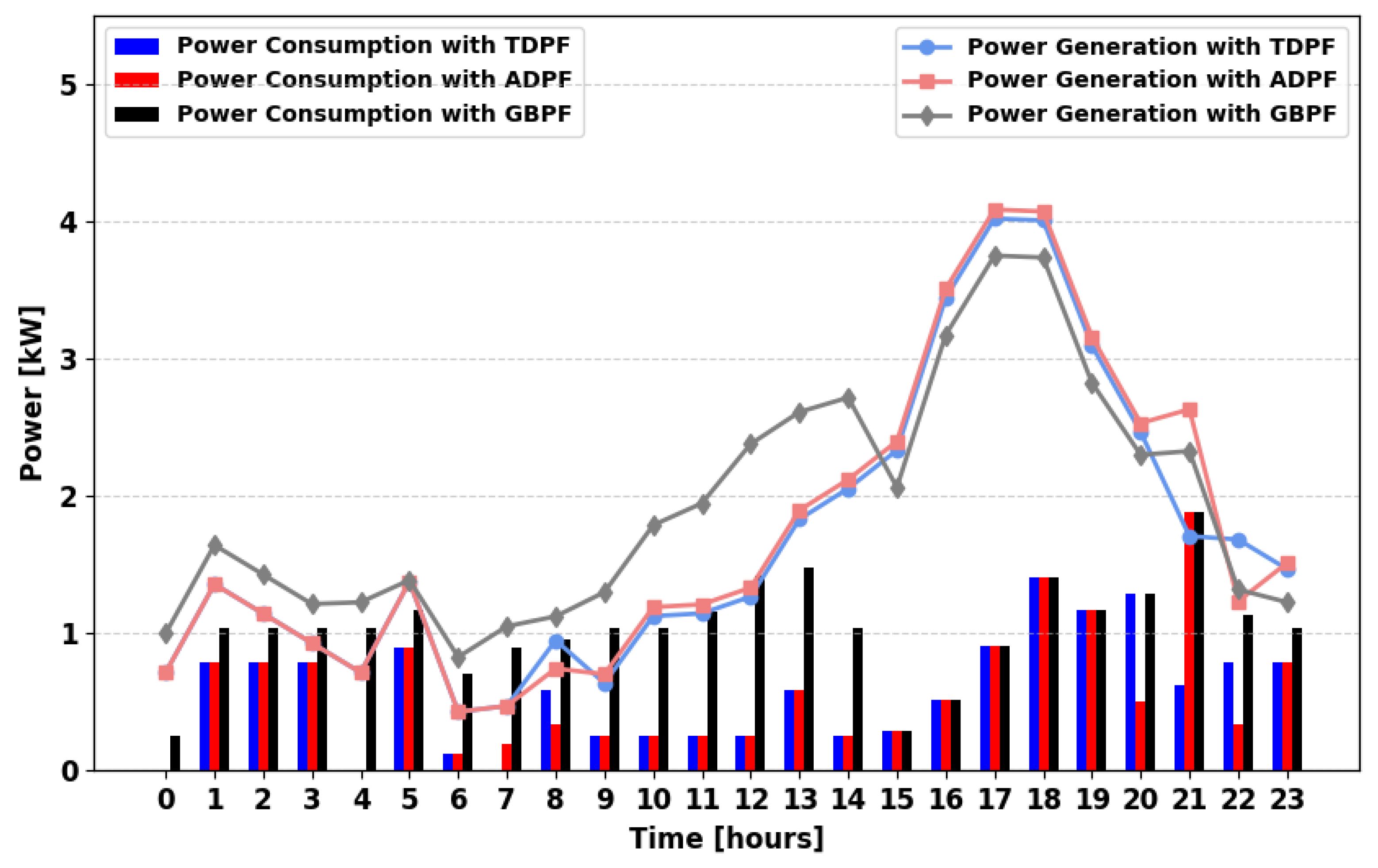
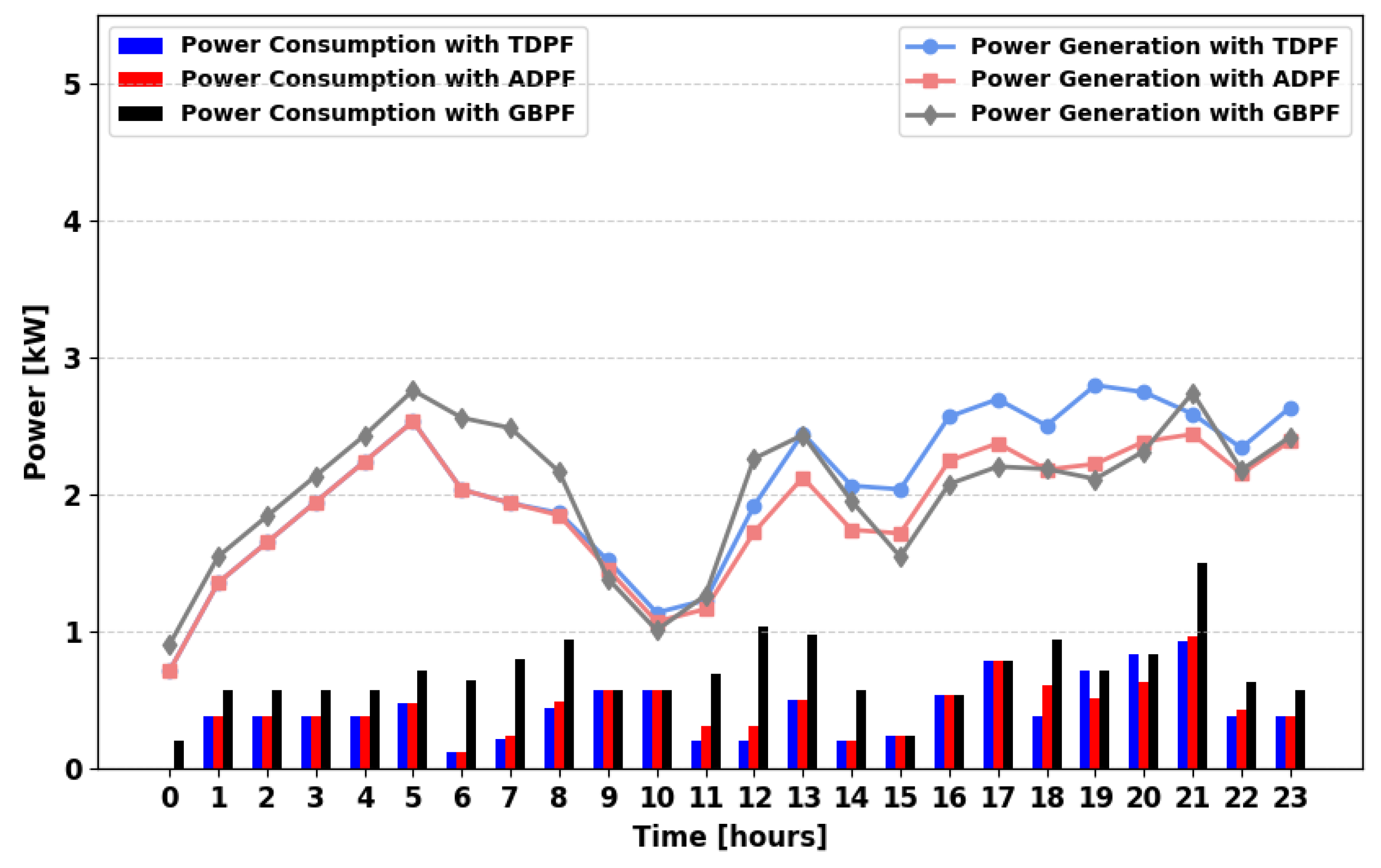
In Figure 9, the power demand satisfaction profile is analyzed throughout the day. During hours 08:00, 09:00, and 22:00, ADPF achieves higher demand fulfillment than TDPF does. This suggests that ADPF is more effective in managing limited power resources from a single generator and storage, optimizing allocation to maintain supply during critical hours.

Figure 9. Power supply and consumption in winter with MPFA/SG.

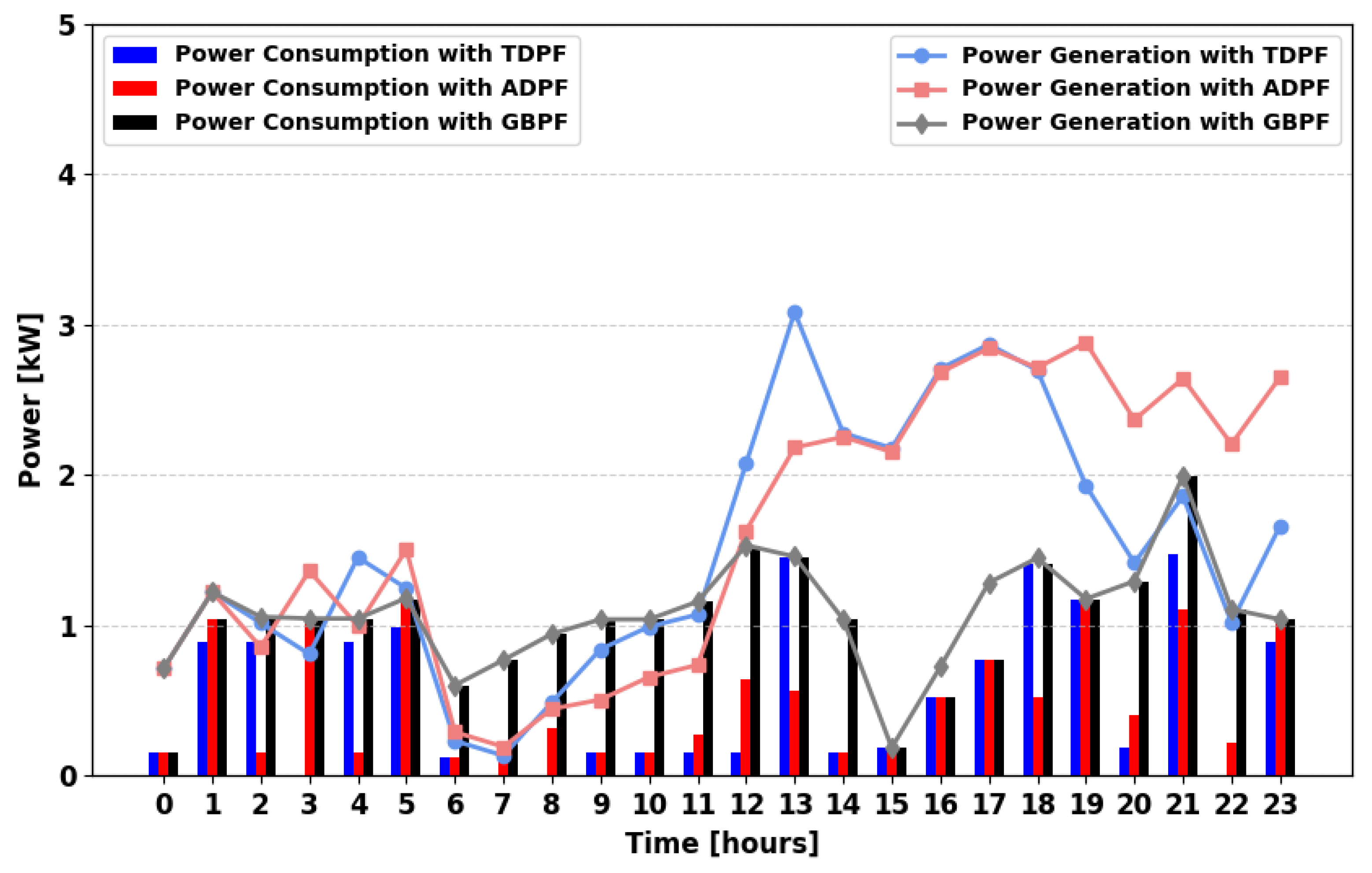
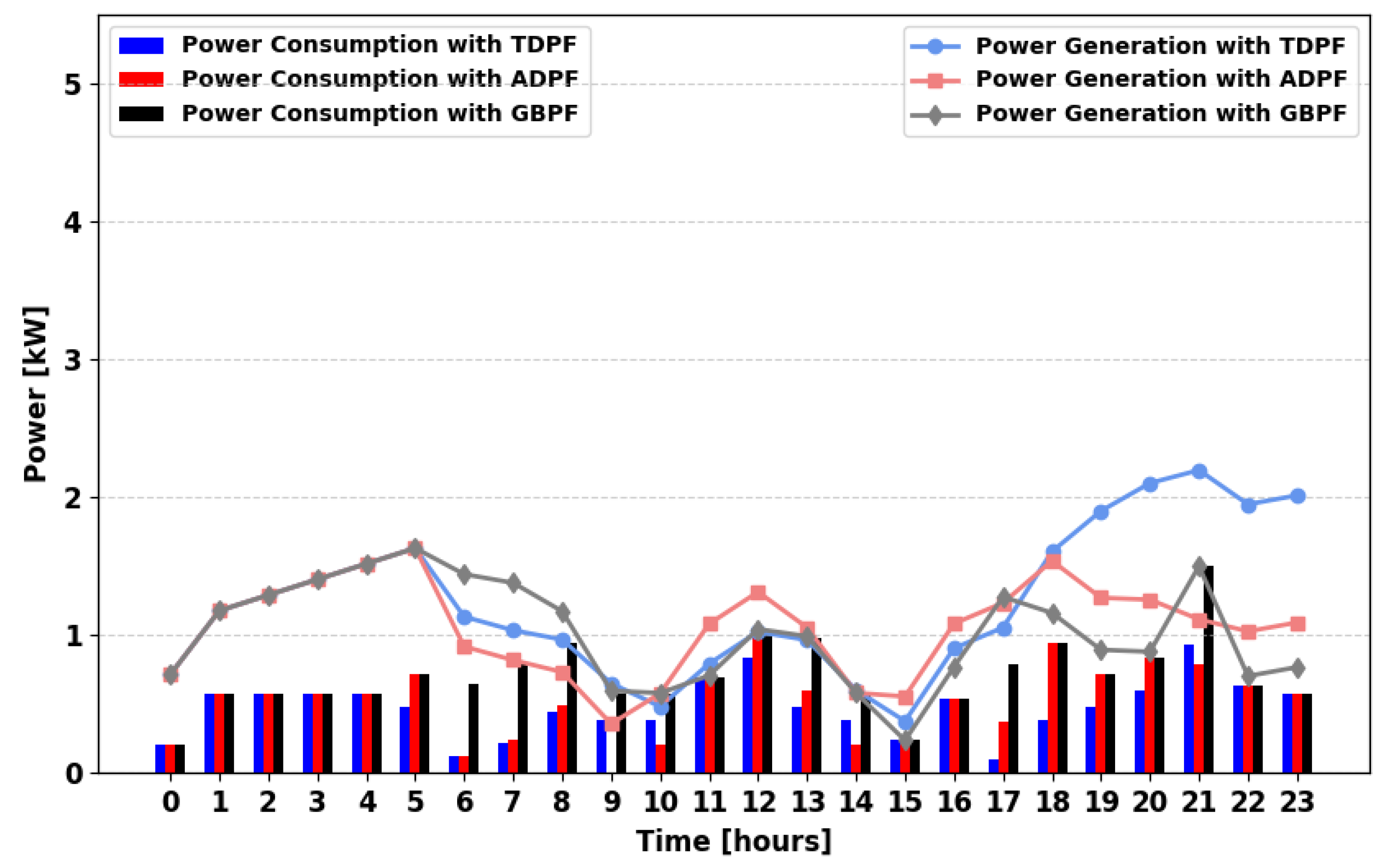
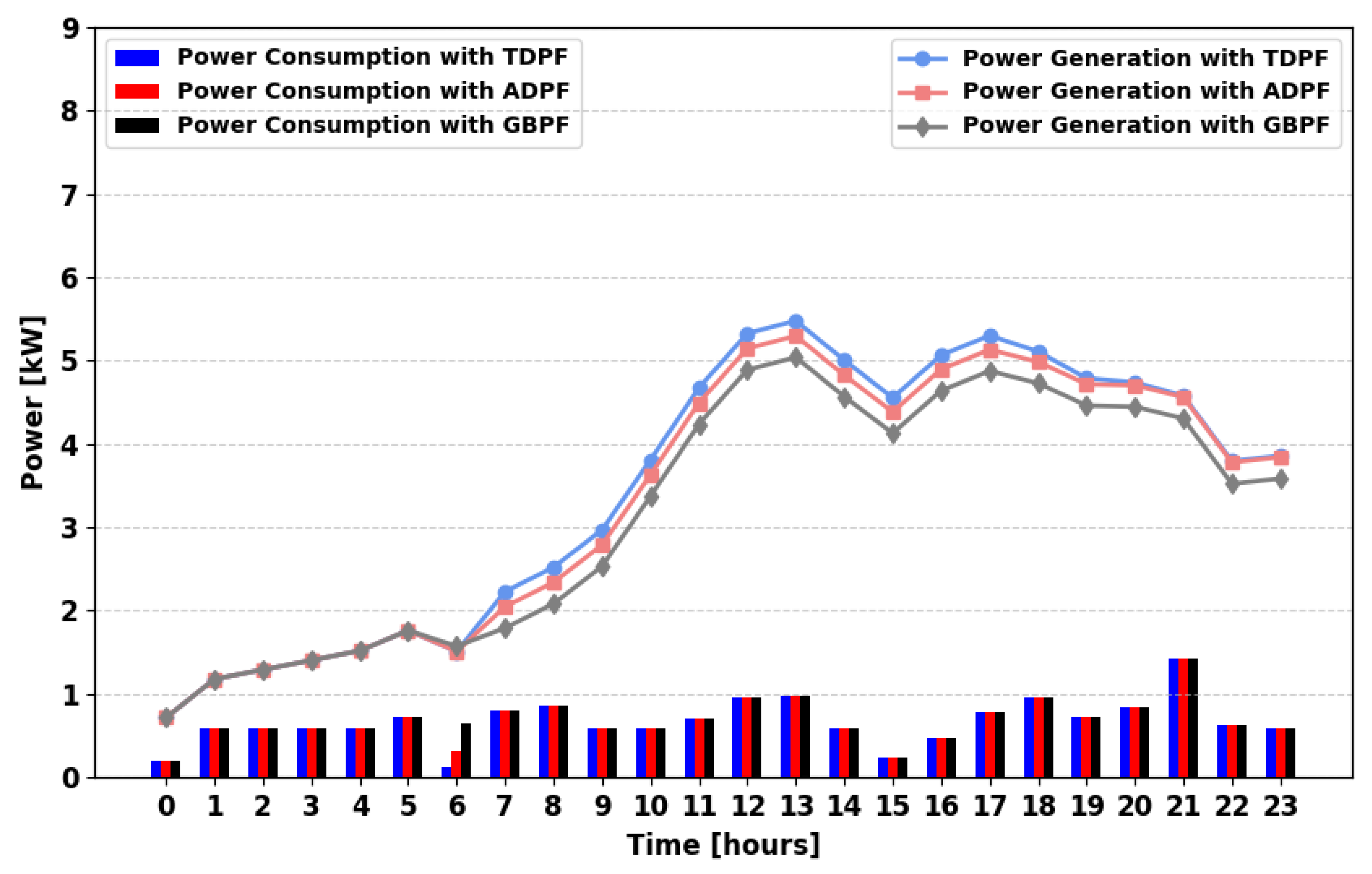
Figure 10 demonstrates an improvement in power availability due to the presence of multiple power generators. ADPF satisfies more demand at key intervals: 04:00, 08:00, 09:00, 12:00, 13:00, 21:00, 23:00, and 24:00, compared to TDPF.

Figure 10. Power supply and consumption in winter with MPFA/MG.

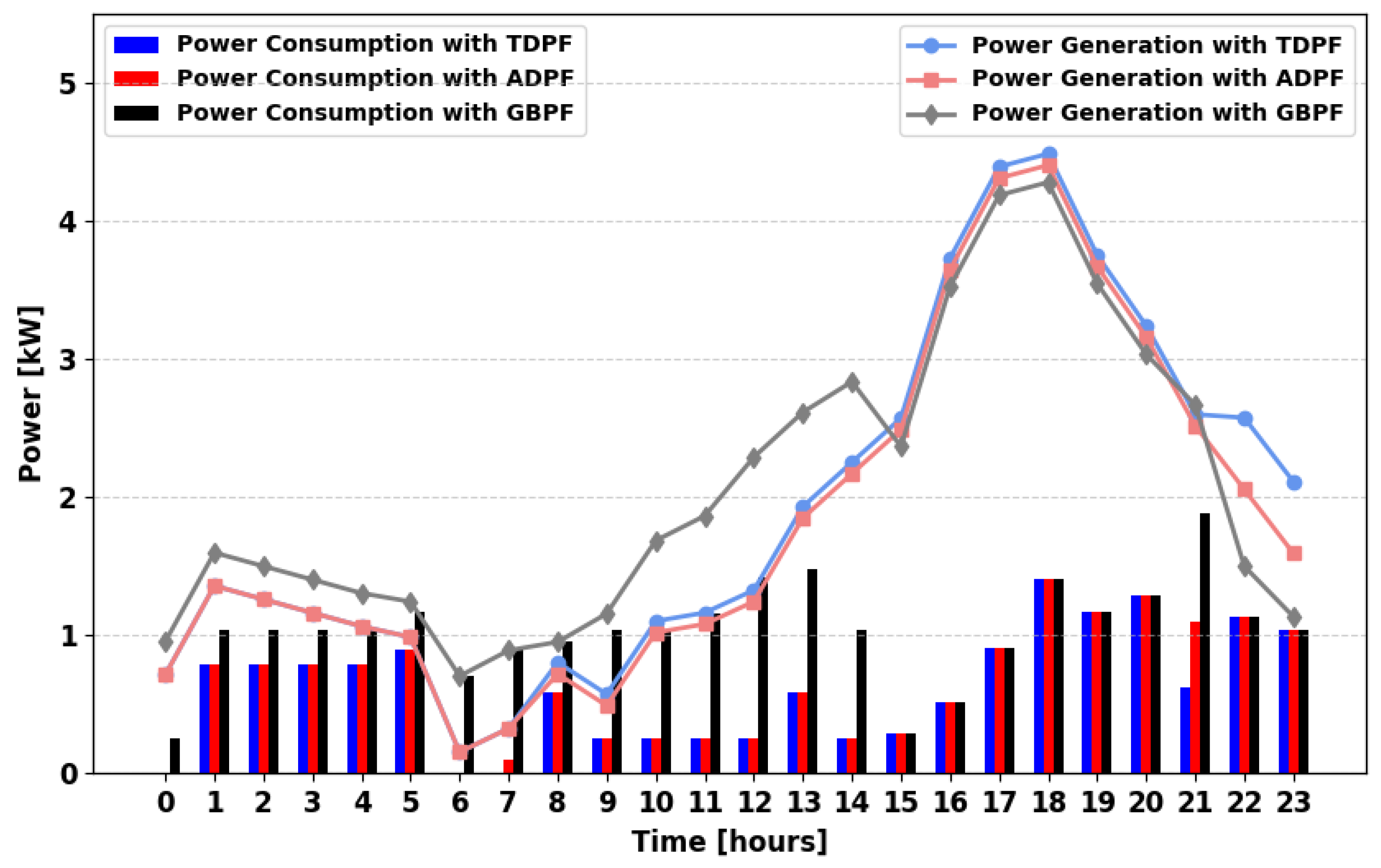
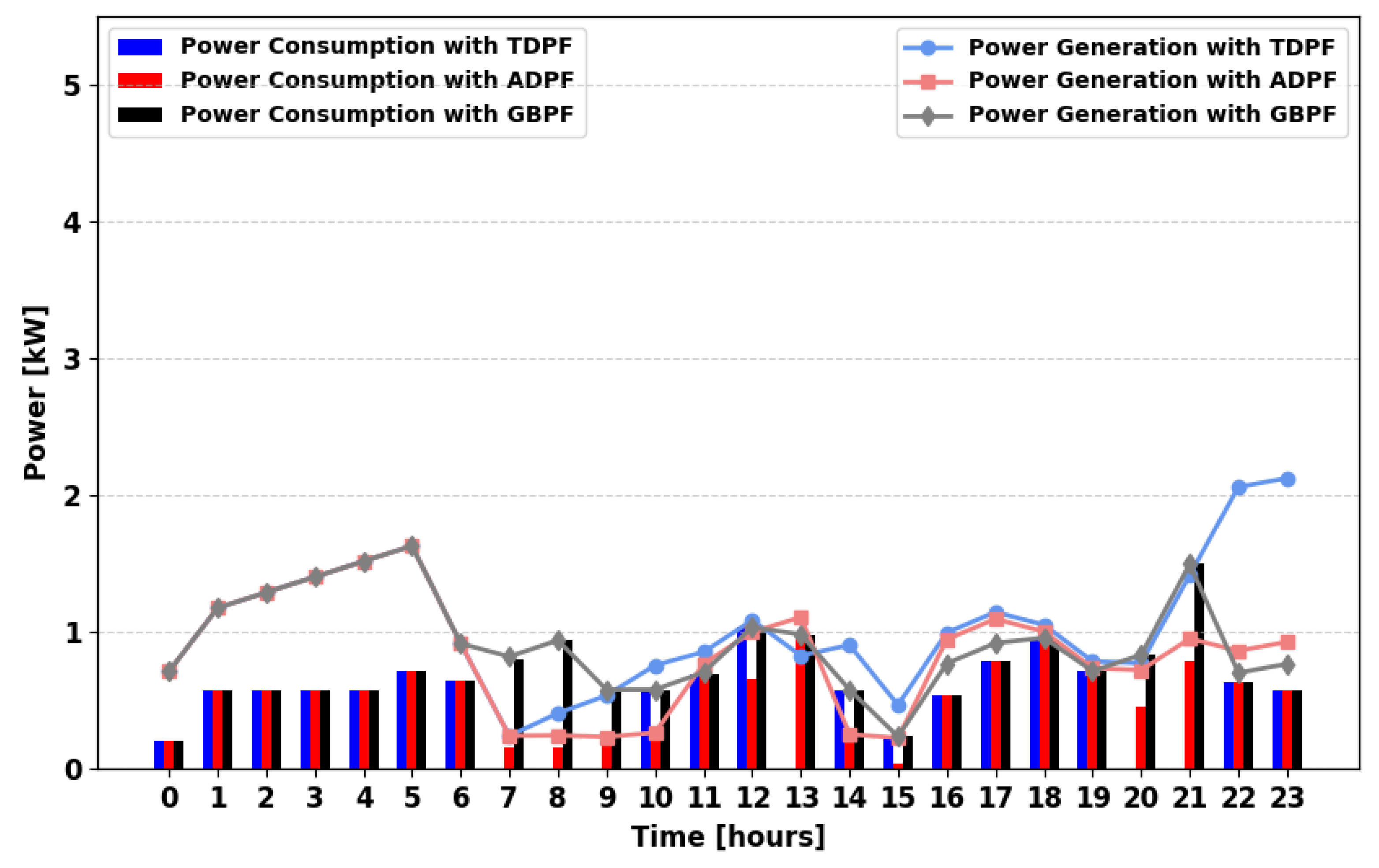
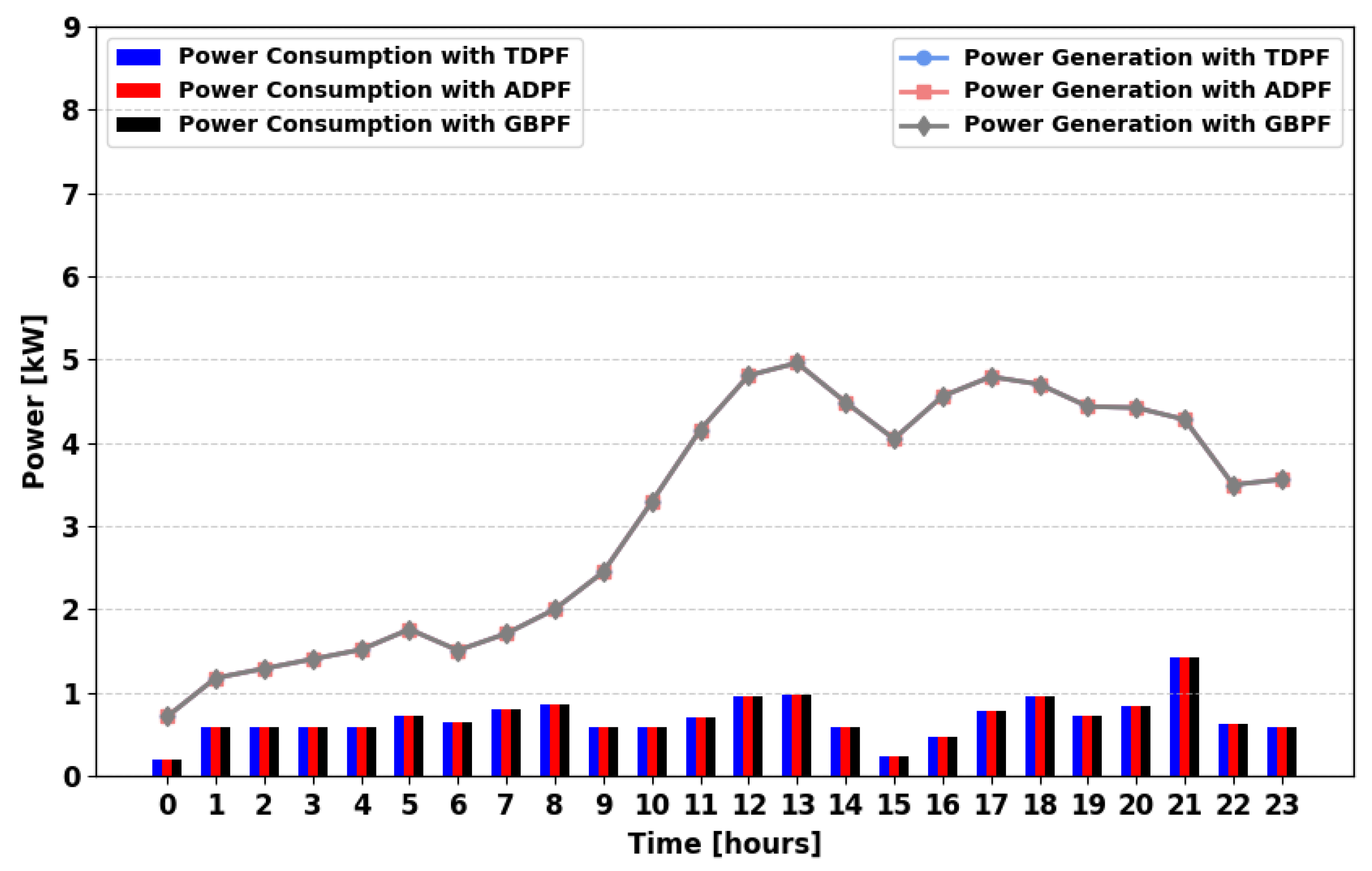
Finally, Figure 11 shows the most efficient and balanced power supply scenario. Here, ADPF ensures greater demand satisfaction during multiple hours, particularly in the morning (08:00–11:00) and later in the evening (19:00, 22:00, and 24:00). The presence of multiple PSs allows surplus energy from PGs to be stored and redistributed effectively, further improving demand fulfillment.

Figure 11. Power supply and consumption in winter with MPFA/MSG.

Across all scenarios, the GBPF algorithm consistently meets the full daily power demand, highlighting its superior performance in ensuring reliable energy supply. The results further emphasize the importance of multi-source generation and grid integration in optimizing energy distribution and reducing supply gaps.

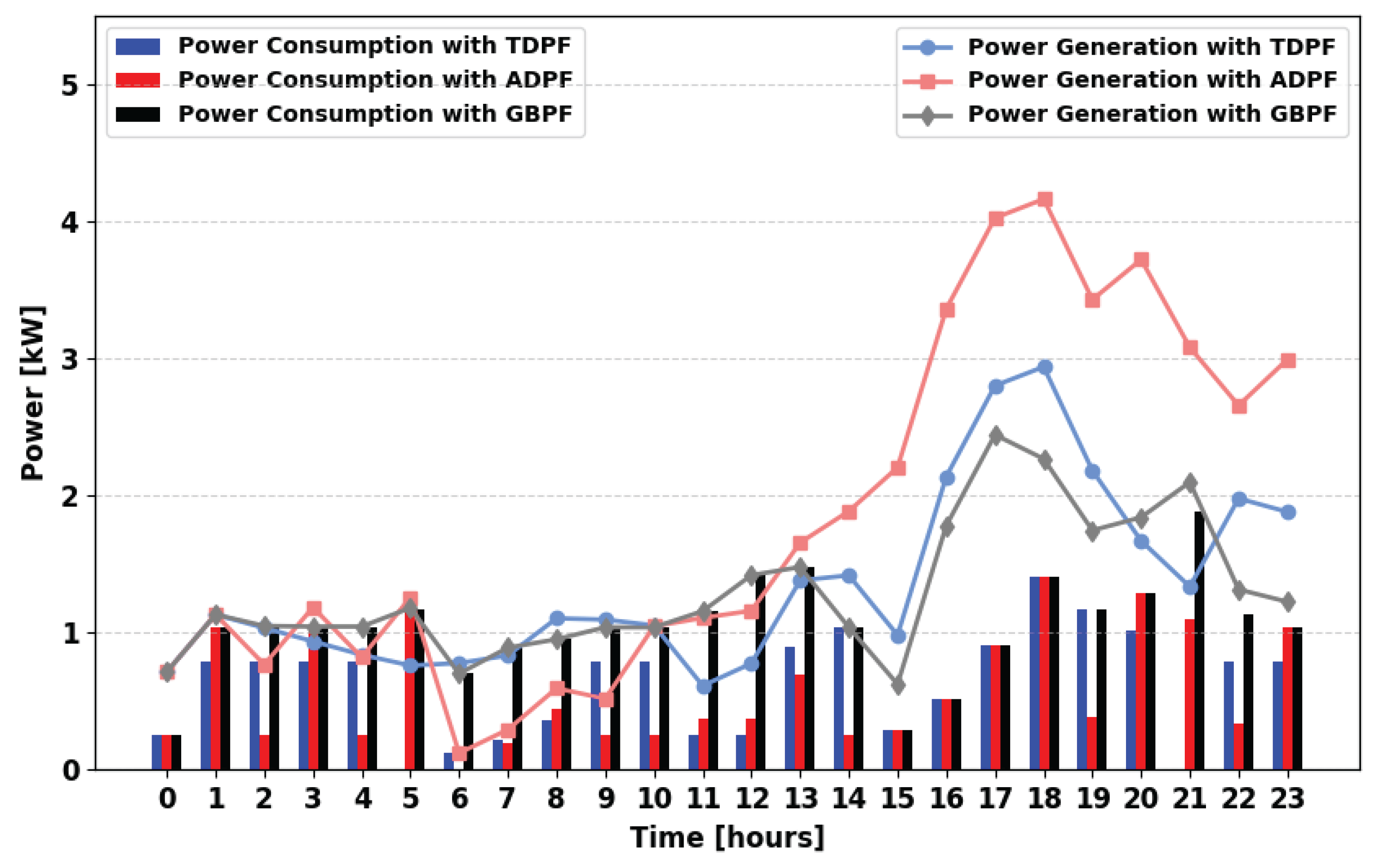
Figure 12 and Figure 13 illustrate the power supply and consumption profiles during the summer season for the MPFA/S and MPFA/SG scenarios. In both cases, the ADPF and TDPF algorithms exhibit nearly identical performance in meeting demand, primarily due to the limited number of connections available. In Figure 14, with the increased number of connections in the MPFA/MG scenario, the TDPF algorithm outperforms ADPF. Specifically, demand satisfaction is higher at critical hours such as 02:00, 03:00, 04:00, 09:00, 10:00, 13:00, 19:00, and 22:00. Conversely, in Figure 15, the ADPF algorithm demonstrates better performance at 01:00, 03:00, 05:00, 20:00, 21:00, and 23:00. In the MPFA/MSG scenario, the ADPF algorithm nearly satisfies the maximum demand across all periods, while the TDPF algorithm either fully meets or intermittently fails to meet the demand at multiple times. Across all evaluated scenarios, the GBPF algorithm consistently achieves full daily power demand satisfaction, confirming its superior reliability and effectiveness during the summer season.

Figure 12. Power supply and consumption in summer with MPFA/S.

Figure 13. Power supply and consumption in summer with MPFA/SG.

Figure 14. Power supply and consumption in summer with MPFA/MG.

Figure 15. Power supply and consumption in summer with MPFA/MSG.

Figure 16 and Figure 17 illustrate the power supply and consumption profiles for the autumn season. Given the relatively lower energy demand during this period, the MPFA/S, MPFA/SG, and MPFA/MG scenarios exhibit similar performance trends across all three evaluated algorithms. In particular, Figure 18, representing the MPFA/MG scenario, shows that during critical hours—specifically, 05:00, 08:00, 12:00, 13:00, and 17:00–20:00 the ADPF algorithm is able to satisfy a higher portion of the demand compared to the TDPF algorithm. Furthermore, Figure 19 highlights the MPFA/MSG scenario, where at hours 7:00–9:00, 20:00, and 21:00, the TDPF algorithm fails to meet the required load, whereas the ADPF algorithm successfully fulfills the demand based on available power supply. This distinction underlines the adaptability of the ADPF method under supply-constrained conditions. Across all considered scenarios, the GBPF algorithm consistently achieves full daily demand satisfaction, demonstrating its robustness and superior capability in ensuring reliable power delivery throughout the autumn season.

Figure 16. Power supply and consumption in autumn with MPFA/S.

Figure 17. Power supply and consumption in autumn with MPFA/SG.

Figure 18. Power supply and consumption in autumn with MPFA/MG.

Figure 19. Power supply and consumption in autumn with MPFA/MSG.

Figure 20, Figure 21, Figure 22 and Figure 23 present the power supply and consumption profiles for the spring season, a period characterized by lower energy demand and relatively high photovoltaic (PV) energy supply. In the MPFA/S scenario, both the ADPF and TDPF algorithms demonstrate comparable performance in terms of demand satisfaction. However, the GBPF algorithm outperforms them during certain periods, leveraging the additional availability of grid power to meet the load requirements better. Specifically, Figure 21, which illustrates the MPFA/SG scenario, highlights that during the early morning hours from 1:00 to 5:00 and midday hours from 11:00 to 14:00, the TDPF algorithm is able to satisfy a greater portion of the demand compared to the ADPF algorithm, likely due to its effective load distribution strategy.

Figure 20. Power supply and consumption in spring with MPFA/S.

Figure 21. Power supply and consumption in spring with MPFA/SG.

Figure 22. Power supply and consumption in spring with MPFA/MG.

Figure 23. Power supply and consumption in spring with MPFA/MSG.

Moreover, Figure 22, focusing on the MPFA/MG scenario, reveals that at 06:00, neither the TDPF nor the ADPF algorithm is able to fully satisfy the load, pointing to a temporary mismatch between supply availability and demand requirements. Nevertheless, as shown in Figure 23, under the more advanced MPFA/MG and MPFA/MSG scenarios, all three algorithms ADPF, TDPF, and GBPF successfully meet the full demand across all time periods. This is largely attributed to the abundant RES supply during the spring season and the extensive logical connections established between devices, which enhance load-sharing flexibility and system robustness. Overall, the results emphasize the importance of optimizing connectivity and leveraging renewable generation to ensure reliable and efficient microgrid operation under varying seasonal conditions.

5.3. Power Loss Results and Discussion

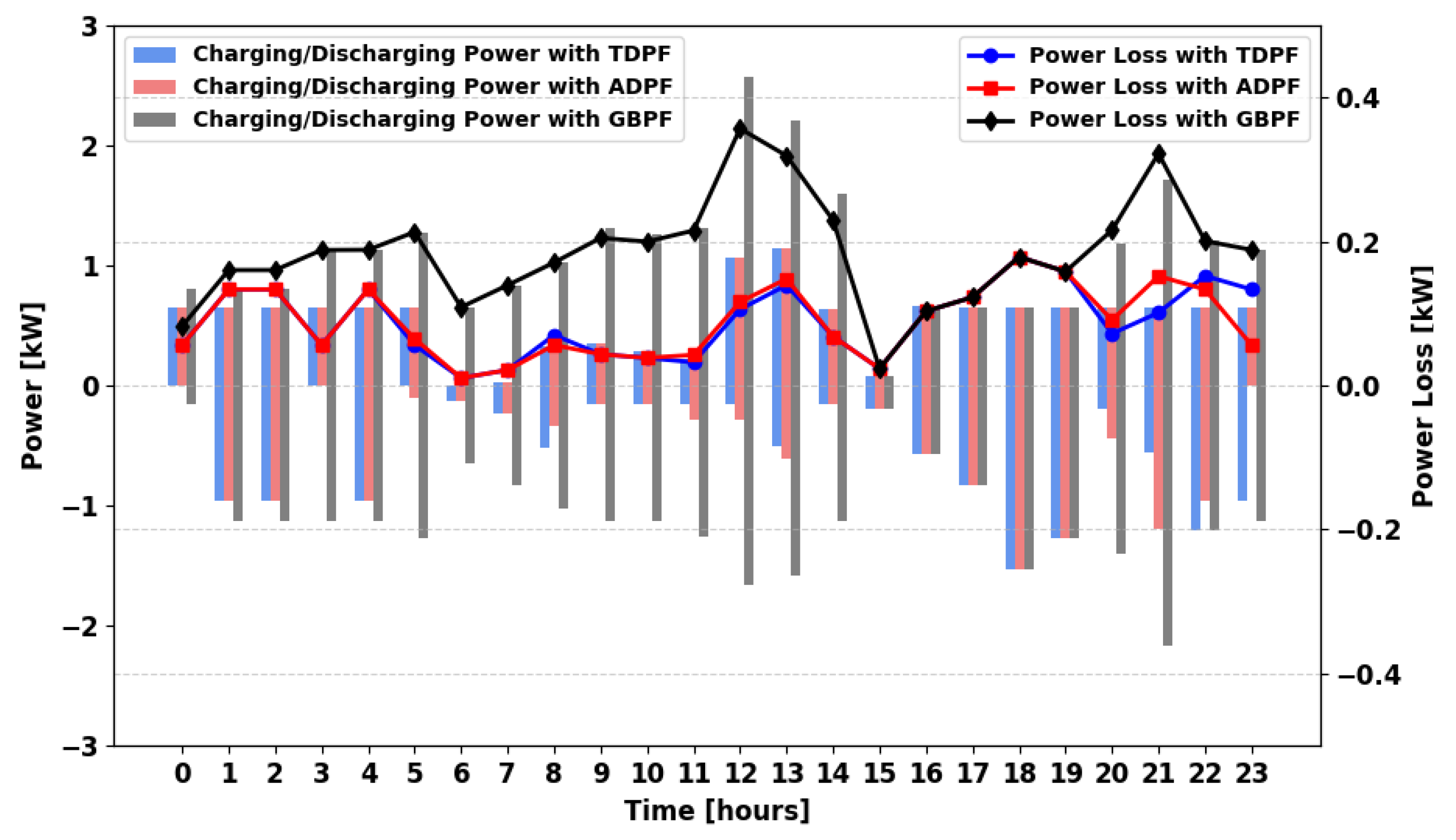
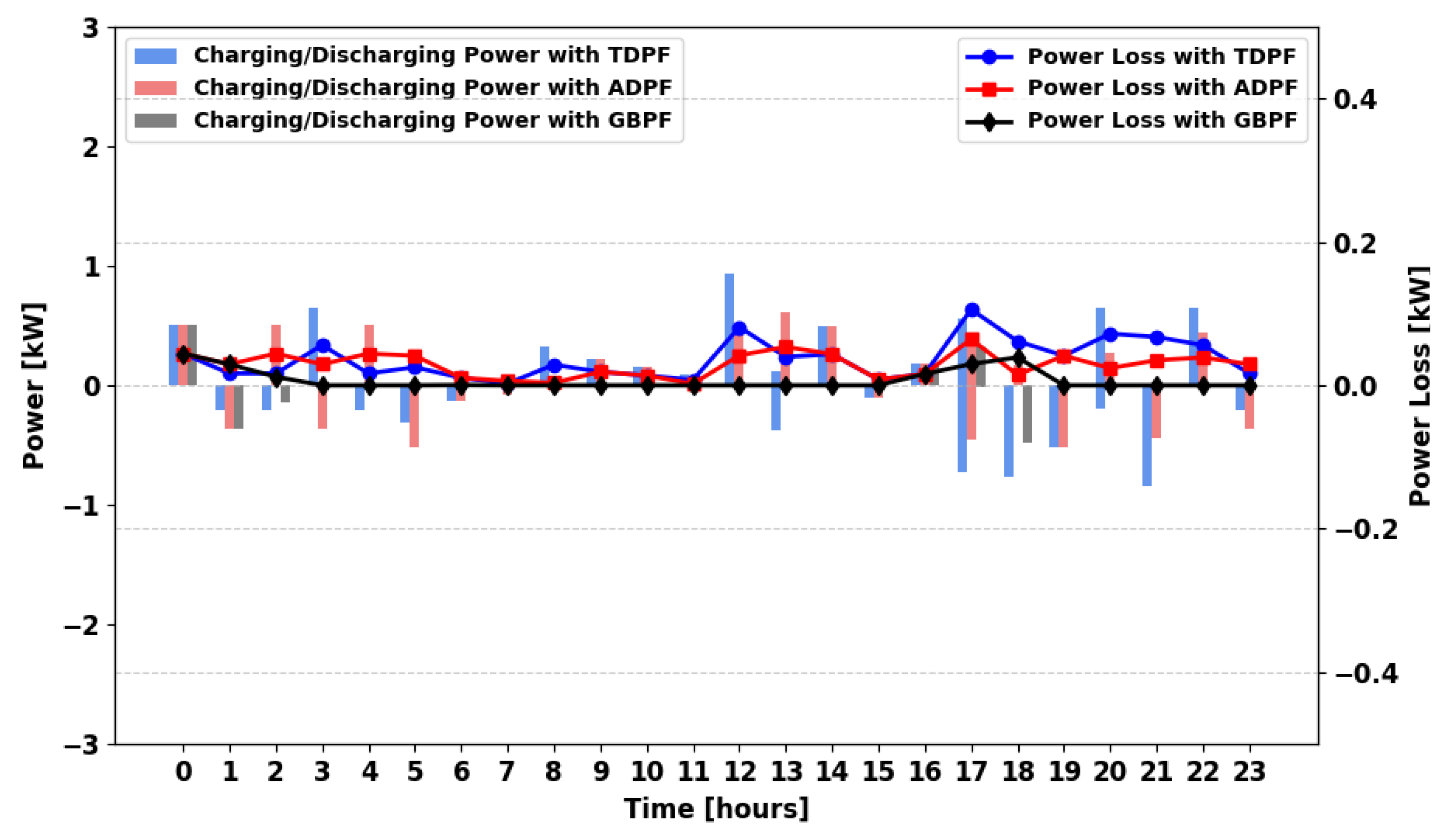
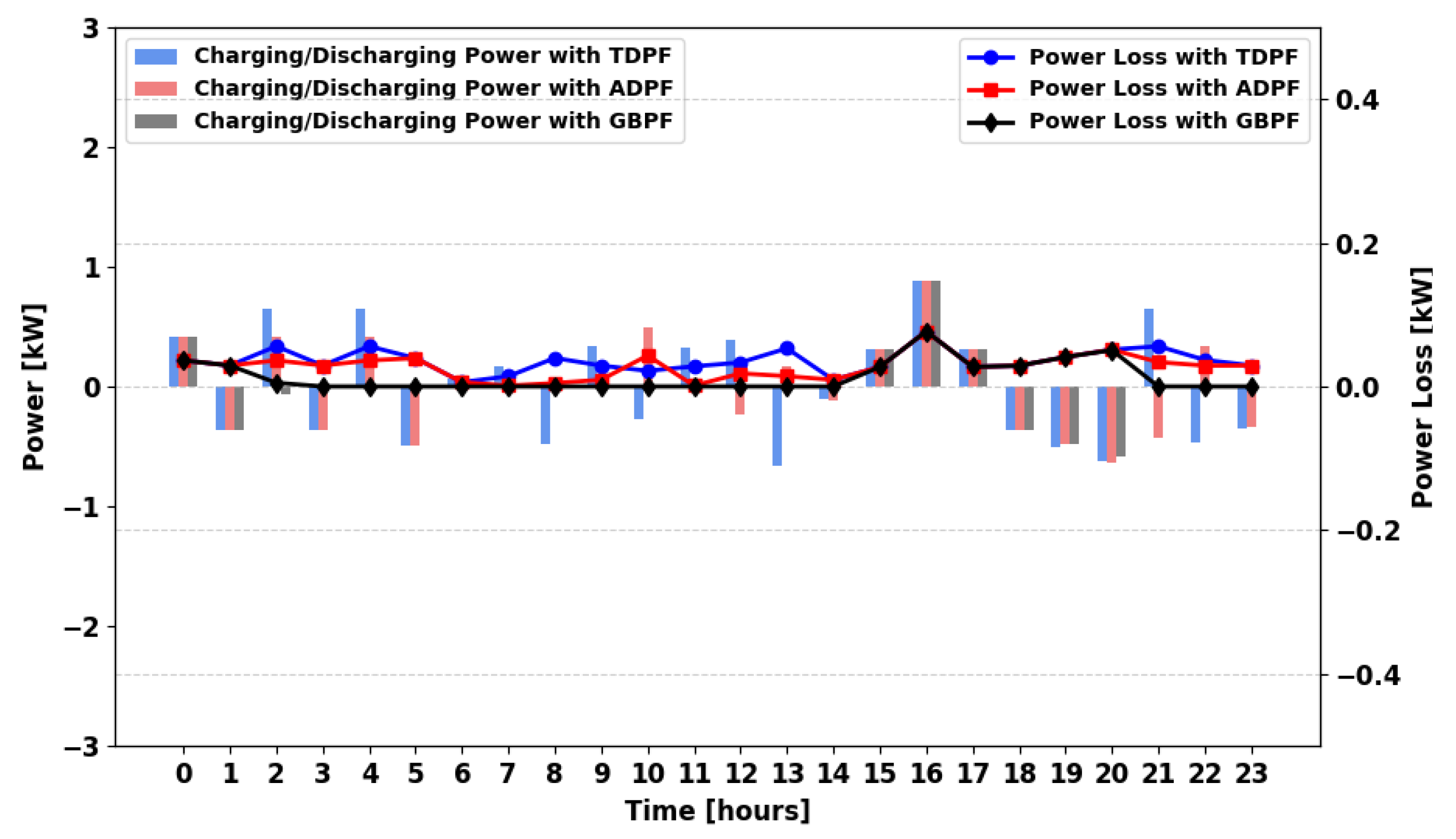
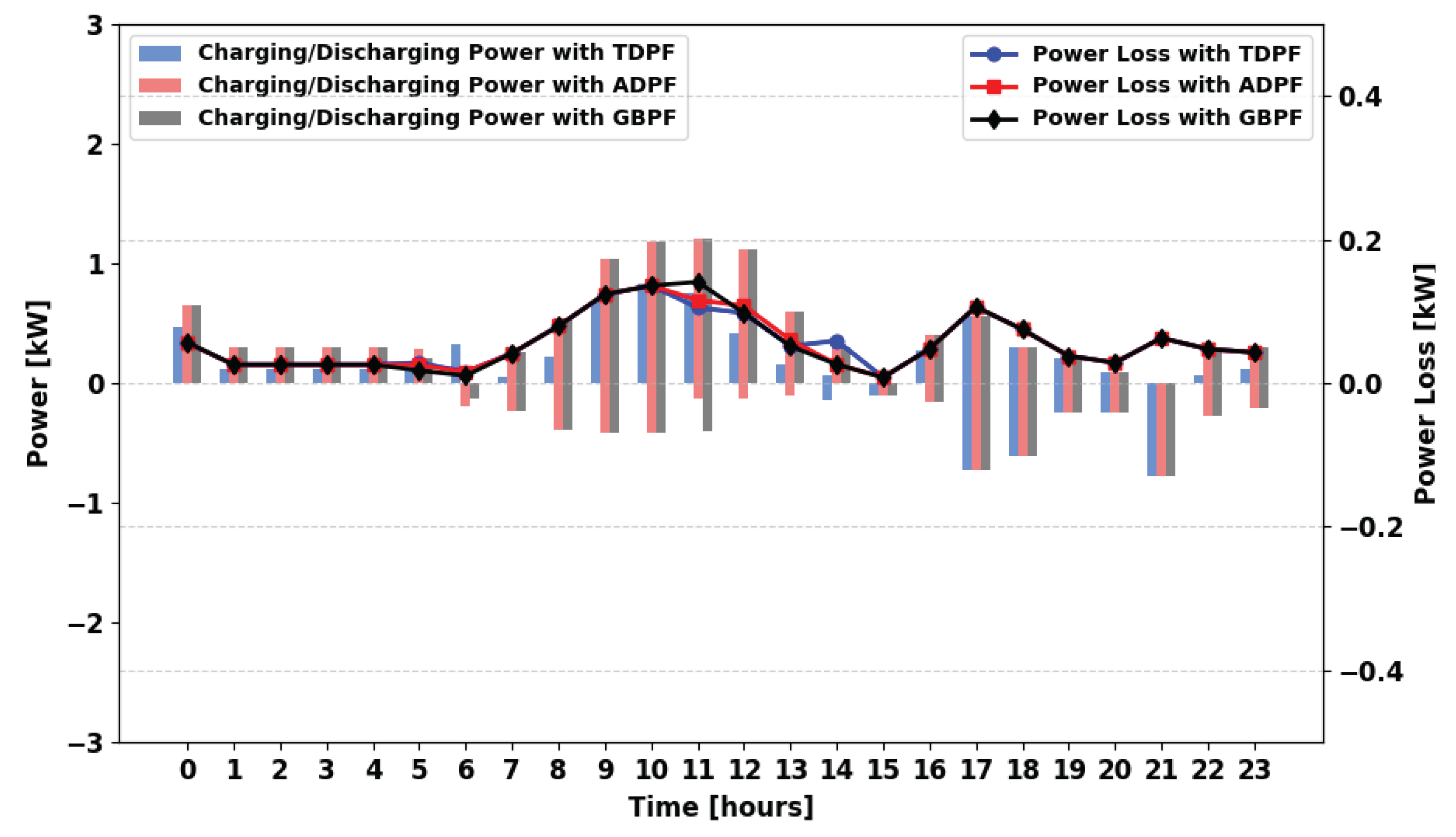
This section analyzes the power loss in different scenarios using various power flow algorithms. For the winter season and in the MPFA/S scenario (Figure 24), the logical connection where power flows primarily from the PS leads to a high frequency of charging and discharging, resulting in significant storage losses. The TDPF and ADPF algorithms exhibit similar storage losses. Under GBPF, 100% demand is guaranteed; grid support often reduces battery cycling and thus storage-related losses, although total imported energy can increase when RES are scarce.

Figure 24. Power loss in winter with MPFA/S.

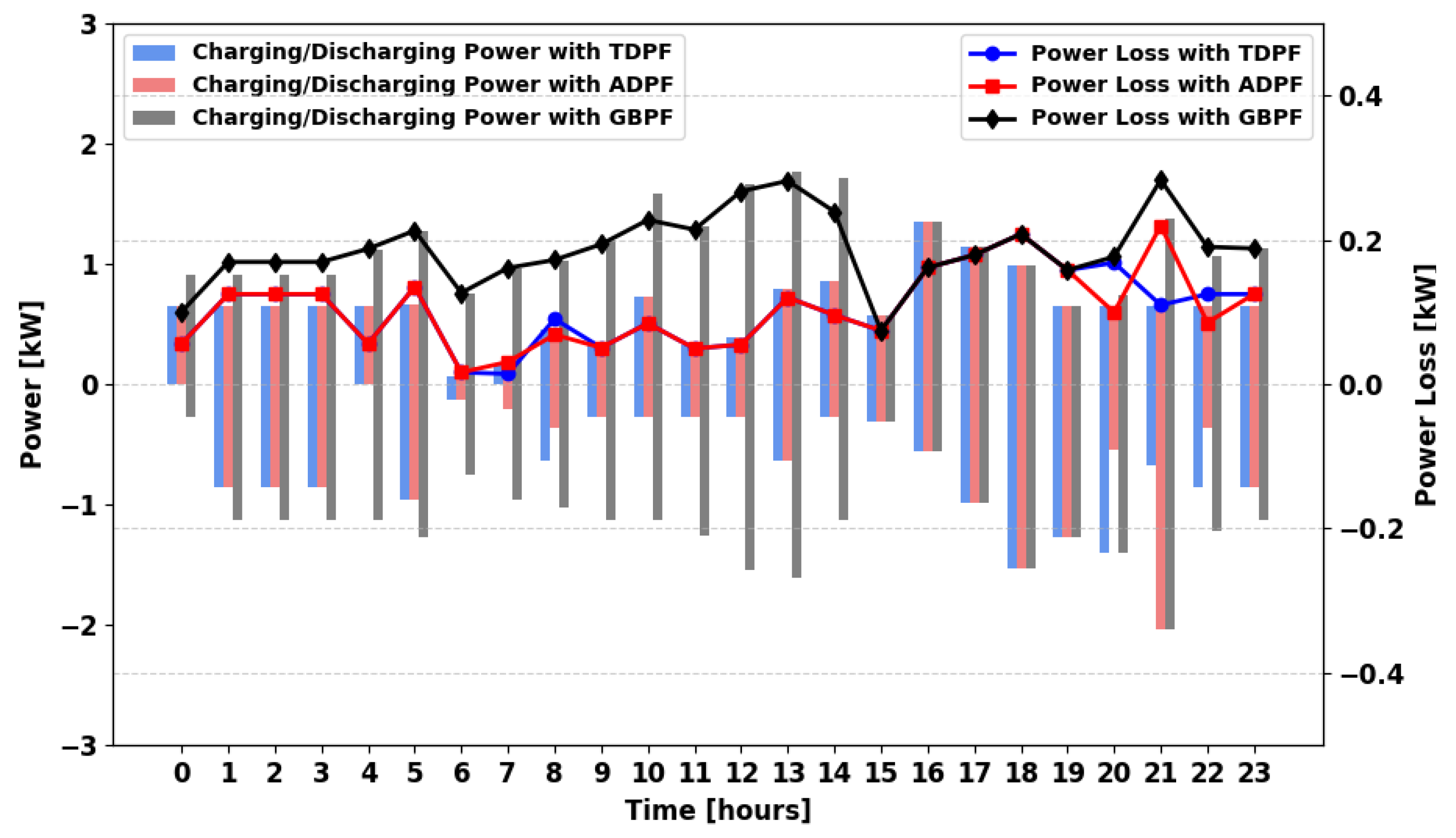
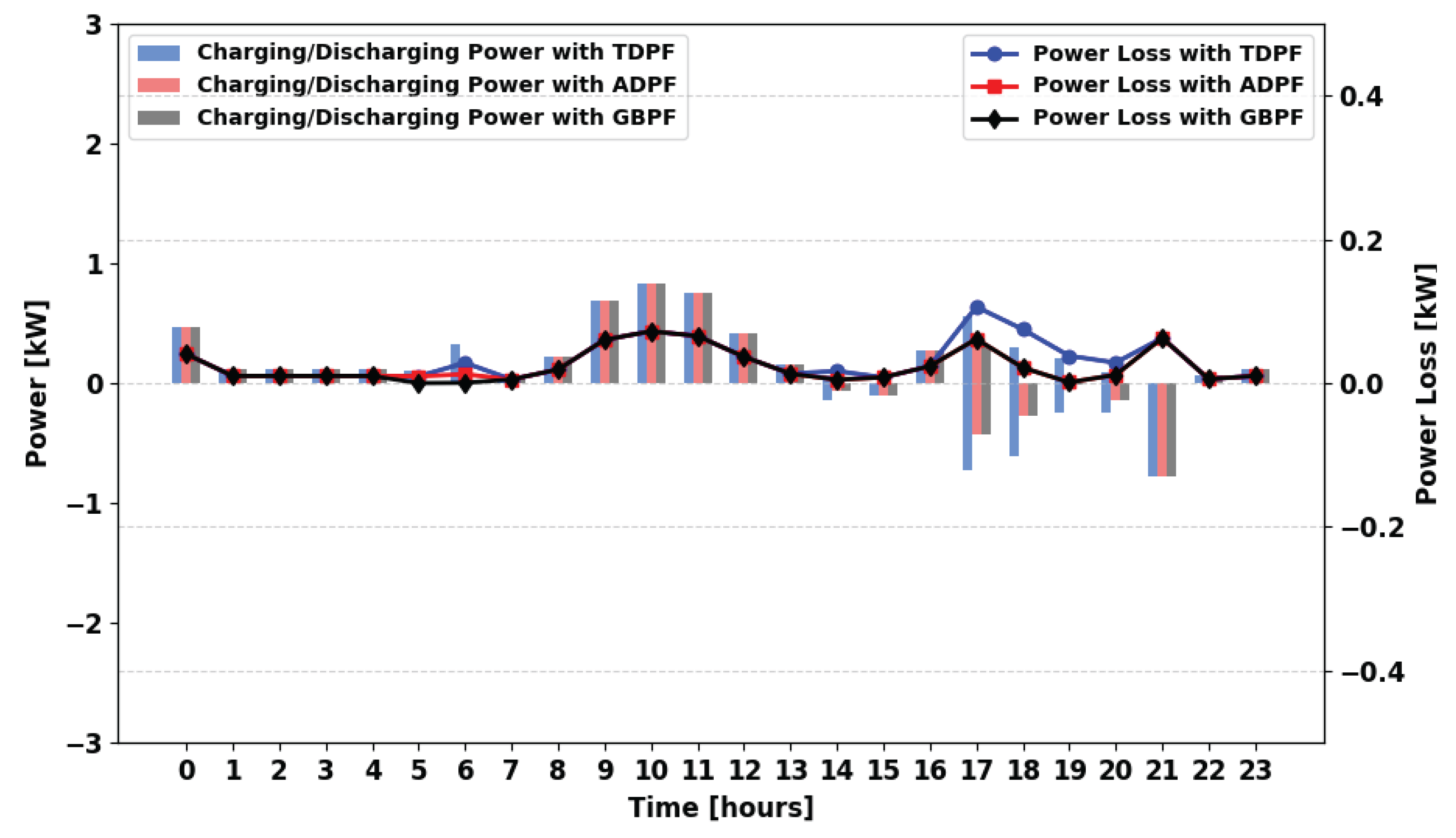
For winter, Figure 25 represents the charging and discharging profile for the MPFA/SG scenario. Here, the logical connection allows power to be drawn from a single generator, reducing dependency on PS and significantly lowering power losses compared to MPFA/S. This highlights the impact of direct generation-based supply in minimizing inefficiencies.

Figure 25. Power loss in winter with MPFA/SG.

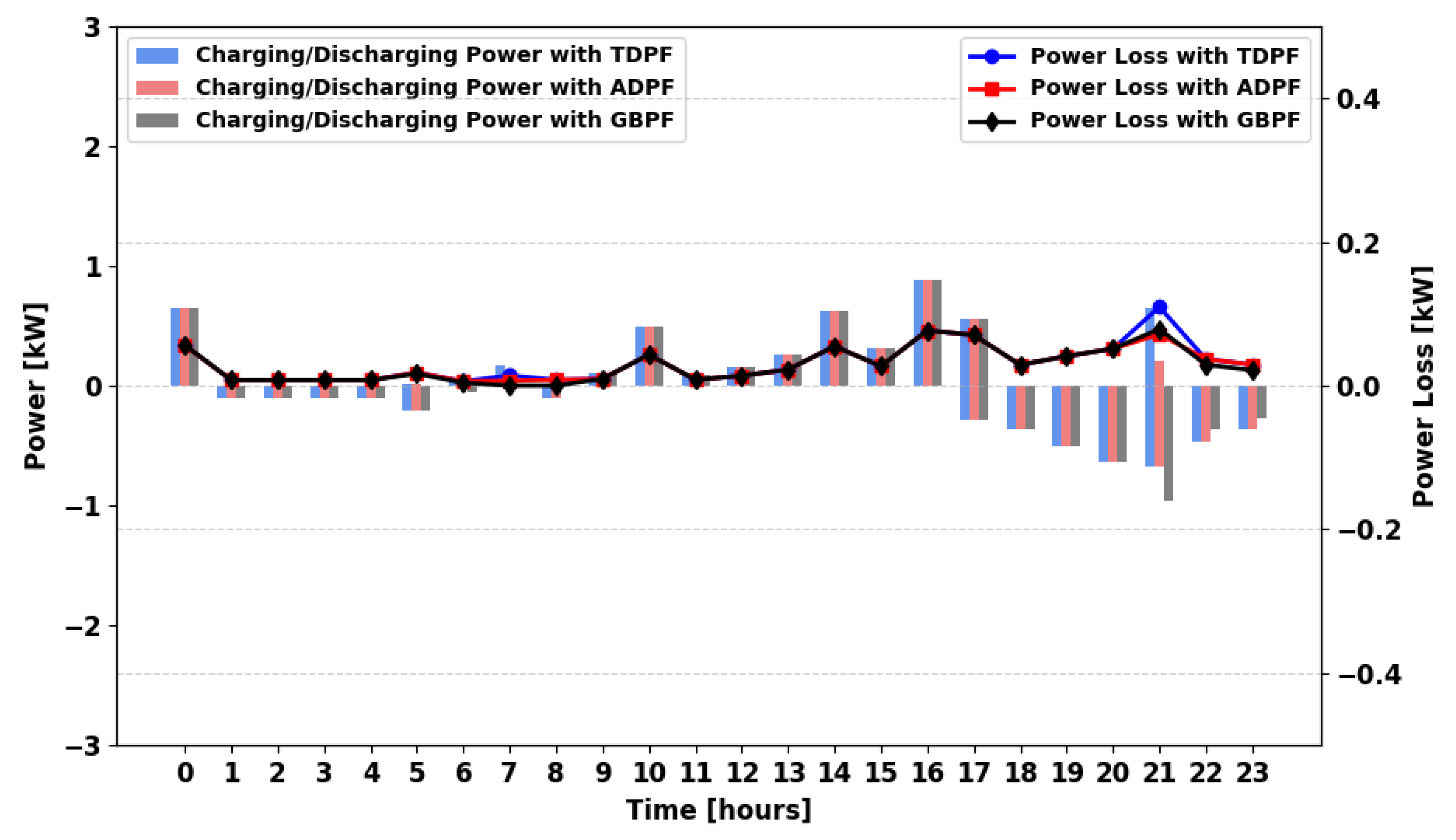
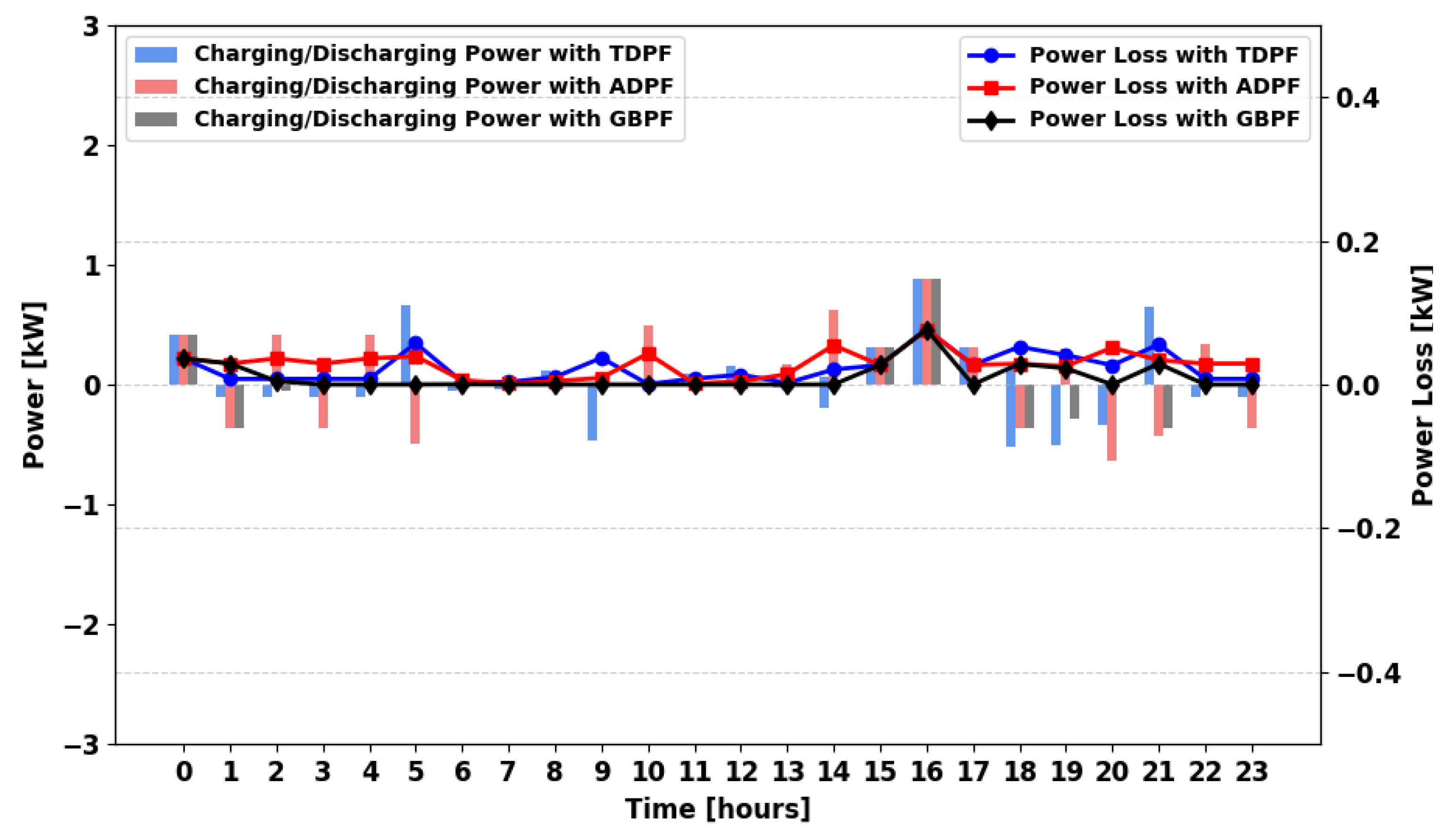
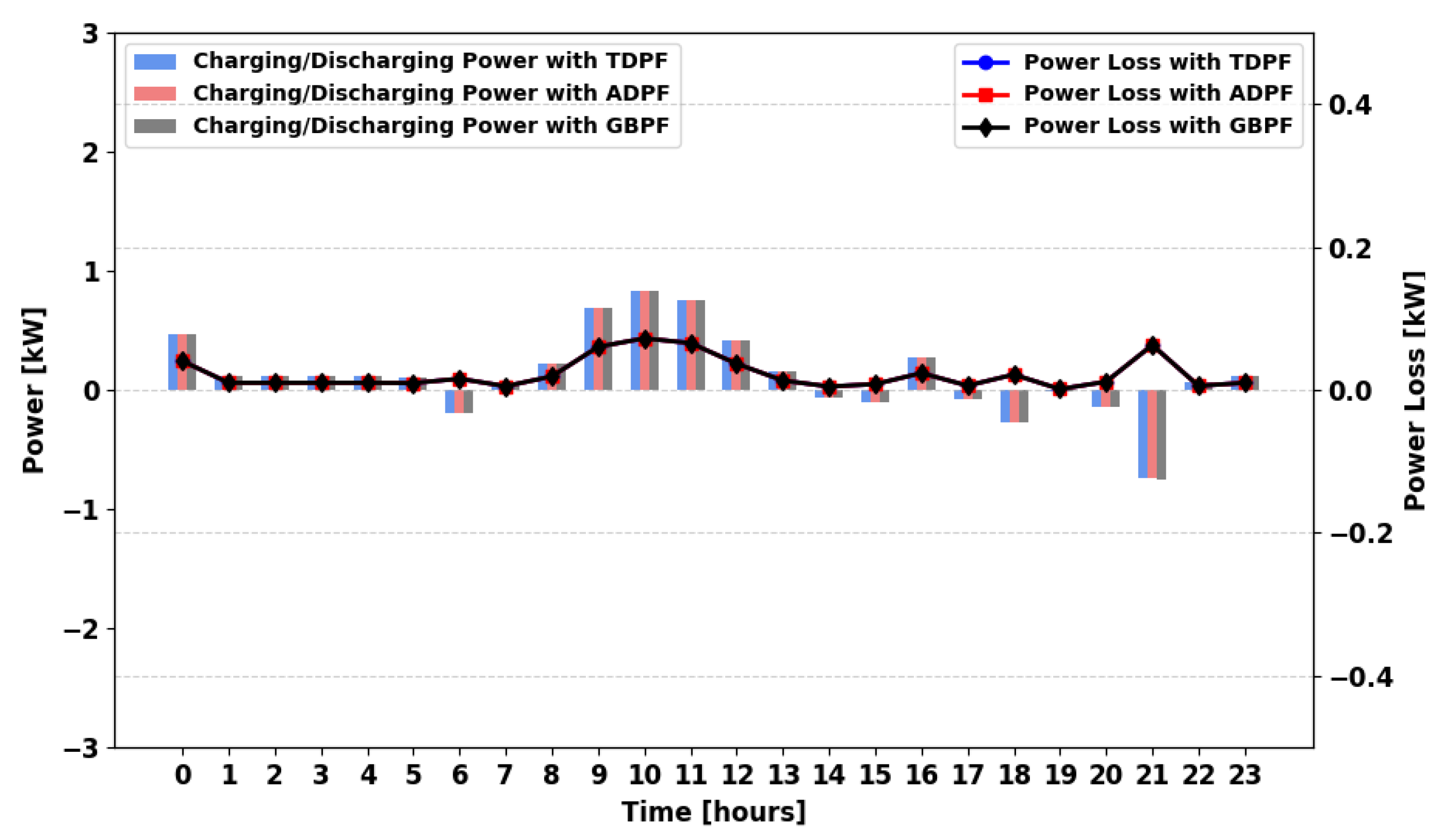
In Figure 26 (MPFA/MG) and Figure 27 (MPFA/MSG), power loss continues to decrease rapidly across scenarios. The introduction of multiple generators and storage systems in these configurations enhances energy availability and distribution efficiency, resulting in further reductions in energy losses. Notably, across all scenarios except MPFA/S, the ADPF algorithm demonstrates lower power losses compared to TDPF. Across MPFA/SG–MPFA/MSG scenarios, power loss in GBPF is significantly lower than in ADPF, benefiting from grid integration that reduces cycling.

Figure 26. Power loss in winter with MPFA/MG.

Figure 27. Power loss in winter with MPFA/MSG.

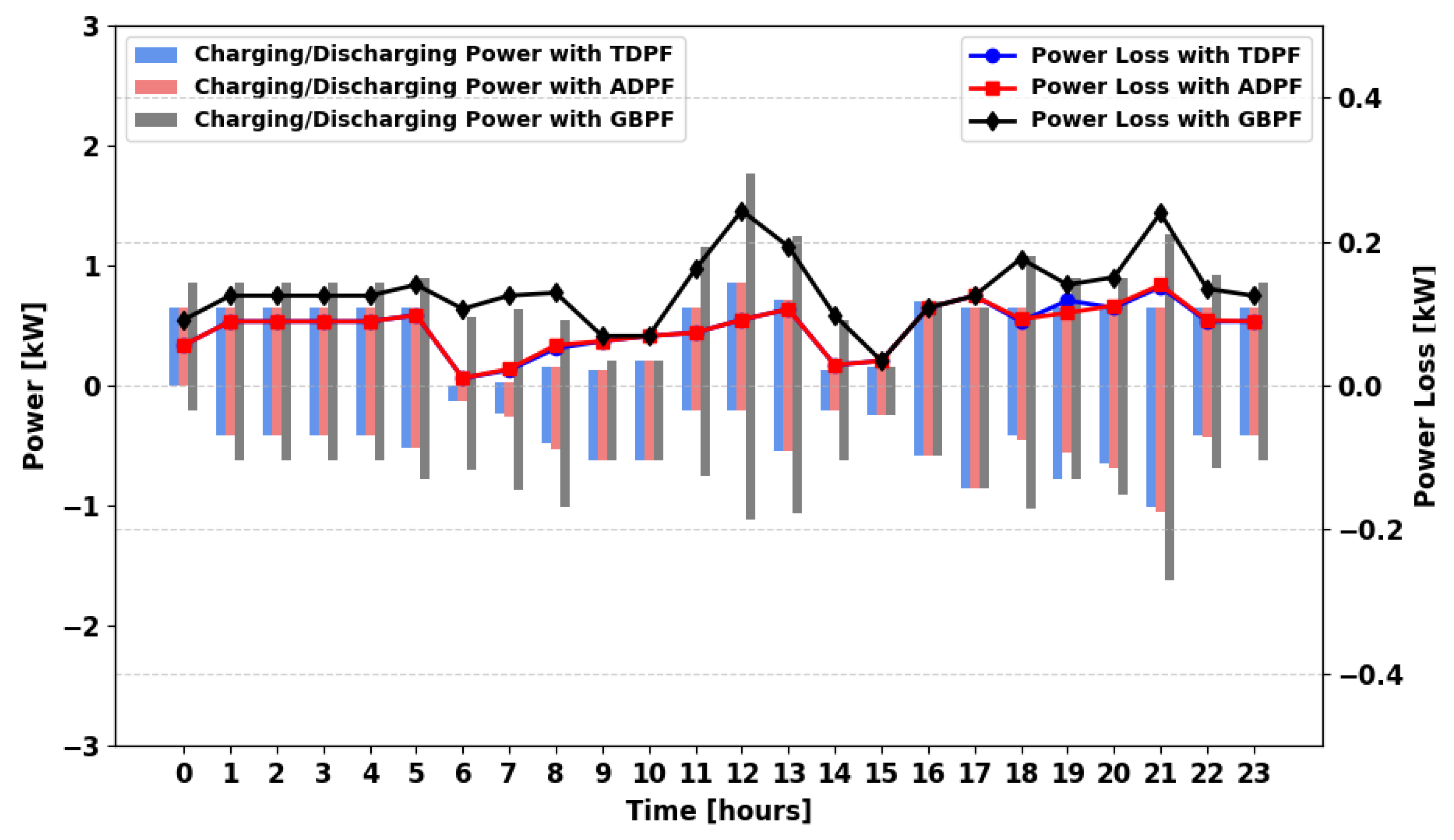
For the summer season, Figure 28, Figure 29, Figure 30 and Figure 31 illustrate the charging/discharging profile and power loss across the three algorithms. In the MPFA/S scenario, limited logical connections lead to high power charging/discharging, resulting in significant losses. The GBPF algorithm ensures complete demand satisfaction and generally yields the lowest storage-related losses due to reduced cycling from grid support (though imported energy can increase when RES are scarce). In MPFA/SG, power loss remains similar across all three algorithms. In MPFA/MG and MPFA/MSG, ADPF exhibits lower losses than TDPF at all time periods, while GBPF consistently has the lowest losses compared to both TDPF and ADPF.

Figure 28. Power loss in summer with MPFA/S.

Figure 29. Power loss in summer with MPFA/SG.

Figure 30. Power loss in summer with MPFA/MG.

Figure 31. Power loss in summer with MPFA/MSG.

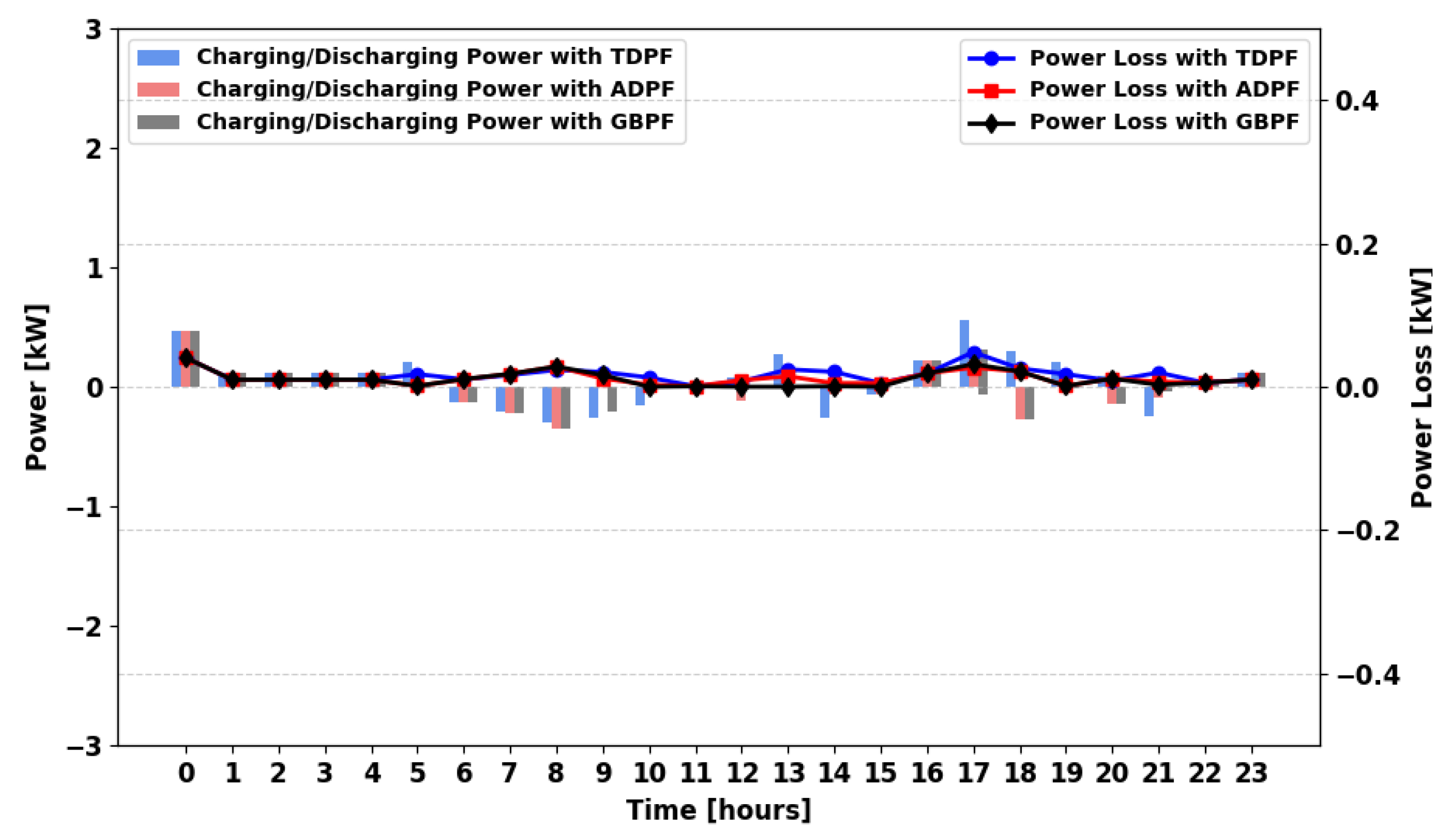
For the autumn season, Figure 32, Figure 33, Figure 34 and Figure 35 present the charging/discharging profile and power loss. Similar to summer, MPFA/S experiences high losses due to frequent charging/discharging. With grid support, GBPF reduces storage cycling and typically yields the lowest storage-related losses while ensuring 100% demand satisfaction. In MPFA/SG, power loss remains similar across all algorithms. In MPFA/MG, ADPF has lower losses than TDPF, while in MPFA/MSG, TDPF exhibits higher losses compared to ADPF, and GBPF maintains the lowest losses.

Figure 32. Power loss in autumn with MPFA/S.

Figure 33. Power loss in autumn with MPFA/SG.

Figure 34. Power loss in autumn with MPFA/MG.

Figure 35. Power loss in autumn with MPFA/MSG.

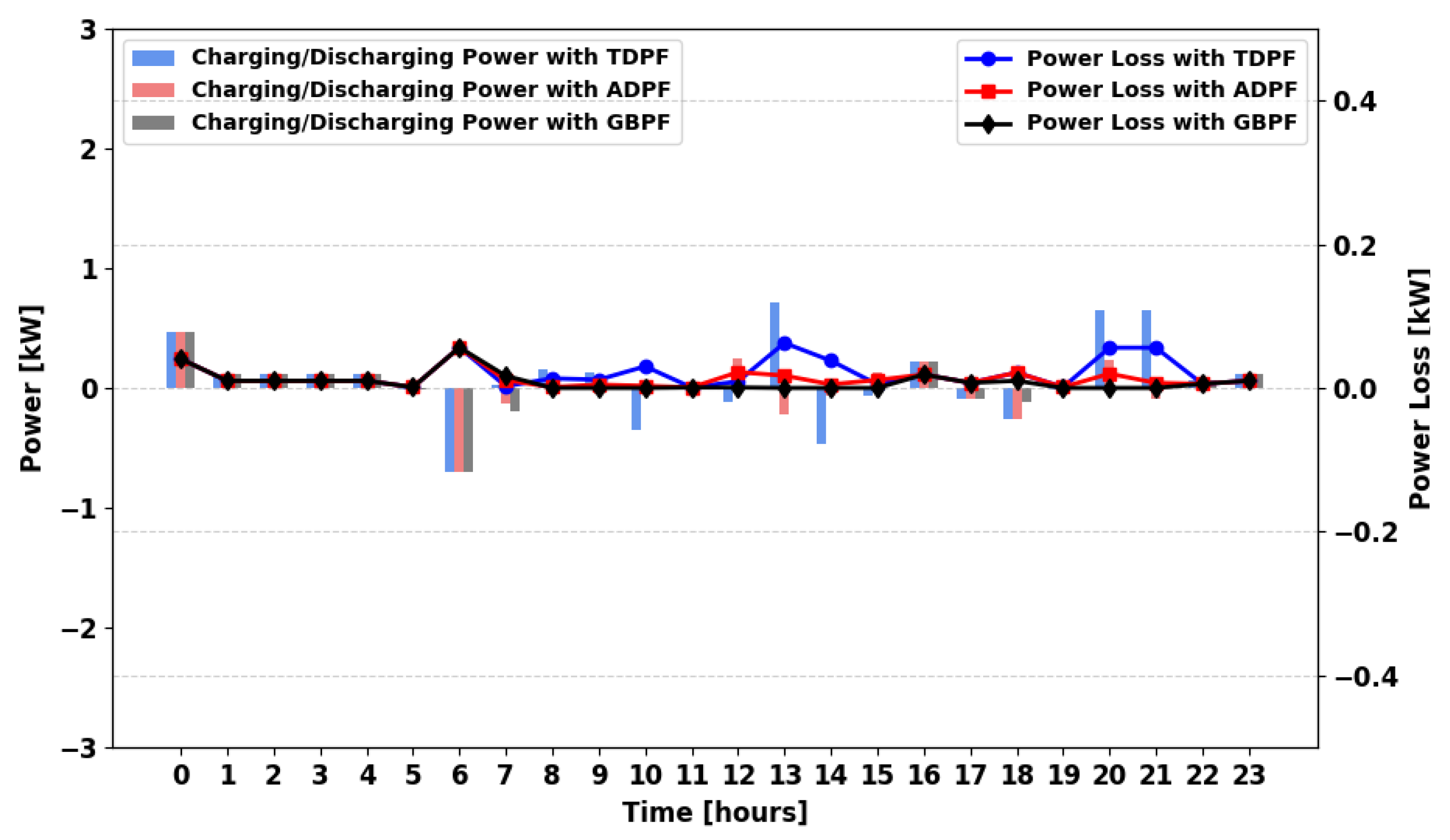
For the spring season, Figure 36, Figure 37, Figure 38 and Figure 39 show the charging/discharging profile and power loss. In MPFA/S, TDPF experiences the lowest losses due to lower demand satisfaction, ADPF has moderate losses, and GBPF achieves full demand satisfaction and generally the lowest storage-related losses; in spring, all three methods show similar losses due to ample RES supply. In MPFA/SG and MPFA/MSG, losses remain similar across algorithms due to the lower demand compared to supply. In MPFA/MG, GBPF outperforms the other two algorithms in minimizing power loss.

Figure 36. Power loss in spring with MPFA/S.

Figure 37. Power loss in spring with MPFA/SG.

Figure 38. Power loss in spring with MPFA/MG.

Figure 39. Power loss in spring with MPFA/MSG.

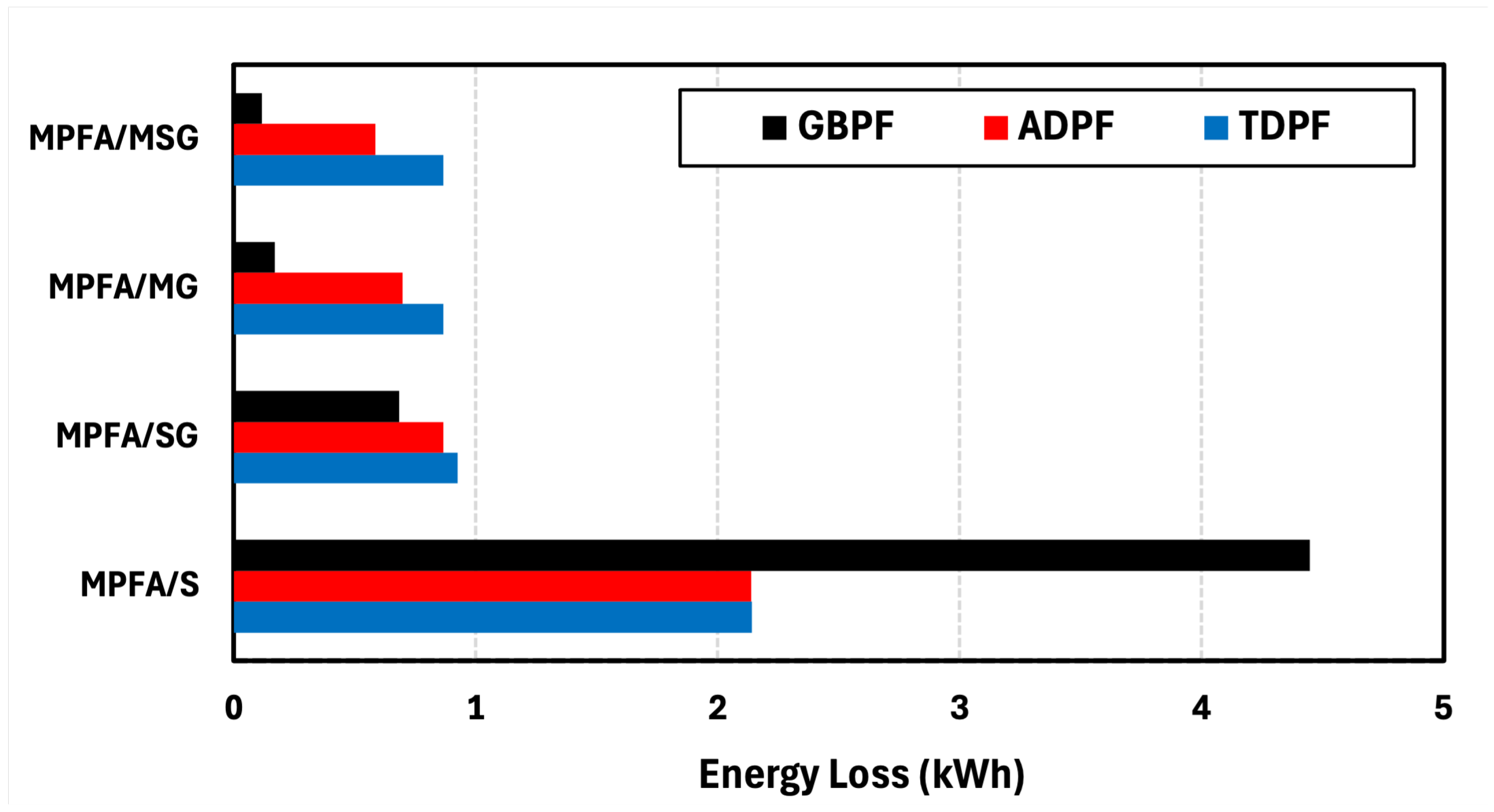
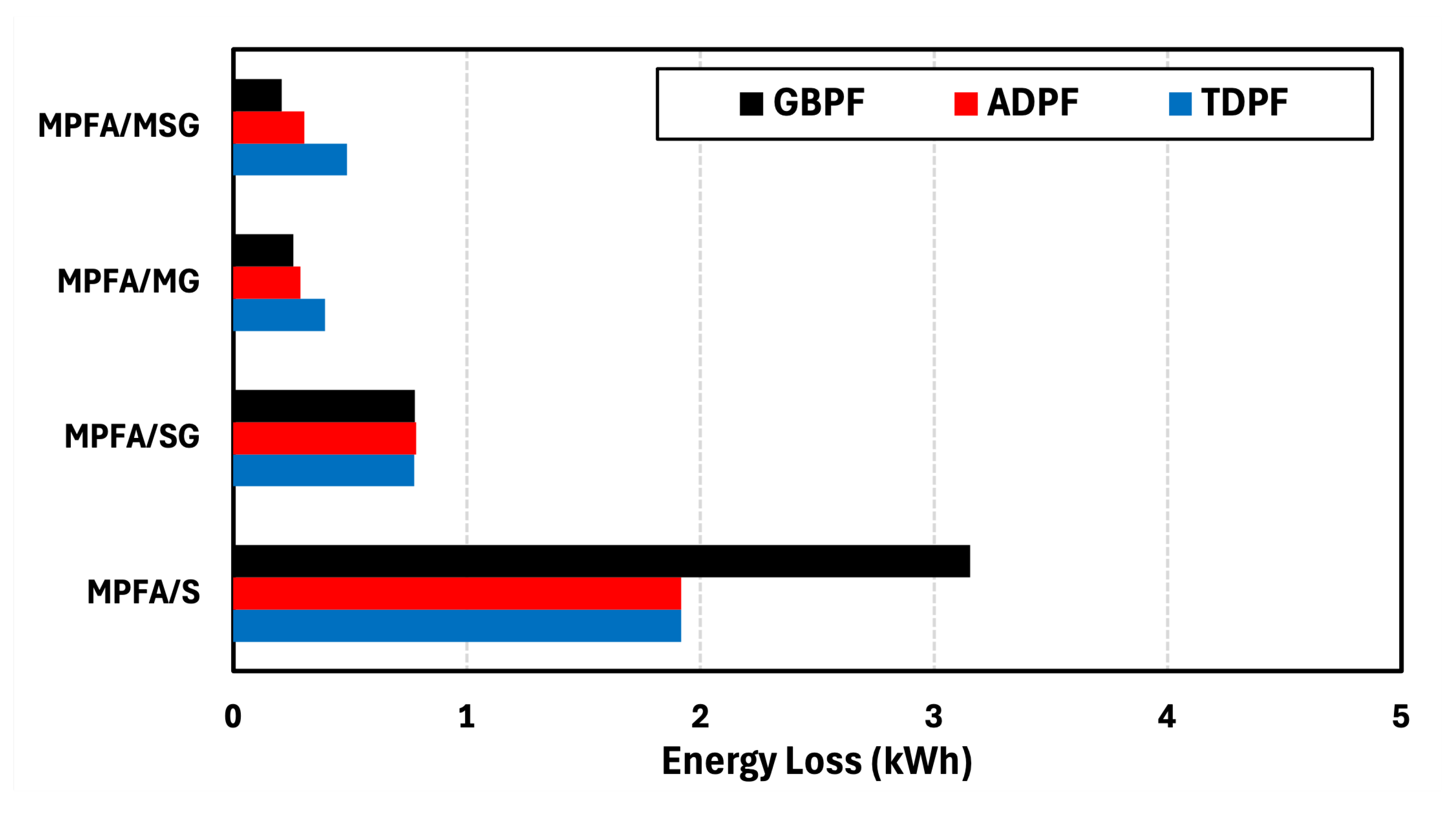
The comparative analysis in Figure 40 for the winter season shows that MPFA/SG achieves an energy loss reduction of 71.64% compared to MPFA/S, while MPFA/MG further reduces energy loss by 30.06% compared to MPFA/SG. The MPFA/MSG scenario provides an additional 9.61% reduction in energy loss compared to MPFA/MG. Regarding algorithm performance, in the MPFA/MSG scenario, the ADPF algorithm reduces energy loss by 32.47% compared to TDPF, whereas GBPF achieves a substantial 80.09% reduction in energy loss relative to ADPF. These results emphasize that energy loss is minimized as more generation and storage units are incorporated into the system. Moreover, GBPF consistently outperforms other algorithms in reducing energy losses due to its ability to supplement local power with the grid, leading to a more efficient energy distribution strategy.

Figure 40. Energy loss for DPFS in winter.

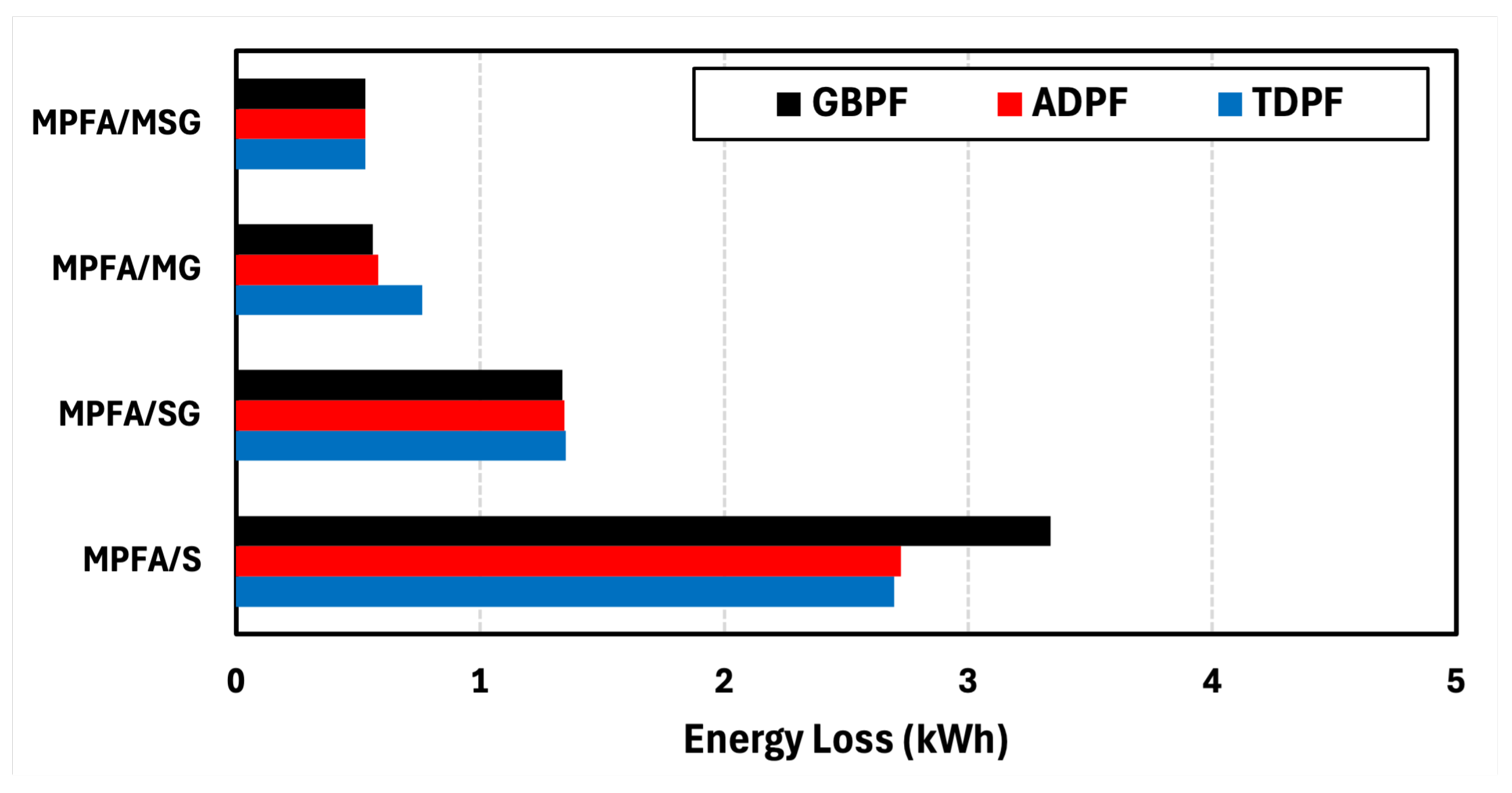
For the summer season (Figure 41), MPFA/SG achieves a 77.38% energy loss reduction compared to MPFA/S, while MPFA/MG further reduces energy losses by 31.34% relative to MPFA/SG. In the MPFA/MSG scenario, ADPF reduces energy losses by 48.94% compared to TDPF, while GBPF achieves a 51.06% energy loss reduction compared to ADPF.

Figure 41. Energy loss for DPFS in summer.

For the autumn season (Figure 42), MPFA/SG reduces energy losses by 66.60% compared to MPFA/S, and MPFA/MG achieves an additional 59.82% energy loss reduction relative to MPFA/SG. In MPFA/MSG, ADPF outperforms TDPF with a 68.20% energy loss reduction, while GBPF reduces energy losses by 31.80% compared to ADPF.

Figure 42. Energy loss for DPFS in autumn.

For the spring season (Figure 43), MPFA/SG achieves a 53.94% energy loss reduction compared to MPFA/S, while MPFA/MG reduces energy losses by 52.73% relative to MPFA/SG. Additionally, MPFA/MSG achieves a 16.49% energy loss reduction compared to MPFA/MG. In this scenario, all three algorithms exhibit similar energy losses due to power consumption being lower than the available RES power supply.

Figure 43. Energy loss for DPFS in spring.

5.4. Cross-Season Summary

Across seasons, enlarging MPFA connectivity (S → SG → MG → MSG) consistently lowers storage-related energy losses and raises demand satisfaction. GBPF guarantees full daily demand and the lowest storage-related losses in most cases due to reduced cycling. ADPF outperforms TDPF under constrained local supply by prioritizing critical loads and smoothing storage usage. To avoid redundancy, detailed hour-by-hour plots are retained in the figures, while aggregate comparisons (daily energy demanded/supplied, daily energy loss, storage throughput) are summarized here.

5.5. Statistical Validation (Supplement)

We computed daily aggregates over multiple representative days per season. Variability across days (mean ± std) for demand satisfaction, daily energy loss, and storage throughput is provided in [8]; no material changes to the rank ordering of methods were observed.

5.6. Overall Results

The comprehensive numerical simulations demonstrate that the proposed MPFA approach, in conjunction with advanced power flow algorithms, significantly enhances the operational efficiency and reliability of smart home distributed power flow systems.

Across all seasonal scenarios, integrating multiple power generation sources and storage units proved crucial in minimizing storage-related losses and ensuring consistent demand fulfillment. Notably, the GBPF algorithm consistently achieved complete daily demand satisfaction; with grid support, it often reduces battery cycling and hence storage-related losses, though total imported energy can increase when RES are scarce. The ADPF algorithm also exhibited strong performance—especially when grid support is limited—by dynamically prioritizing loads and optimizing storage utilization and allocation. Furthermore, the results highlight the importance of leveraging renewable energy resources, optimizing connectivity among appliances, and deploying intelligent control algorithms to ensure stable and efficient power delivery under varying seasonal and operational conditions. Overall, the study validates the effectiveness of the MPFA framework and provides valuable insights for the design of future smart home energy management systems that prioritize sustainability, resilience, and cost-effectiveness.

5.7. Limitations and Practical Considerations

Large-scale hardware-in-the-loop (HIL) verification and dynamic grid-event testing are pending. Battery and hydrogen-system degradation were modeled empirically; converter and thermal losses beyond ${\eta }_c,{\eta }_d$ are neglected. Cost modeling and scalability to larger feeder-level deployments are not included. Implementation-wise, GBPF requires reliable grid availability and metering; ADPF requires priority configuration and limited communications; both are compatible with edge controllers.

6. Conclusions and Future Work

This paper has presented a comprehensive investigation of power flow assignment scenarios and power flow algorithms within the DPFS for smart homes. Four distinct power-flow assignment scenarios—MPFA/S, MPFA/SG, MPFA/MG, and MPFA/MSG—were evaluated, each representing different logical interconnections between PGs, PLs, and PSs. The simulation framework incorporated real experimental data and accounted for seasonal variations to evaluate system performance under realistic and dynamic operating conditions. Simulation results consistently demonstrated that as the logical connectivity among generators, loads, and storage units is enhanced, particularly in the MPFA/MSG scenario, both power losses are minimized and demand satisfaction improves. Among the analyzed algorithms, the GBPF approach achieved the highest levels of demand fulfillment. It exhibited the lowest power losses across all scenarios and seasons, leveraging grid integration to ensure a reliable supply. The ADPF algorithm also provided significant improvements in power allocation efficiency and storage utilization, resulting in reduced user discomfort compared to the TDPF method, especially under supply-constrained conditions.

Overall, the findings highlight the importance of adopting multi-source, multi-storage power flow strategies and intelligent algorithmic control to optimize energy utilization, minimize losses, and enhance the reliability and resilience of smart home energy systems. The study offers a practical framework and actionable insights for future smart home energy management solutions, particularly as the share of RESs and distributed resources continues to rise. Future work includes: (i) optimization-based MPFA dispatch with explicit cost terms (tariffs, degradation), (ii) HIL validation under real grid events, (iii) stochastic PV/FC forecasts and uncertainty-aware scheduling, and (iv) scalability tests on multi-home feeders with communication delays and cyber-physical constraints.