A Cross-Scenario Generalizable Duty Cycle Aggregation Method for Electric Loaders with Scenario Verification

Abstract

With the rapid advancement of construction machinery electrification, optimizing the energy efficiency of electric loaders requires representative duty cycles that accurately capture real-world operating characteristics. However, most existing studies rely on simplified test-track cycles, which fail to reflect the complexity of actual operations. To address this gap, this paper takes a commercial concrete mixing plant as a case study and proposes a cross-scenario generalization method for the duty cycle aggregation of electric loaders. The method integrates multi-source signal acquisition, task-segment partitioning, feature extraction, and dimensionality reduction via Principal Component Analysis (PCA), enabling the clustering of typical operating modes and reconstruction of representative duty cycles through segment concatenation. The aggregated duty cycles are validated using Jensen–Shannon divergence, showing similarity levels above 93% compared with field measurements from mixing plants in Yiwu and Kunshan. These results demonstrate the method’s strong temporal adaptability and cross-scenario transferability. The proposed approach provides a solid foundation for energy consumption assessment, powertrain matching, and control strategy optimization of electric loaders while also supporting the development of duty cycle databases and future industry standardization.

1. Introduction

Electrification of construction machinery has emerged as an effective pathway for improving energy efficiency and reducing carbon emissions in the construction sector [1,2]. Among these machines, wheel loaders—widely used in infrastructure construction, mining, and material handling—have drawn increasing attention due to their high energy consumption and operating intensity [3]. Electric loaders, as sustainable alternatives to conventional diesel models, offer advantages such as zero tailpipe emissions, high energy efficiency, and lower operating costs, making them a key focus of both academia and industry [4,5,6]. However, to fully realize these advantages under diverse real-world conditions, it is essential to understand the operational characteristics and energy consumption patterns of loaders through representative duty cycles [7,8,9].

Existing challenges include limited battery energy density under heavy-load cycles and complex coupling between electric drive and electro-hydraulic systems, which lead to conversion losses and performance fluctuations [10,11,12]. Consequently, duty cycle aggregation research has become a key approach for analyzing large-scale operational data [13], extracting representative working patterns, and supporting powertrain design, energy evaluation, and control optimization [14,15,16].

In the automotive field, standardized driving cycles such as FTP-75, HWFET, NEDC, and WLTC have long been established to reflect different driving conditions, enabling consistent evaluation of vehicle energy performance [15,17,18,19,20,21,22,23,24]. With the growth of China’s new energy vehicle industry, methods such as clustering analysis, principal component analysis, and neural networks have been widely applied to real-world driving data for constructing representative cycles, leading to the establishment of the China Light-duty Vehicle Test Cycle (CLTC) that aligns with domestic conditions [25,26].

However, compared with the automotive field, research on duty cycles for construction machinery remains limited. Loaders exhibit strong task coupling between driving and hydraulic operations, and their operation varies widely due to material type, operator behavior, and environmental conditions. No standardized representative duty cycle currently exists for loaders, restricting energy efficiency studies and control optimization based on real-world data. Although the V-cycle pattern (Figure 1) is commonly adopted in research, it oversimplifies the complex combinations of actions in practical operations. This gap between test-based V-cycles and field operations underscores the necessity of developing data-driven duty cycle aggregation methods that capture both driving and working system dynamics.

Recent studies have started addressing this challenge using data-driven approaches. Wang et al. [27] proposed a radar chart-based evaluation method for duty cycle difficulty, using fuzzy C-means clustering on boom cylinder pressure signals to extract four key features: operation duration, time variation, maximum pressure, and pressure variation rate. These features were plotted on radar charts, and the difficulty level was quantified by the ratio of the enclosed feature area to the total area. Experimental results demonstrated that the method effectively reflected operational differences, although driver experience still had a considerable impact on the outcomes. Ren et al. [28] proposed a duty cycle construction method for electric loaders based on principal component analysis (PCA) and K-means clustering, which effectively captured operational characteristics, with simulation and field test results showing an energy consumption error of only 3.4%. Nevertheless, this method relied on simplified V-cycle tests conducted at proving grounds, limiting its ability to represent the complexity and diversity of real customer operations. Other works have applied time-domain segmentation and similarity analysis, yet they often neglect multi-dimensional coupling between driving and hydraulic systems, resulting in incomplete representation of operational behaviors.

Unlike automotive, where duty cycle studies primarily focus on the driving system, construction machinery involves more complex and diverse operating scenarios. Loader duty cycles include not only driving dynamics but also multiple variables of the working system, meaning that methodologies cannot be directly transferred from the automotive domain. Therefore, current research still faces several challenges: (1) insufficient consideration of multivariable coupling in duty cycle segmentation, which can result in physically inconsistent cycles; (2) lack of a complete workflow for extracting and aggregating typical duty cycles from real-world data; and (3) absence of systematic similarity validation methods for aggregated duty cycles. These gaps highlight the necessity of developing dedicated duty cycle modeling and aggregation methods tailored to electric loaders, combining both driving and working features to better support endurance evaluation and energy optimization.

Among the many operating environments of loaders, commercial concrete mixing plants represent a particularly important scenario. In this setting, loaders are primarily responsible for handling and transporting medium-density materials such as sand, cement, and aggregates. Their operation typically follows a “loading–driving–feeding–return” cycle [29]. Compared with mining or port operations, mixing plant duty cycles are characterized by fixed operating paths, strong cyclic regularity, clearly defined loading requirements, stable work rhythm, and distinct energy consumption patterns [30]. These attributes make concrete mixing plants not only typical high-utilization environments for loaders, but also ideal testbeds for duty cycle modeling and aggregation studies of electric loaders.

The overall research framework of this study is illustrated in Figure 2. In the figure, “F” denotes False and “T” denotes True. Using the commercial concrete mixing plant as a case study, this paper proposes a cross-scenario generalization method for duty cycle aggregation of electric loaders. The approach integrates multi-source signal acquisition, task-segment partitioning, feature extraction, and dimensionality reduction, followed by clustering of operating modes and representative segment selection. Typical duty cycles are then generated through segment concatenation and validated for accuracy. The Jensen–Shannon divergence is employed to quantitatively evaluate the aggregated duty cycles from two perspectives: temporal adaptability and cross-scenario transferability.

The remainder of this paper is organized as follows. Section 2 describes the data acquisition platform, signal sources, and sampling strategy. Section 3 introduces the data preprocessing workflow, including task segmentation, feature extraction, dimensionality reduction, and clustering, as well as the construction of typical duty cycles. Section 4 validates the aggregated duty cycles against field measurements using the Jensen–Shannon divergence, focusing on both temporal adaptability and cross-scenario transferability. Section 5 summarizes the findings and outlines directions for future research.

2. Data Acquisition Scheme

To construct representative duty cycles for electric loaders, real-world operational data were obtained from customer sites through the enterprise’s cloud-based backend platform. This platform enables real-time monitoring and remote storage of machine operating states, ensuring continuous recording of key signals under diverse duty cycles.

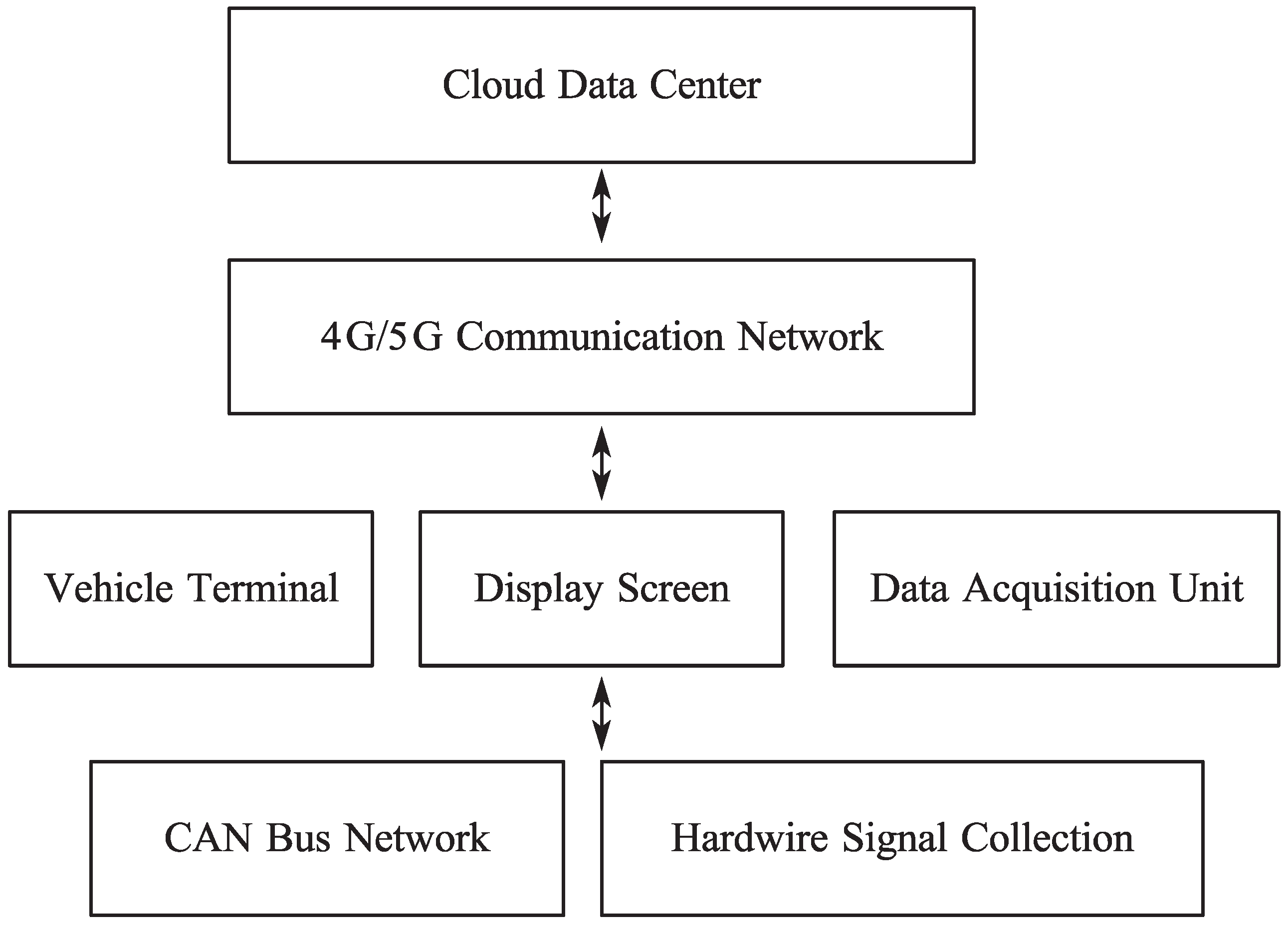
The data acquisition system adopts a distributed architecture, establishing a stable communication link between the onboard terminal and the cloud server. As illustrated in Figure 3, the cloud data platform consists of three core components:

(1)

Onboard Data Acquisition Unit—responsible for real-time collection of operational parameters across loader subsystems. It integrates CAN bus interfaces with hard-wired I/O modules, enabling synchronized acquisition of multi-source signals.

(2)

Data Transmission Module—transmits collected data to the cloud via 4G/5G networks, supporting disconnection-resume mechanisms and data compression.

(3)

Cloud Storage and Processing Center—performs large-scale data classification, storage, preprocessing, and analysis, and provides query, statistical, and visualization services.

To meet the temporal resolution required for duty cycle feature extraction, the upload interval of display-screen data was shortened to 500 ms. The sampling duration covered more than one full-day operational cycle, forming the raw time-series dataset:

$$\mathcal{D}=\{X_i{\}}_{i=1}^N,X_i\in R^{T\times D}$$

(1)

where $T$ denotes the number of time steps, $D$ the dimensionality of signals, and $N$ the number of samples.

The acquired data primarily originated from signals uploaded by the vehicle display unit to the cloud platform, including CAN bus messages and hard-wired signals (

Table 1. Acquired signals.

Signal Type	Source	Acquired Parameters
CAN bus	Traction motor controller	Speed, torque, temperature
	Pump motor controller	Speed, load rate, efficiency
	DC/DC converter	Input/output voltage & current
	PDU	Power distribution status
	BMS	Voltage, current, SOC, temperature
	HVAC system	Temperature, pressure state
	TCU	Gear, oil temperature, pressure
	VCU	Vehicle control information
	Display unit	HMI information
Hard-wired	Radiator fan	Operating state, speed
	Solenoids	Actuation state
	Temperature sensors	Component temperatures
	Pilot pressure	Hydraulic pilot pressure
	Main valve pressure	Main hydraulic valve pressure
	Steering pressure	Steering system pressure
	Brake pressure	Brake system pressure

).

CAN bus signals were collected from the vehicle’s communication network, covering working parameters of electronic control units such as the traction motor controller, pump motor controller, DC/DC converter, PDU (Power Distribution Unit), HVAC system, BMS (Battery Management System), TCU (Transmission Control Unit), VCU (Vehicle Control Unit), and display unit. As message transmission cycles varied across nodes, synchronization of time stamps was required during preprocessing.

Hard-wired signals included direct sensor and actuator inputs/outputs, such as radiator fan states, solenoid actuation, indicator switch signals, and measurements from temperature and pressure sensors. Pressure sensors covered key measurement points, including pilot pressure, main valve pressure, steering pressure, and brake pressure, with a signal range of 0.5–4.5 V (corresponding to 0–350 bar).

The joint acquisition of these multi-source signals provided a comprehensive representation of the loader’s powertrain, electrical, and hydraulic systems during customer operations.

To capture representative duty cycles, two typical mixing plants were selected as data collection sites. At each plant, two electric loaders were deployed for continuous monitoring—six days at the Yiwu plant and seven days at the Kunshan plant—resulting in approximately 624 h of real-world operational data. The dataset covered multiple typical operating conditions, including medium- and high-intensity continuous cycles, as summarized in

Table 2. Summary of data collection.

Data Source	Duration
Yiwu mixing plant	2 loaders × 6 days
Kunshan plant	2 loaders × 7 days

.

3. Construction of Typical Operating Conditions

Since the raw data were collected directly from customer sites, their completeness and consistency were affected by sensor accuracy, communication latency, and environmental interference. As a result, outliers, missing values, and noise interference were present. To ensure the accuracy of subsequent feature extraction and operating condition modeling, the raw data were preprocessed, mainly including the following steps:

3.1. Data Preprocessing

The raw data were collected from manufacturer-calibrated sensors. Post-processing included outlier removal, interpolation, and noise filtering to enhance reliability. After preprocessing, the estimated measurement errors for key sensors, such as motor torque, hydraulic pressure, and speed sensors, were within ±2%, while the relative errors of the extracted features after filtering were maintained below 5%, ensuring that the processed signals accurately represent operational trends.

A physical constraint check was applied to all signals to eliminate values outside the normal operating range. For example, the hydraulic pressure sensor measurement range is 0–350 bar; any values outside this range were identified as abnormal and discarded. In addition, abrupt and unrealistic instantaneous jumps (e.g., motor speed suddenly dropping to negative values) were removed using a gradient-threshold detection method:

$${\left|{\displaystyle \frac{dx}{dt}}\right|}_{t=t_i}>\gamma ·\mathrm{s}\mathrm{t}\mathrm{d}\left({\displaystyle \frac{dx}{dt}}\right)$$

(2)

where $x$ represents the signal variable, $t_i$ is the time point, γ is the mutation detection coefficient (typically 3–5), and std(·) is the standard deviation function.

3.1.1. Missing Value Completion

Data losses caused by communication interruptions or sensor jitter were completed using linear interpolation between adjacent valid points, thereby maintaining time-series continuity and trend consistency and avoiding curve discontinuities:

$$x_{\mathrm{m}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}}(t)=x\left(t_1\right)+{\displaystyle \frac{x\left(t_2\right)-x\left(t_1\right)}{t_2-t_1}}\cdot \left(t-t_1\right)$$

(3)

where $t$ is the missing point, and $\left(t_1,x\left(t_1\right)\right)$, $\left(t_2,x\left(t_2\right)\right)$ are valid data points before and after the missing sample.

3.1.2. Noise Filtering

For signals subject to high-frequency fluctuations, a moving average filter was applied to suppress random noise, enhancing signal smoothness and reliability while preserving overall trends. For signals sensitive to abrupt changes, a weighted moving average filter was used:

$$\widehat{x}(t)={\sum }_{k=-M}^M{w}_k\cdot x(t+k)$$

(4)

where $\widehat{x}(t)$ is the filtered signal, $M$ is the half-window width (typically 3–5), and ${\omega }_k$ are weights, chosen according to a Gaussian or uniform distribution.

3.1.3. Data Alignment and Unification

Since different CAN messages and hardwired signals had inconsistent sampling periods, synchronization across data sources was necessary. A unified sampling interval of 500 ms was adopted, and timestamp alignment with interpolation-based resampling was performed to synchronize all variables in the same time series. This ensured consistency for operating condition curve construction and simulation input.

Table 3. Comparison of Data Volume Before and After Preprocessing (Batching Plant Scenario).

Processing Stage	Data Volume	Change	Retention Rate
Raw data	485,250	–	100%
After outlier removal	471,320	−13,930	97.1%
After missing value fill	473,180	+1860	97.5%
After noise filtering	472,950	−230	97.5%
After time alignment	468,975	−3975	96.6%
Final dataset	468,975	−16,275	96.6%

compares the data volume before and after preprocessing for a concrete batching plant scenario.

3.2. Work Segment Partitioning and Feature Extraction

The overall process of constructing typical operating condition curves is illustrated in Figure 4. This section details each step and the corresponding validation results, using the batching plant scenario as an example.

3.2.1. Work Segment Partitioning

Since loader system variables are strongly coupled (e.g., engine/motor, hydraulics, and drivetrain interactions), unreasonable segmentation may lead to concatenation results that violate physical laws. In this study, engine or motor idle and shutdown states were used as segmentation points for work cycles:

(1)

Idle condition: engine speed or motor speed ≤ 110% of rated idle speed, with output torque < idle torque threshold.

(2)

Shutdown condition: shutdown signal = True followed by data interruption, or engine/motor speed = 0 with torque = 0, while hydraulic signals remain constant at default values.

(3)

Definition: the data between two consecutive idle or shutdown states is defined as a complete work segment.

This segmentation ensures that concatenated segments do not exhibit unrealistic signal jumps or physically inconsistent variable coupling.

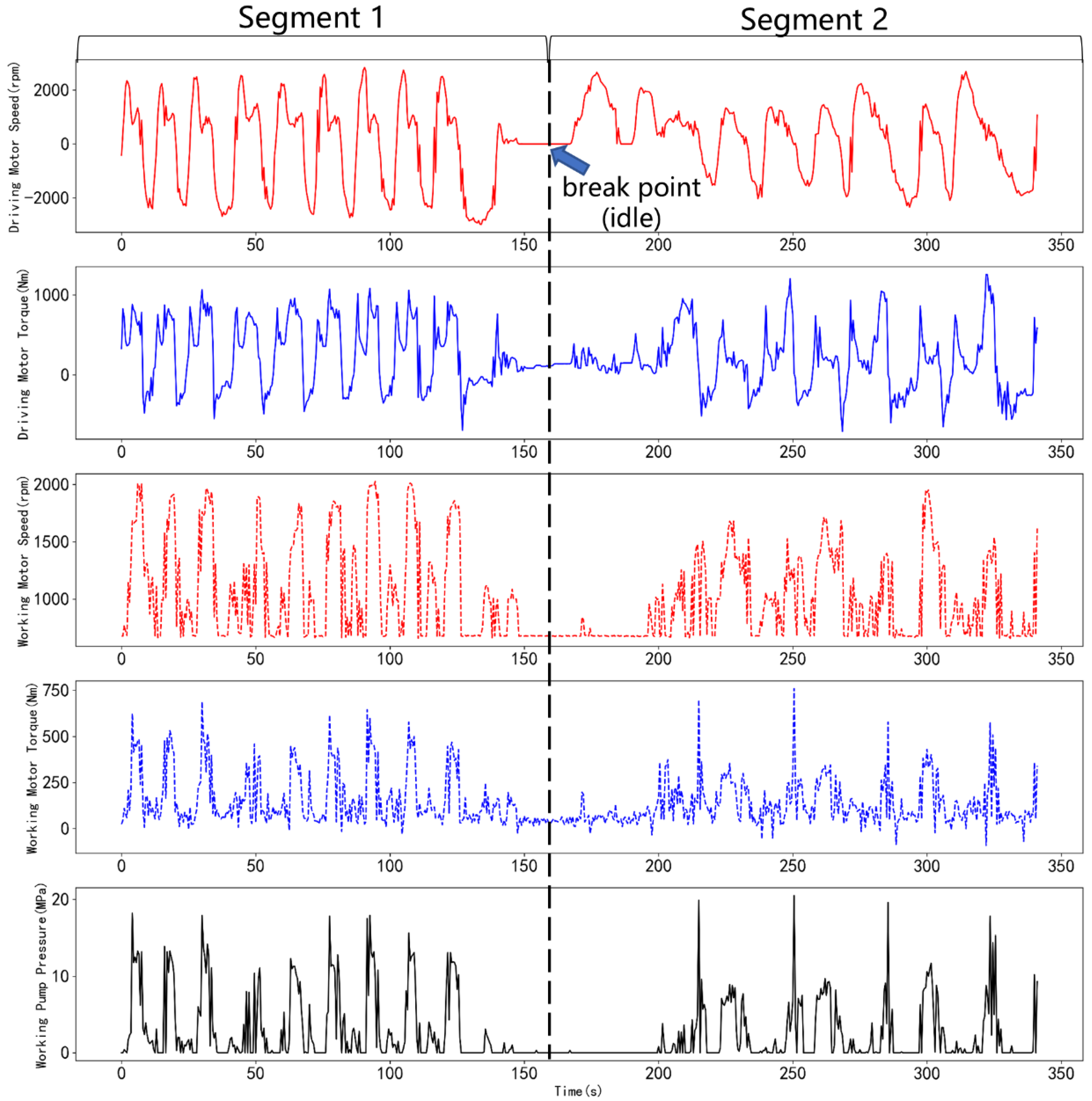
Figure 5 shows a case study where work segments were divided using idle state points, demonstrating the effectiveness of this logic. The dashed line indicates the division between two work segments, with the break point (idle) marked at the transition.

3.2.2. Segment Feature Calculation

Typical operating condition curves are composed of representative work segments. Representative segments were identified by computing characteristic parameters as evaluation criteria. Based on the multi-dimensional feature space theory, a mapping was established:

$$\mathit{\varphi }:\mathcal{X}\to {\mathbb{R}}^{15},\mathbf{s}\mapsto \mathbf{f}={\left[f_1,f_2,...,f_{15}\right]}^T$$

(5)

where $\mathcal{X}$ denotes the work segment data space, $\mathbf{s}$ is a single segment, and $\mathbf{f}$ is a 15-dimensional feature vector. These features capture the operating characteristics and workload intensity of each segment. The selected feature categories and their engineering significance are summarized in

Table 4. List of segment features.

Category	Feature Parameter	Expression	Engineering Significance
Time Features	1. Segment duration	$f_1=∆t_{\mathrm{s}\mathrm{e}\mathrm{g}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}$	Work cycle integrity
	2. Effective work ratio	$f_2={\displaystyle \frac{t_{\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}\mathrm{i}\mathrm{n}\mathrm{g}}}{t_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}$	Equipment utilization
	3. Idle ratio	$f_3={\displaystyle \frac{t_{\mathrm{i}\mathrm{d}\mathrm{l}\mathrm{e}}}{t_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}$	Energy-saving potential
Motion Features	4. Max vehicle speed	$f_4=\mathrm{m}\mathrm{a}\mathrm{x}\left(v\right(t\left)\right)$	Transfer efficiency
	5. Mean acceleration	$f_5={\displaystyle \frac{1}{N}}{\displaystyle \sum _{t=1}^N\parallel a\left(t\right)}\parallel$	Work rhythm intensity
	6. Accel/decel frequency	$f_6={\displaystyle \sum _{t=1}^{N-1}\mathbb{I}(}\parallel a\left(t+1\right)-a\left(t\right)\parallel >\left.a_{th}\right)$	Complexity index
Load Features	7. Mean torque	$f_7={\displaystyle \frac{1}{N}}{\displaystyle \sum _{t=1}^N\tau \left(t\right)}$	Powertrain load level
	8. Hydraulic pressure peak	$f_8=\mathrm{m}\mathrm{a}\mathrm{x}\left(P_{hyd}\left(t\right)\right)$	Hydraulic system limit
	9. Torque standard deviation	$f_9=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{t=1}^N\left(\tau \right(t)}-\overline{\tau }{)}^2}$	Load fluctuation
Work Device Features	10. Boom cycle frequency	$f_{10}={\displaystyle \frac{\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(\mathrm{b}\mathrm{o}\mathrm{o}\mathrm{m}\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{s}\right)}{∆t}}$	Shoveling intensity
	11. Bucket swing range	$f_{11}=\mathrm{m}\mathrm{a}\mathrm{x}\left({\theta }_{\mathrm{b}\mathrm{u}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left({\theta }_{\mathrm{b}\mathrm{u}\mathrm{c}\mathrm{k}\mathrm{e}\mathrm{t}}\right)$	Material control
	12. Work device cycle period	$f_{12}={\displaystyle \frac{∆t}{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}}}$	Standardization index
Energy Efficiency	13. Specific energy consumption	$f_{13}={\displaystyle \frac{\int P\left(t\right)dt}{∆t}}$	Core economic metric
	14. Hydraulic power ratio	$f_{14}={\displaystyle \frac{P_{\mathrm{h}\mathrm{y}\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{u}\mathrm{l}\mathrm{i}\mathrm{c}}}{P_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}$	Energy distribution efficiency
	15. Regen braking ratio	$f_{15}={\displaystyle \frac{E_{\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}\mathrm{n}}}{E_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}$	Key metric for NE loaders

where $N$ is the number of samples, $v\left(t\right)$ is vehicle speed, $a\left(t\right)$ acceleration, $\tau \left(t\right)$ torque, $P_{\mathrm{h}\mathrm{y}\mathrm{d}}$ hydraulic pressure, $I\left(\right)$ indicator function, $a_{\mathrm{t}\mathrm{h}}$ acceleration threshold, and $\overline{\tau }$ mean torque.

.

3.2.3. Feature Dimensionality Reduction and Principal Component Analysis (PCA)

Two major issues must be addressed during raw loader data processing:

(1)

Normalization

Due to unit differences across parameters (e.g., rpm, MPa, mm), min–max normalization was applied:

$$X_{norm}={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}$$

(6)

where $X$ is the raw feature, and $X_{min}$, $X_{max}$ are the min and max values. This mapped all features into the [0, 1] range, eliminating unit bias.

(2)

Feature Space Compression

Directly computing with 15-dimensional features may cause the “curse of dimensionality,” manifesting as exponential growth in computational complexity and model instability due to multicollinearity. Therefore, PCA was applied to reduce dimensionality. Based on eigenvalue decomposition of the covariance matrix:

$$\mathbf{C}={\displaystyle \frac{1}{n-1}}{\mathbf{Z}}^T\mathbf{Z}$$

(7)

where $\mathbf{Z}$ is the standardized feature matrix and n the sample size. Eigenvalue decomposition yields $\mathbf{C}=\mathbf{V}\mathsf{\Lambda }{\mathbf{V}}^T$, with $\mathsf{\Lambda }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({\lambda }_1,{\lambda }_2,...,{\lambda }_{15}\right),{\lambda }_1\ge {\lambda }_2\ge \dots \ge {\lambda }_{15}$, and $\mathbf{V}$ the eigenvector matrix.

The contribution ratio of the $k$-th principal component is:

$${\eta }_k={\displaystyle \frac{{\lambda }_k}{\sum _{i=1}^{15}{\lambda }_i}}$$

(8)

As shown in

Table 5. Principal Component Contribution Ratios.

Principal Component	Contribution	Cumulative Contribution
PC1	49.1%	49.1%
PC2	17.5%	66.6%
PC3	15.5%	82.1%
PC4	9.9%	92.0%
Cumulative		92.0%

, the first four principal components account for 92.0% of the total variance (>85% threshold), successfully reducing the feature space from ${\mathrm{R}}^{15}\mathrm{t}\mathrm{o}{\mathrm{R}}^4$. This provides a lightweight dataset for clustering while retaining 92.0% of the original information.

3.3. Feature-Based Duty Cycle Clustering and Concatenation

3.3.1. Segment Clustering

The reduced-dimensional feature vectors of work segments were classified using clustering algorithms such as K-Means and DBSCAN. For the K-Means algorithm, the objective function is to minimize the sum of squared errors within clusters:

$$J={\sum }_{j=1}^K{\sum }_{i\in C_j}{‖{\mathbf{s}}_i-{\mathit{\mu }}_j‖}^2$$

(9)

where $K$ denotes the number of clusters, $C_j$ represents the $j$-th cluster, ${\mathbf{s}}_i$ is the feature vector of a segment, and ${\mathit{\mu }}_j$ is the centroid of cluster $j$.

To ensure transparent K-value determination and improve reproducibility, an Elbow curve has been added (see Figure 6). The Elbow curve illustrates the within-cluster sum of squares (WCSS) against different K values, and the inflection point indicates where additional clusters bring diminishing returns.

The number of clusters was determined using the elbow method or silhouette coefficient. Each cluster corresponds to a representative operating mode within the target scenario (e.g., short-distance heavy-load loading, long-distance transportation). The clustering results reflect the dominant operational behaviors across different customers and sites.

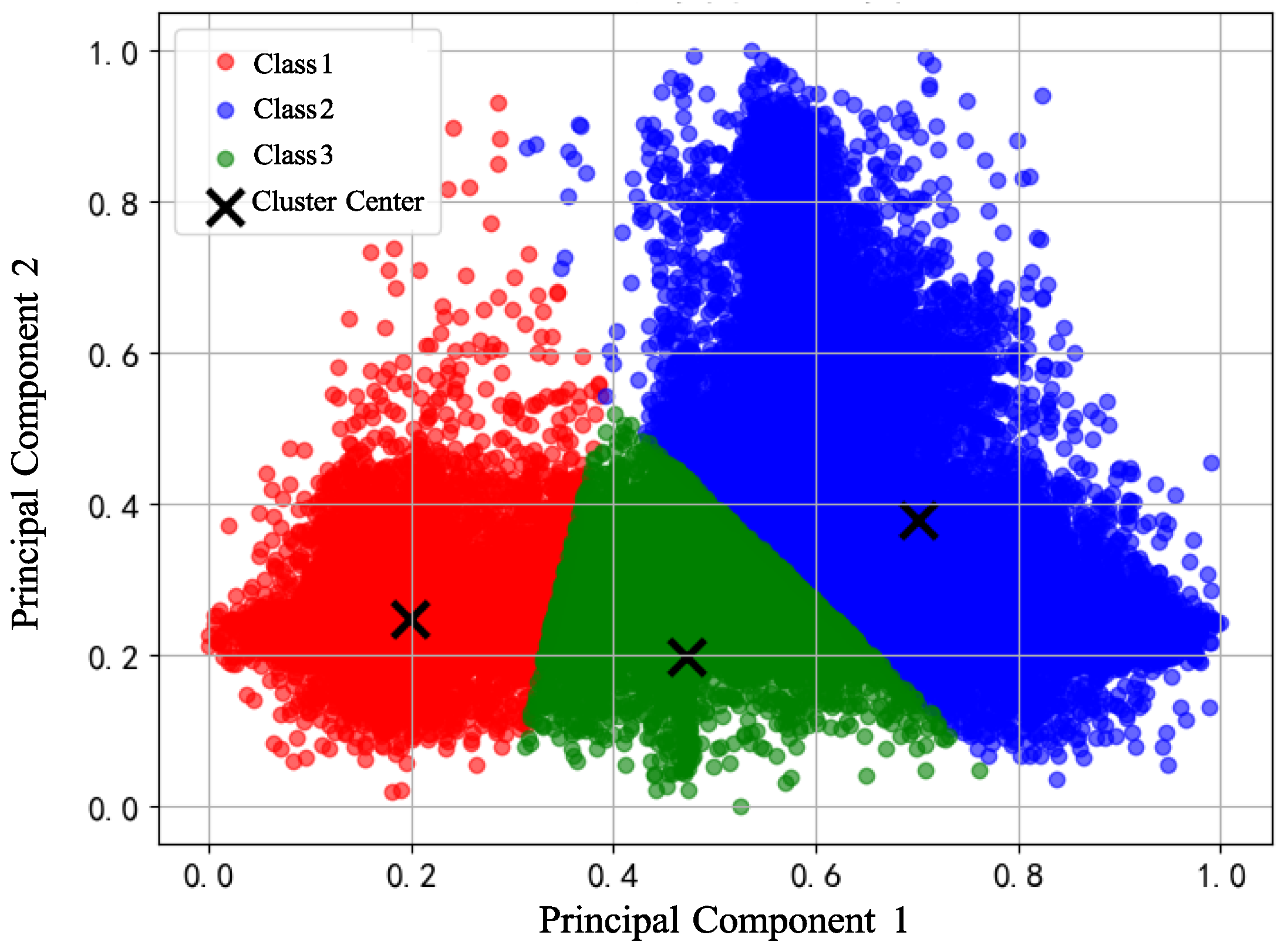
In the case of the concrete batching plant scenario, all kinematic segments were grouped into three clusters. The clustering results are shown in Figure 7, where the x- and y-axes correspond to the first two principal components.

3.3.2. Segment Concatenation

From each cluster, the segment closest to the cluster centroid was selected as the representative segment:

$${\mathbf{s}}_j^{\mathrm{*}}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{{\mathbf{s}}_i\in C_j}{\mathrm{m}\mathrm{i}\mathrm{n}}‖{\mathbf{s}}_i-{\mathit{\mu }}_j‖$$

(10)

where ${\mathbf{s}}_j^{\mathrm{*}}$ denotes the representative segment. The concatenated duty cycle must satisfy physical continuity:

$$\underset{t\to t_c^{-}}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathbf{x}(t)=\underset{t\to t_c^{+}}{\mathrm{l}\mathrm{i}\mathrm{m}}\mathbf{x}(t)$$

(11)

$${\left.{\displaystyle \frac{d\mathbf{x}}{dt}}\right|}_{t=t_c^{+}}-{\left.{\displaystyle \frac{d\mathbf{x}}{dt}}\right|}_{t=t_c^{-}}\le {\mathit{\delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(12)

where $t_c$ is the concatenation time and ${\mathit{\delta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum allowable gradient discontinuity. Representative segments from each cluster were concatenated sequentially according to the actual operational order, resulting in a candidate typical duty cycle curve.

To enhance clarity and reproducibility, the iterative concatenation process has been explicitly defined. The algorithm iteratively merges adjacent segments with similar feature vectors, with a maximum of 50 iterations to prevent excessive computation. Convergence is determined when the relative change in the average segment feature deviation falls below $\epsilon =15\mathrm{\%}$, ensuring computational efficiency and physical continuity. These parameters were determined empirically through repeated experiments to balance accuracy and stability.

3.3.3. Accuracy Validation and Iterative Optimization

The accuracy of the concatenated duty cycle curve was validated by comparing its characteristic features (same set as defined in feature extraction) with those of the overall dataset. The relative error was computed as:

$$\mathsf{\epsilon }={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{F_i^{\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}}-F_i^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{F_i^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}\right|$$

(13)

where $F_i^{\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}}$ and $F_i^{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ denote the i-th feature of the concatenated curve and the overall dataset, respectively, and n is the number of features. If the mean error ε ≤ the predefined threshold (typically 15%), the curve is considered representative and finalized as the typical duty cycle.

If $\epsilon$ > 15%, an iterative optimization process is triggered:

-

Replace or add segments by selecting the second-closest, third-closest, etc., segments from each cluster.

-

Recalculate the error until the threshold is met or the maximum iteration count is reached.

3.4. Typical Duty Cycle Construction for Batching Plant Scenario

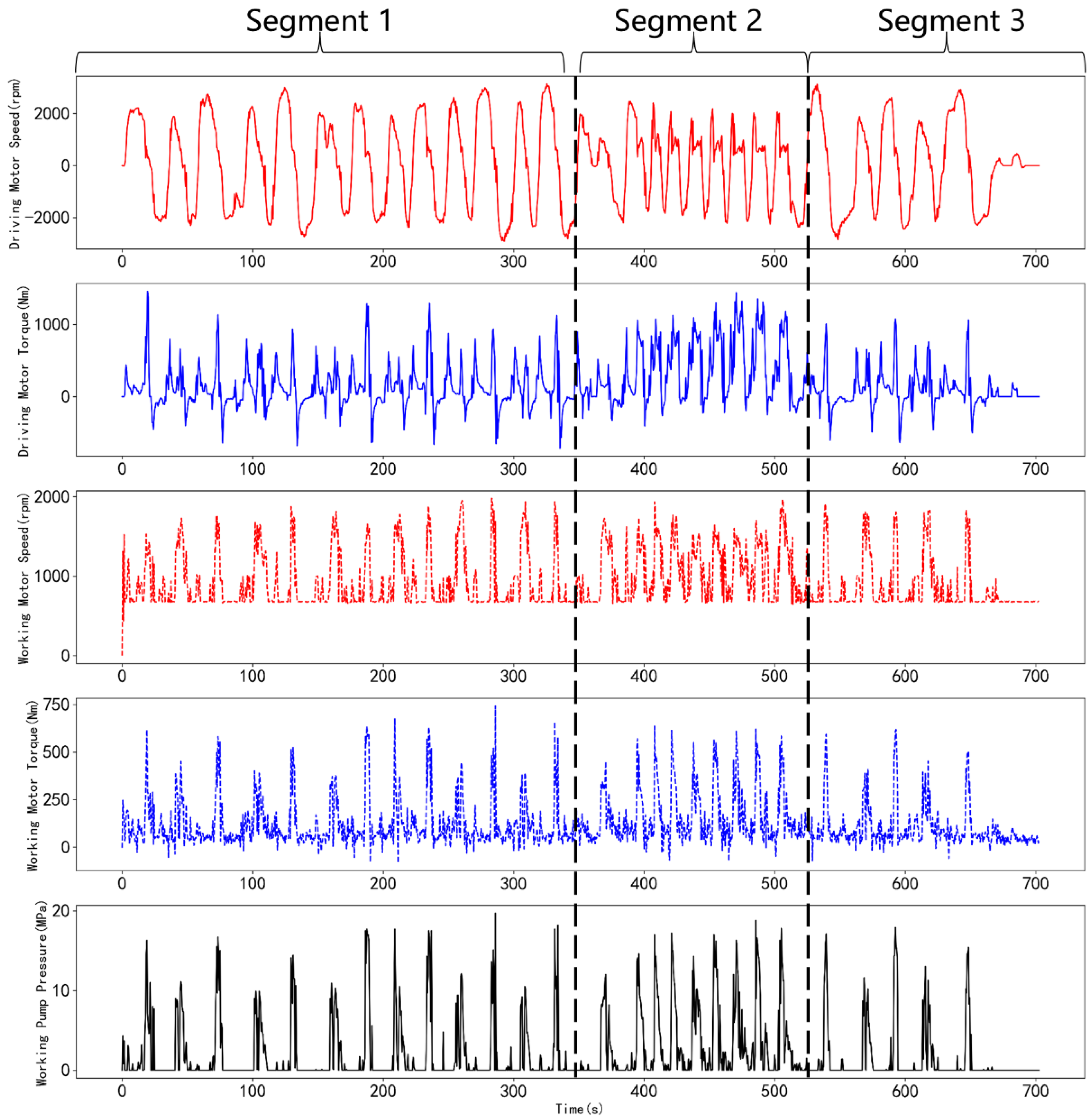
Through segment stitching, accuracy validation, and iterative optimization, the final representative operating condition curve of an electric wheel loader working in a concrete batching plant was obtained, as shown in Figure 8, the dashed line indicates the division between two work segments, with the break point (idle) marked at the transition. Five primary variables are illustrated, including travel motor speed, travel motor torque, working motor speed, working motor torque, and hydraulic system pressure. The complete profile additionally incorporates boom pilot pressure, bucket pilot pressure, throttle opening, brake opening, and gear position, thereby providing a comprehensive characterization of loader operations in this scenario.

Furthermore, clustering analysis of the field data revealed that the representative operating condition is composed of three characteristic operating segments. To gain deeper insights into the working features of each segment, and based on typical loader operation modes in batching plant environments, the entire cycle was decomposed into five canonical action states: idling, digging, working only (e.g., lifting or dumping without travel), traveling only, and combined travel–working operations. This classification not only reflects the energy consumption characteristics of the equipment but also provides an action-level basis for simulation modeling and subsequent control strategy optimization.

To further reveal the compositional differences among segments, the three extracted operating segments were decomposed into the five states above, and the corresponding time proportions were calculated, as shown in

Table 6. Time proportions of action states across three operating segments.

Action State	Segment 1	Segment 2	Segment 3
Idling	0.57	2.29	13.76
Digging	5.57	20.86	4.21
Working only	2.86	1.43	0.28
Traveling only	55.71	28.86	55.06
Combined travel + working	35.29	46.57	26.69

. Distinct differences in action distribution can be observed, highlighting the diversity and temporal variability of loader duty cycles in batching plant operations.

Specifically, in Segment 1, traveling only accounts for the largest share (55.71%), followed by combined travel–working (35.29%). This suggests that the segment primarily represents high-frequency short-distance transport with relatively fewer loading actions, likely corresponding to a stage of efficient operation with sufficient and continuous material supply. Meanwhile, the low shares of idling and working only indicate limited downtime and fewer pure working operations.

In contrast, Segment 2 shows a markedly higher share of digging (20.86%) and the highest level of combined travel–working among the three (46.57%). This reflects intensive operations involving frequent actions such as “digging while traveling” or “lifting while traveling,” possibly due to feed inlet congestion or active excavation from stockpiles.

Notably, Segment 3 exhibits the highest idling proportion (13.76%), far exceeding the other segments. Together with relatively low proportions of digging and working only, this indicates extended waiting or idle states, likely constrained by mixer processing capacity or material scheduling delays. Nevertheless, traveling only still remains dominant (55.06%), suggesting that vehicle movement continues to occupy a major share even during lower-efficiency operation.

In summary, the comparative analysis of three operating segments reveals that batching plant operations are not a single steady-state process but a dynamic alternation of multiple operating modes. This finding provides essential data support and theoretical grounding for constructing more representative evaluation conditions, optimizing energy management strategies, and enhancing overall operational efficiency.

4. Duty Cycle Validation at the Concrete Mixing Plant

4.1. Vehicle Parameters and Site Conditions

The subject of this study is a 5-ton class battery-electric wheel loader. Its main technical specifications are summarized in

Table 7. Main technical specifications of the electric wheel loader.

Parameter	Value	Unit
Overall dimensions	8760 × 3096 × 3540	mm
Travel motor power	Rated 120 (Peak 240)	kW
Travel motor torque	Rated 1000 (Peak 2400)	N·m
Travel motor speed	Rated 1146 (Peak 3500)	rpm
Working motor power	Rated 80 (Peak 160)	kW
Working motor torque	Rated 400 (Peak 800)	N·m
Working motor speed	Rated 1910 (Peak 3000)	rpm
Gearbox ratio	1st: 2.895, 2nd: 1	–
Battery capacity	282/350/359/423	kWh
Total mass	19,000	kg
Rated load	5800	kg
Rated power	200	kW
Bucket capacity	2.7–5	m3
Maximum bucket breakout force	185	kN
Maximum traction force	180	kN
Maximum lifting force	80	kN
Vehicle speed	F1: 0–15, F2: 0–40	km/h
Three-item cycle time	9.7	s
Hydraulic system pressure	19.5	MPa

. The machine adopts a dual-motor drive architecture, with the travel motor and working motor separately responsible for propulsion and implement power. Depending on configuration, the battery capacity ranges from 282 to 423 kWh, sufficient to sustain continuous operation under typical duty cycles. The machine has a total mass of 19 t, a rated load of 5.8 t, a bucket capacity of 2.7–5 m³, a maximum breakout force of 185 kN, and a maximum traction force of 180 kN, demonstrating strong productivity and site adaptability.

Field investigations (Figure 9) reveal that loader duty cycles in concrete mixing plants are highly repetitive and structured. The machine primarily shuttles between aggregate piles and the plant’s charging hopper, with loading cycles recurring every few minutes and totaling several hundred per day. The cycle typically involves repeated short-distance acceleration, low-speed travel, and reversing, coupled with frequent digging, lifting, and dumping operations. Although travel speeds are generally low, the loading and lifting phases impose high loads, keeping the hydraulic system under high-pressure, high-frequency operation for extended periods. Operator differences in accelerator pedal input, lift height control, and cycle rhythm lead to variations in energy consumption.

4.2. Quantitative Validation and Error Analysis

To evaluate the universality and robustness of the constructed typical duty cycle, the concept of cross-scenario generalization is introduced. This concept describes the ability of the aggregated operating profile to maintain representativeness and similarity when applied to data from different temporal or spatial domains.

To validate the representativeness of the constructed typical duty cycle, this study employs Jensen–Shannon ($JS$) divergence to quantify the similarity between the aggregated duty cycle and measured data distributions. $JS$ divergence is a symmetric and bounded metric that effectively characterizes the overlap between two probability distributions. It is defined as:

$$JS(P\parallel Q)={\displaystyle \frac{1}{2}}KL(P\parallel M)+{\displaystyle \frac{1}{2}}KL(Q\parallel M),M={\displaystyle \frac{1}{2}}(P+Q)$$

(14)

where $P$ and Qdenote the two distributions under comparison, $M$ is their mean distribution, and $KL\left(\right)$ represents the Kullback–Leibler divergence:

$$KL(P\parallel Q)={\sum }_{i}P(i)\mathrm{l}\mathrm{o}\mathrm{g}{\displaystyle \frac{P\left(i\right)}{Q\left(i\right)}}$$

(15)

A smaller $KL$ divergence indicates closer similarity, but since $KL$ is asymmetric and unbounded [0, +∞), $JS$ divergence is preferred for practical analysis, with values constrained to [0, log2], In this study, similarity is defined as:

$$\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{y}=1-JS(P\parallel Q)$$

(16)

A value closer to 1 indicates higher similarity.

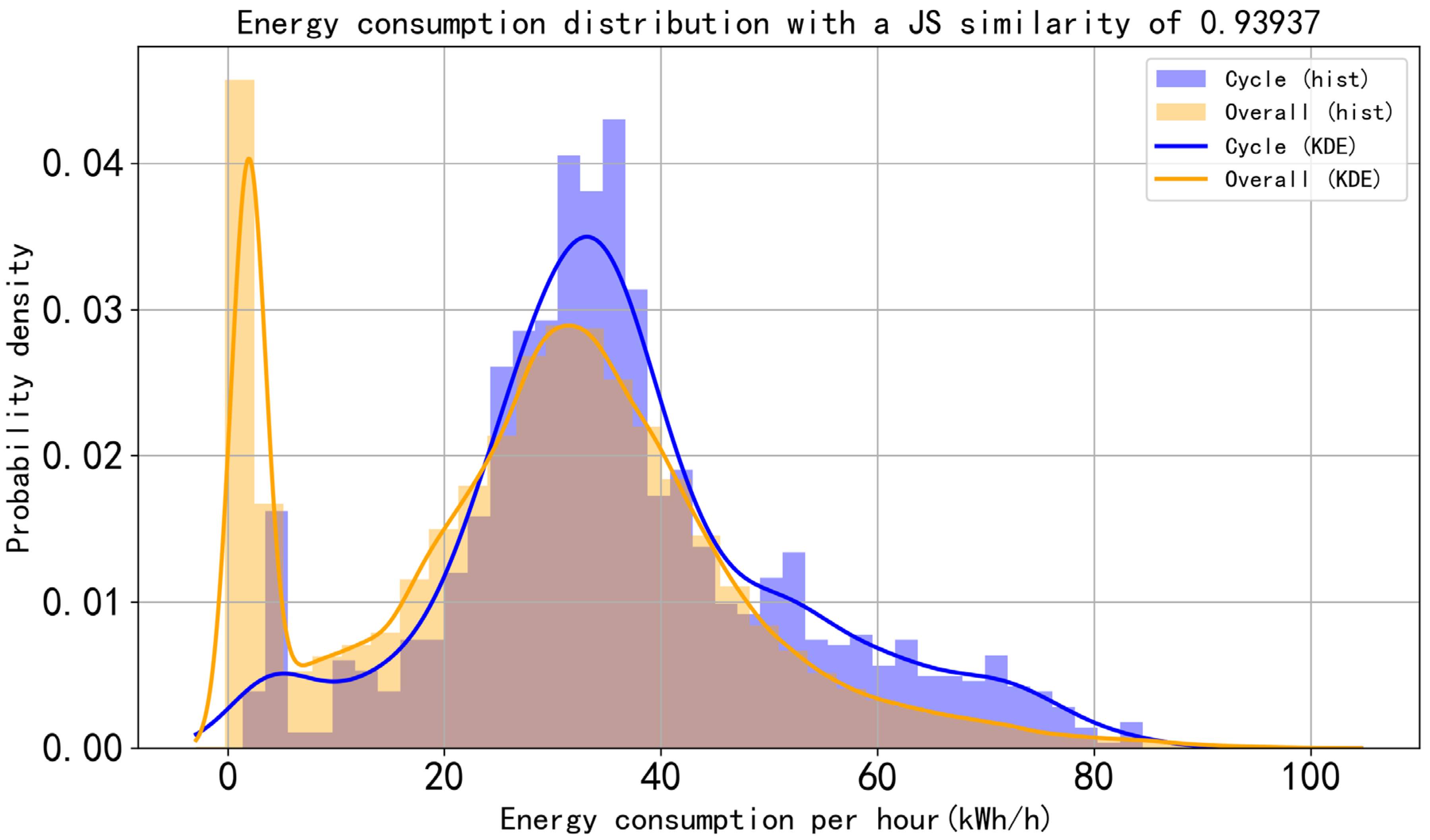
Using four days of data from two loaders operating at the Yiwu mixing plant, the aggregated duty cycle was constructed and compared with the measured energy consumption distributions. As shown in Figure 10, the similarity reached 93.94%, demonstrating that the aggregated cycle effectively preserves the energy-use characteristics of the raw data.

Furthermore, the error between the aggregated condition curve and the overall sample dataset was analyzed. Based on the relative error formula, the deviation of feature parameters was computed (

Table 8. Relative error of characteristic parameters in the typical duty cycle.

Feature Parameters	Unit	Overall Sample Value	Representative Cycle Value	Relative Error
Time Characteristics
1. Average segment duration	s	270.3	233.7	−13.5%
2. Proportion of effective operation time	%	68.7	72.4	+5.4%
3. Proportion of idle time	%	22.5	19.8	−12.0%
Motion Characteristics
4. Maximum vehicle speed	km/h	28.6	26.3	−8.0%
5. Average acceleration	m/s2	0.83	0.76	−8.4%
6. Frequency of rapid acceleration/deceleration	times/min	3.2	3.6	+12.5%
Load Characteristics
7. Average driving motor torque	N·m	168.1	171.9	+2.3%
8. Average working motor torque	N·m	121.7	125.5	+3.1%
9. Peak hydraulic system pressure	MPa	20.8	20.0	−3.8%
Working Device Characteristics
10. Boom lifting/lowering frequency	times/cycle	2.8	3.2	+14.3%
11. Bucket tipping angle		214.5	235.7	+9.9%
12. Working device cycle period	s	17.3	15.2	−12.1%
Energy Efficiency Characteristics
13. Energy consumption per unit time	kWh/h	43.6	45.9	+5.3%
14. Proportion of hydraulic power	%	71.8	66.4	−7.5%
15. Proportion of regenerative braking energy	%	12.7	14.3	+12.6%

). Results show that the relative error of all feature parameters remains within 15%, confirming the validity of the proposed method for constructing representative duty cycles.

The comparison between the aggregated operating profile and the actual operation data collected over four days at the Yiwu concrete batching plant is presented in

Table 9. Comparison of Aggregated Operating Profile and Four-Day Operation Data at Yiwu Batching Plant.

Action Category	Aggregated Profile (%)	Yiwu Plant (Four-Day Average, %)
Idle	5.03	5.37
Excavation	6.34	5.96
Operation only	2.48	2.67
Travel only	51.49	48.90
Travel + Operation combined	34.66	37.10
Average Error	–	6.5%

. The results indicate that the average deviation of action proportion across different categories is 6.5%.

4.3. Validation Across Different Time Periods in the Same Scenario (Time Transferability)

To further evaluate the temporal generalization capability (time transferability) of the aggregated operating conditions, the aggregated load profile was compared with the energy consumption distributions of two loaders at the Yiwu concrete batching plant over the subsequent two days. Time transferability is defined as the ability of the aggregated duty cycle to represent operational states over different time periods within the same site. Mathematically, it is quantified using the same Jensen–Shannon divergence-based similarity metric:

$$\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{y}}_{\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e}}=1-JS(P\parallel Q)$$

(17)

where $P$ is the feature distribution of the aggregated duty cycle constructed from the initial dataset, and $Q$ is the feature distribution of the target future dataset from the same site.

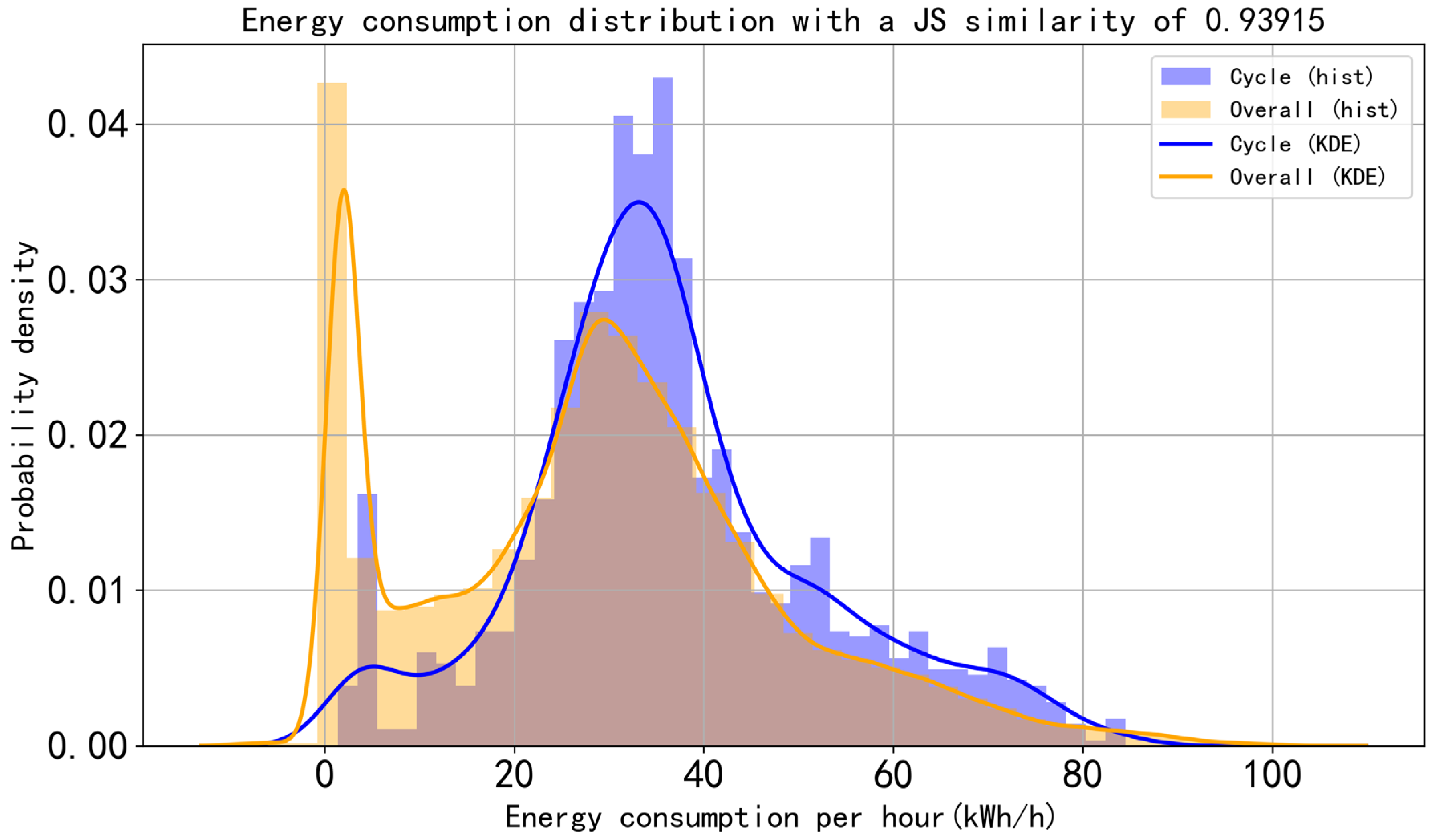
As shown in Figure 11, the similarity remains at 93.915%, indicating that the operating conditions constructed from the historical four-day dataset not only reflect past energy consumption patterns but also remain representative of the operational states over the following period.

The comparison between the aggregated operating profile and the actual operation data collected during the subsequent two days at the Yiwu batching plant (in addition to the initial four days used for constructing the aggregated profile, making six days in total) is shown in

Table 10. Comparison of Aggregated Operating Profile and Subsequent Two-Day Operation Data at Yiwu Batching Plant.

Action Category	Aggregated Profile (%)	Yiwu Plant (Two-Day Average, %)
Idle	5.03	5.49
Excavation	6.34	6.06
Operation only	2.48	2.77
Travel only	51.49	48.92
Travel + Operation combined	34.66	36.76
Average Error	–	7.3%

. The results indicate that the average deviation of action proportions increased to 7.3% compared with the first four-day dataset, but it still remains within the acceptable error margin.

4.4. Validation Across Different Scenarios (Site Transferability)

To assess the cross-scenario transferability of the aggregated load profile, the energy consumption distribution of the aggregated profile from the Yiwu plant was compared with the measured load profile of a single wheel loader at the Kunshan concrete batching plant over seven consecutive days. Site transferability is defined as the ability of the aggregated duty cycle to represent operational states across different sites with similar machinery and operations, and is also quantified using Jensen–Shannon divergence:

$$\mathrm{S}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{t}{\mathrm{y}}_{\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{e}}=1-JS(P\parallel Q)$$

(18)

where $P$ is the feature distribution of the aggregated duty cycle from the reference site, and $Q$ is the feature distribution of the target site. A higher similarity indicates stronger cross-site applicability.

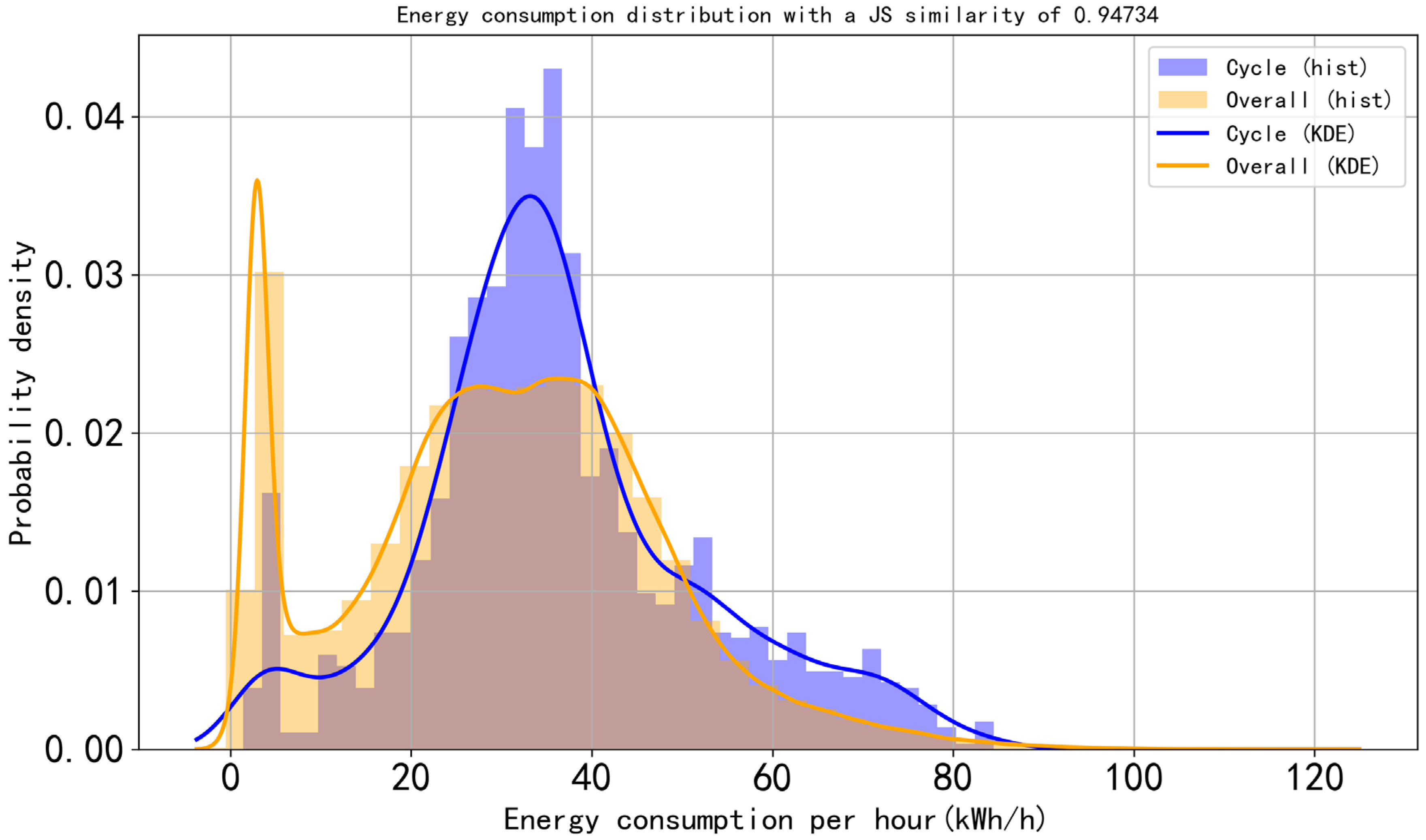
As shown in Figure 12, the similarity reaches 94.734%, demonstrating that the proposed aggregation method not only maintains high consistency within the same operational scenario but also adapts well to different sites and equipment characteristics, indicating strong potential for broader applicability.

The comparison between the aggregated operating profile and the actual operation data collected over seven consecutive days at the Kunshan batching plant is presented in

Table 11. Comparison of Aggregated Operating Profile and Seven-Day Operation Data at Kunshan Batching Plant.

Action Category	Aggregated Profile (%)	Kunshan Plant (Seven-Day Average, %)
Idle	5.03	4.67
Excavation	6.34	5.63
Operation only	2.48	2.76
Travel only	51.49	49.68
Travel + Operation combined	34.66	37.26
Average Error	–	8.1%

. The results show that the average deviation of action proportions is 8.1%, which remains within an acceptable range for representative operating condition construction.

In summary, the Jensen–Shannon divergence-based validation confirms that the proposed operating condition aggregation method exhibits high reliability in preserving original load characteristics, as well as strong time and site transferability, providing a solid foundation for subsequent energy consumption evaluation and control strategy optimization based on typical operating conditions.

5. Discussion

The proposed duty cycle aggregation method provides several notable insights into the operation characteristics and energy consumption analysis of electric loaders. First, by integrating multi-source data acquisition from CAN bus signals, hard-wired sensors, and cloud-based storage platforms, the constructed dataset comprehensively captured the interaction between power, hydraulic, and thermal management systems. This allowed for a more realistic representation of loader dynamics compared to traditional proving ground tests, which often overlook operational diversity.

Second, the feature-based clustering and segment concatenation approach effectively identified typical operating modes, such as idling, short-distance loading, and long-distance transportation. The resulting representative duty cycles preserved both the statistical characteristics and temporal continuity of real-world operations. Validation results demonstrated that the aggregated duty cycles maintained high fidelity with field data, with average feature errors below 10% and Jensen–Shannon divergence values exceeding 93%. The dataset spans six consecutive days, with the first four days used for duty cycle aggregation and the remaining two days reserved for validation. The validation process is temporal rather than random; therefore, no random seed or split ratio is applicable. This consecutive-sampling approach ensures that the aggregated duty cycles are representative of continuous operations while maintaining real-world temporal consistency. These findings confirm the robustness and applicability of the proposed methodology within the studied concrete mixing plant scenario.

Although the operational data utilized in this study were obtained from a specific customer site (a commercial concrete batching plant), the proposed duty cycle modeling and aggregation framework possesses broad applicability and is not confined to this single enterprise. By appropriately adjusting the feature selection, clustering parameters, and segmentation thresholds to align with different operational characteristics, the same methodology can be extended to other application scenarios such as ports, mining sites, and steel mills. This demonstrates the practical versatility of the proposed approach, indicating its potential to support energy efficiency evaluation, component sizing, and control strategy development across diverse real-world working environments.

It is acknowledged that this study primarily focuses on a 5-ton-class electric wheel loader, which may restrict the direct generalization of results to other equipment categories. Variations in system specifications—such as hydraulic capacity, motor power, and vehicle mass—as well as operator behaviors, including loading intensity and travel patterns, can influence the representativeness of the aggregated duty cycles. This limitation has been explicitly addressed in the discussion, emphasizing that further validation across multiple loader classes, operating conditions, and operator profiles would enhance the robustness and scalability of the proposed framework. Therefore, the presented case study should be regarded as a demonstration of the feasibility and effectiveness of the general methodology, rather than as an exhaustive validation across all equipment types.

Although the dataset used in this study comprises 624 h of operation from only two concrete batching plants, which may limit the diversity of operational scenarios, the methodology itself is generalizable. Potential data bias due to limited site diversity is acknowledged, and further validation with datasets from additional sites, such as ports, mining areas, or steel mills, would enhance the robustness and broader applicability of the proposed duty cycle aggregation method.

Third, the results highlight that although minor discrepancies were observed between aggregated cycles and site-specific data—particularly in the proportion of compound “driving + working” operations—the deviations remained within acceptable engineering tolerance. Such differences are attributable to variations in operator habits, material handling intensity, and site-specific logistics, suggesting that further refinement may be achieved by incorporating operator behavior modeling or adaptive weighting strategies in the clustering stage.

Finally, the established representative duty cycles provide a practical foundation for subsequent applications. These include energy efficiency benchmarking, powertrain and hydraulic component sizing, as well as the design of advanced control strategies such as torque distribution and energy recovery. In addition to extending applications to mines and ports, future work explicitly includes AI-based adaptive clustering methods to dynamically identify representative duty cycles under varying operational conditions, online cycle recognition algorithms for real-time duty cycle identification and energy management, and multi-agent fleet analysis to optimize operations and energy efficiency at the fleet level. Moreover, the method contributes to the development of standardized duty cycle databases. Specifically, the aggregated duty cycles can support duty cycle databases aligned with ISO 8178 and SAE J1939 standards, highlighting the potential for standardizing duty cycle evaluation and benchmarking across manufacturers, thereby enhancing the practical and regulatory value of the work. Moreover, the method contributes to the development of standardized duty cycle databases. Specifically, the aggregated duty cycles can support duty cycle databases aligned with ISO 8178 and SAE J1939 standards, highlighting the potential for standardizing duty cycle evaluation and benchmarking across manufacturers, thereby enhancing the practical and regulatory value of the work.

6. Conclusions

This study addresses the energy consumption modeling and operating condition aggregation of electric wheel loaders under typical scenarios at concrete batching plants, proposing an aggregation method with cross-scenario generalization capability. Its effectiveness was validated using multi-scenario datasets. The main conclusions are as follows:

1.

A method for segmenting operating conditions and extracting features was proposed, constructing a multi-dimensional feature parameter system, and dimensionality reduction was achieved via Principal Component Analysis (PCA), which improved clustering efficiency and accuracy.

2.

Using concrete batching plants as a case study, typical load profiles were constructed through cluster analysis, overcoming the limitations of conventional simplified V-shaped cycles that fail to reflect real operational characteristics.

3.

Validation based on the Jensen–Shannon divergence shows that the aggregated load profiles exhibit more than 93% similarity with measured data across different time periods and different equipment, demonstrating the reliability and applicability of the method.

In conclusion, the proposed method effectively characterizes typical operating conditions of electric wheel loaders, providing support for energy consumption assessment and control strategy optimization. Future work will extend the method to more complex scenarios such as mines and ports and integrate machine learning and big data techniques to promote the establishment of cross-vehicle operating condition databases and industry standards.