Abstract
Automated demand response in residential sectors is critical for grid stability, but centralized control strategies fail to address the unique energy profiles of individual households. This paper introduces a decentralized control framework using multi-agent deep reinforcement learning. We assign an independent Soft Actor–Critic (SAC) agent to each building’s battery energy storage system (BESS), enabling it to learn a control policy tailored to local conditions while responding to shared grid signals. Evaluated in a high-fidelity simulation environment of CityLearn using real-world data, our multi-agent system demonstrated a reduction of approximately 50% in both electricity costs and carbon emissions. Crucially, this decentralized approach considerably outperformed all benchmarks, including a rule-based controller, tabular Q-learning, and even a centralized single-agent SAC controller. At the district level, learned policies flatten the net load profile, lowering daily peaks by 16% and ramping by 26%, and improve the load factor. The resulting dispatch patterns are interpretable and consistent with operator objectives such as peak shaving and valley filling. These findings indicate that decentralized reinforcement learning can translate local optimization into system-level benefits and offers a scalable pathway for aggregators and utilities to operationalize the flexibility of residential storage at scale.
1. Introduction
The residential sector in the United States accounts for roughly one-fifth of both national energy use (about 21%) and greenhouse gas releases (near 20%) [1]. To truly achieve zero-emission buildings, electric grid decarbonization and end-use electrification are pivotal, with the help of renewable energy sources (RESs), which include wind and PV arrays [2]. But implementation of this strategy is challenging due to the intermittent nature of RESs. Hence, supply and demand drift apart in ways that threaten voltage stability, raise balancing costs, and shave the market value of variable resources [3,4]. Grid-interactive efficient buildings (GEBs) are intended to counter this misalignment. By improving efficiency, shifting flexible loads, or absorbing surplus generation, such buildings can furnish a portfolio of grid services that includes load shifting, peak clipping, and continuous modulation [5]. Utilities usually activate these capabilities through demand response (DR) programs that either compensate customers directly (for example, direct load control) or rely on price signals such as time-of-use tariffs [6].
Commercial and industrial facilities have embraced DR for years, largely because heavy machinery and process equipment offer substantial flexibility in the grid during peak demand hours [7]. But contrary to that, residential participation is more recent and often relies on distributed energy resources that behave quite differently. Examples include HVAC systems whose setpoints can be modified and electric vehicles that vary their charging rate or supply energy to the grid in vehicle-to-grid configurations or battery energy storage systems (BESSs), which can be utilized during the event of load shifting by acting as energy buffers [8]. However, when each household responds to a demand-response signal on its own, the collective outcome at the system level is not always favorable. A load that is supposed to be curtailed often shifts again a few minutes or hours later, creating a secondary peak rather than a genuine reduction in demand [9]. One remedy that is gaining traction is the use of market-based aggregators. These entities occupy the space between grid operators and individual consumers, coordinating thousands of small, flexible resources such as heat pumps, battery packs, and rooftop PV inverters and packaging their combined capacity for sale in wholesale or ancillary service markets [10]. In effect, the bundled assets behave as a virtual power plant; participating households receive a financial credit that reflects the real-time value of the flexibility they contribute.
Two algorithmic families—model predictive control (MPC) [11] and reinforcement learning control (RLC) [12]—dominate recent work on automated operation of distributed energy resources. Most published work still gravitates toward model-based controllers. MPC has been particularly influential in energy management and formal demand-response trials [13]. The reason for the widespread usage of MPC is the fact that it can optimize well-defined objectives while enforcing equipment and comfort constraints, and it has been shown to coordinate cold storage for comfort-preserving demand response [14] and to manage systems with high penetration of renewable generation under demand-response limits [15]. A parallel stream casts demand response as a scheduling problem and solves it with mixed-integer linear programming (MILP), which requires explicit device models and operating constraints for the relevant appliances [16], with tailored solution strategies proposed to improve tractability and performance [17]. But there are certain disadvantages associated with MPC. Accurate physics-based models can be costly to build and maintain; key parameters may be unavailable because of privacy concerns or may drift as equipment ages [18]. These approaches also lean on high-quality forecasts of uncertain inputs [19], are exposed to modeling error, and are not inherently adaptive [20]. As system size grows and buildings diverge in design and use, the burden of maintaining building-specific models increases, so large-scale deployment may become impractical [21].
Reinforcement learning (RL) offers an alternative that treats demand response as sequential decision making under uncertainty [22]. Because model-free RL does not require prior knowledge of dynamics, it is often easier to implement in practice than traditional optimization. Deep RL, which couples function approximation with RL, has already supported several demand-response demonstrations [23]. These studies indicate that multiple objectives can be handled simultaneously, for example, maintaining thermal comfort while reducing electricity use during events [20] or balancing revenue, user satisfaction, and peak reduction within one control scheme [24]. In residential settings where buildings host different resources and operating rules, DRL has been used to deliver autonomous load management without detailed device models [25]. It may also help hedge against uncertainty in load, on-site generation, weather, and dynamic tariffs [26]. Coordination across many grid-responsive buildings introduces additional challenges. Single-agent DRL can struggle with high-dimensional joint action spaces and with reward specifications that inadvertently create misaligned local incentives. Multi-agent deep reinforcement learning (MADRL) provides a more flexible way to encode cooperation across heterogeneous energy systems and can reduce the risk of conflicting objectives [27]. Information sharing and concurrent learning in a multi-agent setting may shorten training and raise the quality of the learned policies for individual agents [28].
Multi-agent deep reinforcement learning is gaining traction in energy management, particularly for cooperative control tasks that are hard to handle with a single decision maker [29,30]. Recent studies report autonomous demand response across portfolios that mix several energy assets, using multi-agent variants of leading DRL algorithms [31]. Even so, several open issues remain. The first is policy design: agents must learn to cooperate so that aggregate demand actually falls rather than merely shifting from one hour to another. Tailored MADRL schemes have shown clear gains in load shaping when compared with single-agent baselines [32]. The problem is that tailored techniques may not transfer well to generalized buildings, while the translation of the conventional DRL algorithm to a multi-agent setting can cause uncoordinated actions and elevated peaks. Dynamic pricing adds another hurdle; because tariffs respond to load, poorly aligned policies may move the peak rather than flatten it. A second challenge is non-stationarity. As agents share information and react to one another, the environment each agent sees keeps changing, which can destabilize learning unless the method explicitly accounts for it. There are scalability issues as well. As the number of buildings grows, communication overhead rises and training signals can become noisy, so maintaining stable performance may require a careful architecture or communication limits.
Contribution and Structure of Study
The contributions of this paper are outlined as follows:
- We propose and implement a multi-agent control system where each residential building’s battery is managed by an independent Soft Actor–Critic (SAC) agent as shown in Figure 1. This decentralized execution architecture allows each agent to learn policies tailored to its building’s unique load characteristics while coordinating its actions with others through shared environmental signals (e.g., electricity price and carbon intensity), effectively tackling the heterogeneity challenge in residential communities.
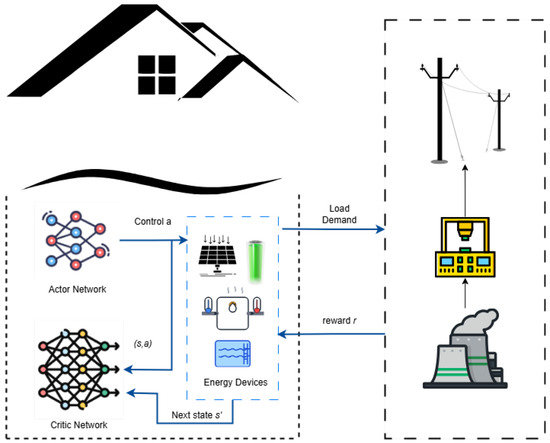 Figure 1. Overview of the multi-agent residential RL demand-response setup.
Figure 1. Overview of the multi-agent residential RL demand-response setup. - We introduce a cost-centric, SoC-aware reward that implements PV self-consumption and curbs wasteful grid exchange. The reward minimizes electricity cost and adds an SoC-dependent term that (i) encourages charging from PV systemswhen available, (ii) avoids importing from the grid when the battery can serve the load, and (iii) avoids exporting before the battery is full. The final reward is presented as a single compact formula with clear normalization.
- We report five KPIs (cost, emissions, average daily peak, ramping, and load factor) at both building and district levels, normalized to a no-storage baseline, and we benchmark against strong centralized controllers (Rule-Based Controller (RBC), Tabular Q Learning (TQL) control, and centralized SAC).
The rest of this paper is structured as follows. Section 2 formally casts the residential demand-response challenge as a Markov decision process, defining the problem’s state, action, and reward components. This section also presents the multi-agent Soft Actor–Critic framework. Section 3 details our methodology, presenting the CityLearn simulation environment, the baseline controllers used for comparison, and the metrics for evaluation, in addition to providing the complete workflow of the problem. Section 4 presents and discusses the empirical results, providing a comparative analysis of the controllers and interpreting the learned behaviors. Finally, Section 5 concludes the paper by summarizing the key findings, acknowledging the study’s limitations, and suggesting avenues for future work.
2. Problem Formulation and Methodology
The objective of this work is to formulate an intelligent control strategy for BESSs in residential buildings. This can be done by charging and discharging each battery in a building to reduce the overall electricity tariff, reduce emissions, and increase grid stability by mitigating peak loads and ramping events. This task can be naturally framed as a sequential decision-making problem under uncertainty, for which the Markov Decision Process (MDP) provides a formal mathematical framework. In this section, we set out the theoretical framework for our reinforcement learning approach. We begin by casting the control task as an MDP, the standard mathematical model for sequential decisions under uncertainty. The MDP specification clarifies the state, action, transition, and reward elements that shape the objective and constraints. With that foundation in place, we then describe how SAC is implemented for the residential energy system, noting the policy and value-function parameterizations, the used training signals, and a few practical choices that appear to matter in this application.
2.1. Markov Decision Process Formulation
An RL problem is modeled as a Markov decision process (MDP), represented by . Here, S is the set of observable states of the controlled environment and may be discrete or continuous. The Markov property assumes that the state at time t summarizes all information relevant for control. A denotes the set of admissible actions or action space available from a state (). As with the state space, A may be discrete or continuous. At each transition, the agent chooses its next action according to a policy , which is understood as a mapping from states to probability distributions over actions (). Interaction with the environment produces a trajectory (). An action represents the agent’s decision within the control setting, selected to pursue the objective encoded by the reward function. P represents the system dynamics in the form of a transition kernel. For any state–action pair and successor state (), the equation expressed as
represents the likelihood of moving to after taking action a in state s. Consistent with the Markov property, this probability is assumed to depend only on the current state and action rather than on earlier history. The reward function assigns an immediate payoff to each transition. Formally, returns the expected one-step reward received when action a taken in state s leads to successor state . This conditional expectation is written as
The discount factor () determines how strongly future rewards contribute to the return. When computing the discounted return, i.e.,
larger values of place more weight on outcomes that occur later in time. At , the agent values long-horizon rewards without discounting, whereas at , it is entirely myopic and attends only to the immediate reward.
The control objective is conveniently expressed through two related value functions: the state-value function () and the action-value function (). Under a policy (), these are defined as
The function quantifies the desirability of being in state s with respect to the control objective, while evaluates the benefit of taking action a in state s, then continuing to follow policy .
2.2. Soft Actor–Critic Deep Reinforcement Learning
SAC adopts an actor–critic design in which two deep networks approximate the value functions: one evaluates actions, and the other estimates the state value. Figure 2 sketches the main components of SAC and the data flow between them. The paragraphs that follow describe these elements and how they interact during training.
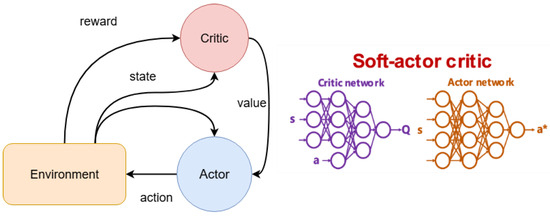
Figure 2.
Actor–critic environmental interactions and ANNs in SAC.
Soft Actor–Critic relies on two cooperating function approximators. The actor, or policy network, receives the current state (s) and proposes an action (). Training does not push the policy toward reward alone. In SAC, the objective also includes policy entropy, which keeps the action distribution sufficiently random and reduces the risk of settling too early on a poor strategy. The actor is updated by a policy-gradient step that uses signals supplied by the critic.
Evaluation of actions is handled by a pair of critic networks that approximate the action-value function (). Using two critics is not a cosmetic choice. Taking the minimum of their predictions during target computation tends to limit overestimation bias and usually makes learning more stable, especially in noisy environments.
A defining feature of SAC is entropy regularization. The objective trades off expected return with the entropy of the policy, with a temperature parameter () controlling the balance. Larger values encourage broader exploration; smaller values place more weight on exploiting what the agent currently believes to be best. In practice, tuning can materially affect both the pace and the reliability of convergence.
SAC learns off-policy and uses a replay buffer. Transitions in the form of are stored and later sampled at random to update the networks. This reuse of past experience increases data efficiency and breaks correlations in sequential data that may otherwise hamper gradient estimates.
Finally, the critic updates use a soft Bellman backup. The target includes not only the immediate reward and the discounted value of the next state but also the entropy of the next-state policy. This soft update encourages a policy that performs well while still assigning probability mass to alternative actions—a balance that appears to matter in control settings with variable prices, emissions, and loads.
2.3. Entropy-Regularized RL in SAC
The standard reinforcement learning objective is to choose a policy that maximizes the expected discounted sum of rewards. Let denote a trajectory generated by policy . The expected return under is the expectation of the discounted cumulative reward over trajectories induced by . Therefore, the optimal policy is
where is the discount factor, is the one-step reward, and denotes the expectation over all trajectories that may occur when the agent follows . The operator selects the policy with the largest expected return, so defines the behavior that maximizes cumulative reward over time.
Entropy regularization is central to SAC. The policy is trained to strike a balance between maximizing expected return and preserving policy entropy [33]. This mechanism ties directly to the exploration–exploitation trade-off: greater entropy typically promotes broader exploration and may yield better learning over longer horizons. It also reduces the risk that the agent settles too quickly on a solution that later proves suboptimal.
For a policy distribution (P) over actions, the entropy measures action uncertainty:
where is the probability of selecting action x under the current policy and the expectation is taken with respect to that policy. Larger entropy values indicate a more uncertain, more exploratory policy because grows as shrinks. In entropy-regularized reinforcement learning, the objective balances return and entropy. The optimal policy solves
where is a trajectory generated by , is the discount factor, R is the one-step reward, and controls the trade-off between reward maximization and exploration.
Soft Value Functions
With entropy regularization, the state-value and action-value functions take the following forms:
The expectation () is taken over all future outcomes when following policy . In other words, is the immediate reward earned at time t, and is the policy entropy in state .
Soft Actor–Critic trains two critic networks by minimizing the mean squared Bellman error over samples drawn from a replay buffer (), where flags terminal transitions. For a critic () with parameters (), the loss is
with a soft target of
The parameters denote slowly updated target-critic weights. The min operator reduces overestimation bias by taking the smaller of the two target Q estimates, while the entropy term () carries the exploration incentive into the backup.
The soft target combines three components: the immediate reward (r), a future reward on the next state that uses the smaller of the two critic estimates to limit overestimation, and an entropy term () that encourages exploration. The variable is a terminal indicator, i.e., at episode end and otherwise, so the bootstrap contribution is included only for non-terminal transitions.
3. Experimental Setup and Evaluation
This section describes the experimental framework used to evaluate the proposed multi-agent reinforcement learning controller for residential demand response. We used a case study built from high-resolution measurements in a community of zero-net-energy homes, which serves as the basis for our simulations. To train and test control agents, we instantiated this scenario within the CityLearn environment so that agents interact with a consistent, repeatable representation of the district. The choice of CityLearn is central to the design. As a standardized testbed for residential demand-response studies, it offers a reproducible setting for multi-agent analysis and avoids the considerable computational burden associated with full co-simulation using detailed physics engines such as EnergyPlus. Figure 3 presents a schematic overview of this entire workflow, illustrating the key stages, from data acquisition and setup of the simulation environment to controller design, experimental execution, and final policy evaluation.
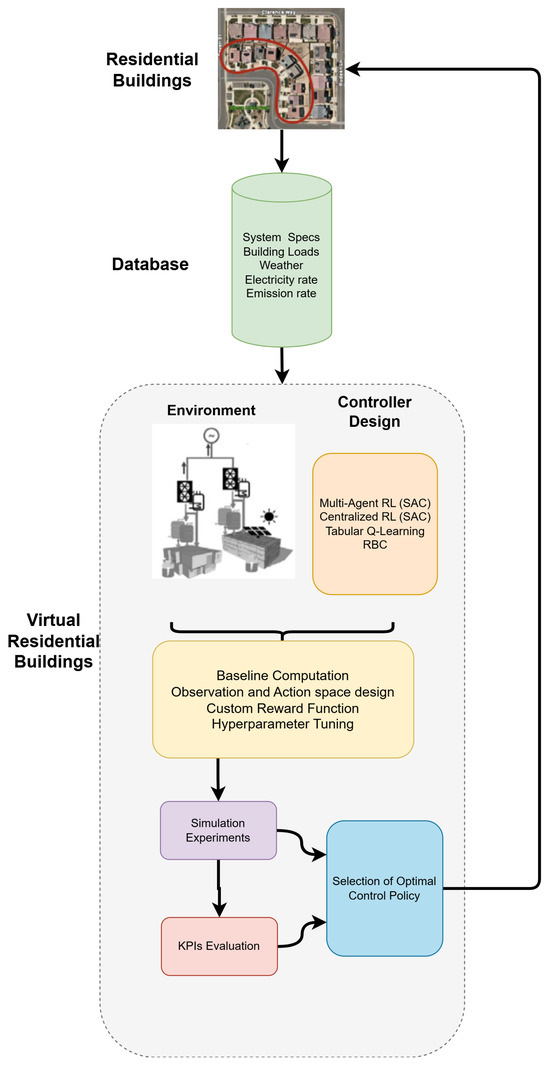
Figure 3.
Schematic of the experimental workflow for controller development and evaluation.
3.1. Case Study
Our assessment framework relies on a dataset drawn from 17 single-family, zero-net-energy households located in the Sierra Crest community in Fontana, California. Different types of residential buildings utilized in the case study are shown in Figure 4. This figure displays the different architectural elevations of the homes in the dataset. These variations in design and size are a primary source of the energy consumption heterogeneity that our decentralized control strategy aims to address. These homes were monitored under the California Solar Initiative, a study that sought to quantify how neighborhoods with high rooftop photovoltaic penetration and on-site battery storage interact with the distribution grid [34].

Figure 4.
Elevation of houses used in the dataset [35].
The study sample consists of 17 single-family prototypes with conditioned floor areas spanning 177 to 269 . Figure 5 summaries each home’s envelope and mechanical profile. The envelope employs high-performance insulation and glazing, while the internal systems rely on premium-efficiency appliances, together with fully electric space-conditioning and water-heating equipment, a configuration expected to curb baseline demand. Circuit-level meters capture sub-minute load traces, and an energy management platform permits either manual scheduling or automated control. A total of 8 of the 17 buildings also contain a lithium-ion battery rated at 5 kW, offering 6.4 kWh of nominal capacity given a 90% round-trip efficiency and a 75% depth of discharge.
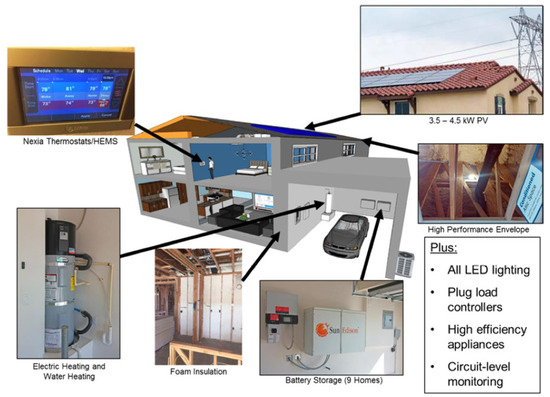
Figure 5.
Various devices installed in a case-study building [35].
This virtual community has already been implemented in the CityLearn Environment to test various control strategies of BESSs. The dataset is present in the CityLearn Environment and is the transformed version of the as-built buildings. This transformed version fixes the data quality issues to address privacy concerns with the aim of making the dataset open-source. To obtain the transformed version of dataset, the raw power traces were first aggregated into hourly energy values expressed in kilowatt-hours. Potential anomalies were then handled: an inter-quartile range filter flagged suspicious spikes, short gaps were filled through linear interpolation, and longer gaps were estimated with a concise supervised learning model that drew on neighboring observations. Each building is equipped with a lithium-ion battery that provides 6.4 kWh of usable capacity, can deliver up to 5 kW, and returns about 90% of its stored energy over a complete charge and subsequent discharge cycle; the analysis assumes the battery pack is free to operate across its full depth of discharge. Finally, space cooling, space heating, domestic hot-water production, and plug consumption were merged into a single non-shiftable category by referencing the aggregate signal recorded at the main service meter.
The simulation framework supplements the building data set with typical meteorological year (TMY3) weather observations recorded at Los Angeles International Airport, along with an hourly carbon-intensity profile (kilograms of equivalent per kilowatt-hour). Price signals reflect Southern California Edison’s TOU-D-PRIME schedule, an option geared toward households that operate behind-the-meter batteries, with the tariffs provided in Table 1. It can be seen in the table that unit prices fall to their lowest level in the short window before sunrise and again after midnight. They remain near their average value throughout the months of October through May, when regional demand is relatively less. On weekends, the utility further relaxes its pricing, so the usual 4 p.m. to 9 p.m. peak period becomes noticeably less expensive, a structure that implicitly rewards residents who can defer or store energy during weekday peaks yet still favor evening use on Saturdays and Sundays.

Table 1.
Energy rates simulated in the CityLearn environment ($/kWh).
3.2. CityLearn Environment
CityLearn provides a reinforcement learning testbed for analyzing demand-response strategies in both single- and multi-agent configurations [36]. The environment inherits the OpenAI Gym interface and follows the multi-agent conventions outlined by Lowe et al. [37]. Because CityLearn relies on pre-computed building loads and internal device models, it eliminates the need for slower co-simulation with EnergyPlus or comparable engines. The main components of CityLearn are shown in Figure 6. The flowchart shows that CityLearn is the testbed for implementing reinforcement learning algorithms, and it provides an environment for building simulation by making use of the data available to this platform through multiple third-party data sources. These inputs configure the central CityLearn environment, which facilitates interaction with the control agents. This interaction follows a standard reinforcement learning loop, in which the environment typically sends the current state and a calculated reward to the agents, who, in turn, process this information and send actions back to the environment to be executed. The goal of this process is to optimize building energy consumption. The effectiveness of the agents’ learned policies is then quantified and output as load-shaping performances metrics, which measure the impact on objectives like peak load reduction and energy cost savings.
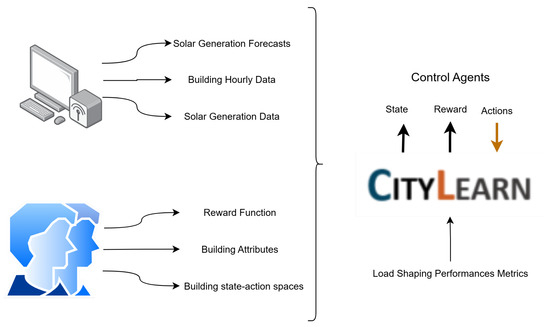
Figure 6.
Flowchart of the CityLearn environment.
Within the platform, several dispatchable systems are explicitly modeled, including air-to-water heat pumps and electric resistance heaters. The dataset also supplies hourly series for additional end uses such as space cooling, domestic hot water, appliance loads, dehumidification, and on-site solar generation. Agents act on an hourly time step, receiving fresh observations and reward signals with each interval. Built-in constraints limit every control decision so that device capacities remain sufficient to satisfy even minute demands. A fallback controller further protects occupant comfort, ensuring that heating and cooling requirements take priority over any energy storage objective pursued by the learning agent. Collectively, these design choices allow researchers to explore advanced control policies while retaining confidence that core comfort needs are met throughout every simulation step.
CityLearn is structured to enable continuous demand response without requiring explicit dispatch signals from the grid. It achieves this by coordinating active energy storage systems to shift loads in time. The platform incorporates detailed models for buildings, electric heaters, heat pumps, thermal energy storage (TES), BESSs, and PV generation.
For the present study, the simulation environment was configured with energy models for two buildings, but the results are reproducible for any number of buildings. Each of the buildings comprises a battery and PV array that match the specifications of those deployed in the real-world community. In the model, batteries accumulate surplus energy from either the PV system or the grid and discharge when the building experiences a net positive load. In the simulation, each building is assigned a control agent responsible for regulating its battery’s SoC by determining, at each time step, the amount of energy to store or release. Because the building load profile is known in advance from measured or simulated data, CityLearn ensures that demand is always met, regardless of the agent’s decisions. An internal backup controller further safeguards system constraints by prioritizing the fulfillment of occupant comfort requirements and essential base loads before allocating energy for battery charging. It also prevents the battery from discharging more than is necessary to meet the building’s current demand.
3.3. Key Performance Indicators
We evaluate each control policy using five minimization metrics: electricity cost, carbon emissions, average daily peak, ramping, and the complement of the load factor . Average daily peak, ramping, and are computed based on the aggregated district net load () at an hourly resolution. Electricity cost and carbon emissions are computed per building from , then averaged across buildings to report a grid-level value. Let h be the number of hours and d be the number of days, and the KPIs are calculated as follows:
The first KPI is imported energy, and it is charged at the hourly tariff ():
Carbon emissions are the second KPI, corresponding to the product of imported energy and hourly carbon intensity (, in kg CO2e per kWh):
The average daily peak (P), which is the third KPI, is defined as the mean of the daily maximum district load (, where d indexes the day of the year).
We also measure ramping as a KPI to measure the hour-to-hour variability of the district profile:
The load factor (L) is defined as the average of the ratio between the monthly mean and the monthly peak of the district hourly load (, where m indexes the months) across months. The quantity of L lies in the range of , so one may maximize L or, equivalently, minimize . This is the last KPI to be measured.
All KPIs are reported relative to a no-battery baseline; hence, they are normalized with the following formula:
Values below indicate improvement over operation without storage or advanced control.
3.4. Action and Observation Space
The effective formulation of the action and observation spaces is fundamental to the agent’s ability to learn an optimal control policy. The observation space must provide a sufficiently rich representation of the environment’s state to enable informed decision-making, while the action space must grant the agent the necessary control authority over the system. Our design is guided by the principle of providing each agent with a comprehensive snapshot of its local building state, key exogenous signals from the wider grid, and predictive information to facilitate proactive control. The agent observes a mix of community variables and building states, as summarized in Table 2. Temporal features consist of two indicators that encode the time structure of the problem and appear in every series. Weather inputs include direct solar irradiance, together with its forecasts obtained from the supplementary meteorological data. The non-shiftable load denotes total building demand prior to any contribution from PV or the battery. Net electricity consumption is computed as the sum of non-shiftable load, PV generation, and battery power. The battery state of charge (SoC) is evaluated during simulation as stored energy divided by rated capacity. Carbon emissions and the net electricity price represent the environmental and economic costs of drawing energy from the grid, respectively. To aid in learning, periodic features use cyclical encodings, discrete features use one-hot encodings, and continuous features are scaled with min–max normalization.

Table 2.
Agent observation variables and associated units.
The action space is a single scalar that specifies the fraction of battery capacity to charge or discharge. Its value lies in the interval of , where negative values request discharge and positive values request charge.
3.5. Reward Function
We want to reduce electricity cost (Equation (13)) and emissions (Equation (14)). Likewise, we want to reduce the peaks and ramping and increase the load factor. One way to achieve this is to teach the agents to charge the batteries when electricity is cheap after 9 p.m. and before 4 p.m., which typically coincides with when the grid is cleaner (lower emissions). But as stated earlier, each building is able to generate power, provided there is solar power. Therefore, we can take advantage of self-generation in the late morning to late afternoon to charge for free and discharge the rest of the day, thereby reducing electricity cost and emissions at the very least. Also, by shifting the early-morning and evening peak loads to the batteries, we can improve on our peak and load-factor KPIs.
We should also teach our agents to ensure that renewable solar generation is not wasted by making use of the PV to charge the batteries when they are charged below capacity. On the flip side, the agents should learn to discharge when there is a net positive grid load and the batteries still have stored energy.
Given these learning objectives, we can now define a reward function that closely satisfies the criteria for which the agent will learn good rewards:
The reward function (r) is designed to minimize electricity cost (C). It is calculated for each building (i) and summed to provide the agent with a reward that is representative of all n buildings. It encourages net-zero energy use by penalizing grid-load satisfaction when there is energy in the battery, as well as penalizing net export when the battery is not fully charged through the penalty term (p). There is neither a penalty nor a reward when the battery is fully charged during net export to the grid, whereas when the battery is charged to capacity and there is net import from the grid, the penalty is maximized.
3.6. Baseline Comparison and Validation
Regarding the baseline comparison, the designed multi-agent controller is tested against various baselines as follows:
- RBC, in which rules are defined for charging and discharging and various rules are set [38];
- An adaptive controller based on tabular Q-Learning, which works with discrete observation and action spaces, so we have to convert the action and observation spaces in to discrete environments [39];
- A decentralized SAC controller, in which two buildings are controlled by one agent [40].
4. Results and Discussion
This section presents the empirical findings from our systematic evaluation of the multi-agent SAC controller for residential demand response. We begin by visualizing and characterizing the operational data for the selected buildings, including their non-shiftable load profiles and solar generation potential, as well as the associated carbon intensity signals. This initial analysis establishes the nature of the control challenge. Following this, we present the results for the no-control baseline, which serves as the reference point for all subsequent comparisons. We then evaluate the performance of several strong centralized benchmark controllers (RBC, TQL, and a decentralized SAC) to situate our approach within the context of existing methods.
4.1. Data Preprocessing and Visualization
Buildings 2 and 7 are selected at random for simulation purposes, and multi-agent SAC is employed for both of the buildings. The reason for the selection of two buildings is the fact that it takes considerable time for each agent to train for a whole year. Therefore, as a proof of concept, only two random buildings are selected, and the results can be extended to any number of buildings, given that the necessary compute is available.
Figure 7 and Figure 8 span one year at hourly resolution and depict the load and solar profile of building 2. The non-shiftable load shows a persistent base between roughly 1 and 4 kWh per hour, with occasional peaks that reach about 6 to 7 kWh. Day-to-day variability is evident, yet the baseline remains relatively stable, indicating that a sizable share of demand is not easily deferred. The PV series follows the expected daily and seasonal pattern. Output drops toward zero at regular intervals that align with night hours, then recovers during daylight. The annual envelope strengthens through midyear and peaks in late summer, after which it gradually weakens.
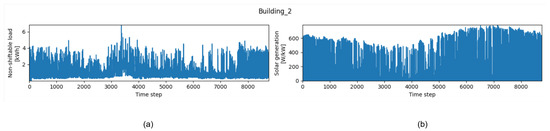
Figure 7.
Load and solar profiles of building 2 over the year. (a) Load profile; (b) solar profile.
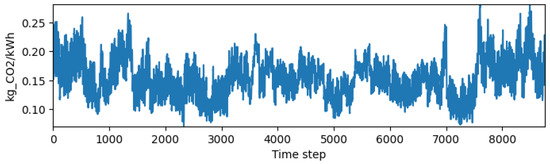
Figure 8.
Intensity of Building 2 over the year.
The carbon-intensity trace fluctuates between about 0.10 and 0.26 kg per kWh over the year. Several multi-day windows of comparatively low intensity appear in mid to late year, while higher plateaus are more common at the beginning and near the end of the record. The lack of a perfect alignment with PV availability is notable. Periods of abundant solar coincide with lower-than-average intensity only part of the time, which implies that carbon-aware control cannot rely on solar output alone.
The patterns of Building 2 indicate that an agent seeking to minimize both cost and emissions should prioritize charging during mid-day hours in summer when PV is strong and intensity is high. Discharge should target evening spikes in non-shiftable load, especially on days with higher-intensity supply. Because the three signals do not consistently move together, a multi-objective policy that adapts by season and learns building-specific habits is likely to perform better than a static rule set.
Relative to Building 2, Building 7 (Figure 9) exhibits a higher and steadier non-shiftable demand—typically, around 3.5 to 5 kWh per hour, with short spikes above 6 kWh. The PV series follows the familiar seasonal envelope, with a broad summer plateau and frequent short interruptions earlier in the year that may reflect cloud cover or brief inverter limits.

Figure 9.
Load and solar profiles of Building 7 over the year.
The grid-carbon intensity trace for Building 7 shown in Figure 10 spans roughly 0.10 to 0.26 kg per kWh and shows the same broad mid-year decline observed for Building 2. As the characteristics of the two buildings differ, multiple policies across both buildings are likely to benefit from seasonally adaptive thresholds and a small reserve that can be deployed on days when evening intensity is elevated.
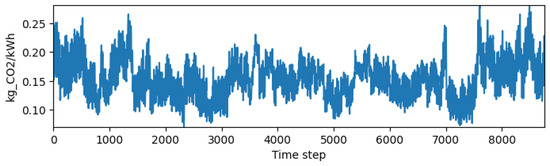
Figure 10.
Intensity of Building 7 over the year.
The meteorological record covers a full year at hourly resolution and reflects a coastal Southern California pattern, as depicted in Figure 11. The outdoor dry-bulb temperature is mostly between 15 and 25 °C, with a broad cool period near the middle of the series at around 8–10 °C, then a gradual return to warmer conditions toward the end. Relative humidity is generally elevated, often between 60 and 90%, with sharper drops during the drier season. Solar inputs follow a clear seasonal envelope. Direct irradiance weakens during the shorter days of winter and strengthens into a long summer plateau, while diffuse irradiance shows a complementary pattern with higher values during cloudier or lower-sun periods. The frequent short dips in both series likely reflect transient cloud cover or brief sensor clipping rather than sustained regime shifts.
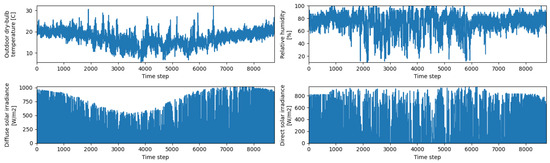
Figure 11.
Weather profile for Buildings 2 and 7.
Because Buildings 2 and 7 experience the same weather parameters as shown in Figure 12, differences in their load and PV profiles should be attributed to building characteristics and use rather than climate. For control design, the weather curves suggest broad mid-day charging opportunities in summer, when direct irradiance is strong, and a greater reliance on diffuse light and stored energy during winter. The mild winters also imply that comfort constraints can usually be met without exhausting storage, although short humid spells may still nudge cooling setpoints and increase latent loads.
Figure 12.
Outside weather of Building 2 and 7.
4.2. Implementation of Baseline
First, the baseline results are presented. A baseline agent is included in the CityLearn environment without controlling available DERs, which, in our case, are battery charge and discharge. The baseline serves as a crucial reference for quantifying the benefits of any control strategy. As expected, the normalized KPIs for cost and emissions shown in Figure 13 are 1.0, indicating the default state without control. More importantly, the baseline load profiles shown in Figure 14 and Figure 15 reveal the central challenge of this research. The distinct average daily load profiles for Building 2 and Building 7 establish the problem of heterogeneity. Building 2 exhibits a sharp evening peak, while Building 7 has a higher, more sustained load. This confirms that a single, rigid control strategy is unlikely to be optimal for both households. Therefore, an effective controller must be able to adapt to these unique local conditions.

Figure 13.
Cost and emissions of individual buildings.
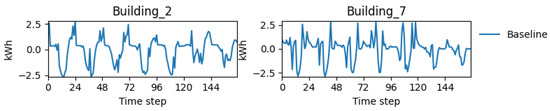
Figure 14.
Load profiles for individual buildings.

Figure 15.
Average daily load profiles of individual buildings.
Figure 14 depicts the load profile for a week for both the selected buildings. Remember that for better clarity, only a weekly record is displayed, and the vertical units depict the load. Consumption remains more or the less the same for Building 2, while Building 7 has reduced consumption during the last day. This shows that there are different load profiles for the different buildings that depend on various factors, such as the number of occupants and their comfort. This fact is also verified in Figure 15, which shows the average daily load profile for both the residential buildings. It can be seen from the graph that the demand of Building 2 is almost negligible during nighttime; then, it decreases to negative values due to solar generation is lowest in the afternoon, whereas it ramps up after 4 p.m. and attains the peak around 10 to 11 p.m., which is also the time when solar is not available. Building 7’s response is a bit different than that of Building 2, as its consumption typically increases from 10 a.m. to 12 p.m. after almost being negligible at night. Then, there is a linear increase in demand from 4 p.m. to 10 p.m., after which it declines to zero.
As there is no BESS control available during the baseline computation, it can be observed that battery SoC remains at zero, as shown in Figure 16, which depicts the fact that batteries are in a discharged state and there is no role of a BESS in the system.
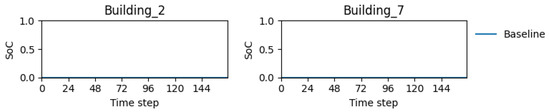
Figure 16.
Battery SoC of each building.
After displaying the individual KPIs, district-level KPIs are observed in Figure 17, which, as expected, shows a value of 1. This indicates that the KPIs remain in their initial state without any control in the system.

Figure 17.
District-level KPIs for baseline.
4.3. Implementation of Baseline Controllers
After the implementation of the baseline, an RBC controller, TQL, and centralized SAC controller are implemented in CityLearn to complete the benchmarking results. All of the implemented controllers are centralized in nature, which means that the same control strategy is applied to all the batteries in both the buildings. Figure 18 shows the cost and emission KPIs for individual buildings. It can be seen that RBC performs the best relative to TQL and the centralized SAC controller. The RBC performs surprisingly well, setting a high benchmark for the learning-based methods. Its effectiveness is rooted in its simple logic, which is well aligned with the strong diurnal patterns of solar generation and electricity tariffs. The RBC executes a static but effective strategy: it charges the battery during mid-day, when solar power is abundant, and discharges during the evening peak. In contrast, the centralized SAC controller (SAC-D), despite its advanced algorithm, struggles to consistently outperform this simple rule. The reason is architectural: the single agent must learn a compromised policy that attempts to serve both buildings simultaneously. This forces it to average the distinct needs of the two homes, resulting in a strategy that is not optimally tailored to either. This finding is significant, as it demonstrates that the choice of a sophisticated algorithm is insufficient if the control framework cannot address the underlying heterogeneity of the system. The poor performance of the TQL controller further highlights the difficulty of applying discrete methods to such a complex and continuous control problem. The simulation profile and average daily profile for both buildings are displayed in Figure 19 and Figure 20, with a relatively flat line in morning hours corresponding to a period when solar is high in demand, which means that batteries are charged at that time in the case of the RBC controller. Furthermore, the load is also reduced during peak evening times, which is indicative of batteries being discharged at that time to reduce grid stress. Hence, the RBC controller performed reasonably well for peak shaving and valley filling, which are the two main objectives of demand response. But the problem with a rule-based controller is that every building has unique characteristics, nd it is quite cumbersome to manually design the rules for optimal battery charging and discharging.
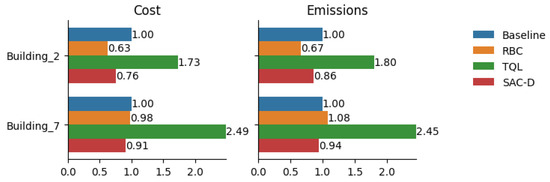
Figure 18.
Building-level KPI values for different controllers.
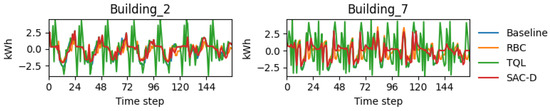
Figure 19.
Load profiles for different controllers.
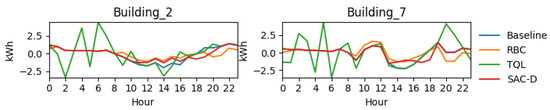
Figure 20.
Average load profiles for different controllers.
Figure 21 shows the pattern of battery charging and discharging. The reason that TQL performs the worst is evident from this chart, as the charging and discharging of batteries are not learned properly and the actions are random at best. Figure 22 shows all the possible values of the Q-table, which shows that there is not enough exploitation of optimal control actions and that the fails to find reasonable patterns. This could be due to limited training episodes as well. The rule-based controller charges and discharges the batteries during the first and second half of the day, respectively, and, hence, achieves better performance than all other implemented controllers.
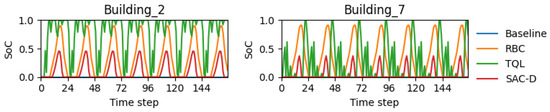
Figure 21.
State of charge for different controllers.
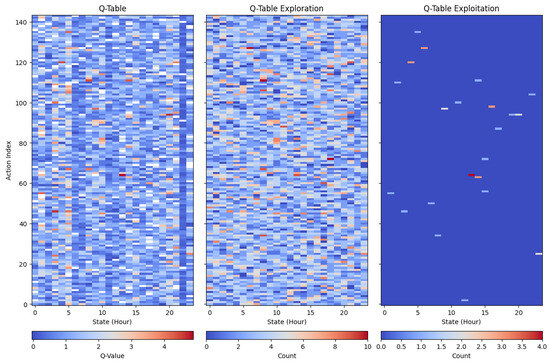
Figure 22.
Exploration vs. exploitation in tabular Q-learning.
District-level KPIs are shown in Figure 23, showing that the RBC also performs the best in all metrics. Our goal is to obtain minimum values for all KPIs below the baseline, with RBC and SAC achieving success with respect to these parameters. TQL, again, performed worst among all the implemented parameters. The next step is to implement the multi-agent SAC controller and perform hyperparameter tuning on the controllers, then compare the result of the multi-agent SAC controller that of a decentralized controller.
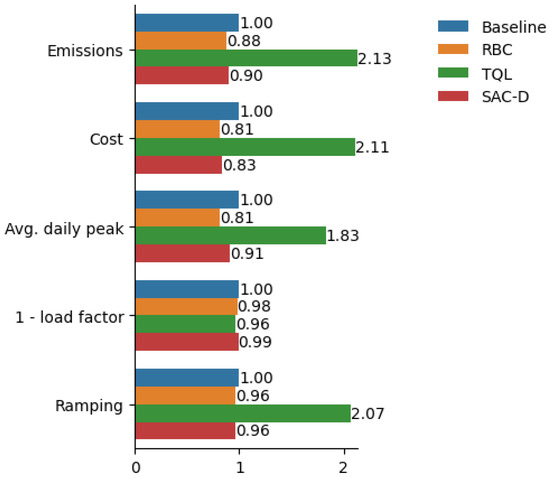
Figure 23.
District-level KPIs for different controllers.
4.4. Implementation of Multi-Agent SAC Controller
This subsection is attributed to implementation of a multi-agent SAC controller and tuning of hyperparameters to achieve the optimal results. The controller was implemented in the rllib library, which is a standard library for the implementation of multi-agent reinforcement learning. We adopt SAC as the RL control approach for battery management, assigning a separate agent to each building’s battery. SAC is a model-free, off-policy method [41]. As an off-policy algorithm, it can recycle past experience, which may reduce the number of interactions needed to learn useful behavior. The method combines an actor and a critic with off-policy updates and an entropy term that encourages exploration and tends to stabilize training. In practice, SAC learns three functions: a stochastic policy (the actor), a soft state–action value function (the critic), and a state value function (V).
The performance of reinforcement learning control algorithms is typically sensitive to hyperparameter choices, so a dedicated tuning phase is required. Each agent employs two hidden layers, with 256 units per layer. Policy updates use mini-batches of 256 samples drawn from a replay buffer of size 100,000. Training runs for 500 episodes. At the beginning of every episode, the environment is reset to its initial state (time step 0), and training proceeds until the terminal step is reached. Multiple episodes allow the agent to explore a broader action space and, over time, to converge toward higher-value decisions across diverse observation patterns, which tends to raise the cumulative reward.
For the hyperparameters that most affect performance (Table 3), we conduct a grid search. The target-network decay () controls the magnitude of each SAC target-network update. The discount factor () trades off immediate versus future returns, with focusing exclusively on the present and valuing the long-horizon reward. The learning rate () determines how quickly estimated Q-values are updated; a larger replaces prior estimates more aggressively and may increase forgetting of past information. The temperature( ) balances exploitation and exploration in the policy, tending toward purely greedy selections at and increasingly exploratory behavior as T approaches 1.

Table 3.
Hyperparameter search grid for SAC.
Results for cost and emissions of multi-agent SAC controllers are reported in Figure 24, where it is shown that SAC in a multi-agent configuration (green bar) performs best, with an almost 50% reduction when employing multi-agent SAC. Considerable effects in emissions are also observed. Figure 25 and Figure 26 show that the load profile is also flat, which is highly desirable, as the buildings are now operating sustainable, with excess power from solar charged during the daytime and discharged during the peak hours of consumption. This reduces gird stress and helps in demand response by shifting the load as desired.
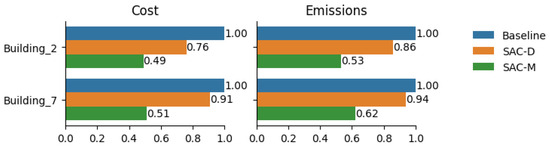
Figure 24.
Building-level KPIs for multi-agent SAC.
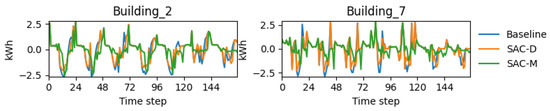
Figure 25.
Load profile for multi-agent SAC.
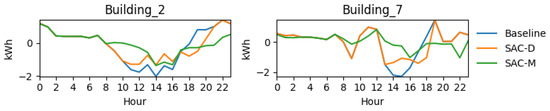
Figure 26.
Average load profile for multi-agent SAC.
The SoC for both buildings (Figure 27) indicates that batteries are charged fully and more or less follows the trend of the RBC-based controller but in a more optimized way. The plot shows that the agents learned a consistent and effective policy: they systematically charge the batteries to near-maximum capacity during the mid-day hours, a period that corresponds perfectly with peak solar generation. This action demonstrates that the agents successfully learned to harvest and store available renewable energy. Subsequently, the traces show a complete discharge of the batteries during the evening hours, specifically between 4 p.m. and 9 p.m., which aligns with the period of highest grid demand and peak electricity prices. The results are even better than those of the RBC-based controller, without the need for manual labor to set the rules for charging and discharging. As depicted in Figure 28, District-level KPIs are also improved significantly in the case of emissions, cost, daily peak, and ramping, where a minimum of 15% and maximum of 50% reduction is achieved. The only KPI that does not improve significantly is the load factor, but its value is still better than all of the controllers. Hence, it is evident that SAC in a decentralized configuration significantly outperforms the battery controller in a centralized configuration. The reason behind decentralized SAC outperforming the centralized configuration is the fact that each controller is now able to independently charge and discharge the battery; thus, the policy for each building is optimal to its locality. By absorbing the mid-day solar surplus and dispatching it to cover the evening load, the batteries act as intelligent energy buffers, effectively shielding the grid from the buildings’ peak demand. This learned behavior is also more pronounced than the static schedule of the RBC. It is an adaptive policy that can adjust to daily variations in weather and load, which is why it not only matches but significantly surpasses the strong RBC benchmark. This in-depth analysis confirms that the success of the multi-agent framework is not superficial but is the direct result of independent agents learning an effective, interpretable, and locally tuned control strategy to achieve significant system-wide benefits.
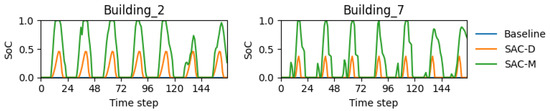
Figure 27.
SoC for each building for multi-agent SAC.
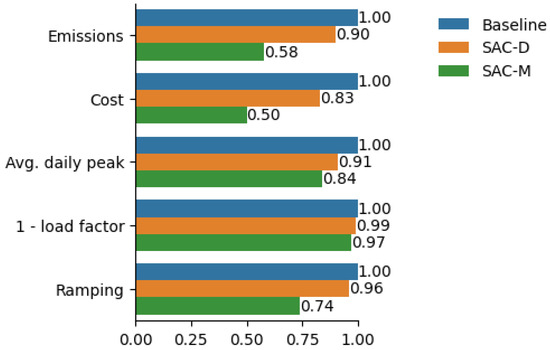
Figure 28.
District-level KPIs for multi-agent SAC.
4.5. Discussion
A closer examination of the results reveals important insights into the nature of residential energy control. The baseline case, with its uncontrolled energy flow, serves as more than a simple benchmark. It illustrates the core challenge of heterogeneity. The distinct consumption and generation signatures of Building 2 and Building 7, despite identical weather, confirm that residential loads are not uniform. This diversity means that effective control strategies must be inherently adaptive and capable of conforming to the specific needs and opportunities of each individual household. A single, rigid control logic is bound to be inefficient when applied across a diverse community.
The performance of the centralized controllers provides a compelling narrative about the limits of generalized approaches. The rule-based controller proved to be a surprisingly formidable benchmark. Its success can be attributed to the strong, predictable diurnal patterns present in both the time-of-use electricity tariffs and the solar generation profiles. A simple time-based heuristic that aligns charging with cheap, sunny hours and discharging with expensive evening peaks captures a substantial portion of the available economic and grid-stabilizing benefits. This outcome reinforces the notion that for problems with clear, cyclical drivers, simple rules can be highly effective. The central problem in using an RBC is its inherent rigidity and its complete inability to handle heterogeneity. Our results provide a clear example of this flaw: the RBC’s fixed schedule was highly effective for Building 2, whose load profile happened to align well with the pre-defined rules. However, the same rules offered almost no benefit to Building 7, demonstrating the ‘one-size-fits-all’ problem. This inflexibility means an RBC cannot adapt to real-world dynamics; it would fail to capitalize on an unusually sunny winter day, could not react to a sudden grid price spike outside its fixed schedule, and would become obsolete if a household’s consumption patterns changed.
Furthermore, the struggles of tabular Q-learning and even the centralized SAC controller are equally telling. These agents, tasked with learning a single policy for both buildings, were forced into a middle ground, averaging the needs of two different systems. This averaging effect diluted the policy’s effectiveness, preventing it from fully exploiting the unique potential within either building and ultimately failing to consistently surpass the simple RBC. The tabular Q-learning agent’s particularly poor performance is attributed to two reasons. First is the curse of dimensionality, which is exacerbated by the necessary discretization of the continuous state space. To create a finite Q-table, continuous variables like SoC, price, and solar forecasts must be binned, leading to a combinatorial explosion in the number of states. The agent can only explore a tiny fraction of this vast state space during training, leaving its value estimates unreliable. Second, this coarse binning leads to a critical loss of information, where the agent cannot distinguish between subtly different but important conditions, causing it to receive conflicting rewards for what it perceives as the same state. This directly results in the observed inconsistent, thrashing behavior. Together, these issues highlight why tabular methods are ill-suited for complex, continuous control problems, reinforcing the need for function approximation methods like those used in SAC.
The superior performance of the multi-agent SAC framework is therefore the central finding of this work, and its success is rooted in its direct confrontation of the issue of heterogeneity. By assigning an independent agent to each building, the system allows for the development of specialized, locally optimal control policies. We can infer that the agent for Building 7, with its higher and steadier load, likely learned a more aggressive discharge strategy for the evening peak, while the agent for Building 2 may have adopted a more conservative policy to handle its sporadic, high-magnitude spikes. This capacity for tailored adaptation is something a centralized controller simply cannot achieve.
The choice of the Soft Actor–Critic algorithm was also pivotal to this success. The energy management problem involves a continuous range of decisions over a long, year-long horizon with significant seasonal variations. The algorithm’s off-policy nature grants it the sample efficiency needed to learn effectively from this extensive dataset, reusing past experiences to speed up learning. Perhaps the most significant finding for future scalability is the evidence of emergent coordination. Although the agents operate independently, their collective behavior produces a coherent, beneficial outcome at the district level: a flatter, more stable grid load. This coordination arises not from direct communication but from the agents’ shared motivation to respond to common environmental signals—namely, the electricity price and carbon intensity. When the price is high, every agent is independently incentivized to discharge its battery, leading to a synchronized reduction in aggregate demand. This suggests that a highly effective and coordinated virtual power plant can be realized without the complexity and communication overhead of a centralized command-and-control system, pointing toward a more resilient and scalable architecture for future smart grids.
It is also important to note the framework’s inherent adaptability to different seasonal regimes. While the presented detailed behavioral results (e.g., Figure 27) highlight a typical high-solar period characteristic of summer, the control logic naturally extends to winter conditions. In summer, the agents maximize value primarily through solar load shifting (charging with excess mid-day PV and discharging during evening cooling peaks). In winter, when solar generation is weak and heating loads are high, the same cost-minimizing reward function will drive the agents toward price arbitrage. Instead of relying on solar, the agents will learn to charge from the grid during the lowest-cost off-peak windows (typically post midnight) to have energy available for the evening heating peak. This ability to autonomously switch between solar-shifting and price-arbitrage strategies based on available signals is a key advantage of the learning-based approach over static rule-based controllers, which would require manual reprogramming to handle such seasonal shifts effectively.
5. Conclusions
This paper presented and evaluated a multi-agent deep reinforcement learning framework for automated demand response in residential buildings equipped with battery energy storage systems. The objective was to develop a decentralized control strategy capable of coordinating individual building actions to achieve collective benefits in terms of economic cost, carbon emissions, and grid stability. By employing the Soft Actor–Critic algorithm, a separate agent was assigned to manage the battery of each building, enabling it to learn control policies tailored to the unique load profiles and photovoltaic generation patterns of its assigned residence while responding to shared environmental signals. The results demonstrated that the proposed multi-agent SAC controller outperformed several centralized controllers, including a rule-based controller, tabular Q-Learning, and a single-agent SAC. The multi-agent approach achieved a considerable reduction in both electricity cost and carbon emissions, with building-level improvements approaching 50%. This performance was realized by effectively learning an optimal battery dispatch strategy: charging during periods of high solar generation and low grid prices and discharging to offset load during evening peak hours. This behavior not only benefited individual households but also produced a significantly flatter aggregate load profile at the district level, leading to marked improvements in critical grid metrics such as average daily peak, ramping, and load factor. The findings confirm that multi-agent systems can successfully counter the heterogeneity inherent in residential communities, which is a critical challenge for centralized controllers. The ability of individual agents to optimize locally while contributing to global objectives presents a viable pathway for integrating distributed energy resources into the grid in a coordinated and beneficial manner. The findings confirm that multi-agent systems can successfully counter the heterogeneity inherent in residential communities, which is a critical challenge for centralized controllers. The ability of individual agents to optimize locally while contributing to global objectives presents a viable pathway for integrating distributed energy resources into the grid in a coordinated and beneficial manner. The primary practical contribution is therefore a control framework that can autonomously manage diverse residential assets at scale, offering utilities and aggregators a viable pathway to coordinate distributed resources without the need for complex, individualized building models. A critical aspect of the multi-agent system’s success is the mechanism of emergent coordination, which allows local decisions to optimize aggregate objectives at the district level. It is important to distinguish between the roles of different shared environmental signals. While meteorological data like temperature and humidity are shared and influence each building’s individual energy needs, the primary drivers of coordination are the shared economic signals, particularly the electricity price. This price signal creates a powerful and identical incentive for all agents to act upon simultaneously. The goal is to optimize the aggregate outcome, which refers to the sum total of the energy drawn from the grid by both buildings, not simply their average. Coordination is an emergent property arising from this shared incentive. For instance, when the grid price peaks, this signal is broadcast to all agents. Each self-interested agent independently determines that its best local action to minimize its own cost is to discharge its battery. The sum of these locally optimal, independent decisions results in a synchronized discharge across the entire district, which effectively flattens the aggregate net-load profile. From a game-theoretic perspective, the reward structure aligns individual incentives with the global objective. The visual evidence for this synchronized behavior is clear in the state-of-charge traces in Figure 27, which show the batteries for the two buildings charging and discharging in near-perfect unison, driven not by communication but by a shared, external economic driver. There are, however, certain limitations. The analysis was conducted on two buildings as a foundational proof of concept, which allows for a deep, behavioral interpretation of the learned policies but does not constitute a comprehensive verification of the framework’s performance at a larger scale. Extending the system to a larger and more diverse fleet of buildings introduces several critical challenges that must be addressed in future work. While our decentralized framework is designed to minimize direct communication overhead by relying on broadcast environmental signals rather than peer-to-peer messaging, the infrastructure required to deliver these signals reliably to hundreds or thousands of agents would need careful design to avoid latency issues. More critically, there is a potential for inter-agent strategy conflicts that can arise from the collective impact of agents on the physical grid. In our current simulation, the grid is treated as an infinite bus, meaning one agent’s actions do not affect the environment another agent observes. However, in a real distribution network, the simultaneous discharge of dozens of batteries could cause local voltage swells or other instabilities. This introduces a form of non-stationarity into the environment, where the agents’ collective actions change the rules of the game. A large-scale deployment would require co-simulation with a power distribution network model to study and mitigate these effects. A further limitation is the policy’s static nature relative to the tariff structure. The agents’ learned policies are highly optimized for the economic conditions present during training and cannot dynamically adapt to significant changes, such as a utility altering the time-of-use (TOU) price gap. In such a scenario, the learned strategy would become sub-optimal, and the agents would require retraining on the new data. This highlights an important avenue for future research into online learning methods that would enable agents to continuously adapt to evolving pricing schemes. The underperformance of Q-learning may reflect the discrete formulation and limited training horizon rather than a fundamental ceiling of value-based methods. Finally, CityLearn relies on precomputed loads and internal device models, so co-simulation with full physics engines could reveal interactions not captured here. There are several avenues for future research as well. As mentioned above, the analysis was conducted on two buildings as a proof of concept. Future work should investigate the scalability and performance of the framework across a larger and more diverse fleet of buildings, incorporating potential network constraints. A key limitation of this study is that it evaluates the controller’s performance on a holistic, aggregate basis over a full year. While the year-long simulation data naturally contains a wide variety of events, including days with significant PV generation fluctuations due to weather, we did not perform a fine-grained analysis of the agent’s behavior during such specific, off-normal conditions. Similarly, we did not explicitly model a “grid emergency” event to test the system’s response to an extreme, short-notice demand-response signal. The analysis of such critical events is a crucial avenue for future research. Further refinement of the reward function could also be explored to target additional grid services or to more explicitly balance competing objectives. Finally, validating the proposed controller within a co-simulation environment that integrates detailed building physics models would further strengthen the findings by capturing more complex thermal and electrical dynamics.
Author Contributions
Conceptualization, S.S., M.A. and A.M.; methodology, S.S., B.L. and Q.G.; software, S.S., Y.K. and B.B.; validation, Q.G., Y.K. and B.B.; formal analysis, M.A., B.L. and A.M.; investigation, S.S., B.L. and M.A.; resources, B.L., Q.G. and Y.K.; data curation, A.M. and Y.K.; writing—original draft preparation, S.S., B.L. and A.M.; writing—review and editing, M.A., Q.G., Y.K. and B.B.; visualization, B.B. and Y.K.; supervision, B.L., Q.G. and Y.K.; project administration, B.L., Q.G. and Y.K.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Beijing Changping District’s Special Program for Science and Technology Deputy Chief under the title, “Construction of a Resource Pool for the New-Type Power Load Management System and Development of Interactive Simulation Software” (2023-806).
Data Availability Statement
Data will be made available upon request to the corresponding author. The data are not publicly available due to [privacy and inclusion of compute APIs].
Acknowledgments
The authors would like to thank Beijing Changping District’s Special Program for Science and Technology.
Conflicts of Interest
Authors Qi Guo, Yi Kang were employed by the company Inner Mongolia Power (Group) Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Goldstein, B.; Gounaridis, D.; Newell, J.P. The carbon footprint of household energy use in the United States. Proc. Natl. Acad. Sci. USA 2020, 117, 19122–19130. [Google Scholar] [CrossRef]
- de Oliveira, R.S.; de Oliveira, M.J.L.; Nascimento, E.G.S.; Sampaio, R.; Nascimento Filho, A.S.; Saba, H. Renewable energy generation technologies for decarbonizing urban vertical buildings: A path towards net zero. Sustainability 2023, 15, 13030. [Google Scholar] [CrossRef]
- Lu, X.; Li, H.; Zhou, K.; Yang, S. Optimal load dispatch of energy hub considering uncertainties of renewable energy and demand response. Energy 2023, 262, 125564. [Google Scholar] [CrossRef]
- Chatuanramtharnghaka, B.; Deb, S.; Singh, K.R.; Ustun, T.S.; Kalam, A. Reviewing demand response for energy management with consideration of renewable energy sources and electric vehicles. World Electr. Veh. J. 2024, 15, 412. [Google Scholar] [CrossRef]
- Neukomm, M.; Nubbe, V.; Fares, R. Grid-Interactive Efficient Buildings; Technical report; US Department of Energy (USDOE): Washington, DC, USA; Navigant: Colorado Springs, CO, USA, 2019.
- Algarvio, H.; Lopes, F. Bilateral contracting and price-based demand response in multi-agent electricity markets: A study on time-of-use tariffs. Energies 2023, 16, 645. [Google Scholar] [CrossRef]
- Golmohamadi, H. Demand-side flexibility in power systems: A survey of residential, industrial, commercial, and agricultural sectors. Sustainability 2022, 14, 7916. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. A review of residential demand response of smart grid. Renew. Sustain. Energy Rev. 2016, 59, 166–178. [Google Scholar] [CrossRef]
- Stanelyte, D.; Radziukyniene, N.; Radziukynas, V. Overview of demand-response services: A review. Energies 2022, 15, 1659. [Google Scholar] [CrossRef]
- Burger, S.; Chaves-Ávila, J.P.; Batlle, C.; Pérez-Arriaga, I.J. A review of the value of aggregators in electricity systems. Renew. Sustain. Energy Rev. 2017, 77, 395–405. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T. Reinforcement learning for building controls: The opportunities and challenges. Appl. Energy 2020, 269, 115036. [Google Scholar] [CrossRef]
- Mariano-Hernández, D.; Hernández-Callejo, L.; Zorita-Lamadrid, A.; Duque-Pérez, O.; García, F.S. A review of strategies for building energy management system: Model predictive control, demand side management, optimization, and fault detect & diagnosis. J. Build. Eng. 2021, 33, 101692. [Google Scholar] [CrossRef]
- Hu, G.; You, F. Multi-zone building control with thermal comfort constraints under disjunctive uncertainty using data-driven robust model predictive control. Adv. Appl. Energy 2023, 9, 100124. [Google Scholar] [CrossRef]
- Chen, W.H.; You, F. Sustainable building climate control with renewable energy sources using nonlinear model predictive control. Renew. Sustain. Energy Rev. 2022, 168, 112830. [Google Scholar] [CrossRef]
- Antunes, C.H.; Alves, M.J.; Soares, I. A comprehensive and modular set of appliance operation MILP models for demand response optimization. Appl. Energy 2022, 320, 119142. [Google Scholar] [CrossRef]
- Pang, S.; Zheng, Z.; Xiao, X.; Huang, C.; Zhang, S.; Li, J.; Zong, Y.; You, S. Collaborative power tracking method of diversified thermal loads for optimal demand response: A MILP-Based decomposition algorithm. Appl. Energy 2022, 327, 120006. [Google Scholar] [CrossRef]
- Sharma, P.; Mathur, H.D.; Mishra, P.; Bansal, R.C. A critical and comparative review of energy management strategies for microgrids. Appl. Energy 2022, 327, 120028. [Google Scholar] [CrossRef]
- Yang, S.; Gao, H.O.; You, F. Model predictive control for Demand-and Market-Responsive building energy management by leveraging active latent heat storage. Appl. Energy 2022, 327, 120054. [Google Scholar] [CrossRef]
- Ceusters, G.; Rodríguez, R.C.; García, A.B.; Franke, R.; Deconinck, G.; Helsen, L.; Nowé, A.; Messagie, M.; Camargo, L.R. Model-predictive control and reinforcement learning in multi-energy system case studies. Appl. Energy 2021, 303, 117634. [Google Scholar] [CrossRef]
- Ajagekar, A.; You, F. Deep reinforcement learning based unit commitment scheduling under load and wind power uncertainty. IEEE Trans. Sustain. Energy 2022, 14, 803–812. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Jin, R.; Zhou, Y.; Lu, C.; Song, J. Deep reinforcement learning-based strategy for charging station participating in demand response. Appl. Energy 2022, 328, 120140. [Google Scholar] [CrossRef]
- Azuatalam, D.; Lee, W.L.; De Nijs, F.; Liebman, A. Reinforcement learning for whole-building HVAC control and demand response. Energy AI 2020, 2, 100020. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X.; Zhao, J.; Li, W.; Li, H.; Wang, Y.; Deng, S.; Zhu, J. Deep reinforcement learning framework for dynamic pricing demand response of regenerative electric heating. Appl. Energy 2021, 288, 116623. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Zhang, X. A dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Aladdin, S.; El-Tantawy, S.; Fouda, M.M.; Eldien, A.S.T. MARLA-SG: Multi-agent reinforcement learning algorithm for efficient demand response in smart grid. IEEE Access 2020, 8, 210626–210639. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef]
- Nagarathinam, S.; Menon, V.; Vasan, A.; Sivasubramaniam, A. Marco-multi-agent reinforcement learning based control of building hvac systems. In Proceedings of the Eleventh ACM International Conference on Future Energy Systems, Melbourne, Australia, 22–26 June 2020; pp. 57–67. [Google Scholar]
- Zhang, Q.; Dehghanpour, K.; Wang, Z.; Qiu, F.; Zhao, D. Multi-agent safe policy learning for power management of networked microgrids. IEEE Trans. Smart Grid 2020, 12, 1048–1062. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, R.; Jiang, J.; Hong, S.H.; Song, W.S. Testbed implementation of reinforcement learning-based demand response energy management system. Appl. Energy 2021, 297, 117131. [Google Scholar] [CrossRef]
- Vazquez-Canteli, J.R.; Henze, G.; Nagy, Z. MARLISA: Multi-agent reinforcement learning with iterative sequential action selection for load shaping of grid-interactive connected buildings. In Proceedings of the 7th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, Virtual Event, 18–20 November 2020; pp. 170–179. [Google Scholar]
- Liu, J.; Gu, X.; Liu, S. Policy optimization reinforcement learning with entropy regularization. arXiv 2019, arXiv:1912.01557. [Google Scholar]
- Narayanamurthy, R.; Handa, R.; Tumilowicz, N.; Herro, C.; Shah, S. Grid Integration of Zero net Energy Communities. 2016 ACEEE Summer Study on Energy Efficiency in Buildings. 2016. Available online: https://www.aceee.org/files/proceedings/2016/data/papers/10_1165.pdf (accessed on 27 October 2025).
- Nweye, K.; Sankaranarayanan, S.; Nagy, Z. MERLIN: Multi-agent offline and transfer learning for occupant-centric operation of grid-interactive communities. Appl. Energy 2023, 346, 121323. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Kämpf, J.; Henze, G.; Nagy, Z. Citylearn v1. 0: An openai gym environment for demand response with deep reinforcement learning. In Proceedings of the 6th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, New York, NY, USA, 13–14 November 2019; pp. 356–357. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Alimohammadisagvand, B.; Jokisalo, J.; Sirén, K. Comparison of four rule-based demand response control algorithms in an electrically and heat pump-heated residential building. Appl. Energy 2018, 209, 167–179. [Google Scholar] [CrossRef]
- Tai, C.S.; Hong, J.H.; Hong, D.Y.; Fu, L.C. A real-time demand-side management system considering user preference with adaptive deep Q learning in home area network. Sustain. Energy Grids Netw. 2022, 29, 100572. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Lee, W.J. Soft actor–critic algorithm featured residential demand response strategic bidding for load aggregators. IEEE Trans. Ind. Appl. 2022, 58, 4298–4308. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Pmlr, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).