Nodal Marginal Price Decomposition Mechanism for the Hydrogen Energy Market Considering Hydrogen Transportation Characteristics
Abstract
1. Introduction
- The study constructs a comprehensive marginal price decomposition framework for hydrogen markets, explicitly incorporating the time-delay characteristics of pipeline transport. This framework introduces the Time-Delay Component (TDC) as a fundamental price element, alongside the traditional energy component (EC), network loss component (NLC) and congestion component (CC), providing a more complete reflection of the physical realities and costs of hydrogen energy delivery. The improved second-order cone programming method is proposed to solve the non-convex problem in hydrogen market modeling. This problem arises from time-period coupling constraints and the Weymouth equation. The method significantly reduces computational complexity.
- We propose an improved second-order cone programming algorithm to address the nonconvexities arising from the Weymouth equation and intertemporal coupling constraints. This method transforms the original problem into a tractable mixed-integer second-order cone programming problem through a series of reformulations and introduces an iterative penalty mechanism to ensure convergence, significantly reducing computational complexity while maintaining high solution accuracy.
- The research quantifies the dominant role and dynamic coupling of each price component under various operational conditions, confirming that the nodal marginal price decomposition mechanism accurately captures the drivers of spot prices, including network congestion, transmission loss, and temporal delay effects. Experiments demonstrate that the improved second-order cone programming algorithm is computationally efficient and scalable for solving real-world problems. Furthermore, comparative analysis of pricing mechanisms reveals the superiority of nodal marginal pricing in facilitating high renewable energy integration and large-scale hydrogen development, providing theoretical and practical support for building an efficient hydrogen market.
2. Hydrogen Market Modeling
2.1. Market Structure and Assumptions
- Market timescales: A static time-series optimization framework using a uniform day-ahead market trading cycle that ignores real-time market dynamics.
- Load Characteristics: Hydrogen loads constitute rigid demand and do not consider demand-side elastic response mechanisms.
- Supply-side structure: All hydrogen producers use electrolytic hydrogen plants, assuming that the electrolysis plant operates at a constant efficiency. Electricity and hydrogen conversion satisfy a linear relationship.
- Pipe network modeling: Neglect topographic elevation differences and radial air pressure gradients, assuming that the pipe network has uniform temperatures and constant flow rates and does not require spatial discretization.
- Market Behavior: Hydrogen producers offer at true marginal cost, no strategic gaming behavior.
2.2. Basic Hydrogen Market Clearing Model
2.2.1. Objective Function
2.2.2. Constraints of the Hydrogen Energy Market Model
- Cost Factor for Hydrogen Production
- 2.
- Hydrogen Market Node Hydrogen Pressure
- 3.
- Electrolytic Hydrogen Production
- 4.
- Pipeline Hydrogen Transmission
- 5.
- Hydrogen Transportation Pipeline Flow
- 6.
- Delay Properties of Hydrogen Transportation
- 7.
- Nodal Hydrogen Balance Constraints
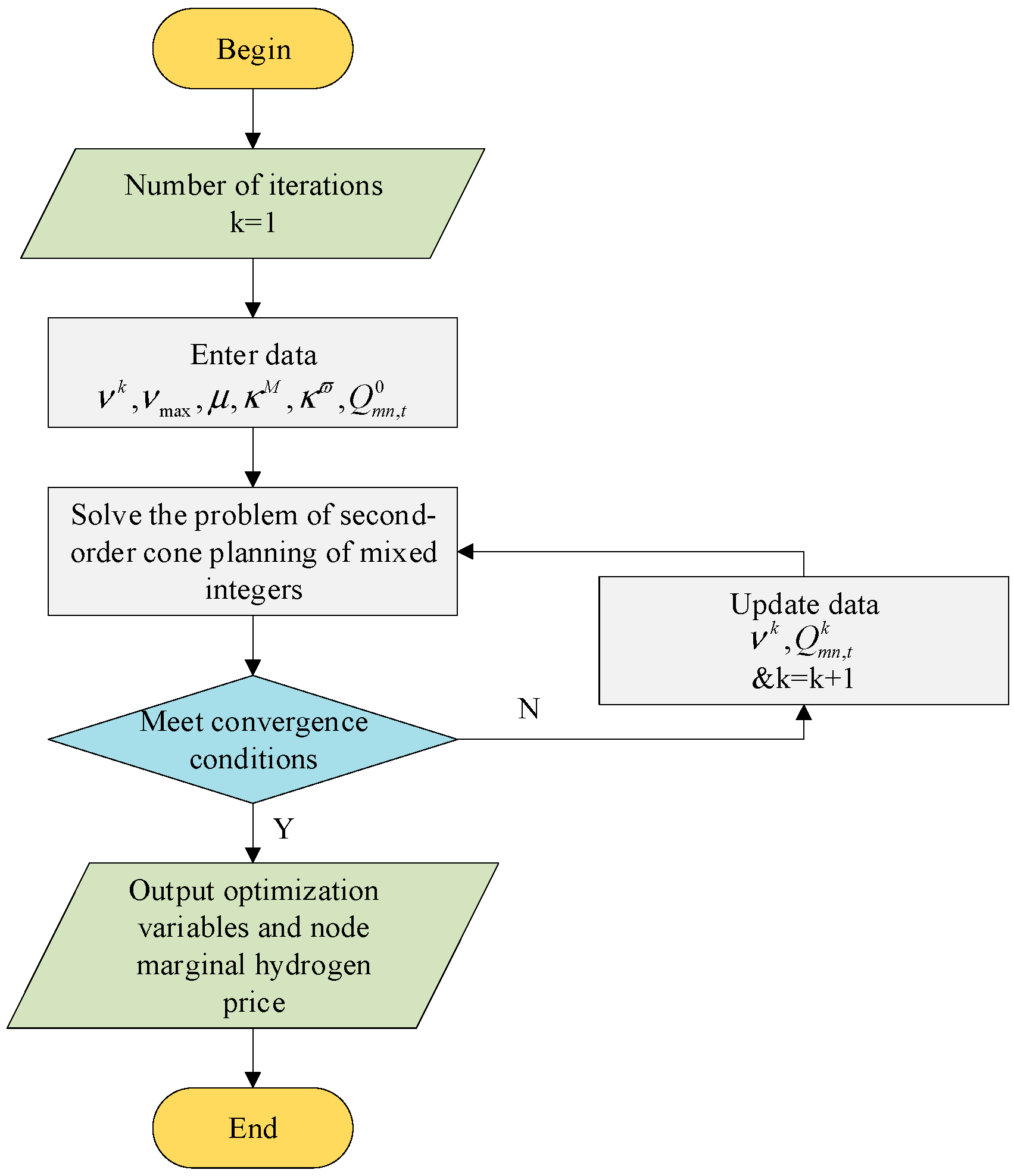
3. Modified Hydrogen Market Clearing Model by Improved Second-Order Cone Algorithm
3.1. Weymouth Equation Model Transformation
3.2. Improved Second-Order Cone Algorithm
4. Implementation of Marginal Price Decomposition in the Hydrogen Market Clearing Model
4.1. A Lagrangian Function for Hydrogen Market Clearing Model
4.2. KKT Conditions for Hydrogen Market Clearing Model
4.3. Jacobian Matrix for Hydrogen Market Clearing Model
4.4. Nodal Marginal Hydrogen Prices for Hydrogen Market Clearing Model
5. Case Studies
5.1. Basic Information
5.2. Comparison of Different Pricing Mechanisms
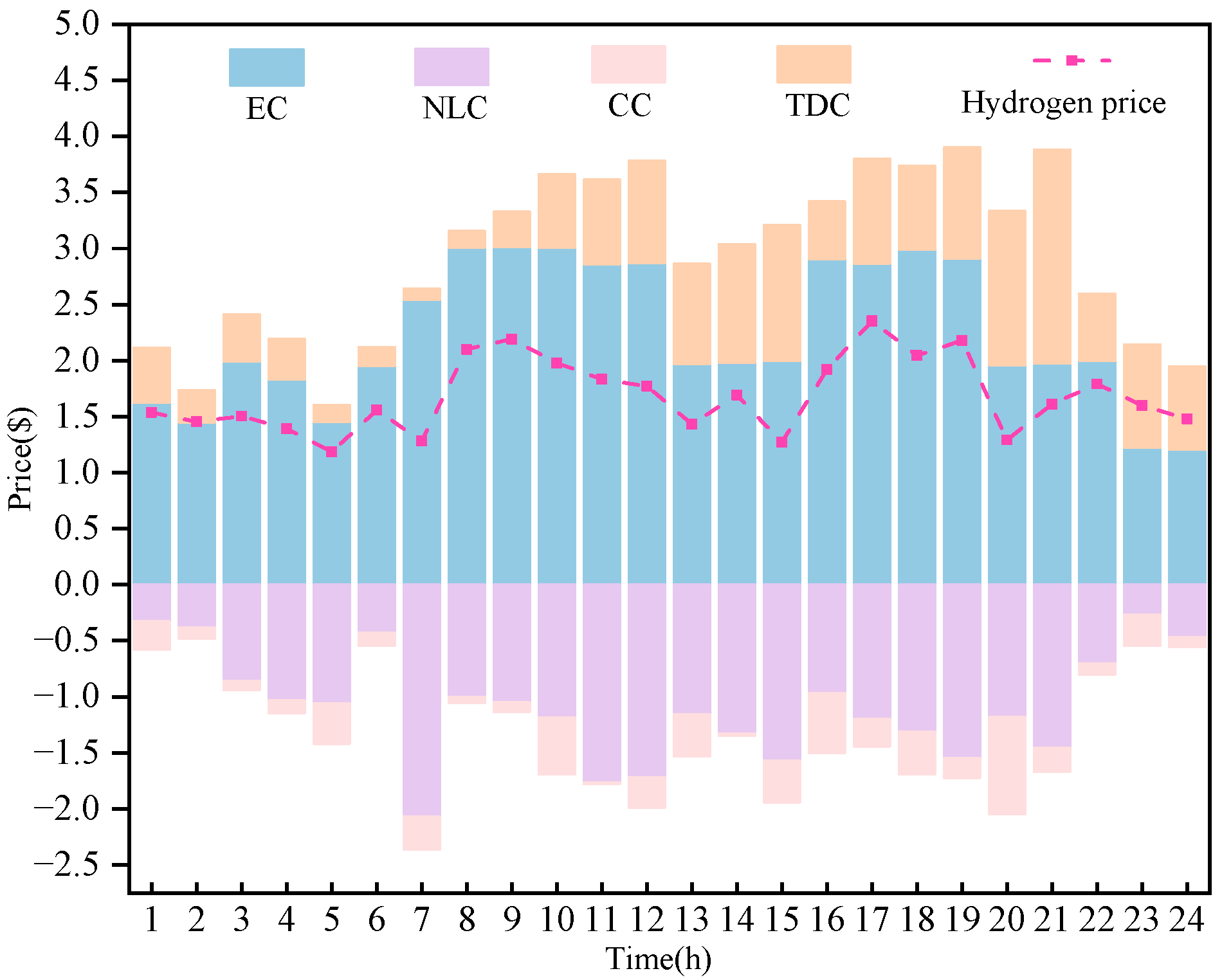
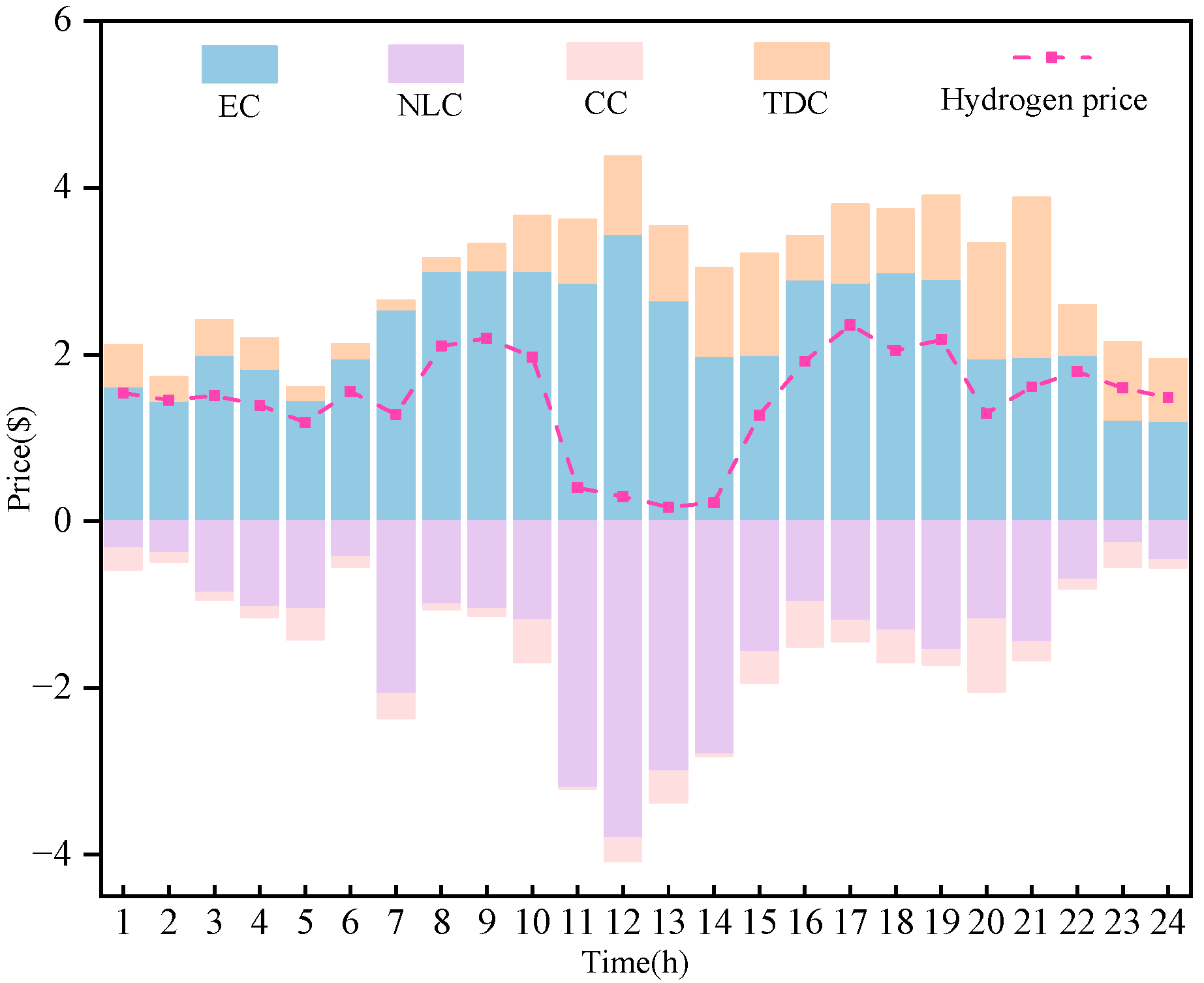
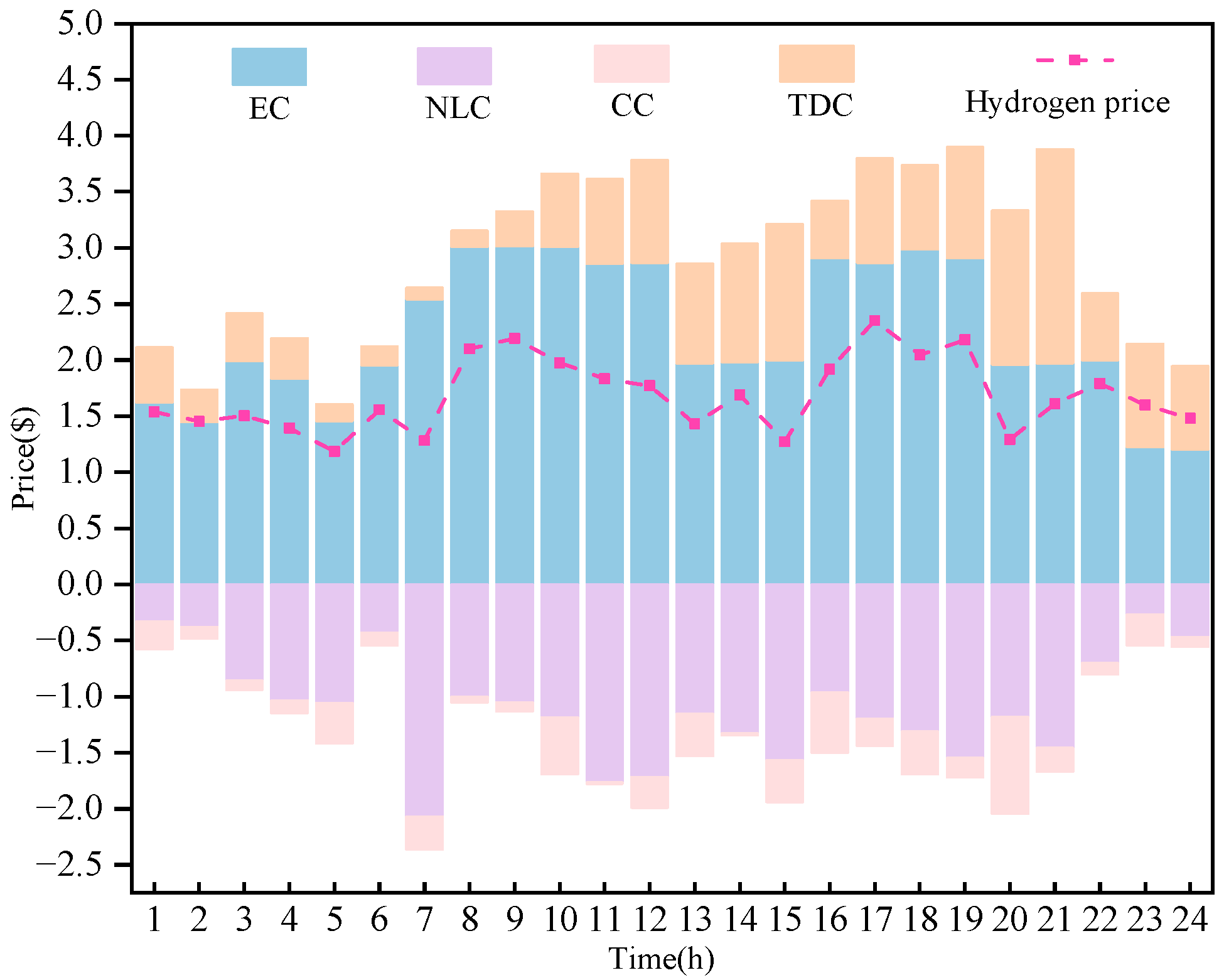
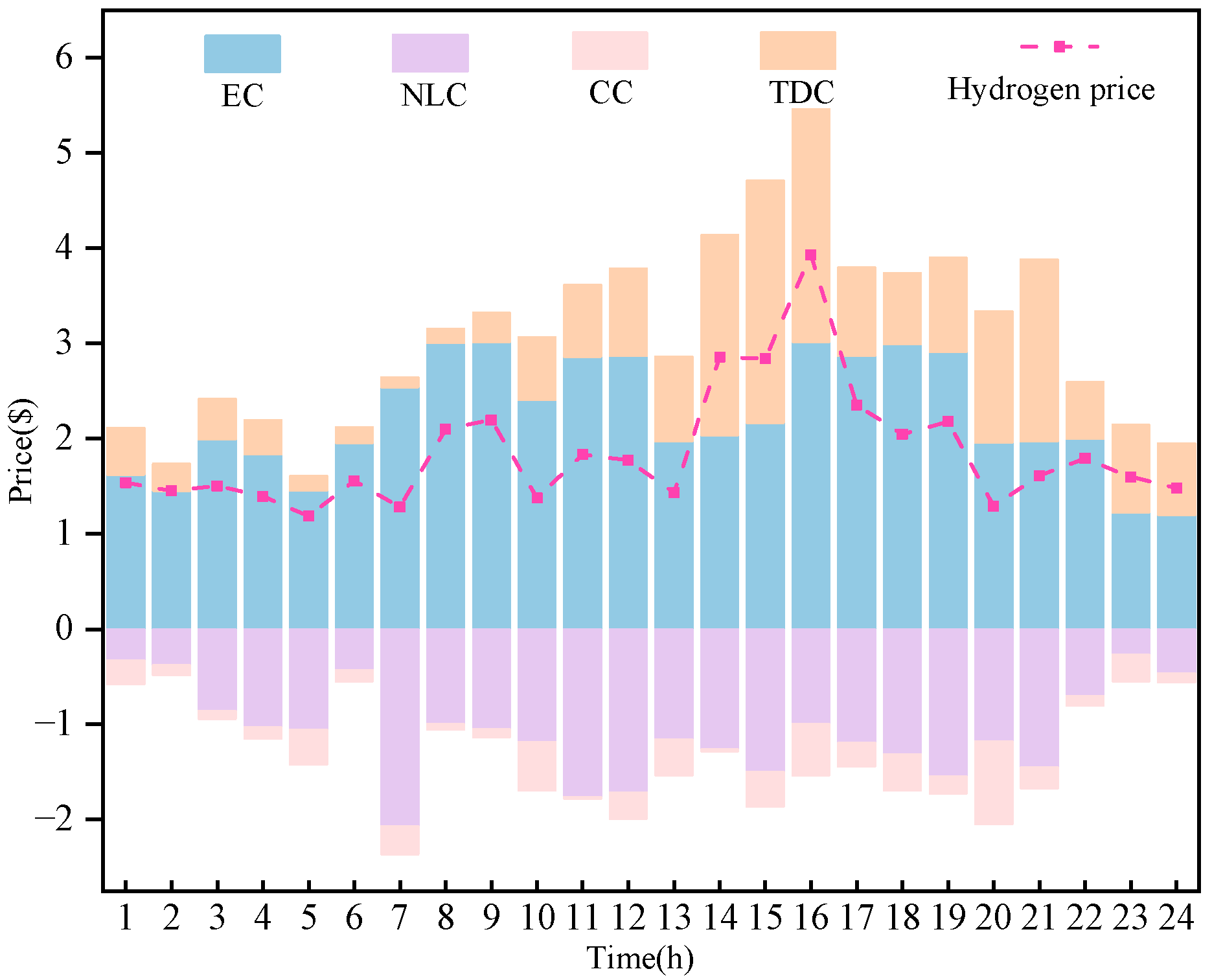
5.3. Decomposition of Nodal Marginal Hydrogen Valence
5.4. The Effect of the Choice of Different Reference Nodes on the Decomposition of Hydrogen Prices
5.5. Scalability Analysis for Large-Scale Integrated Systems
5.6. Distribution of Price Components Under Different Operating Conditions
6. Conclusions and Discussions
- A novel four-dimensional price decomposition framework was established to accurately reflect the full cost of hydrogen transmission. By integrating the TDC with the EC, NLC and CC, the proposed nodal marginal hydrogen price provides a more comprehensive and physically interpretable pricing signal. This framework successfully quantifies the often-overlooked temporal costs associated with the finite propagation speed of hydrogen in pipelines, offering a foundational theory for hydrogen market design.
- The empirical analysis verified the superiority of this mechanism and provided key insights for market operations. Case studies show that the LMP mechanism is dynamically correlated with load and electricity costs and outperforms the average pricing mechanism and time-of-use pricing mechanism in terms of economic efficiency. The research results also quantified the impact of reference node selection on price components and revealed the conditions under which NLC, CC or TDC become dominant price drivers, providing valuable guidance for the future design of the hydrogen energy market and infrastructure planning.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Tian, X.; Chi, Y.; Li, L.; Liu, H. Review of the configuration and transient stability of large-scale renewable energy generation through hybrid DC transmission. CES Trans. Electr. Mach. Syst. 2024, 8, 115–126. [Google Scholar] [CrossRef]
- Sakib, A.N.; Mehjabin, F.; Schmidt, J.B.; Haque, M.; Saha, K.; Bhuiyan, M.H. Harnessing hydrogen: A comprehensive literature review on strategic launching initiatives in the global energy market. Int. J. Energy Res. 2024, 2024, 3265065. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, B.; Huang, W.; Li, Y.; Hou, L.; Xiao, J.; Mao, Z.; Li, X. A review of hydrogen generation, storage, and applications in power system. J. Energy Storage 2024, 75, 109307. [Google Scholar] [CrossRef]
- Zhou, J.; Ji, W.; Cao, X.; He, W.; Fan, J.; Yuan, Y. A current perspective on the renewable energy hydrogen production process. J. Therm. Sci. 2023, 32, 542–596. [Google Scholar] [CrossRef]
- Jiayu, B.; Xingang, W.; Chaoshan, X.; Zhiyong, Y.; Shoutao, T.; He, C. Development status and measures to promote the development of renewable energy in China. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; IEEE: New York, NY, USA, 2021; pp. 1102–1107. [Google Scholar]
- Shang, Y.; Han, D.; Gozgor, G.; Mahalik, M.K.; Sahoo, B.K. The impact of climate policy uncertainty on renewable and non-renewable energy demand in the United States. Renew. Energy 2022, 197, 654–667. [Google Scholar] [CrossRef]
- Li, Y.; Suryadi, B.; Yan, J.; Feng, J.; Bhaskoro, A.G.; Suwanto. A strategic roadmap for ASEAN to develop hydrogen energy: Economic prospects and carbon emission reduction. Int. J. Hydrogen Energy 2023, 48, 11113–11130. [Google Scholar] [CrossRef]
- Nong, K.; Sun, W.; Shen, L.; Sun, D.; Lin, J. Future pathways for green hydrogen: Analyzing the nexus of renewable energy consumption and hydrogen development in Chinese cities. Renew. Energy 2024, 237, 121507. [Google Scholar] [CrossRef]
- Guo, L.; Su, J.; Wang, Z.; Shi, J.; Guan, X.; Cao, W.; Ou, Z. Hydrogen safety: An obstacle that must be overcome on the road towards future hydrogen economy. Int. J. Hydrogen Energy 2024, 51, 1055–1078. [Google Scholar] [CrossRef]
- Li, F.; Liu, D.; Sun, K.; Yang, S.; Peng, F.; Zhang, K.; Guo, G.; Si, Y. Towards a future hydrogen supply chain: A review of technologies and challenges. Sustainability 2024, 16, 1890. [Google Scholar] [CrossRef]
- Han, X.; Yan, H.; Kang, J.; Li, Y. Strategic Analysis of Hydrogen Energy Policies and Technology Layout in Major Countries. In World Hydrogen Technology Convention, Proceedings of the 10th Hydrogen Technology Convention, Foshan, China, 22–26 May 2023; Springer Nature: Singapore, 2023; pp. 435–451. [Google Scholar]
- Peng, D.; Chen, X.; Liu, H.; Guo, N.; Wang, H. Optimal Configuration of Long-Duration Hydrogen Energy Storage for High Proportion New Energy Power System. In Proceedings of the 2023 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chongqing, China, 7–9 July 2023; IEEE: New York, NY, USA, 2023; pp. 1693–1698. [Google Scholar]
- Chen, S.; Zhang, J.; Wei, Z.; Cheng, H.; Lv, S. Towards Renewable-Dominated Energy Systems: Role of Green Hydrogen. J. Mod. Power Syst. Clean Energy 2024, 12, 1697–1709. [Google Scholar] [CrossRef]
- Ferrada, F.; Babonneau, F.; Homem-de-Mello, T.; Jalil-Vega, F. The role of hydrogen for deep decarbonization of energy systems: A Chilean case study. Energy Policy 2023, 177, 113536. [Google Scholar] [CrossRef]
- Tarhan, C.; Çil, M.A. A study on hydrogen, the clean energy of the future: Hydrogen storage methods. J. Energy Storage 2021, 40, 102676. [Google Scholar] [CrossRef]
- Pingkuo, L.; Xue, H. Comparative analysis on similarities and differences of hydrogen energy development in the World’s top 4 largest economies: A novel framework. Int. J. Hydrogen Energy 2022, 47, 9485–9503. [Google Scholar] [CrossRef]
- Han, Z.; Yuan, S.; Dong, Y.; Ma, S.; Bian, Y.; Mao, X. Research on the flexibility margin of an electric–hydrogen coupling energy block based on model predictive control. Front. Energy Res. 2022, 10, 879244. [Google Scholar] [CrossRef]
- Steinbach, S.A.; Bunk, N. The future European hydrogen market: Market design and policy recommendations to support market development and commodity trading. Int. J. Hydrogen Energy 2024, 70, 29–38. [Google Scholar] [CrossRef]
- Gu, Z.; Pan, G.; Gu, W.; Qiu, H.; Lu, S. Robust optimization of scale and revenue for integrated power-to-hydrogen systems within energy, ancillary services, and hydrogen markets. IEEE Trans. Power Syst. 2023, 39, 5008–5023. [Google Scholar] [CrossRef]
- Vechkinzova, E.; Steblyakova, L.P.; Roslyakova, N.; Omarova, B. Prospects for the development of hydrogen energy: Overview of global trends and the Russian market state. Energies 2022, 15, 8503. [Google Scholar] [CrossRef]
- Ramadasu, V.; Reiner, G. Integrated inventory and capacity management for hydrogen production under consideration of fluctuating electricity prices. Int. J. Prod. Res. 2025, 63, 4540–4562. [Google Scholar] [CrossRef]
- Zhao, W.; Ma, J.; Wang, Z.; Li, Y.; Zhang, W. Potential hydrogen market: Value-added services increase economic efficiency for hydrogen energy suppliers. Sustainability 2022, 14, 4804. [Google Scholar] [CrossRef]
- Asghari, M.; Afshari, H.; Jaber, M.Y.; Searcy, C. Strategic analysis of hydrogen market dynamics across collaboration models. Renew. Sustain. Energy Rev. 2025, 208, 115001. [Google Scholar] [CrossRef]
- Sahraie, E.; Kamwa, I.; Moeini, A.; Mohseni-Bonab, S.M. Synergy-based hydrogen pricing in hydrogen-integrated electric power system: Sensitivity analysis. Int. J. Hydrogen Energy 2024, 93, 948–962. [Google Scholar] [CrossRef]
- Guo, H.; Gong, D.; Zhang, L.; Wang, F.; Du, D. Hierarchical game for low-carbon energy and transportation systems under dynamic hydrogen pricing. IEEE Trans. Ind. Inform. 2022, 19, 2008–2018. [Google Scholar] [CrossRef]
- Guo, H.; Gong, D.; Zhang, L.; Mo, W.; Ding, F.; Wang, F. Time-Decoupling Layered Optimization for Energy and Transportation Systems under Dynamic Hydrogen Pricing. Energies 2022, 15, 5382. [Google Scholar] [CrossRef]
- Wang, L.; Jiao, S.; Xie, Y.; Xia, S.; Zhang, D.; Zhang, Y.; Li, M. Two-way dynamic pricing mechanism of hydrogen filling stations in electric-hydrogen coupling system enhanced by blockchain. Energy 2022, 239, 122194. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Chen, Z. Stackelberg-equilibrium-based collaborative charging management strategy for renewable fuel vehicles in regional integrated electricity-hydrogen system. Appl. Energy 2025, 377, 124617. [Google Scholar] [CrossRef]
- Zhu, J.; Meng, D.; Dong, X.; Fu, Z.; Yuan, Y. An integrated electricity-hydrogen market design for renewable-rich energy system considering mobile hydrogen storage. Renew. Energy 2023, 202, 961–972. [Google Scholar] [CrossRef]
- Wang, J.; Shao, Z.; Wu, J.; Wu, L. Day-ahead strategic bidding of multi-energy microgrids participating in electricity, thermal energy, and hydrogen markets: A stochastic bi-level approach. Int. J. Electr. Power Energy Syst. 2024, 163, 110319. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Sun, Y.; Zang, H.; Zhu, Y. Optimal power and gas flow with a limited number of control actions. IEEE Trans. Smart Grid 2017, 9, 5371–5380. [Google Scholar] [CrossRef]
- Gao, H.; Li, Z. A benders decomposition based algorithm for steady-state dispatch problem in an integrated electricity-gas system. IEEE Trans. Power Syst. 2021, 36, 3817–3820. [Google Scholar] [CrossRef]
- Kang, Z.; Ma, X.; Lv, L.; Fang, X.; Wang, Z. A PV Hosting Capacity Assessment Method in Distribution Network Based on Successive Second-Order Cone Programming. In Proceedings of the 2024 4th Power System and Green Energy Conference (PSGEC), Shanghai, China, 22–24 August 2024; IEEE: New York, NY, USA, 2024; pp. 1109–1113. [Google Scholar]
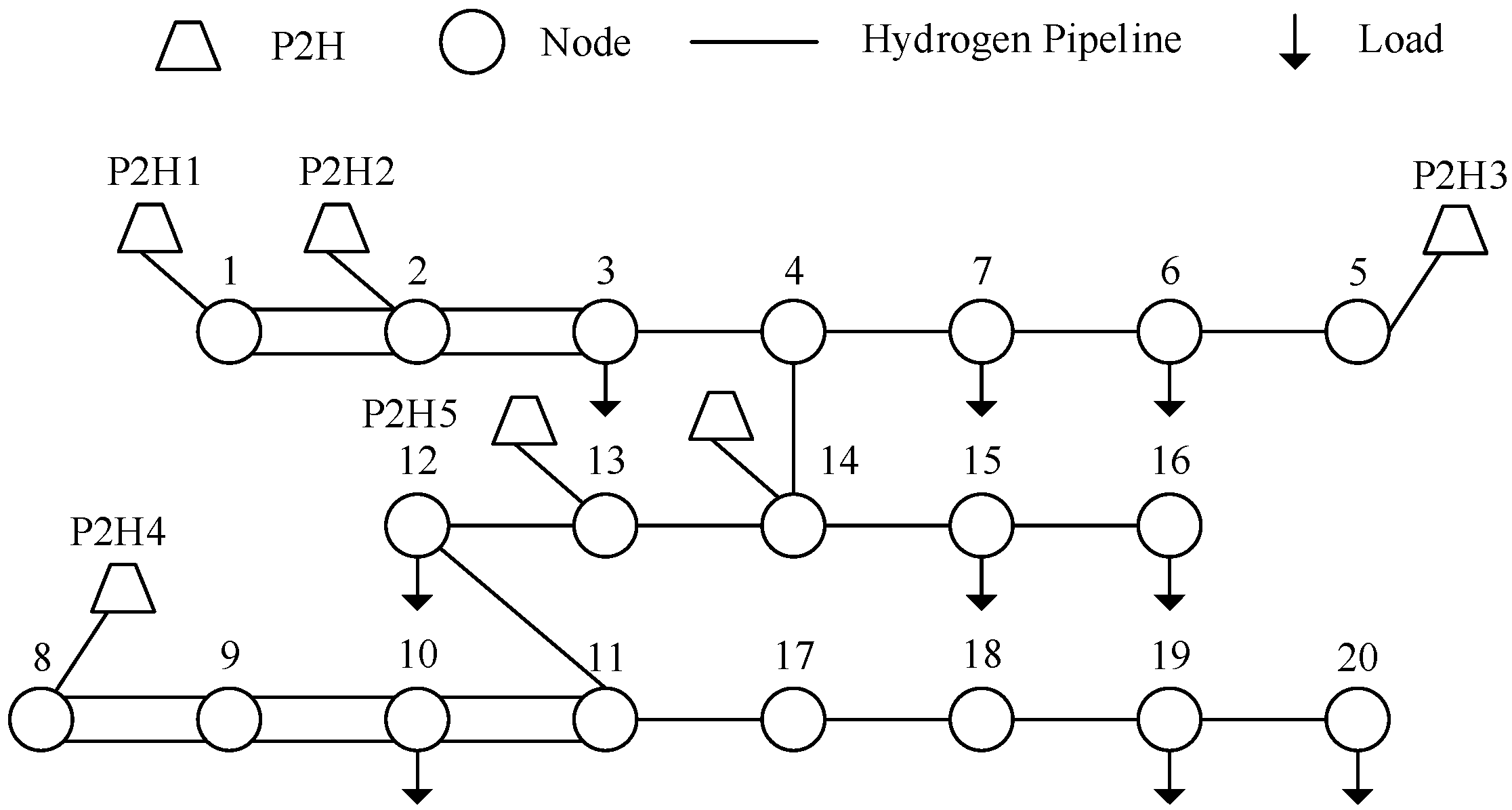

| Node Location Where the Device Is Located | Equipment Capacity (103 kg) | Nodal Average Electricity Price (USD/MWh) |
|---|---|---|
| 1 | 1200 | 32.09 |
| 2 | 1100 | 19.79 |
| 5 | 900 | 26.14 |
| 8 | 1000 | 55.75 |
| 13 | 850 | 38.62 |
| 14 | 1200 | 39.83 |
| Pricing Mechanisms | Time Period | Prices (USD/kg) |
|---|---|---|
| TOUP mechanism | Peak value (8:00–11:00, 17:00–21:00) | 2.3532 |
| Par value (12:00–16:00, 22:00–24:00) | 1.8761 | |
| Valley value (0:00–7:00) | 1.2916 |
| Performance Metric | Belgian 20-Node System | 59-Node Integrated Electricity-Hydrogen Network |
|---|---|---|
| number of variables | 5780 | 18,654 |
| number of constraints | 7844 | 25,732 |
| solving time (seconds) | 63 | 336 |
| number of iterations | 11 | 23 |
| convergence status | converged | converged |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yang, W.; Wang, K.; Zhang, A. Nodal Marginal Price Decomposition Mechanism for the Hydrogen Energy Market Considering Hydrogen Transportation Characteristics. Energies 2025, 18, 5681. https://doi.org/10.3390/en18215681
Li S, Yang W, Wang K, Zhang A. Nodal Marginal Price Decomposition Mechanism for the Hydrogen Energy Market Considering Hydrogen Transportation Characteristics. Energies. 2025; 18(21):5681. https://doi.org/10.3390/en18215681
Chicago/Turabian StyleLi, Shouheng, Wei Yang, Kangkang Wang, and Anan Zhang. 2025. "Nodal Marginal Price Decomposition Mechanism for the Hydrogen Energy Market Considering Hydrogen Transportation Characteristics" Energies 18, no. 21: 5681. https://doi.org/10.3390/en18215681
APA StyleLi, S., Yang, W., Wang, K., & Zhang, A. (2025). Nodal Marginal Price Decomposition Mechanism for the Hydrogen Energy Market Considering Hydrogen Transportation Characteristics. Energies, 18(21), 5681. https://doi.org/10.3390/en18215681






