Energy Management System-Based Multi-Objective Nizar Optimization Algorithm Considering Grid Power and Battery Degradation Cost
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Contributions of the Article
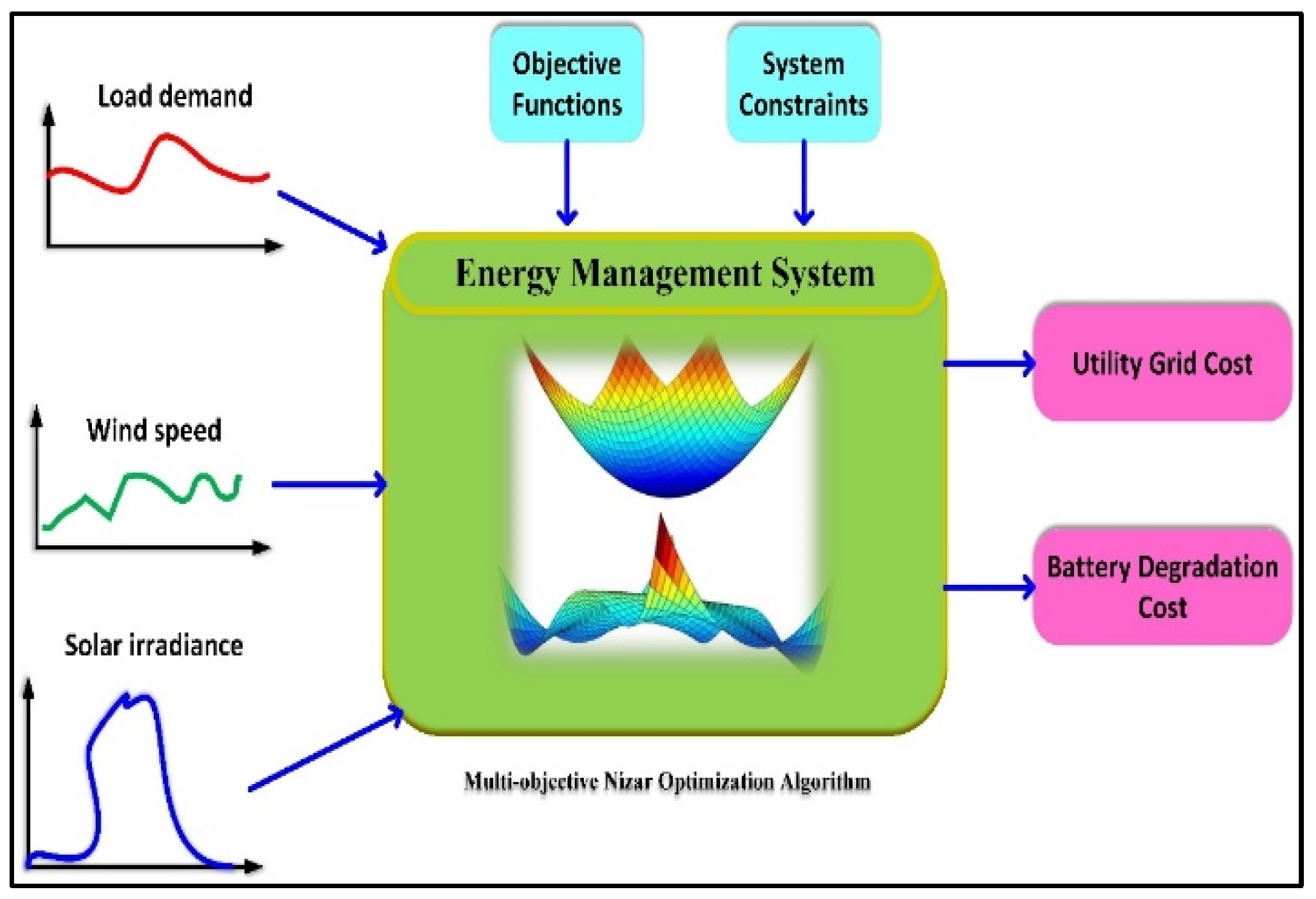
- For the optimal coordination of multi-energy systems in a grid-connected microgrid, a novel energy management system (EMS) framework based on the Nizar Optimization Algorithm (NOA) is proposed. The EMS is balancing power flow among PV, WT, BESS, and grid components under variable weather and load conditions.
- The authors have developed a new multi-objective formulation to minimize the cost of power exchanged with the grid and the cost of battery degradation simultaneously. Besides that, it also maintains high power quality and system stability, thus ensuring a resilient and cost-effective operation.
- Comparative performance evaluation via MATLAB simulations under various weather conditions is conducted for the proposed and well-known EMS methods. The NOA-based EMS proposed shows faster convergence, better dynamic response, and higher economic performance (total cost reduction of USD 17–34, and the degradation cost is 27% lower).
- The proposed EMS, supported by comprehensive validation and sensitivity analyses, is stable, flexible, and scalable, thus presenting a strong case for its implementation in the real world of future smart grid and hybrid microgrid architectures.
2. Modeling of the Proposed System
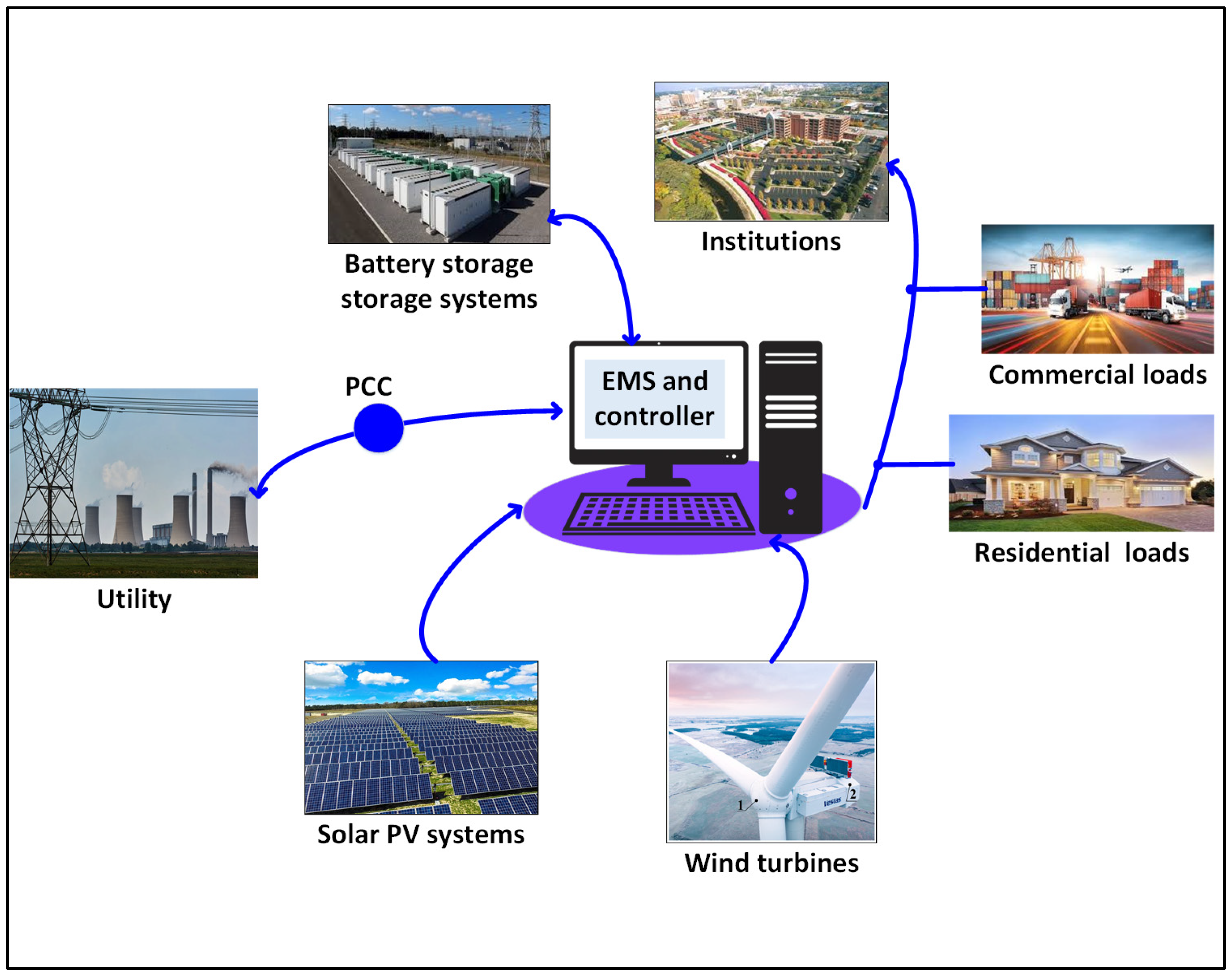
2.1. Microgrid Structure
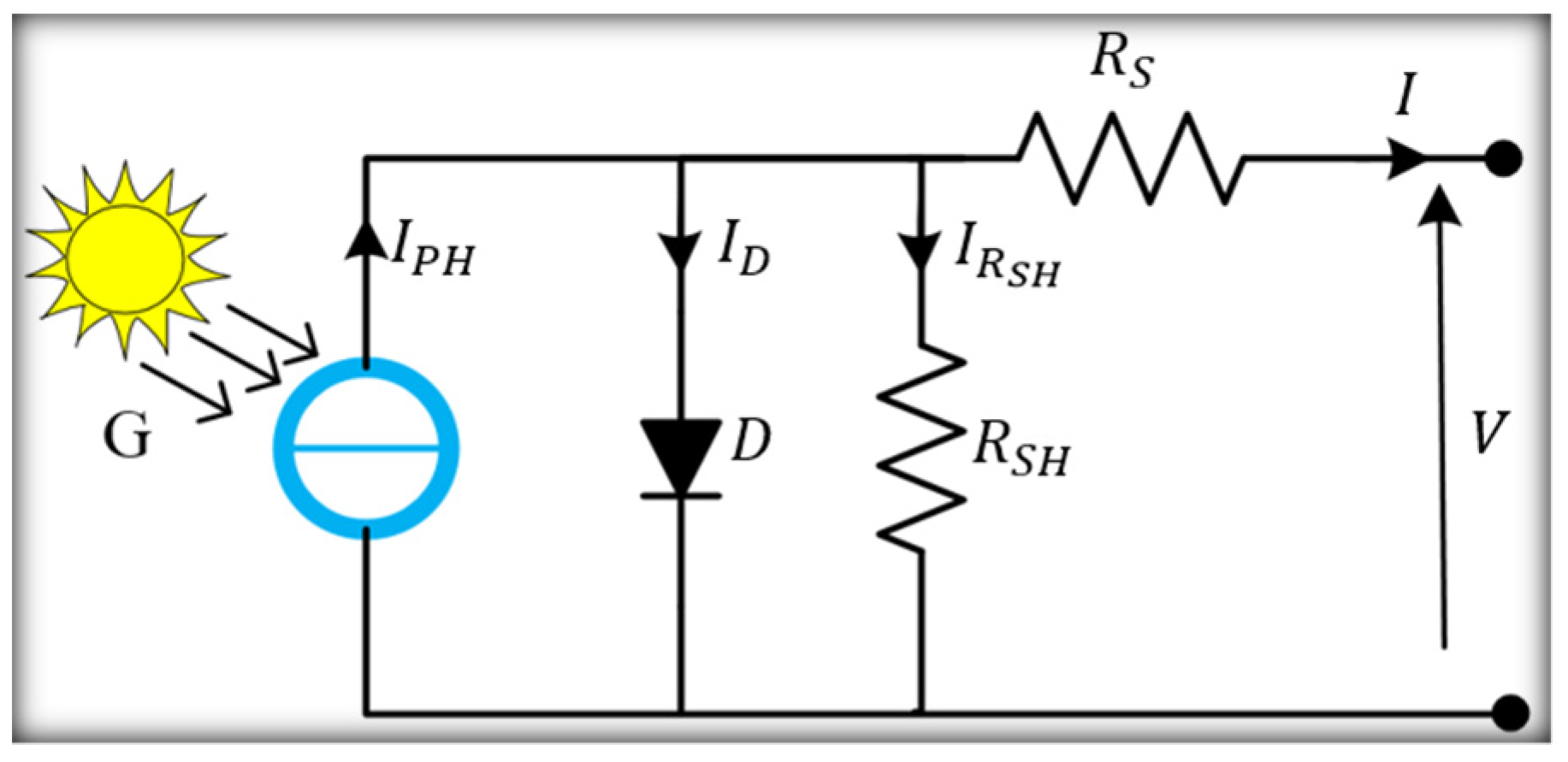
2.2. PV Solar Modeling
2.3. Battery Energy Storage Modeling
2.4. Wind Turbine Modeling
2.5. System Constraints
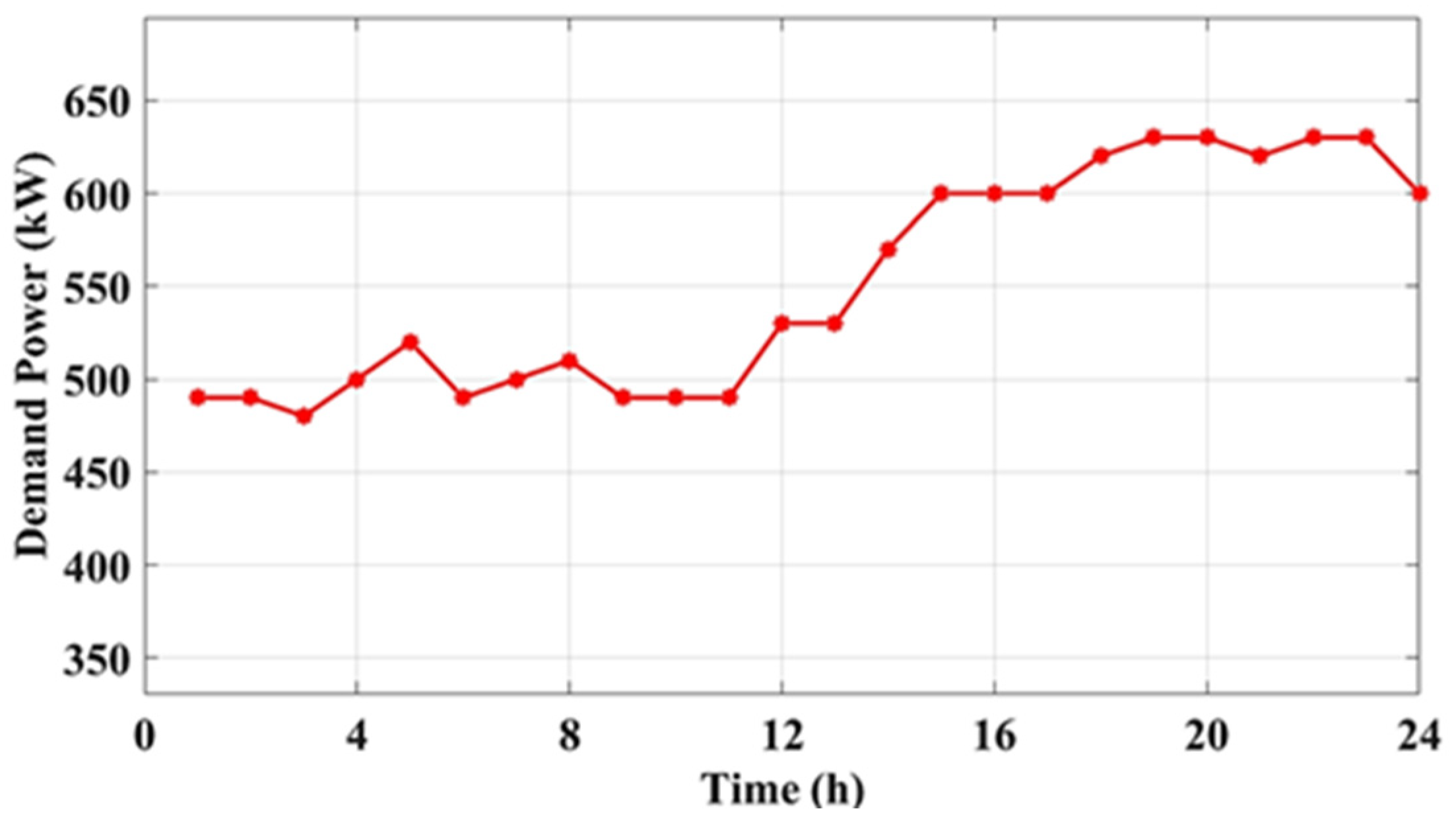
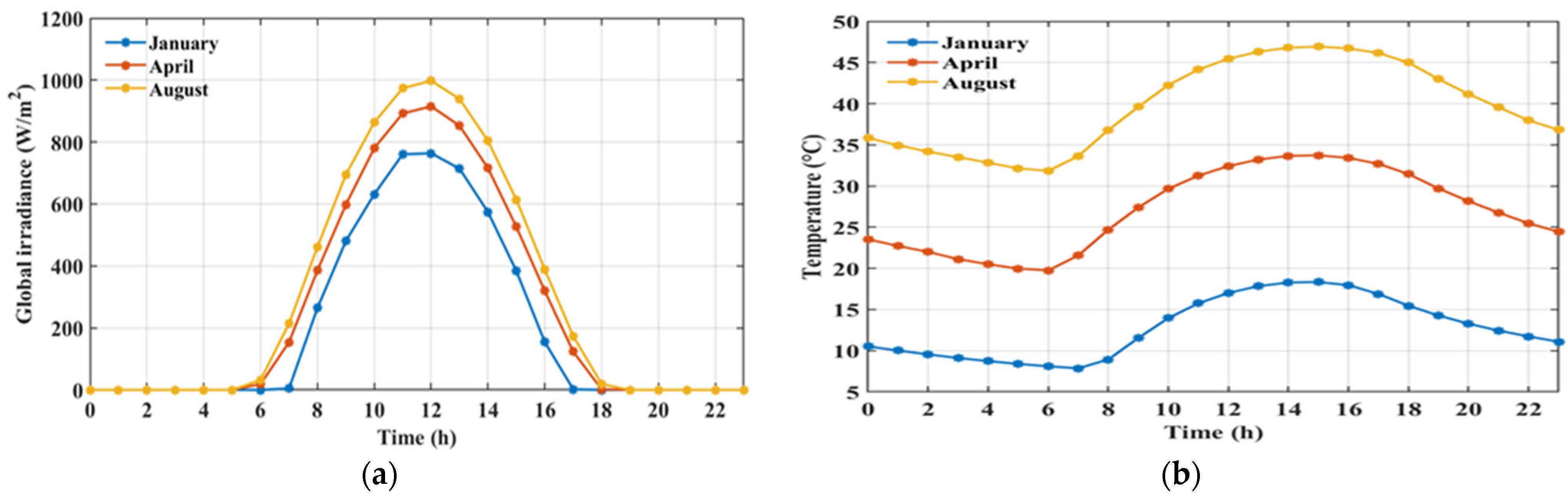
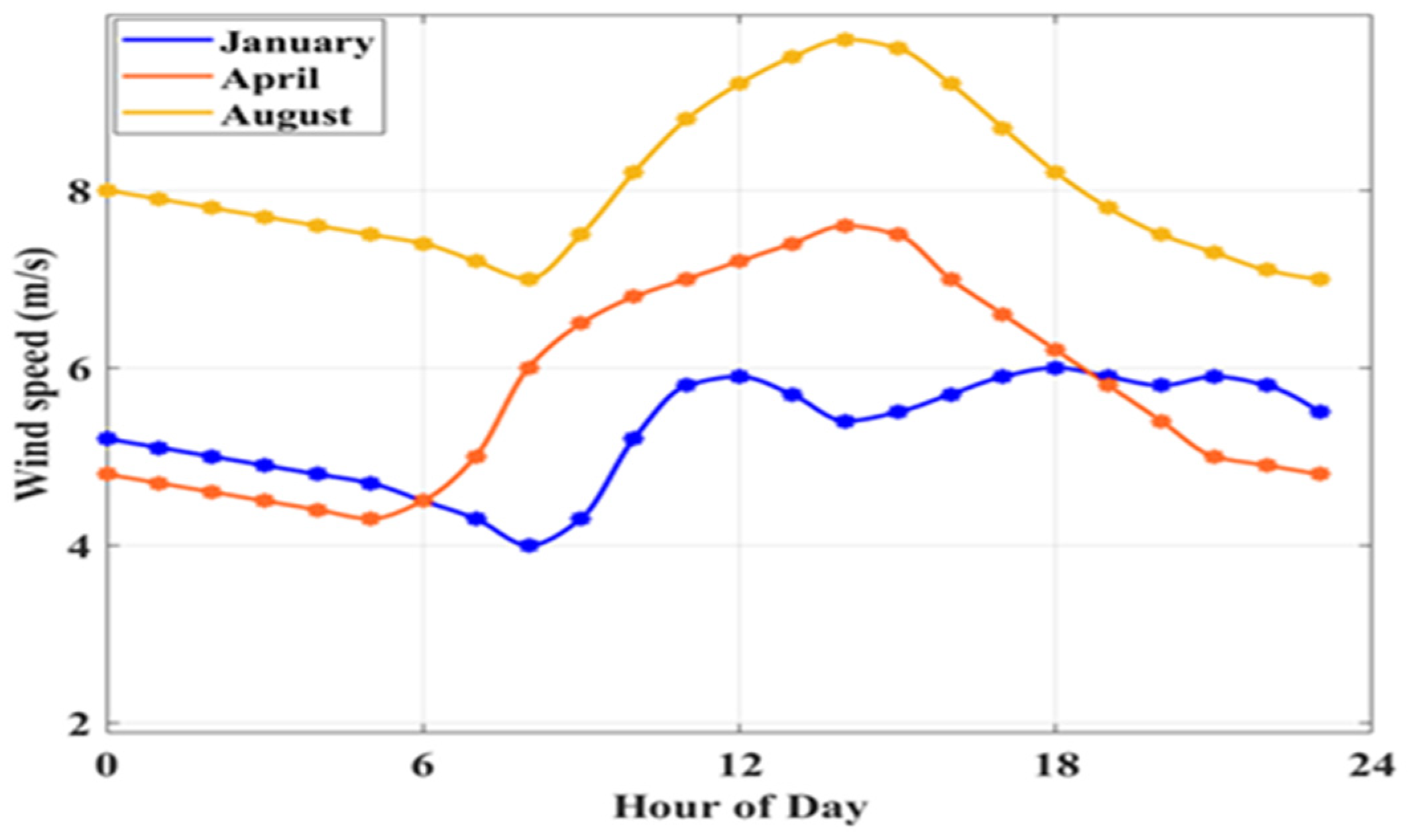
2.6. Load Profile and Weather Conditions
2.7. Problem Formulation and Objective Function
3. Proposed EMS Design
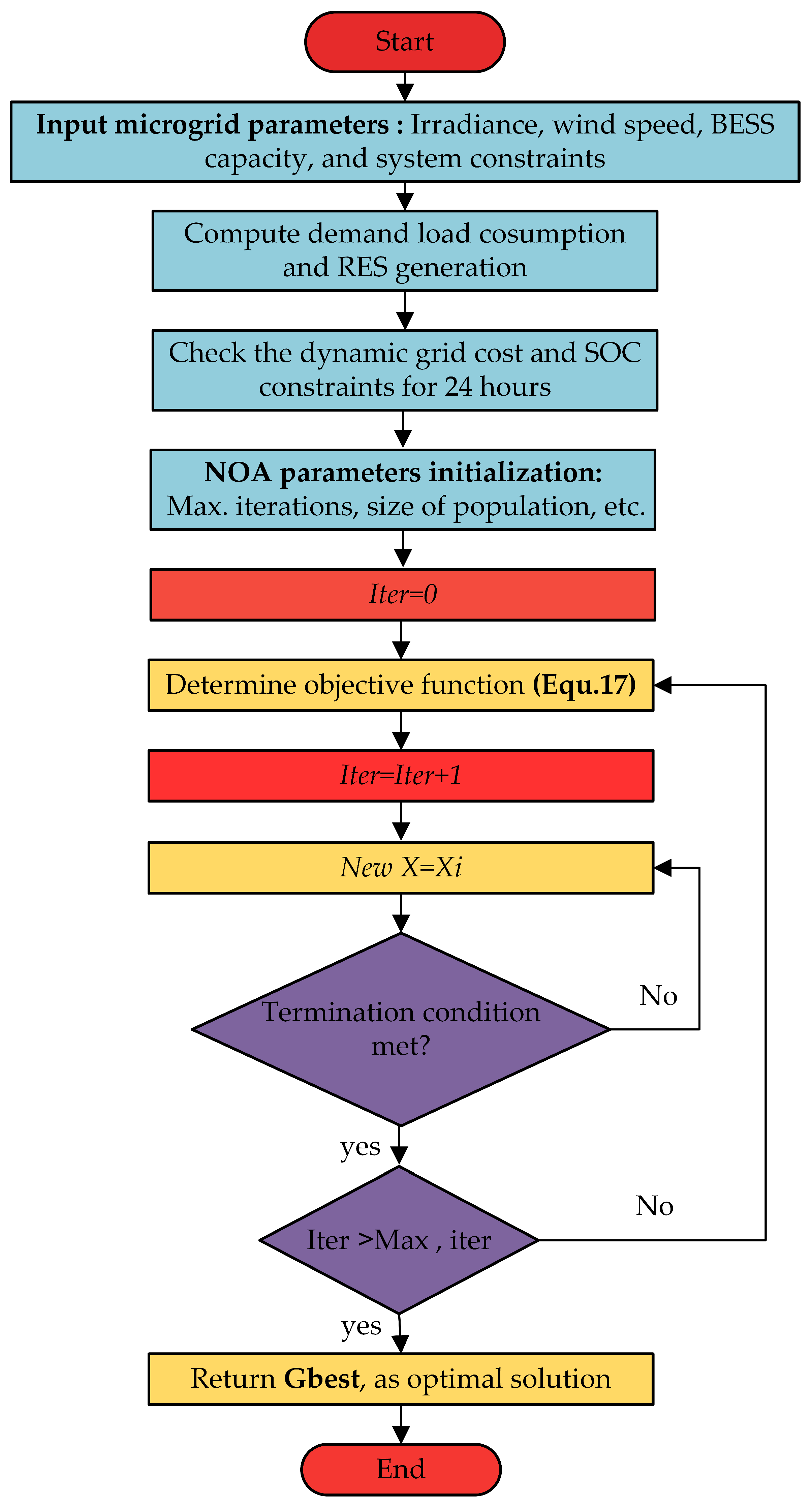
3.1. Multi-Objective Nizar Optimization Algorithm
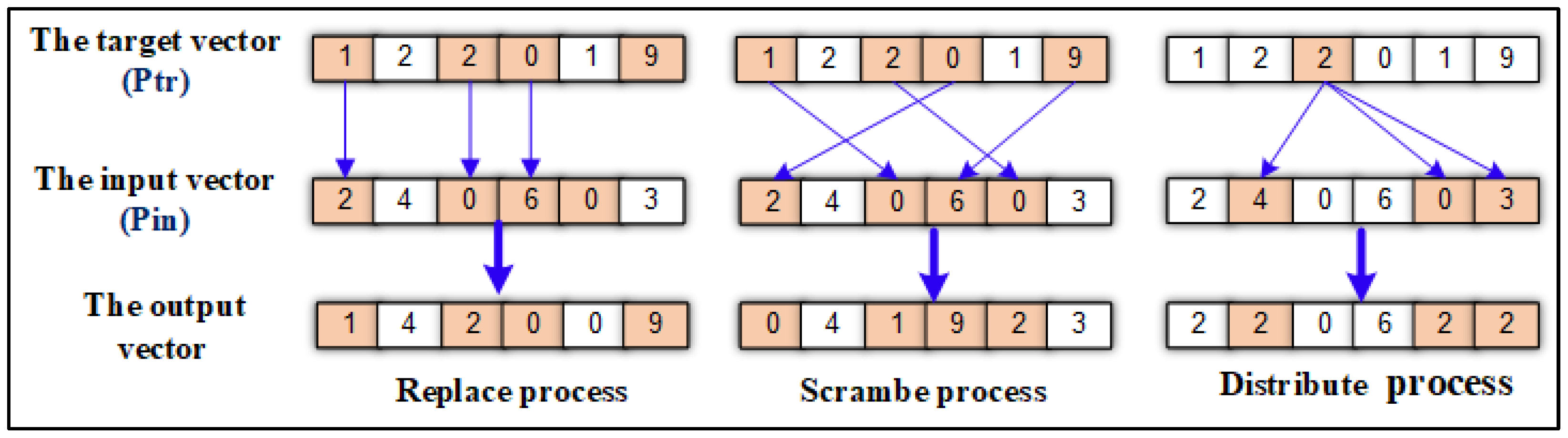
3.2. Effective Mappings
3.3. Effect Transformation Mappings
- The first condition is that the maximum number of iterations (MaxIter) is reached, thus putting a limit on the computational resources to be used.
- The second condition is the absolute difference between the best fitness values of two consecutive iterations being less than a small threshold (|F(t) − F(t−1)| < 10−6), which stands for convergence and a very slight change in the objective function.
4. Results and Discussion
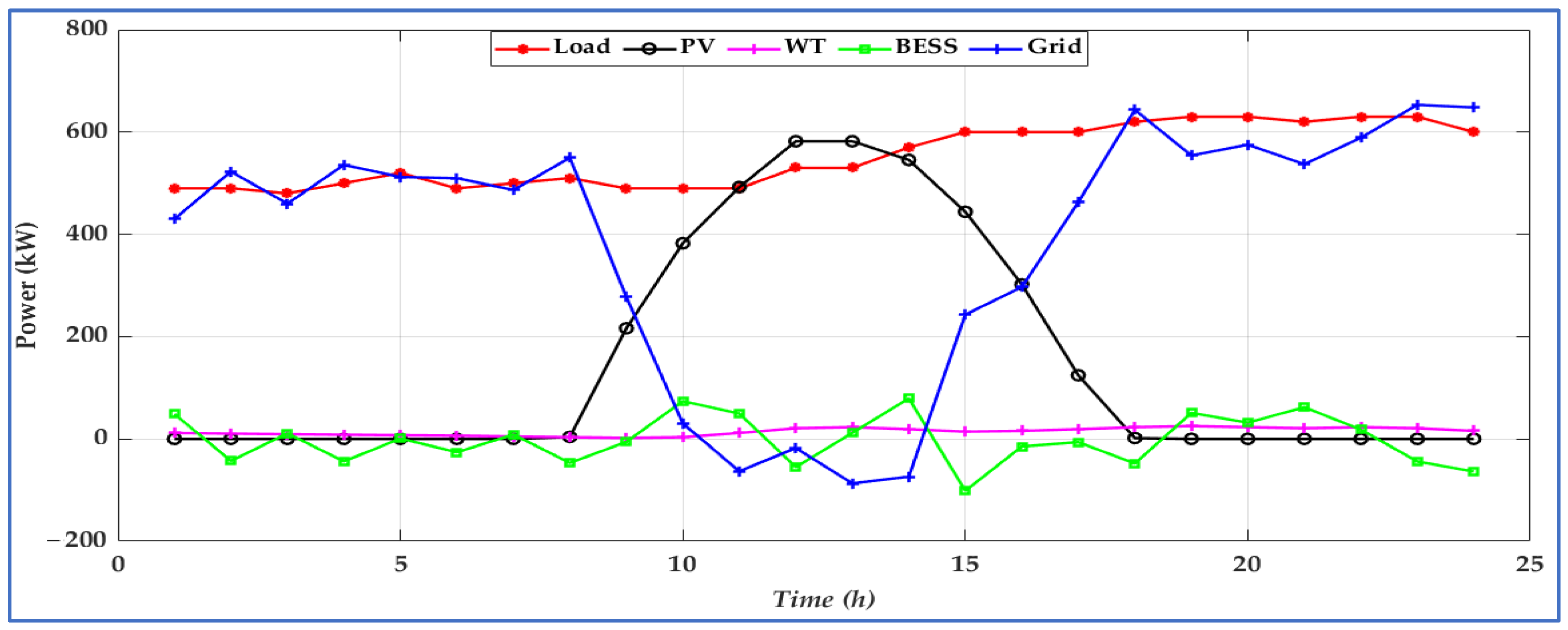
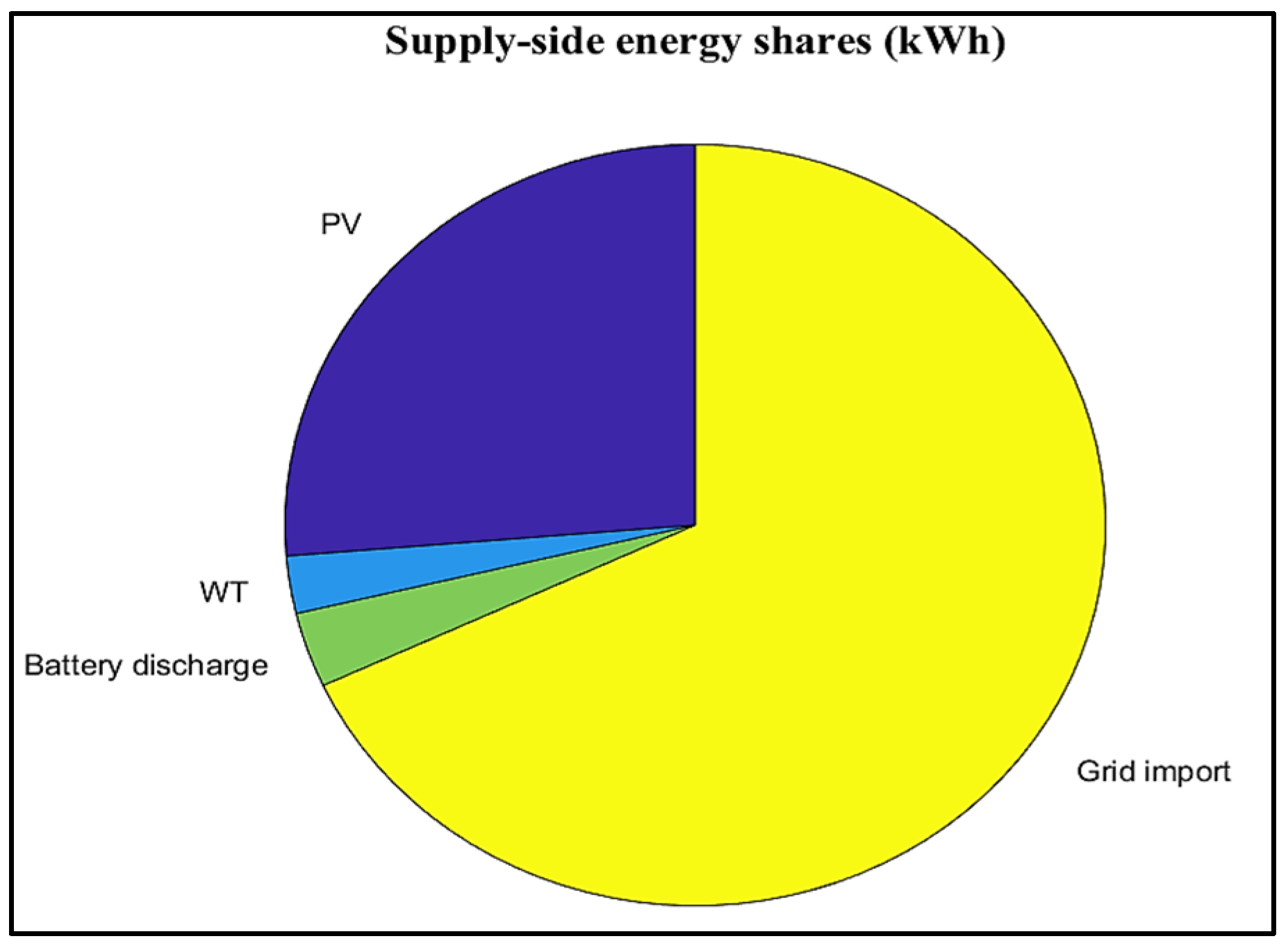
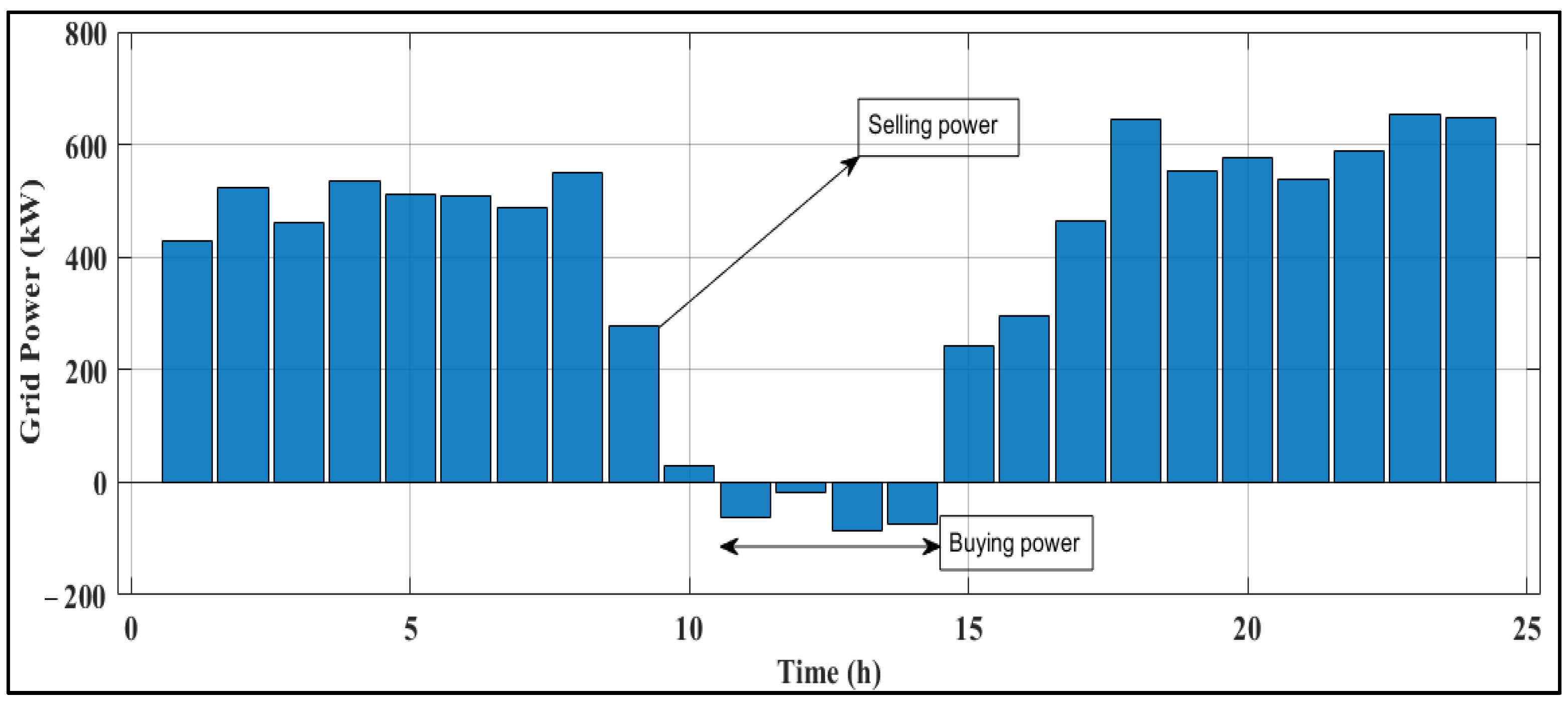
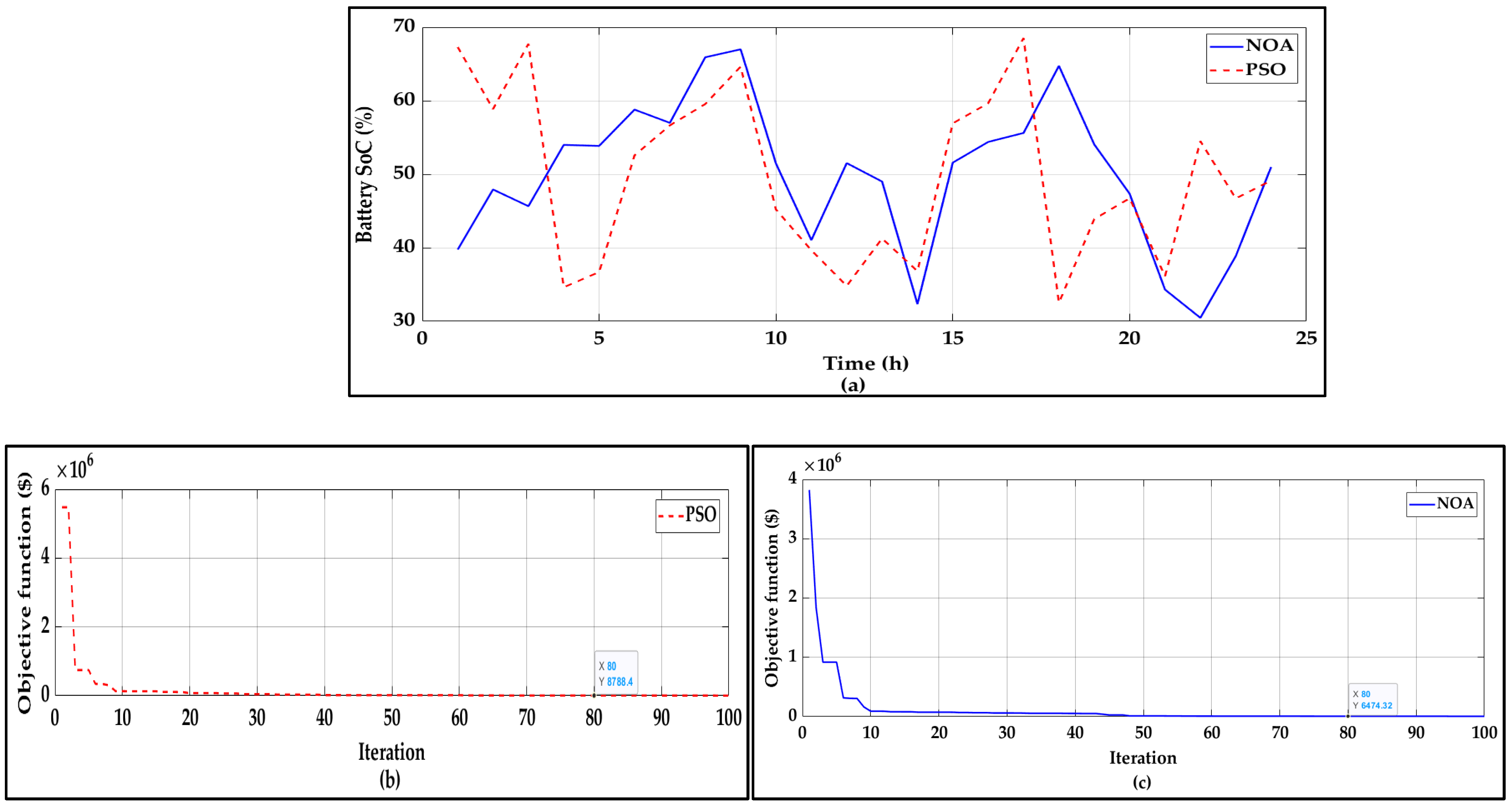
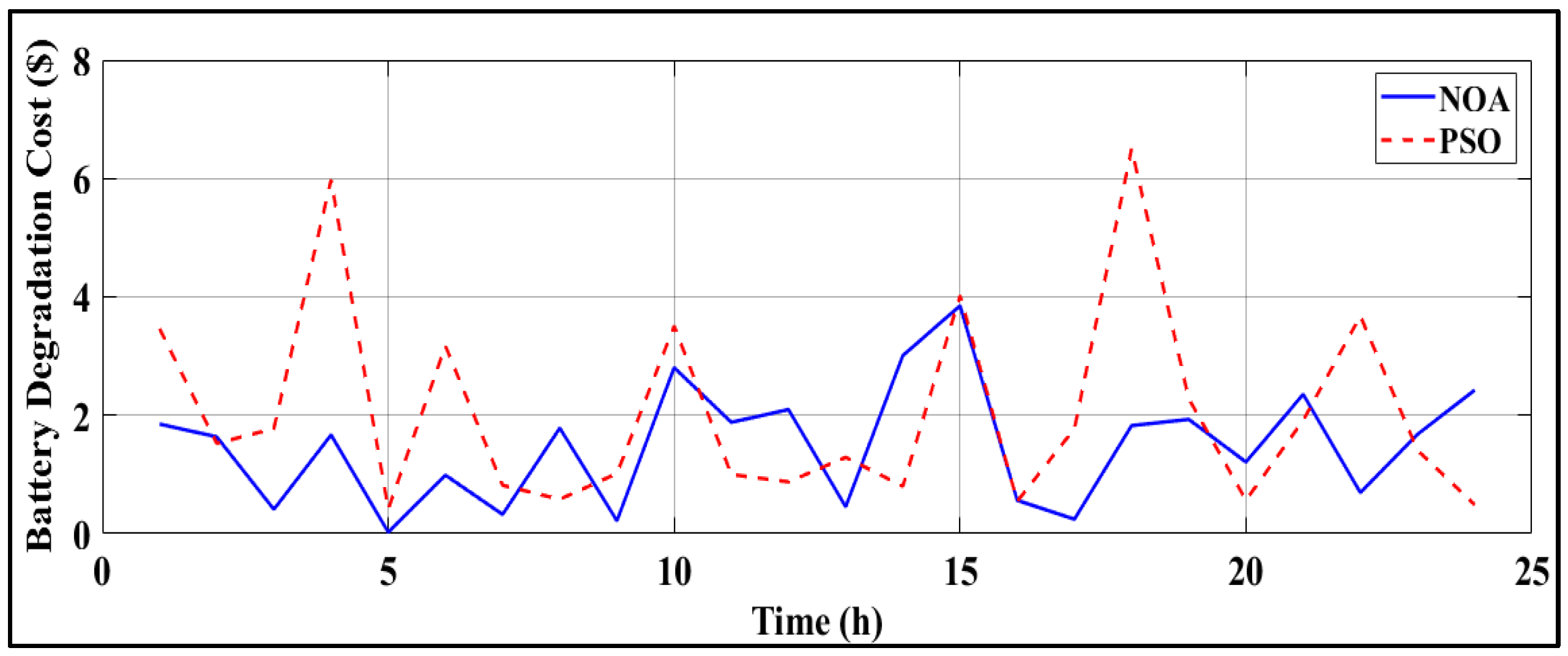
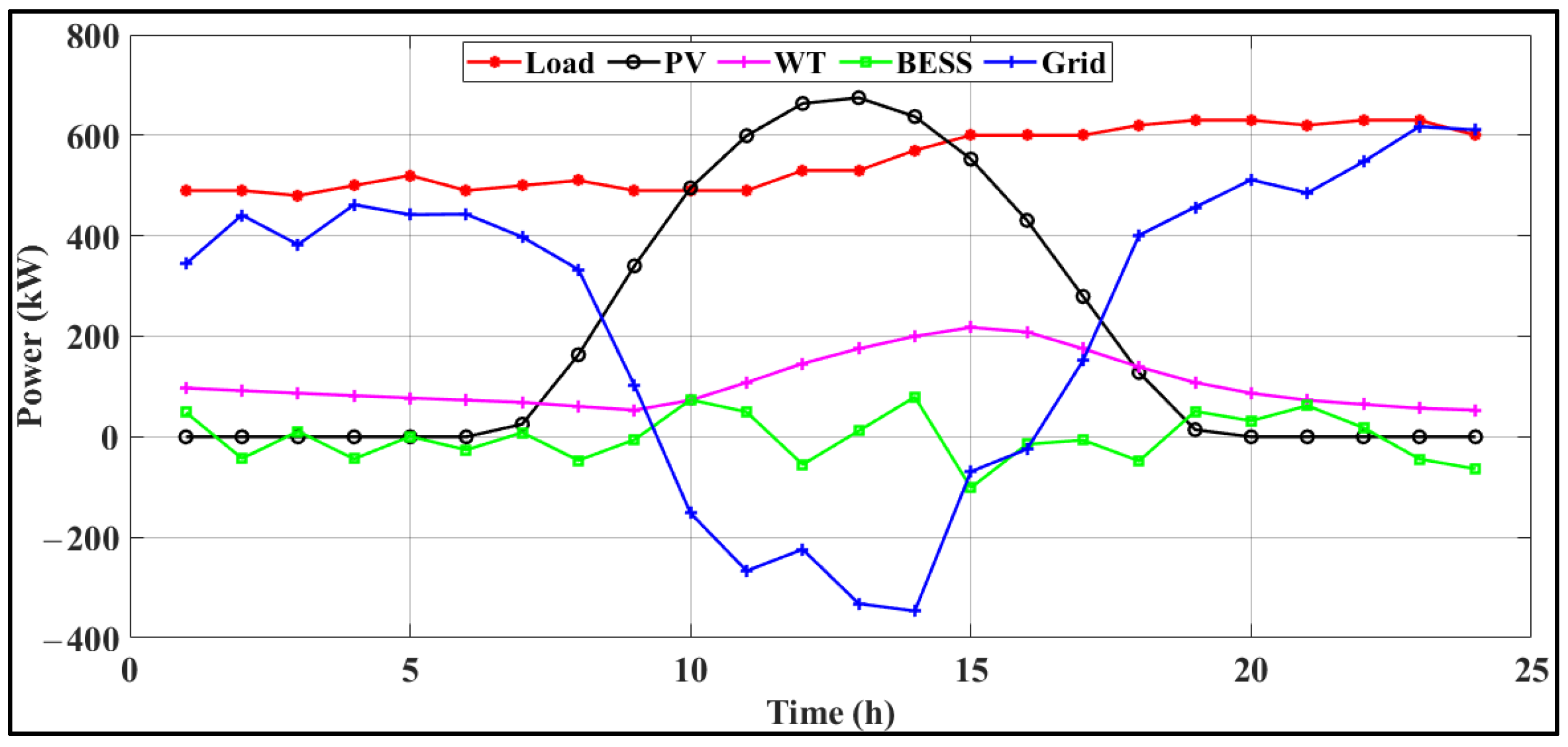
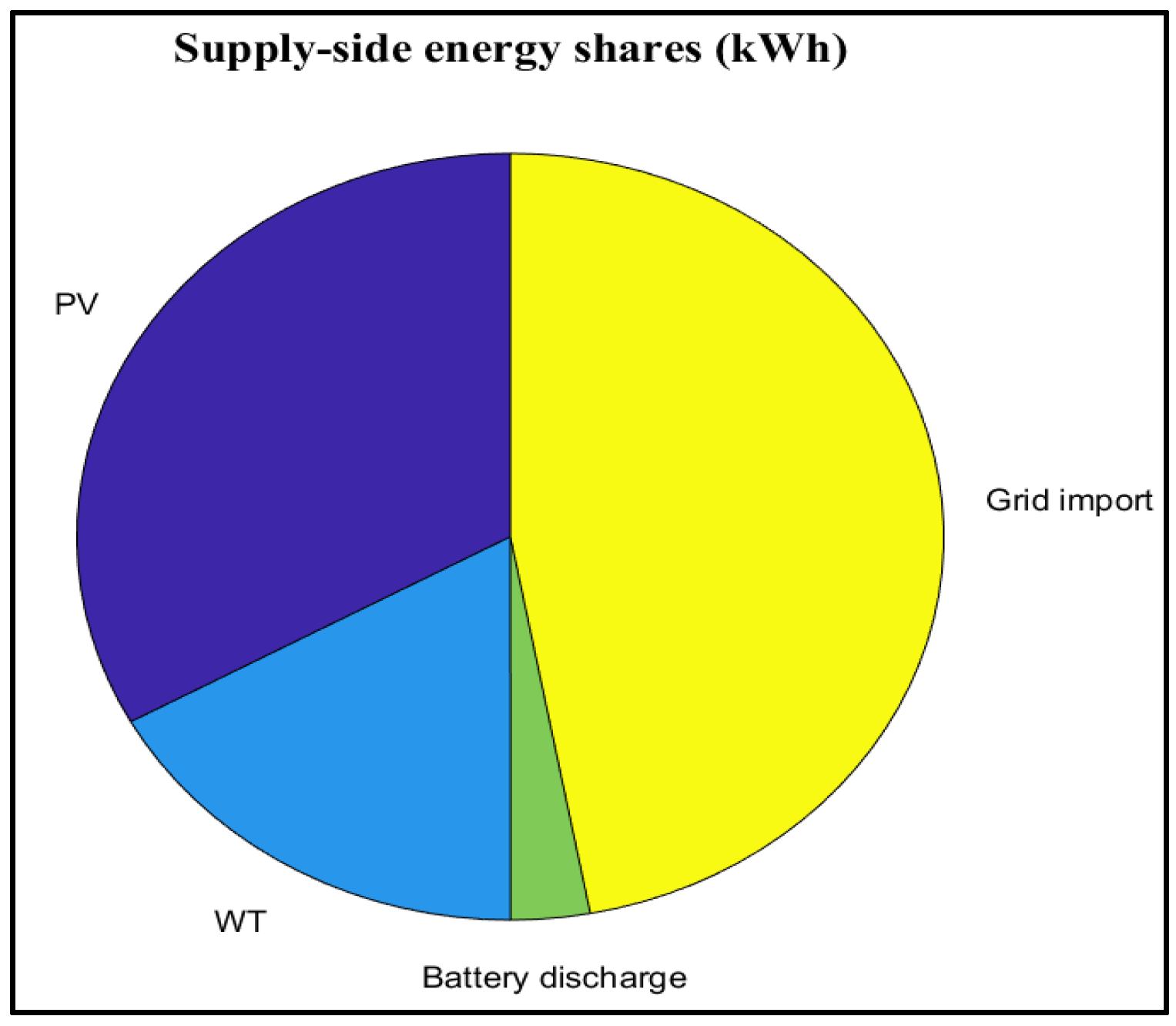
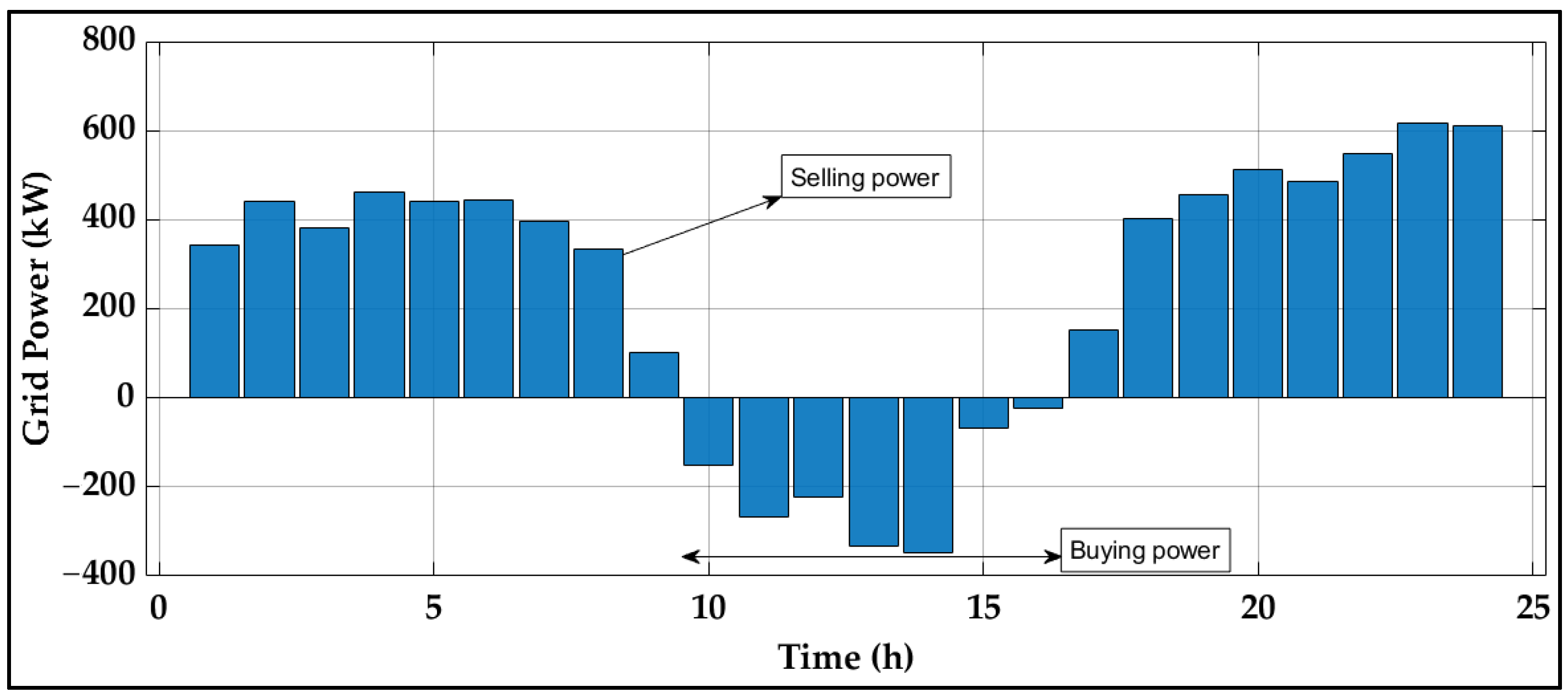
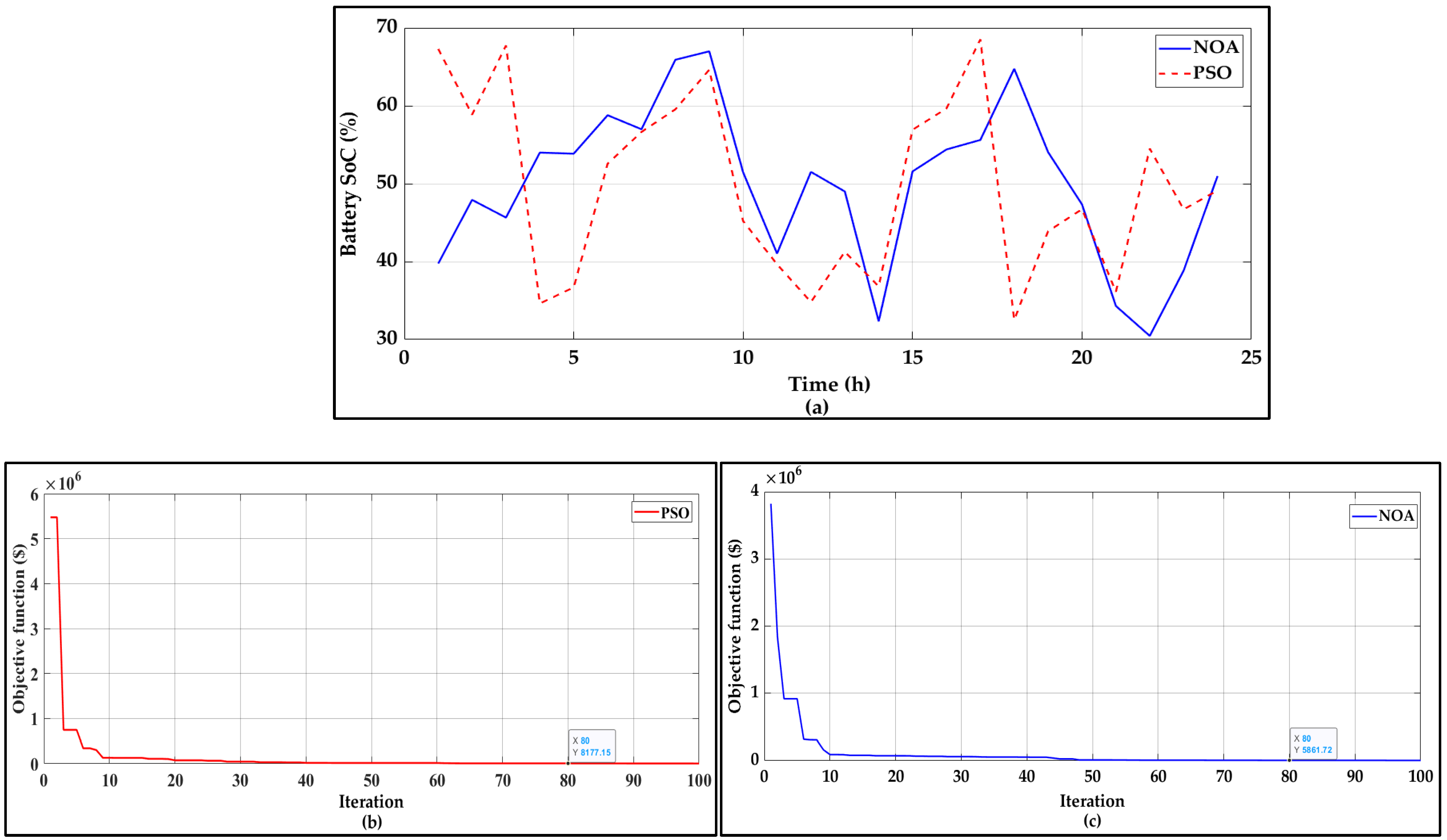
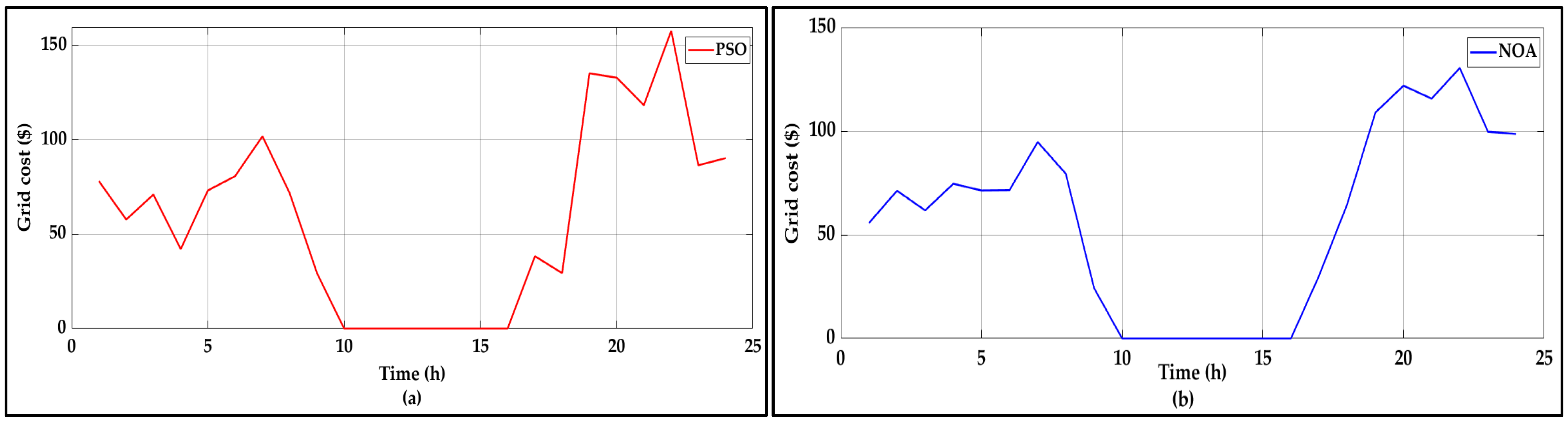
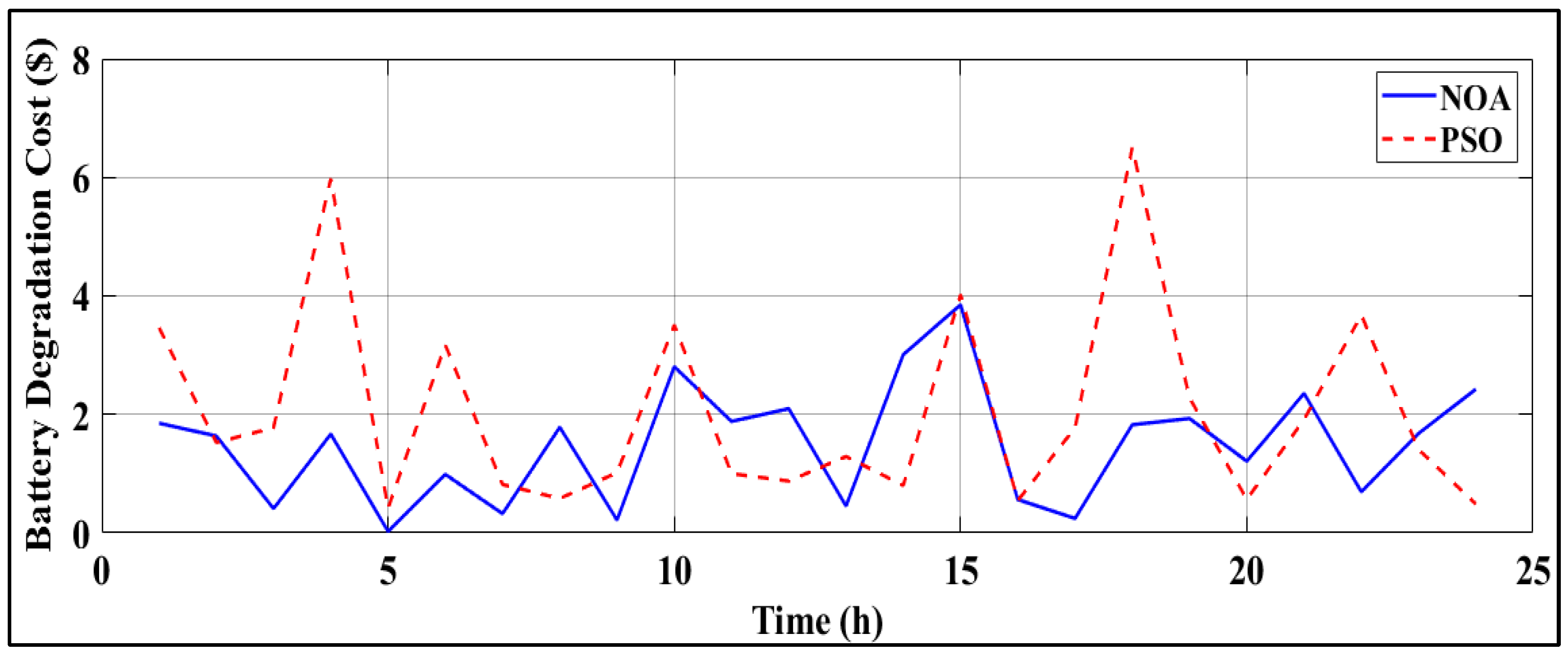
4.1. NOA Performance Under Scenario 1
4.2. NOA Performance Under Scenario 2
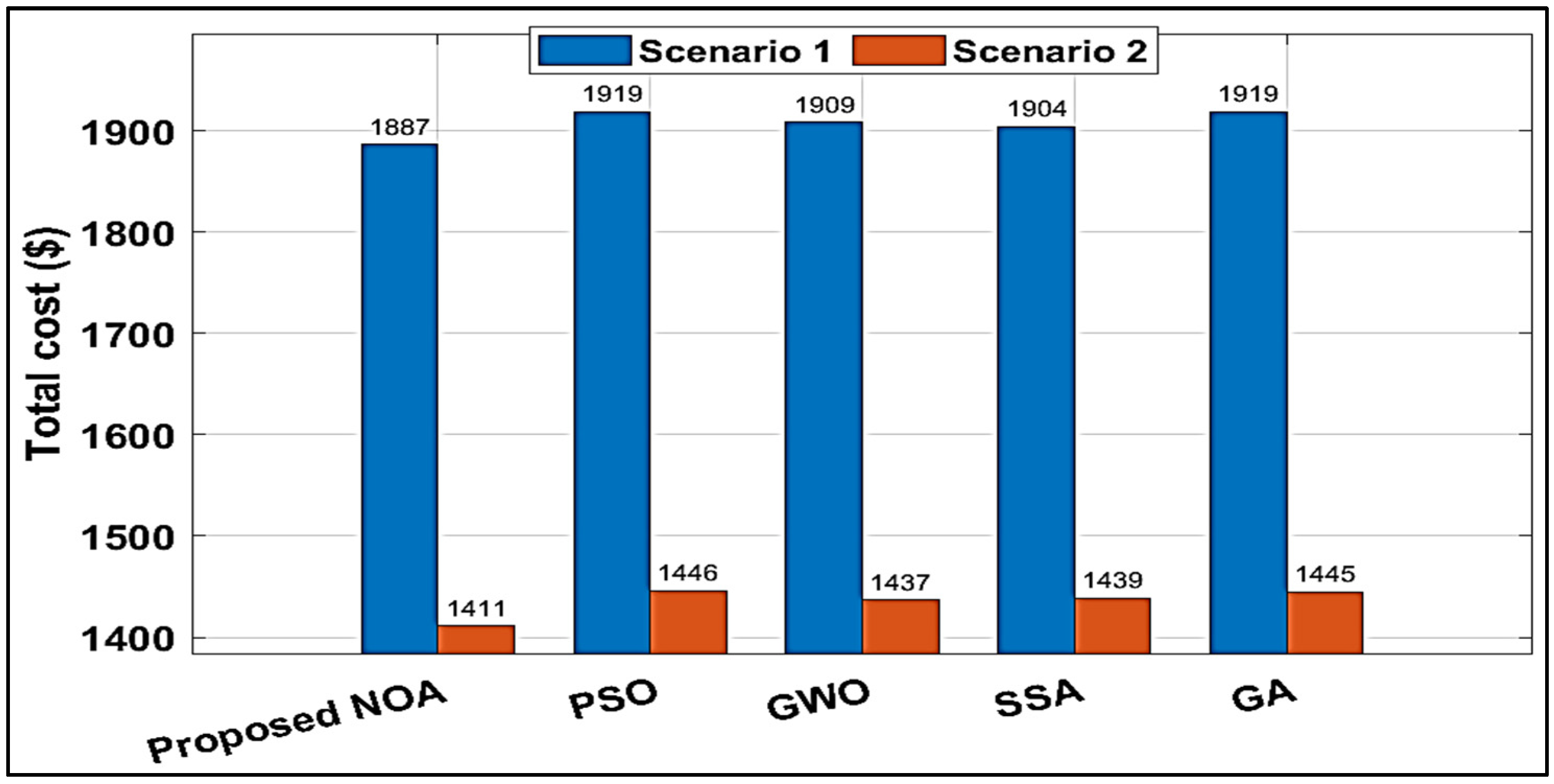
4.3. Comparison with the Existing Algorithms
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qasim, M.A.; Yaqoob, S.J.; Bajaj, M.; Blazek, V.; Obed, A.A. Techno-economic optimization of hybrid power systems for sustainable energy in remote communities of Iraq. Results Eng. 2025, 25, 104283. [Google Scholar] [CrossRef]
- Zubair, M.; Ullah, I.; Alanazi, A.; Alanazi, M.; Hassan, I.; Jan, S.T. Energizing rural Pakistan through optimization of stand-alone hybrid systems with techno-economic, multi-criteria decision and sensitivity analysis. Environ. Dev. Sustain. 2024, 26, 1–49. [Google Scholar] [CrossRef]
- Rehmani, A.M.; Akhter, P. Techno-Economic analysis of hybrid renewable energy systems for rural area energization in Pakistan. In Proceedings of the 2019 3rd International Conference on Energy Conservation and Efficiency (ICECE), Lahore, Pakistan, 23–24 October 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jan, S.T.; Alanazi, A.; Feroz, M.; Alanazi, M. Techno-economic analysis of renewable energy sources’ potential in the rural northern region of Kalam in Pakistan. Environ. Dev. Sustain. 2024, 27, 11117–11160. [Google Scholar] [CrossRef]
- Yaqoob, S.J.; Arnoos, H.; Qasim, M.A.; Agyekum, E.B.; Alzahrani, A.; Kamel, S. An optimal energy management strategy for a photovoltaic/li-ion battery power system for DC microgrid application. Front. Energy Res. 2023, 10, 1066231. [Google Scholar] [CrossRef]
- Yaqoob, S.J.; Ferahtia, S.; Obed, A.A.; Rezk, H.; Alwan, N.T.; Zawbaa, H.M.; Kamel, S. Efficient flatness based energy management strategy for hybrid supercapacitor/lithium-ion battery power system. IEEE Access 2022, 10, 132153–132163. [Google Scholar] [CrossRef]
- Allwyn, R.G.; Al-Hinai, A.; Margaret, V. A comprehensive review on energy management strategy of microgrids. Energy Rep. 2023, 9, 5565–5591. [Google Scholar] [CrossRef]
- Sharma, P.; Mathur, H.D.; Mishra, P.; Bansal, R.C. A critical and comparative review of energy management strategies for microgrids. Appl. Energy 2022, 327, 120028. [Google Scholar] [CrossRef]
- Bruni, G.; Cordiner, S.; Mulone, V.; Rocco, V.; Spagnolo, F. A study on the energy management in domestic micro-grids based on model predictive control strategies. Energy Convers. Manag. 2015, 102, 50–58. [Google Scholar] [CrossRef]
- Joshi, A.; Capezza, S.; Alhaji, A.; Chow, M.Y. Survey on AI and machine learning techniques for microgrid energy management systems. IEEE/CAA J. Autom. Sin. 2023, 10, 1513–1529. [Google Scholar] [CrossRef]
- Ahmad, S.; Shafiullah, M.; Ahmed, C.B.; Alowaifeer, M. A review of microgrid energy management and control strategies. IEEE Access 2023, 11, 21729–21757. [Google Scholar] [CrossRef]
- Gholami, M.; Mousavi, S.A.; Muyeen, S.M. Enhanced microgrid reliability through optimal battery energy storage system type and sizing. IEEE Access 2023, 11, 62733–62743. [Google Scholar] [CrossRef]
- Dhanavath, T.; Injeti, S.K.; Busi, R. Grid-Edge Optimization for Maximizing the Utilization of Solar-Battery and Wind-Biomass Systems in Large-Scale Networked Microgrids to Minimize Annual Overall Cost. J. Act. Passiv. Electron. Devices 2025, 18, 257. [Google Scholar]
- Ibrahim, O.; Aziz, M.J.A.; Ayop, R.; Dahiru, A.T.; Low, W.Y.; Sulaiman, M.H.; Amosa, T.I. Fuzzy logic-based particle swarm optimization for integrated energy management system considering battery storage degradation. Results Eng. 2024, 24, 102816. [Google Scholar] [CrossRef]
- Nammouchi, A.; Aupke, P.; D’andreagiovanni, F.; Ghazzai, H.; Theocharis, A.; Kassler, A. Robust opportunistic optimal energy management of a mixed microgrid under asymmetrical uncertainties. Sustain. Energy Grids Netw. 2023, 36, 101184. [Google Scholar] [CrossRef]
- Raghuwanshi, S.S.; Raghuwanshi, P.; Masih, A.; Singh, P. Modeling and optimization of hybrid renewable energy with storage system using flamingo swarm intelligence algorithms. Energy Storage 2023, 5, e470. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Rahman, M.A.; Begum, R.A.; Mahlia, T.M.I. Particle swarm optimised fuzzy controller for charging–discharging and scheduling of battery energy storage system in MG applications. Energy Rep. 2020, 6, 215–228. [Google Scholar] [CrossRef]
- Minh, N.Q.; Linh, N.D.; Khiem, N.T. A mixed-integer linear programming model for microgrid optimal scheduling considering BESS degradation and RES uncertainty. J. Energy Storage 2024, 104, 114663. [Google Scholar] [CrossRef]
- Shafiei, K.; Seifi, A.; Hagh, M.T. A novel multi-objective optimization approach for resilience enhancement considering integrated energy systems with renewable energy, energy storage, energy sharing, and demand-side management. J. Energy Storage 2025, 115, 115966. [Google Scholar] [CrossRef]
- de Lima, T.D.; Faria, P.; Vale, Z. Optimizing home energy management systems: A mixed integer linear programming model considering battery cycle degradation. Energy Build. 2025, 329, 115251. [Google Scholar] [CrossRef]
- Wang, J.; Lyu, C.; Bai, Y.; Yang, K.; Song, Z.; Meng, J. Optimal scheduling strategy for hybrid energy storage systems of battery and flywheel combined multi-stress battery degradation model. J. Energy Storage 2024, 99, 113208. [Google Scholar] [CrossRef]
- Khani, M.; Moghaddam, M.S.; Noori, T.; Ebrahimi, R. Integrated energy management for enhanced grid flexibility: Optimizing renewable resources and energy storage systems across transmission and distribution networks. Heliyon 2024, 10, e39585. [Google Scholar] [CrossRef]
- Li, L.; Sun, Y.; Han, Y.; Chen, W. Seasonal hydrogen energy storage sizing: Two-stage economic-safety optimization for integrated energy systems in northwest China. IScience 2024, 27, 110691. [Google Scholar] [CrossRef]
- Ankar, S.J.; Pinkymol, K.P. Optimal sizing and energy management of electric vehicle hybrid energy storage systems with multi-objective optimization criterion. IEEE Trans. Veh. Technol. 2024, 73, 11082–11096. [Google Scholar] [CrossRef]
- Apribowo, C.H.B.; Hadi, S.P.; Wijaya, F.D.; Setyonegoro, M.I.B. Early prediction of battery degradation in grid-scale battery energy storage system using extreme gradient boosting algorithm. Results Eng. 2024, 21, 101709. [Google Scholar] [CrossRef]
- Qian, J.; Guo, Y.; Wu, D.; Liu, A.; Han, Z.; Liu, Z.; Zhang, S.; Yang, X. Research on multi-time scale optimization of integrated energy system based on multiple energy storage. J. Energy Storage 2024, 102, 113892. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Zhan, Y.; Yan, R.; Mei, J.; Fu, A.; Jiao, F.; Zeng, R. Multi-scenario optimization and performance evaluation of integrated energy system considering co-scheduling of EVs and stationary energy storage. Renew. Energy 2024, 237, 121927. [Google Scholar] [CrossRef]
- Sharma, P.; Saini, K.K.; Mathur, H.D.; Mishra, P. Improved energy management strategy for prosumer buildings with renewable energy sources and battery energy storage systems. J. Mod. Power Syst. Clean Energy 2024, 12, 381–392. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, D.; Wang, Y. Optimal operation of integrated energy systems considering energy trading and integrated demand response. Energy Rep. 2024, 11, 3307–3316. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C. Enabling high-efficiency economic dispatch of hybrid AC/DC networked microgrids: Steady-state convex bi-directional converter models. Trans. Smart Grid 2024, 16, 45–61. [Google Scholar] [CrossRef]
- Yaqoob, S.J.; Motahhir, S.; Agyekum, E.B. A new model for a photovoltaic panel using Proteus software tool under arbitrary environmental conditions. J. Clean. Prod. 2022, 333, 130074. [Google Scholar] [CrossRef]
- Babu, V.V.; Roselyn, J.P.; Sundaravadivel, P. Multi-objective genetic algorithm based energy management system considering optimal utilization of grid and degradation of battery storage in microgrid. Electr. Eng. 2023, 9, 5992–6005. [Google Scholar] [CrossRef]
- Belboul, Z.; Toual, B.; Bensalem, A.; Ghenai, C.; Khan, B.; Kamel, S. Techno-economic optimization for isolated hybrid PV/wind/battery/diesel generator microgrid using improved salp swarm algorithm. Sci. Rep. 2024, 14, 2920. [Google Scholar] [CrossRef] [PubMed]
- Resen, A.K.; Mahmood, A.A. Data-Driven Selection of the Most Cost-Effective Turbine for Basrah Governorate Using Advanced Software Tools. Iraqi Geol. J. 2025, 58, 190–201. [Google Scholar] [CrossRef]
- Khouni, S.E.; Menacer, T. Nizar optimization algorithm: A novel metaheuristic algorithm for global optimization and engineering applications. J. Supercomput. 2024, 80, 3229–3281. [Google Scholar] [CrossRef]
- Suvitha, A.; Devi, S.R.; Arun, K.K.; Jayakumar, S.; Selvi, R.K.; Rajesha, N. Optimal Charging Control of No-Insulation HTS Magnets using Pontryagin’s Principle and Advanced Nizar Optimization Technique. In Proceedings of the 2025 5th International Conference on Trends in Material Science and Inventive Materials (ICTMIM), Kanyakumari, India, 7–9 April 2025; IEEE: Piscataway Township, NJ, USA, 2025; pp. 428–435. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| PV system | 800 kW, 500 V |
| Wind turbine | 250 kW, 500 V |
| BESS capacity | 250 kWh |
| Utility Grid | 11 kV, 50 Hz |
| AC/DC rectifier | 250 kVA, 800 V |
| DC/DC boost and bidirectional converters | 800 kVA, 800 V |
| Bidirectional converter | 1000 |
| Parameter | Value |
|---|---|
| BESS charge efficiency | |
| BESS discharge efficiency | |
| Battery degradation pricing | |
| Grid buying/selling (off-peak) | |
| Grid buying/selling (peak) | |
| Implemented Scenario | EMS | Grid Power Purchase Cost (USD) | Degradation Cost (USD) | Total Cost (USD) |
|---|---|---|---|---|
| Scenario 1 | Proposed NOA | |||
| PSO | ||||
| GWO | 1908.55 | |||
| SSA | ||||
| GA | ||||
| Scenario 2 | Proposed NOA | |||
| PSO | ||||
| GWO | ||||
| SSA | ||||
| GA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabee, H.W.S.; Majeed, D.M. Energy Management System-Based Multi-Objective Nizar Optimization Algorithm Considering Grid Power and Battery Degradation Cost. Energies 2025, 18, 5678. https://doi.org/10.3390/en18215678
Rabee HWS, Majeed DM. Energy Management System-Based Multi-Objective Nizar Optimization Algorithm Considering Grid Power and Battery Degradation Cost. Energies. 2025; 18(21):5678. https://doi.org/10.3390/en18215678
Chicago/Turabian StyleRabee, Hasan Wahhab Salih, and Doaa Mohsin Majeed. 2025. "Energy Management System-Based Multi-Objective Nizar Optimization Algorithm Considering Grid Power and Battery Degradation Cost" Energies 18, no. 21: 5678. https://doi.org/10.3390/en18215678
APA StyleRabee, H. W. S., & Majeed, D. M. (2025). Energy Management System-Based Multi-Objective Nizar Optimization Algorithm Considering Grid Power and Battery Degradation Cost. Energies, 18(21), 5678. https://doi.org/10.3390/en18215678





