Abstract
CREATE-FXB is a Finite Element Method solver specifically developed to address the fixed boundary problem, namely the determination of the Magnetohydrodynamic equilibrium of an axisymmetric plasma confined within a toroidal nuclear fusion device. Although several solvers are already available and widely used, CREATE-FXB represents a valuable alternative with further improvements, as it introduces a set of distinctive capabilities that extend its applicability and accuracy in modelling this class of problems. Its key features include the design of plasma scenarios in tokamaks, the derivation of linearized plasma response with high accuracy, the treatment of a wide class of current density profiles including non-smooth distributions, and an improved capability of interfacing with other existing codes.
1. Introduction
Numerical models solving the Grad–Shafranov equation in magnetically confined toroidal plasmas are crucial both for the design phase of plasma scenarios [1] and for the development of active magnetic control systems [2]. For these applications, a variety of procedures and associated codes for the calculation of Magnetohydrodynamic (MHD) equilibria are widely used.
Under the axisymmetric assumption, MHD codes deal with forward and inverse problems. Forward codes analyze the fixed boundary problem, i.e., the resolution of the Grad–Shafranov equation inside a prescribed plasma region, and the free boundary problem, where the results provide the overall equilibrium configuration including the plasma shape. Inverse MHD codes are aimed at the optimization of the external currents which maintain a desired plasma shape in equilibrium [3], or the identification of the plasma configuration starting from magnetic measurements [4]. Several solvers adaptable to one or more categories are available in the literature, and their range of applications is very vast. The typical numerical schemes involved are the finite difference method (FD) or the Finite Element Method (FEM).
Some remarkable examples of FD-based codes are Lackner’s code [3], FIESTA [5], essentially used for analysis and control purposes, and the SPIDER module [6], included in scenario simulator FENIX [7]. Their domain of resolution is typically a rectangular grid.
On the other hand, Finite Element Method (FEM) schemes are usually intensely adopted in combination with other codes. The first example is the self-consistent SCED code [8], which couples the FEM analysis of the free boundary MHD problem via FEM to one-dimensional transport equations. The MAXFEA code [9] evaluates the plasma motion and supplies it to codes for electromechanical analyses on the external conductors. The CREATE-NL+ [10] free boundary solver makes transient analyses and also provides the outputs to the CREATE-L code [11] to derive plasma response linearized models.
Unlike the above-mentioned procedures, the present work focuses exclusively on fixed boundary problems. The main application is the evaluation of linearized plasma response models. Indeed, thanks to the perturbative fixed boundary approach proposed in [12], the determination of the plasma response to external poloidal fields can be carried out without explicitly defining the external coil system. Consequently, linear models can be derived without any information about geometry and number of poloidal field coils, improving flexibility. A dramatic reduction in computational effort is the main consequence, since only the plasma region is meshed.
This paper presents a new tool called CREATE-FXB, a FEM solver for fixed boundary problems. With respect to the procedure presented in [12], the code incorporates innovative numerical features that make it particularly suited for the derivation of robust and flexible linearized models. In particular, the implemented novel nodal numerical formulation makes the subsequent linearization procedure robust in the treatment of generic current density profiles, such as those ones provided by transport codes [13,14], no matter about the presence of points of non-regularity. Secondly, as well as the previous tools, the code can work using plasma parameters instead of current density profile as input, i.e., total plasma current, poloidal beta, and internal inductance, but the current density parametrization allows the procedure to match equilibria in a wide range of initial plasma parameters, still preserving a simple parametric expression with few degrees of freedom (DoFs) like in [15]. Finally, using the procedure depicted in [16], both magnetic flux and field are provided with a second-order accuracy.
These aspects make the code highly suitable for the design of plasma scenarios, including the estimation of the equilibrium currents once the geometry of the magnetic system is fixed.
The paper is organized as follows. Section 2 describes the main assumptions. Section 3 presents the Grad–Shafranov equilibrium equation and its numerical resolution with the formulation used by CREATE-FXB. Section 4 illustrates some applications of the procedure. Finally, Section 5 draws the conclusions and discusses potential future developments compatible with the model.
2. Assumptions
2.1. Basic Equations
At a generic point of the plasma region , static (zero plasma velocity v = 0) and stationary (∂/∂t = 0) plasma equilibria are well described by the following basic equations below, obtained by means of simplifications of the more complex MHD model [17,18]:
where is the current density, is the magnetic field, is the vacuum magnetic permeability assumed in the plasma, and p is the kinetic pressure.
Under the 2D axisymmetric assumption in a cylindrical reference coordinate system , the magnetic poloidal flux per radian and the poloidal current function are defined as
Using Ampere’s law (1a) and the divergence-free condition for the magnetic field (1b), both and can be expressed in terms of the two above scalar functions:
where is a 2nd order elliptic operator defined by:
Referring to the plasma region , by substituting (4) and (5) in (1c) and noting that (5) implies:
the Grad–Shafranov (G-S) equation is derived:
The functions and are named free functions.
Two classes of differential problems can be distinguished. In free boundary problems [3,6,10], (8) is coupled with (7), in which the current density is known outside the plasma, namely prescribed in the external conductors, and zero in the vacuum. The problem has to be solved in the whole poloidal plane rz, but the plasma–vacuum interface (the last closed magnetic surface that does not intersect solid walls) is a result of the calculation and is not known in advance.
Instead, in fixed boundary problems [12], the plasma region is assigned. Thus, the differential problem is closed by coupling the PDE to some Dirichlet boundary conditions at the plasma boundary :
The problem resolution requires the expression of . Thus, the free functions must be assigned or derived in some way.
2.2. Current Density Modelling
The current density modelling passes through the derivation of the free functions and . Usually, they are given as function of the non-dimensional variable defined as follows:
where and are the values of the flux per radian at the magnetic axis and at the plasma boundary, respectively.
These functions can be obtained by coupling a simplified one-dimensional version of the Grad–Shafranov equilibrium to the transport equations [13,14], adopting iterative schemes to solve the non-linear system and derive the plasma pressure and poloidal current function . Afterwards, these profiles are given to specific 2D axisymmetric codes coupled to circuit equations like CREATE-NL+ [10] to obtain the time evolution of the poloidal flux map.
An alternative procedure takes and from the suitable family of functions . The variable is a set of shape parameters necessary to model the features of the current density profile as shown in [15]. They represent the DoFs of the parameterization , linked to the main plasma quantities, namely plasma current , poloidal beta , and internal inductance , which can be defined as follows:
where is the magnetic field component in the poloidal plane .
However, different definitions of and can also be employed [18]. The choice of this parameterization is motivated by the fact that the flux surfaces outside the plasma boundary are nearly identical for two equilibria with different current density profiles but the same values of , , and [15]. Therefore, the magnetic coupling of the plasma with the external conductors can be modelled by means of a suitable choice of the parameters.
These parameters are calculated using iterative methods, i.e., by solving (7)–(9) until the desired values of plasma quantities (11) are obtained. The computational effort depends on the number of DoFs. Therefore, the choice of should be made so as to ensure coverage of the widest possible range of plasma quantities with a limited amount of computational effort.
Several methods have been proposed to model the current density profile in terms of . For instance, power functions can be employed for both and , as in the CREATE-L code [11], which usually implements the following formulation:
which corresponds to bell-shaped current density profiles due to the term In this formula, the is a scale factor to match the desired plasma current, while the and quantities are mainly used to control the coordinates of the maximum value of current density, and the internal inductance, respectively.
This bell-shaped expression is relatively simple, but it cannot be used for plasma equilibria characterized by low values of , where the current density typically exhibits a hollow profile and tends to concentrate near the boundary. A new family of functions must be determined to be non-monotonic with for specific values of α correspondent to a low internal inductance. Moreover, it should be as simple as possible, to guarantee convergence with sufficient rate.
The CREATE-FXB code can also use the following parameterization in terms of the four parameters , derived by modifying the McCarthy class of profiles [19]:
which enables the treatment of a wide class of plasmas, as shown in Section 4. It is worth noticing that the filter function plays a key role in shaping the plasma current density.
In some cases, the profiles of both and provided by transport codes may be highly rough and irregular. Examples of treatment of these kinds of profiles are also shown in Section 4, where an innovative technique based on information from the mesh nodes has been adopted.
All these features represent a challenge more for the linearization procedure than for the numerical resolution of the fixed boundary problem: indeed, the coupling between standard FEM with linear triangular elements with iterative fixed-point scheme (Picard iterations) is quite robust to face the non-linearity in the computation of the plasma equilibrium quantities. On the other hand, the derivation of the linearized model becomes challenging, because the linearization involves the numerical calculation of profiles derivatives, which cannot be rigorously evaluated in the non-regularity points. For these reasons, adequate meshing processes and suitable numerical techniques to treat the irregularities of the profile are crucial for derivation of the linear model. In this context, the so-called nodal formulation, a numerical technique formalized in the subsequent paragraphs, represents a suitable way to overcome the limitations of conventional methods. Additionally, a procedure of adaptive refinement of mesh can also be used.
3. Finite Element Method Formulation in CREATE-FXB
3.1. Picard Iterations
Equation (8) is a non-linear elliptical partial differential equation, perfectly suited for the resolution using the standard FEM. The first step is to convert it into the weak formulation, by multiplying all the members by a weight function and applying integration by parts:
The non-linearity appears in the right-hand side, since the toroidal current density depends on the unknown .
The plasma domain is discretized into a set of triangular elements with N nodes, corresponding to the vertices of the triangles. The unknown solution is approximated via a linear combination of shape functions :
where at the -th node, is zero at the other nodes, and is piecewise linear within the elements containing the l-th node.
The unknown variable can thus be represented as a numerical vector of length N rather than as a function, so that independent equations are required to find the solution. These are obtained from weak formulation (14) by applying Galerkin’s approach, which selects :
which, in a compact form, become the matrix relation:
where
At this point, Dirichlet’s boundary conditions must be imposed on (17), according to (9). In this case the last term , which would be needed in case of Neumann boundary conditions, becomes redundant. To this end, the set of nodes is partitioned into two subsets: , corresponding to internal nodes, and , related to the boundary nodes, marked by indices ii and ib, respectively. The same operation is performed for the nodal values of . In system (17) K is then rewritten in block format:
where clearly due to properties of functions, can be ignored since only the first subset of equations is required for the next step, is known (Dirichlet’s boundary condition), and depends on .
Therefore, a Picard scheme is adopted to solve the non-linearity, with the unknown vector uniquely determined by solving, at each step :
until a convergence criterion is satisfied.
Additional information on the well-posedness of system (17) can be found in [20].
3.2. Nodal Formulation for
A critical aspect in solving the Grad–Shafranov equation is the accurate evaluation of the current density , especially in the presence of steep gradients or discontinuities in the equilibrium profiles. Standard approaches use linear triangular elements and Gauss integration, e.g., in the CREATE-NL+ code [10], where the term in (18) is computed iteratively from the values of and the shape functions in each triangle barycentre as well as the map are determined in these points, while the free function values are read from the diagrams and . However, the main issue arises when the profiles present discontinuities. In such cases, if the level at which is discontinuous falls into a bend of elements, the integrals are done with a wrong value of . To address this limitation, a nodal formulation is introduced, in which the current density is reformulated in terms of nodal quantities, ensuring a smoother and more robust treatment of discontinuities.
The main issue arises when the profiles present discontinuities. In such cases, if the level at which is discontinuous falls into a bend of elements, the integrals are calculated with a wrong value of .
In order to properly handle the high steep current density regions within the plasma domain, as well as the possible discontinuities of with respect to , the current density is reformulated as follows:
where and , are computed from and defined at the mesh nodes according to their respective profile functions. In this way, spatial discontinuities resulting from discontinuities in and are smoothed out. As a result, the computation of (the flux source) becomes more accurate, and consequently, so does the evaluation of the flux itself. The singularity in the right-hand side of (21) wherever can easily be handled. Indeed, the flux gradient is typically zero for well-defined values of , namely at the magnetic axis () and at the null points at the plasma boundary ().
The nodal formulation is particularly suited in two cases that are beyond the scope of this paper, namely,
- The free boundary problem in cases where the current density is non-zero at the plasma edge;
- The derivation of the linearized plasma response to external currents and profile variations.
3.3. Accurate Calculation of the Magnetic Flux and Field
The above MHD equilibrium calculation with linear triangles provides a piecewise constant value of the flux gradient and yields magnetic field discontinuities across elements.
To tackle these issues, especially when the derivative of the magnetic field is needed, two different actions are undertaken. The first action is a mesh refinement wherever the discontinuities in the flux gradient and/or the gradients of the current density exceed prescribed thresholds.
The other method is a post-processing algorithm that requires very limited computational effort while ensuring the regularity of field derivatives [21], which is crucial for certain applications. This method is based on Helmholtz’s theorem and employs the Finite Element Method (FEM) with linear shape functions to calculate and in the second-order calculation. With the technique proposed in [16], the poloidal magnetic field can be determined by post-processing the standard FEM flux map as the solution to the minimization problem:
where from (4), , while are suitable non-dimensional constants.
The first and second terms in (22) are related to (1a,b), whereas the third term takes into account the boundary condition. The quantities and , which is the tangential component of , are obtained from the first-order FEM solution of the G-S equation. This formulation ensures continuity and achieves a convergence rate of order O(h2) also for , where h is the mesh size. These properties are highly useful, offering a high level of accuracy and enabling the derivation of reliable linearized models with limited computational effort, especially when compared to other methods, such as [22].
3.4. Optimization of Poloidal Field Coil Currents
The optimization of the number, position, and dimension of the Poloidal Field (PF) coils in a tokamak is a challenging task, due to linear and non-linear constraints related to maintenance requirements, and technological limits on electric power, current density, magnetic fields, and vertical forces [13,14,17,23,24]. Here, the problem of the optimization of the currents of the PF coils in air core tokamaks while keeping their positions fixed has been addressed [9,10,11,12]. It is based on the linearization of the GS equation around the desired plasma equilibrium. An iterative optimization problem, subject to both linear and quadratic constraints, is then solved.
The total flux per radian at the plasma boundary is the sum of two terms:
Here , the flux pre radian due to the PF coils, can readily be computed using Green functions based on elliptic integrals [25]. The calculation of the plasma contribution using elliptic integrals may be cumbersome, since the boundary is in contact with the source currents. A solution having the same degree of accuracy as FEM can be obtained by surrounding the fixed mesh boundary (i.e., the plasma contour) with a halo region made of a few layers of elements, and solving:
where is given by the solution of Section 2.1 in , and vanishes in .
The boundary condition on is computed using Green functions from . This method gets rid of the singularities, since the minimum distance between the points of the boundary and the sources is the thickness of the layer.
The PF coil currents are then optimized using one of the methods described in [13,14,17,23,24]. Since the optimized flux per radian is hardly equal to the difference between and , it is necessary to check whether the free boundary equilibrium is sufficiently close to the desired fixed boundary configuration. This task is fulfilled by a specific version of the CREATE-NL+ code, solving the free boundary equilibrium code in a semicircle of the r-z plane in the first and fourth quadrants, adding further elements to the mesh used for solving the fixed boundary problem. In this version of the free boundary code, the PF equilibrium currents are treated as a set of filaments at the same locations used for Gauss integration of elliptic integrals.
3.5. Linearization
The formulation described in this paper can effectively be used to derive a linearized plasma response model.
By using the perturbative fixed boundary approach of [12], combined with the nodal formulation of in (21), the equilibrium linearized variations can be computed without restrictions on the class of and profiles. The smoothing feature of the nodal formulation, indeed, makes the evaluation of the plasma response (based on the evaluation of Jacobian matrices) robust to each non-regularity of the profiles, such as high-gradient regions, cusps, and discontinuities. Moreover, only the plasma region must be meshed to derive the response model. As a consequence, the linearization procedure is very accurate and flexible to treat any magnetic flux perturbation due to geometry variations in the external conductors, without requiring a mesh in the region outside the plasma. The new linearization procedure can efficiently be employed for plasma identification, magnetic control, optimization of PF coil current waveforms, and all the phases of the design of tokamak magnetic plasma scenarios.
4. Results and Discussion
This section shows the flexibility of parameterization (13) and demonstrates the reliability of the CREATE-FXB code with a number of benchmark cases, obtaining a very good agreement with available analytical solutions and other numerical results in the literature.
4.1. Envelopes for Current Density Parameterization
This section compares the limits of validity of three parameterization choices for the current density in the - plane for an elliptic plasma (Figure 1a).
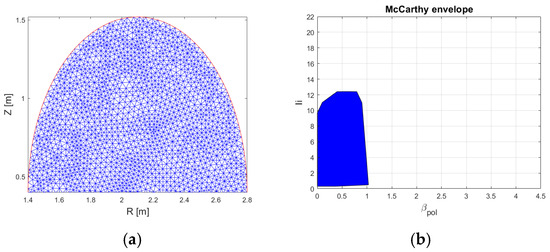
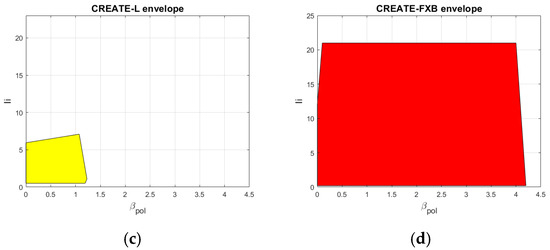
Figure 1.
Limits of validity of three parameterization choices and envelopes in the - plane: (a) upper part of the FEM mesh of the elliptical fixed boundary domain; (b) McCarthy parameterization [19]; (c) CREATE-L parameterization [11]; (d) CREATE-FXB parameterization proposed here in (13).
The CREATE-FXB parameterization proposed here in (13) is able to obtain plasmas with a wide range of and values. Figure 1 shows that the upper bounds (more than 20 for and more than 4 for ) are clearly larger than those obtained with the other parameterizations. As stated in Section 2, the CREATE-FXB parameterization (13) is also able to obtain low values of , i.e., down to about 0.2 like McCarthy’s family, whereas the corresponding lowest value for CREATE-L is about 0.5.
4.2. Circular Plasma with a Large Aspect Ratio and Discontinuous Current Density Profile
The robustness of the nodal formulation is shown by comparing the standard and new numerical solutions with the analytical one, in a circular plasma case with very large aspect ratio:
with and as the major and minor radius, respectively. Under this assumption, the two-dimensional differential problem (8) and (9) reduces to a 1D one [17]. The test is carried out by comparing the straightforward analytical solution of the 1D problem with the FEM solution returned by the 2D axisymmetric solver. A discontinuous current density profile is defined with the following input data:
Figure 2 shows the azimuthal field in the plasma region evaluated both using the standard and the nodal formulation of the current density in the numerical solver. Moreover, for each formulation, the second-order procedure has been applied.
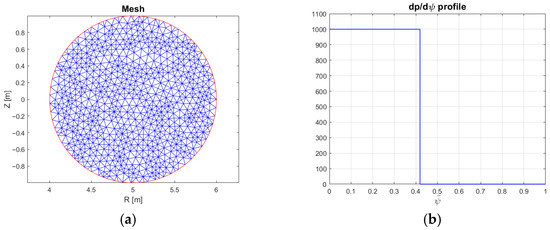
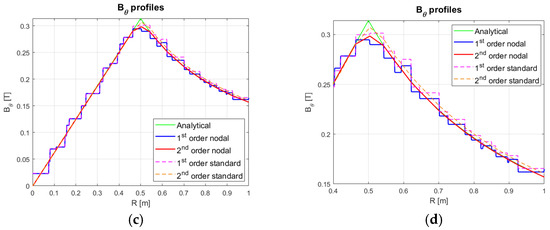
Figure 2.
Analytical and numerical evaluation of the azimuthal magnetic field along the pinch radius at : (a) FEM mesh, with 936 nodes and 1783 elements; (b) profile; (c) comparison between the classic first and second-order magnetic field solutions, using the nodal and the standard formulation of ; (d) zoom at .
As shown in Figure 2d, the continuous red line (second-order nodal result) practically coincides with the continuous green one (analytical result) for R > 0.5.
Two aspects are highlighted in Table 1, which reports the values of the numerical error. Firstly, the nodal formulation provides better results when the discretization is coarse. Secondly, higher accuracy and smoothness of the magnetic field is obtained by post-processing the FEM solution with the method introduced in [16] and summarized in Section 3.3, no matter the involved formulation.

Table 1.
Circular plasma with a large aspect ratio and discontinuous current density profile: numerical errors.
4.3. Non-Circular Low-Aspect-Ratio Plasma Equilibrium
The procedure has been applied also to a number of test cases for which analytical solutions are available. The reference case shown here is a low-aspect-ratio plasma equilibrium described in [26], with
where is the poloidal flux per radian at the magnetic axis, is the radial coordinate of the magnetic axis, and is a non-dimensional constant (there is a typo in [26] in the exponent of ).
The analytic solution of the Grad–Shafranov equation is given by:
By fixing the previous parameters as follows:
and choosing as boundary flux per radian:
the coordinates of the separatrix are shown in Figure 3a.
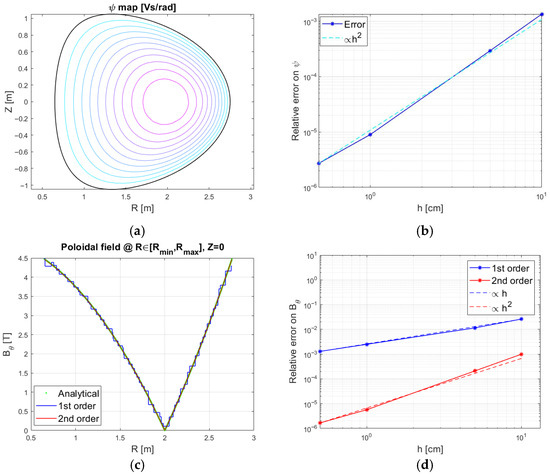
Figure 3.
Non-circular low-aspect-ratio plasma equilibrium. Comparison between numerical and analytic solution: (a) analytical flux levels inside the plasma region; (b) trend of the relative error on the poloidal flux per radian ‖ψan-ψnum‖/‖ψan‖, with ψ at the mesh nodes; (c) Bθ profile along the line at Z = 0; (d) numerical error on the magnetic field ‖B(θ,an)-B(θ,num)‖/‖B(θ,an)‖ at Z = 0.
In this case the nodal and the standard formulations yield exactly the same results, since the current density is linear in each triangular element. Figure 3b shows the trend of the numerical error on the flux with the infinity norm as a function of the maximum element size , which scales with , as shown in [16].
4.4. Optimization of PF Equilibrium Currents in DTT
The fixed boundary solver has been used to determine the set of PF current needed to keep a single plasma in equilibrium in DTT, standing for Divertor Tokamak Test facility, one of the next generation tokamak devices scheduled in the EU European roadmap for nuclear fusion [27].
Figure 4 shows the target plasma boundary at 27 s in the DTT plasma scenario with MA, , , and [28]. The CREATE-FXB code has firstly calculated the fixed boundary equilibrium in , and then the flux per radian due to the plasma , obtained in the region , using the procedure described in Section 3.4.
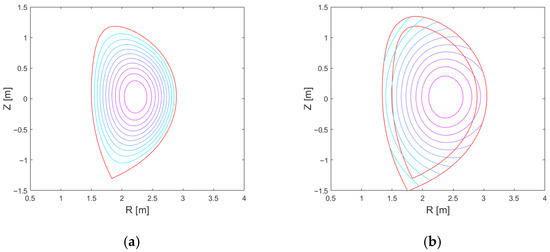
Figure 4.
Target plasma boundary at 27 s in the DTT plasma scenario with = 5.5 MA, , , and [23]: (a) fixed boundary solution obtained by CREATE-FXB in ; (b) (flux per radian due to the plasma) in
Afterwards, the CREATE-FXB code minimizes , which is the difference between (flux per radian due to the PF system at the plasma boundary) and the desired equilibrium value, namely –. The PF system includes 12 circuits and 24 coils. The details are given in [28]. Figure 5a shows the as a function of the maximum current in the circuits . Figure 5b shows the optimal currents in comparison with those reported in [28]. The slight improvement of CREATE-FXB is due to a different choice of the figure of merit, since the procedure used in [28] optimizes the entire scenario, adding further constrains.
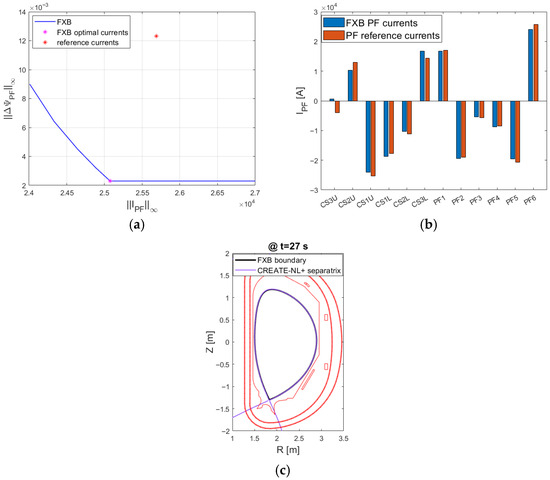
Figure 5.
PF circuit current optimization in DTT plasma scenario at 27 s: (a) minimum value of the discrepancy between PF flux per radian and its desired value as a function of the maximum circuit current; (b) optimal currents in comparison with reference currents in [28]; (c) desired shape and plasma edge provided by the free boundary CREATE-NL+ code using the circuit currents provided by CREATE-FXB (the maximum distance is less than 9 mm).
The validity and the effectiveness of the CREATE-FXB resulting PF currents is demonstrated by solving a free boundary problem using these currents as input data. The test consists of determining, via FEM, the separatrix line confining the plasma region as output from the free boundary solver and verifying the matching with the plasma boundary of the fixed boundary procedure.
The result is shown in Figure 5c, where the free boundary equilibrium obtained by the CREATE-NL+ code using the PF circuit currents obtained by CREATE-FXB provides a plasma boundary almost coincident with the desired shape, since the maximum distance is less than 9 mm.
4.5. Software Performance
The procedure here presented, has been implemented as a new software called CREATE-FXB. The programming language is MATLAB®. Its copyright is being transferred to Consorzio CREATE. Requests to obtain the code should be addressed to create@unina.it with raffaele.albanese@unina.it in cc. The problem described in Section 4.3 has been analyzed with meshes of different sizes. The numerical results have been obtained with an Intel (R) Core(TM) i7–10750H processor at 2.6 GHz and a 32 GB RAM using the MATLAB® version R2023b. With reference to cases 1, 2, and 3 of Table 1, the first-order solution requires 37 ms, 90 ms, and 2.261 s, respectively. The corresponding computational times of the second-order solutions are instead 437 ms, 526 ms, and 5.468 s.
5. Conclusions
In this work, CREATE-FXB is presented as a new fixed boundary solver for the Grad–Shafranov equation, based on the Finite Element Method with an innovative technique. The code provides an efficient and accurate tool for plasma equilibrium analysis in tokamaks, offering robust handling of non-smooth current density profiles, second-order accuracy in the evaluation of magnetic flux and field, and an integrated framework for PF coil current optimization.
Its accuracy has been demonstrated via comparison with various available analytic solutions. Validation against the free-boundary code CREATE-NL+ has confirmed the reliability of the approach for scenario design and equilibrium current estimation. Future extensions will focus on the systematic use of the derived linearized models for plasma identification and control, and on the integration of plasma response-based scenario optimization strategies.
Overall, CREATE-FXB constitutes a flexible and accurate complement to the CREATE code family, enhancing its capability to address fixed boundary problems in tokamak applications.
Author Contributions
Conceptualization, R.A., M.N. and P.Z.; methodology, R.A., M.N. and P.Z.; software, R.A., M.N. and P.Z.; formal analysis, R.A., M.N. and P.Z.; investigation, R.A., M.N. and P.Z.; resources, R.A., M.N. and P.Z.; data curation, R.A., M.N. and P.Z.; writing—original draft preparation R.A., M.N. and P.Z.; writing—review and editing, R.A., M.N. and P.Z.; supervision, R.A.; project administration, R.A.; funding acquisition, R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the PRIN Project P2022KNM7B “TRAINER—Tokamak plasmas daTa-dRiven identificAtIon and magNEtic contRol”, CUP E53D23014670001 funded by EU in NextGenerationEU plan through the Italian “Bando Prin 2022—D.D. 1409 del 14-09-2022” by MUR. This work was also partially supported by the Italian Research Ministry under the PRIN Project 2022JCZJ33. Advanced control techniques for the alternative divertor plasma configurations in nuclear fusion tokamaks, CUP: E53D23000670006.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Blum, J.; Boulbe, C.; Faugeras, B.; Heumann, H. Control Methods for the Optimization of Plasma Scenarios in a Tokamak. In System Modeling and Optimization, Proceedings of the CSMO 2015, Sophia Antipolis, France, 29 June–3 July 2015; Bociu, L., Désidéri, J.A., Habbal, A., Eds.; IFIP Advances in Information and Communication Technology; Springer: Cham, Switzerland, 2016; Volume 494. [Google Scholar] [CrossRef]
- Anand, H.; Bardsley, O.; Humphreys, D.; Lennholm, M.; Welander, A.; Xing, Z.; Barr, J.; Walker, M.; Mitchell, J.; Meyer, H. Modelling, design and simulation of plasma magnetic control for the Spherical Tokamak for Energy Production (STEP). Fusion Eng. Des. 2023, 194, 113724. [Google Scholar] [CrossRef]
- Lackner, K. Computation of ideal MHD equilibria. Comput. Phys. Commun. 1976, 12, 33–44. [Google Scholar] [CrossRef]
- Lao, L.L.; John, H.S.; Stambaugh, R.D.; Kellman, A.G.; Pfeiffer, W. Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 1985, 25, 1611. [Google Scholar] [CrossRef]
- Cunningham, G. High performance plasma vertical position control system for upgraded MAST. Fusion Eng. Des. 2013, 88, 3238–3247. [Google Scholar] [CrossRef]
- Ivanov, A.A.; Khayrutdinov, R.; Medvedev, S.; Poshekhonov, Y. The SPIDER code—Solution of direct and inverse problems for free boundary tokamak plasma equilibrium. Keldysh Inst. Prepr. 2009, 39, 24. [Google Scholar]
- Fable, E.; Janky, F.; Treutterer, W.; Englberger, M.; Schramm, R.; Muraca, M.; ASDEX Upgrade Team. The modeling of a tokamak plasma discharge, from first principles to a flight simulator. Plasma Phys. Control. Fusion 2022, 64, 044002. [Google Scholar] [CrossRef]
- Blum, J.; Le Foll, J.; Thooris, B. The self-consistent equilibrium and diffusion code SCED. Comput. Phys. Commun. 1981, 24, 235–254. [Google Scholar] [CrossRef]
- Miki, N.; Verrecchia, M.; Barabaschi, P.; Belov, A.; Chiocchio, S.; Elio, F.; Ioki, K.; Kikuchi, S.; Kokotkov, V.; Ohmori, J.; et al. Vertical displacement event/disruption electromagnetic analysis for the ITER-FEAT vacuum vessel and in-vessel components. Fusion Eng. Des. 2001, 58, 555–559. [Google Scholar] [CrossRef]
- Albanese, R.; Ambrosino, R.; Mattei, M. CREATE-NL+: A robust control-oriented free boundary dynamic plasma equilibrium solver. Fusion Eng. Des. 2015, 96, 664–667. [Google Scholar] [CrossRef]
- Albanese, R.; Villone, F. The linearized CREATE-L plasma response model for the control of current, position and shape in tokamaks. Nucl. Fusion 1998, 38, 723. [Google Scholar] [CrossRef]
- Portone, A. Perturbed solutions of fixed boundary MHD equilibria. Nucl. Fusion 2004, 44, 265. [Google Scholar] [CrossRef]
- Pereverzev, G.V.; Yushmanov, E.P. ASTRA. Automated System for TRansport Analysis in a Tokamak; Max Planck Institute for Plasma Physics: Garching near Munich, Germany, 2022. [Google Scholar]
- Khayrutdinov, R.R.; Lukash, V.E. Studies of plasma equilibrium and transport in a tokamak fusion device with the inverse-variable technique. J. Comput. Phys. 1993, 109, 193–201. [Google Scholar] [CrossRef]
- Luxon, J.L.; Brown, B.B. Magnetic analysis of non-circular cross-section tokamaks. Nucl. Fusion 1982, 22, 813. [Google Scholar] [CrossRef]
- Albanese, R.; Iaiunese, A.; Zumbolo, P. Solution of Grad-Shafranov equation with linear triangular finite elements providing magnetic field continuity with a second order accuracy. Comput. Phys. Commun. 2023, 291, 108804. [Google Scholar] [CrossRef]
- Freidberg, J.P. Ideal magnetohydrodynamic theory of magnetic fusion systems. Rev. Mod. Phys. 1982, 54, 801–902. [Google Scholar] [CrossRef]
- Wesson, J.; Campbell, D.J. Tokamaks; Clarendon Press: Oxford, UK, 2004; ISBN 9780198509226. [Google Scholar]
- Mc Carthy, P.J. Analytical solutions to the Grad–Shafranov equation for tokamak equilibrium with dissimilar source functions. Phys. Plasmas 1999, 6, 3554–3560. [Google Scholar] [CrossRef]
- Quarteroni, A. Il metodo di Galerkin-elementi finiti per problemi ellittici. In Modellistica Numerica per Problemi Differenziali; Springer: Milano, Italy, 2006; pp. 37–96. [Google Scholar]
- Neittaanmäki, P.; Saranen, J. On finite element approximation of the gradient for solution of Poisson equation. Numer. Math. 1981, 37, 333–337. [Google Scholar] [CrossRef]
- Jardin, S.C. A triangular finite element with first-derivative continuity applied to fusion MHD applications. J. Comput. Phys. 2004, 200, 133–152. [Google Scholar] [CrossRef]
- Lazarus, E.A.; Lister, J.B.; Neilson, G.H. Control of the vertical instability in tokamaks. Nucl. Fusion 1990, 30, 111. [Google Scholar] [CrossRef]
- Albanese, R.; Ambrosino, R.; Castaldo, A.; Loschiavo, V.P. Optimization of the PF coil system in axisymmetric fusion devices. Fusion Eng. Des. 2018, 133, 163–172. [Google Scholar] [CrossRef]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Physicists; Springer: Berlin/Heidelberg, Germany, 2013; Volume 67. [Google Scholar]
- Schnack, D.D. Toroidal Equilibrium; The Grad–Shafranov Equation. In Lectures in Magnetohydrodynamics; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 780, pp. 107–120. [Google Scholar] [CrossRef]
- European Research Roadmap to the Realisation of Fusion Energy. November 2018. Available online: https://euro-fusion.org/wp-content/uploads/2022/10/2018_Research_roadmap_long_version_01.pdf (accessed on 2 May 2019).
- Castaldo, A.; Albanese, R.; Ambrosino, R.; Crisanti, F. Plasma Scenarios for the DTT Tokamak with Optimized Poloidal Field Coil Current Waveforms. Energies 2022, 15, 1702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).