Higher-Order Dynamic Mode Decomposition to Identify Harmonics in Power Systems
Abstract
1. Introduction
- Introduction of a robust harmonic spectrum analysis framework based on HODMD, maintaining accuracy under stressed operating conditions such as transients, microgrids, and distorted waveforms;
- Extension of harmonic analysis to non-stationary signals, enabling accurate extraction of frequency, amplitude, and phase for both fundamental and harmonic components;
- Development of a sliding window HODMD implementation for high resolution time–frequency tracking with amplitude;
- Validation of the proposed method through simulation and real-time experiments, demonstrating robustness to switching harmonics and noise in both simulated and real-world grid operation and monitoring environments.
2. Dynamic Mode Decomposition (DMD)
- Harmonics: integer multiples of a fundamental frequency due to nonlinear loads;
- Interharmonics: frequencies that lie between integer harmonics, often resulting from variable speed drives or power electronic switching;
- DC Components: steady-state offsets that may arise from asymmetrical faults or rectified signals.
- : DC value with/without decaying;
- , : magnitude and phase of the harmonic;
- , , : magnitude, frequency, and angle of the fundamental frequency in Hz;
- , , : magnitude, frequency, and angle of the inter-harmonic component.
2.1. Standard DMD Assumption
2.2. Koopman Operator and Singular Value Decomposition (SVD)
3. Higher-Order Dynamic Mode Decomposition (HODMD)
Algorithm of HODMD
- SVD-Based Truncation: During the first step of HODMD, singular value decomposition (SVD) is applied to the snapshot matrix. This step retains only the most energetic modes, effectively filtering out low-energy noise components.
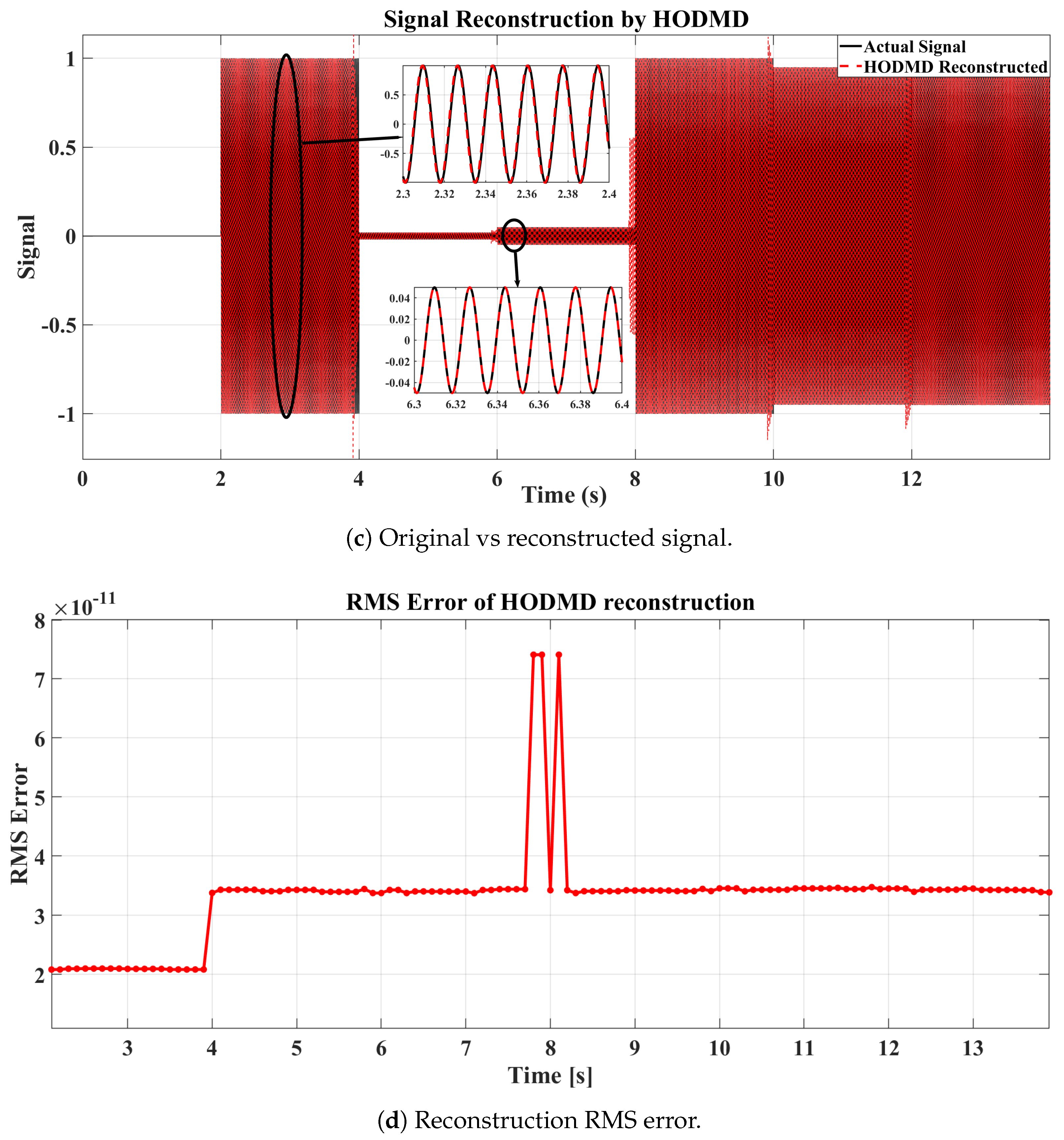
- Reconstruction Error Check: After mode selection, the reconstructed signal is compared to the original data, and the root mean square error (RMSE) is computed. A high RMSE indicates that a relevant mode may have been discarded or misclassified. In such cases, the parameter d or the tolerance is adjusted until the reconstruction error is minimized, ensuring recovery of the missing dominant mode.
4. Results
4.1. Performance Evaluation on Synthetic Signal
4.1.1. Case Study 1: Stationary Signal
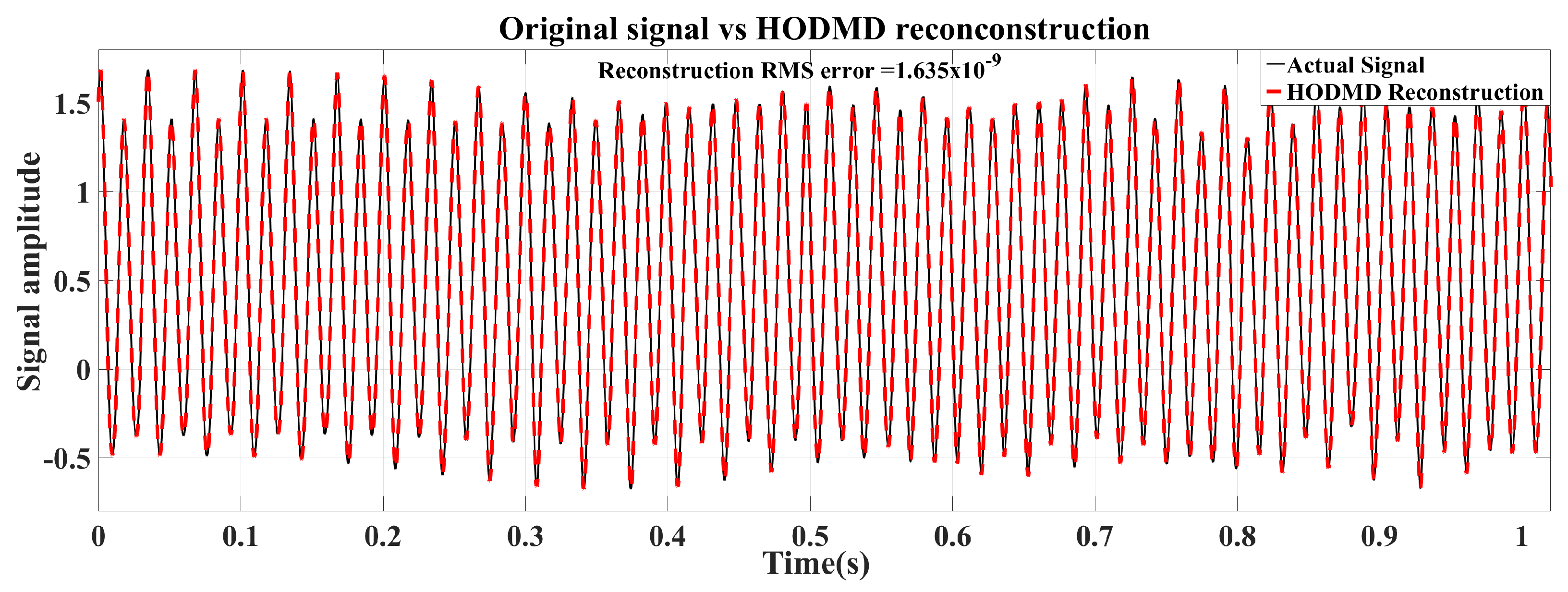
4.1.2. Case Study 2: Hauer’s Signal
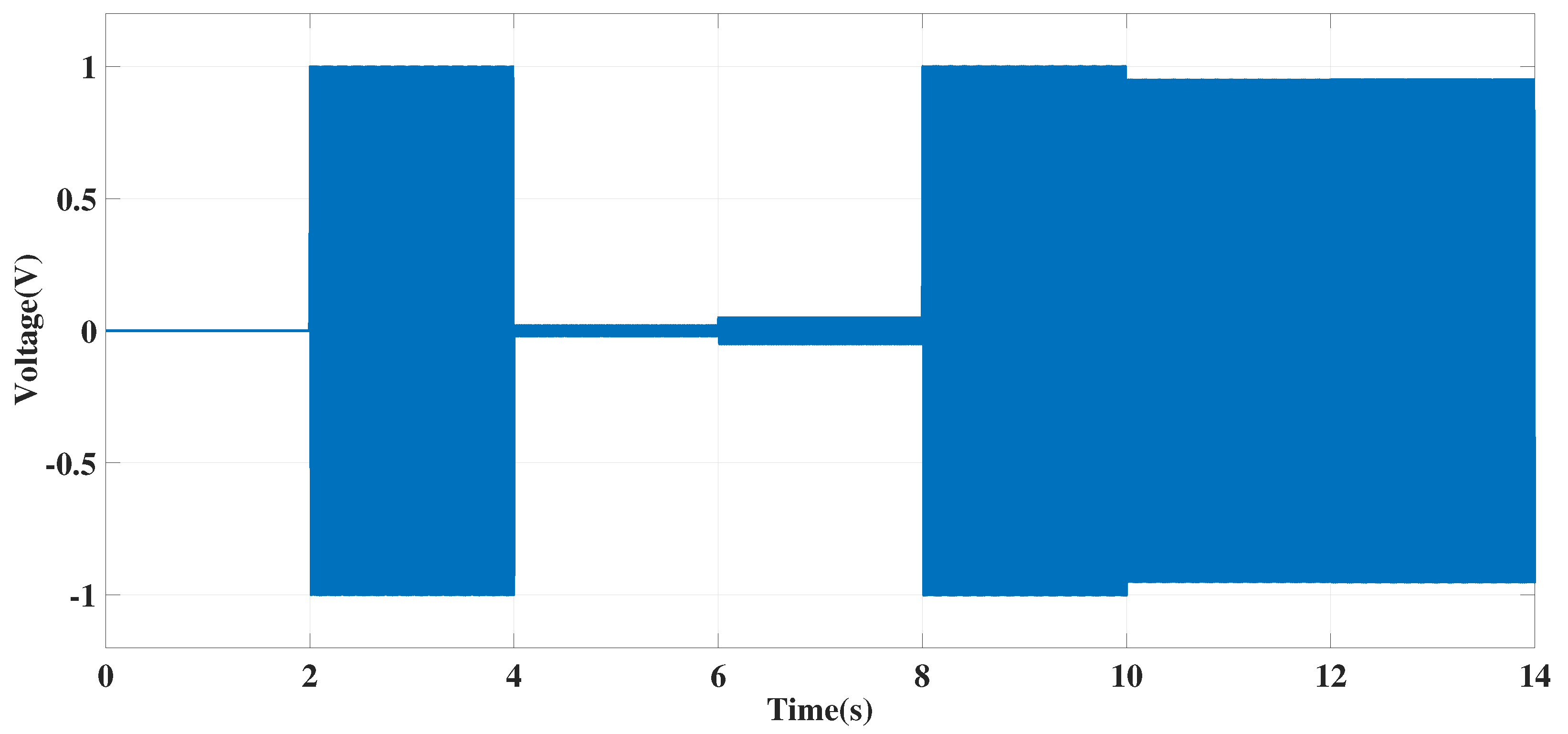
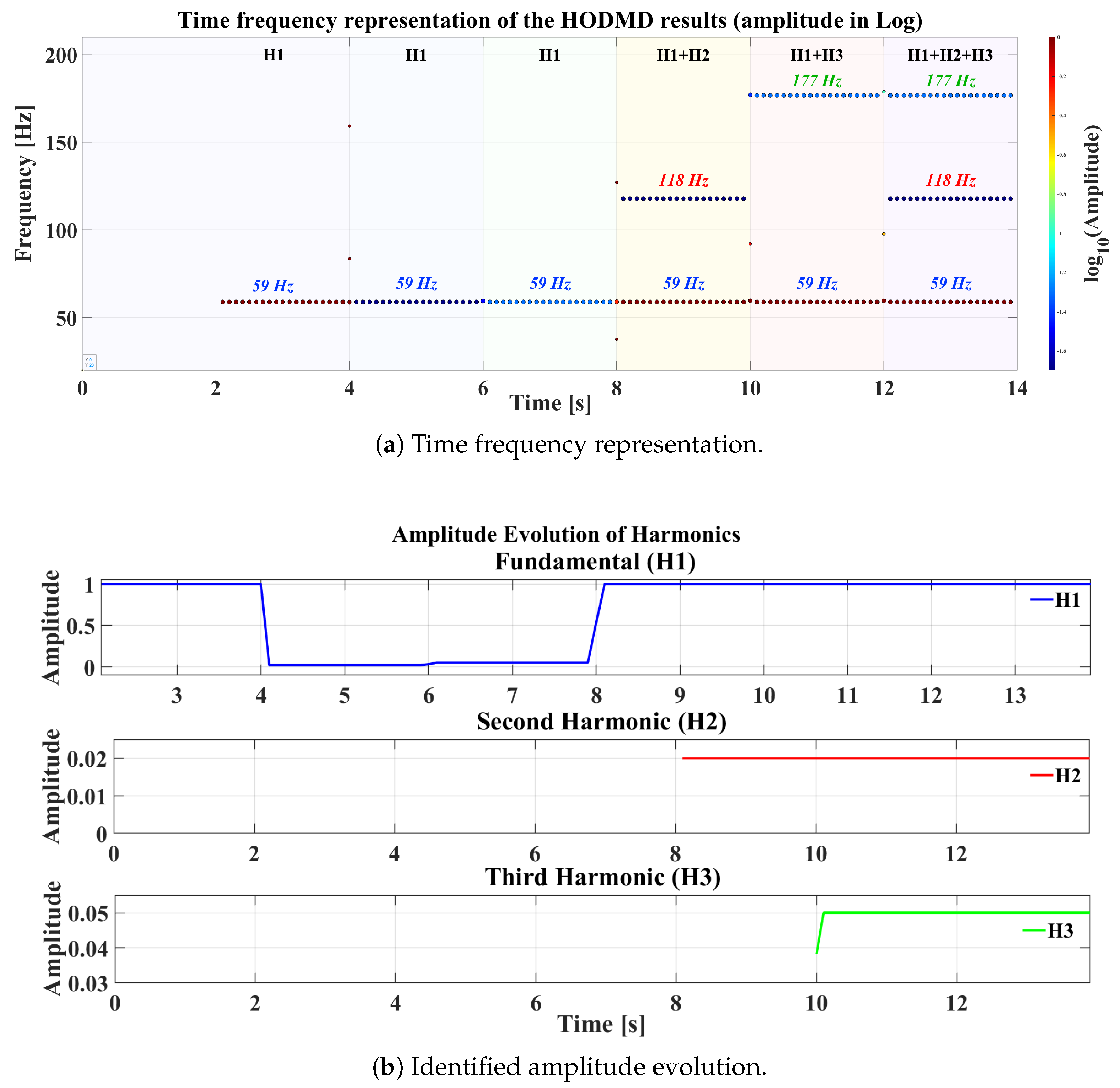
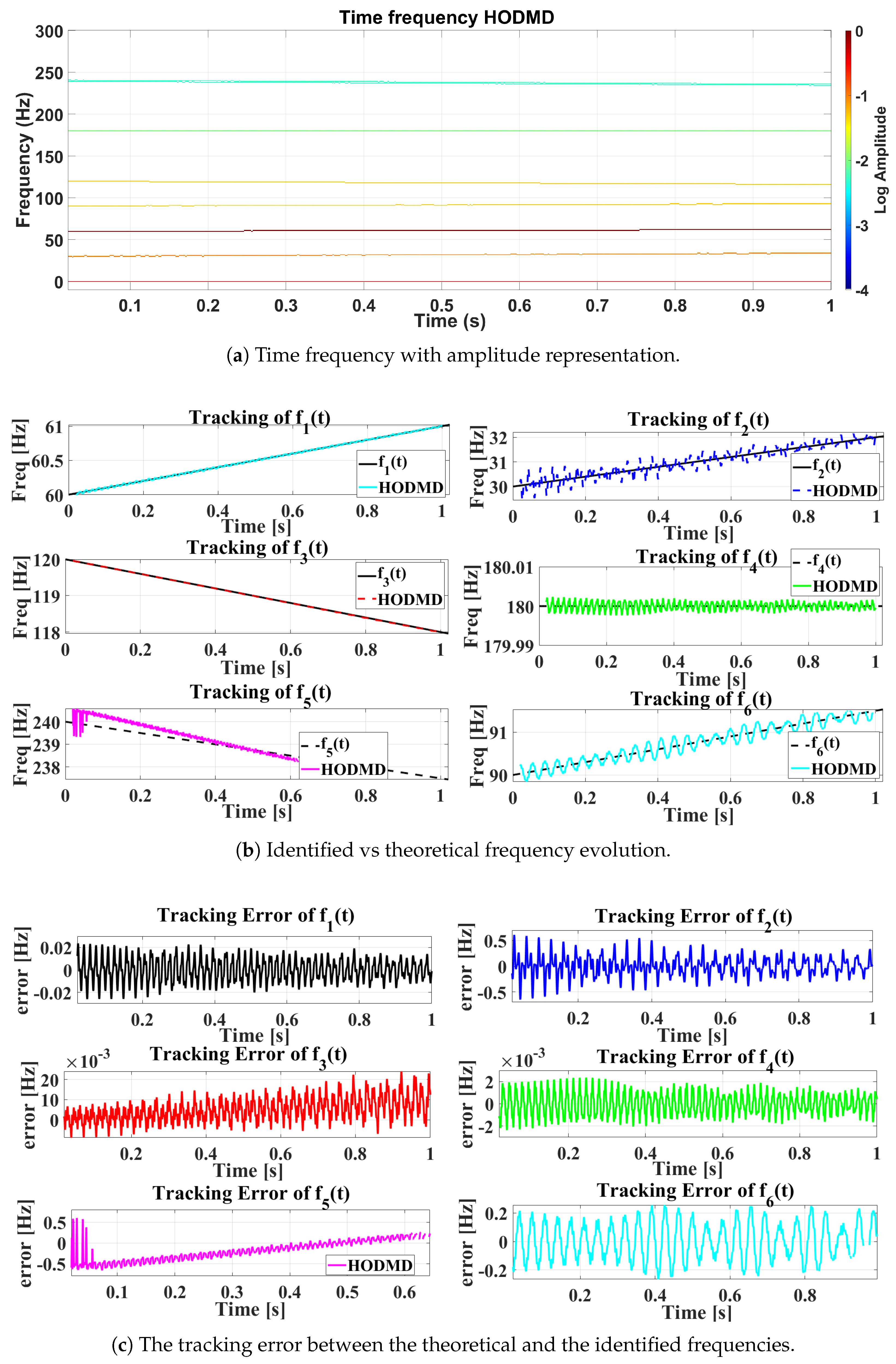
4.1.3. Case Study 3: Non-Stationary Signal
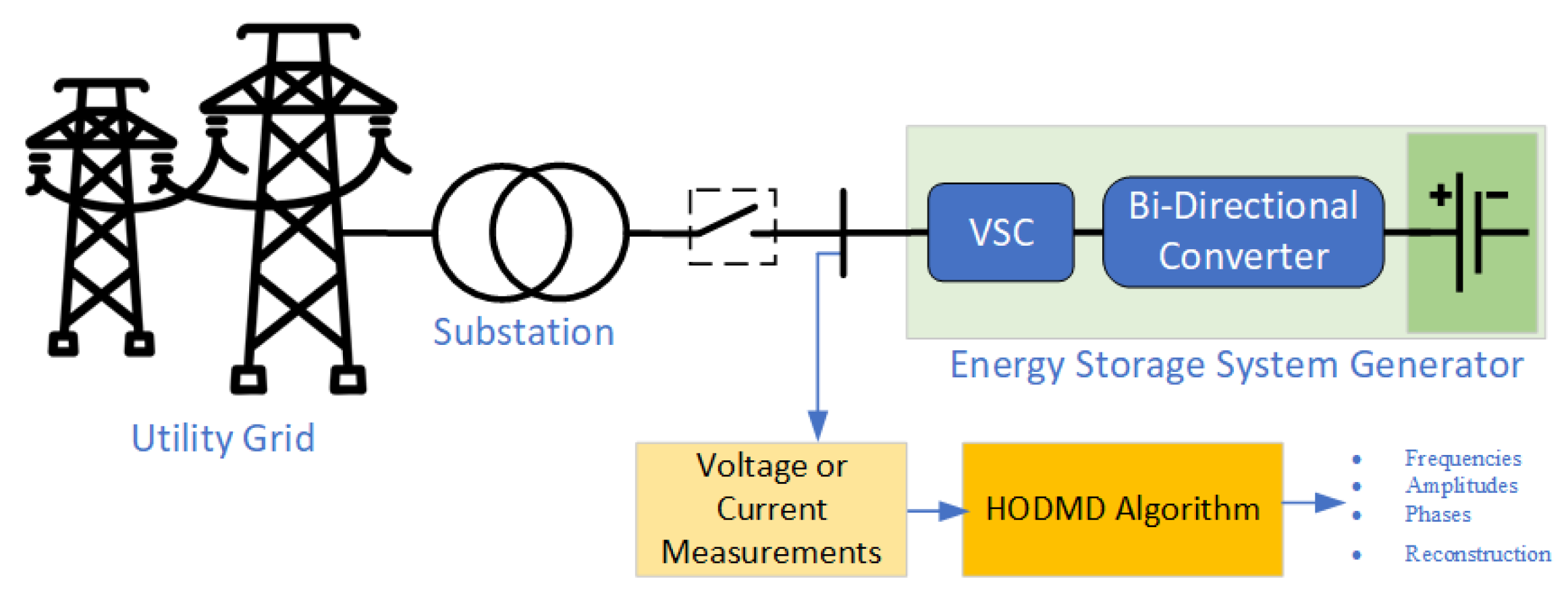
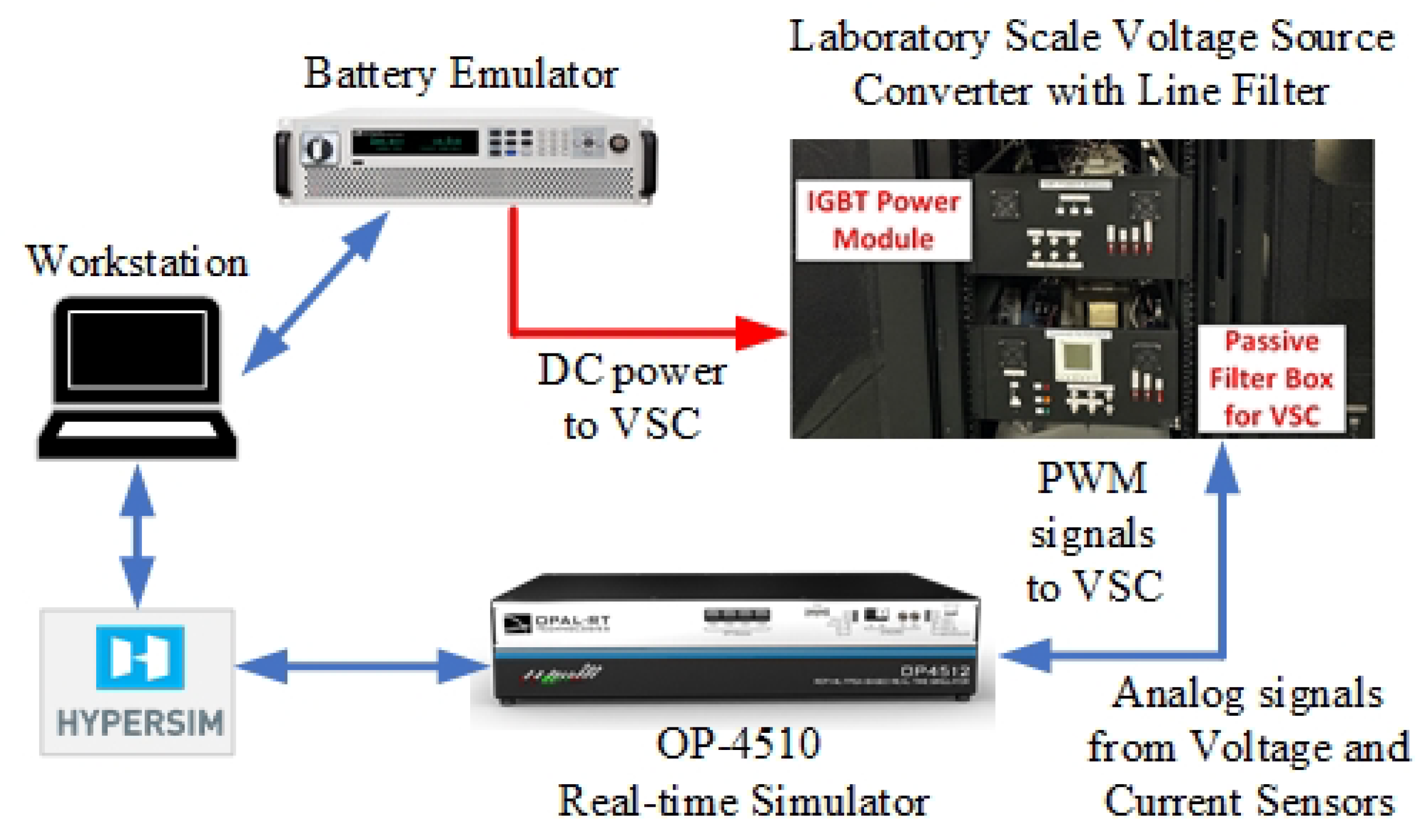
4.2. Performance Evaluation on Laboratory-Scale Experimental Setup
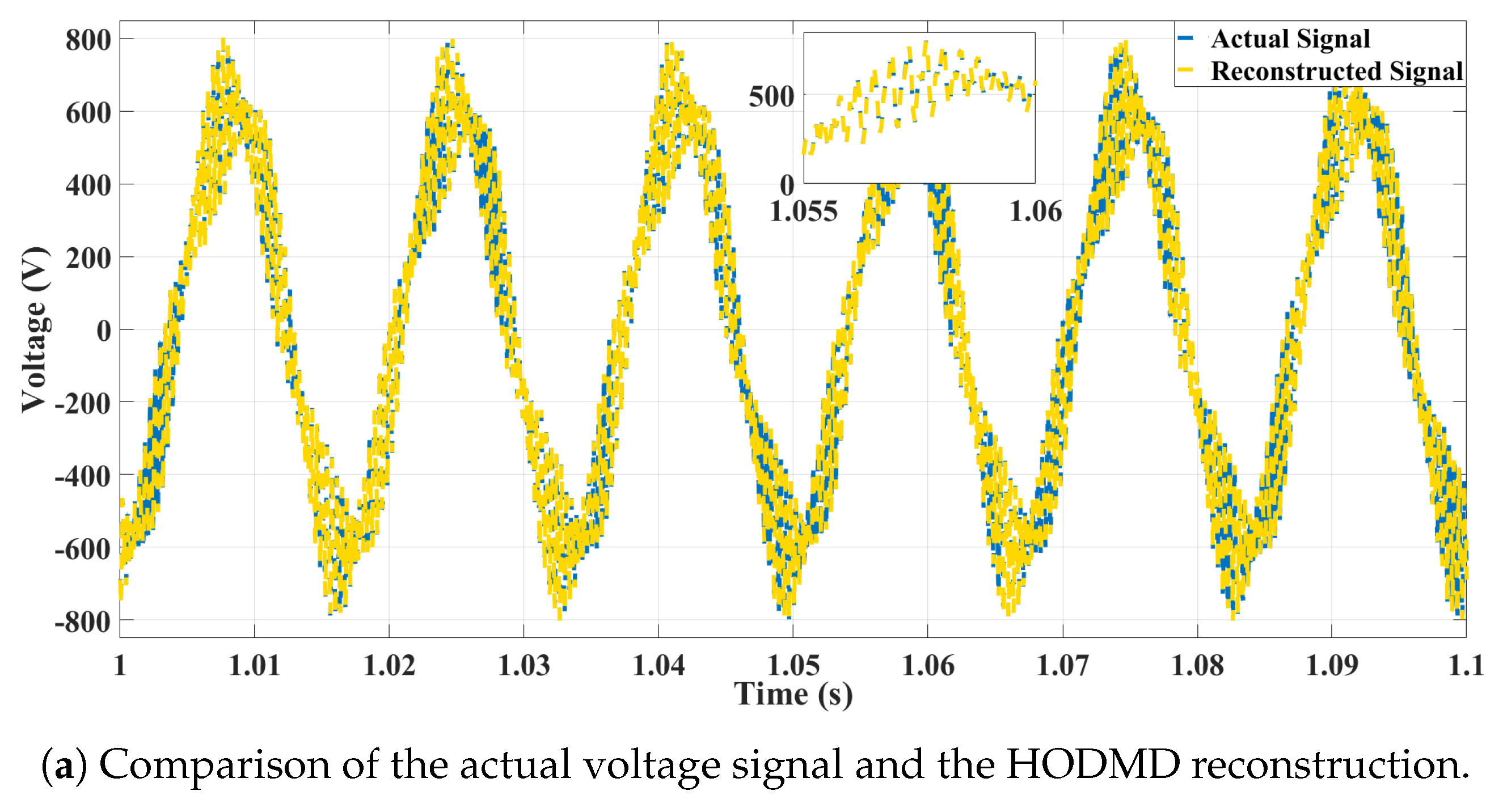
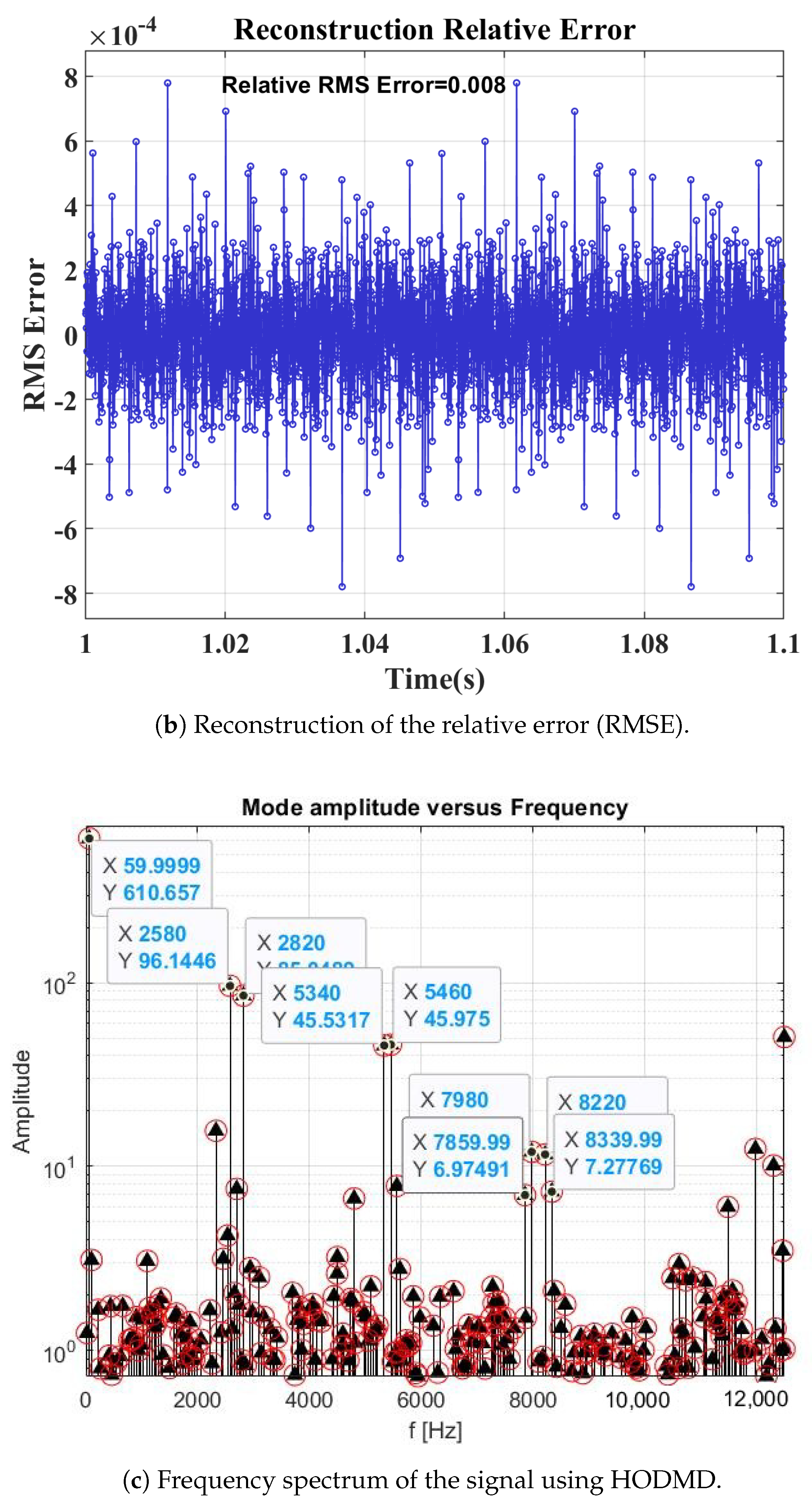
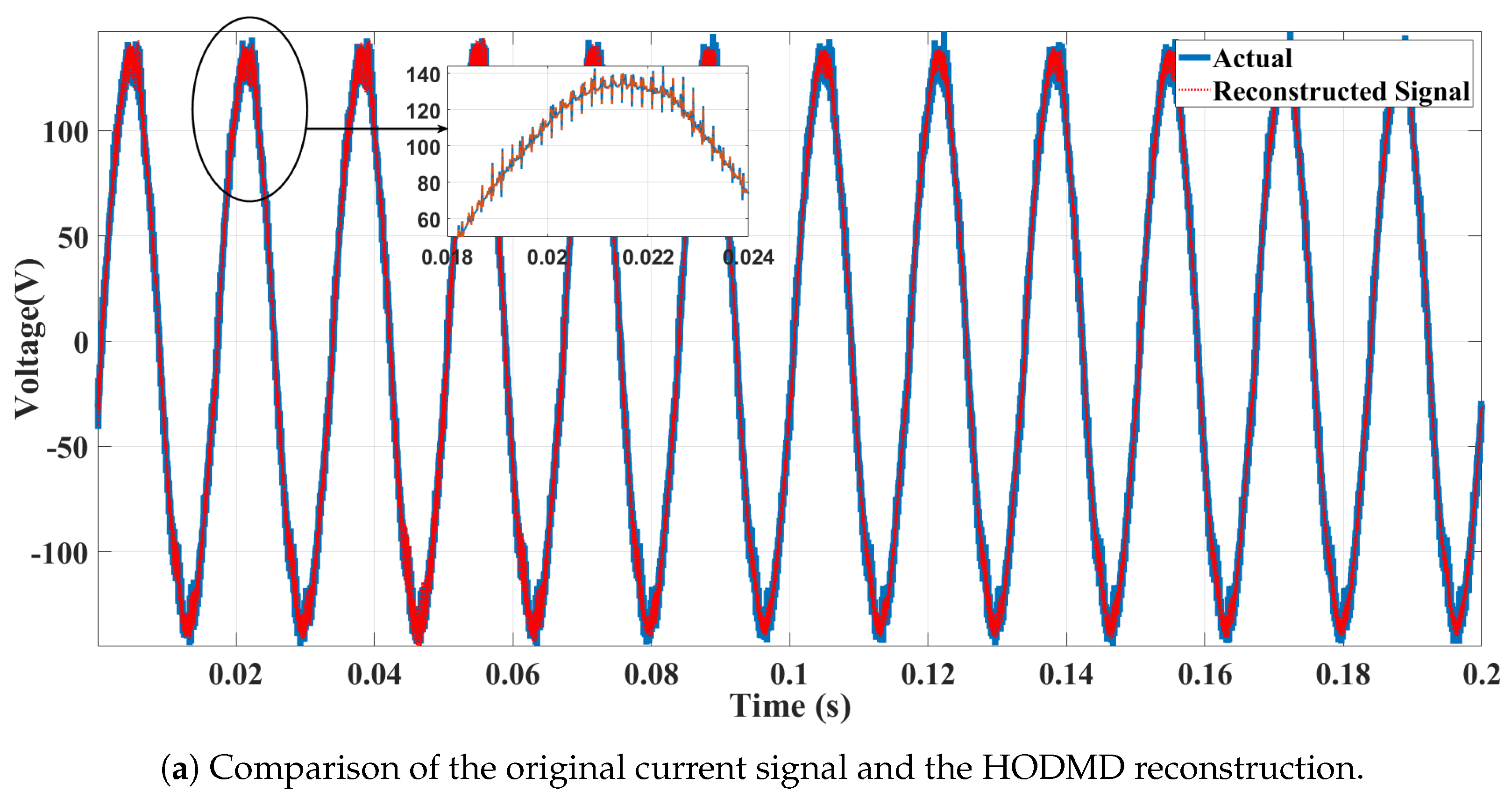
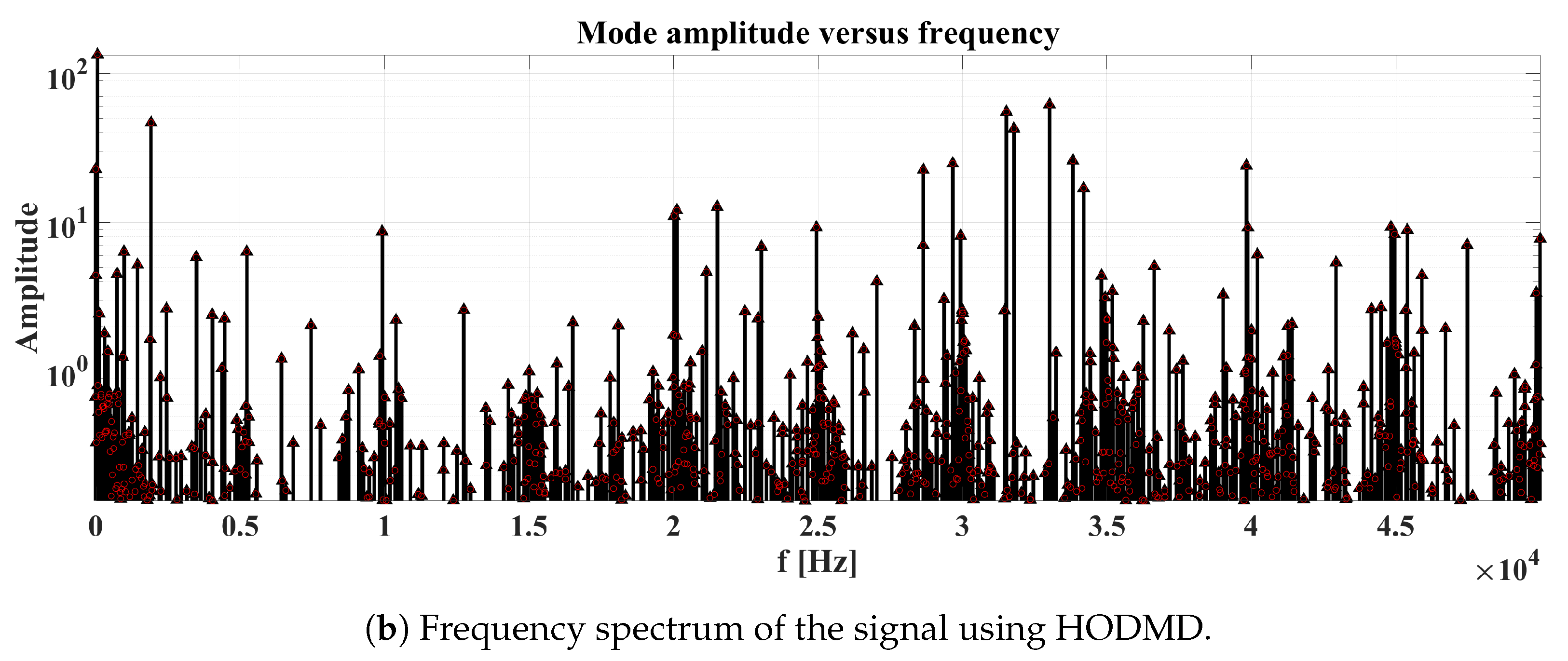
4.2.1. Case Study 4: Measured Signal from a Battery Energy Storage System
Simulation Validation
Experimental Validation
4.2.2. Case Study 5: Frequency-Varying System Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grover, H.; Verma, A.; Bhatti, T.S. A Fast and Robust DOBC-Based Frequency and Voltage Regulation Scheme for Future Power Systems with High Renewable Penetration. Energy Convers. Econ. 2023, 4, 287–302. [Google Scholar] [CrossRef]
- North American Electric Reliability Corporation (NERC). Project 2022-04: Electromagnetic Transient (EMT) Modeling Standard. Available online: https://www.nerc.com/pa/Stand/Pages/Project2022-04EMTModeling.aspx (accessed on 20 August 2025).
- Chen, C.-I.; Chen, Y.-C. Comparative Study of Harmonic and Interharmonic Estimation Methods for Stationary and Time-Varying Signals. IEEE Trans. Ind. Electron. 2014, 61, 397–404. [Google Scholar] [CrossRef]
- Nam, S.-R.; Kang, S.-H.; Kang, S.-H. Real-Time Estimation of Power System Frequency Using a Three-Level Discrete Fourier Transform Method. Energies 2015, 8, 79–93. [Google Scholar] [CrossRef]
- Duric, M.B.; Djurisic, Z. Frequency Measurement in Power Networks in the Presence of Harmonics Using Fourier and Zero Crossing Technique. In Proceedings of the 2005 IEEE Russia Power Tech (PowerTech), St. Petersburg, Russia, 27–30 June 2005; pp. 1–6. [Google Scholar] [CrossRef]
- Xiao, X.; Jiang, X.; Xie, S.; Lu, X.; Zhang, Y. A Neural Network Model for Power System Inter-Harmonics Estimation. In Proceedings of the 2010 IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA), Changsha, China, 23–26 September 2010; pp. 756–760. [Google Scholar] [CrossRef]
- Føyen, S.; Kvammen, M.-E.; Fosso, O.B. Prony’s Method as a Tool for Power System Identification in Smart Grids. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 562–569. [Google Scholar] [CrossRef]
- Priyanga, V.T.; Chandni, M.; Mohan, N.; Soman, K.P. Data-Driven Analysis for Low Frequency Oscillation Identification in Smart Grid Using FB-DMD and T-DMD Methods. In Proceedings of the 2019 9th International Conference on Advances in Computing and Communication (ICACC), Kochi, India, 6–8 November 2019; pp. 51–57. [Google Scholar] [CrossRef]
- Barocio, E.; Pal, B.C.; Thornhill, N.F.; Messina, A.R. A Dynamic Mode Decomposition Framework for Global Power System Oscillation Analysis. IEEE Trans. Power Syst. 2015, 30, 2902–2912. [Google Scholar] [CrossRef]
- Zuhaib, M.; Rihan, M. Identification of Low-Frequency Oscillation Modes Using PMU Based Data-Driven Dynamic Mode Decomposition Algorithm. IEEE Access 2021, 9, 49434–49447. [Google Scholar] [CrossRef]
- Yang, D.; Wang, B.; Cai, G.; Chen, Z.; Ma, J.; Sun, Z.; Wang, L. Data-Driven Estimation of Inertia for Multiarea Interconnected Power Systems Using Dynamic Mode Decomposition. IEEE Trans. Ind. Inform. 2021, 17, 2686–2695. [Google Scholar] [CrossRef]
- Nonomura, T.; Shibata, H.; Takaki, R. Extended-Kalman-Filter-Based Dynamic Mode Decomposition for Simultaneous System Identification and Denoising. PLoS ONE 2019, 14, e0209836. [Google Scholar] [CrossRef]
- Mohan, N.; Soman, K.P. A Data-Driven Technique for Harmonics Monitoring in Emerging Power Grids Using Noise-Aware Dynamic Mode Decomposition. Meas. Sci. Technol. 2020, 31, 015016. [Google Scholar] [CrossRef]
- Indhu, I.S.; Kumar, K.S.; Krishna, U.V.; Mohan, N.; Sowmya, V.; Soman, K.P. Investigating the Significance of Dynamic Mode Decomposition for Fast and Accurate Parameter Estimation in Power Grids. In Proceedings of the 2020 11th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kharagpur, India, 1–5 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Sikha, O.K.; Soman, K.P.; Kumar, S.S. VMD–DMD Coupled Data-Driven Approach for Visual Saliency in Noisy Images. Multimed. Tools Appl. 2020, 79, 1951–1970. [Google Scholar] [CrossRef]
- Rehman, N.U.; Aftab, H. Multivariate Variational Mode Decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef]
- Aadhithya, A.; Mohan, N.; Kumar, S.S.; Soman, K.P.; Poornachandran, P. Prospects of NFMD for Power System Frequency and Amplitude Estimation. In Proceedings of the 2022 7th International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 2–4 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition to Identify and Extrapolate Flow Patterns. Phys. Fluids 2017, 29, 084102. [Google Scholar] [CrossRef]
- Kou, J.; Le Clainche, S.; Zhang, W. A Reduced-Order Model for Compressible Flows with Buffeting Condition Using Higher Order Dynamic Mode Decomposition with a Mode Selection Criterion. Phys. Fluids 2018, 30, 016103. [Google Scholar] [CrossRef]
- Yu, J.; Hao, G.; Guo, J.; Li, X. Synchrosqueezing Superlet Transform: Algorithm and Applications. IEEE Trans. Ind. Electron. 2025, 1–13. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. The Fourier-Based Synchrosqueezing Transform. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 315–319. [Google Scholar] [CrossRef]
- Daubechies, I.; Wang, Y.G.; Wu, H. ConceFT: Concentration of Frequency and Time via a Multitapered Synchrosqueezed Transform. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150193. [Google Scholar] [CrossRef] [PubMed]
- Le Clainche, S.; Vega, J.M. Higher Order Dynamic Mode Decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Koopman, B.O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Vega, J.M.; Le Clainche, S. Higher Order Dynamic Mode Decomposition. In Higher Order Dynamic Mode Decomposition and Its Applications; Elsevier: Amsterdam, The Netherlands, 2021; pp. 29–83. [Google Scholar] [CrossRef]
- Chakir, M.; Kamwa, I.; Le-Huy, H. Extended C37.118.1 PMU Algorithms for Joint Tracking of Fundamental and Harmonic Phasors in Stressed Power Systems and Microgrids. IEEE Trans. Power Deliv. 2014, 29, 1465–1480. [Google Scholar] [CrossRef]
- Kamwa, I.; Samantaray, S.R.; Joos, G. Wide Frequency Range Adaptive Phasor and Frequency PMU Algorithms. IEEE Trans. Smart Grid 2014, 5, 569–579. [Google Scholar] [CrossRef]



| Parameter | Practical Range | Guideline for Selection |
|---|---|---|
| d (Delay Embedding Dimension) | Depends on signal complexity and noise level; trial-and-error tuning | Start with twice the expected number of dominant modes. Increase d until the reconstruction error converges. Stop increasing if the SVD becomes ill conditioned. |
| (SVD Tolerance) | – | Choose to retain at least of the system energy. If runtime becomes excessive without improving accuracy, increase . |
| (Mode Selection Threshold) | – | Select a threshold that filters out noise like modes while retaining physically meaningful weak modes. |
| Method | freq (Hz) | Amp (pu) | (°) | RMSE freq (%) | RMSE Amp (%) | RMSE (%) |
|---|---|---|---|---|---|---|
| HODMD | 0 | 0.5 | N/A | N/A | ||
| 30 | 0.1 | 90 | ||||
| 60 | 1 | 60 | ||||
| 90 | 0.05 | 12.6 | ||||
| 120 | 0.05 | 45 | ||||
| 180 | 0.01 | 180 | ||||
| 240 | 0.01 | −29.79 | ||||
| SST-STFT | 0.0914 | 0.5026 | N/A | N/A | ||
| 30.0849 | 0.0911 | 89.99 | 78 | |||
| 60.0718 | 1 | 60 | ||||
| 90.0718 | 0.0458 | 12.609 | ||||
| 120.1568 | 0.0489 | 44.99 | ||||
| 180.1437 | 0.0101 | 180 | ||||
| 240.1306 | 0.0101 | −29.79 | ||||
| ConceFT-STFT | N/A | N/A | N/A | N/A | N/A | N/A |
| 30.0027 | 0.0844 | −0.638 | 100.708 | |||
| 60.0053 | 1 | 9.166 | 115.276 | |||
| 90.008 | 0.0427 | −5.248 | 141.69 | |||
| 120.0107 | 0.05008 | 5.135 | 88.59 | |||
| 180.01607 | 0.0106 | −0.036 | 99.97 | |||
| 240.0214 | 0.0107 | −1.115 | 94 |
| Frequency | Parameter Variation | ROCOF | Initial Value | Final Value |
|---|---|---|---|---|
| f1 | +1 | 60 | 61 | |
| f2 | +2 | 30 | 32 | |
| f3 | −2 | 120 | 118 | |
| f4 | 0 | 180 | 180 | |
| f5 | −2.5 | 240 | 237.5 | |
| f6 | +1.5 | 90 | 91.5 |
| Frequency | HODMD | ConceFT-STFT | SST-STFT |
|---|---|---|---|
| 30 | |||
| 60 | |||
| 90 | |||
| 120 | |||
| 180 | |||
| 240 |
| Method | freq (Hz) | Amp (pu) | Err freq (%) | Err Amp (%) |
|---|---|---|---|---|
| HODMD | 20 | 0.00126 | 0 | |
| 60 | 1 | 0 | ||
| 100 | 0.00499 | 0 | ||
| 540 | 0.00118 | 0 | ||
| 1380 | 0.00142 | 0 | ||
| 2280 | 0.00131 | 0 | As Reference | |
| 5940 | 0.0024 | 0 | ||
| 8340 | 0.0117 | 0 | ||
| 9420 | 0.00199 | 0 | ||
| 11,760 | 0.00189 | 0 | ||
| STFT | 27.2 | 0.018 | 35.67 | 1334 |
| 67.45 | 1 | 12.413 | 0 | |
| 107.5 | 0.145 | 7.5 | 2797 | |
| 537.08 | 0.001 | 0.54 | 9 | |
| 1378.8 | 0.0012 | 0.083 | 15 | |
| 2279 | 0.0009 | 0.044 | 33 | |
| 5941 | 0.001 | 0.017 | 56 | |
| 8340 | 0.0033 | 0.061 | 72 | |
| 9,420 | 0.0004 | 0.054 | 18 | |
| 11,760 | 0.0016 | 0.063 | 13 | |
| ConceFT-STFT | 18.6 | 0.1712 | 7 | inf |
| 62.05 | 1 | 3.42 | 0 | |
| 101.3 | 0.525 | 1.3 | inf | |
| 540.6 | 0.008 | 0.12 | 584 | |
| 1381 | 0.0047 | 0.08 | 231 | |
| 2280 | 0.0014 | 0 | 10.3 | |
| 5941.4 | 0.001 | 0.02 | 58.3 | |
| 8340.4 | 0.0076 | 0.01 | 35.14 | |
| 9422 | 0.00189 | 0.02 | 38.35 | |
| 11,757.8 | 0.0018 | 0.02 | 6.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdou Dango, A.; Kamwa, I.; Grover, H.; N’Dori, A.; Masoom, A. Higher-Order Dynamic Mode Decomposition to Identify Harmonics in Power Systems. Energies 2025, 18, 5327. https://doi.org/10.3390/en18195327
Abdou Dango A, Kamwa I, Grover H, N’Dori A, Masoom A. Higher-Order Dynamic Mode Decomposition to Identify Harmonics in Power Systems. Energies. 2025; 18(19):5327. https://doi.org/10.3390/en18195327
Chicago/Turabian StyleAbdou Dango, Aboubacar, Innocent Kamwa, Himanshu Grover, Alexia N’Dori, and Alireza Masoom. 2025. "Higher-Order Dynamic Mode Decomposition to Identify Harmonics in Power Systems" Energies 18, no. 19: 5327. https://doi.org/10.3390/en18195327
APA StyleAbdou Dango, A., Kamwa, I., Grover, H., N’Dori, A., & Masoom, A. (2025). Higher-Order Dynamic Mode Decomposition to Identify Harmonics in Power Systems. Energies, 18(19), 5327. https://doi.org/10.3390/en18195327







