Evaluating PWM Solar Charge Regulators for Off-Grid Solar PV Street Lighting Systems Using Linear Regression Approach
Abstract
1. Introduction
2. Pulse Width Modulation and Battery Operation
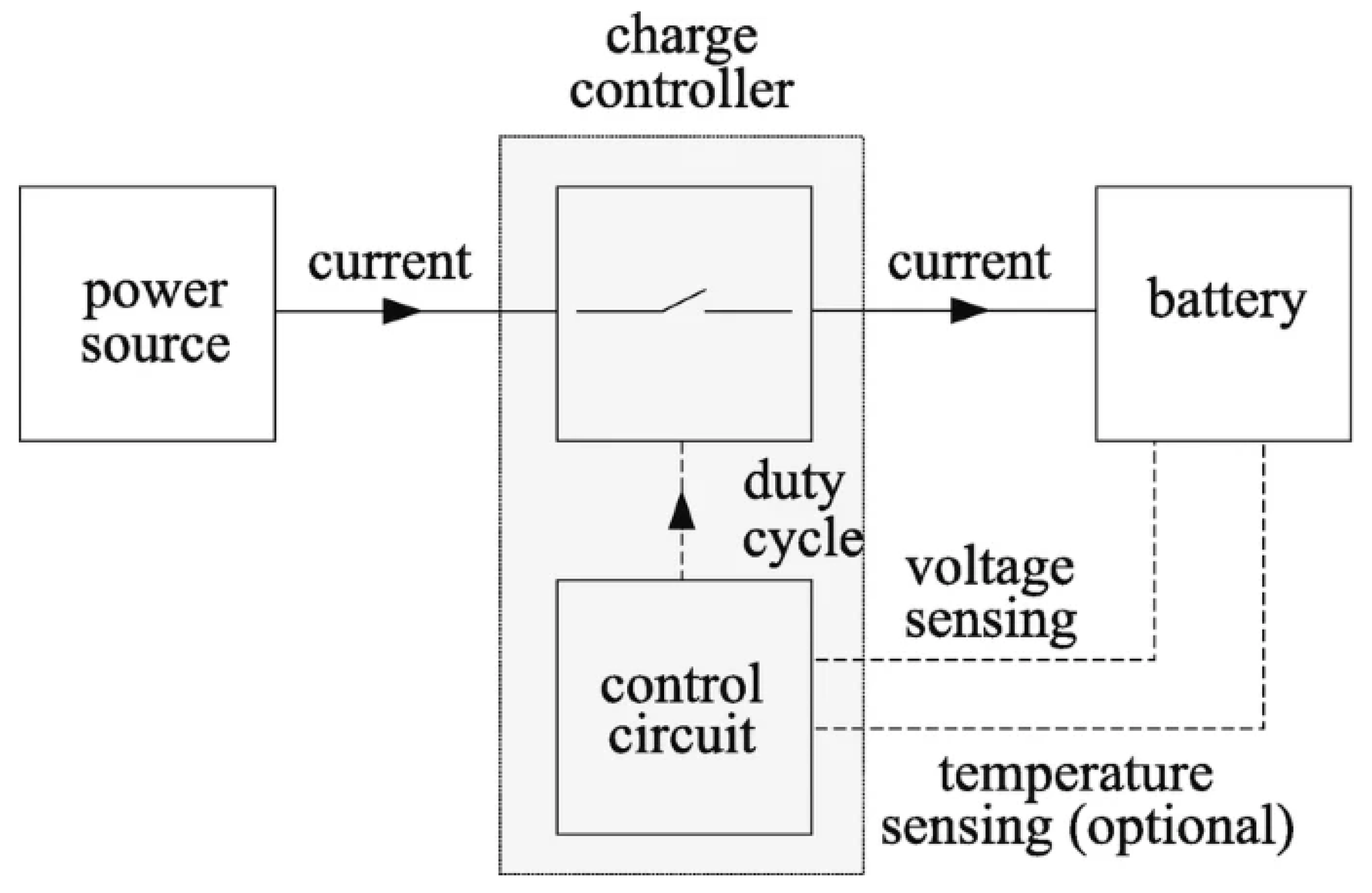
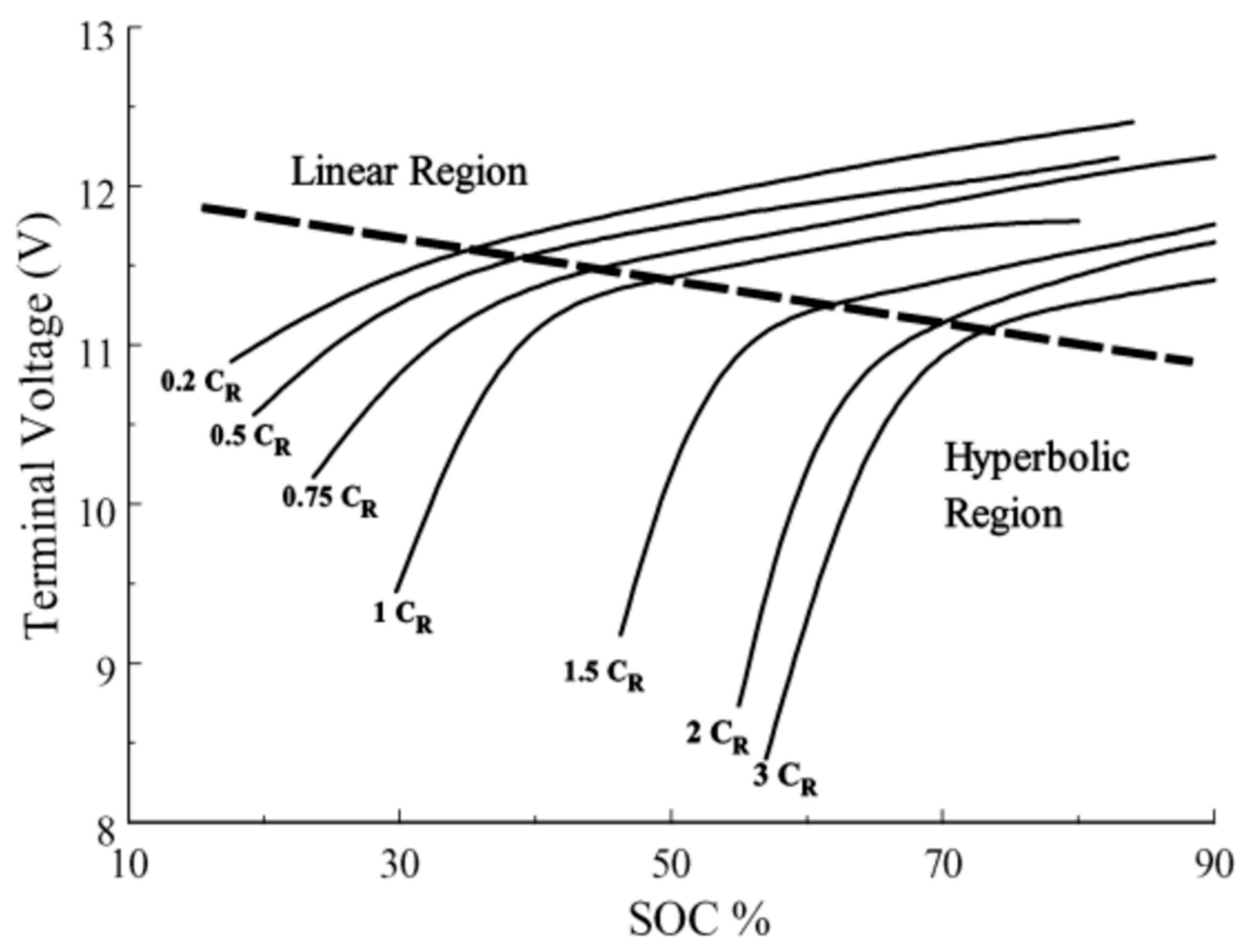
3. Materials and Methods
3.1. Material
3.2. Method
4. Results and Discussion
5. Conclusions
- 1.
- For long-term systems optimization, a more comprehensive efficiency analysis that incorporates coulombic efficiency, energy balance over time, and idle current measurement should be undertaken to study the nonlinear behavior.
- 2.
- Incorporating a full GUM-based analysis for uncertainty in future extended studies, particularly those involving long-term field data or model-based performance extrapolation.
- 3.
- While this study focuses on PWM regulators, the results should not be generalized to all types of charge regulators. Hence, future work will include benchmarking other regulator types, such as MPPT regulators, for further validation.
- 4.
- Additionally, further testing using various battery chemistries—such as Lithium-ion, Nickel-Cadmium (Ni-Cd), and Nickel-Metal Hydride (Ni-MH)—is recommended to study optimal compatibility and system performance in a small-scale solar project.
- 5.
- A future study will be conducted to study the impact of seasonal variations on the performance of the PWM charge regulators.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CO2 | Carbon dioxide |
| DAQ | Data acquisition |
| DoD | Depth of discharge |
| GUM | Guide to the Expression of Uncertainty in Measurement |
| LEDs | Light-emitting diodes |
| LRA | Linear regression algorithm |
| MPPT | Maximum power point tracker |
| NOCT | Normal operating cell temperature |
| PWM | Pulse width modulation |
Appendix A
| Solsum 6.6F | Sunguard SK-6 | Sunsaver SS-6L | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Time | Battery | PV | Load | Battery | PV | Load | Battery | PV | Load |
| H: Min: S | Voltage | Voltage | Current | Voltage | Voltage | Current | Voltage | Voltage | Current |
| (V) | (V) | (A) | (V) | (V) | (A) | (V) | (V) | (A) | |
| 10:26:01 a.m. | 12.474614 | 20.457887 | 0.000161 | 12.482836 | 20.214258 | 0.000180 | 12.488137 | 20.324011 | 0.000090 |
| 10:27:24 a.m. | 12.401295 | 12.882287 | 3.510339 | 12.325702 | 12.447423 | 3.528563 | 12.479800 | 13.000150 | 3.679366 |
| 10:28:54 a.m. | 12.473582 | 12.723818 | 3.577161 | 12.397549 | 12.346145 | 3.324453 | 12.502662 | 13.016042 | 3.779010 |
| 10:30:24 a.m. | 12.337040 | 12.801710 | 3.596600 | 12.261839 | 12.309397 | 3.742393 | 12.435035 | 13.095684 | 3.841944 |
| 10:31:54 a.m. | 12.365597 | 12.665259 | 3.662206 | 12.290222 | 12.295954 | 3.737533 | 12.463819 | 12.956063 | 3.831454 |
| 10:33:24 a.m. | 12.370952 | 12.698255 | 3.645197 | 12.295544 | 12.293264 | 3.681646 | 12.469217 | 12.989793 | 3.805233 |
| 10:34:54 a.m. | 12.382554 | 12.707446 | 3.675571 | 12.307075 | 12.277132 | 3.744822 | 12.480910 | 12.999159 | 3.844566 |
| 10:36:24 a.m. | 12.355780 | 12.723051 | 3.634263 | 12.280465 | 12.294161 | 3.448377 | 12.453924 | 13.015093 | 3.873410 |
| 10:37:54 a.m. | 12.402187 | 12.699225 | 3.786130 | 12.326589 | 12.269066 | 3.733888 | 12.500699 | 12.990689 | 3.743611 |
| 10:39:24 a.m. | 12.369168 | 12.750624 | 3.708374 | 12.293771 | 12.298643 | 3.797065 | 12.467418 | 13.043230 | 3.777699 |
| 10:40:54 a.m. | 12.358458 | 12.720364 | 3.678001 | 12.283126 | 12.289680 | 3.668281 | 12.456623 | 13.012244 | 3.730499 |
| 10:42:24 a.m. | 12.404864 | 12.713032 | 3.633048 | 12.329250 | 12.269066 | 3.755757 | 12.503398 | 13.004715 | 3.752789 |
| 10:43:54 a.m. | 12.356673 | 12.764471 | 3.688935 | 12.281352 | 12.269962 | 3.714449 | 12.454824 | 13.057298 | 3.772455 |
| 10:45:24 a.m. | 12.362028 | 12.718566 | 3.718094 | 12.286675 | 12.304916 | 3.679216 | 12.460222 | 13.010309 | 3.819654 |
| 10:46:54 a.m. | 12.391240 | 12.740369 | 3.693795 | 12.315709 | 12.254725 | 3.676786 | 12.477312 | 13.032577 | 3.843255 |
| 10:48:24 a.m. | 12.371588 | 12.761540 | 3.645197 | 12.296176 | 12.260103 | 3.701085 | 12.482191 | 13.054199 | 3.785565 |
| 10:49:54 a.m. | 12.375161 | 12.744990 | 3.824729 | 12.299727 | 12.265480 | 3.845662 | 12.485796 | 13.037235 | 3.917987 |
| 10:51:24 a.m. | 12.366228 | 12.752360 | 3.716879 | 12.290848 | 12.282510 | 3.668281 | 12.476783 | 13.044743 | 3.796055 |
| 10:52:54 a.m. | 12.401067 | 12.746840 | 3.798280 | 12.325475 | 12.268169 | 3.618469 | 12.511934 | 13.039065 | 3.866854 |
| 10:54:24 a.m. | 12.373374 | 12.786451 | 3.695010 | 12.297951 | 12.277132 | 3.579591 | 12.483994 | 13.079551 | 3.797366 |
| 10:55:54 a.m. | 12.346575 | 12.761580 | 3.660992 | 12.271316 | 12.258310 | 3.741178 | 12.456955 | 13.054084 | 3.814410 |
| 10:57:24 a.m. | 12.442160 | 12.737629 | 3.664636 | 12.366318 | 12.269962 | 3.597815 | 12.553394 | 13.029544 | 3.832765 |
| 10:58:54 a.m. | 12.343001 | 12.839953 | 3.720524 | 12.267764 | 12.261896 | 3.718094 | 12.453349 | 13.134179 | 3.765899 |
| 11:00:24 a.m. | 12.353722 | 12.741299 | 3.697440 | 12.278419 | 12.226045 | 3.653702 | 12.464165 | 13.033237 | 3.831454 |
| 11:01:54 a.m. | 12.368014 | 12.756050 | 3.681646 | 12.292624 | 12.269962 | 3.654917 | 12.478585 | 13.048293 | 3.739677 |
| 11:03:24 a.m. | 12.393920 | 12.774491 | 3.669496 | 12.318372 | 12.281613 | 3.658562 | 12.504723 | 13.067128 | 3.769833 |
| 11:04:54 a.m. | 12.322455 | 12.804952 | 3.736318 | 12.247343 | 12.277132 | 3.612394 | 12.432619 | 13.098247 | 3.794744 |
| 11:06:24 a.m. | 12.351042 | 12.734789 | 3.780056 | 12.275755 | 12.259206 | 3.522488 | 12.461461 | 13.026447 | 3.878654 |
| 11:07:54 a.m. | 12.357754 | 12.780639 | 3.628188 | 12.286120 | 12.337182 | 3.551177 | 12.459659 | 13.073320 | 3.836699 |
| 11:09:24 a.m. | 12.346133 | 12.782481 | 3.692580 | 12.274566 | 12.254725 | 3.592297 | 12.447942 | 13.075167 | 3.902254 |
| 11:10:54 a.m. | 12.332723 | 12.774142 | 3.682860 | 12.261234 | 12.236800 | 3.551177 | 12.434422 | 13.066605 | 3.789500 |
| 11:12:24 a.m. | 12.322891 | 12.763941 | 3.656132 | 12.251459 | 12.236800 | 3.551177 | 12.424508 | 13.056143 | 3.759344 |
| 11:13:54 a.m. | 12.427481 | 12.757444 | 3.676786 | 12.355442 | 12.257415 | 3.551177 | 12.519961 | 13.049461 | 3.739677 |
| 11:15:24 a.m. | 12.333618 | 12.869432 | 3.680431 | 12.262123 | 12.206327 | 3.551177 | 12.435323 | 13.163977 | 3.817032 |
| 11:16:54 a.m. | 12.321102 | 12.775903 | 3.769121 | 12.249680 | 12.243970 | 3.471351 | 12.422705 | 13.068282 | 3.831454 |
| 11:18:24 a.m. | 12.312163 | 12.766613 | 3.747252 | 12.240793 | 12.243970 | 3.676072 | 12.413692 | 13.058747 | 3.784254 |
| 11:19:54 a.m. | 12.314845 | 12.761027 | 3.705944 | 12.243460 | 12.239489 | 3.548679 | 12.416396 | 13.052997 | 3.620367 |
| 11:21:24 a.m. | 12.442677 | 12.767483 | 3.718094 | 12.370551 | 12.237696 | 3.622367 | 12.515282 | 13.059566 | 3.588900 |
| 11:22:54 a.m. | 12.327360 | 12.903719 | 3.741178 | 12.255902 | 12.217082 | 3.629861 | 12.429015 | 13.198892 | 3.956009 |
| 11:24:24 a.m. | 12.313951 | 12.787804 | 3.746037 | 12.242570 | 12.229629 | 3.663582 | 12.415494 | 13.080295 | 3.925855 |
| 11:25:54 a.m. | 12.305012 | 12.777573 | 3.653702 | 12.233683 | 12.230526 | 3.678571 | 12.406481 | 13.069791 | 3.803922 |
| 11:27:24 a.m. | 12.292497 | 12.771966 | 3.736318 | 12.221241 | 12.242178 | 3.589894 | 12.393864 | 13.064025 | 3.664945 |
| 11:28:54 a.m. | 12.273725 | 12.762646 | 3.730243 | 12.202577 | 12.332701 | 3.589894 | 12.374936 | 13.054457 | 3.743611 |
| 11:30:24 a.m. | 12.318421 | 12.746808 | 3.743607 | 12.247015 | 12.211705 | 3.618621 | 12.420002 | 13.038233 | 3.898321 |
| 11:31:54 a.m. | 12.274618 | 12.796902 | 3.704729 | 12.203465 | 12.232319 | 3.777238 | 12.375837 | 13.089440 | 3.883899 |
| 11:33:24 a.m. | 12.368481 | 12.755066 | 3.696225 | 12.296785 | 12.211705 | 3.683566 | 12.470474 | 13.046608 | 3.929788 |
| 11:34:54 a.m. | 12.296072 | 12.856286 | 3.695010 | 12.224796 | 12.176750 | 3.573658 | 12.399919 | 13.163109 | 3.883899 |
| 11:36:24 a.m. | 12.296072 | 12.784687 | 3.708374 | 12.224796 | 12.262792 | 3.704798 | 12.399919 | 13.089771 | 3.793433 |
| 11:37:54 a.m. | 12.254058 | 12.788361 | 3.713234 | 12.183024 | 12.209015 | 3.724781 | 12.357549 | 13.093495 | 3.567923 |
| 11:39:24 a.m. | 12.218301 | 12.748316 | 3.519309 | 12.147475 | 12.203638 | 3.509190 | 12.321490 | 13.052465 | 3.444679 |
| 11:40:54 a.m. | 12.271043 | 12.714758 | 3.738748 | 12.199911 | 12.219771 | 3.673574 | 12.374677 | 13.018078 | 3.844566 |
| 11:42:24 a.m. | 12.304796 | 12.773302 | 3.664636 | 12.231017 | 12.200949 | 3.661085 | 12.406229 | 13.077987 | 3.914054 |
| 11:43:54 a.m. | 12.300325 | 12.809542 | 3.703514 | 12.226573 | 12.211705 | 3.629861 | 12.401721 | 13.115057 | 3.906187 |
| 11:45:24 a.m. | 12.285126 | 12.808560 | 3.804354 | 12.211465 | 12.203638 | 3.626114 | 12.386397 | 13.114015 | 3.858988 |
| 11:46:54 a.m. | 12.394207 | 12.796396 | 3.730243 | 12.319892 | 12.195571 | 3.606130 | 12.496377 | 13.101529 | 3.893077 |
| 11:48:24 a.m. | 12.263667 | 12.913707 | 3.704729 | 12.190134 | 12.180335 | 3.747263 | 12.364761 | 13.221611 | 3.889143 |
| 11:49:54 a.m. | 12.239527 | 12.781358 | 3.752112 | 12.166139 | 12.192883 | 3.741018 | 12.340422 | 13.086069 | 3.784254 |
| 11:51:24 a.m. | 12.252044 | 12.759842 | 3.753327 | 12.178581 | 12.265480 | 3.594890 | 12.353042 | 13.064015 | 3.855054 |
| 11:52:54 a.m. | 12.378113 | 12.776551 | 3.726598 | 12.303895 | 12.182128 | 3.642350 | 12.480151 | 13.081084 | 3.873410 |
| 11:54:24 a.m. | 12.249361 | 12.911703 | 3.763047 | 12.175914 | 12.191987 | 3.636106 | 12.350337 | 13.219431 | 3.903565 |
| 11:55:54 a.m. | 12.273336 | 12.781054 | 3.763047 | 12.199139 | 12.214394 | 3.702301 | 12.375324 | 13.085636 | 3.824899 |
| 11:57:24 a.m. | 12.244891 | 12.809097 | 3.722953 | 12.171471 | 12.165099 | 3.676072 | 12.345830 | 13.115827 | 3.852432 |
| 11:58:54 a.m. | 12.236844 | 12.783695 | 3.730243 | 12.163472 | 12.186610 | 3.713541 | 12.337717 | 13.088274 | 3.928477 |
| 12:00:24 p.m. | 12.277575 | 12.791576 | 3.693795 | 12.167817 | 12.190194 | 3.794723 | 12.366564 | 13.096293 | 3.835388 |
| 12:01:54 p.m. | 12.275785 | 12.825137 | 3.767906 | 12.166043 | 12.163306 | 3.790976 | 12.364761 | 13.130630 | 3.925855 |
| 12:03:24 p.m. | 12.248936 | 12.826930 | 3.744822 | 12.139434 | 12.163306 | 3.733524 | 12.337717 | 13.132432 | 3.820966 |
| 12:04:54 p.m. | 12.249830 | 12.802527 | 3.731458 | 12.140320 | 12.162410 | 3.747263 | 12.338618 | 13.107416 | 3.841944 |
| 12:06:24 p.m. | 12.249830 | 12.807116 | 3.671926 | 12.140320 | 12.153447 | 3.765997 | 12.338618 | 13.112082 | 3.883899 |
| 12:07:54 p.m. | 12.269521 | 12.810773 | 3.863887 | 12.159835 | 12.156136 | 3.736022 | 12.358451 | 13.115790 | 3.891766 |
| 12:09:24 p.m. | 12.240880 | 12.835024 | 3.769121 | 12.131451 | 12.154343 | 3.661085 | 12.329603 | 13.140586 | 3.911432 |
| 12:10:54 p.m. | 12.237301 | 12.808706 | 3.713234 | 12.127903 | 12.153447 | 3.853424 | 12.325998 | 13.113618 | 3.709522 |
| 12:12:24 p.m. | 12.214926 | 12.808615 | 3.647627 | 12.105728 | 12.132833 | 3.711043 | 12.303460 | 13.113488 | 3.806544 |
| 12:13:54 p.m. | 12.231931 | 12.788841 | 3.693795 | 12.122581 | 12.141796 | 3.716039 | 12.320588 | 13.093208 | 3.883899 |
| 12:15:24 p.m. | 12.229246 | 12.810287 | 3.697440 | 12.119920 | 12.130144 | 3.789727 | 12.317884 | 13.115139 | 3.870787 |
| 12:16:54 p.m. | 12.270416 | 12.811127 | 3.834728 | 12.160722 | 12.164203 | 3.733524 | 12.359353 | 13.115961 | 3.845877 |
| 12:18:24 p.m. | 12.191668 | 12.857908 | 3.696225 | 12.105728 | 12.130144 | 3.813457 | 12.303460 | 13.163831 | 3.879966 |
| 12:19:54 p.m. | 12.205068 | 12.803408 | 3.714449 | 12.119033 | 12.115804 | 3.737271 | 12.316983 | 13.107998 | 3.889143 |
| 12:21:24 p.m. | 12.273851 | 12.821126 | 3.696225 | 12.187331 | 12.169580 | 3.642350 | 12.386397 | 13.126107 | 3.788189 |
| 12:22:54 p.m. | 12.206855 | 12.897050 | 3.727813 | 12.120807 | 12.139107 | 3.662623 | 12.318786 | 13.203803 | 3.895699 |
| 12:24:24 p.m. | 12.244373 | 12.830293 | 3.787345 | 12.158061 | 12.139107 | 3.672325 | 12.356648 | 13.135433 | 3.899632 |
| 12:25:54 p.m. | 12.189882 | 12.873386 | 3.701085 | 12.103954 | 12.216186 | 3.639853 | 12.301657 | 13.179519 | 3.849810 |
| 12:27:24 p.m. | 12.178269 | 12.819738 | 3.770336 | 12.092423 | 12.110426 | 3.650806 | 12.289938 | 13.124563 | 3.827521 |
References
- Bachanek, K.H.; Tundys, B.; Wiśniewski, T.; Puzio, E.; Maroušková, A. Intelligent Street lighting in a smart city concepts—A direction to energy saving in cities: An overview and case study. Energies 2021, 14, 3018. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Bidokhti, A.; Fakhrzad, M.B.; Sadegheih, A.; Mehrjerdi, Y.Z. A new model for the use of renewable electricity to reduce carbon dioxide emissions. Energy 2022, 238, 121602. [Google Scholar] [CrossRef]
- Khan, S.; Ahmed, M.M.; Muhaisen, N.A.; Habaebi, M.H.; Ahmed, N.A. Street lighting poles top solar power generation for typical housing area in Kuwait. In Proceedings of the 2019 IEEE International Conference on Innovative Research and Development (ICIRD), Jakarta, Indonesia, 28–30 June 2019; IEEE: New York, NY, USA, 2019; pp. 1–5. [Google Scholar]
- Rofaie, N.S.A.; Phoong, S.W.; Abdul Talib @ Abdul Mutalib, M. Light-Emitting Diode (LED) versus High-Pressure Sodium Vapour (HPSV) Efficiency: A Data Envelopment Analysis Approach with Undesirable Output. Energies 2022, 15, 4589. [Google Scholar] [CrossRef]
- Mahmoud, M.M. Economic applications for led lights in industrial sectors. In Light-Emitting Diodes And Photodetectors: Advances and Future Directions; InTech Open: Rijeka, Croatia, 2021. [Google Scholar]
- Symeonidou, M.M.; Zioga, C.; Papadopoulos, A.M. Life cycle cost optimization analysis of battery storage system for residential photovoltaic panels. J. Clean. Prod. 2021, 309, 127234. [Google Scholar] [CrossRef]
- Dorel, S.; Gmal Osman, M.; Strejoiu, C.V.; Lazaroiu, G. Exploring optimal charging strategies for off-grid solar photovoltaic systems: A comparative study on battery storage techniques. Batteries 2023, 9, 470. [Google Scholar] [CrossRef]
- Koko, S.P. Optimal battery sizing for a grid-tied solar photovoltaic system supplying a residential load: A case study under South African solar irradiance. Energy Rep. 2022, 8, 410–418. [Google Scholar] [CrossRef]
- Nasab, N.M.; Yazdanian, S. The advantages of lead-acid battery for off-grid design. Energy Storage 2024, 6, e595. [Google Scholar] [CrossRef]
- Anuphappharadorn, S.; Sukchai, S.; Sirisamphanwong, C.; Ketjoy, N. Comparison the economic analysis of the battery between lithium-ion and lead-acid in PV stand-alone application. Energy Procedia 2014, 56, 352–358. [Google Scholar] [CrossRef]
- Bizhani, H.; Sani, S.K.; Rezazadeh, H.; Muyeen, S.M.; Rahmani, S. Modeling of an optimum fast charging multi-step constant current profile for lead-acid batteries. IEEE Trans. Ind. Appl. 2022, 59, 2050–2060. [Google Scholar] [CrossRef]
- Carroquino, J.; Escriche-Martínez, C.; Valiño, L.; Dufo-López, R. Comparison of economic performance of lead-acid and li-ion batteries in standalone photovoltaic energy systems. Appl. Sci. 2021, 11, 3587. [Google Scholar] [CrossRef]
- Jahed, A.; Abbaspour, A.; Ahmadi, A. Techno-economic analysis of off-grid hybrid wind-photovoltaic-battery power system by analyzing different batteries for the industrial plant in Shiraz Industrial Town, Iran. Sci. Prog. 2024, 107. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, S. Research on aging mechanism and state of health prediction in lithium batteries. J. Energy Storage 2023, 72, 108274. [Google Scholar] [CrossRef]
- Guo, J.; Li, Y.; Pedersen, K.; Stroe, D.I. Lithium-ion battery operation, degradation, and aging mechanism in electric vehicles: An overview. Energies 2021, 14, 5220. [Google Scholar] [CrossRef]
- Antonov, I.; Kanchev, H.; Hinov, N. Study of PWM solar charge controller operation modes in autonomous DC system. In Proceedings of the 2019 II International Conference on High Technology for Sustainable Development (HiTech), Sofia, Bulgaria, 10–11 October 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar]
- Shi, Z.; Guo, Y.; Li, P.; Sun, H. A boost CLLC converter controlled by PWM and PFM hybrid modulation for photovoltaic power generation. IEEE Access 2020, 8, 112015–112026. [Google Scholar] [CrossRef]
- Schmid, F.; Behrendt, F. Optimal sizing of Solar Home Systems: Charge controller technology and its influence on system design. Sustain. Energy Technol. Assess. 2021, 45, 101198. [Google Scholar] [CrossRef]
- Kibirige, D.; Uzorka, A.; Mustafa, M.M.; Ukagwu, K.J. Design and implementation of a charge controller for solar PV systems for emergency situations in health facilities in rural areas of Uganda. Eng. Sci. Technol. 2024, 5, 326–342. [Google Scholar] [CrossRef]
- Yenku, C.F.; Fendji, M.D.; Fopah-Lele, A.; Tsuanyo, D. Charge-controller optimization on lead-acid battery in solar PV systems: Temperature effects and efficiency improvement. In E3S Web of Conferences, Proceedings of the International Energy 2021—Conference on “Renewable Energy and Digital Technologies for the Development of Africa”, Yaoundé, Cameroon, 18–20 November 2021; EDP Sciences: Les Ulis, France, 2022; Volume 354, p. 01003. [Google Scholar]
- Najmurrokhman, A.; Hambali, T.; Hakim, M.T.; Ismail, N. Solar panel charge controller using PWM regulation for charging lead acid batteries. In Proceedings of the 2022 8th International Conference on Wireless and Telematics (ICWT), Yogyakarta, Indonesia, 21–22 July 2022; IEEE: New York, NY, USA, 2022; pp. 1–4. [Google Scholar]
- Priya, K.S. Linear regression algorithm in machine learning through MATLAB. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 989–995. [Google Scholar] [CrossRef]
- Diyoke, G.C. Analysis and Simulation of Buck Switch Mode DC to DC Power Regulator. Int. J. Tech. Res. Appl 2015, 3, 97–103. [Google Scholar]
- Louie, H. Off-Grid System Battery Operationand Control. In Off-Grid Electrical Systems in Developing Countries; Springer Nature: Cham, Switzerland, 2025; pp. 411–444. [Google Scholar]
- Zhao, X.; Osborne, M.; Lantair, J.; Robu, V.; Flynn, D.; Huang, X.; Fisher, M.; Papacchini, F.; Ferrando, A. Towards integrating formal verification of autonomous robots with battery prognostics and health management. In Software Engineering and Formal Methods, Proceedings of the 17th International Conference on Software Engineering and Formal Methods 2019, Oslo, Norway, 16–20 September 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 105–124. [Google Scholar]
- Relan, R.; Tiels, K.; Timmermans, J.-M.; Schoukens, J. Estimation of best linear approximation from varying operating conditions for the identification of a li-ion battery model. IFAC-Pap. 2017, 50, 4739–4744. [Google Scholar] [CrossRef]
- Sheikh, S.S.; Anjum, M.; Khan, M.A.; Hassan, S.A.; Khalid, H.A.; Gastli, A.; Ben-Brahim, L. A battery health monitoring method using machine learning: A data-driven approach. Energies 2020, 13, 3658. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-charge determination from EMF voltage estimation: Using impedance, terminal voltage, and current for lead-acid and lithium-ion batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the battery model and SOC estimation method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Mu, H.; Wang, C. A novel method on estimating the degradation and state of charge of lithium-ion batteries used for electrical vehicles. Appl. Energy 2017, 207, 336–345. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D.I. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Huang, B.; Liao, H.; Wang, Y.; Liu, X.; Yan, X. Prediction and evaluation of health state for power battery based on Ridge linear regression model. Sci. Prog. 2021, 104, 00368504211059047. [Google Scholar] [CrossRef]
- Dekker, J.; Nthontho, M.; Chowdhury, S.; Chowdhury, S.P. Economic analysis of PV/diesel hybrid power systems in different climatic zones of South Africa. Int. J. Electr. Power Energy Syst. 2012, 40, 104–112. [Google Scholar] [CrossRef]
- Koko, S.P. Optimal Battery Recharging Strategy for a Grid-Tied Solar Photovoltaic-Battery. In Trends in Environmental Sustainability and Green Energy: Proceedings of the 2024 7th International Conference on Green Energy and Environment Engineering, Seoul, Republic of Korea, 4–6 July 2024; Springer Nature: Cham, Switzerland, 2025; p. 198. [Google Scholar]
- Ibrahim, M.M.; Elwany, A.M.; Elansary, L.K. Sustainable technical design and economic–environmental analysis of SMART solar street lighting system in Giza City, Egypt. Int. J. Energy Environ. Eng. 2021, 12, 739–750. [Google Scholar] [CrossRef]
- El-Khozenadar, H.J.; Albardawil, M.A.; Asfour, M.S.; Abu-Khater, I.N.; Nassar, Y.F. DC off-grid PV system to supply electricity to 50 boats at Gaza seaport. In Proceedings of the 2023 8th International Engineering Conference on Renewable Energy & Sustainability (ieCRES), Gaza, Palestine, 8–9 May 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar]
- Saputra, R.; Erawadi, D.; Hendri, Z. Design of Public Street Lighting for Solar Power Plants (PLTS) in Bukit Bio-Bio Village, Kenagarian Sikucua Utara V Koto, Kampung Dalam Padang Pariaman. Innov. J. Intell. Control. Optim. Electr. Syst. 2024, 1, 62–68. [Google Scholar]
- El-Khozondar, H.J.; Asfour, A.A.; Nassar, Y.F.; Shaheen, S.W.; El-Zaety, M.F.; El-Khozondar, R.J.; Khaleel, M.M.; Ahmed, A.A.; Alsharif, A.H. Photovoltaic solar energy for street lighting: A case study at Kuwaiti Roundabout, Gaza Strip, Palestine. Power Eng. Eng. Thermophys 2024, 3, 77–91. [Google Scholar] [CrossRef]
- Sachin, K.; Yadav, V.P.; Mukesh, A.N.; Sharma, P.K.; Solanki, L. Design and development of PWM based solar hybrid charge controller. In Proceedings of the 2021 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 9–11 July 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Yunus Khan, T.M.; Soudagar, M.E.M.; Kanchan, M.; Afzal, A.; Banapurmath, N.R.; Akram, N.; Mane, S.D.; Shahapurkar, K. Optimum location and influence of tilt angle on performance of solar PV panels. J. Therm. Anal. Calorim. 2020, 141, 511–532. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Yang, X.G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.Y. Modeling of lithium plating induced aging of lithium-ion batteries: Transition from linear to nonlinear aging. J. Power Sources 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Noman, A.M.; Haidar, Z.A.; Aljumah, A.S.; Almutairi, S.Z.; Alqahtani, M.H. Forecasting the distortion in solar radiation during midday hours by analyzing solar radiation during early morning hours. Appl. Sci. 2023, 13, 6049. [Google Scholar] [CrossRef]
- Faizal, E.; Winoko, Y.A.; Mustapa, M.S.; Kozin, M. Solar Charger Controller Efficiency Analysis of Type Pulse Width Modulation (PWM) and Maximum Power Point Tracking (MPPT). Asian J. Sci. Eng. 2022, 1, 90–102. [Google Scholar] [CrossRef]
- Sathasivam, S.; Adebayo, S.A.; Velavan, M.; Liang, J.K.W. Determine the parameters for photoelectric effect data using correlation and simple linear regression. J. Qual. Meas. Anal. 2022, 18, 61–70. [Google Scholar]
- Razzouk, J.; Ramos, O.; Ouro-Rodrigues, E.; Samayoa, C.; Wycliffe, N.; Cheng, W.; Danisa, O. Comparison of cervical, thoracic, and lumbar vertebral bone quality scores for increased utility of bone mineral density screening. Eur. Spine J. 2023, 32, 20–26. [Google Scholar] [CrossRef] [PubMed]
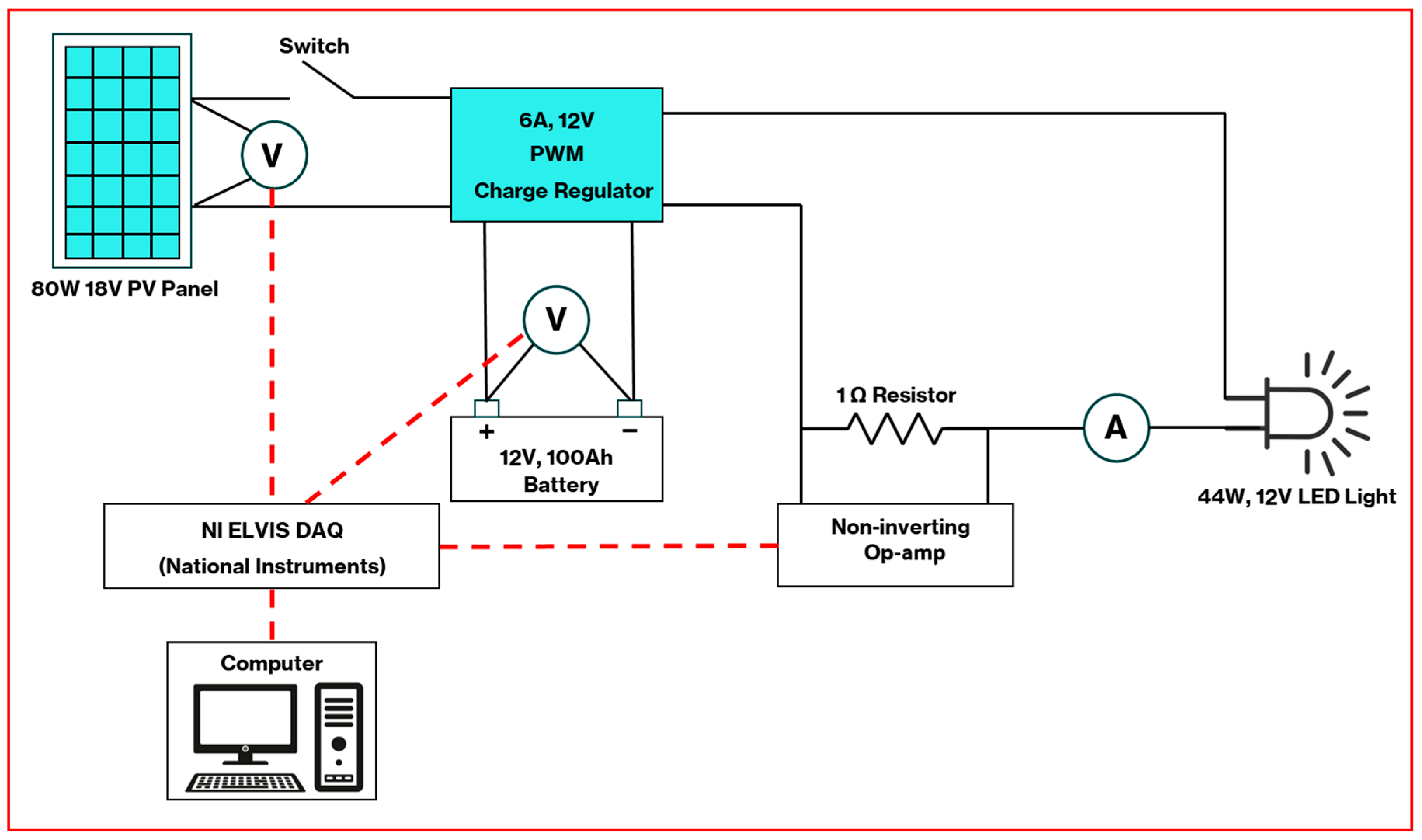
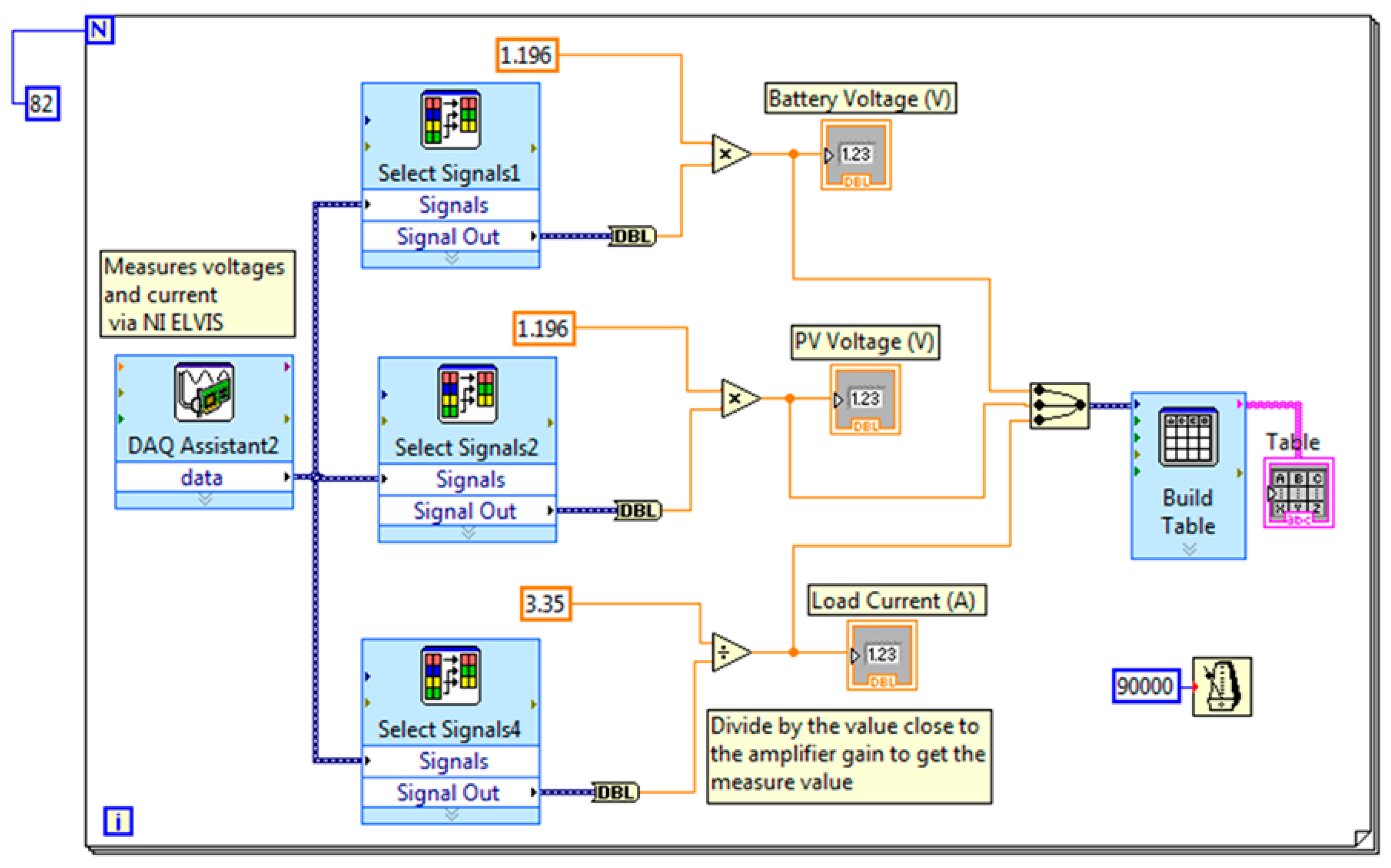
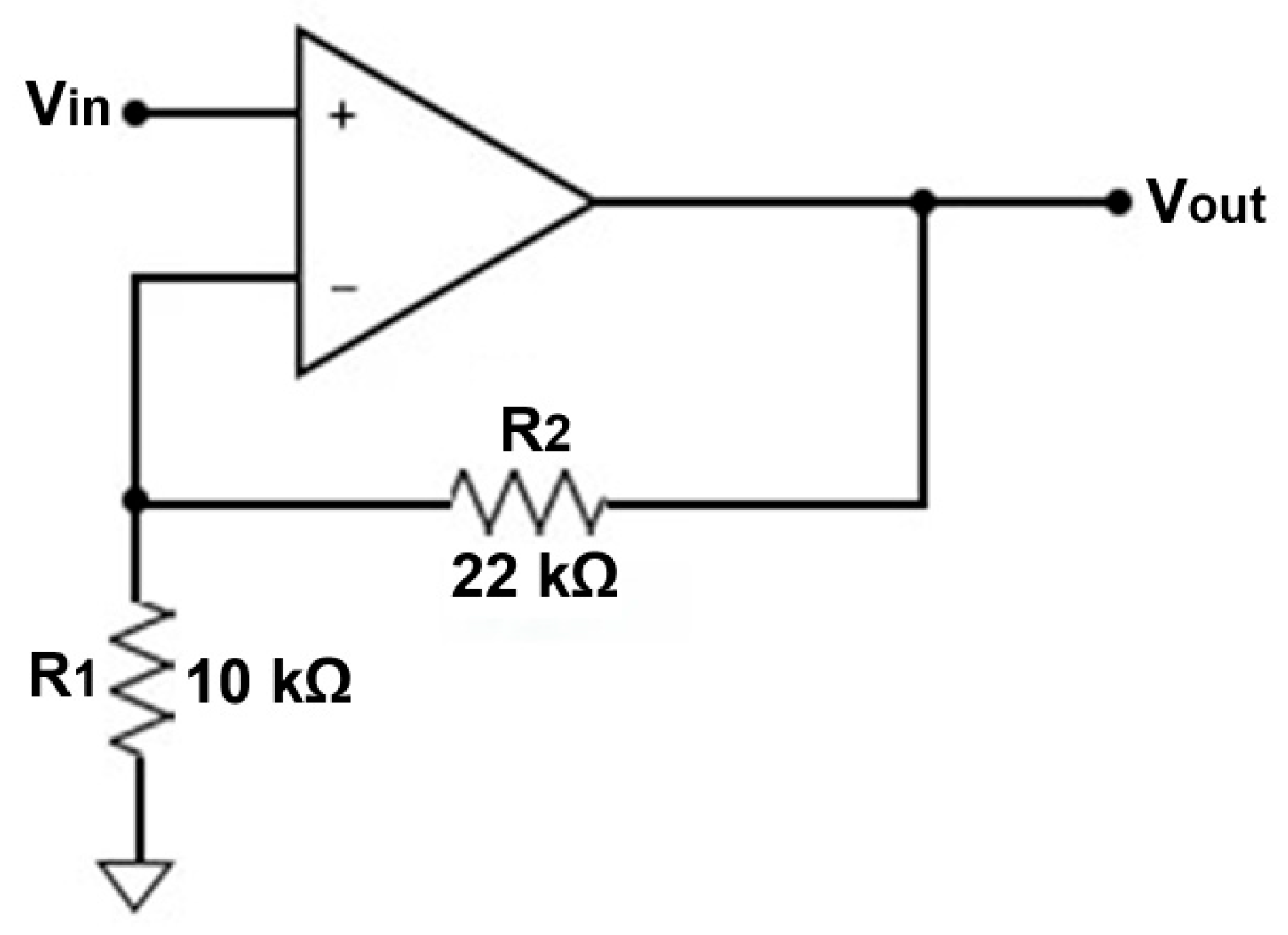

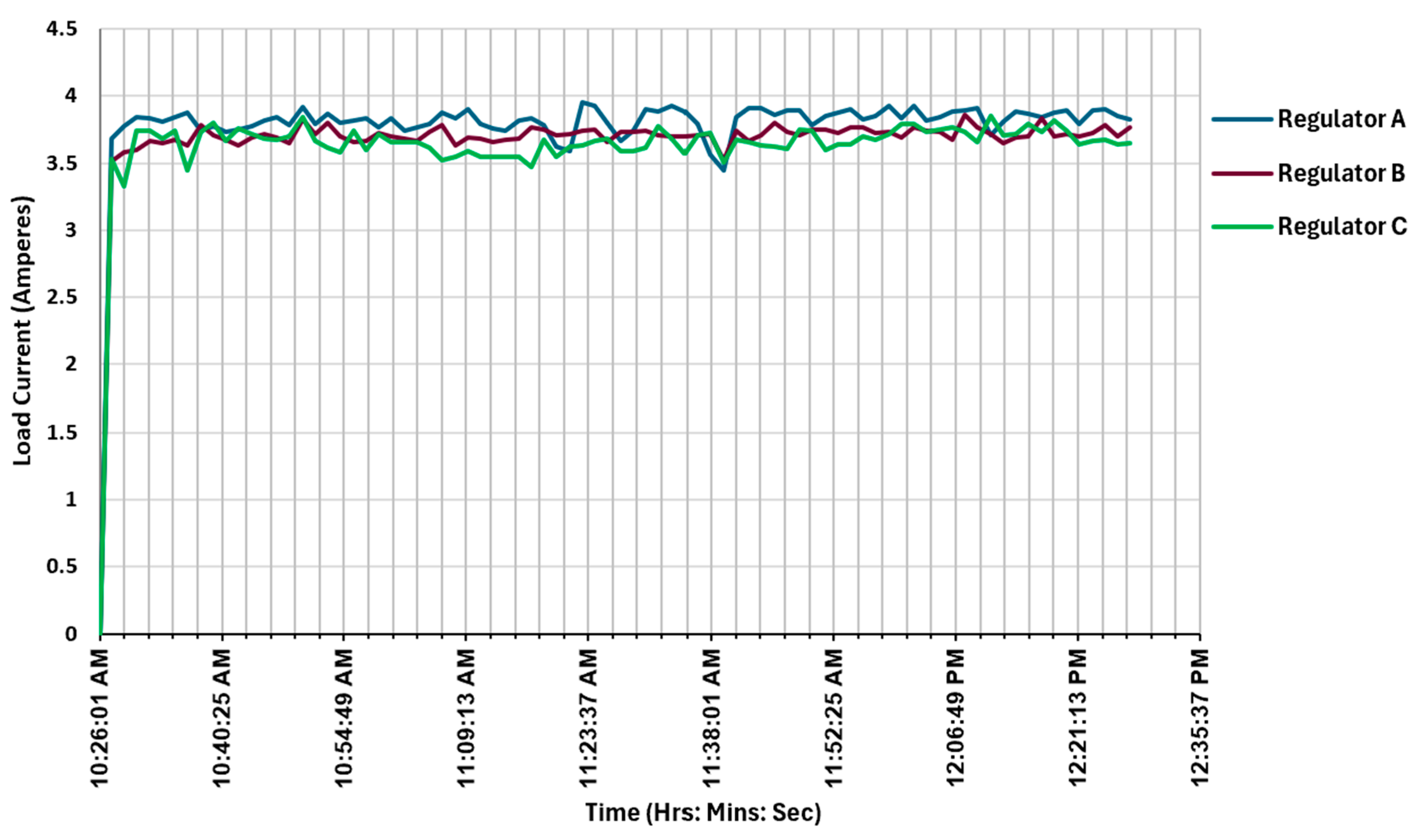
| Components | Specifications |
|---|---|
| Photovoltaic module | Wp = 80 W, Vmp = 18 V, Imp = 4.44 A Voc = 21.6 V, Isc = 4.44 A, 780 × 670 × 30 mm |
| Battery | 100 Ah, 12 V |
| LED light unit | 44 W, 12 V |
| Charge Regulators | Sunsaver SS-6L (Regulator A) | Sunguard SK-6 (Regulator B) | Solsum 6.6F (Regulator C) |
|---|---|---|---|
| System voltage | 12 V | 12 V | 12 V or 24 V |
| Battery voltage range | 6–15 V | 0–15 V | 0–15 V |
| Max. solar voltage | 30 V | 30 V | <47 V |
| Max. solar current | 6 A | 6 A | 6 A |
| Max. load current | 6 A | 6 A | 6 A |
| End of charge voltage | 15.3 V | 15.3 V | 13.9 V |
| Reconnection voltage | 12.6 V | 13.7 V | 12.4 V |
| Operating Temperature Range | −40 °C to +60 °C | −40 °C to +70 °C | −25 °C to +50 °C |
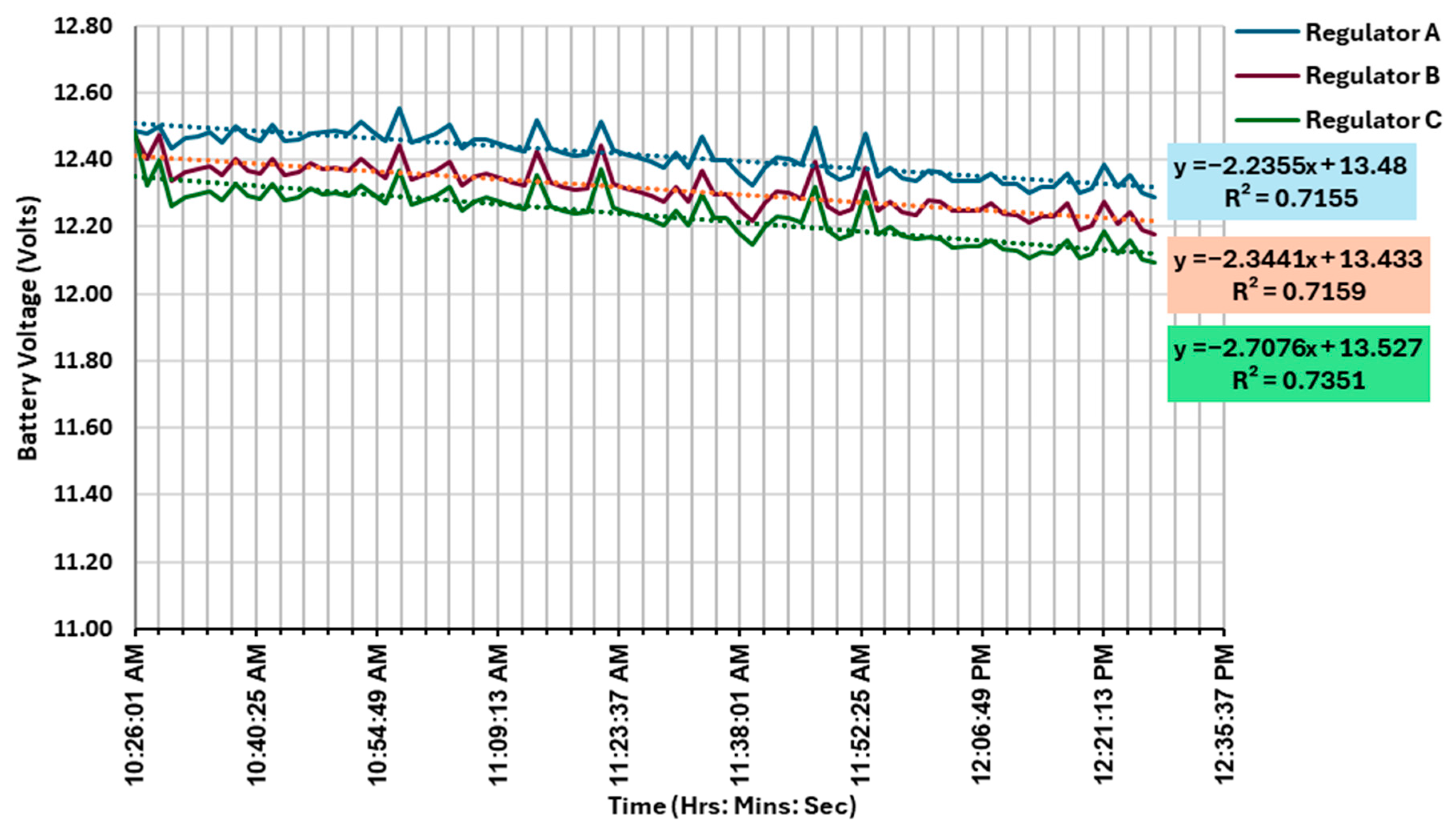
| Number of Data Points (n) Time: H: Min: S | Charge Regulator | Coefficient of Determination (R2) | Slope (m) |
|---|---|---|---|
| n = 10 From: 10:26:01 a.m. To: 10:39:24 a.m. | Regulator A | 0.0150 | −0.814 |
| Regulator B | 0.2937 | −8.081 | |
| Regulator C | 0.3461 | −12.412 | |
| n = 20 From: 10:26:01 a.m. To: 10:54:24 a.m. | Regulator A | 0.0396 | 0.632 |
| Regulator B | 0.1345 | −2.113 | |
| Regulator C | 0.1674 | −3.250 | |
| n = 30 From: 10:26:01 a.m. To: 11:09:24 a.m. | Regulator A | 0.0059 | −0.210 |
| Regulator B | 0.1902 | −1.706 | |
| Regulator C | 0.1927 | −2.172 | |
| n = 40 From: 10:26:01 a.m. To: 11:24:24 a.m. | Regulator A | 0.1370 | −0.980 |
| Regulator B | 0.2256 | −1.606 | |
| Regulator C | 0.2085 | −1.780 | |
| n = 50 From: 10:26:01 a.m. To: 11:39:24 a.m. | Regulator A | 0.4198 | −1.921 |
| Regulator B | 0.4685 | −2.329 | |
| Regulator C | 0.4306 | −2.401 | |
| n = 60 From: 10:26:01 a.m. To: 11:54:24 a.m. | Regulator A | 0.4503 | −1.871 |
| Regulator B | 0.4839 | −2.146 | |
| Regulator C | 0.4591 | −2.207 | |
| n = 70 From: 10:26:01 a.m. To: 12:09:24 p.m. | Regulator A | 0.6127 | −2.124 |
| Regulator B | 0.6095 | −2.227 | |
| Regulator C | 0.6266 | −2.546 | |
| n = 80 From: 10:26:01 a.m. To: 12:24:24 p.m. | Regulator A | 0.6944 | −2.189 |
| Regulator B | 0.6943 | −2.282 | |
| Regulator C | 0.7157 | −2.661 | |
| n = 82 From: 10:26:01 a.m. To: 12:27:24 p.m. | Regulator A | 0.7155 | −2.235 |
| Regulator B | 0.7159 | −2.344 | |
| Regulator C | 0.7351 | −2.708 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koko, S.P.; Sumbwanyambe, M.; Yokwana, X.P. Evaluating PWM Solar Charge Regulators for Off-Grid Solar PV Street Lighting Systems Using Linear Regression Approach. Energies 2025, 18, 5646. https://doi.org/10.3390/en18215646
Koko SP, Sumbwanyambe M, Yokwana XP. Evaluating PWM Solar Charge Regulators for Off-Grid Solar PV Street Lighting Systems Using Linear Regression Approach. Energies. 2025; 18(21):5646. https://doi.org/10.3390/en18215646
Chicago/Turabian StyleKoko, Sandile Phillip, Mbuyu Sumbwanyambe, and Xolani Phillips Yokwana. 2025. "Evaluating PWM Solar Charge Regulators for Off-Grid Solar PV Street Lighting Systems Using Linear Regression Approach" Energies 18, no. 21: 5646. https://doi.org/10.3390/en18215646
APA StyleKoko, S. P., Sumbwanyambe, M., & Yokwana, X. P. (2025). Evaluating PWM Solar Charge Regulators for Off-Grid Solar PV Street Lighting Systems Using Linear Regression Approach. Energies, 18(21), 5646. https://doi.org/10.3390/en18215646







