Thermodynamic Assessment of Carbon Capture Integration in Reheat Gas Turbine Combined Cycles Using Transcritical CO2 and Ammonia–Water Mixtures
Abstract
1. Introduction
- Natural-Gas-Fired Power Plants: While considered a cleaner alternative to coal, natural gas still emits about 180–245 g CO2/kWh. A study by McJeon et al. [19] suggests that the role of natural gas as a transition fuel may still contribute significantly to short-term emissions if not coupled with renewable energy development.
- Oil-Fired Power Plants: Oil has a moderate carbon intensity, emitting approximately 730 g CO2/kWh. Although declining in usage in recent years, oil-fired generation still contributes to emissions in regions with limited alternatives [20].
Research Gap
2. Materials and Methods
2.1. Assumptions
- An ammonia mass fraction of 0.7 is considered, based on Maheshwari and Singh [44];
- Erosion and corrosion of turbine blades due to the use of ammonia and carbon dioxide are not considered;
- Undercooling of working fluids is assumed to be negligible;
- Heat losses during heat transfer processes are neglected;
- Dissociation of ammonia and chemical species present in flue gases is not considered in analysis;
- The uncertainties, like labor issues, timely payment of the electricity bill by the end user, and loan repayment by the organization are not considered in the cost analysis.
2.2. Thermodynamic Modeling and Cost Function of Different Elements
3. Results and Discussion
Validation
4. Conclusions
- (i)
- Unlike previous studies focusing solely on conventional gas–steam cycles or individual working fluids, this study explores hybrid configurations using both ammonia–water and transcritical CO2. The analysis comprehensively compares these options, particularly under carbon capture scenarios, providing new insights into achievable efficiency benchmarks and emission reductions.
- (ii)
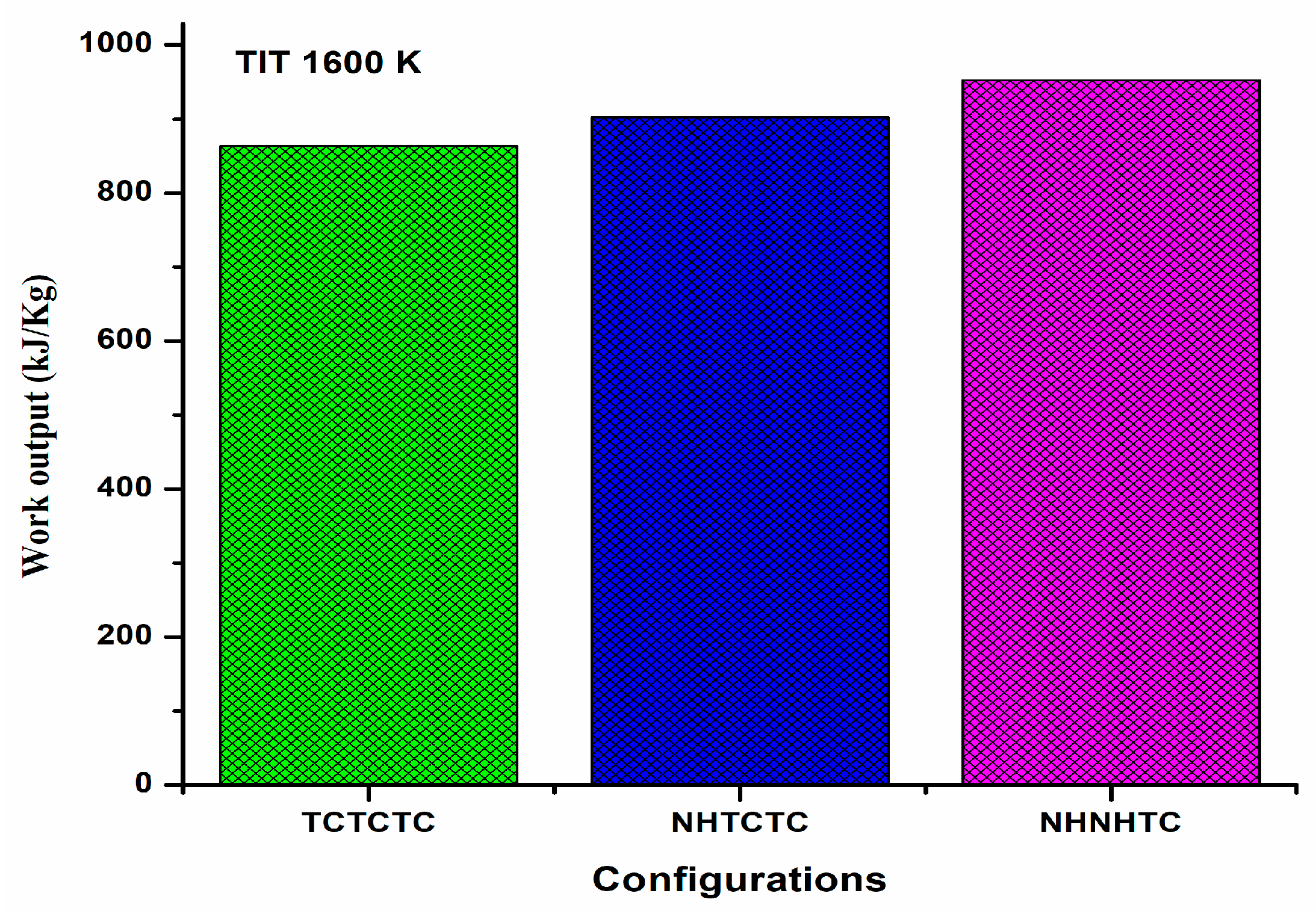
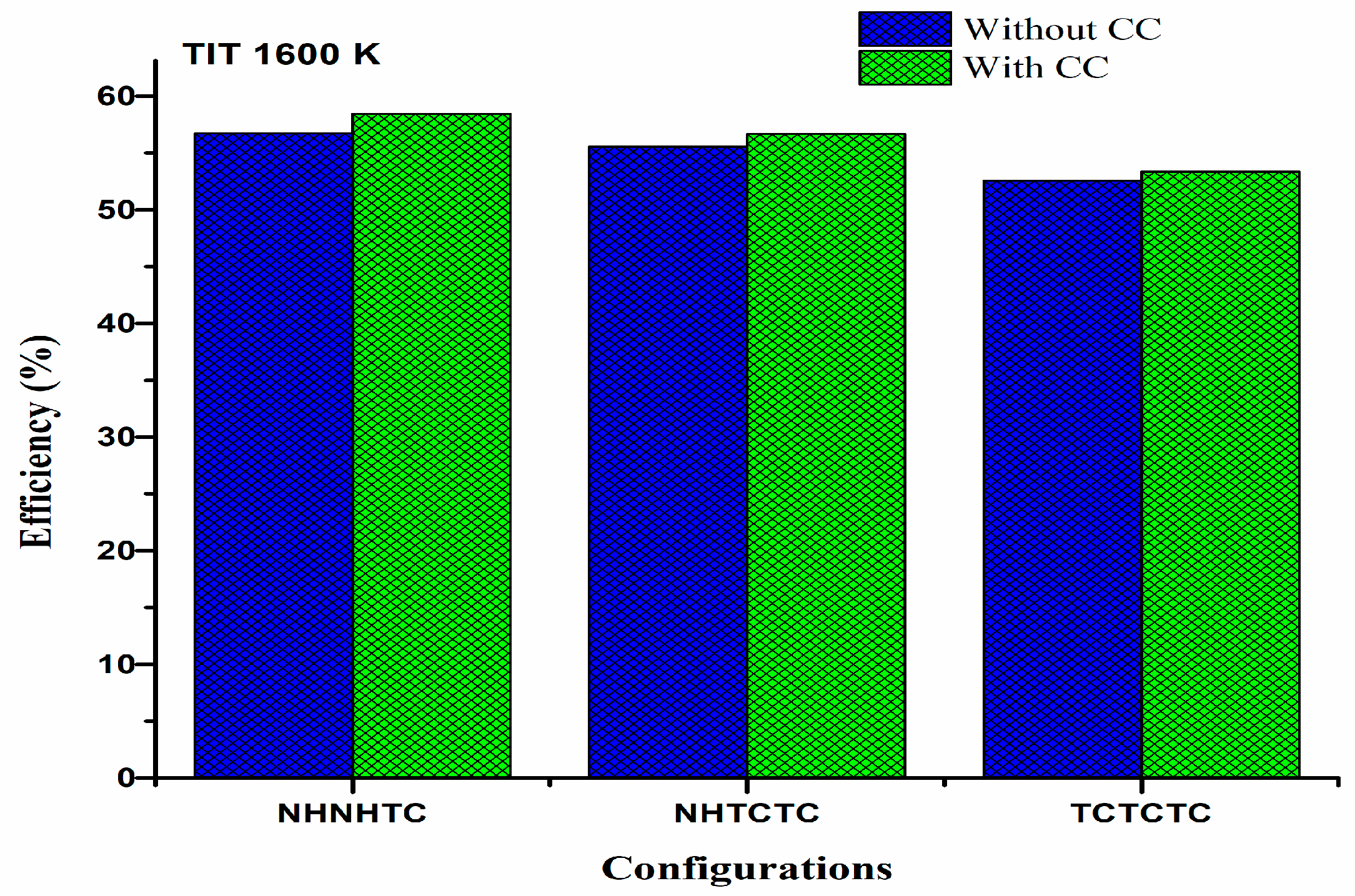
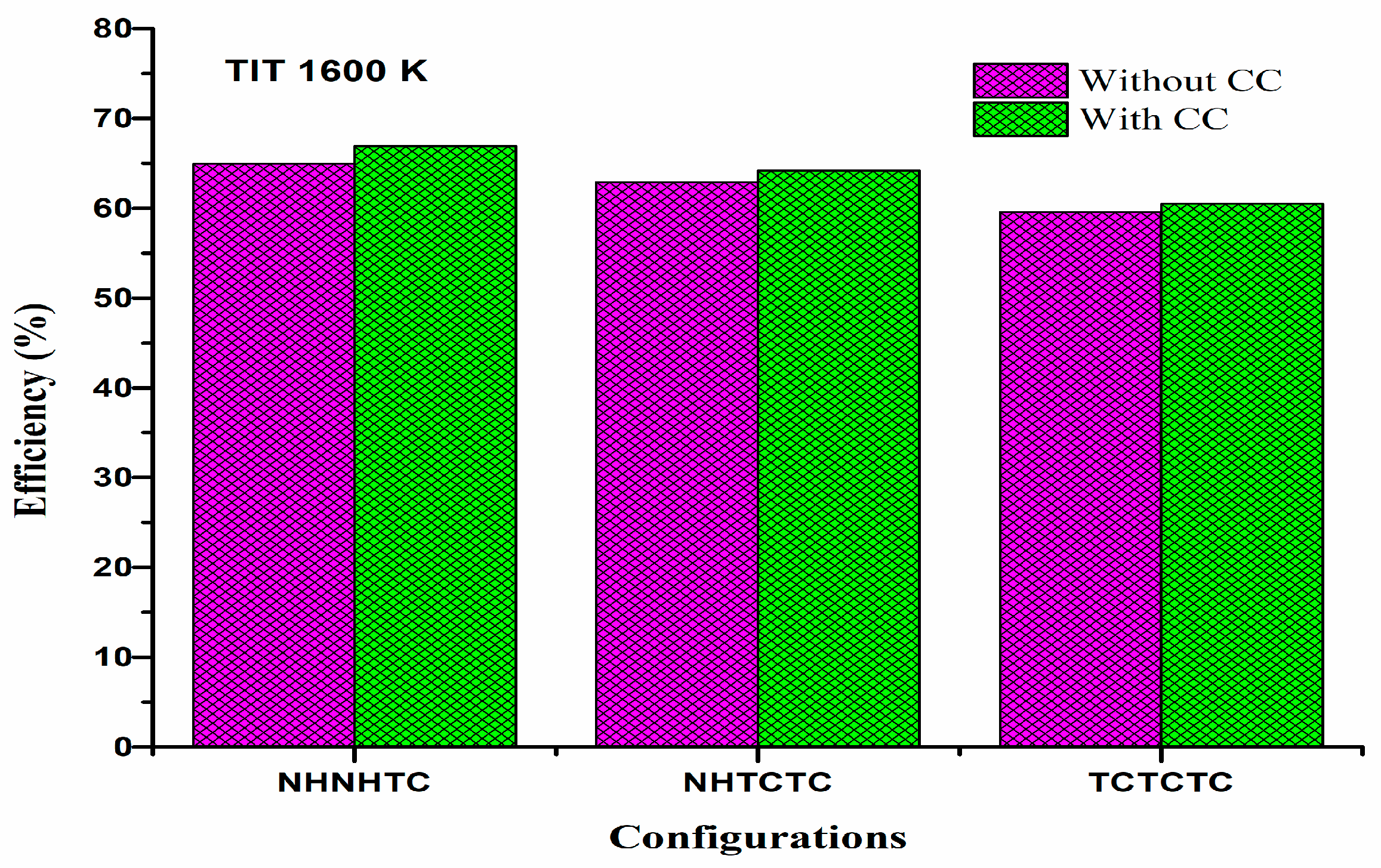
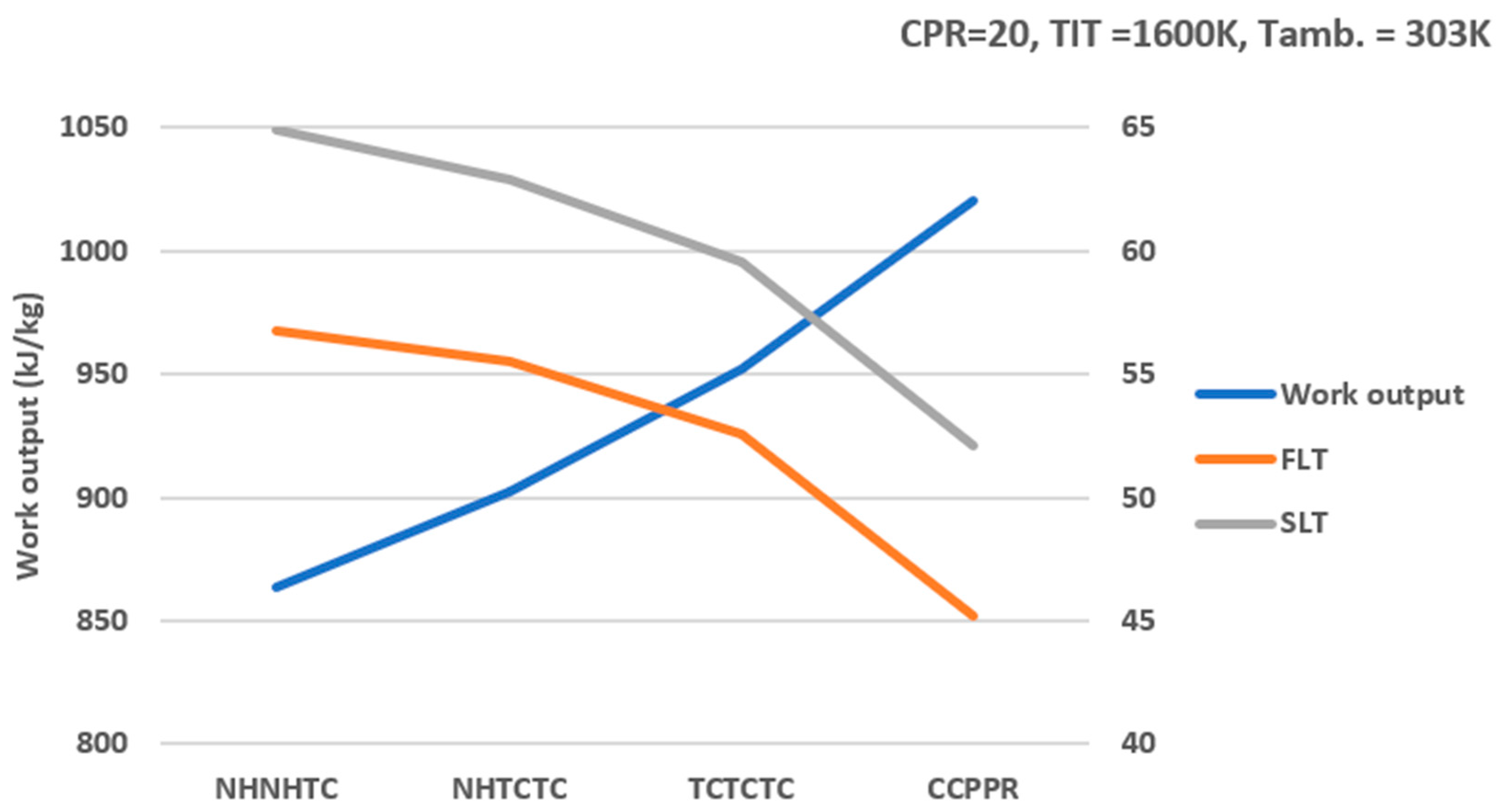
- The NHNHTC configuration demonstrates the highest network output (952.3 kJ/kg) and the best first- (58.45%) and second-law (66.88%) efficiencies, especially when a carbon capture unit is integrated. These values surpass those reported for traditional gas–steam and pure CO2-based cycles.
- (iii)
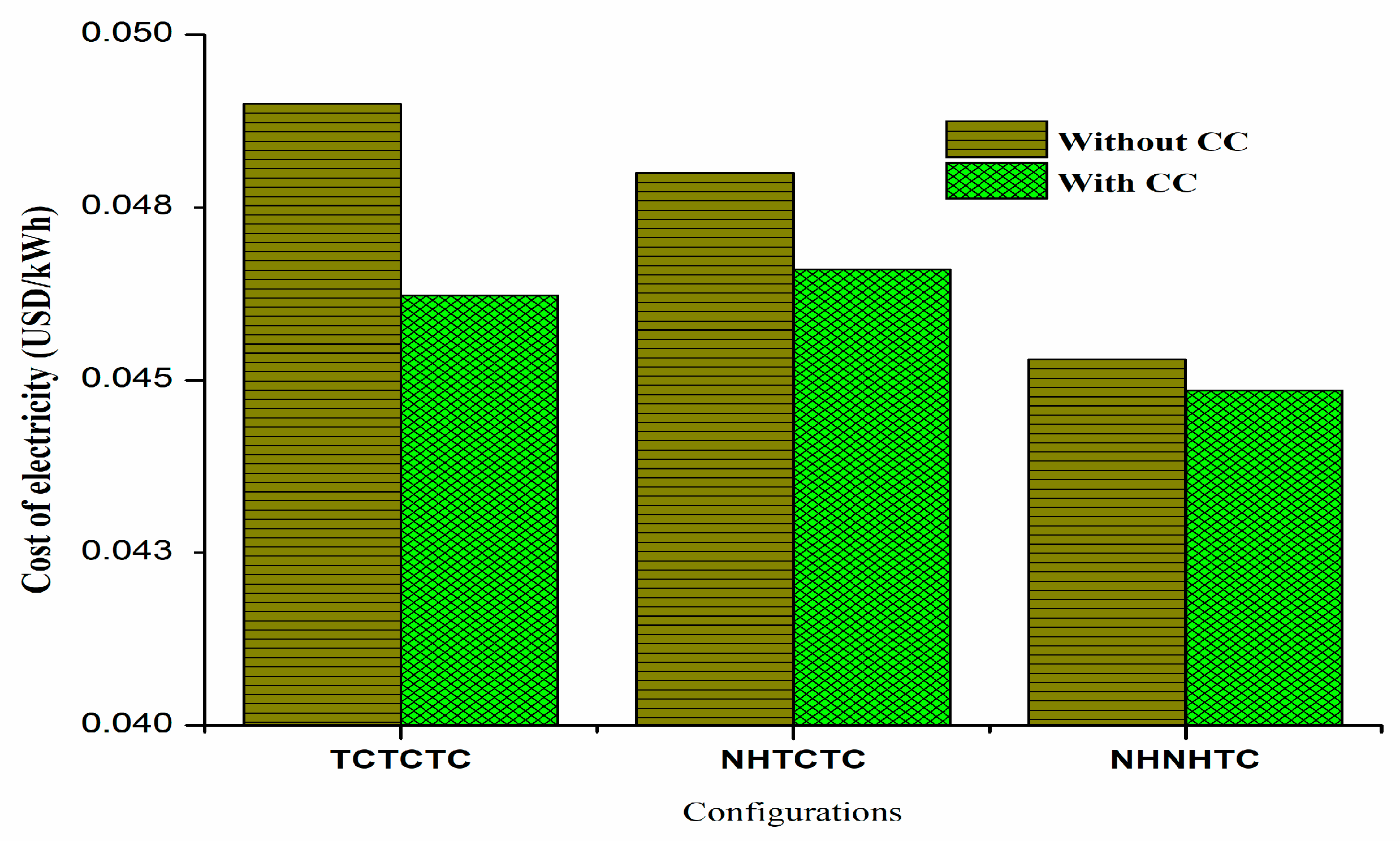
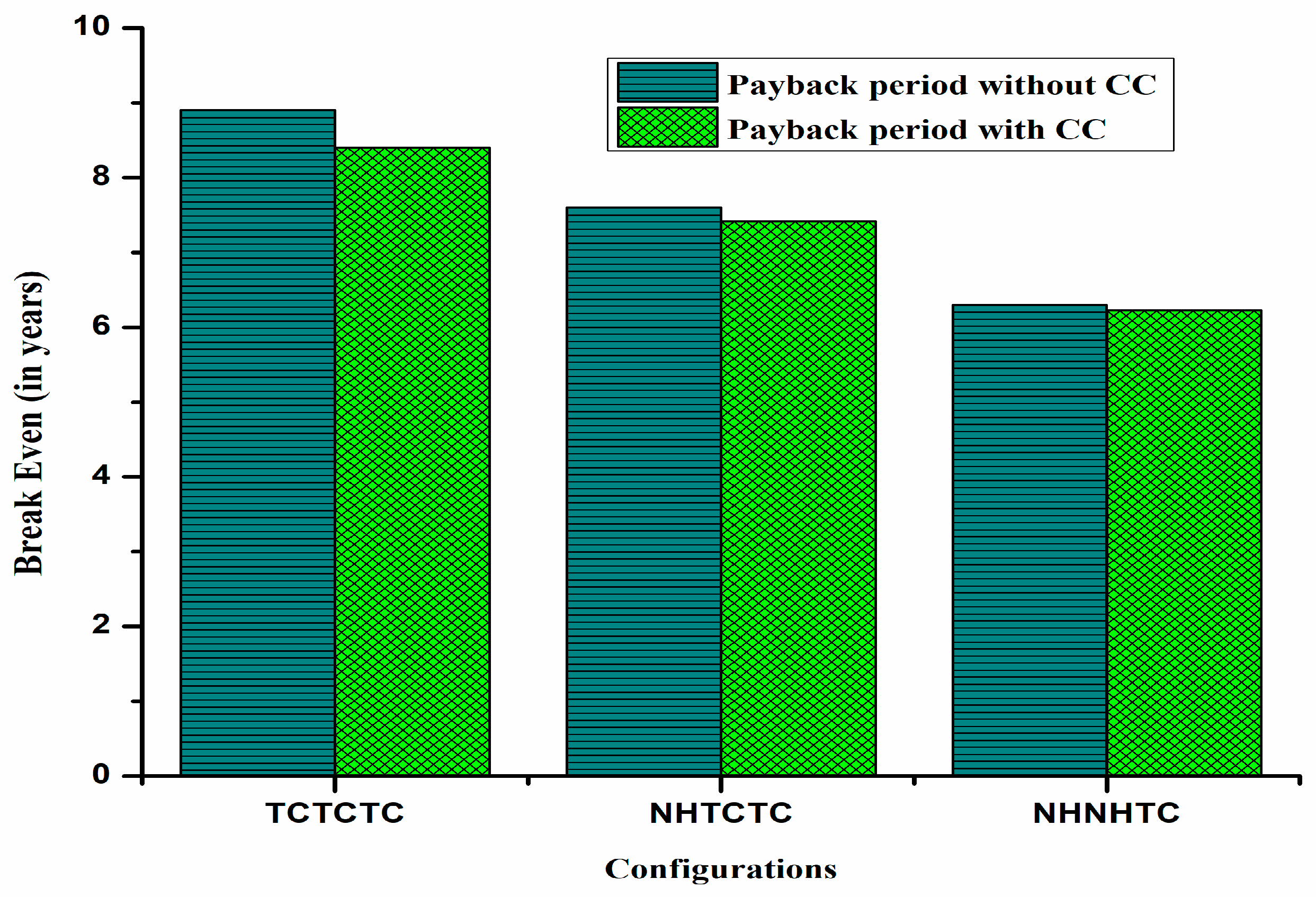
- Although the TCTCTC (all-CO2) configuration has higher electricity costs and longer payback periods, the inclusion of carbon capture across all cycles leads to significant emission reductions (up to 22.81% in TCTCTC) and operational benefits such as fuel savings. These findings indicate that proper cycle selection can meaningfully reduce carbon footprints and enhance economic feasibility, supporting accelerated adoption of carbon capture in modern power plants.
- (iv)
- This study identifies material compatibility, especially for ammonia–water mixtures, as a key barrier for real-world implementation—emphasizing the need for further research into corrosion-resistant design. Additionally, system modifications such as advanced blade cooling strategies and improved system integration are recommended to push performance further.
- (v)
- Experimental validation and pilot tests are needed to confirm projected efficiencies and resolve uncertainties related to ammonia–water dissociation and flue gas chemistry. Future work could also investigate advanced heat recovery and integration techniques to maximize network output and overall system reliability for gas turbine blades, utilizing bottoming cycle working fluids.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABS | Absorber |
| AI | Artificial intelligence |
| C | Compressor/Condenser/Cost function |
| Cost rate associated with inlet and outlet exergy streams | |
| c | Specific cost |
| CC/CCS | Combustion chamber/Carbon Capture and storage |
| CCPP | Combined cycle power plant |
| Cd | Condenser |
| CEP | Condensate extraction pump |
| CHP | Combined heat and power |
| CPRR | Gas–steam combined cycle power plant (used in Figure 18) |
| D/a | Deaerator |
| EC | Emissions captured |
| EO | Emissions output (from CCPP) |
| FHeL | Feed heater |
| FLT | First law of thermodynamics |
| FP | Feed pump |
| G | Generator |
| GT | Gas turbine |
| GWP | Global warming potential |
| HAWT/LAWT | High-/low-pressure ammonia–water turbine |
| HE/HExL | Heat exchanger |
| HPD | High-pressure vessel in HRVG |
| HRSG/HRVG | Heat recovery steam/vapor generator |
| HTb | High-pressure gas turbine |
| LPD | Low-pressure vessel in HRVG |
| LTb | Low-pressure gas turbine |
| M | Mixture |
| MPD | Medium-pressure vessel in HRVG |
| NHNHTC | Ammonia–Ammonia–Transcritical Carbon dioxide |
| NHTCTC | Ammonia–Transcritical–Transcritical Carbon dioxide |
| P1, P2, … | Pump |
| PTC | Parabolic trough collectors |
| RCC | Reheat combustion chamber |
| RGAAC | Reheat gas-turbine-based ammonia–water cycle |
| RHE | Refrigerant heat exchanger |
| SLT | Second law of thermodynamics |
| SpL | Separator |
| ST | Steam Turbine |
| t CO2/T CO2 | Transcritical carbon dioxide |
| TE | Total emissions |
| TCTCTC | Transcritical–Transcritical–Transcritical carbon dioxide |
| USD | Currency ($) used in the United States of America |
| Total cost rate associated with capital investment and operation and maintenance cost | |
| Symbol | Specification (Unit) |
| ac | Capture rate (in %) |
| °F/°C | Degree Fahrenheit/Degree Celsius |
| AT | Approach temperature (in Kelvin) |
| C | Compressor |
| cp/csp | Specific heat at constant pressure (kJ/kg·K)/Molar specific heat |
| CPR | Cycle pressure ratio |
| eI | Emission Intensity (tCO2/kW) |
| g | Gibbs free energy |
| GP | Gross power output (kW) |
| Irreversibility (kJ/sec) | |
| h | Enthalpy (kJ/kg) |
| kWh | Kilowatt-hour |
| LHV | Lower heating value (kJ/kg) |
| M | Molecular weight |
| Mass flow rate (kg/second) | |
| p/P | Pressure (bar) |
| pE | Exhaust pressure (in bar) |
| Po, To | Dead state pressure and temperature (used in exergy equation) |
| PP | Pinch point temperature (in Kelvin) |
| Q | Refrigerating effect/heat input |
| R | Gas constant (kJ/kg·K) |
| s | Entropy (kJ/kg·K) |
| T | Temperature (K) |
| TIT | Turbine inlet temperature |
| W | Work (kJ/kg or kJ/kg of inlet air) |
| x | Ammonia proportion in liquid phase of mixture |
| y | Ammonia proportion in vapor phase of mixture |
| Sub-scripts | |
| Symbol | Specification |
| a | Air/ambient/state point in HRVG profile |
| a, b, c, d | Constants |
| amw | Ammonia–water mixture |
| b | Bubble point |
| c | Compressor |
| cc | Combustion chamber |
| CV | Calorific Value |
| cw/w | Cooling Water |
| d | Dew point |
| e/o | Exit/outlet |
| ex/E | Exhaust gases from turbine |
| f | Fuel/final |
| fg | Flue gas |
| FHE | Feed heater |
| gt | Gas turbine |
| HE/HexL | Heat exchanger |
| hp/HP | High pressure |
| HRSG/HRVG | Heat recovery steam/vapor generator |
| i | Inlet/initial |
| ip/IP | Intermediate pressure |
| is | Isentropic |
| j | jth pressure level |
| lp/LP | Low pressure |
| M | Mechanical |
| mix | Mixture |
| p | Polytropic (if not used with ‘c’) |
| p | Pump |
| R | Reduced |
| ri | Rich |
| sol. | Solution |
| T | Transcritical (if used before CO2) |
| w | Water |
| we | Weak |
| wo | Working |
| Greek Letter | |
| α | Cost (USD) |
| ∆ | Difference |
| ε | Effectiveness of heat exchanging element |
| Efficiency | |
| ω | Variable used in economic analysis |
| γ | Variable used in economic analysis |
| Superscripts (used in Appendixes A and B) | |
| CI | Capital investment |
| E | Excess |
| g | Gas phase |
| l | Liquid phase |
| m,n | Constants |
| OM | Operation and maintenance |
Appendix A. Evaluation of Phase of the Mixture
Appendix B
Appendix C
| State Point | NHNHTC | |||
|---|---|---|---|---|
| Pressure (Bar) | Temperature (K) | Enthalpy (kJ/kg) | Entropy (kJ/kg·K) | |
| 1 | 1.013 | 323 | 449.2 | 3.95 |
| 2 | 1.013 | 303 | 429 | 3.89 |
| 3 | 20 | 704.3 | 987.33 | 3.905 |
| 4 | 19.6 | 1600 | 2129 | 7.09 |
| 5 | 4.64 | 1057 | 1560.2 | 6.91 |
| 6 | 4.54 | 1600 | 2129 | 7.54 |
| 7 | 1.08 | 1062 | 1580.46 | 7.34 |
| 8 | 1.015 | 378 | 503.74 | 6.2 |
| 9 | 200 | 773 | 2810 | 6.82 |
| 10 | 140 | 550 | 2623 | 6.1 |
| 11 | 140 | 570 | 1823 | 6.23 |
| 12 | 5.5 | 369 | 1679 | 5.91 |
| 13 | 5.5 | 343 | 1602 | 5.75 |
| 14 | 5.5 | 298 | 1498 | 5.44 |
| 15 | 67 | 298 | 233 | 0.81 |
| 16 | 67 | 312 | 290.55 | 1.03 |
| 17 | 67 | 343 | 435.7 | 1.44 |
| 18 | 67 | 310 | 288.23 | 1.01 |
| 19 | 67 | 298 | 233 | 0.81 |
| 20 | 140 | 298 | 236 | 0.79 |
| 21 | 140 | 313 | 307 | 1.03 |
| 22 | 200 | 313 | 311 | 1.08 |
| 23 | 140 | 400 | 745 | 2.4 |
| 24 | 140 | 690 | 2427 | 5.86 |
| 25 | 200 | 426 | 887 | 2.58 |
| 26 | 120 | 400 | 499 | 1.97 |
| 27 | 41.6 | 280 | 425 | 1.8 |
| 28 | 41.6 | 280 | 217.3 | 1.05 |
| 29 | 41.6 | 298 | 223 | 1.05 |
| 30 | 41.6 | 298 | 223 | 1.05 |
| 31 | 120 | 298 | 232 | 1.05 |
References
- Benini, E. Progress in Gas Turbine Performance; Intech: Rijeka, Croatia, 2013. [Google Scholar]
- Zhang, C.; Janeway, M. Optimization of Turbine Blade Aerodynamic Designs Using CFD and Neural Network Models. Int. J. Turbomach. Propuls. Power 2022, 7, 20. [Google Scholar] [CrossRef]
- Zhu, C.; Zhang, Y.; Wang, M.; Deng, J.; Cai, Y.; Wei, W.; Guo, M. Simulation and Comprehensive Study of a New Trigeneration Process Combined with a Gas Turbine Cycle, Involving Transcritical and Supercritical CO2 Power Cycles and Goswami Cycle. J. Therm. Anal. Calorim. 2024, 149, 6361–6384. [Google Scholar] [CrossRef]
- Mohammed, A.; Al-Mansour, M.; Ghaithan, A.M.; Alshibani, A. An Optimization Approach for Improving Steam Production of Heat Recovery Steam Generator. Sci. Rep. 2025, 15, 3860. [Google Scholar] [CrossRef] [PubMed]
- Abdollahian, A.; Ameri, M. Effect of Supplementary Firing on the Performance of a Combined Cycle Power Plant. Appl. Therm. Eng. 2021, 193, 117049. [Google Scholar] [CrossRef]
- Powell, K.M.; Rashid, K.; Ellingwood, K.; Tuttle, J.; Iverson, B.D. Hybrid Concentrated Solar Thermal Power Systems: A Review. Renew. Sustain. Energy Rev. 2017, 80, 215–237. [Google Scholar] [CrossRef]
- Wojcik, J.D.; Wang, J. Feasibility Study of Combined Cycle Gas Turbine (CCGT) Power Plant Integration with Adiabatic Compressed Air Energy Storage (ACAES). Appl. Energy 2018, 221, 477–489. [Google Scholar] [CrossRef]
- Fan, C.; Zhang, C.; Chen, Y. Dynamic Operation Characteristics of Ocean Thermal Energy Conversion Using Kalina Cycle. Renew. Energy 2024, 231, 120909. [Google Scholar] [CrossRef]
- Abdelghafar, M.M.; Hassan, M.A.; Kayed, H. Comprehensive Analysis of Combined Power Cycles Driven by SCO2-Based Concentrated Solar Power: Energy, Exergy, and Exergoeconomic Perspectives. Energy Convers. Manag. 2024, 301, 118046. [Google Scholar] [CrossRef]
- Scaife, A.D. Improve Predictive Maintenance through the Application of Artificial Intelligence: A Systematic Review. Results Eng. 2023, 21, 101645. [Google Scholar] [CrossRef]
- Asghar, A.; Hussain, A.; Kamal, K.; Alkahtani, M.; Mohammad, E.; Mathavan, S. Sustainable Operations of a Combined Cycle Power Plant Using Artificial Intelligence Based Power Prediction. Heliyon 2023, 9, e19562. [Google Scholar] [CrossRef]
- Yuce, B.E. Energy and Exergy Optimization of Kalina Cycle System-34 with Detailed Analysis of Cycle Parameters. Case Stud. Therm. Eng. 2024, 61, 105066. [Google Scholar] [CrossRef]
- Wang, L.; Huang, X.; Babaei, M.; Liu, Z.; Yang, X.; Yan, J. Full-Scale Utilization of Geothermal Energy: A High-Efficiency CO2 Hybrid Cogeneration System with Low-Temperature Waste Heat. J. Clean. Prod. 2023, 403, 136866. [Google Scholar] [CrossRef]
- Brzęczek, M.; Kotowicz, J. Integration of Alternative Fuel Production and Combined Cycle Power Plant Using Renewable Energy Sources. Appl. Energy 2024, 371, 123738. [Google Scholar] [CrossRef]
- Drago, C.; Gatto, A. Policy, Regulation Effectiveness, and Sustainability in the Energy Sector: A Worldwide Interval-Based Composite Indicator. Energy Policy 2022, 167, 112889. [Google Scholar] [CrossRef]
- Oecd Publishing (Oecd). World Energy Outlook 2020; Paris Organisation For Economic Co-Operation And Development Oecd: Paris, France, 2020. [Google Scholar]
- Ritchie, H.; Rosado, P.; Roser, M. Energy Production and Consumption; Our World in Data: Oxford, England, 2020. [Google Scholar]
- Stark, M.; Cataudella, F.; Mayer, J. A Cleaner Future for Coal Power Plants and Communities; World Economic Forum: Davos, Switzerland, 2022; Available online: https://www.weforum.org/stories/2022/03/a-cleaner-life-for-coal-power-plants (accessed on 20 March 2025).
- McJeon, H.; Edmonds, J.; Bauer, N.; Clarke, L.; Fisher, B.; Flannery, B.P.; Hilaire, J.; Krey, V.; Marangoni, G.; Mi, R.; et al. Limited Impact on Decadal-Scale Climate Change from Increased Use of Natural Gas. Nature 2014, 514, 482–485. [Google Scholar] [CrossRef]
- Agathokleous, E.; Barceló, D.; Calabrese, E.J. US EPA: Is There Room to Open a New Window for Evaluating Potential Sub-Threshold Effects and Ecological Risks? Environ. Pollut. 2021, 284, 117372. [Google Scholar] [CrossRef]
- Canton, H. The Europa Directory of International Organizations 2021; Routledge: London, UK, 2021. [Google Scholar] [CrossRef]
- Ochu, E.R.; Friedmann, S.J. CCUS in a Net-Zero U.S. Power Sector: Policy Design, Rates, and Project Finance. Electr. J. 2021, 34, 107000. [Google Scholar] [CrossRef]
- Tooryan, F.; HassanzadehFard, H.; Collins, E.R.; Jin, S.; Ramezani, B. Smart Integration of Renewable Energy Resources, Electrical, and Thermal Energy Storage in Microgrid Applications. Energy 2020, 212, 118716. [Google Scholar] [CrossRef]
- Kumar Shukla, A.; Ahmad, Z.; Sharma, M.; Dwivedi, G.; Nath Verma, T.; Jain, S.; Verma, P.; Zare, A. Advances of Carbon Capture and Storage in Coal-Based Power Generating Units in an Indian Context. Energies 2020, 13, 4124. [Google Scholar] [CrossRef]
- Sharma, M.; Pavithran, A.; Shukla, A.K. Thermodynamic investigation on coal fired emission free s-CO2 power cycles. Energy Equip. Syst. 2024, 12, 197–216. [Google Scholar]
- Kumar Rai, S.; Sharma, M.; Kumar Shukla, A. Parametric evaluation of a cascaded novel system based on biomass, solar, and SCO2 power cycle. Energy Equip. Syst. 2025, 13, 93–114. [Google Scholar]
- Meng, J.; Wei, M.; Song, P.; Tian, R.; Hao, L.; Zheng, S. Performance Evaluation of a Solar Transcritical Carbon Dioxide Rankine Cycle Integrated with Compressed Air Energy Storage. Energy Convers. Manag. 2020, 215, 112931. [Google Scholar] [CrossRef]
- Gu, Z.; Liu, Z.; Yang, S.; Xie, N.; Ma, K. Exergy and Environmental Footprint Analysis for a Green Ammonia Production Process. J. Clean. Prod. 2024, 455, 142357. [Google Scholar] [CrossRef]
- Wolf, V.; Bertrand, A.; Leyer, S. Analysis of the Thermodynamic Performance of Transcritical CO2 Power Cycle Configurations for Low Grade Waste Heat Recovery. Energy Rep. 2022, 8, 4196–4208. [Google Scholar] [CrossRef]
- Zare, V.; Mahmoudi, S.M.S.; Yari, M. Ammonia–Water Cogeneration Cycle for Utilizing Waste Heat from the GT-MHR Plant. Appl. Therm. Eng. 2012, 48, 176–185. [Google Scholar] [CrossRef]
- 2016 ANNUAL REPORT. 2017. Available online: https://area-eur.be/sites/default/files/2017-05/AREA%20Annual%20Report%202016%20%28web%29.pdf (accessed on 24 March 2025).
- Wang, J.; Zhao, P.; Niu, X.; Dai, Y. Parametric Analysis of a New Combined Cooling, Heating and Power System with Transcritical CO2 Driven by Solar Energy. Appl. Energy 2012, 94, 58–64. [Google Scholar] [CrossRef]
- Anwar, M.; Mehdizadeh, A.; Karimi, N. Waste Heat Recovery from a Green Ammonia Production Plant by Kalina and Vapour Absorption Refrigeration Cycles: A Comparative Energy, Exergy, Environmental and Economic Analysis. Sustain. Energy Technol. Assess. 2024, 69, 103916. [Google Scholar] [CrossRef]
- Mishra, R.S.; Singh, H. Detailed Parametric Analysis of Solar Driven Supercritical CO2 Based Combined Cycle for Power Generation, Cooling and Heating Effect by Vapor Absorption Refrigeration as a Bottoming Cycle. Therm. Sci. Eng. Prog. 2018, 8, 397–410. [Google Scholar] [CrossRef]
- Valdimarsson, P.; Eliasson, L. Factors influencing the economics of the Kalina power cycle and situations of superior performance. In Proceedings of the International Geothermal Conference, Reykjavík, Iceland, 14–17 September 2003; pp. 14–17. [Google Scholar]
- Wall, G.; Chuang, C.C.; Ishida, M. Exergy study of the Kalina cycle. Anal. Des. Energy Syst. Anal. Ind. Process. 1989, 10, 73–77. [Google Scholar]
- Desideri, U.; Bidini, G. Study of Possible Optimisation Criteria for Geothermal Power Plants. Energy Convers. Manag. 1997, 38, 1681–1691. [Google Scholar] [CrossRef]
- Leibowitz, H.M.; Micak, H.A. Design of a 2MW Kalina cycle binary module for installation in Husavik, Iceland. Trans. Geotherm. Resour. Counc. 1999, 23, 75–80. [Google Scholar]
- Vijayaraghavan, S.; Goswami, D.Y. On Evaluating Efficiency of a Combined Power and Cooling Cycle. Adv. Energy Syst. 2002, 125, 287–295. [Google Scholar] [CrossRef]
- Whittaker, P. Corrosion in the Kalina cycle: An investigation into corrosion problems at the Kalina cycle geothermal power plant in Húsavík, Iceland. Ph.D. Thesis, University of Iceland, Reykjavík, Iceland, University of Akureyri, Akureyri, Iceland, 2009. [Google Scholar]
- Svoboda, R.; Denk, J.; Maggi, C. Influence of carbon dioxide on corrosion in steam turbines. Power Plant Chem. 2003, 5, 581–586. [Google Scholar]
- Maheshwari, M.; Singh, O. Comparative Evaluation of Different Combined Cycle Configurations Having Simple Gas Turbine, Steam Turbine and Ammonia Water Turbine. Energy 2019, 168, 1217–1236. [Google Scholar] [CrossRef]
- Prakash, D.; Singh, O. Thermo-Economic Study of Combined Cycle Power Plant with Carbon Capture and Methanation. J. Clean. Prod. 2019, 231, 529–542. [Google Scholar] [CrossRef]
- Maheshwari, M.; Singh, O. Exergoeconomic Study of Reheat Combined Cycle Configurations Using Steam and Ammonia-Water Mixture for Bottoming Cycle Parameters. J. Therm. Eng. 2023, 9, 1272–1290. [Google Scholar] [CrossRef]
- Yari, M.; Mehr, A.S.; Zare, V.; Mahmoudi, S.M.S.; Rosen, M.A. Exergoeconomic Comparison of TLC (Trilateral Rankine Cycle), ORC (Organic Rankine Cycle) and Kalina Cycle Using a Low Grade Heat Source. Energy 2015, 83, 712–722. [Google Scholar] [CrossRef]
- Maheshwari, M. Thermodynamic Analysis of Combined Power Cycle with Ammonia Water Mixture for Power Generation. Inflibnet.ac.in. 2019. Available online: http://hdl.handle.net/10603/309491 (accessed on 19 February 2025).
- Sanjay, Y.; Singh, O.; Prasad, B.N. Energy and Exergy Analysis of Steam Cooled Reheat Gas–Steam Combined Cycle. Appl. Therm. Eng. 2007, 27, 2779–2790. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. Simple Functions for Fast Calculations of Selected Thermodynamic Properties of the Ammonia-Water System. Int. J. Refrig. 1995, 18, 228–234. [Google Scholar] [CrossRef]
- Soleimani Alamdari, G. Simple Functions for Predicting Thermodynamic Properties of Ammonia-Water Mixture (RESEARCH NOTE). Int. J. Eng. 2007, 20, 94–104. [Google Scholar]
- Ziegler, B.; Trepp, C. Equation of State for Ammonia-Water Mixtures. Int. J. Refrig. 1984, 7, 101–106. [Google Scholar] [CrossRef]
- Owebor, K.; Oko, C.O.C.; Diemuodeke, E.O.; Ogorure, O.J. Thermo-Environmental and Economic Analysis of an Integrated Municipal Waste-To-Energy Solid Oxide Fuel Cell, Gas-, Steam-, Organic Fluid- and Absorption Refrigeration Cycle Thermal Power Plants. Appl. Energy 2019, 239, 1385–1401. [Google Scholar] [CrossRef]
- CFI Team. Levelized Cost of Energy (LCOE); Corporate Finance Institute: Vancouver, BC, Canada, 2024; Available online: https://corporatefinanceinstitute.com/resources/valuation/levelized-cost-of-energy-lcoe/ (accessed on 22 March 2025).

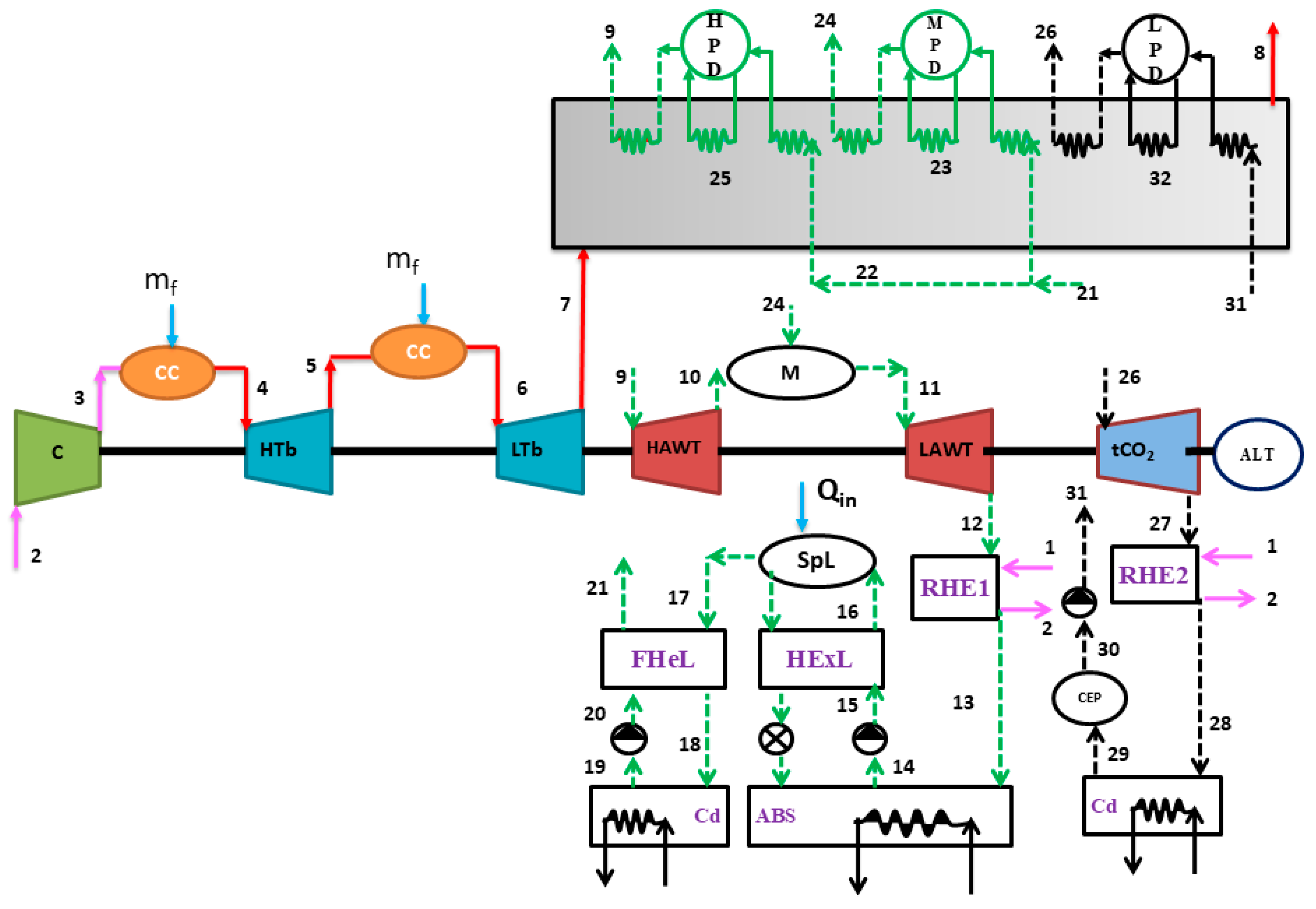


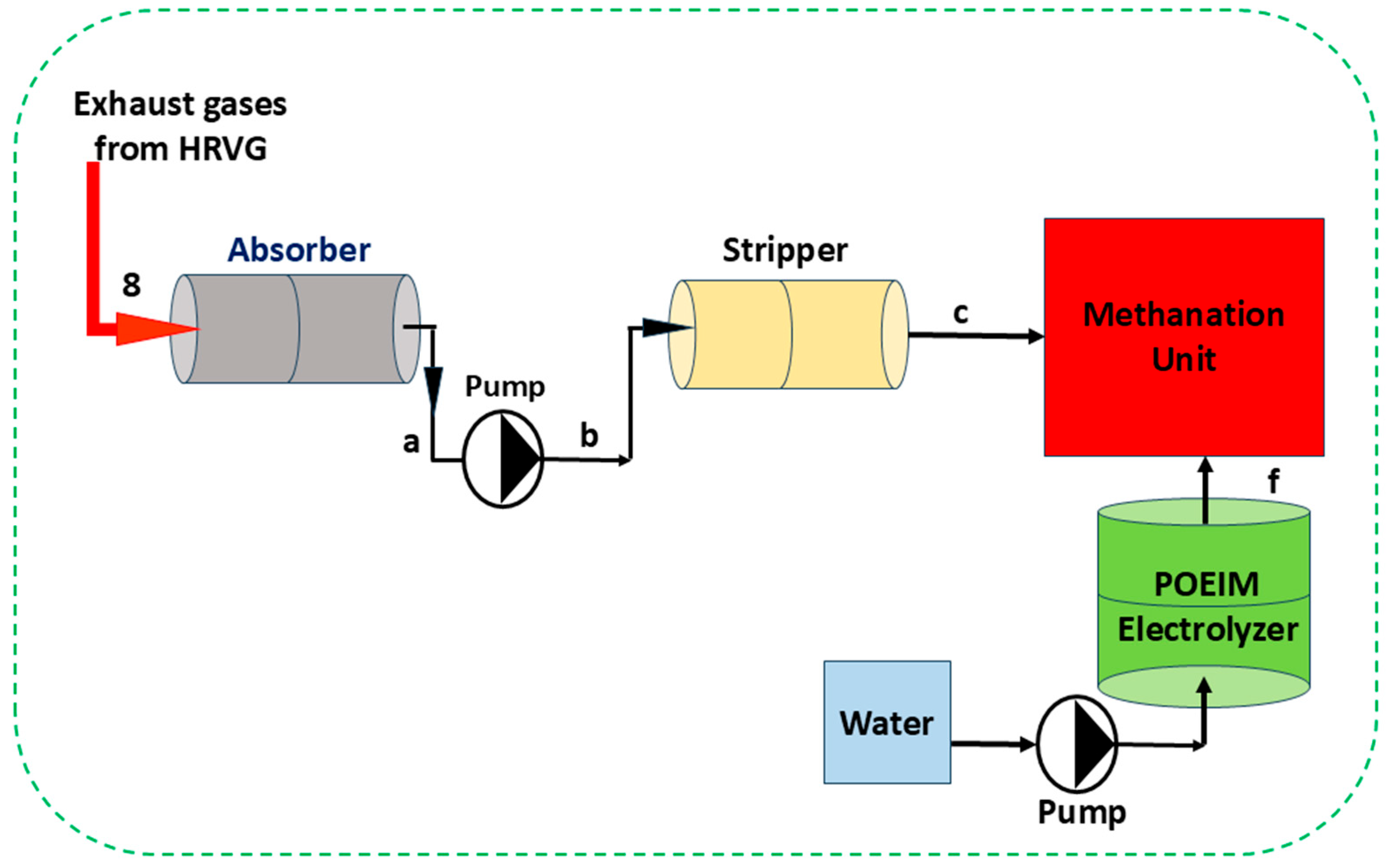
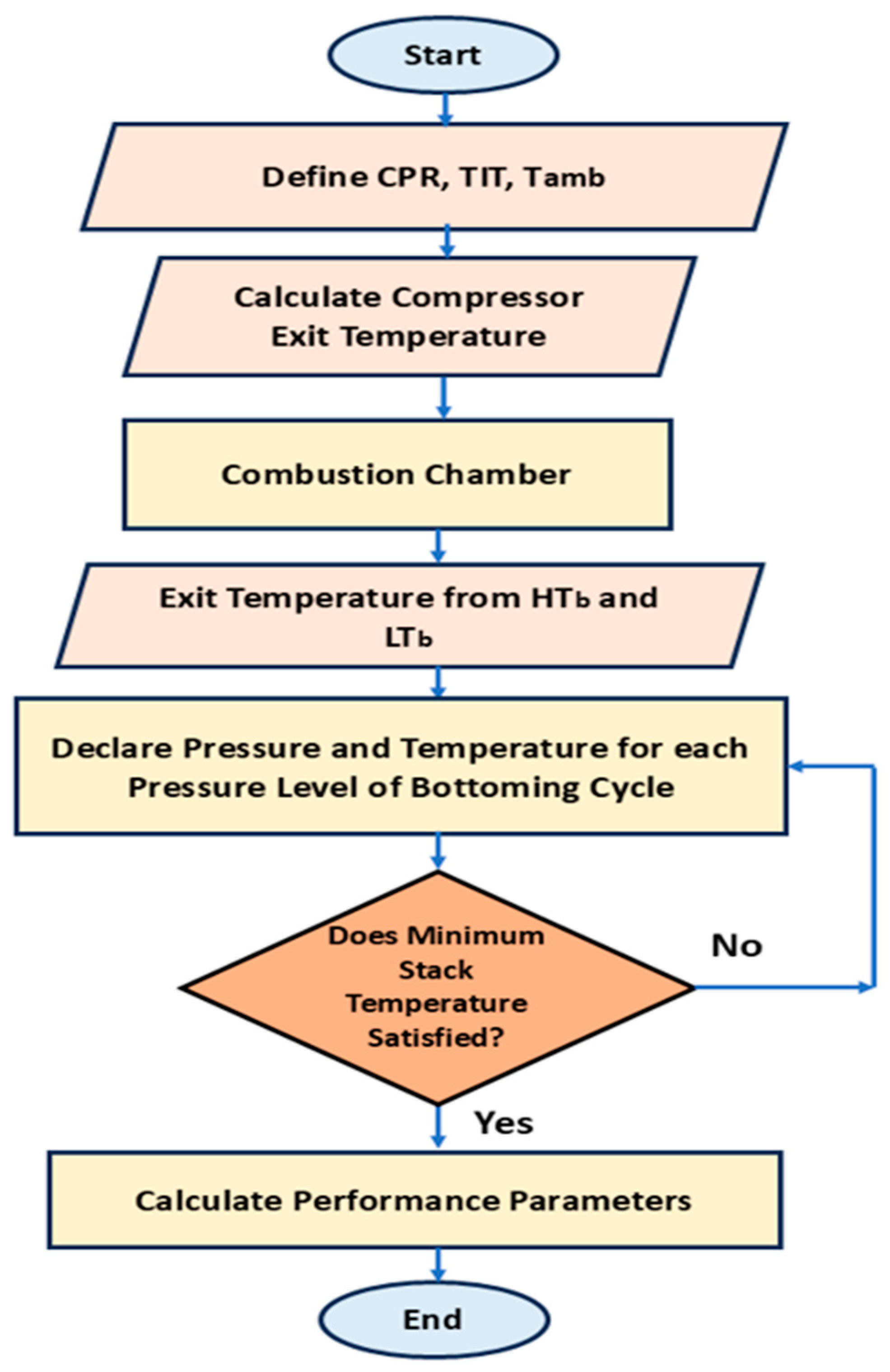

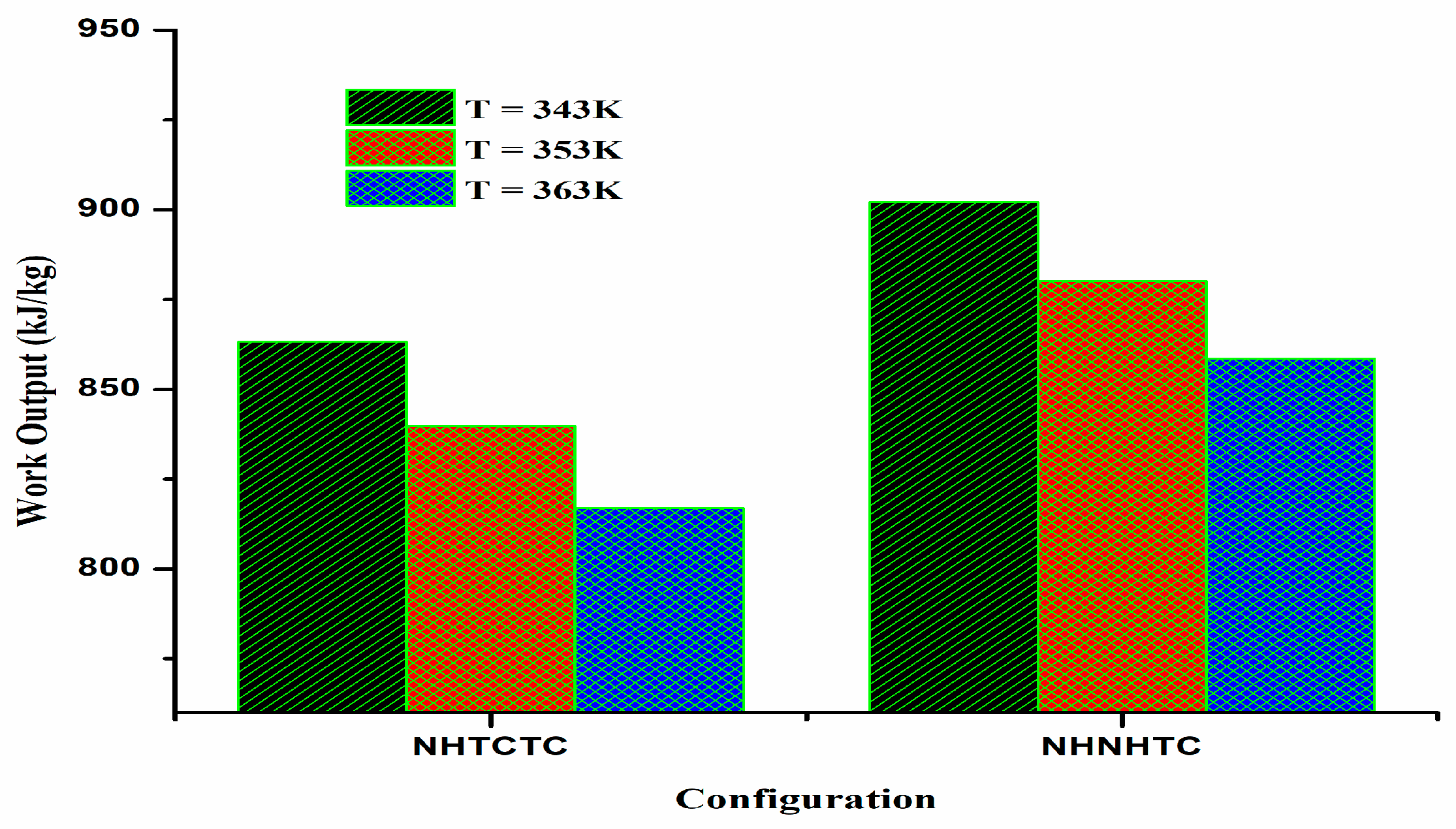
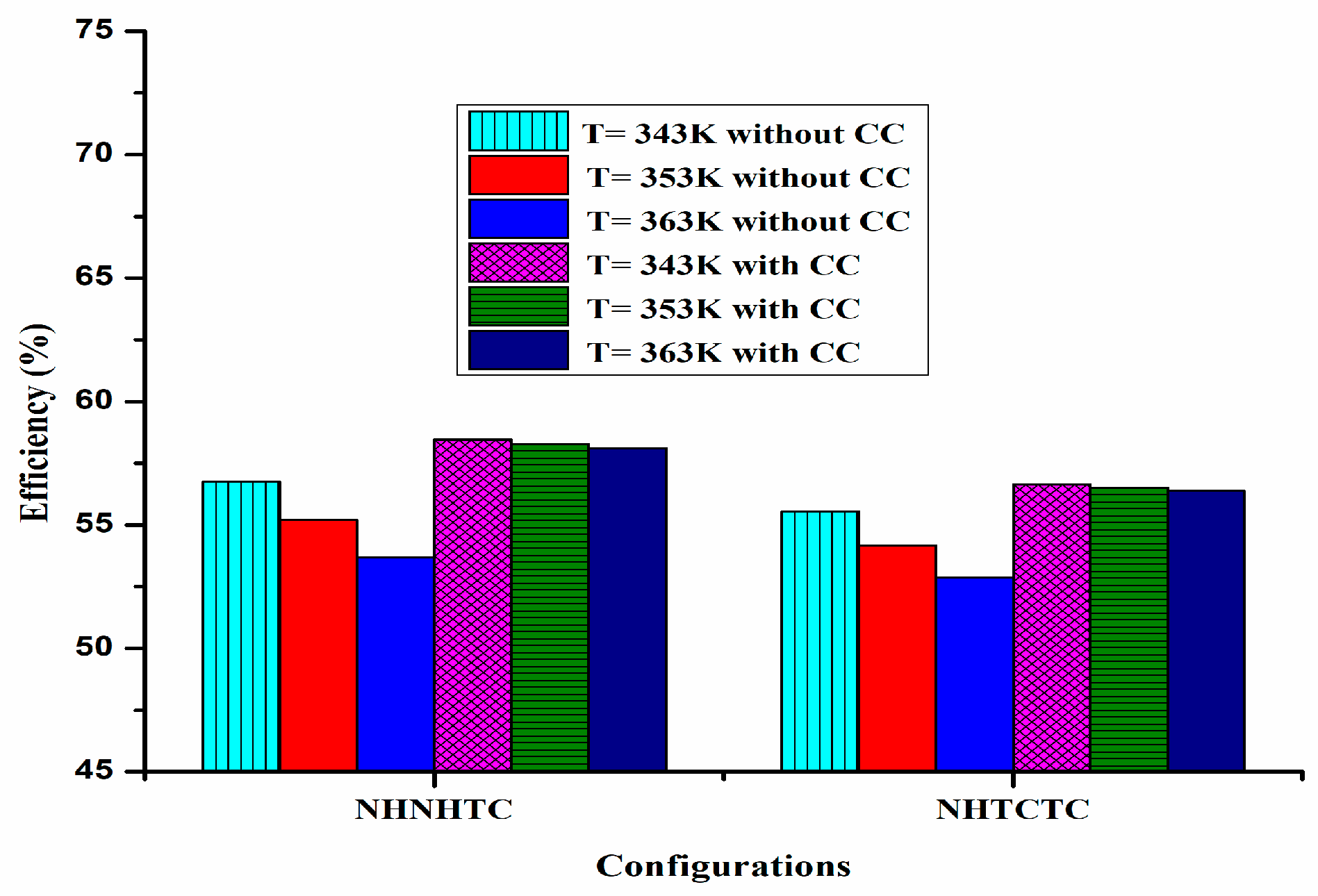

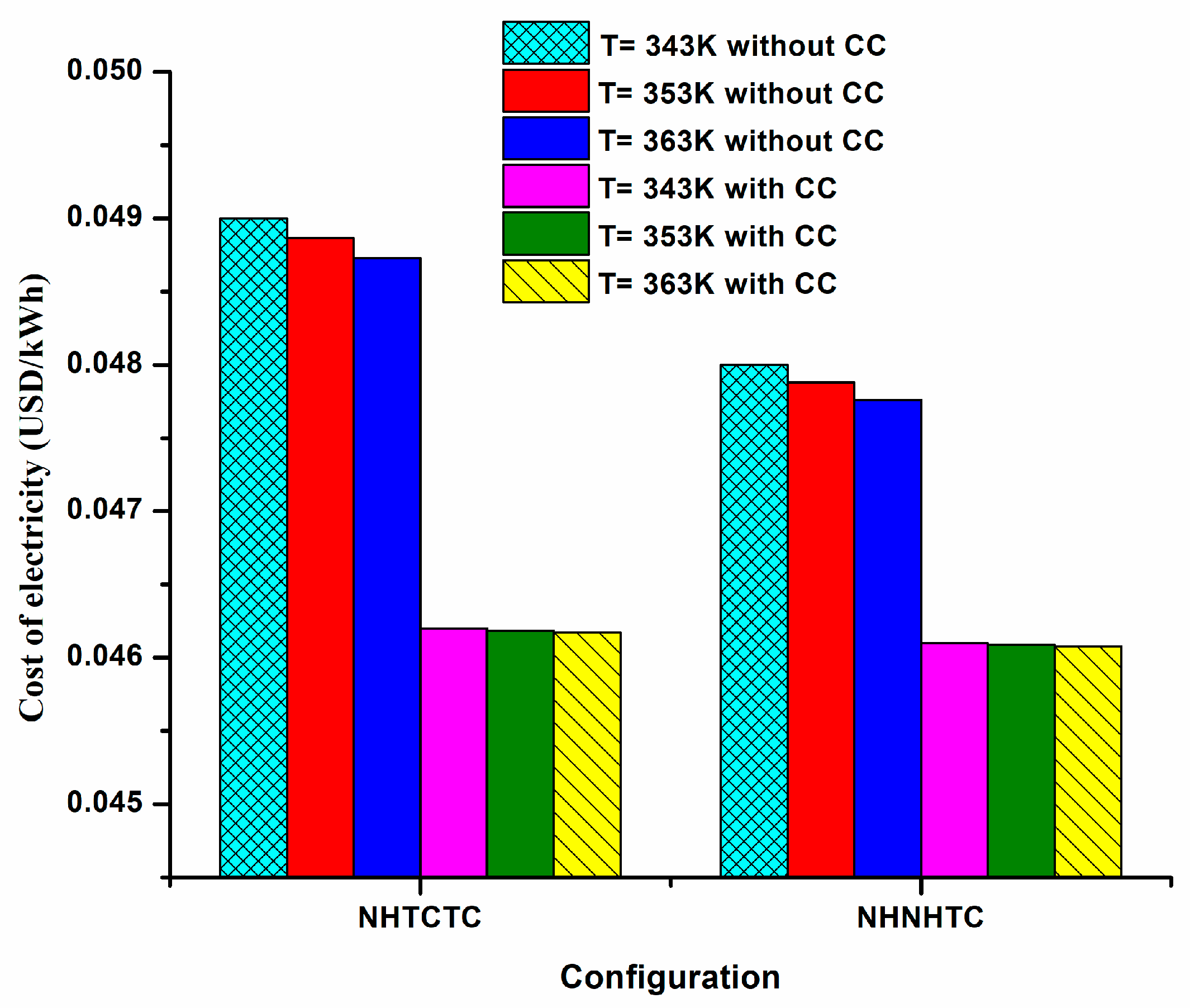
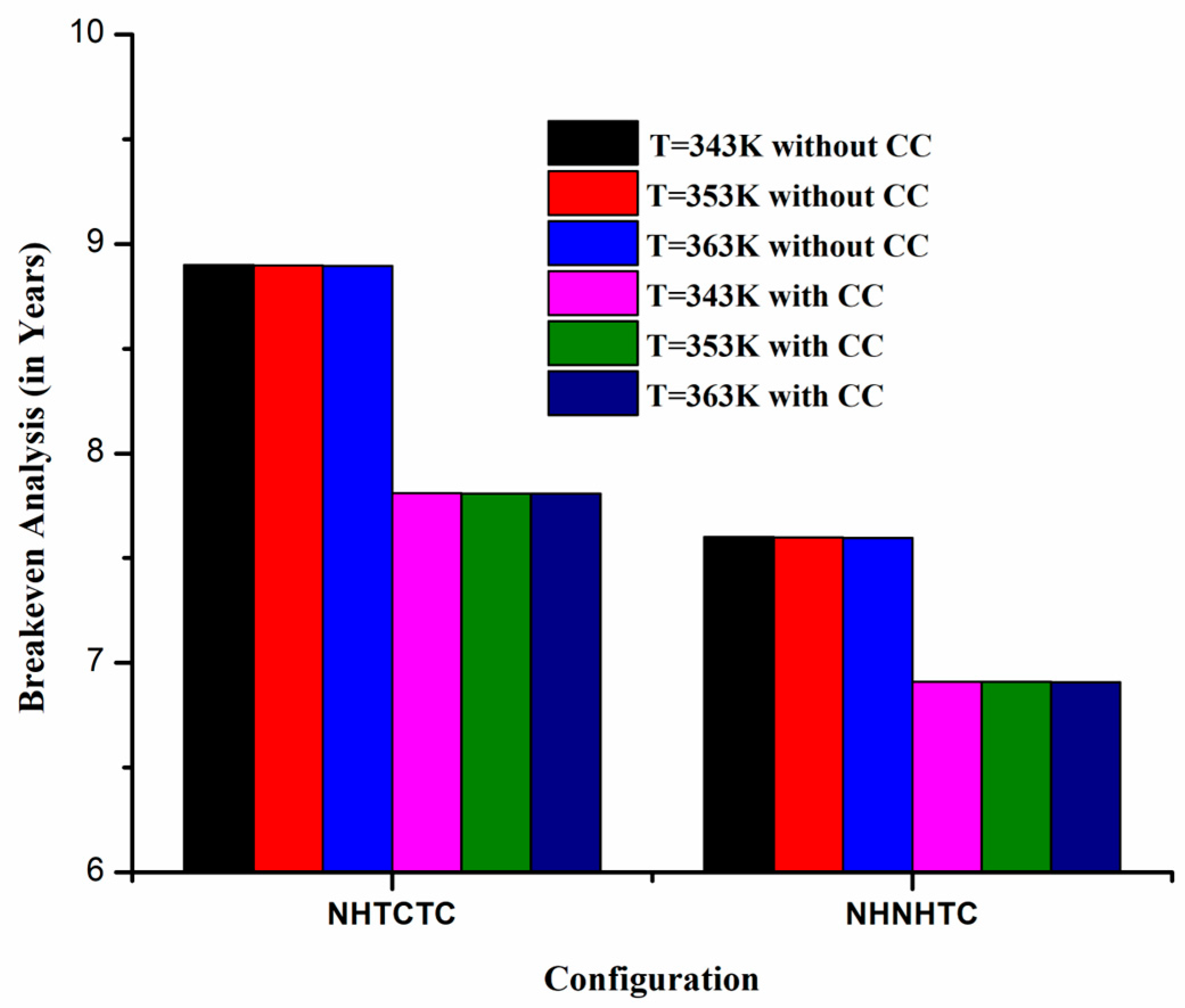
| S.No. | Parameter | Transcritical CO2 Summary | Ammonia–Water Mixture Summary | Comparative Insight |
|---|---|---|---|---|
| 1. | Efficiency | Often exceeds traditional Rankine cycles, especially in waste heat and CSP systems. Meng et al. [27]. | High latent heat of ammonia + water properties offer strong efficiency in bottoming cycles. Gu et al. [28]. | Ammonia–water excels at moderate temperatures; CO2 advantageous where high-grade waste is available. |
| 2. | Waste heat recovery | Significant gains in low-grade heat recovery; efficient for industrial/renewable recovery [29]. | Cogeneration shows 9–15% higher energy utilization vs. CO2 systems in several studies [30]. | Both strong; ammonia–water is superior for deep waste heat recovery in hybrids. |
| 3. | Environmental impact | Non-toxic, GWP = 1, minimal climate risk [31]. | Zero GWP, climate-friendly, but corrosion risk in equipment [31]. | Both are environmentally preferred; ammonia–water needs careful plant material selection. |
| 4. | Combined heat and power systems | Used in CCHP; high turbine inlet pressure may lower efficiency [32]. | Integrated into CHP for waste heat; excellent for combined cooling and power [33]. | Ammonia–water is ideal where CHP and versatility matter most. |
| Reference | Bottoming Fluid(s) | Carbon Capture | Reheat | Economic Analysis | Direct Fluid Comparison? |
|---|---|---|---|---|---|
| Zhu et al. [3] | CO2/Hybrid | No | No | Yes | No |
| Maheshwari & Singh [42] | Ammonia–Water | No | Yes | Yes | No |
| Abdelghafar et al. [9] | Supercritical CO2 + Solar | No | No | Yes | No |
| Prakash & Singh [43] | Steam + Methanation | Yes | Yes | Yes | No |
| Present Work | Ammonia–Water | Yes | Yes | Yes | Yes |
| Component | Diagrammatic Representation | Input Parameters Considered for Analysis | First-Law Analysis of the Component | Second-Law Analysis/Irreversibility in the Component | Cost of Operating Thermodynamic Element |
|---|---|---|---|---|---|
| RHE |  | ε = 98% AT = 20.0 K PP = 20.0 K | |||
| Compressor | 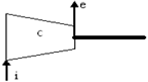 | = 92.0% = 98.5% | |||
| CC/RCC | 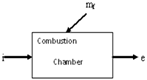 | = 99.5% = 2% of inlet pressure LHV = 48,990 kJ/kg | |||
| Gas turbine |  | = 92.0% pE = 1.08 bar | |||
| HRVG | 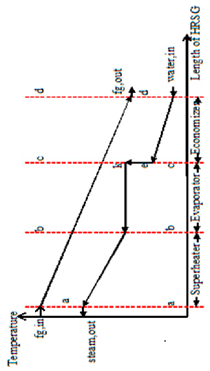 | ε = 98.0% ploss = 10% and 6% of entry pressure for bottoming cycle and on the gas side Tmin.ex = 353.0 K AT = 20.0 K PP = 20.0 K HPD = 200 bar (Max.) Tmax.,HPD = 873 K, Tmax.,MPD = 673.0 K (Max.) Tmax.,LPD = 500 K (Max.) | Generation of T-CO2 in high-pressure vessel of triple-pressure HRVG is given as Generation of T-CO2 in intermediate-pressure vessel of triple-pressure HRVG can be written as Generation of T-CO2 in low-pressure vessel of triple-pressure HRSG can be written as Temperature of stack is calculated as | ||
| Bottoming cycle turbine | 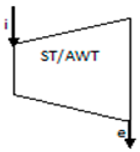 | = 88.0% | |||
| Absorber | 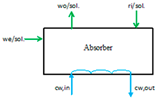 | ε = 98.0% AT = 20.0 K PP = 20.0 K | |||
| Pump |  | = 88.0% | |||
| HE |  | ε = 98.0% AT = 20.0 K PP = 20.0 K | |||
| Separator |  |
| S.No. | Parameter | Value |
|---|---|---|
| 1 | Capture rate | 90% |
| 2 | Carbon price (USD/tCO2) | 5.5 |
| 3 | Intensity of carbon being emitted (tCO2/kW) | 0.55 × 10−3 |
| 4 | Solvent type | Mono ethanol-Amine |
| Configuration | First-Law Efficiency (%) | Second-Law Efficiency (%) | CO2 Reduction (%) | Payback Period (years) |
|---|---|---|---|---|
| NHNHTC | 58.45 | 66.88 | 15.0 | 6.22 |
| NHTCTC | 56.65 | 64.16 | 22.12 | 7.41 |
| TCTCTC | 53.36 | 60.46 | 22.81 | 8.39 |
| Configuration | Parameter Considered | Present Study Values | Published Literature Values | % Error | Reference |
|---|---|---|---|---|---|
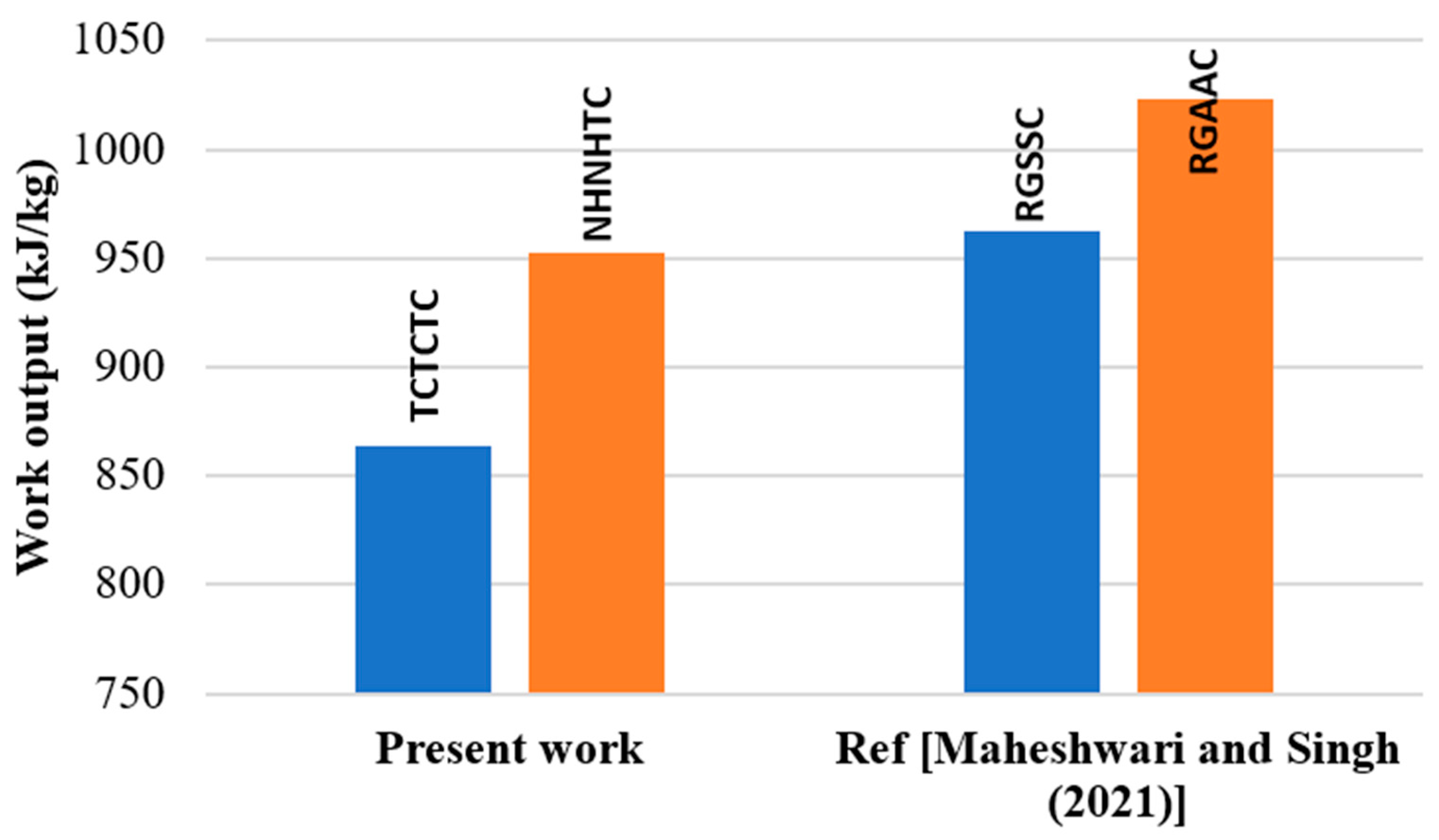
| NHNHTC | First-law efficiency (%) | 58.45 | 54.8 | 6.07 | Ref. [47] |
| NHNHTC | % Carbon reduction | 15 | 14.3 | 4.60 | Ref. [43] |
| NHNHTC | Work output (kJ/kg) | 952.3 | 981.2 | 2.94 | Ref. [46] |
| TCTCTC | Work output (kJ/kg) | 863.3 | 898.02 | 3.97 | Ref. [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maheshwari, M.; Shukla, A.K.; Rathore, P.K.S.; Amar, A.K. Thermodynamic Assessment of Carbon Capture Integration in Reheat Gas Turbine Combined Cycles Using Transcritical CO2 and Ammonia–Water Mixtures. Energies 2025, 18, 5642. https://doi.org/10.3390/en18215642
Maheshwari M, Shukla AK, Rathore PKS, Amar AK. Thermodynamic Assessment of Carbon Capture Integration in Reheat Gas Turbine Combined Cycles Using Transcritical CO2 and Ammonia–Water Mixtures. Energies. 2025; 18(21):5642. https://doi.org/10.3390/en18215642
Chicago/Turabian StyleMaheshwari, Mayank, Anoop Kumar Shukla, Pushpendra Kumar Singh Rathore, and Arbind Kumar Amar. 2025. "Thermodynamic Assessment of Carbon Capture Integration in Reheat Gas Turbine Combined Cycles Using Transcritical CO2 and Ammonia–Water Mixtures" Energies 18, no. 21: 5642. https://doi.org/10.3390/en18215642
APA StyleMaheshwari, M., Shukla, A. K., Rathore, P. K. S., & Amar, A. K. (2025). Thermodynamic Assessment of Carbon Capture Integration in Reheat Gas Turbine Combined Cycles Using Transcritical CO2 and Ammonia–Water Mixtures. Energies, 18(21), 5642. https://doi.org/10.3390/en18215642







