State of Health Aware Adaptive Scheduling of Battery Energy Storage System Charging and Discharging in Rural Microgrids Using Long Short-Term Memory and Convolutional Neural Networks

Abstract

This study presents a novel LSTM–CNN-based adaptive scheduling framework (LSTM-CNN–AS) designed to improve real-time energy management and extend the lifespan of lithium-ion Battery Energy Storage Systems (BESS) in rural and resource-constrained microgrids. In contrast to conventional methods that prioritize economic optimization, the proposed framework incorporates state of health (SOH) aware control and adaptive closed-loop scheduling to enhance operational reliability and battery longevity. The architecture combines Long Short-Term Memory (LSTM) and Convolutional Neural Networks (CNN) for accurate SOH estimation, with lightweight Multi-Layer Perceptron (MLP) models supporting real-time scheduling and state of charge (SOC) regulation. Operational safety is maintained by keeping SOC within 20–80% and SOH above 70%. The proposed model training and validation are conducted using two real-world datasets: the Mendeley Lithium-Ion SOH Test Dataset and the DKA Solar System Dataset from Alice Springs, both sampled at 5-min intervals. Performance is evaluated across three operational scenarios, which are 2C charging with random discharge; random charging with 3C discharge; and fully random profiles, achieving up to 44% reduction in MAE and an R²; score of 0.9767. A one-month deployment demonstrates a 30% reduction in charging time and 40% lower operational costs, confirming the framework’s effectiveness and scalability for rural microgrid applications.

1. Introduction

Renewable energy adoption has accelerated across rural Australia, with photovoltaic systems (PV) emerging as a predominant source of electricity generation. As of 2024, PV installations contribute approximately 23% of the Northern Territory’s microgrid capacity, with a governmental target of achieving 50% renewable energy penetration by 2030 [1]. However, the integration of intermittent renewable resources poses several operational challenges, including frequency deviations, voltage instability, and peak demand stress, all of which threaten the reliability and stability of isolated grids. Battery Storage System (BESS) have been widely recognized as key enablers of renewable energy integration, offering the capability to buffer surplus energy and supply it during periods of shortfall. Nevertheless, the deployment of BESS in remote regions such as the Northern Territory is constrained by substantial logistical costs, limited infrastructure, and technical resource limitations. These constraints necessitate the adoption of advanced and efficient grid-BESS coordination strategies to ensure stable and economical system operation [2,3]. A range of control and optimization strategies have been investigated to address these challenge, including active power control, frequency regulation, and flexible load management [4,5,6]. Among these, flexible load control has demonstrated the most promising potential due to its ability to dynamically adjust demand-side consumption patterns in real time without compromising occupant comfort or critical services. Unlike conventional demand-side management approaches, flexible loads such as HVAC systems, electric vehicle chargers, and smart appliances can be temporally shifted or curtailed in accordance with grid conditions and renewable generation profiles. This demand-side flexibility enhances grid responsiveness and reduces dependence on costly peaking generators. In resource constrained environments, flexible load management also offers a cost-effective alternative to extensive infrastructure upgrades, alleviating the burden on transmission and distribution systems. It facilitates higher penetration of variable renewables while maintaining power quality and reliability. Furthermore, effective BESS integration can be augmented through strategies such as optimized charge/discharge scheduling, predictive maintenance, and accurate estimation of the state of charge (SOC) and state of health (SOH), thereby prolonging battery lifespan and ensuring operational resilience [7]. Therefore, investigating BESS charging and discharging scheduling in conjunction with load flexibility is essential for optimizing energy distribution between the grid and BESS.

The remaining sections of this research paper are organized as follows: Section 2: Related Work will critically review existing research on smart grid and BESS distribution techniques, with particular emphasis on the methodologies employing closed-loop control strategies. Section 3: Research Gap and Contribution will systematically analyze the current limitations in these approaches and present the novel methodology proposed in this study to address the identified gaps. Section 4: Electricity Distribution State of Art analyzes energy usage behavior and energy harvesting in a local town in Alice Springs, Northern Territory, Australia. Section 5: Methodology presents the proposed scheduling system, including SOH model estimation, the MLP-Power for scheduling BESS charging and discharging, and the MLP-SOC model for supervising and validating MLP-Power mismatches. Additionally, the methodology outlines the preprocessing of raw data and the evaluation approaches used to assess each component of the proposed scheduling system, ensuring accuracy and reliability in energy management. The Section 6: Result and Discussion section displays the experimental result and analyzes the robustness and efficiency of the LSTM-CNN–AS framework. Lastly, the Section 7: Conclusion section will summarise and evaluates whether the framework achieved the research aims.

2. Related Works

In the domain of BESS charging and discharging scheduling, most studies concentrate on optimization strategies, such as enhancing energy forecasting models and employing bio-inspired optimization techniques. Notably, more than 80% of research focuses on linear programming and smart meter integration, primarily assessing peak demand variations and conducting economic evaluations to refine charging and discharging operations. By contrast, only 20% of studies focus on data-driven methodologies, while merely 5% explore closed-loop machine learning techniques, highlighting a substantial research gap in adaptive and intelligent BESS management.

As shown Table 1, Sridhar Chouhan et al. employed a linear programming approach to define the operational limits of active power, peak shaving constraints, SOC, and discharge restrictions [8]. This method provides an optimized power management strategy; however, its reliance on predefined constraints and a limited feedback mechanism reduces its adaptability to real-time fluctuations and uncertainties in energy demand and supply. The rigidity poses significant challenges in accommodating dynamic variations, including fluctuations in renewable energy generation, shifts in load demand, and unforeseen system disturbances. Similarly, the convolutional neural network long short-term memory (CNN-LSTM) model proposed by M. A. Tovar Rosas integrates CNNs with LSTM networks to capture spatiotemporal dependencies in energy forecasting and optimization [9]. While this hybrid approach demonstrates strong predictive capabilities, it also exhibits high computational complexity. Additionally, it does not incorporate a real-time feedback mechanism to dynamically adjust predictions on the basis of evolving system conditions, thereby limiting its ability to address uncertainty effectively. In the context of rural microgrids, these computational demands pose significant barriers due to limited edge computing resources and unreliable communication links. The absence of adaptive feedback mechanisms may reduce its robustness when deployed in practical, large-scale energy management systems. In addition, R. Moslemi et al. introduced a clustering-based method for energy management that segments operational states based on historical data patterns [10]. This technique enhances system understanding by identifying key operational regimes, which can be leveraged for improved forecasting and optimization. However, the framework’s primary limitation lies in its inability to learn and adapt to real-time variations, as seen in time-series neural network models. Additionally, the framework lacks a feedback mechanism, which restricts its capacity to dynamically adjust predictions based on evolving system conditions.

In additional, D. Khoury et al. [11] introduced an intelligent energy management system designed to mitigate blackouts and preserve battery SOH. The proposed system maintained SOH at approximately 33% and reduced blackout occurrences by 56% compared with a classical energy management system. However, the framework lacks adaptive feedback capabilities, limiting its ability to respond effectively to sudden uncertainties or dynamically adjust control strategies in real time. Lastly, M. G. M. Abdolrasol et al. [12] integrated a binary particle swarm optimization algorithm to optimize an artificial neural network (ANN) based scheduling controller for managing renewable energy resources in a virtual power plant. This approach is an effective means of enhancing the decision-making accuracy of the ANN controller. However, the training process required 8 h, 57 min, and 12 s, which presents scalability challenges when applied to larger datasets and limits feasibility for real-time adaptive feedback control. Moreover, the study does not address how the framework handles sudden uncertainties or operational deviations.

Hybrid deep learning architectures such as convolutional neural network–bi-directional long short-term memory (CNN-Bi-LSTM) and CNN-LSTM have been extensively applied to state-of-health (SOH) prediction, demonstrating strong capabilities in extracting complex degradation features and capturing long-term temporal dependencies that traditional statistical or shallow models often fail to represent [13,14]. These models are particularly effective for handling sequential battery data, enhancing predictive accuracy under diverse operating conditions, and extending the forecasting horizon. However, these benefits come at the cost of increased architectural complexity, longer training times, and higher computational demands, which limit scalability and hinder real-time deployment. Moreover, their dependence on large volumes of high-quality labeled data makes them sensitive to noise, imbalance, and domain transfer challenges.

Recent studies [15,16] have shown that machine learning–based control strategies can achieve significant operational gains, including an 18% increase in prosumer energy utilization and a 30% improvement in stacked net revenue. Despite these advances, key limitations remain. For instance, the RNN-based framework in [15] prioritizes predictive accuracy but does not incorporate downstream control objectives such as active power compensation or SOH balancing. Similarly, while [16] reports considerable economic benefits, the absence of a closed-loop control framework restricts the system’s ability to adapt effectively to real-time operational deviations. These gaps underscore the need for machine learning–driven control architectures that are explicitly embedded within adaptive closed-loop mechanisms to enhance robustness and reliability, particularly given the wide diversity of lithium-ion chemistries [17] and their dynamic operational characteristics. By continuously assessing and updating estimated remaining capacity in real time, closed-loop control strategies can adapt to evolving battery behaviors and optimize operation, thereby extending system lifetime and enabling more reliable deployment across a range of applications. In this regard, multilayer perceptron (MLP)–based controllers have recently emerged as lightweight yet effective alternatives for closed-loop battery energy storage system (BESS) operation. By approximating nonlinear system dynamics, MLPs can deliver control accuracy [18] comparable to model predictive control (MPC) while requiring substantially fewer computational resources. This trade-off is particularly advantageous in rural or resource-constrained regions, where access to high-performance computing infrastructure is limited. The combination of real-time adaptability and reduced complexity positions MLP-driven control as a practical pathway toward reliable and efficient energy management in such contexts, where computational efficiency is as critical as predictive accuracy. Furthermore, while machine learning–based charging and discharging strategies hold promise, their effectiveness often hinges on accurately identifying peak demand periods within distribution networks. Many existing approaches [19,20] rely on deterministic or rule-based thresholds, which may inadequately capture the variability of real-world load patterns. In contrast, unsupervised learning methods such as clustering [21] offer more flexible and data-driven tools for uncovering latent structures in demand profiles. Incorporating such methods into BESS control frameworks could further enhance load balancing, mitigate grid stress, and improve the economic viability of distributed energy systems.

Complementing these efforts, recent work [22] has advanced second-life battery management by leveraging deep generative transfer learning frameworks to synthesize voltage dynamics and perform domain alignment, effectively addressing challenges of data scarcity and heterogeneity in relative remaining capacity estimation. While such methods demonstrate strong performance in predictive estimation, our work diverges by prioritizing a closed-loop control perspective. Specifically, we employ datasets from lithium-ion batteries to forecast the SOH of lithium-ion–based BESS under diverse current profiles, ensuring that the model can accommodate heterogeneous aging behaviors and limited data availability. Unlike offline prediction approaches, our framework integrates machine learning models directly within the control loop, allowing predictions to be continuously refined with real-time feedback. Furthermore, this integration enables adaptive decision-making that not only estimates system states but also dynamically optimizes operational strategies. By grounding control decisions in continuously refreshed data, the framework simultaneously enhances adaptability and mitigates the challenges of data scarcity and heterogeneity as they arise in practice. Crucially, in rural regions where electricity supply is highly sensitive to environmental fluctuations and user behavior, this adaptive closed-loop architecture strengthens system resilience. By stabilizing power delivery under uncertain conditions, the proposed approach reduces degradation risks and enhances long-term reliability, ultimately ensuring more consistent and sustainable access to electricity.

Table 1. Comparison of different BESS control frameworks and techniques.

Framework Name	Scheduling Technique	Input Parameter	ML Model Applied	Adaptive Closed Loop Control
BESS charge, discharge schedule using linear programming [8]	Linear programming (software control)	Electric demand, economics	No	No
Itineraries for charging and discharging a BESS using energy predictions based on a CNN-LSTM model [9]	CNN-LSTM	Electric demand, diffuse horizontal irradiance, global horizontal irradiance, wind speed, temperature, atmospheric pressure	Yes	No
Demand charge management solution [10]	Clustering	Electric demand, electricity price	Yes	No
Intelligent energy management system [11]	ANN	Cycle charging, load following and combined dispatched	Yes	No
Artificial neural network based particle swarm optimization [12]	ANN	Time, solar, wind speed, grid hourly prices and SOC	Yes	No
Hybrid PV-BESS-grid integrated fast EV charging stations [23]	Linear programming (hardware control) and snake optimization tuning	Power of EV, BESS, grid and PV	No	Yes
Smart control of BESS in PV integrated EV charging station [24]	Linear programming	power demand, power electric vehicle, power BESS	No	No

Table 1. Comparison of different BESS control frameworks and techniques.

Framework Name	Scheduling Technique	Input Parameter	ML Model Applied	Adaptive Closed Loop Control
BESS charge, discharge schedule using linear programming [8]	Linear programming (software control)	Electric demand, economics	No	No
Itineraries for charging and discharging a BESS using energy predictions based on a CNN-LSTM model [9]	CNN-LSTM	Electric demand, diffuse horizontal irradiance, global horizontal irradiance, wind speed, temperature, atmospheric pressure	Yes	No
Demand charge management solution [10]	Clustering	Electric demand, electricity price	Yes	No
Intelligent energy management system [11]	ANN	Cycle charging, load following and combined dispatched	Yes	No
Artificial neural network based particle swarm optimization [12]	ANN	Time, solar, wind speed, grid hourly prices and SOC	Yes	No
Hybrid PV-BESS-grid integrated fast EV charging stations [23]	Linear programming (hardware control) and snake optimization tuning	Power of EV, BESS, grid and PV	No	Yes
Smart control of BESS in PV integrated EV charging station [24]	Linear programming	power demand, power electric vehicle, power BESS	No	No

3. Research Gap and Contribution

LSTM-CNN SOH Forecasting Model

Previous research from the Related Works section has primarily focused on improving the precision of mathematical programming and machine learning models to optimize the charging and discharging schedules of BESS. These studies predominantly emphasize economic efficiency, aiming to minimize costs and maximize revenue. However, limited attention has been given to the functional longevity of BESS and the implementation of closed-loop control in scheduling, both of which are essential for real-time adaptability and system stability. While these advancements enhance operational efficiency, they also introduce significant challenges for integration and control engineering due to high computational demands and concerns regarding environmental sustainability. This challenge is particularly critical in rural areas, as illustrated in Figure 1, specifically at the DKA Solar System Centre located in Alice Springs, Northern Territory, where access to advanced computing infrastructure is limited. In particular, during a representative operating period, solar generation reaches approximately 161.7 kW, of which 27.88 kW is consumed by the local load, 2.55 kW is stored in the BESS, and the remaining 131.27 kW is exported to the grid. These values represent the typical power flow distribution observed during daytime operation, providing the baseline for further system enhancement and integration. To address these gaps, this research proposes a novel approach known as LSTM-CNN adaptive scheduling (AS), as shown in Figure 2. The framework aims:

• A predictive SOH model integrating LSTM and CNN is proposed to improve BESS longevity. The LSTM captures long-term dependencies in degradation trends, while the CNN extracts local spatial features. This hybrid architecture enables accurate SOH estimation with low computational overhead, suitable for real-time deployment in resource-constrained environments.
• A closed-loop control framework based on two multilayer perceptron (MLP) models is developed to optimize BESS operations. Compared with alternative strategies, reinforcement learning (RL) requires extensive environment interaction and reward supervision, making it sensitive to noise and highly fluctuating user behavior, which can lead to unstable or inefficient training in real-world microgrids. Model predictive control (MPC), while theoretically powerful, imposes substantial computational demands that limit real-time feasibility. In contrast, MLPs provide a lightweight, feedforward architecture capable of capturing complex nonlinear relationships, achieving rapid inference, and generalising effectively under unseen or noisy conditions. Within this framework, MLP-Power regulates charge/discharge cycles, maintaining SOC between 20–80% and SOH above 70%, while balancing grid and renewable energy supply. Simultaneously, MLP-SOC detects scheduling mismatches and updates system actions in real time, enhancing reliability, efficiency, and operational resilience.
• Model robustness is validated under three degradation scenarios: 2C_Random, Random_3C, and Random_Random. The scheduling system is assessed using real-time data, comparing system performance with and without the proposed method. Evaluation metrics include charging/discharging profiles, revenue, net power, and weekly SOH fluctuation, demonstrating improved efficiency and scheduling accuracy.

4. Electricity Distribution Optimization via Load Clustering and Peak Shaving

Two key factors must be examined before integrating the control framework into the BESS system in the Northern Territory which are environmental impacts and user behaviours. Variations in humidity, wind direction, and global solar radiation can influence not only the electricity generation of photovoltaic systems but also the behaviour of end users in response to environmental conditions. These changes can affect how and when energy is consumed, directly impacting the BESS system’s ability to effectively manage community loads. A thorough understanding of user behaviour, particularly under varying environmental scenarios, is essential for identifying operational constraints and optimising peak shaving strategies during the BESS system’s charging and discharging cycles. This study applies Pearson and Spearman correlation analyses to examine the linear and nonlinear relationships within the DKA PV datasets and Site Demand datasets [25], an open access platform share quality data related to solar power located in the Northern Territory, Australia. As illustrated in Figure 3, solar radiation emerges as the most influential weather variable affecting the active power output of the PV system, while other environmental factors show only weak or negligible correlations. Additionally, Figure 4 confirms that solar radiation consistently maintains a moderate impact on active power trends. 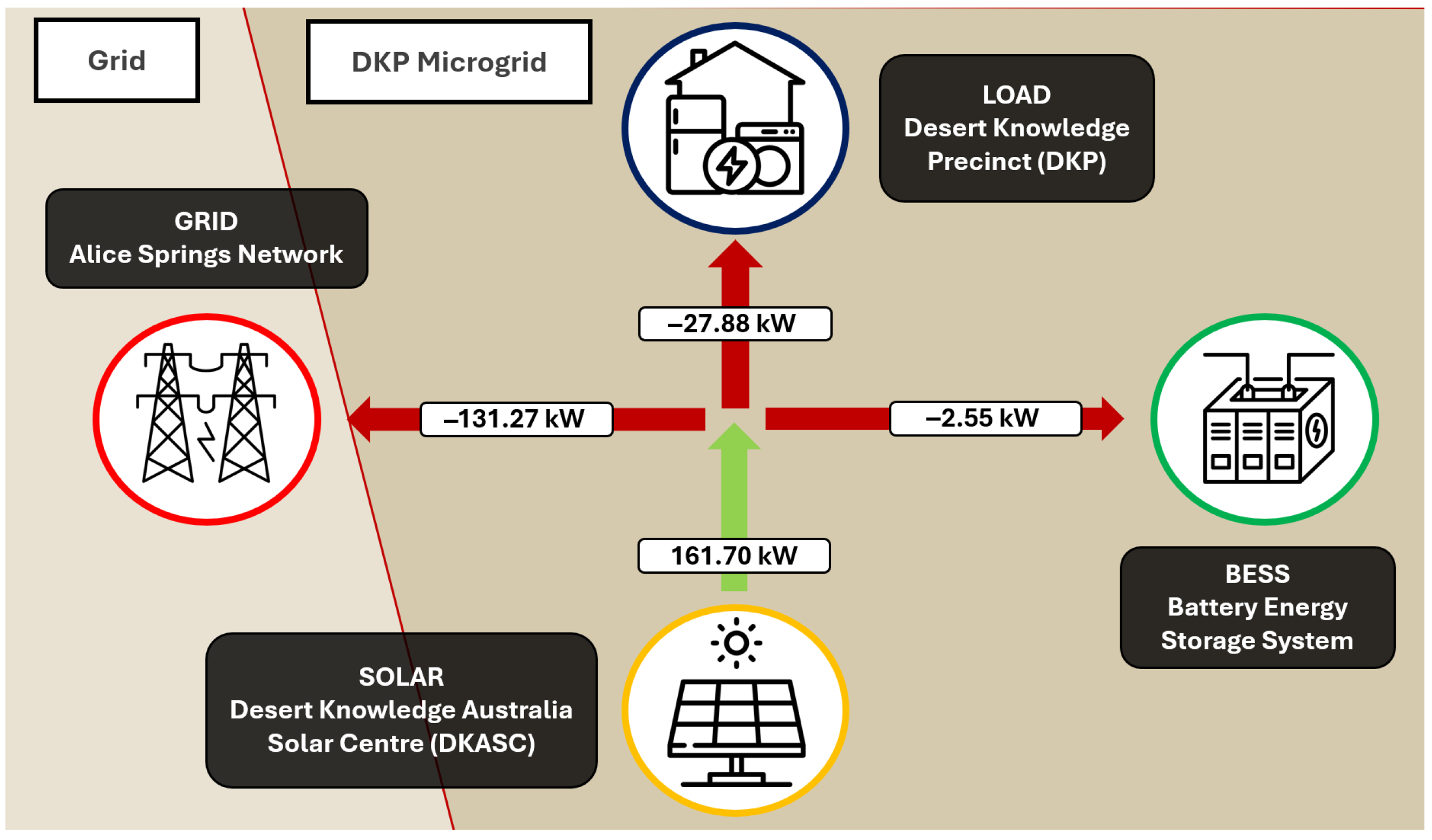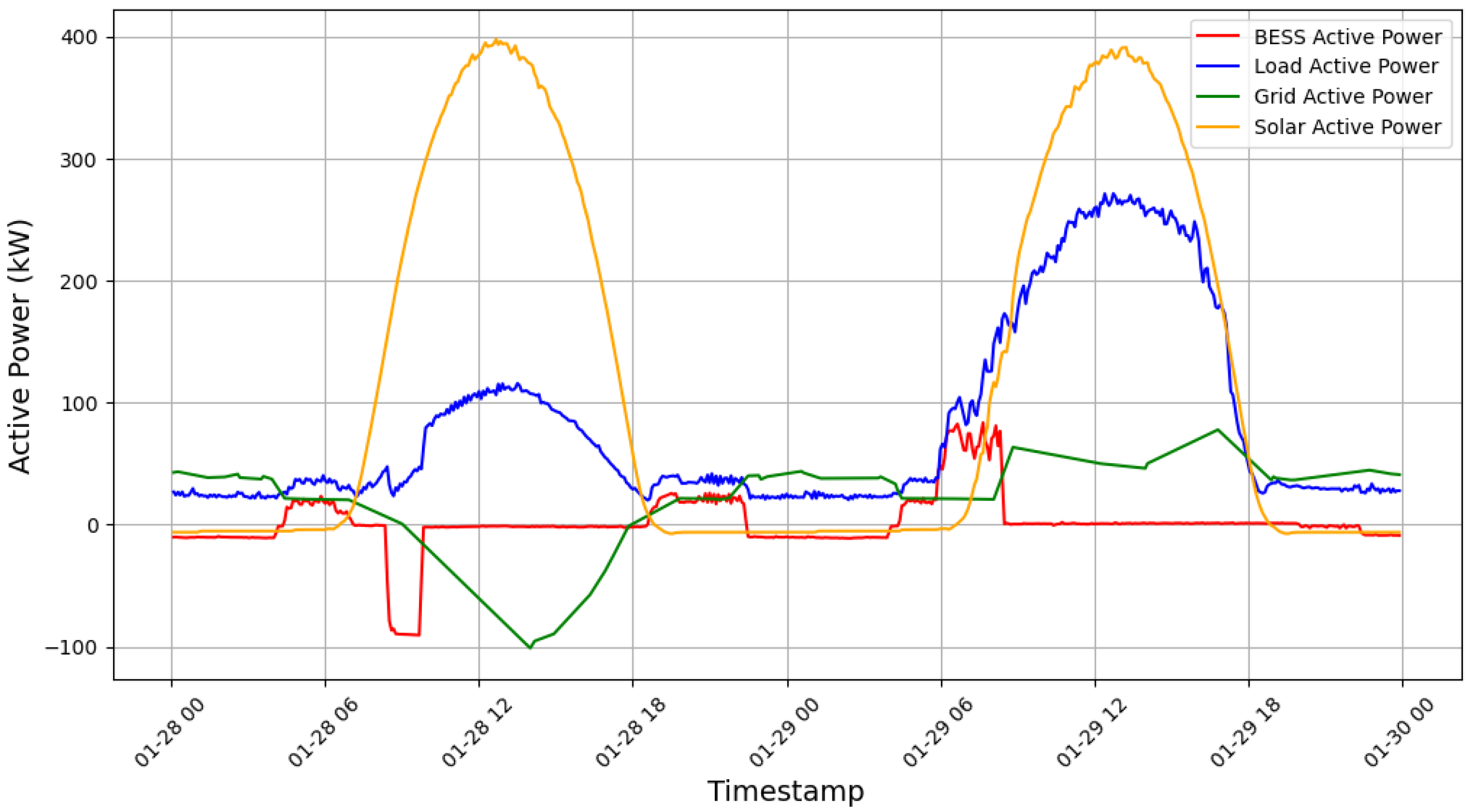From Figure 5, at the DKA Solar System Centre, the most significant electricity production and distribution occur between 6:00 a.m. and 6:00 p.m., with a pronounced increase from 6:00 a.m. to 12:00 p.m., followed by a gradual decline until 6:00 p.m. On 28 January during the early morning rise period (7:00 a.m. to 9:00 a.m.), the BESS begins charging, coinciding with sudden increases in load demand and limited solar generation. During the evening peak load period (6:00 p.m. to 9:00 p.m.) on the same day, when active power demand is high and solar generation is insufficient, the BESS discharges actively to support the photovoltaic system, ensuring load demands are met and contributing to grid stability by mitigating potential power deficits.

Based on the analysis of energy usage characteristics at the DKA Solar System Centre, this study introduces several mathematical constraints related to peak shaving to construct the LSTM-CNN–AS control framework:

• SOH and SOC Constraints: The BESS system operates under strict constraints to ensure long-term reliability and prevent performance degradation. A minimum SOH of 70% is enforced, while the SOC is maintained within the 20–80% range to preserve battery efficiency and life span.
• Discharging Priority: The framework prioritizes discharging power to supply local loads and export to the grid. This approach ensures power adequacy during peak demand periods and contributes to maintaining stability within the microgrid.
• Operational State Clustering: Given the observed pattern similarities among key variables, the study applies a clustering algorithm to classify the BESS, PV, and Site Demand active power values alongside solar radiation into three distinct operational states: charging (+1), discharging (–1), and idle (0). This clustering method enables adaptive scheduling and control under varying solar and demand conditions. The mathematical of operation clustering could be derive as:

$$C_{-1}=\left\{x_i\in X\mid f\left(x_i\right)=-1\right\}$$

(1)

$$C_0=\left\{x_i\in X\mid f\left(x_i\right)=0\right\}$$

(2)

$$C_{+1}=\left\{x_i\in X\mid f\left(x_i\right)=+1\right\}$$

(3)

where $f:X\to \{-1,0,+1\}$ be a function that maps each data point to a system state, $x_i$ is a single data point from the dataset, $C_{-1}$ is the set of data points in the discharging state, $C_0$ is the set of data points in the idle state, and $C_{+1}$ is the set of data points in the charging state. A consecutive state counting strategy is employed to mitigate excessive and repetitive charging activity. This technique systematically tracks the sequential occurrences of identical system states, specifically charging and discharging events within the clustered data. By quantifying these consecutive patterns, the method enables the identification and suppression of prolonged or frequent transitions that may indicate operational inefficiency. The mathematical formulation of this clustering informed counting mechanism is presented as follows:

$$C_i=\left\{\begin{array}{cc}{C}_{i-1}+1,\hfill & \mathrm{if}{S}_i=S_{i-1}\wedge S_i\ne 0\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

where $C_i$ is the count of consecutive charging/discharging events at time step i, $S_i\in \{-1,0,1\}$ denotes the BESS state (discharging, idle, charging) and only non-idle states ($S_i\ne 0$) are counted.

5. Methodology

In this section, the research paper introduces the architecture of the LSTM-CNN–AS framework and the datasets used for training. This approach includes integrating an SOH model to forecast battery health and life span while analyzing battery charging and discharging cycles. Additionally, two MLP models are designed to control the charging power target SOH and SOC and validate SOC the BESS, forming a closed-loop control system. The proposed framework is verified using two approaches: SOH model benchmarking and systematic benchmarking, ensuring a comprehensive evaluation of its performance.

5.1. Data Preparation

This paper utilizes two data collections: the DKA Solar System dataset [25] located in Alice Springs, Northern Territory and the Mendeley dataset—Lithium-Ion Laboratory SOH Test [26]. The Mendeley Dataset is used to forecast the SOH of lithium-ion-based BESS systems, while the DKA Solar System dataset is used to train and evaluate the scheduling and charging behavior of the MLP control model. Both data collections were recorded at 5-min intervals to ensure consistent temporal resolution. Each data collection was split, with 80% used for training and 20% for testing. Several preprocessing steps are applied to prepare the Mendeley dataset for SOH prediction. First, type labeling is performed to identify charging (−1), discharging (1), and idle (0) states, followed by counting consecutive occurrences of each state. SOH is calculated as the ratio of the current capacity to the nominal capacity of the battery, whereas the SOC for each cycle is determined using the corresponding maximum capacity column. A unique battery ID is generated for tracking purposes. The dataset is filtered to maintain 5-min intervals, ensuring compatibility with the DKA dataset. The data are kept in sequential order to preserve the time-series structure and grouped into categories: 2C_Random, Random_3C, and Random_Random. The 2C_Random category corresponds to charging at 2C rate and discharging at a random rate. In the Random_Random category, both charging and discharging occur at random rates. The Random_3C is applied the charging rate being variable and the discharge rate set to 3C rate.

The Mendeley contains degradation data from 77 nominally identical 18,650 lithium-ion batteries manufactured by LISHEN, with positive electrodes of LiCoO₂ + LiNi_0.5Co_0.2Mn_0.3O₂ and graphite negative electrodes [27]. Each battery has a rated capacity of 2.4 Ah, a nominal voltage of 3.7 V, and voltage limits of 3.0–4.2 V. Degradation tests were conducted at 25 °C, with charging/discharging within voltage limits and a 0.048 A cut-off current. For BESS optimization, the DKA Solar System dataset simulates charging and discharging under the same assumptions as the Mendeley tests, and the modeling remains reliable for any lithium-based battery, such as lithium iron phosphate, provided the framework is constrained to lithium-ion chemistries.

For the DKA Solar System dataset, preprocessing for the two MLP models predicting active power and SOC involves handling missing values, applying type labeling, and creating a column to count consecutive occurrences of charging, discharging, or idle states. Additionally, two columns are introduced to store the SOC and SOH values from the previous time step, along with a column that captures the difference between the current and previous SOC values. In the DKA Solar System dataset, linear interpolation fills missing values by drawing a straight line between adjacent non-missing points, followed by the removal of any remaining NaN rows. Only data before 1 June 2025, are analyzed, as values beyond this date are unavailable. Additionally, an SOH column is generated using the SOH prediction model to enhance charge and discharge scheduling, ensuring more efficient energy management in the system.

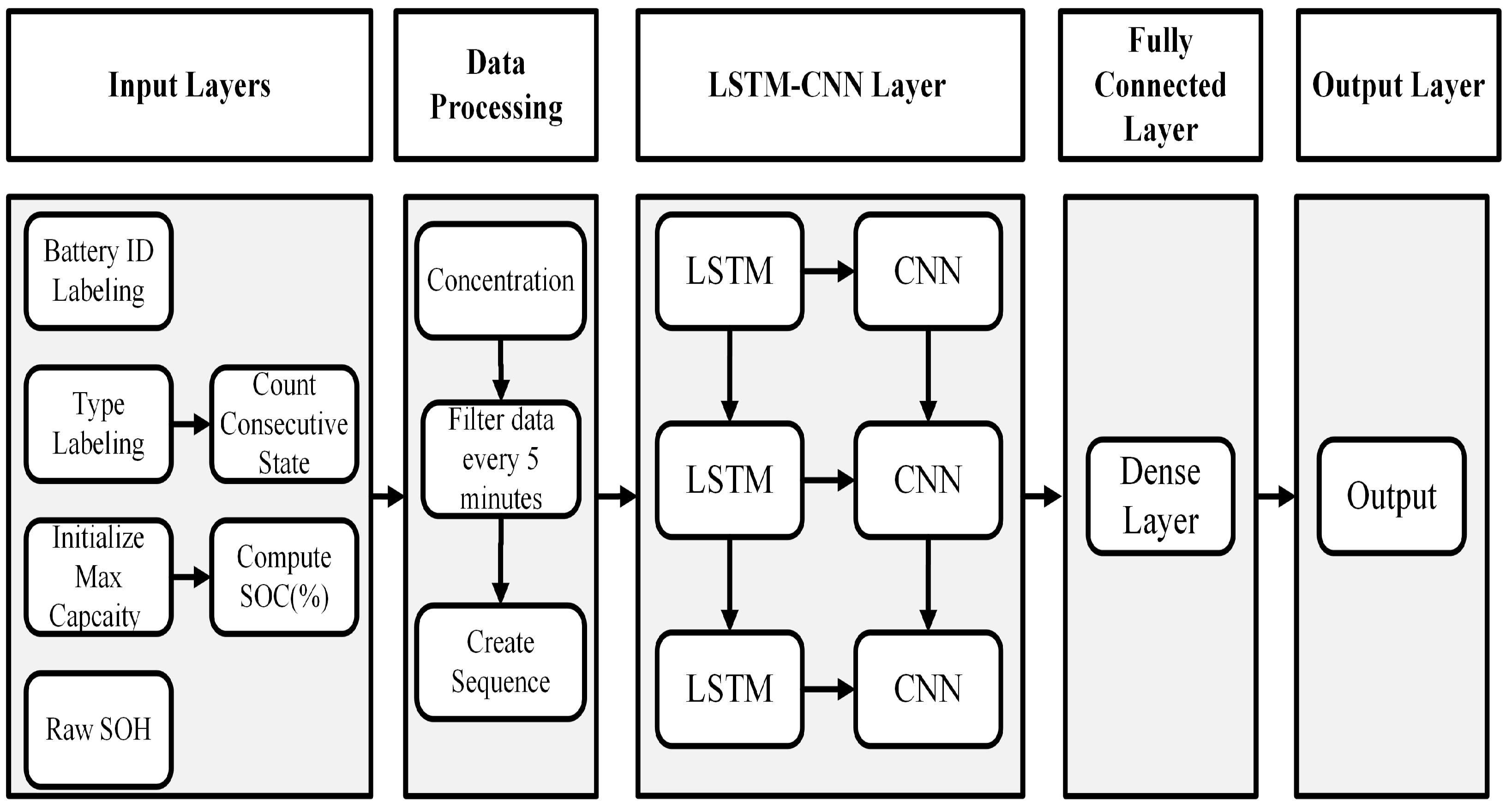
This paper proposes an LSTM-CNN model to forecast the SOH of lithium-based BESS, illustrated in Figure 6. The LSTM cell is designed to retain information related to long-term dependencies and patterns within an input sequence. The LSTM $i^{th}$ cell at layer m consists of two output cell states ($c_i^m$), the hidden state ($h_i^m$), and three inputs, which are the hidden state of the previous cell ($h_{i-1}^m$), previous cell state ($c_{i-1}^m$), and input data ($h_i^{m-1}$). The flow of information into and out of the memory cell is governed by gating mechanisms, which play a critical role in controlling the internal state of the cell [28,29]. These gates employ sigmoid activation functions followed by element-wise multiplication operations, enabling the network to learn which information to retain and discard. The LSTM architecture comprises three primary gates: the input gate ($i{g}_i^m$), the forget gate ($f{g}_i^m$), and the output gate ($o{g}_i^m$). The input gate controls the incorporation of new information into the cell state, while the output gate determines the extent to which the cell state contributes to the hidden state at each time step. The forget gate decides which components of the previous cell state should be preserved or discarded, thereby enabling the model to effectively manage long-term dependencies and prevent the accumulation of irrelevant information over time [30]. The LSTM cell equations can be derived as [31]:

$${(h}_i^m,c_i^m)=C(h_{i-1}^m,c_{i-1}^m,h_i^{m-1}).$$

(5)

$${{\mathrm{ig}}_i^m(h}_{i-1}^m,h_i^{m-1})=\sigma ({w_{ig,m-1}h}_i^{m-1}-{w_{ig,m-1}h}_{i-1}^m,+b_{ig}),$$

(6)

$${{\mathrm{fg}}_i^m(h}_{i-1}^m,h_i^{m-1})=\sigma ({w_{fg,m-1}h}_i^{m-1}-{w_{fg,m-1}h}_{i-1}^m,+b_{fg}),$$

(7)

$${{\mathrm{og}}_i^m(h}_{i-1}^m,h_i^{m-1})=\sigma ({w_{og,m-1}h}_i^{m-1}-{w_{og,m-1}h}_{i-1}^m,+b_{og}),$$

(8)

where $w_{ig,m-1}$, $w_{fg,m-1}$, $w_{og,m-1}$, $b_{ig}$, $b_{fg}$, $b_{og}$ is the weights that update continuously, during training and $\sigma$ is the sigmoid function. The returned cell state and hidden state are derived as Equations (9) and (10):

$$c_i^m=f{g}_i^m·c_{i-1}^m·{ug}_i,$$

(9)

$$h_i^m=o{g}_i^m·tanh\left(c_i^m\right).$$

(10)

Following the LSTM layer, a CNN layer is integrated to process the resulting sequence of hidden states, thereby enhancing the model’s ability to extract meaningful features. While LSTM networks are well suited for capturing long-term temporal dependencies, they may fail to detect localized variations and transient patterns critical to accurate battery health assessment [32]. CNNs address this limitation by applying localized filters that extract fine-grained features across the temporal dimension. This layered architecture leverages the complementary strengths of both models, resulting in improved robustness, sensitivity to subtle signal changes, and overall predictive accuracy in SOH estimation. The CNN operation is mathematically expressed as [32]:

$$y_i=\sum _{k=0}^{K-1}{w}_k·h_{i+k}+b$$

(11)

where $y_i$ is the output feature at position i, $h_{i+k}$ represents the input hidden states from the LSTM, $w_k$ are the filter weights, K is the kernel size, and b is a bias term. In addition, the model hyperparameters, including 128 LSTM cells and 16 CNN filters, were systematically optimized through grid search combined with cross-validation on the training set to maximize predictive performance. This rigorous approach provides transparency in model selection and ensures that both the architecture and training procedure can be reliably reproduced and benchmarked in future studies.

The model was trained using the mean squared error (MSE) loss function and the Adam optimization algorithm, selected for their effectiveness in regression-based learning tasks. MSE defined as the average of the squared differences between predicted and actual values, emphasizes larger errors, thereby promoting precise convergence during optimization. Although MSE is sensitive to outliers, its mathematical simplicity and consistent gradient behavior contribute to stable training dynamics in continuous-valued prediction problems. The Adam optimizer, initialized with a learning rate of 0.001, adaptively updates individual learning rates based on first and second-order moment estimates of the gradients. This approach facilitates faster convergence and enhanced stability in the presence of sparse or noisy gradients. As illustrated in

Table 2. Model components and corresponding hyperparameters.

Component	Hyperparameter	Value
LSTM	Units	128
Conv1D	Filters	16
	Activation	ReLU
Dense (1)	Units	128
	Activation	RelU
Dense (2)	Units	1
Optimizer	Type	Adam
	Learning rate	0.001
Training	Batch size	32
	Epochs	50
Loss Optimisation		MAE

, the model training was conducted over 50 epochs with a batch size of 32, providing a practical balance between convergence speed and generalization capability. The choice of 50 epochs allows the model sufficient iterations to learn underlying patterns in the data without overfitting, while the batch size of 32 is commonly used in deep learning due to its efficient use of memory and ability to stabilize gradient updates. This combination of loss function, optimizer, and training configuration ensured efficient learning and improved predictive performance across the dataset.

5.2. SOH Forecasting Model Benchmark

This section presents the architecture and advantages of currently utilized models in the SOH prediction field. These models serve as benchmarks for performance comparison with the proposed LSTM-CNN model, facilitating a comprehensive evaluation of its predictive capabilities.

5.2.1. M-LSTM

The Multilayered LSTM model is a stack of m layers of LSTM cells. This multilayered architecture enhances the model’s capacity to capture complex temporal dependencies by learning hierarchical representations of sequential data [32]. Lower layers tend to extract short-term patterns, while higher layers focus on more abstract, long-range dependencies. This depth allows the model to better generalize across varying input dynamics, improving robustness and predictive accuracy. Additionally, the stacked structure increases the expressive power of the network, enabling it to model intricate relationships that may not be captured by a single-layer LSTM, particularly in high-dimensional or noisy datasets.

5.2.2. M-LSTM-SA

The M-LSTM with self attention (SA) is an advanced architecture that enhances the standard M-LSTM model by integrating a self-attention mechanism to better capture long-range dependencies and the relative importance of time steps in sequential data [32]. While M-LSTM learns hierarchical temporal features by stacking multiple LSTM layers, the self-attention layer further improves performance by dynamically assigning weights to each time step based on their relevance to the prediction task [32]. In SOH forecasting, this combination improves temporal sensitivity, enabling the model to focus on the most informative historical points. It also enhances robustness to noise and irregularities by reducing reliance on local patterns, and contributes to model interpretability by identifying critical time steps through attention weights. The SA mechanism can be derived as [32]:

$${\mathrm{SA}}_i=\sum _{j=1}^T{\alpha }_{ij}{V}_j$$

(12)

where ${\alpha }_{ij}$ is the attention weight, and $V_j$ is the value vector.

5.2.3. Bi-LSTM

Bi-LSTM is an advanced recurrent neural network variant, it captures both past and future dependencies in sequential data by integrating two LSTM layers operating in opposite directions; one from past to future and the other from future to past. This bidirectional structure enhances contextual information retention, making it particularly effective for time-series forecasting of BESS SOH dynamics [33]. The forward LSTM cell processes the hidden state, cell state, and input sequence from past to future. Meanwhile the backward LSTM cell processes the hidden state, cell state, and input sequence, but in reverse order, moving from future to past to capture future context dependencies. Finally, hidden states from both directions are combined to form the final output in Equation (13) [33].

$$(h_i^f,c_i^f)=\mathrm{LSTM}(h_{i-1}^f,c_{i-1}^f,x_i)(h_i^b,c_i^b)=\mathrm{LSTM}(h_{i+1}^b,c_{i+1}^b,x_i)$$

(13)

where at each time step i, the forward LSTM processes the sequence from left to right, producing a hidden state $h_i^f$ and cell state $c_i^f$ based on the previous hidden and cell states along with the current input $x_i$. Simultaneously, the backward LSTM processes the sequence from right to left, generating $h_i^b$ and $c_i^b$ from future states and the same input $x_i$.

5.2.4. Bi-LSTM–CNN

The Bi-LSTM–CNN model combines the strengths of both Bi-LSTM and CNNs, integrating temporal sequence learning with efficient feature extraction. The Bi-LSTM component captures long-range dependencies and temporal dynamics from both past and future time steps, which is particularly beneficial for modeling the nonlinear and time-dependent nature of battery degradation [34]. Meanwhile, the CNN component enhances the model’s ability to automatically extract local patterns and spatial correlations from multivariate time-series data. This hybrid architecture improves the robustness, accuracy, and generalization of SOH forecasting, especially under varying operational conditions, aging mechanisms, and sensor noise [35].

5.2.5. ANN

The ANN model presents several advantages that make it a valuable tool in predictive modeling frameworks. Its relatively simple architecture supports rapid training and requires minimal computational resources, making it well suited for real-time applications or environments with constrained processing capacity. ANNs are particularly effective at modeling complex nonlinear relationships between input features and target variables, especially in datasets exhibiting strong static or cross-sectional patterns [36]. The structure of fully connected layers enables rich interactions among input features, thereby enhancing the model’s ability to learn intricate dependencies and improve predictive performance [37].

$$y=\varphi (Wx+b)$$

(14)

where x is the input vector, W is the weight matrix, b is the bias term, and $\varphi$ is a RELU activation function.

5.3. Adaptive Scheduling Framework

The proposed adaptive scheduling framework employs two distinct MLP models: one dedicated to estimating the active power requirement, denoted as MLP-Power, and another for real-time tracking and updating of the SOC, referred to as MLP-SOC. The MLP architecture is selected for its computational efficiency and scalability, offering rapid training convergence and minimal inference latency. Although architecturally lightweight, MLPs demonstrate a strong capability in modeling complex, non linear relationships within high-dimensional datasets, effectively capturing patterns without necessitating temporal dependencies [38].Furthermore, due to their simplicity and low computational overhead, MLPs are well suited for deployment on resource-constrained platforms such as embedded systems and FPGAs, enabling real-time inference in edge computing environments. Mathematically, both MLP models can be described as compositions of affine transformations and nonlinear activation functions [39], expressed as:

$$a^{\left(0\right)}=x$$

(15)

$$z^{\left(l\right)}=W^{\left(l\right)}{a}^{(l-1)}+b^{\left(l\right)},a^{\left(l\right)}={\sigma }^{\left(l\right)}\left(z^{\left(l\right)}\right),\mathrm{for}l=1,2,\dots ,L-1$$

(16)

$$y=f^{\left(L\right)}\left(z^{\left(L\right)}\right),\mathrm{where}{z}^{\left(L\right)}=W^{\left(L\right)}{a}^{(L-1)}+b^{\left(L\right)}$$

(17)

where x is the input vector; $a^{\left(l\right)}$ is the activation of layer l; ${\sigma }^{\left(l\right)}$ is the activation function at layer l; W and b are the weight matrix and bias vector at layer l and L, respectively; $f^{\left(L\right)}$ is the output activation function. The final output of the MLP is denoted by y. The MLP-Power model is constructed to estimate the active power input necessary to transition the battery system toward a specified target SOC and SOH. The input feature set includes the temporal change in SOC, the previously estimated SOH, and the current active power applied to the system. Leveraging these parameters, the model predicts the optimal power requirement, as shown in Figure 7. Additionally, MLP-SOC is utilized to infer the updated SOC based on the prior SOC and SOH values in conjunction with the present active power input, as illustrated in Figure 7. The predicted SOC from the MLP-SOC model will also be used to inform and allow the MLP-Active Power model to adjust the amount of power required for charging and discharging accordingly. This modeling approach facilitates both prospective power estimation and real-time SOC prediction, which are critical for adaptive scheduling in energy-constrained environments.

An intelligent closed-loop scheduling system is proposed to autonomously manage the charging and discharging cycles of a battery, with the principal objective of prolonging battery life span by preserving the SOH. The control strategy is governed by a scheduling algorithm, detailed in Algorithm 1, which dynamically orchestrates operational decisions based on real-time assessments of battery status. During discharge, the system continuously monitors and updates both the SOH and SOC, ensuring that the power delivered to the load adheres to predefined safety and performance constraints. In the charging phase, the system predicts and adjusts the charging power in a proactive manner to maintain the SOH above a critical threshold of 70%, while constraining the SOC within the optimal range of 20% to 80%. These operational bounds are selected to mitigate electrochemical degradation and extend the effective service life of the battery. Upon completion of each control cycle, essential system parameters, including SOH, SOC, active power, operational mode, system state, and the frequency of consecutive state occurrences are updated to enhance the accuracy of subsequent predictions. This adaptive mechanism ensures that the scheduling framework remains robust, responsive, and capable of optimizing performance under varying real-world conditions. The complete operational workflow of the system is illustrated in Figure 8.

Algorithm 1 Battery Scheduling Algorithm

1: Initialize columns for SOC, SOH, Type, Active Power, etc.   2: for $i=Lo$ to $step$ do   3:     Retrieve previous values: $SO{C}_{prev},SO{H}_{prev}$   4:     if $Type=1$ then                                                                    ▹ Discharge   5:         $SO{C}_{change}\leftarrow 0-SO{C}_{prev}$   6:         $P_{active}\leftarrow f_{active\_power}(SO{C}_{change},SO{H}_{prev})$   7:         $P_{active}^{\left(new\right)}\leftarrow max(P_{active},P_{active}^{\left(current\right)})$   8:         $SOC\leftarrow f_{SOC}(P_{active}^{\left(new\right)},SO{H}_{prev},SO{C}_{prev})$   9:     else if $Type=-1$ then                                                              ▹ Charge 10:         $SOC\leftarrow f_{SOC}(P_{active},SO{H}_{prev},SO{C}_{prev})$ 11:         $consecutive\_state\_count\leftarrow g\left(Type\right)$ 12:         $X\leftarrow \mathrm{Historical}\mathrm{data}\mathrm{of}\mathrm{SOC}\mathrm{and}\mathrm{state}\mathrm{count}$ 13:         $SOH\leftarrow f_{SOH}\left(X\right)$ 14:         while $SOC>SO{C}_{prev}$ and $SOH<SO{H}_{prev}$ do 15:            $SOC\leftarrow SOC-0.5$ 16:            $SOH\leftarrow f_{SOH}\left(X\right)$ 17:         end while 18:         if $SOC<SO{C}_{prev}$ then 19:            $SOC\leftarrow SO{C}_{prev},Type\leftarrow 0,State\leftarrow “Idle”$ 20:         else 21:            $SO{C}_{change}\leftarrow SOC-SO{C}_{prev}$ 22:            $P_{active}^{\left(new\right)}\leftarrow f_{active\_power}(SO{C}_{change},SO{H}_{prev})$ 23:         end if 24:     end if 25:     $consecutive\_state\_count\leftarrow g\left(Type\right)$ 26:     $X\leftarrow \mathrm{Historical}\mathrm{data}\mathrm{of}\mathrm{SOC}\mathrm{and}\mathrm{state}\mathrm{count}$ 27:     $SOH\leftarrow f_{SOH}\left(X\right)$ 28:     if $Type=0$ then                                                                                ▹ Idle 29:         $P_{active}^{\left(new\right)}\leftarrow 0$, $SOH\leftarrow SO{H}_{prev}$ 30:     end if 31: end for 32: Output updated data table with SOC, SOH, Active Power, etc.

5.4. Evaluation SOH Forecasting Model Metrics

To evaluate the precision and robustness of the SOH forecasting model, this study presents mean absolute error (MAE), normalized root mean squared error (NRMSE) and R-squared score (R²). MAE quantifies prediction accuracy by computing the average of the absolute differences between predicted and actual values, relative to the actual values. Specifically, it involves calculating the absolute error for each prediction, normalizing it by the corresponding actual value, and then averaging these normalized errors across the entire dataset [40]. The resulting scalar value reflects the average magnitude of prediction errors, with lower MAE values indicating superior model performance. The NRMSE assesses the accuracy of the prediction model by quantifying the normalized average magnitude of the residuals between predicted and actual values [40]. It is computed by taking the square root of the mean of the squared residuals and normalizing this value by the range of the actual data. A lower NRMSE signifies higher predictive accuracy. The R² also known as the coefficient of determination, measures the proportion of variance in the dependent variable that is explained by the independent variables in the model [40]. As formulated, the R² score ranges from 0 to 1, with higher values indicating a better model fit. An R² of 1 denotes that the model perfectly accounts for the variance in the data.

5.5. Systematic Assessment for LSTM-CNN–AS Framework

To comprehensively assess the effectiveness of the proposed LSTM-CNN–AS framework, this study adopts a rigorous three-pronged evaluation strategy: (1) a quantitative analysis of the MLP-based SOC Updated Model and MLP-based Active Power Controller integrated within the LSTM-CNN–AS framework, evaluated using standard predictive performance metrics outlined in Section 5.5; (2) a comparative investigation of the BESS SOH evolution over a one-month operational period, with five representative days selected for detailed temporal and behavioral analysis; and (3) a one-month economic evaluation comparing charging/discharging costs and total operational profits before and after deploying the proposed framework. The quantitative analysis focuses on evaluating the model’s predictive accuracy, robustness, and generalization capabilities under varying operational conditions. The SOH-based comparative study examines the framework’s ability to enhance system reliability and preserve battery longevity by mitigating degradation effects. The economic assessment aims to quantify the potential financial benefits of the proposed framework, particularly for cost-sensitive and resource-constrained applications such as rural microgrids, by highlighting improvements in operational efficiency and profitability.

The assessment scenario is designed to reflect real-world conditions and is based on high-resolution operational data recorded from the DKA Solar Centre. The systematic evaluation covers the period from 1 February 2025 to 28 February 2025. This period is selected to capture diverse operational patterns and stress factors relevant to battery performance. Data from the DKA Solar Centre is openly accessible, as indicated in the Data Availability section. According to [41], the total cost of charging and discharging operations is computed using the following function, where x denotes the energy usage duration in hours (kWh):

$$\mathrm{Total}\mathrm{Price}=55.42+0.28117\times x$$

(18)

This cost function is applied consistently throughout the economic evaluation to ensure a standardized and reproducible comparison.

5.6. Computing Resources

The experiments are conducted on a machine equipped with an 11th Gen Intel^® Core^TM i5-11400H CPU operating at 2.70 GHz, featuring 6 cores and 12 logical processors. The system includes 8 GB of RAM and a 512 GB NVMe PCIe SSD for storage. For graphical computations, an NVIDIA RTX 3050 GPU with 4 GB of dedicated memory is utilized. The experimental software applications are implemented using Python 3.12 and TensorFlow 2.16.

6. Results and Discussions

In this section, the performance of the SOH model is rigorously compared with benchmark models, and the LSTM-CNN–AS framework is evaluated based on a systematic benchmark.

6.1. SOH Model

Table 3. Model performance comparison. Bold values indicate the model with superior performance.

Dataset	Model	Metric Values
		MAE	NRMSE	${\mathit{R}}^{\mathbf{2}}$ Score
2C_Random	M-LSTM	1.7431	0.0405	0.9691
	Bi-LSTM	1.6608	0.0371	0.9740
	LSTM-CNN	1.4361	0.0352	0.9767
	Bi-LSTM-CNN	1.6316	0.0380	0.9728
	M-LSTM-SA	1.6558	0.0414	0.9676
	ANN	2.8982	0.0551	0.9428
Random_3C	M-LSTM	1.3741	0.0458	0.9706
	Bi-LSTM	1.2878	0.0461	0.9702
	LSTM-CNN	0.8300	0.0340	0.9838
	Bi-LSTM-CNN	1.4536	0.0467	0.9694
	M-LSTM-SA	1.3618	0.0495	0.9656
	ANN	3.3466	0.0951	0.8733
Random_Random	M-LSTM	1.9364	0.0353	0.9734
	Bi-LSTM	1.4229	0.0343	0.9749
	LSTM-CNN	1.3251	0.0351	0.9736
	Bi-LSTM-CNN	1.4104	0.0320	0.9781
	M-LSTM-SA	1.6658	0.0396	0.9664
	ANN	3.5106	0.0666	0.9051

compares the performance of six models across three datasets using MAE, NRMSE, and $R^2$. Bold values indicate the best performance per dataset, with LSTM-CNN generally achieving the highest scores.

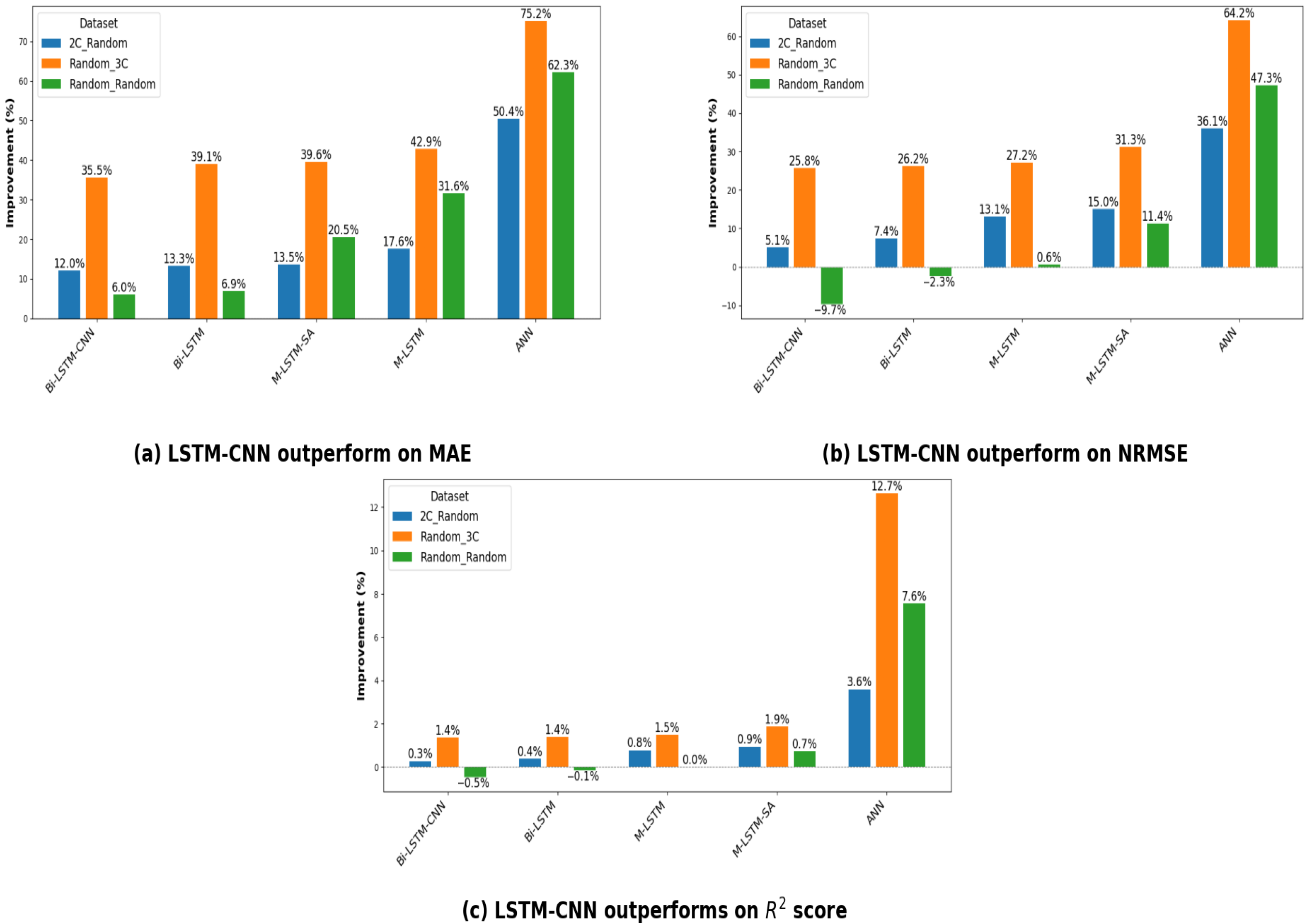
In terms of MAE (Table 3 and Figure 9a), the proposed LSTM-CNN consistently surpasses all benchmark models, achieving improvements ranging from 6% to 75.2%. This substantial margin highlights its superior capability in capturing nonlinear degradation dynamics and maintaining high accuracy under diverse operating conditions. Such performance directly addresses the challenge of data heterogeneity, demonstrating that the model can generalize effectively across batteries with different usage histories and operating regimes.

For NRMSE (Figure 9b), the model achieves gains of 0.6% to 64.2%. Although it exhibits a relative underperformance compared with Bi-LSTM-CNN and Bi-LSTM by 9.7% and 2.3%, respectively, on the Random_Random dataset, it consistently outperforms both on the more challenging 2C_Random and Random_3C datasets. These results confirm that the LSTM-CNN architecture is particularly robust in scenarios involving diverse degradation trajectories, where conventional recurrent architectures may fail to capture domain-specific variations.

Regarding the $R^2$ metric (Figure 9c), the model delivers improvements ranging from 0.3% to 12.7% over the baselines, with only marginal decreases of 0.5% and 0.1% on the Random_Random dataset. Despite these slight drops, the overall correlation remains consistently strong across all datasets, further reinforcing the model’s generalization capacity under heterogeneous conditions.

Taken together, these results demonstrate that the LSTM-CNN achieves not only high predictive accuracy but also resilience to heterogeneity in data distributions and degradation modes. This combination of accuracy, robustness, and adaptability establishes the model as a reliable and scalable solution for real-world SOH estimation in lithium-ion batteries, where data scarcity and heterogeneity are often the primary obstacles.

6.2. LSTM-CNN-AS Assesment

As presented in

Table 4. Prediction performance of the proposed model on the DKA-Solar-BESS dataset.

Datasets	Predict	MAE	NRMSE	R2
DKA-Solar-BESS	Active Power	1.4211	0.0148	0.9511
	SOC	0.1417	0.0051	0.9995

and Figure 10 and Figure 11, the LSTM-CNN–AS framework demonstrates high efficiency in achieving both precision and robustness when predicting the active power output and the SOC of the BESS. The model achieves an MAE of 1.4211 for active power prediction and 0.1417 for SOC, indicating a strong ability to minimize prediction errors across different output variables. 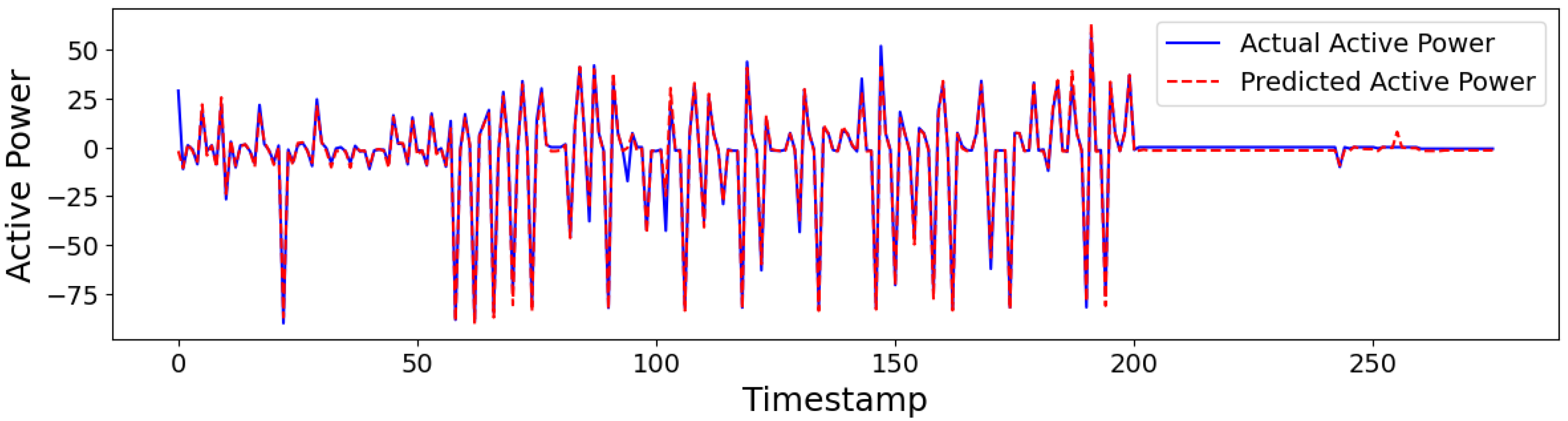Furthermore, the framework attains an R² value of 0.9511 for active power and an impressive 0.9995 for SOC, highlighting the model’s excellent capacity to capture the complex dynamics and nonlinear behavior of the BESS. These results confirm the LSTM–CNN-AS framework’s effectiveness in delivering highly accurate forecasts, which is critical for optimizing battery operation and ensuring system reliability. Overall, the outstanding predictive performance of this framework positions it as a promising tool for advanced energy management strategies in grid-connected BESSs.

The one-month comparative analysis confirms the superior performance of the proposed LSTM–CNN–AS framework in managing the BESS, as shown in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. A one-month horizon was selected to encompass a representative range of operational conditions, including fluctuations in load demand and user consumption patterns. This duration is sufficiently long to evaluate both short-term dynamics and emerging operational trends, while keeping the computational complexity of simulation and interpretation tractable.

Across all scenarios (Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16), the intelligent scheduling mechanism consistently optimizes the charging process to preserve SOH. On the left-hand side of the figures, the uncontrolled charging profiles lead to accelerated degradation, evidenced by a steep decline in SOH. Notably, the SOH fluctuates irregularly. This phenomenon occurs because the model was tested on a publicly available dataset, as described in the Data Preparation section, rather than on data collected under controlled laboratory conditions. Consequently, maintenance activities and internal factory operations that were not captured in the dataset may have contributed to unstable charging and discharging behavior, leading to fluctuations in SOC and the resulting variations observed in the SOH patterns. Therefore, in this paper, our study aims to refine the charge–discharge control process within the available dataset to minimize SOH reduction, as observed on the left-hand side of Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

Additionally, the robustness of the proposed model in predicting SOH trends has been validated in Figure 17, where the predicted values align closely with the ground truth. Furthermore, the proposed intelligent scheduling algorithm (Algorithm 1) demonstrates well-regulated charging behavior, effectively mitigating abrupt SOH drops and flattening the degradation trajectory, as illustrated on the right-hand side of Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

These findings confirm that charging and discharging behaviors directly influence battery longevity, and that the integration of adaptive, intelligent scheduling is essential to prolong battery health. Moreover, rural grid systems are often characterized by unstable and highly variable current conditions, emphasizing the necessity for lifetime prediction methods that perform reliably under cross-operational scenarios, where adaptive feature alignment and physics-informed learning can further enhance degradation trajectory forecasting.

Specifically, the framework maintains SOH above 70%, prevents SOC from falling below 20%, and reduces charging time by more than 30%, thereby enhancing both reliability and long-term durability. Importantly, user demand satisfaction is always prioritized. Therefore, during discharge intervals, the system consistently ensures adequate power supply despite inevitable SOH decline, as highlighted by the red-shaded regions in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

Thus, the proposed intelligent scheduling strategy simultaneously preserves battery health, minimizes charging stress, guarantees user energy supply, and improves overall system efficiency. These results underscore its potential as a practical and scalable solution for real-world BESS operation.

This framework was selected for detailed analysis based on earlier comparisons with several benchmark models, including LSTM-only and CNN-only variants, which consistently showed inferior performance in terms of SOC/SOH management and scheduling efficiency. Therefore, to focus on economic and operational benefits, only the best-performing model is analyzed in depth in this section.

In addition,

Table 5. Economic assessment before and after one-month LSTM-CNN–AS deployment. Bold values indicate the framework with superior performance.

	Charging Power (MWh)	Discharge Power (MWh)	Total Power	Charging Revenue (AUD)	Discharging Revenue (AUD)	Total Revenue (AUD)
Without Schedule Model	47.68	29.56	77.24	21,426.87	13,285.51	34,738.96
With Schedule Model	17.81	30.19	48.00	8002.52	13,567.27	21,596.37

shows that the LSTM-CNN–AS framework demonstrates strong economic performance by reducing the total operational cost of the BESS by 40%. This substantial reduction is primarily driven by the framework’s ability to optimise charging strategies, resulting in an 66% decrease in the total power required for charging. By minimising energy consumption and avoiding inefficient, prolonged charging cycles, the framework not only lowers electricity expenses but also reduces battery wear, thereby decreasing maintenance costs over time. This improvement is particularly significant in the context of supporting net-zero energy policies of the Northern Territory, as it enhances the overall energy efficiency and sustainability of the system. Furthermore, by increasing the effectiveness of charging cycles and promoting smarter energy usage, the framework extends the operational life span of the BESS. These combined benefits make the LSTM-CNN–AS framework a valuable approach for advancing environmental goals and economic savings in modern energy storage applications.

6.3. Limitations of the Proposed Model

Despite the strong performance of the LSTM-CNN–AS framework, several limitations remain. First, although the framework performs well under controlled conditions, its robustness to noisy or unseen real-world data has not been rigorously quantified; for instance, the effect of sensor errors at different intensities on prediction accuracy remains untested. Second, while short-term forecasts have been validated, long-term prediction capability is only demonstrated for one month, leaving the cumulative effect of SOH prediction bias over extended horizons unassessed. Third, evaluation is restricted to two datasets with relatively controlled settings, which may not fully capture variability across lithium-ion chemistries, system scales, or deployment environments. Finally, the proposed integration of explainable AI lacks a clear technical path or feasibility assessment.

7. Conclusions

This study presents the LSTM-CNN–AS framework, an intelligent and lightweight solution designed to improve the accuracy of SOH and SOC estimation in lithium-ion battery systems. By combining the temporal learning strength of LSTM networks with the feature extraction capabilities of CNN, and integrating adaptive scheduling, the framework enables smarter battery management in grid-connected and remote energy systems. The framework was rigorously evaluated using diverse datasets, including 2C_Random, Random_3C, and Random_Random profiles. Results consistently demonstrated its strong predictive capability, highlighted:

• For the 2C Random dataset, the LSTM-CNN model outperformed the Bi-LSTM-CNN model by 12% in both MAE and NRMSE, achieving an R² of 0.9767 for SOH estimation.
• For the 3C dataset, the LSTM-CNN model delivered a 44% reduction in MAE and a 2% increase in R², with an NRMSE of 0.0340.
• For the Random_Random dataset, the LSTM-CNN model maintained solid performance, improving MAE by 8% while preserving accurate trend tracking with an R² of 0.9736.
• For SOC estimation, the framework showed exceptional precision, reaching an R² of 0.9995 with minimal error.
• Over a one-month simulation, the framework effectively preserved battery health by maintaining SOH above 70% and avoiding deep discharges, keeping SOC consistently above 20%.

These outcomes highlight the framework’s potential to not only monitor but also enhance battery performance over time. Its efficient control of charging and discharging extends battery life span and supports reliable operation, particularly in scenarios where stability and resource efficiency are essential. Further work will aim to enhance robustness under real-world noise, and uncertainty improve long-term forecasting, and incorporate explainable AI for greater model transparency.