Comparative Analysis of DCIR and SOH in Field-Deployed ESS Considering Thermal Non-Uniformity Using Linear Regression
Abstract
1. Introduction
- Temperature-Compensated Degradation Inference. A polynomial regression methodology was developed and validated to compensate state-of-health (SOH) and DCIR to 30 °C and 23 °C, respectively. Compensation reduced dispersion and clarified inter-year trends in both DCIR and SOH under heterogeneous field conditions while remaining practical with sparse temperature sensing, yielding per-year compensation tables.
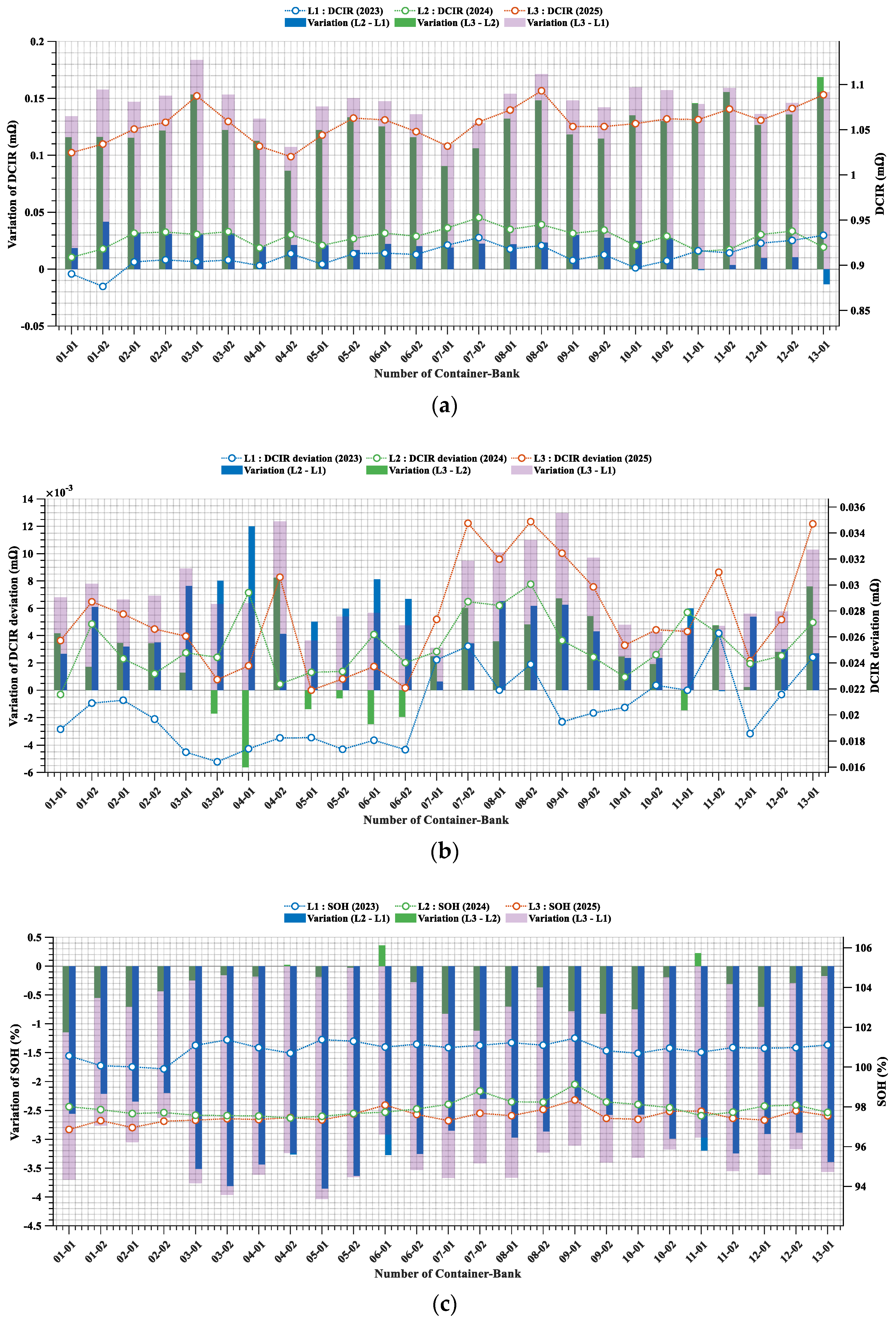
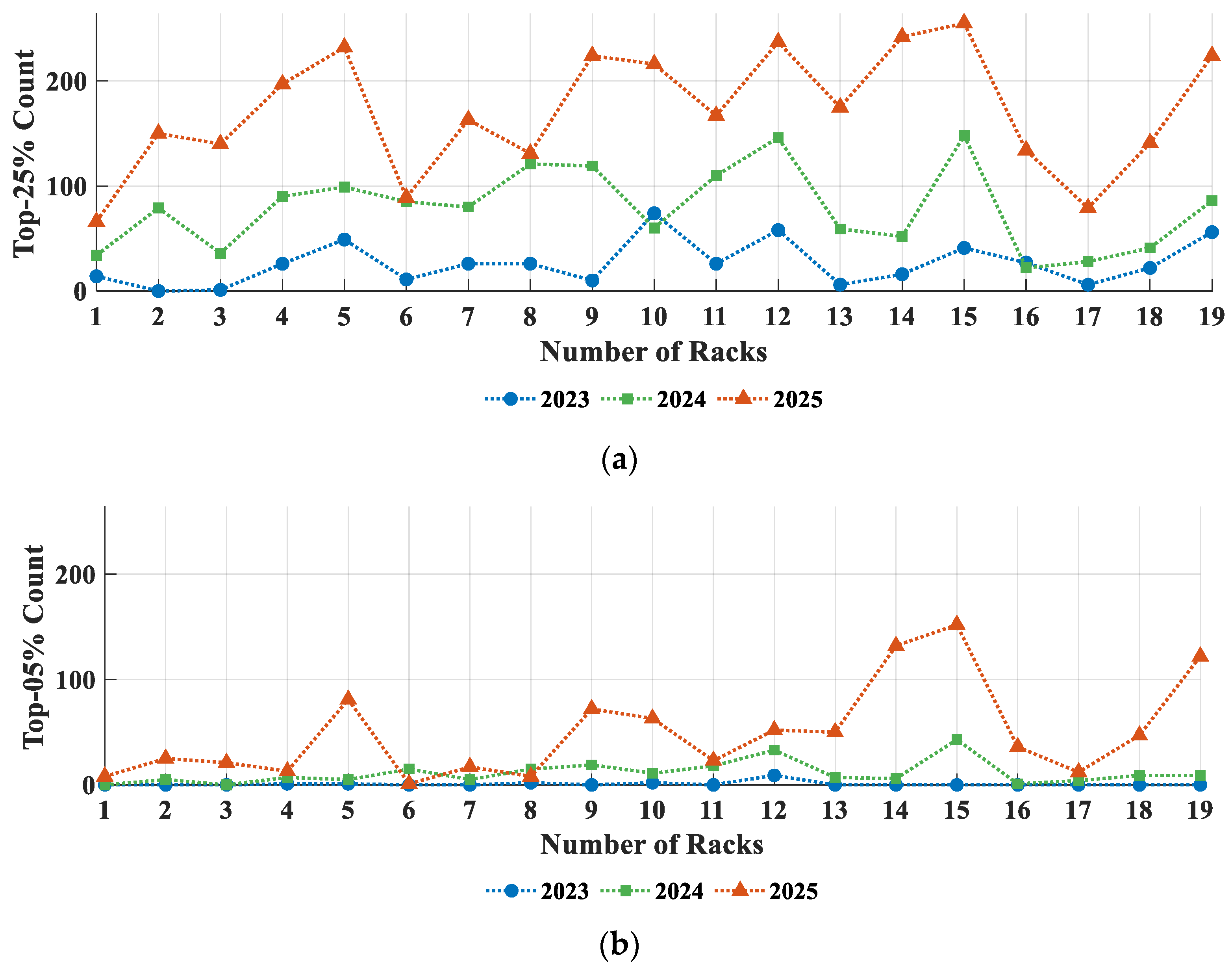
- Quantification of Intra-Bank Heterogeneity. Beyond mean shifts, bank-level dispersion metrics (e.g., DCIR standard deviation and upper-tail fractions such as top 25%/top 5% cells) increased monotonically with aging. These variability indicators provided early-warning signals complementary to average SOH/DCIR, revealing progressive imbalances across cells, racks, and banks.
- Spatial Diagnostics and Structural Effects (Bank 03-01). Rack–module heatmaps of DCIR and temperature identified a localized hotspot near Racks 14–15, where SOH decline and DCIR growth intensified concurrently. The hotspot aligned with heating, ventilation, and air conditioning (HVAC)-driven airflow asymmetry and episodic fan operation; uncompensated DCIR distributions broadened during fan activity, whereas temperature-compensated maps isolated degradation-driven changes—motivating HVAC co-design and targeted monitoring.
2. Operation of the ESS and Data Acquisition
2.1. System Architecture and Field Data Acquisition
2.2. SOH and DCIR Evaluation
2.2.1. SOH Estimation Using the Coulomb Counting Approach
2.2.2. DCIR Evaluation Using the HPPC Test
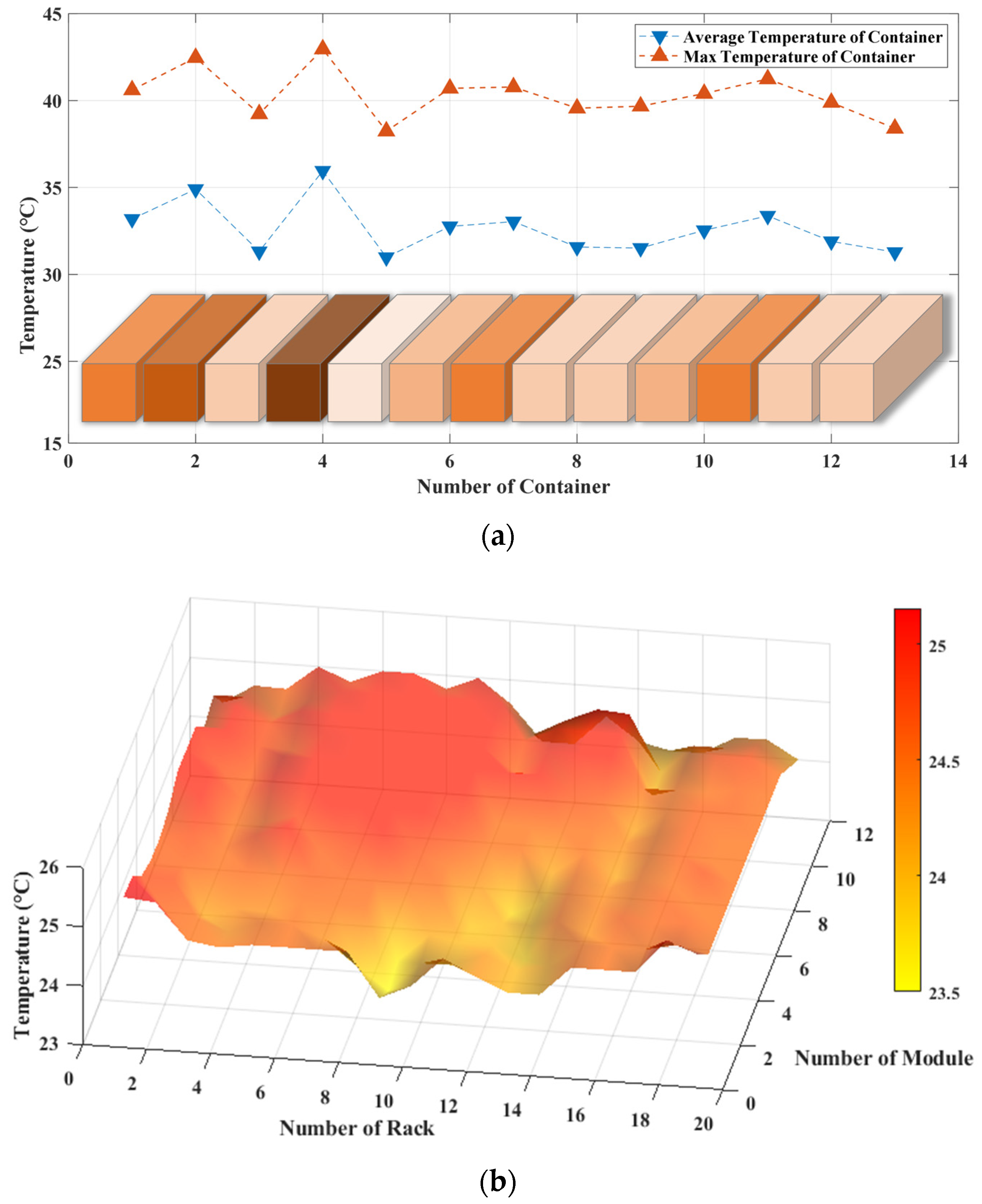
2.3. Thermal Non-Uniformity Across Different Scales
3. Derivation of Temperature-Compensated DCIR Using Linear Regression Analysis
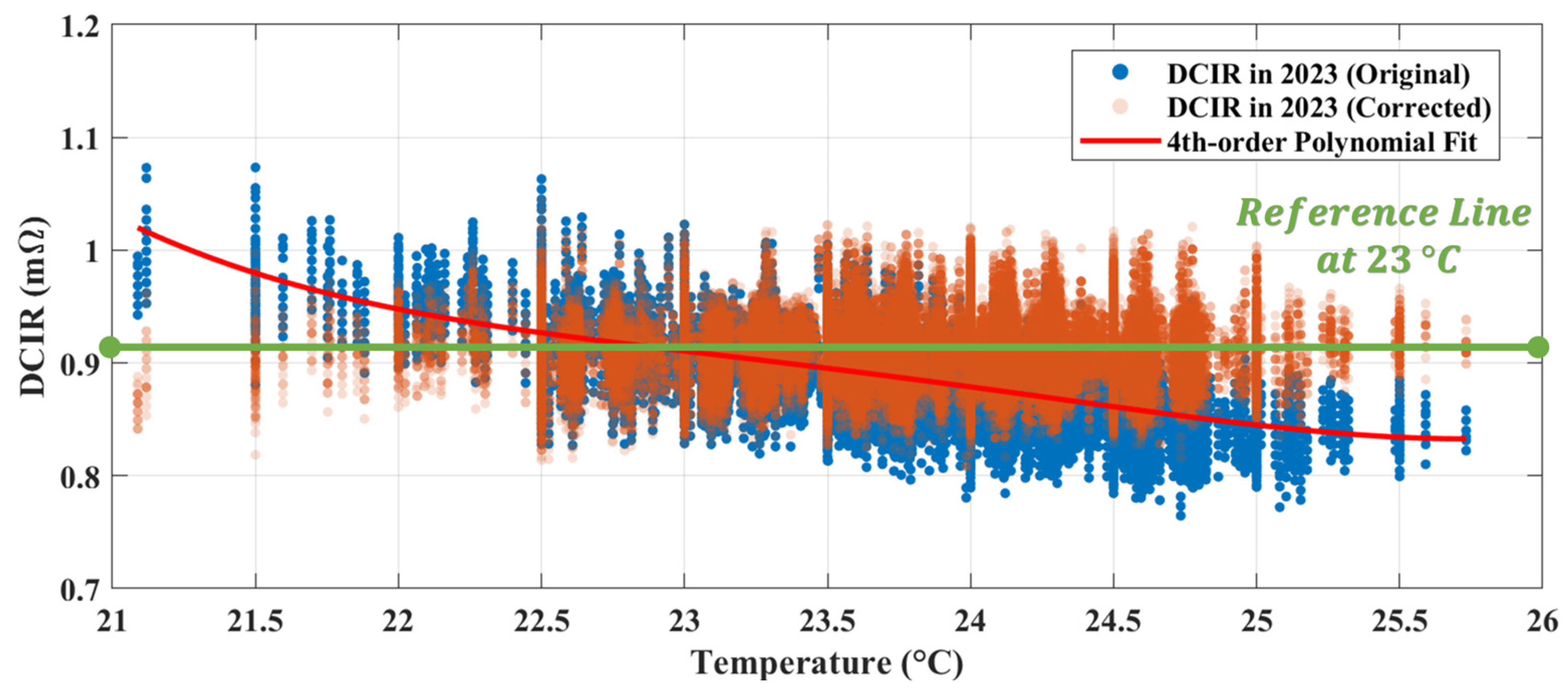
3.1. Thermal Dependence of DCIR
3.1.1. Polynomial Regression for Temperature Compensation
3.1.2. Temperature Compensation of DCIR
3.2. Degradation Assessment Based on DCIR Measurements with Temperature Compensation
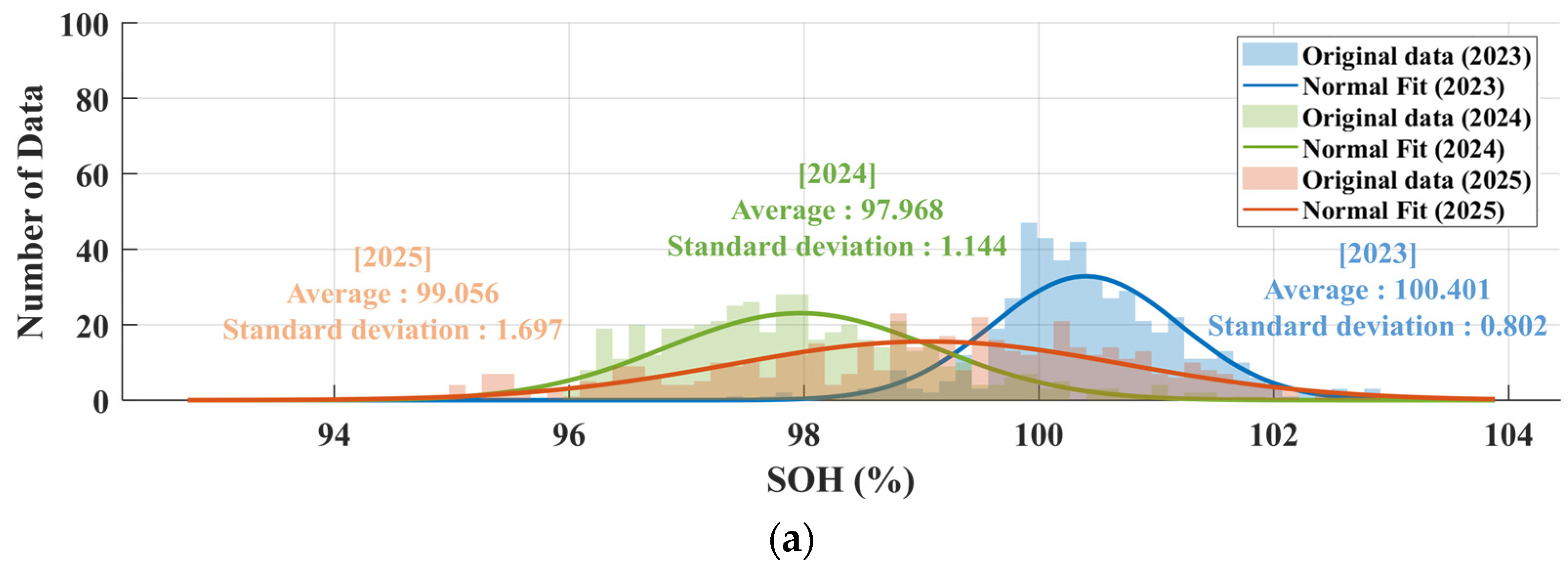
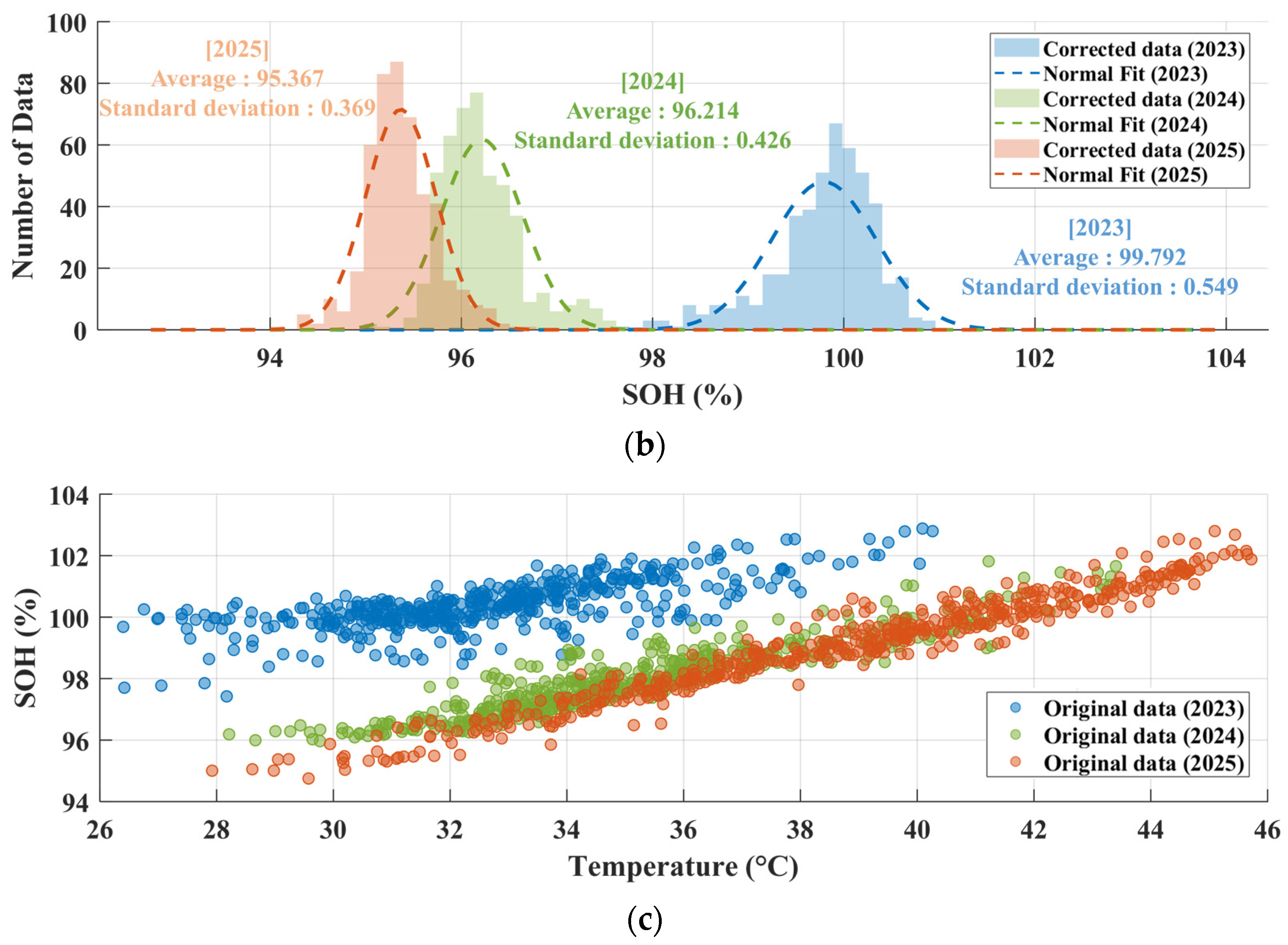
3.3. Degradation Assessment Based on Capacity-Based SOH Measurements with Temperature Compensation
4. Temperature-Compensated Degradation Analysis: Bank-Level Correlations and Structural Effects
4.1. Bank-Level Analysis of Correlated Trends in SOH Degradation and DCIR Growth
4.2. Case Study of Bank 03-01: Escalation of Abnormal Degradation
4.3. Case Study of Bank 03-01: Analysis of Structural Effects and Temperature Compensation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESS | Energy Storage System |
| DCIR | Direct Current Internal Resistance |
| SOH | State-of-health |
| SOC | State-of-charge |
| HPPC | Hybrid Pulse Power Characterization |
| FR | Frequency Regulation |
| LIBs | Lithium-Ion Batteries |
| ICA | Incremental Capacity Analysis |
| EIS | Electrochemical impedance spectroscopy |
| LAM | Loss of Active Material |
| LLI | Loss of Lithium Inventory |
| HVAC | Heating, Ventilation, and Air Conditioning |
| BMS | Battery Management System |
| DOD | Depth-of-discharge |
| OCV | Open-circuit Voltage |
| CFD | Computational Fluid Dynamics |
| MAPE | Mean Absolute Percentage Error |
References
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Tasneem, O.; Tasneem, H.; Xian, X. Lithium-Ion Battery Technologies for Grid-Scale Renewable Energy Storage. Next Res. 2025, 2, 100297. [Google Scholar] [CrossRef]
- Gräf, D.; Marschewski, J.; Ibing, L.; Huckebrink, D.; Fiebrandt, M.; Hanau, G.; Bertsch, V. What drives capacity degradation in utility-scale battery energy storage systems? The impact of operating strategy and temperature in different grid applications. J. Energy Storage 2022, 47, 103533. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, M.; Zhang, M.; Cai, T.; Huang, Y.; Xu, M. Advancements, Challenges, and Future Trajectories in Advanced Battery Safety Detection. Electrochem. Energy Rev. 2025, 8, 10. [Google Scholar] [CrossRef]
- Pillai, P.; Desai, S.; Pattipati, K.R.; Balasingam, B. An Improved Approach to Estimate the Internal Resistance of a Battery During the HPPC Test. arXiv 2025, arXiv:2505.06410. [Google Scholar]
- Krupp, A.; Ferg, E.; Schuldt, F.; Derendorf, K.; Agert, C. Incremental capacity analysis as a state of health estimation method for lithium-ion battery modules with series-connected cells. Batteries 2020, 7, 2. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. On the use of electrochemical impedance spectroscopy to characterize and model the aging phenomena of lithium-ion batteries: A critical review. J. Power Sources 2021, 505, 229860. [Google Scholar] [CrossRef]
- Schreiber, M.; Lin, Y.; Sommer, A.; Wassiliadis, N.; Torricos, P.M.; Rogge, M.; Lewerenz, M.; Grosu, C.; Endisch, C.; Jossen, A.; et al. Apparent vs. true battery aging: Impact of various load characteristics on accelerated aging tests. J. Energy Storage 2025, 127, 116924. [Google Scholar] [CrossRef]
- Che, Y.; Stroe, D.I.; Sui, X.; Vilsen, S.B.; Hu, X.; Teodorescu, R. Battery aging behavior evaluation under variable and constant temperatures with real loading profiles. In Proceedings of the 2023 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Sulzer, V.; Mohtat, P.; Aitio, A.; Lee, S.; Yeh, Y.T.; Steinbacher, F.; Khan, M.U.; Lee, J.W.; Siegel, J.B.; Stefanopoulou, A.G.; et al. The challenge and opportunity of battery lifetime prediction from field data. Joule 2021, 5, 1934–1955. [Google Scholar] [CrossRef]
- Cao, W.; Zhou, Y.; Kuang, Z.; Sun, W.; Wu, H.; Dong, T. Multi-scale modelling of battery cooling systems for grid frequency regulation with high C-rate amplitude and non-uniform cell heat generation. Sci. Rep. 2025, 15, 6508. [Google Scholar] [CrossRef]
- Hossain Ahmed, S.; Kang, X.; Bade Shrestha, S.O. Effects of temperature on internal resistances of lithium-ion batteries. J. Energy Resour. Technol. 2015, 137, 031901. [Google Scholar] [CrossRef]
- Cavalheiro, G.M.; Iriyama, T.; Nelson, G.J.; Huang, S.; Zhang, G. Effects of nonuniform temperature distribution on degradation of lithium-ion batteries. J. Electrochem. Energy Convers. Storage 2020, 17, 021101. [Google Scholar] [CrossRef]
- Li, S.; Zhang, C.; Zhao, Y.; Offer, G.J.; Marinescu, M. Effect of thermal gradients on inhomogeneous degradation in lithium-ion batteries. Commun. Eng. 2023, 2, 74. [Google Scholar] [CrossRef]
- Reniers, J.M.; Howey, D.A. Digital twin of a MWh-scale grid battery system for efficiency and degradation analysis. Appl. Energy 2023, 336, 120774. [Google Scholar] [CrossRef]
- Lyu, D.; Zhang, B.; Zio, E.; Xiang, J. Battery cumulative lifetime prognostics to bridge laboratory and real-life scenarios. Cell Rep. Phys. Sci. 2024, 5, 102164. [Google Scholar] [CrossRef]
- Shi, Y.; Xu, B.; Wang, D.; Zhang, B. Using battery storage for peak shaving and frequency regulation: Joint optimization for superlinear gains. IEEE Trans. Power Syst. 2017, 33, 2882–2894. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef]
- Kirkaldy, N.; Samieian, M.A.; Offer, G.J.; Marinescu, M.; Patel, Y. Lithium-ion battery degradation: Comprehensive cycle ageing data and analysis for commercial 21,700 cells. J. Power Sources 2024, 603, 234185. [Google Scholar] [CrossRef]
- Rosewater, D.; Ferreira, S. Development of a frequency regulation duty-cycle for standardized energy storage performance testing. J. Energy Storage 2016, 7, 286–294. [Google Scholar] [CrossRef]
- Edison, C. Considerations for ESS Fire Safety; DNV GL: Oslo, Norway, 2017. [Google Scholar]
- Sun, Z.; He, W.; Wang, J.; He, X. State of Health Estimation for Lithium-Ion Batteries with Deep Learning Approach and Direct Current Internal Resistance. Energies 2024, 17, 2487. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, S.J.; Lee, J.M.; Cho, B.H. A new direct current internal resistance and state of charge relationship for the Li-ion battery pulse power estimation. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, South Korea, 22–26 October 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Bayoumi, E.; Hassan, E.; El-Khattam, W.; Ibrahim, A.M. Implications of lithium-ion cell temperature estimation methods for intelligent battery management and fast charging systems. Bull. Pol. Acad. Sci. Tech. Sci. 2024, 72, e149171. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Ebenezer, K.; Wang, S.; Li, X.; Tao, J.; Fernandez, C.; Blaabjerg, F. Enhancing State of Charge Prediction of Lithium-Ion Batteries Through Linear Polynomial Regression–Support Vector Machine Modeling with Temperature Varying and Open Circuit Voltage Compensation; Elsevier: Amsterdam, The Netherlands, 2025. [Google Scholar]
- Razi, M.F.I.M.; Daud, Z.H.C.; Asus, Z.; Mazali, I.I.; Ardani, M.I.; Hamid, M.K.A. Li-NMC Battery Internal Resistance at Wide Range of Temperature. J. Adv. Res. Fluid. Mech. Therm. Sci. 2022, 99, 9–16. [Google Scholar]
- Lv, S.; Wang, X.; Lu, W.; Zhang, J.; Ni, H. The influence of temperature on the capacity of lithium ion batteries with different anodes. Energies 2021, 15, 60. [Google Scholar] [CrossRef]
- Dechent, P.; Greenbank, S.; Hildenbrand, F.; Jbabdi, S.; Sauer, D.U.; Howey, D.A. Estimation of Li-Ion Degradation Test Sample Sizes Required to Understand Cell-to-Cell Variability. Batter. Supercaps 2021, 4, 1821–1829. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, J.; Lu, Y.; Yan, K.; Guan, Y.; Zhao, F.; Tang, R.; Shen, W.; Li, N.; Su, Y.; et al. Spatially heterogeneous degradation in LiFePO 4//graphite pouch batteries under temperature accelerated aging process. EES Batter. 2025, 1, 1279–1290. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, X.; Tran, M.K.; Fowler, M.; Ouyang, M.; Burke, A.F. Battery safety: Fault diagnosis from laboratory to real world. J. Power Sources 2024, 598, 10–1016. [Google Scholar] [CrossRef]





| Number of Year | Degree | MAPE | |||
|---|---|---|---|---|---|
| 2023 | 1 | 0.3956 | 2.0476 | ||
| 2 | 0.3957 | 2.0475 | |||
| 3 | 0.3961 | 2.0474 | |||
| 4 | 0.3991 | 2.0448 | |||
| 5 | 0.3993 | 2.0415 | |||
| 6 | 0.3995 | 2.0411 | |||
| 7 | 0.3997 | 2.0408 | |||
| 8 | 0.3998 | 2.0408 | |||
| 2024 | 1 | 0.7755 | 2.3187 | ||
| 2 | 0.7804 | 2.2858 | |||
| 3 | 0.7804 | 2.2855 | |||
| 4 | 0.7804 | 2.2843 | |||
| 5 | 0.7807 | 2.2840 | |||
| 6 | 0.7807 | 2.2837 | |||
| 7 | 0.7808 | 2.2833 | |||
| 8 | 0.7808 | 2.2827 | |||
| 2025 | 1 | 0.8679 | 2.4738 | ||
| 2 | 0.8716 | 2.4355 | |||
| 3 | 0.8716 | 2.4358 | |||
| 4 | 0.8718 | 2.4343 | |||
| 5 | 0.8719 | 2.4346 | |||
| 6 | 0.8719 | 2.4344 | |||
| 7 | 0.8723 | 2.4319 | |||
| 8 | 0.8723 | 2.4315 |
| Temperature (°C) | Uncompensated DCIR (mΩ) | Compensation Factor | Compensated DCIR at 23 °C (mΩ) |
|---|---|---|---|
| 21.0 | 1.0309 | 0.8833 | 0.9106 |
| 22.0 | 0.9478 | 0.9608 | 0.9106 |
| 23.0 | 0.9106 | 1.0000 | 0.9106 |
| 24.0 | 0.8788 | 1.0362 | 0.9106 |
| 25.0 | 0.8449 | 1.0777 | 0.9106 |
| 26.0 | 0.8353 | 1.0902 | 0.9106 |
| Figure 10 | Max (mΩ) | Min (mΩ) | Average (mΩ) | Range (mΩ) |
| (a) | 0.9325 | 0.8739 | 0.9039 | 0.0586 |
| (b) | 0.9671 | 0.8991 | 0.9342 | 0.0680 |
| (c) | 1.1294 | 1.0378 | 1.0875 | 0.0916 |
| (d) | 0.9096 | 0.8437 | 0.8742 | 0.0659 |
| (e) | 0.9335 | 0.8557 | 0.8859 | 0.0778 |
| (f) | 1.2220 | 0.9268 | 1.0713 | 0.2952 |
| Figure 10 | Max (°C) | Min (°C) | Average (°C) | Range (°C) |
| (g) | 24.6162 | 22.6162 | 23.9371 | 2.0000 |
| (h) | 24.9330 | 22.7564 | 24.2906 | 2.1766 |
| (i) | 26.6709 | 21.1680 | 23.3935 | 5.5029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mun, T.; Noh, C.; Lee, S.-E. Comparative Analysis of DCIR and SOH in Field-Deployed ESS Considering Thermal Non-Uniformity Using Linear Regression. Energies 2025, 18, 5640. https://doi.org/10.3390/en18215640
Mun T, Noh C, Lee S-E. Comparative Analysis of DCIR and SOH in Field-Deployed ESS Considering Thermal Non-Uniformity Using Linear Regression. Energies. 2025; 18(21):5640. https://doi.org/10.3390/en18215640
Chicago/Turabian StyleMun, Taesuk, Chanho Noh, and Sung-Eun Lee. 2025. "Comparative Analysis of DCIR and SOH in Field-Deployed ESS Considering Thermal Non-Uniformity Using Linear Regression" Energies 18, no. 21: 5640. https://doi.org/10.3390/en18215640
APA StyleMun, T., Noh, C., & Lee, S.-E. (2025). Comparative Analysis of DCIR and SOH in Field-Deployed ESS Considering Thermal Non-Uniformity Using Linear Regression. Energies, 18(21), 5640. https://doi.org/10.3390/en18215640







