Next Article in Journal
Energy-Efficient Last-Mile Logistics Using Resistive Grid Path Planning Methodology (RGPPM)
Next Article in Special Issue
Nonlinear Pressure Fluctuation Management for Ejector-Based Hydrogen Recirculation System in Large-Power Vehicular PEMFCs
Previous Article in Journal
Collaborative Estimation of Lithium Battery State of Charge Based on the BiLSTM-AUKF Fusion Model
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 18
Issue 21
10.3390/en18215623
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Simulation Analysis of Cu2O Solar Cells

by
Sinuo Chen
1,2,
Lichun Wang
1,2,
Chunlan Zhou
1,2,*,
Jinli Yang
1,2 and
Xiaojie Jia
1,2
1
The Key Laboratory of Solar Thermal Energy and Photovoltaic System, Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China
2
University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Energies 2025, 18(21), 5623; https://doi.org/10.3390/en18215623
Submission received: 30 September 2025 / Revised: 22 October 2025 / Accepted: 23 October 2025 / Published: 26 October 2025
(This article belongs to the Special Issue Functional Materials for Advanced Energy Applications)
Browse Figures
Versions Notes

Abstract

Cu2O solar cells are regarded as a promising emerging inorganic photovoltaic technology due to their power conversion efficiency (PCE) potential and material sustainability. While previous studies primarily focused on the band offset between n-type buffer layers and Cu2O optical absorption, this work systematically investigated an ETL/buffer/p-Cu2O/HTL heterojunction structure using SCAPS-1D simulations. Key design parameters, including bandgap (Eg) and electron affinity (χ) matching across layers, were optimized to minimize carrier transport barriers. Furthermore, the doping concentration and thickness of each functional layer (ETL: transparent conductive oxide; HTL: hole transport layer) were tailored to balance electron conductivity, parasitic absorption, and Auger recombination. Through this approach, a maximum PCE of 14.12% was achieved (Voc = 1.51V, Jsc = 10.52 mA/cm2, FF = 88.9%). The study also identified candidate materials for ETL (e.g., GaN, ZnO:Mg) and HTL (e.g., ZnTe, NiOx), along with optimal thicknesses and doping ranges for the Cu2O absorber. These findings provide critical guidance for advancing high-performance Cu2O solar cells.

1. Introduction

Due to its sustainable nature and remarkable optoelectronic properties, characterized by a high absorption coefficient (1 × 106 cm−1) and elevated carrier mobility (100 cm2/V⋅s), Cu2O, as a p-type semiconductor material with a direct bandgap of 1.1–2.1 eV, has been highly sought in the field of photovoltaic solar cell technology [1,2,3,4]. Cu2O and c-Si have minimal spectral sensitivity overlaps, making it possible to fabricate a high PCE of Cu2O/Si four-terminal tandem solar cells. With the improvement in Cu2O-based solar cell performance, the PCE of Cu2O/Si tandem solar cells may exceed 30% in the future, indicating significant research potential [5,6,7]. ZnO is a sustainable n-type direct bandgap semiconductor with a wide bandgap of 3.1 eV, forming a type-II heterojunction structure with Cu2O [8,9,10,11,12]. Therefore, ZnO–Cu2O solar cells are currently the most promising and best-performing type of Cu2O-based solar cells. In addition to the challenges posed by Cu2O material synthesis technology and the deposition process, the significant band offset between the ZnO and Cu2O layers serves as the main limiting factor for the performance of ZnO–Cu2O solar cells. In early ZnO–Cu2O solar cells without a buffer layer, the PCE did not exceed 4% [13,14,15]. According to Anderson’s band alignment theory, shown in Equations (1) and (2), to simultaneously reduce the conduction band offset (CBO) and valence band offset (VBO), the differences in electron affinity and bandgap between adjacent materials must be minimized as much as possible [16,17]:
CBO: ∆EC = χ2 − χ1,
VBO: ∆EV = (χ2 + Eg2) − (χ1 + Eg1),
where ∆EC is the CBO between material 1 and material 2, ∆EV is the CBO between material 1 and material 2, χ1 and χ2 signify the electron affinity of material 1 and material 2, respectively, and Eg1 and Eg2 denote the bandgap of material 1 and material 2, respectively.
In 2020, Nakagawa et al. compared the CBO between p-Cu2O and four n-type semiconductor materials including Ga2O3, ZnO:Sn, Zn–Ge–O, and ZnO, and found that Ga2O3 was possibly a comparatively suitable ETL due to the smallest CBO [6]. In 2022, Toshiba utilized Zn1–xSnxOy/Ga2O3 as buffer layers to fabricate ZnO:Al/Zn1−xSnxOy/Ga2O3/Cu2O/SnO2:Sb/InOx:Sn heterojunction solar cells and achieved the highest PCE record value of 9.5% [18]. In 2024, Toshiba developed a transparent Cu2O solar cell with the AZO/n-Cu2O/p-Cu2O/AZO structure, achieving a record efficiency of 10.5% in small-area devices [19]. However, there is still significant room for optimization, as this value remains far from the maximum theoretical PCE value of 20% based on the Shockley–Queisser model [20].
Numerical modeling still remains a useful and valuable method for predicting the optimal parameters of each functional layer in solar cells and exploring the optimal optimization solutions for state-of-the-art solar cell designs. One-dimensional solar cell capacitance simulators (SCAPS-1D) have been developed by researchers at the University of Gent in Belgium to initially handle polycrystalline thin film solar cells, particularly Cu(In,Ga)Se2 and CdTe-based solar cells [21]. The major advantages of SCAPS-1D have covered transient state analysis, graded structure calculation, intra-band tunneling, and multivalent defects modeling through several versions updated since 1996 [21,22,23,24,25,26]. Previous simulation studies of ZnO–Cu2O solar cells have often utilized SCAPS-1D [27,28,29], primarily by adjusting the doping concentration and specified thickness of ZnO in the TCO layer, Cu2O layer, and the specific buffer layers or ETL such as Zn–Ge–O [30], CdS [29], Ga2O3 [31], ZnO and CdS double buffer layers [29], and CuO [32] to explore the optimal solutions.
In this study, we utilized SCAPS-1D (v3.3.10) to systematically optimize an ETL/buffer/p-Cu2O/HTL heterojunction thin-film solar cell. While previous simulations have largely focused on simpler heterojunctions such as TiO2/Cu2O or ZnO/Cu2O, often with limited parameter exploration, our work introduces a more comprehensive device architecture that incorporates both electron and hole transport layers [28,33]. This design enables improved carrier management and reduced recombination losses, which are essential for enhancing device performance. We first examined the energy band alignment by analyzing the influence of χ and bandgap of the ETL, buffer, and HTL layers—key factors that have not been fully addressed in earlier modeling efforts. Based on optimized Eg and χ values, we propose several candidate materials for the buffer and HTL including GaN or Mg-doped ZnO for the ETL, and ZnTe or NiOx for the HTL. Subsequently, we systematically evaluated the effects of layer thickness and doping concentration across the buffer, HTL, and Cu2O absorber. This multi-parameter optimization strategy offers a holistic view of the trade-offs between carrier collection, optical absorption, and Auger recombination—aspects often overlooked in studies that tune only a subset of parameters. Our approach not only helps reconcile performance discrepancies reported in the literature, but also provides a reproducible framework for the design of high-efficiency Cu2O solar cells.

2. Simulation Methods

Figure 1 presents a schematic diagram of the ETL/buffer/p-Cu2O/HTL solar cell. All simulations were carried out under standard conditions (AM1.5G spectrum, 1000 W m−2, T = 300 K) using SCAPS-1D software (version 3.3.10). Table 1 lists the characteristic parameters of the functional layers (ETL, buffer, Cu2O and HTL) used in the simulation, indicating that the band gaps and electron affinities of the ETL, buffer and HTL layers were treated as variables. In addition, the doping concentrations and thicknesses of the ETL, Buffer, Cu2O and HTL layers were varied to explore how high electron conductivity could be achieved while ensuring minimal Auger recombination and parasitic optical absorption. The initial parameters for the ETL, buffer, p-Cu2O, and HTL in Table 1 were based on standard values for ZnO (Al), Ga2O3, Cu2O, and Cu2O (P+), respectively. The simulation employed Ag electrodes with a work function of 4.8 eV [13,34,35].

3. Results and Discussion

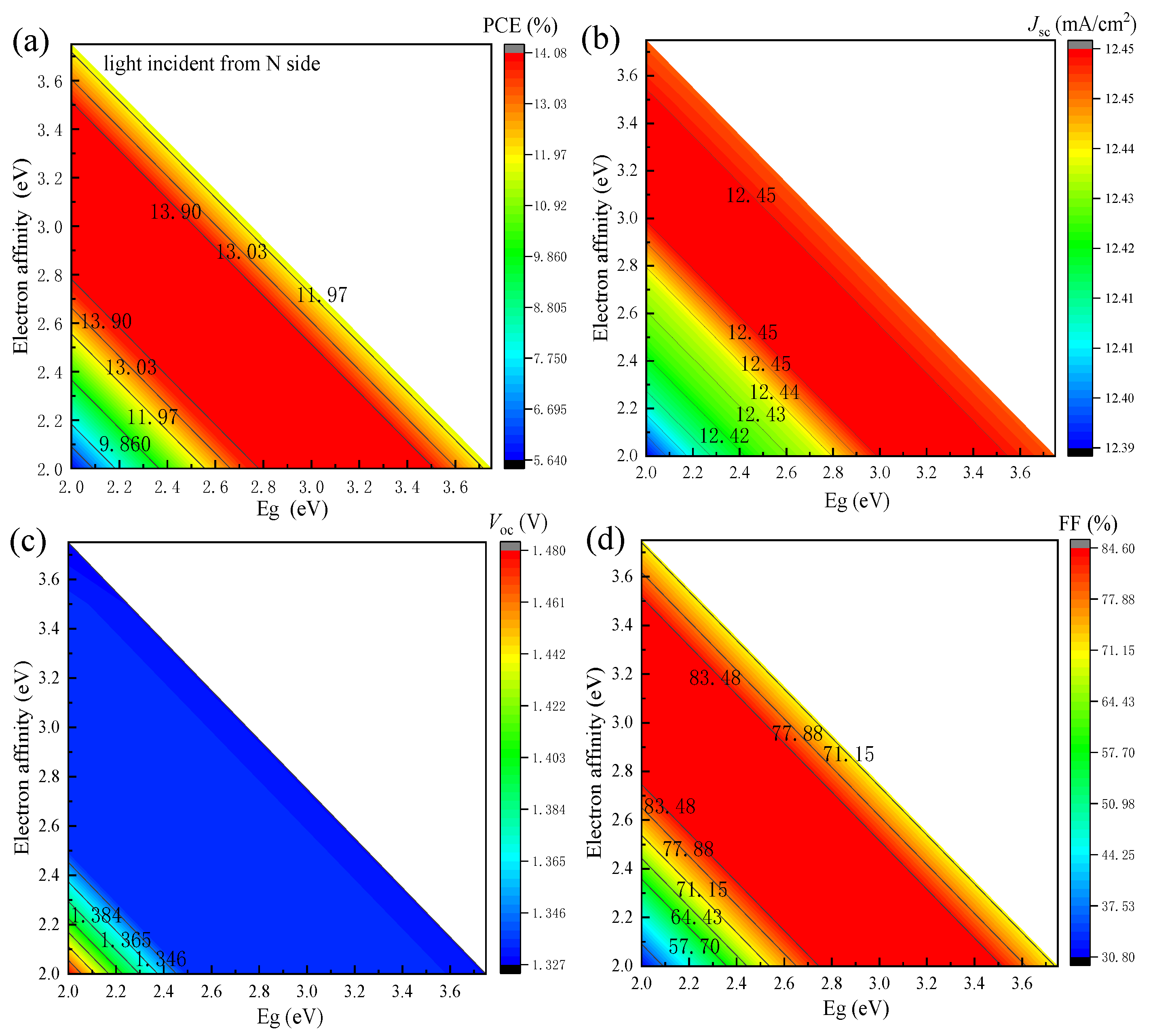
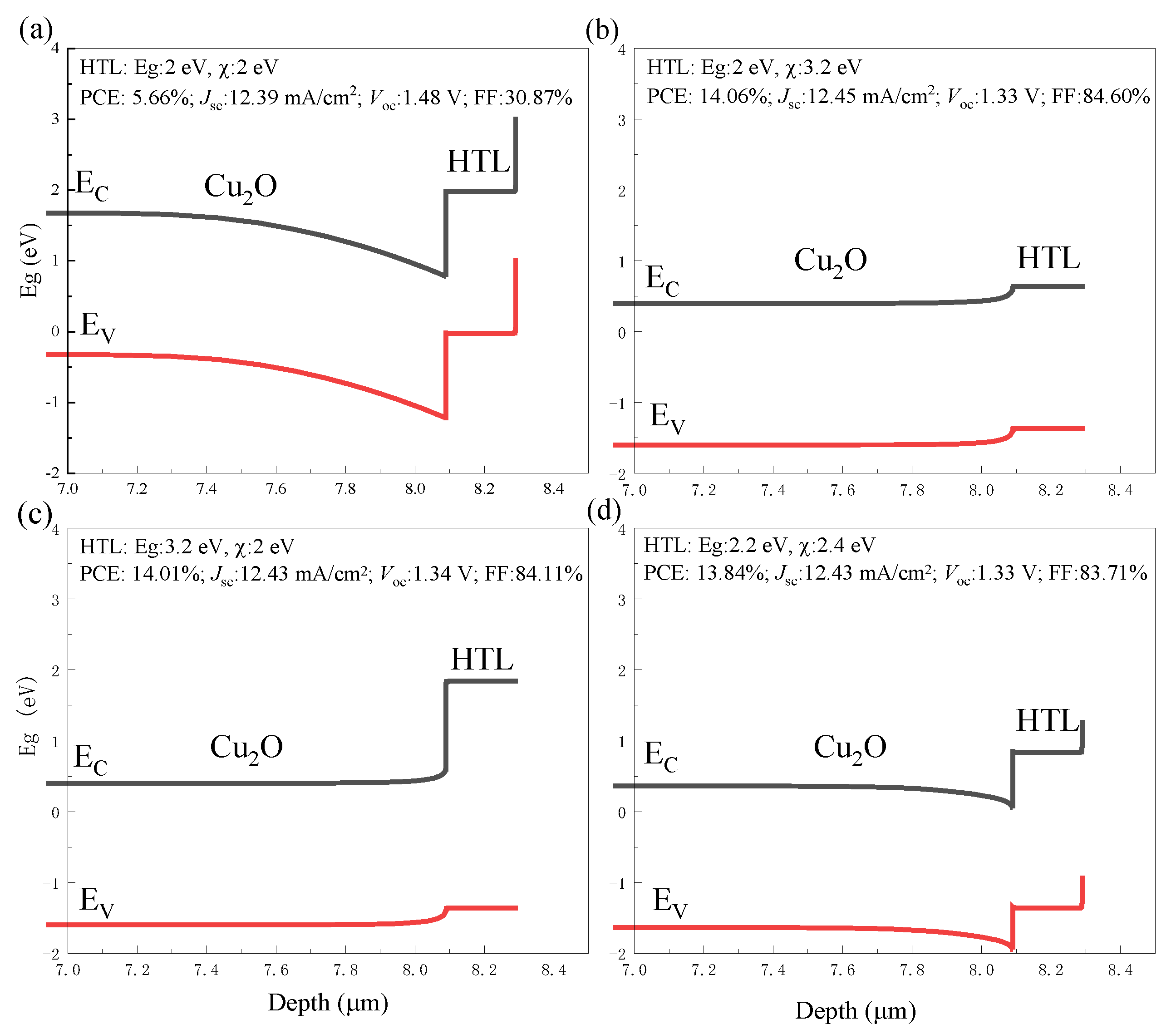
3.1. The Effect of Bandgap and Electron Affinity of the ETL and Buffer Layers

Toshiba’s latest 10.5% Cu2O solar cell employs the stack ZnO(Al)/n-buffer/p-Cu2O/ZnO(Al)/glass (10 × 3 mm2, AM1.5G, open-circuit voltage (Voc) = 0.86 V, short-circuit current density (Jsc) = 15.8 mA cm−2, fill factor (FF) = 71.2%). In line with this architecture, the present simulations initialized the structure with ZnO(Al) as the electron-transport layer (ETL) and Cu2O(P+) as the hole-transport layer (HTL). In the absence of a buffer, the ZnO(Al)/Cu2O/Cu2O(P+) device exhibits an S-shaped J–V curve (Figure 2a) because the large CBM and VBM offset between ZnO(Al) and Cu2O creates a substantial electron barrier that impedes carrier transport. Inserting a 10 nm buffer lowers this barrier; however, the thicker buffer introduces significant parasitic absorption, reducing the Jsc. Figure 2b illustrates the band alignment before and after buffer insertion. By tuning the electron affinity of the ETL, the CBM and VBM positions can be adjusted to further minimize the band offset and barrier height. The simulations fixed the Cu2O absorber at 10 μm thickness with a doping concentration of 1 × 1015 cm−3, the ETL at 80 nm with 1 × 1020 cm−3, and the buffer at 2 nm with 1 × 1020 cm−3, while systematically varying the Eg and electron affinity of the ETL and buffer to investigate their influence on band alignment and solar-cell performance, thereby identifying more suitable ETL, buffer, and HTL layers based on the optimal Eg and electron affinity values.
Compared with the Jsc and Voc, the electron affinity (χ) of both the electron transport layer (ETL) and the buffer layer exerted a more pronounced influence on the fill factor (FF) of solar cells. As summarized in Table 2, when the buffer layer’s electron affinity was set equal to that of the Cu2O absorber (3.2 eV), an increase in the ETL’s electron affinity from 3.5 eV to 3.9 eV caused a downshift in the CBM of the ETL. This enlarged the CBO between the ETL and buffer layers, thereby introducing a higher electron extraction barrier, as illustrated in Figure 3a. Consequently, the FF decreased from 88.29% to 85.85%, while Voc and Jsc remained largely unchanged. To mitigate this barrier, the electron affinity difference between the ETL and buffer layers should be minimized. This leads to two optimal χ combinations: buffer χ = 3.2 eV with ETL χ = 3.5 eV, and buffer χ = 3.5 eV with ETL χ = 3.9 eV. Due to the relatively small CBO at the buffer/Cu2O interface in these cases, the performance degradation remained limited—the efficiency only dropped from 13.64% to 13.26%. However, when the buffer’s electron affinity increased to 3.9 eV, the FF declined sharply to 79.14%, which can be attributed to the more significant band offset at the buffer/Cu2O interface.
By fixing the electron affinity of both the buffer and ETL at 3.9 eV, we further systematically examined the effect of bandgap alignment among the buffer, ETL, and Cu2O layers on device performance. Under constant electron affinity, the CBM position remained fixed, while variations in the bandgap (Eg) solely altered the valence band maximum (VBM). As shown in Figure 3b, buffer layers with Eg = 5 eV and 4 eV introduced considerable hole transport barriers at the buffer/Cu2O interface. These barriers progressively diminished as the Eg decreased. This observation wase further corroborated by the current density–voltage (J–V) characteristics: pronounced S-shaped curves appeared at Eg = 5 eV and 4 eV—indicative of notable band offsets—while such distortions disappeared when the Eg was reduced to 3 eV and 2 eV (Figure 3d). Correspondingly, as listed in Table 2, reducing the buffer Eg from 5 eV to 2 eV led to a marked enhancement in device performance: the power conversion efficiency improved from 12.21% to 13.62%, Voc rose from 1.392 V to 1.479 V, and Jsc increased from 11.08 mA/cm2 to 12.28 mA/cm2.
These simulation results can be further elucidated and validated through the analysis of defect-mediated recombination dynamics and quantum efficiency (QE), as illustrated in Figure 4a,b. The analysis must consider the critical role of defects, as they fundamentally govern recombination processes in solar cells. Figure 4a demonstrates that when the buffer layer bandgap was 5 eV, enhanced recombination rates emerged at the ETL/buffer interface, where the combination of a high defect density (1.0 × 1018 cm−3) with deep-level states at 0.60 eV in the ETL layer and 1.20 eV in the buffer layer, along with the hole transport barrier formed between these layers, created optimal conditions for severe recombination. This defect-enhanced environment impeded hole movement toward the back contact collection region and strongly promoted trap-assisted recombination at defect centers. The short carrier lifetimes (10 ns) and limited diffusion lengths (0.28–0.51 μm for electrons, 0.088–0.0011 μm for holes) further confirmed the dominant role of defects in these recombination processes. This defect-driven recombination phenomenon directly caused the observed short-wavelength spectral response losses, as evidenced in Figure 4b. Notably, under optimized valence band offset conditions, minimizing the buffer layer bandgap proves essential not only for suppressing parasitic absorption effects, but also for mitigating the detrimental impact of these defects on carrier collection efficiency. Consequently, the device performance exhibited a comprehensive improvement: the PCE increased from 12.21% to 13.62%, the Voc rose by 87 mV, and the Jsc improved by 1.2 mA/cm2 (Table 2).
A combined analysis of defect engineering and band alignment suggests that materials with electron affinities in the range of 3.5–3.9 eV (e.g., GaN or Mg-doped ZnO) are optimal for the ETL layer. These materials not only fulfill the band alignment requirements, but also exhibit shallow defect levels, which help reduce non-radiative recombination losses. Furthermore, their excellent interface compatibility with Cu2O minimizes interfacial defect states, thereby enhancing carrier transport across the heterojunction. The superior electron mobility of GaN (~1000 cm2/V·s) particularly facilitates rapid electron extraction while suppressing bulk recombination, contributing significantly to the improved Jsc and FF. These findings provide critical theoretical guidance for the further optimization of Cu2O-based heterojunction solar cells. Specifically, under optimized valence band offset conditions, minimizing the buffer layer bandgap helps suppress parasitic absorption while maintaining favorable band alignment for efficient carrier transport. Based on band alignment theory and material feasibility, we systematically evaluated various ETL and buffer candidate materials. For the ETL layer, ZnO:Mg (Eg = 3.6 eV, χ = 3.4 eV) and GaN (Eg = 3.4 eV, χ = 3.5 eV) exhibited ideal electron affinity matching (3.5–3.9 eV), with GaN demonstrating superior electron mobility (~1000 cm2/V·s), facilitating efficient electron transport and collection [35]. For the buffer layer, GaP (Eg = 2.4 eV, χ = 3.6 eV) not only met band structure requirements (Eg: 2–5 eV, χ: 3.2–3.5 eV), but also exhibited significantly higher hole mobility (~100 cm2/V·s) compared with Ga2O3 (~10 cm2/V·s) [37]. Notably, GaN can be reliably grown via metal–organic chemical vapor deposition (MOCVD), while GaP can achieve high-quality epitaxial growth via molecular beam epitaxy (MBE), ensuring excellent process compatibility for both materials [38]. In contrast, although Ga2O3 (Eg = 4.7 eV, χ = 3.5 eV) exhibited suitable band alignment, its low carrier mobility and high growth temperature (>800 °C) may limit practical applications [39]. These results offer valuable insights into interface engineering and material selection for high-performance Cu2O-based solar cells.

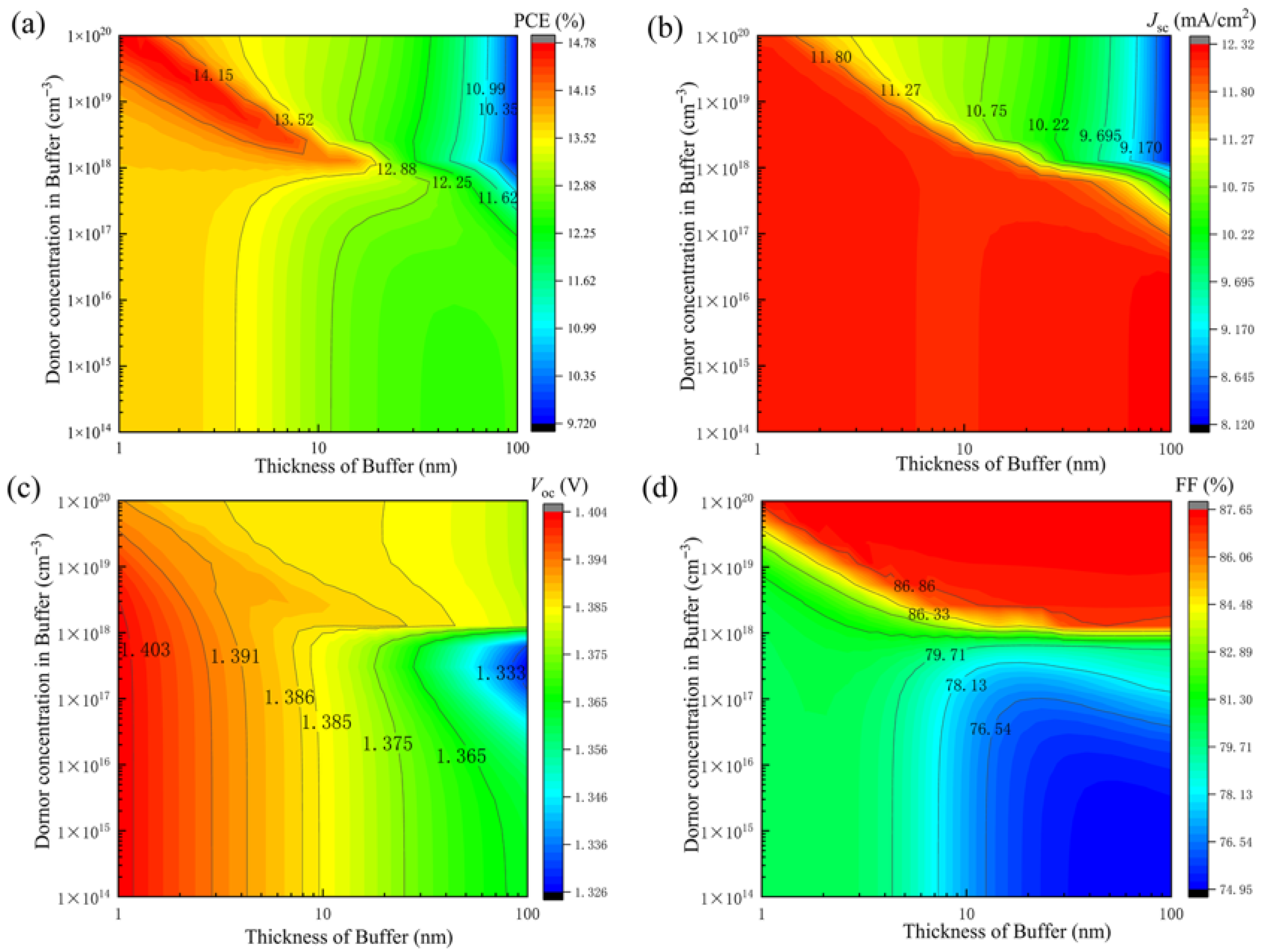
3.2. Influence of Buffer Thickness and Doping Concentration

The thickness and doping level of the buffer may have significant impacts on solar cell performance, considering parasitic absorption, carrier transport resistance, and Auger recombination. The effect of buffer layer thickness and doping concentration is discussed according to the appropriate value range of electron affinity and the bandgap of the ETL and buffer layer parameters described in Section 3.1.
The optimal buffer is both highly doped (or equivalently possesses a high carrier concentration) and ultrathin. The highest PCE was obtained when the buffer doping level and thickness were in the ranges of 1 × 1018–1 × 1020 cm−3 and 1–10 nm, respectively, as illustrated in Figure 5a–d. A trade-off among the Jsc, Voc, and FF dictates the precise combination of doping and thickness that yields the maximum PCE. For instance, when the buffer was doped to 1 × 1019 cm−3 and thinned to 8 nm, the Cu2O solar cell reached its peak efficiency of 14.78%. Consequently, higher performance in this cell architecture demands a thinner buffer with elevated doping.
The underlying mechanism governing the doping/thickness combinations shown in Figure 5b–d stems from the competing effects of parasitic optical absorption, recombination, and electronic conductivity within the buffer. First, a thin and lightly-doped buffer mitigates parasitic absorption, thereby enhancing Jsc; this trend was especially pronounced when the doping fell below 1 × 1018 cm−3. Simultaneously, reduced thickness and lower doping suppressed Auger recombination, boosting Voc (Figure 5c). However, these conditions do not favor a high fill factor (Figure 5d). Because the buffer’s electronic conductivity scales with the product of doping and thickness, a high FF can still be achieved in ultrathin films (~1–8 nm), provided the doping exceeds 1 × 1019 cm−3; conversely, if the doping is below 1 × 1019 cm−3, a thickness larger than 8 nm becomes tolerable. Extremely thin buffers may allow quantum tunnelling, which could further benefit carrier transport by enabling electron passage while blocking hole recombination; however, this phenomenon lies beyond the scope of the present simulation. From an experimental standpoint, fabricating an 8 nm (or thinner) buffer with a doping concentration of 1 × 1019 cm−3 and sufficiently low defect density is challenging, and therefore the simulation did not consider buffer thicknesses below 8 nm.

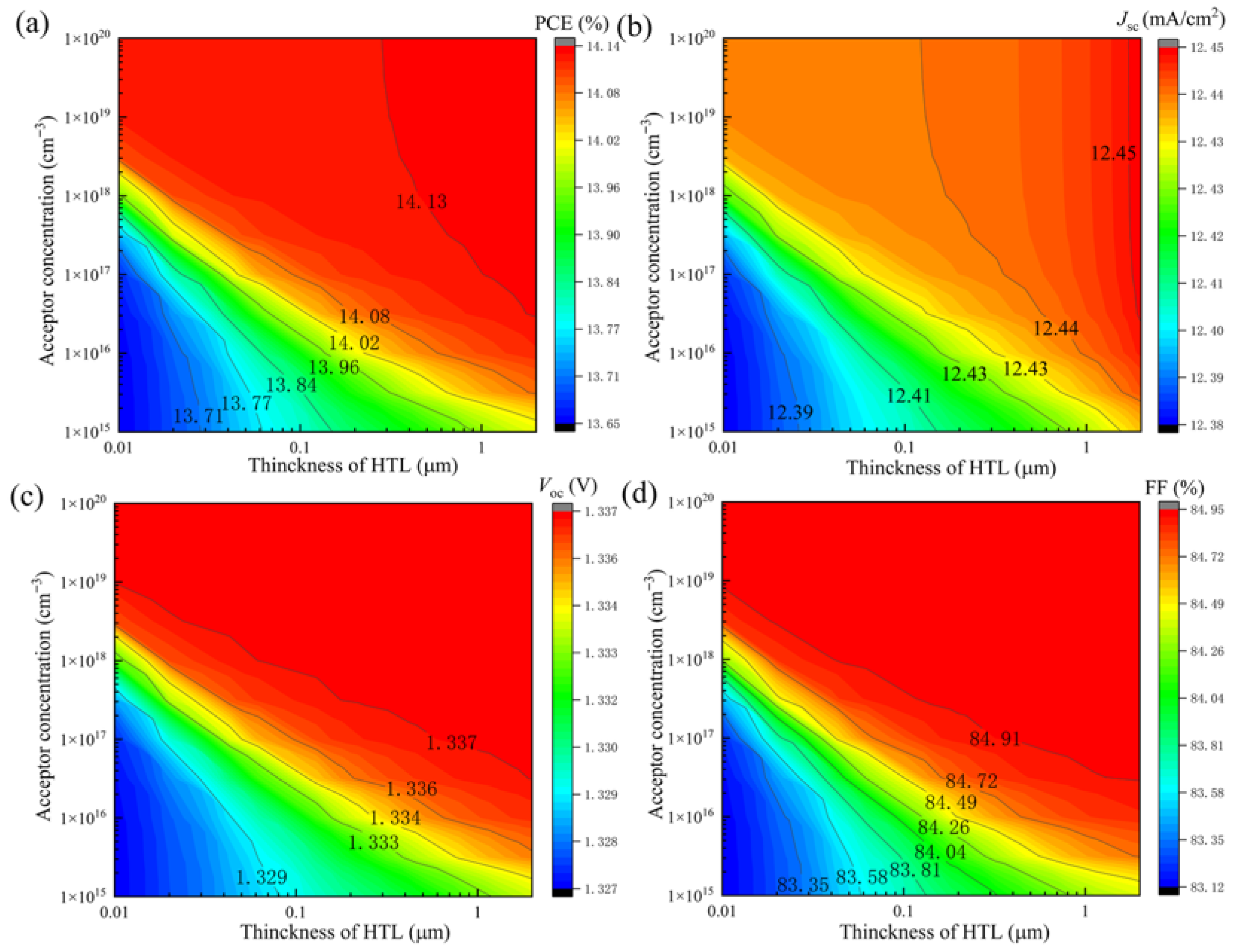
3.3. The Impact of the Bandgap, Electron Affinity, Thickness, and Doping Concentration of the HTL Layer

As previously mentioned, to minimize hole transport barriers between the Cu2O absorption layer and HTL, careful matching of band gaps and electron affinities is essential. Figure 6 demonstrates the impact of HTL layer electron affinity and Eg on the photovoltaic parameters (PCE, Jsc, Voc, and FF) of the Cu2O solar cells. The results revealed that optimal device performance occurred when both parameters fell within 2.7–3.6 eV (red zone in Figure 6), with maximum efficiency requiring specific Eg-χ combinations: either low Eg with high χ (e.g., Eg = 2.4 eV, χ = 3.6 eV) or high Eg with low χ (e.g., Eg = 3.6 eV, χ = 2.0 eV). This behavior, similar to our ETL findings, primarily influences FF through band offset modulation. The selected HTL materials must satisfy Eg (2–3.5 eV), χ (1.9–3.76 eV), and Ev (χ + Eg = 4.7–5.5 eV) to ensure proper alignment with Cu2O (Ev≈5.1 eV). While heavily doped Cu2O serves as an effective HTL by creating a back-surface field, alternative materials offer distinct advantages: SiCx (Eg = 2–2.25 eV, χ = 3.76 eV) provides excellent lattice matching; ZnTe (Eg = 2.26 eV, χ = 3.53 eV) offers superior p-type dopability; and NiOx(Cu) (Eg = 3.75 eV, χ = 1.9 eV) enables solution processing. These materials have demonstrated successful integration in similar heterostructures. This comprehensive evaluation of band alignment and material properties provides justification for our material selections while maintaining all original simulation results and conclusions [40,41,42,43].
Figure 7 shows the energy band diagrams of the Cu2O/HTL interface, illustrating the influence of the HTL layer’s band gap and electron affinity on solar cell performance. In Figure 7a,b, we maintained the HTL layer’s band gap equal to that of the Cu2O absorber layer (2 eV) while comparing the band offset under two conditions: when the electron affinity difference across the Cu2O/HTL junction was either large or small. As shown in Figure 7a, when the electron-affinity offset was large, the CBM of Cu2O and that of the HTL were separated by a substantial energy. The resulting large CBO erected a significant barrier to electron transport from the Cu2O absorber into the HTL, which lowered the fill factor to 30.86% and reduced the power-conversion efficiency (PCE) to 5.66%. Conversely, when the electron-affinity difference was small, the CBO was reduced and the electron barrier height diminished, promoting efficient carrier extraction and raising the fill factor to 84.60% and the PCE to 14.06%, as depicted in Figure 7b. Nevertheless, even with a large electron-affinity offset, the device performance can still be optimized by adjusting the HTL band gap. When the HTL band gap was increased to 3.2 eV and its electron affinity was set to 2 eV, the HTL CBM was 1.2 eV above the Cu2O CBM (Figure 7c). Although the CBO remained at 1.2 eV, the larger HTL band gap yielded a smaller VBO at the Cu2O/HTL interface, leading to a PCE of 14.01% (Jsc = 12.43 mA cm−2, Voc = 1.34 V, FF = 84.11%). Finally, choosing an HTL band gap of 2.2 eV and an electron affinity of 2.4 eV produced a CBO of 0.8 eV and a VBO of 0.4 eV (Figure 7d). These moderate band offsets yielded a PCE of 13.84% (Jsc = 12.43 mA/cm2, Voc = 1.33 V, FF = 83.71%).
In terms of the effect of doping concentration and thickness of HTL, the increase in PCE for the solar cells was approximately 0.5% when using an elevated doping level with a thickness range of 10 nm to 1 μm, as shown in Figure 8a–d. The performance improvement mainly came from the enhancement of FF for the same reason as ETL. The thickness of HTL had a tiny impact on the light absorption, which had little effect on Jsc. An optimal PCE of 14.14% was obtained as the HTL layer with the following parameters: thickness of 100 nm, doping concentration of 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV. The thickness of the Cu2O absorption layer decreased from 10 to 8 μm, which caused the PCE to decline from 14.78% to 14.14%, as shown in Figure 5a. Therefore, further investigation of the parameters for the Cu2O absorption layer was required.

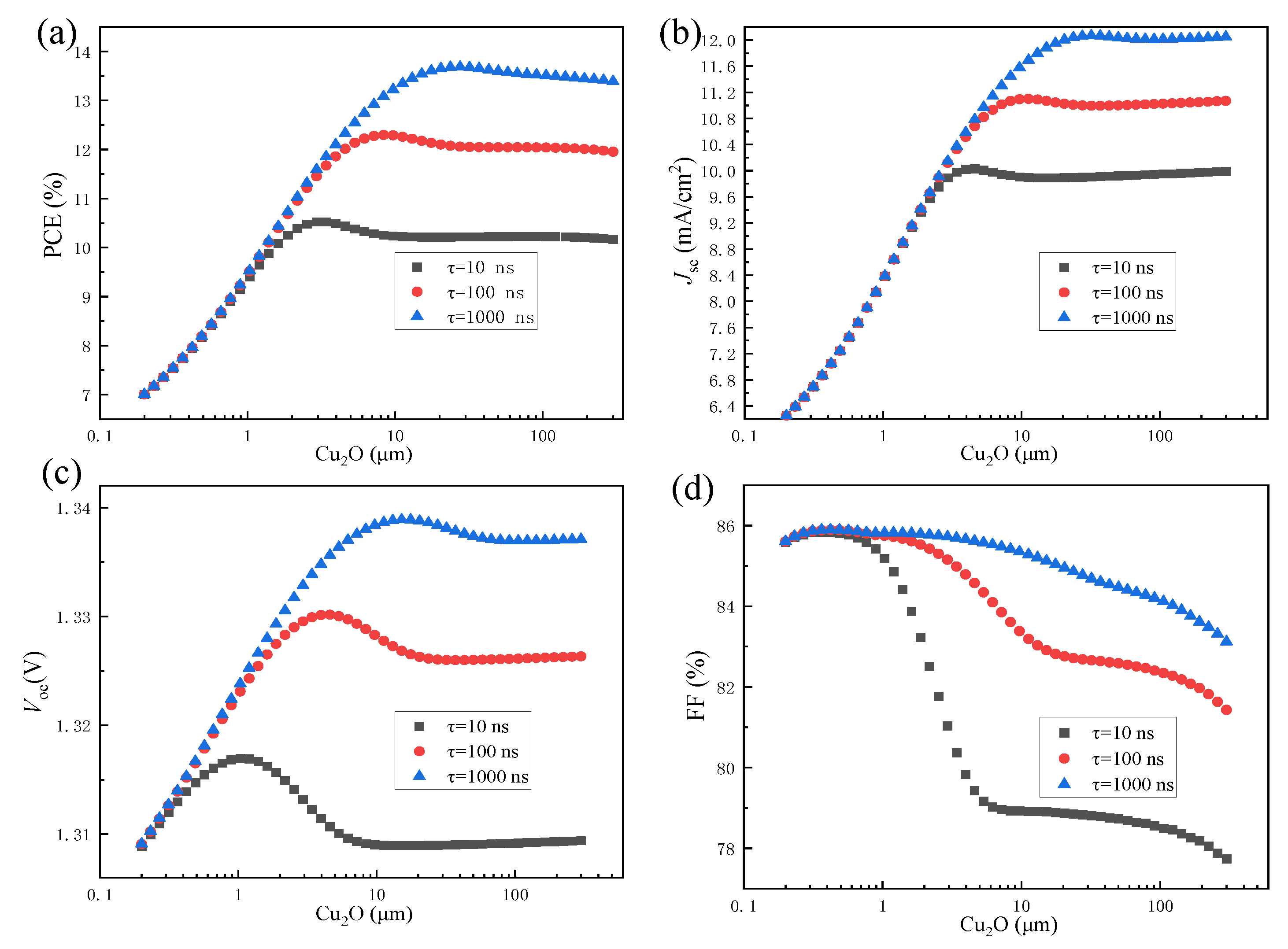
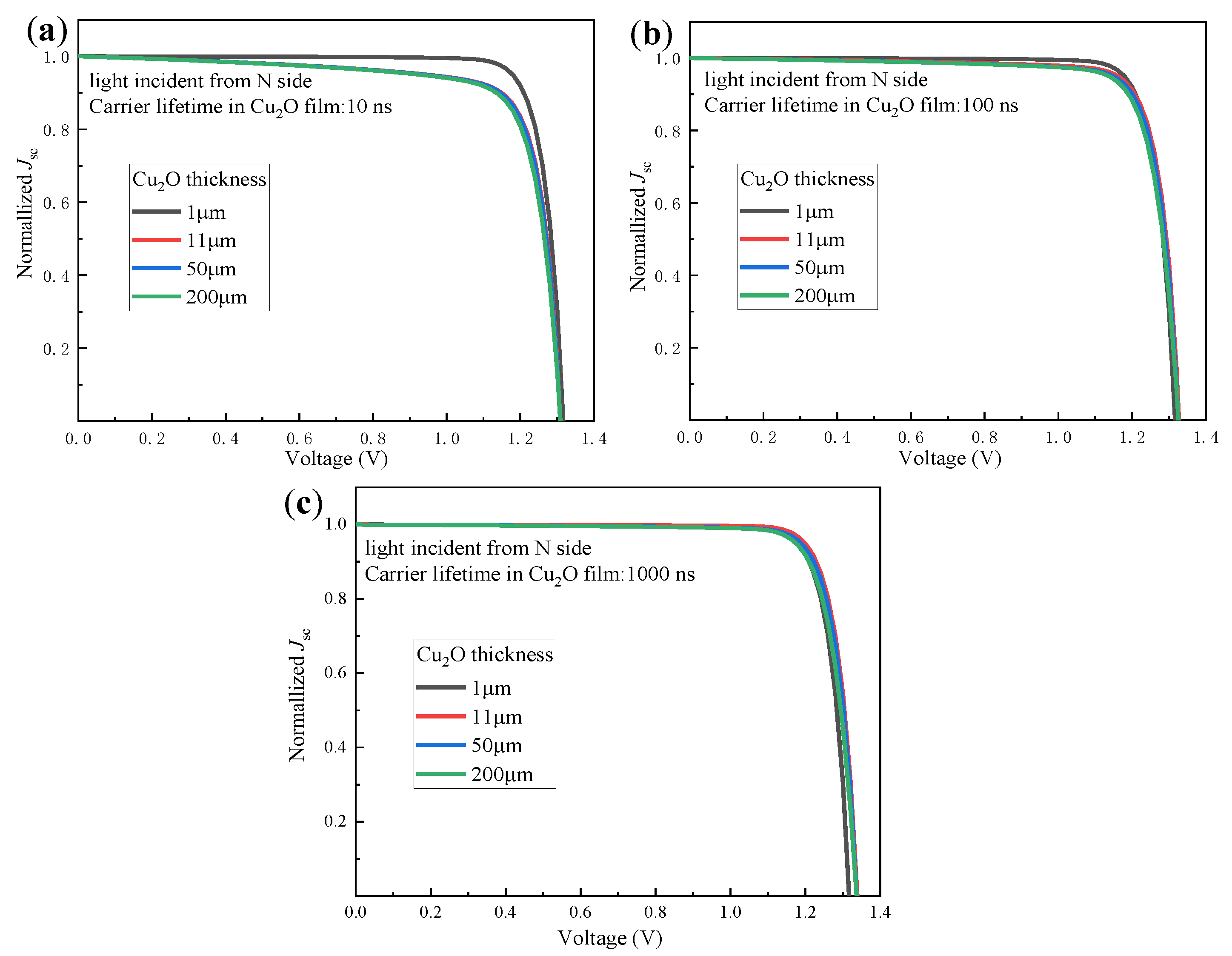
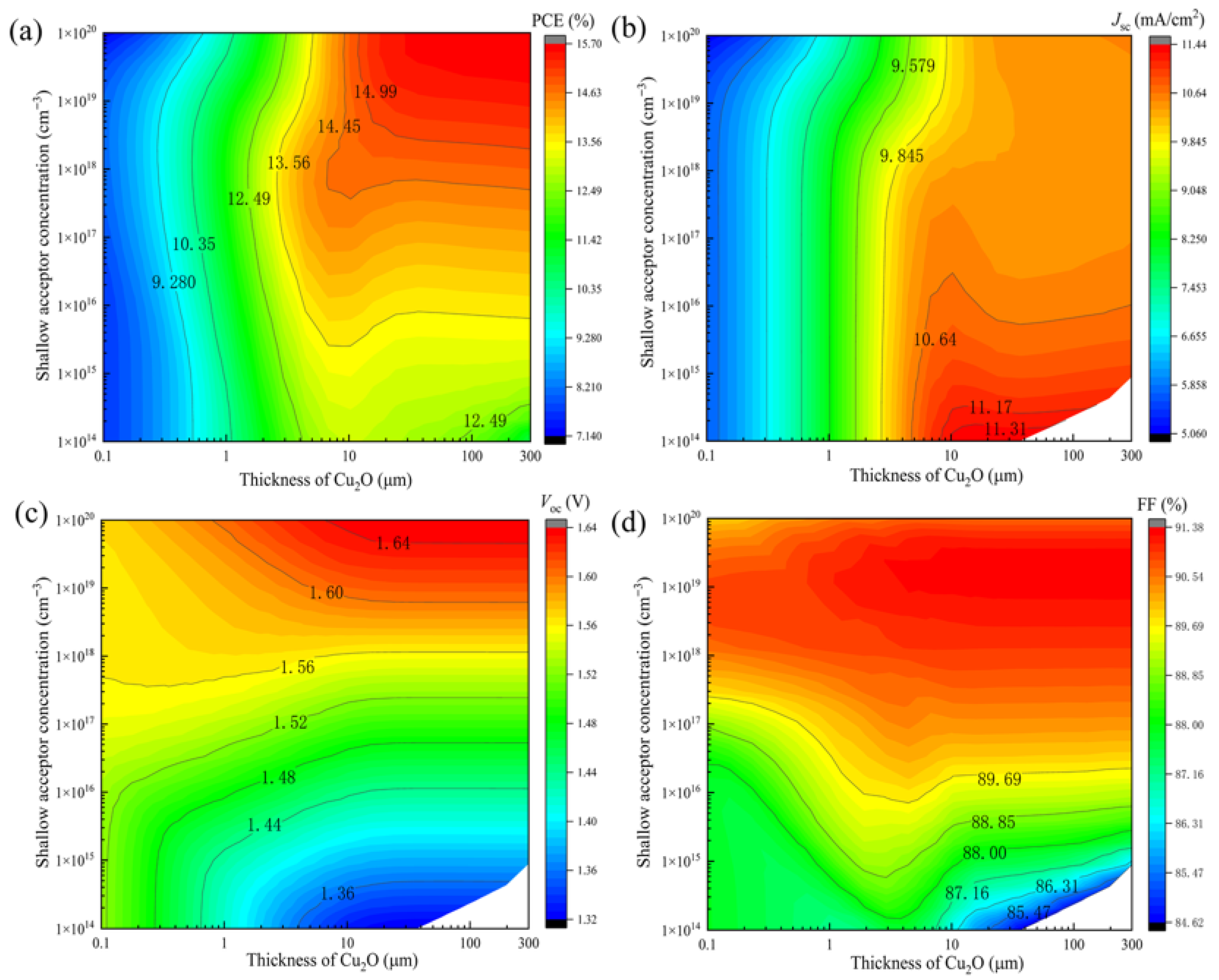
3.4. The Effect of Carrier Lifetime, Thickness, and Doping Concentration of the Cu2O Absorber Layer

The minority carrier lifetime, thickness, and doping concentration of the Cu2O absorber will affect the light absorption, carrier diffusion, and recombination as well as the performance of the Cu2O-based solar cell. Figure 9a–d illustrates the impact of minority carrier lifetime and Cu2O absorption layer thickness on the performance of Cu2O-based solar cells, where the higher the minority carrier lifetime, the better the performance of the device with a lifetime ranging from 10 to 1000 ns. This is because increasing the minority carrier lifetime would cause the carrier to have a sufficient diffusion length for collection. Furthermore, the trends shown in the curves in Figure 9a–c indicate that the PCE, Jsc, and Voc values initially increased with an increase in Cu2O thickness, followed by a slight decrease before stabilizing. The reason behind this pattern is evident. Within the range of carrier diffusion length, increasing the thickness of the Cu2O absorption layer helped to enhance light absorption and carrier concentration. Conversely, if the Cu2O absorption layer thickness exceeded its carrier diffusion length, the carrier recombination in the Cu2O bulk limited its diffusion to the buffer layer for collection.
This conclusion is fully corroborated by the quantum-efficiency (QE) simulations presented in Figure 10. Within the 10–100 ns minority-carrier-lifetime window, Cu2O layers of 8 μm and 50 μm yielded identical QE curves, a direct consequence of Cu2O’s intense absorption in the visible range (400–600 nm). Due to its direct band gap of 2 eV, the absorption coefficient rose sharply at short wavelengths, so photogeneration was concentrated near the buffer interface. Over this lifetime, range carrier collection is limited by the minority-carrier diffusion length rather than by the optical absorption depth; therefore, increasing the Cu2O thickness brings no appreciable QE gain. The saturation observed around 550 nm mirrors the intrinsic absorption edge of Cu2O and explains why Jsc is capped under these conditions. When the lifetime was extended to 1000 ns, the QE in the long-wavelength region (>600 nm) improved markedly. High-lifetime carriers can now traverse the thicker absorber without excessive recombination, underscoring the intricate coupling between spectral absorption and carrier transport. At these wavelengths, the lower photon energy increases the absorption depth, making lifetime the dominant limit on Jsc. The wavelength-dependent collection efficiency thus embodies the competition between photogeneration and carrier extraction in the Cu2O solar cells. Complementing the QE results, Figure 8d reveals a sharp decline in fill factor with increasing thickness, especially when the lifetimes fell below 100 ns. This behavior can be clarified by the current–voltage characteristics in Figure 11a–c. Higher recombination within thicker Cu2O layers manifests as increased leakage current, reflected in lower shunt resistance (Rsh). At 10 ns lifetime (Figure 11a), Rsh dropped rapidly once the Cu2O thickness exceeded 1 μm, directly degrading FF. Raising the lifetime to 100 ns (Figure 11b) and further to 1000 ns (Figure 11c) mitigated the thickness dependence of Rsh, making its contribution negligible. However, a pronounced rise in series resistance (Rse) remained evident, continuing to erode FF. Hence, even under these improved lifetime conditions, the resistive losses of the Cu2O layer must still be carefully considered.
Figure 12a–d presents the influence of Cu2O absorber doping concentration and thickness on the PCE, Jsc, Voc and FF, obtained for a p-type Cu2O layer with a minority-carrier lifetime of 100 ns. A thicker absorber enhances the Jsc, whereas a lower doping level reduces defect-assisted trapping and Auger recombination losses. As shown in Figure 12b, the maximum Jsc of 11.44 mA/cm2 was reached at a low doping concentration (1 × 1014–1 × 1015 cm−3) when the thickness exceeded 10 µm. Raising the doping concentration is required to increase the Voc irrespective of thickness (Figure 12c); nevertheless, the simulated range of 1 × 1019–1 × 1020 cm−3 lies beyond the experimentally viable window for Cu2O. Practical devices should therefore limit the bulk doping to 1 × 1014–1 × 1017 cm−3 and rely on interface passivation to preserve long diffusion lengths while still achieving a high Voc. Both higher doping and greater thickness improved the Cu2O film conductivity and the device FF, but the effect of doping dominated (Figure 12d). Under the simulation conditions, the optimal PCE of 14.12% (Voc = 1.51 V, Jsc = 10.52 mA/cm2, FF = 88.9%) was predicted for a Cu2O absorber layer with a doping concentration of 1 × 1014–1 × 1017 cm−3 and a thickness of 13–150 µm. It should be noted that although a PCE exceeding 15% can be achieved when the doping concentration of Cu2O reaches 1 × 1019–1 × 1020 cm−3, such heavy bulk doping would provoke increased Auger recombination, lead to a collapse in minority-carrier lifetime and diffusion length, cause band-gap narrowing, and induce tunnelling leakage. Therefore, in experimental work, the doping of Cu2O should be limited to 1 × 1014–1 × 1017 cm−3, and efforts should focus on interface engineering and defect passivation rather than indiscriminate doping to enhance Voc and overall performance. These findings indicate that an optimized ETL/buffer/Cu2O/HTL solar cell requires a moderately doped Cu2O absorber layer with a carrier lifetime exceeding 100 ns, enabling absorber thicknesses on the order of tens of micrometers.
The high simulated Voc and FF presented here contrast with the typically lower values reported for real ZnO–Cu2O solar cells. This discrepancy arises primarily from three non-ideal factors prevalent in fabricated devices but not accounted for in the idealized simulation: (1) significant band offsets at the heterojunction interface, which impede carrier transport and promote recombination, thereby degrading both Voc and FF [13,15]; (2) pronounced interface defects and impurities (e.g., Cu or CuO phases), which act as recombination centers and shunt paths, further reducing Voc, FF [14]; and (3) impure Cu2O bulk material with high defect density, which shortens the minority-carrier lifetime well below the 100 ns used in the simulation.
To bridge this gap and achieve the high performance predicted by the simulation, future work should prioritize interface and defect engineering over merely pursuing high bulk doping. Specifically, inserting suitable buffer layers (e.g., Ga2O3 or Zn1–xGexO) can mitigate the large band offsets and improve band alignment [34,44]. Simultaneously, advanced deposition techniques with precise control over process parameters (e.g., O2 flux) are essential to suppress the formation of secondary phases and reduce interface state density [40]. Moreover, reducing thin-film surface roughness, suppressing interface defects, controlling oxidation extent, and passivating defects such as Cu and CuO are equally critical for enhancing device performance [45,46]. By combining a moderately doped, high-lifetime Cu2O absorber (as identified in our simulation) with such interface optimization strategies, the practical Voc and FF of Cu2O solar cells can be significantly enhanced toward their theoretical potential.

4. Conclusions

Using SCAPS-1D, we carried out a systematic investigation of the optimal parameters for every functional layer in an ETL/buffer/Cu2O/HTL Cu2O solar cell in order to maximize device performance. The simulations revealed that selecting materials with closely matched electron affinities effectively shrinks the CBO and lowers the barrier created by band bending, thereby facilitating carrier transport. Adjusting the band gap of a material shifts its VBM and can therefore be used to reduce the VBO. In addition, we performed a comprehensive study of the doping concentrations and thicknesses of the ETL, buffer, and HTL layers to balance the competing demands of series resistance, Auger recombination and parasitic absorption. The optimal buffer layer was 8 nm thick and doped at 1 × 1019 cm−3, whereas the optimal HTL was about 100 nm thick and doped at 1 × 1020 cm−3. For the Cu2O absorber, the best performance was obtained with doping between 1 × 1014 and 1 × 1017 cm−3 and a thickness in the 13–150 µm range. Candidate materials for each functional layer are proposed: (1) ETL: ZnO:Mg, GaN; (2) Buffer: GaP, GaN, Ga2O3; (3) HTL: Cu2O, SiCx, NiOx(Cu), and ZnTe. These findings provide valuable guidance for the structural design and process optimization of Cu2O solar cells.

Author Contributions

Methodology, S.C. and C.Z.; Software, S.C.; Resources, S.C., L.W., C.Z., J.Y. and X.J.; Writing—original draft, S.C. and C.Z.; Writing—review & editing, S.C. and C.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 62104228) and the Research Program of Institute of Electrical Engineering, Chinese Academy of Sciences (Grant No. E1551401).

Data Availability Statement

The core experimental datasets and analytical results supporting this study are fully documented within the main body of this article. All processed data points and statistical analyses referenced throughout this work can be directly traced to the corresponding sections in the main text.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lakshmanan, A.; Alex, Z.C.; Meher, S.R. Recent advances in cuprous oxide thin film based photovoltaics. Mater. Today Sustain. 2022, 20, 100244. [Google Scholar] [CrossRef]
  2. Farhad, S.F.U.; Hossain, A.; Tanvir, N.I.; Akter, R.; Patwary, A.M.; Shahjahan, M.; Rahman, M.A. Structural, optical, electrical, and photoelectrochemical properties of cuprous oxide thin films grown by modified silar method. Mater. Sci. Semicond. Process. 2019, 95, 68–75. [Google Scholar] [CrossRef]
  3. Hsu, Y.-K.; Wu, J.-R.; Chen, M.-H.; Chen, Y.-C.; Lin, Y.-G. Fabrication of homojunction Cu2O solar cells by electrochemical deposition. Appl. Surf. Sci. 2015, 354, 8–13. [Google Scholar] [CrossRef]
  4. Cui, J.; Gibson, U.J. A simple two-step electrodeposition of Cu2O/ZnO nanopillar solar cells. J. Phys. Chem. C 2010, 114, 6408–6412. [Google Scholar] [CrossRef]
  5. Mitroi, M.R.; Ninulescu, V.; Fara, L. Tandem solar cells based on Cu2O and c-si subcells in parallel configuration: Numerical simulation. Int. J. Photoenergy 2017, 2017, 7284367. [Google Scholar] [CrossRef]
  6. Nakagawa, N.; Shibasaki, S.; Honishi, Y.; Yamazaki, M.; Hiraoka, Y.S.; Yamamoto, K. Development of a zn-based n-layer in cuprous oxide top cells for high-efficiency tandem photovoltaics. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, ON, Canada, 15 June–21 August 2020; pp. 0983–0985. [Google Scholar]
  7. Chen, S.; Wang, L.; Zhou, C.; Yang, J. A review of Cu2O solar cell. J. Renew. Sustain. Energy 2023, 15, 062701. [Google Scholar] [CrossRef]
  8. Yang, M.; Zhu, L.; Li, Y.; Cao, L.; Guo, Y. Asymmetric interface band alignments of Cu2O/ZnO and ZnO/Cu2O heterojunctions. J. Alloys Compd. 2013, 578, 143–147. [Google Scholar] [CrossRef]
  9. Martin, G.; Botchkarev, A.; Rockett, A.; Morkoc, H. Valence-band discontinuities of wurtzite gan, aln, and inn heterojunctions measured by x-ray photoemission spectroscopy. Appl. Phys. Lett. 1996, 68, 2541–2543. [Google Scholar] [CrossRef]
  10. Dong, C.J.; Yu, W.X.; Xu, M.; Cao, J.J.; Chen, C.; Yu, W.W.; Wang, Y.D. Valence band offset of Cu2O/in2o3 heterojunction determined by x-ray photoelectron spectroscopy. J. Appl. Phys. 2011, 110, 139. [Google Scholar] [CrossRef]
  11. Kramm, B.; Laufer, A.; Reppin, D.; Kronenberger, A.; Hering, P.; Polity, A.; Meyer, B.K. The band alignment of Cu2O/ZnO and Cu2O/gan heterostructures. Appl. Phys. Lett. 2012, 100, 094102. [Google Scholar] [CrossRef]
  12. Guo, Y.M.; Zhu, L.P.; Jiang, J.; Hu, L.; Ye, C.L.; Ye, Z.Z. Valence band offset of n-ZnO/p-mgxni1-xo heterojunction measured by x-ray photoelectron spectroscopy. Appl. Phys. Lett. 2012, 101, 052109. [Google Scholar] [CrossRef]
  13. Hussain, S.; Cao, C.; Nabi, G.; Khan, W.S.; Usman, Z.; Mahmood, T. Effect of electrodeposition and annealing of ZnO on optical and photovoltaic properties of the p-Cu2O/n-ZnO solar cells. Electrochim. Acta 2011, 56, 8342–8346. [Google Scholar] [CrossRef]
  14. Zang, Z. Efficiency enhancement of ZnO/Cu2O solar cells with well oriented and micrometer grain sized Cu2O films. Appl. Phys. Lett. 2018, 112, 042106. [Google Scholar] [CrossRef]
  15. Mittiga, A.; Salza, E.; Sarto, F.; Tucci, M.; Vasanthi, R. Heterojunction solar cell with 2% efficiency based on a Cu2O substrate. Appl. Phys. Lett. 2006, 88, 163502. [Google Scholar] [CrossRef]
  16. Koda, D.S.; Bechstedt, F.; Marques, M.; Teles, L.K. Trends on band alignments: Validity of anderson’s rule in sns 2-and snse 2-based van der waals heterostructures. Phys. Rev. B 2018, 97, 165402. [Google Scholar] [CrossRef]
  17. Shiel, H.; Hutter, O.S.; Phillips, L.J.; Swallow, J.E.; Jones, L.A.; Featherstone, T.J.; Smiles, M.J.; Thakur, P.K.; Lee, T.L.; Dhanak, V.R.; et al. Natural band alignments and band offsets of Sb2Se3 solar cells. ACS Appl. Energy Mater. 2020, 3, 11617–11626. [Google Scholar] [CrossRef]
  18. Toshiba. Toshiba Boosts Transparent Cu2O Tandem Solar Cell to a New High. Available online: https://www.global.toshiba/ww/technology/corporate/rdc/rd/topics/22/2209-02.html (accessed on 22 October 2025).
  19. Yoshio, S.; Wada, A.; Shibasaki, S.; Nakagawa, N.; Mizuno, Y.; Honishi, Y.; Wakamatsu, K.; Toyota, M.; Yamamoto, T.; Sano, J.; et al. Thermal stability of cuprous oxide top cells for high-efficiency Cu2O/si tandem solar cells. In Proceedings of the 2024 IEEE 52nd Photovoltaic Specialist Conference (PVSC), Seattle, WA, USA, 9–14 June 2024; pp. 0149–0151. [Google Scholar]
  20. Shockley, W.; Queisser, H.J. Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
  21. Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin Solid Film. 2000, 361, 527–532. [Google Scholar] [CrossRef]
  22. Niemegeers, A.; Burgelman, M. Numerical modelling of ac-characteristics of cdte and cis solar cells. In Proceedings of the Conference Record of the Twenty Fifth IEEE Photovoltaic Specialists Conference-1996, Washington, DC, USA, 13–17 May 1996; pp. 901–904. [Google Scholar]
  23. Verschraegen, J.; Burgelman, M. Numerical modeling of intra-band tunneling for heterojunction solar cells in scaps. Thin Solid Film. 2007, 515, 6276–6279. [Google Scholar] [CrossRef]
  24. Degrave, S.; Burgelman, M.; Nollet, P. Modelling of polycrystalline thin film solar cells: New features in scaps version 2.3. In Proceedings of the 3rd World Conference onPhotovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; pp. 487–490. [Google Scholar]
  25. Decock, K.; Khelifi, S.; Burgelman, M. Modelling multivalent defects in thin film solar cells. Thin Solid Film. 2011, 519, 7481–7484. [Google Scholar] [CrossRef]
  26. Burgelman, M.; Marlein, J. Analysis of graded band gap solar cells with scaps. In Proceedings of the 23rd European Photovoltaic Solar Energy Conference, Valencia, Spain, 1–5 September 2008; pp. 2151–2155. [Google Scholar]
  27. Sekkat, A.; Bellet, D.; Chichignoud, G.; Kaminskicachopo, A. Unveiling key limitations of ZnO/Cu2O all-oxide solar cells through numerical simulations. ACS Appl. Energy Mater. 2022, 5, 5423–5433. [Google Scholar] [CrossRef]
  28. Sawicka-Chudy, P.; Sibiński, M.; Wisz, G.; Rybak-Wilusz, E.; Cholewa, M. Numerical analysis and optimization of Cu2O/Tio2 CuO/Tio2, heterojunction solar cells using scaps. J. Phys. Conf. Ser. 2018, 1033, 012002. [Google Scholar] [CrossRef]
  29. Fentahun, D.A.; Tyagi, A.; Kar, K.K. Numerically investigating the AZO/Cu2O heterojunction solar cell using ZnO/Cds buffer layer. Opt.—Int. J. Light Electron Opt. 2020, 228, 166228. [Google Scholar] [CrossRef]
  30. Chevallier, C.; Bose, S.; Hamady, S.O.S.; Fressengeas, N. Numerical investigations of the impact of buffer germanium composition and low cost fabrication of Cu2O on AZO/ZnGeO/Cu2O solar cell performances. Eur. Phys. J. Photovolt. 2021, 12, 3. [Google Scholar] [CrossRef]
  31. Rizi, M.T.; Abadi, M.S.; Ghaneii, M. Two dimensional modeling of Cu2O heterojunction solar cells based-on β-ga2o3 buffer. Optik 2018, 155, 121–132. [Google Scholar] [CrossRef]
  32. Lam, N.D. Modelling and numerical analysis of ZnO/CuO/Cu2O heterojunction solar cell using scaps. Eng. Res. Express 2020, 2, 025033. [Google Scholar] [CrossRef]
  33. Koné, K.E.; Bouich, A.; Soro, D.; Soucase, B.M. Insight of ZnO/CuO and ZnO/Cu2O solar cells efficiency with scaps simulator. Opt. Quantum Electron. 2023, 55, 616. [Google Scholar] [CrossRef]
  34. Minami, T.; Nishi, Y.; Miyata, T. High-efficiency Cu2O-based heterojunction solar cells fabricated using a Ga2O3 thin film as n-type layer. Appl. Phys. Express 2013, 6, 044101. [Google Scholar] [CrossRef]
  35. Giri, P.; Chakrabarti, P. Effect of Mg doping in ZnO buffer layer on ZnO thin film devices for electronic applications. Superlattices Microstruct. 2016, 93, 248–260. [Google Scholar] [CrossRef]
  36. Nishi, Y.; Miyata, T.; Minami, T. The impact of heterojunction formation temperature on obtainable conversion efficiency in n-ZnO/p-Cu2O solar cells. Thin Solid Film. 2013, 528, 72–76. [Google Scholar] [CrossRef]
  37. Hong, S.K.; Hanada, T.; Makino, H.; Chen, Y.; Ko, H.J.; Yao, T.; Tanaka, A.; Sasaki, H.; Sato, S. Band alignment at a ZnO/GaN (0001) heterointerface. Appl. Phys. Lett. 2001, 78, 3349–3351. [Google Scholar] [CrossRef]
  38. Matsumoto, K.; Yamaoka, Y.; Ubukata, A.; Arimura, T.; Piao, G.; Yano, Y.; Tokunaga, H.; Tabuchi, T. Opportunities and challenges in gan metal organic chemical vapor deposition for electron devices. Jpn. J. Appl. Phys. 2016, 55, 05FK04. [Google Scholar] [CrossRef]
  39. Yang, D.; Zhao, B.; Yang, T.; Lai, R.; Lan, D.; Friend, R.H.; Di, D. Toward stable and efficient perovskite light-emitting diodes. Adv. Funct. Mater. 2022, 32, 2109495. [Google Scholar] [CrossRef]
  40. Shibasaki, S.; Honishi, Y.; Nakagawa, N.; Yamazaki, M.; Mizuno, Y.; Nishida, Y.; Sugimoto, K.; Yamamoto, K. Highly transparent Cu2O absorbing layer for thin film solar cells. Appl. Phys. Lett. 2021, 119, 242102. [Google Scholar] [CrossRef]
  41. Chawki, N.; Rouchdi, M.; Alla, M.; Fares, B. Simulation and analysis of high-performance hole transport material srzrs3-based perovskite solar cells with a theoretical efficiency approaching 26%. Sol. Energy 2023, 262, 111913. [Google Scholar] [CrossRef]
  42. Suthar, D.; Patel, S.; Chander, S.; Kannan, M.; Dhaka, M. Enhanced physicochemical properties of znte thin films as potential buffer layer in solar cell applications. Solid State Sci. 2020, 107, 106346. [Google Scholar] [CrossRef]
  43. Yin, X.; Guo, Y.; Xie, H.; Que, W.; Kong, L.B. Nickel Oxide as Efficient Hole Transport Materials for Perovskite Solar Cells. Sol. Rrl 2019, 3, 1900001. [Google Scholar] [CrossRef]
  44. Minami, T.; Nishi, Y.; Miyata, T. Efficiency enhancement using a zn1− xgex-o thin film as an n-type window layer in Cu2O-based heterojunction solar cells. Appl. Phys. Express 2016, 9, 052301. [Google Scholar] [CrossRef]
  45. Ţălu, Ş.; Yadav, R.P.; Šik, O.; Sobola, D.; Dallaev, R.; Solaymani, S.; Man, O. How topographical surface parameters are correlated with cdte monocrystal surface oxidation. Mater. Sci. Semicond. Process. 2018, 85, 15–23. [Google Scholar] [CrossRef]
  46. Werner, F.; Veith-Wolf, B.; Spindler, C.; Barget, M.R.; Babbe, F.; Guillot, J.; Schmidt, J.; Siebentritt, S. Oxidation as key mechanism for efficient interface passivation in cu (in, Ga) Se2 thin-film solar cells. Phys. Rev. Appl. 2020, 13, 054004. [Google Scholar] [CrossRef]
Energies 18 05623 g001
Figure 1. Structure schematic diagram of the Cu2O heterojunction solar cell used.
Figure 1. Structure schematic diagram of the Cu2O heterojunction solar cell used.
Energies 18 05623 g001
Energies 18 05623 g002
Figure 2. (a) J–V curves of the solar cell before and after the introduction of the buffer layer and (b) band diagrams of the solar cell before and after the introduction of the buffer layer.
Figure 2. (a) J–V curves of the solar cell before and after the introduction of the buffer layer and (b) band diagrams of the solar cell before and after the introduction of the buffer layer.
Energies 18 05623 g002
Energies 18 05623 g003
Figure 3. (a,b) Band diagrams of buffer layers with different bandgap (Eg) and electron affinity (χ) values at a doping concentration of 1 × 1020 cm−3 (simulation parameters: ETL: 80 nm, 1 × 1020 cm−3; Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV; buffer: 2 nm, 1 × 1020 cm−3; HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV). (c,d) Current density–voltage (J–V) characteristics of the Cu2O solar cells with varying bandgap and electron affinity combinations.
Figure 3. (a,b) Band diagrams of buffer layers with different bandgap (Eg) and electron affinity (χ) values at a doping concentration of 1 × 1020 cm−3 (simulation parameters: ETL: 80 nm, 1 × 1020 cm−3; Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV; buffer: 2 nm, 1 × 1020 cm−3; HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV). (c,d) Current density–voltage (J–V) characteristics of the Cu2O solar cells with varying bandgap and electron affinity combinations.
Energies 18 05623 g003
Energies 18 05623 g004
Figure 4. (a) The depth distribution of the carrier recombination rate in the ETL/buffer/Cu2O interface with different bandgaps in the ETL layer, (b) quantum efficiency graph for Cu2O heterojunction solar cells with different bandgaps in the ETL layer (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 4 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 1 × 1020 cm–3, χ: 3.9 eV. HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 4. (a) The depth distribution of the carrier recombination rate in the ETL/buffer/Cu2O interface with different bandgaps in the ETL layer, (b) quantum efficiency graph for Cu2O heterojunction solar cells with different bandgaps in the ETL layer (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 4 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 1 × 1020 cm–3, χ: 3.9 eV. HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g004
Energies 18 05623 g005
Figure 5. The impact of the buffer layer doping concentration and thickness on various parameters of the Cu2O solar cells: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 5. The impact of the buffer layer doping concentration and thickness on various parameters of the Cu2O solar cells: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g005
Energies 18 05623 g006
Figure 6. Impact of changing the band gap and electron affinity of the HTL layer on the performance of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3).
Figure 6. Impact of changing the band gap and electron affinity of the HTL layer on the performance of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3).
Energies 18 05623 g006
Energies 18 05623 g007
Figure 7. Energy band diagrams at the Cu2O/HTL interface for different values of band gap and electron affinity in the HTL layer. (a) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2 eV, χ: 2 eV). (b) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2 eV, χ: 3.2 eV). (c) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 3.2 eV, χ: 2 eV). (d) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2.2 eV, χ: 2.4 eV) (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3).
Figure 7. Energy band diagrams at the Cu2O/HTL interface for different values of band gap and electron affinity in the HTL layer. (a) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2 eV, χ: 2 eV). (b) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2 eV, χ: 3.2 eV). (c) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 3.2 eV, χ: 2 eV). (d) Band diagram with Cu2O absorber (Eg: 2 eV, χ: 3.2 eV) and HTL (Eg: 2.2 eV, χ: 2.4 eV) (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 10 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 200 nm, 1 × 1020 cm−3).
Energies 18 05623 g007
Energies 18 05623 g008
Figure 8. Impact of doping concentration and film thickness of the HTL layer on the performance of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for the simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 8 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV, HTL: Eg: 2 eV, χ: 3.2 eV).
Figure 8. Impact of doping concentration and film thickness of the HTL layer on the performance of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for the simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 8 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV, HTL: Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g008
Energies 18 05623 g009
Figure 9. The influence of carrier lifetime and Cu2O layer thickness on the performance parameters of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 9. The influence of carrier lifetime and Cu2O layer thickness on the performance parameters of the Cu2O heterojunction solar cell: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g009
Energies 18 05623 g010
Figure 10. The influence of carrier lifetime and Cu2O layer thickness on quantum efficiency (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 10. The influence of carrier lifetime and Cu2O layer thickness on quantum efficiency (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g010
Energies 18 05623 g011
Figure 11. I–V curves for the Cu2O layers with varying minority carrier lifetimes and thicknesses: (a) τ = 10 ns, (b) τ = 100 ns, and (c) τ = 1000 ns (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 8 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 11. I–V curves for the Cu2O layers with varying minority carrier lifetimes and thicknesses: (a) τ = 10 ns, (b) τ = 100 ns, and (c) τ = 1000 ns (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: 8 μm, 1 × 1015 cm−3, Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g011
Energies 18 05623 g012
Figure 12. The influence of Cu2O layer doping concentration and thickness on the performance of the Cu2O solar cells: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Figure 12. The influence of Cu2O layer doping concentration and thickness on the performance of the Cu2O solar cells: (a) PCE, (b) Jsc, (c) Voc, and (d) FF (the other parameters required for simulation were as follows: ETL: 80 nm, 1 × 1020 cm−3, Eg: 3.5 eV, χ: 3.9 eV. Cu2O: Eg: 2 eV, χ: 3.2 eV. Buffer: 8 nm, 1 × 1019 cm−3, Eg: 2 eV, χ: 3.5 eV. HTL: 100 nm, 1 × 1020 cm−3, Eg: 2 eV, χ: 3.2 eV).
Energies 18 05623 g012
Table 1. Baseline parameters for modeling the Cu2O solar cell.
Table 1. Baseline parameters for modeling the Cu2O solar cell.
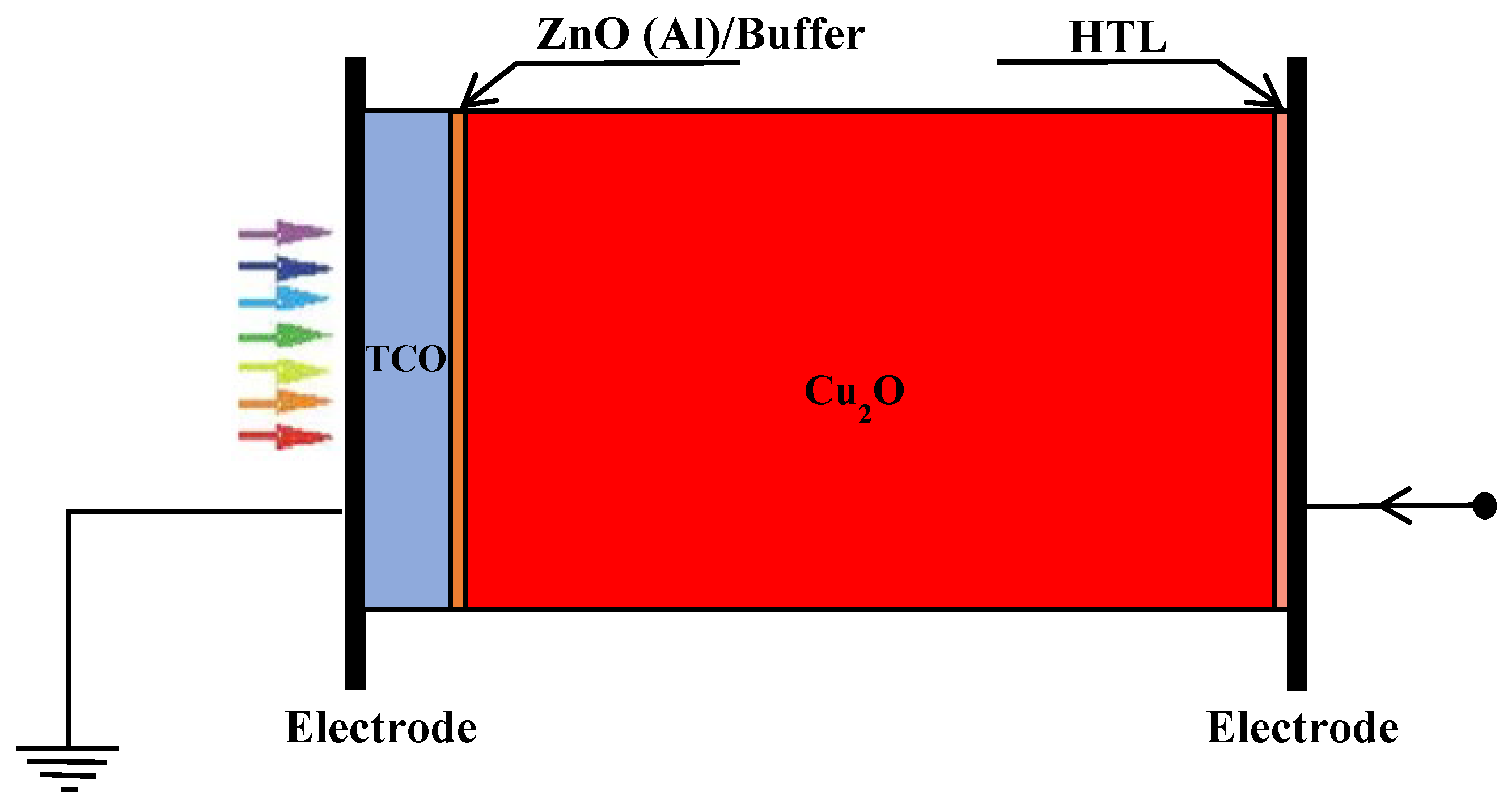
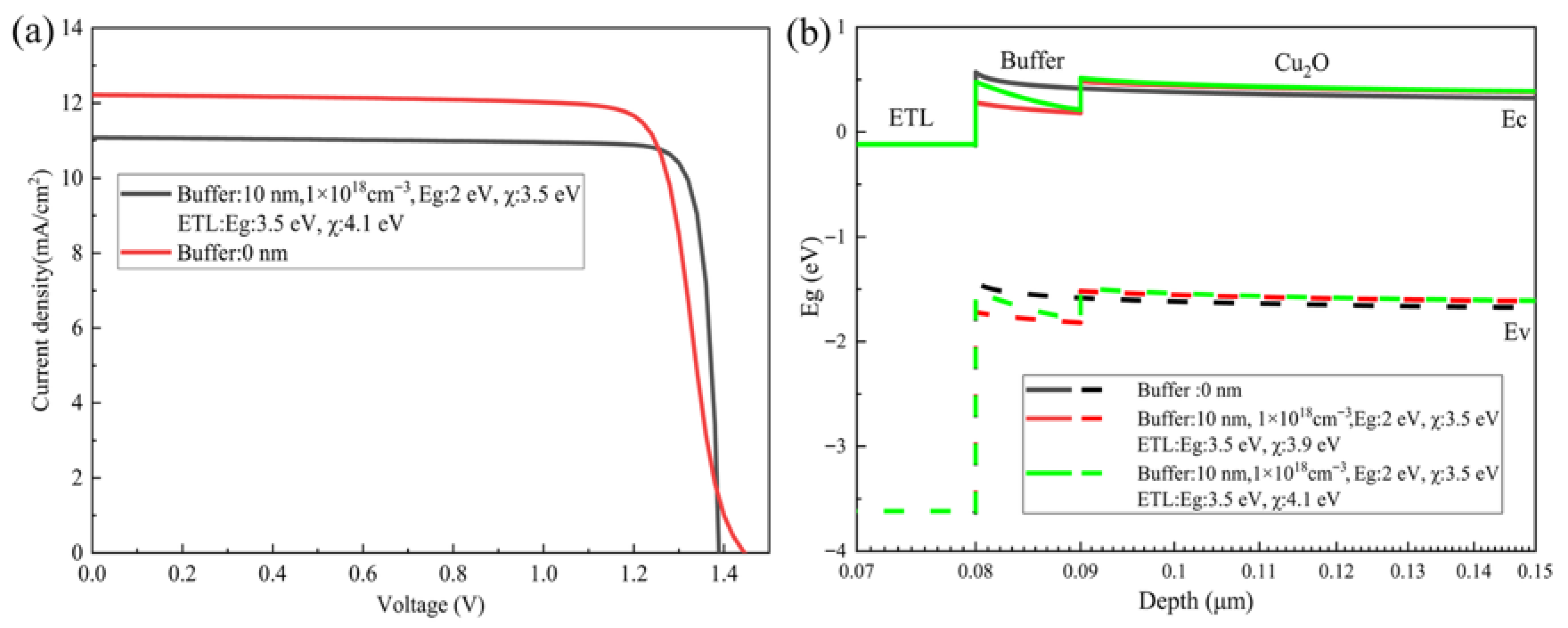
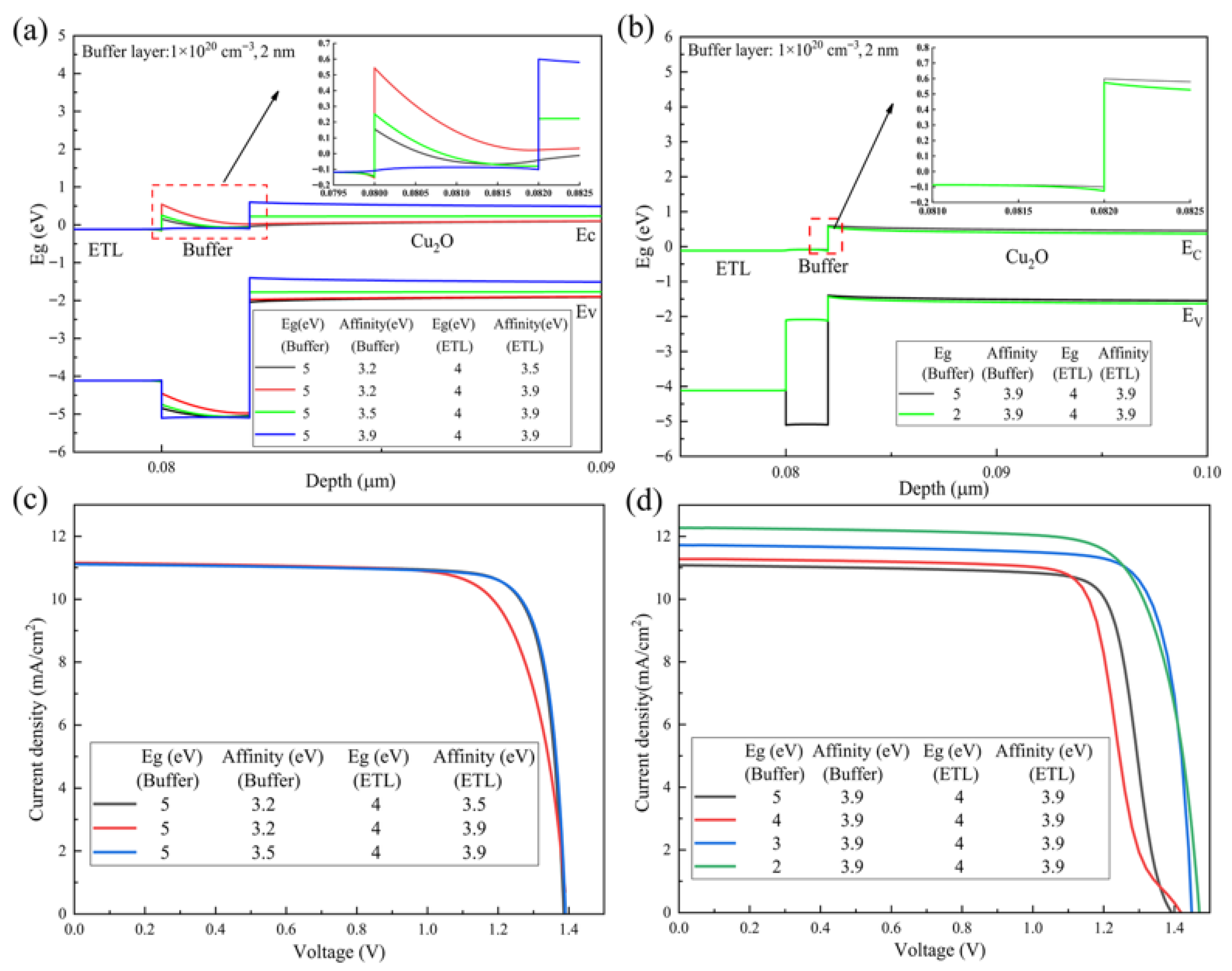
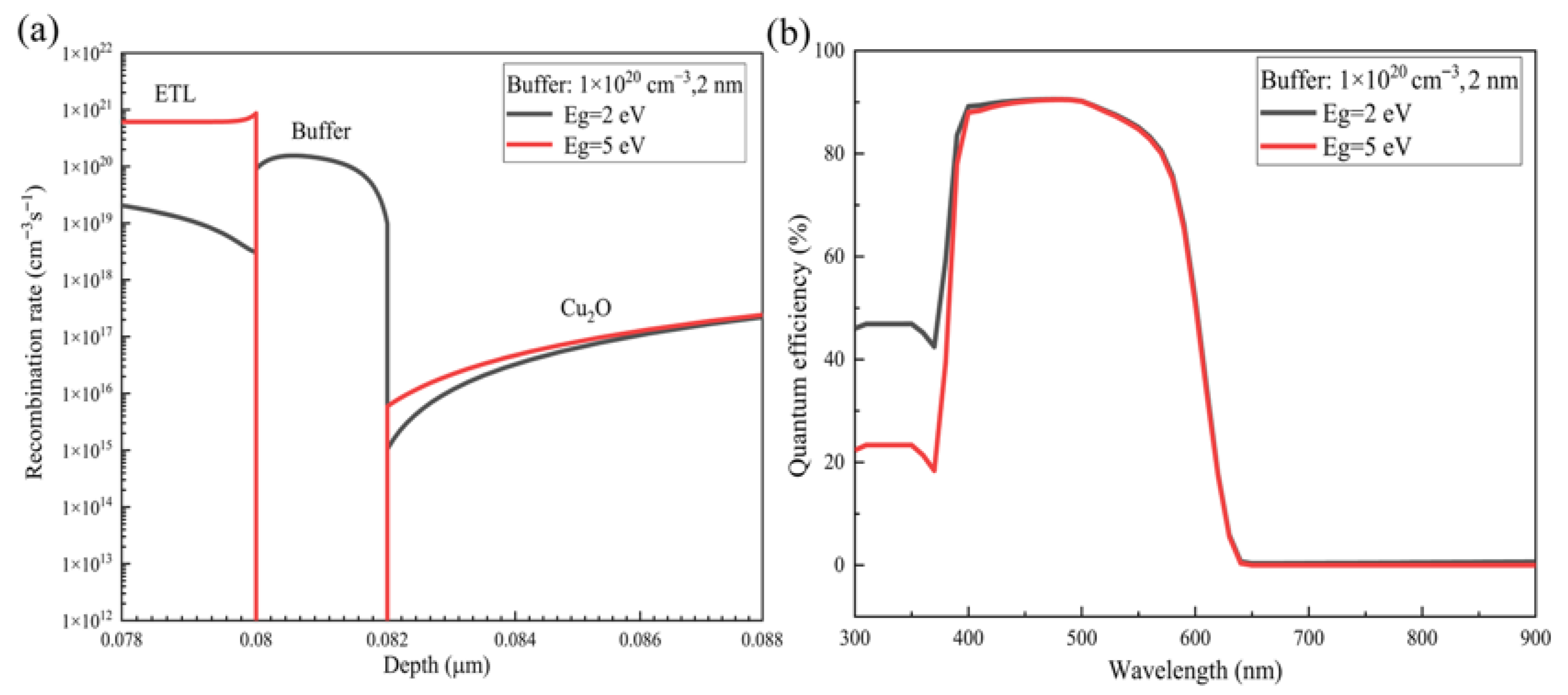
ParameterETLBuffer [28,34]Cu2OHTL
Thickness (μm)0.08VariedVariedVaried
Band gap (eV)VariedVaried213Varied
electron affinity (eV)VariedVaried3.233Varied
Donor concentration (cm−3)1.000 × 1020Varied00
Acceptor concentration (cm−3)00VariedVaried
Dielectric permittivity (relative)8.9106.1807.6007.600
CB effective density of states (cm−3)8.090 × 10183.718 × 10181.050 × 10191.050 × 1019
VB effective density of states (cm−3)9.420 × 10191.137 × 10192.250 × 10192.250 × 1019
Electron thermal velocity (cm/s)1.000 × 1071.000 × 1071.000 × 1071.000 × 107
Hole thermal velocity (cm/s)1.000 × 1071.000 × 1071.000 × 1071.000 × 107
Electron mobility (cm2/Vs)3050200200
Hole mobility (cm2/Vs)35100100
Total defect density (cm−3)1.0 × 10181.0 × 10181.0 × 10131.0 × 1013
Energy level (eV)0.601.200.600.60
Electron lifetime (ns)1.0 × 1011.0 × 1011.4 × 1021.4 × 102
Hole lifetime (ns)1.0 × 1011.0 × 10−41.4 × 1021.4 × 102
Electron diffusion length (μm)2.8 × 10−15.1 × 10−18.6 × 1012.7 × 101
Hole diffusion length (μm)8.8 × 10−21.1 × 10−36.1 × 1011.9 × 101
Table 2. The impact of bandgap and electron affinity in the ETL and buffer layer on the performance of the solar cells (Cu2O layer: thickness of 10 μm, doping concentration of 1 × 1015 cm−3, ETL: 80 nm, 1 × 1020 cm−3, buffer layer: thickness of 2 nm, dopant concentration of 1 × 1020 cm−3.).
Table 2. The impact of bandgap and electron affinity in the ETL and buffer layer on the performance of the solar cells (Cu2O layer: thickness of 10 μm, doping concentration of 1 × 1015 cm−3, ETL: 80 nm, 1 × 1020 cm−3, buffer layer: thickness of 2 nm, dopant concentration of 1 × 1020 cm−3.).
ParameterETLBuffer [35,36]Cu2OHTL
Thickness (μm)0.08VariedVariedVaried
Band gap (eV)VariedVaried213Varied
electron affinity (eV)VariedVaried3.233Varied
Donor concentration (cm−3)1.000 × 1020Varied00
Acceptor concentration (cm−3)00VariedVaried
Dielectric permittivity (relative)8.9106.1807.6007.600
CB effective density of states (cm−3)8.090 × 10183.718 × 10181.050 × 10191.050 × 1019
VB effective density of states (cm−3)9.420 × 10191.137 × 10192.250 × 10192.250 × 1019
Electron thermal velocity (cm/s)1.000 × 1071.000 × 1071.000 × 1071.000 × 107
Hole thermal velocity (cm/s)1.000 × 1071.000 × 1071.000 × 1071.000 × 107
Electron mobility (cm2/Vs)3050200200
Hole mobility (cm2/Vs)35100100
Bulk density (cm−3)1.0 × 10181.0 × 10181.0× 10131.0 × 1013
Energy level (eV)0.601.200.600.60
Electron lifetime (ns)1.0 × 1011.0 × 1011.4 × 1021.4 × 102
Hole lifetime (ns)1.0 × 1011.0 × 10−41.4 × 1021.4 × 102
Electron diffusion length (μm)2.8 × 10−15.1 × 10−18.6 × 1012.7 × 101
Hole diffusion length (μm)8.8 × 10−21.1 × 10−36.1 × 1011.9 × 101
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Chen, S.; Wang, L.; Zhou, C.; Yang, J.; Jia, X. Simulation Analysis of Cu2O Solar Cells. Energies 2025, 18, 5623. https://doi.org/10.3390/en18215623

AMA Style

Chen S, Wang L, Zhou C, Yang J, Jia X. Simulation Analysis of Cu2O Solar Cells. Energies. 2025; 18(21):5623. https://doi.org/10.3390/en18215623

Chicago/Turabian Style

Chen, Sinuo, Lichun Wang, Chunlan Zhou, Jinli Yang, and Xiaojie Jia. 2025. "Simulation Analysis of Cu2O Solar Cells" Energies 18, no. 21: 5623. https://doi.org/10.3390/en18215623

APA Style

Chen, S., Wang, L., Zhou, C., Yang, J., & Jia, X. (2025). Simulation Analysis of Cu2O Solar Cells. Energies, 18(21), 5623. https://doi.org/10.3390/en18215623

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop