Modeling Hydrogen-Assisted Combustion of Liquid Fuels in Compression-Ignition Engines Using a Double-Wiebe Function
Abstract
1. Introduction
Double- and Triple-Wiebe Functions
2. Materials—Experimental Setup
Uncertainty Analysis
3. Methodology
3.1. Modeling Combustion Rate
- Qin—heat accumulated in the total mass of fuel mfuel delivered to the engine cylinder,
- mfuel—mass of the fuel dose,
- LHVfuel—lower heating value of the fuel.
- Qin(α)—heat released from starting combustion up to the time where the engine piston is located at specific position determined by the crank angle α,
- mfuel(α)—mass of the fuel dose combusted from the beginning of combustion until the crank angle α.
- ΔU—internal energy change before and after combustion,
- Qin—heat accumulated in the fuel dose mFuel,
- Qout—heat transferred outside the engine,
- Qloss—heat losses,
- W—useful work generated by the piston on the crankshaft.
- κ—the ratio of specific heats (cp/cv) of the gases filling the engine cylinder at constant pressure and constant volume, respectively,
- p(α)—in-cylinder combustion pressure,
- V(α)—in-cylinder volume,
- α—crank angle (CA) deg,
- Qwall(α)—heat losses to walls.
- SOC—start of combustion,
- mfuel,net (α)—is mass of fuel combusted following this relation mfuel (α)-mfuel,loss(α).
- CHRmax—is the cumulative heat at the end of combustion.
3.2. Wiebe Function Parameter Study
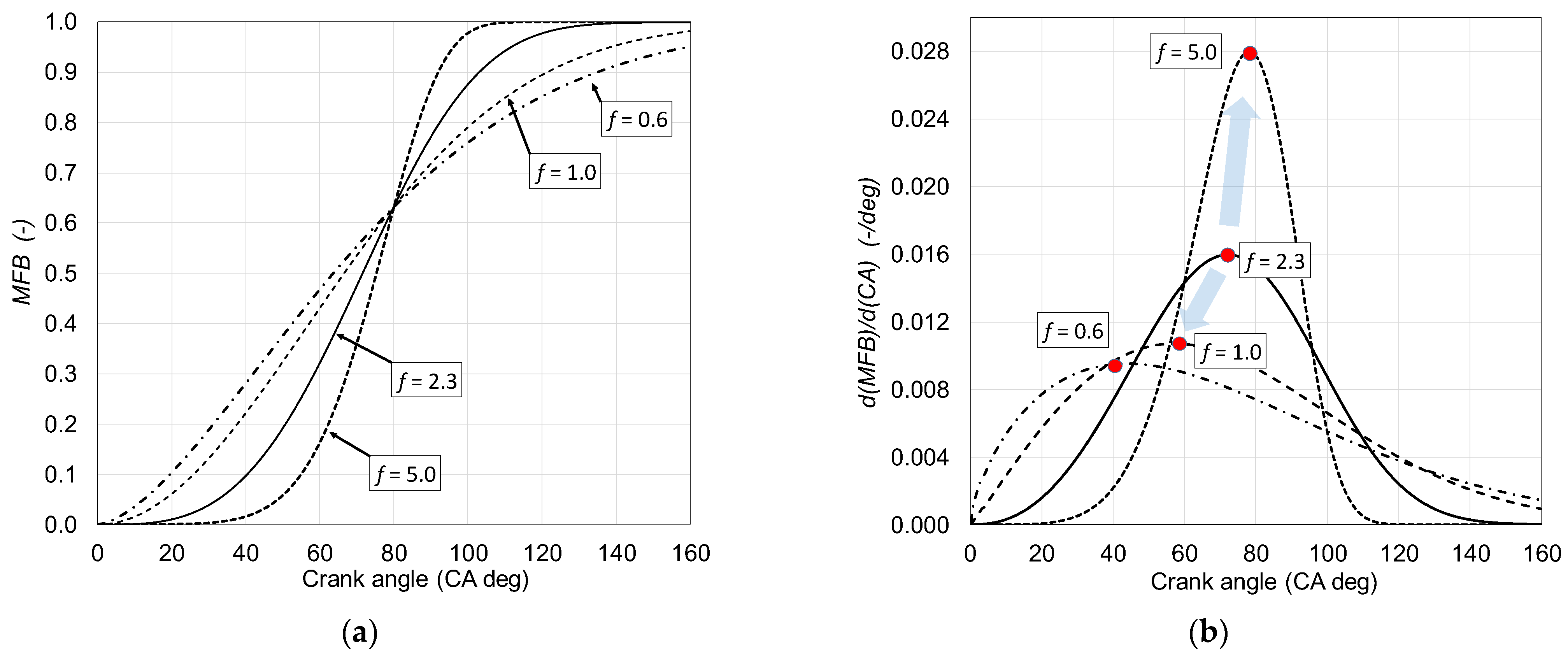
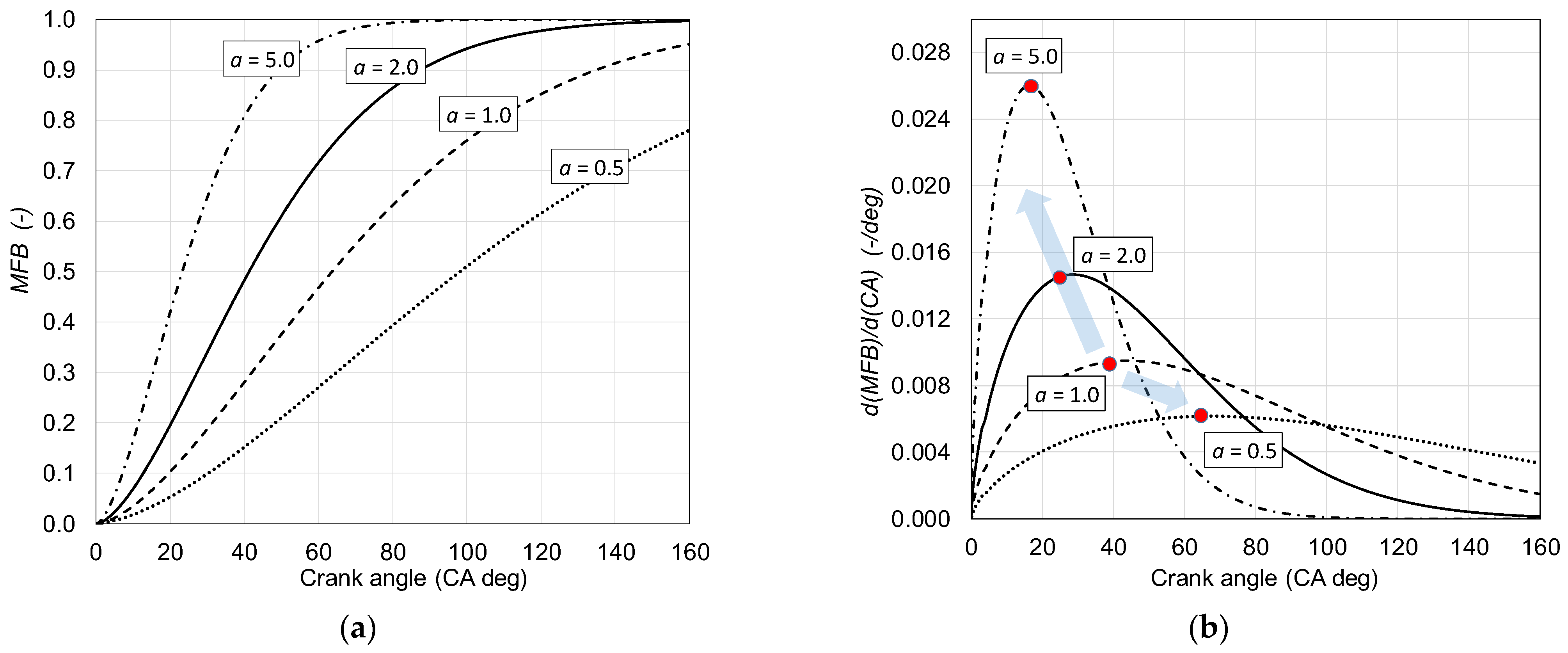
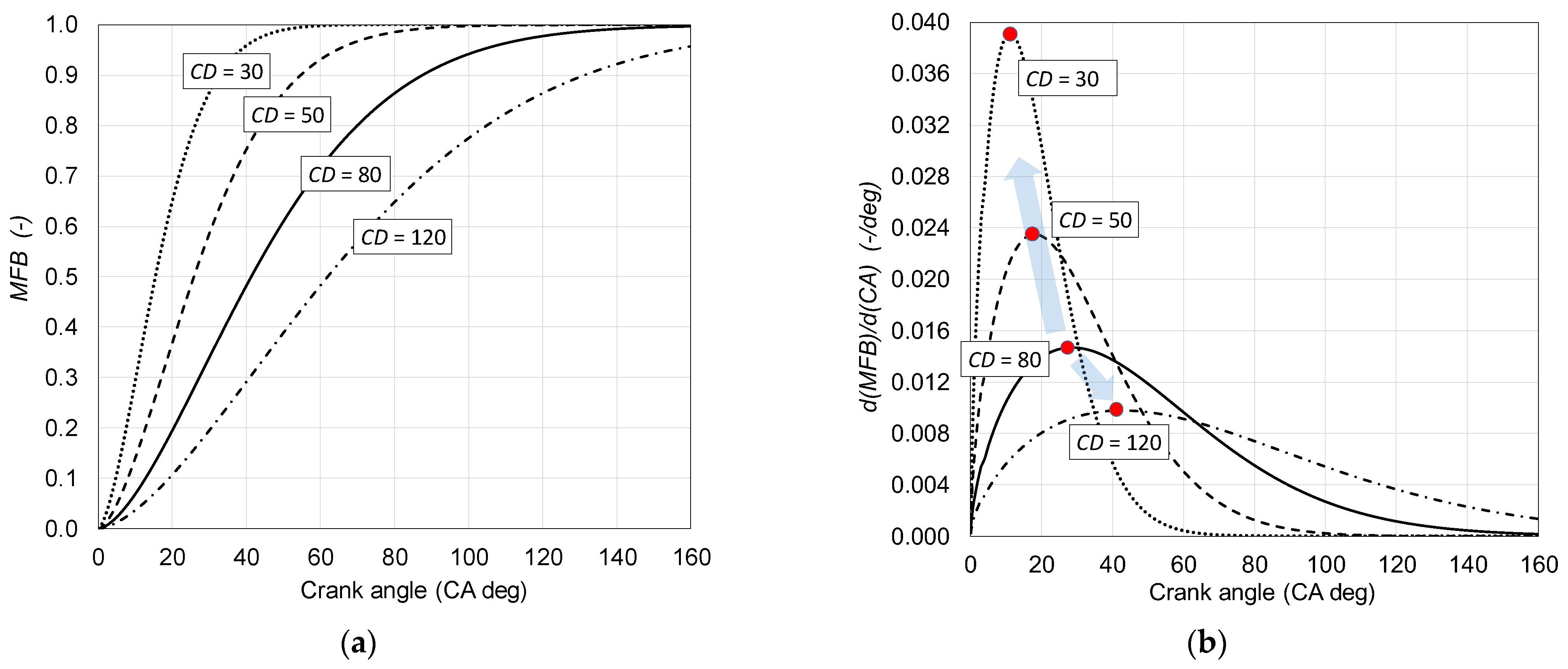
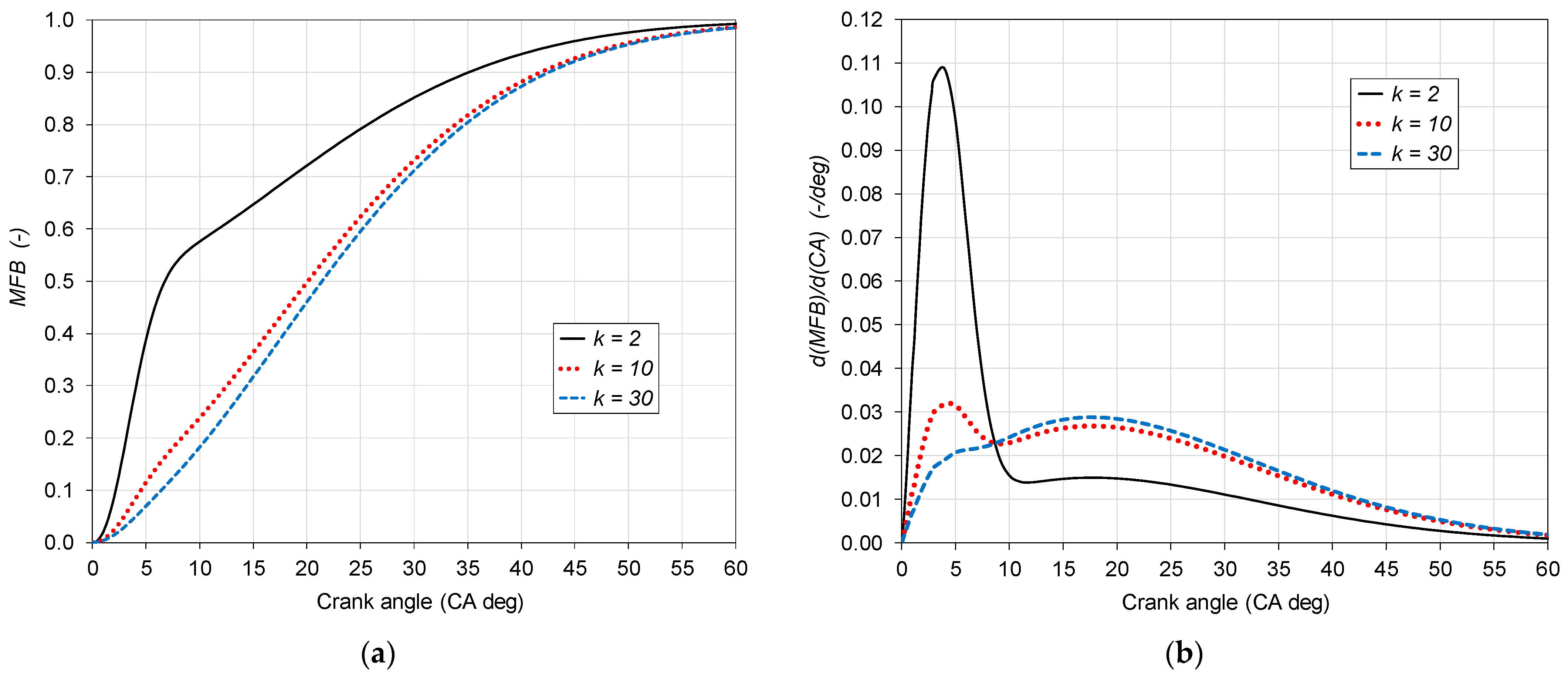
3.2.1. Single-Wiebe Function
- a—is the exponential coefficient influencing combustion duration,
- f—shape factor,
- α—crank angle (CA) in deg,
- αSOC—crank angle for start of combustion in CA deg,
- CD—combustion duration in CA deg.
3.2.2. Double-Wiebe Function
- βi—is the fraction of each combustion phase,
- δi—equals 1 if α − αi > 0.
- subscript 1 denotes the first, assumed as the premixed combustion phase,
- subscript 2 denotes the second, considered the diffusion combustion phase,
- k—let one call it the phase importance factor of these premixed and diffusion combustion phases.
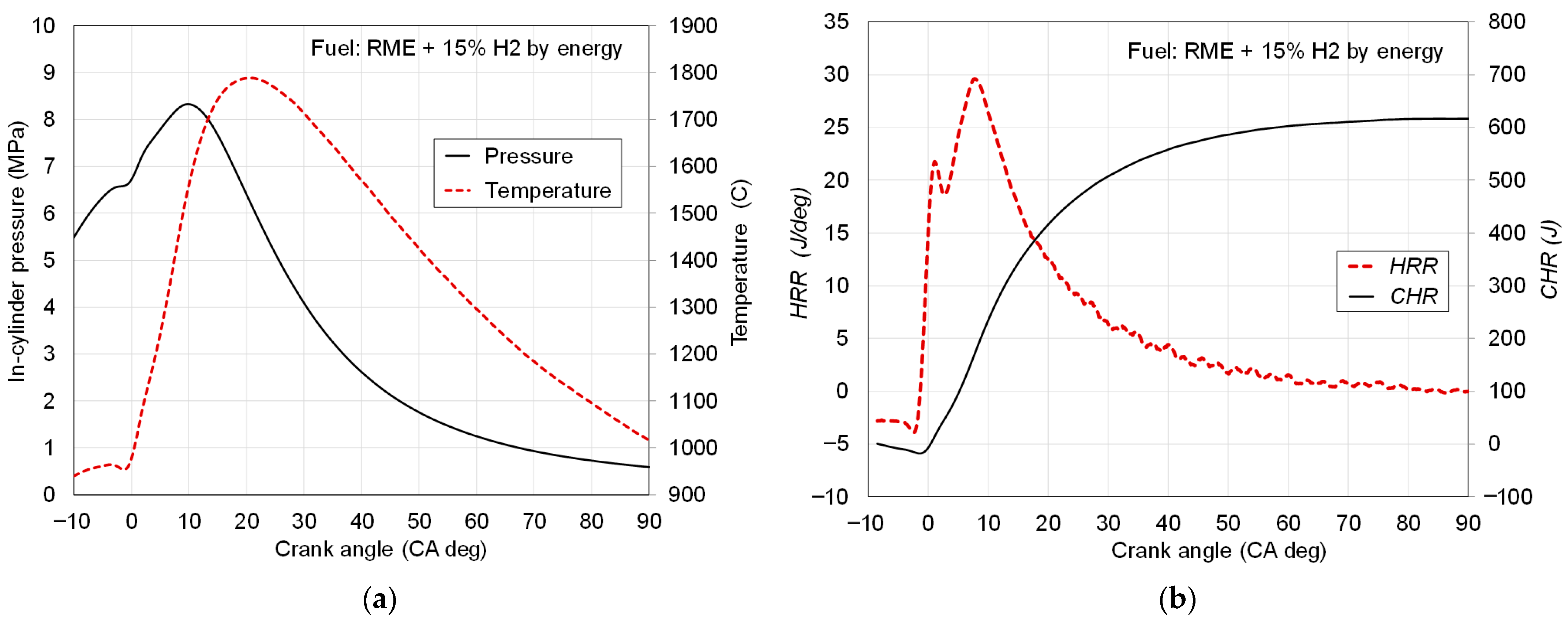
4. Results and Discussion
- In-cylinder pressure, mean in-cylinder temperature, HRR, and MFB obtained from experiments;
- Fitting the double-Wiebe function to experimental data;
- Discussion summary.
4.1. In-Cylinder Pressure, In-Cylinder Mean Temperature, HRR and MFB
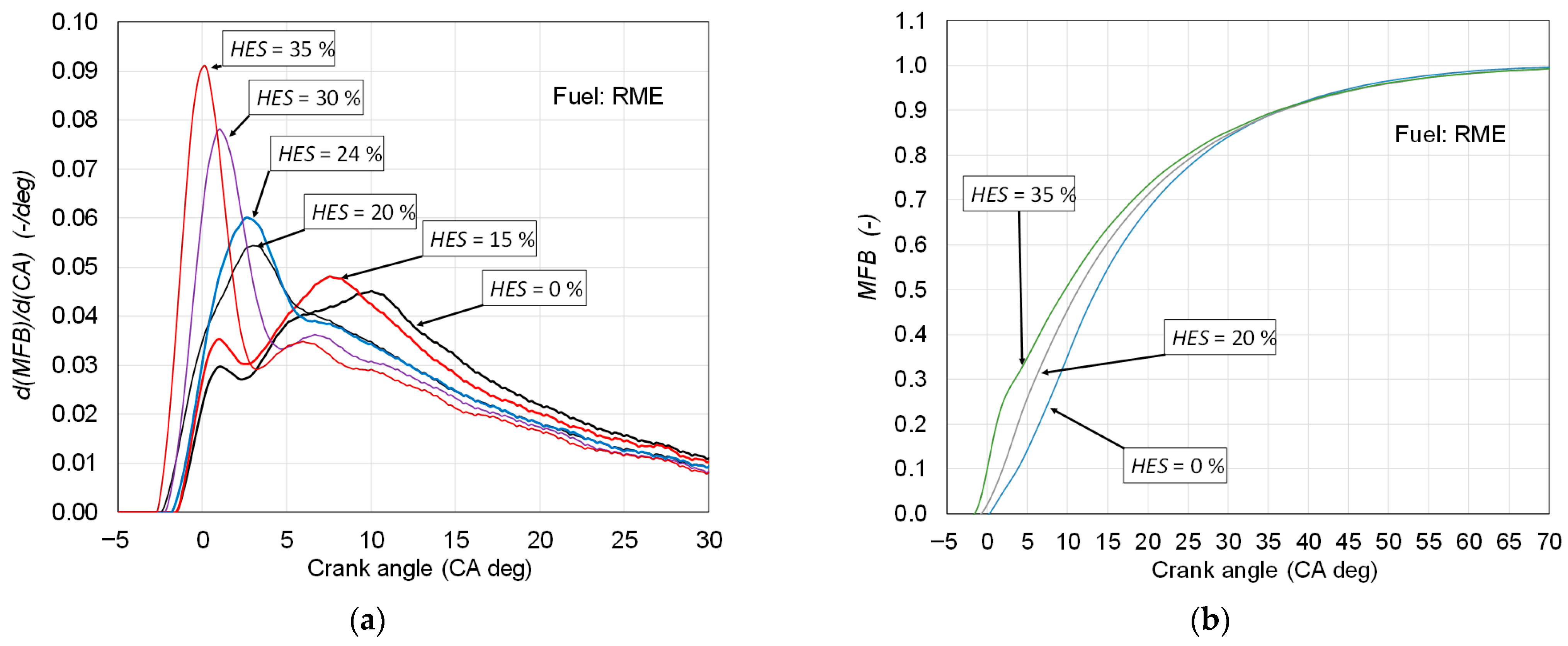
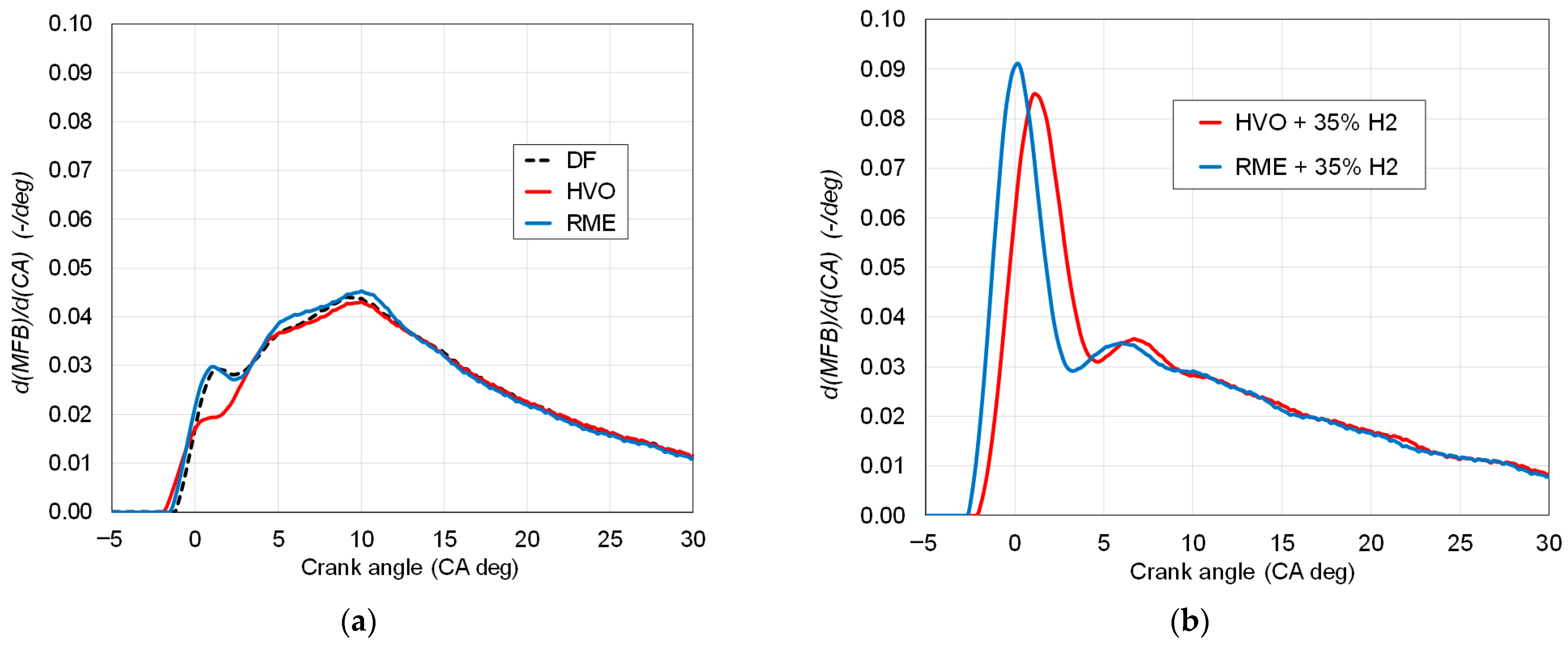
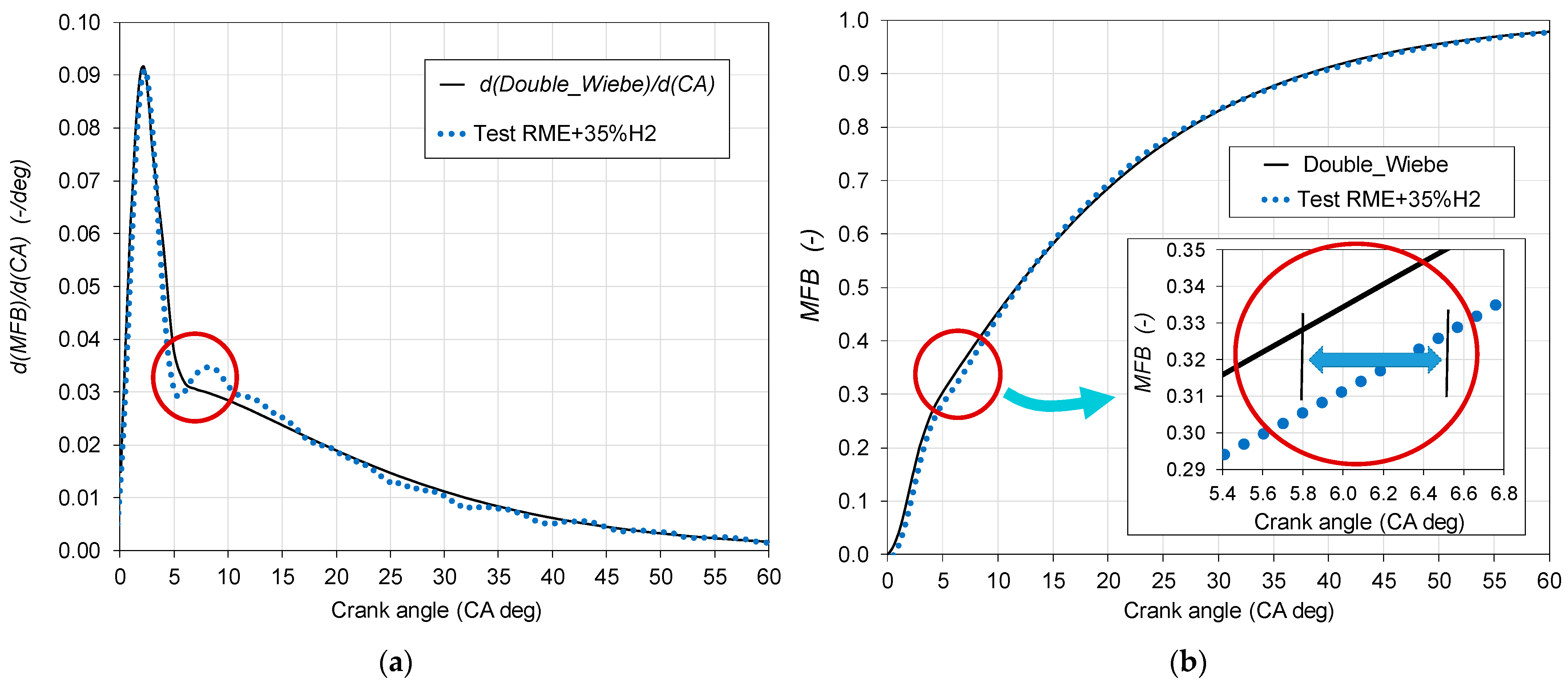
4.2. Adapting the Double-Wiebe Function
4.3. Recommendations for the Double-Wiebe Parameters
- The first combustion phase is strictly affected by hydrogen. As found from Table 5, the two following parameters f1 and CD1 have to be changed with hydrogen addition.
- Typically, the parameter f1 decreases from 1.8 to [0.9, 1.0] (with increasing HES from 0 to 35% HES).
- The parameter CD1 gets shortened from 28 CA deg to [8, 10] CA deg while changing HES from 0 to 35%.
- The parameter a1 is recommended to equal 10.
- The second combustion phase does not change with hydrogen addition; hence, the values can be the same for all the tests ignoring hydrogen addition as proposed:
- a2 = 10, f2 = [0.25, 0.26], CD2 = [125, 130]. This was confirmed in tests with pure diesel fuel as well as tests with RME and HVO without hydrogen added.
- The phase importance factor k varies from 7 to 6 with HES increasing from 0 to 35%.
- The coefficients f1, CD1, f2, CD2 and k can be determined using the linear interpolation with change in HES from 0 to 35%.
5. Conclusions
- The addition of hydrogen increases the combustion rate during the initial phase, which is primarily dominated by premixed combustion.
- When hydrogen is added to diesel-like fuels, two distinct peaks appear in the heat release rate, corresponding to the first (premixed) and second (diffusion) combustion phases. Therefore, the double-Wiebe function was proposed as an optimal tool for modeling this process.
- Modeling of such a combustion should be based on the derivative of the double-Wiebe function rather than on the Wiebe function itself. For this purpose, the normalized heat release rate obtained from experimental data was used to calibrate the derivative of the double-Wiebe function.
- The parameters presented in Table 6 for the double-Wiebe function were determined with an R2 value exceeding 0.98. Hence, they are proposed as universal parameters for modeling the co-combustion of hydrogen with RME or HVO.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 0-D, 1-D | Zero-, One-Dimensional |
| BMEP | Brake Mean Effective Pressure |
| CA | Crank angle |
| CD | Combustion duration |
| CHR | Cumulative heat released |
| CI | Compression-ignition |
| DF | Diesel fuel |
| HES | Hydrogen energy share |
| HRR | Heat release rate |
| HVO | Hydrotreated vegetable oil |
| HVP | Hydrogen volumetric percentage |
| IC | Internal combustion |
| LHV | Lower heating value |
| MFB | Mass fraction burnt |
| NHRR | Normalized heat release rate |
| RME | Rapeseed methyl ester |
| SOC | Start of combustion |
References
- Barış, O.; Güler, İ.; Yaşgül, A. The Effect of Different Charging Concepts on Hydrogen Fuelled Internal Combustion Engines. Fuel 2023, 343, 127983. [Google Scholar] [CrossRef]
- Szwaja, S.; Pukalskas, S.; Juknelevicius, R.; Rimkus, A. Combustion Analysis of the Renewable Fuel HVO and RME with Hydrogen Addition in a Reciprocating Internal Combustion Engine. Energies 2025, 18, 3381. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Zhang, Y.; Zhao, D.; Li, Q.; Huang, M.; Hao, Q.; Du, J.; Song, Y.; Ming, Z.; Wang, J. Premixed Combustion and Emission Characteristics of Methane Diluted with Ammonia under F-Class Gas Turbine Relevant Operating Condition. Front. Energy Res. 2023, 11, 1120108. [Google Scholar] [CrossRef]
- Schuller, T.; Poinsot, T.; Candel, S. Dynamics and Control of Premixed Combustion Systems Based on Flame Transfer and Describing Functions. J. Fluid Mech. 2020, 894, P1. [Google Scholar] [CrossRef]
- Olanrewaju, F.O.; Li, H.; Andrews, G.E.; Phylaktou, H.N. Improved Model for the Analysis of the Heat Release Rate (HRR) in Compression Ignition (CI) Engines. J. Energy Inst. 2020, 93, 1901–1913. [Google Scholar] [CrossRef]
- Depcik, C.; Mattson, J.; Alam, S.S. Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines. Energies 2023, 16, 2514. [Google Scholar] [CrossRef]
- Serrano, R.; Uriondo, Z.; Portillo, L.D.; Basterretxea, A. A Study on the Optimal Adjustment of a Turbocharged Marine Compression-Ignition Engine with Double Pilot Fuel Injection Operating under a diesel─H2 Dual Fuel. Appl. Therm. Eng. 2025, 270, 126233. [Google Scholar] [CrossRef]
- Jalivar, G.; Neshat, E. Novel Thermodynamic Model for Simulation of Hydrogen/Diesel Fueled PCCI Engine. Heliyon 2025, 11, e42140. [Google Scholar] [CrossRef]
- Saeed Akhtar, M.U.; Asfand, F.; Khan, M.I.; Mishra, R.; Ball, A. Comparative Analysis to Assess the Effects of Hydrogen Injection Techniques on Performance and Emission Characteristics of a Compression-Ignition Engine. Case Stud. Therm. Eng. 2025, 73, 106724. [Google Scholar] [CrossRef]
- Feyijimi, C.; Depcik, C. Predictive Zero-Dimensional Combustion Modeling in Internal Combustion Engines with Residual Fraction and Exhaust Gas Recirculation. J. Eng. Gas Turbines Power 2025, 147, 1–34. [Google Scholar] [CrossRef]
- Osetrov, O.; Haas, R. Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach. Energies 2025, 18, 3004. [Google Scholar] [CrossRef]
- Wang, B.; Pamminger, M.; Vojtech, R.; Wallner, T. Impact of Injection Strategies on Combustion Characteristics, Efficiency and Emissions of Gasoline Compression Ignition Operation in a Heavy-Duty Multi-Cylinder Engine. Int. J. Engine Res. 2020, 21, 1426–1440. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, H.; Zhou, L.; Li, Y.; Liang, J. Effect of Injection Strategy on the Combustion and Knock in a Downsized Gasoline Engine with Large Eddy Simulation; SAE Technical Paper 2020-01-0244; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Zamboni, G. A Study on Combustion Parameters in an Automotive Turbocharged Diesel Engine. Energies 2018, 11, 2531. [Google Scholar] [CrossRef]
- Yeliana, Y.; Cooney, C.; Worm, J.; Michalek, D.J.; Naber, J.D. Estimation of Double-Wiebe Function Parameters Using Least Square Method for Burn Durations of Ethanol-Gasoline Blends in Spark Ignition Engine over Variable Compression Ratios and EGR Levels. Appl. Therm. Eng. 2011, 31, 2213–2220. [Google Scholar] [CrossRef]
- Rassweiler, G.M.; Withrow, L. Motion Pictures of Engine Flames Correlated with Pressure Cards. SaE Trans. 1938, 33, 185–204. [Google Scholar]
- Wang, Q.; Yang, R.; Sun, X.; Liu, Z.; Zhang, Y.; Fu, J.; Li, R. The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method. Processes 2022, 10, 717. [Google Scholar] [CrossRef]
- Beccari, S.; Pipitone, E. A New Simple Function for Combustion and Cyclic Variation Modeling in Supercharged Spark Ignition Engines. Energies 2022, 15, 3796. [Google Scholar] [CrossRef]
- Thakkar, K.; Kachhwaha, S.S.; Kodgire, P.; Srinivasan, S. Combustion Investigation of Ternary Blend Mixture of Biodiesel/n-Butanol/Diesel: CI Engine Performance and Emission Control. Renew. Sustain. Energy Rev. 2021, 137, 110468. [Google Scholar] [CrossRef]
- Serrano, J.R.; Climent, H.; Guardiola, C.; Piqueras, P. Methodology for Characterisation and Simulation of Turbocharged Diesel Engines Combustion during Transient Operation. Part 2: Phenomenological Combustion Simulation. Appl. Therm. Eng. 2009, 29, 150–158. [Google Scholar] [CrossRef]
- Xu, S.; Anderson, D.; Hoffman, M.; Prucka, R.; Filipi, Z. A Phenomenological Combustion Analysis of a Dual-Fuel Natural-Gas Diesel Engine. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 231, 66–83. [Google Scholar] [CrossRef]
- Awad, S.; Varuvel, E.G.; Loubar, K.; Tazerout, M. Single Zone Combustion Modeling of Biodiesel from Wastes in Diesel Engine. Fuel 2013, 106, 558–568. [Google Scholar] [CrossRef]
- Tipanluisa, L.; López-Martínez, J.; Casanova, J.; Fonseca, N. Three-Stage Combustion Modeling of a Binary Mixture-Fueled CI CRDI Engine; Vizán Idoipe, A., García Prada, J.C., Eds.; Springer International Publishing: Cham, Switzerland, 2023; ISBN 978-3-031-38562-9. [Google Scholar]
- Kamaltdinov, V.G.; Lysov, I.O.; Nikiforov, S.S. Diesel Engine Operating Cycle Optimization with Simulation of Combustion Process by Double-Wiebe Function. Procedia Eng. 2015, 129, 873–878. [Google Scholar] [CrossRef][Green Version]
- Yang, R.; Ran, Z.; Ristow Hadlich, R.; Assanis, D. A Double-Wiebe Function for Reactivity Controlled Compression Ignition Combustion Using Reformate Diesel. J. Energy Resour. Technol. 2022, 144, 112301. [Google Scholar] [CrossRef]
- Hellström, E.; Stefanopoulou, A.; Jiang, L. A Linear Least-Squares Algorithm for Double-Wiebe Functions Applied to Spark-Assisted Compression Ignition. J. Eng. Gas Turbines Power 2014, 136, 091514. [Google Scholar] [CrossRef]
- Liu, Y. A Method for Real-Time Combustion Metrics Estimation Using Wiebe Model in Diesel Engine. Prim. Sci. Eng. 2024, 4, 28–46. [Google Scholar]
- Zhu, J.; Du, P.; Zhang, G.; Song, H.; Li, B.; Long, W.; Dong, D. Development and Validation of a Modeling and Calibration Method for Diesel-Like Multistage Combustion Based on a Modified Multi-Wiebe Function. ACS Omega 2022, 7, 11756–11769. [Google Scholar] [CrossRef]
- Salvà, E.P.; Gallo, W.L.R. Determination of the Apparent Heat Release for Diesel Engines. In Proceedings of the 22nd International Congress of Mechanical Engineering (COBEM 2013), Ribeirão Preto, Brazil, 3–7 November 2013; pp. 2030–2039. [Google Scholar]
- Maroteaux, F.; Saad, C.; Aubertin, F. Development and Validation of Double and Single Wiebe Function for Multi-Injection Mode Diesel Engine Combustion Modelling for Hardware-in-the-Loop Applications. Energy Convers. Manag. 2015, 105, 630–641. [Google Scholar] [CrossRef]
- Yasar, H.; Soyhan, H.S.; Walmsley, H.; Head, B.; Sorusbay, C. Double-Wiebe Function: An Approach for Single-Zone HCCI Engine Modeling. Appl. Therm. Eng. 2008, 28, 1284–1290. [Google Scholar] [CrossRef]
- Pesic, R.; Davinic, A.; Taranovic, D.; Miloradovic, D.; Petkovic, S. Experimental Determination of Double Vibe Function Parameters in Diesel Engines with Biodiesel. Therm. Sci. 2010, 14, 197–208. [Google Scholar] [CrossRef]
- Lebedevas, S.; Žaglinskis, J.; Drazdauskas, M. Development and Validation of Heat Release Characteristics Identification Method of Diesel Engine under Operating Conditions. J. Mar. Sci. Eng. 2023, 11, 182. [Google Scholar] [CrossRef]
- Tang, Y.; Li, H.; Jiang, Y.; Liang, W.; Zhang, J. The Control-Oriented Heat Release Rate Model for a Marine Dual-Fuel Engine under All the Operating Modes and Loads. J. Mar. Sci. Eng. 2023, 11, 64. [Google Scholar] [CrossRef]
- Alam, S.S.; Rosa, S.W.; Depcik, C.; Preetham Burugupally, S.; McDaniel, E.; Hobeck, J.D. Modification of the Wiebe Function for Methane-Air and Oxy-Methane- Based Spark-Ignition Engines. Fuel 2021, 303, 121218. [Google Scholar] [CrossRef]
- Szwaja, S.; Grab-Rogalinski, K. Hydrogen Combustion in a Compression Ignition Diesel Engine. Int. J. Hydrogen Energy 2009, 34, 4413–4421. [Google Scholar] [CrossRef]
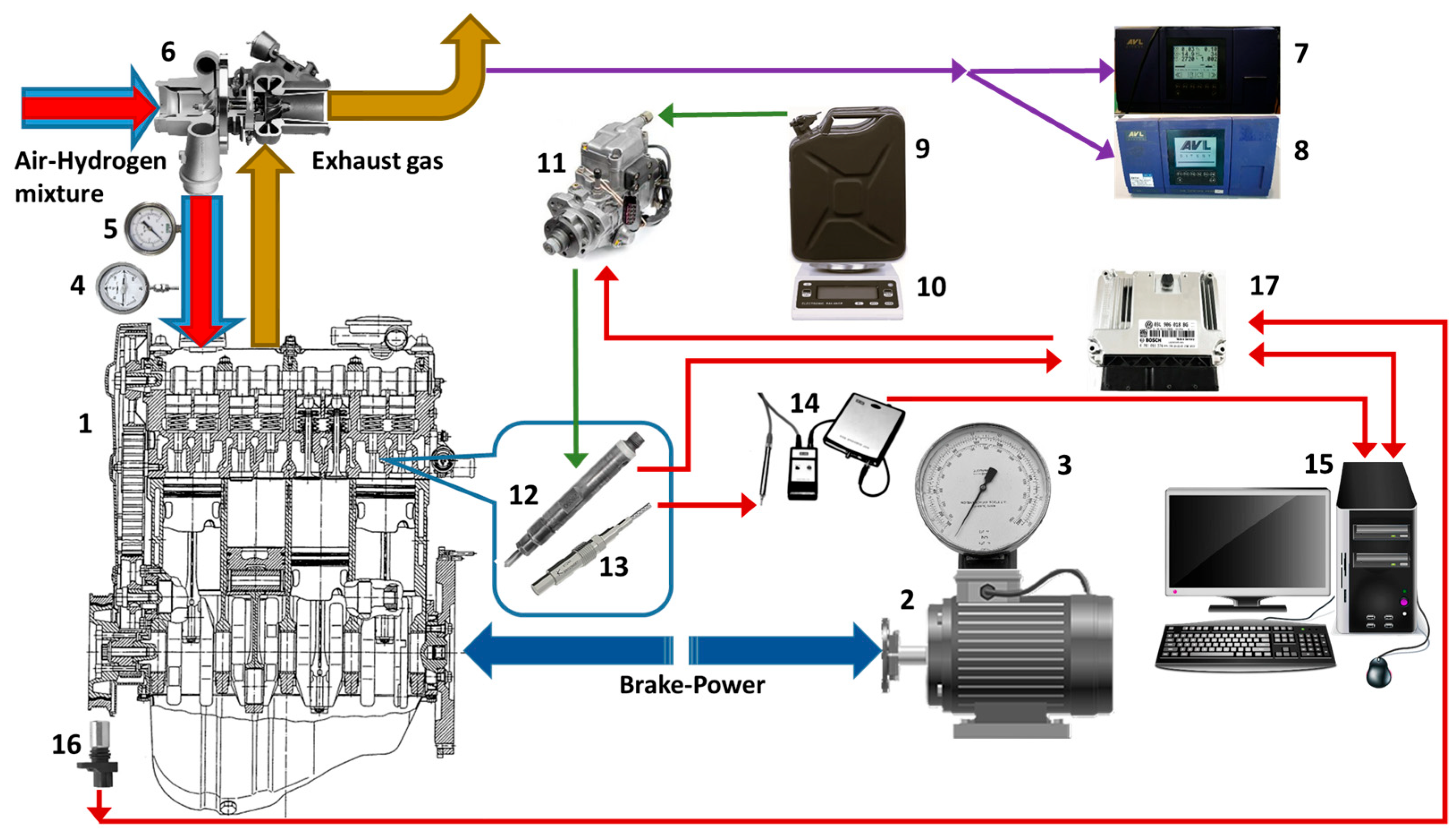


| Number of cylinders | 4 |
| Displacement | 1896 cm3 |
| Compression ratio | 19.5 |
| Rated power | 66 kW/4000 rpm |
| Maximum torque | 180 Nm/2000–25,000 rpm |
| Intake valve opening | 16° bTDC |
| Intake valve closing | 25° aBDC |
| Exhaust valve opening | 28° bBDC |
| Exhaust valve closing | 19° aTDC |
| Fuel injection | Single direct injection |
| Fuel pump design | Axial piston distribution pump |
| Nozzle type | Hole-type |
| Nozzle and holder assembly | double spring |
| Nozzle opening pressure | 200 bar |
| Parameter/Quantity | Units | Data |
|---|---|---|
| Fuels | - | Diesel Fuel, HVO, RME Hydrogen from 0 to 35% (by energy) |
| Load as BMEP | kPa | 600 |
| Injection timing | CA deg aTDC | −5 |
| Engine speed | rpm | 2000 |
| HVP (m3/m3 ∙ 100%) | HES (J/J ∙ 100%) |
|---|---|
| 0 | 0 |
| 2.6 | 15 |
| 3.5 | 20 |
| 4.2 | 24 |
| 5.3 | 30 |
| 6.2 | 35 |
| Parameter/Quantity | Units | Uncertainty |
|---|---|---|
| CA0–10 | CA deg | 1.12 |
| CA10–90 | CA deg | 1.25 |
| Peak in HRR | J/deg | 4.28 |
| Peak in NHRR | -/deg | 0.006 |
| Combustion Parameters from Tests | Wiebe Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | HES | P1 | LocP1 | P2 | LocP2 | 1st Wiebe | 2nd Wiebe | R2 | |||||
| % | Deg | Deg | Deg | Deg | a1 | f1 | CD1 | a2 | f2 | CD2 | k | ||
| Fuel: HVO + H2 | |||||||||||||
| 1 | 0 | 0.020 | 1.0 | 0.043 | 10.0 | 10 | 1.8 | 28 | 10 | 0.26 | 130 | 7 | 0.9862 |
| 2 | 15 | 0.022 | 1.0 | 0.048 | 8.1 | 10 | 1.5 | 28 | 10 | 0.25 | 130 | 7 | 0.9863 |
| 3 | 24 | 0.064 | 3.7 | ni | ni | 10 | 1.8 | 16 | 10 | 0.25 | 130 | 7 | 0.9913 |
| 4 | 35 | 0.085 | 1.1 | 0.035 | 6.8 | 10 | 1.0 | 8 | 10 | 0.19 | 140 | 6 | 0.9906 |
| Fuel: RME + H2 | |||||||||||||
| 5 | 0 | 0.029 | 1.04 | 0.045 | 10.2 | 10 | 1.6 | 28 | 10 | 0.26 | 125 | 6 | 0.9867 |
| 6 | 15 | 0.035 | 1.06 | 0.048 | 7.6 | 10 | 1.4 | 24 | 10 | 0.26 | 130 | 7 | 0.9899 |
| 7 | 24 | 0.061 | 2.7 | ni | ni | 10 | 0.9 | 14 | 10 | 0.26 | 125 | 6 | 0.9877 |
| 8 | 35 | 0.091 | 0.3 | 0.034 | 6.1 | 10 | 0.9 | 10 | 10 | 0.26 | 125 | 6 | 0.99876 |
| Fuel: Diesel fuel | |||||||||||||
| 9 | 0 | 0.029 | 1.3 | 0.044 | 9.1 | 10 | 1.8 | 28 | 10 | 0.25 | 130 | 7 | 0.9876 |
| RME or HVO + hydrogen | HES | |
| 0 ⟶ 35% | ||
| 1st Combustion Phase | a1 | 10 |
| f1 | 1.8 ⟶ 0.9 | |
| CD1 | 28 ⟶ 8 CA deg | |
| 2nd Combustion Phase | a2 | 10 |
| f2 | [0.25, 0.26] | |
| CD2 | [125, 130] | |
| k | 7 ⟶ 6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szwaja, S.; Pukalskas, S.; Juknelevičius, R.; Rimkus, A. Modeling Hydrogen-Assisted Combustion of Liquid Fuels in Compression-Ignition Engines Using a Double-Wiebe Function. Energies 2025, 18, 5622. https://doi.org/10.3390/en18215622
Szwaja S, Pukalskas S, Juknelevičius R, Rimkus A. Modeling Hydrogen-Assisted Combustion of Liquid Fuels in Compression-Ignition Engines Using a Double-Wiebe Function. Energies. 2025; 18(21):5622. https://doi.org/10.3390/en18215622
Chicago/Turabian StyleSzwaja, Stanislaw, Saugirdas Pukalskas, Romualdas Juknelevičius, and Alfredas Rimkus. 2025. "Modeling Hydrogen-Assisted Combustion of Liquid Fuels in Compression-Ignition Engines Using a Double-Wiebe Function" Energies 18, no. 21: 5622. https://doi.org/10.3390/en18215622
APA StyleSzwaja, S., Pukalskas, S., Juknelevičius, R., & Rimkus, A. (2025). Modeling Hydrogen-Assisted Combustion of Liquid Fuels in Compression-Ignition Engines Using a Double-Wiebe Function. Energies, 18(21), 5622. https://doi.org/10.3390/en18215622










