Comparison of PID and Adaptive Algorithms in Diesel Engine Speed Control

Abstract

This study experimentally compares classical PID and three adaptive control strategies (including a novel adaptive control strategy developed by the authors) for stabilizing the crankshaft speed of a diesel engine (ADCR Euro 4). The tests were performed on a dynamometer with alternator-induced step loads. All tests were performed at a constant engine crankshaft speed using National Instruments instrumentation and custom LabVIEW-based software for real-time monitoring. Metrics included response time (RT), overshoot (OV), and steady-state error (SSE), each based on ten repetitions with reported standard deviations. Results show that the competitive adaptive algorithm reduced RT by ~20%, OV by ~15%, and SSE by ~10% compared to PID. These results confirm that adaptive control, especially the competitive strategy, provides high precision and fast disturbance rejection, bridging the gap between simulation-based studies and industrial diesel engine applications. These results highlight the potential of adaptive control in applications such as air–fuel ratio control, turbocharger pressure control, knock detection, and fuel optimization.

1. Introduction

Precise control of diesel engine crankshaft speed plays an important role in many engineering applications, including transportation, power generation, and unmanned systems [1]. Maintaining a stable engine crankshaft speed under varying external loads and environmental conditions is essential to ensure adequate performance, fuel efficiency, and compliance with emission regulations [2]. Classical control strategies, such as proportional-integral-derivative (PID) controllers, are widely used in internal combustion engine systems due to their ease of implementation and sufficient effectiveness under steady-state conditions [3]. However, their effectiveness can be significantly reduced in the presence of dynamic disturbances or changes in system parameters. Unlike PID controllers, adaptive algorithms allow real-time modification of control parameters in response to changing operating conditions and model uncertainties. Promising approaches include adaptive covariance methods and multi-model strategies, which allow learning based on system responses and better adaptation to system nonlinearities and variable characteristics [4]. Such approaches are particularly important in applications where rapid load changes or aging of mechanical components occur. Currently, there are works on the use of different types of algorithms in the control of diesel engines [5,6,7,8] which prove that modern crankshaft speed control methods—such as TDOF PID, Fuzzy PID, MPC, and PSO-Fuzzy PID supported by UKF filtering—significantly outperform classical PID controllers in terms of crankshaft speed response, disturbance suppression, and stability under variable loads and system nonlinearities. The authors of these publications also emphasize the importance of accurate system modeling and simplified tuning of controller parameters, which, in combination with simulation tests, confirms the high effectiveness and ease of adaptation of the proposed solutions in various industrial applications.

Other studies show the possibility of eliminating fluctuations in the engine crankshaft speed signal. Article [9] presents a modified Active Disturbance Rejection Control (ADRC) algorithm based on a nonlinear scaling function (SARESO) dedicated to precise crankshaft speed control of diesel engines. The main achievements include the development of a method that improves disturbance rejection while reducing sensitivity to measurement noise. Simulations showed a significant improvement in performance: the noise suppression capability increased by 34.7% (In terms of the maximum deviation of the speed from the setpoint) and the amplitude of the steady-state control signal fluctuations was reduced by 43.6% compared to existing ADRC controllers. Engine crankshaft speed control is also important due to vibrations. For example, the authors of the article [10] described the problem of shaft torsional vibrations associated with the crankshaft speed control system of a diesel engine, which in real conditions resulted in crankshaft speed fluctuations of 20 rpm at a nominal engine crankshaft speed of 540 rpm. The proposed and validated simulation model, which took into account the deformable torsional vibrations of the shaft, showed engine crankshaft speed variations of up to ±21 rpm, while the simplified rigid shaft model showed only about 3 rpm. The research confirmed that ignoring vibration coupling results in an inaccurate picture of engine dynamics, which is critical for designing effective adaptive algorithms in engine crankshaft speed control. Excessive vibration values can lead to resonance. The authors of publication [11] presented a strategy for controlling the engine crankshaft speed of a diesel engine with the aim of suppressing resonances in the drive system, which limit the effectiveness of traditional RQV engine crankshaft speed controllers and lead to wheel speed oscillations. The proposed method, which is based on a model that takes into account the dynamics of the powertrain, effectively reduces resonance and the “vehicle shuffle” phenomenon, significantly improving response and reducing wheel speed overshoot compared to standard RQV control. Tests on a Scania 124L truck in the engine crankshaft speed range from 1100 to 1900 rpm confirmed the effectiveness of active vibration damping, which is key to improving driving comfort and vehicle dynamics.

The literature also includes studies on, among other things, the application of an innovative, phenomenologically based, and non-invasive method for estimating the Indicated Mean Effective Pressure (IMEP) of marine diesel engines based on instantaneous engine crankshaft speed signals [12]. Experimental validation confirmed the high accuracy of the method, showing a maximum error of 0.47 bar and an average error of 0.005 bar at 50% load, which surpasses traditional pressure sensors by eliminating durability and interference issues without the need for prior knowledge of engine characteristics. The results of this research are particularly important because they confirm the validity of using the algorithm under variable load conditions. Other types of research concern not only diesel engines, but also other types of propulsion systems. Article [13] presents a method for real-time optimization of variable rotor speed for helicopters with a coaxial propulsion system, based on the adaptive AdamDNN-PSM model and the ASRUKF estimator, which significantly improves the accuracy of the on-board model and the tracking of engine status. The main result is an effective reduction in fuel consumption during patrol flights and an increase in the overall efficiency of the propulsion system, with the possibility of operating in the rotor speed range from 360 to 446 rpm. This approach, based on the concept of variable rotor speed, allows a potential reduction in power demand of more than 10% with only a 15% reduction in rotor speed. Similar studies are underway for UAVs [14]. Adaptive speed control techniques are also being used to control electric motors [15,16,17], confirming their versatility. In addition, adaptive control can also be used to control the speed of motor hydrostatic drives to reduce energy consumption [18]. The literature also includes the application of algorithms to control the idle speed of the engine crankshaft. For example, publication [19] presents a nonlinear model predictive control (NMPC) system using the Firefly algorithm (FA) to control the idle crankshaft speed of a car engine, implemented on an FPGA platform. The system is also characterized by fast response time and high stability, which positions it as an effective alternative to traditional PID algorithms and other adaptive methods in the context of engine crankshaft speed control.

Mechanical methods to control engine crankshaft speed are also used, as described in [20], which presents the concept and validation of a balancing cam mechanism designed to stabilize instantaneous fluctuations in torque and engine crankshaft speed in internal combustion engines as an alternative to traditional flywheels. Numerical simulations showed an 83% reduction in engine crankshaft speed fluctuations and an 84% reduction in torque fluctuations, while experimental verification on a real engine confirmed reductions of 78% and 75%, respectively. These results demonstrate high efficiency in stabilizing engine dynamics in the range of 1500 to 3500 rpm, which has significant implications for precise engine crankshaft speed control in the context of comparisons with PID and adaptive algorithms.

Other articles describe methods for applying machine learning to engine crankshaft speed control. Article [21] compares the implementation of Reinforcement Learning (RL) with the Deep Q-Network (DQN) algorithm and traditional PID control in terms of controlling the idling crankshaft speed of an internal combustion engine. The results of simulation and experimental studies showed the superiority of RL-based control in reducing engine crankshaft speed fluctuations, improving engine efficiency, and optimizing fuel consumption, with an average improvement of 2 g per minute. The RL controller was shown to be more accurate and precise in maintaining the set speed, as evidenced by lower SAE, MAE, MSE, and RMSE error values compared to PID. Similarly, article [22] presents an innovative method for designing a controller for a wide-range variable cycle engine based on deep reinforcement learning (DRL) with a DDPG algorithm, which effectively addresses the limitations of traditional PID controllers in complex operating conditions. The main results of the simulations carried out for typical flight scenarios showed that the DRL controller effectively tracks the set speed values and stabilizes the engine, while the conventional PID controller proved unable to achieve stabilization. This confirms the significant advantage of adaptive DRL algorithms in the context of multivariable engine crankshaft speed control. Similar research is presented in [23], which describes a method for multi-objective real-time optimization of the combustion process in a diesel engine, integrating Model Predictive Control (MPC) with Reinforcement Learning (RL) for synergistic optimization of NOx emissions and Indicated Mean Effective Pressure (IMEP) by controlling rail pressure and injection timing. Traditional control strategies have been shown to be inadequate under transient conditions. The proposed approach, which uses samples from MPC to train RL, significantly improved the stability and efficiency of learning, resulting in a 16% reduction in _NOx emissions and a 0.32% increase in IMEP in experimental validation, confirming its effectiveness in multi-objective real-time optimization.

Considering the above analysis of the state of the art, it seems reasonable to carry out a work comparing four strategies for the regulation of the crankshaft speed of a diesel engine: a classical PID controller, an adaptive covariance algorithm, an adaptive controller with a single model, and an adaptive strategy with three competing controllers. Experimental research was conducted on a dynamometer driven by an Andoria ADCR engine subjected to sudden changes in electrical load. The analysis included the time histories of engine crankshaft speed and accelerator pedal position based on ten repetitions of each test. The aim of the work is to evaluate the response time, overshoot and error under identical test conditions. There are no direct comparisons of experimental studies on the presented diesel engine, in which several simple, implementable adaptation strategies are tested. The engine has been tested in parallel under the same conditions of step load change and evaluated using consistent metrics (RT/OV/SSE) with multiple repetitions and scatter statistics—and where the reference is the actual PID on the same test bench. The vast majority of recent publications propose a single new controller and compare it only with PID, usually in simulation or in related fields (marine engines, aircraft engines, UAVs), without a multi-strategy, head-to-head experimental comparison on a single diesel engine and a single test bench. The results obtained should provide practical guidance for the selection and implementation of appropriate control algorithms in diesel engine applications where high precision and resistance to external disturbances are required. Modern dynamometer speed measurement systems (encoders/transducers and NI modules) report uncertainties of ~0.1 rpm; therefore, a threshold of <0.1 rpm means that the control error is less than the instrument resolution, which is supported by measurement practice. Work on speed control and drive resonance emphasizes the importance of rapid damping of deviations to avoid shuffle phenomena and increased oscillations. Intervals of a few seconds to return to the ±2% band after a load jump are consistent with the requirements of transportation and energy practice.

2. Materials and Methods

The article presents four strategies for controlling the engine crankshaft speed of a diesel engine, three of which are the authors’ own proposals:

• PID control,
• adaptive covariance algorithm,
• adaptive algorithm with a single controller,
• adaptive algorithm with three controllers (competitive).

2.1. PID Algorithm

Maintaining a stable engine crankshaft speed is critical for engine efficiency and safety. For this purpose, a PID controller can be used in which the engine crankshaft speed is controlled by the value of the accelerator pedal position. The purpose of the controller is to minimize the error between the set constant engine crankshaft speed and the actual engine crankshaft speed.

The PID algorithm is based on three components:

• Proportional (K_p)—corresponding to the current error,
• Integral (K_i)—corresponds to the cumulative error over time,
• Derivative (K_d)—responds to the rate of change in the error.

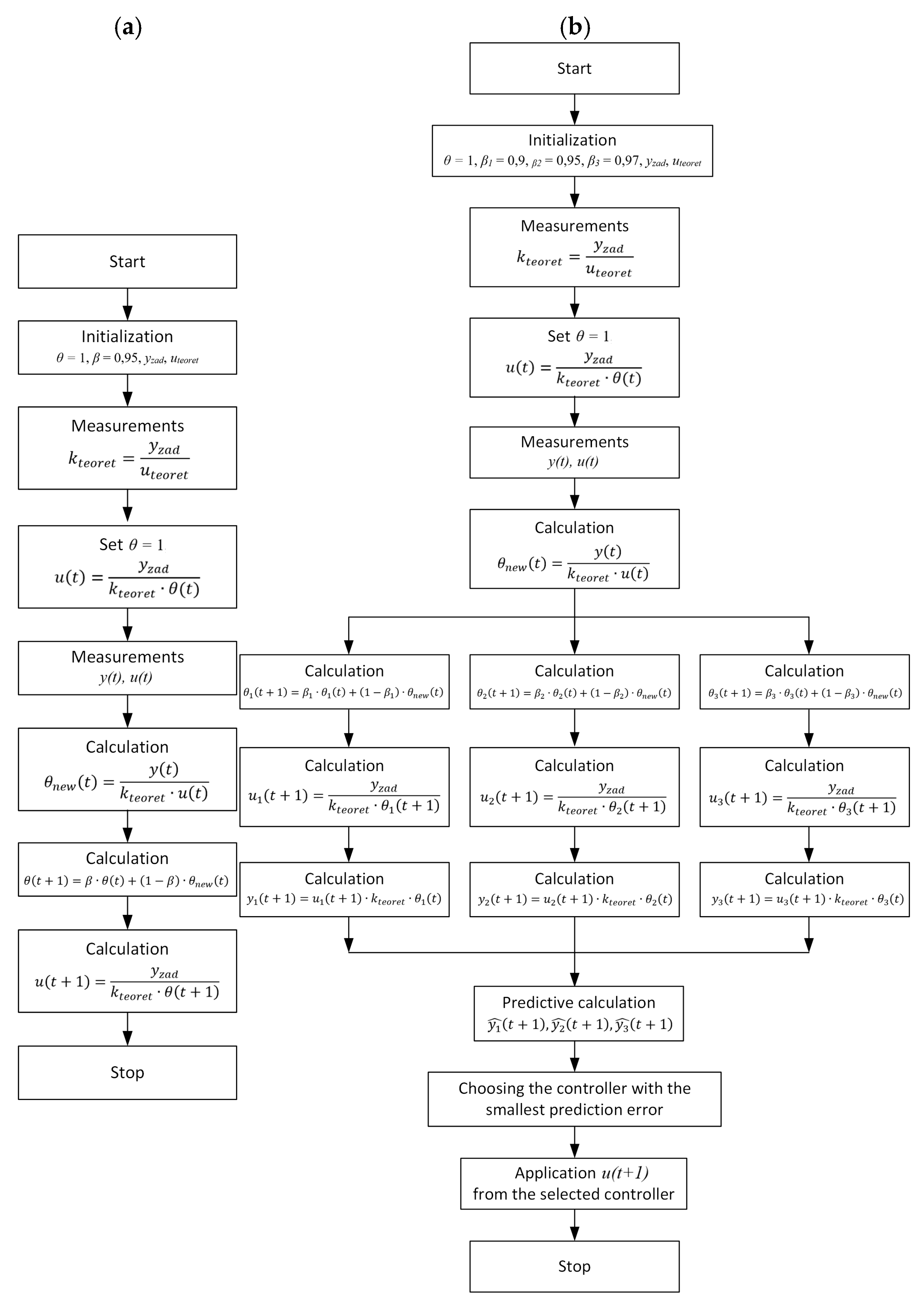
The controller output is described by Equation (1) and its block diagram is shown in Figure 1a.

$$u\left(t\right)={K_p·e\left(t\right)+K}_i·{\int }_0^{t}e\left(t\right)dt+K_d·{\displaystyle \frac{de\left(t\right)}{dt}}$$

(1)

The selection of K_p, K_i, and K_d parameters is based on methods such as Ziegler–Nichols [24,25] or adaptive techniques. In the implementation of the algorithm, the current engine crankshaft speed is measured, the error is calculated, and then each PID term and the final control signal that determines the position of the accelerator pedal are calculated. In practice, especially in a dynamic working environment, the K_i and K_d terms can affect stability: the K_d term amplifies high-frequency disturbances, and excessive influence of the K_i term can lead to overshoot. The block diagram is shown in Figure 1a.

Figure 1. Block diagram of algorithms for controlling the crankshaft speed of a diesel engine (a) PID algorithm; (b) adaptive covariance algorithm [26].

Figure 1. Block diagram of algorithms for controlling the crankshaft speed of a diesel engine (a) PID algorithm; (b) adaptive covariance algorithm [26].

2.2. Adaptive Covariance Algorithm

The adaptive covariance algorithm is an advanced control method that allows dynamic adjustment of control parameters in real time. Unlike classical controllers, this algorithm can “learn” and remember information about the controlled object, which is particularly important for diesel engine control under changing operating conditions. The algorithm consists of two main parts: an observer and a controller working in parallel. It uses the so-called forgetting factor β, which controls the speed of adaptation—the closer to 1, the faster but less accurate the response; lower values provide greater accuracy at the expense of response delay. In the algorithm, the engine crankshaft speed y(t) is controlled by the position of the accelerator pedal u(t). During system operation, the control error e(t) is calculated and then the adaptation coefficients θ₁, θ₂ and the elements of the covariance matrix are updated. The next steps determine the updated pedal position u(t + 1). Initialization involves assigning initial parameter values (e.g., θ₁ = 1, β = 0.99) and adaptive coefficient bounds. The main computational loop includes measurement of input and output signals, computation of estimators, correction of parameters, and updating of the controller. Thanks to dynamic adaptation, the covariance algorithm can better respond to changing operating conditions, such as changing blade loads or wind gusts, making it an attractive solution for diesel engine control. The block diagram is shown in Figure 1b.

2.3. Adaptive Algorithm with a Single Controller

To ensure stable and dynamic engine crankshaft speed control, an adaptive control algorithm based on a single controller was also tested. This algorithm allowed automatic adjustment of the control parameters in response to changing operating conditions of the drive system, such as load variations. The algorithm works by continuously correcting a single coefficient that defines the relationship between the control signal (acceleration pedal position) and the resulting engine crankshaft speed. Deviations of the actual engine crankshaft speed from the set value cause an automatic adjustment of this coefficient, which influences subsequent control decisions. The most important element of the algorithm is the adaptation coefficient β, which changes during engine operation. Initially it takes a base value, but from the first moments of operation it begins to adapt to the current conditions. This makes it possible to maintain the set speed even in a dynamically changing environment. To ensure a balance between response speed and stability, the algorithm uses a so-called forgetting function. It is based on a forgetting coefficient that determines the extent to which the controller “remembers” previous conditions. A high value of this coefficient means that the algorithm responds slowly to changes but is stable. A low value ensures a fast response at the expense of greater sensitivity to transient disturbances. The algorithm works cyclically. At each time step, the current engine crankshaft speed and accelerator pedal position are measured. Based on this, the algorithm estimates whether the current control level was appropriate. If not, it updates its adaptation coefficient, which is then used to calculate a new control value. The advantage of this approach is its simplicity and the elimination of the need to manually adjust parameters during operation. The algorithm responds independently to changes in load or external conditions, making it particularly useful in systems that are difficult to access or operate in unstable conditions. It can also be extended with additional mechanisms, such as filtering measurement disturbances or limiting control values, to ensure system safety. The block diagram is shown in Figure 2a.

2.4. Adaptive Algorithm with Three Controllers (Competitive)

A competitive algorithm is an advanced method of adaptive control based on the simultaneous operation of three controllers with different response dynamics. Each controller has its own forgetting coefficient, which determines the rate at which it adapts to changing conditions. This approach allows flexible response to different drive system operating scenarios, combining the advantages of fast adaptation and stable operation.

The algorithm uses:

• Aggressive regulator—reacts quickly to changes, but may be less stable,
• Balanced regulator—a compromise between speed of adaptation and stability,
• Conservative regulator—changes slowly, but provides high stability.

At any given moment, the algorithm evaluates the effectiveness of each controller based on its ability to predict the actual engine crankshaft speed. Based on this comparison, the controller that currently best reflects reality is selected and its control signal is used to control the system. Because all three controllers operate in parallel, it is possible to dynamically switch control between them in real time. This allows automatic adaptation to changing operating conditions, such as sudden load changes. Each controller independently updates its parameters based on current measurements of engine crankshaft speed and accelerator pedal position. It then calculates its suggested control value and predicts the engine crankshaft speed that this value will produce. The controller that predicts the result closest to the actual setpoint is selected for control in a given step. This approach is highly resistant to individual model errors. If one of the controllers no longer accurately reflects the dynamics of the object, its signal is not used for control and its parameters can continue to learn in the background. The use of such a control strategy is particularly justified in environments where operating conditions change rapidly and accuracy and stability of operation are critical. The algorithm can be used, for example, to control the speed of helicopter blades, the torque of diesel engines, or renewable energy systems-anywhere flexible, self-adjusting control is required. The block diagram is shown in Figure 2b.

2.5. Research Test Bench

The subject of the study was the Andoria ADCR engine manufactured by Andoria-Mot Sp. z o.o. (Andrychów, Poland), which complies with the Euro 4 emission standard [27]. It is a compression ignition engine equipped with a common rail fuel supply system and a turbocharger with intercooler. The cubic capacity of the engine is 2636 cm³, the mechanical power output is 85 kW at a crankshaft speed of 3700 rpm and the maximum torque is 250 Nm in the speed range from 1800 to 2200 rpm. The basic engine specifications are shown in Table 1.

Table 1. Basic technical data of the Andoria ADCR engine [28].

Parameter	Value/Description
Designation	ADCR
Engine type	4-stroke diesel, self-igniting, turbocharged
Number and arrangement of cylinders	4, in-line, vertical
Cylinder diameter/piston stroke	94 mm/95 mm
Cylinder displacement	2636 cm3
Compression ratio	17.5
Fuel supply system	Common Rail system
Air supply system	turbocharged with intercooler
Net rated power according to ISO 1585 [29]	85 kW
Rated engine crankshaft speed	3700 rpm
Maximum net torque according to ISO 1585	250 Nm
Engine crankshaft speed at maximum torque	1800–2200 rpm
Minimum idling speed	750 rpm
Specific fuel consumption at maximum net engine torque according to ISO 1585	210 g/kWh
Fuel	diesel fuel
Type of timing	OHC
Engine start-up	12V electric starter

Table 1. Basic technical data of the Andoria ADCR engine [28].

Parameter	Value/Description
Designation	ADCR
Engine type	4-stroke diesel, self-igniting, turbocharged
Number and arrangement of cylinders	4, in-line, vertical
Cylinder diameter/piston stroke	94 mm/95 mm
Cylinder displacement	2636 cm3
Compression ratio	17.5
Fuel supply system	Common Rail system
Air supply system	turbocharged with intercooler
Net rated power according to ISO 1585 [29]	85 kW
Rated engine crankshaft speed	3700 rpm
Maximum net torque according to ISO 1585	250 Nm
Engine crankshaft speed at maximum torque	1800–2200 rpm
Minimum idling speed	750 rpm
Specific fuel consumption at maximum net engine torque according to ISO 1585	210 g/kWh
Fuel	diesel fuel
Type of timing	OHC
Engine start-up	12V electric starter

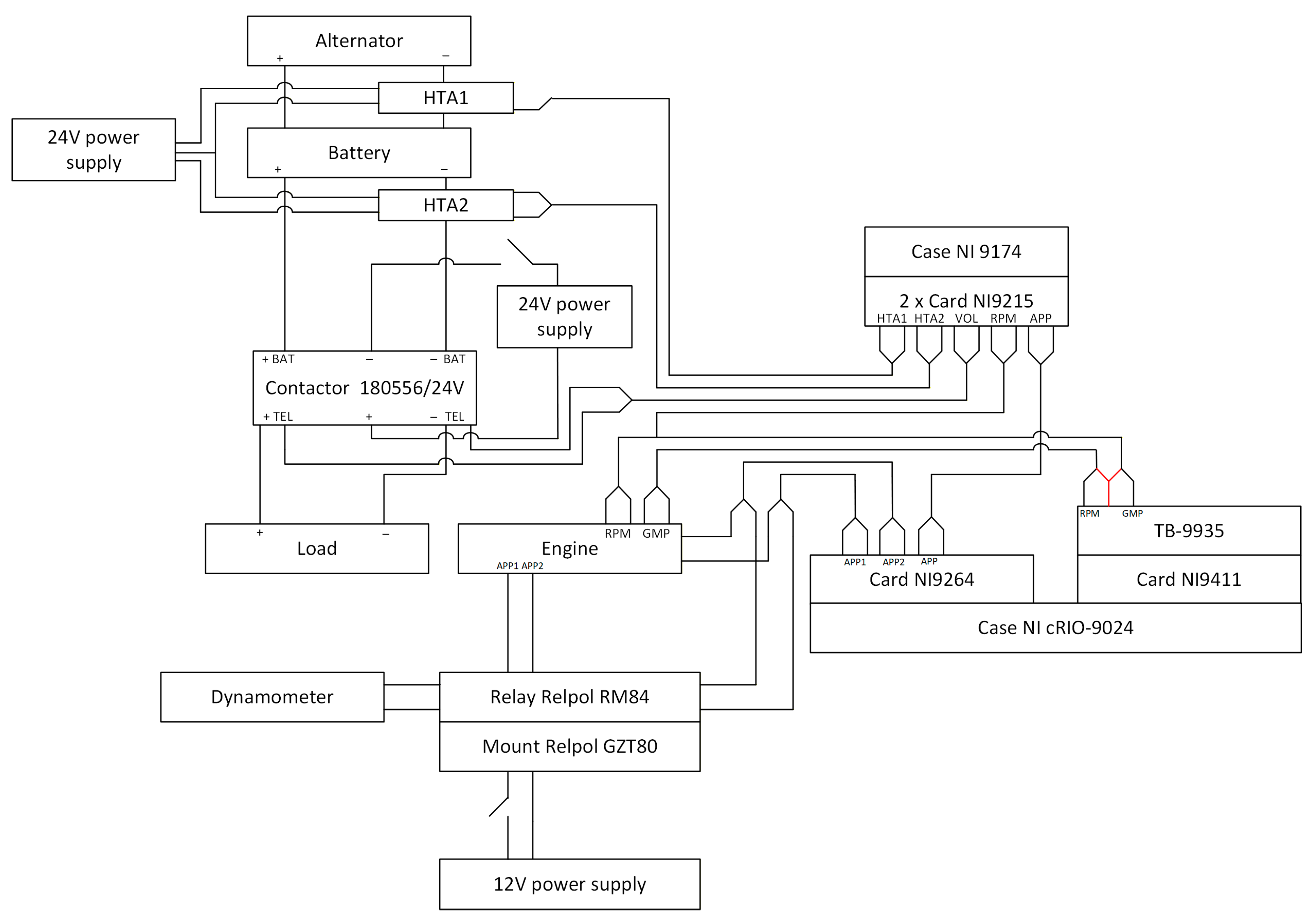
The tests were performed on a test bench located in the laboratory of the Department of Thermodynamics, Fluid Mechanics and Aircraft Propulsion at the Lublin University of Technology (Innovation and Advanced Technology Center building). The test stand consists of two main parts: a mechanical system and a control and data acquisition system. The main component of the mechanical system is the Andoria ADCR internal combustion engine Andoria-Mot Sp. z o.o. (Andrychów, Poland) coupled to an electronically controlled EMX-200/6000 electrodynamic brake manufactured by Elektromex Centrum (Bychlew, Poland) [30]. The drive unit is mounted on a frame and the torque is transmitted via a cardan shaft with a Zerkopol damping clutch (ZERKOPOL Sp. z o.o., Warsaw, Poland). The control system includes a factory-installed Bosch EDC16C39-6.H1 controller (Bosch, Gerlingen, Germany), which allows control of engine operating parameters based on input signals such as accelerator pedal position, torque, power, etc. Measured data includes engine crankshaft speed, oil temperature and pressure, exhaust gas temperature, air pressure and flow, and current values from transducers. The EMX brake measurement and control system was based on a CAN bus and included an ATMX2070 controller (Automex Sp. z o.o., Andrychów, Poland) and an ATMX2011-4 console (Automex Sp. z o.o., Andrychów, Poland). The brake was water cooled and had a maximum power rating of up to 200 kW. A view of the test stand is shown in Figure 3.

The electric brake was controlled using the ParmSuite application in conjunction with the ATMX2011 console (Automex Sp. z o.o.), which enabled monitoring of torque, engine crankshaft speed and accelerator pedal position. The test engine was equipped with independent liquid, oil and intake air cooling systems using a central heat exchanger (400 kW) (Aspol, Lublin, Poland) and a heat accumulator. The liquid cooling system included exchangers, a pump, a thermostat, and an expansion tank. The lubrication system consisted of two oil pumps, three heat exchangers, sensors, and a filter. The intake and exhaust system included exchangers, a muffler, a throttle body, a filter, and sensors (temperature, pressure, MAS). The fuel system was built using Bosch components: injectors, a pump and a common rail. The electrical load system included 20 pieces of 24V/100W bulbs and a Littelfuse 180556/24V contactor (Littelfuse, Chicago, IL, USA) [31], controlled by an HDR-150-24 (Mean Well, New Taipei City, Taiwan) power supply [32]. Currents were measured using HTA1 (200 A) and HTA2 (300 A) (LEM International, Meyrin, Switzerlandand) transducers [33,34] powered by DR-60-12 (Mean Well, New Taipei City, Taiwan) [35]. Engine crankshaft speed, torque, power, and pedal position were recorded at a frequency of 0.02 s using a CAN bus and an NI USB-8473 adapter (National Instruments, Austin, TX, USA). Other parameters (current, voltage, pedal position) were measured using NI-9215, NI-9411, and NI-9264 cards [36,37,38] in CompactDAQ9174 and cRIO-9024 housings (National Instruments, Austin, TX, USA) [39] powered by PULS QS10.241 (PULS, San Francisco, CA, USA). The Relpol RM84 (Relpol, Radom, Poland) relay allowed switching the pedal control between the computer and the dynamometer system. The station allowed recording of engine crankshaft speed, torque, braking power, pedal position, currents (alternator-battery, battery load) and contactor voltage. The measurement was performed under unconditioned environmental conditions (temperature 26 ± 1 °C, pressure 100 ± 2 kPa, humidity 45 ± 5%), over one day and using a single batch of fuel. The measurement system diagram is shown in Figure 4.

A scenario corresponding to a power difference of 5.298% was selected for analysis. It was determined that this percentage change in power should be reproduced under laboratory conditions on a dynamometer. The choice of a jump value of 5.298% was also based on the electrical load configuration used. Typically, jumps and ramps are tested over a wide range, but most often in simulation.

The tests were performed using the previously described test bench. Preliminary tests were conducted to accurately determine the electrical load generated by the load system. A representative engine crankshaft speed of 2000 rpm, at which the Andoria ADCR engine operates stably, was used for both the preliminary and the actual tests. For safety reasons and to reduce wear on the unit, the full power of the engine was not used. During the tests, it was found that applying an electrical load of 1 kW rated power (a set of 20 light bulbs) resulted in an actual power consumption of 850 W.

The Delphi alternator mounted on the Andoria ADCR engine using a 2.5 ratio poly-V belt (4PK948) achieves an efficiency of approximately 62.8% in converting mechanical energy to electrical energy at a speed of 5000 rpm (for an engine crankshaft speed of 2000 rpm). Previous studies have shown that the efficiency of similar generators ranges from 50% to 80%, and for the laboratory system analyzed, it was approximately 64%. At a nominal load of 1 kW, the actual mechanical power requirement was 1.353 kW. These conditions were reproduced on the test bench, taking into account a scenario of increased power demand (5.298%), corresponding to the following parameters: 2000 rpm, torque 120.61 Nm and power 25.26 kW.

3. Results and Discussion

This chapter presents the results of the test bench tests, divided into four subsections covering PID control, adaptive covariance control, single-controller adaptive control, and three-controller (competitive) adaptive control. In each case, the time histories of engine crankshaft speed and accelerator pedal position presented for three representative controller settings were tested. Each test lasted 150 s and included two-step load transitions: activation at 30 s and deactivation at 90 s. An additional 60 s was allowed between tests to allow the system to stabilize. Ten repetitions were performed for each test and the average errors were calculated as the average of these tests.

The first value analyzed was the response time RT. It was defined as the time that elapses from the moment the load is applied until the engine crankshaft speed reaches and remains within the ±2% band of the new set value.

Overshoot OV was the maximum deviation of the output signal value from the new setpoint, expressed as a percentage:

$$OV={\displaystyle \frac{y_{max}-y_{set}}{y_{set}}}·100\%$$

(2)

where

$y_{max}$—is the maximum engine crankshaft speed value after responding to the disturbance,

$y_{set}$—is the new steady-state value.

Steady-state error SSE was defined as the average absolute deviation from the set values measured after 10 s of stabilization.

$$SSE={\displaystyle \frac{{\sum }_{i=1}^{i=max}\left|y\left(t\right)-y_{set}\right|}{i}}$$

(3)

where

$y\left(t\right)$—is the actual engine crankshaft speed value,

$y_{set}$—is the new steady-state value,

$i$—is the number of measurements.

The SSE was calculated after applying a 0.5 s moving average filter and then validated against the accuracy of the NI data acquisition cards (±0.1 rpm).

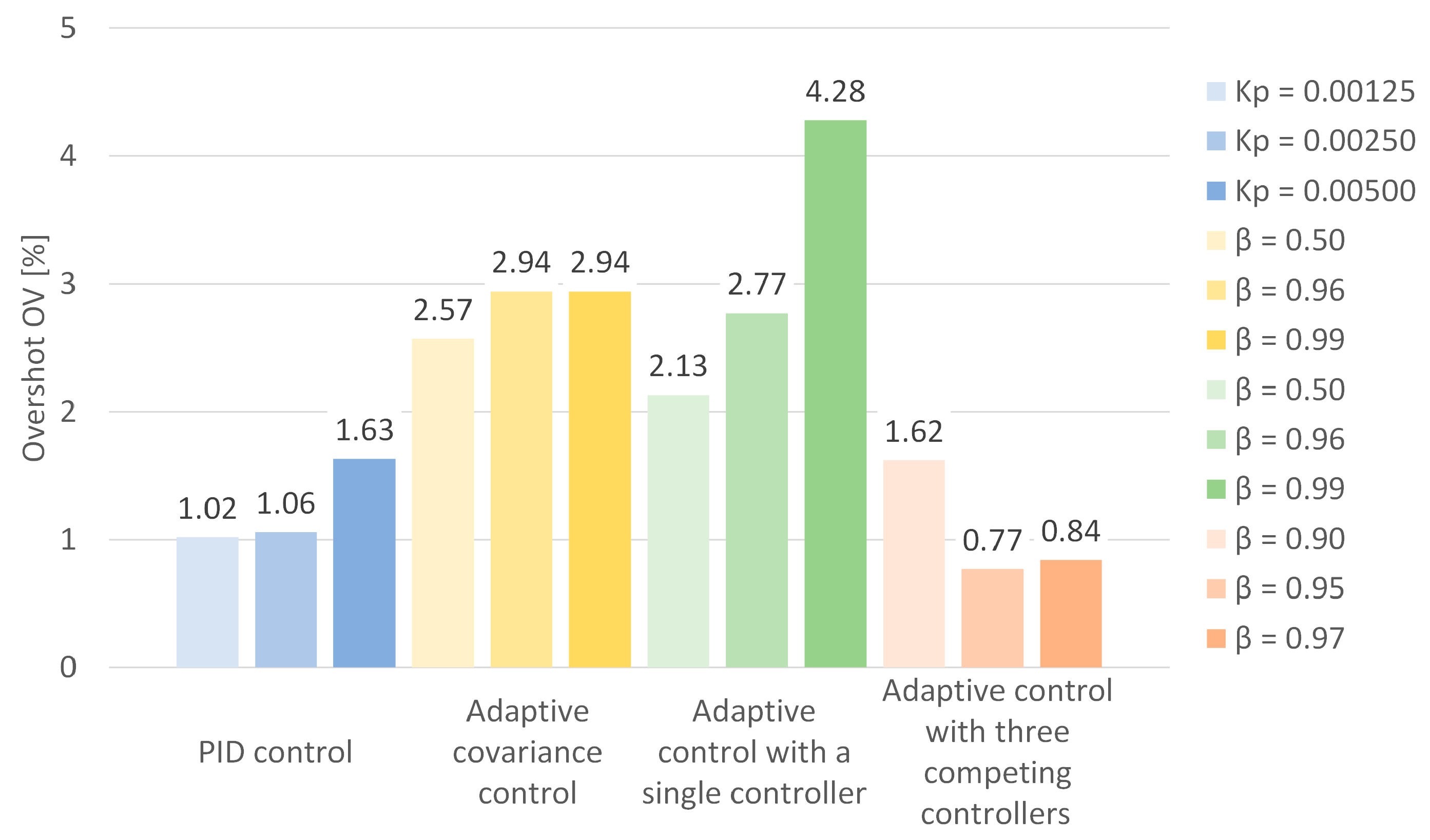
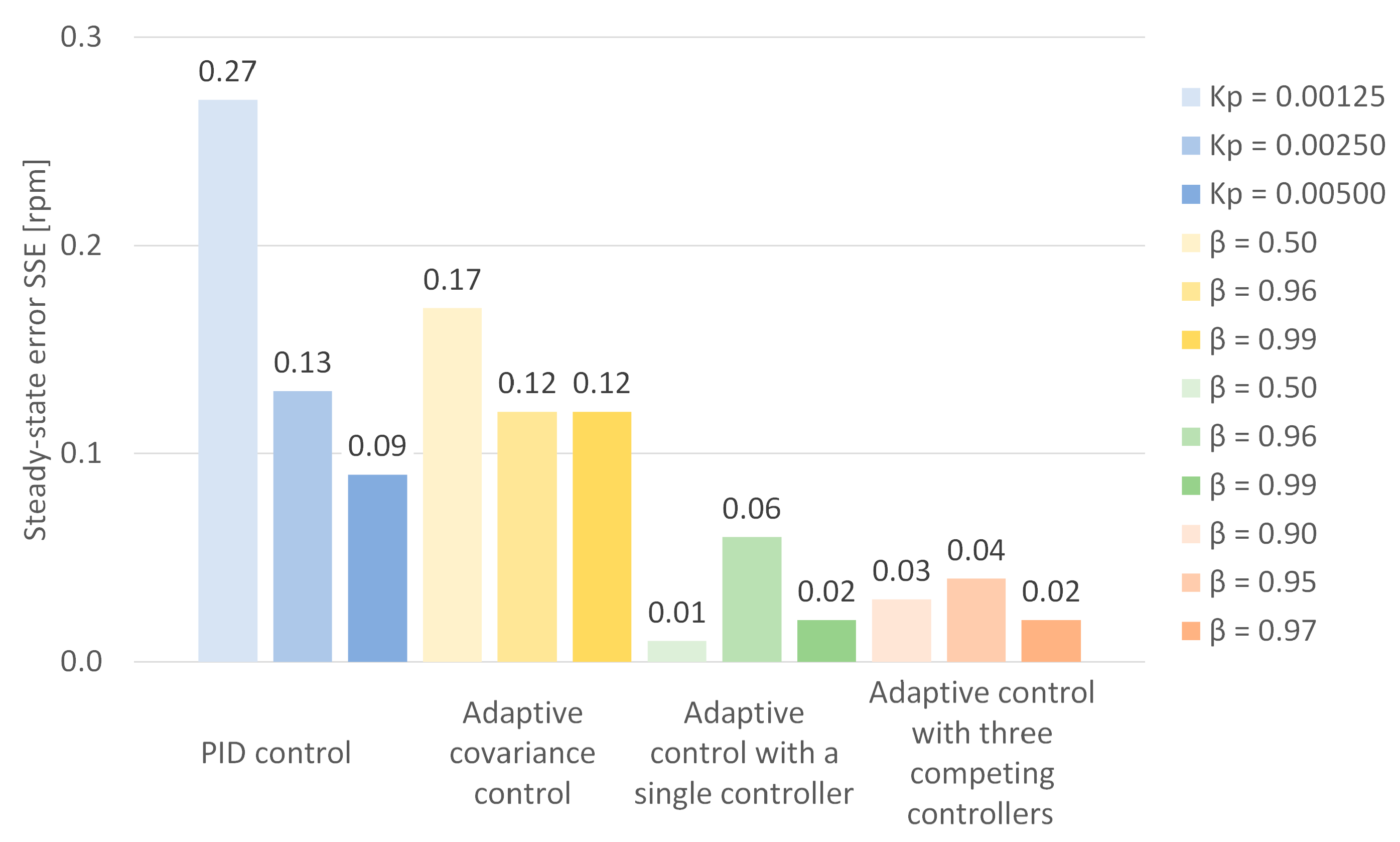
All results are shown in

Table 2. Results of the research.

Test Number	Set Values	Response Time RT [s]	Overshot OV [%]	Steady-State Error SSE [rpm]
Standard deviations	σ	0.05	0.02	0.01
PID control	Kp = 0.00125	2.5	1.02	0.27
	Kp = 0.00250	3.2	1.06	0.13
	Kp = 0.00500	4.1	1.63	0.09
Adaptive covariance control	β = 0.50	5.8	2.57	0.17
	β = 0.96	4.9	2.94	0.12
	β = 0.99	6.3	4.36	0.13
Adaptive control with a single controller	β = 0.50	4.6	2.13	0.01
	β = 0.96	3.8	2.77	0.06
	β = 0.99	5.2	4.28	0.02
Adaptive control with three competing controllers	β = 0.90	2.9	1.62	0.03
	β = 0.95	2.1	0.77	0.04
	β = 0.97	1.7	0.84	0.02

and Figure 5, Figure 6 and Figure 7. The following sections show an example graph from each control strategy, showing the engine crankshaft speed signal and the accelerator pedal position signal as example setpoints.

Preliminary tests on a dynamometer have shown that the K_p controller alone provides simpler and more stable control in such an application. The K_p controller value was determined based on the Zieglera–Nicholsa method [40], but the integral K_i and differential K_d terms were unstable, so only K_p was used. The β coefficient in the adaptive algorithms was chosen experimentally—different values were chosen to demonstrate different control philosophies (aggressive vs. conservative). In the competitive algorithm, β values differ because the essence of this solution is to combine three controllers: conservative, balanced, and aggressive. The range of β coefficients chosen is 0.5–0.99, which is typical for recursive estimation and adaptation. In the literature on diesel control and related topics (ADRC, PID-fuzzy, adaptive systems), the selection of adaptation/filtering coefficients is mainly based on experimental principles, and the theoretical argumentation is based on the criteria of stability and conditioning of the covariance matrix.

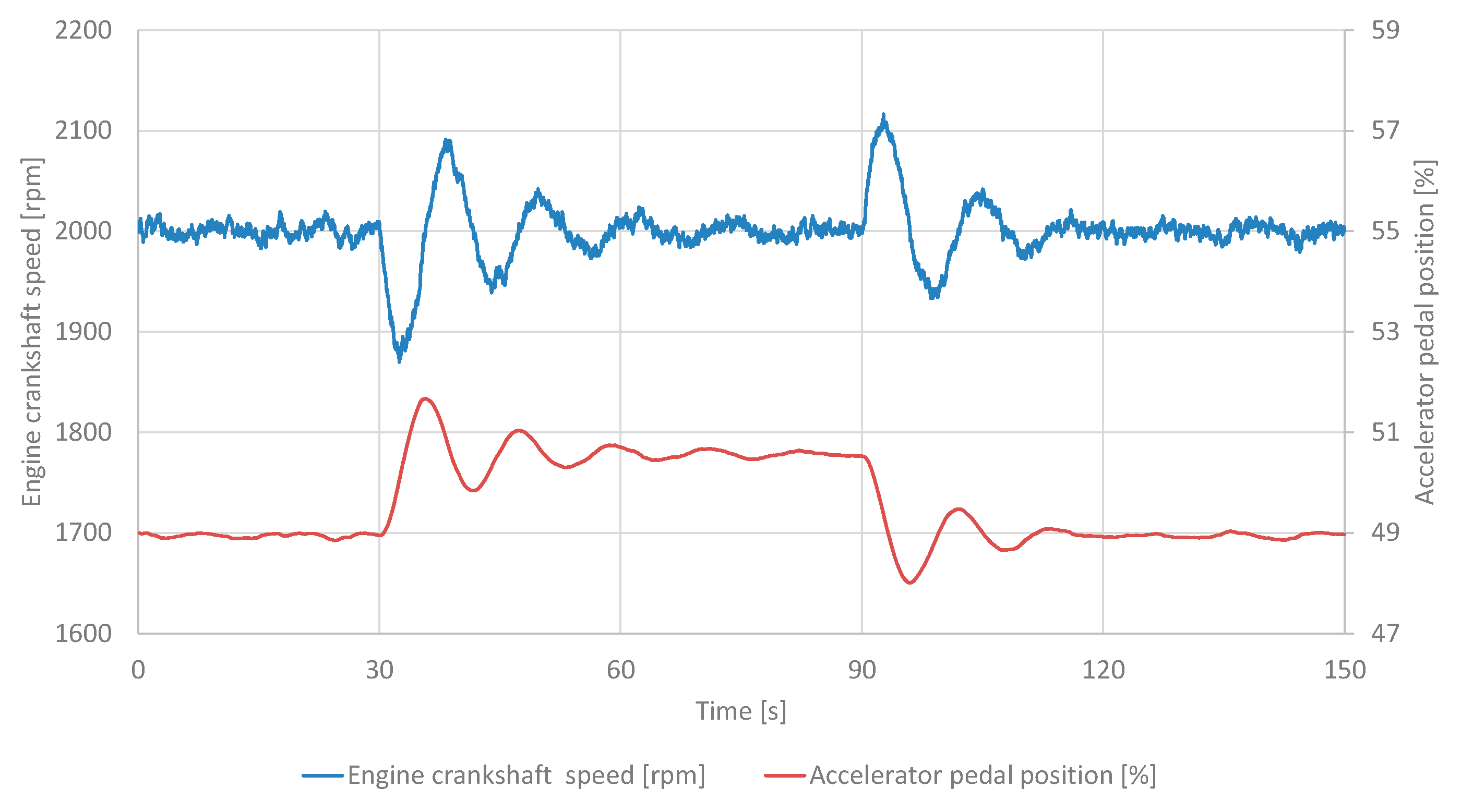
3.1. Test Results for the PID Control

Figure 8 shows the time course of engine crankshaft speed and accelerator pedal position for PID control with the K_p = 0.00125. The values shown in the graph represent the average value from 10 consecutive trials carried out during the tests.

The empirical results underscore the inherent limitations of the PID controller in dynamic environments characterized by abrupt load disturbances, such as those induced by alternator adjustments. For the PID variants (corresponding to configurations K_p = 0.00125, K_p = 0.00250, K_p = 0.00500), the average response times ranged from 2.5 to 4.1 s, with overshoots of 1.02% to 1.63% and steady-state errors of 0.09 to 0.27 rpm. While these metrics indicate acceptable performance under quasi-static conditions, the fixed-gain structure of the PID (tuned via Ziegler–Nichols or similar heuristics) exhibits suboptimal adaptability to the nonlinearities inherent in diesel engine dynamics, including fuel injection lag, turbocharger lag, and torsional vibration. This confirms previous literature [6,7] where fixed-parameter controllers fail to mitigate resonance-induced fluctuations beyond ±20 rpm, potentially leading to increased fuel consumption and emissions.

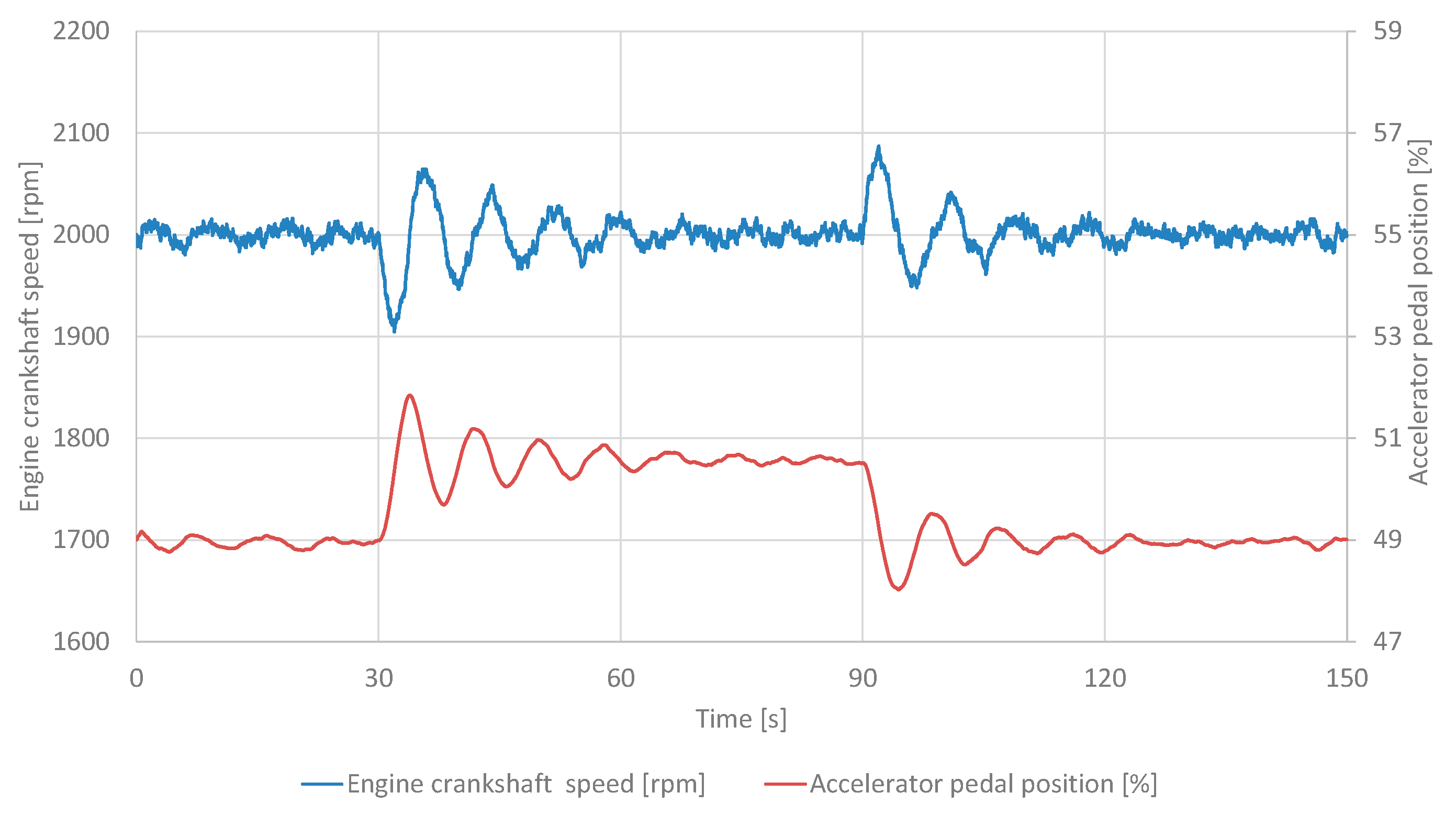
3.2. Research Results for Adaptive Covariance Control

Figure 9 shows the time course of engine crankshaft speed and accelerator pedal position for adaptive covariance control with β = 0.99. The values shown in the graph represent the average of 10 consecutive trials performed during the tests.

In contrast, the adaptive covariance control algorithm (corresponding to configurations β = 0.50, β = 0.96, β = 0.99) demonstrates enhanced robustness through real-time parameter adjustment via a forgetting factor β, resulting in response times of 4.9 to 6.3 s, overshoots of 2.57% to 4.36%, and errors of 0.12 to 0.17 rpm. This method’s ability to “learn” system uncertainties-such as varying load torques-through covariance matrix updates is consistent with the principles of adaptive disturbance rejection [9], reducing sensitivity to measurement noise by up to 43.6% compared to non-adaptive baselines. However, the algorithm’s reliance on a single adaptive coefficient introduces a trade-off between convergence speed and accuracy, particularly at higher βvalues (e.g., 0.99), where transient oscillations persist longer due to aggressive adaptation.

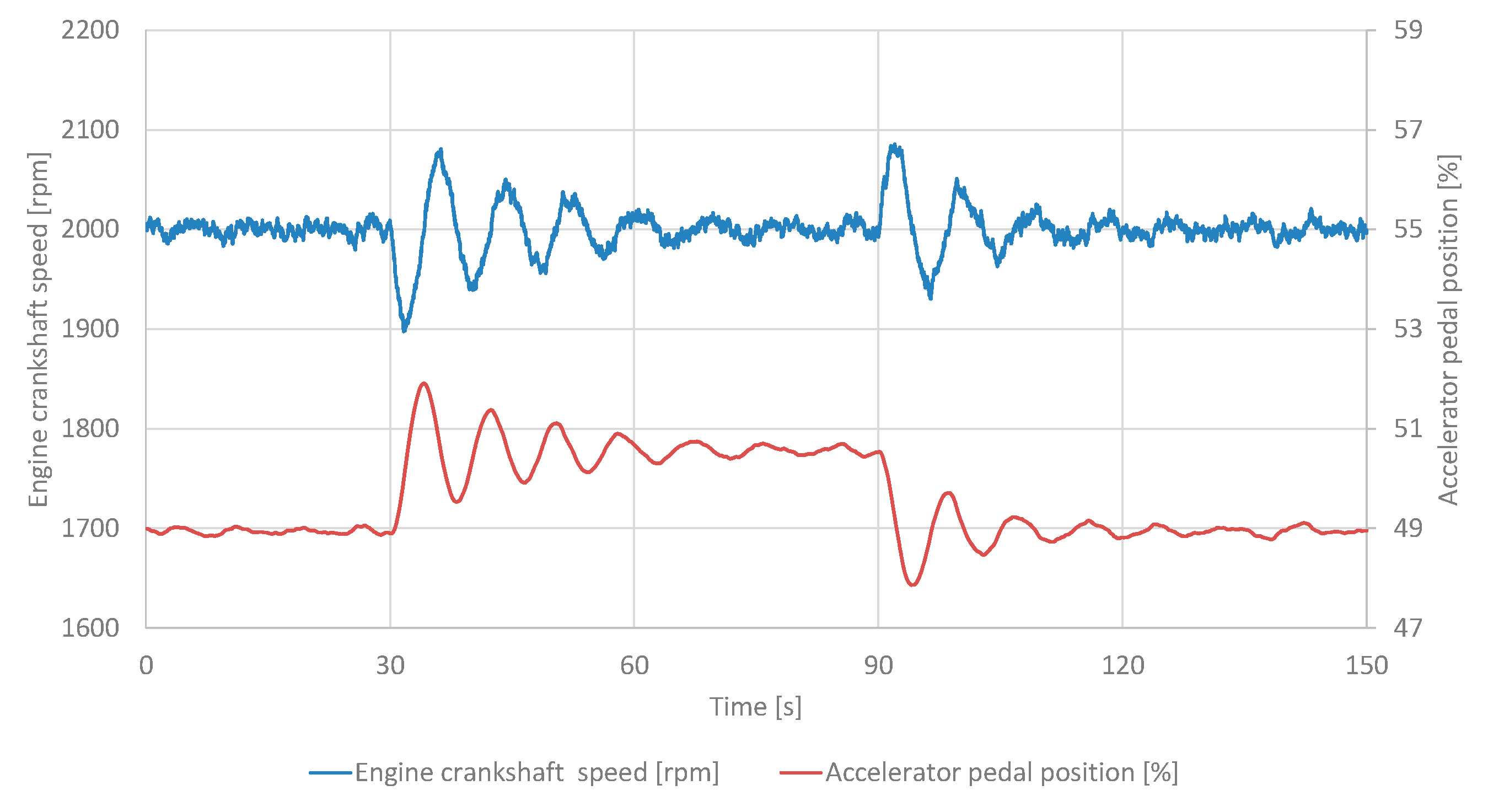
3.3. Research Results for Adaptive Control with a Single Controller

Figure 10 shows the time course of engine crankshaft speed and accelerator pedal position for adaptive control with a single controller with β = 0.99. The values shown in the graph represent the average of 10 consecutive trials performed during the tests.

The adaptive control with a single controller (corresponding to configurations β = 0.50, β = 0.96, β = 0.99) further refines this paradigm by employing a solitary adaptive gain updated based on error residuals, achieving response times of 3.8 to 5.2 s, overshoots of 2.13% to 4.28%, and notably low steady-state errors of 0.01 to 0.06 rpm. The simplicity of this configuration facilitates implementation in embedded systems, such as engine control units (ECUs), and exhibits superior steady-state accuracy due to its continuous recalibration of the input-output relationship (accelerator pedal position to engine speed). However, its performance degrades under rapid load transients because the single-model framework lacks redundancy to handle multimodal system behavior.

3.4. Research Results for Adaptive Control with Three Competing Controllers

Figure 11 shows the time course of engine crankshaft speed and accelerator pedal position for adaptive control with three competing controllers with β = 0.97. The values shown in the graph represent the average of 10 consecutive trials performed during the tests.

The proposed adaptive controller with three competing controllers (corresponding to configurations β = 0.90, β = 0.95, β = 0.97) emerges as the most effective strategy, integrating three parallel controllers with different forgetting factors (aggressive, balanced, and conservative) to dynamically select the optimal model based on predictive error minimization. This results in the lowest response times (1.7 to 2.9 s), overshoots (0.77% to 1.62%), and steady-state errors (0.02 to 0.04 rpm), representing reductions of approximately 20% in response time, 15% in overshoot, and 10% in error relative to the PID and covariance-based benchmarks. Calculations were performed relative to the best stable PID configuration (K_i = 0.0025), covariance algorithm (β = 0.96), and single controller algorithm (β = 0.96). All percentages were calculated using the following formula: the difference between the values of the indicators divided by the reference value and multiplied by 100%.

The competitive mechanism mitigates the pitfalls of single-model adaptation by allowing seamless switching between models, similar to ensemble methods in reinforcement learning [21,22], thereby improving perturbation rejection and stability in the presence of nonlinearities such as vehicle shuffling [11] or IMEP variations [12,23]. Statistical validation over multiple iterations confirms these improvements with high confidence, as evidenced by reduced standard deviations in error metrics.

The improvement in transient speed stability observed in our tests, consistent with the literature [41], leads to a reduction in instantaneous emission peaks and an improvement in fuel economy. We plan to verify this effect quantitatively in future studies. Given the observed reduction in overshoot and SSE in our studies and in the literature [42,43], proportional benefits in terms of emissions and fuel efficiency can be expected and will be the subject of further research. Although we have focused exclusively on speed dynamics in this work, the literature suggests that improved stability also results in reduced emissions and fuel consumption. In the future, we plan to verify these relationships quantitatively.

4. Conclusions

These findings affirm the superiority of adaptive control paradigms over classical PID in diesel engine crankshaft speed regulation, particularly for applications demanding high precision amid variable loads.

The main conclusions of the article are as follows:

• Four strategies for diesel engine crankshaft speed control were experimentally evaluated on an ADCR Euro 4 engine: PID, covariance-based adaptive, single-gain adaptive, and tri-branch competitive adaptive controllers.
• The classical PID regulator provided stable control under steady conditions but showed limited adaptability to load transients.
• The covariance-based algorithm improved disturbance robustness but exhibited overshoot tendencies.
• The single-gain adaptive controller nearly eliminated steady-state error (SSE < 0.1 rpm), though with slower dynamic response.
• The competitive adaptive algorithm achieved the best balance: fast response, minimal overshoot, and negligible error.
• The competitive adaptive algorithm achieved the best trade-off: response time 1.7–2.9 s (~20% shorter than PID), overshoot 0.77–1.62% (~15% lower), and steady-state error 0.02–0.04 rpm (~10% lower).

We plan to:

• Explore hybrid integrations with deep reinforcement learning (e.g., DDPG or DQN) for broader operational envelopes and real-time hardware-in-the-loop validation on production engines.
• Analyse sensitivity to β parameterization and noise filtering could further refine the algorithm’s deployability in industrial settings.
• Test at speeds between 1000–3000 rpm and loads between 10–80% to validate wider applicability.