Abstract
Reliable multilevel inverter IGBT modules require precise loss and heat management, particularly in severe traction applications. This paper presents a comprehensive modeling framework for three-level T-type neutral-point clamped (TNPC) inverters using a high-power Insulated Gate Bipolar Transistor (IGBT) module that combines model predictive control (MPC) with space vector pulse width modulation (SVPWM). The particle swarm optimization (PSO) algorithm is used to methodically tune the MPC cost function weights for minimization, while achieving a balance between output current tracking, stabilization of the neutral-point voltage, and, consequently, a uniform distribution of thermal stress. The proposed SVPWM-MPC algorithm selects optimal switching states, which are then utilized in a chip-level loss model coupled with a Cauer RC thermal network to predict transient chip-level junction temperatures dynamically. The proposed framework is executed in MATLAB R2024b and validated with experiments, and the SemiSel industrial thermal simulation tool, demonstrating both control effectiveness and accuracy of the electro-thermal model. The results demonstrate that the proposed control method can sustain neutral-point voltage imbalance of less than 0.45% when operating at 25% load and approximately 1% under full load working conditions, while accomplishing a uniform junction temperature profile in all inverter legs across different working conditions. Moreover, the results indicate that the proposed control and modeling structure is an effective and common-sense way to perform coordinated electrical and thermal management, effectively allowing for predesign and reliability testing of high-power TNPC inverters.
1. Introduction
Multilevel inverters are increasingly used in high-power industrial drives and traction applications to meet stringent efficiency and reliability standards. Among them, the three-level T-type Neutral Point Clamped (TNPC) inverter has garnered significant interest due to its ability to produce high-quality voltage waveforms, reduce voltage stress on components, and achieve lower total harmonic distortion (THD) compared to standard two-level configurations [1,2]. Nonetheless, these advantages present significant challenges in electro-thermal control, especially when operating IGBT modules under high current and switching stress [3,4].
Imbalanced neutral-point voltages and unequal power loss distribution in TNPC inverters can accelerate thermal fatigue events, such as solder joint deterioration, lower junction temperature (Tj), and reduced module lifespan [5]. For effective thermal management, detailed modeling of conduction and switching losses is required, along with real-time control systems capable of dynamically addressing voltage imbalances and uniformly distributing thermal stress.
Model Predictive Control (MPC) has evolved as a reliable solution for improving output current quality and assuring DC-link voltage stability in multilevel inverters [6,7]. MPC outperforms traditional control methods that rely solely on the reference voltage vector and fixed duty cycles by predicting future scenarios and selecting optimal switching actions [8]. Incorporating Space Vector Pulse Width Modulation (SVPWM) enables the control system to utilize a broader range of switching states, thereby increasing flexibility and improving output waveform quality [9,10].
The effectiveness of MPC significantly relies on the proper tuning of its cost function weights, which affect the balance between opposing goals, such as present tracking and neutral-point voltage regulation [11]. Manually tweaking designs through trial and error often results in inefficient or prolonged changes. Recent research has investigated sophisticated metaheuristic algorithms, such as genetic algorithms (GA) and Particle Swarm Optimization (PSO), to automate the tuning procedure, ensuring optimal weight selection and reducing the predictive cost function in real time [12].
Additionally, thermal modeling of IGBT modules under actual inverter settings is critical. While analytical and simulation-based techniques, such as Foster and Cauer RC networks [13], are often used to measure junction temperatures, they typically yield inaccurate results in scenarios involving rapidly varying loads and switching [14]. Reliable transient Tj estimation, which considers localized heating effects that standard average models may overlook, is possible by combining dynamic thermal networks with accurate chip-level loss modeling [15].
Recent research has expanded the usage of Model Predictive Control (MPC) and Space Vector Pulse Width Modulation (SVPWM) in multilevel inverters by combining predictive state selection and flexible vector modulation to improve current tracking and voltage management [16,17,18]. Numerous studies have demonstrated that MPC-SVPWM approaches enhance dynamic performance compared to classic PI or hysteresis controllers by directly anticipating future load currents and optimizing switching sequences at each sample instance. Hybrid frameworks have been proposed to address switching limits and reduce computational requirements while maintaining high modulation index efficiency and low harmonic distortion [19,20]. In three-level TNPC configurations, MPC–SVPWM techniques have been demonstrated to be particularly efficient in mitigating neutral-point voltage variations under varying load and grid conditions [21,22].
Precise thermal modeling of IGBT modules is crucial for accurately predicting junction temperatures, minimizing thermal stress, and extending device life, particularly under dynamic switching and high-current conditions [23,24,25]. Approaches to estimating losses based on device-specific elements such as conduction voltage drop and switching energies have consistently been used to calculate power dissipation, which is then integrated into thermal RC networks for transient Tj forecasts [26,27,28]. Recent research has improved these methods by using modified thermal models that accurately describe the thermal impedance of individual semiconductor chips within multilevel modules [29,30]. Sophisticated measurement approaches, including online monitoring of electrical characteristics and real-time estimating and machine learning algorithms, have evolved to provide precise junction temperature feedback without the use of obtrusive sensors [31,32,33]. To improve reliability predictions and fault avoidance in power converters, localized hotspots and dynamic thermal imbalances can be detected by combining chip-level loss evaluations with electrothermal networks [34,35].
Recent studies have demonstrated the benefits of integrating electro-thermal models with real-time control methods to achieve coordinated electrical and thermal management. The TNPC inverter can attain precise voltage balancing and stable thermal profiles across diverse load conditions by integrating MPC-SVPWM control with PSO-based weight modification and a comprehensive Cauer thermal network. In applications requiring high reliability, these frameworks provide valuable guidance for preventive maintenance and lifecycle predictions.
This study builds upon previous work by introducing a comprehensive control and electrothermal modeling method for three-level TNPC inverters. A PSO-optimized MPC-SVPWM control approach dynamically adjusts cost function weights in real time to achieve optimal neutral-point voltage stabilization and current regulation. To quickly determine junction temperatures, the resulting switching states are fed into a chip-level loss computation and then combined with a transient thermal RC network. The results of MATLAB simulations demonstrate the technique’s ability to maintain a uniform temperature distribution across the inverter’s three legs while ensuring the DC-link balance remains within the standard limits. Furthermore, SemiSel simulations and direct experimental measurements for cross-validation confirm the accuracy of the electrothermal models.
The rest of the paper is structured as follows: Section 2 outlines the topology of the target system, detailing the design specifications of the TNPC inverter, the TNPC-IGBT module employed, and the load profile. Section 3 introduces the proposed MPC-SVPWM approach for controlling the three-level inverter. Section 4 focuses on the developed electro-thermal model of the TNPC-IGBT module used in the designed inverter circuit. Section 5 discusses the MATLAB simulation outcomes, analysis, and validation of the electro-thermal model through the SemiSel thermal simulation benchmark. Section 6 describes the experimental setup and validation, and Section 7 concludes the paper.
2. Three-Level Inverter Topology and Design Specifications
A three-phase inverter employing three-level TNPC-IGBT modules, as illustrated in Figure 1a, is often utilized for medium-voltage and high-power applications due to its efficiency and lower switching losses. Producing three voltage levels (0, Vdc/2, and −Vdc/2) rather than the two levels found in a typical topology improves power quality. It also reduces harmonic distortion, making it suitable for traction systems and renewable energy [36]. The Semikron SEMiX405TMLI12E4B IGBT module (Semikron International GmbH, Nürnberg (Nuremberg), Germany) shown in Figure 1b is employed for the intended inverter, which has a rating of 1200 V/400 A, with peak junction and case temperatures of 175 °C and 125 °C, respectively. Even though this commercial class of IGBT modules has a rating for higher voltage and current, they are commonly advised to be used at reduced stress with a maximum limit of (≈70–80% of rated values) in both industrial practice and research practice for the guarantee of safe operation, lifespan, and to accommodate small testing facilities in the laboratory. In this work paper, operating limits were confined to 450 V and 100 A, while module specification parameters on the datasheet rated at 300 V and 400 A were successfully scaled to get the operating point of defined voltage and current. The utilized IGBT module also features a negative temperature coefficient (NTC) thermistor, which enables precise monitoring of the case temperature [37]. In practice, especially during non-uniform cooling, heat being released by one die can affect the temperatures of neighboring dies. However, it is worth noting that, while the NTC thermistor only measures a general case temperature, chip-level modeling, SemiSel simulation, and the controlled experiments with active cooling incorporate some mutual thermal coupling between semiconductor dies.
The inverter topology under investigation consists of four transistors (T1–T4) and their corresponding free-wheeling diodes (D1–D4) for each TNPC leg. Under balanced operation, the outer switches (S1, S4) endure the full DC-link voltage (Vdc), whereas the inner switches (S2, S3) connected to the neutral point experience only (Vdc/2). IGBT module losses during conduction and switching can be measured to calculate junction temperatures using a thermal model, which determines the maximum temperature and its precise location within the module.
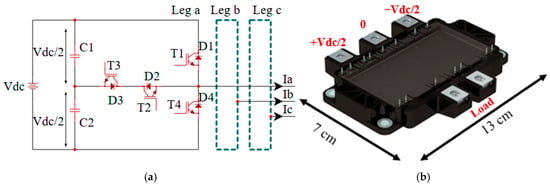
Figure 1.
Three-level inverter schematic and corresponding Semikron IGBT module leg: (a) inverter schematic with Switches (T1–T4) and diodes (D1–D4) are arranged across the split DC-link capacitors (C1, C2); (b) a physical image of a Semikron IGBT module (one-leg) [37], that shows the terminal correspondence to the schematic, where the output terminals and +Vdc/2 and −Vdc/2 represent the electrical connections of one inverter leg.
In this work, a coordinated MPC-SVPWM scheme is used to regulate neutral point voltage, minimizing DC-link imbalance and enabling precise current tracking across loads. In accordance with earlier studies on three-level inverters in traction and renewable applications [38,39,40], which generally have operating ranges of 1–10 kHz, the switching frequency was selected to be 5 kHz. This value preserves industrial compatibility, permits a realistic electro-thermal evaluation, and allows for real-time implementation viability on DSP platforms. SVPWM ensures deep modulation and effective voltage selection, while the MPC cost function, adjusted by PSO, balances THD minimization, neutral point stabilization, and reduced switching losses. The TNPC topology optimizes switching occurrences among IGBTs to ensure uniform thermal stress. A chip-level loss model calculates conduction and switching losses for each IGBT per cycle, utilizing a Cauer-type thermal RC network to determine real-time junction temperatures. The control method ensures electrical and thermal symmetry, allowing a single-leg model for loss and thermal analysis. Table 1 outlines the specifications of the TNPC inverter prototype.

Table 1.
Circuit specification of the target three-level inverter.
3. Proposed MPC-SVPWM Scheme for Three-Level Inverter
3.1. Conventional SVPWM for Three-Level Inverters
SVPWM is widely employed in multilevel inverters because it offers improved DC bus utilization, a consistent switching frequency, and reduced harmonic distortion compared to conventional sinusoidal PWM [36]. In a three-level T-type neutral-point clamped (TNPC) inverter, SVPWM utilizes the current switching states to generate a reference output voltage vector within the hexagonal space vector plane.
In conventional SVPWM, the inverter output voltages (Va, Vb, Vc) are first transformed using the Clarke transformation into a stationary reference vector Vref, in the α-β system. The TNPC provides three voltage levels per phase: −Vdc/2, 0, and +Vdc/2, resulting in a total of 33 = 27 switching states. These switching states are mapped onto the α-β plane, forming the hexagonal voltage space vector diagram shown in Figure 2, which is subdivided into six identical sectors.
The voltage vectors in this diagram are categorized into four groups: (1) large vectors (e.g., V6, V12), (2) medium vectors (e.g., V15, V21), (3) small vectors (e.g., V17, V18), and (4) zero vectors (V1, V14, V27). The switching states are expressed by a triplet [Sa, Sb, Sc], where Sx∈ {−1,0,1} related to the voltage level of the phase x (−Vdc/2, 0, and +Vdc/2), respectively.
The Clarke transformation is given by:
The resulting reference vector magnitude and angle are then calculated as:
For a particular sector:
where Ts is the total sampling period, v1 and v2 are the two adjacent active voltage vectors in the space vector diagram, v0 is the zero-voltage vector, T1, T2, and T0 are the dwell times for the respective voltage vectors.
As an illustrative example, the switching state [1, 0, −1] generates the active vector V6 located in Sector 1. The Clarke transformation (Equation (1)) is utilized to map this vector to the α-β plane at 60° counter to the α-axis. With each switching cycle, Vref is synthesized using time-weighted combinations of two active vectors (e.g., V6 and V2) and one zero vector (e.g., V14), as illustrated in Figure 2.
The position of Vref within the hexagon determines the active and zero vectors selected for SVPWM. Conventional SVPWM achieves high modulation depths, smooth reference tracking, and low total harmonic distortion (THD), but has limitations in high current applications, including thermal “hot spots” and neutral-point voltage imbalance. To address these challenges, this work proposes a hybrid control methodology that combines SVPWM with Model Predictive Control (MPC). In the proposed scheme, SVPWM controls the vector path and dwell times to enhance voltage and current performance and increase the device reliability, whereas MPC is used to optimize the selection of switching states.
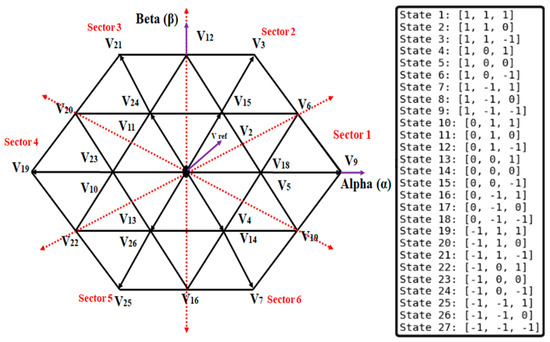
Figure 2.
Hexagonal voltage space vector diagram for the three-level TNPC inverter [15].
3.2. MPC Cost Function Formulation
Maintaining DC-link voltage imbalance within ±5% in multilevel TNPC inverters is crucial, as imbalances exceeding 10% can cause device stress, capacitor failure, and increased losses [6,7]. A coordinated MPC-SVPWM approach is proposed to assist SVPWM in optimizing switching states, aiming for neutral voltage imbalance below 3%, load balance, and reducing electro-thermal stress.
Figure 3 depicts the block structure of the proposed MPC with the SVPWM scheme for balanced operation of the three-level TNPC inverter. In the proposed scheme, the control goal is achieved by minimizing a cost function that considers both load current monitoring accuracy and neutral point voltage variation. For each control step, the MPC assesses all valid switching states and chooses the one that minimizes the cost function:
where and are weighting factors, is the reference current for phase x ∈ {a, b, c}, k is the control step, is the predicted current at the next sampling instant, and are the current and predicted neutral point voltages, respectively.
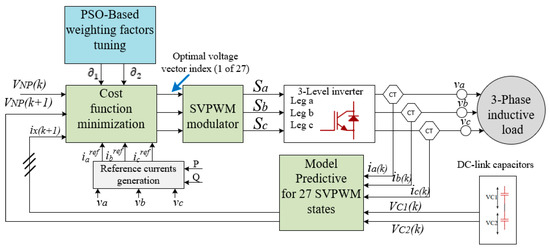
Figure 3.
Structure of MPC with SVPWM scheme for balanced operation of a three-level inverter: The MPC evaluates all 27 SVPWM switching states using a cost function with appropriate weighting terms (δ1, δ2). The best vector selected from the MPC is sent into the SVPWM modulator to provide gate signals that keep the DC-link voltage balanced and improve reference tracking.
The difference in voltage between the upper DC-link capacitor voltage (VC1), and lower DC-link capacitor voltage (VC2), determines the neutral point voltage as:
The capacitor voltages are updated based on the capacitor currents and the sampling period Ts, as:
The capacitor currents iC1 and iC2 can be obtained based on the load currents and the switching states of the three legs, given by:
where Sx1,2 ∈ {0, 1} is the switching states contributing to phase leg x ∈ {a, b, c} to the capacitors C1 (Sx1) and C2 (Sx2).
Table 2 presents the truth table for the capacitor current in the TNPC inverter phase leg, showing the relationship between switching states and capacitor currents.

Table 2.
TNPC inverter capacitor current truth table.
MPC aids in ensuring balanced load currents by monitoring reference currents obtained from active (P) and reactive (Q) power requirements via dq-axis and inverse Park transformation matrix (computations as specified:
where θ is the electrical angle of the reference frame.
The inverse Park transformation matrix (is usually defined as:
At the control step (k + 1), the load current can be predicted as:
where L and R are the load inductance and resistance values.
3.3. PSO-Based Cost Function Weighting Optimization
The thoughtful choice of the weighting parameters and within the cost function of the model predictive control (MPC) method greatly influences its effectiveness. These elements manage the balance between stabilizing the neutral-point voltage and precisely monitoring the load current. Improper tuning can lead to poor tracking, greater neutral-point imbalance, or significant thermal stress on the IGBT module.
To overcome the limitations of static, offline-tuned parameters, this study presents an online Particle Swarm Optimization (PSO) framework is presented to adjust weighting coefficients [, ] in real time. This real-time adjustment improves control stability under changing load and temperature conditions while also improving the MPC’s response to transient disturbances.
Alongside the MPC loop in the online implementation, a simplified PSO algorithm updates , and , every N control cycle based on the system’s most recent performance metrics. The optimization seeks to lower a combined performance index, where each particle in the swarm represents a possible solution pair [, ]:
where ISEcurrent is the integral of the squared error between the reference and predicted load currents, ISENPV is the integral of the squared neutral-point voltage deviation, ω1 and ω2 are defined scaling coefficients.
The fitness components are defined as:
Each particle updates its position in the search space according to the standard PSO update rules as:
where is the position of particle I at iteration k; is its velocity; is the best solution found by particle I; g is the global best solution found by the entire swarm; ω is the inertia weight; c1 and c2 are acceleration coefficients; and r1 and r2 are random numbers uniformly distributed between 0 and 1.
The proposed PSO is carried out to reduce computational load by using a smaller swarm size and a limited number of iterations. The adjusted [∂1, ∂2] pair is then fed into the MPC controller for the next control interval. The key PSO parameter values used to optimize the weighting factor in this setup are shown in Table 3. The small swarm size (Np = 10) and limited generations (Gmax = 5) were chosen to decrease the computational requirements for real-time execution on the DSP MCU. This ensures that the online PSO update fits within the control cycle while still achieving stable convergence. These decisions were based on a preliminary sensitivity analysis of DC-link imbalance and RMS current tracking error, which established appropriate search ranges for ∂1 and ∂2. Furthermore, the selected PSO settings align with common ranges seen in recent studies [41,42,43], where inertia weight values between 0.4 and 0.9 and acceleration coefficients c1 and c2 ranging from 1 to 2 are frequently used.

Table 3.
PSO parameter settings.
3.4. Optimized Switching State
To ensure accurate load current tracking and uphold a stable neutral-point voltage balance, the switching state in the proposed SVPWM–MPC approach is enhanced at each sampling moment. The integrated MPC framework assesses all potential switching states to determine the one that minimizes the predictive cost function, unlike conventional SVPWM, which relies solely on the reference voltage vector and fixed duty cycles for producing gate signals.
During each control step, the MPC prediction model evaluates the expected future voltages of the DC-link capacitors and load currents for every potential switching state. The cost function for each candidate is evaluated using the weighting factors α and β, which are adjusted through PSO to balance neutral-point voltage deviation and tracking error. The SVPWM method selects the switching scenario that results in the least expensive outcome for execution. The following illustration demonstrates the ideal switching state S*:
This meticulous switching state selection ensures that the inverter maintains the intended switching frequency while also providing strict current regulation and neutral point balance within set bounds. Figure 4 depicts the complete flowchart of the proposed PSO-enhanced SVPWM-MPC technique for the three-level TNPC inverter.
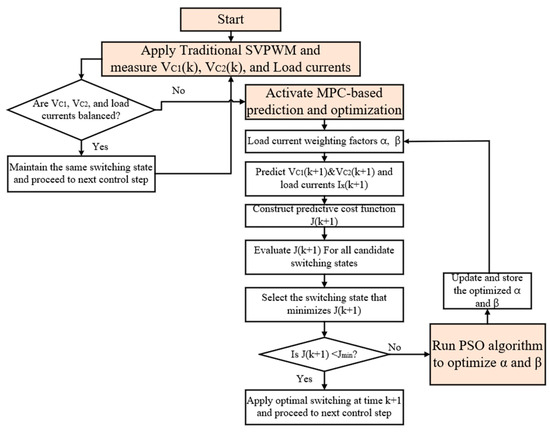
Figure 4.
Flowchart of the proposed PSO-enhanced MPC-SVPWM control scheme in a three-level TNPC inverter.
4. Electro-Thermal Modeling of the TNPC-IGBT Module
4.1. Loss Model Using Optimized Switching States and Datasheet Parameters
Precisely assessing power losses in multilevel IGBT inverters is critical for predicting thermal performance and guaranteeing long-term reliability. This section develops a loss model that incorporates the impact of SVPWM switching states on conduction and switching losses in TNPC modules. The model computes diode and transistor chip loss sequences for each SVPWM state while accounting for current polarity and real-time dynamics. These exact loss predictions improve average power forecasts and have a direct impact on junction temperature simulations and lifespan evaluations.
The overall power loss of the chip (Pi) is calculated by summing the conduction losses (Pcon) and the switching losses (Psw) as shown:
4.1.1. Chip Conduction Loss Evaluation
Each chip (either transistor or diode) conducts current during a specific portion of the switching period. The instantaneous conduction loss (Pcon) over a switching cycle Ts is given by:
This can be approximated using average and RMS current values for each conduction interval:
where Vce and VF are the transistor and diode typical on-state voltage drops; rc and rD are dynamic resistances, derived from the module’s datasheet.
The average and RMS conduction currents for each chip are computed as:
The timing diagram in Figure 5 illustrates the specific conduction-state mapping for every power chip in phase A of the three-level TNPC inverter configuration. The graph illustrates the load current waveform, Ia (in per unit), alongside the switching state, Sa. During each segment of the switching cycle, the active chips, either transistors (T1–T4) or diodes (D1–D4), are determined according to the polarity of the current and the state of switching. This detailed chip-level mapping is essential for an accurate assessment of conduction losses, as it facilitates the precise identification of current routes and their durations during each PWM cycle.
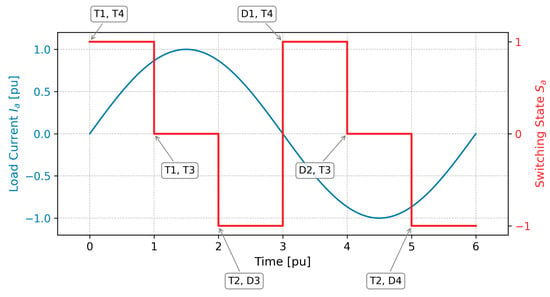
Figure 5.
Chip-level conduction mapping for TNPC inverter.
Figure 6 demonstrates the approach used to calculate real-time, chip-level conduction losses in the TNPC-IGBT module. It evaluates the conduction status and current flow of each chip, computes the average and RMS conduction currents for a single SVPWM cycle, and considers the current SVPWM switching state along with the related load current waveform. Conduction losses are determined by applying these values along with device-specific parameters.
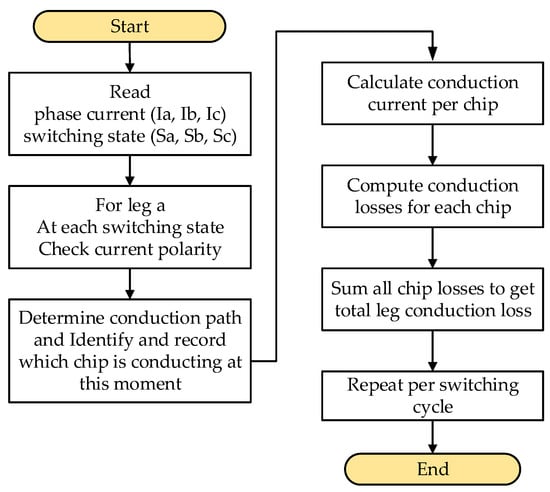
Figure 6.
Steps of the proposed on-line chip-level conduction loss evaluation with the PWM cycle.
4.1.2. Chip Switching Loss Evaluation
Switching losses during both turn-on and turn-off are essential at high frequencies, influenced by load current, DC-link voltage, and junction temperature. In TNPC, the inner transistors (T2, T3) switch more frequently than the outer ones (T1, T4), resulting in unequal switching losses that necessitate chip-level evaluation. The overall switching losses comprise the energy associated with transistor switching as well as diode reverse recovery, and are expressed as:
where fsw is the switching frequency, is the transistor energy losses, and is the diode reverse recovery energy.
The chip’s switching energy is modeled as a function of the collector current, junction temperature, and input DC voltage, and can be expressed as:
where is the reference switching energy at = 400 A, = 300 V, = 150 °C, derived from the module’s datasheet double pulse testing data. k is the voltage exponent coefficient, and α is the temperature coefficient, indicating the dependency of switching energy on voltage and temperature.
It is important to remember that when an IGBT is turned off, the collector current does not instantly decrease to zero. Instead, because of the stored charge in the drift area, a tail current continues to exist, which makes a substantial contribution to the turn-off energy, especially at high current and high temperatures. Since the double-pulse measurement records the entire turn-off transient, the datasheet-based switching energy ( naturally includes both the voltage fall and the tail current contribution, even if Equations (24) and (25) do not specifically isolate this tail current item. The tail current energy can be independently stated as follows for more thorough modeling:
and imposed directly to the turn-off loss. In this work; however, as the datasheet reference switching losses consider the tail behavior, we rely on the practical datasheet-based scaling that described in (25), following the manufacturer’s datasheet and application notes [37,44].
While the inverter operates, real-time switching occurrences are identified using SVPWM patterns and observed phase currents. The inverter’s state logic, as detailed in Table 4, monitors the turn-on/off chips (T1–T4) along with the diode reverse recovery losses (through D1–D4).

Table 4.
TNPC inverter chip-level switching events mapping [15]. The “—” indicates that no active switching device is involved; current flow is through freewheeling paths.
Figure 7 illustrates an approach for determining real-time chip-level switching losses in TNPC modules. It detects phase currents and employs SVPWM switching states to identify turn-on/off events, as well as the direction of current flow. The inverter’s operating logic, as presented in Table 4, separates active switching chips (T1–T4) and associates diode activity (D1–D4) using reverse recovery effects. Each event’s chip ID, polarity, and current direction are recorded. Energy values are adjusted based on current, DC-link voltage, and temperature. Overall losses are estimated by multiplying detected events by energy losses during a single SVPWM cycle as:
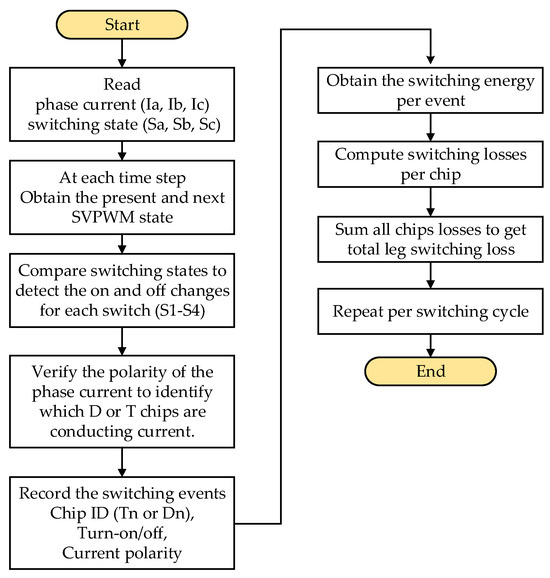
Figure 7.
Steps of the proposed on-line chip-level switching loss evaluation with the PWM cycle.
4.2. Thermal Model-Based Cauer Transient Network
Figure 8 illustrates the Cauer thermal model, which describes heat transmission within the physical framework of an IGBT module by depicting each chip as a ladder-like succession of RC stages. This establishes a direct relationship between the thermal model and the actual device, providing a better understanding of where heat builds and how it disperses.
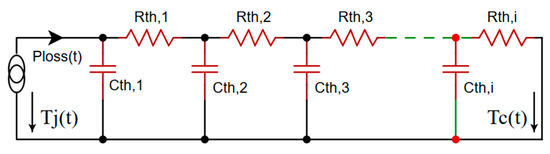
Figure 8.
IGBT module multi-stage Cauer thermal model.
Each node follows the differential equation of the thermal ladder:
where i is the ladder stage, Ti refers to the node temperature at stage i. (at i = 1, Ti = junction temperature (Tj)).
In practice, the thermal conductivity of materials varies with junction and case temperature, so the semiconductor chip’s thermal resistance is not constant but temperature-dependent. To account this, we apply a linear correction relative to a reference junction temperature Tj,0:
where is the nominal thermal resistance of the i-th Cauer element at the reference temperature , and β is a temperature-dependent coefficient (1/°C).
As the junction temperature deviates from its reference value (as given in the module datasheet), this formulation enables the thermal resistance to dynamically change (increase or decrease). Using switching and conduction losses as inputs, the model produces the transient junction temperature:
where is expressed by:
where τi is the time constant of the ith Cauer stage. is the weight, which depends on the network structure.
Datasheets typically provide Foster-model parameters as:
The Cauer configuration can be obtained from the Foster parameters in the module’s datasheet. First, this function in (29) is converted into a single rational form as:
Subsequently, applying a Euclidean algorithm [30], the rational expression is converted into a continued fraction to achieve the Cauer form as shown:
From the continued fraction, the physical layer-based parameters Rthi and Cthi can be identified, reflecting the actual thermal impedance from the junction to the case (Zthjc), enabling real-time junction temperature prediction for time-domain simulation platforms.
Figure 9 illustrates the extended block diagram that includes the proposed method for evaluating power loss and thermal performance of TNPC-IGBT modules in balanced three-level inverters. The process begins with optimal inverter management for balanced operation. Next, chip-level power losses are evaluated using SVPWM switching signals, and current flow is tracked in real time. These losses are utilized as inputs in the Cauer model-based thermal network simulation, which calculates the junction temperature at the chip level and provides critical insights into thermal performance, reliability, durability, and safe operation across various situations.
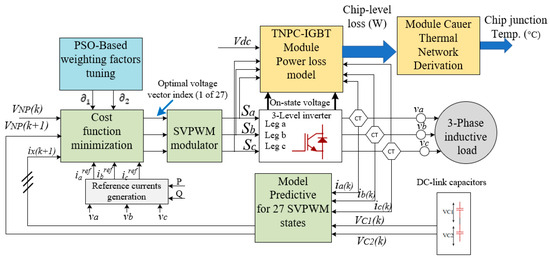
Figure 9.
Block diagram of the proposed framework for balanced operation and electro-thermal modeling in a three-level inverter.
5. Results, Discussions, and Validation
5.1. Inverter Steady-State and Dynamic Performances with Proposed Control
The comprehensive modeling of the 3-phase, 3-level TNPC-IGBT inverter, employing the proposed control method for balanced operation throughout the module’s three phases, along with loss modeling for chip-level power loss and thermal profile assessment, is performed in MATLAB R2022a software. The entire system was modeled via MATLAB software through code-based modeling. All subsystems, including the three-level TNPC inverter, the RL load, the direct MPC algorithm, and the capacitor voltage balancing system, were modeled numerically, enabling full flexibility and transparency of the equations. The switching behavior of the inverter was represented using discrete device-level models that generate the output voltages entirely from the switching state. The load was modeled as a series RL branch with no additional filters included, which enabled the direct evaluation of interacting inverter voltages and the subsequent load current. The MPC controller was coded to predict system states (currents and capacitor voltages) using the discrete-time system equations, and the cost function was evaluated at each sampling step to determine the optimal switching state.
The simulations were carried out on a personal computer with an Intel® Core™ i7-12700H processor (2.3 GHz, 14 cores), (Intel Corporation, Santa Clara, CA, USA) and 64 GB RAM under a Windows 10 Pro environment. The control and optimization environment operated under a switching frequency of 5 kHz throughout the simulation, where the simulations were designed to mirror real-time control. The algorithm was computationally efficient such that, through zero-order PSO, there was a relatively small overall computational demand (number of swarms of 10 and Gmax = 5 overall generations), allowing the weighting parameters [∂1, ∂2] to converge extremely fast at each control interval. Overall, these features resulted in simulation outputs that realistically reflect values consistent with feasible real-time implementation, given the timing and performance constraints.
Figure 10 illustrates the simulation of the three-phase load currents alongside the tracking load current that aligns with the generated reference current (for phase a), utilizing the proposed controller of the designed TNPC inverter circuit. This is achieved through optimized MPC cost function weighting factors implemented via PSO algorithms, at Vdc = 450 V, with load currents of 25 A, 75 A, and 100 A, demonstrating accurate tracking of the phase current with the reference current and balanced three-phase load currents across a wide load range.
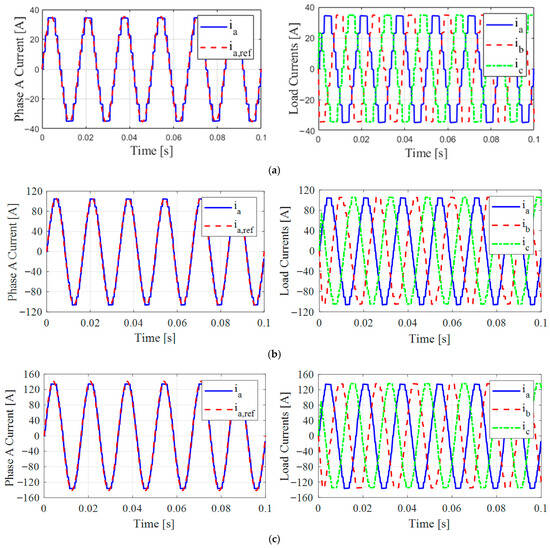
Figure 10.
Load current (phase a) tracking the reference current and three-phase load current waveforms using the proposed control strategy at (a) 25 A, (b) 75 A, and (c) 100 Load scenarios.
Figure 11 shows the dynamic performance of the proposed SVPWM-MPC approach in regulating the DC-link capacitor voltages VC1 and VC2 while minimizing the neutral-point imbalance percentage under various load situations (25 A, 75 A, and 100 A) at Vdc = 450 V. The controller efficiently keeps both capacitor voltages close to the nominal 225 V, and the imbalance % is successfully reduced in all load scenarios.
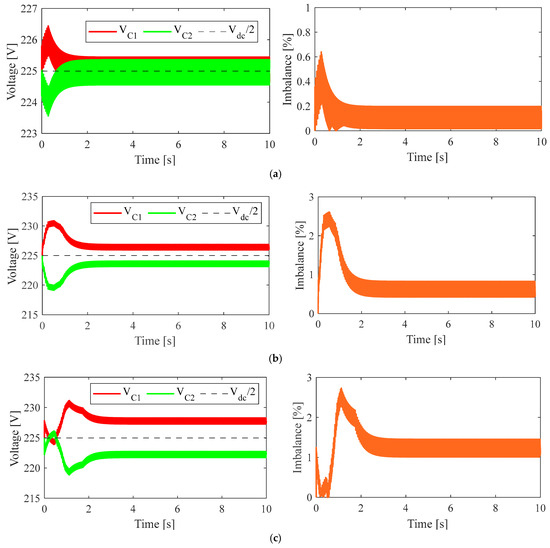
Figure 11.
DC link capacitor voltage and neutral point imbalance percentage measurements using the proposed control strategy at (a) 25 A, (b) 75 A, and (c) 100 Load scenarios.
At reduced loads (25 A), there are minor oscillations that quickly stabilize with a 0.25% imbalance; however, at greater loads (75–100 A), the system stabilizes more quickly and exhibits excellent voltage symmetry, keeping the imbalance at 1.1% even when fully loaded. These results confirm that the proposed control approach guarantees stable neutral-point regulation and effective voltage balancing across an extensive operating range.
To evaluate the MPC-SVPWM control method’s dynamic response to sudden load changes, at t = 3 s, the load current reference increased from 75 A to 100 A. The results in Figure 12 show minimal short-term fluctuations and a gradual increase in load current without significant distortion. The voltage imbalance at the neutral point remains within acceptable limits, and the DC-link capacitors (VC1 and VC2) are well-regulated. A slight temporary imbalance occurs initially but stabilizes quickly, demonstrating the control system’s robustness and adaptability in response to sudden load variations while maintaining consistent performance and power distribution.
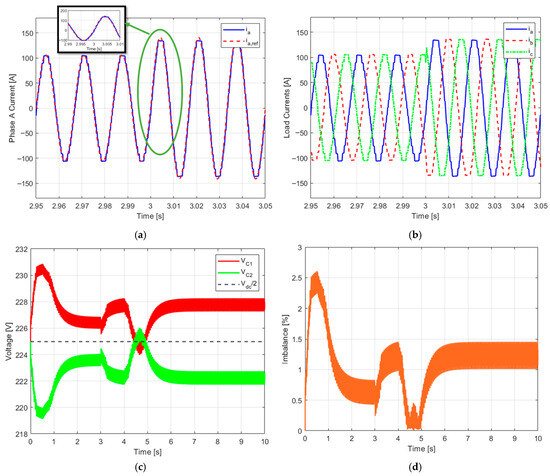
Figure 12.
Dynamic response of the three-level inverter under the proposed control during step load increase from 75 to 100 A at t = 3 s: (a) load current tracking, (b) load currents, (c) capacitor voltages, and (d) neutral point imbalance (%).
5.2. Chip-Level Power Loss Evaluation
Upon verifying the balanced function of the three-level inverter, the power loss algorithm at the module chip level is started. It employs optimized switching states and load current polarity to identify conduction states and switching events. The energy values for switching, specifically Eon, Eoff, and Err, employed in this calculation were obtained from the manufacturer’s datasheet [37], which presents standard double-pulse test (DPT) data performed at Vin = 300 V, IC = 400 A, and Tj, nom = 150 °C. These reference values are available in Table 5. To adjust the DPT results for actual inverter performance used in this work, scaling factors for collector current, bus voltage, and junction temperature were incorporated into the calculation of switching loss, as indicated in (24).

Table 5.
Typical switching energy data for the utilized TNPC-IGBT module [37].
At a 450 V DC input voltage, and with two distinct load conditions of 25 A and 100 A. Figure 13 and Figure 14 illustrate the distribution of power losses among the various semiconductor chips within the three legs of the module. With a 25 A load, the module incurs a loss of approximately 143.5 W, nearly evenly spread across the three phases (leg a = 47.8 W, leg b = 47.7 W, and leg c = 48 W). Conversely, under full load (100 A), the loss amounts to roughly 610.7 W. The loss distribution indicates that the inner switch chips (T2, T3, D2, and D3) incur a greater amount of power loss compared to the outer switch chips (T1, T4, D1, and D4), with the peak loss level noted in transistors T2 and T3 at around 43.6 W at 100 A and nearly 13.2 W at the 25 A state.
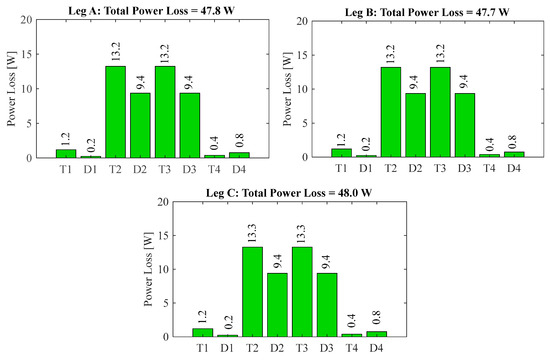
Figure 13.
TNPC-IGBT module chip-level loss distribution at 25 A, 450 V DC, and 100 °C case temperature.
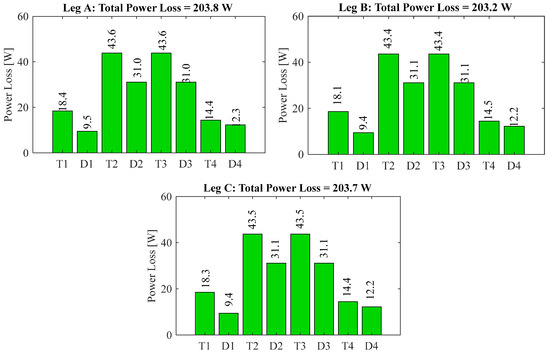
Figure 14.
TNPC-IGBT module chip-level loss distribution at 100 A, 450 V DC, and 100 °C case temperature.
5.3. Chip-Level Junction Temperatures Estimation
Using the proposed transient thermal model and power loss distributions from Figure 13 and Figure 14, the TNPC-IGBT module’s junction temperature profile was simulated at a constant case temperature of 100 °C. Figure 15 shows thermal profiles for different semiconductor chips at a moderate load of 25 A, while Figure 16 displays profiles at full load of 100 A, highlighting varying junction temperature increases based on chip type and location.
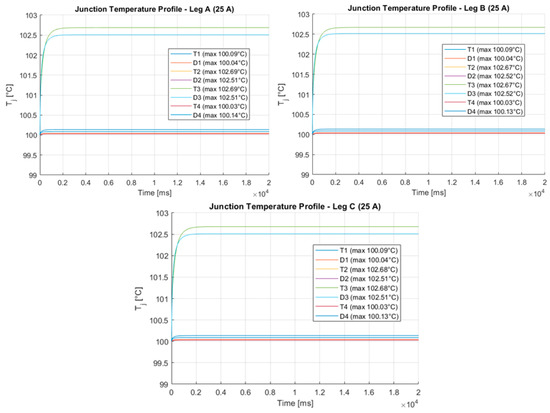
Figure 15.
TNPC-IGBT module junction temperature profile at 25 A, 450 V DC, and 100 °C case temperature.
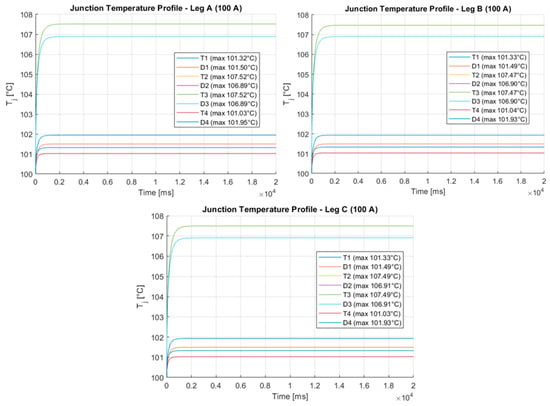
Figure 16.
TNPC-IGBT module junction temperature profile at 100 A, 450 V, and 100 °C case temperature.
When a load of 25 A is applied (Figure 15), the outer chips (T1, T4, D1, and D4) only experience a small temperature rise, with temperatures remaining stable around 100.04–100.14 °C, relative to the inner chips (T2, T3, D2, and D3) which elevated more than 102.51 °C and 102.69 °C junction temperatures due to higher conduction losses and localized thermal impedance. At the 100 A load (Figure 16), the junction temperature increases even more substantially; the inner transistors (T2, T3) and diodes (D2, D3) see temperatures go to peaks of between 106.90 °C and 107.52 °C; however, the outer chips remain cooler, with peaks of near 101–101.95 °C, being able to spread more heat with lower losses. Most importantly, note that the temperature of the three legs of the TNPC module remains almost identical with a variation of a maximum of ~1 °C of inner T2 or T3 chips, and D2 and D3 diodes, for low and high loads evenly, confirming that the current was not only evenly shared but that the thermal management was also efficiently managed during slow and high loads, respectively, under the MPC-SVPWM strategy.
5.4. Electro-Thermal Model Validation
A thermal simulation of a three-phase inverter circuit using the SEMiX405TMLI12E4B TNPC-IGBT module (Semikron International GmbH, Nürnberg (Nuremberg), Germany) was conducted with SVPWM control at a frequency of 5 kHz. The simulation, executed using Semikron’s SemiSel software version 6, validated the power loss distribution and junction temperature profiles under consistent test conditions. SemiSel software provides reliable predictions for power losses and thermal efficiency, enabling optimal IGBT selection and design efficiency while reducing testing duration. It serves as a benchmark for validating prior analytical and experimental findings. However, it is limited to simulating the TNPC-IGBT inverter with balanced three-leg operation, focusing on the outcomes of module leg-a for comparison. In the simulation process, the heatsink temperature is adjusted to simulate the thermal profile at a constant case temperature of 100 °C.
Figure 17 illustrates the SemiSel simulation outcomes of the IGBT module’s power losses under a 25 A loading scenario and a 100 °C case temperature, revealing that the module’s overall loss is approximately 141.53 W, which is close to the value derived from the proposed framework (143.5 W), highlighting the framework’s high precision in estimating power loss under low loading conditions. Furthermore, Figure 18 shows the junction temperature (Tj) and heatsink temperature (Ts) profiles for various semiconductor chips, indicating a peak junction temperature of approximately 102.30 °C at the inner diode chips (D2 and D3), which was also recorded to be around 101.90 °C at the same location using the proposed framework.
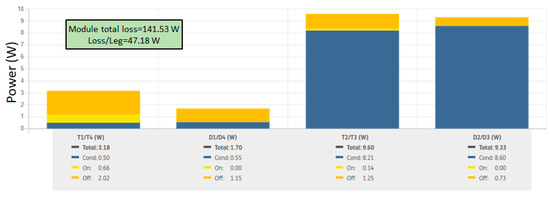
Figure 17.
Chip-level Power loss estimation using Semikron SemiSel simulation at 25 A load and a case temperature of 100 °C.
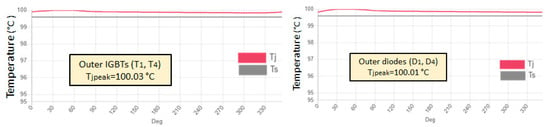
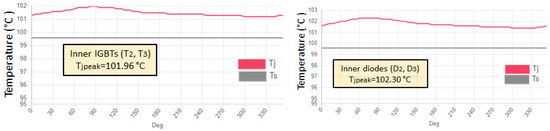
Figure 18.
Junction temperature estimation using Semikron SemiSel simulation at 25 A load and a case temperature of 100 °C.
Figure 19 displays the SemiSel simulation results for power losses of the IGBT module at a 100 A load and a case temperature of 100 °C, indicating that the overall module loss is approximately 594 W, which is in close agreement with the value obtained from the proposed framework (610.7 W), highlighting the framework’s accuracy in predicting power loss under high-current conditions. Additionally, Figure 20 illustrates the Tj and Ts profiles for different semiconductor chips, revealing a maximum junction temperature of approximately 107.10 °C at the inner diode chips (D2 and D3), which is similar to the value of around 106.10 °C noted at the same location using the proposed framework.
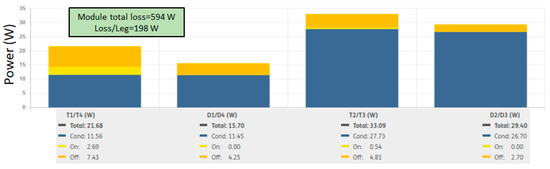
Figure 19.
Chip-level Power loss estimation using Semikron SemiSel simulation at 100 A load and a case temperature of 100 °C.
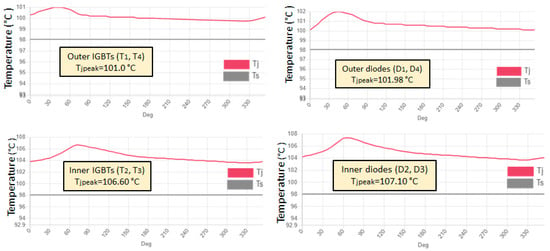
Figure 20.
Junction temperature estimation using Semikron SemiSel simulation at 100 A load and a case temperature of 100 °C.
6. Experimental Setup and Validation
The experimental testing configuration of the three-level three-phase TNPC-IGBT inverter is illustrated in Figure 21, which was designed to test the effectiveness of the proposed MPC-SVPWM control strategy for the purpose of maintaining a DC-link imbalance and balancing load currents, as well as validating the proposed electro-thermal model of the IGBT module utilized in the experiments through direct experimental measurements of total power losses and peak and minimum junction temperatures of the IGBT module.
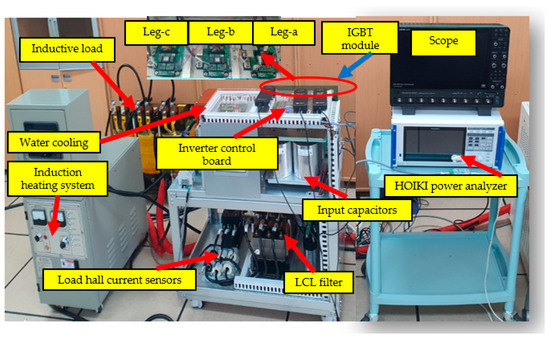
Figure 21.
Experimental setup of the designed 3-level TNPC-IGBT inverter.
The configuration mainly includes a three-level TNPC-IGBT module (SEMiX405TMLI12E4B), an LCL filter (L = 150 uH, C = 100 uF, L = 100 uH) for smooth load current waveforms, an inverter control circuit with the DSP MCU TMS320 F28337D (Texas Instruments Inc., Dallas, TX, USA), and a highly inductive load (R = 8.5 mΩ, L = 3 mH) with 100 A and 200 V ratings. The HOIKI PW8001 (Hioki E.E. Corporation, Ueda, Nagano, Japan) power analyzer is used to monitor the three-phase load voltage and currents, as well as to measure the input and output power of the utilized IGBT module, to validate the total power losses obtained with the proposed framework. An induction heating system with water cooling is employed to keep the case temperature at 100 °C, simulating the harsh thermal environment found in traction applications. The OTP-M-100 (OpSens Solutions Inc., Quebec City, QC, Canada) fiber optic temperature sensor is used to directly measure the peak junction temperature (Tjpeak) and minimum junction temperature (Tjmin) at the point specified by the created thermal model for junction temperature validation.
In the tested TNPC-IGBT module (SEMiX405TMLI12E4B), an NTC temperature chip was integrated to act as a stand-in for monitoring the module’s general case temperature status, as illustrated in Figure 22a. The value of the negative temperature coefficient (NTC) resistance value, which is commonly expressed as a function of temperature, can be computed using the formula shown in the module datasheet [37] as follows:
where R100 and B100/125 are constants defined by the properties of the NTC chip; these values can be sourced from the module’s datasheet.
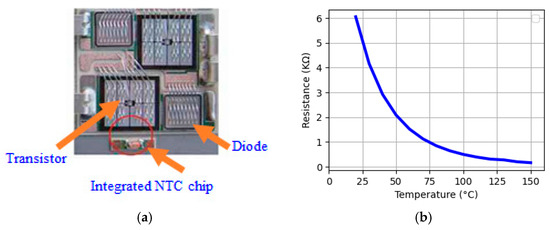
Figure 22.
Semikron (SEMiX405TMLI12E4B) TNPC-IGBT module (NTC) sensor [15]: (a) NTC position, (b) R-T curve of the NTC.
To observe the general case temperature, the NTC resistance (RNTC) must be measured and linked to the integrated NTC’s resistance R-T characteristics. Figure 22b shows the measured R-T profile of the integrated NTC sensor contained in the Semikron SE-MiX405TMLI12E4B IGBT module. The case temperature on all three inverter legs was kept at the measurement value, with an induction heating system with a water-cooling system, during a measurement under a defined electrical load.
The inverter circuit is subjected to a DC-link voltage of 450 V and the PWM signals produced by the proposed control scheme. The proposed control technique is implemented and tested at two different loading circumstances of 25 A and 100 A, and the DC-link capacitor voltages and the three-phase load currents’ RMS values are tracked. Figure 23a shows the collector-emitter voltage across switch S1 (Vce_S1) and the DC-link voltages (VC1 and VC2) at an input DC-link voltage of 450 V and a load current of 25 A, with VC1 at 224 V and VC2 at 226 V, resulting in a 0.45% imbalance. Figure 23b presents similar measurements at the same input voltage but with a load current of 100 A, showing VC1 at 222.5 V and VC2 at 227.5 V, leading to an imbalance percentage of around 1%. Both figures confirm the proposed inverter control system’s effective management of DC-link voltage imbalance and reduced voltage ripple contents with different load currents.
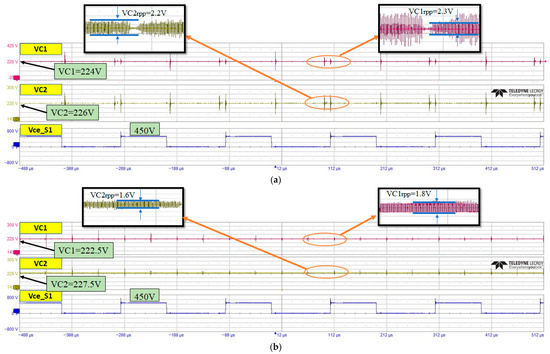
Figure 23.
DC-link capacitor voltages (VC1, VC2) and outer-upper switch collector emitter voltage (Vce_S1) waveforms at Vdc = 450 V and load currents of: (a) 25 A, (b) 100 A.
Figure 24 illustrates the experimental waveforms and the RMS level readings of the three phases as recorded by the HIOKI 8001 power analyzer at load currents of 25 A (Figure 24a) and 100 A (Figure 24b), respectively. These show the magnitude and phase balance of the three-phase currents in the three-level TNPC-IGBT module being tested, with a relative RMS error tracking approximately 1% at 25 A conditions and around 0.86% at 100 A conditions, as related to the load reference RMS current value.
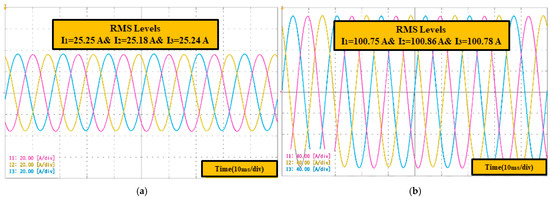
Figure 24.
Three-phase load currents and RMS levels of the designed inverter at Vdc = 450 V and load currents of: (a) 25 A, (b) 100 A.
After checking the load current balancing and DC-link voltage stabilization, the induction heating system manages heatsink temperatures, keeping the case temperature of the three module legs around 100 °C. An NTC sensor monitors temperature, while a HOIKI PW8001 power analyzer tracks input and output power to determine total power losses. One module remains open (encapsulated) to measure junction temperatures at specified locations via a fiber optic sensor. Table 6 presents detailed module junction temperatures and power losses at varying load currents obtained from different measurement frameworks.

Table 6.
Comparison of module junction temperatures and power loss evaluations from different techniques.
At a 25 A load current, the estimated minimum junction temperature (Tj,min) from the proposed modeling framework and thermal simulation align closely, differing by only 0.03% (100.04 °C compared to 100.01 °C). The directly measured value is about 100.40 °C varied by only 0.36% from the proposed framework. The peak junction temperature (Tj,peak) varies by only 0.39 °C between the proposed framework (102.69 °C) and thermal simulation (102.30 °C), while the directly measured value (103.0 °C) remained within the 0.30% margin again. Similarly, the estimated power loss for the proposed model (143.5 W) was closely similar to the thermal simulation (141.53 W) and direct measurement (148 W) results, yielding a maximum relative deviation of approximately 2.2%.
As the load current rises to 100 A, thermal stress increases as well, which causes junction temperatures to rise. The Tj,min values rise to 102.51 °C (proposed model framework), 101.0 °C (thermal simulation), and 102.9 °C (direct measuring) with a relative difference below 1.5%. Additionally, the Tj,peak variation remains low, with a 0.42 °C difference between the proposed and simulation Tj,peak (107.52 °C to 107.10 °C) and 0.08 °C to the measured Tj,peak (107.6 °C) all resulting in a relative error below 0.5%. Total power losses are also in close agreement with 610.7 W (proposed model framework), 594 W (thermal simulation), and 616 W (direct measurement), resulting in an absolute maximum relative error of 2.7%.
These small relative errors across all operating conditions validate that the proposed electro-thermal modeling framework provides a precise and reliable estimate of junction temperatures and total power losses, showing a high degree of agreement with both SemiSel industrial simulation and experimental measurement platforms.
The key contributions of this research can be outlined as:
- Integrated MPC–SVPWM framework: The fusion of MPC and SVPWM creates a unique control system that guarantees precise current tracking and upholds neutral-point voltage stability.
- Cost function tuning with PSO: The MPC cost function weights are systematically adjusted using Particle Swarm Optimization (PSO), producing an appropriate balance between thermal consistency and electrical regulation.
- Chip-level electro-thermal modeling: Integrating dynamic power loss estimation with a Cauer-style RC thermal network results in a comprehensive IGBT module model, facilitating online prediction of transient junction temperatures at the chip level, simplifying the design and selection of the IGBT modules in multilevel inverters in the predesign process without the requirement of complicated testing.
- Enhanced thermal equilibrium and reliability: The system guarantees consistent thermal stress distribution across inverter components, minimizing hot-spot development and increasing module longevity under fluctuating load scenarios.
- Generality and design-stage applicability: The proposed modeling framework is not limited to a specific manufacturer (e.g., Semikron), but can be used for any high-power IGBT module, providing a flexible resource for accurate module selection before circuit production, thus minimizing design time and expenses.
- Facilitated reliability assessment: By offering direct access to chip-level junction temperature information, the framework simplifies reliability evaluation and lifespan estimation, facilitating better design and maintenance choices.
7. Conclusions
This paper presents a comprehensive modeling and control framework to evaluate the electro-thermal performance of three-level T-type neutral-point clamped (TNPC) inverters with high-power IGBT modules. By integrating Model Predictive Control (MPC) and Space Vector Pulse Width Modulation (SVPWM), it addresses electrical regulation and thermal management. Particle Swarm Optimization (PSO)-based weighting adjustment was established using parameter ranges documented in the recent literature, and a preliminary sensitivity analysis of DC-link imbalance and RMS current tracking error is used to adjust MPC cost function weights for achieving current tracking accuracy, neutral-point voltage stability, and thermal uniformity. This resulted in a better selection of switching sequences, which improves the output waveform quality and promotes balanced power dissipation across semiconductor chips, thereby increasing thermal reliability. The incorporation of a chip-level electro-thermal model, which connects a thorough Cauer-type RC thermal network with dynamic power loss estimation, is an important component of this study, enabling the precise prediction of junction temperatures for every chip in the IGBT module.
The proposed SVPWM-MPC technique demonstrates excellent DC-link voltage regulation capabilities across a range of operating scenarios, maintaining a neutral-point voltage imbalance of approximately 0.45% under light loads and 1% under heavy loads. Furthermore, a comparison with the industry-standard SemiSel simulation benchmark and also with experimental direct measurements was used to validate the proposed thermal model. At both low (25 A) and high (100 A) load levels, the investigation of minimum and maximum junction temperatures, as well as overall power losses, showed good consistency, with relative errors continuously falling below 3%. The model’s suitability for accurate reliability assessment and thermal control in high-power inverter circumstances is reinforced by these minor differences, which confirm the accuracy of the electro-thermal estimation.
To conclude, combining MPC, SVPWM, PSO, and electro-thermal modeling into a unified simulation framework offers an effective approach for evaluating and monitoring the optimal electrical and thermal performance in three-level inverters with IGBT modules, while significantly reducing cost and development times during the selection and predesign stages of multilevel inverter systems.
Author Contributions
Conceptualization, A.H.O. and J.B.; methodology, A.H.O. and J.B.; software, A.H.O. and C.K. validation, A.H.O. and J.B., C.K. and D.-W.K.; formal analysis, A.H.O.; investigation, A.H.O. and J.B.; resources, A.H.O.; data curation, C.K. and D.-W.K.; writing, A.H.O. and C.K.; writing—review and editing, A.H.O. and J.B.; visualization, A.H.O. and J.B.; supervision, J.B.; funding acquisition, J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Regional Innovation System & Education (RISE) program through the Chungnam RISE, funded by the Ministry of Education (MOE) and the Chungnam, Republic of Korea (2025-RISE-12-022).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Choudhary, A.; Kumar, R.; Letha, S.S.; Bakhsh, F.I.; Singh, A.; Khan, M.J. Review of recent trends of advancements in multilevel inverter topologies with reduced power switches and control techniques. IET Power Electron. 2024, 1–35. [Google Scholar] [CrossRef]
- Munawar, S.; Iqbal, M.S.; Adnan, M.; Akbar, M.A.; Bermak, A. Multilevel Inverters Design, Topologies, and Applications: Research Issues, Current, and Future Directions. IEEE Access 2024, 12, 149320–149350. [Google Scholar] [CrossRef]
- Silva, C.E.; Reis, G.L.; Alzamora, A.M.; de Paula, H. Reliability Analysis of IGBT Modules of Multilevel Inverters Operating in Hostile Mining Environments. IEEE Trans. Ind. Appl. 2025, 61, 6798–6809. [Google Scholar] [CrossRef]
- Nyamathulla, S.; Chittathuru, D.; Muyeen, S.M. An Overview of Multilevel Inverters Lifetime Assessment for Grid-Connected Solar Photovoltaic Applications. Electronics 2023, 12, 1944. [Google Scholar] [CrossRef]
- Wang, D.; Hemming, S.; Yang, Y.; Poorfakhraei, A.; Zhou, L.; Liu, C.; Emadi, A. Multilevel Inverters for Electric Aircraft Applications: Current Status and Future Trends. IEEE Trans. Transp. Electrif. 2024, 10, 3258–3282. [Google Scholar] [CrossRef]
- Tang, W.; Chen, Z.; Chen, Y.; Liu, Y.; Wang, T.; Chen, Z. Multi-voltage-vector-based modulated model predictive controller for three-level NPC inverters with neutral-point voltage balancing. J. Power Electron. 2024, 24, 934–945. [Google Scholar] [CrossRef]
- Harbi, I.; Rodriguez, J.; Liegmann, E.; Makhamreh, H.; Heldwein, M.L.; Novak, M.; Rossi, M.; Abdelrahem, M.; Trabelsi, M.; Ahmed, M.; et al. Model-Predictive Control of Multilevel Inverters: Challenges, Recent Advances, and Trends. IEEE Trans. Power Electron. 2023, 38, 10845–10868. [Google Scholar] [CrossRef]
- Rodriguez, J.; Garcia, C.; Mora, A.; Davari, A.; Rodas, J.; Garcia, D.F.V.; Elmorshedy, M.F.; Wang, F.; Zuo, K.; Tarisciotti, L.; et al. Latest Advances of Model Predictive Control in Electrical Drives—Part II: Applications and Benchmarking with Classical Control Methods. IEEE Trans. Power Electron. 2022, 37, 5047–5061. [Google Scholar] [CrossRef]
- Le, H.-P.N.; Pham, K.D.; Nguyen, N.-V. Analyses, Modeling, and SVPWM Control of a Three-Level T-NPC Inverter to Reduce Common-Mode Voltage Under Open-Circuit Fault in a Neutral-Point Switch. IEEE Access 2024, 12, 104708–104727. [Google Scholar] [CrossRef]
- Nandhini, E.; Sivaprakasam, A. A review of various control strategies based on space vector pulse width modulation for the voltage source inverter. IETE J. Res. 2022, 68, 3187–3201. [Google Scholar] [CrossRef]
- Babaie, M.; Mehrasa, M.; Sharifzadeh, M.; Al-Haddad, K. Floating Weighting Factors ANN-MPC Based on Lyapunov Stability for Seven-Level Modified PUC Active Rectifier. IEEE Trans. Ind. Electron. 2022, 69, 387–398. [Google Scholar] [CrossRef]
- Shadmand, B.; Balog, R.S.; Rub, H.A. Auto-tuning the cost function weight factors in a model predictive controller for a matrix converter VAR compensator. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3807–3814. [Google Scholar]
- Du, X.; Zhang, J.; Li, G.; Yu, Y.; Qian, C.; Du, R. Junction Temperature Extraction of the Power Semiconductor Device. In Thermal Reliability of Power Semiconductor Device in the Renewable Energy System; Springer Nature: Singapore, 2022; pp. 73–106. [Google Scholar]
- Andresen, M.; Ma, K.; Buticchi, G.; Falck, J.; Blaabjerg, F.; Liserre, M. Junction Temperature Control for More Reliable Power Electronics. IEEE Trans. Power Electron. 2018, 33, 765–776. [Google Scholar] [CrossRef]
- Okilly, A.H.; Harmony, P.N.; Kim, C.; Kim, D.-W.; Baek, J. Estimation of Peak Junction Hotspot Temperature in Three-Level TNPC-IGBT Modules for Traction Inverters Through Chip-Level Modeling and Experimental Validation. Energies 2025, 18, 3829. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, X.; Zhu, J.; Du, W.; Ye, J.; Bai, Y. Advances in Space Vector Modulation Techniques for Multilevel Inverters: A Comprehensive Review. Chin. J. Electr. Eng. 2025, 11, 63–77. [Google Scholar] [CrossRef]
- Tuluhong, A.; Song, T.; Chang, Q.; Xu, Z. A Review of Neutral-Point Voltage Balancing and Common-Mode Voltage Suppression Methods in Three-Level Converters. Electronics 2025, 14, 936. [Google Scholar] [CrossRef]
- Bebboukha, A.; Chouaib, L.; Meneceur, R.; Elsanabary, A.; Anees, M.A.; Mekhilef, S.; Zaitsev, I.; Bajaj, M.; Bereznychenko, V. A reduced vector model predictive controller for a three-level neutral point clamped inverter with common-mode voltage suppression. Sci. Rep. 2024, 14, 15108. [Google Scholar] [CrossRef]
- Bakini, H.; Mesbahi, N.; Kermadi, M.; Mekhilef, S.; Zahraoui, Y.; Mubin, M.; Seyedmahmoudian, M.; Stojcevski, A. An Improved Mutated Predictive Control for Two-Level Voltage Source Inverter with Reduced Switching Losses. IEEE Access 2024, 12, 25797–25808. [Google Scholar] [CrossRef]
- Li, K.; Xiao, F.; Liu, J.; Mai, Z.; Lian, C.; Gao, S.; Fu, K. Space Vector Pulsewidth Modulation Strategy for ANPC-5L Inverter Based on Model Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3020–3035. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Q.; Jiang, Y.; Hu, W.; Chen, Z. A Hybrid SVPWM-MPTC Control Strategy of Three-Level NPC Inverter-Fed PMSM Under the Balanced and Unbalanced DC Links. IEEE Trans. Energy Convers. 2024, 39, 1865–1878. [Google Scholar] [CrossRef]
- Guo, F.; Yang, T.; Li, C.; Bozhko, S.; Wheeler, P. Active Modulation Strategy for Capacitor Voltage Balancing of Three-Level Neutral-Point-Clamped Converters in High-Speed Drives. IEEE Trans. Ind. Electron. 2022, 69, 2276–2287. [Google Scholar] [CrossRef]
- Guo, C.; Zhu, Y.; Tong, L. Junction Temperature Prediction for Multi-chip IGBT Modules Based on an Improved 3D Thermal Network Model and Experimental Results. Results Eng. 2025, 27, 106072. [Google Scholar] [CrossRef]
- Abuelnaga, A.; Narimani, M.; Bahman, A.S. A Review on IGBT Module Failure Modes and Lifetime Testing. IEEE Access 2021, 9, 9643–9663. [Google Scholar] [CrossRef]
- Hosseinabadi, F.; Chakraborty, S.; Bhoi, S.K.; Prochart, G.; Hrvanovic, D.; Hegazy, O. A comprehensive overview of reliability assessment strategies and testing of power electronics converters. IEEE Open J. Power Electron. 2024, 5, 473–512. [Google Scholar] [CrossRef]
- Okilly, A.H.; Choi, S.; Kwak, S.; Kim, N.; Lee, J.; Moon, H.; Baek, J. Estimation Technique for IGBT Module Junction Temperature in a High-Power Density Inverter. Machines 2023, 11, 990. [Google Scholar] [CrossRef]
- Haque, M.S.; Moniruzzaman, M.; Choi, S.; Kwak, S.; Okilly, A.H.; Baek, J. A Fast Loss Model for Cascode GaN-FETs and Real-Time Degradation-Sensitive Control of Solid-State Transformers. Sensors 2023, 23, 4395. [Google Scholar] [CrossRef]
- Tian, W.; Chen, N. Multiphysics Coupling in IGBT Modules: A Review. J. Electron. Packag. 2024, 146, 040801. [Google Scholar] [CrossRef]
- Liu, G.; Li, X.; Wang, Y.; Huang, X.; Chang, G.; Luo, H. A method to derive the coupling thermal resistances at junction-to-case level in multichip power modules. IEEE Trans. Power Electron. 2023, 38, 1747–1756. [Google Scholar] [CrossRef]
- Ma, H.; Yang, Y.; Fan, Z.; Huang, T.; Xiang, W.; Wen, Y.; Cobreces, S. A Fourier Series-Based Steady-State Thermal Resistance Model for Power Module. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3912–3924. [Google Scholar] [CrossRef]
- Moniruzzaman, M.; Okilly, A.H.; Choi, S.; Baek, J.; Mannan, T.I.; Islam, Z. A Comprehensive Study of Machine Learning Algorithms for GPU based Real-time Monitoring and Lifetime Prediction of IGBTs. In Proceedings of the 2024 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 25–29 February 2024; pp. 2678–2684. [Google Scholar]
- Jones-Jackson, S.; Rodriguez, R.; Yang, Y.; Lopera, L.; Emadi, A. Overview of current thermal management of automotive power electronics for traction purposes and future directions. IEEE Trans. Transp. Electrif. 2022, 8, 2412–2428. [Google Scholar] [CrossRef]
- Wei, K.; Wang, W.; Hu, Z.; Du, M. Condition Monitoring of IGBT Modules Based on Changes of Thermal Characteristics. IEEE Access 2019, 7, 47525–47534. [Google Scholar] [CrossRef]
- Wang, J.; Chen, W.; Wu, Y.; Zhang, J.; Wang, L.; Liu, J. Chip-Level Electrothermal Stress Calculation Method of High-Power IGBT Modules in System-Level Simulation. IEEE Trans. Power Electron. 2022, 37, 10546–10561. [Google Scholar] [CrossRef]
- Wu, X.; Yang, X.; Ye, J.; Liu, G. Novel Prognostics for IGBTs Using Wire-Bond Contact Degradation Model Considering On-Chip Temperature Distribution. IEEE Trans. Power Electron. 2024, 40, 4411–4424. [Google Scholar] [CrossRef]
- Okilly, A.H.; Kim, C.; Baek, J. Experimental Implementation of a 3-Level TNPC-IGBT Inverter for Uniform Stress Distribution and THD Mitigation: MPC-Driven Switching Optimization, LCL Filter Integration, and Real-Time Stress Monitoring. IEEE Access 2025, 13, 152762–152781. [Google Scholar] [CrossRef]
- Semikron: SEMiX405TMLI12E4B. Power Modules and Systems. Available online: https://www.semikron-danfoss.com/products/p/semix405tmli12e4b-21919490 (accessed on 25 December 2024).
- Zhao, M.; Ge, Q.; Zhu, J.; Wang, K.; Zhang, B.; Zhao, L. Improved Synchronized SVPWM Strategy for High-Power Three-Level Active Neutral Point Clamped Traction Inverter. IEEE Trans. Power Electron. 2025, 40, 3189–3209. [Google Scholar] [CrossRef]
- Lin, Z.; Du, W.; Bai, Y.; Iu, H.H.C.; Fernando, T.; Zhang, X. Carrier-Based Implementation of SVPWM for a Three-Level Simplified Neutral Point Clamped Inverter with XOR Logic Gates. Electronics 2025, 14, 1408. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mascarella, D.; Joós, G.; Cyr, J.-M.; Xu, J. A Dual Three-Level T-NPC Inverter for High-Power Traction Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 668–678. [Google Scholar] [CrossRef]
- Watanabe, K.; Xu, X. Nonlinear crossing strategy-based particle swarm optimizations with time-varying acceleration coefficients. Appl. Intell. 2024, 54, 7229–7277. [Google Scholar] [CrossRef]
- Li, Y. Particle swarm optimization based neural network automatic controller for stability steering control of four-wheel drive electric vehicle. Front. Mech. Eng. 2024, 10, 1378175. [Google Scholar] [CrossRef]
- Anssari, O.M.H.; Badamchizadeh, M.; Ghaemi, S. Designing of a PSO-Based Adaptive SMC with a Multilevel Inverter for MPPT of PV Systems Under Rapidly Changing Weather Conditions. IEEE Access 2024, 12, 41421–41435. [Google Scholar] [CrossRef]
- Danfos SEMIKRON. Determining Switching Losses of IGBT Modules. Application Note AN 14-003. August 2024. Available online: https://assets.danfoss.com/documents/latest/444047/AB501641682475en-000201.pdf (accessed on 3 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).