Experimental Characterization and Modelling of a Humidification–Dehumidification (HDH) System Coupled with Photovoltaic/Thermal (PV/T) Modules
Abstract
1. Introduction
2. Humidifier and Dehumidifier Models
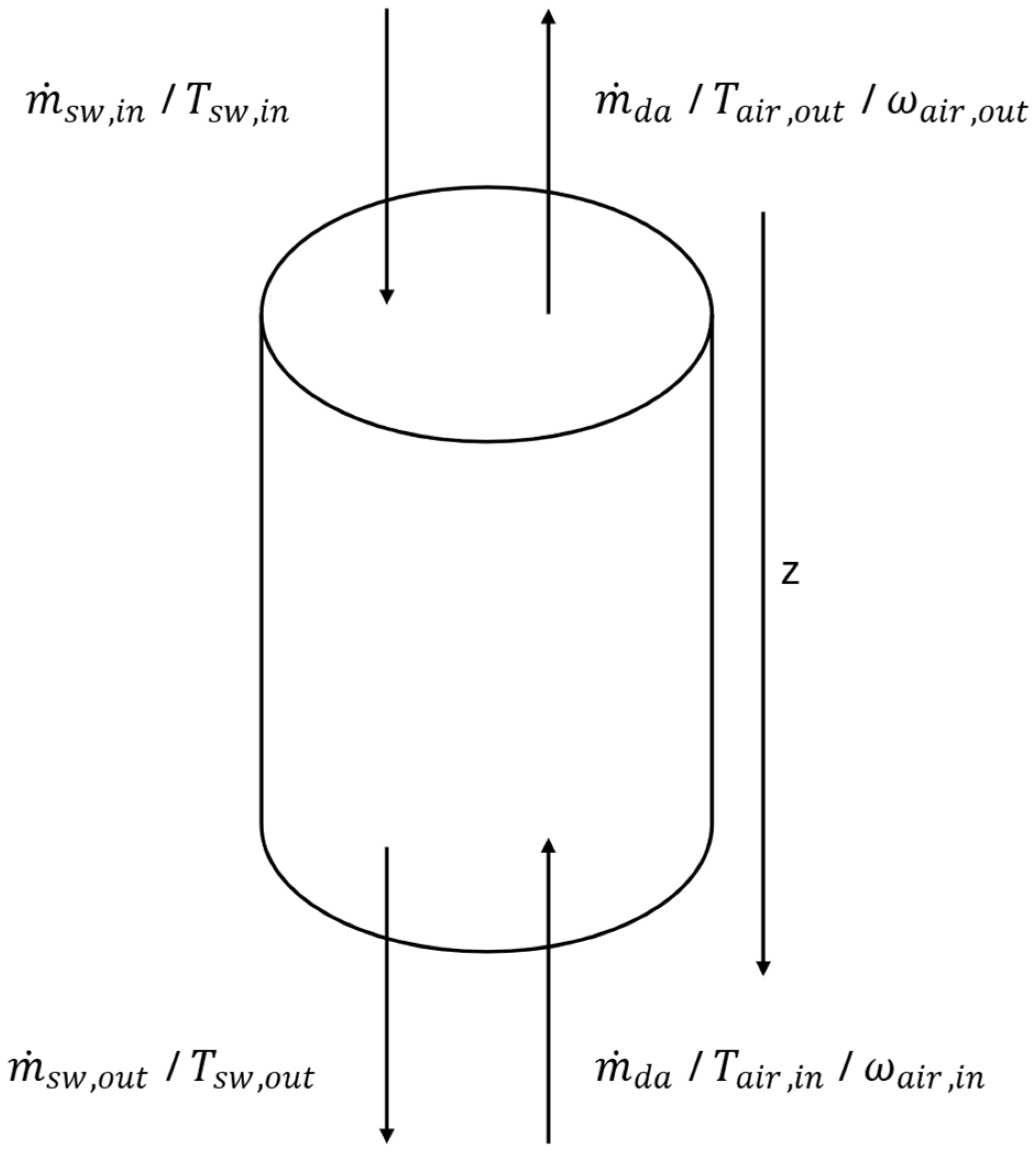
2.1. Humidifier
- The heat exchanger operates in steady-state conditions.
- Kinetic energy and potential energy are negligible.
- The cylinder is adiabatic and there is no heat exchange to the outside.
- Saline water and moist air properties are constant in each volume.
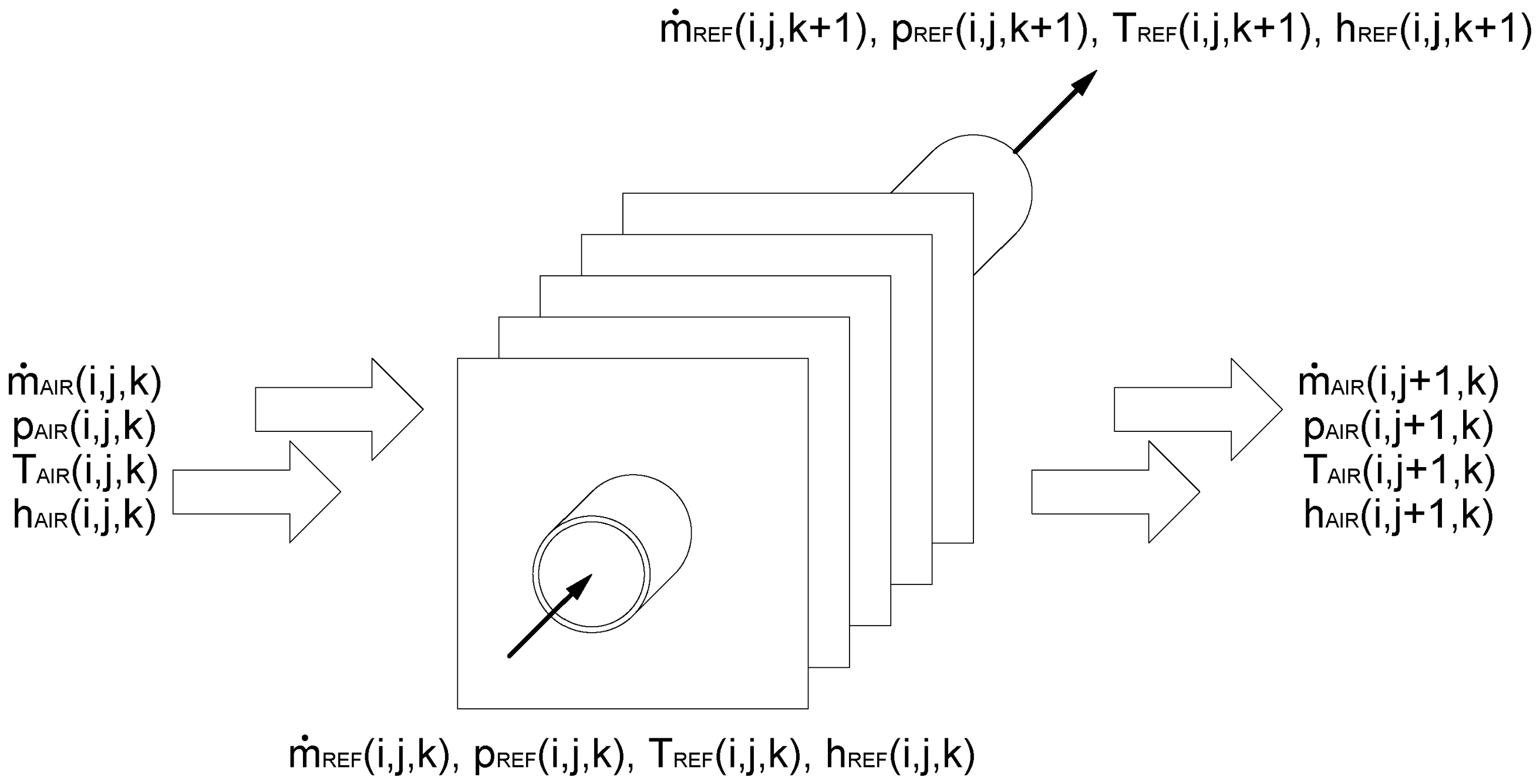
2.2. Dehumidifier
- The heat exchanger operates in steady-state conditions.
- Kinetic energy and potential energy are negligible.
- Axial heat conduction through tube thickness is negligible.
- Radiation heat transfer with the surrounding elements is negligible.
- Return bends, joints, splits and headers are adiabatic.
- Saline water and moist air properties are constant in each volume.
- Condensation enthalpy of vapor is added to the total heat absorbed by water.
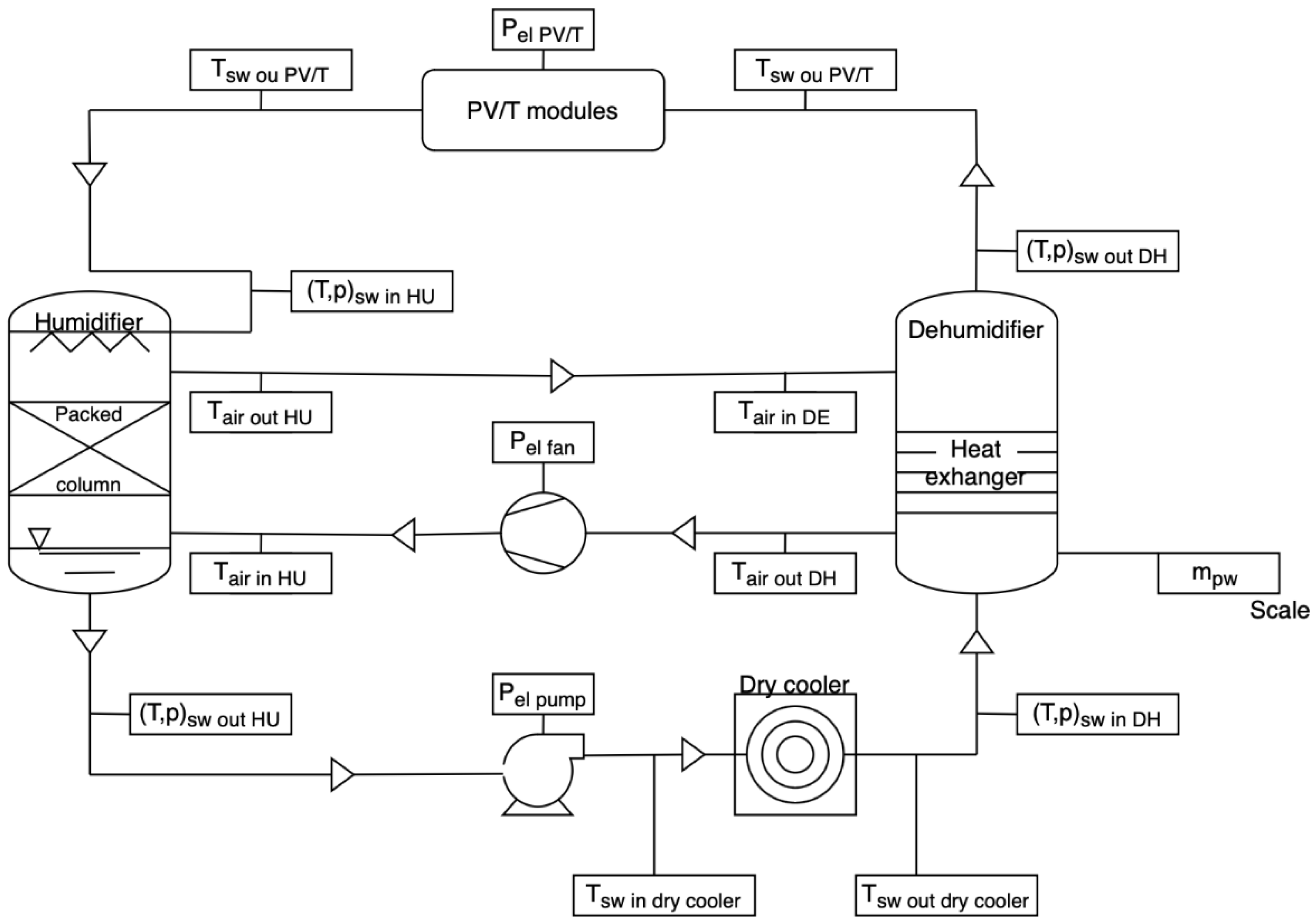
3. Experimental Setup
Measurement and Control Instruments
4. Experimental Activities
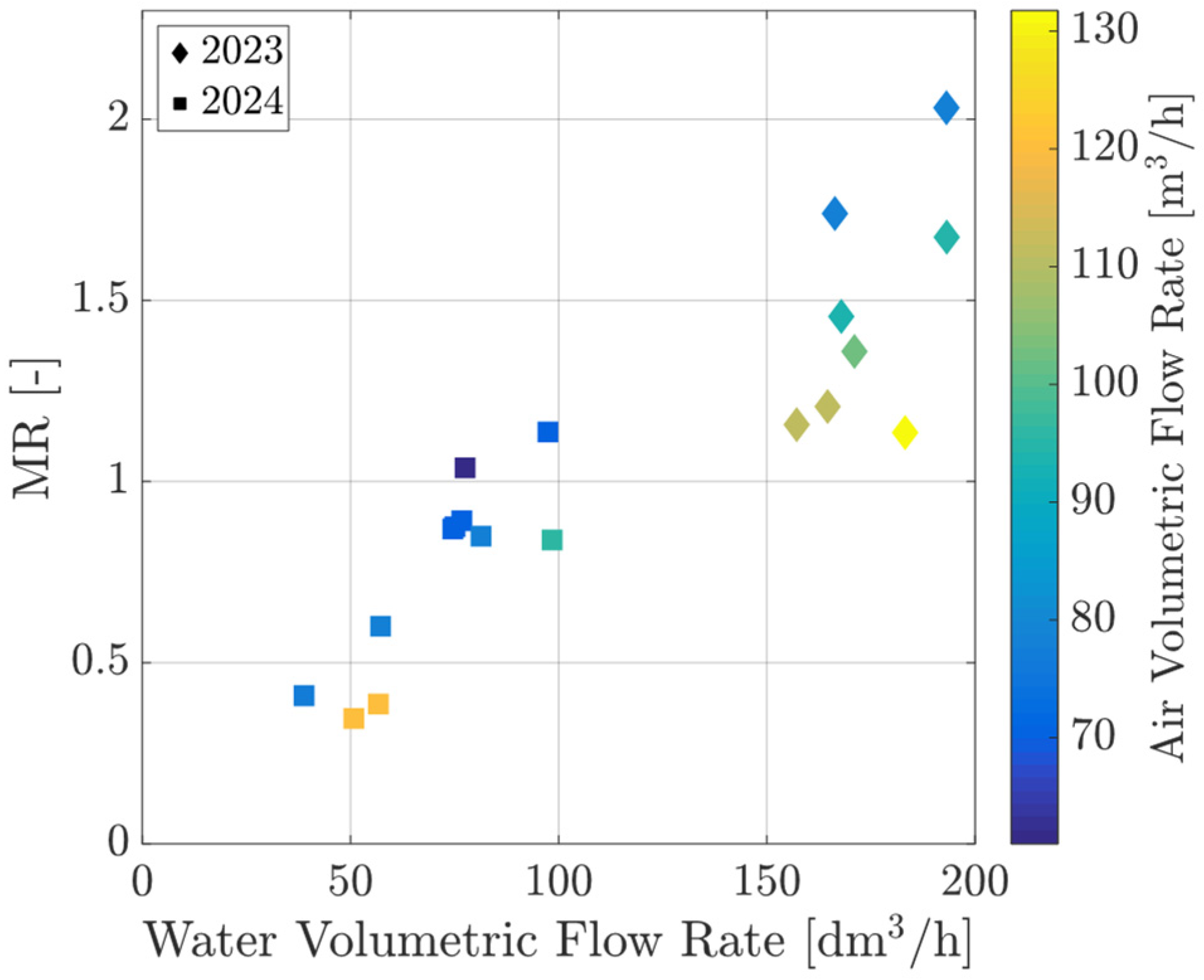
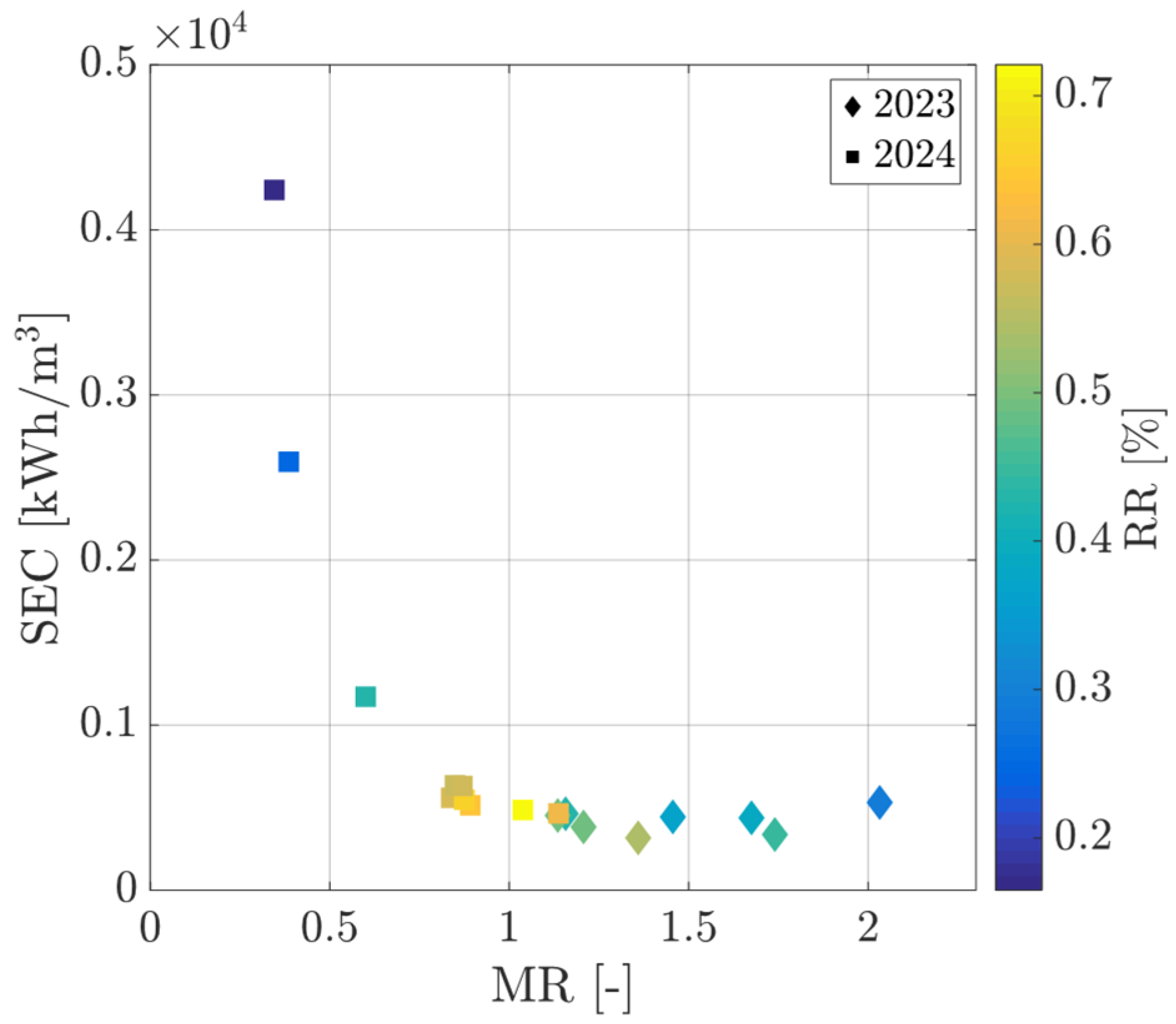
- Mass flow ratio: it expresses the ratio between the flow rates of saline water and air circulating in the plant.
- Recovery ratio: it expresses the percentage ratio between pure water mass flow rate and saline water mass flow rate.
- Gain output ratio: the ratio between the latent heat of evaporation of the distillate produced and the total thermal input absorbed by the solar collectors.
- Specific electrical consumption: the amount of electricity that the auxiliaries (pump and fan) consume to produce one cubic meter of fresh water.
- Thermal energy consumption: the amount of thermal energy recovered by the saline water flow in the PV/T modules
- Specific thermal consumption: the amount of thermal energy recovered by the saline water flow in the PV/T modules to produce one cubic meter of fresh water.
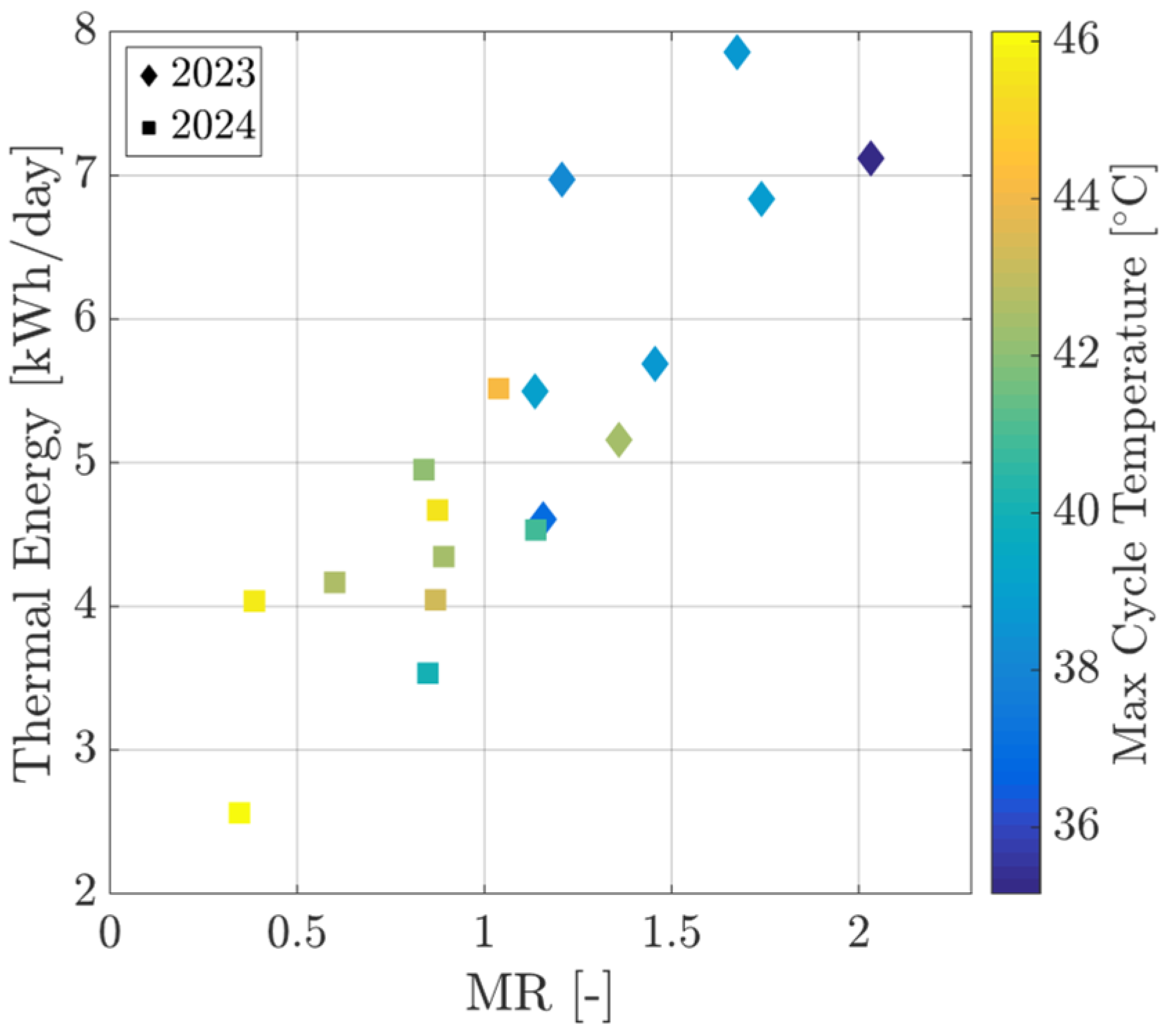
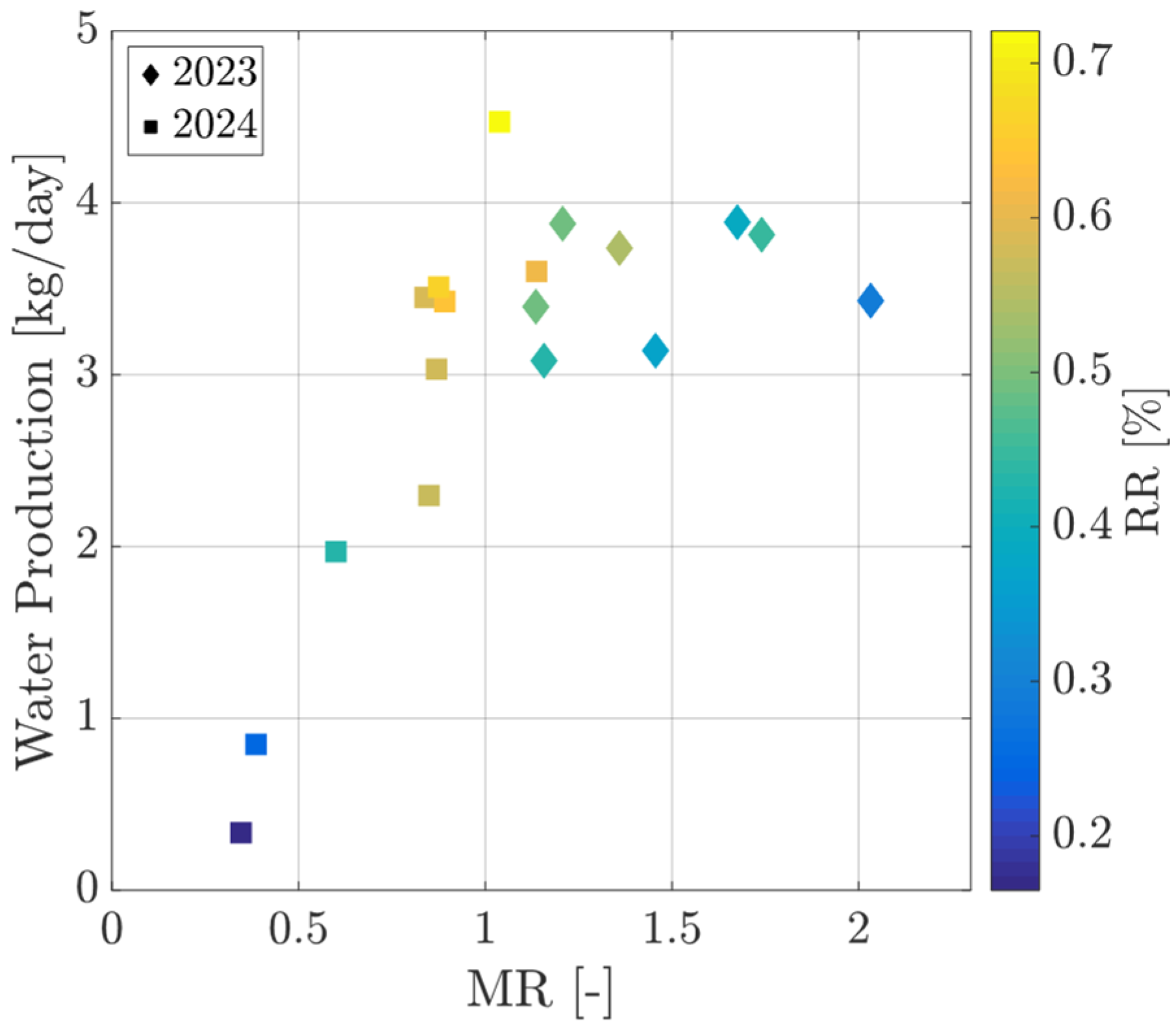
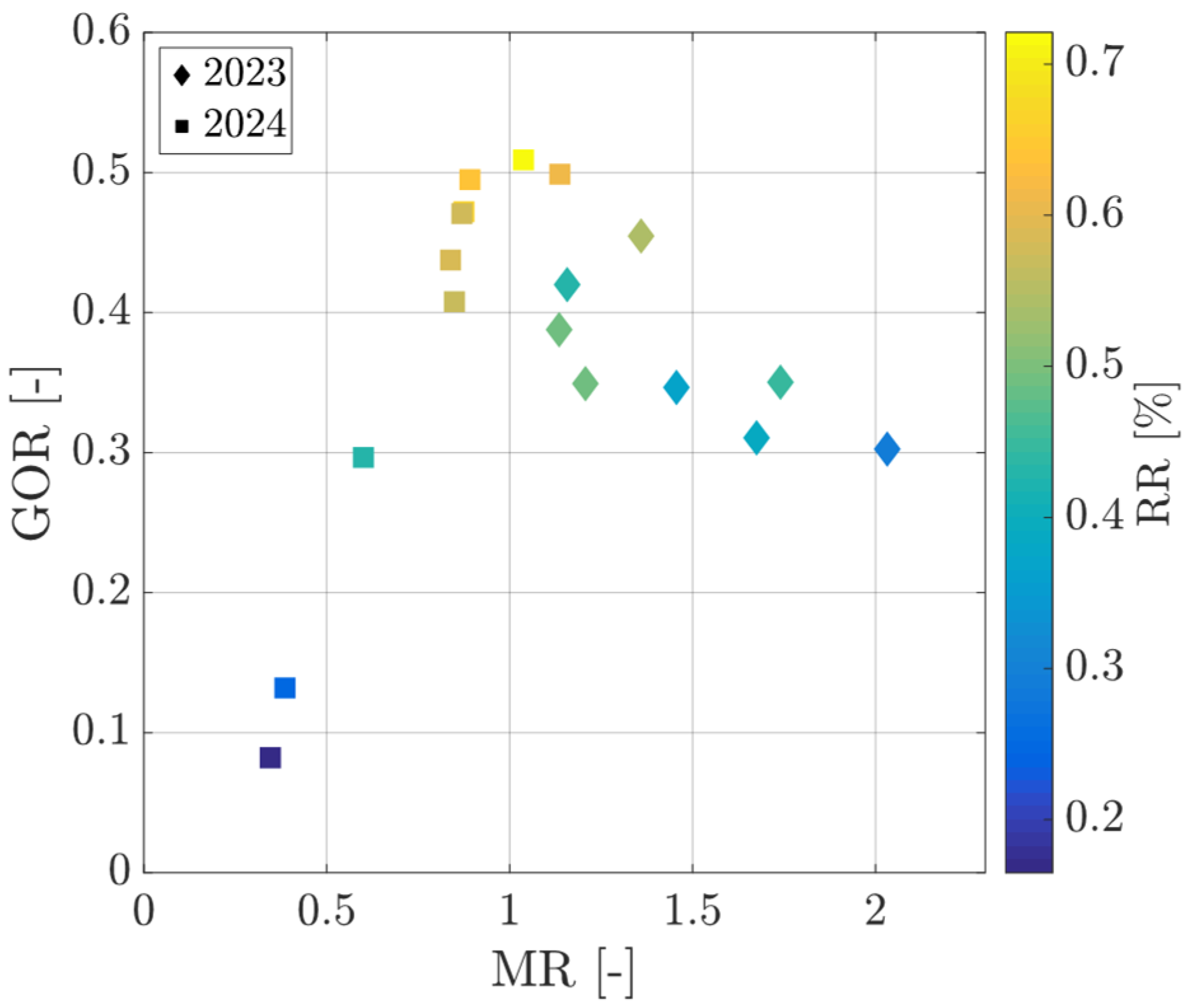
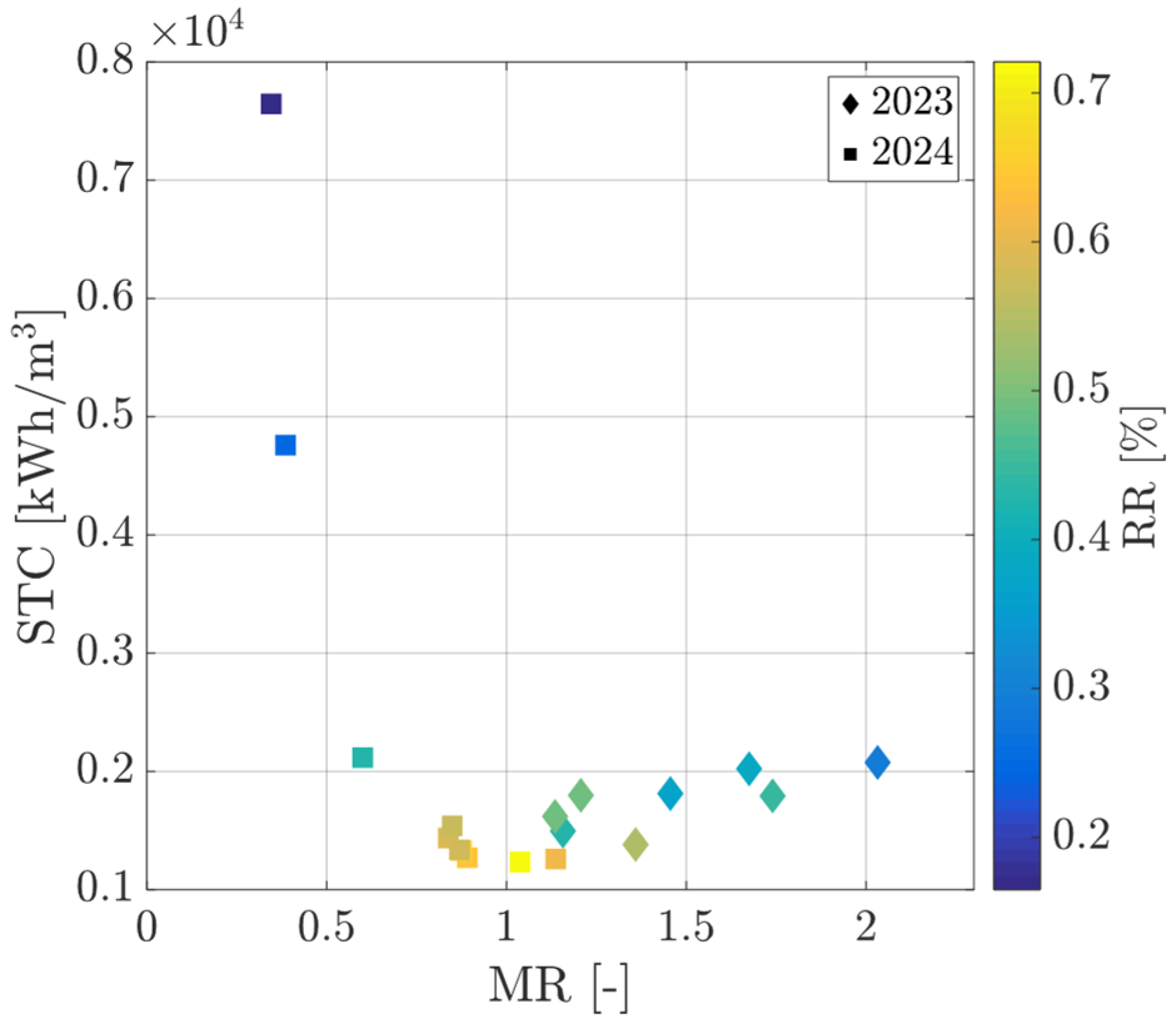
5. Results and Discussion
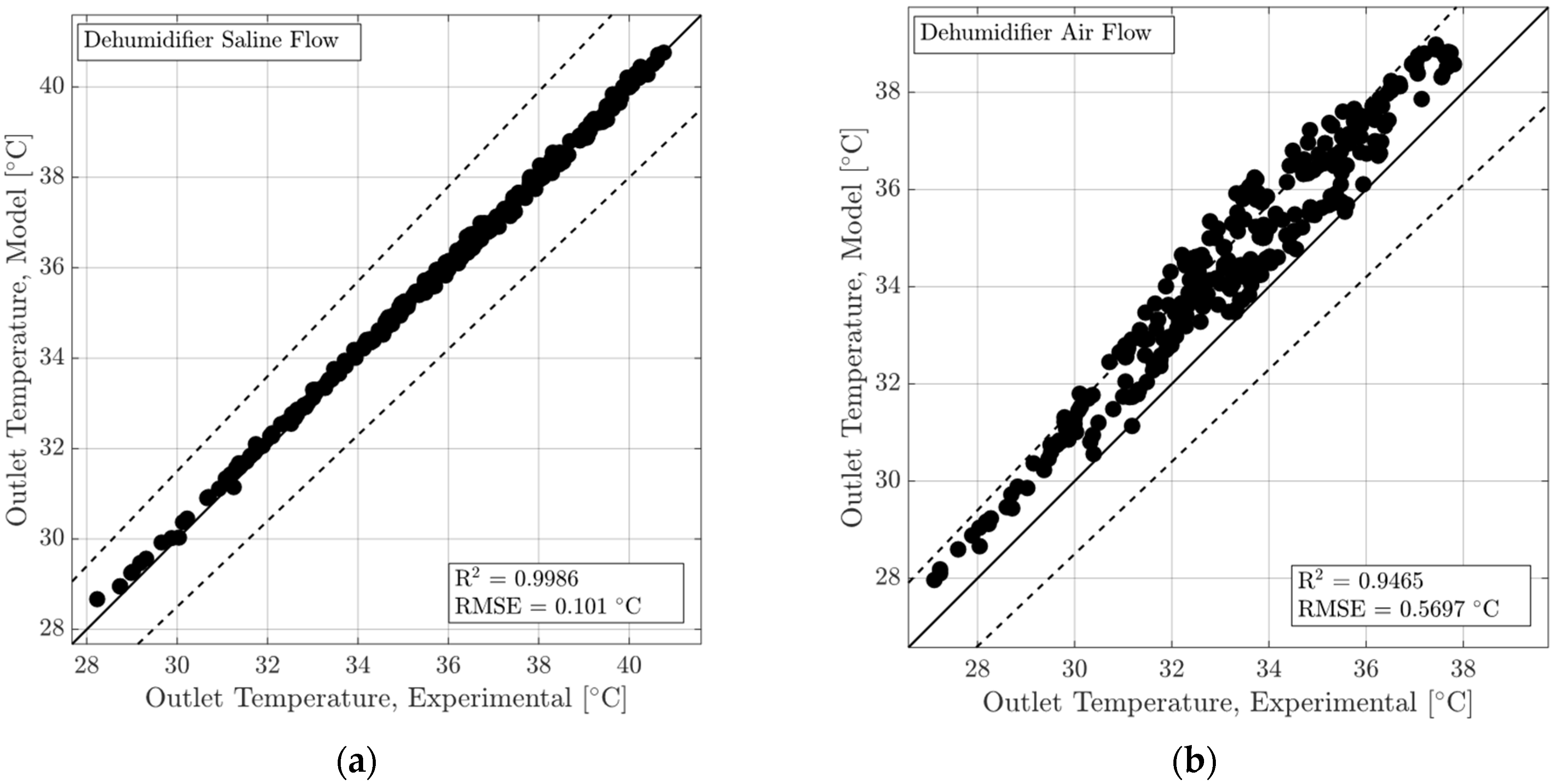
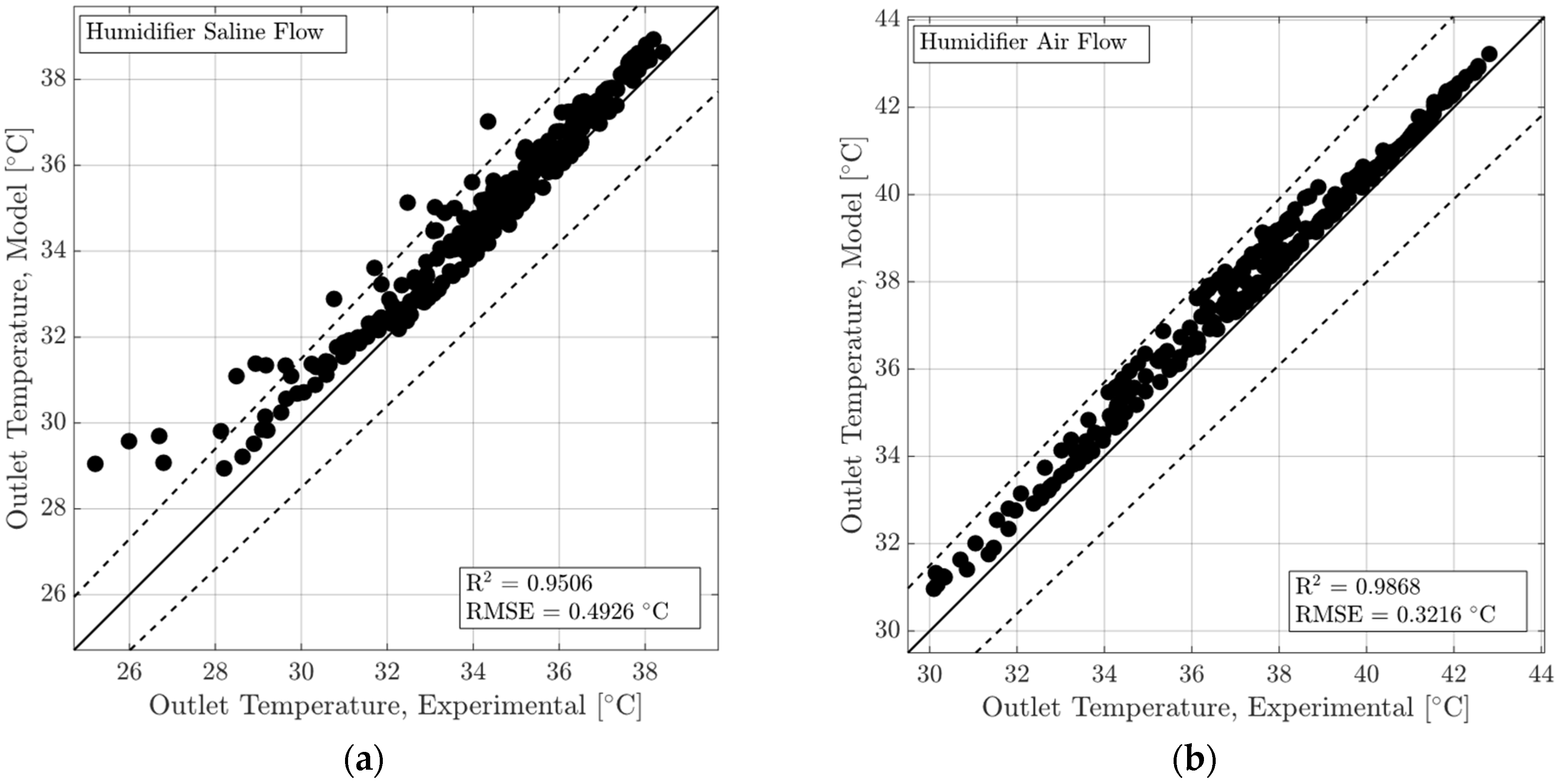
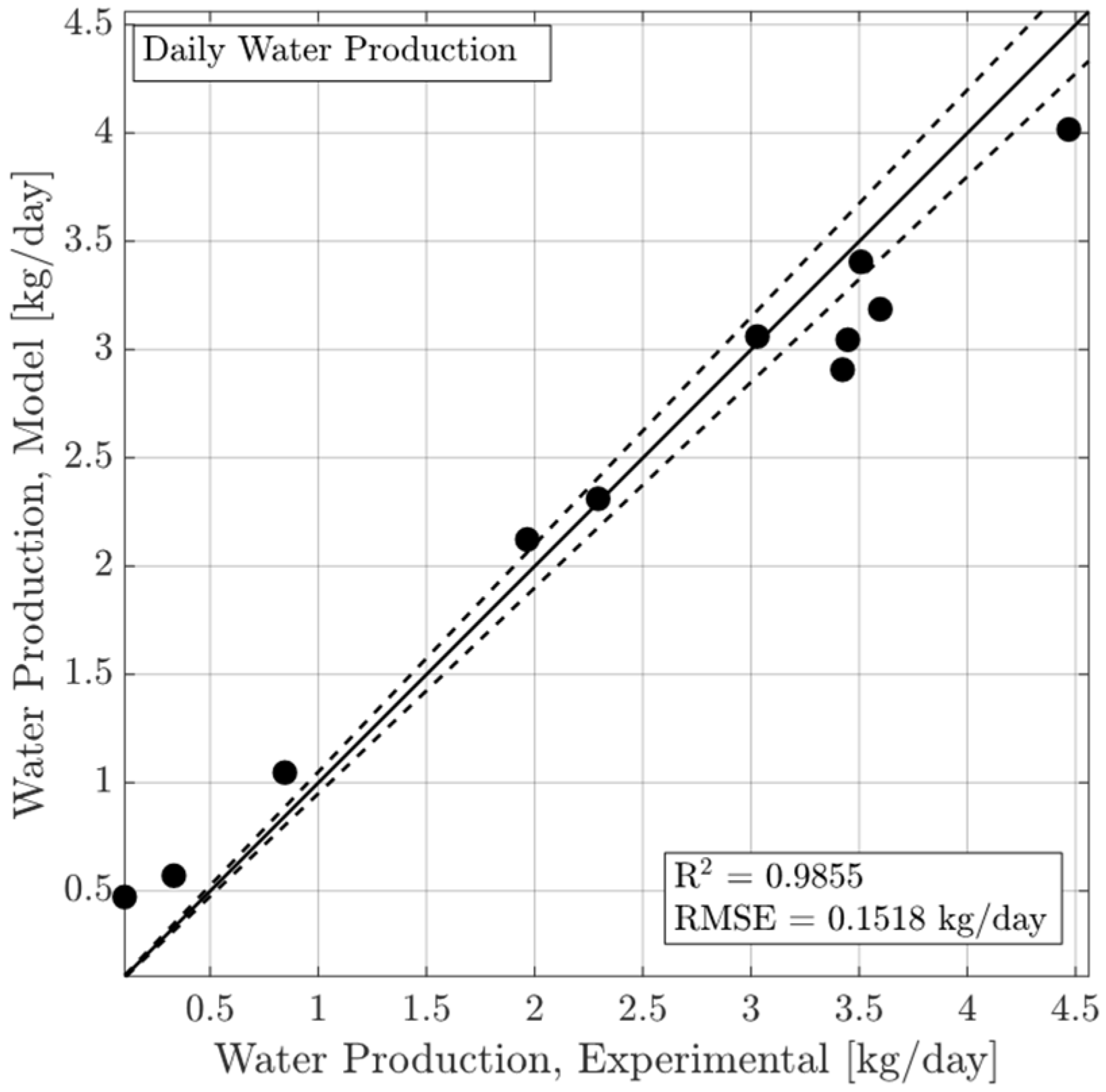
Numerical Model and Experimental Data Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| AH | Air Heated |
| CACW | Closed Air Closed Water |
| CAOW | Closed Air Open Water |
| DHI | Diffuse Horizontal Irradiance |
| GHI | Global Horizontal Irradiance |
| GOR | Gain Output Ratio |
| HDH | Humidification Dehumidification |
| MD | Membrane Distillation |
| MED | Multi-Effect Distillation |
| MR | Mass flow Ratio |
| MSF | Multi-Stage Flash distillation |
| PV | Photovoltaic |
| PVT | Photovoltaic Thermal |
| RO | Reverse Osmosis |
| RR | Recovery Ratio |
| SEC | Specific Electrical Consumption |
| SDG | Sustainable Development Goals |
| STC | Specific Thermal Consumption |
| TEC | Thermal Energy Consumption |
| VCC | Vapor Compression Chiller |
| WH | Water Heated |
| Humidity ratio of air | |
| Cross sectional area | |
| Dehumidifier heat exchange effectiveness | |
| Density | |
| Heat | |
| Heat transfer coefficient | |
| Height | |
| Latent heat of vaporization of water | |
| Lewis factor | |
| Mass flow rate | |
| Mass transfer coefficient | |
| Merkel number | |
| Pressure | |
| Pressure drop | |
| Specific enthalpy | |
| Specific heat | |
| Specific mass flow rate | |
| Specific packing area | |
| Temperature | |
| Air | |
| Dry air | |
| Moist air | |
| Pure water | |
| Saline water | |
| Vapour |
References
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 25 August 2025).
- Goal 6: Ensure Access to Water and Sanitation for All. Available online: https://www.un.org/sustainabledevelopment/water-and-sanitation/ (accessed on 20 August 2025).
- World Bank. The Role of Desalination in an Increasingly Water-Scarce World. 2019. Available online: https://hdl.handle.net/10986/31416 (accessed on 11 July 2025).
- Rajesh, S.; Chiranjeevi, C. Hybrid thermal desalination systems for sustainable development—A critical review. Sol. Energy 2024, 270, 112364. [Google Scholar] [CrossRef]
- Curto, D.; Franzitta, V.; Guercio, A. A review of the water desalination technologies. Appl. Sci. 2021, 11, 670. [Google Scholar] [CrossRef]
- Mistry, K.H.; Mitsos, A.; Lienhard, J.H. Optimal operating conditions and configurations for humidification–dehumidification desalination cycles. Int. J. Therm. Sci. 2011, 50, 779–789. [Google Scholar] [CrossRef]
- Sonkar, M.; Kanathala, Y.; Naik, B.K. Recent developments in solar-driven adsorption and humidification-dehumidification based hybrid desalination system: A state-of-the-art review. Sol. Compass 2025, 15, 100125. [Google Scholar] [CrossRef]
- Urban, J.J. Emerging Scientific and Engineering Opportunities Within the Water-Energy Nexus. Joule 2017, 1, 665–688. [Google Scholar] [CrossRef]
- Giwa, A.; Akther, N.; Al Housani, A.; Haris, S.; Hasan, S.W. Recent advances in humidification dehumidification (HDH) desalination processes: Improved designs and productivity. Renew. Sustain. Energy Rev. 2016, 57, 929–944. [Google Scholar] [CrossRef]
- Shaikh, J.S.; Ismail, S. A review on recent technological advancements in humidification dehumidification (HDH) desalination. J. Environ. Chem. Eng. 2022, 10, 108890. [Google Scholar] [CrossRef]
- Giwa, A.; Fath, H.; Hasan, S.W. Humidification–dehumidification desalination process driven by photovoltaic thermal energy recovery (PV-HDH) for small-scale sustainable water and power production. Desalination 2016, 377, 163–171. [Google Scholar] [CrossRef]
- Faegh, M.; Behnam, P.; Shafii, M.B. A review on recent advances in humidification-dehumidification (HDH) desalination systems integrated with refrigeration, power and desalination technologies. Energy Convers. Manag. 2019, 196, 1002–1036. [Google Scholar] [CrossRef]
- Khodadadi, M.; Sheikholeslami, M. Review on poly-generation application of photovoltaic/thermal systems. Sustain. Energy Technol. Assess. 2022, 52, 102172. [Google Scholar] [CrossRef]
- Zubair, S.M.; Antar, M.A.; Elmutasim, S.M.; Lawal, D.U. Performance evaluation of humidification-dehumidification (HDH) desalination systems with and without heat recovery options: An experimental and theoretical investigation. Desalination 2018, 436, 161–175. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Antar, M.A.; Zubair, S.M.; Elbashir, A.M. Optimum thermal design of humidification dehumidification desalination systems. Desalination 2014, 349, 10–21. [Google Scholar] [CrossRef]
- Mahmoud, A.; Fath, H.; Ahmed, M. Enhancing the performance of a solar driven hybrid solar still/humidification-dehumidification desalination system integrated with solar concentrator and photovoltaic panels. Desalination 2018, 430, 165–179. [Google Scholar] [CrossRef]
- Pourafshar, S.T.; Jafarinaemi, K.; Mortezapour, H. Development of a photovoltaic-thermal solar humidifier for the humidification-dehumidification desalination system coupled with heat pump. Sol. Energy 2020, 205, 51–61. [Google Scholar] [CrossRef]
- Rafiei, A.; Alsagri, A.S.; Mahadzir, S.; Loni, R.; Najafi, G.; Kasaeian, A. Thermal analysis of a hybrid solar desalination system using various shapes of cavity receiver: Cubical, cylindrical, and hemispherical. Energy Convers. Manag. 2019, 198, 111861. [Google Scholar] [CrossRef]
- He, W.; Lu, Y.; An, H.; Zhou, X.; Su, P.; Han, D. Parametric analysis of humidification dehumidification desalination driven by photovoltaic/thermal (PV/T) system. Energy Convers. Manag. 2022, 259, 115520. [Google Scholar] [CrossRef]
- Elsafi, A.M. Integration of humidification-dehumidification desalination and concentrated photovoltaic-thermal collectors: Energy and exergy-costing analysis. Desalination 2017, 424, 17–26. [Google Scholar] [CrossRef]
- Anand, B.; Srinivas, T. Performance evaluation of photovoltaic/thermal–HDH desalination system. Appl. Sol. Energy 2017, 53, 243–249. [Google Scholar] [CrossRef]
- Ravajiri, E.S.; Hasanloo, M.; Jalali, A.; Houshfar, E. Techno-economic analysis and tri-objective optimization of a novel HDH desalination with PVT and vapor-compression chiller for sustainable water supply in remote areas. Sustain. Cities Soc. 2024, 101, 105211. [Google Scholar] [CrossRef]
- Gabrielli, P.; Gazzani, M.; Novati, N.; Sutter, L.; Simonetti, R.; Molinaroli, L.; Manzolini, G.; Mazzotti, M. Combined water desalination and electricity generation through a humidification-dehumidification process integrated with photovoltaic-thermal modules: Design, performance analysis and techno-economic assessment. Energy Convers. Manag. X 2019, 1, 100004. [Google Scholar] [CrossRef]
- Zhani, K.; Ben Bacha, H. Experimental investigation of a new solar desalination prototype using the humidification dehumidification principle. Renew. Energy 2010, 35, 2610–2617. [Google Scholar] [CrossRef]
- Nafey, A.; Fath, H.; El-Helaby, S.; Soliman, A. Solar desalination using humidification–dehumidification processes. Part II. An experimental investigation. Energy Convers. Manag. 2004, 45, 1263–1277. [Google Scholar] [CrossRef]
- Hermosillo, J.-J.; Arancibia-Bulnes, C.A.; Estrada, C.A. Water desalination by air humidification: Mathematical model and experimental study. Sol. Energy 2012, 86, 1070–1076. [Google Scholar] [CrossRef]
- Chang, Z.; Zheng, H.; Yang, Y.; Su, Y.; Duan, Z. Experimental investigation of a novel multi-effect solar desalination system based on humidification–dehumidification process. Renew. Energy 2014, 69, 253–259. [Google Scholar] [CrossRef]
- Ghazy, A. Experimental thermal and electrical performances of a PVT-air collector coupled to a humidification-dehumidification (HDH) cycle. Int. J. Renew. Energy Dev. 2023, 12, 520–527. [Google Scholar] [CrossRef]
- Taheri, S.; Faghih Khorasani, A.; Mozafari Shamsi, M. Evaluating the Performance of a Humidification-Dehumidification Desalination System Integrated with Photovoltaic-Thermal Collectors. J. Renew. Energy Environ. 2024, 11, 1–9. [Google Scholar] [CrossRef]
- Colombini, R.; Molinaroli, L.; Simonetti, R.; Colombo, L.P.M.; Manzolini, G. Numerical analysis of different designs of roll-bond absorber on PV/T module and performance assessment. Appl. Therm. Eng. 2021, 192, 116873. [Google Scholar] [CrossRef]
- Bombarda, P.; Di Marcoberardino, G.; Lucchini, A.; Leva, S.; Manzolini, G.; Molinaroli, L.; Pedranzini, F.; Simonetti, R. Thermal and electric performances of roll-bond flat plate applied to conventional PV modules for heat recovery. Appl. Therm. Eng. 2016, 105, 304–313. [Google Scholar] [CrossRef]
- Gatley, D.P. Understanding Psychrometrics, 3rd ed.; ASHRAE: Peachtree Corners, GA, USA, 2013. [Google Scholar]
- Kloppers, J.C. A Critical Evaluation and Refinement of the Performance Prediction of Wet-Cooling Towers. Ph.D. Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2003. Available online: https://scholar.sun.ac.za/handle/10019.1/1476 (accessed on 10 July 2025).
- Bosnjakovic, F.; Knoche, K.F. Technische Thermodynamik Teil I; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Joppolo, C.M.; Molinaroli, L.; Pasini, A. Numerical analysis of the influence of circuit arrangement on a fin-and-tube condenser performance. Case Stud. Therm. Eng. 2015, 6, 136–146. [Google Scholar] [CrossRef]
- Celen, A.; Dalkilic, A.S.; Wongwises, S. Experimental analysis of the single phase pressure drop characteristics of smooth and microfin tubes. Int. Commun. Heat Mass Transf. 2013, 46, 58–66. [Google Scholar] [CrossRef]
- Wang, C.-C.; Hsieh, Y.-C.; Lin, Y.-T. Performance of Plate Finned Tube Heat Exchangers Under Dehumidifying Conditions. 1997. Available online: http://asmedigitalcollection.asme.org/heattransfer/article-pdf/119/1/109/5507775/109_1.pdf?casa_token=VP8XVZLvIm0AAAAA:qs73IVOWvFRq__lkv31AAv6yU29ttmCCbE6ppY5OC1LBVVZv6K02AU_hdI-a7m_eODrYTWVlVzA (accessed on 10 July 2025).
- ESDU 98005; Design and Performance Evaluation of Heat Exchangers: The Effectiveness-NTU Method. (Part 3: Graphical and Analytical Data); Accuris: Englewood, CO, USA, 2014.









| Instrument | Manufacturer and Model | Range | Accuracy |
|---|---|---|---|
| Water Flowmeter | Endress + Hauser Proline Promag P300, Reinach, Switzerland | 0–6 m3/h | ±0.5% R.V. |
| Air Flowmeter | Endress + Hauser Proline Prowirl R200, Reinach, Switzerland | 0–821 m3/h | ±1.0% R.V. |
| Scale | Kern 572-55, Balingen-Frommern, Germany | 0–20 kg | ±0.25 g |
| Thermometer | Tersid PT100, Sesto San Giovanni (MI), Italy | 0–90 °C | Class A |
| Pressure Gauge | Huba Control 528, Würenlos, Switzerland | 0–4 bar | ±0.3% F.S. |
| Wattmeter | Cewe Instrument DPT221-441, Segrate (MI), Italy | 0–1100 W | ±0.5% F.S. |
| Component | Manufacturer and Model | Main Characteristics |
|---|---|---|
| Pump | Wilo MHI 202-1, Dortmund, Germany | Rated flow rate: 6 m3/h Rated head: 23.5 m Rated power: 0.55 kW |
| Fan | Fläkt W20-160-2-1, Herne, Germany | Rated flow rate: 2000 m3/h Rated pressure: 1000 Pa Rated power: 1.1 kW |
| PVT | Eclipse ECL250P, Nozza di Vestone (BS), Italy | Electrical peak power: 250 W |
| Inverter | SolarEdge SE3500, Munich, Germany | Rated output power: 3.5 kW |
| Humidifier | Dehumidifier | ||
|---|---|---|---|
| Column height | 2.8 m | Frontal tube length | 0.25 m |
| Column width | 0.2 m | Inner tubes diameter | 0.0085 m |
| Surface area to volume ratio | 300 m2/m3 | Tube transversal distance | 0.025 m |
| Tube longitudinal distance | 0.025 m | ||
| Fin distance | 0.0032 m | ||
| Fin thickness | 0.0005 m | ||
| Fin Type | Corrugated | ||
| Rows tubes number | 16 | ||
| Frontal tubes number | 6 | ||
| Duration | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| h:mm:ss | ||||||||||||||
| 11/09/2023 | 4:01:33 | 171.03 | 102.72 | 0.0475 | 0.0350 | 1.359 | 3.317 | 5.159 | 1.185 | 3.737 | 1380.7 | 317.1 | 0.543 | 0.455 |
| 14/09/2023 | 4:34:14 | 157.16 | 110.88 | 0.0437 | 0.0377 | 1.157 | 2.644 | 4.606 | 1.428 | 3.082 | 1494.8 | 463.4 | 0.429 | 0.420 |
| 25/09/2023 | 4:46:40 | 164.59 | 111.32 | 0.0457 | 0.0379 | 1.207 | 4.266 | 6.972 | 1.487 | 3.879 | 1797.3 | 383.4 | 0.493 | 0.349 |
| 28/09/2023 | 5:12:51 | 193.20 | 94.17 | 0.0537 | 0.0320 | 1.675 | 3.947 | 7.858 | 1.705 | 3.888 | 2021.4 | 438.5 | 0.386 | 0.311 |
| 02/10/2023 | 5:09:35 | 166.34 | 78.04 | 0.0462 | 0.0266 | 1.740 | 3.876 | 6.836 | 1.286 | 3.815 | 1792.1 | 337.2 | 0.444 | 0.350 |
| 03/10/2023 | 6:04:14 | 193.13 | 77.59 | 0.0536 | 0.0264 | 2.032 | 3.773 | 7.119 | 1.824 | 3.431 | 2075.0 | 531.6 | 0.293 | 0.303 |
| 09/10/2023 | 5:06:13 | 167.87 | 94.13 | 0.0466 | 0.0320 | 1.456 | 3.934 | 5.689 | 1.395 | 3.140 | 1811.5 | 444.2 | 0.367 | 0.347 |
| 10/10/2023 | 3:48:17 | 183.20 | 131.75 | 0.0509 | 0.0448 | 1.135 | 3.091 | 5.497 | 1.537 | 3.396 | 1618.7 | 452.5 | 0.487 | 0.388 |
| 18/06/2024 | 6:00:00 | 97.41 | 69.92 | 0.0271 | 0.0238 | 1.137 | 3.865 | 4.532 | 1.674 | 3.601 | 1258.7 | 464.9 | 0.616 | 0.499 |
| 19/06/2024 | 6:00:00 | 98.44 | 95.83 | 0.0273 | 0.0326 | 0.839 | 4.164 | 4.951 | 1.929 | 3.451 | 1435.0 | 559.0 | 0.584 | 0.437 |
| 27/06/2024 | 7:00:00 | 76.75 | 70.28 | 0.0213 | 0.0239 | 0.892 | 4.967 | 4.346 | 1.763 | 3.426 | 1268.3 | 514.7 | 0.638 | 0.495 |
| 28/06/2024 | 8:00:00 | 77.54 | 60.98 | 0.0215 | 0.0208 | 1.038 | 6.444 | 5.516 | 2.170 | 4.472 | 1233.5 | 485.2 | 0.721 | 0.509 |
| 05/07/2024 | 5:00:00 | 81.36 | 78.22 | 0.0226 | 0.0266 | 0.849 | 3.735 | 3.535 | 1.461 | 2.297 | 1539.4 | 636.0 | 0.565 | 0.408 |
| 09/07/2024 | 8:00:00 | 57.22 | 77.82 | 0.0159 | 0.0265 | 0.600 | 5.273 | 4.167 | 2.309 | 1.969 | 2116.4 | 1172.6 | 0.430 | 0.297 |
| 10/07/2024 | 6:00:00 | 56.71 | 119.99 | 0.0158 | 0.0408 | 0.386 | 5.066 | 4.037 | 2.201 | 0.848 | 4758.4 | 2594.7 | 0.249 | 0.132 |
| 11/07/2024 | 4:00:00 | 50.81 | 119.93 | 0.0141 | 0.0408 | 0.346 | 3.597 | 2.562 | 1.421 | 0.335 | 7644.5 | 4240.8 | 0.165 | 0.082 |
| 18/07/2024 | 6:00:00 | 38.84 | 77.56 | 0.0108 | 0.0264 | 0.409 | 3.593 | 1.975 | 1.089 | 0.108 | 18,359.1 | 10,122.9 | 0.046 | 0.034 |
| 22/07/2024 | 7:05:00 | 75.09 | 70.07 | 0.0209 | 0.0238 | 0.875 | 5.566 | 4.670 | 1.923 | 3.511 | 1329.9 | 547.7 | 0.660 | 0.472 |
| 23/07/2024 | 7:00:00 | 74.59 | 70.03 | 0.0207 | 0.0238 | 0.869 | 4.807 | 4.045 | 1.914 | 3.032 | 1334.0 | 631.2 | 0.581 | 0.471 |
| KPI | Instantaneous, % | Daily, % |
|---|---|---|
| MR | 1.12 | 0.0067 |
| RR | 0.68 | 0.0041 |
| Eth | 4.82 | 0.0266 |
| GOR | 4.84 | 0.0389 |
| SEC | 0.78 | 0.0047 |
| STC | 4.84 | 0.0268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picotti, G.; Simonetti, R.; Molinaroli, L.; Manzolini, G. Experimental Characterization and Modelling of a Humidification–Dehumidification (HDH) System Coupled with Photovoltaic/Thermal (PV/T) Modules. Energies 2025, 18, 5586. https://doi.org/10.3390/en18215586
Picotti G, Simonetti R, Molinaroli L, Manzolini G. Experimental Characterization and Modelling of a Humidification–Dehumidification (HDH) System Coupled with Photovoltaic/Thermal (PV/T) Modules. Energies. 2025; 18(21):5586. https://doi.org/10.3390/en18215586
Chicago/Turabian StylePicotti, Giovanni, Riccardo Simonetti, Luca Molinaroli, and Giampaolo Manzolini. 2025. "Experimental Characterization and Modelling of a Humidification–Dehumidification (HDH) System Coupled with Photovoltaic/Thermal (PV/T) Modules" Energies 18, no. 21: 5586. https://doi.org/10.3390/en18215586
APA StylePicotti, G., Simonetti, R., Molinaroli, L., & Manzolini, G. (2025). Experimental Characterization and Modelling of a Humidification–Dehumidification (HDH) System Coupled with Photovoltaic/Thermal (PV/T) Modules. Energies, 18(21), 5586. https://doi.org/10.3390/en18215586







