Study on CO2 Induced Gas Channeling in Tight Gas Reservoirs and Optimization of Injection Production Parameters
Abstract
1. Introduction
2. Model Construction and Numerical Methods
2.1. Geological Background and Modeling Domain
2.2. Governing Equations and Coupled Physical Fields
- Darcy Flow Governing Equation
- 2.
- Dilute Species Transport Equation
2.3. Boundary Conditions and Solution Method
2.4. Grid Partitioning and Independence Test
3. Simulation Schemes and Variable Design
3.1. Single-Factor Simulation Variables and Grouping Design
- Fracture parameter design: number, inclination, and permeability (Groups A/B/C)
- 2.
- Injection parameter design: constant-pressure injection (Group D)
- 3.
- Reservoir heterogeneity setting (Group E)
3.2. Multi-Factor Experimental Design
4. Results and Discussion
4.1. Single-Factor Simulation Results
- Effect of fracture number
- 2.
- Effect of fracture inclination
- 3.
- Effect of fracture width
- 4.
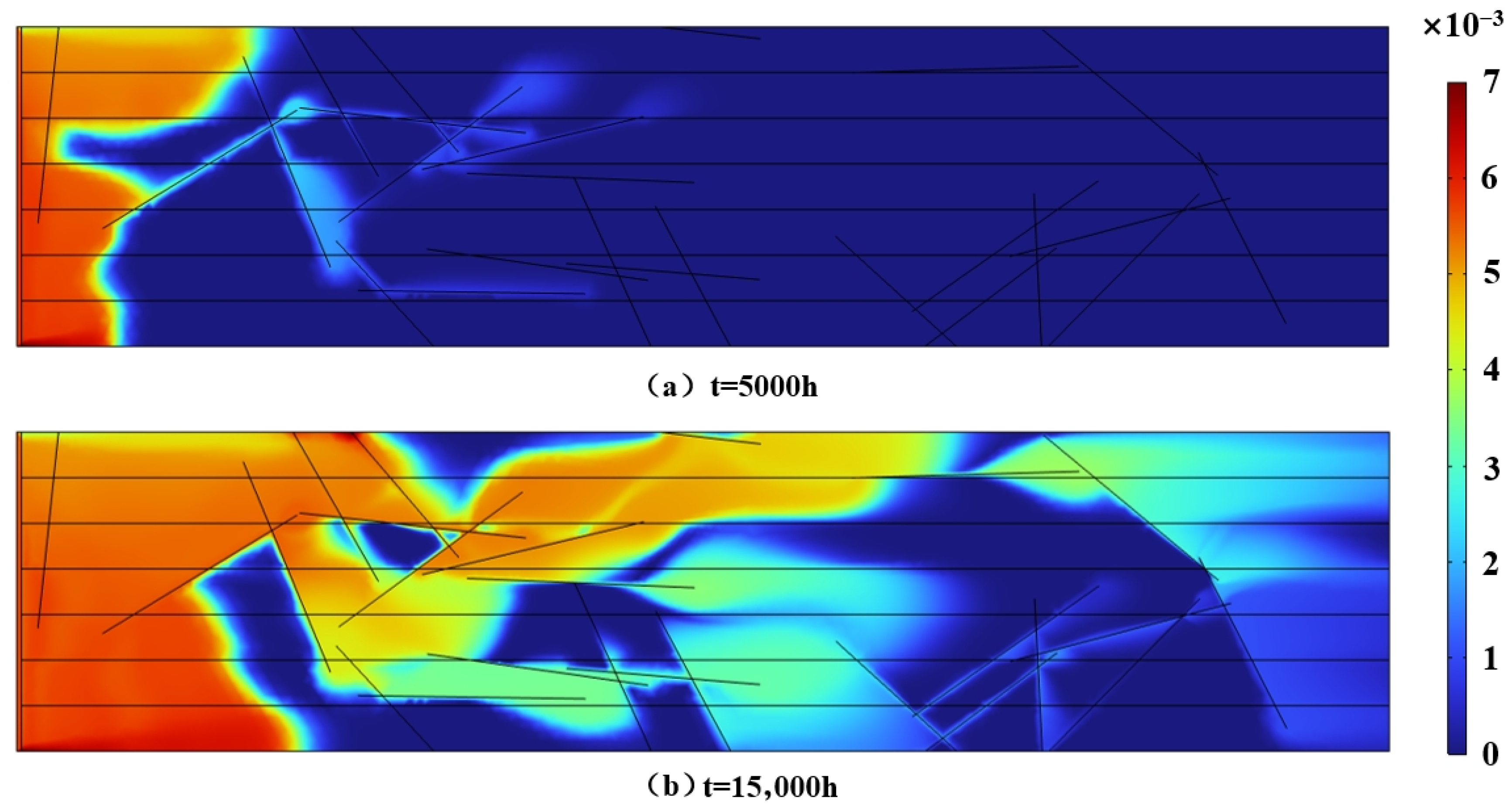
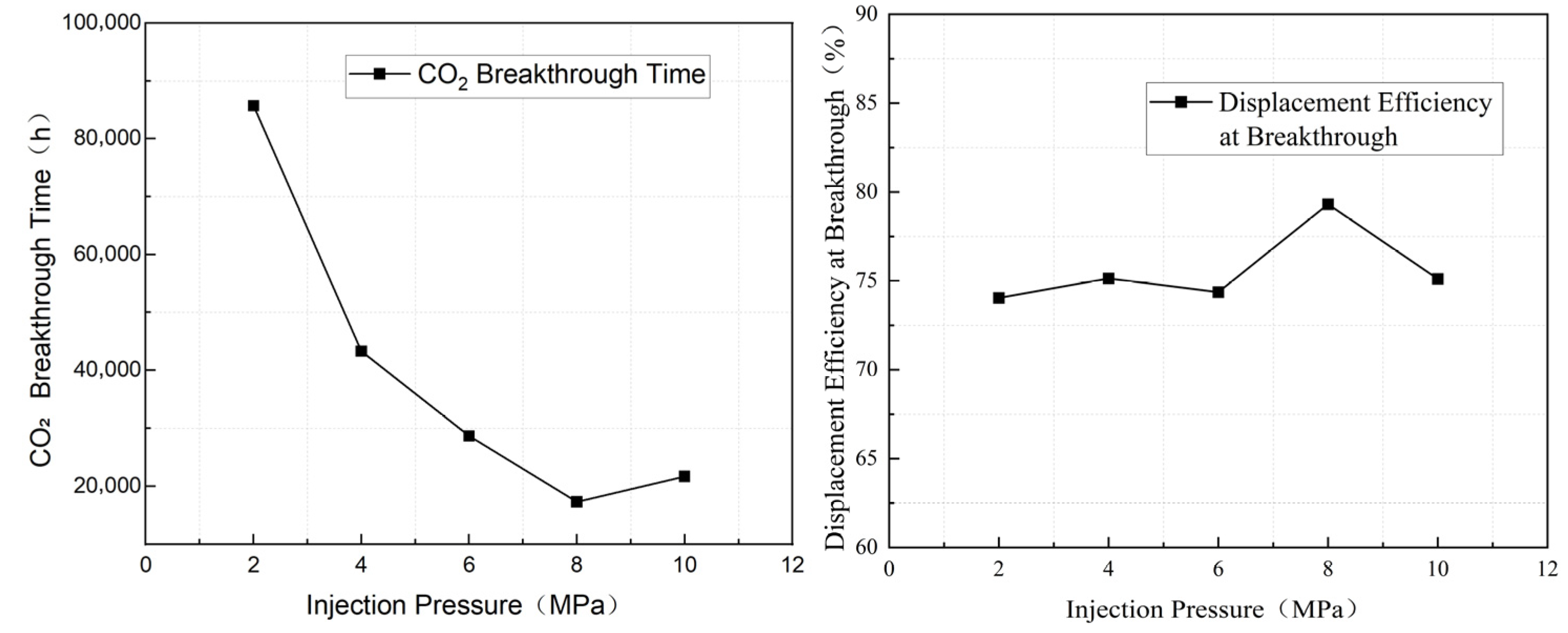
- Effect of injection pressure
- 5.
- Effect of permeability contrast
4.2. Response Surface Analysis Results
- Establishment of the second-order mathematical model
- 2.
- Validation and significance testing of the second-order model
- 3.
- Interaction analysis based on response surfaces
- Fracture number and fracture width
- 2.
- Fracture number and injection pressure
- 3.
- Fracture number and fracture inclination
- 4.
- Optimization and validation of experimental conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, X.; He, D.; Wei, Y.; Guo, J.; Jia, C. Enhanced gas recovery: Theory, technology, and prospects. Nat. Gas Ind. B 2023, 10, 393–405. [Google Scholar] [CrossRef]
- Sun, Y.; Zuo, L.; Li, X.; Liu, X. Enhancing shale gas recovery by carbon dioxide injection: A method of carbon capture, utilization and storage (CCUS). Process. Saf. Environ. Prot. 2023, 179, 484–492. [Google Scholar] [CrossRef]
- Fahandezhsaadi, M.; Amooie, M.A.; Hemmati-Sarapardeh, A.; Ayatollahi, S.; Schaffie, M.; Ranjbar, M. Laboratory evaluation of nitrogen injection for enhanced oil recovery: Effects of pressure and induced fractures. Fuel 2019, 253, 607–614. [Google Scholar] [CrossRef]
- Xiong, L.; Chen, D.; Yang, Y.; Zhang, L.; Li, S.; Wang, Q. Accumulation mechanism and enrichment model of deep tight sandstone gas in second member of Upper Triassic Xujiahe Formation, Xinchang structural belt, Sichuan Basin, SW China. Pet. Explor. Dev. 2025, 52, 907–920. [Google Scholar] [CrossRef]
- Mabuza, M.; Premlall, K.; Daramola, M.O. Modelling and thermodynamic properties of pure CO2 and flue gas sorption data on South African coals using Langmuir, Freundlich, Temkin, and extended Langmuir isotherm models. Int. J. Coal. Sci. Technol. 2022, 9, 45. [Google Scholar] [CrossRef]
- English, J.M.; English, K.L. An overview of carbon capture and storage and its potential role in the energy transition. First Break 2022, 40, 35–40. [Google Scholar] [CrossRef]
- Liu, J.; Xie, L.-Z.; He, B.; Zhao, P.; Ding, H.-Y. Performance of free gases during the recovery enhancement of shale gas by CO2 injection: A case study on the depleted Wufeng–Longmaxi shale in northeastern Sichuan Basin, China. Pet. Sci. 2021, 18, 530–545. [Google Scholar] [CrossRef]
- Rezk, M.G.; Adebayo, A.R. An insight into hydrogen and carbon dioxide displacement and trapping efficiencies in carbonate formations through NMR and core flooding. Int. J. Hydrogen Energy 2024, 86, 890–898. [Google Scholar] [CrossRef]
- Al-Hashami, A.; Ren, S.R.; Tohidi, B. CO2 Injection for enhanced gas recovery and geo-storage: Reservoir simulation and economics. In Proceedings of the SPE Europec/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005. [Google Scholar]
- Zhang, K.; Lau, H.C.; Chen, Z. Regional carbon capture and storage opportunities in Alberta, Canada. Fuel 2022, 322, 124224. [Google Scholar] [CrossRef]
- Fu, L.; Shao, Y.; Shao, M.; Zhu, T.; Li, X.; Yang, Z.; Zou, J.; Fan, M.; Liao, K. Application and research progress of CO2 stimulation technology in unconventional oil and gas reservoirs: A review and prospect. Energy Fuels 2023, 37, 19400–19418. [Google Scholar] [CrossRef]
- Cook, P.J. 11—The CO2CRC otway project in Australia. In Geological Storage of Carbon Dioxide (CO2); Gluyas, J., Mathias, S., Eds.; Woodhead Publishing: London, UK, 2013; pp. 251–277. [Google Scholar] [CrossRef]
- Thiez, P.L.; Mosditchian, G.; Torp, T.; Feron, P.; Ritsema, I.; Zweigel, P.; Lindeberg, E. An innovative European integrated project: Castor—CO2 from capture to storage. In Greenhouse Gas Control Technologies 7; Rubin, E.S., Keith, D.W., Gilboy, C.F., Wilson, M., Morris, T., Gale, J., Thambimuthu, K., Eds.; Elsevier Science Ltd.: Oxford, UK, 2005; pp. 2047–2050. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Yang, S.-L.; Bi, L.-F.; Gao, X.-Y.; Shen, B.; Hu, J.-T.; Luo, Y.; Zhao, Y.; Chen, H.; Li, J. A technical review of CO2 flooding sweep-characteristics research advance and sweep-extend technology. Pet. Sci. 2025, 22, 255–276. [Google Scholar] [CrossRef]
- van der Burgt, M.J.; Cantle, J.; Boutkan, V.K. Carbon dioxide disposal from coal-based IGCC’s in depleted gas fields. Energy Convers. Manag. 1992, 33, 603–610. [Google Scholar] [CrossRef]
- Patel, M.J.; May, E.F.; Johns, M.L. High-fidelity reservoir simulations of enhanced gas recovery with supercritical CO2. Energy 2016, 111, 548–559. [Google Scholar] [CrossRef]
- Tian, M.; Wu, Y.; Shi, Y.; Cao, G.; Sun, Y.; Li, M.; Wang, W.; Gao, L.; Wang, Z.; Li, Y. Experimental Investigation on Temperature-Resistant CO2 Foam Flooding in a Heterogenous Reservoir. Energies 2025, 18, 89. [Google Scholar] [CrossRef]
- Hasan, M.; Eliebid, M.; Mahmoud, M.; Elkatatny, S.; Shawabkeh, R. Enhanced gas recovery (EGR) methods and production enhancement techniques for shale & tight gas reservoirs. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar]
- Zhao, X.; Chen, Z.; Wang, B.; Liao, X.; Li, D.; Zhou, B. A Multi-medium and Multi-mechanism model for CO2 injection and storage in fractured shale gas reservoirs. Fuel 2023, 345, 128167. [Google Scholar] [CrossRef]
- Omari, A.; Wang, C.; Li, Y.; Xu, X. The progress of enhanced gas recovery (EGR) in shale gas reservoirs: A review of theory, experiments, and simulations. J. Pet. Sci. Eng. 2022, 213, 110461. [Google Scholar] [CrossRef]
- Wang, Z.; Kong, Y.; Li, W. Review on the development of China’s natural gas industry in the background of “carbon neutrality”. Nat. Gas Ind. B 2022, 9, 132–140. [Google Scholar] [CrossRef]
- Luo, F.; Xu, R.-N.; Jiang, P.-X. Numerical investigation of the influence of vertical permeability heterogeneity in stratified formation and of injection/production well perforation placement on CO2 geological storage with enhanced CH4 recovery. Appl. Energy 2013, 102, 1314–1323. [Google Scholar] [CrossRef]
- Li, Y.; Fan, A.; Yang, R.; Sun, Y.; Lenhardt, N. Braided deltas and diagenetic control on tight sandstone reservoirs: A case study on the Permian Lower Shihezi Formation in the southern Ordos Basin (central China). Sediment. Geol. 2022, 435, 106156. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, C.; Ouyang, S.; Luo, B.; Zhao, D.; Sun, W.; Awan, R.S.; Lu, Z.; Li, G.; Zang, Q. Investigation of pore-throat structure and fractal characteristics of tight sandstones using HPMI, CRMI, and NMR methods: A case study of the lower Shihezi Formation in the Sulige area, Ordos Basin. J. Pet. Sci. Eng. 2022, 210, 110053. [Google Scholar] [CrossRef]
- Yu, T.; Yin, Z. Integrated characterization of a tight sandstone gas reservoir: Member 8 Permian Shihezi Formation, Su49-01 Block, Sulige gas field, Ordos Basin, China. In Proceedings of the SPG/SEG 2016 International Geophysical Conference, Beijing, China, 20–22 April 2016. Global Meeting Abstracts. [Google Scholar] [CrossRef]
- Koohbor, B.; Colombano, S.; Harrouet, T.; Deparis, J.; Lion, F.; Davarzani, D.; Ataie-Ashtiani, B. The effects of water table fluctuation on LNAPL deposit in highly permeable porous media: A coupled numerical and experimental study. J. Contam. Hydrol. 2023, 256, 104183. [Google Scholar] [CrossRef]
- Huang, Y.; Pang, Z.; Kong, Y.; Watanabe, N. Assessment of the high-temperature aquifer thermal energy storage (HT-ATES) potential in naturally fractured geothermal reservoirs with a stochastic discrete fracture network model. J. Hydrol. 2021, 603, 127188. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, R.; Li, K.; Wang, Z.; Gu, K.; He, W. Performance analysis and design optimization of a novel Trombe wall system using CFD and response surface method. Energy 2025, 324, 136031. [Google Scholar] [CrossRef]
- Tiwari, S.; Kumar, A.; Gupta, N.; Tiwari, G.; Sharma, P. Hydrogen storage systems performance and design parameters using response surface methods and sensitivity analysis. Renew. Sustain. Energy Rev. 2024, 202, 114628. [Google Scholar] [CrossRef]
- Assareh, M.; Yavari, P.; Jamil, M.; Rafiei, B.; Assareh, E. Thermodynamic analysis of a multiple energy production system based on geothermal energy for commissioning in Canada and optimization by response surface method (RSM). Energy 2024, 302, 131669. [Google Scholar] [CrossRef]
- Rahimi-Esbo, M.; Rezaei Firouzjaee, M.; Bagherian Farahabadi, H.; Alizadeh, E. Performance investigation of a standalone renewable energy system using response surface methodology (RSM): 4E analysis and multi-objective optimization. Energy Convers. Manag. 2024, 299, 117752. [Google Scholar] [CrossRef]
- Li, F.; Cai, X.; Zhang, Y.; Guo, X.; Jiang, M. Mechanical and permeability analysis and optimization of recycled aggregate pervious concrete based on response surface method. JRM 2022, 11, 1745–1762. [Google Scholar] [CrossRef]
- Sun, Q.; Gupta, R.; Zhu, Z.; Sharma, A.; Qiang, S. A new mathematical model for elastic modulus prediction in mortar and concrete. J. Build. Eng. 2025, 100, 111761. [Google Scholar] [CrossRef]
- Hagglund, C.R.; Duranceau, S.J. Application of mathematical models to predict permeate water quality in pilot- and full-scale reverse osmosis processes. J. Water Process Eng. 2025, 76, 108167. [Google Scholar] [CrossRef]
- Deng, L.; Han, D.; Zhang, L.; Wang, S. Bridge influence surface identification using a physical informed neural network and its application on load transverse localisation. Eng. Struct. 2025, 339, 120618. [Google Scholar] [CrossRef]
- Seo, J.; Linzell, D.G. Use of response surface metamodels to generate system level fragilities for existing curved steel bridges. Eng. Struct. 2013, 52, 642–653. [Google Scholar] [CrossRef]
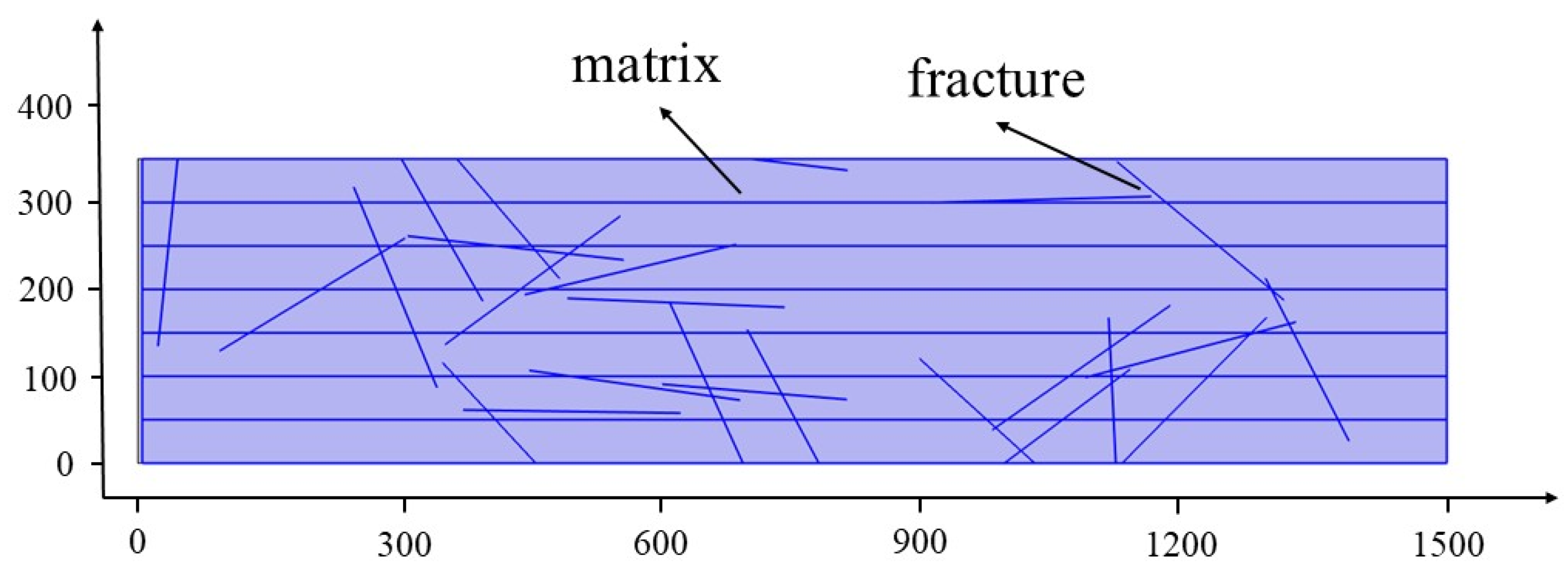
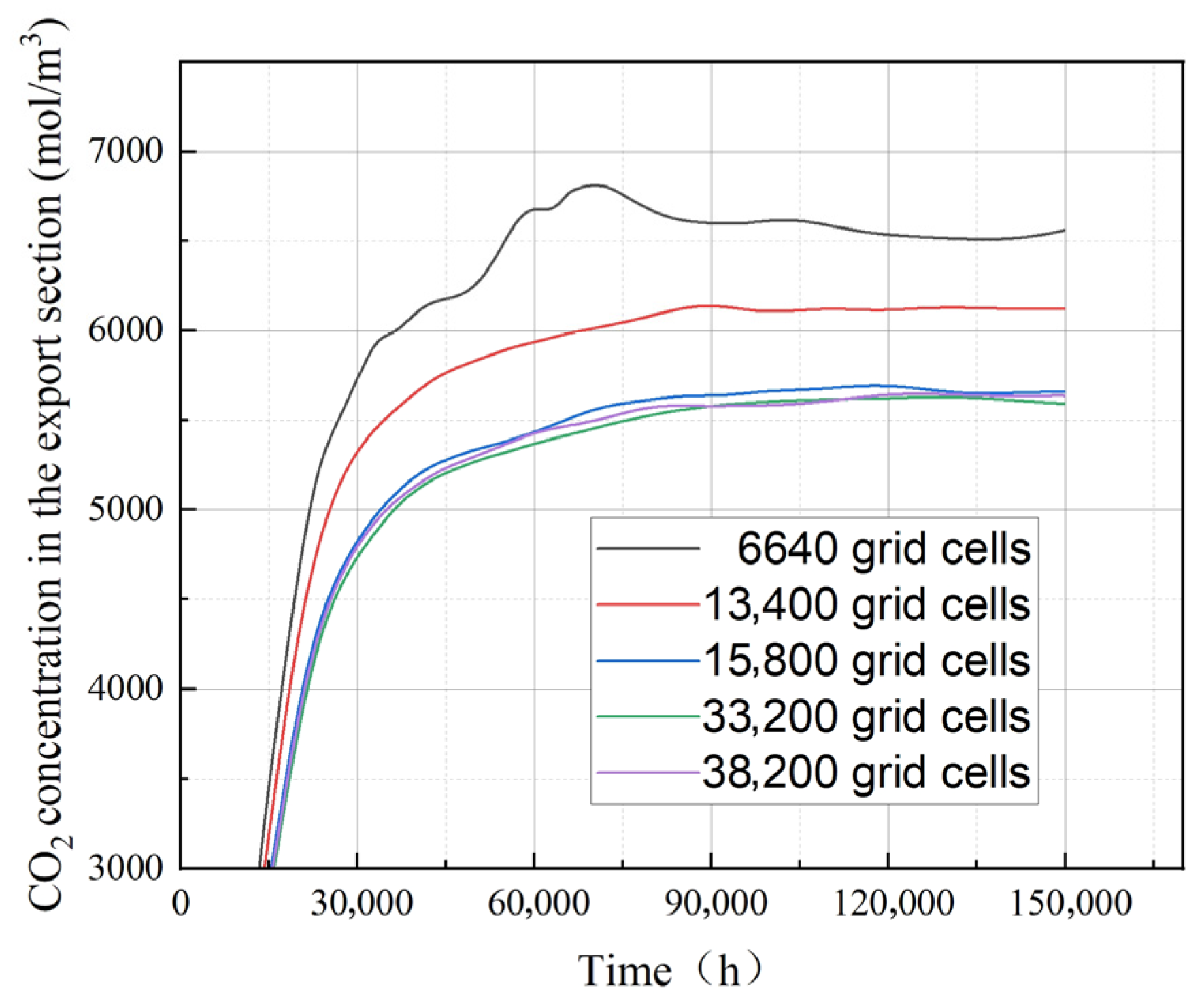


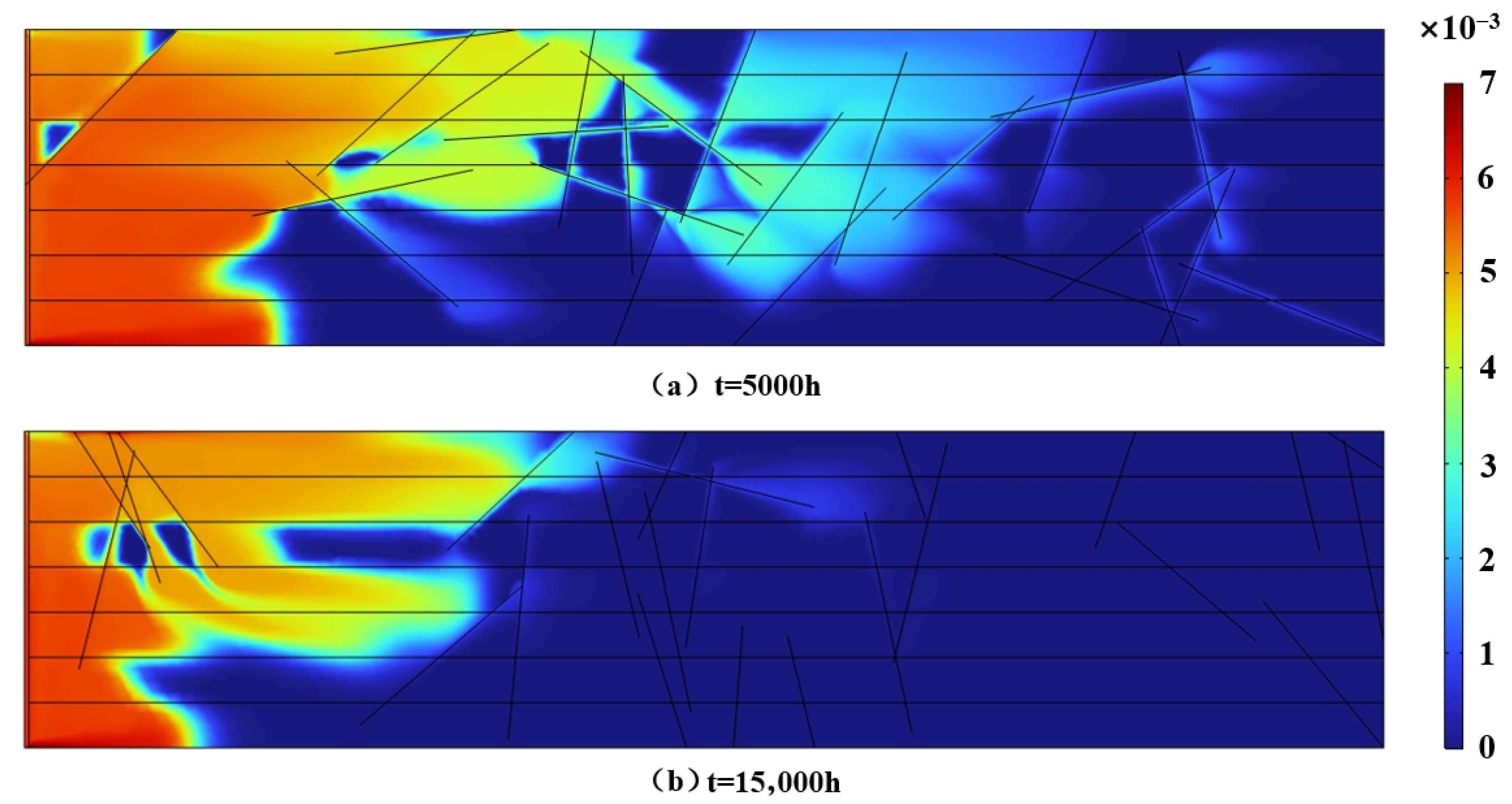

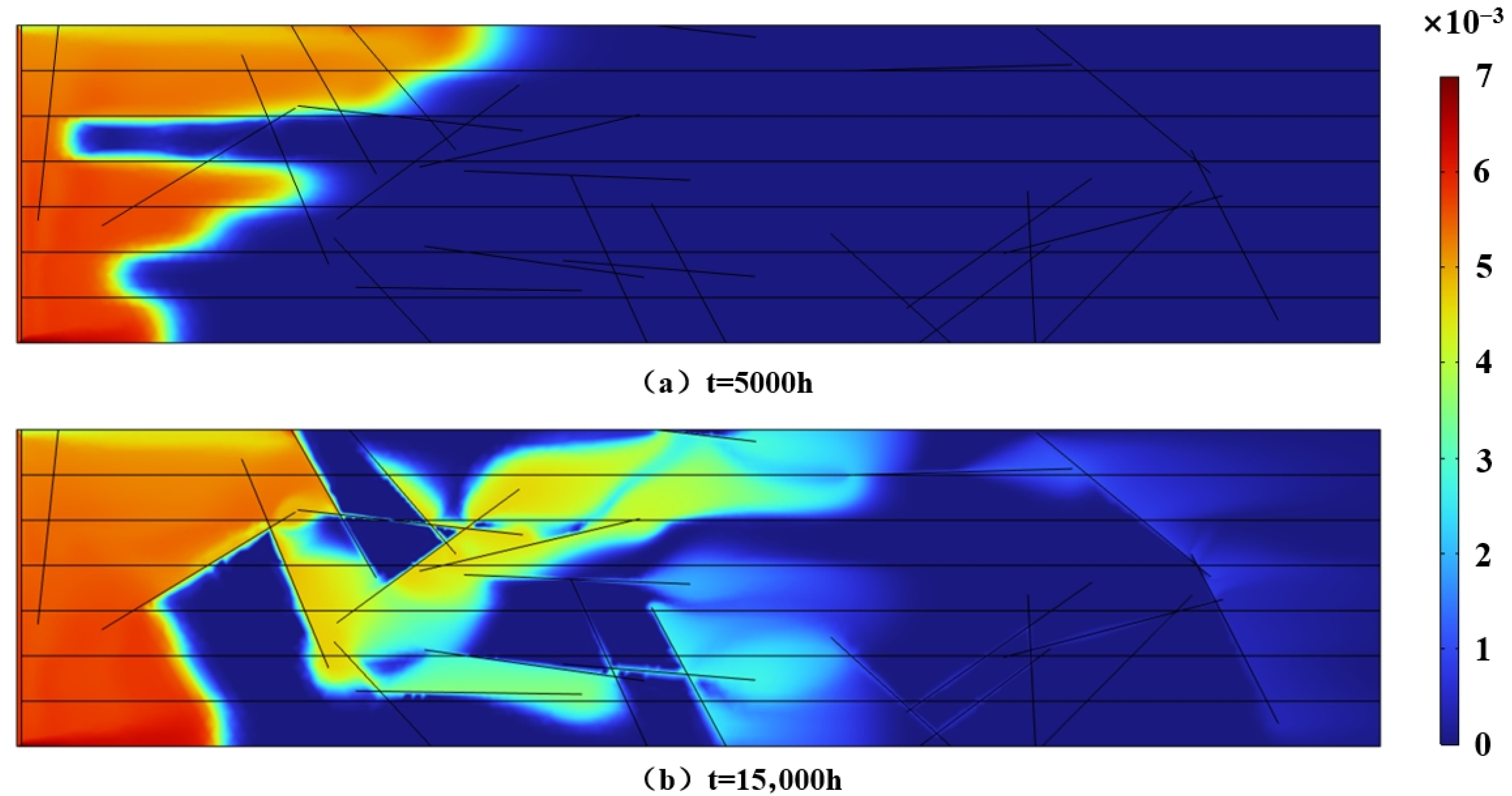








| Category | Controlling Factor | Parameter Levels | Control Approach |
|---|---|---|---|
| A | Number of fractures | 5, 15, 25, 50, 75 | Control fracture number with fixed distribution |
| B | Fracture inclination (°) | 0, 30, 60, 90, 120 | Uniform distribution |
| C | Fracture permeability (width) | 5, 1, 0.5, 0.1, 0.05 mm | Control fracture conductivity |
| D | Injection–production pressure differential (MPa) | 2, 4, 6, 8, 10 | Constant-pressure injection |
| E | Permeability contrast (mD) | 0.7, 3.0, 4.5, 7.7, 9.9 | Control layered permeability configuration |
| Level | Factors | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| −1 | 5 | 0 | 0.2525 | 2 | 0.7 |
| 0 | 40 | 60 | 0.0005 | 6 | 5.3 |
| 1 | 75 | 120 | 0.5 | 10 | 9.9 |
| Category | A | B | C | D | E | Breakthrough Time |
|---|---|---|---|---|---|---|
| 1 | 40 | 60 | 0.002525 | 2 | 9.9 | 21,401 |
| 2 | 75 | 0 | 0.002525 | 6 | 5.3 | 15,001 |
| 3 | 5 | 60 | 5 × 10−5 | 6 | 5.3 | 13,701 |
| 4 | 40 | 60 | 0.002525 | 10 | 9.9 | 3201 |
| 5 | 40 | 60 | 0.002525 | 6 | 5.3 | 6601 |
| 6 | 5 | 60 | 0.002525 | 10 | 5.3 | 13,001 |
| 7 | 40 | 60 | 5 × 10−5 | 2 | 5.3 | 40,801 |
| 8 | 40 | 60 | 0.005 | 10 | 5.3 | 4001 |
| 9 | 5 | 60 | 0.002525 | 6 | 9.9 | 11,001 |
| 10 | 40 | 60 | 0.005 | 6 | 0.7 | 23,101 |
| 11 | 40 | 0 | 5 × 10−5 | 6 | 5.3 | 13,501 |
| 12 | 75 | 60 | 5 × 10−5 | 6 | 5.3 | 13,401 |
| 13 | 40 | 60 | 5 × 10−5 | 6 | 0.7 | 20,901 |
| 14 | 5 | 120 | 0.002525 | 6 | 5.3 | 21,301 |
| 15 | 40 | 60 | 0.002525 | 6 | 5.3 | 21,001 |
| 16 | 40 | 120 | 0.005 | 6 | 5.3 | 9901 |
| 17 | 40 | 60 | 0.002525 | 10 | 0.7 | 5601 |
| 18 | 75 | 60 | 0.002525 | 6 | 0.7 | 2001 |
| 19 | 40 | 120 | 0.002525 | 2 | 5.3 | 27,401 |
| 20 | 5 | 0 | 0.002525 | 6 | 5.3 | 13,601 |
| 21 | 40 | 120 | 5 × 10−5 | 6 | 5.3 | 13,601 |
| 22 | 40 | 60 | 0.002525 | 6 | 5.3 | 6501 |
| 23 | 40 | 60 | 0.005 | 6 | 9.9 | 5701 |
| 24 | 40 | 60 | 5 × 10−5 | 6 | 9.9 | 6901 |
| 25 | 40 | 0 | 0.002525 | 6 | 0.7 | 20,501 |
| 26 | 40 | 0 | 0.002525 | 2 | 5.3 | 37,601 |
| 27 | 40 | 60 | 0.005 | 2 | 5.3 | 19,901 |
| 28 | 40 | 60 | 0.002525 | 6 | 5.3 | 6501 |
| 29 | 5 | 60 | 0.005 | 6 | 5.3 | 21,701 |
| 30 | 40 | 60 | 0.002525 | 6 | 5.3 | 6501 |
| 31 | 40 | 120 | 0.002525 | 10 | 5.3 | 4901 |
| 32 | 75 | 60 | 0.002525 | 2 | 5.3 | 2101 |
| 33 | 40 | 60 | 0.002525 | 6 | 5.3 | 6501 |
| 34 | 40 | 60 | 0.002525 | 2 | 0.7 | 28,001 |
| 35 | 40 | 60 | 5 × 10−5 | 10 | 5.3 | 8101 |
| 36 | 40 | 120 | 0.002525 | 6 | 9.9 | 2101 |
| 37 | 40 | 0 | 0.002525 | 10 | 5.3 | 7501 |
| 38 | 5 | 60 | 0.002525 | 2 | 5.3 | 48,701 |
| 39 | 5 | 60 | 0.002525 | 6 | 0.7 | 17,301 |
| 40 | 40 | 120 | 0.002525 | 6 | 0.7 | 16,401 |
| 41 | 40 | 0 | 0.005 | 6 | 5.3 | 12,601 |
| 42 | 75 | 60 | 0.005 | 6 | 5.3 | 1001 |
| 43 | 75 | 120 | 0.002525 | 6 | 5.3 | 501 |
| 44 | 40 | 0 | 0.002525 | 6 | 9.9 | 6501 |
| 45 | 75 | 60 | 0.002525 | 6 | 9.9 | 201 |
| 46 | 75 | 60 | 0.002525 | 10 | 5.3 | 301 |
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p | Significance |
|---|---|---|---|---|---|---|
| Model | 4.594 × 109 | 20 | 2.297 × 108 | 7.52 | <0.0001 | significant |
| A | 9.891 × 108 | 1 | 9.891 × 108 | 32.40 | <0.0001 | |
| B | 6.806 × 107 | 1 | 6.806 × 107 | 2.23 | 0.1479 | |
| C | 2.009 × 109 | 1 | 2.009 × 109 | 65.81 | <0.0001 | |
| D | 5.891 × 107 | 1 | 5.891 × 107 | 1.93 | 0.1771 | |
| E | 3.686 × 108 | 1 | 3.686 × 108 | 12.07 | 0.0019 | |
| AB | 1.040 × 108 | 1 | 1.040 × 108 | 3.41 | 0.0768 | |
| AC | 2.873 × 108 | 1 | 2.873 × 108 | 9.41 | 0.0051 | |
| AD | 1.232 × 108 | 1 | 1.232 × 108 | 4.04 | 0.0555 | |
| AE | 5.063 × 106 | 1 | 5.063 × 106 | 0.1658 | 0.6873 | |
| BC | 7.056 × 107 | 1 | 7.056 × 107 | 2.31 | 0.1410 | |
| BD | 1.960 × 106 | 1 | 1.960 × 106 | 0.0642 | 0.8021 | |
| BE | 2.890 × 106 | 1 | 2.890 × 106 | 0.0947 | 0.7609 | |
| CD | 1.444 × 107 | 1 | 1.444 × 107 | 0.4729 | 0.4980 | |
| CE | 4.410 × 106 | 1 | 4.410 × 106 | 0.1444 | 0.7071 | |
| DE | 22,500.00 | 1 | 22,500.00 | 0.0007 | 0.9786 | |
| A2 | 3.713 × 105 | 1 | 3.713 × 105 | 0.0122 | 0.9131 | |
| B2 | 8.063 × 107 | 1 | 8.063 × 107 | 2.64 | 0.1167 | |
| C2 | 3.896 × 108 | 1 | 3.896 × 108 | 12.76 | 0.0015 | |
| D2 | 5.666 × 107 | 1 | 5.666 × 107 | 1.86 | 0.1853 | |
| E2 | 1.409 × 105 | 1 | 1.409 × 105 | 0.0046 | 0.9464 | |
| Residual | 7.633 × 108 | 25 | 3.053 × 107 | |||
| Lack of Fit | 5.886 × 108 | 20 | 2.943 × 107 | 0.8421 | 0.6497 | not significant |
| Pure Error | 1.747 × 108 | 5 | 3.495 × 107 | |||
| Cor Total | 5.358 × 109 | 45 |
| Item | Fracture Density (Number) | Injection Pressure (MPa) | Fracture Inclination (°) | Fracture Width (m) | Permeability Contrast | Breakthrough Time (h) | Sweep Efficiency (%) |
|---|---|---|---|---|---|---|---|
| Optimized parameters | 11.8 | 2.28 | 105.4 | 0.00458 | 0.97 | 46,984 | 87.68 |
| Simulation validation | 12 | 2.3 | 105.4 | 0.00458 | 1 | 42,990 | 84.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, H.; Cheng, G.; Guo, J.; Wang, R.; Ning, B.; Wang, X.; Yuan, H.; Liu, H. Study on CO2 Induced Gas Channeling in Tight Gas Reservoirs and Optimization of Injection Production Parameters. Energies 2025, 18, 5584. https://doi.org/10.3390/en18215584
Yan H, Cheng G, Guo J, Wang R, Ning B, Wang X, Yuan H, Liu H. Study on CO2 Induced Gas Channeling in Tight Gas Reservoirs and Optimization of Injection Production Parameters. Energies. 2025; 18(21):5584. https://doi.org/10.3390/en18215584
Chicago/Turabian StyleYan, Haijun, Gang Cheng, Jianlin Guo, Runxi Wang, Bo Ning, Xinglong Wang, He Yuan, and Huaxun Liu. 2025. "Study on CO2 Induced Gas Channeling in Tight Gas Reservoirs and Optimization of Injection Production Parameters" Energies 18, no. 21: 5584. https://doi.org/10.3390/en18215584
APA StyleYan, H., Cheng, G., Guo, J., Wang, R., Ning, B., Wang, X., Yuan, H., & Liu, H. (2025). Study on CO2 Induced Gas Channeling in Tight Gas Reservoirs and Optimization of Injection Production Parameters. Energies, 18(21), 5584. https://doi.org/10.3390/en18215584






