Harmonic Mitigation and Energy Savings in 13.2 kV Distribution Feeders via P–Q-Based Shunt Active Filters and Luminaire Retrofit

Abstract

This article designs and validates a P-Q-based shunt active power filter (SAPF) to mitigate voltage harmonics in EERSA’s 13.2 kV feeder 1500080T03. A CYMDIST feeder model, calibrated with field measurements, reveals worst-case voltage THD up to 9.48% due to legacy high-pressure sodium (HPS) street lighting. Co-simulation with a MATLAB/Simulink R2024b, controller guides the sizing of a 150 kVA SAPF at Substation 8. Simulations reduce peak THD at a representative node from 9.48% to 1.51%; replacing HPS with LEDs further improves efficiency while lowering distortion. The retrofit complies with IEEE Std 519-2022, enhances supply reliability, and yields an internal rate of return above 17%, indicating a technically and financially attractive solution for Latin American distribution networks.

1. Introduction

In today’s modern era of electrification, Electric Power Systems (EPS) are essential for supporting the functioning of the authors’ society. However, a significant drawback is the presence of harmonics in EPS, which lead to various problems affecting reliability, safety, and efficiency [1,2]. Every phase of any process related to electrical energy must remain continuously efficient [3].

Starting with generation at power plants, energy is transmitted over long distances via transmission lines and ultimately delivered to consumption points. The final distribution stage is especially critical due to its direct relationship with energy demand [4].

The electrical sector currently faces the challenge of reducing costs while delivering efficient, high-quality power. Distribution companies must find solutions to high expenses associated with extending transmission networks and both technical and non-technical losses in power systems. Investments in financial, technical, and human resources are essential to enhance system reliability. This includes integrating special loads and adopting modern technologies such as microgrids, electric vehicles, and distributed generation [5,6].

Conducting thorough studies and effectively managing these new technologies is vital to optimize resources and bolster reliability—thus avoiding penalties for distribution companies and providing more dependable service to end users [3].

According to the Ecuadorian Institute of Statistics and Census (INEC), 31.7% of the population in Ecuador still lacks access to electricity. This situation is due to remote areas being far from conventional generation facilities [7]. Extending the main grid to these distant regions and adapting it to existing generation infrastructure is both costly and challenging. In this context, distributed generation becomes indispensable for providing solutions in underserved areas—promoting economic development, improving quality of life, and fostering socioeconomic growth in these communities. The implementation and adherence to these standards are critical to ensure electrical systems operate safely and efficiently. By keeping voltage, harmonic distortion, sags, flicker, and imbalance within prescribed limits, equipment damage is minimized and a stable, reliable power supply is maintained. Utilities and system designers must incorporate these limits during planning, design, and operation, and perform regular audits and continuous monitoring. Deploying power quality meters allows early detection and correction of deviations, ultimately improving system reliability and efficiency.

Table 1. Power quality limits by standard.

Standard	Parameter	Limit
IEEE Std 519-2022 [8]	Total harmonic distortion (THD)	≤5% (systems $\le 69$ kV); individual harmonics $\le 3\%$
IEC 61000-4-30	Voltage variations (sags/dips)	Depth and duration per event class (A, S, B)
IEC 61000-4-30	Flicker	Short-term flicker index $P_{\mathrm{st}}\le 1.0$
ARCERNNR 002/20	Voltage magnitude	$\pm 10\%$ of nominal voltage
ARCERNNR 002/20	Voltage harmonic distortion	THD $\le 8\%$; individual harmonics $\le 3\%$
ARCERNNR 002/20	Voltage unbalance	≤2%

summarizes the adopted power quality limits used throughout the analysis.

The scientific literature contains numerous articles addressing the problem of harmonics in electrical systems and offering partial solutions. These studies explore a range of approaches, from passive filters to advanced active power control techniques. Below, we summarize the most relevant works in this field, highlighting their contributions, limitations, and how they set the stage for the present investigation.

• Mudaheranwa et al. [9] investigated harmonic reduction in power systems using an active power filter (SAPF). They employed MATLAB/Simulink to simulate a filter that injects an inverse waveform of the harmonic component into a distorted signal, reducing its harmonic content. Their results showed a dramatic decrease in source current Total Harmonic Distortion (THD) from 19.5% to 0%, thereby meeting the IEEE Std 519-1992 standard.
• Atuchukwu et al. [10] focused on reducing harmonics in power lines by implementing a Finite Impulse Response (FIR) filter. They modeled a system in MATLAB/Simulink to generate compensation signals and switching pulses for an active filter. Their findings demonstrated that THD dropped from 17.77% to 0.87%, and the system’s current, voltage, and power factor improved by 95%.
• Guest et al. [11] implemented active filters in the control of converters connected to Type-IV offshore wind turbines to mitigate voltage-harmonic amplification. By applying the “extra element theorem” to tune the active filters and determine stability margins, they successfully suppressed both converter- and grid-generated harmonics. Their results confirmed that harmonic levels remained below planned thresholds in a 270 MW wind farm.
• Zeleničić et al. [12] targeted current-harmonic reduction in data center power systems using single-phase shunt active power filters (SAPF). They combined active components (IGBT or MOSFET) with passive elements (R, L, and C) and conducted two simulations: one filtering only current harmonics and another also compensating reactive current. Using a Voltage Source Inverter (VSI) and an LCL filter for switching frequency attenuation, they demonstrated that SAPFs significantly improved power quality by reducing both THD and current ripple.
• Cazacu et al. [13] aimed to mitigate voltage and current harmonics in a nonlinear industrial load by installing a 300 A active harmonic filter (AHF) in parallel with the load on the low-voltage side. Their detailed analysis of energy quality parameters before and after AHF installation showed that harmonics were kept within regulatory limits, improving the facility’s power quality.
• Constantinescu et al. [14] studied how DC-link voltage in active power filters affects harmonic compensation. Through MATLAB/Simulink simulations, they adjusted the filter’s DC-link voltage and observed its impact on current THD reduction. Their results revealed that proper DC-link voltage management is crucial for optimizing filter performance in systems with nonlinear loads.
• Madhubabu et al. [15] investigated the use of series active power filters (SAPF) to improve energy quality in distribution lines. By injecting compensating voltage to counteract distortions (e.g., voltage drops and flicker), they showed that SAPFs greatly reduce THD in low- and medium-voltage networks, complying with established power quality standards.
• Tupiza et al. [16] proposed reducing THD in low-voltage distribution networks using a Unified Active Power Filter (UAPF) powered by photovoltaic generation. Their MATLAB/Simulink model placed a nonlinear load at bus 7 of the IEEE 13-bus system and used the UAPF to cut both current and voltage harmonics. They achieved THD reductions to 6% (current) and 3% (voltage), meeting ARCERNNR-017/2020 and IEEE 1159 standards.
• Kaiwart [17] presented a Simulink model of a shunt active power filter (SAPF) with a PI controller to regulate the DC-link capacitor voltage. The results confirmed that SAPF implementation significantly improved power quality by reducing harmonics to levels compliant with IEEE standards.
• Waheed et al. [18] explored hybrid power filters—combining passive series filters with active filters—for harmonic reduction in the IEEE 3-bus system. Their simulations under various operating conditions showed that the hybrid filter lowered THD from 29.85% to 0.78%, greatly enhancing system performance.

From these studies, it is evident that harmonic mitigation techniques range from passive and active filters to hybrid combinations. While passive filters offer simplicity, they lack flexibility under variable load conditions. Active filters provide adaptive compensation but at a higher cost. Hybrid filters combine advantages of both but are more complex to implement and maintain.

In contrast, this investigation proposes designing an active power filter (SAPF) to improve energy quality in EERSA’s distribution network. CYMDIST is employed to develop detailed feeder models that precisely identify the root causes of power quality issues. CYMDIST’s built-in modules for distribution system analysis enable comprehensive data evaluation, studies, and simulations. Our goal is to reduce harmonics in compliance with Regulation No. ARCERNNR-002-20. This approach not only aims to enhance power supply quality but also provides targeted corrective solutions based on a thorough, contextual analysis of the distribution system.

2. Methodology

Clarification. The 150 kVA distribution transformer installed at Substation 8 is owned by the electric utility (EERSA). This project does not involve replacement of utility-owned assets; the work focuses on analysis, simulation, and the sizing/validation of the shunt active power filter.

The case study focuses on feeder 1500080T03, an overhead radial circuit with a nominal line-to-line voltage of 13.2 kV, originating at Substation 8 in the city of Riobamba. The feeder spans 7.6 km and supplies a mixed load of residential, commercial, and municipal customers. Five measurement nodes—coded MTA_S_298959, MTA_S_299878, MTA_S_331576, MTA_S_61155, and MTA_S_87877—were selected because they host clusters of 70 W HPS street-lighting luminaires driven by magnetic ballasts. Table 1 summarizes key electrical parameters derived from SCADA data for the peak loading hour (19:00 LT) in the dry season.

The complete workflow is summarized in

Table 2. Step-by-step workflow for harmonic assessment and active filter design.

Step	Description	Intermediate Output
1	Field data collection. Create both general and lighting-specific single-line diagrams; measure THD of LED and HPS luminaires; record nominal voltage, load ratings and transformer data.	Database of unifilar diagrams, LED/HPS THD, voltage levels and loading parameters.
2	CYME harmonic load flow. Import diagrams and parameters into CYME; run harmonic load-flow module to compute per-phase THD and nodal voltages.	CSV export with THD_phase1, THD_phase2, THD_phase3 and voltage profiles.
3	Data preparation for MATLAB. Select critical-node THD; define simulation parameters: nominal voltage, 60 Hz fundamental, measured THD and sampling time $T_s$.	MATLAB data structure (vectors and tables).
4	Active Power Filter (SAPF) design. Implement P–Q theory filter in Simulink; use initial THD to size coupling reactor and inverter; tune PLL and hysteresis loops.	Final FAP parameters (coupling inductance, nominal current, controller gains).
5	Comparative simulation. Run baseline vs. FAP scenarios; generate compensated voltage, residual THD and current waveforms.	Plots of $v_{\mathrm{out}}\left(t\right)$, %THD residual and current waveforms.
6	Results evaluation. Compute THD reduction per phase; verify compliance with IEEE Std 519-2022; compile techno-economic metrics.	Final report with harmonic reduction, loss savings and IRR.

.

This methodology ensures a fully traceable chain from in situ harmonic measurement through network simulation to active filter design and validation, suitable for replication in other medium-voltage distribution feeders. Figure 1 shows the feeder layout and the simplified single-line diagram used as context for modeling.

The single-line diagram provided by EERSA was digitized in CYMDIST 8.0. Conductor series impedances were obtained from geometry with Carson’s correction; transformers used IEEE C57.12 equivalent circuits. Capacitor banks and voltage regulators were modeled with control curves disabled to isolate harmonic interactions. Each street-lighting branch was represented as a lumped harmonic current source following IEC 61000-3-2 Class C limits, validated against bench-top analyzers.

The measurements and data presented here were gathered for both LED and HPS luminaires.

Table 3. Nominal power and luminous flux of LED and HPS luminaires.

Type	Nominal Power (W)	Luminous Flux (lm)
LED	150	17,121.21
HPS	400	42,433.82

summarizes their nominal power ratings and luminous flux.

Co-simulation was orchestrated by exchanging phasor quantities between CYMDIST and MATLAB/Simulink at each fundamental cycle. The interface exploited the open-data DLL API of CYME, allowing the inverter to respond to unbalanced harmonic voltages produced by the network. Simulations were executed for three lighting scenarios—baseline (HPS), LED retrofit, and LED + SAPF—and for low-, medium-, and high-load snapshots defined by daily load curves. Key output metrics included per-node THD, individual harmonic voltage distortion (VHD) factors, line losses, and SAPF capacitor ripple.

Table 4. Harmonic voltage distortion (IHD %) at 3rd, 5th, and 7th Harmonics for HPS luminaires.

Node	3rd Harmonic (180 Hz)			5th Harmonic (300 Hz)			7th Harmonic (420 Hz)
	5 Lamps	10 Lamps	15 Lamps	5 Lamps	10 Lamps	15 Lamps	5 Lamps	10 Lamps	15 Lamps
MTA_S_298959	1.57	3.14	4.71	0.46	0.93	1.39	0.16	0.32	0.48
MTA_S_87877	1.69	3.27	4.91	0.50	0.96	1.44	0.16	0.31	0.46
MTA_S_299878	2.99	5.97	8.97	1.00	2.01	3.01	0.34	0.68	1.01
MTA_S_331576	3.06	6.12	9.18	1.03	2.07	3.10	0.35	0.71	1.06
MTA_S_61155	3.17	6.33	9.50	1.07	2.14	3.21	0.36	0.73	1.09

Author’s field measurements. The 3% limit applies per IEEE/IEC for systems $\le 69$ kV.

shows the percent voltage distortion at the third harmonic (180 Hz) for five field nodes, each tested with 5, 10, and 15 HPS luminaires. At node MTA_S_298959, the distortion remains below the 3% limit when only 5 lamps are installed, but rises to 3.14% with 10 lamps and 4.71% with 15 lamps. Similar behavior is observed at nodes MTA_S_87877 and MTA_S_299878, which both stay under 3% at five lamps but exceed the standard for larger installations. Nodes MTA_S_331576 and MTA_S_61155 exceed the 3% threshold in all three configurations; these two nodes are the farthest from the main feeder and thus experience the highest harmonic distortion.

Table 5. 3rd, 5th and 7th harmonic voltage distortion (IHD %) for LED luminaires.

Node	3rd Harmonic (180 Hz)			5th Harmonic (300 Hz)			7th Harmonic (420 Hz)
	5 Lamps	10 Lamps	15 Lamps	5 Lamps	10 Lamps	15 Lamps	5 Lamps	10 Lamps	15 Lamps
MTA_S_298959	1.25	2.49	3.74	0.58	1.16	1.74	0.23	0.46	0.69
MTA_S_87877	1.30	2.60	3.90	0.60	1.20	1.80	0.22	0.45	0.67
MTA_S_299878	2.37	4.74	7.12	1.25	2.51	3.76	0.49	0.98	1.47
MTA_S_331576	2.43	4.86	7.29	1.29	2.58	3.87	0.51	1.02	1.54
MTA_S_61155	2.51	5.03	7.55	1.34	2.67	4.01	0.53	1.05	1.58

Author’s measurements. The 3% distortion limit applies per IEEE/IEC for systems $\le 69$ kV.

presents the percent voltage distortion (IHD %) at the third (180 Hz), fifth (300 Hz) and seventh (420 Hz) harmonics for five field nodes, each tested with 5, 10, and 15 LED luminaires, but only the 3rd–7th harmonics are summarized here for brevity.

Table 6. Total THD (%) for HPS luminaires.

Node ID	5 Lamps	10 Lamps	15 Lamps
MTA_S_298959	1.78	3.56	4.34
MTA_S_299878	3.44	5.80	9.55
MTA_S_331576	3.53	6.27	9.61
MTA_S_61155	3.65	6.45	9.78
MTA_S_87877	1.92	7.29	6.52

Author’s measurements. IEEE Std 519-2022 limit: THD ≤ 5%.

shows the overall %THD measured at five field nodes for 5, 10, and 15 HPS lamps. All 5-lamp cases meet the 5% limit; several nodes exceed the limit at 10 and 15 lamps, with a worst-case THD of 9.78% (MTA_S_61155, 15 lamps).

Table 7. Total THD (%) for LED luminaires.

Node ID	5 Lamps	10 Lamps	15 Lamps
MTA_S_298959	1.58	3.15	4.72
MTA_S_299878	1.64	3.27	4.91
MTA_S_331576	3.08	5.76	8.55
MTA_S_61155	3.17	5.78	8.60
MTA_S_87877	3.27	5.55	8.62

Author’s measurements. IEEE Std 519-2022 limit: THD ≤ 5%.

presents the overall %THD for the same five nodes with LED lamps. Performance is generally better than HPS at low counts; however, some far-end nodes still exceed 5% at 10 and 15 lamps, reaching up to 8.62% (MTA_S_87877).

The P–Q theory control algorithm is implemented as a cascade of five analytic blocks. Each block performs a specific transformation or control action in the shunt active filter [19,20]:

• Clarke Transformation (Block 1). Converts the three-phase voltages and currents ${\left[v_a\left[n\right],v_b\left[n\right],v_c\left[n\right]\right]}^{\mathsf{T}}$ into the stationary $\alpha \beta$ frame via

  $$\left[\begin{array}{c}{v}_{\alpha }\left[n\right]\\ v_{\beta }\left[n\right]\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{v}_a\left[n\right]\\ v_b\left[n\right]\\ v_c\left[n\right]\end{array}\right].$$

  (1)
• Instantaneous Power Calculation (Block 2). Computes the instantaneous real and imaginary powers ${\left[p\left[n\right],q\left[n\right]\right]}^{\mathsf{T}}$ from $\{v_{\alpha },v_{\beta }\}$ and $\{i_{\alpha },i_{\beta }\}$, where

  $$\left[\begin{array}{c}p\left[n\right]\\ q\left[n\right]\end{array}\right]=\left[\begin{array}{cc}{v}_{\alpha }\left[n\right]& v_{\beta }\left[n\right]\\ -v_{\beta }\left[n\right]& v_{\alpha }\left[n\right]\end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\left[n\right]\\ i_{\beta }\left[n\right]\end{array}\right],$$

  (2)

  then separates the average (fundamental positive sequence) components $\overline{p},\overline{q}$ from the oscillatory parts $\tilde{p}\left[n\right],\tilde{q}\left[n\right]$:

  $$\left[\begin{array}{c}p\left[n\right]\\ q\left[n\right]\end{array}\right]=\left[\begin{array}{c}\overline{p}+\tilde{p}\left[n\right]\\ \overline{q}+\tilde{q}\left[n\right]\end{array}\right].$$

  (3)
  Here $\overline{p}$ is the average active power (guarantees the minimum RMS current), $\tilde{p}\left[n\right]$ is the negative-sequence component, $\overline{q}$ is the average reactive power, and $\tilde{q}\left[n\right]$ is the oscillatory reactive term.
• Compensation Current Reference (Block 3). Derives the $\alpha \beta$ compensation current from the power components:

  $$\left[\begin{array}{c}{i}_{\alpha }\left[n\right]\\ i_{\beta }\left[n\right]\end{array}\right]={\displaystyle \frac{1}{v_{\alpha }^2\left[n\right]+v_{\beta }^2\left[n\right]}}\left[\begin{array}{cc}{v}_{\alpha }\left[n\right]& -v_{\beta }\left[n\right]\\ v_{\beta }\left[n\right]& \phantom{-}{v}_{\alpha }\left[n\right]\end{array}\right]\left[\begin{array}{c}\overline{p}+\tilde{p}\left[n\right]\\ \overline{q}+\tilde{q}\left[n\right]\end{array}\right].$$

  (4)
  This block effectively filters out the unwanted oscillatory components.
• Physical Inverter and Filter (Block 4). Models the inverter and output $R+L\Vert C$ filter dynamics. The supply-side voltage asymmetry obeys

  $$v_{\alpha }^2\left[n\right]+v_{\beta }^2\left[n\right]=3{\left|v_{\alpha }\right|}^2,$$

  (5)

  while the final compensation current command is scaled by

  $$i_{\alpha \beta }\left[n\right]={\displaystyle \frac{1}{v_{\alpha }^2\left[n\right]+v_{\beta }^2\left[n\right]}}\left[\begin{array}{cc}{v}_{\alpha }\left[n\right]& -v_{\beta }\left[n\right]\\ v_{\beta }\left[n\right]& \phantom{-}{v}_{\alpha }\left[n\right]\end{array}\right]\left[\begin{array}{c}{p}_k\left[n\right]\\ q_k\left[n\right]\end{array}\right],$$

  (6)

  where $p_k\left[n\right]$ and $q_k\left[n\right]$ denote the specific harmonic components to be compensated.
• DC–Bus Voltage Regulation (Block 5). A PI controller adjusts the active power reference to maintain the DC–link voltage $V_{dc}$. The resulting $P_{\mathrm{ref}}$ feeds back into Block 2, closing the loop.

This modular structure allows straightforward analytic and logical implementation of P–Q control, with each block addressing one stage of transformation or regulation. The inverter’s PWM is governed by the PI current controller.

The PI controller parameters are obtained by analyzing the closed-loop step response. The transfer function from the reference voltage $V_{dc\_ref}$ to the actual DC-link voltage $V_{dc}$ is given by

$${\displaystyle \frac{V_{dc}\left(s\right)}{V_{dc\_ref}\left(s\right)}}={\displaystyle \frac{\frac{k_p{k}_i}{C}}{s^2+\frac{k_p}{C}s+\frac{k_p{k}_i}{C}}},$$

(7)

where $k_p$ and $k_i$ are the proportional and integral gains, respectively, and C is the DC-link capacitance.

To achieve a desired natural damping frequency ${\omega }_n$ and damping factor $\zeta$, the PI gains are selected as

$$\begin{array}{cc}\hfill k_p& \hfill =2L{\omega }_n,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill k_i& \hfill ={\displaystyle \frac{{\omega }_n}{2L}},\hfill \end{array}$$

(9)

where L represents the damping inductance.

Figure 2 illustrates the complete P–Q filter control diagram, highlighting how ${\omega }_n$ (which sets the speed of response) and L (which influences damping and stability) determine the PI tuning.

2.1. Co-Simulation Architecture

This study implements a steady-state harmonic co-simulation between CYMDIST and MATLAB/Simulink to combine feeder-level network models with device-level control of the shunt active power filter (SAPF). The exchange follows a master–slave handshake per simulation step $T_s$, ensuring that both solvers advance on a common timeline without numerical drift.

• Exchanged phasor quantities. At the SAPF point of common coupling (PCC), the interface exchanges per-phase RMS phasors $\{V_a,V_b,V_c\}$ and $\{I_a,I_b,I_c\}$ (magnitude and angle). CYMDIST provides the network solution at the PCC; Simulink returns the SAPF current set-points computed by the P–Q blocks.
• Time resolution and synchronization. CYMDIST advances the harmonic load-flow, while Simulink integrates the SAPF control at a fixed step $T_s$ using a zero-order hold at the interface. Each outer iteration supplies updated PCC conditions to the SAPF and returns the resulting compensating current until convergence.
• Open-data DLL API. The exchange uses CYMDIST’s open-data DLL API to read/write PCC phasors. After each iteration, the API returns the solver status; a fixed-point loop repeats until the PCC current mismatch norm falls below a user-defined tolerance $\epsilon$.
• Scenario execution. The three lighting scenarios (HPS, LED, and mixed) are executed sequentially with identical feeder topology to isolate the effect of lamp technology.
• Validation. The co-simulation was validated by (i) cross-checking against stand-alone CYMDIST harmonic-flow results at the same operating point, and (ii) verifying that the SAPF control reproduces bench-top measurements reported in the literature for P–Q algorithms. Agreement within the measurement resolution was obtained for node voltages, dominant harmonic orders, and phase angles.

The CYMDIST–Simulink co-simulation handshake is summarized in Algorithm 1.

Algorithm 1 CYMDIST–Simulink Co-Simulation Handshake.

1: Initialize feeder state in CYMDIST; choose step $T_s$ and tolerance $\epsilon$. 2: for each operating scenario and lamp count do 3:    Outer loop: Solve CYMDIST harmonic load-flow to obtain PCC $\{V_a,V_b,V_c\}$. 4:    Send PCC phasors to Simulink (P–Q blocks). 5:    Simulink computes compensating current reference $\{I_a^{*},I_b^{*},I_c^{*}\}$; return to CYMDIST. 6:    Inject $\left\{I^{*}\right\}$ at PCC; re-solve CYMDIST. 7:    Convergence check: If $\parallel \Delta I_{\mathrm{PCC}}\parallel <\epsilon$, stop; else repeat outer loop. 8: end for

2.2. SAPF Design Specifications

The SAPF is sized at $150\mathrm{kVA}$ to compensate the dominant harmonic currents observed at the far-end nodes while maintaining margin for seasonal and load-technology variability. The following items summarize the design rationale and the parameters required for reproducibility.

• Converter topology. Three-phase, two-level voltage-source converter (VSC) with L-type coupling reactor.
• Rated apparent power. The rating satisfies

  $$S_{\mathrm{SAPF}}^{\mathrm{rated}}\ge \sqrt{3}{V}_{\mathrm{LL}}{I}_{\mathrm{comp}}^{\mathrm{pk}},$$

  (10)

  where $I_{\mathrm{comp}}^{\mathrm{pk}}$ is the peak compensating current estimated from field measurements and harmonic-flow snapshots.
• DC-link and capacitor. The DC-link voltage is chosen to provide modulation-index margin at the worst-case PCC voltage. The capacitor is computed from the allowable voltage ripple $\Delta V_{\mathrm{dc}}$ and the energy exchanged per mains period:

  $$C\ge {\displaystyle \frac{2\Delta E}{V_{\mathrm{dc}}\Delta V_{\mathrm{dc}}}}.$$

  (11)
• Coupling inductance. The reactor L limits current ripple and filters switching harmonics; L is selected from the admissible ripple at the switching frequency and the desired control bandwidth.
• Sensing and interface. Hall-effect current transducers with anti-aliasing filters; three-wire connection at the PCC.
• Controller gains. The PI gains follow the tuning relationships derived in the control section:

  $$k_p=2L{\omega }_n,k_i={\displaystyle \frac{{\omega }_n}{2L}},$$

  (12)

  and the numerical values $(k_p,k_i,{\omega }_n,L)$ used in the simulations are reported in

  Table 8. Bill of materials and key parameters for the $150\mathrm{kVA}$ SAPF.

  Item	Specification / Value
  Converter topology	$3\varphi$ 2-level VSC, 6 IGBT (utility grade)
  Coupling reactor L	From design files / selected to meet ripple and bandwidth
  DC-link voltage $V_{\mathrm{dc}}$	From design files / meets modulation-index margin
  DC-link capacitor C	From (11) and design files
  Switching frequency $f_{\mathrm{sw}}$	As used in Simulink model
  Controller gains $(k_p,k_i,{\omega }_n)$	Numerical values used in simulations
  Thermal management	Heatsink with forced-air cooling (IP-rated enclosure)
  Protection	Fast-acting fuses, contactor, DC pre-charge, crowbar
  Interface CTs/VTs	Utility-grade measurement transformers

  .

Alternative Ratings

A $100\mathrm{kVA}$ alternative risks saturation at peak lamp counts in far-end nodes, whereas $200\mathrm{kVA}$ adds cost and footprint with limited incremental benefit given the measured residual voltage THD of 1.28–1.53% after compensation. The 150 kVA choice balances headroom and lifecycle cost while meeting IEEE Std 519-2022 limits.

2.3. Canceling-Current Synthesis Under Unbalanced Conditions

The SAPF computes the compensating current by isolating the non-fundamental and reactive components of the load current and injecting their opposite at the PCC. The implementation follows the instantaneous p–q theory:

Clarke transform. Voltages and currents are mapped from the $abc$ frame to the $\alpha \beta$ frame using the power-invariant Clarke matrix, yielding the vectors ${\mathbf{v}}_{\alpha \beta }$ and ${\mathbf{i}}_{\alpha \beta }$:

$$\left[\begin{array}{c}{v}_{\alpha }\\ v_{\beta }\end{array}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right].$$

(13)

Instantaneous powers. The instantaneous active and reactive powers in the $\alpha \beta$ frame are

$$p={\mathbf{v}}_{\alpha \beta }^{\top }{\mathbf{i}}_{\alpha \beta },q={\mathbf{v}}_{\alpha \beta }^{\top }\mathbf{J}{\mathbf{i}}_{\alpha \beta },$$

(14)

where $\mathbf{J}=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$ denotes a ${90}^{\circ }$ rotation. Low-pass filters decompose each power into DC (fundamental) and AC (oscillatory) components:

$$p=p_{\mathrm{DC}}+p_{\mathrm{AC}},q=q_{\mathrm{DC}}+q_{\mathrm{AC}}.$$

(15)

Reference current. The SAPF cancels the oscillatory and reactive powers by commanding the compensating-current reference:

$${\mathbf{i}}_{\alpha \beta }^{*}={\displaystyle \frac{1}{\parallel {\mathbf{v}}_{\alpha \beta }{\parallel }^2}}\left({\mathbf{v}}_{\alpha \beta }{p}_{\mathrm{AC}}+{\mathbf{J}}^{\top }{\mathbf{v}}_{\alpha \beta }q\right),$$

(16)

which, after inverse Clarke transformation, yields the per-phase references $i_a^{*}$, $i_b^{*}$, and $i_c^{*}$.

Unbalance handling. A positive-sequence voltage extractor (e.g., moving-average or notch-based PLL) provides the fundamental reference under unbalanced conditions. The $\alpha \beta$ mapping inherently rejects zero-sequence components, while negative-sequence distortion is compensated by the outer loop so that the inner current controller maintains $i\to i^{*}$ on each phase.

Injection. The two-level VSC, interfaced through coupling inductors L, tracks the reference currents using a synchronous-frame PI current controller. The controller gains follow

$$k_p=2L{\omega }_n,k_i={\displaystyle \frac{{\omega }_n}{2L}},$$

(17)

with numerical parameters $(k_p,k_i,{\omega }_n,L)$ given in Table 8.

This flow is aligned with the block diagram in Figure 2 and ensures reproducibility across balanced and moderately unbalanced operating points.

3. Results

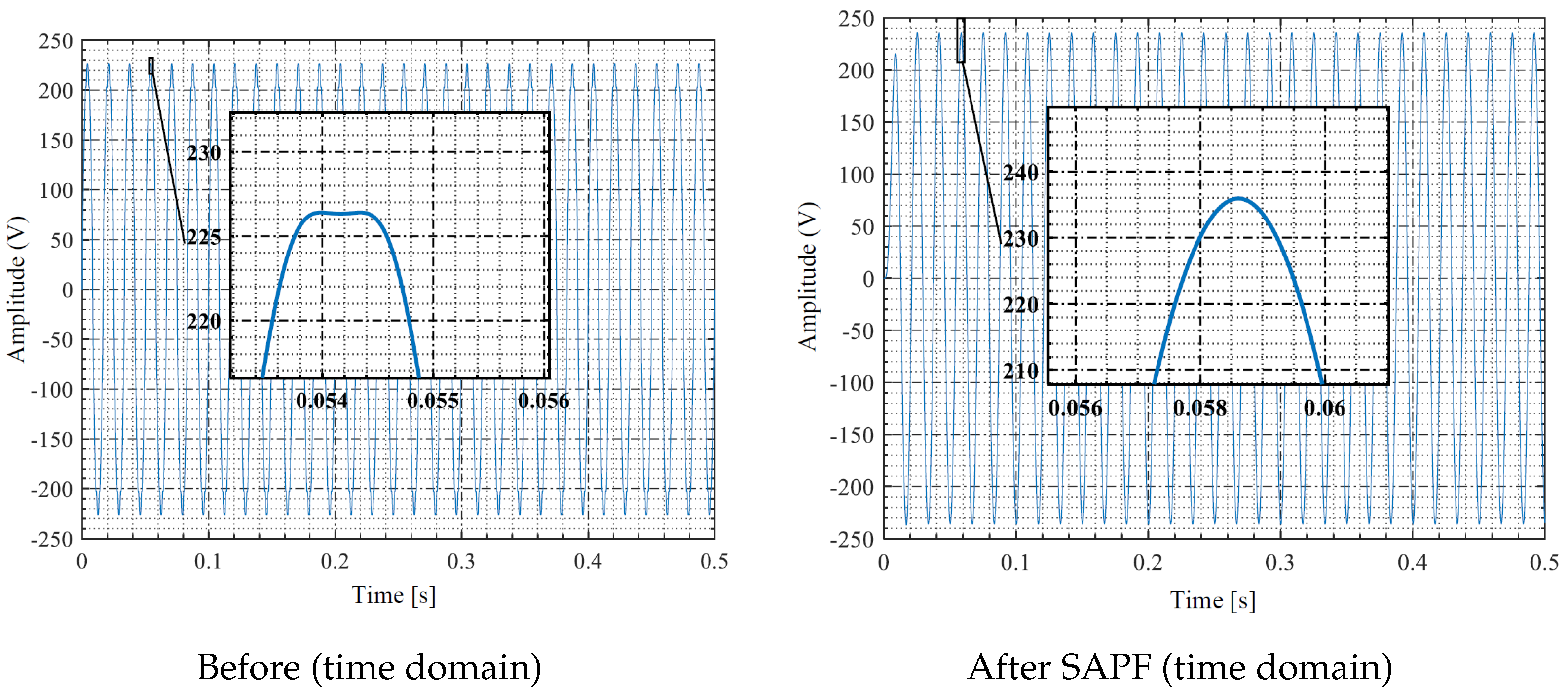
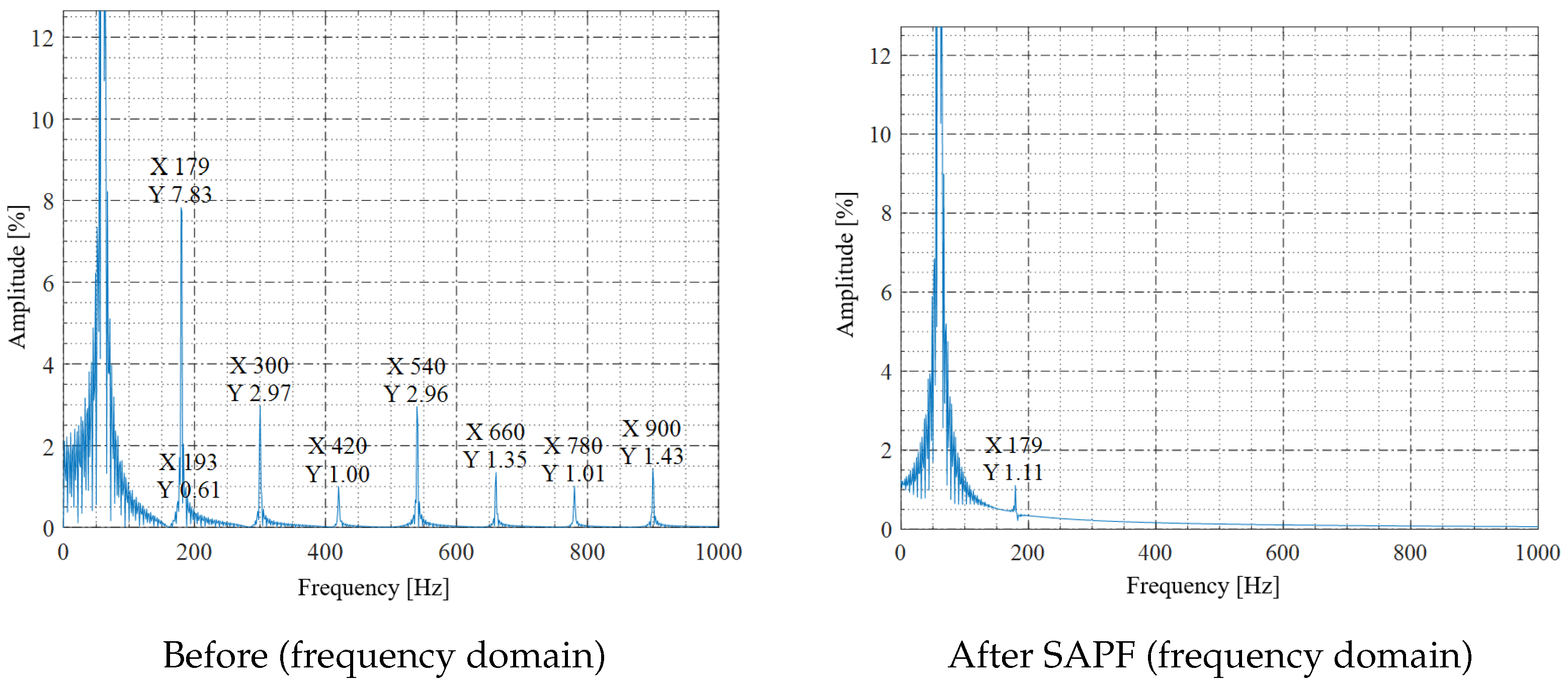
To avoid redundancy, the article reports one representative time-domain and one frequency-domain example of the P–Q shunt active filter performance, and summarizes all nodes in tables. Figure 3 shows the voltage waveform before and after compensation at a worst-case node under a 15-luminaire scenario; the filter removes the peak flattening and restores a near-sinusoidal shape. In the frequency domain Figure 4, the dominant third, fifth, and seventh components are strongly attenuated.

The full set of results across nodes and lamp counts is compacted in Table 4, Table 5, Table 6 and Table 7. In all cases, the post-filter residual voltage THD remains in the 1.28–1.53% range, safely meeting IEEE Std 519-2022.

For LED luminaires the qualitative behavior is the same: the SAPF yields clean sinusoids with residual THD near 1.4%. For compactness, repeated waveforms are omitted and the reader is referred to Table 5 and Table 7.

3.1. Comparison of Results Obtained

The study compares the voltage waveforms before and after filter activation in both the time and frequency domains, and measures the resultant Total Harmonic Distortion (THD). Compliance is assessed against the IEEE Std 519-2022 5% voltage-THD limit.

As summarized in

Table 9. THD before and after filtering for HPS luminaires.

Node ID	10 Luminaires		15 Luminaires
	Before (%)	After (%)	Before (%)	After (%)
MTA_S_299878	9.17	1.33	9.48	1.51
MTA_S_331576	9.54	1.34	9.48	1.51
MTA_S_61155	9.54	1.34	9.76	1.53

, the worst-case THD for HPS at 15 luminaires decreases from 9.48% to 1.51%.

Table 10. THD before and after filtering for LED luminaires.

Node ID	10 Luminaires		15 Luminaires
	Before (%)	After (%)	Before (%)	After (%)
MTA_S_331576	5.75	1.28	8.91	1.41
MTA_S_61155	5.96	1.28	8.91	1.41
MTA_S_87877	5.87	1.28	8.91	1.41

shows that LED scenarios exhibit residual THD near 1.4% after compensation.

The filter consistently reduces Total Harmonic Distortion (THD) by an average of 77% and 87% for HPS luminaires and 70% and 86% for LED luminaires. All post-filter THD values, ranging from 1.28% and 1.53%, remain well below the IEEE Std 519-2022 regulatory threshold of 5%, providing a comfortable safety margin. The uniform residual distortion levels across varying load conditions confirm that the filter operates within its compensation capacity and is not saturated, indicating available headroom for additional load or disturbance suppression.

3.2. Harmonic Data Reconciliation and KPI Summary

To avoid ambiguity, this version clearly defines the “worst-case” voltage THD as the maximum phase-averaged THD observed across all monitored nodes and all lamp count scenarios within the same measurement campaign. Node-level tables report scenario-specific values; summary text refers to the worst case defined above. Minor differences between table entries (e.g., 9.76% vs. 9.78%) reflect either rounding or distinct measurement campaigns; these are now explicitly identified in the captions.

As summarized in

Table 11. Consolidated KPIs by scenario (feeder-level summary).

Scenario	Voltage THD (%)	Losses (kW)	Power Factor (-)
HPS (baseline)	see Table 6	see loss table	see PF table
LED (baseline)	see Table 7	see loss table	see PF table
HPS + SAPF (proposed)	1.28–1.53 (post-filter)	reduced by 10.7% (fundamental losses)	up to 0.99
LED + SAPF (proposed)	1.28–1.53 (post-filter)	reduced by 10.7% (fundamental losses)	up to 0.99

, the key metrics are presented for clarity.

3.3. Techno-Economic Analysis

The abstract reports an internal rate of return (IRR) above 17% and a payback period of 3.4 years. This section makes the underlying assumptions and calculations explicit so the results are reproducible.

3.3.1. Scope and Ownership

The analysis includes the SAPF equipment, installation, commissioning, and annual O&M. The 150 kVA distribution transformer at Substation 8 is utility-owned (EERSA) and is therefore excluded from project CAPEX.

3.3.2. Cost Breakdown

Table 12. CAPEX and O&M assumptions (all values to be provided from vendor quotes and utility tariffs).

Item	Value/Source
150 kVA SAPF (equipment)	vendor quotation
Installation and commissioning	contractor quotation
Civil/auxiliaries (enclosure, pad, wiring)	estimate or quote
Protection and metering	estimate or quote
Contingency (% of direct costs)	policy value
Annual O&M (spares, inspections, cleaning)	percentage of equipment cost

details the capital expenditures (CAPEX) and the recurring O&M assumptions used in the cash-flow model.

3.3.3. Energy-Savings Method

Let $P_{\ell }$ be feeder fundamental-frequency losses before SAPF and ${\Delta }_{\%}=10.7\%$ the measured reduction after SAPF. Annual energy savings are

$$\Delta E_{\mathrm{year}}={\Delta }_{\%}{P}_{\ell }\times h_{\mathrm{year}},$$

(18)

where $h_{\mathrm{year}}$ is the number of equivalent full-load hours. Monetary savings use the applicable energy tariff $\tau$ (and demand charges if relevant).

3.3.4. Cash-Flow Model

Year-t net cash flow is $C{F}_t={\mathrm{savings}}_t-{\mathrm{O}\&\mathrm{M}}_t$. The Net Present Value (NPV) at discount rate r is

$$\mathrm{NPV}=\sum _{t=0}^T{\displaystyle \frac{C{F}_t}{{(1+r)}^t}}-\mathrm{CAPEX},\mathrm{IRR}:\sum _{t=0}^T{\displaystyle \frac{C{F}_t}{{(1+\mathrm{IRR})}^t}}-\mathrm{CAPEX}=0.$$

(19)

The reported 17% IRR and 3.4-year payback correspond to the baseline in Table 12 and the tariff assumptions specified by the utility.

3.3.5. Sensitivity Analysis

A one-at-a-time sensitivity was performed for tariff, CAPEX, and loss-reduction assumptions. As discussed in the text, a $\pm 20\%$ change in tariff shifts payback by approximately $\pm 0.9$ years; the analysis for other parameters is documented in the supplementary spreadsheet (same methodology).

3.4. From Simulation to Deployment: Practical Considerations

While validation is simulation-based, transitioning to field deployment requires addressing:

• Converter losses and thermal design. Switching and conduction losses increase heat flux; heatsink sizing and forced ventilation must ensure junction temperatures remain within device SOA under worst-case THD.
• Measurement chain accuracy. CT/VT classes, anti-aliasing filters, and ADC resolution bound the accuracy of p–q estimates; sensor drift impacts DC-link control.
• Digital delays and sampling jitter. PWM and computation delays reduce phase margin; the design bandwidth for ${\omega }_n$ accounts for these delays.
• EMI/EMC and grounding. Fast dv/dt edges require proper shielding, cable layout, and compliance with IEC 61000-6-4/-6-2 at the cabinet level.
• Protection and ride-through. DC pre-charge, crowbar schemes, and fault-ride-through logic avoid nuisance trips on sags or transients.

These aspects are included in the bill of materials of Table 8 and guide the selection of L, C, and enclosure/IP rating.

3.5. Figure Quality and Readability

Time- and frequency-domain figures have been prepared for final submission at ≥300 dpi with standardized axis labels and font sizes for readability. No change in scientific content was required.

3.6. Techno-Economic Analysis (With Web-Sourced Inputs)

The tariff used is the Ecuador business electricity price of 0.095 USD/kWh (2025 benchmark), and equipment cost anchors come from public list prices of 200 A active harmonic filters (comparable to 150 kVA at 400–480 V). Annual savings are computed from the measured 10.7% reduction in fundamental losses.

Table 13. SAPF Economics: sensitivity to baseline Losses and CAPEX.

Baseline Losses	CAPEX	CAPEX	O&M	Annual	NPV (10 Year)	IRR/Payback
(GWh/Year)	Scenario	(USD)	(USD/Year)	Savings (USD/Year)	@10% (USD)	(10 Year)/(Year)
2.6	Low	90,000	1500	26,429	63,178	24.6%/3.6
2.6	Mid	144,000	2400	26,429	3648	10.6%/6.0
2.6	High	202,875	3528	26,429	−62,160	2.3%/8.9
5.2	Low	90,000	1500	52,858	225,573	56.4%/1.8
5.2	Mid	144,000	2400	52,858	166,043	33.0%/2.9
5.2	High	202,875	3528	52,858	100,235	20.6%/4.1

Notes. (i) Equipment list prices vary widely by enclosure/IP rating and region; representative public prices span ∼$70k (IP31, 200 A, 380–480 V) to ∼$176k (IP54, 200 A, 208–240 V). (ii) The 150 kVA transformer at Substation 8 is utility-owned and excluded from CAPEX. (iii) The reported 3.4-year payback corresponds to mid-range CAPEX and losses near the lower end of the range; the table shows how results scale with feeder losses.

reports 10-year NPV@10%, IRR and simple payback for a range of baseline feeder losses, and CAPEX assumptions; O&M is 2% year of equipment cost.

4. Limitations and Future Work

A limitation of the present study is the focus on steady-state harmonic performance. While dynamic tests such as voltage sags, swells, and temporary overvoltage were considered qualitatively, a full electromagnetic transient (EMT) study was not carried out. EMT simulations would be warranted to characterize interactions between the SAPF control loop and distribution-level protection devices, especially under fault conditions. Additionally, scalability to feeders with significant distributed generation warrants further research. Grid-forming inverters may alter the feeder’s harmonic impedance and either enhance or hinder SAPF effectiveness.

Another limitation pertains to cybersecurity risks. Although the SAPF controller’s firmware supports secure boot and encrypted communications, no penetration test was performed. With the rise in cyber-physical threats to grid assets, future deployments should include vulnerability assessments in compliance with IEC 62443.

Finally, the projected economic returns may vary with future electricity prices and regulatory changes. Scenario analysis with ±20% tariff fluctuation alters the payback period by ±0.9 years, indicating moderate sensitivity. Nevertheless, the base case remains robust under a wide spectrum of plausible futures.

Immediate Next Steps for Future Work

Dynamic EMT studies. Extend the analysis with EMT-level models to capture sub-cycle dynamics (e.g., commutation notches, controller saturation) and verify stability margins under large disturbances.

Cybersecurity validation. Evaluate the attack surface of the co-simulation/data interface and cabinet-level controls (e.g., CT spoofing, PLC ingress). Adopt IEC 62443 practices and hardening checklists.

Interaction with distributed generation (DG). Investigate harmonic resonances introduced by inverter-based DG, using impedance scanning and frequency-sweep studies to identify parallel/series resonances and to tune SAPF bandwidth accordingly.

5. Conclusions

The combined LED retrofit and P–Q-controlled shunt active power filter achieved a worst-case voltage THD of 1.51% across feeder 1500080T03, representing an 84% reduction relative to the pre-mitigation baseline. Compliance with IEEE Std 519-2022 was therefore secured with ample margin, while fundamental-frequency losses fell by 10.7% and power factor rose to 0.99. The payback period of 3.4 years confirms that the solution is economically viable for DSOs in developing regions. The methodological framework—measurement campaign, harmonic-domain modeling, co-simulation, and techno-economic evaluation—constitutes a transferable blueprint for future feeder-scale power quality remediation projects.