Sustaining Battery Life: Deep-Cycle Lead-Acid Battery Through Acoustic Simulation and System Modeling
Abstract
1. Introduction
- A developed mathematical model that captures the effect of ultrasonic waves on the lifecycle of DCLA batteries, addressing a critical gap in existing battery research using MATLAB Simulink.
- A comparative evaluation of battery efficiency, capacity retention, and service life under scenarios with and without ultrasonic excitation, providing quantitative insights into performance differences.
- It explores ultrasonic excitation as a potential retrofit strategy to enhance durability and energy efficiency, particularly in off-grid PV systems where lead-acid batteries remain widely used.
2. Purpose/Problem Description
2.1. Problem Context
2.2. Research Gap and Study Objectives
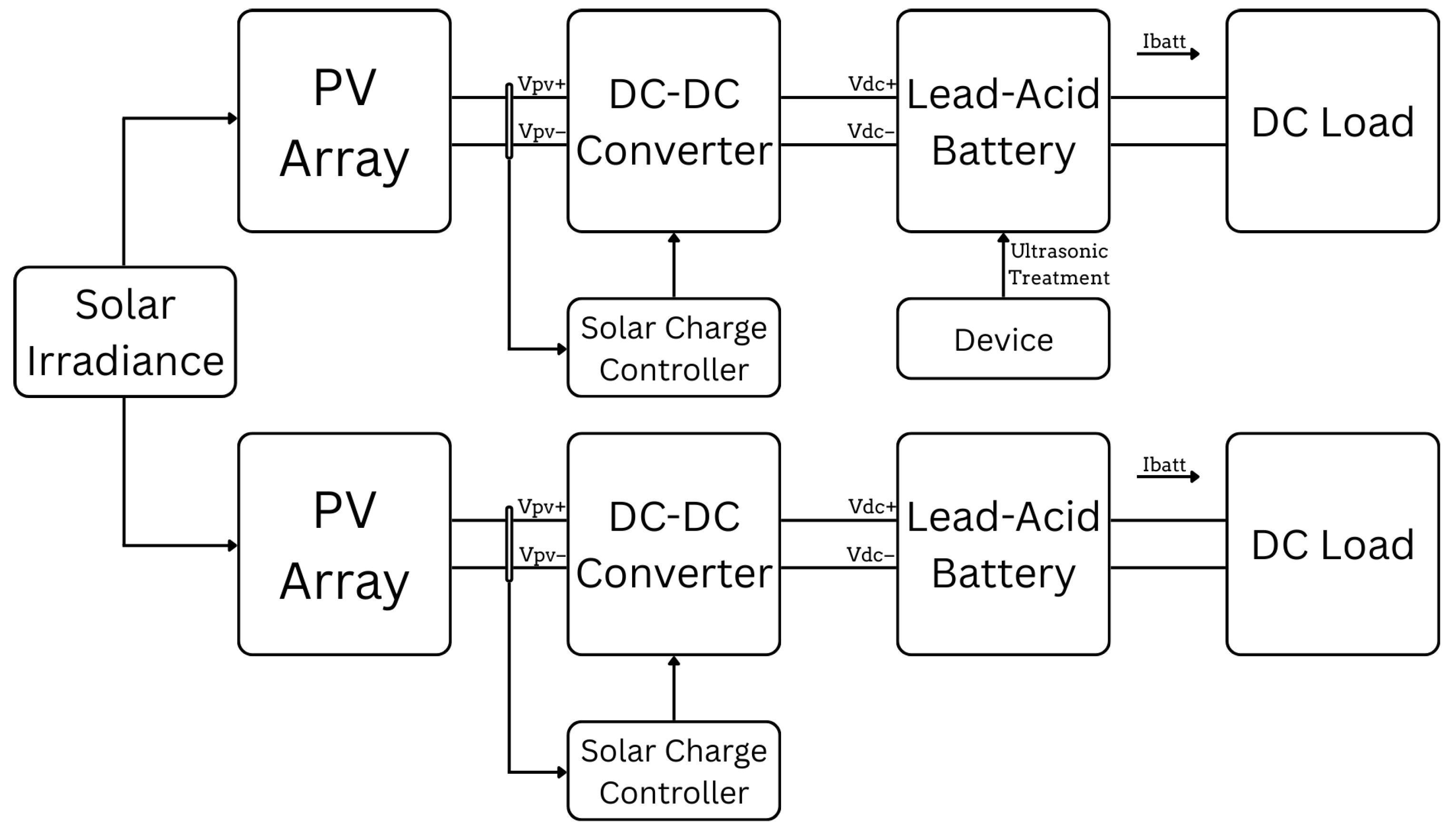
2.3. System Designs
2.3.1. Modified Standalone Photovoltaic (PV) System
2.3.2. Charge Controller
2.3.3. DC-DC Converter
2.3.4. Ultrasonic Device
2.3.5. Lead-Acid Battery
2.3.6. DC Load
3. Methodology
3.1. Simulation Procedure of the PV System
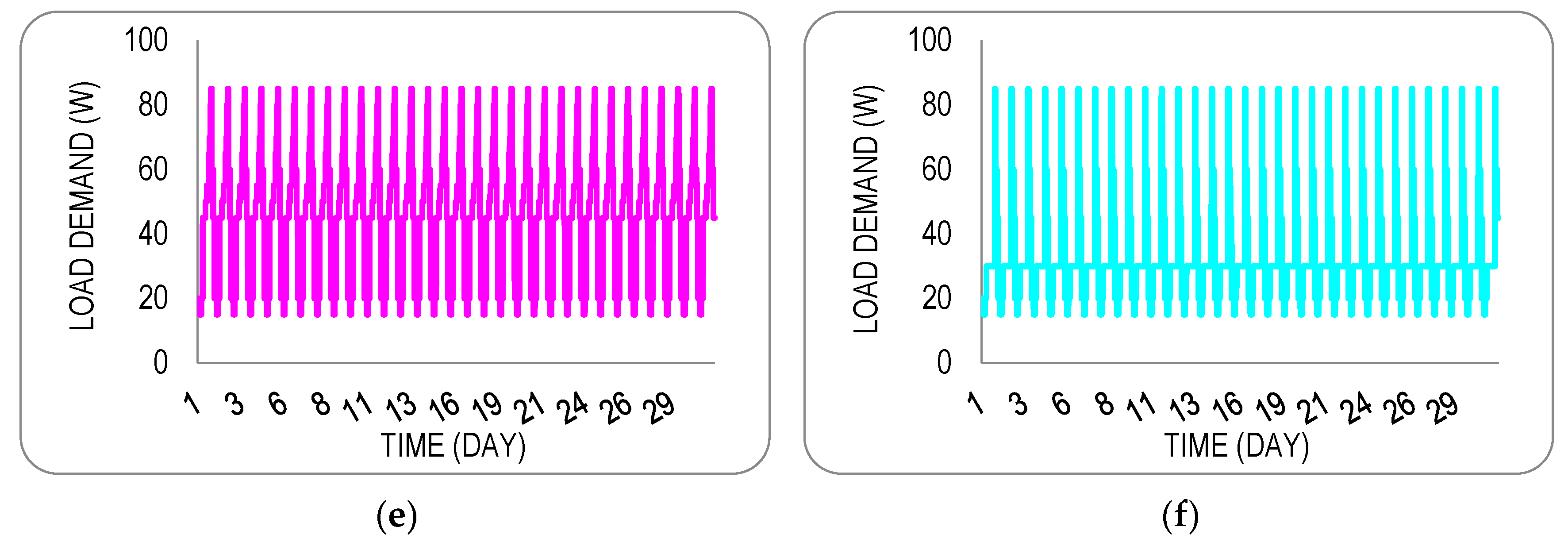
3.1.1. Constant Load
3.1.2. Uniform Random Load
3.1.3. Estimated Household DC Load Profile with Sudden Load Spikes
3.1.4. Estimated Household DC Load Profile Without Sudden Load Spikes
3.1.5. Estimated Household DC Load Profile with Gradual Load Increase
3.1.6. Estimated Intermittent Household DC Load Profile
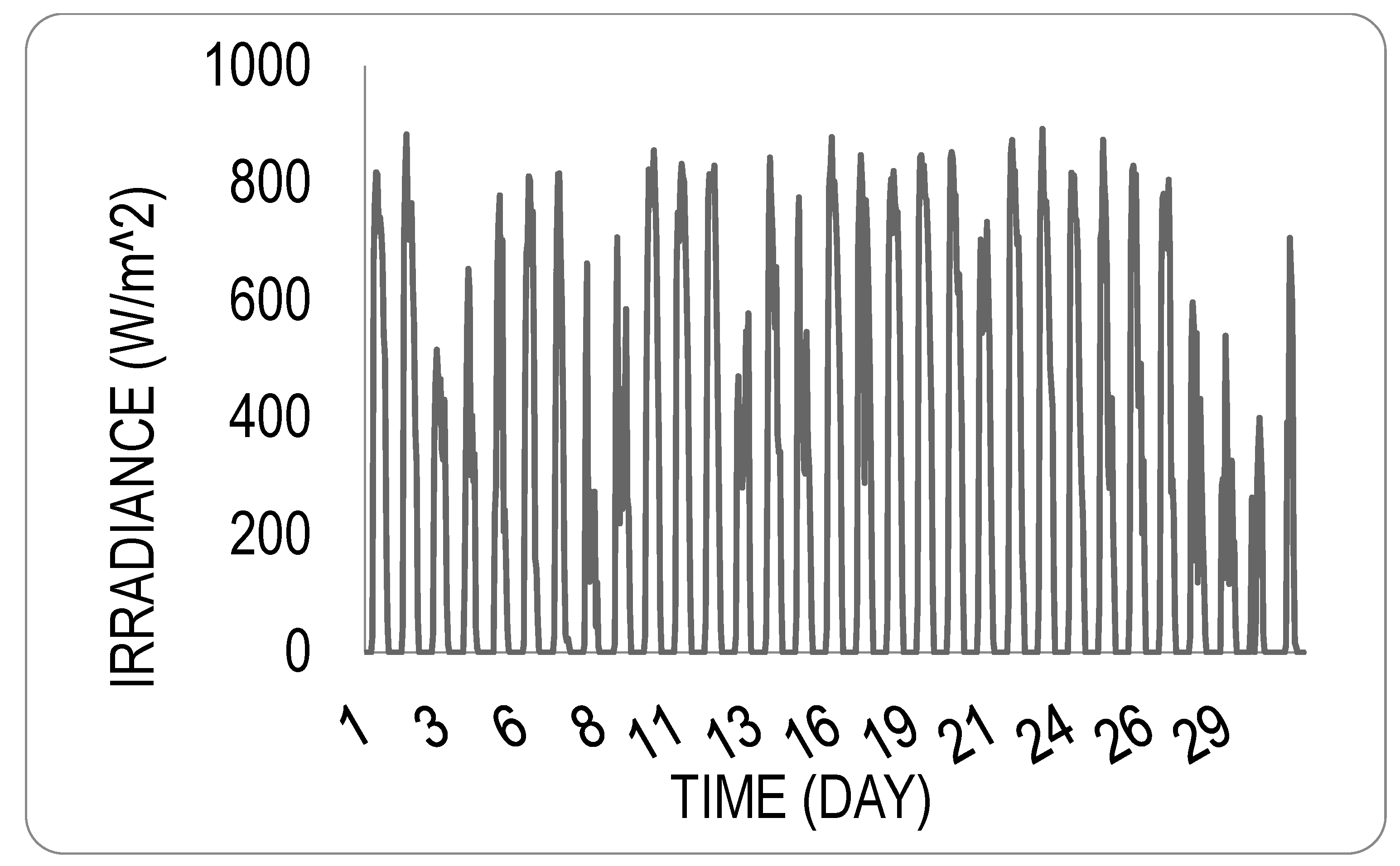
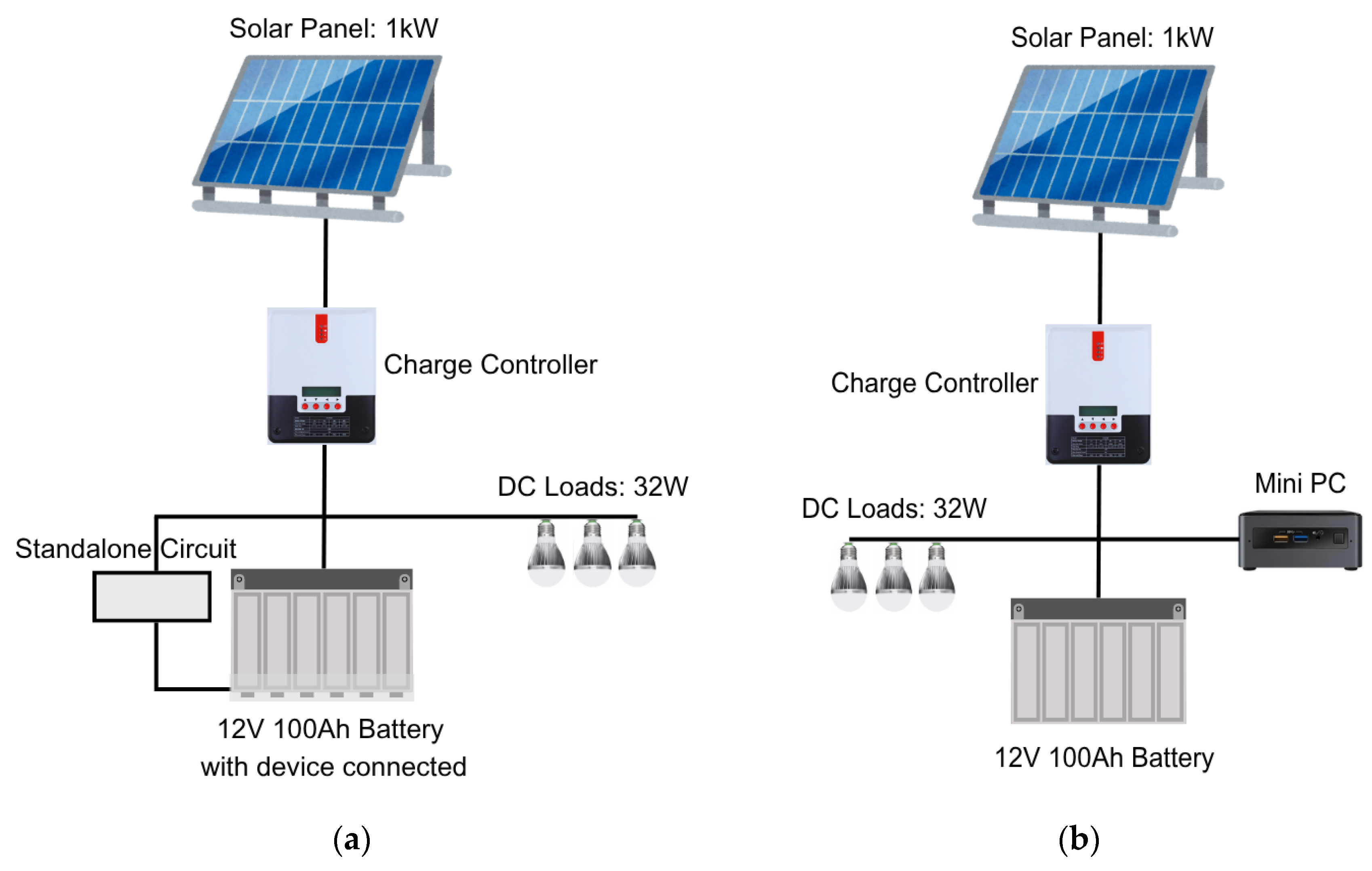
3.2. Experimental Data Collection (Microgrid Measurements)
3.3. DC House Set-Up for DCLA Battery Testing
3.4. Evaluation and Verification Process
4. Results and Discussion
4.1. Results
4.2. Evaluation and Verification
4.3. Discussion
4.4. Practical Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skyllas-Kazacos, M. Electro-chemical energy storage technologies for wind energy systems. Stand-Alone Hybrid Wind. Energy Syst. 2010, 10, 323–365. [Google Scholar] [CrossRef]
- Byrne, R.H.; Nguyen, T.A.; Copp, D.A.; Chalamala, B.R.; Gyuk, I. Energy Management and Optimization Methods for Grid Energy Storage Systems. IEEE Access 2018, 6, 13231–13260. [Google Scholar] [CrossRef]
- Chua, K.H.; Lim, Y.S.; Morris, S. Peak Reduction for Commercial Buildings Using Energy Storage. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 012008. [Google Scholar] [CrossRef]
- Hau, L.C.; Lim, Y.S.; Chua, K.H. Active Control Strategy of Energy Storage System for Reducing Maximum Demand Charges under Limited Storage Capacity. J. Energy Eng. 2017, 143, 04017010. [Google Scholar] [CrossRef]
- Varshney, K.; Varshney, P.K.; Gautam, K.; Tanwar, M.; Chaudhary, M. Current trends and future perspectives in the recycling of spent lead acid batteries in India. Mater. Today Proc. 2020, 26, 592–602. [Google Scholar] [CrossRef]
- Sommerville, R.; Zhu, P.; Rajaeifar, M.A.; Heidrich, O.; Goodship, V.; Kendrick, E. A qualitative assessment of lithium-ion battery recycling processes. Resour. Conserv. Recycl. 2020, 161, 105219. [Google Scholar] [CrossRef]
- Jolly, R.; Rhin, C. The recycling of lead-acid batteries: Production of lead and polypropylene. J. Power Sources 1994, 54, 77–82. [Google Scholar] [CrossRef]
- Radja, K.; Selami, N.; Khadra, K.; Abdelkader, F.; Laid, G. Sustainable practices in lead acid battery recycling. Braz. Appl. Sci. Rev. 2025, 9, e76719. [Google Scholar] [CrossRef]
- Delgado-Sanchez, J.-M.; Lillo-Bravo, I. Influence of degradation processes in lead–acid batteries on the technoeconomic analysis of photovoltaic systems. Energies 2020, 13, 4075. [Google Scholar] [CrossRef]
- Spiers, D. Chapter IIB-2—Batteries in PV Systems. In Practical Handbook of Photovoltaics: Fundamentals and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 721–776. [Google Scholar] [CrossRef]
- Catherino, H.A.; Feres, F.F.; Trinidad, F. Sulfation in lead–acid batteries. J. Power Sources 2004, 129, 113–120. [Google Scholar] [CrossRef]
- Casey, A.J.; D’Arpino, M. Performance of Sodium-Ion and Lithium-Ion Batteries for Energy Storage System Applications. In Proceedings of the 2025 IEEE Electrical Energy Storage Applications and Technologies Conference (EESAT), Charlotte, NC, USA, 20–21 January 2025. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, T.; Chen, J.; Gao, B.; Yu, M.; Zhu, J. Advances in safety of lithium-ion batteries for energy storage: Hazard characteristics and active suppression techniques. Energy Rev. 2025, 4, 100117. [Google Scholar] [CrossRef]
- Bullock, K.R. Lead-acid battery research and development—A vital key to winning new business. J. Power Sources 2003, 116, 8–13. [Google Scholar] [CrossRef]
- Deveau, J.; White, C.; Swan, L.G. Lead-acid battery response to various formation levels—Part A: Recommended formation levels for off-grid solar and conventional applications. Sustain. Energy Technol. Assess. 2015, 11, 1–10. [Google Scholar] [CrossRef]
- Naidenov, V.; Markov, U. Influence of ultrasonic waves on the formation of lead-acid batteries. J. Power Sources 2012, 217, 236–242. [Google Scholar] [CrossRef]
- El Filali, A.; Laadissi, E.M.; Khalfi, J.; Zazi, M. Lead-acid battery desulfation using a high-frequency pulse desulfator in standalone PV systems. Int. J. Appl. Power Eng. 2024, 13, 853–861. [Google Scholar] [CrossRef]
- Al Riza, D.F.; Gilani, S.I.U.H. Standalone photovoltaic system sizing using peak sun hour method and evaluation by TRNSYS simulation. Int. J. Renew. Energy Res. 2014, 4, 109–114. [Google Scholar]
- Habeeb, A.; Hizam, H.; Othman, M.L.; AbdulWahab, N.I.; Rohouma, W. Design Simulation and Performance Evaluation of a Standalone Photovoltaic System for a Health Care Facility in Malaysia. Energies 2023, 16, 5342. [Google Scholar] [CrossRef]
- Tan, R.H.G.; Er, C.K.; Solanki, S.G. Modeling of Photovoltaic MPPT Lead Acid Battery Charge Controller for Standalone System Applications. In Proceedings of the 2020 10th International Conference on Power, Energy and Electrical Engineering (CPEEE 2020), E3S Web of Conferences, Tokyo, Japan, 19–21 June 2020; Volume 182, p. 03005. [Google Scholar] [CrossRef]
- Vignesh, S.; Megalingam, R.K. Design & simulation of a PV system under varying temperatures for maximum power by considering the variation of efficiency with temperature in Simulink. In Proceedings of the 2022 IEEE IAS Global Conference on Emerging Technologies (GlobConET), Arad, Romania, 20–22 May 2022; pp. 349–354. [Google Scholar] [CrossRef]
- Balasubramanian, M.S.; Dheeban, S.S.; Kumar, C.S. Design of standalone PV system. Int. J. Sci. Technol. Res. 2019, 8, 684–688. [Google Scholar]
- Rivadulla, G.A.T.; Apolinario, G.F.D.G.; Pacis, M.C. Optimizing Hybrid Microgrid Power Systems for Local Power Distribution: A Study on Combined Photovoltaic and Fuel Cell Systems in the Philippines. Energies 2023, 16, 5906. [Google Scholar] [CrossRef]
- Singh, A.; Karandikar, P.B. A broad review on desulfation of lead-acid battery for electric hybrid vehicle. Microsyst. Technol. 2016, 22, 1679–1685. [Google Scholar] [CrossRef]
- Alvarado, M.; Bulfa, A., Jr.; Aquino, A. Ultrasonic influence on germination and early growth of bell pepper seeds. In Proceedings of the International Exchange and Innovation Conference on Engineering & Sciences (IEICES), Fukuoka, Japan, 17–18 October 2024; Volume 10, pp. 19–25. [Google Scholar] [CrossRef]
- Kumar, M.S.; Mayavan, S.; Ganesan, M.; Ambalavanan, S. Effect of using sonicated sulphuric acid as an electrolyte in a lead acid battery. RSC Adv. 2015, 5, 76065–76067. [Google Scholar] [CrossRef]
- Zippenfenig, P. Open-Meteo.com Weather API [Computer Software], version 1.4.0; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- Trina Solar. Available online: https://static.trinasolar.com/sites/default/files/AU_Datasheet_Vertex_DEG18MC.20(II)_2020C.pdf (accessed on 4 August 2025).
- Klima, J. Application of ultrasound in electrochemistry. An overview of mechanisms and design of experimental arrangement. Ultrasonics 2011, 51, 202–209. [Google Scholar] [CrossRef]
- Wang, H.; Cui, X.; Zhang, C.; Gao, H.; Du, W.; Chen, Y. Promotion of Ionic Conductivity of PEO-Based Solid Electrolyte Using Ultrasonic Vibration. Polymers 2020, 12, 1889. [Google Scholar] [CrossRef] [PubMed]
- Kitaronka, S. Lead-Acid Battery. Bachelor’s Thesis, Siirt University, Siirt, Türkiye, 2022. [Google Scholar] [CrossRef]
- Charlangsut, N.; Rugthaicharoencheep, N. Enhancing Voltage and Power Stability in Distribution System with Photovoltaic from the Benefits of Battery Energy Storage. Energies 2025, 18, 577. [Google Scholar] [CrossRef]
- Li, G.; Kong, J.; Song, L.; Zhu, Y.; Liu, M.; Liu, C.; Wang, J. Study on voltage consistency characteristics of lithium-ion battery energy storage system. J. Phys. Conf. Ser. 2024, 2788, 012050. [Google Scholar] [CrossRef]
- Law, A.M. Simulation Modeling and Analysis, 5th ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Vicari, L.A.; de Lima, V.A.; de Moraes, A.S.; Lopes, M.C. Remaining Capacity Estimation of Lead-acid Batteries Using Exponential Decay Equations. Orbital Electron. J. Chem. 2021, 13, 392–398. [Google Scholar] [CrossRef]
- Reddy, T.B.; Linden, D. Linden’s Handbook of Batteries, 4th ed.; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-0-07-162419-0. [Google Scholar]
- Kebede, A.A.; Coosemans, T.; Messagie, M.; Jemal, T.; Behabtu, H.A.; Van Mierlo, J.; Berecibar, M. Techno-Economic Analysis of Lithium-Ion and Lead-Acid Batteries in Stationary Energy Storage Application. J. Energy Storage 2021, 40, 102748. [Google Scholar] [CrossRef]




| Item | Parameters | Values |
|---|---|---|
| PV | Module | Trina [28] |
| Maximum Power per Module | 500.402 W | |
| Cells per module | 150 | |
| No. of string series | 1 | |
| No. of string parallel | 2 | |
| Open circuit voltage | 51.5 V | |
| Short-circuit current | 12.3 A | |
| Voltage at the maximum power point | 43.4 V | |
| Current at maximum power point | 11.53 A | |
| Solar Charge Controller | Boost Voltage | 14.3 V |
| Boost Duration | 2 h | |
| Float Voltage Max | 13.8 V | |
| Float Voltage Min | 13.6 V | |
| Lead-acid Battery | Nominal Voltage | 12 V |
| Rated Capacity | 100 Ah | |
| Initial state-of-charge | 78% | |
| Battery response time | 1 s |
| Scenario | System | SoC | ||
|---|---|---|---|---|
| Max | Min | Mean | ||
| 1 | Test | 100 | 41.8 | 78.5 |
| Control | 100 | 0 | 37.4 | |
| 2 | Test | 100 | 42.7 | 78.8 |
| Control | 100 | 0 | 37.9 | |
| 3 | Test | 100 | 0 | 38.0 |
| Control | 100 | 0 | 24.6 | |
| 4 | Test | 100 | 0 | 36.3 |
| Control | 100 | 0 | 28.6 | |
| 5 | Test | 100 | 0 | 30.2 |
| Control | 100 | 0 | 22.2 | |
| 6 | Test | 100 | 0 | 71.0 |
| Control | 100 | 0 | 33.2 | |
| Scenario | System | Battery Voltage | ||
|---|---|---|---|---|
| Max | Min | Mean | ||
| 1 | Test | 14.4 | 12.4 | 13.2 |
| Control | 14.4 | 10.5 | 12.6 | |
| 2 | Test | 14.4 | 12.4 | 13.2 |
| Control | 14.4 | 10.5 | 12.6 | |
| 3 | Test | 14.4 | 10.5 | 12.7 |
| Control | 14.4 | 10.5 | 12.1 | |
| 4 | Test | 14.4 | 10.5 | 12.7 |
| Control | 14.4 | 10.5 | 12.3 | |
| 5 | Test | 14.4 | 10.5 | 12.3 |
| Control | 14.4 | 10.5 | 12.0 | |
| 6 | Test | 14.4 | 12.3 | 13.1 |
| Control | 14.4 | 10.5 | 12.5 | |
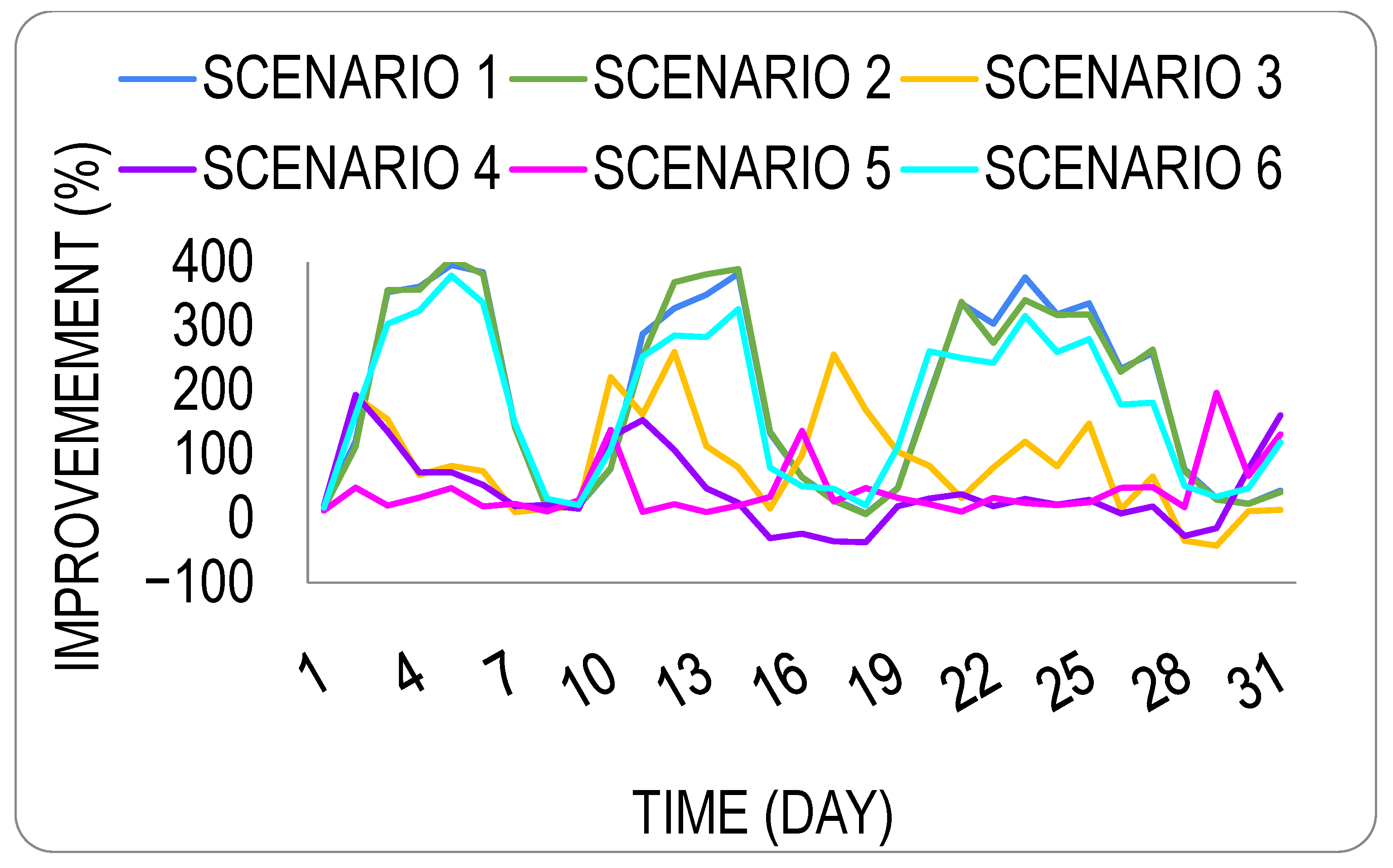
| Day | Improvement (%) | |||||
|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | Scenario 6 | |
| 1 | 16.88 | 16.03 | 18.20 | 19.47 | 12.39 | 17.08 |
| 2 | 120.78 | 111.97 | 190.26 | 192.98 | 48.03 | 161.93 |
| 3 | 353.03 | 356.09 | 154.58 | 135.83 | 20.36 | 303.44 |
| 4 | 361.41 | 357.13 | 67.92 | 71.92 | 32.57 | 324.17 |
| 5 | 395.64 | 405.13 | 82.03 | 72.32 | 47.47 | 379.19 |
| 6 | 384.03 | 380.96 | 74.15 | 52.5 | 18.93 | 336.58 |
| 7 | 143.52 | 141.70 | 10.18 | 19.31 | 23.21 | 148.74 |
| 8 | 16.48 | 15.83 | 15.38 | 21.13 | 11.08 | 30.85 |
| 9 | 19.63 | 19.78 | 18.58 | 15.32 | 28.57 | 20.92 |
| 10 | 77.70 | 78.56 | 220.35 | 127.05 | 138.35 | 107.91 |
| 11 | 288.13 | 252.66 | 162.27 | 153.69 | 10.33 | 252.47 |
| 12 | 327.83 | 368.68 | 259.81 | 106.78 | 22.45 | 285.66 |
| 13 | 349.10 | 381.17 | 112.82 | 47.22 | 10.09 | 282.92 |
| 14 | 381.90 | 389.09 | 79.99 | 24.58 | 20.38 | 326.43 |
| 15 | 133.02 | 135.62 | 15.57 | −30.71 | 33.59 | 79.25 |
| 16 | 64.52 | 64.32 | 99.21 | −23.53 | 136.68 | 50.2 |
| 17 | 30.32 | 27.76 | 255.79 | −35.78 | 26.63 | 46.44 |
| 18 | 7.86 | 6.88 | 169.51 | −36.86 | 47.57 | 20.62 |
| 19 | 47.56 | 46.79 | 103.98 | 19.16 | 32.3 | 111.59 |
| 20 | 193.12 | 189.61 | 82.16 | 31.09 | 22.35 | 260.71 |
| 21 | 335.52 | 337.89 | 32.18 | 38.1 | 10.57 | 250.64 |
| 22 | 303.78 | 273.89 | 79.81 | 19.12 | 32.28 | 242.85 |
| 23 | 375.96 | 340.69 | 119.85 | 30.43 | 24.16 | 315.86 |
| 24 | 318.28 | 317.45 | 81.59 | 21.53 | 20.87 | 259.7 |
| 25 | 335.72 | 318.42 | 148.42 | 29.01 | 25.09 | 279.76 |
| 26 | 233.34 | 228.77 | 14.30 | 7.97 | 47.81 | 177.66 |
| 27 | 258.44 | 263.50 | 65.52 | 18.93 | 49.08 | 180.74 |
| 28 | 76.94 | 74.19 | −34.59 | −26.96 | 17.96 | 50.8 |
| 29 | 31.65 | 29.59 | −42.20 | −14.99 | 196.17 | 34.03 |
| 30 | 23.18 | 22.60 | 11.47 | 77.27 | 66.71 | 47.03 |
| 31 | 43.46 | 41.13 | 13.51 | 160.98 | 131.19 | 119.03 |
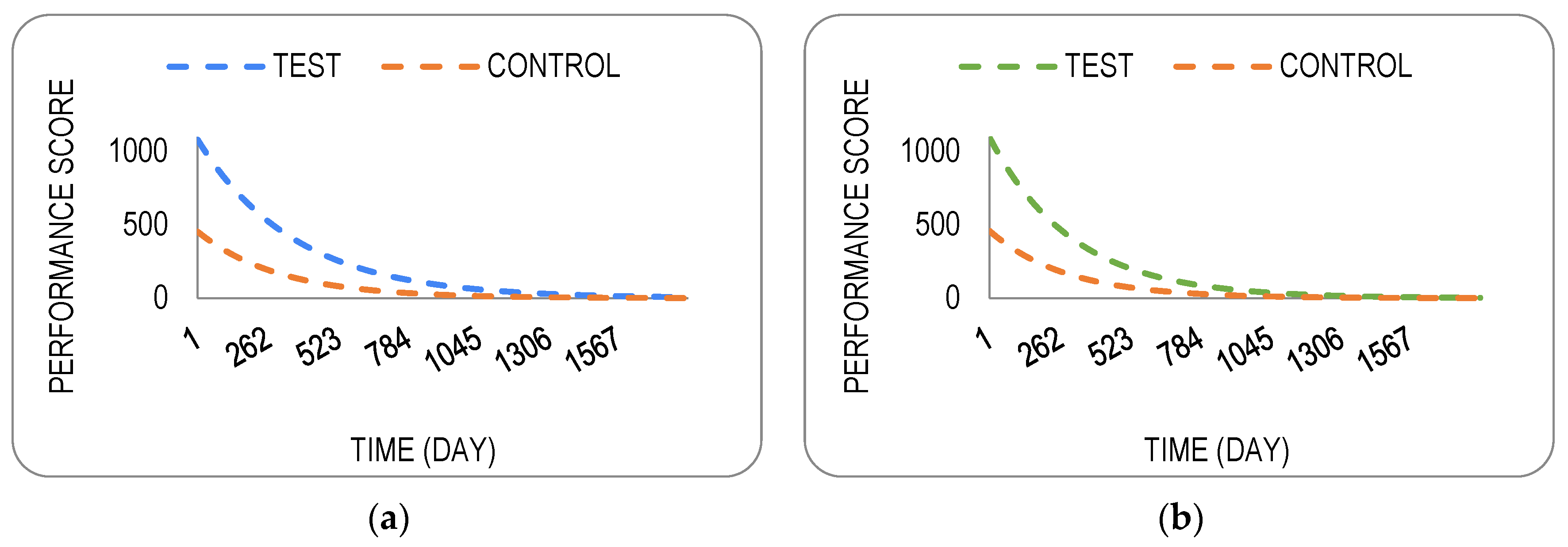
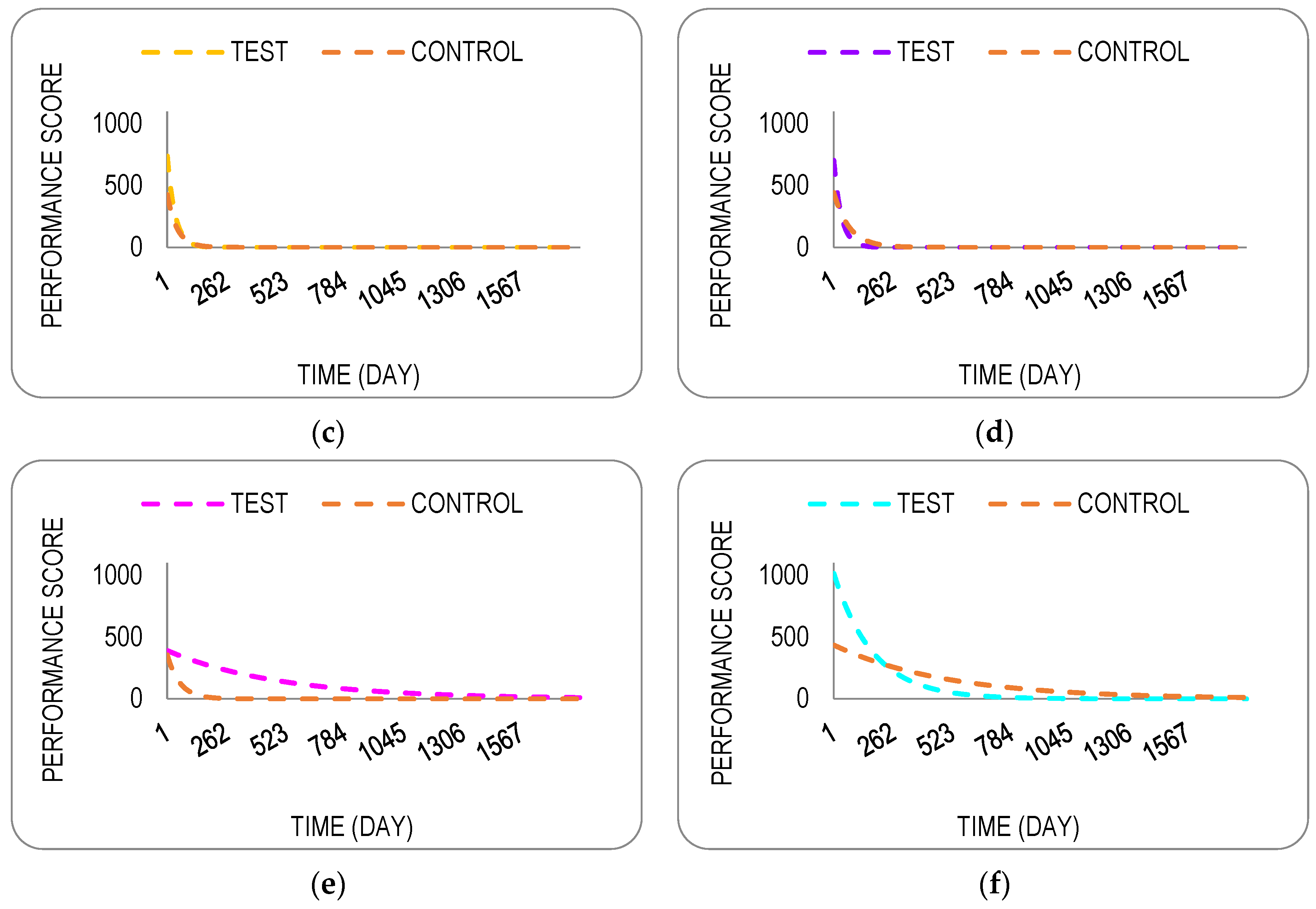
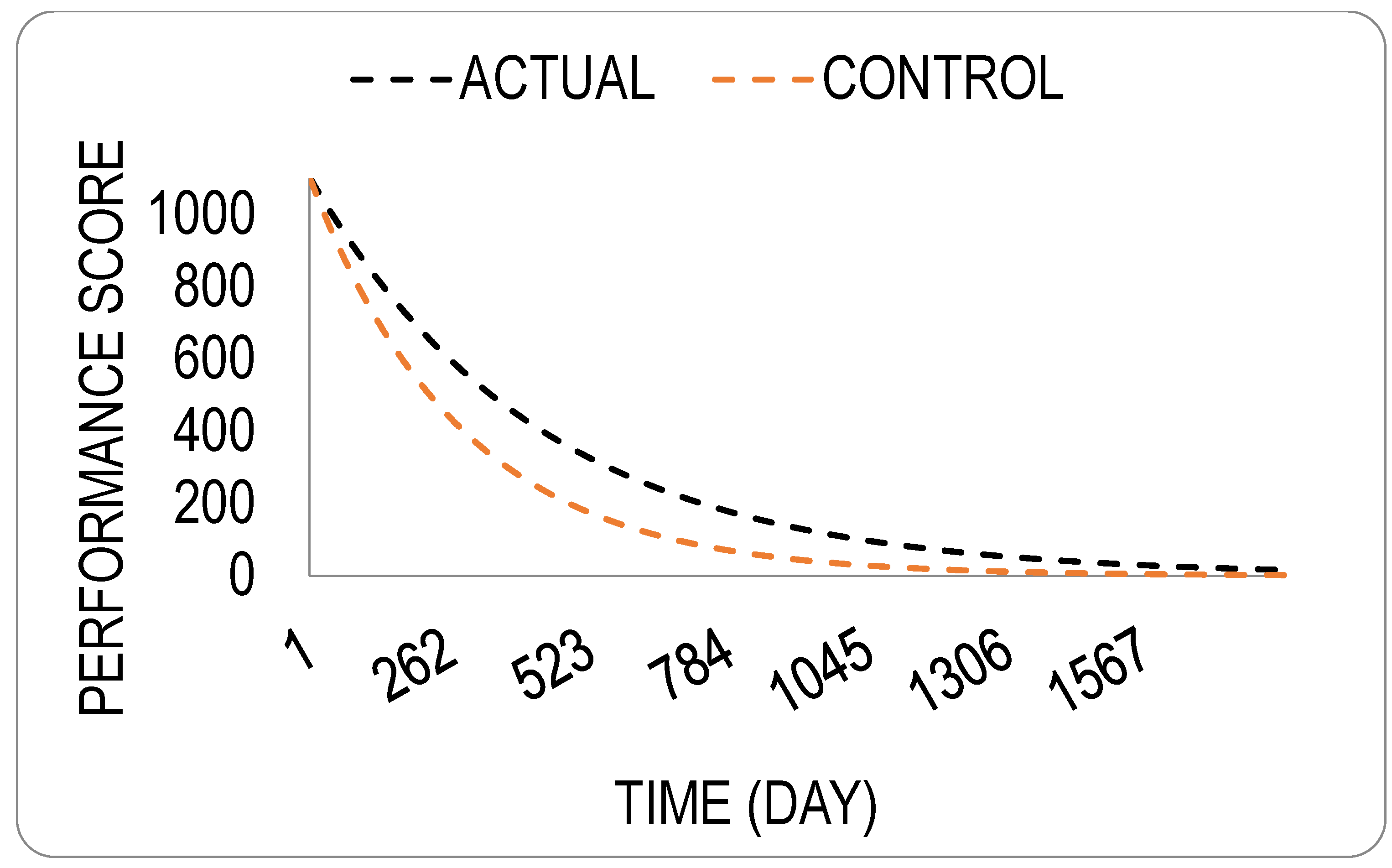
| Scenario | Accumulated Performance Score | Improvement % | |
|---|---|---|---|
| Test | Control | ||
| 1 | 685,503.47 | 382,414.14 | 121.12 |
| 2 | 688,662.57 | 387,169.60 | 119.42 |
| 3 | 319,517.96 | 243,488.76 | 61.87 |
| 4 | 301,967.28 | 288,051.63 | 29.32 |
| 5 | 244,167.26 | 217,680.27 | 38.37 |
| 6 | 615,151.44 | 337,961.97 | 124.53 |
| Actual | 467,334.70 | 313,006.84 | 49.30 |
| Scenario | Error % |
|---|---|
| 1 | 145.68 |
| 2 | 142.23 |
| 3 | 25.50 |
| 4 | 40.53 |
| 5 | 22.17 |
| 6 | 152.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacleb, N.R.A.; Ardiente, A.A.; Apolinario, G.F.D.G. Sustaining Battery Life: Deep-Cycle Lead-Acid Battery Through Acoustic Simulation and System Modeling. Energies 2025, 18, 5576. https://doi.org/10.3390/en18215576
Pacleb NRA, Ardiente AA, Apolinario GFDG. Sustaining Battery Life: Deep-Cycle Lead-Acid Battery Through Acoustic Simulation and System Modeling. Energies. 2025; 18(21):5576. https://doi.org/10.3390/en18215576
Chicago/Turabian StylePacleb, Napski Rudolph A., Alexis A. Ardiente, and Gerard Francesco D. G. Apolinario. 2025. "Sustaining Battery Life: Deep-Cycle Lead-Acid Battery Through Acoustic Simulation and System Modeling" Energies 18, no. 21: 5576. https://doi.org/10.3390/en18215576
APA StylePacleb, N. R. A., Ardiente, A. A., & Apolinario, G. F. D. G. (2025). Sustaining Battery Life: Deep-Cycle Lead-Acid Battery Through Acoustic Simulation and System Modeling. Energies, 18(21), 5576. https://doi.org/10.3390/en18215576






