VMD-LSTM-Based Model Predictive Control for Hybrid Energy Storage Systems with Auto-Tuning Weights and Constraints
Abstract
1. Introduction
- The introduction of the MPC-ATWC strategy represents a significant advancement. By auto-tuning weights and constraints, this strategy not only improves energy management efficiency but also prolongs battery life.
- The proposed VMD-LSTM model significantly improves the prediction accuracy of velocity and road gradient, thus leading to a more accurate power demand prediction.
- A combination of rule-based and fuzzy logic-based strategies is introduced to auto-tune the weights and constraints, optimizing UC utilization while alleviating the burden on batteries.
2. System Modeling
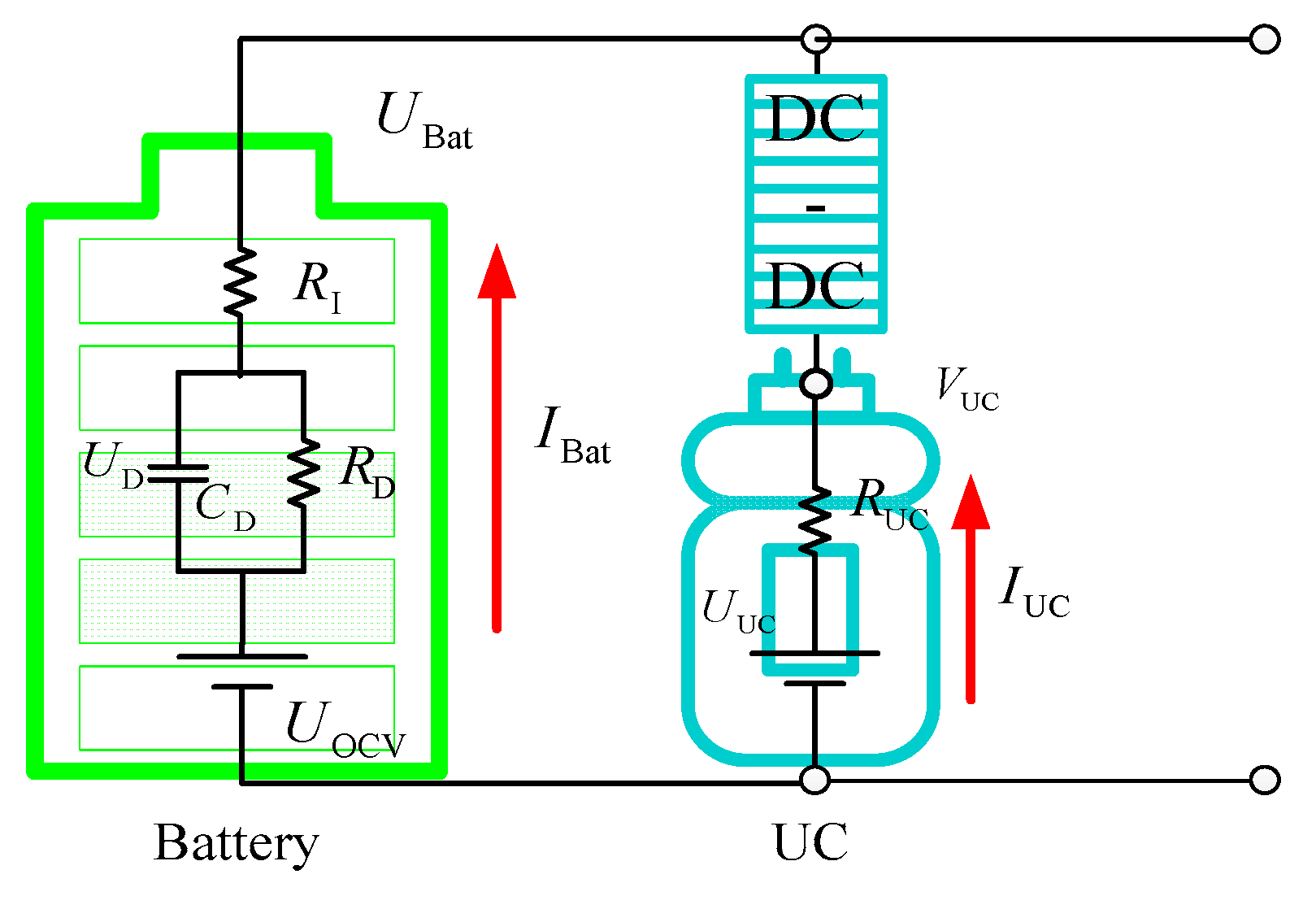
2.1. Vehicle and HESS Structure
2.2. HESS System Modeling
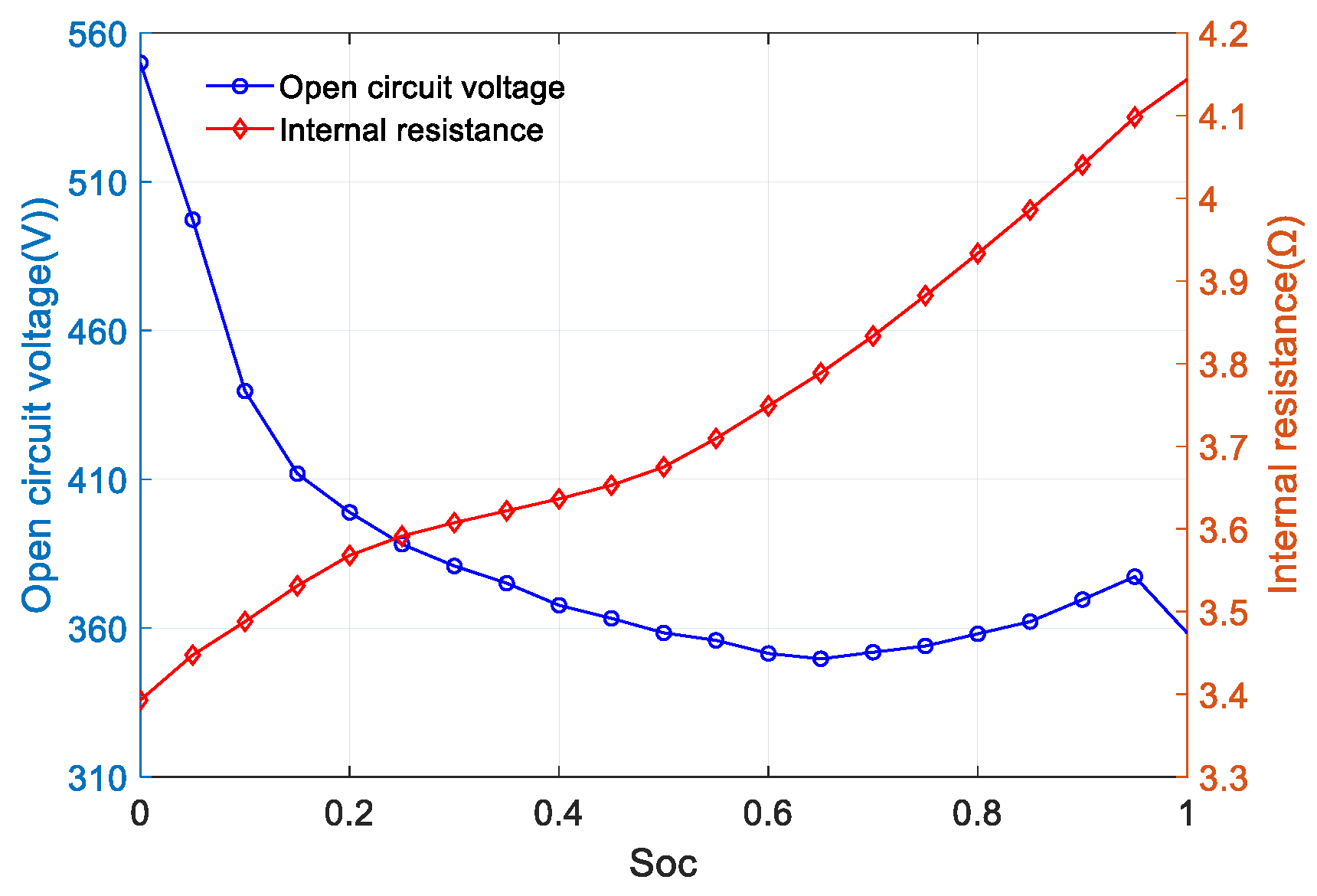
2.3. Model of Battery Lifetime Decay
3. Auto-Tuning Weight- and Constraint-Based MPC Method
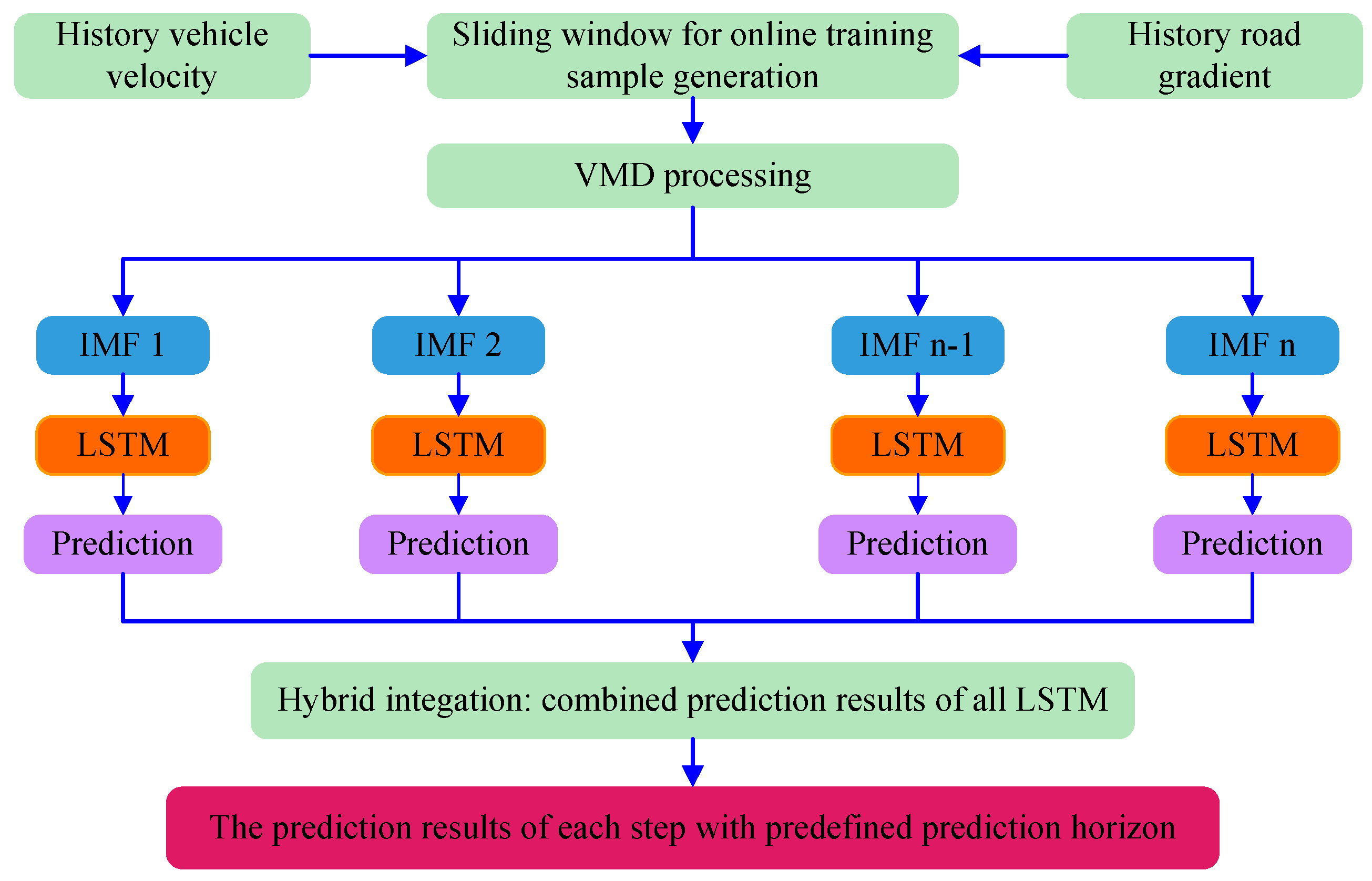
3.1. The Power Demand Prediction with VMD-LSTM
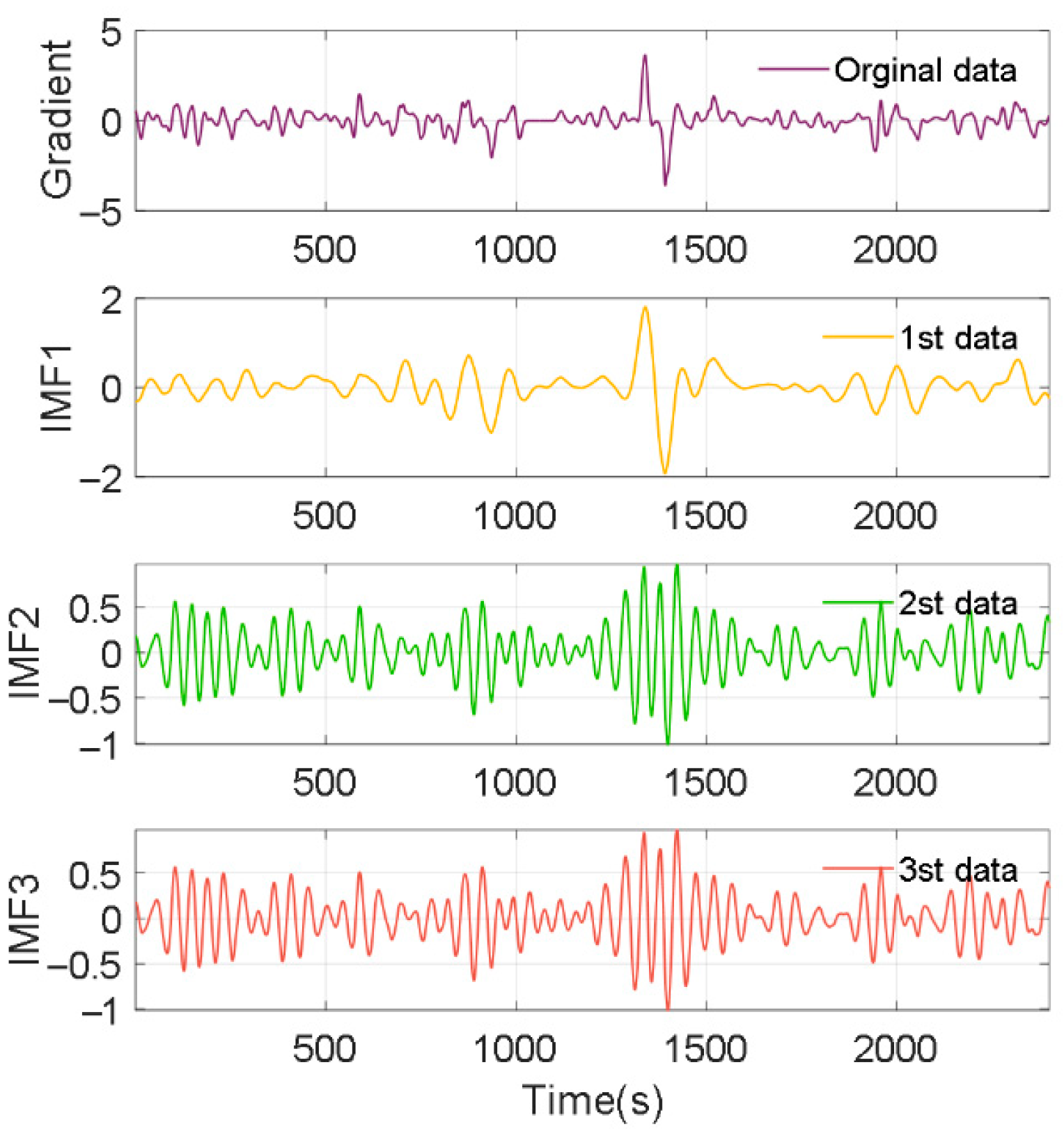
3.1.1. Model of the VMD
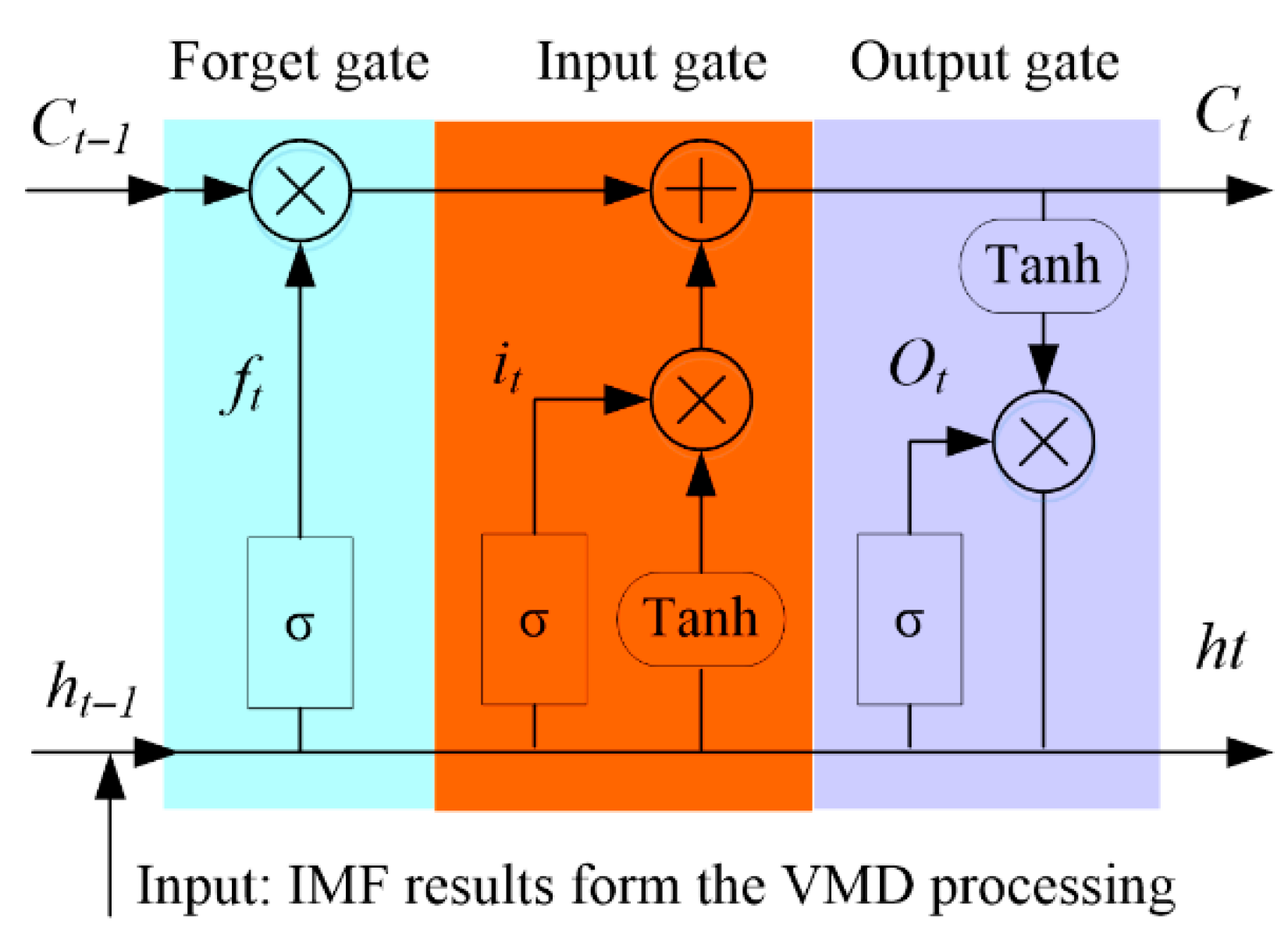
3.1.2. Model of the LSTM
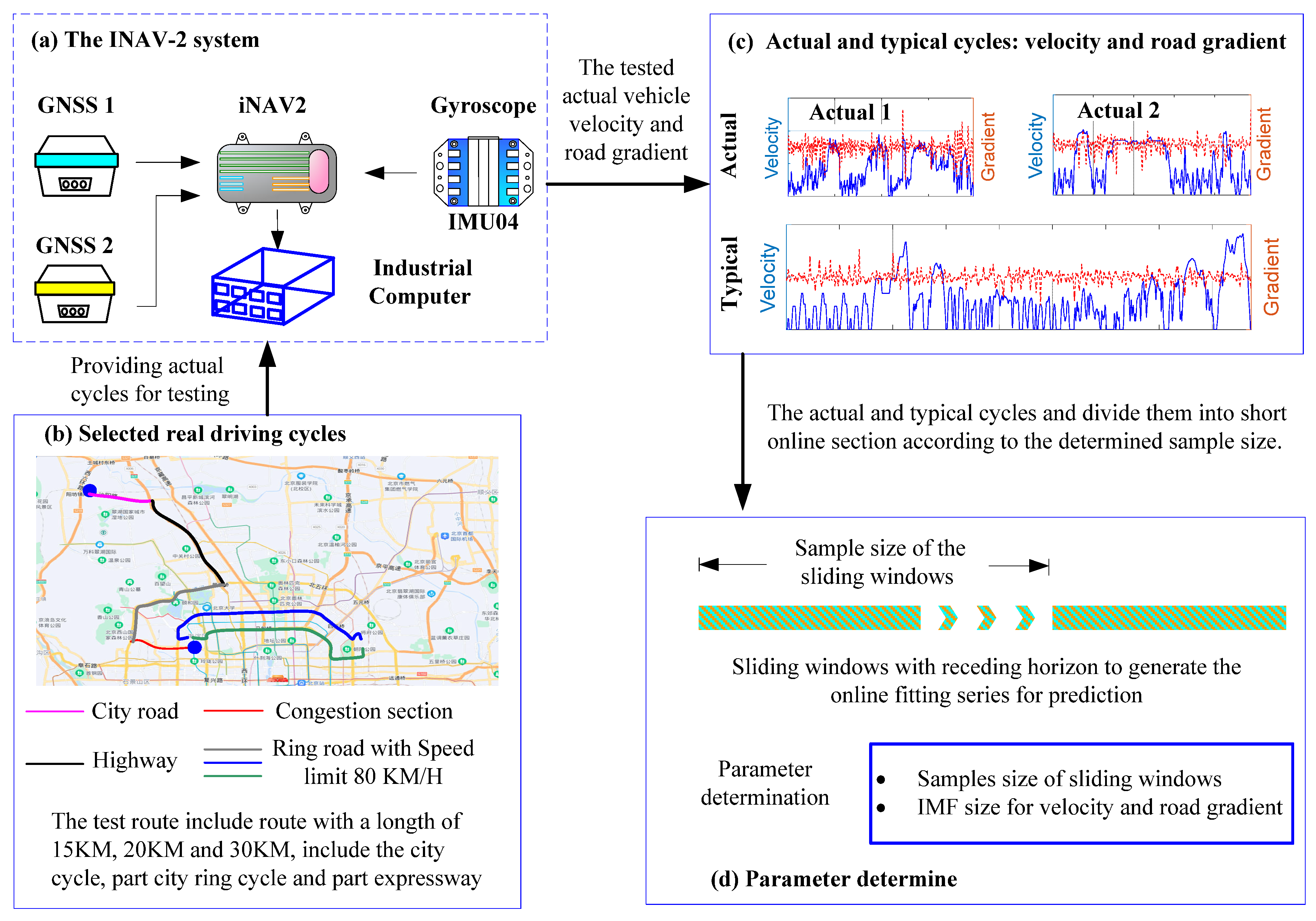
3.1.3. Actual Driving Cycle Test
3.2. Formulation of the Adaptive MPC
3.2.1. The MPC Modeling
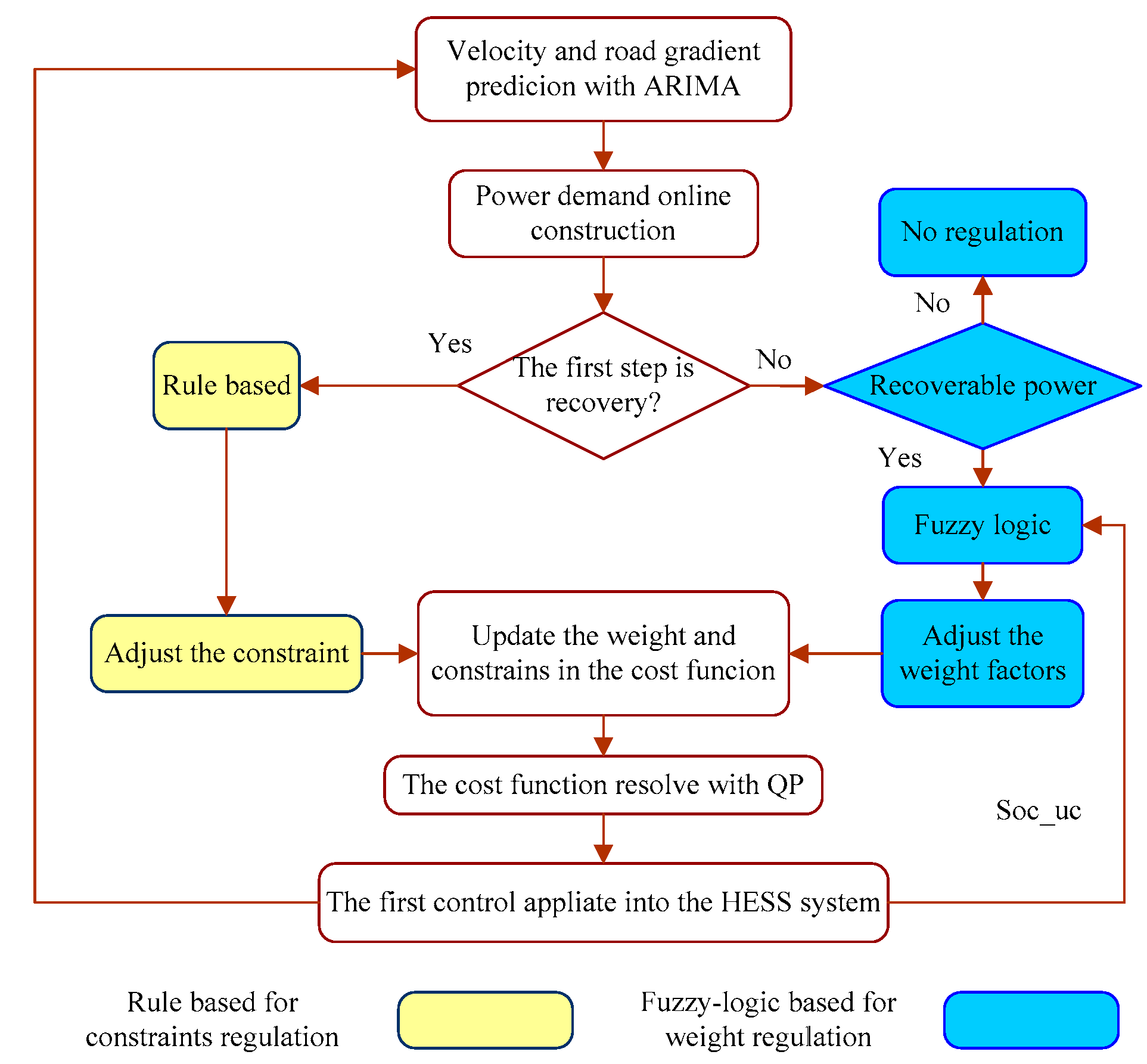
3.2.2. Auto-Tune Weights and Constraints with Rule-Based and Fuzzy Logic-Based Methods
4. Results and Discussion
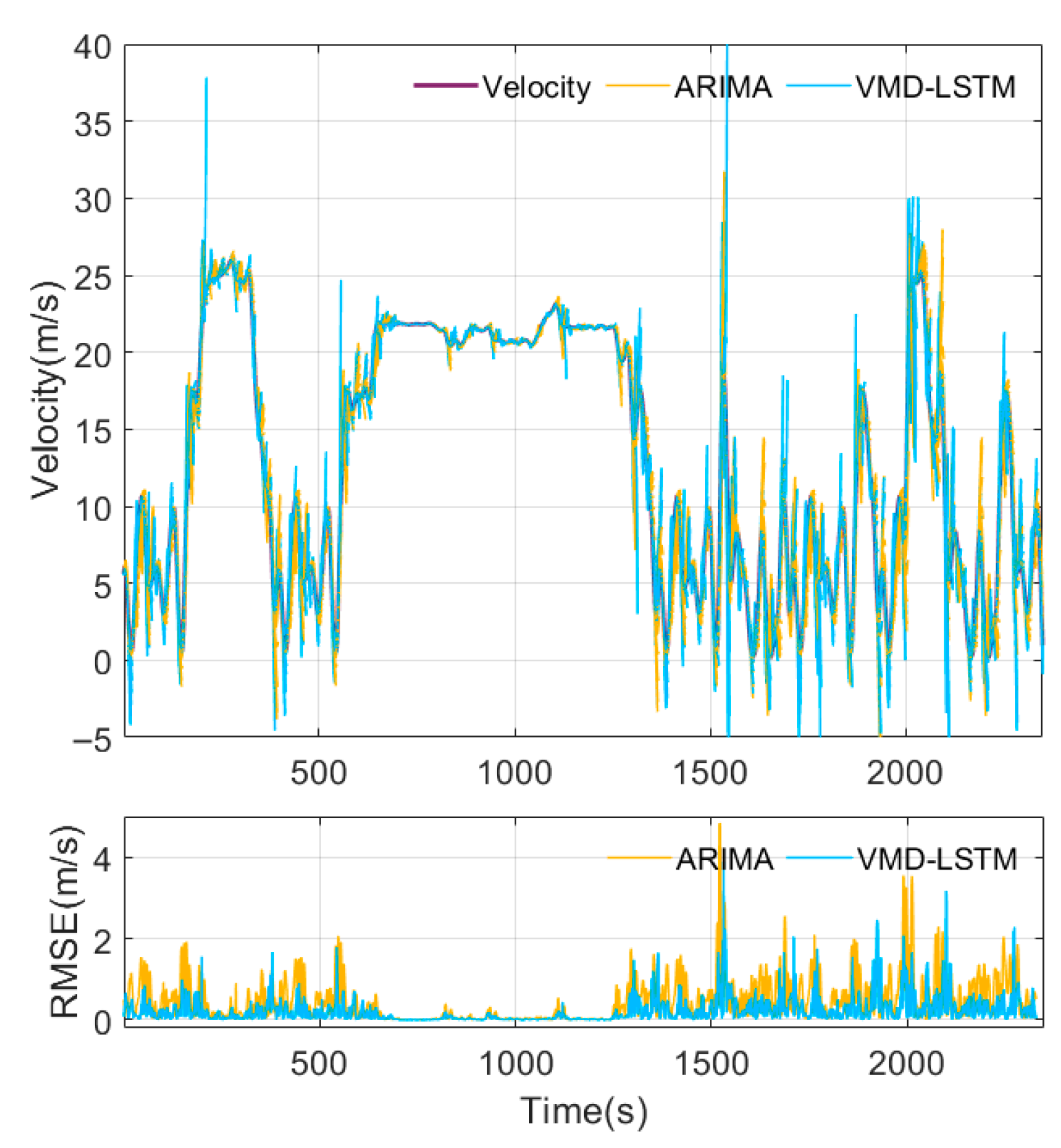
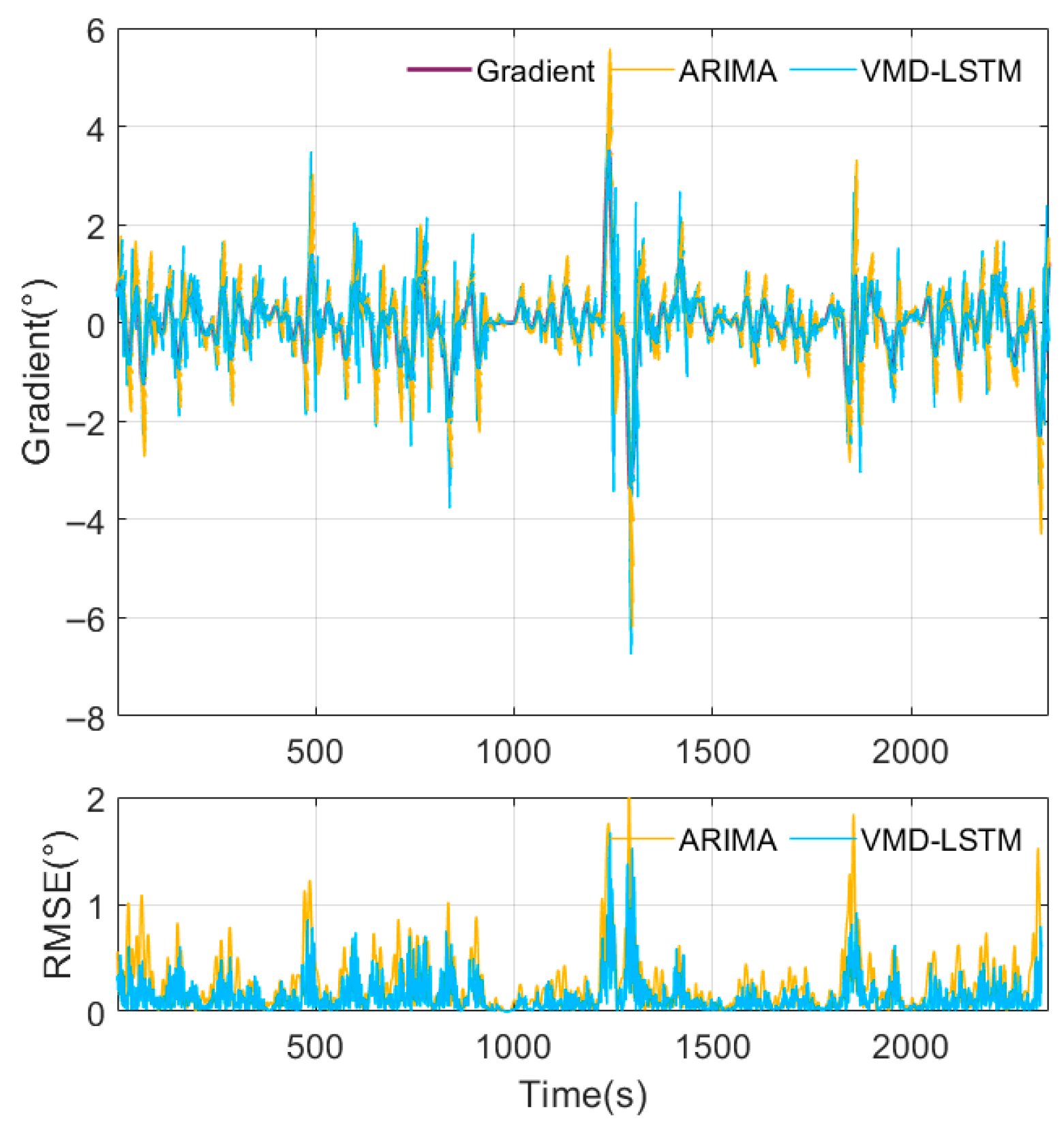
4.1. The VMD-LSTM Prediction Performance
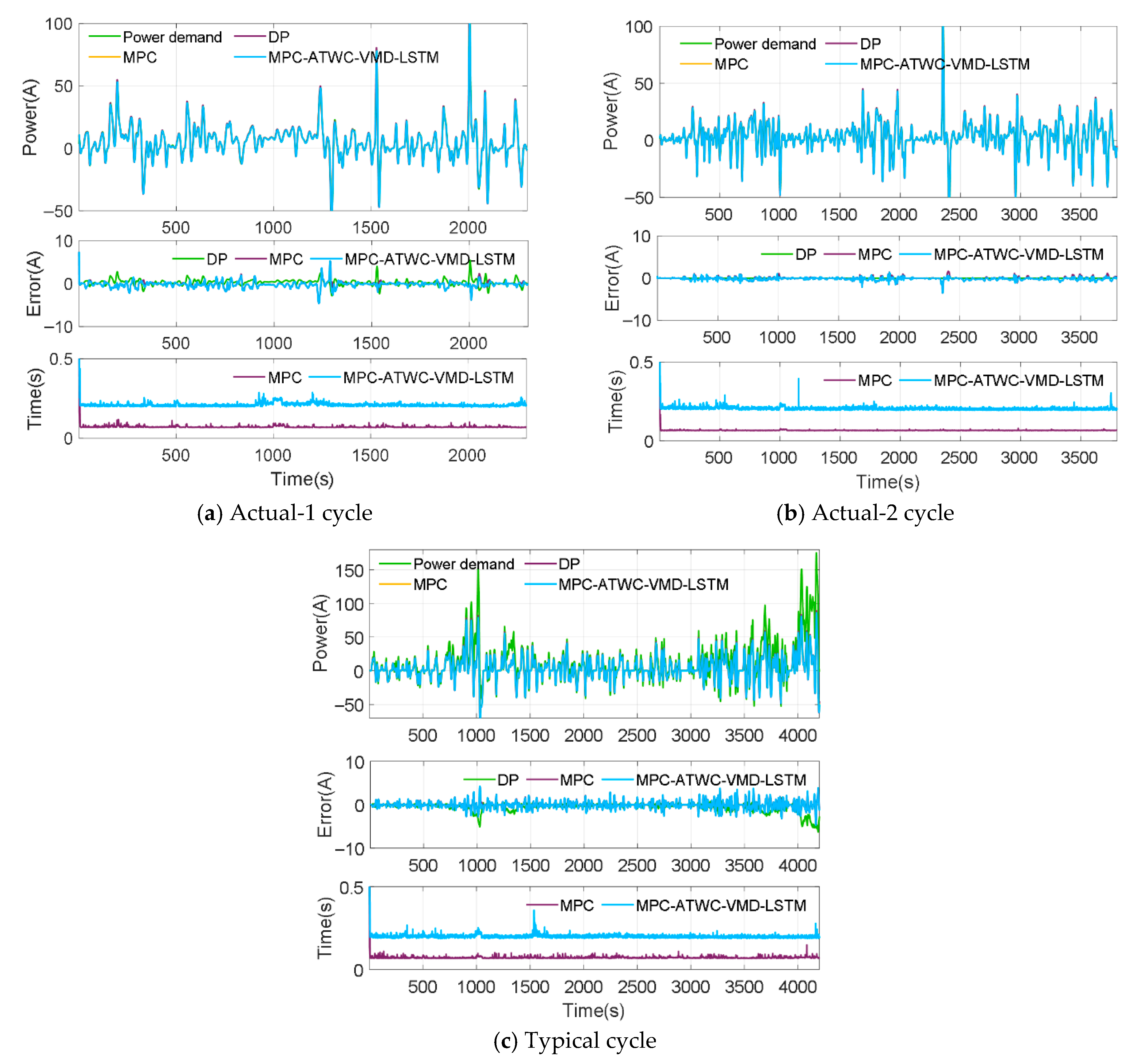
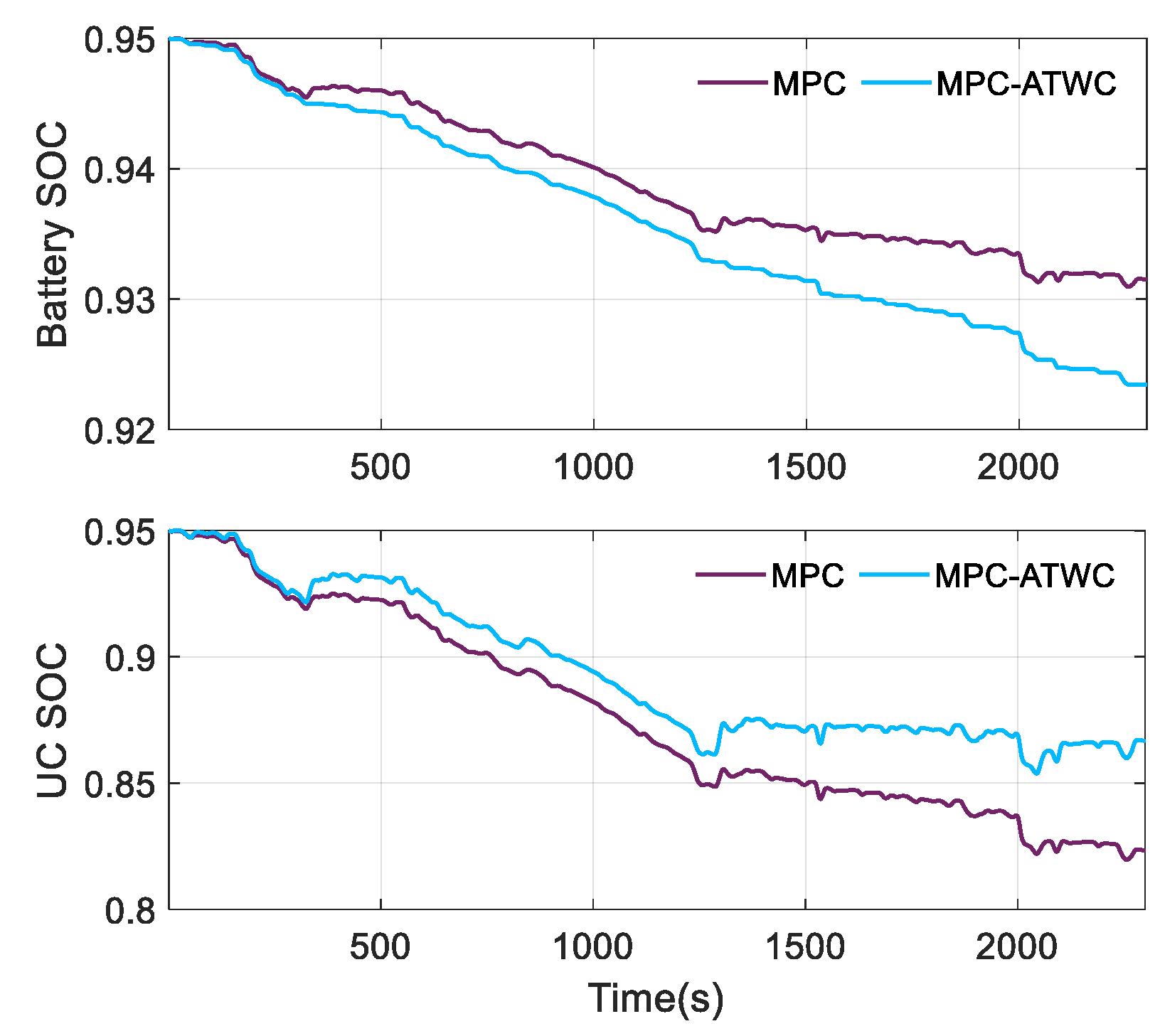
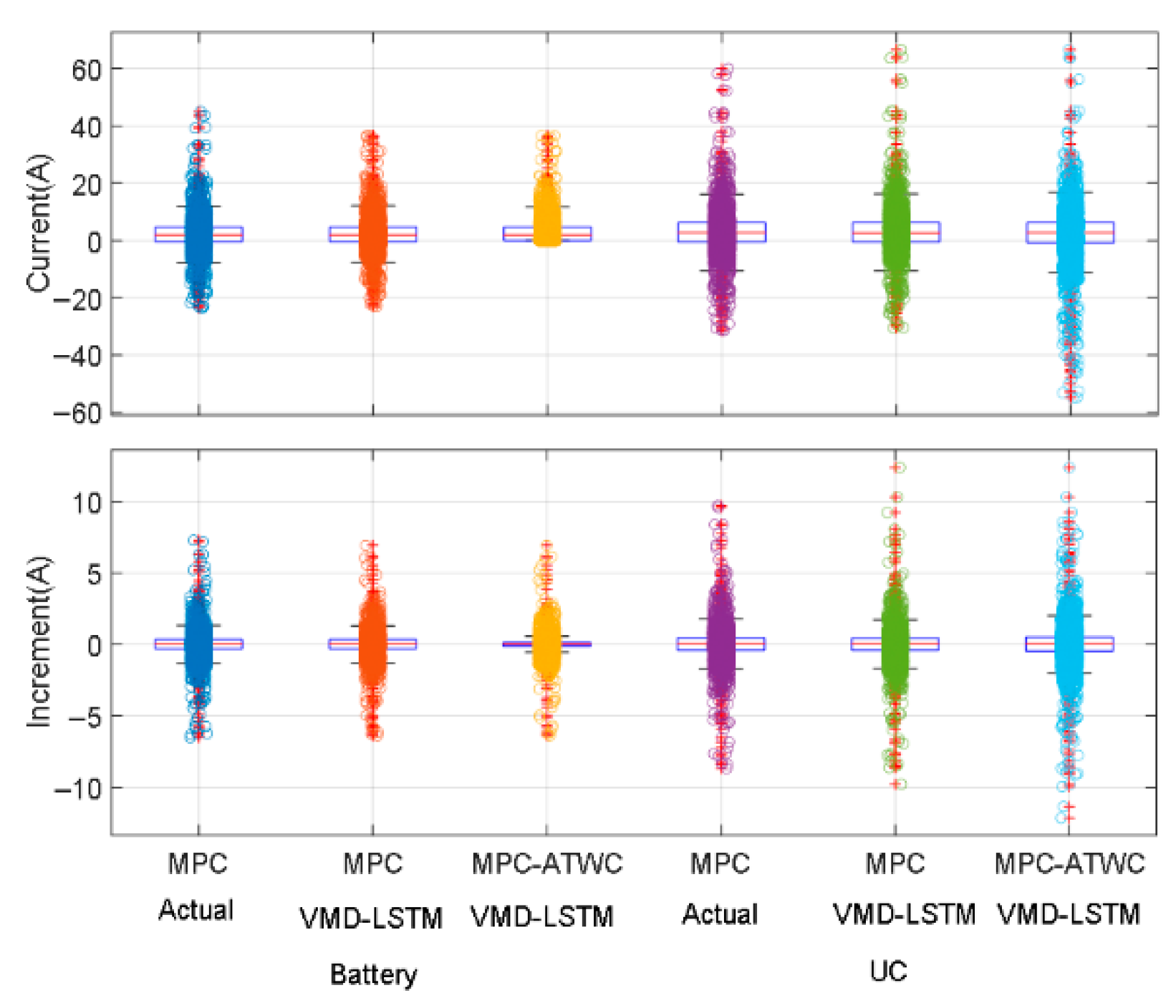
4.2. The Power-Tracking Performance of the Proposed Strategy
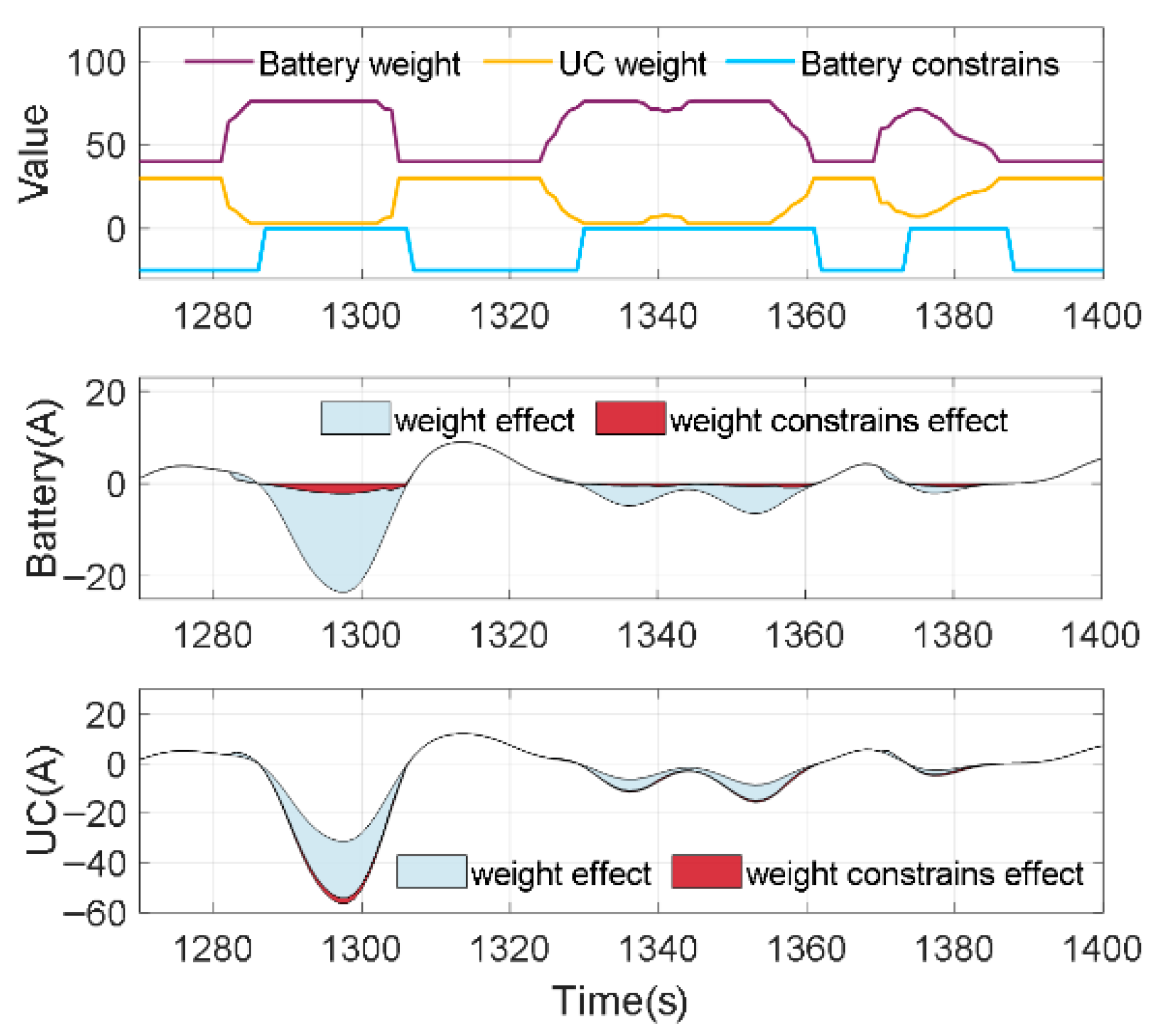
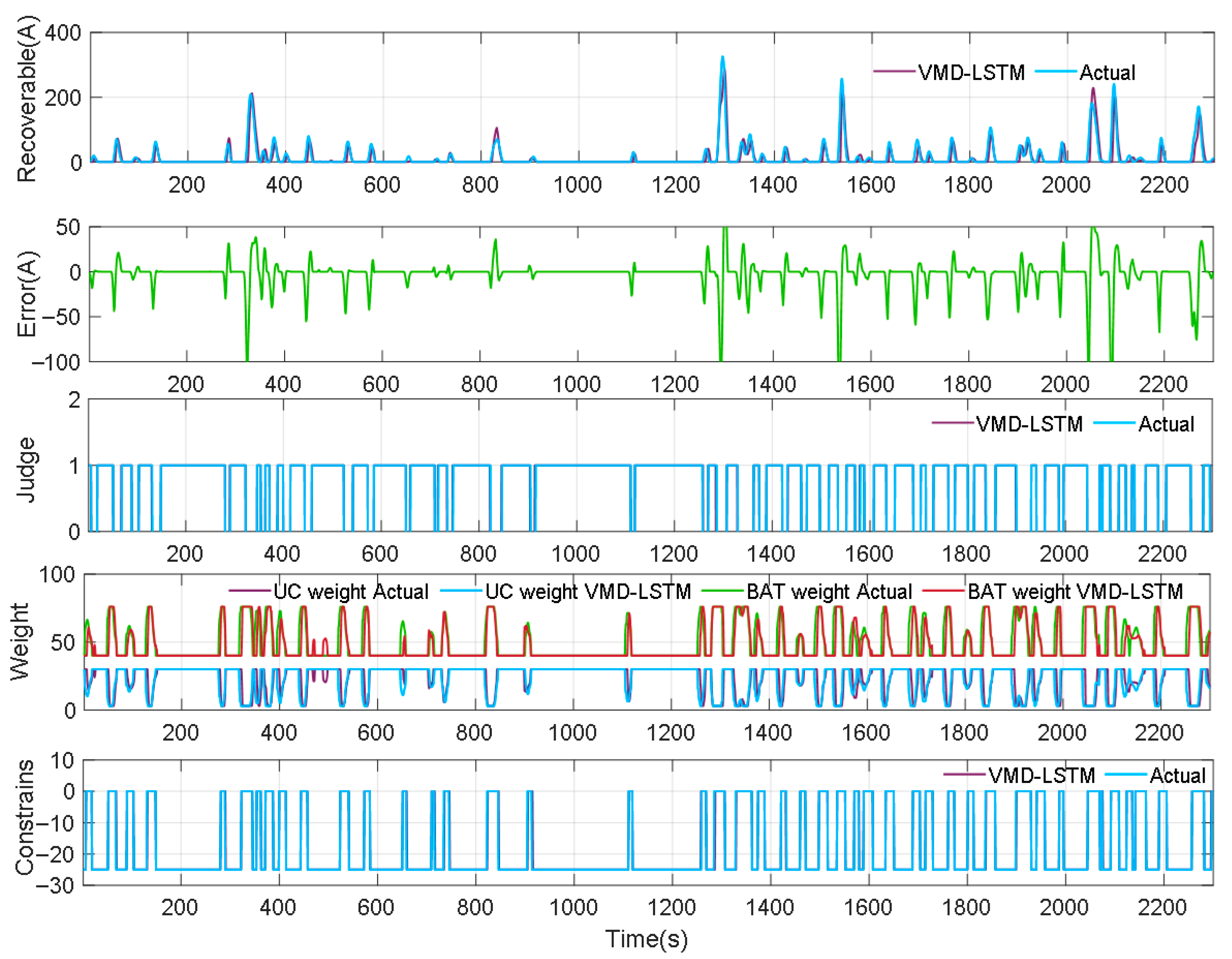
4.3. Effect of Weight and Constraints on Power Allocation
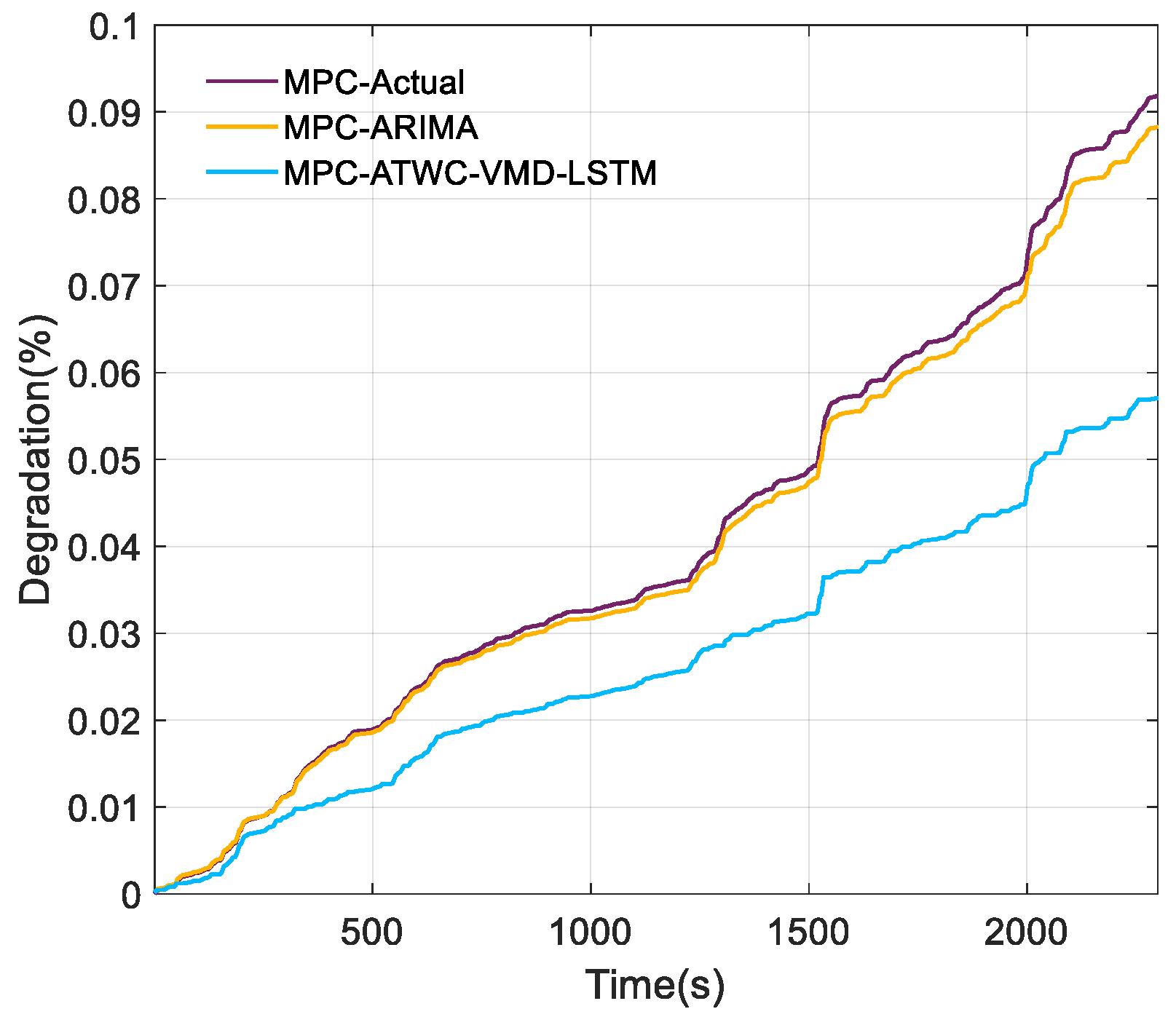
4.4. Overall Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
References
- Gao, D.; Luo, Z.; Liu, C.; Fan, S. A Survey of Hybrid Energy Devices Based on Supercapacitors. Green Energy Environ. 2023, 8, 972–988. [Google Scholar] [CrossRef]
- Li, F.; Gao, Y.; Wu, Y.; Xia, Y.; Wang, C.; Hu, J.; Huang, Z. Incentive Learning-Based Energy Management for Hybrid Energy Storage System in Electric Vehicles. Energy Convers. Manag. 2023, 293, 117480. [Google Scholar] [CrossRef]
- Luo, Y.; Fang, S.; Niu, T.; Fan, A.; Liao, R. Hierarchical Power Management of Shipboard Hybrid Energy Storage System Under Multiple Pulse Loads. IEEE Trans. Ind. Appl. 2024, 60, 1380–1395. [Google Scholar] [CrossRef]
- Ma, B.; Guo, X.; Li, P. Adaptive Energy Management Strategy Based on a Model Predictive Control with Real-Time Tuning Weight for Hybrid Energy Storage System. Energy 2023, 283, 129128. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, X.; Liu, Q.; Li, S.; Xu, Y. Review Article: A Comprehensive Review of Energy Management Strategies for Hybrid Electric Vehicles. Mech. Sci. 2022, 13, 147–188. [Google Scholar] [CrossRef]
- Zhang, S.; Xiong, R. Adaptive Energy Management of a Plug-in Hybrid Electric Vehicle Based on Driving Pattern Recognition and Dynamic Programming. Appl. Energy 2015, 155, 68–78. [Google Scholar] [CrossRef]
- Wang, H.; He, H.; Li, J.; Bai, Y.; Chang, Y.; Yan, B. Adaptive MPC Based Real-Time Energy Management Strategy of the Electric Sanitation Vehicles. Appl. Sci. 2021, 11, 498. [Google Scholar] [CrossRef]
- Zhu, T.; Wills, R.G.A.; Lot, R.; Ruan, H.; Jiang, Z. Adaptive Energy Management of a Battery-Supercapacitor Energy Storage System for Electric Vehicles Based on Flexible Perception and Neural Network Fitting. Appl. Energy 2021, 292, 116932. [Google Scholar] [CrossRef]
- Yang, N.; Han, L.; Liu, R.; Wei, Z.; Liu, H.; Xiang, C. Multiobjective Intelligent Energy Management for Hybrid Electric Vehicles Based on Multiagent Reinforcement Learning. IEEE Trans. Transp. Electrif. 2023, 9, 4294–4305. [Google Scholar] [CrossRef]
- Asensio, E.M.; Magallán, G.A.; Pérez, L.; De Angelo, C.H. Short-Term Power Demand Prediction for Energy Management of an Electric Vehicle Based on Batteries and Ultracapacitors. Energy 2022, 247, 123430. [Google Scholar] [CrossRef]
- Zheng, C.; Li, W.; Liang, Q. An Energy Management Strategy of Hybrid Energy Storage Systems for Electric Vehicle Applications. IEEE Trans. Sustain. Energy 2018, 9, 1880–1888. [Google Scholar] [CrossRef]
- Nie, Z.; Song, H.; Lian, Y.; Shi, Z. BiLSTM-ATTENTION-CNN Predictive Energy Management Based on ISSA Optimization for Intelligent Fuel Cell Hybrid Vehicle Platoon. Energy 2025, 324, 135860. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Z.; Liu, J.; Wu, Q. Coordinated Mechanical Loads and Power Optimization of Wind Energy Conversion Systems with Variable-Weight Model Predictive Control Strategy. Appl. Energy 2019, 236, 307–317. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Li, G.; Liu, Y.; Huang, Y.; Cunningham, G.; Early, J. Integrated Velocity Prediction Method and Application in Vehicle-Environment Cooperative Control Based on Internet of Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 2639–2654. [Google Scholar] [CrossRef]
- Ewusie, J.E.; Soobiah, C.; Blondal, E.; Beyene, J.; Thabane, L.; Hamid, J.S. Methods, Applications and Challenges in the Analysis of Interrupted Time Series Data: A Scoping Review. J. Multidiscip. Healthc. 2020, 13, 411–423. [Google Scholar] [CrossRef]
- Quan, S.; Wang, Y.-X.; Xiao, X.; He, H.; Sun, F. Real-Time Energy Management for Fuel Cell Electric Vehicle Using Speed Prediction-Based Model Predictive Control Considering Performance Degradation. Appl. Energy 2021, 304, 117845. [Google Scholar] [CrossRef]
- Guo, L.; Liu, H.; Han, L.; Yang, N.; Liu, R.; Xiang, C. Predictive Energy Management Strategy of Dual-Mode Hybrid Electric Vehicles Combining Dynamic Coordination Control and Simultaneous Power Distribution. Energy 2023, 263, 125598. [Google Scholar] [CrossRef]
- Guo, J.; He, H.; Sun, C. ARIMA-Based Road Gradient and Vehicle Velocity Prediction for Hybrid Electric Vehicle Energy Management. IEEE Trans. Veh. Technol. 2019, 68, 5309–5320. [Google Scholar] [CrossRef]
- Wang, W.; Ma, B.; Guo, X.; Chen, Y.; Xu, Y. A Hybrid ARIMA-LSTM Model for Short-Term Vehicle Speed Prediction. Energies 2024, 17, 3736. [Google Scholar] [CrossRef]
- Chen, H.; Lu, T.; Huang, J.; He, X.; Yu, K.; Sun, X.; Ma, X.; Huang, Z. An Improved VMD-LSTM Model for Time-Varying GNSS Time Series Prediction with Temporally Correlated Noise. Remote Sens. 2023, 15, 3694. [Google Scholar] [CrossRef]
- Ji, Q.; Han, L.; Jiang, L.; Zhang, Y.; Xie, M.; Liu, Y. Short-Term Prediction of the Significant Wave Height and Average Wave Period Based on the Variational Mode Decomposition–Temporal Convolutional Network–Long Short-Term Memory (VMD–TCN–LSTM) Algorithm. Ocean Sci. 2023, 19, 1561–1578. [Google Scholar] [CrossRef]
- Ding, T.; Wu, D.; Shen, L.; Liu, Q.; Zhang, X.; Li, Y. Prediction of Significant Wave Height Using a VMD-LSTM-Rolling Model in the South Sea of China. Front. Mar. Sci. 2024, 11, 1382248. [Google Scholar] [CrossRef]
- Ramasamy, V.; Kannan, R.; Muralidharan, G.; Sidharthan, R.K.; Veerasamy, G.; Venkatesh, S.; Amirtharajan, R. Comprehensive Review on Advanced Process Control of Cement Kiln Process with the Focus on MPC Tuning Strategies. J. Process Control 2023, 121, 85–102. [Google Scholar] [CrossRef]
- Gomozov, O.; Trovao, J.P.F.; Kestelyn, X.; Dubois, M.R. Adaptive Energy Management System Based on a Real-Time Model Predictive Control With Nonuniform Sampling Time for Multiple Energy Storage Electric Vehicle. IEEE Trans. Veh. Technol. 2017, 66, 5520–5530. [Google Scholar] [CrossRef]
- Sun, J.; Li, Z.; Li, J.; Wu, G.; Xia, Y. Hybrid Power System with Adaptive Adjustment of Weight Coefficients Multi-Objective Model Predictive Control. Int. J. Electr. Power Energy Syst. 2023, 153, 109296. [Google Scholar] [CrossRef]
- Zhan, S.; Chen, Y.; Ringwood, J.V. Terminal Weight and Constraint Design for Wave Energy Converter Economic Model Predictive Control Problems. Int. J. Robust Nonlinear Control 2023, 35, 2694–2716. [Google Scholar] [CrossRef]
- Bakibillah, A.S.M.; Kamal, M.A.S.; Tan, C.P.; Hayakawa, T.; Imura, J. Fuzzy-Tuned Model Predictive Control for Dynamic Eco-Driving on Hilly Roads. Appl. Soft Comput. 2021, 99, 106875. [Google Scholar] [CrossRef]
- Zhao, R.C.; Wong, P.K.; Xie, Z.C.; Zhao, J. Real-Time Weighted Multi-Objective Model Predictive Controller for Adaptive Cruise Control Systems. Int. J. Automot. Technol. 2017, 18, 279–292. [Google Scholar] [CrossRef]
- Liu, H.; Chen, G.; Li, D.; Wang, J.; Zhou, J. Energy Active Adjustment and Bidirectional Transfer Management Strategy of the Electro-Hydrostatic Hydraulic Hybrid Powertrain for Battery Bus. Energy 2021, 230, 120794. [Google Scholar] [CrossRef]
- Yang, C.; Sun, T.; Wang, W.; Li, Y.; Zhang, Y.; Zha, M. Regenerative Braking System Development and Perspectives for Electric Vehicles: An Overview. Renew. Sustain. Energy Rev. 2024, 198, 114389. [Google Scholar] [CrossRef]
- Lü, X.; Li, S.; He, X.; Xie, C.; He, S.; Xu, Y.; Fang, J.; Zhang, M.; Yang, X. Hybrid Electric Vehicles: A Review of Energy Management Strategies Based on Model Predictive Control. J. Energy Storage 2022, 56, 106112. [Google Scholar] [CrossRef]
- Ju, F.; Murgovski, N.; Zhuang, W.; Wang, Q.; Wang, L. Predictive Cruise Controller for Electric Vehicle to Save Energy and Extend Battery Lifetime. IEEE Trans. Veh. Technol. 2023, 72, 469–482. [Google Scholar] [CrossRef]
- Yan, M.; Li, G.; Li, M.; He, H.; Xu, H.; Liu, H. Hierarchical Predictive Energy Management of Fuel Cell Buses with Launch Control Integrating Traffic Information. Energy Convers. Manag. 2022, 256, 115397. [Google Scholar] [CrossRef]
- Wu, G.; Wang, C.; Zhao, W.; Meng, Q. Integrated Energy Management of Hybrid Power Supply Based on Short-Term Speed Prediction. Energy 2023, 262, 125620. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, D.; Zeng, X.; Zhang, X.; Song, D. Multi-Objective Real-Time Energy Management for Series–Parallel Hybrid Electric Vehicles Considering Battery Life. Energy Convers. Manag. 2023, 290, 117234. [Google Scholar] [CrossRef]
- Uddin, M.; Mekhilef, S.; Rivera, M.; Rodriguez, J. Imposed Weighting Factor Optimization Method for Torque Ripple Reduction of IM Fed by Indirect Matrix Converter with Predictive Control Algorithm. J. Electr. Eng. Technol. 2015, 10, 227–242. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Coskun, S.; Pang, H.; Cui, Y.; Xi, J. Energy Management Strategies for Hybrid Electric Vehicles: Review, Classification, Comparison, and Outlook. Energies 2020, 13, 3352. [Google Scholar] [CrossRef]
- Chen, H.; Xiong, R.; Lin, C.; Shen, W. Model Predictive Control Based Real-Time Energy Management for a Hybrid Energy Storage System. CSEE J. Power Energy Syst. 2020, 7, 862–874. [Google Scholar] [CrossRef]
- Zhou, Y.; Ravey, A.; Péra, M.-C. Real-Time Cost-Minimization Power-Allocating Strategy via Model Predictive Control for Fuel Cell Hybrid Electric Vehicles. Energy Convers. Manag. 2021, 229, 113721. [Google Scholar] [CrossRef]
- Feng, Y.; Dong, Z. Optimal Energy Management with Balanced Fuel Economy and Battery Life for Large Hybrid Electric Mining Truck. J. Power Sources 2020, 454, 227948. [Google Scholar] [CrossRef]
- Jia, C.; Cui, J.; Qiao, W.; Qu, L. Real-Time Model Predictive Control for Battery-Supercapacitor Hybrid Energy Storage Systems Using Linear Parameter-Varying Models. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 251–263. [Google Scholar] [CrossRef]
- Hou, J.; Yao, D.; Wu, F.; Shen, J.; Chao, X. Online Vehicle Velocity Prediction Using an Adaptive Radial Basis Function Neural Network. IEEE Trans. Veh. Technol. 2021, 70, 3113–3122. [Google Scholar] [CrossRef]







| Parameter | ||||||
| Value | 500 V | 77 Ah | 500 V | 165 F | 0.98 | 1500 kg |
| Parameter | ||||||
| Value | 3 m2 | 0.011 | 0.55 | 1.03 | 0.0032 | −15,162 |
| Parameter | (K) | |||||
| Value | 1516 | 8.314 | 0.849 | 25 | 0.0025 |
| Parameters | Value | Parameters | Value | Parameters | Value |
| −0.5 V | 2.5 V | 50 A | |||
| 0.3 | 0.95 | −25 A | |||
| 0.5 | 0.95 | 30 | |||
| 150 A | −150 A | 40 |
| Parameters | Strategy | ARMSE | Compute Time(s) | |||
|---|---|---|---|---|---|---|
| 7 s | 9 s | 11 s | 13 s | |||
| Velocity (m/s) | VMD-LSTM | 0.26 | 0.41 | 0.52 | 0.74 | 0.285 |
| ARIMA | 0.31 | 0.49 | 0.71 | 0.94 | 0.195 | |
| RBF-NN | 0.98 | 1.18 | 1.36 | 1.58 | 0.103 | |
| LSTM | 0.84 | 1.02 | 1.14 | 1.65 | 0.098 | |
| Gradient (°) | VMD-LSTM | 0.21 | 0.32 | 0.53 | 0.65 | 0.292 |
| ARIMA | 0.32 | 0.42 | 0.73 | 0.97 | 0.183 | |
| RBF-NN | 0.3 | 0.42 | 0.63 | 0.73 | 0.095 | |
| LSTM | 0.41 | 0.51 | 0.61 | 0.75 | 0.093 | |
| Cycle | Prediction | Strategy | Utilization (%) | UC Utilization Improvement (%) | ERC | Battery Life Prolonged (%) | Time(s) | |
|---|---|---|---|---|---|---|---|---|
| Battery | UC | |||||||
| Actual-1 | Actual | DP | 40.62 | 59.38 | NAN | 425 | NAN | NAN |
| Actual | MPC | 42.85 | 57.14 | −2.24 | 435 | 2.35 | 0.073 | |
| Actual | MPC-ATWC | 31.59 | 68.41 | 9.03 | 506 | 19.06 | 0.132 | |
| LSTM | MPC-ATWC | 33.48 | 66.52 | 7.14 | 492 | 15.76 | 0.192 | |
| VMD-LSTM | MPC-ATWC | 32.23 | 67.77 | 8.39 | 512 | 20.47 | 0.380 | |
| Actual-2 | Actual | DP | 40.15 | 59.85 | NAN | 552 | NAN | NAN |
| Actual | MPC | 42.79 | 57.21 | −2.64 | 584 | 5.79 | 0.091 | |
| Actual | MPC-ATWC | 27.30 | 72.70 | 12.85 | 625 | 13.22 | 0.125 | |
| LSTM | MPC-ATWC | 28.79 | 71.21 | 11.36 | 611 | 10.68 | 0.201 | |
| VMD-LSTM | MPC-ATWC | 27.79 | 72.21 | 12.36 | 634 | 14.86 | 0.392 | |
| Typical | Actual | DP | 40.52 | 59.48 | NAN | 368 | NAN | NAN |
| Actual | MPC | 42.81 | 57.19 | −2.29 | 398 | 8.15 | 0.082 | |
| Actual | MPC-ATWC | 27.51 | 72.49 | 13.01 | 438 | 19.02 | 0.102 | |
| LSTM | MPC-ATWC | 29.88 | 70.12 | 10.64 | 425 | 15.48 | 0.185 | |
| VMD-LSTM | MPC-ATWC | 28.32 | 71.68 | 12.19 | 456 | 23.91 | 0.372 | |
| Overall | 10.98 | 19.75 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Ma, B.; Li, P.-H. VMD-LSTM-Based Model Predictive Control for Hybrid Energy Storage Systems with Auto-Tuning Weights and Constraints. Energies 2025, 18, 5559. https://doi.org/10.3390/en18215559
Yang Y, Ma B, Li P-H. VMD-LSTM-Based Model Predictive Control for Hybrid Energy Storage Systems with Auto-Tuning Weights and Constraints. Energies. 2025; 18(21):5559. https://doi.org/10.3390/en18215559
Chicago/Turabian StyleYang, Yi, Bin Ma, and Peng-Hui Li. 2025. "VMD-LSTM-Based Model Predictive Control for Hybrid Energy Storage Systems with Auto-Tuning Weights and Constraints" Energies 18, no. 21: 5559. https://doi.org/10.3390/en18215559
APA StyleYang, Y., Ma, B., & Li, P.-H. (2025). VMD-LSTM-Based Model Predictive Control for Hybrid Energy Storage Systems with Auto-Tuning Weights and Constraints. Energies, 18(21), 5559. https://doi.org/10.3390/en18215559







