Power Analysis Produced by Virtual Inertia in Single-Phase Grid-Forming Converters Under Frequency Events Intended for Bidirectional Battery Chargers
Abstract
1. Introduction
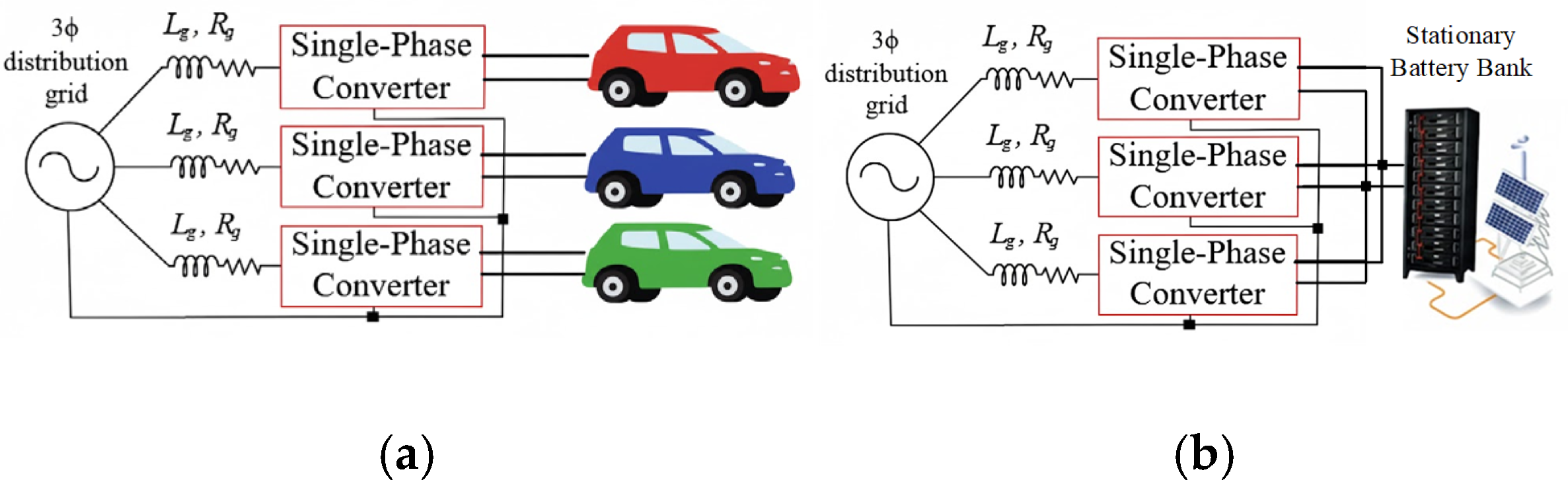
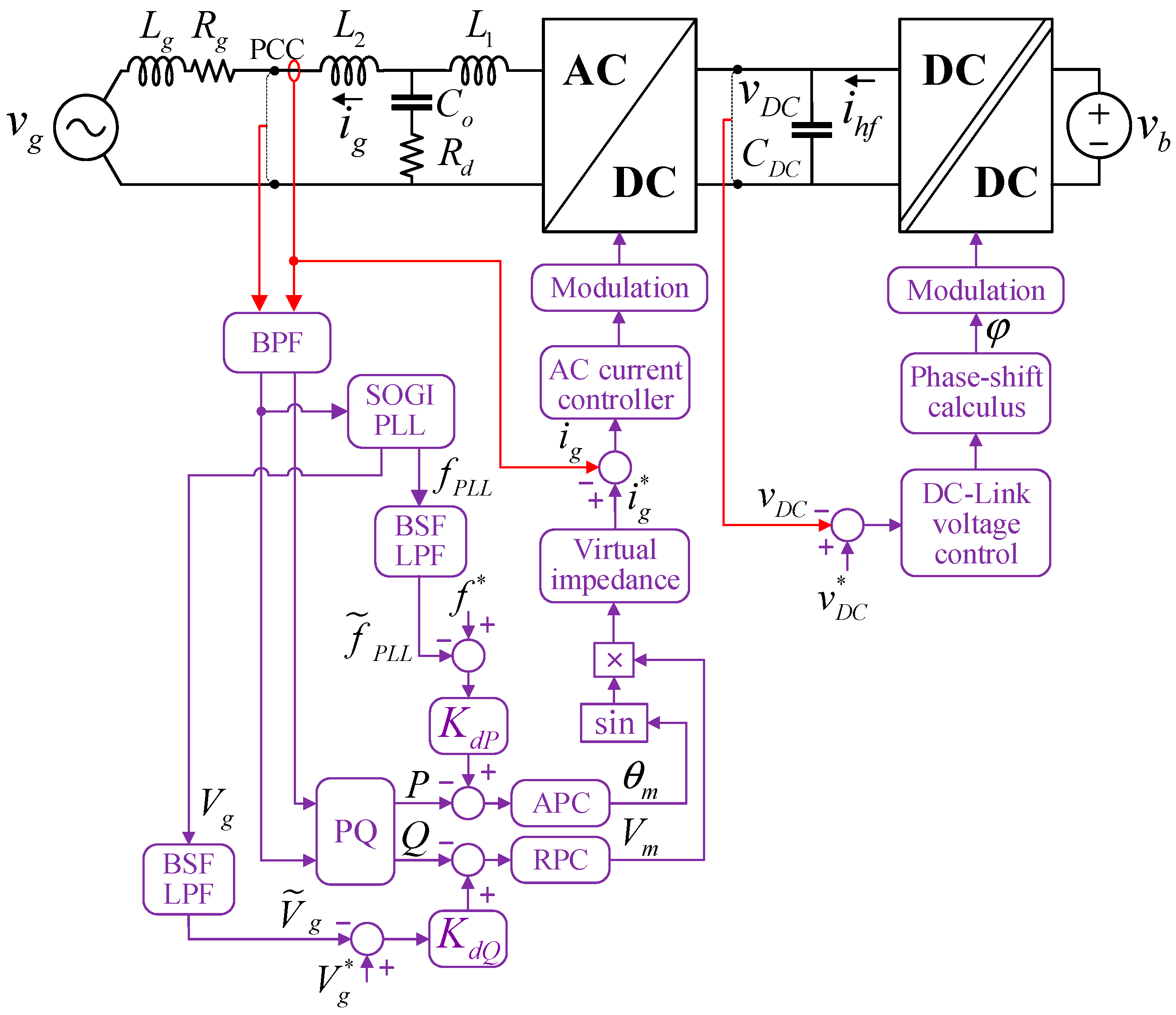
2. GFM Converter Control Strategy Implemented on a Single-Phase Isolated Bidirectional Battery Charger
2.1. Synchronous Generator
2.2. Power Transferred Between Two Sources
3. System Design
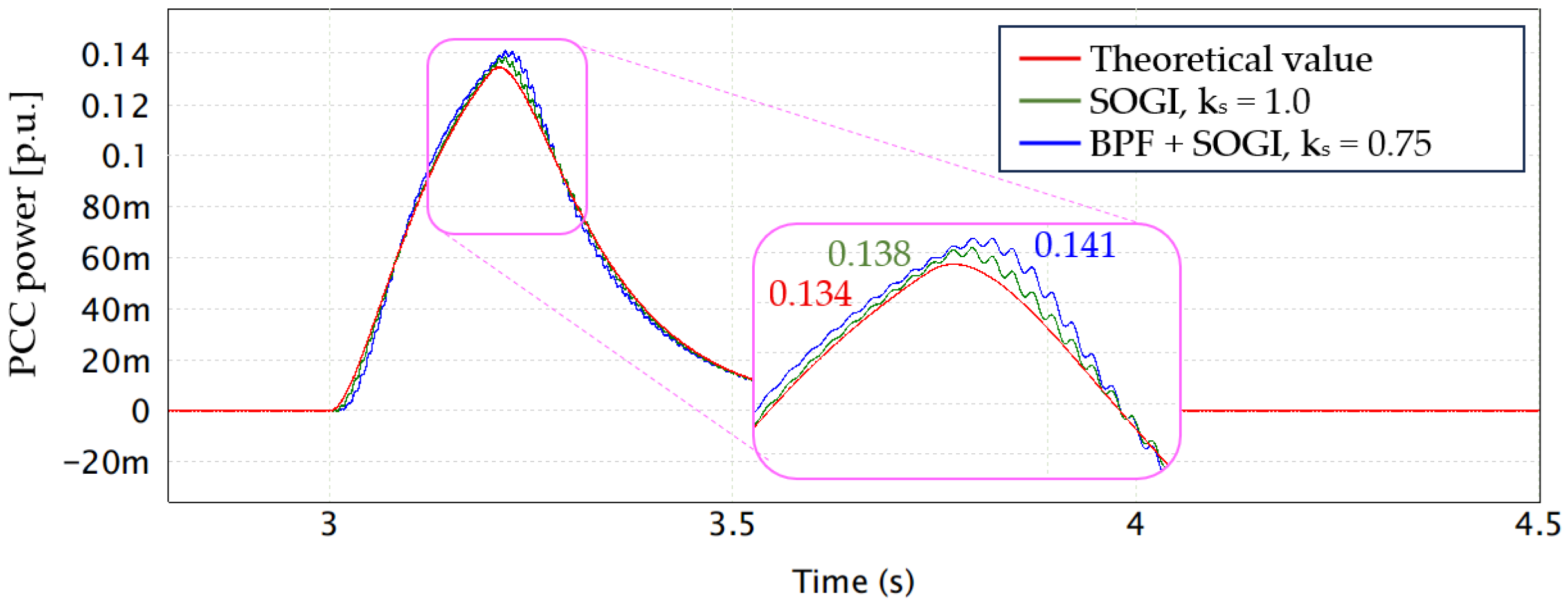
3.1. Band Pass Filter (BPF) and SOGI-PLL
3.2. Active Power Control (APC)
3.3. Reactive Power Control (RPC)
3.4. Droop Control
3.5. AC Current Control
3.6. DC-Link Voltage Control
4. Virtual Inertia Calculation for a Step-Shaped Frequency Disturbance
4.1. Underdamped Response
4.2. Critically Damped Response
4.3. Overdamped Response
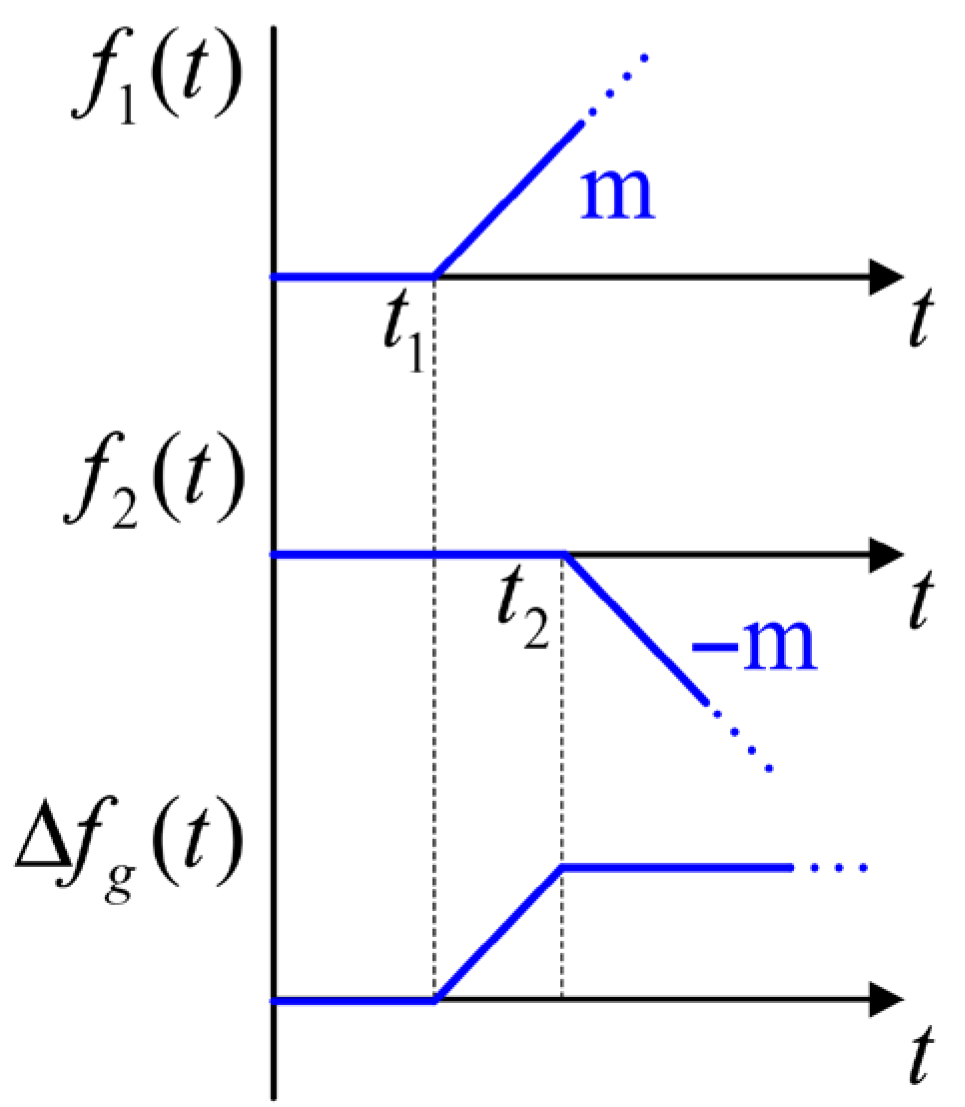
5. Virtual Inertia Calculation for Ramp-Shaped Frequency Variation
5.1. Underdamped Response
5.2. Critically Damped Response
5.3. Overdamped Response
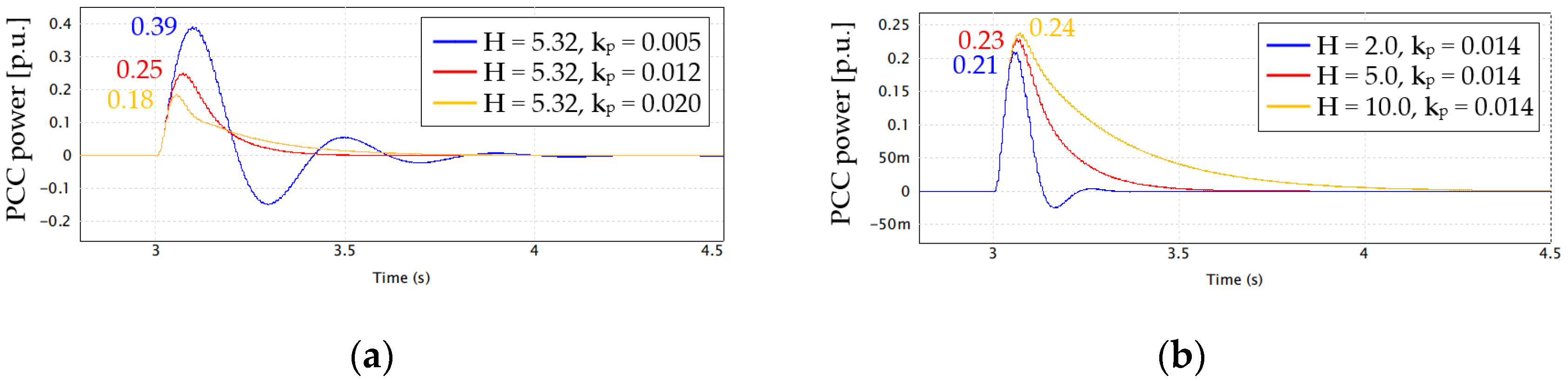
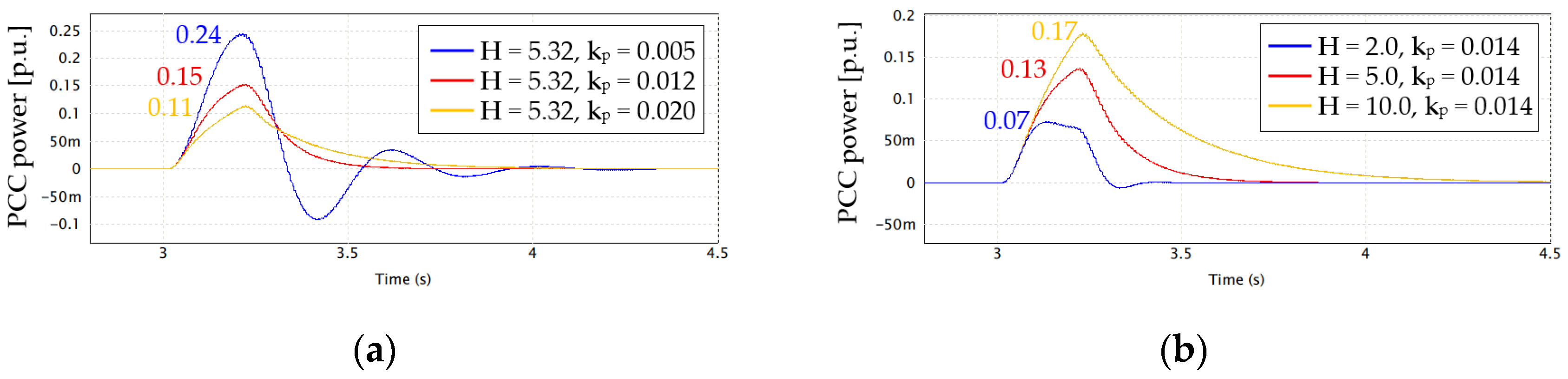
6. Simulation Results
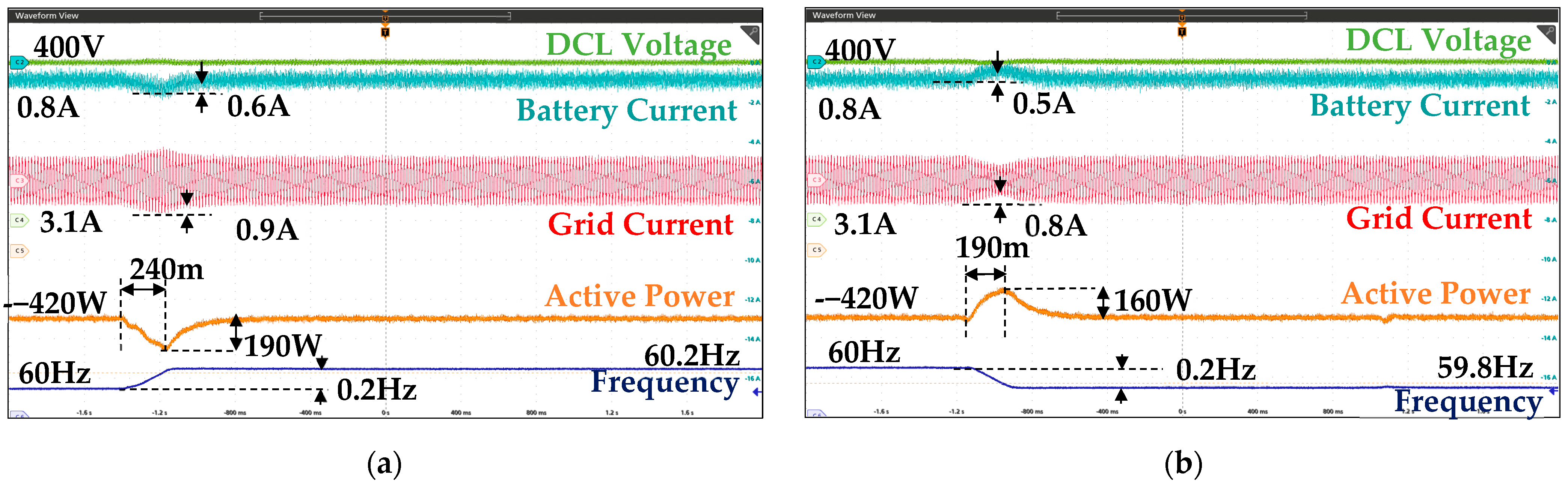
7. Experimental Results
7.1. Power Management
7.2. Power Response Under Step-Shaped Frequency Disturbance
7.3. Power Response Under Ramp-Shaped Frequency Disturbance
7.4. Voltage Response
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alam, M.S.; Al-Ismail, F.S.; Salem, A.; Abido, M.A. High-Level Penetration of Renewable Energy Sources into Grid Utility: Challenges and Solutions. IEEE Access 2020, 8, 190277–190299. [Google Scholar] [CrossRef]
- Du, W.; Tuffner, F.K.; Schneider, K.P.; Lasseter, R.H.; Xie, J.; Chen, Z.; Bhattarai, B. Modeling of Grid-Forming and Grid-Following Inverters for Dynamic Simulation of Large-Scale Distribution Systems. IEEE Trans. Power Deliv. 2021, 36, 2035–2045. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Topics Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Jafari, M.; Gharehpetian, G.B.; Anvari-Moghaddam, A. On the Role of Virtual Inertia Units in Modern Power Systems: A Review of Control Strategies, Applications and Recent Developments. Int. J. Electr. Power Energy Syst. 2024, 159, 110067. [Google Scholar] [CrossRef]
- Shobug, M.A.; Chowdhury, N.A.; Hossain, M.A.; Sanjari, M.J.; Lu, J.; Yang, F. Virtual Inertia Control for Power Electronics-Integrated Power Systems: Challenges and Prospects. Energies 2024, 17, 2737. [Google Scholar] [CrossRef]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Grid-Supporting Inverters with Improved Dynamics. IEEE Trans. Ind. Electron. 2019, 66, 3655–3667. [Google Scholar] [CrossRef]
- Qoria, T.; Rokrok, E.; Bruyere, A.; François, B.; Guillaud, X. A PLL-Free Grid-Forming Control with Decoupled Functionalities for High-Power Transmission System Applications. IEEE Access 2020, 8, 197363–197378. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed Power System Virtual Inertia Implemented by Grid-Connected Power Converters. IEEE Trans. Power Electron. 2018, 33, 8488–8499. [Google Scholar] [CrossRef]
- Peng, Q.; Fang, J.; Yang, Y.; Liu, T.; Blaabjerg, F. Maximum Virtual Inertia From DC-Link Capacitors Considering System Stability at Voltage Control Timescale. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 79–89. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An Improved Virtual Inertia Control for Three-Phase Voltage Source Converters Connected to a Weak Grid. IEEE Trans. Power Electron. 2019, 34, 8660–8670. [Google Scholar] [CrossRef]
- Quan, X.; Yu, R.; Zhao, X.; Lei, Y.; Chen, T.; Li, C.; Huang, A.Q. Photovoltaic Synchronous Generator: Architecture and Control Strategy for a Grid-Forming PV Energy System. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 936–948. [Google Scholar] [CrossRef]
- Paucara, J.; Peña, J.; Espinoza, R.; Sal y Rosas, D. Control Strategy to Provide Frequency Support Functionality Using a Supercapacitor-Based Energy Storage System. In Proceedings of the 2021 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 25–28 October 2021. [Google Scholar] [CrossRef]
- Liu, T.; Dai, Y.; Peng, Q.; Zeng, X.; Chen, G.; Meng, J. Inertia Emulation-Oriented Evaluation Method of Sustaining Power Boundary for Lithium-Ion Battery Energy Storage System. IEEE Trans. Energy Convers. 2024, 39, 2362–2376. [Google Scholar] [CrossRef]
- Wu, Q.; Chu, X.; Fan, Y.; Liu, L.; Sun, X. Consistency Algorithm-Based SOC Balancing Scheme of Retired Non-Equal Capacity Lithium Battery in Virtual Synchronous Generator Controlled Microgrids. IEEE Access 2025, 13, 9073–9088. [Google Scholar] [CrossRef]
- Dozein, M.G.; De Corato, A.M.; Mancarella, P. Virtual Inertia Response and Frequency Control Ancillary Services From Hydrogen Electrolyzers. IEEE Trans. Power Syst. 2023, 38, 2447–2459. [Google Scholar] [CrossRef]
- Reißner, F.; De Carne, G. Virtual Synchronous Machine integration on a Commercial Flywheel for Frequency Grid Support. IEEE Trans. Power Electron. 2024, 39, 12086–12090. [Google Scholar] [CrossRef]
- Sarojini, R.K.; Palanisamy, K.; Sanjeevikumar, P.; Nielsen, J.B.-H. Inertia emulation control technique based frequency control of grid connected single-phase rooftop photovoltaic system with battery and supercapacitor. IET Renew. Power Gener. 2020, 14, 1156–1163. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A battery/ultracapacitor hybrid energy storage system for implementing the power management of virtual synchronous generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Sun, C.; Ali, S.Q.; Joos, G.; Bouffard, F. Design of Hybrid-Storage-Based Virtual Synchronous Machine With Energy Recovery Control Considering Energy Consumed in Inertial and Damping Support. IEEE Trans. Power Electron. 2022, 37, 2648–2666. [Google Scholar] [CrossRef]
- Bernal, M.; Rocca, R.; Fernández, G.; Paz, M.; Galán, N. Grid Impact of Frequency Regulation Provided by V2Gs Aggregated at HV, MV, and LV Level. IEEE Access 2023, 11, 76768–76780. [Google Scholar] [CrossRef]
- Liu, T.; Wang, P.; Peng, Q.; Zhang, M.; Wang, T.; Meng, J. Operation-area-constrained Adaptive Primary Frequency Support Strategy for Electric Vehicle Clusters. J. Mod. Power Syst. Clean Energy 2023, 11, 1982–1994. [Google Scholar] [CrossRef]
- Kaur, K.; Singh, M.; Kumar, N. Multiobjective Optimization for Frequency Support Using Electric Vehicles: An Aggregator-Based Hierarchical Control Mechanism. IEEE Syst. J. 2019, 13, 771–782. [Google Scholar] [CrossRef]
- Amamra, S.-A.; Marco, J. Vehicle-to-grid aggregator to support power grid and reduce electric vehicle charging cost. IEEE Access 2019, 7, 178528–178538. [Google Scholar] [CrossRef]
- Restrepo, M.; Morris, J.; Kazerani, M.; Cañizares, C.A. Modeling and testing of a bidirectional smart charger for distribution system EV integration. IEEE Trans. Smart Grid 2018, 9, 152–162. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Dey, S.; Mallik, A. Optimal Utilization of Bidirectional EVs For Grid Frequency Support in Power Systems. IEEE Trans. Power Deliv. 2023, 38, 998–1010. [Google Scholar] [CrossRef]
- Roveri, A.; Mallemaci, V.; Mandrile, F.; Bojoi, R. Power Decoupling Methods for Grid Support Provided by Ultra-Fast Bidirectional Chargers. IEEE Open J. Ind. Electron. Soc. 2025, 6, 107–119. [Google Scholar] [CrossRef]
- Ke, S.; Ding, L.; Shi, X.; Fan, P.; Wang, H.; Chen, L.; Yang, J.; Chung, C.Y. Response Characteristics and Regulation Feasibility of DC Charging Station Controlled by GFM/GFL Virtual Inertia for Grid Frequency Stability. IEEE Trans. Transp. Electrif. 2025, 11, 7743–7758. [Google Scholar] [CrossRef]
- Paucara, J.D.; Peña, J.C.U.; Sal y Rosas, D. HESS Management for Virtual Inertia, Frequency, and Voltage Support Through Off-Board EV Bidirectional Chargers. IEEE Open J. Ind. Electron. Soc. 2024, 5, 376–385. [Google Scholar] [CrossRef]
- Suul, J.A.; D’Arco, S.; Guidi, G. Virtual Synchronous Machine Based Control of a Single-Phase Bi-directional Battery Charger for Providing Vehicle-to-Grid Services. IEEE Trans. Ind. Appl. 2016, 52, 3234–3244. [Google Scholar] [CrossRef]
- Sal y Rosas, D.; Zarate, A. Single-Phase Grid-Forming Strategy with Power Decoupling Implementation for Electrolytic-Capacitor-Free EV Smart Battery Charger. Energies 2023, 16, 894. [Google Scholar] [CrossRef]
- Bhowmik, P.; Satpathy, P.R.; Thanikanti, S.B.; Jana, N. A novel virtual inertia emulation technique for the single-phase electric vehicle charging topology. Comput. Electr. Eng. 2022, 101, 108114. [Google Scholar] [CrossRef]
- Pantaleon, E.; Sal y Rosas, D.; Tafur, J. Single-Phase Grid Forming Control Strategy for an Isolated and Bidirectional EV Battery Charger. In Proceedings of the 2024 Energy Conversion Congress & Expo Europe (ECCE Europe), Darmstadt, Germany, 2–6 September 2024. [Google Scholar]
- Jafari, H.; Moghaddami, M.; Olowu, T.O.; Sarwat, A.I.; Mahmoudi, M. Virtual Inertia-Based Multipower Level Controller for Inductive Electric Vehicle Charging Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2447–2459. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill Education: Columbus, OH, USA, 1994. [Google Scholar]
- Su, K.; Xie, X.; Gong, Z.; Liu, H.; Sun, D.; Wang, Y. Fast Frequency Response Analysis for Grid-Following and Grid-Forming Controlled BESS Considering Voltage Coupling Effect. IEEE Trans. Power Deliv. 2025, 40, 2412–2425. [Google Scholar] [CrossRef]
- Rocabert, J.; Garcia, B.; Candela, J.I.; Villón, J.D.; Rodriguez, P. Evaluation of the Grid-Forming Inertial Response for Power Reference and Grid-Supporting Functionalities. In Proceedings of the 2024 IEEE 15th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Luxembourg, 23–26 June 2024; pp. 1–6. [Google Scholar]












| Parameter | Variable | Value |
|---|---|---|
| Rated active power | 1200 W | |
| Grid voltage | 220 V, 60 Hz | |
| DC-link voltage | 400 V | |
| Battery voltage | 400 V | |
| DABSR switching frequency | 120 kHz | |
| VSI switching frequency | 30 kHz | |
| LCL filter | , , , | 1.2 mH, 0.4 mH, 4.7 µF, 8.2 Ω |
| DC-link capacitor | 700 µF | |
| Tank impedance | , | 328 µH, 6.6 nF |
| Transformer T1 turns ratio | 1 |
| Control Loop | Bandwidth | Parameter | Value |
|---|---|---|---|
| APC | 1.2 Hz | 5.321 | |
| 0.014 | |||
| RPC | 1.0 Hz | 2.82 | |
| AC current | 1200 Hz | 0.033 | |
| 30 | |||
| 0.31 | |||
| DC-link voltage | 30 Hz | 0.1319 | |
| 1.4137 | |||
| SOGI-PLL | 60 Hz | 0.75 | |
| Frequency droop | - | 1 | |
| Voltage droop | - | 4 |
| APC Parameters | Theoretical | Simulation | Error (%) | ||||
|---|---|---|---|---|---|---|---|
| H | kp | Ppk | ts | Ppk | ts | Ppk | ts |
| 5.32 | 0.005 | 0.326 | 0.629 | 0.39 | 0.78 | 19.6 | 24.0 |
| 5.32 | 0.012 | 0.201 | 0.443 | 0.25 | 0.43 | 24.4 | 2.9 |
| 5.32 | 0.020 | 0.140 | 0.823 | 0.18 | 0.77 | 28.6 | 6.4 |
| 2.0 | 0.014 | 0.152 | 0.282 | 0.21 | 0.22 | 38.2 | 22.0 |
| 5.0 | 0.014 | 0.180 | 0.509 | 0.23 | 0.49 | 27.8 | 3.7 |
| 10.0 | 0.014 | 0.197 | 1.09 | 0.24 | 1.04 | 21.8 | 4.6 |
| APC Parameters | Theoretical | Simulation | Error (%) | ||||
|---|---|---|---|---|---|---|---|
| H | kp | Ppk | ts | Ppk | ts | Ppk | ts |
| 5.32 | 0.005 | 0.218 | 0.752 | 0.24 | 0.89 | 10.1 | 18.4 |
| 5.32 | 0.012 | 0.146 | 0.588 | 0.15 | 0.59 | 2.7 | 0.3 |
| 5.32 | 0.020 | 0.109 | 0.978 | 0.11 | 0.97 | 0.9 | 0.8 |
| 2.0 | 0.014 | 0.069 | 0.437 | 0.07 | 0.38 | 1.4 | 13.0 |
| 5.0 | 0.014 | 0.131 | 0.658 | 0.13 | 0.66 | 0.8 | 0.3 |
| 10.0 | 0.014 | 0.168 | 1.23 | 0.17 | 1.22 | 1.2 | 0.8 |
| Parameter | Proposed Work | Study [12] | Study [13,15] | Study [14] |
|---|---|---|---|---|
| Validated V2G functionalities | VI, f-w droop, v-var droop | VI, f-w droop, v-var droop | VI, f-w droop, v-var droop | f-w droop, v-var droop |
| AC-DC structure | VSI cascaded to a DABSR DC-DC | VSI cascaded to a DABSR DC-DC | VSI only | VSI cascaded to a DABSR DC-DC |
| Galvanic isolation | Yes | Yes | No | Yes |
| Power support calculation | Yes | Yes | No | No |
| Control strategy | GFM | GFL | GFM | GFM |
| Storage system | EV Battery | DCL Capacitors + Battery | EV Battery | EV Battery |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantaleon, E.; Paucara, J.; Sal y Rosas, D. Power Analysis Produced by Virtual Inertia in Single-Phase Grid-Forming Converters Under Frequency Events Intended for Bidirectional Battery Chargers. Energies 2025, 18, 5560. https://doi.org/10.3390/en18215560
Pantaleon E, Paucara J, Sal y Rosas D. Power Analysis Produced by Virtual Inertia in Single-Phase Grid-Forming Converters Under Frequency Events Intended for Bidirectional Battery Chargers. Energies. 2025; 18(21):5560. https://doi.org/10.3390/en18215560
Chicago/Turabian StylePantaleon, Erick, Jhonatan Paucara, and Damián Sal y Rosas. 2025. "Power Analysis Produced by Virtual Inertia in Single-Phase Grid-Forming Converters Under Frequency Events Intended for Bidirectional Battery Chargers" Energies 18, no. 21: 5560. https://doi.org/10.3390/en18215560
APA StylePantaleon, E., Paucara, J., & Sal y Rosas, D. (2025). Power Analysis Produced by Virtual Inertia in Single-Phase Grid-Forming Converters Under Frequency Events Intended for Bidirectional Battery Chargers. Energies, 18(21), 5560. https://doi.org/10.3390/en18215560





