Numerical Modelling of Gas Mixing in Salt Caverns During Cyclic Hydrogen Storage
Abstract
1. Introduction
2. Materials and Methods
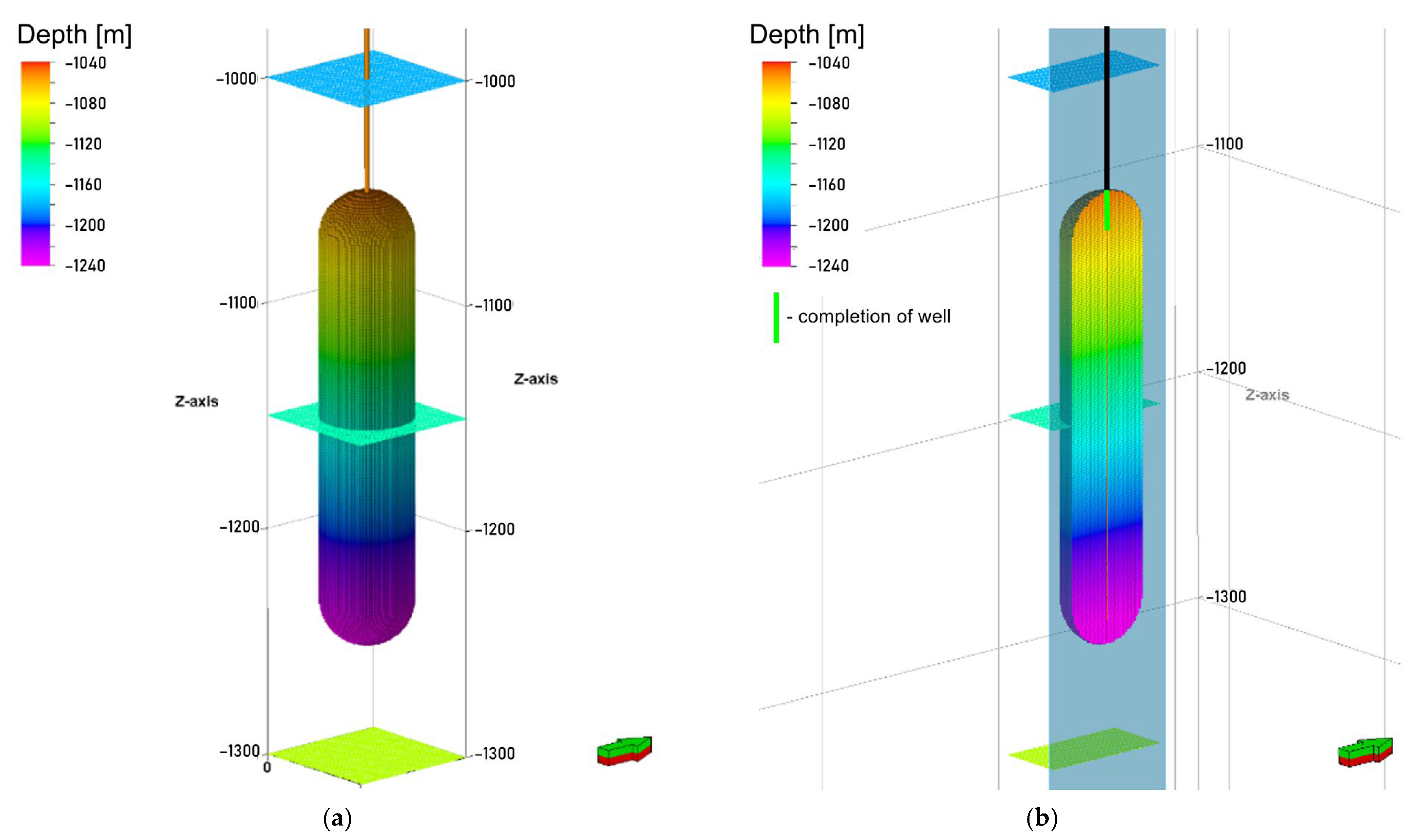
2.1. Salt Cavern Model
2.2. Fluid Properties
2.3. Phase Permeability
2.4. Model Initialization
2.5. Simulation Model Validation
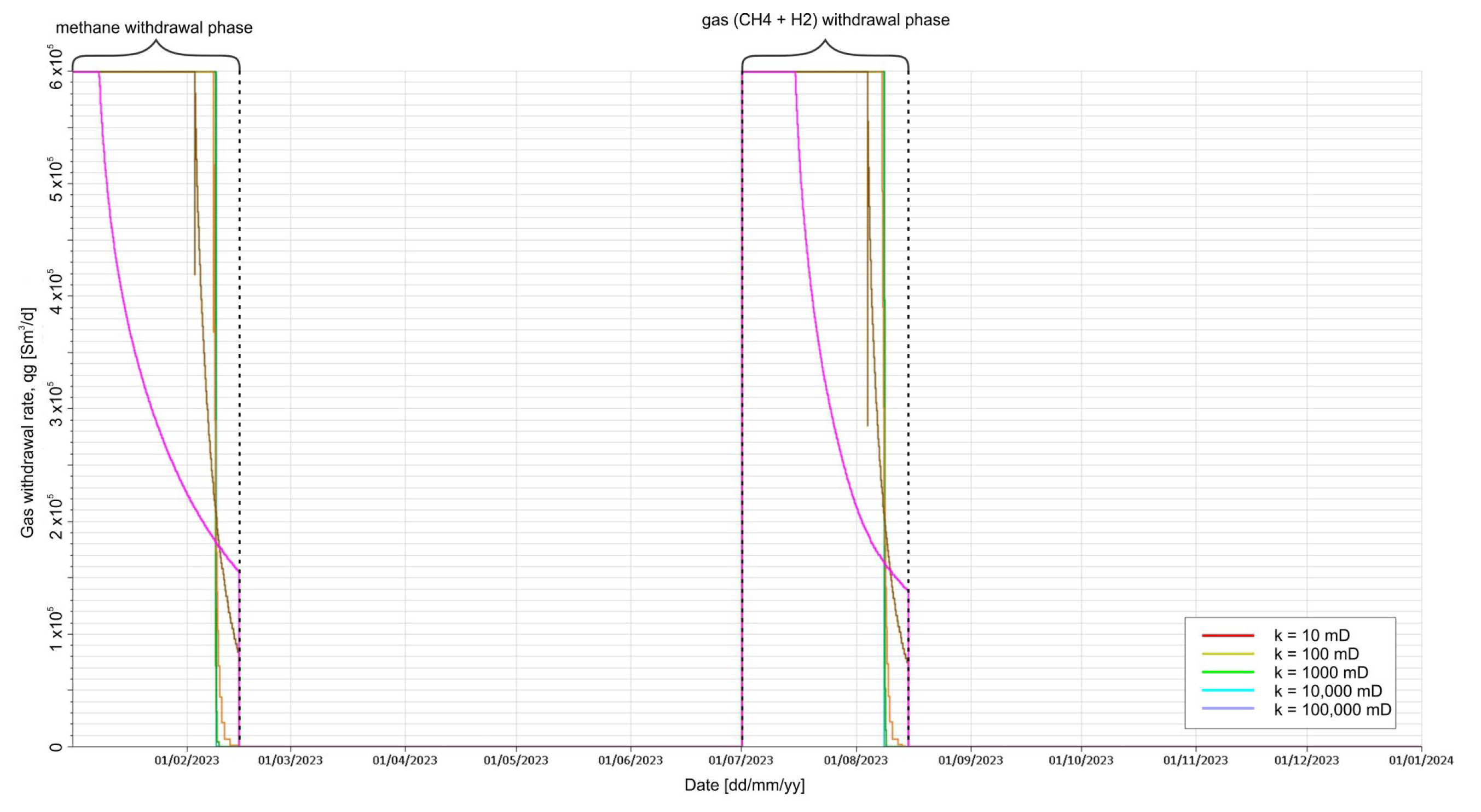
- Precycle, i.e., original gas withdrawal (CH4),
- H2 injection phases,
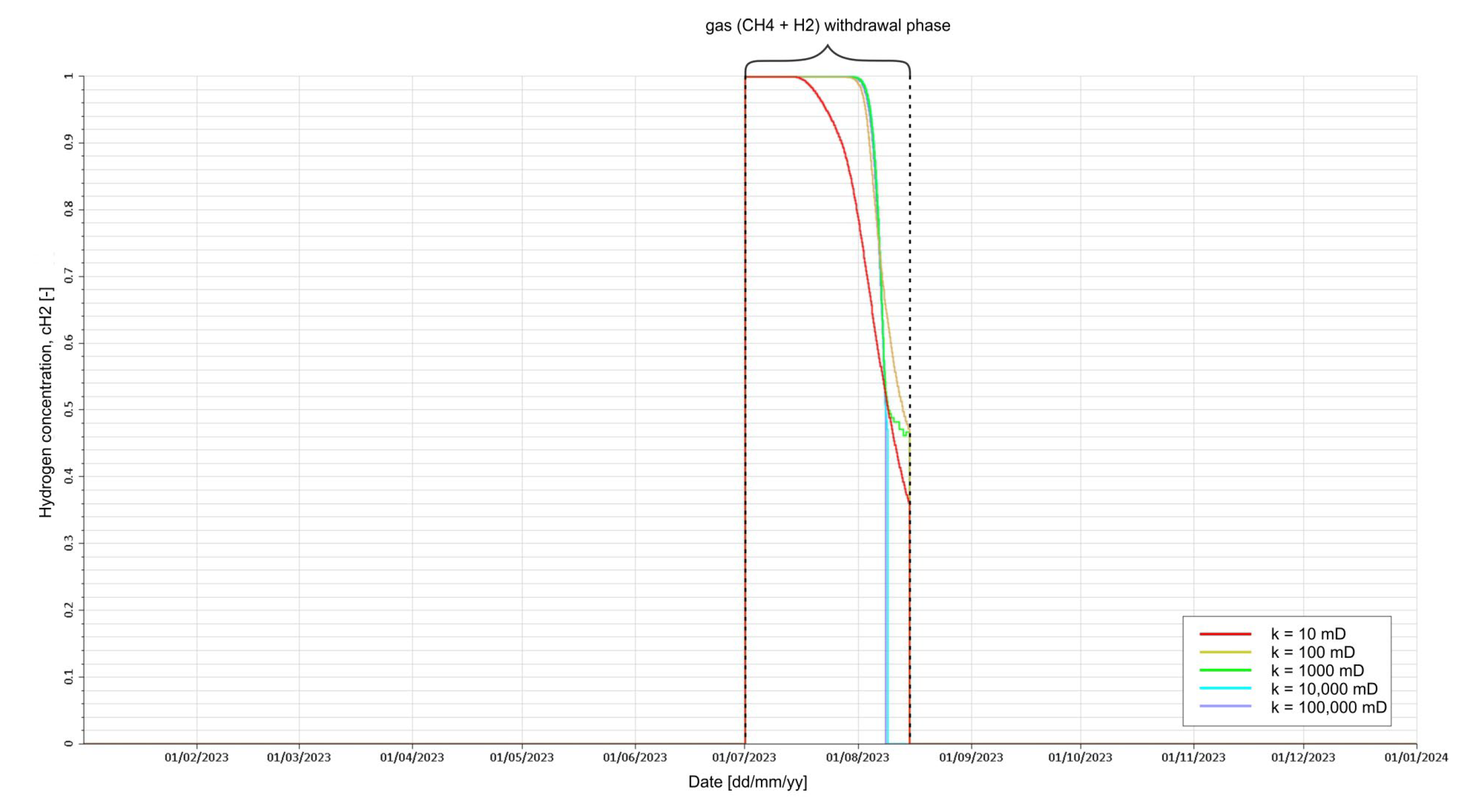
- Withdrawal of gas from the cavern (H2 with CH4).
2.6. Dispersion
2.6.1. Physical and Numerical Dispersion
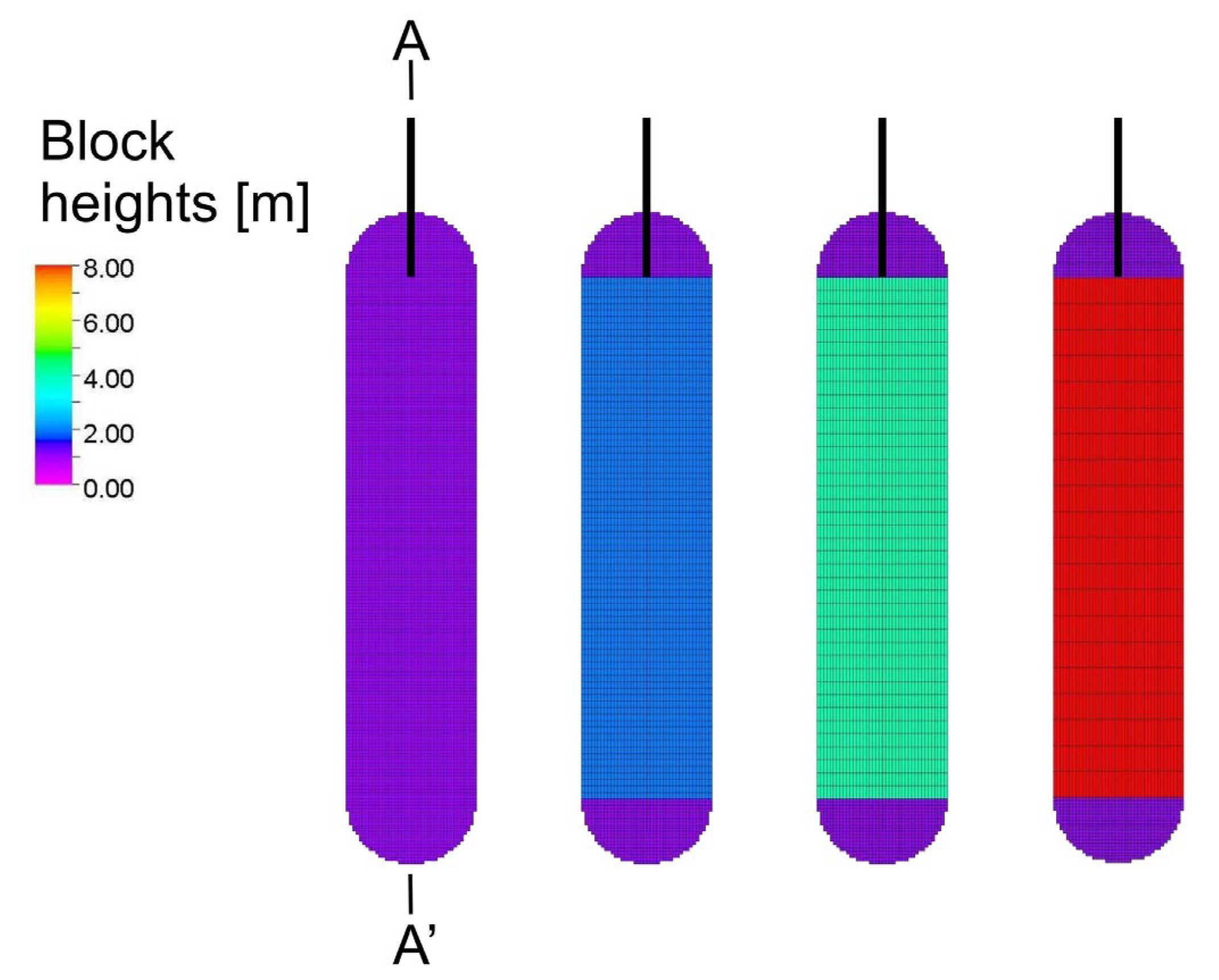
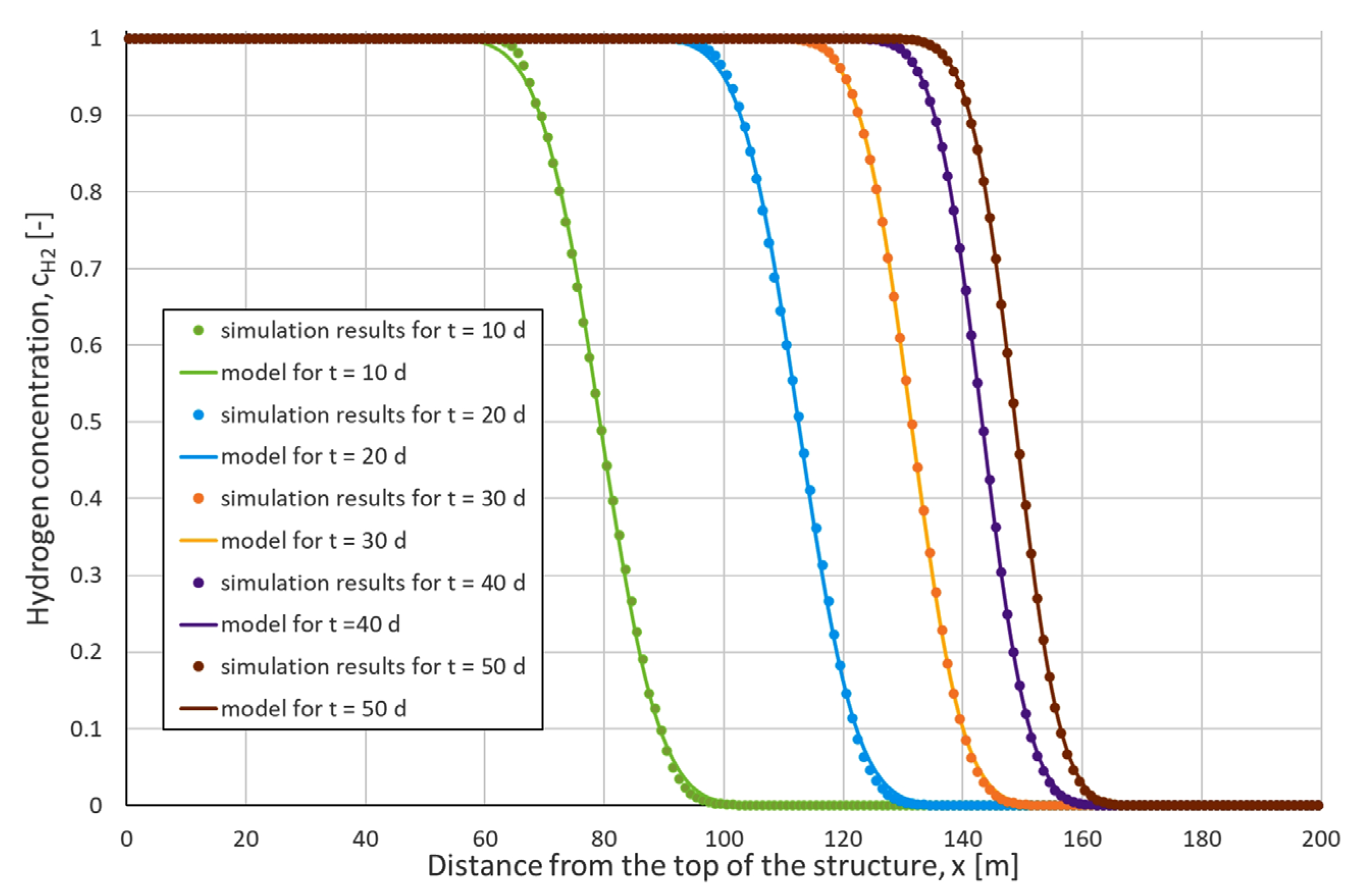
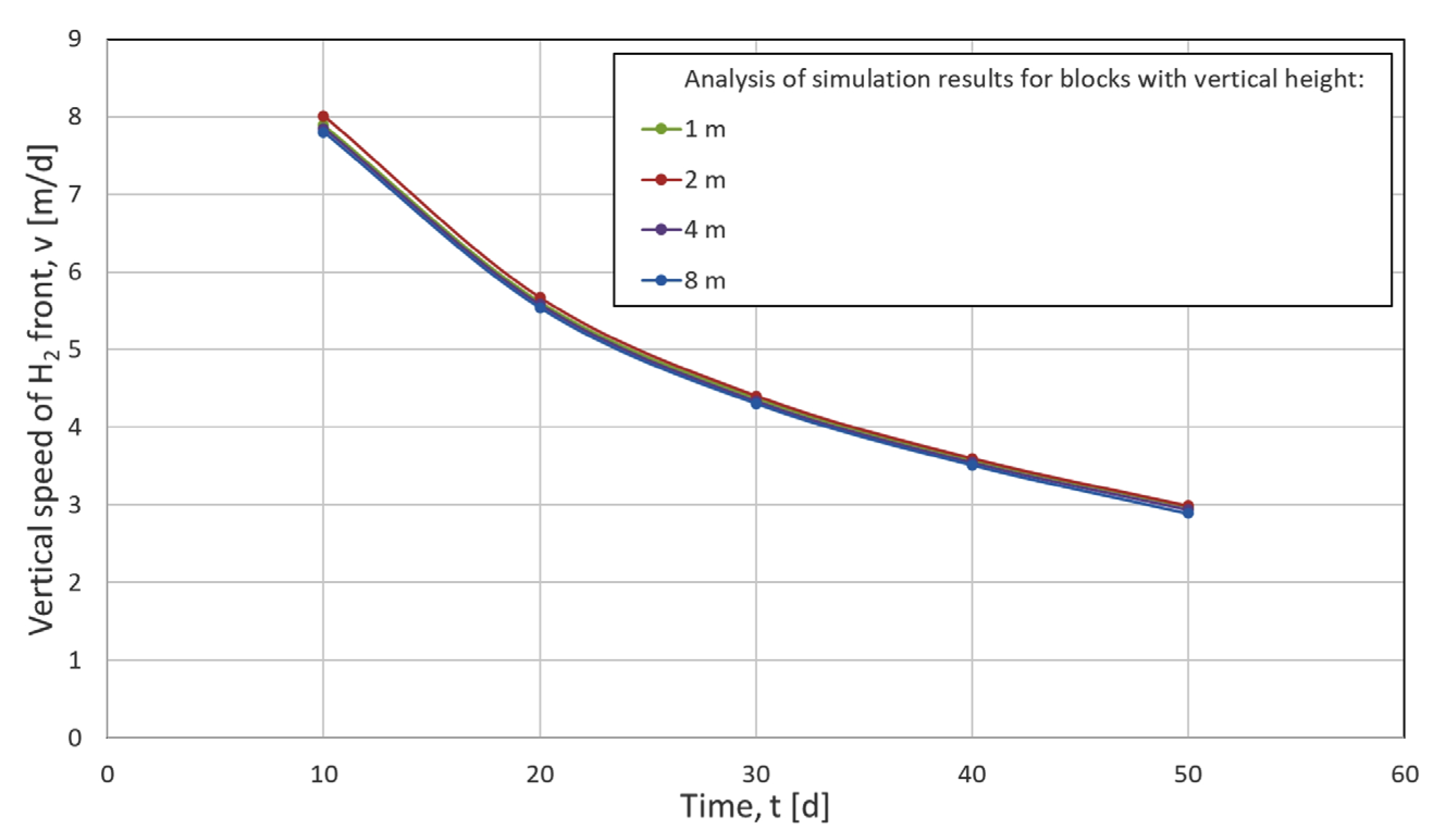
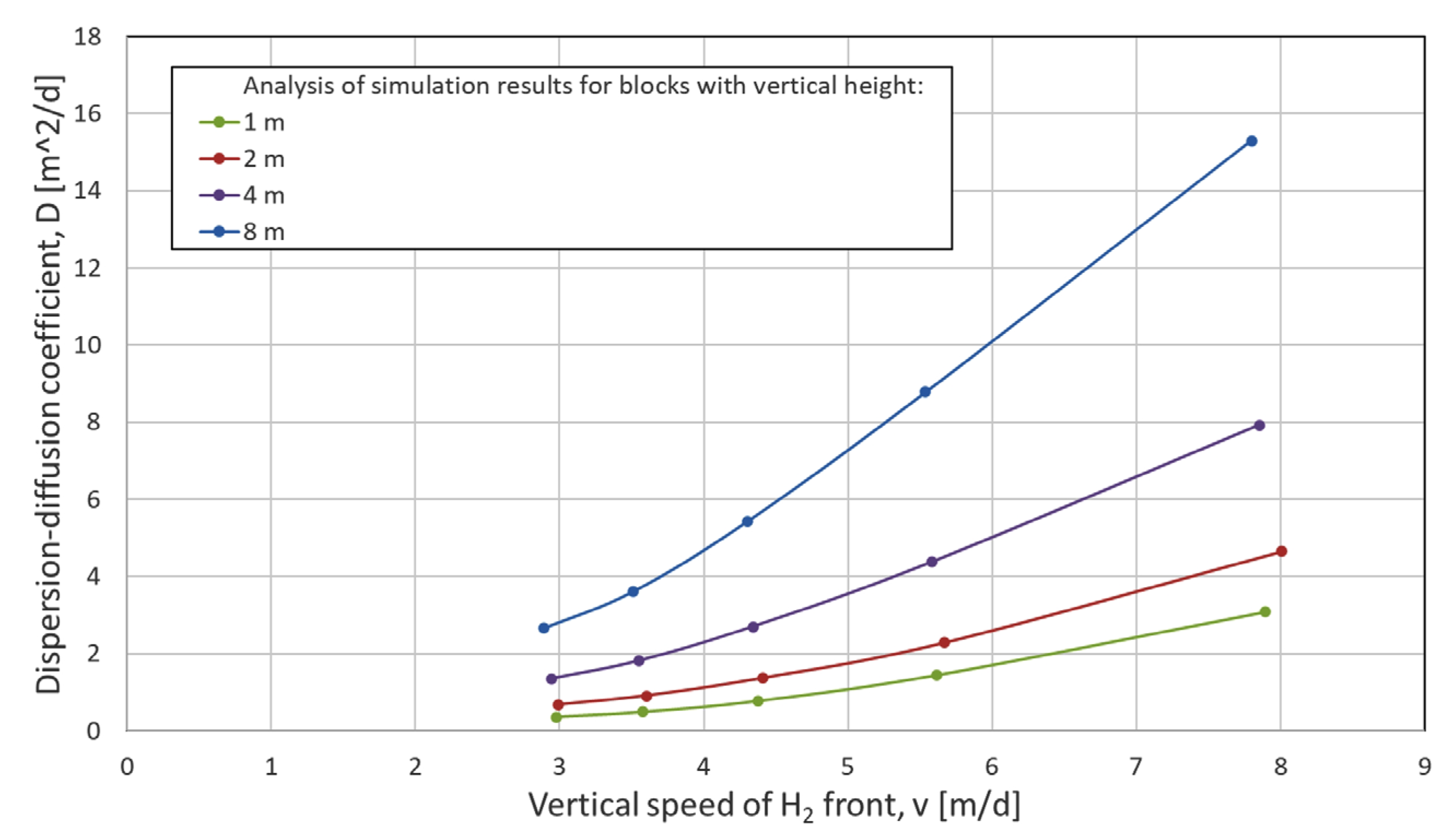
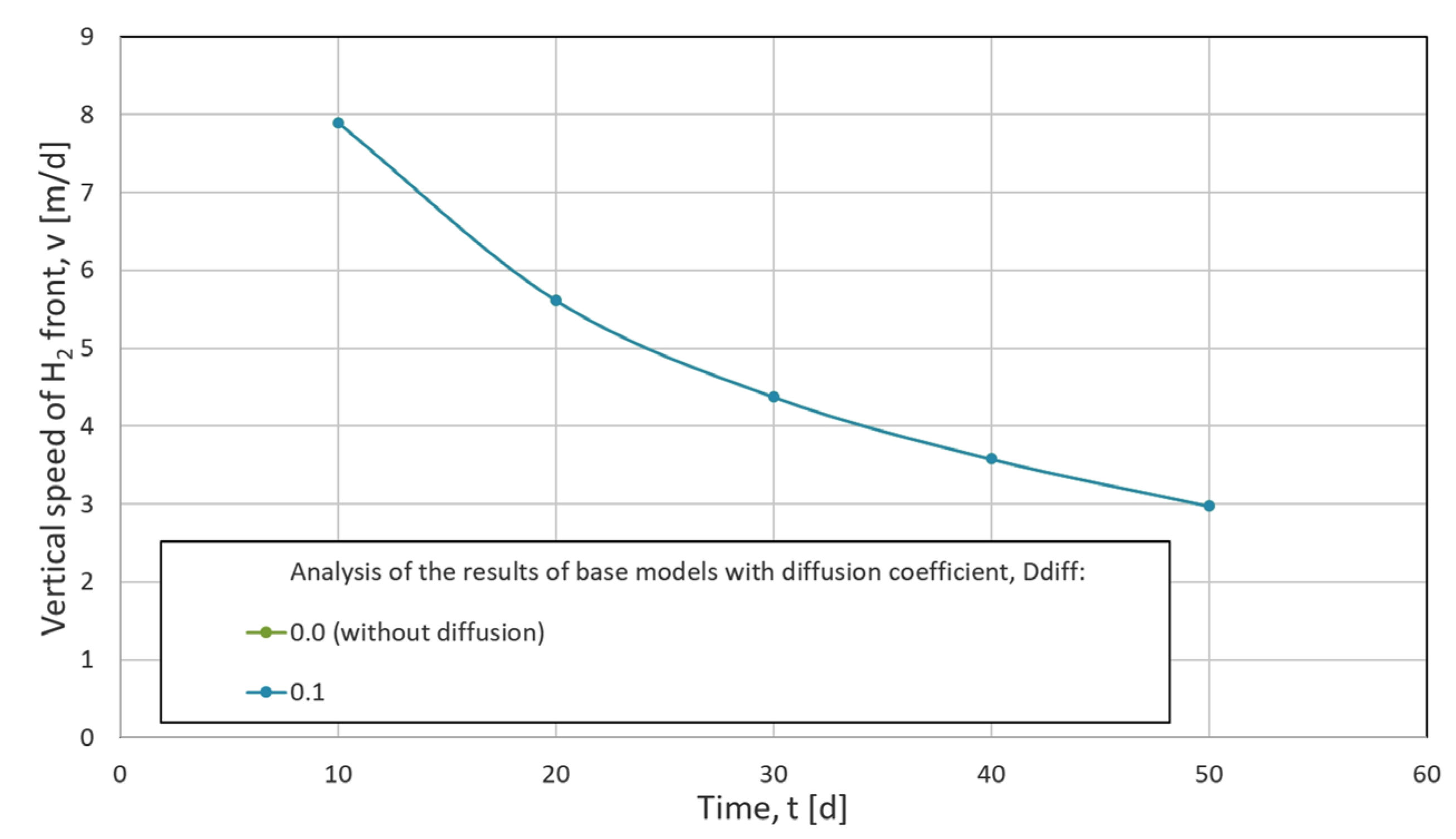
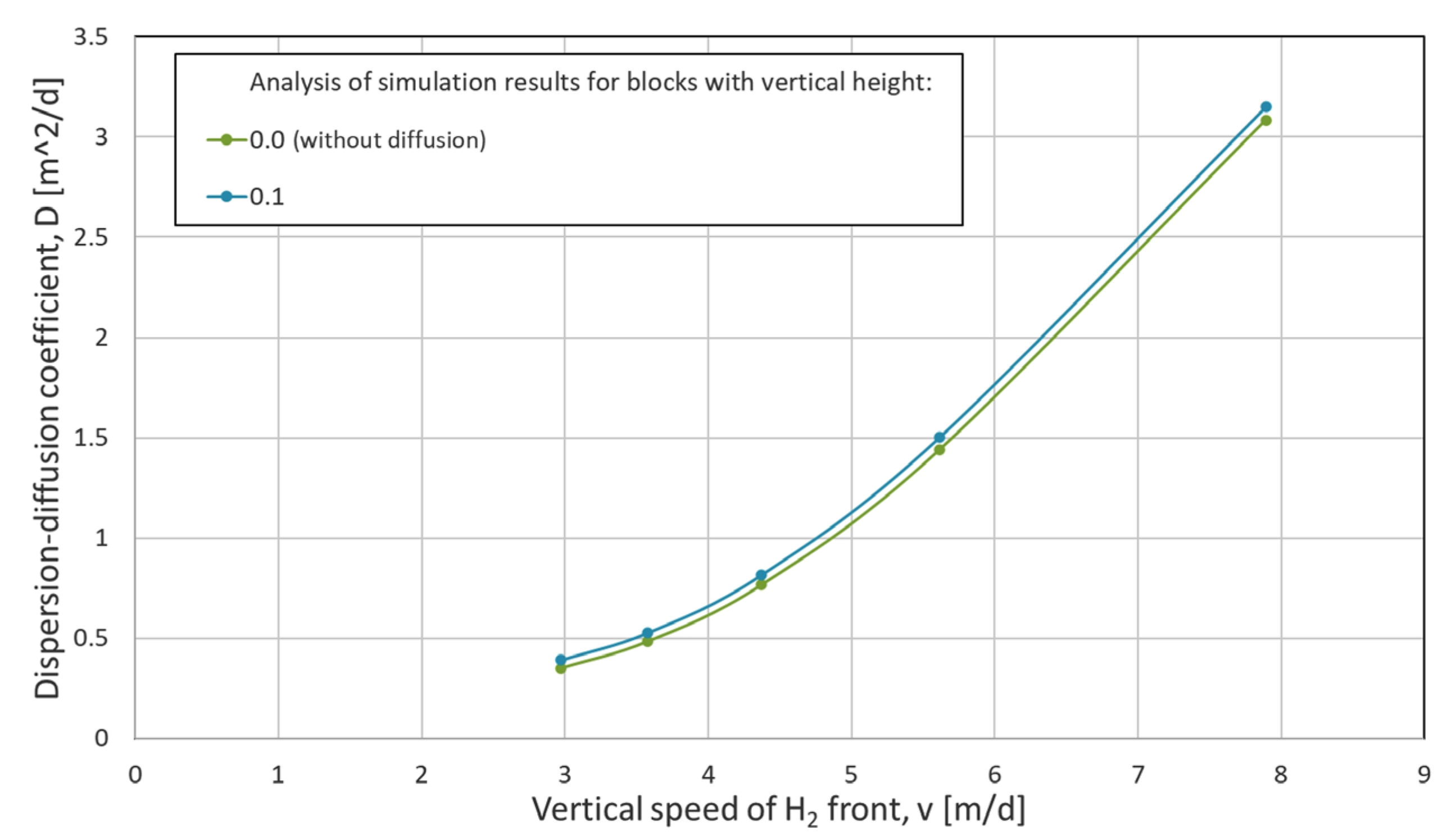
2.6.2. Numerical Dispersion Analysis
- v—velocity of convection [m/d],
- x—distance from the structure ceiling [m],
- D—dispersion–diffusion coefficient [m2/d],
- t—time [d].
2.7. Diffusion
2.7.1. Molecular Diffusion
2.7.2. Diffusion Coefficients
- P—pressure [bar],
- σ—medium molecular size,
- Ω—Lennard-Jones potential,
- T—temperature [°C],
- Mw—molecular mass [g/mol].
2.7.3. Gas Diffusion Analysis
2.7.4. Diffusion Effects During Stand-Ups
3. Results
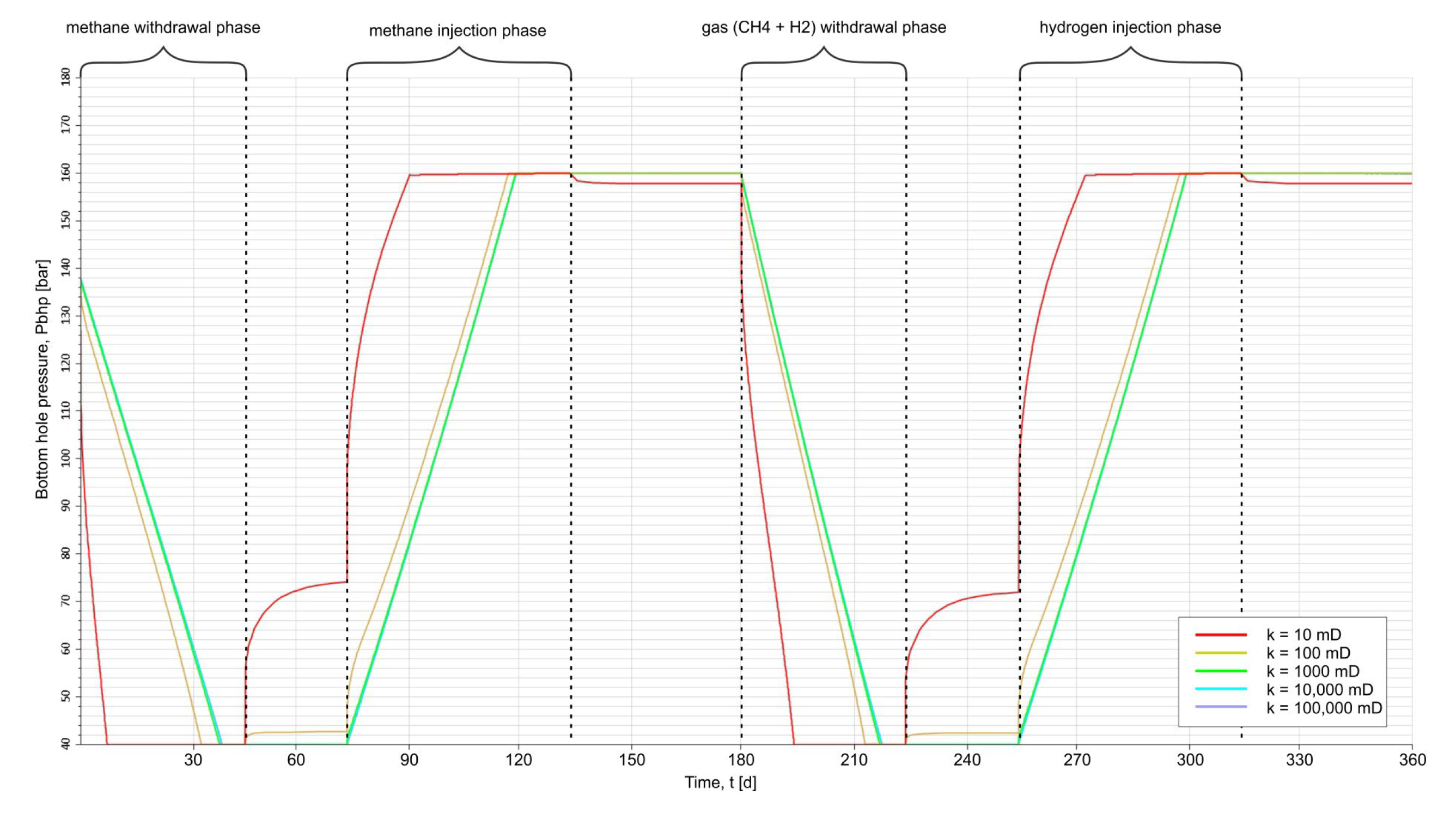
3.1. Assumptions of Storage Operation
- −
- Composition of the injected gas, cH2 = 100%,
- −
- Injection and production (withdrawn) well providing access to the cavern top (Figure 5),
- −
- Two phases of H2 injection per year, i.e., 1.01–14.02, 1.07–14.08,
- −
- Two phases of H2 withdrawal per year, i.e., 15.03–14.05, 15.09–14.11,
- −
- Stand-ups between the above-mentioned phases,
- −
- H2 injection rate, qg,inj = 500,000 Nm3/d,
- −
- H2 withdrawal rate, qg,prod = 600,000 Nm3/d,
- −
- Initial pressure in UHS, Pini = 140 bar,
- −
- Storage temperature, Tres = 57 °C,
- −
- Maximum bottom pressure in the pumping phase, Pbhp,inj,max = 160 bar,
- −
- Minimum bottom pressure in the gas withdrawal phase, Pbhp,prod,min = 40 bar.
3.2. Results of Simulation Forecasts
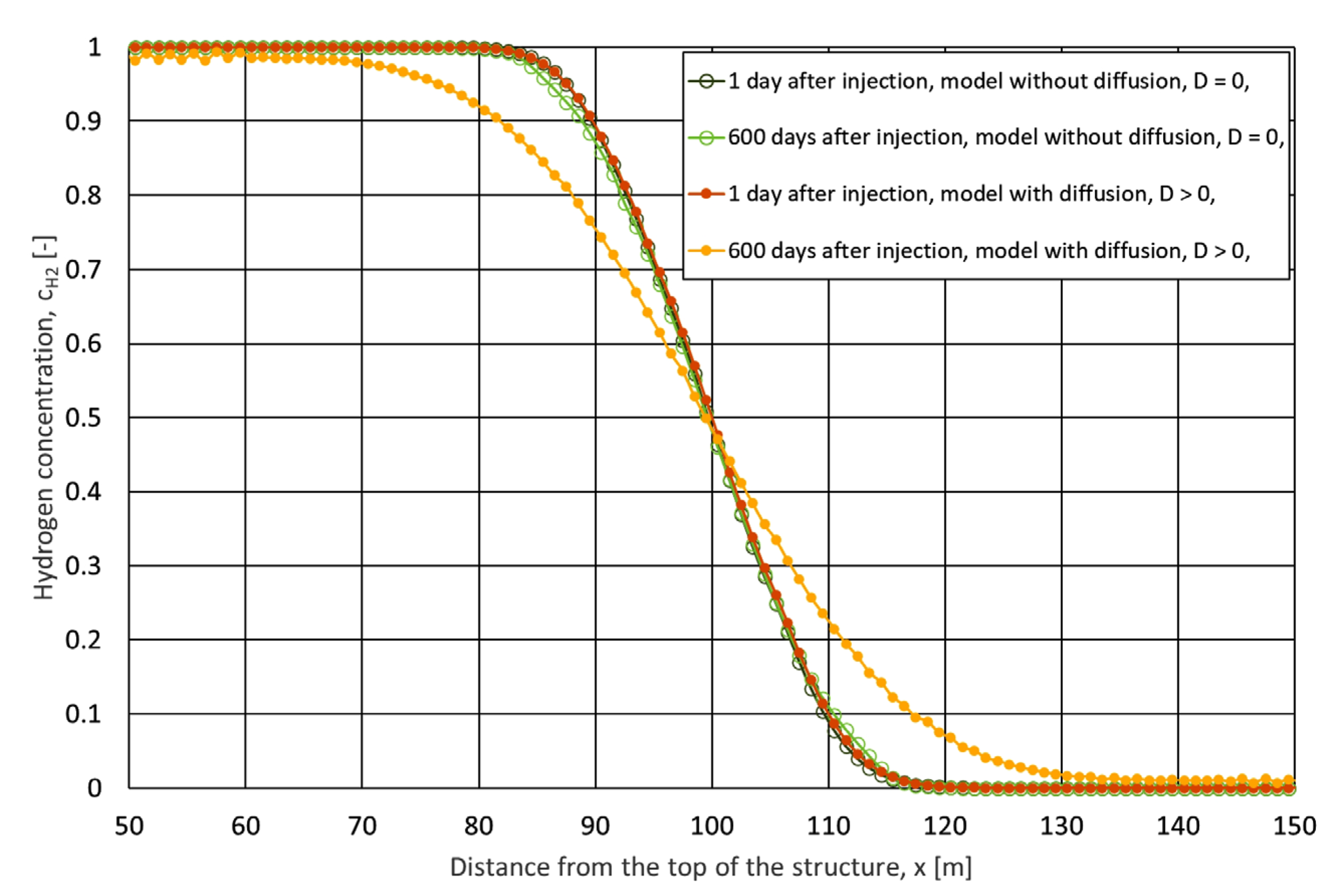
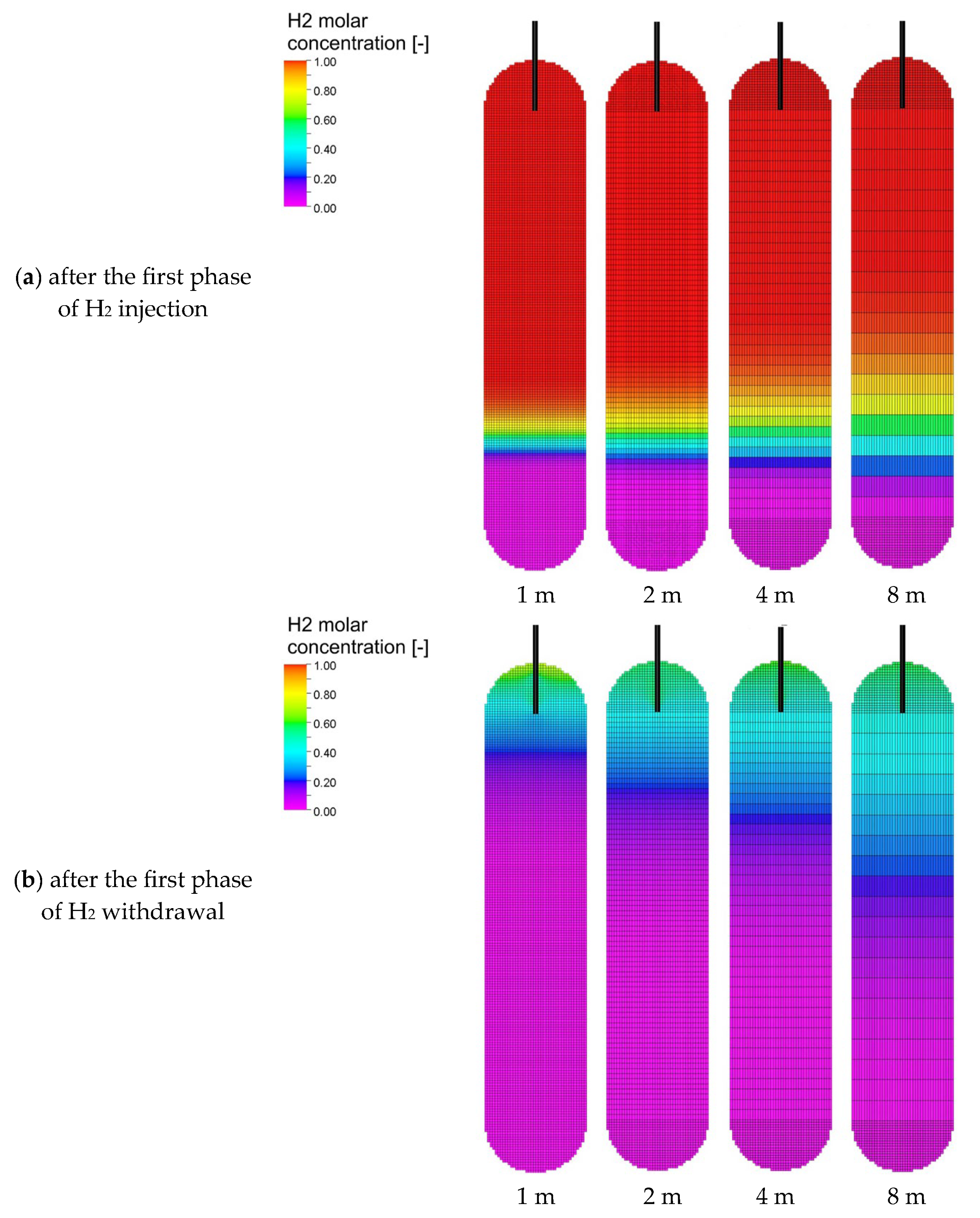
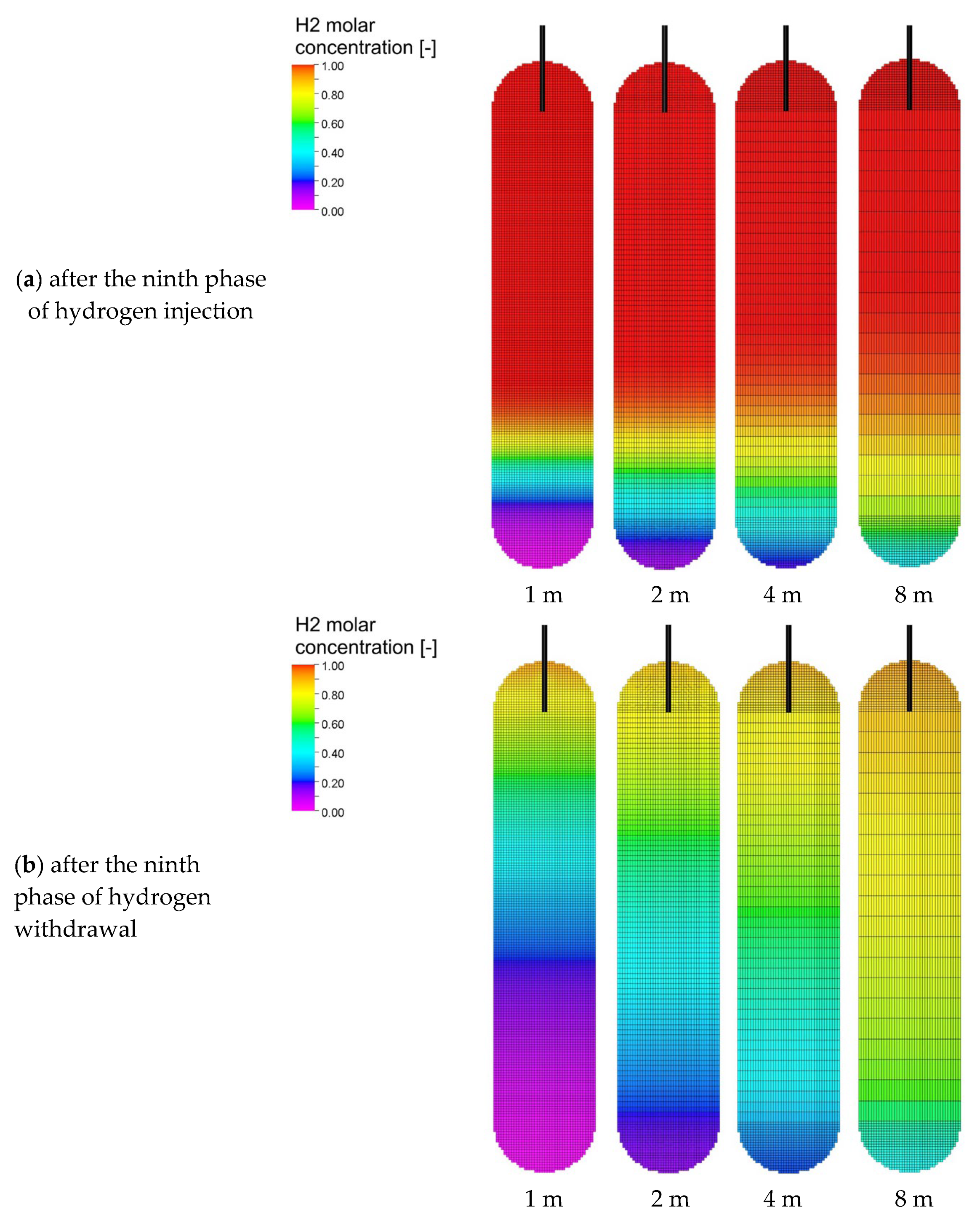
3.3. Analysis of H2 Saturation Distributions
4. Discussion
Limitations and Outlook
5. Conclusions
- The Eclipse 300 commercial compositional simulator, developed by Schlumberger, has been confirmed to be effective for modelling the operation of UHS located in a salt cavern, represented as an ultra-permeable porous rock.
- For the simulations carried out, no significant influence of gravitational segregation on the modelling results was found.
- Physical dispersion modelled as numerical dispersion is identified as the primary driver of mixing during the operation of UHS. This phenomenon has a significant influence on the composition of withdrawn gas.
- Molecular diffusion does not have a significant impact on the modelling of flows caused by the pressure gradient in the cavern, but it may be important in a situation where there are no such flows, i.e., during the so-called stand-ups.
- Both of the above phenomena should be taken into account to properly model the operation of the UHS, especially to calibrate such a model before it is applied to forecast the future performance of a cavern as a UHS facility.
- The location of the injection and production wells, along with the well pattern, may be important for the simulation results, and should be the subject of further research.
- A research gap has been identified: to the authors’ best knowledge, no prior publication has systematically quantified the combined effects of dispersion and diffusion on the modelling of UHS operation or their impact on the composition of withdrawn gas during cyclic operations. This work provides a methodological framework for these assessments and practical guidance for forecasting the composition of withdrawn gas, which is crucial for the gas calorific value.
- The study is subject to limitations (no geomechanical coupling, turbulence, or experimental validation), which will be addressed in future work by integrating dispersion–diffusion modelling with geomechanical analysis, CFD simulations, and laboratory/field data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ciechanowska, M. Hydrogen Strategy for a Climate-Neutral Europe. Naft.-Gaz 2020, 2020, 951–954. [Google Scholar] [CrossRef]
- Liléo, S.; Berge, E.; Undheim, O.; Klinkert, R.; Bredesen, R.E.; Vindteknikk, K. Long-Term Correction of Wind Measurements State-of-the-Art, Guidelines and Future Work; Elforsk Report 13:18; Elforsk AB: Stockholm, Sweden, 2013. [Google Scholar]
- Miziołek, M.; Filar, B.; Kwilosz, T. Hydrogen Storage in Depleted Natural Gas Fields. Naft.-Gaz 2022, 2022, 219–239. [Google Scholar] [CrossRef]
- Budak, P.; Szpunar, T. How Does the Composition of Natural Gas/Hydrogen Mixture Fluctuates during Exploitation of a Gas Cavern. Naft.-Gaz 2020, 2020, 799–806. [Google Scholar] [CrossRef]
- Blicharski, J. Analytical Modelling of the Gas Storage Process in Partially Depleted Natural Gas Deposits—Selected Issues. In AGH Disserations Monographs; AGH University of Science and Technology: Krakow, Poland, 2018; Available online: https://winntbg.bg.agh.edu.pl/skrypty4/0633/modelowanie.pdf (accessed on 28 November 2023).
- Caglayan, D.G.; Weber, N.; Heinrichs, H.U.; Linßen, J.; Robinius, M.; Kukla, P.A.; Stolten, D. Technical Potential of Salt Caverns for Hydrogen Storage in Europe. Int. J. Hydrog. Energy 2020, 45, 6793–6805. [Google Scholar] [CrossRef]
- Tarkowski, R.; Uliasz-Misiak, B. Towards Underground Hydrogen Storage: A Review of Barriers. Renew. Sustain. Energy Rev. 2022, 162, 112451. [Google Scholar] [CrossRef]
- Such, P. Magazynowanie Wodoru w Obiektach Geologicznych. Naft.-Gaz 2020, 76, 794–798. [Google Scholar] [CrossRef]
- Zivar, D.; Kumar, S.; Foroozesh, J. Underground Hydrogen Storage: A Comprehensive Review. Int. J. Hydrogen Energy 2021, 46, 23436–23462. [Google Scholar] [CrossRef]
- Filar, B.; Miziołek, M.; Kwilosz, T. Assessment of Hydrogen Production Costs with the Use of Energy from a Photovoltaic Installation Build in Poland. Naft.-Gaz 2022, 2022, 451–459. [Google Scholar] [CrossRef]
- Gahleitner, G. Hydrogen from Renewable Electricity: An International Review of Power-to-Gas Pilot Plants for Stationary Applications. Int. J. Hydrog. Energy 2013, 38, 2039–2061. [Google Scholar] [CrossRef]
- Zeljaś, D. Magazyny Gazu Ziemnego w Cechsztyñskich Formacjach Solnych Elementem Bezpieczeñstwa Energetycznego Polski. Przegląd Geol. 2020, 68, 824–832. [Google Scholar]
- Amid, A.; Mignard, D.; Wilkinson, M. Seasonal Storage of Hydrogen in a Depleted Natural Gas Reservoir. Int. J. Hydrog. Energy 2016, 41, 5549–5558. [Google Scholar] [CrossRef]
- Li, Q.; Han, Y.; Liu, X.; Ansari, U.; Cheng, Y.; Yan, C. Hydrate as a By-Product in CO2 Leakage during the Long-Term Sub-Seabed Sequestration and Its Role in Preventing Further Leakage. Environ. Sci. Pollut. Res. 2022, 29, 77737–77754. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wang, F.; Xu, N.; Wang, Y.; Bai, B. Settling Behavior and Mechanism Analysis of Kaolinite as a Fracture Proppant of Hydrocarbon Reservoirs in CO2 Fracturing Fluid. Colloids Surf. A Physicochem. Eng. Asp. 2025, 724, 137463. [Google Scholar] [CrossRef]
- Szott, W.; Miłek, K. Numerical Procedure to Effectively Assess Sequestration Capacity of Geological Structures. Naft.-Gaz 2021, 77, 783–794. [Google Scholar] [CrossRef]
- Jaworski, J.; Kułaga, P.; Kukulska-Zając, E. Wybrane Zagadnienia Dotyczące Wpływu Dodatku Wodoru Do Gazu Ziemnego Na Elementy Systemu Gazowniczego. Naft.-Gaz 2019, 75, 625–632. [Google Scholar] [CrossRef]
- Feldmann, F.; Hagemann, B.; Ganzer, L.; Panfilov, M. Numerical Simulation of Hydrodynamic and Gas Mixing Processes in Underground Hydrogen Storages. Environ. Earth Sci. 2016, 75, 1165. [Google Scholar] [CrossRef]
- Hogeweg, S.; Strobel, G.; Hagemann, B. Benchmark Study for the Simulation of Underground Hydrogen Storage Operations. Comput. Geosci. 2022, 26, 1367–1378. [Google Scholar] [CrossRef]
- Taylor, G.I. Dispersion of Soluble Matter in Solvent Flowing Slowly through a Tube. Proc. R. Soc. Lond. A Math. Phys. Sci. 1953, 219, 186–203. [Google Scholar] [CrossRef]
- Aris, R. On the Dispersion of a Solute in Pulsating Flow through a Tube. Proc. R. Soc. Lond. A Math. Phys. Sci. 1960, 259, 370–376. [Google Scholar] [CrossRef]
- Kneafsey, T.J.; Pruess, K. Laboratory Flow Experiments for Visualizing Carbon Dioxide-Induced, Density-Driven Brine Convection. Transp. Porous Media 2010, 82, 123–139. [Google Scholar] [CrossRef]
- Arekhov, V.; Zhainakov, T.; Clemens, T.; Wegner, J. Measurement of Effective Hydrogen-Hydrocarbon Gas Diffusion Coefficients in Reservoir Rocks. In Proceedings of the SPE Europe C—Europe Energy Conference featured at the 84th EAGE Annual Conference & Exhibition, Vienna, Austria, 5 June 2023; SPE: London, UK, 2023. [Google Scholar]
- Lester, D.R.; Metcalfe, G.; Trefry, M.G. Is Chaotic Advection Inherent to Porous Media Flow? Phys. Rev. Lett. 2013, 111, 174101. [Google Scholar] [CrossRef]
- Azin, R.; Nasiri, A.; Entezari, A.J.; Montazeri, G.H. Investigation of Underground Gas Storage in a Partially Depleted Gas Reservoir. In Proceedings of the CIPC/SPE Gas Technology Symposium 2008 Joint Conference, Calgary, AB, Canada, 16 June 2008; SPE: London, UK, 2008. [Google Scholar]
- Lysyy, M.; Fernø, M.; Ersland, G. Seasonal Hydrogen Storage in a Depleted Oil and Gas Field. Int. J. Hydrog. Energy 2021, 46, 25160–25174. [Google Scholar] [CrossRef]
- Bauer, S. Underground Sun Conversion; RAG Austria AG: Vienna, Austria, 2021. [Google Scholar]
- Ozarslan, A. Large-Scale Hydrogen Energy Storage in Salt Caverns. Int. J. Hydrog. Energy 2012, 37, 14265–14277. [Google Scholar] [CrossRef]
- Londe, L. Underground Storage of Hydrocarbons: Advantages, Lessons Learnt and Way Forward. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 13–16 November 2017; p. SPE-188218-MS. [Google Scholar]
- Siekierski, M.; Majewska, K.; Mroczkowska-Szerszeń, M. Metody Efektywnego i Bezpiecznego Magazynowania Wodoru Jako Warunek Powszechnego Jego Wykorzystania w Transporcie i Energetyce. Naft.-Gaz 2023, 79, 114–130. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, H.S.; Zhang, X.J.; Keatley, P.; Huang, M.J.; Vorushylo, I.; Wang, Y.D.; Hewitt, N.J. Techno-Economic Modelling of Large Scale Compressed Air Energy Storage Systems. In Proceedings of the Energy Procedia, Berlin, Germany, 7–9 April 2017; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; Volume 105, pp. 4034–4039. [Google Scholar]
- Huang, Y.; Rolfe, A.; Vorushylo, I.; Keatley, P.; Byrne, R.; Macartain, P.; Flynn, D.; Hewitt, N. Integration of Compressed Air Energy Storage with Wind Generation into the Electricity Grid. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Tomsk, Russia, 30 October 2018; Institute of Physics Publishing: Bristol, UK, 2018; Volume 188. [Google Scholar]
- Kaliski, M.; Janusz, P.; Szurlej, A. Podziemne magazyny gazu jako element krajowego systemu gazowego. Naft.-Gaz 2010, 66, 325–332. [Google Scholar]
- Filar, B.; Miziołek, M.; Cicha-Szot, R.; Moska, A.; Kwilosz, T.; Szpunar, T. Analysis of the Possibility of Increasing the Working Capacity of Underground Gas Storage Facilities in Poland. Naft.-Gaz 2024, 80, 571–580. [Google Scholar] [CrossRef]
- Groenenberg, R.; Koornneef, J.; Sijm, J.; Janssen, G.; Morales-Espana, G.; Van Stralen, J.; Hernandez-Serna, R.; Smekens, K.; Juez-Larré, J.; Goncalvez, C.; et al. Large-Scale Energy Storage in Salt Caverns and Depleted Fields (LSES)-Project Findings; TNO: Den Haag, The Netherlands, 2020. [Google Scholar]
- Höpken, L.; Bekebrok, H.; Pluta, A.; Langnickel, H.; Savchenko, I.; Ohm, M.; Steinmann, O.; Zobel, M.; Dyck, A.; Agert, C. Modelling Green Hydrogen Storage in Salt Caverns: Implications of Future Storage Demands on Cavern Operation. J. Energy Storage 2025, 119, 116150. [Google Scholar] [CrossRef]
- Jeannin, L.; Myagkiy, A.; Vuddamalay, A. Modelling the Operation of Gas Storage in Salt Caverns: Numerical Approaches and Applications. Sci. Technol. Energy Transit. (STET) 2022, 77, 6. [Google Scholar] [CrossRef]
- Ruiz Maraggi, L.M.; Moscardelli, L.G. Modeling Hydrogen Storage Capacities, Injection and Withdrawal Cycles in Salt Caverns: Introducing the GeoH2 Salt Storage and Cycling App. Int. J. Hydrog. Energy 2023, 48, 26921–26936. [Google Scholar] [CrossRef]
- Ghaedi, M.; Gholami, R. Characterization and Assessment of Hydrogen Leakage Mechanisms in Salt Caverns. Sci. Rep. 2025, 15, 185. [Google Scholar] [CrossRef]
- Qian, X.; You, S.; Wang, R.; Yue, Y.; Liao, Q.; Dai, J.; Tian, S.; Liu, X. Underground Hydrogen Storage in Salt Cavern: A Review of Advantages, Challenges, and Prospects. Sustainability 2025, 17, 5900. [Google Scholar] [CrossRef]
- Wallace, R.L.; Cai, Z.; Zhang, H.; Guo, C. Numerical Investigations into the Comparison of Hydrogen and Gas Mixtures Storage within Salt Caverns. Energy 2024, 311, 133369. [Google Scholar] [CrossRef]
- Bowen, H.; Xianzhen, M.; Yu, L.; Shuchen, L.; Wei, L.; Chao, W. Effects of Cushion Gas Pressure and Operating Parameters on the Capacity of Hydrogen Storage in Lined Rock Caverns (LRC). Renew. Energy 2024, 235, 121317. [Google Scholar] [CrossRef]
- Tackie-Otoo, B.N.; Haq, M.B. A Comprehensive Review on Geo-Storage of H2 in Salt Caverns: Prospect and Research Advances. Fuel 2024, 356, 129609. [Google Scholar] [CrossRef]
- Ramesh Kumar, K.; Honorio, H.; Chandra, D.; Lesueur, M.; Hajibeygi, H. Comprehensive Review of Geomechanics of Underground Hydrogen Storage in Depleted Reservoirs and Salt Caverns. J. Energy Storage 2023, 73, 108912. [Google Scholar] [CrossRef]
- Speirs, D.C.D.; Bere, A.; Roberts, D. Geomechanical Modelling of Salt Caverns under Operational Loading from Hydrogen Storage. In Proceedings of the International Geomechanics Symposium, Abu Dhabi, United Arab Emirates, 7 November 2022; The American Rock Mechanics Association: Alexandria, VA, USA, 2022. [Google Scholar]
- Fu, Y.; Jiang, Y.; Dutta, A.; Mohanram, A.; Pietras, J.D.; Bazant, M.Z. Multicomponent Gas Diffusion in Porous Electrodes. J. Electrochem. Soc. 2015, 162, F613–F621. [Google Scholar] [CrossRef]
- Vaartstra, G.; Lu, Z.; Grossman, J.C.; Wang, E.N. Numerical Validation of the Dusty-Gas Model for Binary Diffusion in Low Aspect Ratio Capillaries. Phys. Fluids 2021, 33, 121701. [Google Scholar] [CrossRef]
- Szott, W.; Gołąbek, A. Symulacyjne modelowanie procesów mieszania się gazów w warunkach złożowych. Naft.-Gaz 2014, 3, 151–161. [Google Scholar]
- Szott, W.; Miłek, K. Numerical Simulations of Hydrogen Storage in a Partially Depleted Gas Reservoir. Naft.-Gaz 2022, 78, 41–55. [Google Scholar] [CrossRef]
- Schlumberger-Private An Internal Documentation on General Considerations for Modelling Hydrogen Storage with Eclipse; Unpublished Internal Documentation; Schlumberger: Houston, TX, USA, 2023.
- Neumiller, J. Feasibility of Using Wind Energy and CAES Systems in a Variety of Geologic Systems. In Proceedings of the EUROPEC/EAGE Conference and Exhibition, Amsterdam, The Netherlands, 8–11 June 2009; p. SPE-121934-MS. [Google Scholar]
- Branch of KPMG Mogilno. Available online: https://pgnig.pl/podziemne-magazyny-gazu (accessed on 28 November 2023).
- Fang, Y.; Hou, Z.; Yue, Y.; Chen, Q.; Liu, J. Numerical Study of Hydrogen Storage Cavern in Thin-Bedded Rock Salt, Anning of China. In Mechanical Behavior of Salt; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Stopa, J.; Stanislaw, R.; Kosowski, P. The Role of Salt Caverns in Underground Gas Storage. Miner. Resour. Manag. 2008, 24, 11–23. [Google Scholar]
- Bijeljic, B.; Blunt, M.J. A Physically Based Description of Dispersion in Porous Media. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 24 September 2006; SPE: London, UK, 2006. [Google Scholar]
- Ogata, A.; Banks, R.B. A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media; USGS: Reston, VA, USA, 1961. [Google Scholar]
- Miłek, K.; Szott, W.; Gołąbek, A. Simulation Study of Displaced Methane Displaced in Formation Waters by Injecting Acid Gases as Part of Their Sequestration. Naft.-Gaz 2013, 69, 112–122. Available online: https://inig.pl/magazyn/nafta-gaz/NAFTA-GAZ-2013-02-02.pdf (accessed on 16 October 2025).
| Component | Molecular Weight [kg/kmole] | Tcrit [K] | Pcrit [bar] | Vcrit [m3/kg-mole] | Zcrit [-] | Vol Shift [-] | Acentric Factor [-] | Parachor [dyne/cm] | Omega A [-] | Omega B [-] |
|---|---|---|---|---|---|---|---|---|---|---|
| H2 | 2.016 | 33.2 | 12.97 | 0.065 | 0.3054 | 0 | −0.22 | 34 | 0.4573 | 0.0778 |
| C1 | 16.043 | 190.6 | 46.00 | 0.099 | 0.2874 | 0 | 0.013 | 77 | 0. 4573 | 0.0778 |
| T [°C] | P [bar] | D [m2/d] |
|---|---|---|
| 28 | 40 | 0.1547 |
| 57 | 40 | 0.4492 |
| 57 | 155.14 | 0.1158 |
| 57 | 221.1 | 0.0811 |
| 57 | 301.89 | 0.0595 |
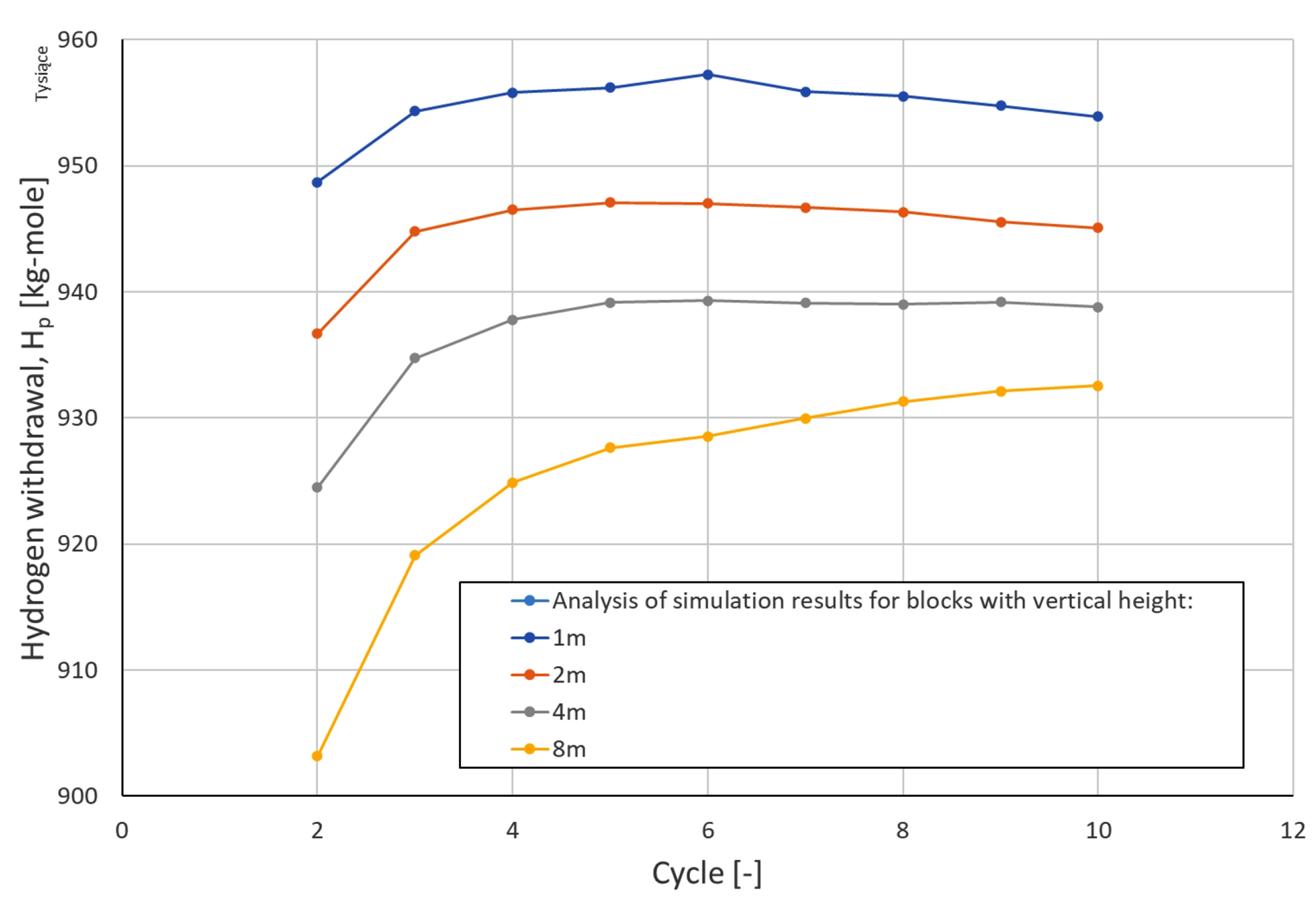
| Cycle\Block Height | Hydrogen Withdrawal [kg mole] | |||
|---|---|---|---|---|
| 1 m | 2 m | 4 m | 8 m | |
| 2 | 948,717 | 936,696 | 924,471 | 903,182 |
| 3 | 954,342 | 944,787 | 934,760 | 919,090 |
| 4 | 955,813 | 946,493 | 937,789 | 924,867 |
| 5 | 956,214 | 947,087 | 939,170 | 927,630 |
| 6 | 957,226 | 946,999 | 939,294 | 928,545 |
| 7 | 955,878 | 946,672 | 939,113 | 929,974 |
| 8 | 955,521 | 946,315 | 939,005 | 931,303 |
| 9 | 954,779 | 945,546 | 939,193 | 932,127 |
| 10 | 953,913 | 945,088 | 938,802 | 932,545 |
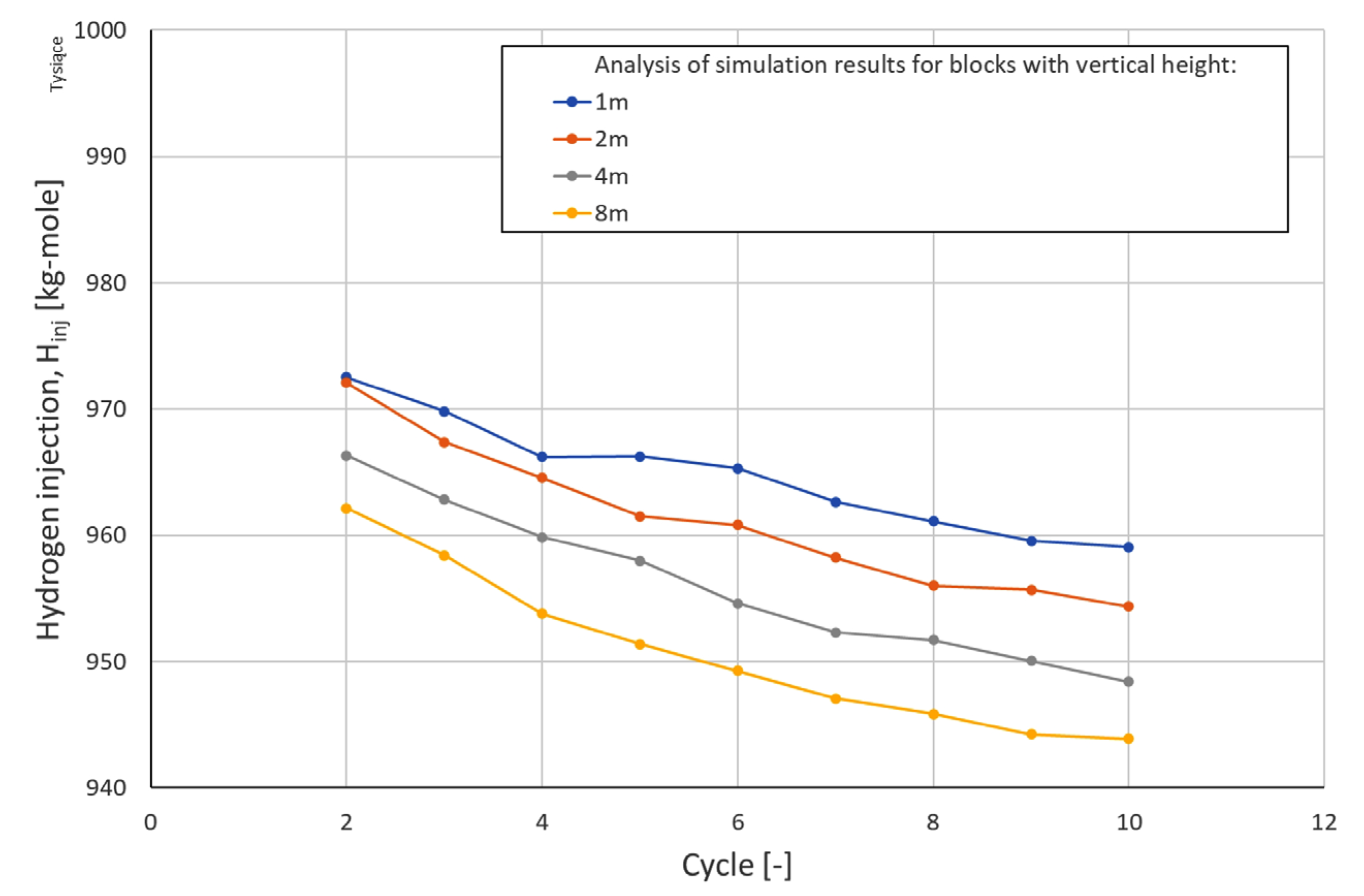
| Cycle\Block Height | Hydrogen Injection [kg mole] | |||
|---|---|---|---|---|
| 1 m | 2 m | 4 m | 8 m | |
| 2 | 974,788 | 974,448 | 971,842 | 970,326 |
| 3 | 972,519 | 972,091 | 966,308 | 962,151 |
| 4 | 969,844 | 967,395 | 962,818 | 958,425 |
| 5 | 966,208 | 964,552 | 959,864 | 953,802 |
| 6 | 966,246 | 961,505 | 957,996 | 951,384 |
| 7 | 965,321 | 960,804 | 954,627 | 949,282 |
| 8 | 962,665 | 958,235 | 952,327 | 947,089 |
| 9 | 961,115 | 956,023 | 951,722 | 945,857 |
| 10 | 959,554 | 955,680 | 950,075 | 944,233 |
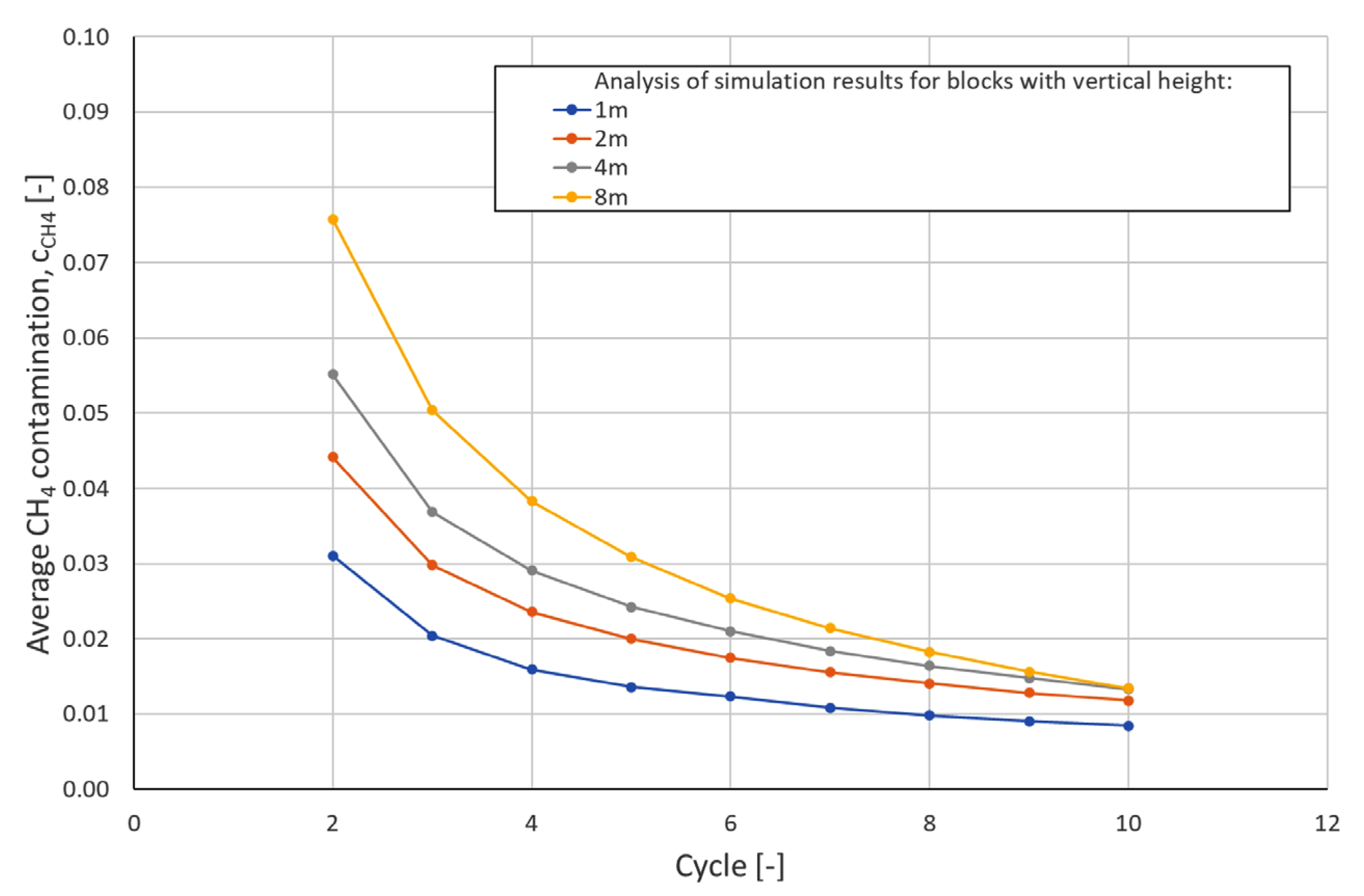
| Cycle\Block Height | Hydrogen Contamination [mol/mol] | |||
|---|---|---|---|---|
| 1 m | 2 m | 4 m | 8 m | |
| 2 | 0.0311 | 0.0441 | 0.0552 | 0.0758 |
| 3 | 0.0204 | 0.0298 | 0.0368 | 0.0504 |
| 4 | 0.0159 | 0.0236 | 0.0291 | 0.0383 |
| 5 | 0.0136 | 0.0200 | 0.0242 | 0.0309 |
| 6 | 0.0123 | 0.0175 | 0.0210 | 0.0254 |
| 7 | 0.0108 | 0.0156 | 0.0184 | 0.0214 |
| 8 | 0.0098 | 0.0141 | 0.0164 | 0.0183 |
| 9 | 0.0091 | 0.0128 | 0.0148 | 0.0156 |
| 10 | 0.0085 | 0.0118 | 0.0133 | 0.0134 |
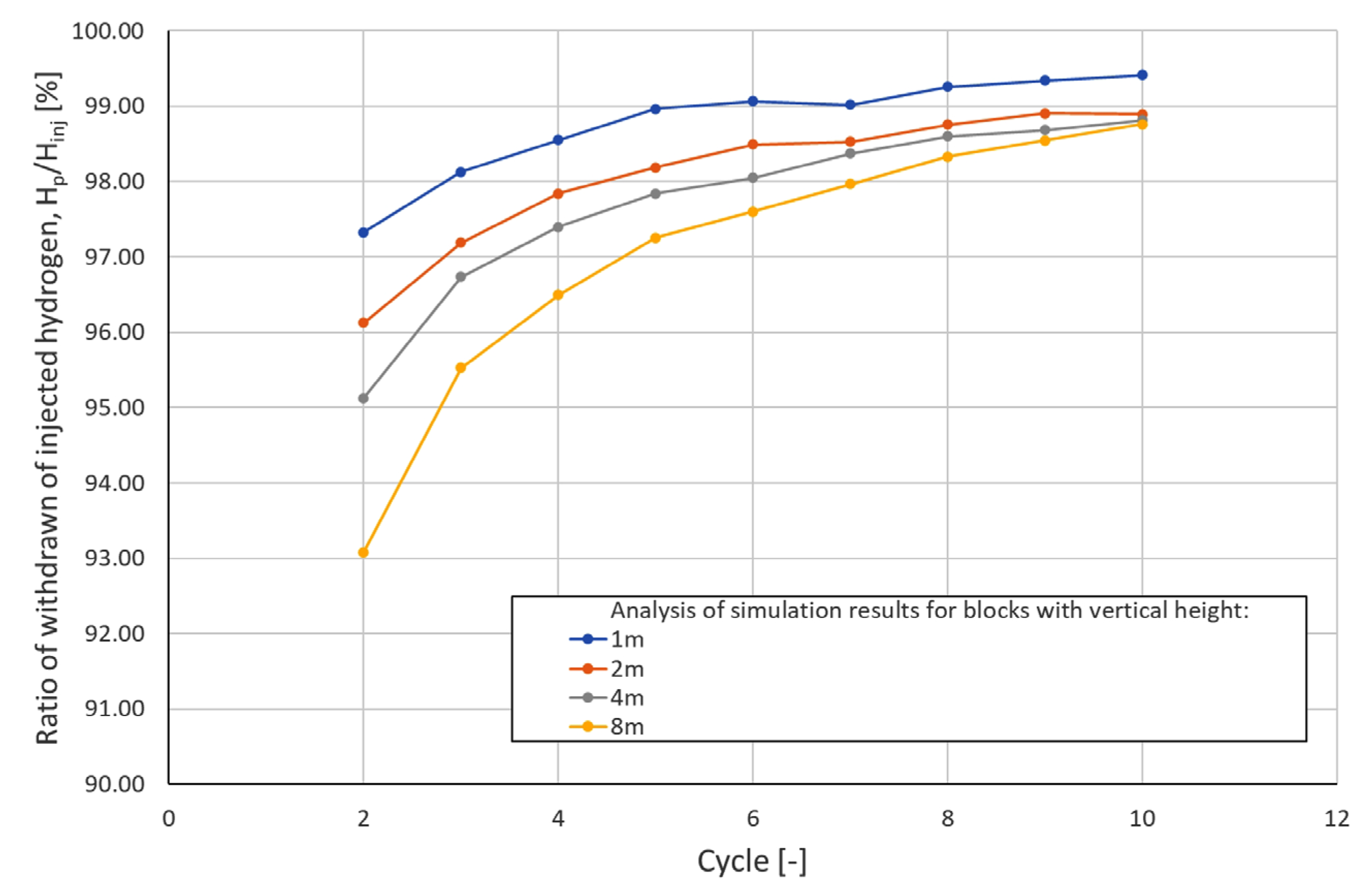
| Cycle\Block Height | Ratio of Withdrawn to Injected Hydrogen in Subsequent Cycles [%] | |||
|---|---|---|---|---|
| 1 m | 2 m | 4 m | 8 m | |
| 2 | 97.33 | 96.13 | 95.13 | 93.08 |
| 3 | 98.13 | 97.19 | 96.74 | 95.52 |
| 4 | 98.55 | 97.84 | 97.40 | 96.50 |
| 5 | 98.97 | 98.19 | 97.84 | 97.26 |
| 6 | 99.07 | 98.49 | 98.05 | 97.60 |
| 7 | 99.02 | 98.53 | 98.37 | 97.97 |
| 8 | 99.26 | 98.76 | 98.60 | 98.33 |
| 9 | 99.34 | 98.90 | 98.68 | 98.55 |
| 10 | 99.41 | 98.89 | 98.81 | 98.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miłek, K.; Szott, W. Numerical Modelling of Gas Mixing in Salt Caverns During Cyclic Hydrogen Storage. Energies 2025, 18, 5528. https://doi.org/10.3390/en18205528
Miłek K, Szott W. Numerical Modelling of Gas Mixing in Salt Caverns During Cyclic Hydrogen Storage. Energies. 2025; 18(20):5528. https://doi.org/10.3390/en18205528
Chicago/Turabian StyleMiłek, Krzysztof, and Wiesław Szott. 2025. "Numerical Modelling of Gas Mixing in Salt Caverns During Cyclic Hydrogen Storage" Energies 18, no. 20: 5528. https://doi.org/10.3390/en18205528
APA StyleMiłek, K., & Szott, W. (2025). Numerical Modelling of Gas Mixing in Salt Caverns During Cyclic Hydrogen Storage. Energies, 18(20), 5528. https://doi.org/10.3390/en18205528






