LightGBM Medium-Term Photovoltaic Power Prediction Integrating Meteorological Features and Historical Data
Abstract
1. Introduction
2. Data and Preprocessing
2.1. Introduction to the Dataset
2.2. Data Preprocessing
2.3. Feature Importance Analysis
2.4. Evaluation Metrics
- MSE, defined as the average of the squared differences between predicted and actual values (Equation (1)), is particularly sensitive to large deviations because errors are magnified by squaring.
- 2.
- RMSE, shown in Equation (2), is the square root of MSE and thus provides a more intuitive measure of prediction error in the same units as the target variable. Both MSE and RMSE indicate better performance when their values are smaller.
- 3.
- MAE, presented in Equation (3), calculates the average absolute difference between predicted and actual values. Unlike MSE and RMSE, MAE does not square the errors, making it less sensitive to outliers and therefore a robust indicator of general predictive accuracy.
- 4.
- Finally, R2, shown in Equation (4), measures the proportion of variance in the actual data explained by the model. An R2 value closer to 1 indicates stronger explanatory power, while a value near 0 suggests that the model performs no better than using the mean of the observations.
3. LightGBM Photovoltaic Power Generation Prediction Model
3.1. LightGBM Algorithm
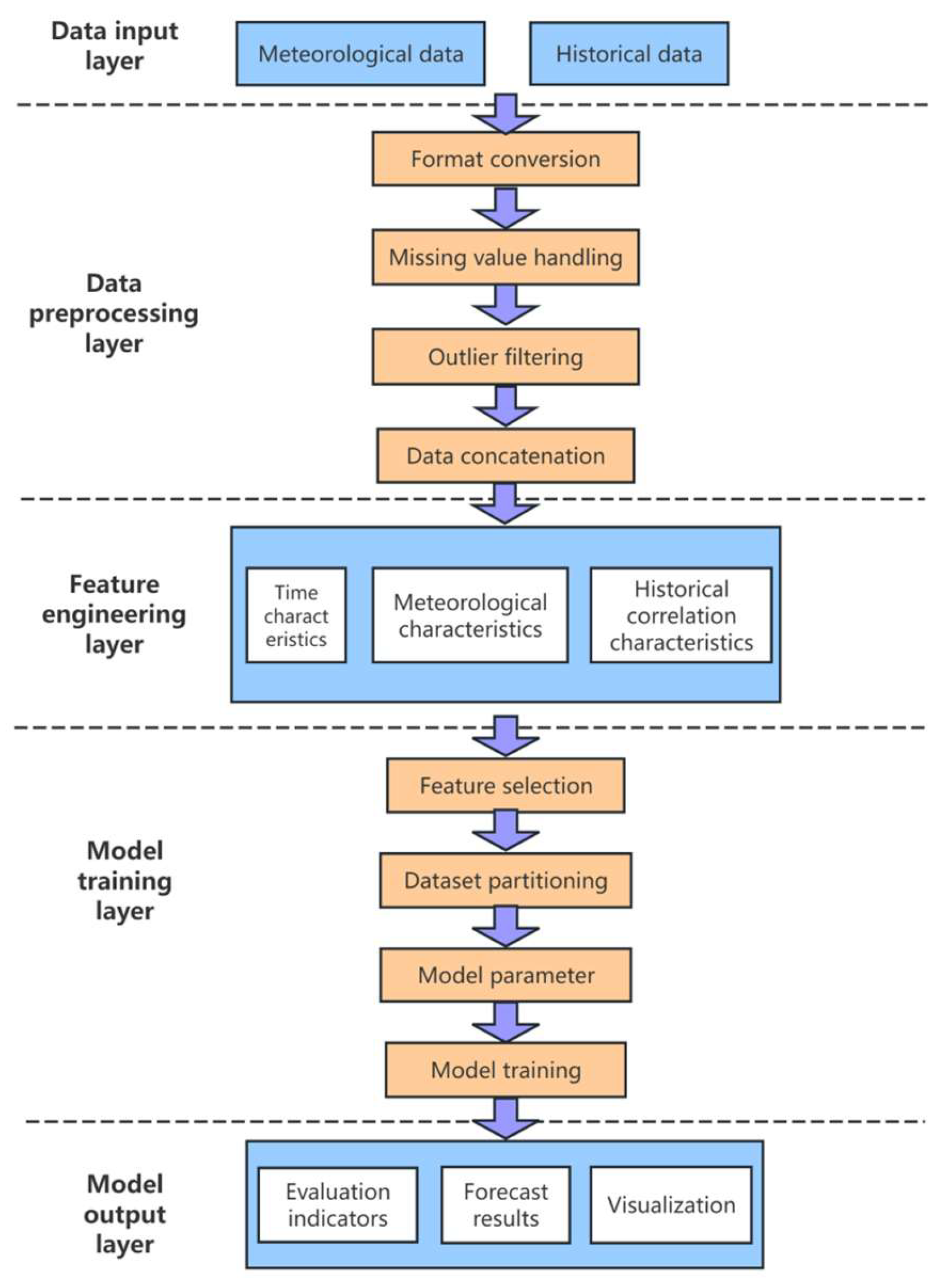
3.2. Construction of LightGBM Model Integrating Meteorological Features and Historical Data
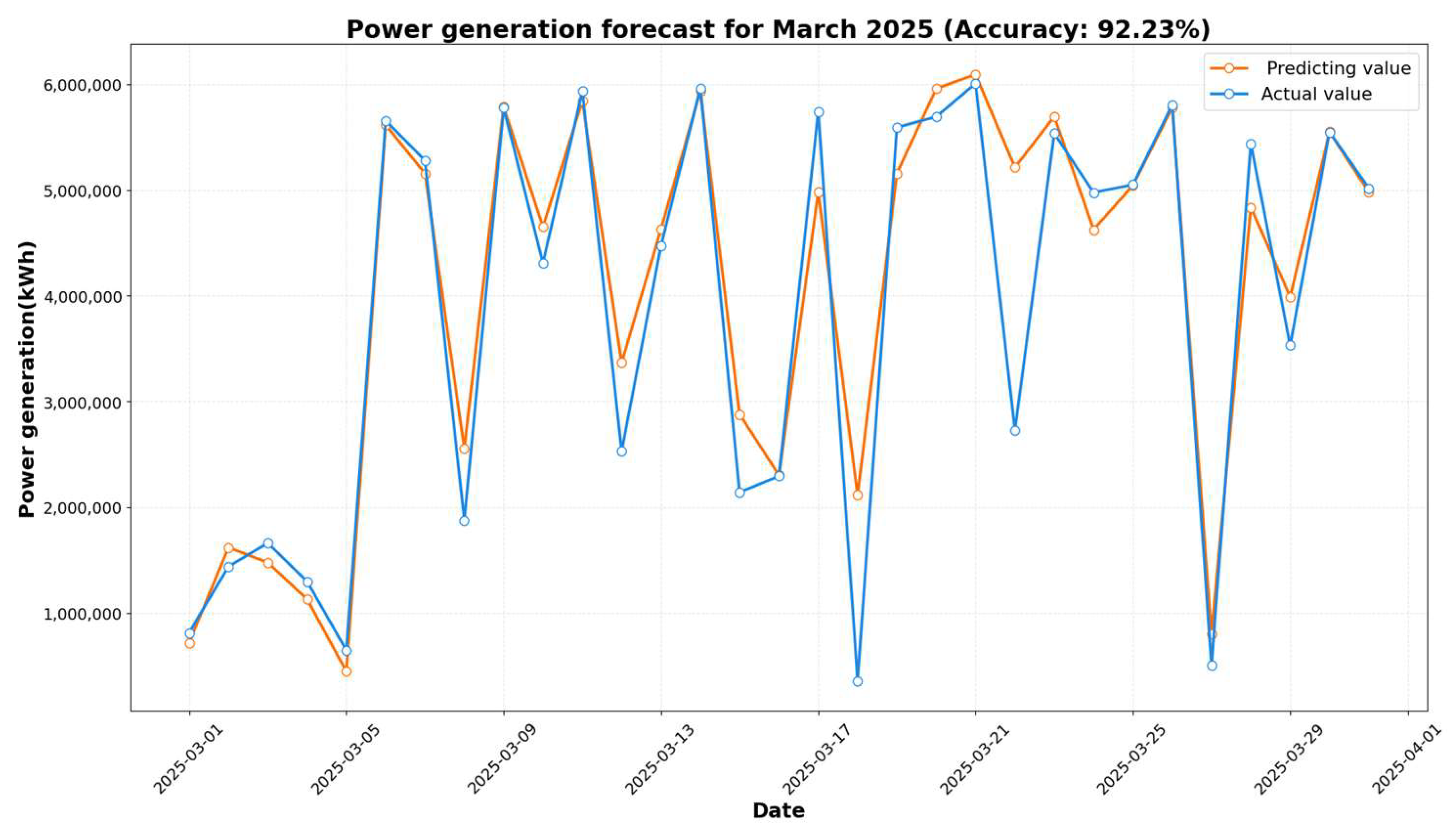
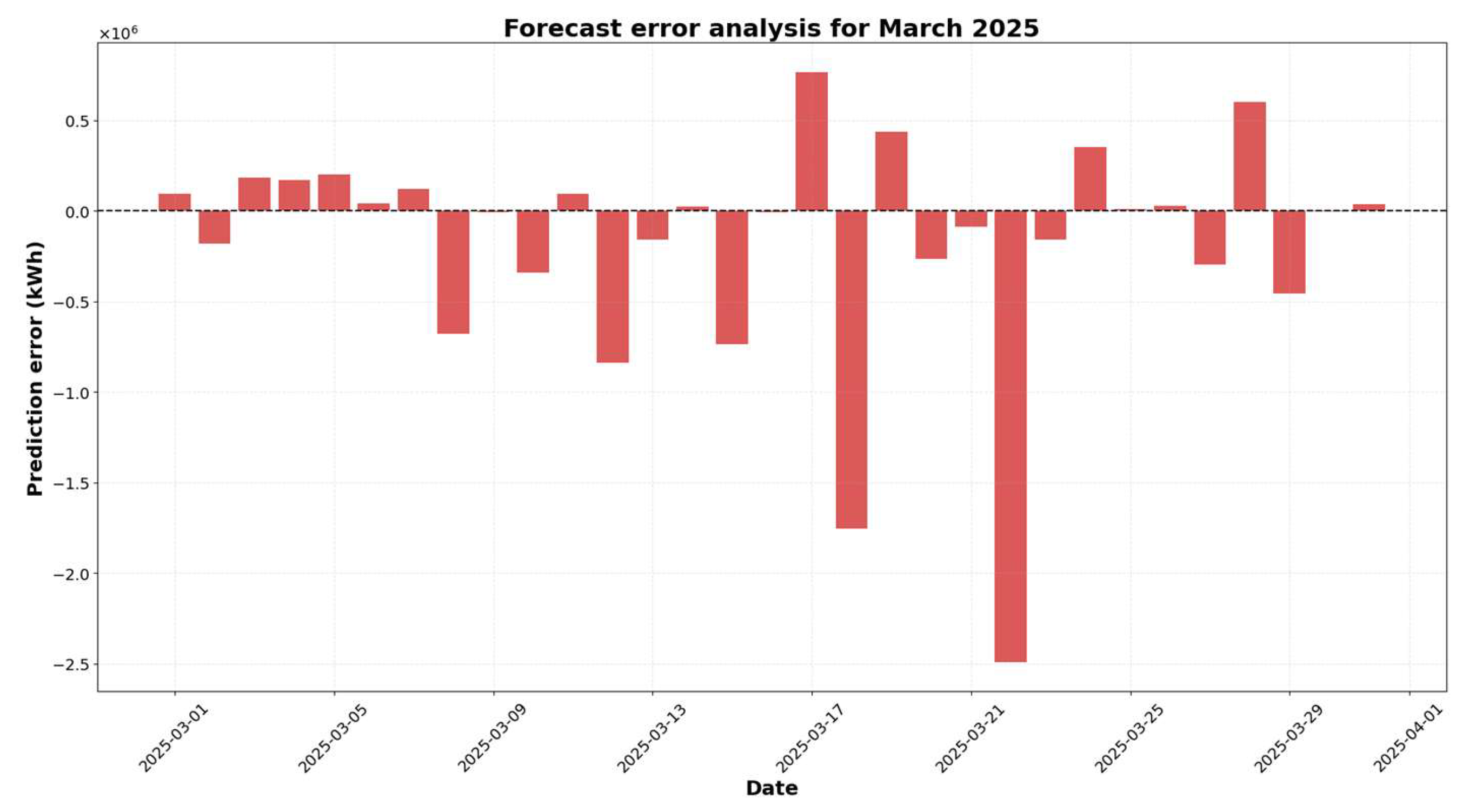
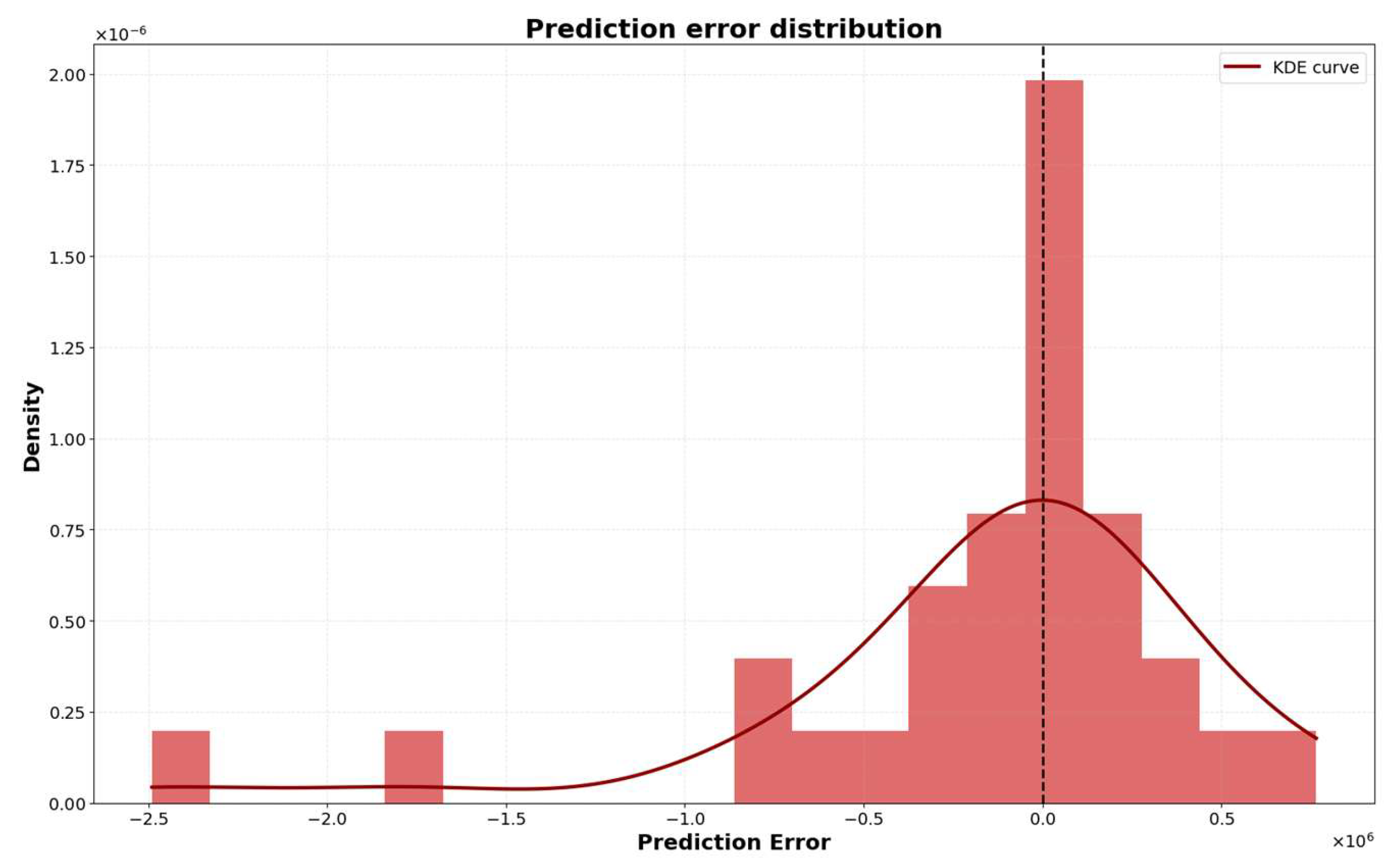
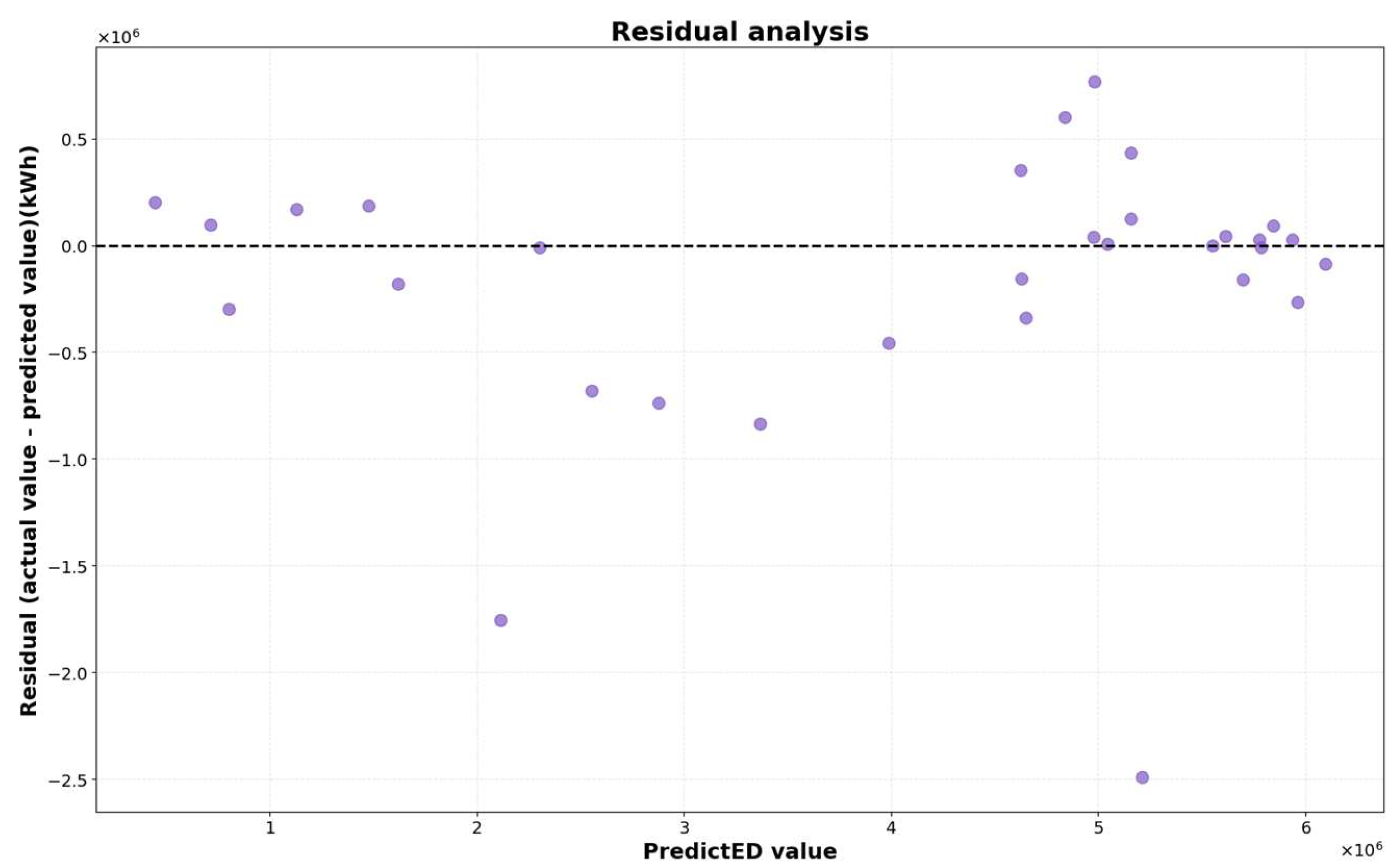
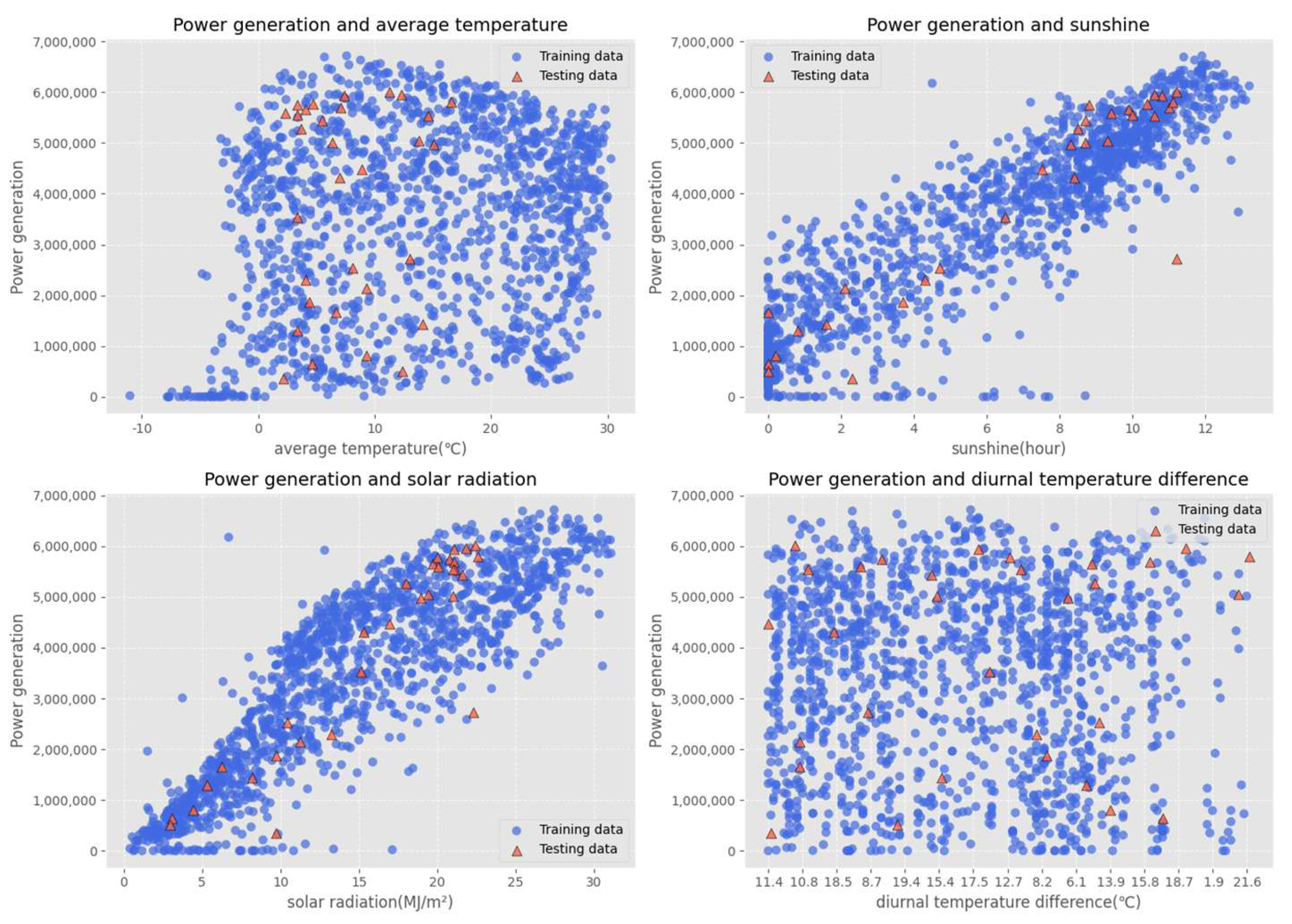
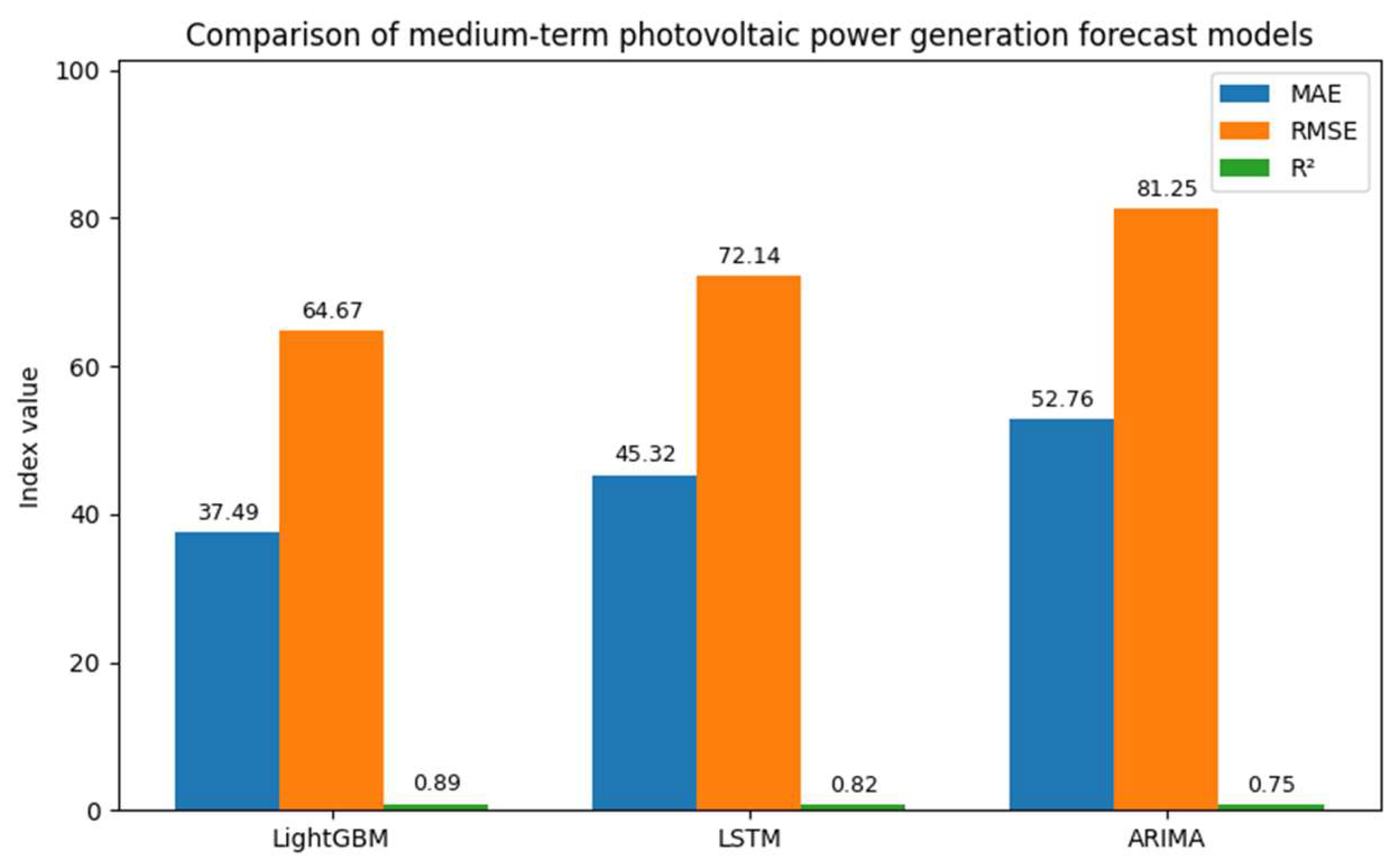
4. Analysis of Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV | Photovoltaic |
| RFE | Recursive feature elimination |
| IEA | International energy agency |
| NWP | Numerical weather prediction |
| SVM | Support vector machines |
| ANN | Artificial neural networks |
| ELM | Extreme learning machines |
| RNNs | Recurrent neural networks |
| LSTM | Long short-term memory |
| LightGBM | Light gradient boosting machine |
| MAE | Mean absolute error |
| RMSE | Root mean square error |
| KDE | Kernel density estimation |
References
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of Photovoltaic Power Forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Hossain, M.S.; Mahmood, H. Short-Term Photovoltaic Power Forecasting Using an LSTM Neural Network and Synthetic Weather Forecast. IEEE Access 2020, 8, 172524–172533. [Google Scholar] [CrossRef]
- Wan, A.; Chang, Q.; AL-Bukhaiti, K.; He, J. Short-Term Power Load Forecasting for Combined Heat and Power Using CNN-LSTM Enhanced by Attention Mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Zhang, M.; Zhen, Z.; Liu, N.; Zhao, H.; Sun, Y.; Feng, C.; Wang, F. Optimal Graph Structure Based Short-Term Solar PV Power Forecasting Method Considering Surrounding Spatio-Temporal Correlations. IEEE Trans. Ind. Appl. 2023, 59, 345–357. [Google Scholar] [CrossRef]
- Alhussein, M.; Aurangzeb, K.; Haider, S.I. Hybrid CNN-LSTM Model for Short-Term Individual Household Load Forecasting. IEEE Access 2020, 8, 180544–180557. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, S.; Chen, W.; Ma, J.; Wang, C.; Chen, J. LightGBM-Integrated PV Power Prediction Based on Multi-Resolution Similarity. Processes 2023, 11, 1141. [Google Scholar] [CrossRef]
- Kim, T.; Ko, W.; Kim, J. Analysis and impact evaluation of missing data imputation in day-ahead PV generation forecasting. Appl. Sci. 2019, 9, 204. [Google Scholar] [CrossRef]
- Hourly Photovoltaic Power Prediction Based on Signal Decomposition and Deep Learning. Available online: https://www.researchgate.net/publication/379104488_Hourly_photovoltaic_power_prediction_based_on_signal_decomposition_and_deep_learning (accessed on 12 October 2025).
- Huang, Y.; Wang, A.; Jiao, J.; Xie, J.; Chen, H. Short-Term PV Power Forecasting Based on CEEMDAN and Ensemble DeepTCN. IEEE Trans. Instrum. Meas. 2023, 72, 2526012. [Google Scholar] [CrossRef]
- Faruque, M.O.; Hossain, M.A.; Alam, S.M.M.; Islam, M.R.; Islam, M.R.; Guo, Y. A Hybrid LSTM-LightGBM Model for Precise Short-Term Wind Power Forecasting. In Proceedings of the 2023 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Tianjin, China, 27–29 October 2023; pp. 1–2. [Google Scholar]
- Robust Photovoltaic Power Forecasting Model Under Complex Meteorological Conditions. Available online: https://www.mdpi.com/2227-7390/13/11/1783 (accessed on 12 October 2025).
- Onorato, G. Bayesian Optimization for Hyperparameters Tuning in Neural Networks. arXiv 2024, arXiv:2410.21886. [Google Scholar] [CrossRef]
- Macaire, J.; Zermani, S.; Linguet, L. New Feature Selection Approach for Photovoltaïc Power Forecasting Using KCDE. Energies 2023, 16, 6842. [Google Scholar] [CrossRef]
- Zhou, H.; Zheng, P.; Dong, J.; Liu, J.; Nakanishi, Y. Interpretable Feature Selection and Deep Learning for Short-Term Probabilistic PV Power Forecasting in Buildings Using Local Monitoring Data. Appl. Energy 2024, 376, 124271. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A Comprehensive Review on Ensemble Deep Learning: Opportunities and Challenges. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Wang, K.; Shan, S.; Dou, W.; Wei, H.; Zhang, K. A Robust Photovoltaic Power Forecasting Method Based on Multimodal Learning Using Satellite Images and Time Series. IEEE Trans. Sustain. Energy 2025, 16, 970–980. [Google Scholar] [CrossRef]
- Xiang, X.; Li, X.; Zhang, Y.; Hu, J. A Short-Term Forecasting Method for Photovoltaic Power Generation Based on the TCN-ECANet-GRU Hybrid Model. Sci. Rep. 2024, 14, 6744. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic Forecasting of Wind Power Generation Using Extreme Learning Machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; Monash University: Clayton, VIC, Australia, 2018. [Google Scholar]
- Elsaraiti, M.; Merabet, A. Solar Power Forecasting Using Deep Learning Techniques. IEEE Access 2022, 10, 31692–31698. [Google Scholar] [CrossRef]
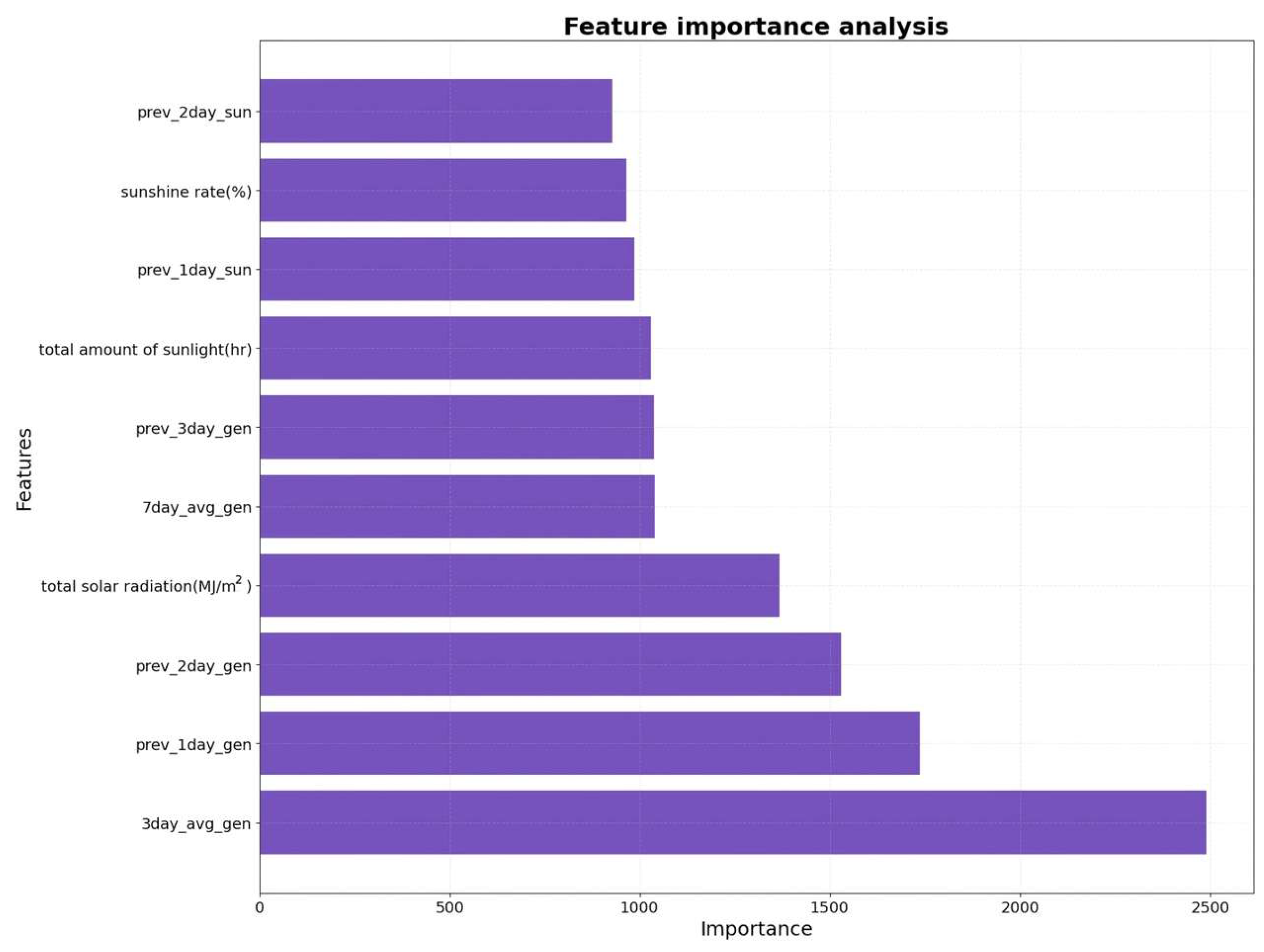
| Rank | Feature Name | Type | Relative Importance | Proxy Elimination Order |
|---|---|---|---|---|
| 1 | prev_1day_gen | Lagged Target | Highest | Last (Most Important) |
| 2 | 7day_avg_gen | Rolling Statistic | Very High | - |
| 3 | prev_2day_gen | Lagged Target | High | - |
| 4 | 3day_avg_gen | Rolling Statistic | High | - |
| 5 | prev_3day_gen | Lagged Target | High | - |
| 6 | total solar radiation (MJ/m2) | Meteorological | Medium | - |
| 7 | total amount of sunlight (hr) | Meteorological | Medium | - |
| … | … | … | … | … |
| N | is_holiday | Calendar | Lowest | First |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Lee, S.-H.; Choi, Y.-S.; Lee, K.-M. LightGBM Medium-Term Photovoltaic Power Prediction Integrating Meteorological Features and Historical Data. Energies 2025, 18, 5526. https://doi.org/10.3390/en18205526
Yang Y, Lee S-H, Choi Y-S, Lee K-M. LightGBM Medium-Term Photovoltaic Power Prediction Integrating Meteorological Features and Historical Data. Energies. 2025; 18(20):5526. https://doi.org/10.3390/en18205526
Chicago/Turabian StyleYang, Yu, Soon-Hyung Lee, Yong-Sung Choi, and Kyung-Min Lee. 2025. "LightGBM Medium-Term Photovoltaic Power Prediction Integrating Meteorological Features and Historical Data" Energies 18, no. 20: 5526. https://doi.org/10.3390/en18205526
APA StyleYang, Y., Lee, S.-H., Choi, Y.-S., & Lee, K.-M. (2025). LightGBM Medium-Term Photovoltaic Power Prediction Integrating Meteorological Features and Historical Data. Energies, 18(20), 5526. https://doi.org/10.3390/en18205526





