Multi-Objective Optimization of Mobile Battery Energy Storage and Dynamic Feeder Reconfiguration for Enhanced Voltage Profiles in Active Distribution Systems
Abstract
1. Introduction
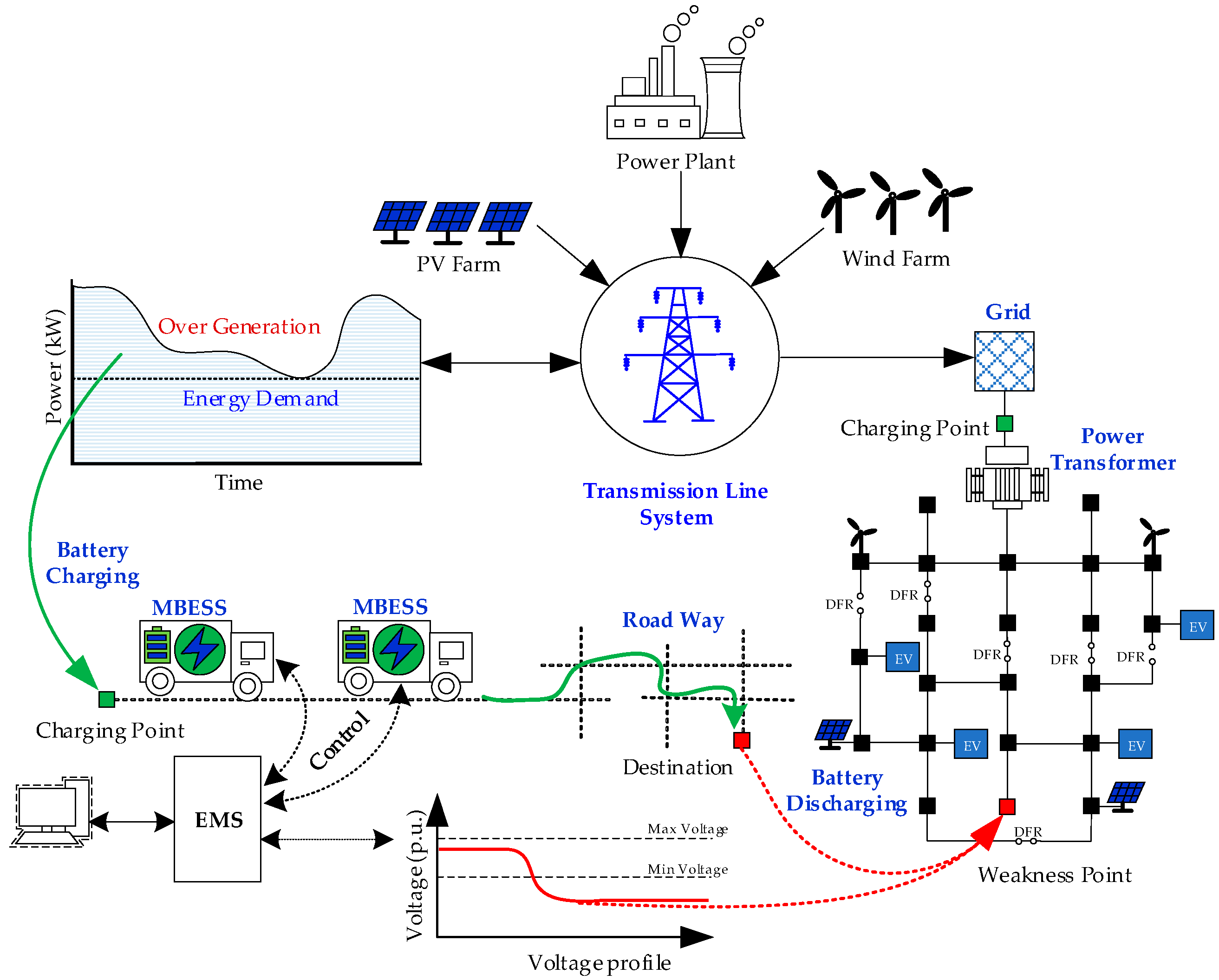
1.1. Background and Motivation
1.2. Literature Review and Research Gaps
1.2.1. Literature Review
1.2.2. Research Gaps
1.3. Purpose, Contributions, and Structure
1.3.1. The Purpose of This Study
1.3.2. Primary Contributions
- An operational framework that integrates MBESS with DFR First item.
- 2.
- NSGA-III for multi-objective co-optimization.
- 3.
- Identifying compromises solution.
- 4.
- Proper testbed and circumstances.
- 5.
- Practical recommendations for implementation.
2. Problem Formulation
2.1. Load Flow Analysis
2.1.1. Power Flow Calculation
2.1.2. Total Active Power Loss and Reactive Power Loss
2.1.3. Voltage Deviation Index (VDI)
2.1.4. Fast Voltage Stability Index
2.2. Photovoltaic System Modeling
2.3. Wind Turbine System Modeling
2.4. Electric Vehicles Charging Station (EVCS) Modeling
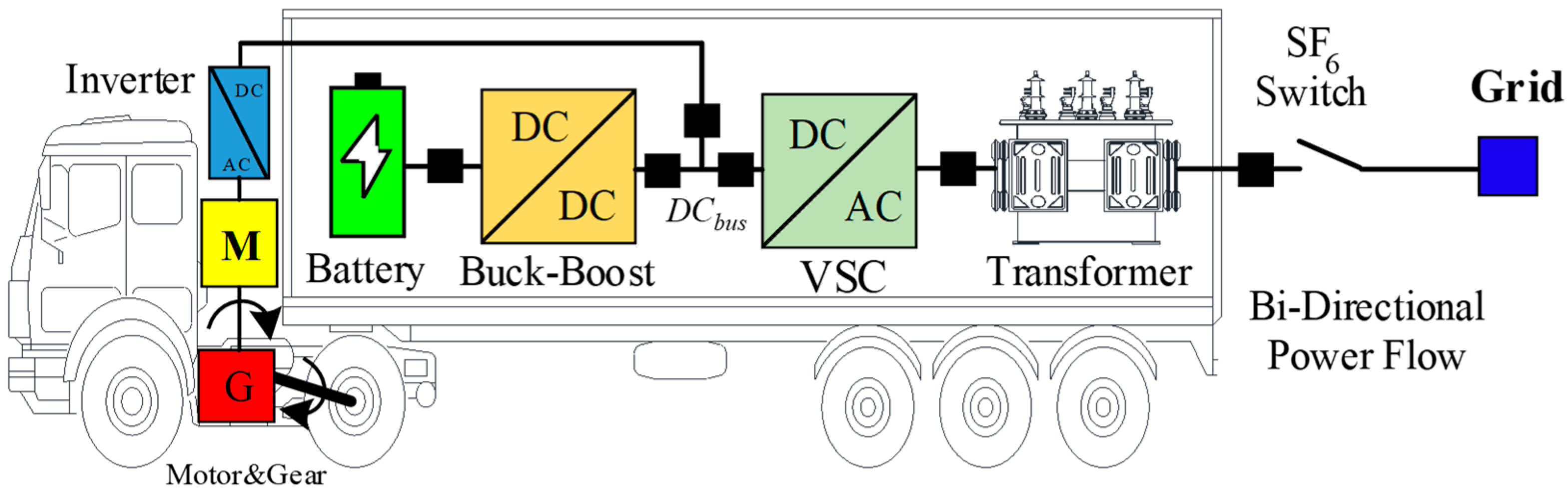
2.5. Mobile Battery Energy Storage System (MBESS) Modelling
2.5.1. Battery Energy Storage System (BESS) Modelling
2.5.2. Electric Vehicle Truck (EVT) Modelling
2.5.3. The MESS Operating Cost Modeling
2.5.4. Dynamic Feeder Reconfiguration (DFR) Background
- (A)
- A disconnecting switch (DS) is used to control the transfer of power under off-load operation; that is the reason for using air insulation for breaking current interruptions.
- (B)
- A load break switch (LBS) is used to control and transfer the power to the load, the same as the DS, but can also operate under load with SF6 insulation for breaking current interruption and installation between feeders.
- (C)
- An auto recloser switch is used to control and transfer the power to the load, the same as the LBS, but with additional functions for the protection under fault control and installation from the root feeder and backup scheme.
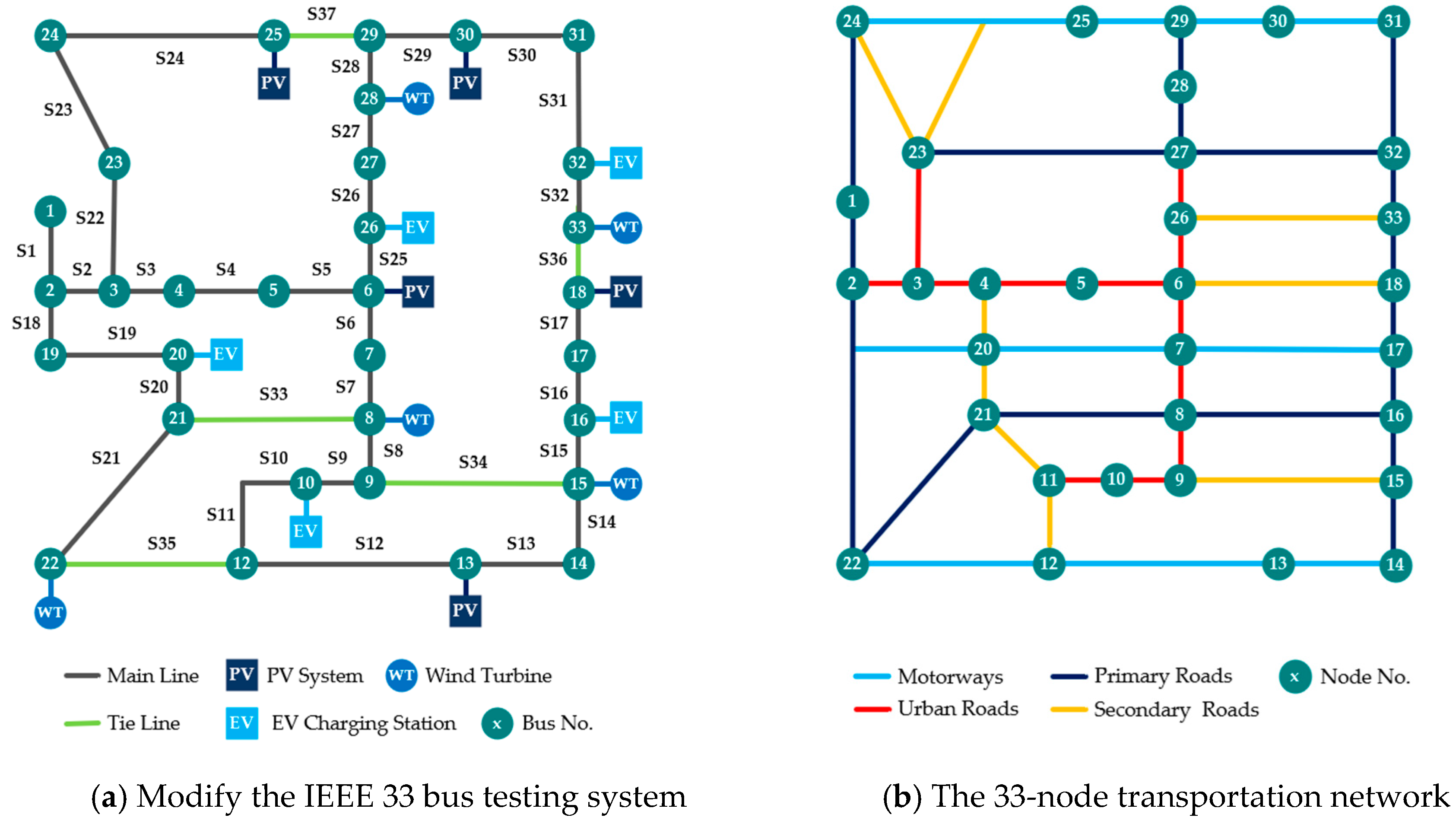
2.6. Transportation System Model Modeling
2.6.1. Bureau of Public Roads (BPR) Function
2.6.2. Travel Distance and Time Matrix
- Travel Distance Matrix:
- Travel Time Matrix (T) is presented as follows:
2.6.3. Shortest Path Analysis Based on the Dijkstra’s Algorithm
| Algorithm 1 Dijkstra (Graph, source) |
| 1. Initialize distances: - - For each vertex v in Graph: - - Mark all nodes as unvisited - Create a priority queue (min-heap) and insert (source, 0) 2. While the priority queue is not empty: - from the priority queue - Mark node u as visited 3. Relaxation step: - For each adjacent node v of u: - - - into the priority queue 4. Repeat until all nodes are processed or the queue is empty 5. for all nodes v (shortest distances from source) |
2.7. Carbon Dioxide Emission Calculation
3. Methodology
3.1. Energy Management Using NSGA-III
3.1.1. NSGA-III Algorithms
3.1.2. Compromised Solution and Normalization
- 1.
- Objective Normalization
- 2.
- Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)
3.2. Objective Function
3.3. Inequality Constraint and Limits
3.4. Test System for ADS and Transportation Network
3.5. Simulation Parameters
3.6. Case Study
4. Results and Discussion
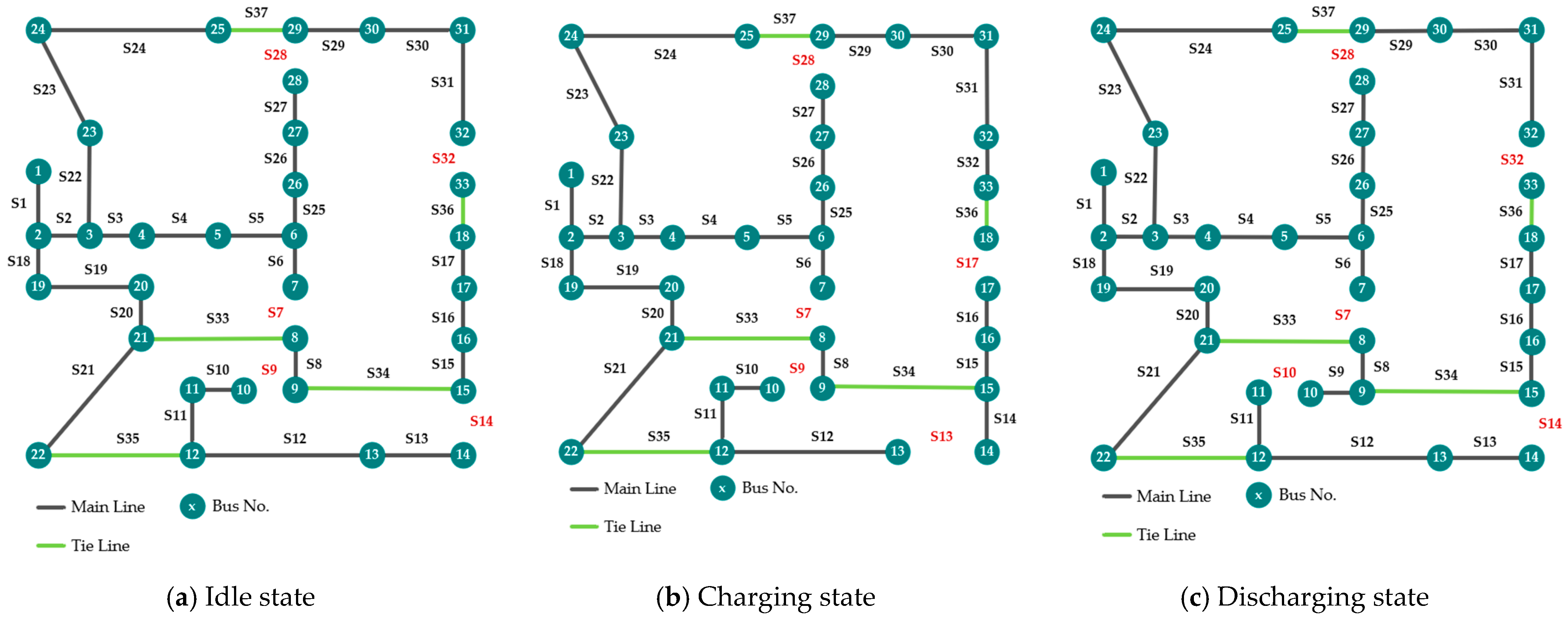
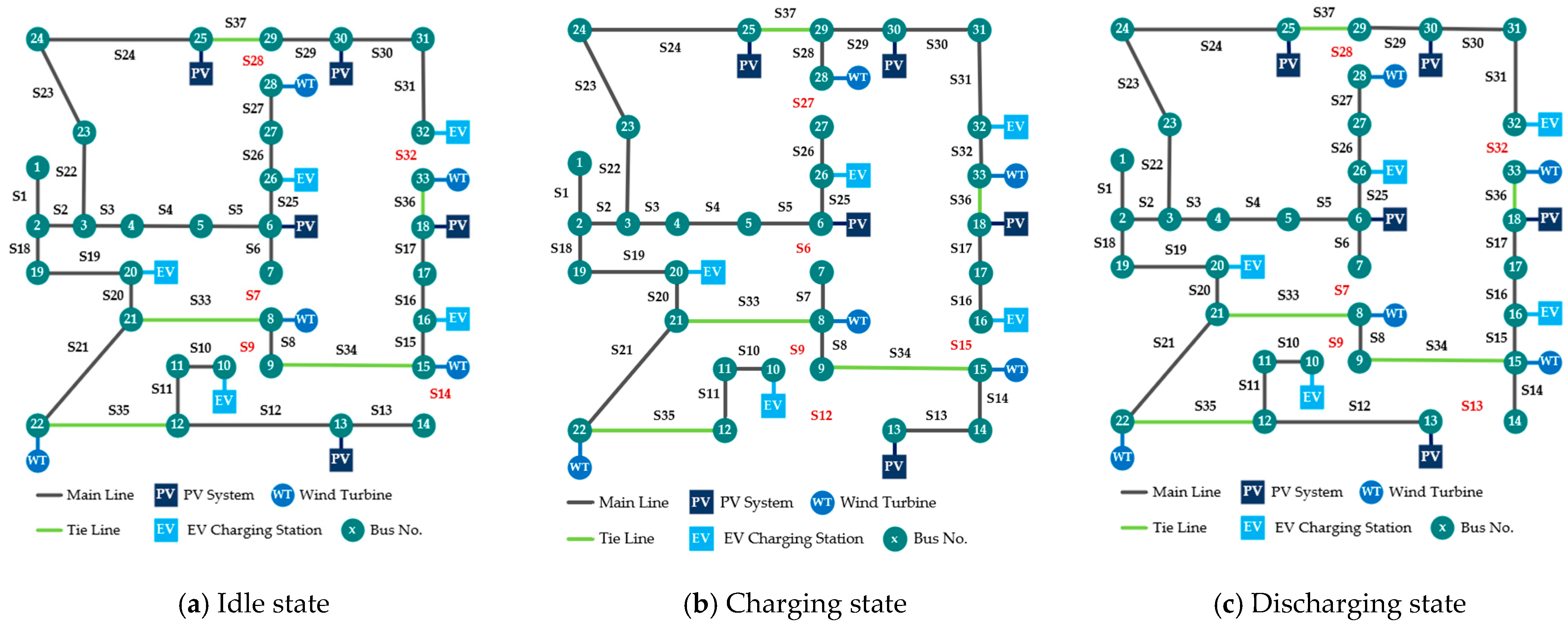
4.1. MBESS Location and Feeder Reconfiguration
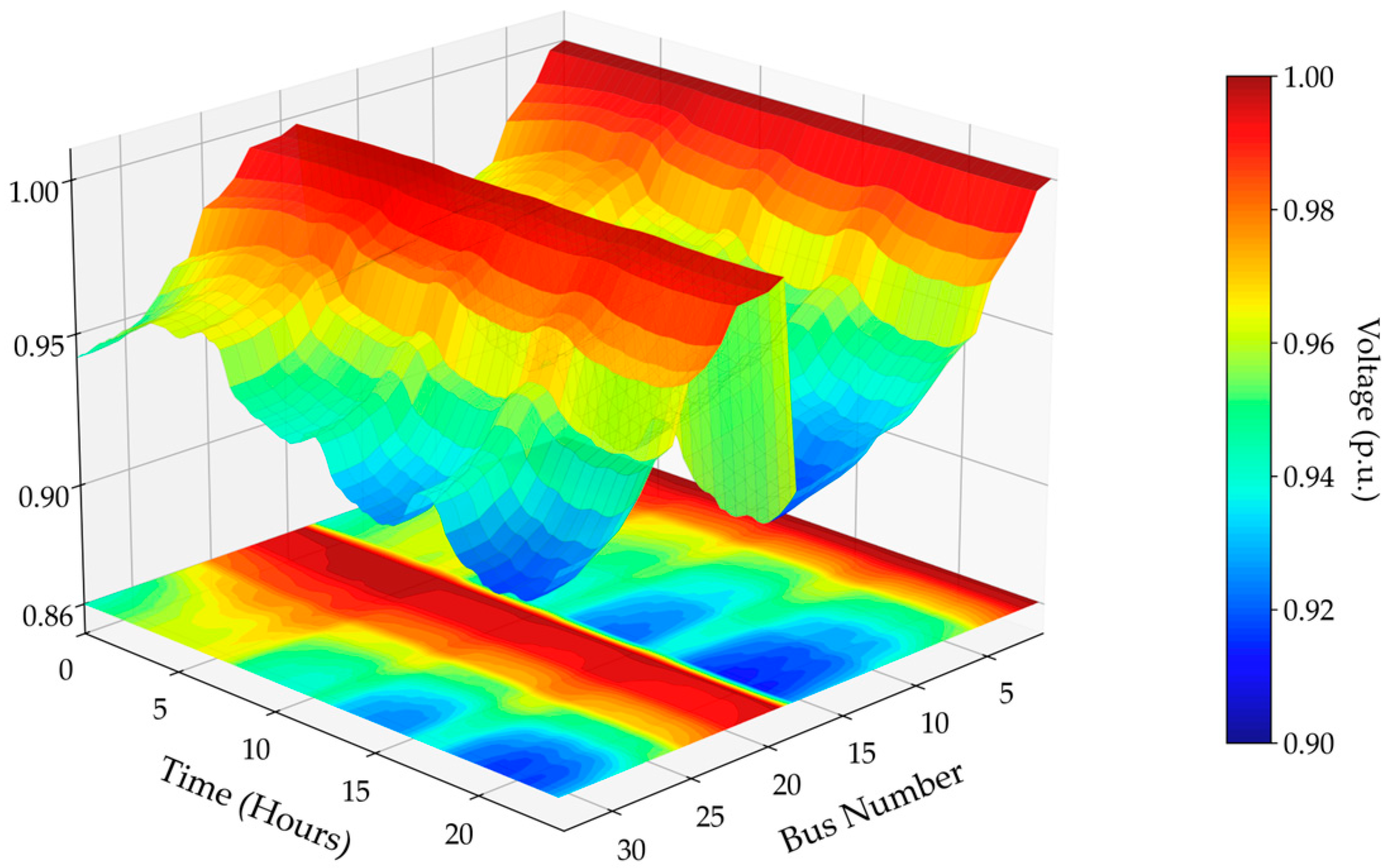
4.2. Results of Scenario 1 (Case 1 to Case 3)
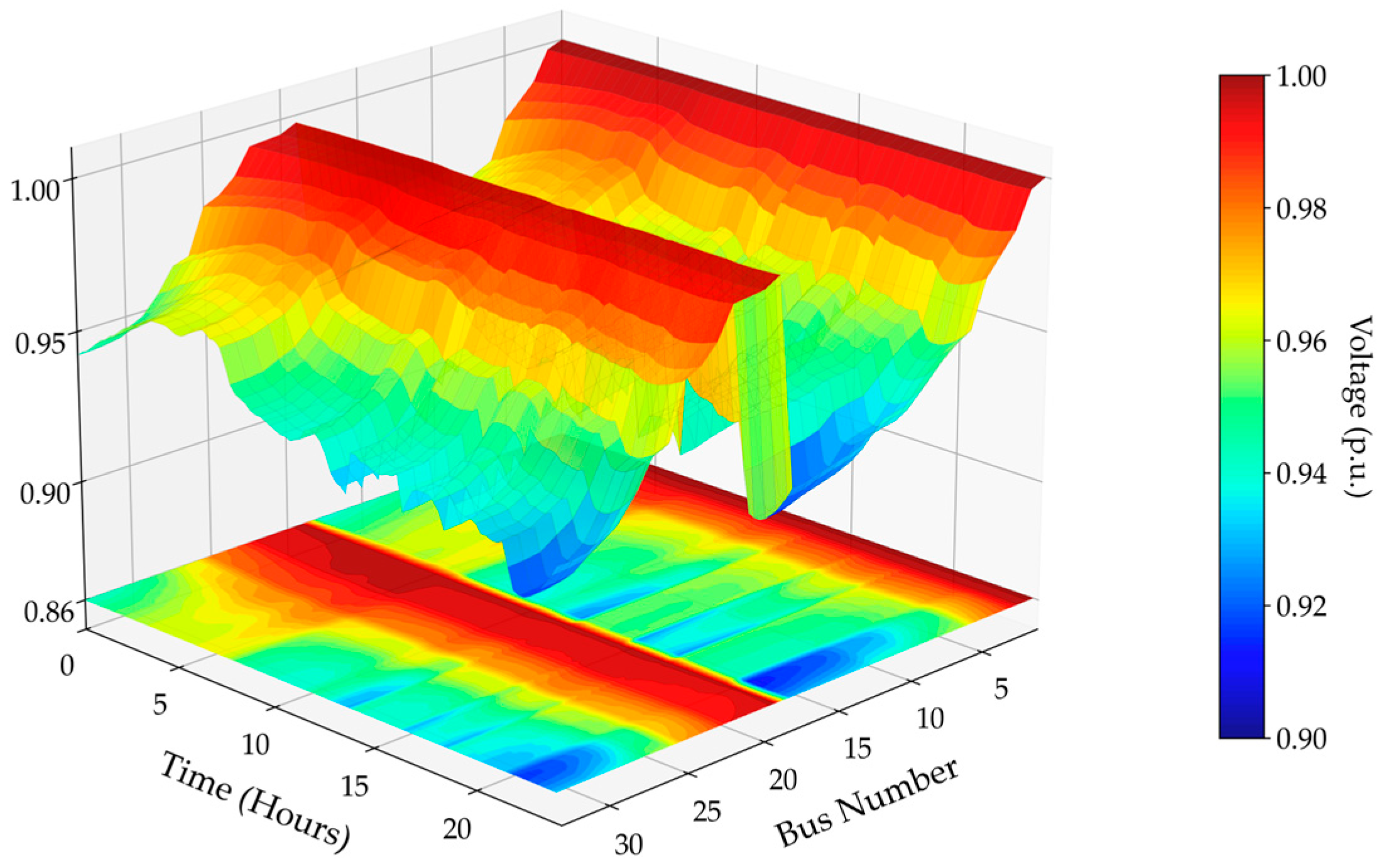
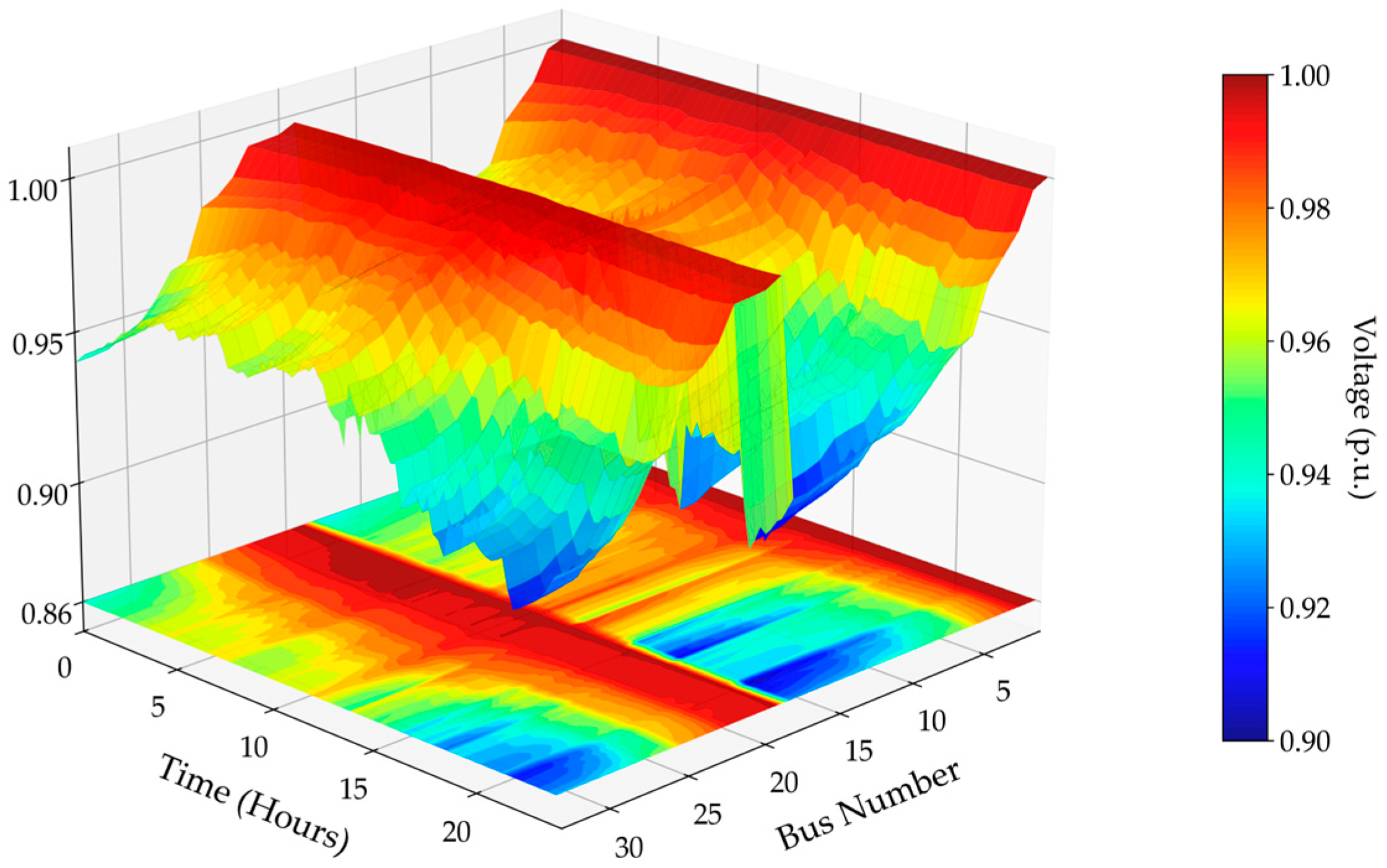
4.3. Results of Scenario 2 (Case 4 to Case 6)
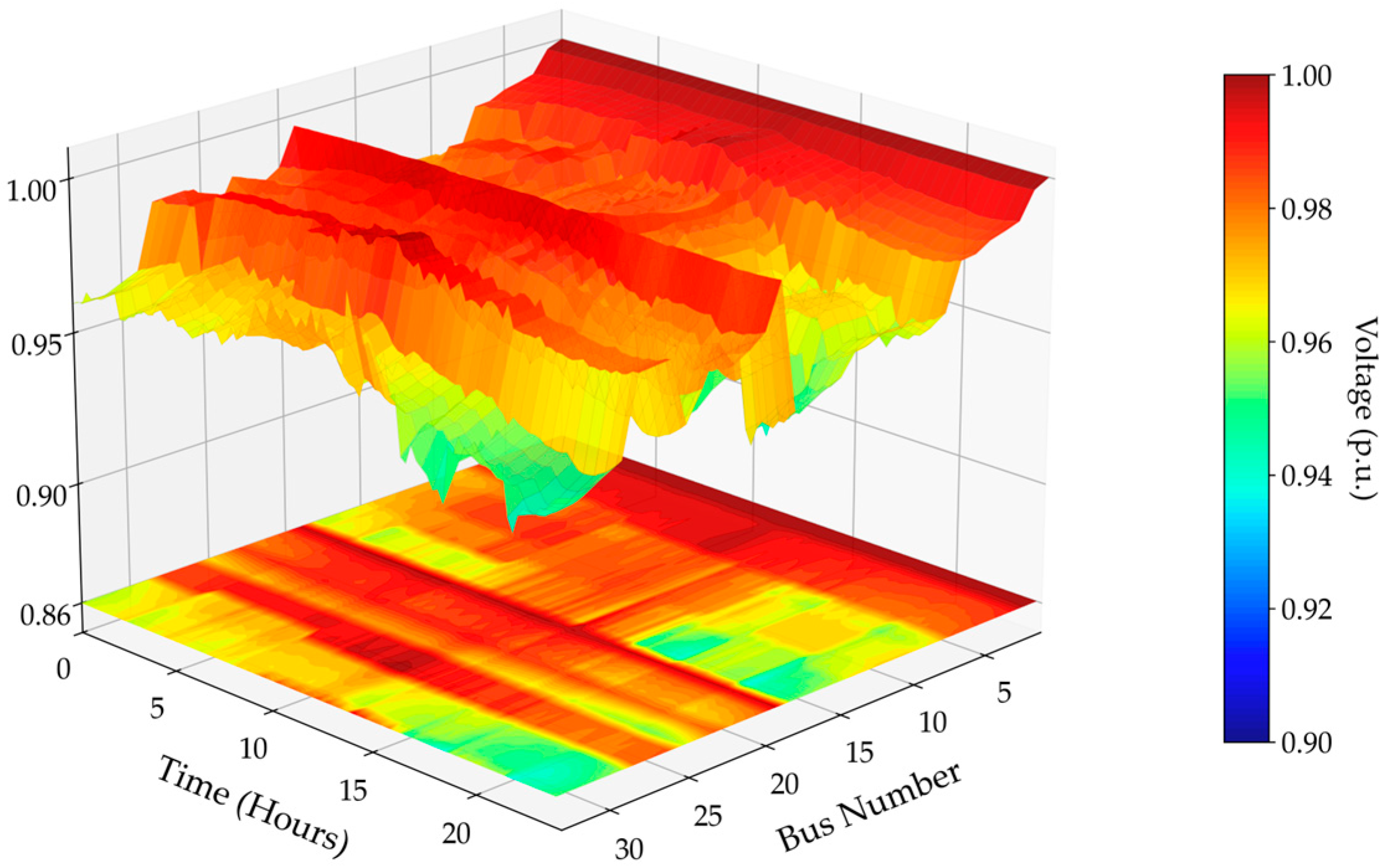
4.4. Discussion
4.4.1. Technical Performance Analysis
4.4.2. Economic and Environmental Performance
4.4.3. Multi-Objective Optimization Insights
- Feeder reconfiguration (DFR) reshapes network topology to minimize impedance and create favorable operating conditions for MBESS deployment, as demonstrated by the varying switching configurations in Table 5.
- Optimal MBESS siting leverages the reconfigured topology to maximize locational value, with siting locations shifting among buses 15, 16, 18, and 32 depending on scenario conditions (Table 4).
- Transportation constraints including travel distances (32.8–54.6 km) and energy consumption (36.08–60.06 kWh) were explicitly modeled, ensuring practical mobility feasibility and preventing unrealistic dispatch behavior.
4.4.4. Practical Implications
4.4.5. Study Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alonso, R.F.; Zambroni de Souza, A.C. Resilience of active networks with optimal mobile energy storage systems management. Electr. Power Syst. Res. 2023, 217, 109152. [Google Scholar] [CrossRef]
- Nick, M.; Cherkaoui, R.; Paolone, M. Optimal Planning of Distributed Energy Storage Systems in Active Distribution Networks Embedding Grid Reconfiguration. IEEE Trans. Power Syst. 2018, 33, 1577–1590. [Google Scholar] [CrossRef]
- Ma, J.; Feng, X.; Lei, J.; Ling, J.; Hua, M. Multi-objective Configuration Method for Mobile Energy Storage Aimed at Enhancing the Resilience of Regional Power Grid. J. Phys. Conf. Ser. 2023, 2662, 12002. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Flexible Optimal Operation of Battery Storage Systems for Energy Supply Networks. IEEE Trans. Power Syst. 2013, 28, 2788–2797. [Google Scholar] [CrossRef]
- Abdeltawab, H.H.; Mohamed, Y.A.-R.I. Mobile Energy Storage Scheduling and Operation in Active Distribution Systems. IEEE Trans. Ind. Electron. 2017, 64, 6828–6840. [Google Scholar] [CrossRef]
- Lotfi, H.; Nikkhah, M.H.; Hajiabadi, M.E. Dynamic Reconfiguration for Energy Management in EV and RES-Based Grids Using IWOA. World Electr. Veh. J. 2025, 16, 412. [Google Scholar] [CrossRef]
- Jacob, R.A.; Bhattacharya, A.; Sharma, S. Feasibility study and analysis of battery energy storage system and network reconfiguration in active distribution network. In Proceedings of the 2017 IEEE Region 10 Symposium (TENSYMP), Cochin, India, 14–16 July 2017. [Google Scholar]
- Tong, L.; Zhao, S.; Jiang, H.; Zhou, J.; Xu, B. Multi-Scenario and Multi-Objective Collaborative Optimization of Distribution Network Considering Electric Vehicles and Mobile Energy Storage Systems. IEEE Access 2021, 9, 55690–55697. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Mobile and self-powered battery energy storage system in distribution networks—Modeling, operation optimization, and comparison with stationary counterpart. J. Energy Storage 2021, 42, 103068. [Google Scholar] [CrossRef]
- Ahmed, H.M.A.; Sindi, H.F.; Azzouz, M.A.; Awad, A.S.A. Optimal Sizing and Scheduling of Mobile Energy Storage Toward High Penetration Levels of Renewable Energy and Fast Charging Stations. IEEE Trans. Energy Convers. 2022, 37, 1075–1086. [Google Scholar] [CrossRef]
- Sun, W.; Qiao, Y.; Liu, W. Economic scheduling of mobile energy storage in distribution networks based on equivalent reconfiguration method. Sustain. Energy Grids Netw. 2022, 32, 100879. [Google Scholar] [CrossRef]
- Jeon, S.; Choi, D.-H. Joint optimization of Volt/VAR control and mobile energy storage system scheduling in active power distribution networks under PV prediction uncertainty. Appl. Energy 2022, 310, 118488. [Google Scholar] [CrossRef]
- Xia, S.; Wang, Z.; Gao, X.; Li, W. Optimal planning of mobile energy storage in active distribution network. IET Smart Grid 2024, 7, 1–12. [Google Scholar] [CrossRef]
- Liu, J.; Lin, S.; He, S.; Liu, W.; Liu, M. Multiobjective Optimal Dispatch of Mobile Energy Storage Vehicles in Active Distribution Networks. IEEE Syst. J. 2023, 17, 804–815. [Google Scholar] [CrossRef]
- Ganivada, P.K.; El-Fouly, T.H.; Zeineldin, H.H.; Al-Durra, A. Optimal siting and sizing of mobile-static storage mix in distribution systems with high renewable energy resources penetration. Electr. Power Syst. Res. 2024, 226, 109860. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J. Optimal Scheduling Strategy for Distribution Network with Mobile Energy Storage System and Offline Control PVs to Minimize the Solar Energy Curtailment. Energies 2024, 17, 2234. [Google Scholar] [CrossRef]
- Linag, F.; Ni, J.; Yu, Z.; Zhang, K.; Zhao, Q.; Wang, S. Fixed and mobile energy storage coordination optimization method for enhancing photovoltaic integration capacity considering voltage offset. Front. Energy Res. 2024, 12, 1351324. [Google Scholar] [CrossRef]
- Guo, H.; Wu, S.; Shi, T.; Wang, F.; Gong, D. Coordinated Operation of Active Distribution Network and Mobile Energy Storage Using Stackelberg Game. IEEE Trans. Ind. Inform. 2025, 21, 4423–4434. [Google Scholar] [CrossRef]
- Lai, X.; Du, H.; Long, F.; An, Y.; Cai, M. A Mobile Energy Storage Configuration Method for Power Grids Considering Power Losses and Voltage Stability. Processes 2025, 13, 1079. [Google Scholar] [CrossRef]
- Miao, L.; Di, L.; Zhao, J.; Liu, H.; Hu, Y.; Wei, X. Optimal Scheduling of Active Distribution Networks with Hybrid Energy Storage Systems Under Real Road Network Topology. Processes 2025, 13, 1492. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, Y.; Chen, L.; Zuo, J.; Wang, W.; Xu, C. The Optimal Dispatch for a Flexible Distribution Network Equipped with Mobile Energy Storage Systems and Soft Open Points. Energies 2025, 18, 2701. [Google Scholar] [CrossRef]
- Qiao, J.; Mi, Y.; Shen, J.; Xia, D.; Li, D.; Wang, P. Active and reactive power coordination optimization for active distribution network considering mobile energy storage system and dynamic network reconfiguration. Electr. Power Syst. Res. 2025, 238, 111080. [Google Scholar] [CrossRef]
- Farzin, H.; Chehrazi, F.; Saniei, M. Multi-objective planning of mobile energy storage unit in active distribution network considering reliability. J. Energy Storage 2025, 109, 115138. [Google Scholar] [CrossRef]
- Li, Z.; Sun, H.; Xue, Y.; Jin, X.; Wang, P. Resilience-Oriented Asynchronous Decentralized Restoration Considering Building and E-Bus Coresponse in Electricity-Transportation Networks. IEEE Trans. Transp. Electrif. 2025, 11, 11701–11713. [Google Scholar] [CrossRef]
- Wang, K.; Xue, Y.; Guo, Q.; Shahidehpour, M.; Zhou, Q.; Wang, B.; Sun, H. A Coordinated Reconfiguration Strategy for Multi-Stage Resilience Enhancement in Integrated Power Distribution and Heating Networks. IEEE Trans. Smart Grid 2023, 14, 2709–2722. [Google Scholar] [CrossRef]
- Nuamkoksung, P.; Sanga-ngam, W.; Suthamno, K.; Klayklueng, T.; Marsong, S.; Sonasang, S.; Bhumkittipich, K.; Ngoc Vo, D.; Buayai, K.; Kerdchuen, K.; et al. Integrated Control of DERs Placement and Network Reconfiguration in EV-Charging Distribution Systems Using Multi-Optimization Techniques. Eng. Access 2025, 11, 301–318. [Google Scholar]
- Kongjeen, Y.; Eiampong, W.; Buayai, K.; Kerdchuen, K. Voltage Stability Analysis in Microgrids System with Photovoltaic Solar Energy under Uncertainty of Loads Variation. GMSARN Int. J. 2023, 17, 156–162. [Google Scholar]
- Purlu, M.; Turkay, B.E. Optimal Allocation of Renewable Distributed Generations Using Heuristic Methods to Minimize Annual Energy Losses and Voltage Deviation Index. IEEE Access 2022, 10, 21455–21474. [Google Scholar] [CrossRef]
- Chitgreeyan, N.; Pilalum, P.; Kongjeen, Y.; Kongnok, R.; Buayai, K.; Kerdchuen, K. Modified MATPOWER for Multi-Period Power Flow Analysis with PV Integration. GMSARN Int. J. 2025, 19, 165–174. [Google Scholar]
- Jaramillo, M.D.; Carrión, D.F.; Muñoz, J.P. A Novel Methodology for Strengthening Stability in Electrical Power Systems by Considering Fast Voltage Stability Index under N − 1 Scenarios. Energies 2023, 16, 3396. [Google Scholar] [CrossRef]
- Gupta, S.K.; Mallik, S.K.; Kumar, D.; Kumar, S. Voltage stability assessment of the power system using novel line voltage collapse index. Eng. Res. Express 2024, 6, 25324. [Google Scholar] [CrossRef]
- Mokred, S.; Wang, Y.; Chen, T. Modern voltage stability index for prediction of voltage collapse and estimation of maximum load-ability for weak buses and critical lines identification. Int. J. Electr. Power Energy Syst. 2023, 145, 108596. [Google Scholar] [CrossRef]
- Pilalum, P.; Taksana, R.; Chitgreeyan, N.; Sa-nga-ngam, W.; Marsong, S.; Buayai, K.; Kerdchuen, K.; Kongjeen, Y.; Bhumkittipich, K. Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks. Smart Cities 2025, 8, 102. [Google Scholar] [CrossRef]
- Lencastre, P.; Yazidi, A.; Lind, P.G. Modeling Wind-Speed Statistics beyond the Weibull Distribution. Energies 2024, 17, 2621. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Mao, S.; Zhang, Y.; Rodriguez, F.; Wang, S.; Hao, C. Real-World Performance of Battery Electric Heavy-Duty Vehicles in China; The International Council on Clean Transportation: Washington, DC, USA, 2023; Available online: https://theicct.org/publication/hdv-china-real-world-performance-apr23/ (accessed on 4 August 2025).
- Amini, M.; Nazari, M.H.; Hosseinian, S.H. Predictive energy management strategy for battery energy storage considering battery degradation cost. IET Renew. Power Gener. 2023, 17, 1119–1138. [Google Scholar] [CrossRef]
- Liu, S.; Yan, J.; Yan, Y.; Zhang, H.; Zhang, J.; Liu, Y.; Han, S. Joint operation of mobile battery, power system, and transportation system for improving the renewable energy penetration rate. Appl. Energy 2024, 357, 122455. [Google Scholar] [CrossRef]
- Gore, N.; Arkatkar, S.; Joshi, G.; Antoniou, C. Modified Bureau of Public Roads Link Function. Transp. Res. Rec. 2023, 2677, 966–990. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Zhou, B. Analytical Model for Travel Time-Based BPR Function with Demand Fluctuation and Capacity Degradation. Math. Probl. Eng. 2019, 2019, 5916479. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, Y.; Dong, S. Public Traffic Congestion Estimation Using an Artificial Neural Network. ISPRS Int. J. Geo-Inf. 2020, 9, 152. [Google Scholar] [CrossRef]
- Scarlat, N.; Prussi, M.; Padella, M. Quantification of the carbon intensity of electricity produced and used in Europe. Appl. Energy 2022, 305, 117901. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K.; Roy, P.C. Investigating the Normalization Procedure of NSGA-III. In Evolutionary Multi-Criterion Optimization; Deb, K., Goodman, E., Coello Coello, C.A., Klamroth, K., Miettinen, K., Mostaghim, S., Reed, P., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 229–240. ISBN 978-3-030-12598-1. [Google Scholar]
- Tanabe, R. Investigating normalization in preference-based evolutionary multi-objective optimization using a reference point. Appl. Soft Comput. 2024, 159, 111646. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A comparative analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Fan, G.; Du, Z.; Lin, X.; Chen, N. Mobile power sources pre-allocation and dispatch strategy in power-transportation coupled network under extreme weather. IET Renew. Power Gener. 2024, 18, 1129–1148. [Google Scholar] [CrossRef]
- Global Petrol Prices. Electricity Prices. 2025. Available online: https://www.globalpetrolprices.com/electricity_prices/ (accessed on 5 August 2025).
- Schade, C.; Egging-Bratseth, R. Battery degradation: Impact on economic dispatch. Energy Storage 2024, 6, e588. [Google Scholar] [CrossRef]
- Basma, H.; Rodríguez, F. A Total Cost of Ownership Comparison of Truck Decarbonization Pathways in Europe. 2023. Available online: https://theicct.org/publication/total-cost-ownership-trucks-europe-nov23/ (accessed on 31 July 2025).
- IEA. Electricity 2025. 2025. Available online: https://www.iea.org/reports/electricity-2025 (accessed on 5 August 2025).




| References | Authors | [8] | [9] | [10] | [11] | [12] | [13] | [14] | [15] | [16] | [17] | [18] | [19] | [20] | [21] | [22] | [23] | Proposed |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Year | 2021 | 2021 | 2022 | 2022 | 2022 | 2023 | 2023 | 2024 | 2024 | 2024 | 2025 | 2025 | 2025 | 2025 | 2025 | 2025 | 2025 | |
| Objective function | Loss | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| VDI | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| FVSI | ✓ | ✓ | ||||||||||||||||
| Cost | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| CO2 | ✓ | ✓ | ||||||||||||||||
| Coordinated with | PV | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| WT | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| EV Charger | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||||
| DFR | ✓ | ✓ | ✓ | |||||||||||||||
| Transportation Constraints | Distance | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| Time | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| Traffic Delay | ✓ | ✓ | ✓ | ✓ | ||||||||||||||
| Routing | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||||
| Optimizer | CPLEX | CPLEX | GA | Gurobi | CPLEX | Gurobi | Gurobi | CC-PSO2 | MILP | PSO-GSA | MILP | MOPSO | NSGA-III | NSGA-III | PADM | NSGA-II | NSGA-III |
| Descriptions | Parameters | Value/Unit |
|---|---|---|
| Mobile Battery Energy Storage | ||
| - Battery capacity | 2000 kWh | |
| - Power | 200 kW | |
| - Efficiency | 0.95 | |
| EV Truck | ||
| - Battery capacity | 540 kWh | |
| - Energy consumption | 1.1 kW/km | |
| - Efficiency | 0.95 | |
| Photovoltaic system | ||
| - PV power | 400, 300, 350, 250, 200 kW | |
| - Position of PV | Bus No. 6, 13, 18, 25, 30 | |
| Wind Turbine (WT) | ||
| - WT power | 300, 250, 200, 300, 250 kW | |
| - Position of WT | Bus No. 8, 15, 22, 28, 33 | |
| EV charging station | ||
| - EV charging power | 176, 300, 110, 140, 150 kW | |
| - Position of EV charging | Bus No. 10, 16, 20, 26, 32 | |
| Cost and emission | ||
| - Electricity price [47] | 0.165 $/kWh | |
| - Battery degradation rate [48] | 0.04 $/kWh | |
| - Transport rate [49] | 0.94 $/km | |
| - Gride emission factor [50] | 0.445 kg /kWh | |
| NSGA-III algorithm | ||
| - Populations | Pop. | 100 |
| - Generations | Gen. | 100 |
| MBESS Operating | Charging | Load 0.55 p.u. |
| Discharging | Load 0.87 p.u. | |
| Idle | Otherwise | |
| DFR Operating | Operating 1 | Charging |
| Operating 2 | Discharging | |
| Operating 3 | Idle |
| Scenarios | Case Study | DERs | MBESS | DFR | ||
|---|---|---|---|---|---|---|
| WT | PV | EVCS | ||||
| Scenario 1: | Case:1 ADS Base Case | - | - | - | - | - |
| Case:2 ADS with MBESS | - | - | - | ✓ | - | |
| Case:3 ADS with MBESS and DFR | - | - | - | ✓ | ✓ | |
| Scenario 2: | Case:4 ADS and DERs Integration | ✓ | ✓ | ✓ | - | - |
| Case:5 ADS and DERs Integration with MBESS | ✓ | ✓ | ✓ | ✓ | - | |
| Case:6 ADS and DERs Integration with MBESS and DFR | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Case | MBESS | Target Bus No. | Route & Path (Nodes) | Distance (km) | Time (min) | Energy (kWh) |
|---|---|---|---|---|---|---|
| Case 2 | MBESS 1 | 15 | 54.6 | 64.3 | 60.06 | |
| MBESS 2 | 32 | 32.8 | 41.6 | 36.08 | ||
| MBESS 3 | 18 | 47.8 | 59.9 | 52.58 | ||
| Case 3 | MBESS 1 | 16 | 46.4 | 52.1 | 51.04 | |
| MBESS 2 | 18 | 47.8 | 59.9 | 52.58 | ||
| MBESS 3 | 32 | 32.8 | 41.6 | 36.08 | ||
| Case 5 | MBESS 1 | 15 | 54.6 | 64.3 | 60.06 | |
| MBESS 2 | 32 | 32.8 | 41.6 | 36.08 | ||
| MBESS 3 | 18 | 47.8 | 59.9 | 52.58 | ||
| Case 6 | MBESS 1 | 17 | 40.2 | 34 | 44.22 | |
| MBESS 2 | 18 | 47.8 | 59.9 | 52.58 | ||
| MBESS 3 | 32 | 32.8 | 41.6 | 36.08 |
| Case | Operating State | Switches Open |
|---|---|---|
| Case 3 | Idle | 7, 9, 14, 32, 28 |
| Charging | 7, 9, 13, 17, 28 | |
| Discharging | 7, 10, 14, 32, 28 | |
| Case 6 | Idle | 7, 9, 14, 32, 28 |
| Charging | 6, 9, 12, 15, 27 | |
| Discharging | 7, 9, 13, 32, 28 |
| Objective | Case 1 | Case 2 | Case 3 | Improvement Case 1 & Case 2 (%) | Improvement Case 1 & Case 3 (%) | Improvement Case 2 & Case 3 (%) |
|---|---|---|---|---|---|---|
| F1: Active Power loss (MWh) | 2.674 | 2.537 | 1.870 | 5.12 | 30.07 | 26.29 |
| F2: Reactive Power loss (Mvarh) | 1.782 | 1.574 | 1.259 | 11.67 | 29.35 | 20.01 |
| F3: Voltage Deviation Index | 0.037 | 0.035 | 0.022 | 5.41 | 40.54 | 37.14 |
| F4: Fast Voltage Stability Index | 2.139 | 2.102 | 2.087 | 1.73 | 2.43 | 0.71 |
| F5: Total Operating Cost ($/day) | 13,596 | 13,891 | 13,632 | −2.17 | −0.26 | 1.86 |
| F6: CO2 Emissions (kg CO2/day) | 30,195 | 30,591 | 30,289 | −1.31 | −0.31 | 0.99 |
| Objective | Case 4 | Case 5 | Case 6 | Improvement Case 4 & Case 5 (%) | Improvement Case 4 & Case 6 (%) | Improvement Case 5 & Case 6 (%) |
|---|---|---|---|---|---|---|
| F1: Active Power loss (MWh) | 2.428 | 2.310 | 1.753 | 4.86 | 27.80 | 24.11 |
| F2: Reactive Power loss (Mvarh) | 1.628 | 1.433 | 1.192 | 11.98 | 26.78 | 16.82 |
| F3: Voltage Deviation Index | 0.037 | 0.031 | 0.021 | 16.22 | 43.24 | 32.26 |
| F4: Fast Voltage Stability Index | 2.134 | 2.099 | 2.086 | 1.64 | 2.25 | 0.62 |
| F5: Total Operating Cost ($/day) | 12,465 | 12,734 | 12,499 | −2.16 | −0.27 | 1.85 |
| F6: CO2 Emissions (kg CO2/day) | 20,807 | 21,213 | 20,954 | −1.95 | −0.71 | 1.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marksan, P.; Buayai, K.; Ratchapan, R.; Sa-nga-ngam, W.; Bhumkittipich, K.; Kerdchuen, K.; Stadler, I.; Marsong, S.; Kongjeen, Y. Multi-Objective Optimization of Mobile Battery Energy Storage and Dynamic Feeder Reconfiguration for Enhanced Voltage Profiles in Active Distribution Systems. Energies 2025, 18, 5515. https://doi.org/10.3390/en18205515
Marksan P, Buayai K, Ratchapan R, Sa-nga-ngam W, Bhumkittipich K, Kerdchuen K, Stadler I, Marsong S, Kongjeen Y. Multi-Objective Optimization of Mobile Battery Energy Storage and Dynamic Feeder Reconfiguration for Enhanced Voltage Profiles in Active Distribution Systems. Energies. 2025; 18(20):5515. https://doi.org/10.3390/en18205515
Chicago/Turabian StyleMarksan, Phuwanat, Krittidet Buayai, Ritthichai Ratchapan, Wutthichai Sa-nga-ngam, Krischonme Bhumkittipich, Kaan Kerdchuen, Ingo Stadler, Supapradit Marsong, and Yuttana Kongjeen. 2025. "Multi-Objective Optimization of Mobile Battery Energy Storage and Dynamic Feeder Reconfiguration for Enhanced Voltage Profiles in Active Distribution Systems" Energies 18, no. 20: 5515. https://doi.org/10.3390/en18205515
APA StyleMarksan, P., Buayai, K., Ratchapan, R., Sa-nga-ngam, W., Bhumkittipich, K., Kerdchuen, K., Stadler, I., Marsong, S., & Kongjeen, Y. (2025). Multi-Objective Optimization of Mobile Battery Energy Storage and Dynamic Feeder Reconfiguration for Enhanced Voltage Profiles in Active Distribution Systems. Energies, 18(20), 5515. https://doi.org/10.3390/en18205515















