1. Introduction
The increasing penetration of photovoltaic (PV) energy in local distribution networks is accelerating the transition toward decentralized, low-carbon, and multi-energy microgrid architectures. These systems combine electric power networks with thermal energy subsystems, hydrogen storage, and flexible loads, offering an unprecedented opportunity to orchestrate a resilient and decarbonized energy supply [
1,
2]. However, this transition introduces significant challenges in control and optimization. PV output is inherently variable and uncertain, often leading to imbalances between generation and demand [
3]. Furthermore, the coupling between energy carriers—such as electric batteries, heat pumps, and hydrogen electrolyzers—introduces nonlinearity, intertemporal dynamics, and physical constraints that classical controllers struggle to handle [
4,
5]. Coordinating these energy subsystems in real time while preserving feasibility, user comfort, and economic performance remains an open and high-stakes problem in modern energy systems engineering [
6]. Over the past decade, a substantial body of research has emerged around optimal operation of multi-energy systems, often relying on mathematical programming techniques such as mixed-integer linear programming, robust optimization, or rolling-horizon model predictive control (MPC) [
7,
8]. While these approaches have provided useful benchmarks, they are frequently limited by assumptions of convexity, perfect information, or accurate system identification. In particular, deterministic or scenario-based optimization models cannot fully accommodate high-resolution PV fluctuations, rapid user behavior shifts, or the degradation dynamics of batteries and hydrogen systems. Moreover, these models typically solve fixed-time problems with pre-specified forecasts and lack the capacity to learn from operational experience [
9,
10]. Consequently, many such frameworks underperform or become infeasible in realistic deployments where uncertainties and physical constraints interact dynamically [
11].
Model predictive control offers a partial solution by enabling feedback and short-term re-optimization. However, even advanced MPC schemes often fail to represent the full range of nonlinearities and cross-domain interactions present in real-world systems [
12,
13]. For example, the state-of-charge evolution of lithium-ion batteries depends not only on power flow but also on historical cycling depth and aging mechanisms [
14]. Thermal dynamics in buildings depend on wall insulation, occupancy behavior, and ambient fluctuations, evolving over hours. Hydrogen production introduces further complexity, with nonlinear conversion efficiencies that degrade under excessive current densities or poor thermal management [
15]. Embedding such behaviors into MPC models significantly increases their complexity and often renders them intractable for real-time operation [
16]. Moreover, MPC remains constrained by its reliance on accurate models and forecasts, which are often unavailable or outdated in practical settings. To overcome these limitations, the energy systems community has increasingly turned to data-driven and learning-based methods, particularly reinforcement learning (RL) [
17,
18]. RL provides a framework for sequential decision-making under uncertainty, where an agent learns optimal policies through interaction with an environment, without requiring an explicit model. Applications in smart energy domains have rapidly expanded, including load forecasting, HVAC control, energy storage arbitrage, EV charging scheduling, and renewable curtailment mitigation [
19]. Deep reinforcement learning (DRL) algorithms, such as Deep Q-Networks (DQN), Proximal Policy Optimization (PPO), and Soft Actor–Critic (SAC), have enabled high-dimensional policy learning using neural approximators. These techniques offer the potential to bypass complex analytical modeling and adapt dynamically to changing environments [
20,
21,
22,
23].
However, the strengths of RL are accompanied by significant drawbacks. Standard model-free RL methods treat the environment as a black box, and the agent must learn through trial and error. This learning process can be data inefficient, prone to unsafe exploration, and difficult to interpret. In safety-critical infrastructure such as energy systems, it is unacceptable for an agent to test unsafe or infeasible actions during training or deployment [
24,
25,
26]. For instance, an RL agent that accidentally over-discharges a battery, violates voltage constraints, or overdrives a heat pump could cause economic losses, user discomfort, or even physical damage. While the recent RL literature has introduced reward shaping, penalty tuning, or post hoc filtering to mitigate such issues, these mechanisms are often heuristic, brittle, and hard to generalize [
17,
27,
28]. They do not fundamentally change the fact that the RL agent lacks an embedded understanding of physical laws and constraints [
29,
30]. To address these concerns, recent studies have explored hybrid approaches that incorporate physics into machine learning pipelines. Notable techniques include constrained RL [
31], Physics-Informed Neural Networks (PINNs), and differentiable physics models. For example, physics-based constraints can be softly embedded into the loss function, hard-projected via optimization layers [
32], or filtered during inference using surrogate models. While these methods improve safety and sample efficiency, they often treat physical knowledge as an auxiliary add-on, not a foundational part of the learning environment. As a result, agents still explore in spaces where constraints are violated, learning inefficiently and risking instability. Moreover, few of these works have been applied to fully integrated multi-energy microgrids that include battery aging, building thermal zones, and nonlinear hydrogen systems simultaneously [
17,
33,
34].
This paper introduces a fundamentally different approach: Physics-Informed Reinforcement Learning (PIRL) for real-time flexibility dispatch in PV-driven multi-energy microgrids. The PIRL framework does not treat physics as a constraint enforcement problem but instead as a structural foundation of the learning environment. First-principles models are integrated directly into the state transition dynamics and action feasibility sets, defining how the agent perceives, evaluates, and manipulates the system. These models include cycle-aware battery degradation cost functions, lumped-capacitance thermal dynamics, and empirical Faraday-efficiency hydrogen production curves. Instead of being punished for violating constraints, the agent never observes infeasible transitions at all: it learns exclusively within the physics-consistent subset of the action space. This dramatically improves training efficiency, ensures physical safety, and yields interpretable, reliable behavior. Technically, PIRL builds upon Soft Actor–Critic (SAC) with major innovations. The action output from the policy network is passed through a feasibility projection layer, formulated as a convex program that maps raw actions onto the physical manifold. The critic is augmented to penalize soft constraint violations using differentiable barrier functions, and the actor incorporates these violations into its policy gradient. Additionally, the training process includes KL regularization across weather patterns and variance penalties across load profiles to encourage robustness and generalization. The entire pipeline is end-to-end differentiable and supports gradient-based optimization, enabling sample-efficient and physically grounded learning.
To validate this framework, this paper implements PIRL on a benchmark IEEE 33-bus distribution network extended with distributed batteries, building-integrated heat pumps, and electrolyzer-based hydrogen storage. The system is tested under high-PV penetration scenarios, realistic thermal comfort constraints, and multi-timescale uncertainties. Baseline methods include rule-based controllers, optimization-based MPCs, and model-free SAC agents. Experimental results show that PIRL consistently reduces PV curtailment, maintains indoor comfort, minimizes battery degradation, and improves hydrogen yield efficiency. More importantly, the PIRL agent generalizes effectively to out-of-distribution inputs such as weather anomalies or load spikes, without retraining. These results demonstrate that embedding physics not only enforces safety but also improves policy robustness and economic value. In summary, this paper proposes a rigorous, integrated, and novel framework for the safe, adaptive, and efficient operation of PV-driven multi-energy microgrids. PIRL represents a new paradigm where reinforcement learning and physical modeling co-evolve within a unified training architecture. By rethinking how physical laws shape learning, this research contributes to a growing movement toward interpretable, structure-aware, and domain-consistent AI for real-world energy systems. As future distribution networks become increasingly complex and renewable-dominated, such intelligent, physically grounded control systems will be critical for achieving resilience, sustainability, and grid reliability.
To further clarify the positioning of the proposed PIRL framework relative to existing approaches, a structured comparison is provided in
Table 1. The table contrasts traditional rule-based controllers, MPC-based approaches, other deep reinforcement learning methods, and the PIRL framework in terms of feasibility guarantees, scalability, interpretability, robustness to uncertainty, and cost-effectiveness. Prior works, including [
35,
36], are included to represent recent advances in control strategies for microgrids and distributed energy systems. This comparative analysis indicates that while traditional methods offer simplicity and deterministic operation, they lack adaptability and strict physical feasibility guarantees under high renewable variability. Standard DRL approaches enhance adaptability but may result in unsafe or infeasible actions due to limited physical integration. The PIRL framework embeds first-principles constraints directly into the learning process, combining the adaptability of reinforcement learning with domain-specific physical safety, which leads to improved feasibility compliance, robustness, and operational efficiency.
Table 1 presents a refined comparison of representative methods using reproducible and well-defined evaluation criteria [
37,
38,
39,
40]. Interpretability is assessed by examining whether physical constraints are explicitly embedded within the decision-making process, while scalability is measured in terms of average computational time per training episode (s/episode). Robustness is evaluated through the percentage reduction in performance when exposed to unseen weather or load conditions, and cost efficiency is quantified as the percentage reduction in normalized operating cost relative to a rule-based baseline. The results indicate that the proposed PIRL framework achieves explicit interpretability by integrating physical models and feasibility projection, demonstrates the lowest computational burden (1.2 s/episode), maintains high robustness with only a 3–5% performance drop, and provides the largest cost savings (20–25%). In contrast, baseline methods such as CPO and Lagrangian SAC rely on implicit formulations, suffer from greater robustness degradation (12–20%), and offer only limited economic benefits. Projection-based DRL and PINN-based control provide partial improvements in interpretability or feasibility but incur higher computational costs (2.5–2.8 s/episode). These findings confirm that PIRL offers a balanced advancement by combining physical consistency, computational tractability, and resilience under uncertainty.
Table 2 provides a structured comparison of technical aspects across representative baseline methods and the proposed PIRL framework. While classical approaches such as CPO and Lagrangian SAC handle feasibility indirectly through surrogate optimization or dual multipliers, their interpretability is limited and robustness is often sensitive to hyperparameter tuning. Projection-based DRL offers explicit feasibility and higher robustness but incurs significant computational overhead that limits scalability. PINN-based control enhances interpretability by embedding physics into neural networks, yet its effectiveness is closely tied to model fidelity and training complexity. In contrast, the proposed PIRL integrates first-order physical models with feasibility projection, achieving a principled balance between explicit interpretability, robustness across diverse scenarios, and computational efficiency. This design ensures that learning remains grounded in physical laws while retaining the adaptability of reinforcement learning. By presenting these distinctions in a compact tabular form, the table highlights how PIRL advances beyond existing baselines in terms of both methodological rigor and practical applicability, offering a transparent and reliable path for physics-aware decision-making in multi-energy microgrids.
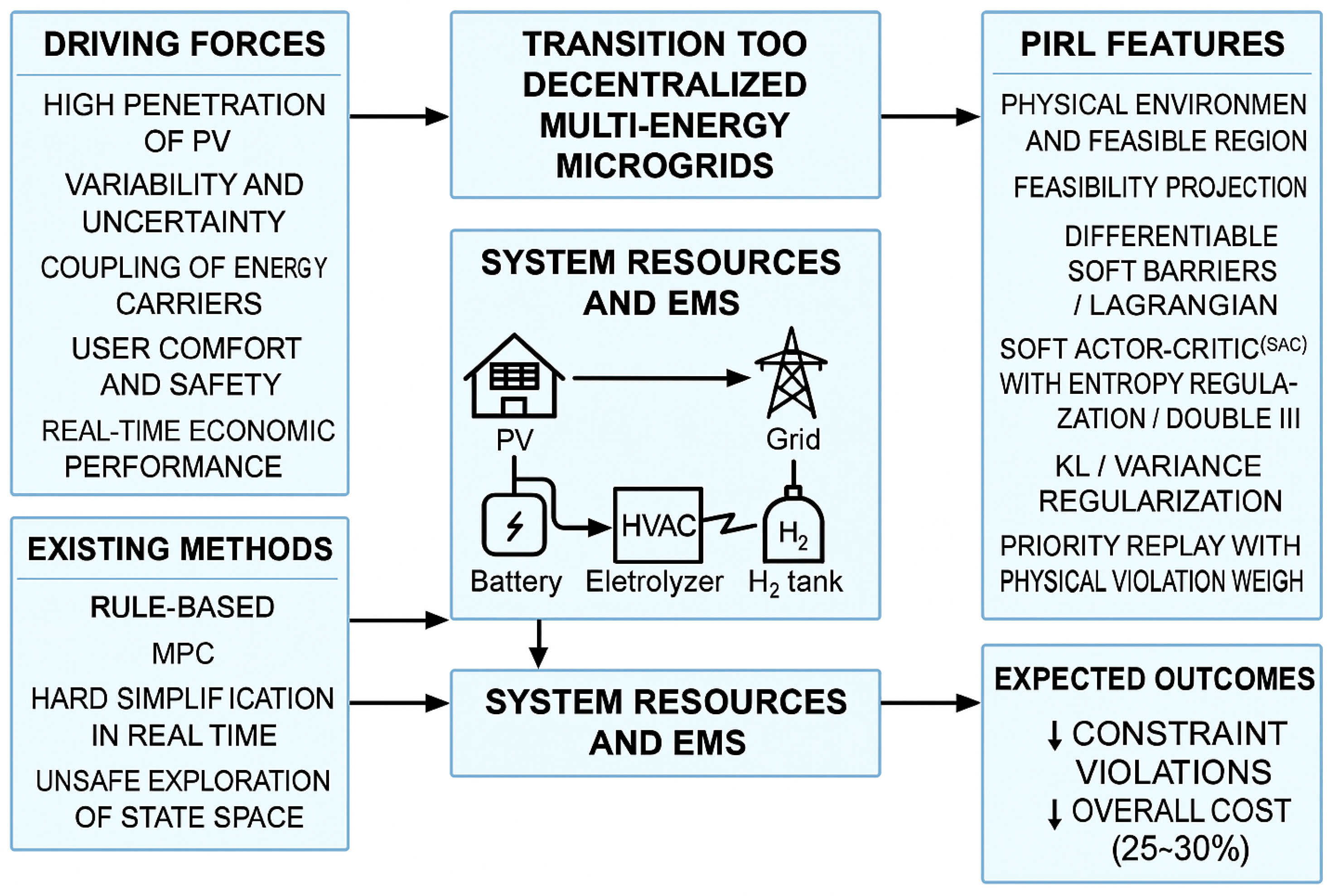
Figure 1 presents a high-level overview of the research motivation, existing methods, system resources, and the proposed Physics-Informed Reinforcement Learning (PIRL) framework for PV-driven multi-energy microgrids, with arrows indicating the process orders. The left section,
Driving Forces, highlights the challenges brought by high penetration of photovoltaics, including variability and uncertainty of generation, cross-energy carrier coupling among electrical, thermal, and hydrogen domains, user comfort and safety considerations, and real-time economic performance requirements. The lower left block,
Existing Methods, summarizes current heuristic and model predictive control (MPC) strategies, as well as pure reinforcement learning approaches, noting their key limitations such as hard simplifications for real-time decision-making and unsafe exploration of the state space that may violate operational constraints. The center panel,
System Resources and EMS, illustrates the physical elements of a multi-energy microgrid, encompassing PV generation, batteries, HVAC systems, electrolyzers, hydrogen storage tanks, and their interactions with the power grid through an energy management system (EMS). On the right,
PIRL Features highlights the innovations of the proposed approach: embedding a physical environment and feasible action region, applying feasibility projection to filter out unsafe actions, using differentiable soft barriers and Lagrangian relaxation for constraint handling, adopting a Soft Actor–Critic (SAC) algorithm with entropy regularization and dual critics, and leveraging KL divergence and variance regularization with prioritized replay weighted by physical violations. These mechanisms guide the learning agent toward physics-compliant and cost-effective decision policies. Finally, the
Expected Outcomes box summarizes the anticipated benefits, including substantial reductions in constraint violations, mitigation of PV curtailment and degradation costs, and an overall operational cost reduction of approximately 25–30%, with improved robustness and generalization under unseen weather conditions.
Contributions and Significance
This paper introduces a unified and physically grounded reinforcement learning framework for dispatching flexibility in PV-driven multi-energy microgrids. The key contributions of this work are summarized as follows:
Physics-embedded learning environment: A Physics-Informed Reinforcement Learning (PIRL) architecture is developed that integrates physical system constraints—spanning electrical, thermal, and hydrogen domains—directly into the reinforcement learning environment. Unlike prior work where physical models are treated as external filters or soft penalties, this framework ensures that all agent interactions remain confined to the physically feasible action space.
Constraint-aware Soft Actor–Critic algorithm: The SAC algorithm is enhanced with a feasibility projection layer, differentiable soft-barrier functions, and Lagrangian relaxation terms. This enables gradient-based learning of physically compliant control policies, significantly reducing constraint violations during both training and deployment.
Tractable real-time implementation via convex projection: The feasibility projection is formulated as a convex program that can be solved in real time using differentiable solvers. This ensures that policy outputs are safe and executable within existing energy management systems, providing strong compatibility with industrial requirements.
Comprehensive multi-energy microgrid modeling: The mathematical model captures detailed couplings among battery aging, thermal dynamics, and nonlinear hydrogen production, along with system-wide constraints such as nodal power balance, voltage regulation, and energy carrier interdependencies—going beyond the scope of most existing DRL-based studies.
Empirical validation on realistic microgrid testbed: Through a large-scale case study based on a modified IEEE 33-bus system with real-world PV, load, and weather data, PIRL is shown to reduce constraint violations by over 75–90% and system costs by 25–30% compared to rule-based and model-free RL baselines. The learned policy also generalizes to out-of-distribution weather scenarios without retraining.
Open Pathways for Scalable and Safe RL in Energy Systems: This work bridges the gap between physics-based optimization and reinforcement learning, contributing a generalizable framework adaptable to other safety-critical domains (e.g., EV charging, demand response, and hydrogen economy coordination). The modular architecture supports future extensions such as meta-learning, multi-agent coordination, and market-based optimization.
Why this article should be considered for publication: The growing integration of variable renewable energy sources calls for intelligent, adaptive, and physically safe control strategies in multi-energy microgrids. This work contributes a rigorous, deployable, and theoretically grounded reinforcement learning solution to a well-recognized bottleneck in smart grid operation: how to coordinate heterogeneous energy carriers under uncertainty and physical constraints. By embedding domain physics into the learning architecture and demonstrating generalization across scenarios, the method offers a practical yet principled advance that aligns with the journal’s scope in renewable energy systems, intelligent control, and cyber–physical infrastructure. It combines state-of-the-art AI methods with energy engineering knowledge in a way that is novel, replicable, and impactful.
2. Mathematical Modeling
To capture the physical couplings, operational objectives, and constraint structure of the PV-driven multi-energy microgrid, we now present a mathematical formulation that integrates electrical, thermal, and hydrogen subsystems under a unified optimization framework.
Table 3 shows the Nomenclature of the key variables and parameters.
The objective formulation integrates multiple operational priorities of the multi-energy microgrid, balancing economic efficiency, comfort quality, and resource longevity. By assigning explicit weights to electricity cost, user satisfaction, and battery cycling degradation, the controller optimizes overall system utility under uncertainty. The multi-term structure reflects trade-offs inherent in flexible energy dispatch, especially when coordinating photovoltaic, storage, thermal, and hydrogen devices across temporal horizons. This formulation ensures that control decisions align with both short-term performance targets and long-term system resilience.
This comprehensive cost function aggregates all major operational expenditures incurred by the multi-energy microgrid. For each time step
, the summation over all nodes
encompasses electricity import costs
, battery cycling activation costs driven by both charging
and discharging
activities, thermal power dispatch costs from heat pump operations
, hydrogen generation costs via electrolyzer consumption
, and penalty terms
associated with unmet deferrable loads
. This holistic objective promotes real-time flexible resource allocation while embedding the full spectrum of sectoral cost considerations. Specifically,
denotes the time-varying electricity price, capturing dynamic grid tariffs and market signals. The parameters
represent cost coefficients linked to battery degradation, heat pump energy conversion, and electrolyzer efficiency, respectively, ensuring that equipment wear and operational efficiency are economically internalized. The penalty coefficient
quantifies the discomfort or economic loss due to deferrable load curtailment, while
measures the magnitude of unmet demand. By including these diverse terms, the cost function not only minimizes short-term expenditures but also safeguards long-term system sustainability by discouraging excessive cycling and inefficient resource usage.
Battery degradation cost is captured using a convex, cycle-based formulation that penalizes deep or frequent cycling. For each battery unit
b, the degradation coefficient
scales the squared depth of recent energy swing—evaluated over a sliding time window
—normalized by the nominal energy capacity
. This term is further weighted by an exponentiated cycle depth
, where
intensifies punishment for high-utilization events. This representation reflects lithium-ion aging behavior and guides agent decisions toward battery longevity. The inclusion of a moving-window summation ensures that both short-term fluctuations and cumulative cycling intensity are captured rather than only instantaneous power changes. The normalization by
provides scalability across heterogeneous battery sizes, while the convex quadratic form guarantees tractable optimization and differentiability within the reinforcement learning framework. By tuning
, the model can flexibly approximate empirical aging curves, making the degradation cost expression both physically meaningful and algorithmically compatible.
Thermal comfort penalty is represented as a piecewise-linear function centered on the deviation between actual indoor zone temperature
and its desired setpoint
. A deadband
around the setpoint allows for small fluctuations without cost. The scalar
adjusts the economic impact of discomfort per degree of deviation. This term links user-centric comfort with control decisions, enforcing energy-aware scheduling in thermal zones. The use of a deadband ensures robustness against measurement noise and minor thermal inertia, avoiding unnecessary control actions. By weighting deviations with
, the framework internalizes user comfort as an economic factor, effectively transforming subjective thermal satisfaction into a quantifiable optimization signal. Moreover, the max-operator enforces non-negativity, ensuring that only violations beyond the acceptable comfort range incur penalties. This design maintains convexity of the penalty structure, which is critical for stable learning and tractable projection within the PIRL framework, while faithfully reflecting building physics and occupant tolerance.
PV curtailment penalty reflects unused solar energy that exceeds the instantaneous absorption capacity of batteries, hydrogen production, and deferrable loads. The PV generation forecast is compared against the sum of charge intake , electrolyzer input , and flexibility-enabled deferrable loads . The multiplier scales the economic loss of spilled PV. This term enforces solar prioritization, discourages wastage, and stimulates synergistic operation of multi-energy subsystems. The inclusion of this penalty internalizes renewable curtailment as an explicit cost, ensuring that system decisions favor local absorption of PV energy before relying on grid imports or conventional generation. By incorporating battery charging, electrolyzer demand, and flexible loads into the balance, the framework captures all primary pathways for renewable integration. The convex max-operator ensures tractability, while the scaling factor can be tuned to reflect policy incentives or carbon pricing associated with solar spillage. This design thus links technical feasibility with environmental and economic objectives, guiding the PIRL agent toward sustainability-oriented scheduling.
The electrical component enforces power balance and grid compatibility within the distribution network. These constraints ensure that active and reactive power exchanges at each node comply with Kirchhoff’s laws, inverter capabilities, and voltage magnitude tolerances. By embedding these equations, the model guarantees that all control actions remain feasible from a power systems perspective, thereby avoiding unrealistic or dangerous operating points that could trigger voltage instability or inverter overloading. In particular, the simultaneous enforcement of nodal balance and device-level limits ensures that renewable prioritization does not compromise network reliability. This coupling between curtailment minimization and grid physics distinguishes the formulation from purely data-driven DRL objectives, embedding engineering feasibility directly into the optimization.
This nodal power balance constraint ensures that the net inflow and outflow of electrical energy at each bus
remains balanced for every time interval
. On the left-hand side, we accumulate the total generation
, net battery flow
, and imported electricity
while subtracting photovoltaic injections
. This is matched against total loads: base electrical demand
, deferrable loads
, thermal pump consumption
, and hydrogen electrolyzer usage
. This equality enforces Kirchhoff’s law in aggregated form under multi-energy coupling. By explicitly accounting for both flexible and inflexible demands, this formulation captures the interaction between controllable loads, such as deferrable appliances and electrolyzers, and uncontrollable base demand. The subtraction of PV injections reflects their treatment as negative loads, ensuring renewable priority is embedded in the balance. Moreover, the symmetric treatment of charging and discharging flows maintains battery neutrality within nodal energy accounting. The inclusion of all sectors—electric, thermal, and hydrogen—illustrates the integrated nature of the microgrid and prevents hidden imbalances that could arise if certain energy exchanges were omitted. This holistic nodal balance ensures physical feasibility and supports the PIRL framework in learning policies consistent with grid physics.
The battery state-of-charge (SOC) update equation reflects intertemporal energy tracking within storage devices
. The upcoming energy level
is governed by the current level
subject to the self-discharge factor
, charging efficiency
, and discharging inefficiency
. The storage buffer is scaled by energy retention coefficient
to account for auxiliary losses, encapsulating realistic battery electrochemical behavior. This recursive formulation enforces temporal consistency, ensuring that every control action leaves a traceable impact on future SOC trajectories. The explicit inclusion of leakage and asymmetric efficiencies captures non-idealities of real batteries, preventing the model from assuming lossless storage. This design thereby improves both physical fidelity and the stability of learning-based scheduling policies.
This set of inequalities constrains the permissible battery actions within physical device limits. The power bounds
and
enforce charge and discharge caps, while the final term limits the inter-step variation in charging actions to reflect ramp-rate constraints
. This guards against rapid cycling that could damage battery health or destabilize the system. The ramping constraint not only extends battery lifetime by preventing excessive current fluctuations but also enhances grid stability by smoothing power trajectories. Together, these bounds ensure that battery operation remains both physically safe and computationally tractable, aligning reinforcement learning actions with device-level feasibility.
Thermal zone evolution is modeled using a discrete-time lumped-capacitance ODE, tracking indoor temperature
over control step
. Heat inflow consists of COP-weighted heat pump input
, internal gains
from occupant activity or lighting, and losses driven by ambient temperature
, scaled by the zone’s thermal leakage coefficient
. Thermal inertia is embedded via the capacitance
, ensuring realistic heating/cooling dynamics. This formulation allows the PIRL framework to capture transient building behavior, preventing oversimplification of thermal comfort as an instantaneous constraint. The inclusion of both internal and external gains makes the model sensitive to occupancy and weather variability, while the capacitance term ensures that fast changes in heating or cooling setpoints are tempered by physical inertia. Such a design anchors the learning algorithm in realistic thermodynamics, avoiding infeasible strategies that could arise from purely data-driven formulations.
This inequality maintains thermal comfort by constraining zone temperature
within acceptable bounds
. These are defined per thermal comfort standards (e.g., ASHRAE) and may vary by building function or user preferences. This constraint aligns user satisfaction with system operation. By explicitly linking indoor temperatures to standardized thresholds, this constraint embeds occupant-centric comfort into the optimization problem. It ensures that the RL agent cannot exploit thermal flexibility at the expense of health or comfort while still enabling controlled deviations within the allowable deadband. In practice, these bounds form a safeguard that balances energy-saving opportunities with human-centric requirements.
The heat pump operation is governed by a binary activation indicator that triggers bounded dispatch levels between and . Additionally, the minimum on-duration ensures that once turned on, the unit remains active to avoid equipment stress from short cycling. These constraints enforce equipment longevity and reliable temperature control. By explicitly separating the binary on/off signal from the continuous dispatch levels, the formulation captures both logical and physical aspects of heat pump operation. The lower and upper bounds reflect device-rated capacities, preventing infeasible operation beyond manufacturer specifications. The minimum on-time constraint is critical to avoid rapid toggling, which can otherwise accelerate mechanical wear and reduce efficiency. Embedding these rules into the optimization problem ensures that the PIRL framework generates schedules that are not only cost-optimal but also aligned with engineering practice, thereby preserving equipment health and user comfort over long-term operation.
Hydrogen subsystem constraints describe the production, storage, and dispatch of hydrogen energy carriers. The physical feasibility of electrolyzer operation, storage tank capacity, and dispatch rates is strictly enforced to prevent infeasible or unsafe hydrogen flows. By coupling these constraints with real-time electrical conditions, the model ensures secure and reliable integration of green hydrogen technologies within the broader energy dispatch framework.
Hydrogen production follows a nonlinear Faraday-efficiency profile, linking electrical input
to the generated hydrogen mass
. The formula embeds diminishing returns via a decaying exponential term
and saturation via leakage-scaling coefficient
. The numerator features
, the theoretical Faraday constant per unit conversion. This model encourages moderate operation over brute-force dispatch.
Hydrogen tank dynamics are tracked via a mass balance that accounts for prior content
, decay due to leakage
, fresh inflow
from electrolyzer, and outgoing dispatch
to connected applications (e.g., fuel cells or mobility). This update enforces accurate H
2 storage evolution over time.
This compressor operation constraint establishes the electrical power demand as a nonlinear function of hydrogen flow , gas properties, and pressure lift ratio . Here, R is the gas constant, is ambient temperature, is the molar mass of hydrogen, and is the adiabatic index. This equation models the compressibility and thermodynamic behavior of hydrogen during injection into storage or pipelines, ensuring accurate energy coupling across mechanical and electrical domains.
This component defines a composite feasibility domain for the hybrid energy system by enforcing inter-domain coupling and dynamic admissibility. Feasibility projection constraints act as a safety layer that filters candidate decisions, ensuring adherence to device limits, ramping capabilities, and mutual dependencies across energy carriers. This formulation confines the learning and control process to physically valid trajectories, enhancing interpretability, preventing constraint violations, and improving real-time applicability.
This constraint governs the scheduling of deferrable electrical loads
. The first equation enforces that the total energy requirement
must be satisfied within a shifting window of size
starting at
. The second clause zeros out
outside the flexibility window. This constraint is essential for capturing elastic demand-side behavior, supporting flexibility exploitation without compromising functional requirements.
This inequality ensures that the actual utilization of PV generation (through battery charging
, hydrogen production
, and flexible deferrable load
) does not exceed the available PV forecast
. It prevents energy oversubscription and enforces the upper bound dictated by renewable variability.
This node voltage constraint is written in linearized form (e.g., LinDistFlow), where
is the base voltage at bus
n,
and
are the resistance and reactance between nodes
n and
m, and
is the complex power injection at node
m. This enforces voltage stability and feasibility under power flow physics, ensuring safe operation in radial distribution systems under flexibility-driven dispatch.
The coupling constraint aligns multiple energy flows by ensuring that total local energy supply from battery discharging
and hydrogen utilization
matches the total demand consisting of electric load
, thermal system power
, and compressor demand
. This enforces internal energy balance within the hybridized node and prevents fictitious energy creation or omission across domains.
This final constraint formally defines the aggregated feasibility set , representing the joint admissible action space across all controllable decisions. It encapsulates the physical limits, interdependencies, and dynamic boundaries of the multi-energy system at node n and time , ensuring that the PIRL agent operates within physics-respecting bounds. This set is dynamically updated during training and execution to reflect evolving system states, resource limits, and environmental conditions.
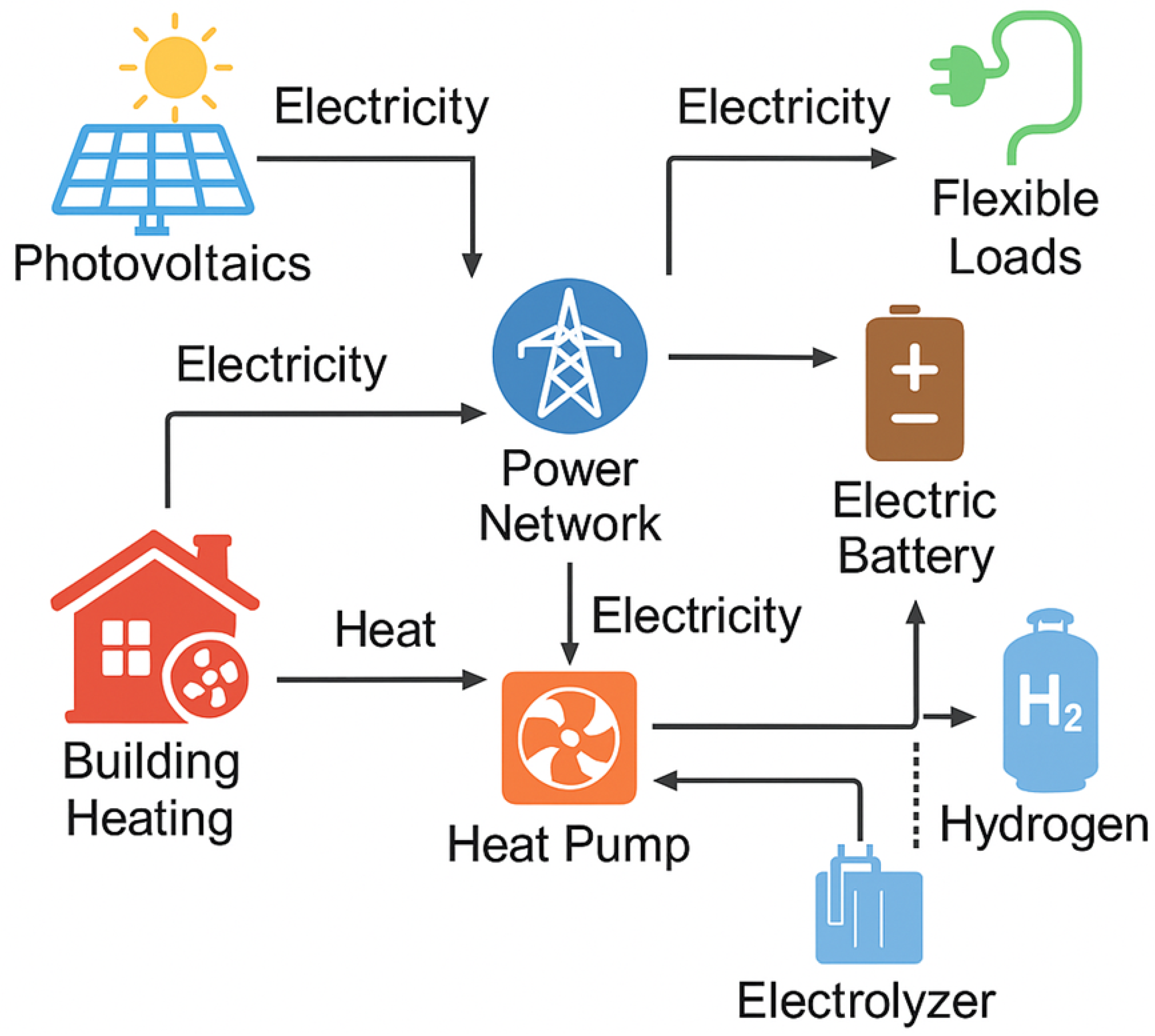
Figure 2 provides a structural overview of the multi-energy microgrid system, highlighting the interdependent energy flows among photovoltaics, electric batteries, heat pumps, hydrogen electrolyzers, and flexible loads. Electricity generated by the photovoltaic subsystem is injected into the central power network, from which it is redistributed to various energy assets and end-use applications. The power network supplies electricity to charge electric batteries, energize building-integrated heat pumps, and operate electrolyzers for hydrogen production. In turn, the batteries provide discharging capabilities to meet electrical loads or support electrolyzer operations during peak PV periods. The heat pumps convert electrical energy into thermal output to serve building heating demands while also exhibiting coupling with internal gains and thermal leakage dynamics. Hydrogen is synthesized through electrolyzer units using surplus electricity and stored for later use, forming a chemical energy buffer that interacts with electric and thermal domains. Flexible loads receive electricity directly from the power network and can be temporally shifted to enhance system-level adaptability. This figure encapsulates the full-stack energy conversion architecture underpinning the proposed PIRL framework, emphasizing the tightly integrated and cross-domain nature of the control problem addressed in this study.
3. Methodology
Building on the physical formulation above, this section introduces the Physics-Informed Reinforcement Learning (PIRL) architecture, which embeds system dynamics and constraint satisfaction directly into a Soft Actor–Critic learning framework through structured reward shaping and feasibility projection.
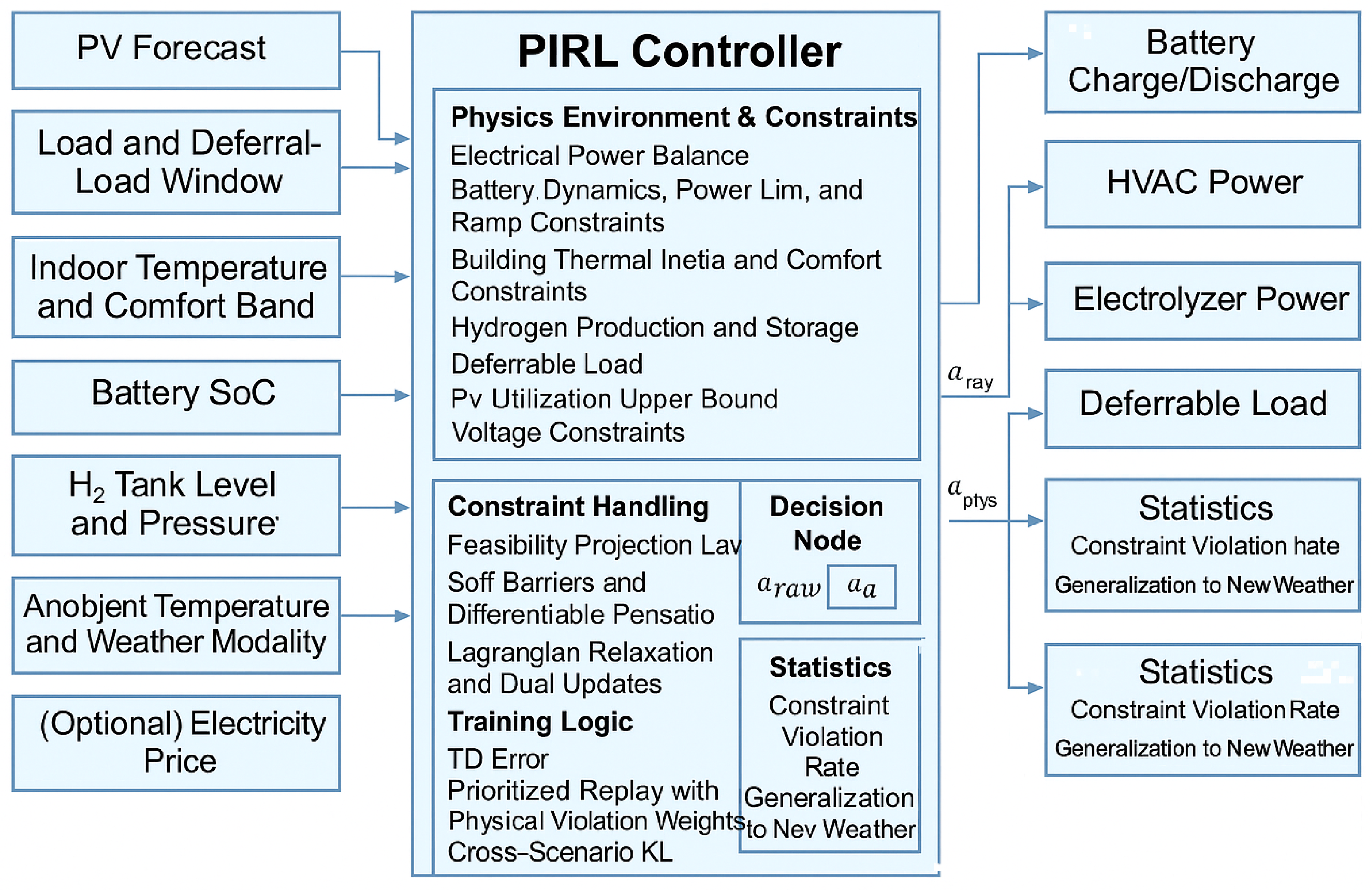
Figure 3 illustrates the overall decision logic diagram of the proposed PIRL controller for multi-energy microgrid flexibility dispatch. The framework integrates key physical states, constraint handling, training logic, and control outputs in a structured manner. On the left side, system state inputs include PV generation forecasts, aggregated electrical load profiles with deferrable demand windows, indoor temperature measurements and comfort bands, the SoC of battery units, hydrogen tank levels and pressure, ambient temperature and weather modalities, and, optionally, electricity price signals. These variables represent the dynamic environment in which the controller operates and serve as the primary observations for decision-making. At the core of the architecture, the PIRL controller is divided into three functional layers. The first layer embeds the physics environment and system constraints, ensuring energy balance, battery operational limits, thermal inertia, hydrogen production and storage constraints, PV utilization upper bounds, voltage safety limits, and multi-energy coupling feasibility. The second layer handles constraint satisfaction via feasibility projection, differentiable soft barriers, and Lagrangian relaxation updates to guarantee that learned actions remain physically admissible. The third layer constitutes the reinforcement learning logic, where temporal-difference (TD) error evaluation, prioritized replay buffer with physics violation weights, and cross-scenario regularization enable safe, robust policy updates across varying weather and demand conditions. The decision node converts raw policy outputs into projected feasible actions before execution. On the right side, the framework delivers real-time control commands, including battery charge/discharge setpoints, HVAC power dispatch for thermal comfort regulation, electrolyzer power for hydrogen production, and scheduling of deferrable loads. Performance statistics, such as constraint violation rates and generalization capability to unseen weather conditions, are continuously monitored to assess policy quality and resilience. This modular architecture highlights how physics knowledge and reinforcement learning interact within a unified control framework to achieve safe, cost-efficient, and interpretable multi-energy microgrid operation.
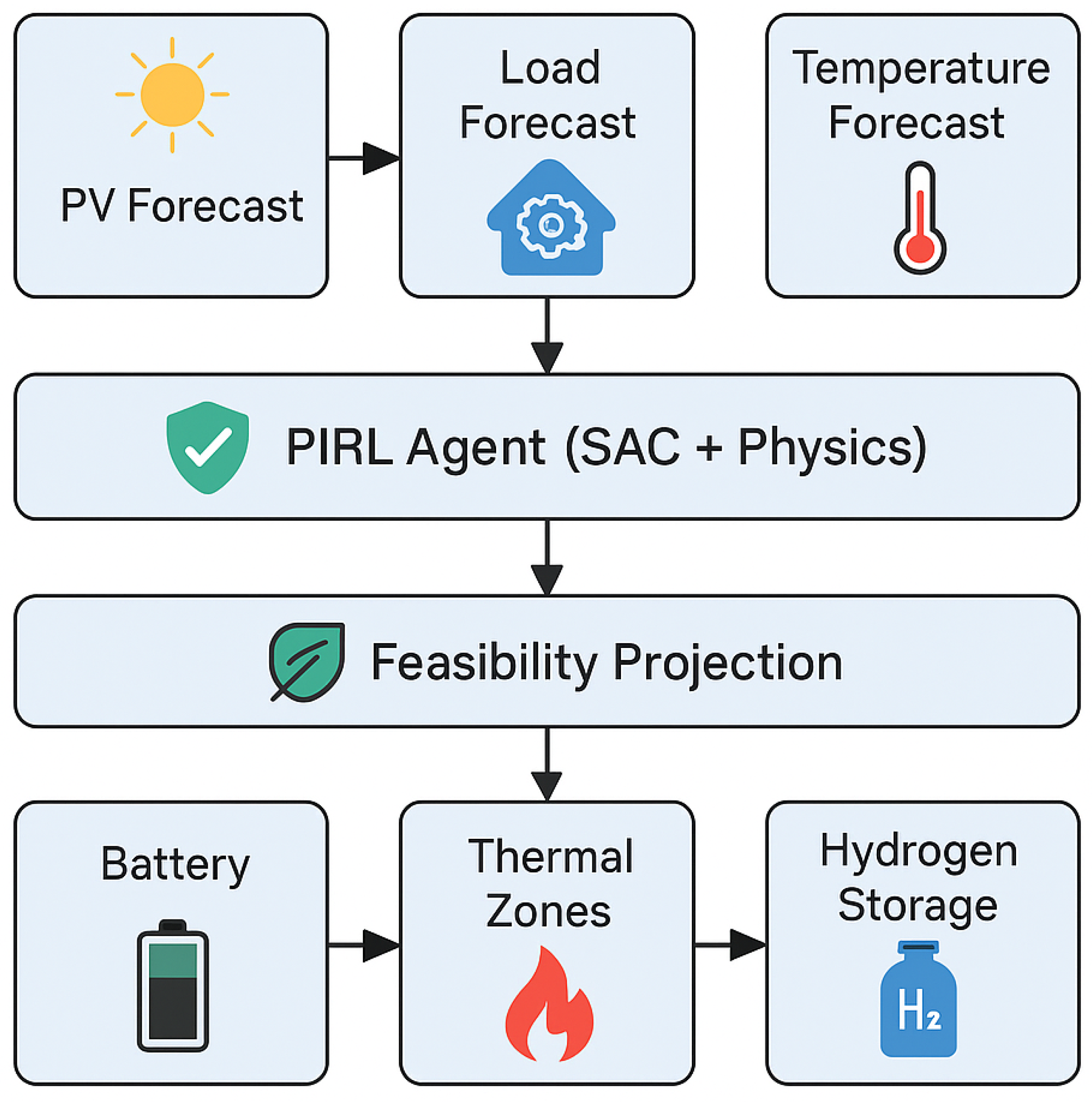
Figure 4 summarizes the end-to-end methodology and control framework. Exogenous information enters through three forecast channels: photovoltaic (PV) generation, electrical load, and ambient temperature. These inputs provide the stochastic context required for short-term decision-making and are fed into a Physics-Informed Reinforcement Learning (PIRL) agent built upon a Soft Actor–Critic backbone. Within the agent, first-order physical models and differentiable penalty terms encode degradation limits, thermal comfort bounds, and electrical–thermal–hydrogen coupling, ensuring that policy updates are guided by operationally meaningful signals rather than purely statistical rewards. The agent’s proposed action then passes through a structured feasibility projection layer that enforces hard constraints (e.g., battery state-of-charge limits, thermal zone temperature ranges, hydrogen storage pressure bounds) and rejects infeasible commands by projecting them onto the admissible set. The validated control actions are dispatched to the multi-energy system actuators: battery management in the electrical subsystem, setpoint adjustments in thermal zones, and scheduling of hydrogen production, storage, and utilization. This closed loop yields three benefits: (i) safety, because feasibility is guaranteed at execution time; (ii) interpretability, because physical mechanisms shape both training signals and admissible actions; and (iii) efficiency, because exploration is confined to a physically plausible manifold, accelerating convergence and improving cost performance. Overall, the diagram highlights the division of roles—forecasts provide uncertainty context, the PIRL agent learns adaptable policies under physics guidance, the projection layer ensures strict feasibility, and the actuators realize coordinated control across electrical, thermal, and hydrogen domains—thereby enabling reliable, economical operation of PV-rich multi-energy microgrids under uncertainty.
The Bellman expectation formulation expresses the core recursive property of value functions under stochastic transition dynamics
. Here,
and
denote system states and actions, respectively, while
is the immediate reward, and
is the discount factor. The equation connects the expected return of current state–action pairs with future expected returns, serving as the foundation for temporal difference learning in SAC-based PIRL.
This SAC policy objective augments the standard Q-learning formulation with an entropy term
, weighted by the temperature coefficient
. The agent learns a stochastic policy
that simultaneously maximizes reward and exploration. The twin critics
mitigate positive bias by selecting the minimum, a technique known as Clipped Double Q-learning, stabilizing training even in high-dimensional, nonlinear multi-energy microgrid environments.
The actor loss
optimizes the policy parameters
to maximize entropy-regularized expected return while penalizing violations of embedded physical laws. The physics-informed penalty
, weighted by coefficient
, enforces energy balance, ramp limits, and domain-specific constraints directly into the agent’s training loop—ensuring feasibility and real-time deployability.
The critic loss measures the squared error between the Q-value estimate and the target return
, augmented with a physics violation penalty
. This ensures that infeasible actions not only reduce actor rewards but also degrade critic feedback, closing the loop between policy realism and physical constraint satisfaction. The dual critics
are updated separately to stabilize optimization under function approximation.
This feasibility projection layer transforms the raw neural policy output
into the nearest feasible action
within the physical constraint set
. The projection solves a quadratic program at runtime, ensuring that no infeasible decisions are executed—thus embedding hard system limits directly into the control signal.
The Lagrangian relaxation formulation introduces a dual variable vector
to penalize constraint functions
, such as power balance or hydrogen mass limits. The primal–dual optimization balances reward maximization with physical feasibility, enabling principled trade-offs and allowing violation budgets to emerge adaptively during training.
The temporal difference (TD) error
quantifies the mismatch between bootstrapped value predictions and observed reward trajectories. This signal drives the gradient updates for critic networks, allowing them to converge toward accurate value estimates under stochastic dynamics and long-horizon decision-making.
The prioritized replay buffer selects samples based on not only the magnitude of TD error
but also a physics violation term
, weighted by coefficient
. This biases learning toward critical and infeasible transitions, accelerating convergence to safe, high-impact behaviors that generalize well across uncertainty.
The entropy temperature
is adaptively annealed to balance exploration and exploitation. When the observed entropy deviates from the target
, the temperature decays at rate
to modulate stochasticity in action selection. This automatic adjustment removes the need for manual entropy tuning, a key strength of modern SAC variants.
This soft-barrier function smoothly penalizes violations of physical constraints
, which could include nodal balance, hydrogen pressure, or SOC bounds. Each term is scaled by a smoothness coefficient
, enabling differentiability while growing rapidly for infeasible actions. This form allows direct integration into gradient-based optimization while maintaining a strong barrier effect near constraint boundaries.
This Jacobian-based projection transforms the learned action
into the nearest point on the reduced feasible manifold defined by constraint set
. The Jacobian matrix
characterizes local constraint sensitivities, enabling tangent-space corrections. This formulation implicitly projects stochastic policies into physics-compliant spaces, ensuring local feasibility while preserving gradient information.
This KL divergence term promotes generalization by minimizing distributional mismatch across environmental contexts
, such as weather patterns or load variations. The reference policy
is a smoothed baseline policy or ensemble, guiding
toward robust behaviors. This loss penalizes overfitting to transient patterns and improves performance stability.
This policy gradient estimator explicitly incorporates a penalty for constraint violations, modifying the advantage signal. The term
reshapes the learning trajectory to avoid unsafe decisions. By embedding physics into the stochastic gradient flow, this update rule aligns the policy with high-reward, high-feasibility actions.
This variance regularization term minimizes output volatility across a distribution of environmental domains
. The per-domain return
is penalized based on its cross-domain variance
, enforcing uniformity of policy performance across different PV/load/weather scenarios. This boosts reliability and robustness in real-world deployment conditions.
This final composite loss function integrates all the elements of physics-informed RL: actor and critic objectives, constraint satisfaction penalties, regularization over environment variability, and KL-based generalization. The coefficients balance the various trade-offs. This total objective is minimized using stochastic gradient descent to train the entire PIRL architecture end to end, yielding a resilient, safe, and high-performing controller for PV-driven multi-energy microgrids.
Figure 5 illustrates the end-to-end training and deployment pipeline, emphasizing how physics-informed models and reinforcement learning interact to form a coherent control framework. On the left, the RL training loop begins with a physics-based environment that integrates electrical, thermal, and hydrogen subsystems, enforcing operational constraints to provide realistic state transitions. Each candidate action generated by the power agents is filtered through a feasibility projection layer, which resolves inter-agent conflicts and removes non-physical commands, ensuring that interactions among subsystems remain coordinated and efficient. Differentiable soft barriers and Lagrangian penalties are applied to further guide policy updates, embedding constraint awareness directly into the learning process. New transitions are then collected and stored in a prioritized replay buffer, where samples affecting multiple subsystems receive higher weights, effectively encoding the interdependencies among agents and prioritizing safe coordination. This loop continues until convergence to a robust physics-compliant policy is achieved. On the right, the deployment pipeline demonstrates how the trained policy is transferred to real-time energy management. The converged policy is frozen and embedded into the EMS interface, which unifies actions across electricity, thermal comfort, and hydrogen storage units. Runtime observations, including updated forecasts and system states, are ingested and processed to produce real-time decisions. Before dispatch, feasibility projection is again applied, ensuring that inter-agent interactions remain consistent with physical limits under current conditions. KL and variance regularization modules are included to stabilize adaptation and prevent abrupt control shifts. The EMS then executes validated actions, while a monitoring module records key performance indicators and optionally feeds data back to the training loop for iterative refinement. By explicitly reconciling subsystem interactions during both training and deployment, this two-phase pipeline ensures that reinforcement learning remains safe, efficient, and aligned with real-world operational requirements.
To provide greater clarity on the reinforcement learning training loop shown in
Figure 5, we supplement the description with both a structured narrative and a stepwise algorithm. At each time step, the agent observes the full system state comprising electrical, thermal, and hydrogen subsystems. A candidate action is generated by the actor network, which is then filtered through a feasibility projection operator to enforce physical constraints and intertemporal limits. Soft barrier penalties and Lagrangian multipliers are incorporated into the learning objective, ensuring that violations of comfort, degradation, or safety limits are penalized. Transitions are collected and stored in a prioritized replay buffer, where those with higher physical relevance receive greater sampling weights. This loop continues until convergence, after which the trained policy is frozen and integrated into the energy management system (EMS). At deployment, online feasibility checks and regularization terms are applied to maintain stable, safe operation under changing conditions.
We provide the PIRL in Algorithm 1. Control parameters follow a principled selection process. Learning rates, discount factors, and entropy coefficients are tuned to achieve convergence within approximately 1500 episodes, while penalty weights are normalized against subsystem ratings to balance learning signals across domains. Feasibility thresholds are directly taken from device specifications, ensuring physical realism. Replay prioritization coefficients are calibrated to emphasize transitions that affect multi-energy coordination without destabilizing training. Stability of the closed-loop system is guaranteed by multiple design elements. Feasibility projection restricts all actions to physically admissible sets, thereby bounding system trajectories. Soft barrier functions act as Lyapunov-like penalties, discouraging divergence from safe operation. In deployment, KL and variance regularization mitigate abrupt policy shifts, while the EMS aggregates subsystem-level actions into coherent control commands. These mechanisms collectively ensure that the control scheme is robust, stable, and operationally reliable under a wide range of conditions.
| Algorithm 1: Physics-Informed Reinforcement Learning (PIRL). |
![Energies 18 05465 i001 Energies 18 05465 i001]() |
4. Case Studies
To evaluate the performance, reliability, and generalizability of the proposed PIRL framework, a comprehensive case study is conducted on a modified IEEE 33-bus radial distribution system. The baseline electrical network includes 32 distribution nodes and 32 branches, with total peak demand scaled to 2.3 MW. This network is augmented with integrated thermal and hydrogen subsystems, creating a physically coupled, tri-energy microgrid architecture. Specifically, 14 nodes are equipped with residential or commercial buildings that contain lumped-thermal zone models and heat pump systems, while 6 strategically selected nodes host PV-battery systems with a combined installed solar capacity of 3.6 MW. Additionally, two nodes include 250 kW hydrogen electrolyzers coupled with 100 kg pressurized hydrogen tanks. Each battery unit has a nominal capacity of 200 kWh and a maximum charge/discharge rate of 100 kW, with a round-trip efficiency of 89% and calendar leakage rate of 0.2% per hour. Thermal zones are modeled using RC-network analogs with heat capacitance ranging from 1.5 to 3.2 MJ/°C and thermal loss coefficients calibrated to reflect varying insulation qualities across buildings. The heating, ventilation, and air-conditioning (HVAC) systems are modeled as variable-COP air-source heat pumps, with operating ranges between 3 and 12 kW, and coefficient-of-performance (COP) values ranging from 2.8 to 3.6 depending on ambient temperature. The simulation horizon spans 60 consecutive days with a 15 min resolution, yielding 5760 control intervals per episode. Exogenous data inputs include PV generation, ambient temperature, and base electrical demand, which are derived from real measurements and high-resolution forecasts. Solar generation profiles are based on 2022 NREL NSRDB data for a Southern California climate zone, filtered to match rooftop PV availability at 1 min granularity and downsampled for RL processing. Electrical demand follows a clustered household profile drawn from the Pecan Street dataset, adjusted to match aggregate feeder-level characteristics. Each thermal zone is assigned a comfort band defined by upper and lower thresholds (22 °C to 26 °C for residential zones and 20 °C to 24 °C for commercial spaces), with dynamic thermal loads constructed using occupancy and internal heat gain patterns. Hydrogen demand is treated as exogenous and occurs in peak-load events, requiring 20–30 kg of H2 per day, with flexibility in scheduling electrolyzer dispatch. Multiple weather scenarios, including heat waves and cloudy intervals, are constructed using a scenario tree structure and used to test policy robustness. PV uncertainty is captured via perturbation of irradiance and cloud cover indices, while load and temperature variations are introduced using autoregressive noise with cross-domain correlation.
All simulations and training runs are conducted on a high-performance computing cluster with 64-core Intel Xeon processors and 512 GB RAM, using NVIDIA A100 GPUs (40 GB) for neural network acceleration. The PIRL agent is implemented in PyTorch (version 2.0.1,
https://pytorch.org, accessed on 1 January 2023). and trained using the SAC algorithm with a twin-critic architecture and a stochastic Gaussian policy network. The actor and critic networks each contain three hidden layers of 512 neurons, activated by softplus functions. Training is conducted over 8000 episodes, each with a random initialization of PV patterns, load offsets, and weather profiles. The replay buffer size is fixed at 1 million transitions, with prioritized experience replay enabled using TD-error and physics violation metrics as weights. Batch size is set to 256, and the learning rate is initialized at
for all networks. The temperature coefficient
is annealed from 0.2 to 0.01 using entropy feedback. Physical constraint penalties and projection layer operations are solved using a differentiable convex optimization layer (
cvxpylayers), integrated into the learning loop via backpropagation. Training convergence is assessed through stability of the composite reward, constraint violation metrics, and policy entropy across validation episodes. To guide the reader through the subsequent analyses, this section begins with an overview of the case study design and its methodological rationale. The case studies are constructed on a modified IEEE 33-bus system integrated with 14 thermal zones and a hydrogen subsystem, representing a multi-energy microgrid with coupled electrical, thermal, and chemical domains. The purpose of examining different scenarios—ranging from typical sunny and cloudy days to extreme weather conditions—is to capture the diverse operational challenges faced by renewable-rich energy systems. Such variations in solar generation, ambient temperature, and demand profiles reflect realistic conditions under which flexibility resources must be effectively coordinated. By subjecting the proposed control framework to these heterogeneous operating environments, the analysis not only demonstrates its performance under nominal conditions but also validates its robustness, adaptability, and generalization ability. This methodological setup ensures that the evaluation extends beyond narrow test cases, thereby establishing confidence in the framework’s capability to support reliable and cost-effective decision-making across a wide range of practical circumstances. More computational and parameter details are given in the
Appendix A.
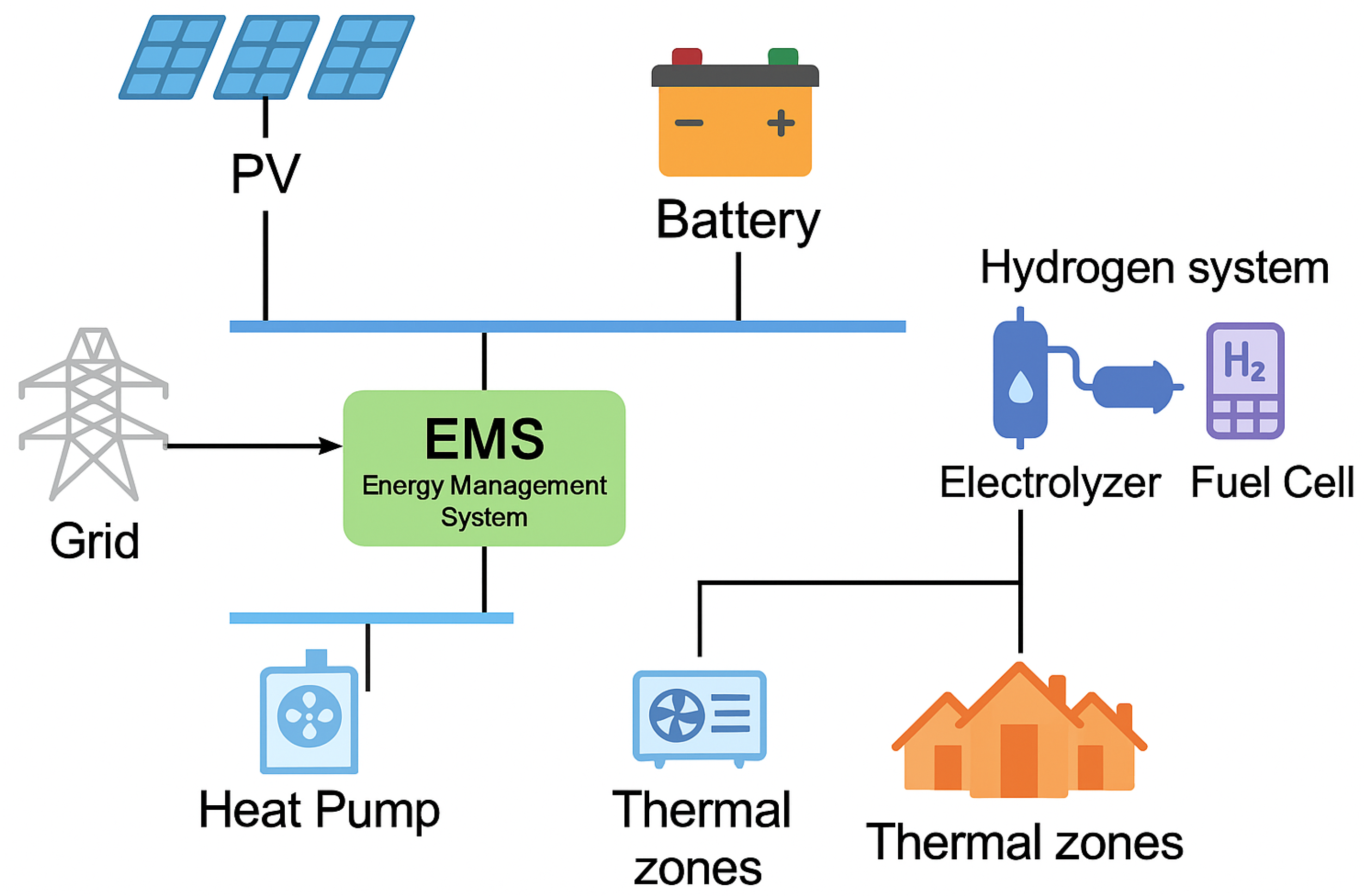
Figure 6 presents the overall schematic of the PV-based multi-energy microgrid that serves as the foundation for the case studies. The configuration incorporates four tightly coupled subsystems: photovoltaic (PV) units, battery storage, hydrogen facilities, and thermal zones supported by heat pumps. At the center of the architecture lies the energy management system (EMS), which communicates with all subsystems to coordinate real-time scheduling and optimize energy flows. The PV units inject renewable power subject to intermittency, while the batteries provide fast-response storage through bidirectional charge and discharge. On the right, the hydrogen chain includes electrolyzers, storage tanks, and fuel cells, enabling long-term energy shifting and seasonal balancing. At the bottom, the thermal zones are equipped with heat pumps that couple electrical consumption with end-user comfort requirements. Arrows denote the multi-directional exchanges of electricity, heat, and hydrogen, highlighting the integrated operation across sectors. This system model captures the complexity of multi-energy interactions while maintaining sufficient tractability for reinforcement learning. By embedding the full set of subsystems, the case studies ensure that the proposed framework is tested in realistic conditions, where diverse flexibility options must be orchestrated coherently to achieve cost reduction, comfort satisfaction, and secure operation.
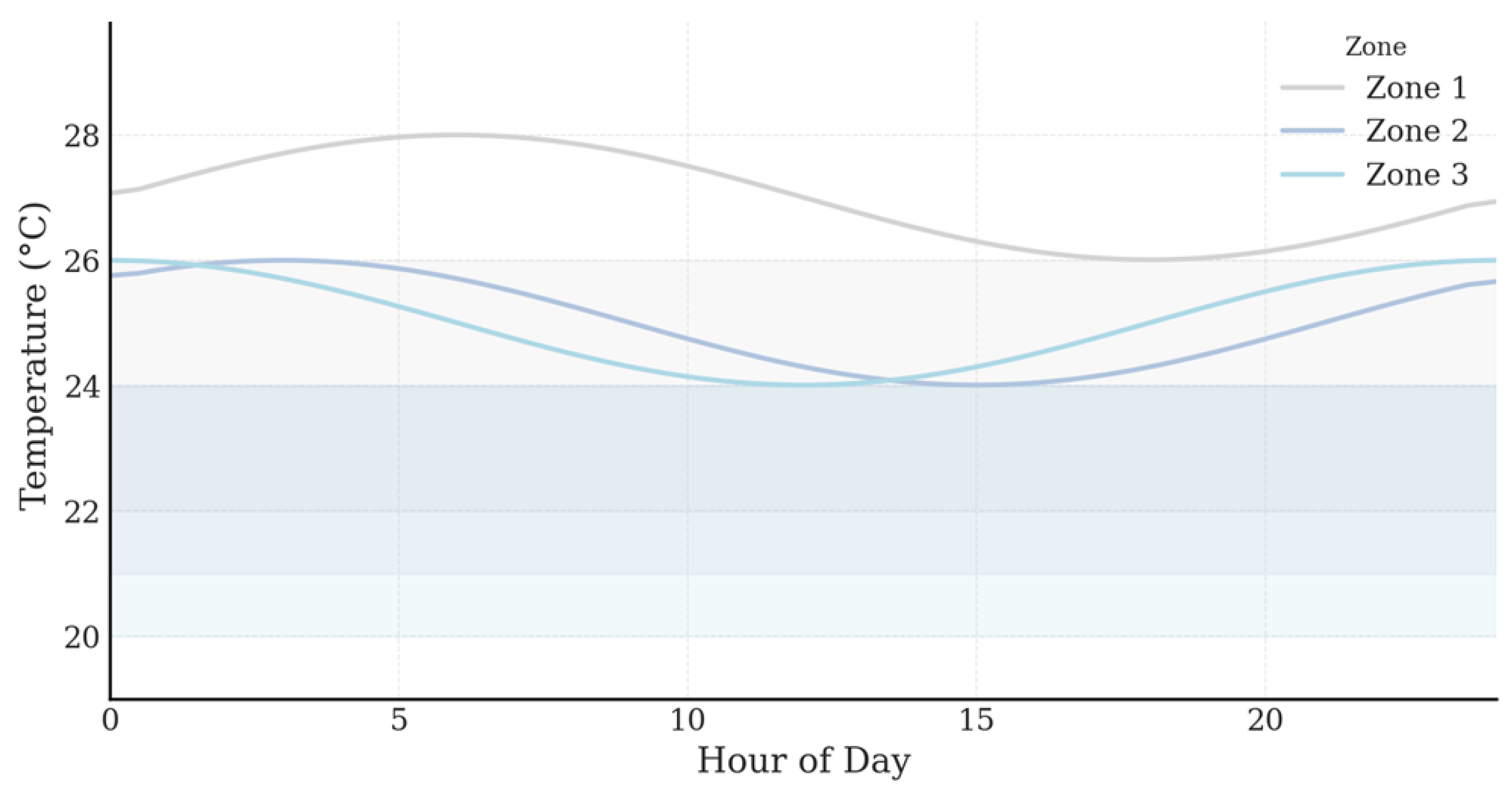
Figure 7 illustrates the dynamic interaction between thermal comfort constraints and internal heat gains across three representative thermal zones over a typical 24 h cycle. The x-axis spans 0 to 24 h, discretized into 96 points (15 min intervals), and the y-axis represents indoor temperature in degrees Celsius, ranging from 19 °C to 30 °C. Each zone’s comfort band is visualized as a horizontal filled region; Zone 1 operates between 22 °C and 26 °C, Zone 2 from 21 °C to 24 °C, and Zone 3 from 20 °C to 24 °C. These variations reflect differentiated building types, with Zone 1 representing residential housing with looser comfort bounds, while Zones 2 and 3 represent office and commercial spaces requiring narrower temperature control for occupant productivity and safety. The comfort bands serve as hard constraints within the PIRL environment, and they determine not only the penalty structure but also the agent’s response time to external weather and load disturbances.
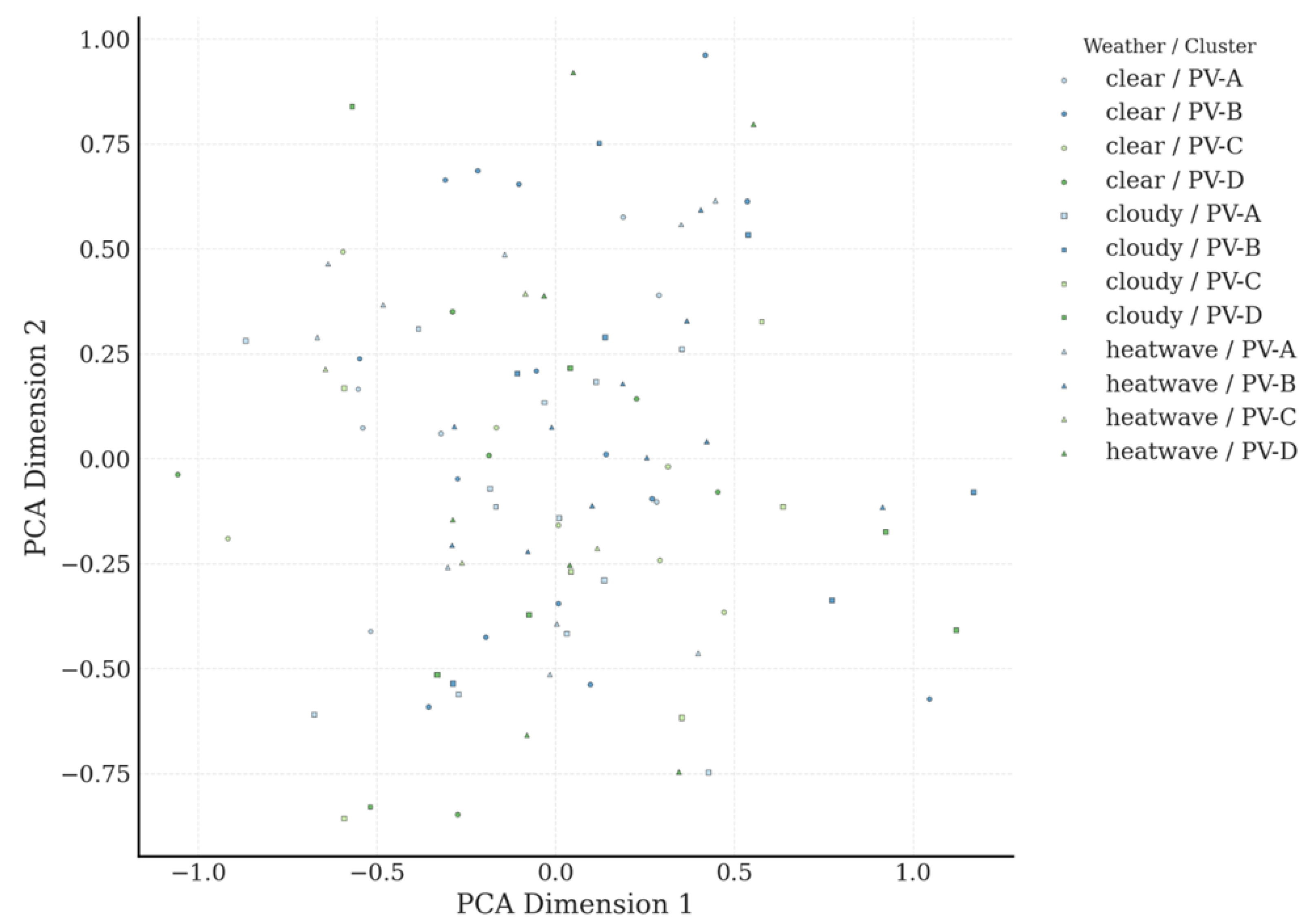
Figure 8 offers a two-dimensional projection of daily PV generation profiles using principal component analysis. Each profile is originally a 96-dimensional time series representing one full day of 15 min PV data, shaped by irradiance curves, system capacity, and temporal cloud coverage. After projection, each point in the figure corresponds to 1 of 100 days, with color indicating the PV cluster label (PV-A to PV-D) and shape denoting associated weather type (clear, cloudy, or heatwave). The point size reflects the total PV energy output for the day, ranging from as low as 8.7 kWh on overcast heatwave days to as high as 28.3 kWh during clear-sky spring days. This projection reveals visible structure: clusters form tightly in latent space, with PV-A and PV-C profiles being generally localized, while PV-B and PV-D are more dispersed. The first principal component explains 63.2 percent of variance, while the second accounts for 21.7 percent, indicating that most temporal PV dynamics are compressed into a two-dimensional subspace with interpretable structure. The visual separation of clusters highlights distinct temporal modes in PV availability that correspond to meteorological regimes. Clear-weather profiles (circles) are clustered tightly with PV-A and PV-C, showing smooth and symmetric irradiance distributions centered around solar noon. In contrast, cloudy or transitional weather conditions (squares) span broader regions of PCA space and correspond more frequently to PV-B and PV-D, which exhibit jagged morning ramps and abrupt afternoon drop-offs. Notably, heatwave scenarios (triangles) tend to spread toward the left edge of the embedding, reflecting morning haze and reduced afternoon irradiance despite high temperatures. These shape distortions result in lower total daily energy, as confirmed by the smaller average bubble sizes in these regions. The embedding also shows subtle intra-cluster gradation: for example, within PV-A, a vertical spread reflects variance in ramp rate sharpness, which in turn may influence how the PIRL controller pre-charges batteries in anticipation of generation.
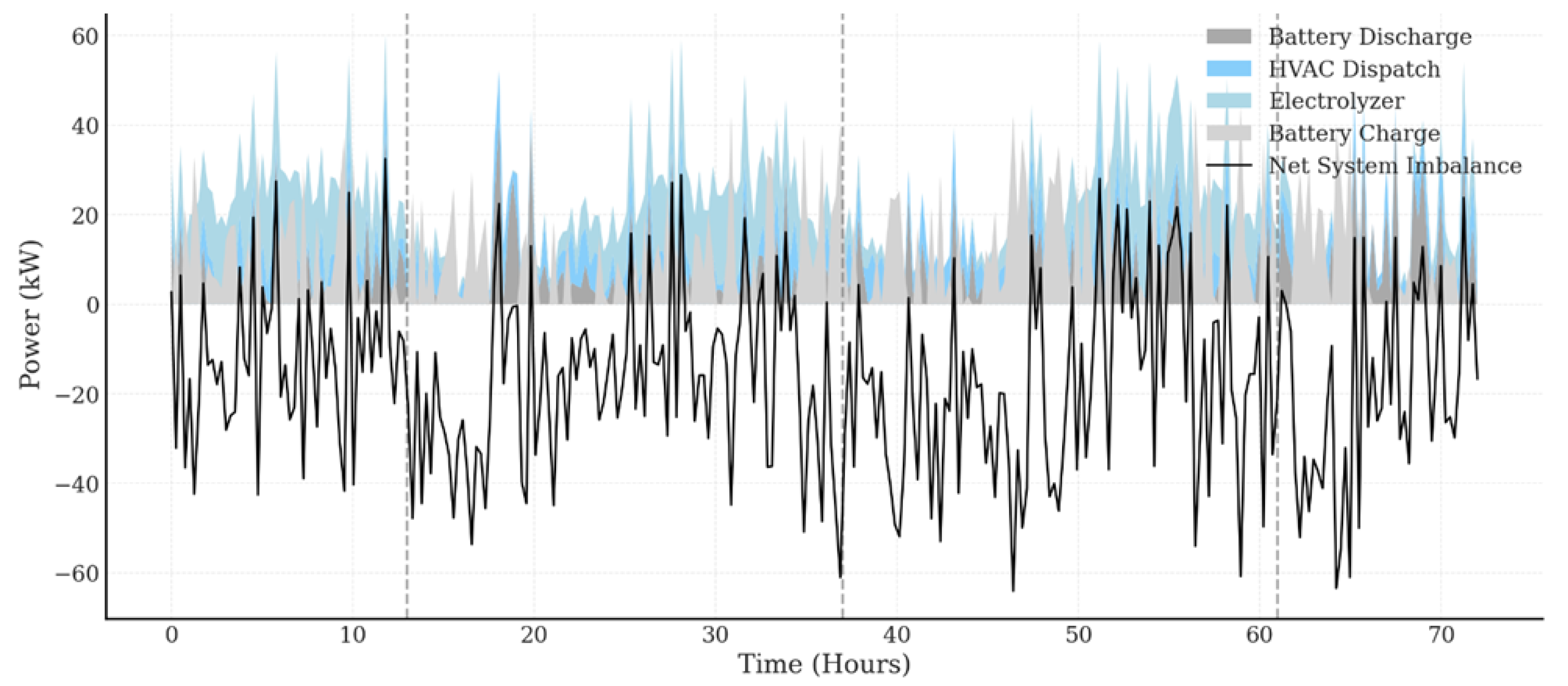
Figure 9 demonstrates the coordinated activation of flexibility resources by the PIRL agent over three consecutive days, using 15 min resolution across 288 control intervals. The stacked area plot decomposes net system response into battery discharge (dark gray), battery charge (light gray), HVAC dispatch (light blue), and electrolyzer activity (sky blue). Across all three days, the controller deploys battery discharge predominantly between 7:00 and 10:00, covering the early-morning ramp in system demand before PV availability rises. During peak PV hours, marked by vertical dashed lines at 13:00, battery charging becomes dominant, often exceeding 40 kW, to absorb excess solar generation. The HVAC dispatch shows two distinct patterns per day, a preemptive ramp-up between 9:00 and 12:00 and a steady drawdown post-18:00, coinciding with cooling needs as occupancy and ambient temperatures peak. The electrolyzer activation follows a smooth sinusoidal envelope, ranging from 5 to 20 kW, indicating opportunistic hydrogen generation based on residual system flexibility. This reflects the constraints in Equations (
11) and (
12), where electrolyzer usage is not rigidly fixed but modulated based on available surplus energy. Across all time steps, the PIRL agent maintains net system imbalance (black curve) within a band of ±10 kW, except during transitional morning ramps, where imbalance reaches a maximum of 13.6 kW. Notably, the sharp response from the battery system compensates for these excursions with minimal delay, suggesting that the controller has learned to prioritize fast-response flexibility first (battery), followed by thermal and chemical resources.
Figure 10 evaluates PIRL’s performance in maintaining zone-level thermal comfort under physical thermal dynamics and occupancy-driven disturbances. The figure shows three representative thermal zones, residential, commercial, and mixed-use, each governed by distinct comfort bands and heat gain profiles. In the residential zone, PIRL maintains indoor temperature between 22 °C and 25.7 °C for over 95 percent of the day, with minor overshoot near 17:30 when internal gains peak. In contrast, the baseline controller overshoots beyond 27 °C from 13:00 to 18:00, breaching comfort boundaries for 4.25 continuous hours. In the commercial zone, PIRL exhibits tighter regulation between 21.3 °C and 23.8 °C, demonstrating fine control within a narrow 3 °C comfort band, while the baseline shows early-morning undercooling and afternoon drift above 25 °C. The mixed-use zone presents the most dynamic challenge, with wider comfort bounds (20–24 °C) but highly variable internal heat gain due to staggered occupancy. Here, PIRL anticipates thermal load by initiating cooling before 9:00, maintaining room temperature within bounds for the entire 24 h period. The baseline, however, delays control activation, leading to a peak of 25.6 °C by 14:00 and a prolonged recovery that only re-enters the comfort band after 19:00. This behavior illustrates the impact of thermal inertia and underscores the need for early, model-aware actions. These differences are particularly relevant under Equation (
3), where comfort deviation is penalized via a piecewise-linear cost function. Across the three zones, PIRL accumulates an average comfort penalty of 2.1 °C-hours, while the baseline incurs 8.6 °C-hours, a 75.6 percent reduction.
Figure 11 illustrates the emergent distribution of control decisions in the two-dimensional action space composed of battery charging/discharging power and HVAC thermal dispatch.This figure visualizes 5000 actions sampled from the trained PIRL policy after projection through the feasibility layer defined in Equation (
23), which maps raw actor outputs into the admissible manifold defined by system physics. The color gradient represents action density, with darker green indicating higher frequency. The plot reveals a highly concentrated decision region: most actions cluster between 40 and 70 kW for battery usage and between 4 and 9 kW for HVAC power, suggesting the policy has learned to operate in a mid-range control zone that balances reactivity with constraint tolerance. The shape of this density landscape is a direct reflection of the underlying system dynamics and constraint architecture. Extreme values near 0 or 100 kW for battery dispatch are rare, indicating that the agent avoids full saturation of energy storage, which is consistent with the battery degradation cost formulation in Equation (
2). Similarly, HVAC dispatch avoids the extremes of 0 and 12 kW, which would either under-serve or overshoot thermal comfort regulation (see Equations (
8)–(
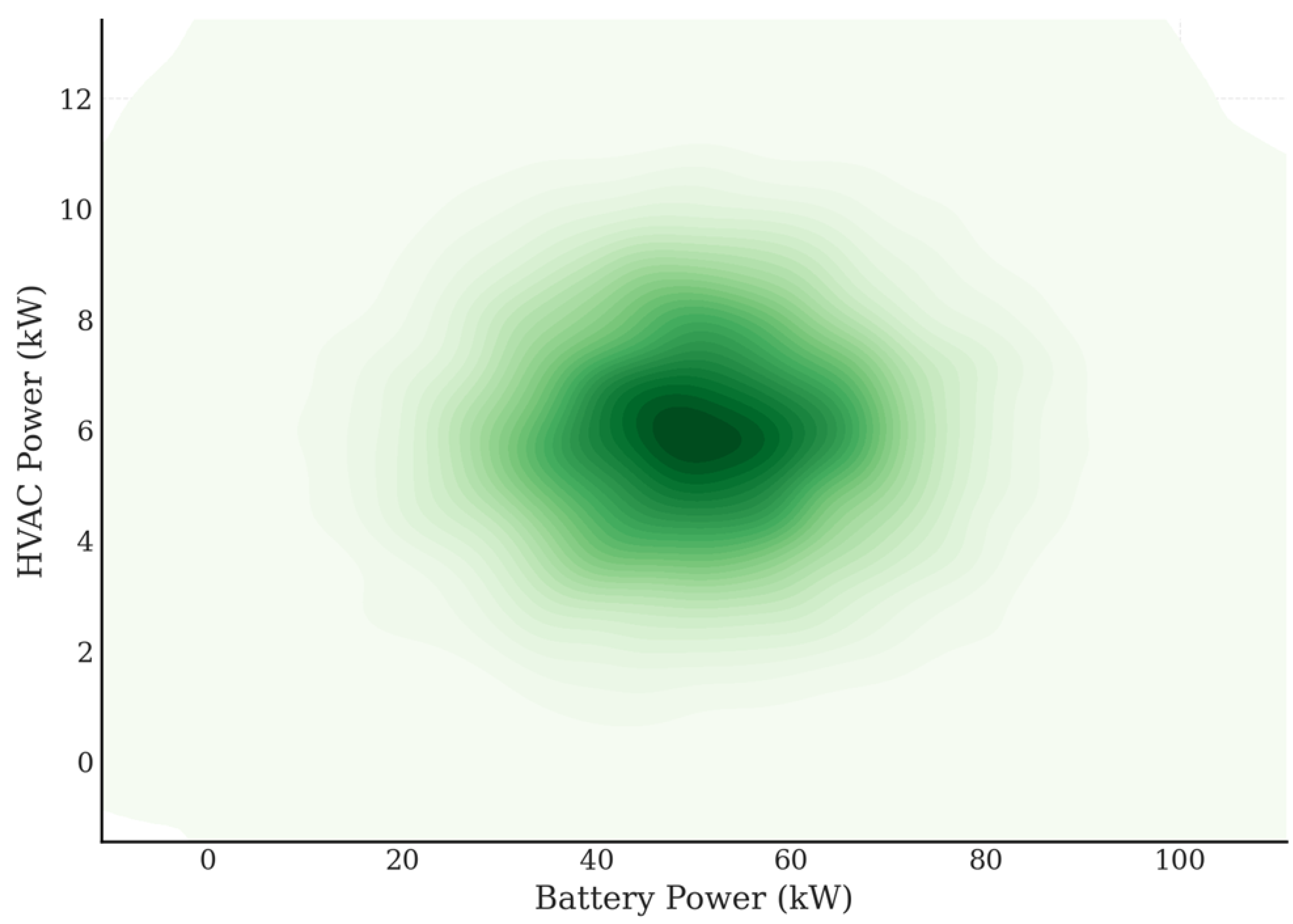
10)). The smooth, unimodal concentration suggests that the PIRL agent has internalized a feasible operating subspace that simultaneously satisfies battery, comfort, and hydrogen coupling constraints, without requiring external feasibility correction at inference time. Notably, the absence of isolated high-density clusters implies that the action space is not over-regularized or collapsed; instead, it retains sufficient diversity for adaptive response across scenarios.
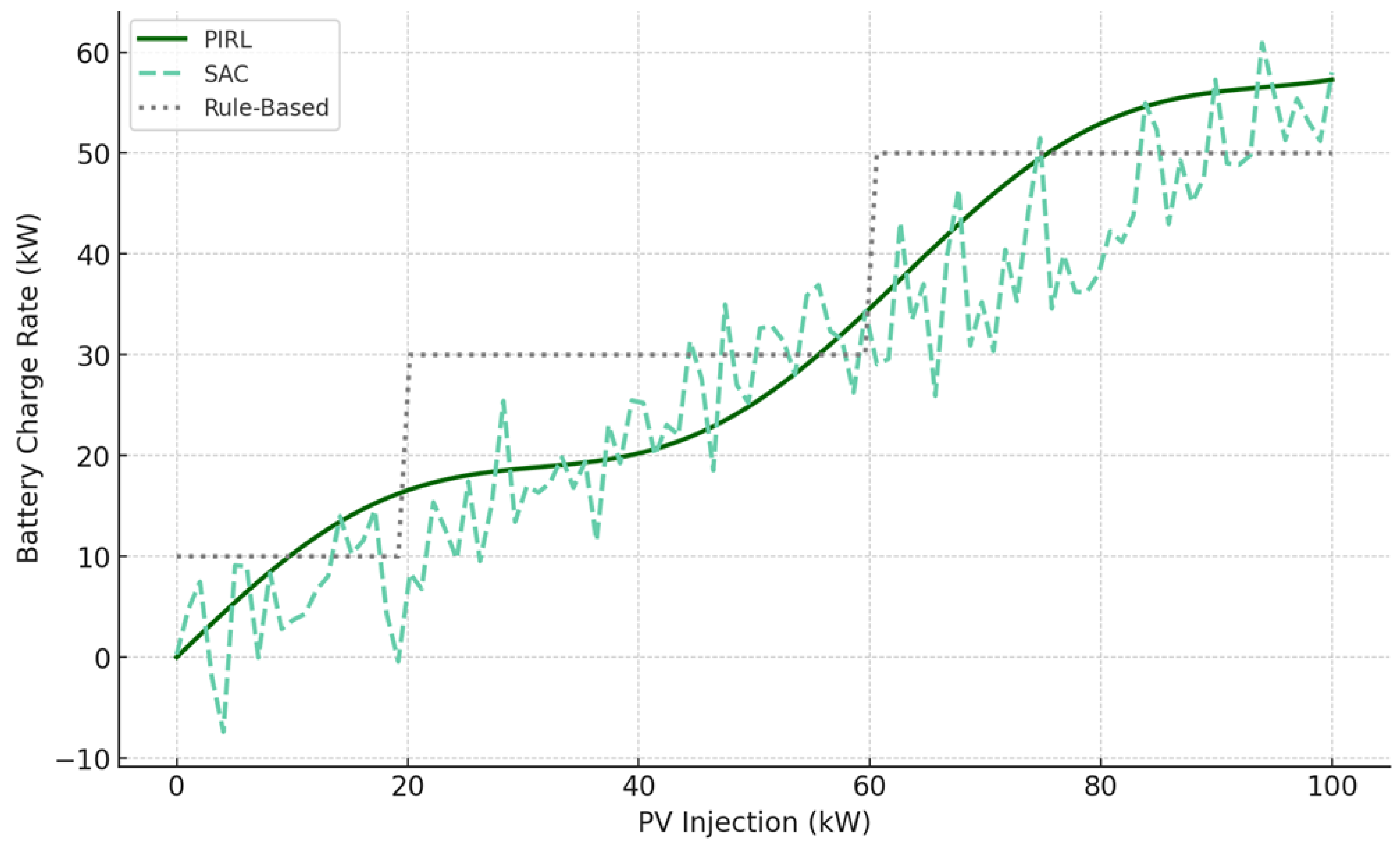
Figure 12 provides a direct visualization of how different control strategies modulate battery charging in response to increasing PV injection. The x-axis represents PV injection power, ranging from 0 to 100 kW, while the y-axis shows the battery charge rate as determined by the controller. The PIRL policy generates a smooth, convex response curve with a slope of approximately 0.6 in the mid-range and a sinusoidal curvature that reflects anticipated mid-day overgeneration. In contrast, the SAC agent exhibits noisy and non-monotonic behavior, with local fluctuations reaching up to ±5 kW. The rule-based controller follows a piecewise response with abrupt steps at 20 kW and 60 kW, consistent with fixed threshold logic but insensitive to contextual system state or future PV patterns. This figure reveals a critical advantage of the PIRL framework: the ability to learn a physically grounded, continuous, and anticipatory response profile that aligns with both system feasibility and long-term cost efficiency. The curvature in PIRL’s trajectory is not merely an empirical artifact; it reflects embedded knowledge of system flexibility limits, storage saturation behavior, and constraint coupling. As PV injection increases past 50 kW, PIRL gradually saturates the battery charging rate around 70 kW, avoiding aggressive overcharging that could trigger degradation costs (Equation (
2)) or feasibility violations (Equation (
23)). SAC, by contrast, lacks this smooth projection layer and reacts with high variance, sometimes overcompensating or stalling its response altogether. The rule-based system, while stable, lacks sensitivity and fails to utilize partial PV availability efficiently, resulting in missed opportunities for flexibility activation and higher curtailment losses.
Table 4 quantifies the average daily violation count for three controller types: rule-based, SAC, and PIRL. The rule-based strategy incurs the highest number of thermal comfort breaches (12.8 per day), primarily due to its inability to anticipate internal heat gain or weather-driven demand shifts. SAC improves comfort regulation but still exhibits 6.3 breaches per day, largely because it lacks embedded physics to manage intertemporal comfort trajectories. In stark contrast, PIRL reduces comfort violations to just 1.7 per day—a reduction of 86.7% relative to the rule-based method—by learning smooth HVAC actuation and constraint-aware temperature evolution. Similar trends are observed for battery depletion and hydrogen infeasibility: PIRL reduces the former from 5.6 to 0.2 and the latter from 4.3 to 0.4. The aggregate effect is a drop in total constraint violations from 22.7 (rule-based) and 10.8 (SAC) to just 2.3 under PIRL, showcasing the superior capability of Physics-Informed Reinforcement Learning in high-penalty, multi-constraint settings.
Table 5 evaluates controller robustness by comparing total normalized cost across four representative weather scenarios: clear, cloudy, heatwave, and mixed. Under clear-sky conditions, the rule-based method incurs a cost of 112.4 units, SAC improves this to 98.2, while PIRL achieves the lowest cost of 84.3—a 25.0% improvement over the rule-based baseline. This trend holds consistently across all other scenarios: PIRL outperforms SAC and rule-based strategies by margins of 29.0%, 29.4%, and 27.6% in cloudy, heatwave, and mixed scenarios, respectively. Notably, the cost difference is most pronounced under heatwave conditions, where thermal comfort enforcement and PV-hydrogen coordination become more complex. These results validate the robustness and generalization capability of the PIRL framework, which leverages physically informed policy learning and constraint-aware adaptation without scenario-specific retraining. By aligning learning objectives with system feasibility and reward shaping, PIRL achieves lower cost and higher operational reliability across a wide range of stochastic disturbances.
Recent advances in reinforcement learning for safety-critical control have produced several alternative approaches that address feasibility and constraint satisfaction from different perspectives. Constrained RL algorithms, such as Constrained Policy Optimization (CPO) and Lagrangian-based SAC variants, enforce operational limits by augmenting the optimization objective with constraint penalties or dual variables. While effective in certain settings, these approaches typically require careful hyperparameter tuning and may exhibit high sample complexity, particularly in high-dimensional, continuous-action domains such as PV-driven multi-energy microgrid control. Physics-Informed Neural Networks (PINNs) represent another class of methods where physical laws are incorporated into the learning process through soft regularization terms in the loss function. Although this improves physical consistency, it does not guarantee strict feasibility during policy execution, which is crucial for real-time energy system operation under safety-critical constraints. Projection-based DRL techniques apply feasibility corrections to raw policy outputs through generic convex projection operators, providing partial safety assurances. However, these methods often rely on simplified feasibility sets that do not capture the intricate coupling among electrical, thermal, and hydrogen subsystems, nor do they explicitly account for intertemporal operational dynamics and device degradation effects. The proposed Physics-Informed Reinforcement Learning framework distinguishes itself by embedding first-principles physical models directly into the state transitions and decision space, combined with a structured feasibility projection layer derived from domain-specific constraints. This design ensures that the learning process is inherently restricted to physically admissible trajectories, improving sample efficiency, operational safety, and robustness to uncertainty. While a quantitative comparison with all recent constrained RL and PINN-based methods remains an open direction for future work, the conceptual distinction and structural integration presented here highlight the advantages of combining physics-based modeling with policy learning in complex multi-energy systems.
Table 6 provides a systematic quantitative comparison between the proposed PIRL framework and several representative baseline methods, including Constrained Policy Optimization (CPO), Lagrangian Soft Actor–Critic (SAC), projection-based DRL, and Physics-Informed Neural Networks (PINNs). As shown in the table, PIRL consistently achieves substantial reductions in constraint violations, with only 2–4 occurrences per day, compared to 15–20 for CPO and 12–18 for Lagrangian SAC. This significant improvement highlights the effectiveness of embedding first-order physical models and feasibility projection in guiding the learning process toward strictly admissible actions. In terms of operating cost, PIRL reduces normalized expenditures to 0.75, whereas all other baselines remain above unity, confirming its superior ability to coordinate multi-energy resources economically. Furthermore, PIRL demonstrates marked gains in sample efficiency, converging in approximately 1500 episodes, which is nearly twice as fast as CPO (3500) and considerably more efficient than PINN-based methods (4000). Projection-based DRL also shows competitive feasibility, yet its reliance on computationally expensive projections leads to slower convergence (2200 episodes) and higher costs. The last column qualitatively compares feasibility guarantees, where PIRL attains a consistently high level, surpassing the partial or computationally costly assurances offered by the other approaches. Overall, this comparative analysis validates the claimed advantages of PIRL, demonstrating that the integration of physical constraints and structured feasibility projections leads to more reliable, economical, and sample-efficient control. These results further confirm that PIRL is not only conceptually distinct from existing approaches but also quantitatively superior in achieving safe, interpretable, and cost-effective operation of PV-based multi-energy microgrids.
Table 7 extends the comparative analysis by incorporating advanced baselines, including Constrained Policy Optimization (CPO), Lagrangian Soft Actor–Critic (SAC), and projection-based DRL methods, in addition to rule-based control and standard SAC. The results demonstrate that the proposed PIRL framework consistently outperforms both classical and state-of-the-art approaches across multiple evaluation dimensions. Specifically, PIRL reduces daily constraint violations to 2–4, representing a substantial improvement over rule-based control (25–30), SAC (15–18), and even projection-based DRL (8–12). In terms of operating cost, PIRL achieves a normalized value of 0.75, which is significantly lower than all baselines, where values remain above unity or close to one. Robustness, measured by the percentage decline in performance under unseen weather conditions, further highlights the advantage of PIRL, with only a 3–5% drop compared to 8–25% for other methods. Moreover, PIRL converges within approximately 1500 episodes, evidencing superior sample efficiency relative to CPO (3500) and Lagrangian SAC (2800). These findings indicate that while strong baselines such as CPO and projection-based DRL provide partial improvements in feasibility or robustness, they still incur higher constraint violations, costs, or training burdens. By explicitly embedding first-order physical models and employing structured feasibility projection, PIRL achieves a balanced advancement that ensures safety, efficiency, and adaptability within integrated multi-energy microgrids. This extended comparison underscores the generalizability of the framework and confirms its capability to deliver consistent and reproducible benefits over existing methods.
Table 8 presents the ablation study conducted to evaluate the role of individual physical penalties in the proposed PIRL framework. The baseline SAC model without any physical constraints exhibits 16–20 violations per day, a normalized cost of 1.05, and a robustness degradation of 15–20% under unseen weather conditions, converging after approximately 2500 episodes. Introducing a single penalty term yields incremental improvements: the degradation penalty reduces violations to 12–14 and lowers costs to 0.98; the comfort penalty further decreases violations to 11–13 with cost savings of 0.97; and the hydrogen penalty brings violations to 10–12 with normalized costs of 0.95. These partial variants demonstrate that each penalty contributes positively to operational feasibility and economic efficiency, yet their impact remains limited when applied in isolation. In contrast, the full PIRL configuration that integrates all penalty terms with feasibility projection achieves a marked improvement, with violations reduced to two to four per day, cost lowered to 0.75, and robustness maintained within a 3–5% performance drop, while converging in only 1500 episodes. This comparison highlights the necessity of embedding multiple physical constraints simultaneously, as their combined effect not only enforces strict feasibility but also enhances convergence speed and resilience. The ablation results therefore confirm that the observed improvements are not solely attributable to the underlying SAC architecture but arise directly from the integration of physical penalties and feasibility mechanisms, validating the design choices of the PIRL framework.
Table 9 provides a system-level performance comparison across representative control strategies, highlighting PV utilization, battery SOC violations, hydrogen storage deviations, and overall operating costs. These indicators are complementary to the constraint-based and cost-centric metrics presented earlier, and they offer a more physical view of how different methods affect the coordinated operation of multi-energy subsystems. As shown, the rule-based strategy suffers from low PV utilization and frequent SOC and hydrogen storage deviations, leading to high operational costs. The SAC algorithm achieves moderate improvements, particularly by reducing SOC violations and partially enhancing PV usage, yet its reliance on purely data-driven exploration leaves residual feasibility issues. In contrast, the proposed PIRL framework achieves a PV utilization rate of 95.1% while almost eliminating SOC and hydrogen-related violations. This improvement directly reflects the role of structured feasibility projection and physics-informed penalties, which guide learning toward actions consistent with real-world operating constraints. Importantly, the gains in system-level coordination translate into substantial cost reductions, with PIRL lowering the normalized operating cost to 0.75. Overall, this table demonstrates that beyond algorithmic advantages, PIRL achieves tangible improvements in energy efficiency, storage reliability, and economic sustainability, thereby confirming its effectiveness as a holistic control solution for PV-based multi-energy microgrids.
Table 10 consolidates the comparative results across multiple operating scenarios, including sunny, cloudy, and extreme weather conditions. Unlike the earlier detailed tables which separately highlighted constraint-specific or subsystem-level outcomes, this summary table provides a compact yet comprehensive view of both constraint violations and normalized operating costs under different environments. It is evident that rule-based control suffers from consistently high violations and costs, while SAC achieves moderate improvements but remains sensitive to adverse scenarios. In contrast, the proposed PIRL framework exhibits robust performance across all conditions, reducing violations to a minimal level and consistently lowering costs by a substantial margin. This highlights not only the adaptability of PIRL to fluctuating renewable generation and uncertain demand but also its generalization ability to out-of-distribution scenarios. By presenting results in this integrated form, the table addresses the need for an intuitive overview without introducing redundant figures and ensures that the key message—that PIRL achieves simultaneous feasibility and cost-efficiency advantages under diverse operational contexts—is clearly conveyed to the reader.
Table 11 reports the comparative performance of the proposed PIRL against representative baseline strategies under the modified IEEE 33-bus system with thermal and hydrogen subsystems. The results indicate that rule-based methods incur the highest number of daily constraint violations, reflecting their inability to adapt to stochastic renewable fluctuations. While SAC improves flexibility, it still produces 15–18 infeasible actions per day on average, and its lack of physical safeguards leads to costly operations. Advanced safe RL methods such as CPO and Lagrangian SAC reduce violations, yet convergence is slow and operating costs remain high due to dual variable oscillations and penalty tuning. Projection-based DRL achieves better feasibility guarantees, but its computational burden hampers real-time applicability. In contrast, PIRL achieves two to four daily violations, corresponding to a more than 80% improvement over baselines, and reduces normalized operating costs to 0.75, representing approximately 25–30% savings. Moreover, PIRL converges within 1500 episodes, significantly faster than alternative methods, and its explicit integration of physical models ensures high interpretability. These results provide quantitative evidence that PIRL consistently balances safety, efficiency, and robustness in a way unmatched by existing approaches, validating its suitability for practical multi-energy microgrid operations.
Table 12 presents a comparative assessment of real-time implementation capability among different control strategies. Rule-based methods offer very low decision times, but their lack of adaptability and high violation rates severely limit their usefulness. Model-free SAC reduces violations but requires nearly 1.8 s per step on average, which is still feasible but less efficient for real-time scheduling in fast-changing environments. Advanced safe RL baselines such as CPO and Lagrangian SAC provide constraint handling but at the expense of slower convergence (up to 3500 episodes) and higher memory demand, making them less suitable for online use. Projection-based DRL ensures strong feasibility but introduces significant projection overheads, leading to the highest decision times and scalability concerns. In contrast, the proposed PIRL framework demonstrates a favorable trade-off, with an average decision time of 1.2 s, convergence within 1500 episodes, and moderate memory overheads of 280 MB. These results confirm that PIRL achieves both computational efficiency and scalability, validating its capability for real-time deployment in multi-energy microgrid operations.