Trajectory Optimization for Airborne Wind Energy Systems Based on a Multi-Strategy Improved Salp Swarm Algorithm

Abstract

Airborne Wind Energy (AWE) systems offer benefits such as high altitude access to stronger and more stable winds, reduced environmental impact, and cost effective infrastructure. However, these systems face several challenges including complex flight trajectory optimization, limited control robustness, and unstable power generation. This paper focuses on optimizing the flight trajectory of a tethered rigid wing AWE system to maximize power generation. A mathematical model of the system is constructed, and a constrained trajectory optimization problem is formulated. The multiple shooting method is employed for discretization, and a Multi-Strategy Improved Salp Swarm Algorithm (MISSA) is proposed to solve the optimization problem. Simulation results indicate that MISSA can generate a closed optimal trajectory, significantly enhance power output, and demonstrate superior performance in addressing complex trajectory optimization challenges.

1. Introduction

Growing global energy demands have intensified energy shortages, highlighting the urgent need to develop renewable energy solutions [1,2]. Conventional wind turbines, which consist of rotor blades, towers, and foundations, are constrained by high construction and maintenance costs as well as inherent structural limitations. As a result, their maximum operational altitude is restricted to approximately 300 m, representing the upper technological limit of traditional wind energy systems [3].

With the rapid advancement of clean energy technologies, Airborne Wind Energy (AWE) systems, which can harness stronger and more stable winds at higher altitudes, have emerged as a promising research direction in wind power generation [4]. Compared with traditional wind turbines, AWE offers distinct advantages, including lower infrastructure costs, higher operational altitudes, and reduced environmental impact. The tether is the “lifeline” of an AWE system, and its material properties directly impact the system’s safety, efficiency, and operational altitude. Advancements in tether materials, particularly toward making them lighter, stronger, more durable, and smarter, will be a critical step in unlocking the full potential of AWE systems [5]. These features make AWE particularly suitable for regions with variable wind conditions or complex terrain, thereby demonstrating strong engineering potential [6].

As shown in Figure 1, AWE systems operate by guiding a tethered aircraft along a periodic flight trajectory to drive ground-based generation units for energy conversion. The design of this trajectory plays a decisive role in determining power generation efficiency, tether stability, and operational safety. An optimized trajectory not only increases energy output per unit time but also enhances the overall system robustness and control performance. Consequently, trajectory optimization has become a central research focus in AWE technology [7].

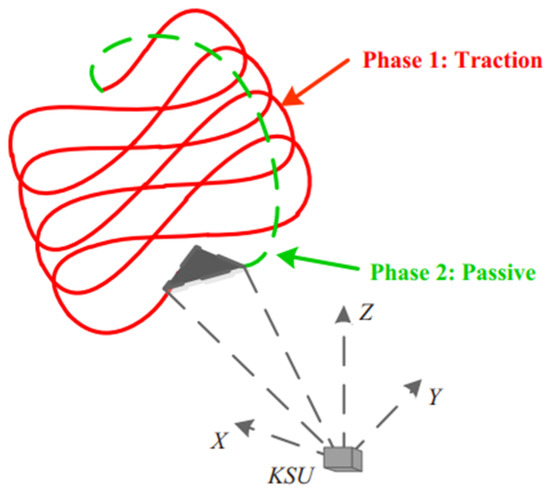
Figure 1. Schematic diagram of the AWE system flight trajectory.

Currently, trajectory optimization approaches fall into two primary categories: one relies on analyzing predefined paths (e.g., figure-eight, circular, elliptical trajectories), while the other formulates the problem as a constrained nonlinear programming (NLP) problem. The latter incorporates the aircraft’s dynamic model and uses numerical optimization to obtain an optimal solution. Due to the strong nonlinearity, coupling, and multiple constraints involved, various optimization strategies have been proposed, including gradient-based methods such as Sequential Quadratic Programming (SQP) and swarm intelligence algorithms like Particle Swarm Optimization (PSO) and Genetic Algorithms (GA), which aim to improve solution quality and global convergence capabilities [8,9,10,11].

The Salp Swarm Algorithm (SSA) is a swarm intelligence optimization technique inspired by the chain-like movement behavior of salps. Its simplicity, strong global search capability, and low parameter dependence make it suitable for solving complex nonlinear problems [12]. However, SSA still faces limitations in local search accuracy and convergence stability when applied to high-dimensional, multi-constrained trajectory optimization problems.

To address these challenges, this study focuses on a tethered rigid-wing AWE system. A complete dynamic model is developed, and a trajectory optimization problem is formulated with power generation maximization as the objective. The multi-constrained NLP problem is discretized using the direct shooting method, and three algorithms, SQP, SSA, and a Multi-Strategy Improved Salp Swarm Algorithm (MISSA), are employed for solution. Their optimization performance is compared and analyzed [13]. Simulation results demonstrate that MISSA significantly improves solution accuracy, convergence stability, and global search capability, thereby providing robust optimization support for the efficient operation of AWE systems.

2. Airborne Wind Energy System Modeling

2.1. Tethered Aircraft Modeling

The overall structure of an airborne wind energy system can be divided into three major components: the traction device, tether, and ground equipment [14], as illustrated in Figure 2. The traction device is one of the key parts of the airborne wind energy system. According to material properties, the traction device can be classified into flexible and rigid types [15]. The flight mode of the airborne wind energy system depends on the physical characteristics of the traction device and is categorized into crosswind mode and non-crosswind mode. In crosswind mode, the aircraft is controlled to fly along an optimized trajectory within a plane nearly perpendicular to the ground. In this mode, the airborne wind energy system harvests energy from the relative wind. In the non-crosswind mode, the aircraft hovers in the air with near-zero velocity relative to the ground and harvests energy from the absolute wind [16,17].

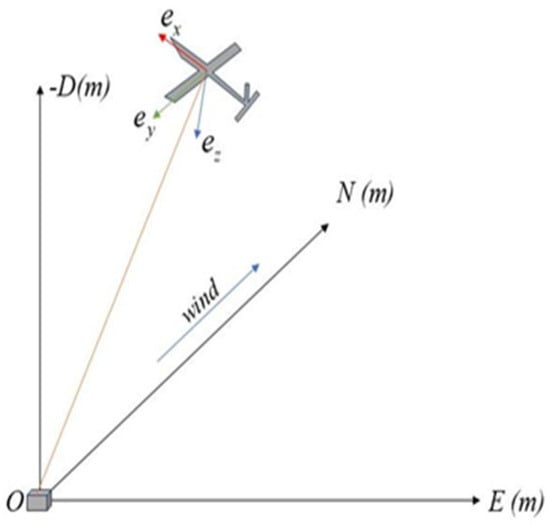
Figure 2. Schematic diagram of airborne wind energy device.

From the perspective of the technological evolution of airborne wind energy (AWE) systems, the mainstream solutions can be classified into three branches: the aerodynamic parafoil traction, the rigid-wing tethered aircraft, and the station-keeping airborne platform. This paper focuses on the rigid-wing tethered aircraft system, which provides notable improvements in both structural performance and energy conversion efficiency. The rigid-wing aircraft is fabricated using aerospace-grade composite materials, achieving a bending stiffness more than 18 times greater than that of conventional flexible kite structures and a wing loading capacity exceeding 3.5 kN/m². Due to this structural design, the aircraft maintains minimal variations in attitude angles within the operational altitude range of 300 to 1500 m. In contrast, flexible systems are susceptible to significant attitude fluctuations under wind speed disturbances, whereas the rigid-wing configuration substantially enhances positioning stability.

Regarding the energy transmission mechanism, this study adopts the lift-cycle power generation mode to mitigate the transmission losses commonly observed in traditional drag-mode systems due to tether-induced drag. In the lift-cycle mode, the aircraft continuously adjusts its angle of attack within vertical wind shear, thereby converting aerodynamic lift into traction torque. This approach enhances energy conversion efficiency while simultaneously reducing transmission losses. The proposed rigid-wing aircraft employs a carbon-fiber main beam structure and is equipped with an intelligent variable angle-of-attack control system capable of millisecond-level attitude corrections under gusty wind conditions.

To facilitate physical description during the modeling process of the airborne wind energy system, both ground and body coordinate systems are established. The right-hand rule is followed when defining the coordinate systems. The ground coordinate system is fixed on the earth’s surface, choosing the North-East-Down (O-NED) coordinate frame. The body coordinate system is fixed on the aircraft and moves synchronously with it. As shown in Figure 2, the origin of the body coordinate system (O-XYZ) is at the aircraft’s center of mass. Its three axes in the ground coordinate system are represented by vectors $e_x$, $e_y$ and $e_z$.

Assuming that the three components of the velocity $v^b$ projection of the fuselage in the body coordinate system are $v_x^b$, $v_y^b$ and $v_z^b$ respectively, then

$$v^b=v_x^{b}i+v_y^{b}j+v_z^{b}k,$$

(1)

In the formula, $i$, $j$ and $k$ are the unit vectors in the body coordinate system.

Now consider the differential of fuselage speed to time, namely ${\displaystyle \frac{\mathrm{d}{v}^b}{\mathrm{d}t}}$, according to formula (1), it can be concluded that:

$${\displaystyle \frac{\mathrm{d}{v}^b}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}{v}_x^b}{\mathrm{d}t}}i+{\displaystyle \frac{\mathrm{d}{v}_y^b}{\mathrm{d}t}}j+{\displaystyle \frac{\mathrm{d}{v}_z^b}{\mathrm{d}t}}k+v_x^b{\displaystyle \frac{\mathrm{d}i}{\mathrm{d}t}}+v_y^b{\displaystyle \frac{\mathrm{d}j}{\mathrm{d}t}}+v_z^b{\displaystyle \frac{\mathrm{d}k}{\mathrm{d}t}},$$

(2)

Since the unit vector derivatives ${\displaystyle \frac{\mathrm{d}i}{\mathrm{d}t}}$, ${\displaystyle \frac{\mathrm{d}j}{\mathrm{d}t}}$ and ${\displaystyle \frac{\mathrm{d}k}{\mathrm{d}t}}$ in the formula are the speed of the vector endpoint, and the vector endpoint passes through the:

$$\left\{\begin{array}{l}{\displaystyle \frac{\mathrm{d}i}{\mathrm{d}t}}=\omega \times i\hfill \\ {\displaystyle \frac{\mathrm{d}j}{\mathrm{d}t}}=\omega \times j\hfill \\ {\displaystyle \frac{\mathrm{d}k}{\mathrm{d}t}}=\omega \times k\hfill \end{array}\right.,$$

(3)

Substituting formula (3) into (2) can obtain:

$${\displaystyle \frac{\mathrm{d}{v}^b}{\mathrm{d}t}}={\dot{v}}^b+{\omega }^b\times v^b,$$

(4)

According to Newton’s second law, the mathematical expression of the aircraft’s motion can be written as:

$$m\cdot {\dot{v}}^b+m\cdot ({\omega }^b\times v^b)=f_t^b+f_a^b+f_g^b,$$

(5)

To simplify the expression and eliminate the Coriolis force in the above equation, it is rewritten as:

$$m\cdot {\dot{v}}^b=R_{nb}\cdot (f_t^b+f_a^b+f_g^b),$$

(6)

Let $J$ be the inertia matrix of the aircraft, also known as the inertia tensor, whose expression is as follows:

$$J=\left[\begin{array}{ccc}{J}_{xx}& J_{xy}& J_{xz}\\ J_{yx}& J_{yy}& J_{yz}\\ J_{zx}& J_{zy}& J_{zz}\end{array}\right],$$

(7)

The diagonal elements of $J$ represent the resistance of the aircraft’s mass to rotational motion around the three axes as fixed axes. Since the mass distribution of the tethered aircraft is not uniform, the off-diagonal elements of the inertia matrix are not zero, representing the situation where a torque applied around one axis generates an angular acceleration around another axis. $J_{xy}$ represents the situation where a torque applied in the OX axis direction generates an angular acceleration around the OY axis.

According to the Euler equation of rigid body motion:

$$J\cdot {\dot{\omega }}^b+{\omega }^b\times J\cdot {\omega }^b=m_a^b,$$

(8)

$m_a^b$ is the aerodynamic moment acting on the aircraft. The term ${\omega }^b\times J\cdot {\omega }^b$ in the above equation is the torque generated by precession.

This paper assumes that the tether connection point to the aircraft is located at the center of mass of the aircraft. For the tether, when the ratio of the tether tension to the tether’s gravity and aerodynamic force is high, the tether can be considered to be in a fully extended state. The force $f_t^b$ applied by the tether to the aircraft’s center of mass can be decomposed into the tether’s gravity $f_{t_g}^b$, the aerodynamic force $f_{t_a}^b$ acting on the tether, and the tether tension $f_{t_{\lambda }}^b$:

$$\left\{\begin{array}{l}{f}_{t_{\lambda }}^b=R_{bn}{f}_{t_{\lambda }}^n\\ f_{t_g}^b=R_{bn}({\widehat{e}}_z{\rho }_t{g}_{D}l)\\ f_{t_a}^b=-D_t\left[\begin{array}{c}\cos \alpha \\ 0\\ \sin \alpha \end{array}\right]\end{array}\right.,$$

(9)

In the above equation, ${\rho }_t$, $g_D$, $D_t$, and $\alpha$ are the line density of the rope, gravitational acceleration, equivalent drag of the tether, and the angle of attack of the aircraft, respectively. The direction vector ${\widehat{e}}_z={\left[0,0,1\right]}^T$.

The forces acting on the aircraft include aerodynamic force and gravity. Since the aerodynamic force is uniformly distributed on the surface of the aircraft, for convenience of analysis, this paper provides an expression for the aerodynamic force acting on the center of mass of the aircraft. The aerodynamic force $f_a^b={[X,Y,Z]}^T$ acting on the aircraft is expressed as:

$$\left\{\begin{array}{l}X=\overline{q}S{C}_X\\ Y=\overline{q}S{C}_Y\\ Z=\overline{q}S{C}_Z\end{array}\right.,$$

(10)

In the above equation, $S$ is the wing area of the aircraft.

Let $\delta ={\left[{\delta }_a,{\delta }_e,{\delta }_r\right]}^T$, where the components are the deflection angles of the aileron, elevator, and rudder, respectively. Their rates of change are $\dot{\delta }=v_{\delta }$, where $v_{\delta }={\left[v_{{\delta }_a},v_{{\delta }_e},v_{{\delta }_r}\right]}^T$ represents the rates of change in the deflection angles of the aileron, elevator, and rudder, respectively. $C_i(i=X,Y,Z)$ are dimensionless body axis aerodynamic force coefficients, calculated specifically according to the following Equation (11):

$$\left\{\begin{array}{l}{C}_X=C_{X_q}\widehat{q}+C_{X_{{\delta }_e}}{\delta }_e+C_{X_0}\\ C_Y=C_{Y_{\beta }}\beta +C_{Y_p}\widehat{p}+C_{Y_r}\widehat{r}+C_{Y_{{\delta }_a}}{\delta }_a+C_{Y_{{\delta }_r}}{\delta }_r\\ C_Z=C_{Z_q}\widehat{q}+C_{Z_{{\delta }_e}}{\delta }_e+C_{Z_0}\end{array}\right.,$$

(11)

The expression for the aircraft’s gravity $f_g^b$ is as follows:

$$f_g^b=R_{bn}\left[\begin{array}{c}0\\ 0\\ m{g}_D\end{array}\right]=m{g}_D\left[\begin{array}{c}-\sin \theta \\ \cos \theta \sin \varphi \\ \cos \theta \cos \varphi \end{array}\right],$$

(12)

In Equation (12) $m$ and $g_D$ are the mass of the aircraft and gravitational acceleration, respectively. Since the aircraft’s gravity can be considered to act at the center of mass of the aircraft, it does not generate additional torque.

2.2. Ground Equipment Modeling

Since the launch and landing of the aircraft are not within the scope of this study, the ground equipment does not consider the devices required for launch and recovery during modeling. The ground equipment mainly consists of a generator and a winch mechanism connected to the generator. Its mathematical model can be expressed as:

$$P=\dot{E}=f_{t_{\lambda }}{\omega }_d{r}_d,$$

(13)

In Equation (13), $P$ is the instantaneous power generated by the system, $\dot{E}$ is the system’s power generation, ${\omega }_d$ is the rotational speed of the winch mechanism, and $r_d$ is the drum radius. $f_{t_{\lambda }}$ is the tension of the tether, which can be expressed as:

$$f_{t_{\lambda }}=\lambda {‖p^n‖}_2=\lambda l,$$

(14)

At the same time, since the rate of change in the tether length $v_1=l={\omega }_d{r}_d$, it can be expressed as:

$$P=\dot{E}=f_{t_{\lambda }}{v}_1,$$

(15)

Additionally, the ground equipment’s winch applies an additional tether acceleration $a_1$ to control the tether retraction.

3. Aircraft Trajectory Optimization for Airborne Wind Energy Systems

3.1. Problem Description

From the perspective of optimal control theory, the trajectory optimization problem can be formulated as a nonlinear functional extremum problem subject to differential constraints. To address this, the direct method is employed, where the trajectory is first discretized and the problem is transformed into a nonlinear programming (NLP) formulation. A numerical optimization algorithm is then applied to solve the NLP, and its performance is evaluated based on the final results, yielding an optimized reference trajectory.

In direct numerical solution methods, the core strategy is to discretize the continuous time domain into a finite set of computational nodes and reformulate the infinite-dimensional control problem as a high-dimensional parameter optimization problem through basis function expansion. This procedure reconstructs the original control problem within a nonlinear programming framework, whose key components include the formulation of the objective function, enforcement of dynamic equation constraints, and specification of boundary conditions [18].

The construction of the objective function generally follows three paradigms: the Mayer-type indicator, which considers only discrete terminal state evaluations; the Lagrange-type indicator, which emphasizes continuous cumulative evaluations over the entire process; and the Bolza-type indicator, which combines both. During the numerical solution, special discretization of the time domain is required, and orthogonal collocation methods are typically employed to improve the accuracy of approximate solutions. At the trajectory planning stage, the iterative efficiency and convergence stability of different optimization algorithms must be evaluated, with particular attention to their capacity for handling large-scale sparse matrices. By balancing discretization accuracy with computational cost, an optimal trajectory curve that satisfies both dynamic constraints and optimality conditions can ultimately be obtained.

In airborne wind energy systems, maximizing power generation efficiency is the primary objective. Consequently, power output should serve as the core performance indicator in system modeling and optimization. At the same time, to ensure structural safety and long-term operational stability of the aircraft, the optimization objectives must also account for the system’s capacity to withstand mechanical stresses. Excessive control inputs, high angular accelerations, and large lateral forces resulting from significant sideslip angles may compromise structural integrity. Therefore, the following constraints must be explicitly incorporated into the optimization design:

(1)

Dynamic balance constraint for angle of attack: Based on stall boundary conditions and the valid range of the aerodynamic model, impose an upper threshold on the angle of attack to maintain a balance between lift enhancement and attached flow stability [19].

(2)

Sideslip angle suppression constraint: Apply bidirectional amplitude limits on sideslip angle to mitigate nonlinear aerodynamic coupling effects and lateral–longitudinal dynamic interference.

(3)

Airspeed envelope constraint: Define upper and lower bounds for airspeed according to aerodynamic characteristics to ensure stable flight [20].

(4)

Flight altitude protection constraint: Introduce a dynamic compensation mechanism for minimum flight altitude to provide safety redundancy for obstacle avoidance [21].

(5)

Tether tension safety constraint: Establish a dynamic threshold for tether tension based on material strength to control fatigue damage and prevent slackening.

(6)

Aircraft attitude angle constraint: Define operational limits for roll and pitch angles to avoid spatial interference between the tether and aircraft while simplifying control architecture [22].

(7)

Winch actuation constraint: Restrict feasible ranges of tether retraction speed and acceleration according to ground mechanism capabilities.

(8)

Angular velocity constraint: Limit angular velocity within the aircraft’s flight envelope.

(9)

Periodic stability constraint: Determine the cycle time T by analyzing the duration of each cycle in experimental tests.

(10)

Tether length constraint: Constrain tether length within the storage capacity of the ground winch mechanism.

The trajectory optimization problem for the established airborne system power generation model is summarized as follows, $\forall t\in [0,T]$:

$$\begin{array}{l}\underset{x(\cdot ),u(\cdot )}{min}J=T{\displaystyle {\int }_0^T({{\displaystyle \parallel u\left(t\right)\parallel }}_{{\displaystyle {\sum }_u^{-1}}}^2+{{\displaystyle \parallel {\dot{\omega }}^b\left(t\right)\parallel }}_{{\displaystyle {\sum }_{\omega }^{-1}}}^2+{\sigma }_{\beta }^{-1}{\beta }^2\left(t\right))dt}-{\displaystyle \frac{E\left(T\right)}{T}}\\ s.t. \dot{x}\left(t\right)=f\left(x\left(t\right),u\left(t\right),t\right)\end{array},$$

(16)

Here, ${\dot{\omega }}^b\left(t\right)$ and $\beta$ are the angular acceleration and sideslip angle of the aircraft, respectively. $x(t)$ and $u(t)$ are the state variables and control variables of the system, respectively. ${\displaystyle {\sum }_u^{-1}}$, ${{\displaystyle \sum }}_{\omega }^{-1}$, ${\sigma }_{\beta }^{-1}$ are represented by the control input and angular acceleration of the aircraft, respectively. When solving the optimal control problem shown in Equation (16), the flight state and physical environment constraints (17) and control and boundary condition constraints (18) must also be satisfied. The specific numerical values for the parameters and bounds used in constraints (17) and (18) are listed in Table 1.

$$\left\{\begin{array}{l}{\alpha }_{\min }\le \alpha \left(t\right)\le {\alpha }_{\max }\\ {\beta }_{\min }\le \beta \left(t\right)\le {\beta }_{\max }\\ V_{T_{\min }}\le V_T\left(t\right)\le V_{T_{\max }}\\ h{\left(t\right)}_{\min }\le h\left(t\right)\\ f_{t_{{\lambda }_{\min }}}\le f_{t_{\lambda }}\left(t\right)\le f_{t_{{\lambda }_{\max }}}\\ {\theta }_{\min }\le \theta \left(t\right)\le {\theta }_{\max }\end{array}\right.,$$

(17)

$$\left\{\begin{array}{l}{v}_{l_{\min }}\le v_l\left(t\right)\le v_{l_{\max }}\\ a_{l_{\min }}\le a_l\left(t\right)\le a_{l_{\max }}\\ {\omega }_{\min }^b\le {\omega }^b\left(t\right)\le {\omega }_{\max }^b\\ {\delta }_{\min }\le \delta \left(t\right)\le {\delta }_{\max }\\ v_{{\delta }_{\min }}\le v_{\delta }\left(t\right)\le v_{{\delta }_{\max }}\\ x\left(0\right)-x\left(T\right)=0\\ l_{\min }<l<l_{\max }\end{array}\right.,$$

(18)

Table 1. Constraint range.

Variable Name	Symbol	Minimum	Maximum
Angle of attack	$\alpha$	−6 deg	13 deg
Sideslip angle	$\beta$	−20 deg	20 deg
Airspeed	$V_T$	13 m/s	32 m/s
Height	$h$	100 m	—
Tethering force	$f_{t_{\lambda }}$	50 N	1800 N
Rolling angle	$\varphi$	−50 deg	50 deg
Pitch angle	$\theta$	−40 deg	40 deg
Tether length	$l$	100 m	700 m
tether speed	$v_l$	−15 m/s	20 m/s
Tether acceleration	$a_l$	−3 m/s2	3 m/s2
Fuselage angular velocity	${\omega }^b$	−50 deg/s	50 deg/s
Aileron deflection angle	${\delta }_a$	−20 deg	20 deg
Deflection angle of elevator	${\delta }_e$	−30 deg	30 deg
Rudder deflection angle	${\delta }_r$	−30 deg	30 deg
Servo motor speed	$v_{\delta }$	−0.6 rad/s	0.6 rad/s
Period of trajectory	$T$	20 s	60 s

Currently, among the methods for transforming trajectory optimization problems, the shooting method is the most classic. The shooting method includes direct shooting and multiple shooting methods.

The multiple shooting method (flowchart as shown in Figure 3), as an enhanced algorithm of the classical direct method, achieves a leap in accuracy through a segmented integration strategy compared to the error accumulation problem faced by the traditional direct shooting method in long integration intervals (stemming from the global error characteristics of numerical solutions to differential equations). Using a multiple discrete framework for the time domain, the continuous time axis is divided into mutually nested finite subintervals. Each subinterval independently constructs an initial value problem solver, and the state variable reset operation at the nodes effectively blocks the cross-interval propagation path of local truncation errors. The initial value problem-solving process in each subinterval has natural parallelism. By constructing a double-layer iterative loop system, the inner loop performs subinterval differential algebraic equation solving, and the outer loop implements nonlinear programming parameter optimization. Compared with the simple direct shooting method, the multiple shooting method uses segmented integration technology to simultaneously discretize control variables and state variables, has higher computational accuracy and better convergence characteristics, and is therefore considered to be able to effectively solve optimal control problems [23]. The processing steps of the direct multiple shooting method for trajectory optimization problems are as shown in Figure 3:

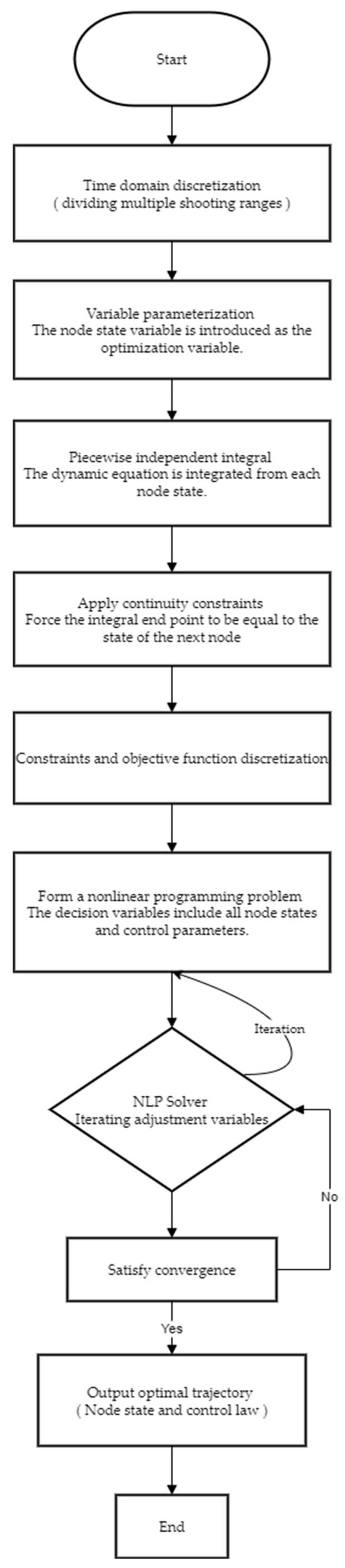
Figure 3. Multiple shooting methods flowchart.

(1)

Time domain transformation

To facilitate the processing of time-varying domain T problems, time domain transformation is introduced:

$$t:\left[0,T\right]\to \tau \left[0,1\right],\tau ={\displaystyle \frac{t}{T}},$$

(19)

Through the above equation, the time domain of the optimization problem can be transformed from $\left[0,T\right]$ to the interval $\left[0,1\right]$. After this processing, the state variables and control variables are converted into functions of $\tau \in \left[0,1\right]$. Since the terminal time $T$ is a variable parameter, an augmented state variable $\dot{T}\left(\tau \right)=0$ is introduced, that is, the terminal time is also regarded as an optimization variable.

(2)

Control variable discretization

The transformed time domain $\left[0,1\right]$ is equally divided into N segments: $0={\tau }_0<{\tau }_1<\dots {\tau }_N=1$. The size of N depends on the required accuracy. It is chosen based on a trade-off between computational efficiency and trajectory accuracy: a larger N provides a finer time discretization and improves the approximation of the continuous dynamics, but also increases computational cost. In this study, N was selected through convergence testing, i.e., by increasing N until further refinement produced a negligible improvement in accuracy.

An N-dimensional parameter vector $q_i$ is introduced to approximate the control variable u(τ) in segments:

$$q_i,\tau \in [{\tau }_i,{\tau }_{i+1}),i=0,1,\cdot \cdot \cdot ,N-1,$$

(20)

To ensure its completeness, the control variable value at the terminal time is set to $u\left(1\right)=q_N=q_{N-1}$.

(3)

State variable parameterization

Let the series of values of the state variable $x(\tau )$ at time collocation points ${\tau }_i$ be equal to the N-dimensional vector $s_i$. At this time, N initial value problems within time segments are obtained, in the following form:

$$\begin{array}{l}\dot{x}(\tau )=T·f(x(T\tau ),q_i)\\ x({\tau }_i)=s_i\end{array},$$

(21)

The state variables at the collocation points need to meet the requirements of the above equation. The solution of the N initial value problems within time segments obtained from the above equation is N independent trajectories on the time region $\tau \in ({\tau }_i,{\tau }_{i+1})$, denoted as $x_i(\tau ;s_i,q_i)$, as shown in Figure 4.

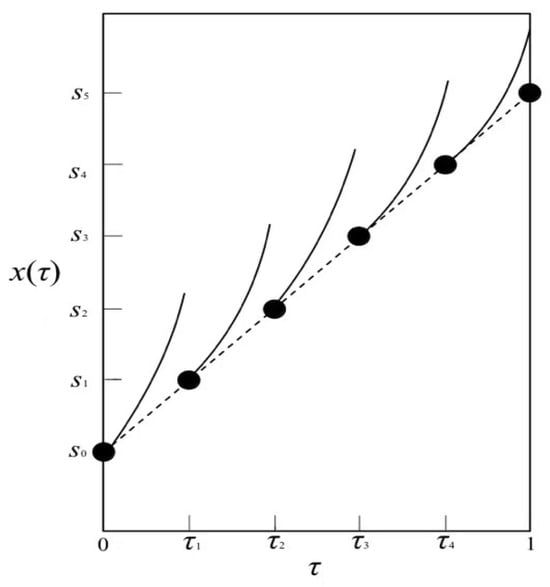
Figure 4. Parameterized state variables.

To ensure the continuity of each segment of differential state trajectories, state connection conditions are added: $s_{i+1}=x_i({\tau }_{i+1},s_i,q_i)$, where the state value $s_0$ of the first node is equal to the initial value $x_0$ of the optimization problem.

(4)

Transformation of performance indicators

Substitute each independent differential state trajectory $x({\tau }_i)$ into $L(\cdot )$, and solve the Lagrange integral performance indicator through integration:

$$L_i(s_i,q_i)={\displaystyle \underset{{\tau }_i}{\overset{{\tau }_{i+1}}{\int }}T·L_i(x(T({\tau }_i),q_i)d\tau },$$

(22)

(5)

Discretization of path constraints

Using nodes ${\tau }_0,{\tau }_1,\dots {\tau }_N$, the infinite-dimensional path inequality constraints can be transformed into N + 1-dimensional inequality constraints: $C(s_i,q_i)\ge 0$. After the above steps, the original trajectory optimization problem is transformed into the following nonlinear programming problem through the multiple shooting method:

$$\begin{array}{l}\underset{q_{0,\cdot \cdot \cdot ,}{q}_{N-1,s_0,\cdot \cdot \cdot ,s_N}}{min}J={\displaystyle \sum _{i=0}^{N-1}{L}_i(s_i,q_i)+\varphi (s_0,s_N)}\\ s.t.\left\{\begin{array}{l}{s}_{i+1}-x_i({\tau }_{i+1},s_i,q_i)=0,\cdot \cdot \cdot ,i=0,1,\cdot \cdot \cdot ,N-1\\ s_0=x_0\\ B(s_0,s_N)=0\\ C(s_i,q_i)\ge 0,i=0,1,\cdot \cdot \cdot N\end{array}\right.\end{array},$$

(23)

Then, the transformed large-scale nonlinear programming problem is solved using NLP algorithms.

For nonlinear programming problems, traditional exact algorithms require that the performance indicators and constraint functions have good mathematical characteristics, such as continuous differentiability and convex feasible domains, which limit the solution of complex large-scale nonlinear programming problems.

Modern heuristic algorithms are a class of optimization algorithms inspired by natural phenomena, biological behaviors, or physical processes, mainly used to solve complex, high-dimensional, nonlinear combinatorial or continuous optimization problems. Unlike traditional exact algorithms, they find approximate optimal solutions through the balance of exploration and utilization, and are particularly suitable for NLP problems. Modern heuristic algorithms do not depend on the selection of initial values, and the iterative update strategy does not depend on the gradient characteristics of the system. With the improvement of modern computer computing power, the solution of parameter optimization problems has begun to tend to use modern heuristic algorithms.

The Salp Swarm Algorithm (SSA) is a new swarm intelligence optimization algorithm proposed by Mirjalili et al. in 2017, which has the characteristics of strong evolutionary ability, fast search speed, and strong optimization ability [24].

3.2. Salp Swarm Algorithm (SSA)

The Salp Swarm Algorithm (SSA) employs a chain-like method to simulate the foraging behavior of salp colonies. SSA requires minimal parameters and has low computational demands, with intuitive formulas that are easy to understand.

Assuming the target search space for salp individuals is N × D-dimensional, where N is the population size and D is the spatial dimension (number of optimization variables), the salp population can be represented as:

$$X=\left[\begin{array}{cccc}{x}_1^1& x_2^1& \dots & x_D^1\\ x_1^2& x_2^2& \dots & x_D^2\\ ⋮& ⋮& & ⋮\\ x_1^N& x_2^N& \dots & x_D^N\end{array}\right],$$

(24)

Salp individuals locate food sources through chain-like movements, gradually reducing the distance to the target. The SSA divides the salp population into two categories: leader population and follower population, which collectively enable exploration in complex environments. In the N × D-dimensional space, the leader’s position is updated according to:

$$X_j^i=\left\{\begin{array}{l}{F}_j+c_1\left[(u{b}_j-l{b}_j)c_2+l{b}_j\right], c_3\ge {\displaystyle \frac{1}{2}}\\ F_j-c_1\left[(u{b}_j-l{b}_j)c_2+l{b}_j\right], c_3<{\displaystyle \frac{1}{2}}\end{array}\right.,$$

(25)

Here, $X_j^i$ represents the position of leader $i$ in dimension $j$, $F_j$ is the food source position in dimension $j$, and $c_2$, $c_3$ are random values between 0 and 1. $u{b}_j$ and $l{b}_j$ are the upper and lower bounds of the search space in dimension $j$. The parameter $c_1$ is a crucial decreasing factor in SSA, which nonlinearly decreases as iterations progress:

$$c_1=2e^{-{({\displaystyle \frac{4l}{L}})}^2},$$

(26)

where $l$ is the current iteration count and $L$ is the maximum number of iterations.

Followers update their positions according to:

$$X_j^i={\displaystyle \frac{X_j^i+X_j^{i-1}}{2}},$$

(27)

where $i\ge 2$. Followers primarily enhance local search precision when the salp population concentrates in a specific region.

3.3. Multi-Strategy Improved Salp Swarm Algorithm (MISSA)

The standard SSA has limitations in population initialization, food source position updates, and follower position updates. Liu Qing et al. proposed an adaptive SSA based on Baker mapping, improving the algorithm’s performance [25].

3.3.1. Population Initialization Using Baker Chaotic Mapping

The original SSA employs random initialization, which may fail to adequately cover the search space. To address this, Baker chaotic mapping is used to generate uniformly distributed initial populations with strong traversal uniformity and fast iteration speed. Compared with other chaotic mappings, Baker mapping offers longer scrambling periods and produces populations with greater diversity. Specifically, the Baker map generates chaotic sequences $F(i,j)$ in the interval $\left[0,1\right]$, which are used to initialize the SSA population:

$$X_j^i(0)=F(i,j)\cdot (u_{bj}-l_{bj})+l_{bj},$$

(28)

3.3.2. Food Source Position Update with t-Distribution Perturbation

Since leader positions depend on the food source, its location directly affects optimization results. To prevent premature convergence, t-distribution random perturbations are introduced:

$$F_d^{\prime }=F_d+F_d\cdot t(T),$$

(29)

where $t(T)$ is a t-distribution random perturbation with degrees of freedom equal to the iteration count $T$. As iterations increase, the perturbation diminishes, balancing global exploration and local exploitation.

3.3.3. Follower Position Update with Adaptive Inertia Weight

In the standard SSA, the positions of follower individuals exhibit strong correlations with their adjacent neighbors, which may cause the algorithm to become trapped in local optima. An adjustable inertia weight $\omega (t)$ is introduced:

$$\begin{array}{l}{X}_i^j={\displaystyle \frac{1}{2}}(X_i^j+\omega (t)X_i^{j-1})\\ \omega (t)\left|=\right|{\omega }_{\min }+{\displaystyle \frac{1}{\lambda }}({\omega }_{\max }-{\omega }_{\min })gammaincinv(\lambda ,1-{\displaystyle \frac{t}{Maxltr}})\end{array}$$

(30)

Here, $gammaincinv$ is the inverse incomplete gamma function. When ${\omega }_{\max }=0.9$, ${\omega }_{\min }=0.4$, and $\lambda =0.1$, the function exhibits near-linear decay in early iterations and near-exponential decay later, dynamically balancing exploration and exploitation.

The flowchart of MISSA is shown in Figure 5.

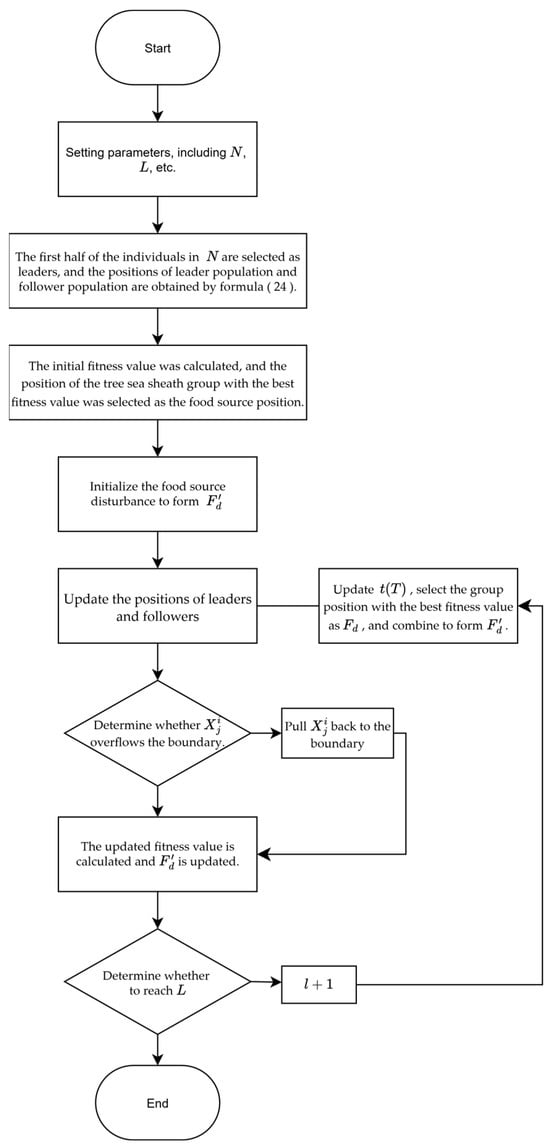
Figure 5. MISSA flowchart.

4. Simulation Results

In order to improve power generation efficiency, trajectory design for the AWE system was performed in MATLAB2023b using a rigid aircraft as the traction element. The simulation parameters are summarized in Table 2.

Table 2. Model parameters.

Variable Name	Symbol	Number
The mass of aircraft AP2	$m$	36.8 kg
Moment of inertia around the x-axis	$J_x$	25 kg·m2
Moment of inertia around the y-axis	$J_y$	32 kg·m2
Moment of inertia around the z-axis	$J_z$	56 kg·m2
xz coupling moment of inertia	$J_{xz}$	0.47 kg·m2
Wingspan	$b$	55 m
Chord length	$\overline{c}$	0.55 m
Tether line density	${\rho }_t$	0.0046 kg/m3
Drag coefficient	$C_{D_t}$	1.2
Tether diameter	$d_t$	0.002 m
Gravity	$g_D$	9.81 m/s2
Air density	$\rho$	1.225 kg/m3
Reference altitude	$h_0$	100 m
Wind speed at reference altitude	$w_0$	10 m/s
Wing area	$S$	3 m2
Wind shear exponent	$z_0$	0.15

To solve the proposed trajectory optimization problem, the multiple shooting method was used to discretize the entire period into 20 equally spaced time nodes, converting the original trajectory optimization into a nonlinear programming (NLP) problem. The population size for both the SSA and MISSA was set to 30, with a maximum of 1000 iterations. The NLP problem was solved using the SQP, SSA, and MISSAs.

4.1. Power Generation Comparison

The energy output curves of the high-altitude wind energy system obtained through optimization are shown in Figure 6, while the variation in tether length is shown in Figure 7. The period duration and average power output for each algorithm are listed in Table 3.

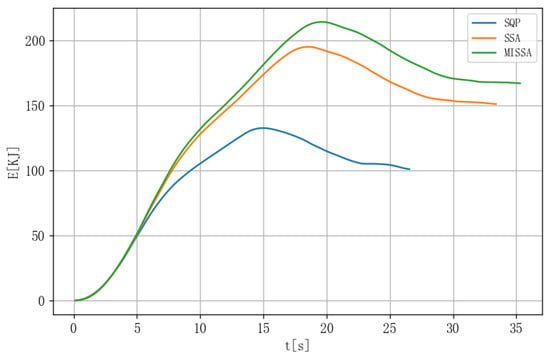
Figure 6. System Energy Generation.

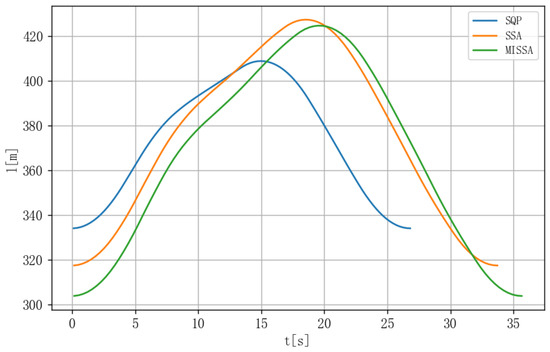
Figure 7. Tether Length Variation.

Table 3. Comparison of Algorithm Performance.

Algorithm	Period Time	Average Power Output
SQP	26.811 s	3.76678 kW
SSA	33.7293 s	4.47901 kW
MISSA	35.6575 s	4.6856 kW

The variation in stop times observed in Figure 6 and Figure 7 arises from the optimization of each algorithm for maximum energy generation. Each algorithm converges to a distinct locally optimal closed-orbit trajectory, which inherently possesses a different period length, as reported in Table 3. Only a single cycle is shown, as it fully represents the steady-periodic reference trajectory used for controller design. During real-time operation, the controller drives the system to accurately follow this pre-computed trajectory in every cycle.

It can be observed from Table 3 that the MISSA achieves the highest average power output. The SQP algorithm, which relies on gradient-based updates, is prone to becoming trapped in local minima due to its limited ability to escape them. By contrast, the original SSA exhibits stronger global search capabilities and a greater capacity to avoid local optima. The improved MISSA further enhances these characteristics, reinforcing both global exploration and local exploitation, and thereby delivering superior performance compared to SSA. Due to differences in algorithm complexity and the resulting optimized trajectories, the cycle times will consequently vary. All three algorithms complete the optimization within a few seconds on an ordinary computer, and the differences in computation time are negligible compared with their dependence on computing power.

From the tether length variation in Figure 7, it can be observed that the tether first extends and then retracts during each cycle. By comparing this with the power generation curve, it is evident that during the tether extension phase, the system is in the traction stage, where the tether drives the ground equipment to generate power. When the tether reaches its maximum length, the system enters the retrieval stage, during which energy is consumed by the ground station to reel the tether back in, completing a full cycle. Overall, the energy generated during the extension phase significantly exceeds the energy consumed during retraction, resulting in a considerable average power output.

4.2. Optimized Trajectories

The optimized trajectories obtained by different algorithms are illustrated in Figure 8, Figure 9 and Figure 10. It can be seen that the trajectories generally exhibit circular shapes. This suggests that under crosswind conditions, a circular flight trajectory is optimal for maximizing power output, which is consistent with the conclusion in the literature that the AWE system’s aircraft should follow circular or figure-eight flight paths. From the tether variation curves, it can be confirmed that the tether consistently extends first and then retracts in a complete cycle.

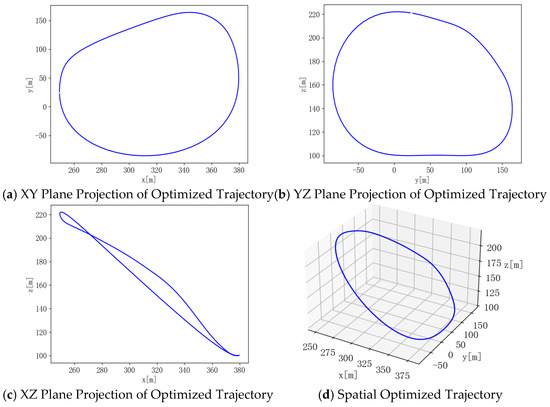
Figure 8. SQP Optimized Trajectory.

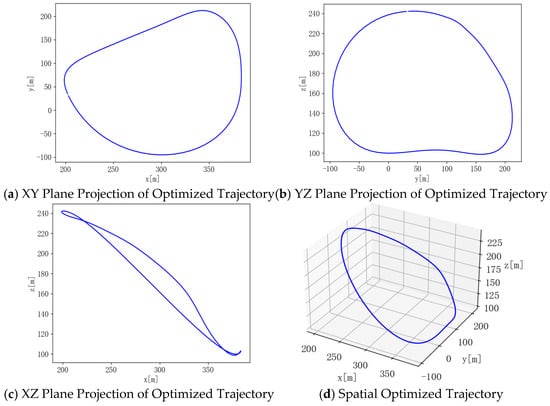
Figure 9. SSA Optimized Trajectory.

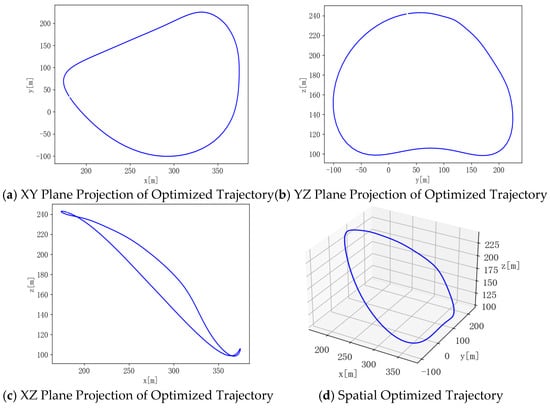
Figure 10. MISSA Optimized Trajectory.

5. Conclusions

This paper established a comprehensive dynamic model for a rigid-aircraft-based airborne wind energy (AWE) system. A trajectory optimization method was proposed with the objective of maximizing energy output under multiple constraints. The original optimization problem was transformed into a nonlinear programming (NLP) model and discretized using a multiple shooting method, effectively enhancing the solution accuracy and feasibility.

Three optimization algorithms were applied to solve the NLP problem: the Sequential Quadratic Programming (SQP) algorithm, the original Sparrow Search Algorithm (SSA), and a multi-strategy improved SSA (MISSA). Simulation results show that the SQP algorithm, due to its dependence on initial values and gradients, is prone to getting trapped in local optima. The SSA demonstrates a better ability to escape local optima but suffers from slower convergence and lower precision. To address these issues, this study introduced MISSA, which incorporates multiple search strategies to enhance both global exploration and local exploitation. The simulation results confirm that the MISSA outperforms both SQP and SSA, achieving a 24.4% improvement in average power output compared to SQP.

This research validates the potential of MISSA in complex constrained trajectory optimization problems and provides a practical and effective method for improving the power generation efficiency of AWE systems. Future work may include incorporating wind disturbances and robust multi-cycle optimization strategies to develop adaptive trajectory control under real-world wind field conditions, providing theoretical and algorithmic support for the engineering implementation of AWE systems.

In addition, further research will focus on the integration of advanced sensing technologies and wind field prediction models. By leveraging real-time sensor data and machine learning-based forecasting methods, the system could adapt more effectively to fluctuating wind conditions, thereby enhancing both efficiency and safety. Moreover, combining predictive control with fault-tolerant mechanisms may enable the AWE system to maintain stable operation under sudden wind speed variations or extreme weather events. Such advancements would contribute to building more resilient, efficient, and commercially viable AWE solutions in the future.